Smooth Trajectory Planning at the Handling Limits for Oval Racing
Abstract
:1. Introduction
1.1. Related Work
1.2. Contribution and Outline of the Paper
- 1.
- The main idea is to treat the initial edges differently from the other edges in a spatio temporal graph. Our sampling-based approach for the generation of the initial edges uses jerk-optimal curves, whose smoothness reduces lateral acceleration deflections and thus increases vehicle stability, especially during braking maneuvers.
- 2.
- We propose a concept for the selection of the end conditions of the jerk-optimal curves in order to adapt the initial edges to the racing scenario and thus get closer to the handling limits of the vehicle. We introduce the concept using the already proposed graph structure described in [16].
2. Material and Methods
2.1. Frenét Frame and Graph Structure
2.2. Local Planning Framework
2.3. Start State Identification
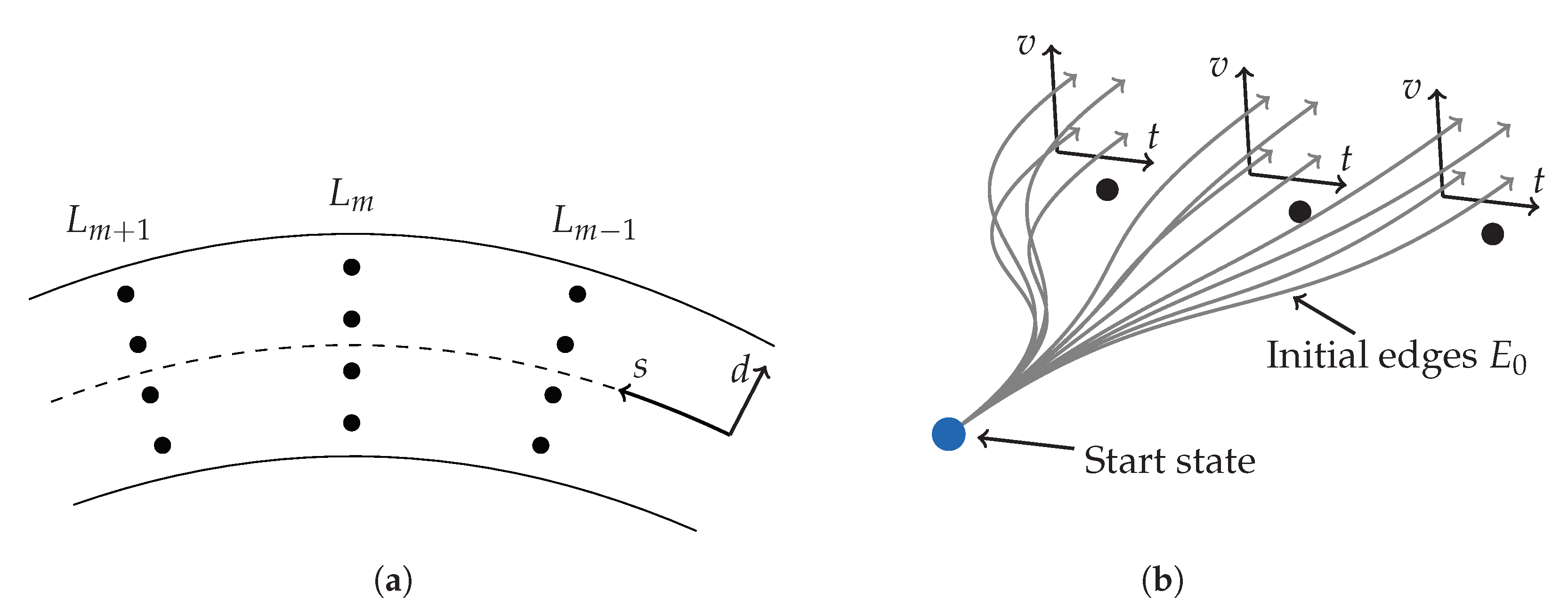
2.4. Initial Edge Generation
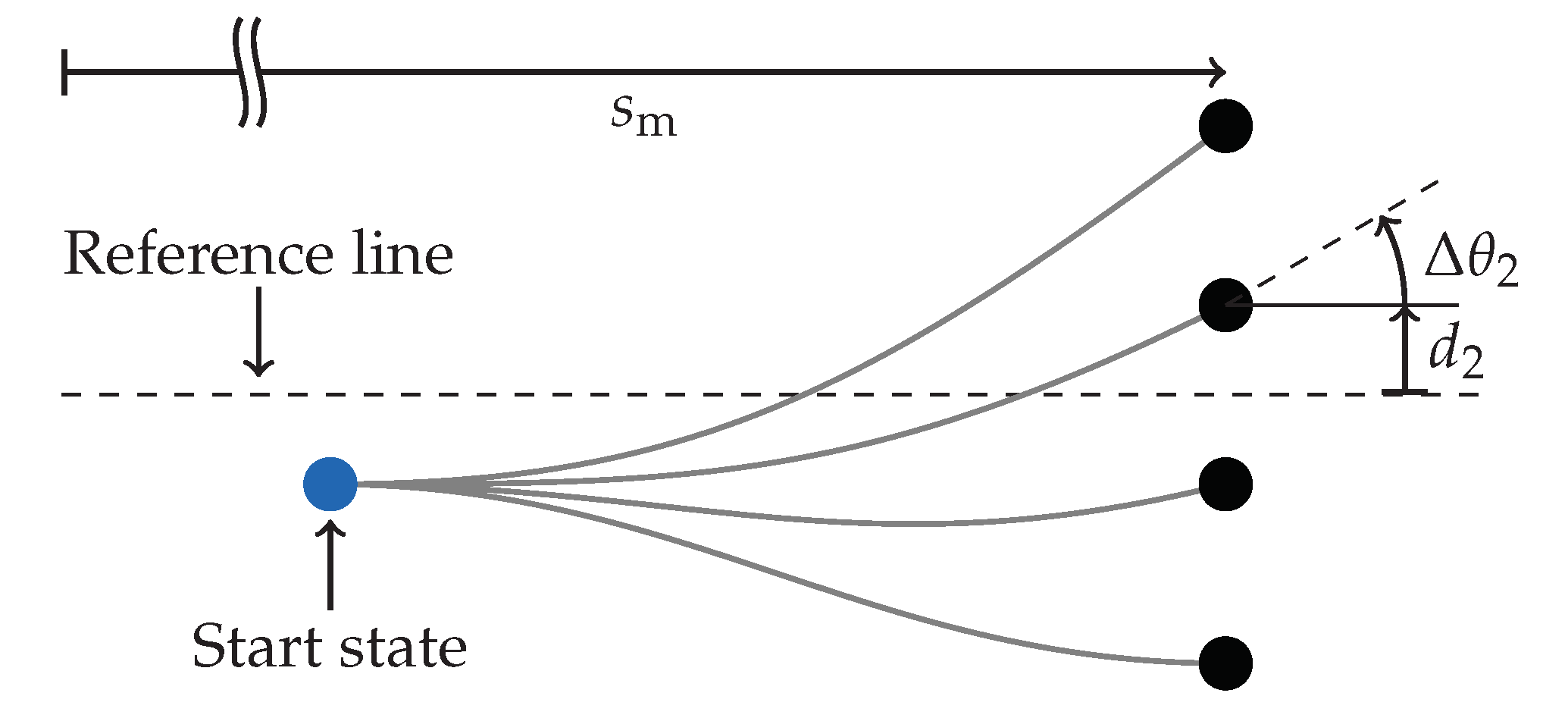
2.4.1. Coordinate Transformation
2.4.2. Jerk-Optimal Movement
2.4.3. Integration into Graph Structure
2.4.4. Performance Improvement for Racing-Scenarios
2.4.5. Stopping to Standstill
3. Results
3.1. Autonomous Driving Software Architecture
3.2. Simulation Results
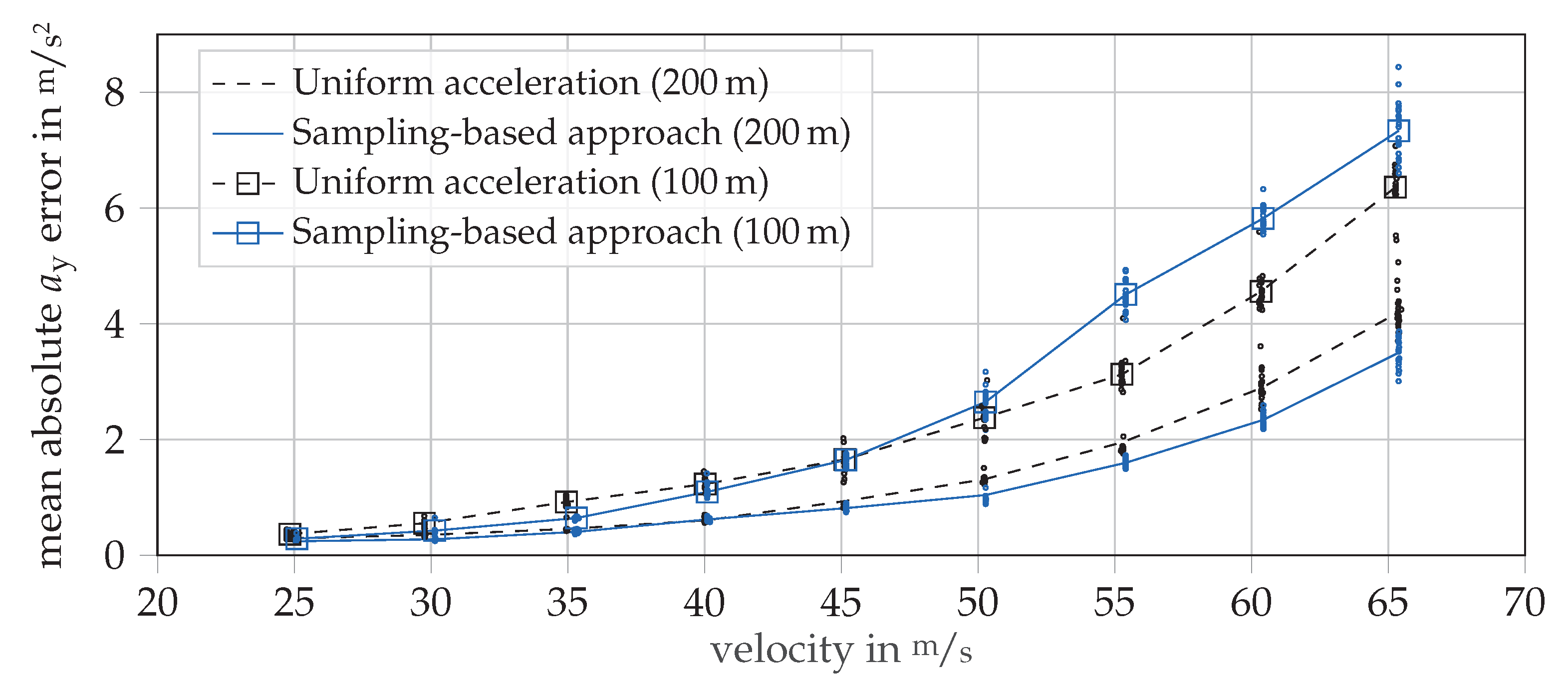
3.2.1. Single-Vehicle Driving
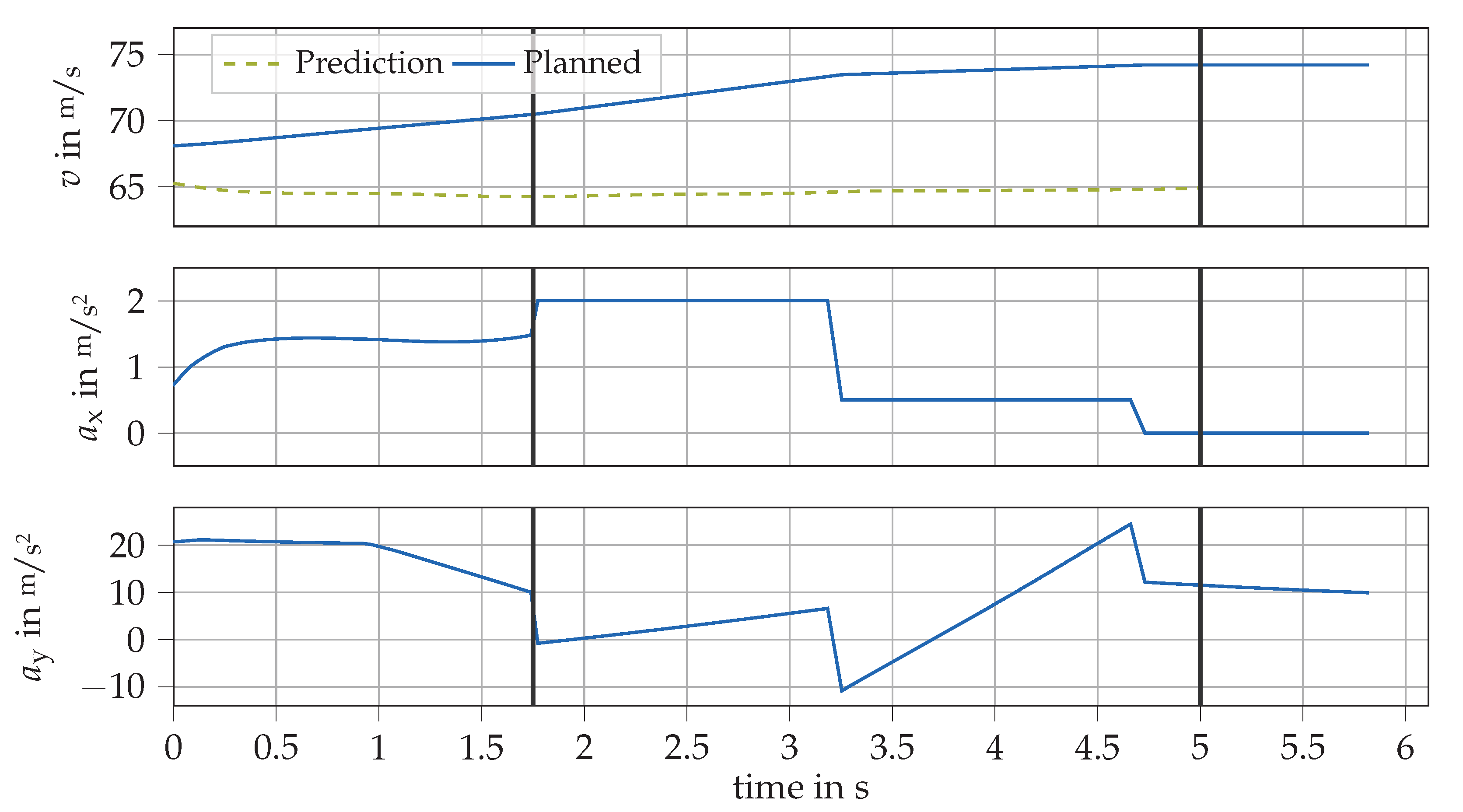
3.2.2. Braking Maneuver
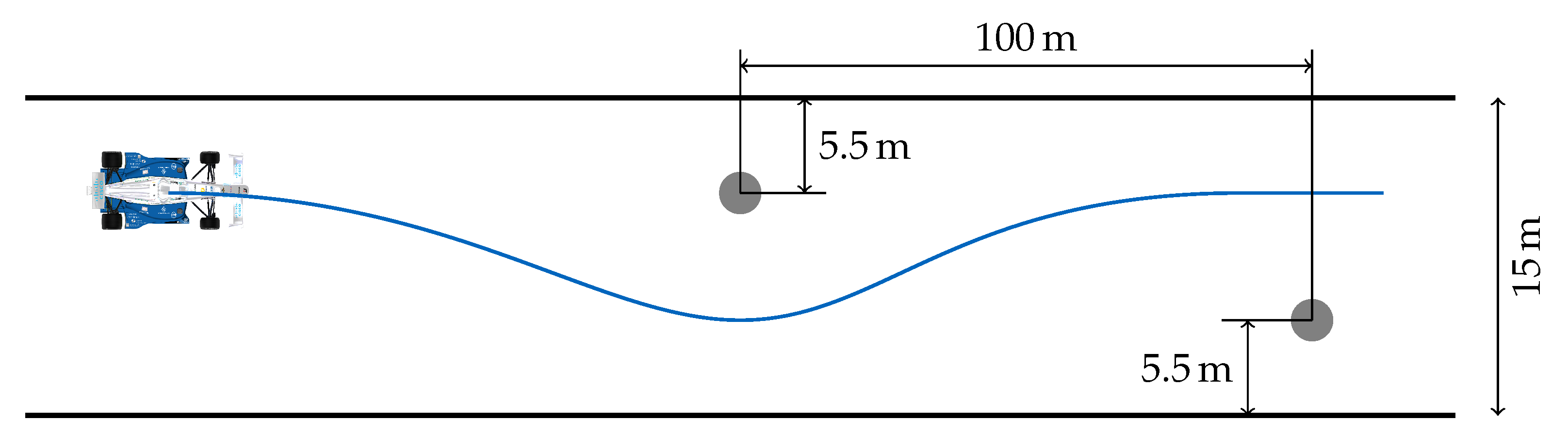
3.2.3. Object Evasion
3.3. Experimental Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AC@CES | Autonomous Challenge at CES |
| IAC | Indy Autonomous Challenge |
| IMS | Indianapolis Motor Speedway |
| LVMS | Las Vegas Motor Speedway |
| ODD | Operational Design Domain |
| PVD | Path-Velocity Decomposition |
| RRT | Rapidly Exploring Random Trees |
References
- Jiang, A. Research on the Development of Autonomous Race Cars And Impact on Self-driving Cars. J. Phys. Conf. Ser. 2021, 1824, 012009. [Google Scholar] [CrossRef]
- Betz, J.; Zheng, H.; Liniger, A.; Rosolia, U.; Karle, P.; Behl, M.; Krovi, V.; Mangharam, R. Autonomous Vehicles on the Edge: A Survey on Autonomous Vehicle Racing. IEEE Open J. Intell. Transp. Syst. 2022, 3, 458–488. [Google Scholar] [CrossRef]
- Herrmann, T.; Christ, F.; Betz, J.; Lienkamp, M. Energy Management Strategy for an Autonomous Electric Racecar using Optimal Control. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 720–725. [Google Scholar] [CrossRef]
- Christ, F.; Wischnewski, A.; Heilmeier, A.; Lohmann, B. Time-optimal trajectory planning for a race car considering variable tyre-road friction coefficients. Veh. Syst. Dyn. 2021, 59, 588–612. [Google Scholar] [CrossRef]
- Heilmeier, A.; Wischnewski, A.; Hermansdorfer, L.; Betz, J.; Lienkamp, M.; Lohmann, B. Minimum curvature trajectory planning and control for an autonomous race car. Veh. Syst. Dyn. 2020, 58, 1497–1527. [Google Scholar] [CrossRef]
- Paden, B.; Čáp, M.; Yong, S.Z.; Yershov, D.; Frazzoli, E. A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles. IEEE Trans. Intell. Veh. 2016, 1, 33–55. [Google Scholar] [CrossRef] [Green Version]
- Subosits, J.K.; Gerdes, J.C. From the Racetrack to the Road: Real-Time Trajectory Replanning for Autonomous Driving. IEEE Trans. Intell. Veh. 2019, 4, 309–320. [Google Scholar] [CrossRef]
- Liniger, A.; Domahidi, A.; Morari, M. Optimization-based autonomous racing of 1:43 scale RC cars. Optim. Control Appl. Methods 2015, 36, 628–647. [Google Scholar] [CrossRef] [Green Version]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments. Int. J. Robot. Res. 2010, 29, 485–501. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Technical Report 98-11; Iowa State University, Department of Computer Science: Ames, IA, USA, 1998. [Google Scholar]
- Karaman, S.; Frazzoli, E. Optimal Kinodynamic Motion Planning using Incremental Sampling-based Methods. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 7681–7687. [Google Scholar] [CrossRef]
- Otte, M.; Frazzoli, E. RRTX: Real-Time Motion Planning/Replanning for Environments with Unpredictable Obstacles. In Algorithmic Foundations of Robotics XI; Akin, H.L., Amato, N.M., Isler, V., van der Stappen, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume 107, pp. 461–478. [Google Scholar] [CrossRef]
- Jeon, J.h.; Cowlagi, R.V.; Peters, S.C.; Karaman, S.; Frazzoli, E.; Tsiotras, P.; Iagnemma, K. Optimal Motion Planning with the Half-Car Dynamical Model for Autonomous High-Speed Driving. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 188–193. [Google Scholar] [CrossRef]
- Kant, K.; Zucker, S.W. Toward Efficient Trajectory Planning: The Path-Velocity Decomposition. Int. J. Robot. Res. 1986, 5, 72–89. [Google Scholar] [CrossRef]
- Werling, M.; Ziegler, J.; Kammel, S.; Thrun, S. Optimal Trajectory Generation for Dynamic Street Scenarios in a Frenét Frame. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 987–993. [Google Scholar] [CrossRef]
- Stahl, T.; Wischnewski, A.; Betz, J.; Lienkamp, M. Multilayer Graph-Based Trajectory Planning for Race Vehicles in Dynamic Scenarios. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 3149–3154. [Google Scholar] [CrossRef]
- McNaughton, M.; Urmson, C.; Dolan, J.M.; Lee, J.W. Motion Planning for Autonomous Driving with a Conformal Spatiotemporal Lattice. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4889–4895. [Google Scholar] [CrossRef]
- Carmo, M.P.d. Differential Geometry of Curves and Surfaces, 2nd ed.; Dover Publications Inc.: Mineola, NY, USA, 2016. [Google Scholar]
- Ziegler, J.; Bender, P.; Dang, T.; Stiller, C. Trajectory Planning for Bertha—A Local, Continuous Method. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 450–457. [Google Scholar] [CrossRef]
- Werling, M.; Groll, L. Low-level controllers realizing high-level decisions in an autonomous vehicle. In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1113–1118. [Google Scholar] [CrossRef]
- Takahashi, A.; Hongo, T.; Ninomiya, Y.; Sugimoto, G. Local Path Planning And Motion Control For Agv In Positioning. In Proceedings of the IEEE/RSJ International Workshop on Intelligent Robots and Systems’, (IROS ’89) ’The Autonomous Mobile Robots and Its Applications, Tsukuba, Japan, 4–6 September 1989; pp. 392–397. [Google Scholar] [CrossRef]
- Werling, M.; Kammel, S.; Ziegler, J.; Gröll, L. Optimal trajectories for time-critical street scenarios using discretized terminal manifolds. Int. J. Robot. Res. 2012, 31, 346–359. [Google Scholar] [CrossRef]
- Rowold, M.; Ögretmen, L.; Kerbl, T.; Lohmann, B. Efficient Spatio-Temporal Graph-Search for Local Trajectory Planning on Oval Race Tracks. Actuators 2022. accepted. [Google Scholar]
- Betz, J.; Betz, T.; Fent, F.; Geisslinger, M.; Heilmeier, A.; Hermansdorfer, L.; Herrmann, T.; Huch, S.; Karle, P.; Lienkamp, M.; et al. TUM Autonomous Motorsport: An Autonomous Racing Software for the Indy Autonomous Challenge. arXiv 2022, arXiv:2205.15979. [Google Scholar] [CrossRef]
- Wischnewski, A.; Herrmann, T.; Werner, F.; Lohmann, B. A Tube-MPC Approach to Autonomous Multi-Vehicle Racing on High-Speed Ovals. IEEE Trans. Intell. Veh. 2022. [Google Scholar] [CrossRef]
- Chair of Automatic Control TUM. Smooth Trajectory Planning at the Handling Limits for Oval Racing. Available online: https://www.youtube.com/watch?v=H4tl_ggR1cc (accessed on 2 November 2022).





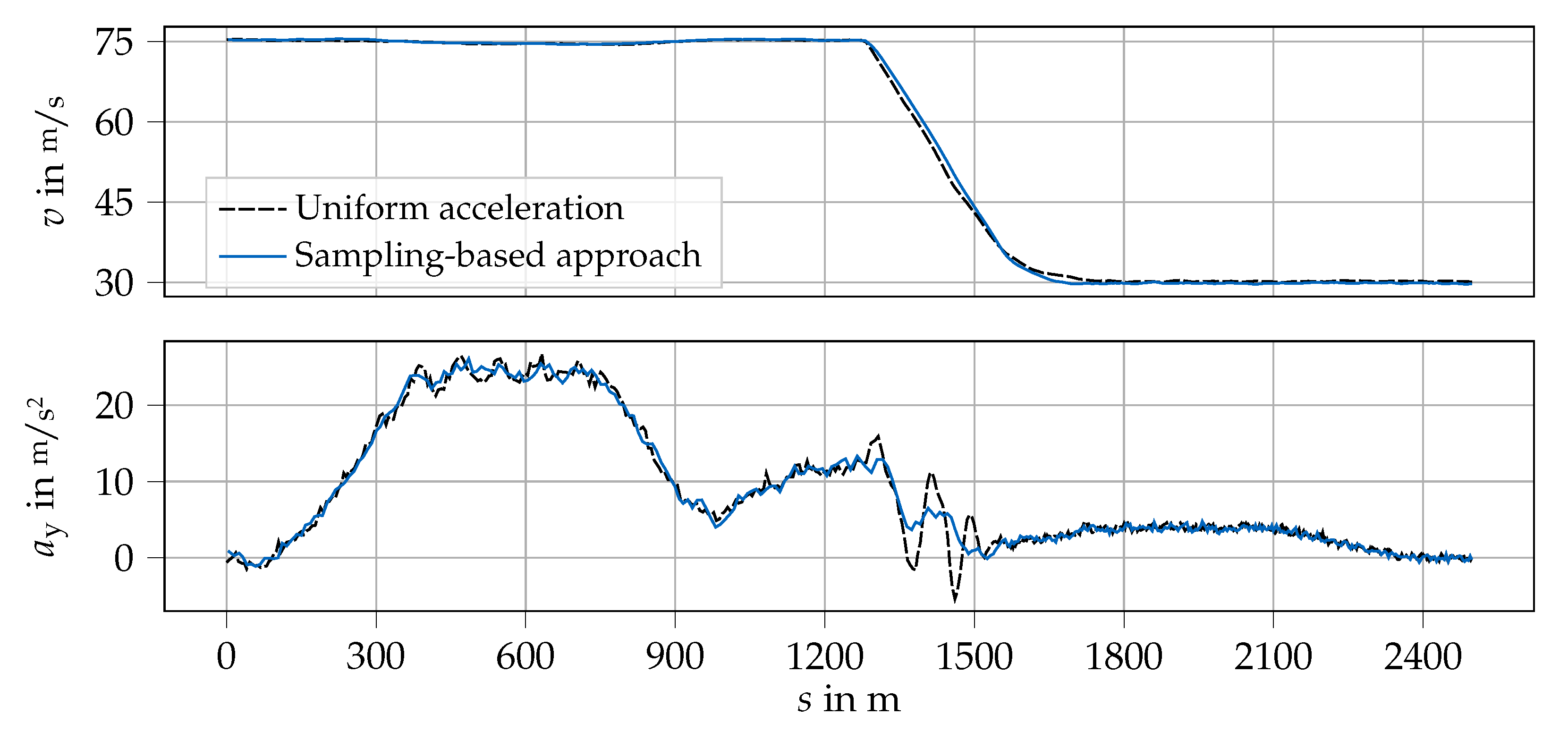

| Standing Start Lap | Flying Lap (Mean/Variance) | |
|---|---|---|
| Uniform acceleration | 47.814 s | 30.431 s/0.001 s2 |
| Sampling-based approach | 51.854 s | 30.001 s/0.004 s2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ögretmen, L.; Rowold, M.; Ochsenius, M.; Lohmann, B. Smooth Trajectory Planning at the Handling Limits for Oval Racing. Actuators 2022, 11, 318. https://doi.org/10.3390/act11110318
Ögretmen L, Rowold M, Ochsenius M, Lohmann B. Smooth Trajectory Planning at the Handling Limits for Oval Racing. Actuators. 2022; 11(11):318. https://doi.org/10.3390/act11110318
Chicago/Turabian StyleÖgretmen, Levent, Matthias Rowold, Marvin Ochsenius, and Boris Lohmann. 2022. "Smooth Trajectory Planning at the Handling Limits for Oval Racing" Actuators 11, no. 11: 318. https://doi.org/10.3390/act11110318
APA StyleÖgretmen, L., Rowold, M., Ochsenius, M., & Lohmann, B. (2022). Smooth Trajectory Planning at the Handling Limits for Oval Racing. Actuators, 11(11), 318. https://doi.org/10.3390/act11110318





