Abstract
Usually, polyhedra are viewed as the underlying constructive cells of packing or tiling in many disciplines, including crystallography, protein folding, viruses structure, building architecture, etc. Here, inspired by the flexible origami polyhedra (commonly called origami flexiballs), we initially probe into their intrinsic metamaterial properties and robotized methods from fabrication to actuation. Firstly, the topology, geometries and elastic energies of shape shifting are analyzed for the three kinds of origami flexiballs with extruded outward rhombic faces. Provably, they meet the definitions of reconfigurable and transformable metamaterials with switchable stiffness and multiple degrees of freedom. Secondly, a new type of soft actuator with rhombic deformations is successfully put forward, different from soft bionic deformations like elongating, contracting, bending, twisting, spiraling, etc. Further, we redesign and fabricate the three-dimensional (3D) printable structures of origami flexiballs considering their 3D printability and foldability, and magnetically actuated them through the attachment of magnetoactive elastomer. Lastly, a fully soft in-pipe robot prototype is presented using the origami flexiball as an applicable attempt. Experimental work clearly suggests that the presented origami flexiball robot has good adaptability to various pipe sizes, and also can be easily expanded to different scales, or reconfigured into more complex metastructures by assembly. In conclusion, this research provides a newly interesting and illuminating member for the emerging families of mechanical metamaterials, soft actuators and soft robots.
1. Introduction
Recently, increasingly innovative research cases [1,2] indicate that origami has far exceeded its traditional definition of manual cutting and folding arts. Its remarkable characteristics, including reversible foldability, adaptive multistability and tunable stiffness, have provided extensive innovative inspirations for scientists and engineers to develop nontraditional structures, mechanisms and materials, such as deployable structures [3,4], mechanical metamaterials [5,6,7], soft actuators or robots [8,9,10], biomedical devices or capsules [11,12], stretchable or flexible electronics [13,14,15] and other attractive possibilities [16,17].
Undoubtedly, origami has been recognized as a powerful and exciting inspiration source to chase the long-standing human dream: the whole physical system is fully programmable including its geometric deformation, material properties and even behavior under external stimulation. By deeply exploiting the novelty of origami, more and more concepts of traditional disciplines are revolutionarily refreshed. For example, a variety of origami-based mechanical metamaterials are demonstrated, such as tunable negative Poisson’s ratio [18], autonomous deployability [19], anisotropic multistability [20], self-locking [21], etc. On another hand, many new types of soft actuators or soft robots with novel deformation modes have been developed, including (but not limited to) self or active folding [22], variable stiffness [23], twisting motion [24], curvilinear deployment [9] and adaptive envelopes [25]. However, most research mainly focuses on a few crease patterns: Miura-ori pattern [25], waterbomb base [13,26], Yoshimura pattern [27] and Ron Resch pattern [28,29]. There are still many exquisite origami structures worthy of further exploration.
The initial motivation of this work is to reveal the intrinsic metamaterial properties of flexible origami polyhedra (commonly called origami flexiballs). Traditionally viewed as the underlying constructive cells of packing or tiling problems, polyhedra have fascinated scientists of many disciplines, including crystallography [30], protein folding [31], virus structure [32] and building architecture [33]. Here, we regard them as flexible and reconfigurable frameworks, and probe into their new properties from metamaterial perspectives.
Further inspired by the flexible origami polyhedra, we hope to break through the deformation patterns of current soft actuators. Usually, the research community of soft robotics pays more attention to soft bionic deformations like bending [34], stretching [35], twisting [36], spiraling [37], coiling [38], etc. In this work, however, we intend to construct a new type of soft actuator through magnetically stimulating the basic origami rhombic cell.
This paper is organized as follows. Firstly, the intrinsic metamaterial mechanisms of origami flexiballs are clarified through the analysis of their topology, geometries and elastic energies during shape shifting. Next the fabrication and actuation methods of the origami flexiball are introduced. Lastly, a fully soft in-pipe robot prototype is experimentally presented as an applicable attempt.
2. Intrinsic Metamaterial Mechanisms of Origami Flexiball
The source of our research inspiration is a popular and interesting origami flexiball with transformable rhombuses, in which modular sheet units are folded and snapped together into a flexible polyhedron with extruded outward faces, such as the rhombic triacontahedron shown in Figure 1.

Figure 1.
Origami flexiball: (a) flat folding pattern, (b) modular unit sheet, (c) snapping modular units, (d) flexible triacontahedron with extruded outward rhombic faces, (e–g) some kinds of switchable ultimate patterns.
While this origami model provides a geometric starting point for our research, our focus here is not on manual folding crafts, but on its flexible deformation originating from simple building block assembly. From this view, we intuitively anticipate that it should have some kind of relationship with the concept of metamaterials, which have remarkable mechanical properties depending on repeating unit cells rather than the properties of bulk materials in nature.
2.1. Topology and Geometry of Origami Flexiball
As a geometric demonstration, there are only three isometrically symmetrical polyhedra with rhombic cells: rhombic hexahedron (RHD, i.e., cube), rhombic dodecahedron (RDD) and rhombic triacontahedron (RTD) [33]. Table 1 and Table 2 together present the topology and geometries of these three types of origami flexiballs. Euler’s theorem in topology implies that the Euler characteristic of the simple polyhedron is two, namely, the number of vertices V, the number of edges E and the number of faces F conform to

Table 1.
Topology and geometries of origami flexiballs.

Table 2.
Vertex type and snapping module.
Further, the RDD has two types of vertices: eight vertices with three edges, and six vertices with four edges. The RTD has another two types of vertices: twenty vertices with three edges, and twelve vertices with five edges. The acute angles of their congruent rhombic faces are, respectively, , and . The theoretically dihedral angles (the angles between adjacent faces) of these three rhombic polyhedra are, respectively, , and.
In geometry, these rhombic polyhedra have many types of symmetries, because they are convex, face-transitive (isohedral) and isotoxal (edge-transitive). In addition, the rhombic dodecahedron is a parallelohedron with four sets of parallel edges.
With the assumption that the faces are rigid and connected at the edges by revolute joints, convex polyhedra are always rigid. However, once we regard them as frameworks without rigid faces, they will have certain motion degrees of freedom (DOFs) and sometimes possess peculiar kinematic properties [39].
2.2. Energy Landscape of Origami Flexiball
Obviously, the great motion mobility or shape shifting of the origami flexiball can make them absorb elastic energies of multiple magnitudes. However, due to the low rigidity of paper sheets, it is very difficult to accurately build a general framework for the elastic energy calculation of origami structures. Here, we suppose that the paper faces remain rigid during deformations, that is, they do not store any energy. Then, we only estimate the fold elastic energy of one crease by parameterizing its torsional stiffness , the rest crease angle and the opening angle . The widely accepted formula [5,20,40] is written as
Further, the total elastic energy of the whole origami flexiball can be approximated by
Meanwhile, during the origami flexiball deformation by manually applying a force, its volume also changes remarkably. If ignoring the origami sheets’ own volumes, the total volume of the origami flexiball only includes two parts: the internal polyhedron cavity , and all volumes of the extruded rhombic cavity , that is, they will fulfill the following equation:
Table 3 lists the possible maximum volumes and the corresponding elastic energies of the three types of origami flexiballs with the same edge length , and the rest crease angle

Table 3.
Volumes and elastic energies of origami flexiballs.
Further, we depicted the volumes versus the elastic energies of four switchable ultimate patterns of the three types of origami flexiballs, as shown in Figure 2, Figure 3, Figure 4. In the figures, we marked the crease opening angles and the numbers of different patterns by . Although this evaluation approach is somewhat rough, the energy landscapes of shape-shifting origami flexiballs are still clearly described. Firstly, we can see that the changes of elastic energies vary with the directions of elastic deformation. Secondly, during the transformations of different ultimate patterns, large volume reductions are also produced. Taking an RTD as an example, the maximum volume reduction happens between the fully expanded Pattern #1 and the fully compressed Pattern #4, and the maximum volume ratio is approximately 14-fold. Thirdly, it is important to note that for the same origami flexiball, the relationship between the volumes of different ultimate patterns and their elastic energies is highly nonlinear. Further, Pattern # 1 of the RHD and Pattern #3 of the RDD have the same volume value, but the elastic energy of the former is more than 20 times that of the latter. Pattern #1 of the RDD and Pattern #3 of the RTD are very close in volume, but the elastic energy of the latter is more than 15 times that of the former. This fully demonstrates that the elastic energy of an origami flexiball not only depends on the numbers of unit cells and their topological connections, but also depends on the motions of crease opening angles.
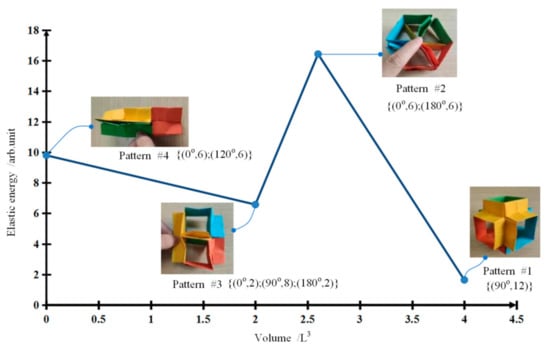
Figure 2.
Shape shifting, energy landscape and cavity volume of rhombic hexahedron origami.
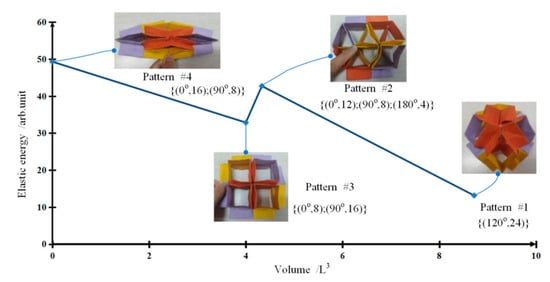
Figure 3.
Shape shifting, energy landscape and cavity volume of rhombic dodecahedron origami.
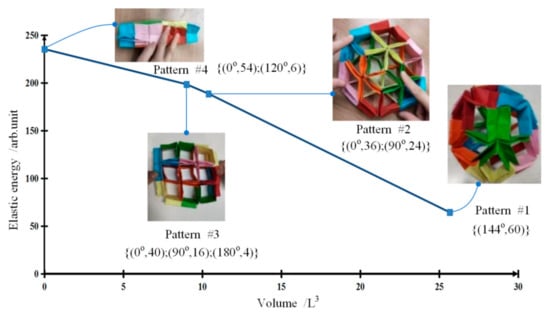
Figure 4.
Shape shifting, energy landscape and cavity volume of rhombic triacontahedron origami.
2.3. Intrinsic Metamaterial Properties of Origami Flexiball
Obviously, according to the above analysis, if viewing the highly flexible and deformable rhombic module as an underlying unit cell, the presented RHD/RDD/RTD origami flexiballs exactly satisfy the definition of an origami-inspired transformable metamaterial with multiple degrees of freedom, which was put forward by Johannes et al. [41]. Further, both the RHD and RDD are parallelohedrons, which can tessellate in a certain space by translational copies of themselves. In light of this, they can be viewed as second-order underlying cells to be assembled into more complex reconfigurable structures like the three-dimensional (3D) printable origami assemblages [42].
Undoubtedly, here we introduce a new type of origami flexiball metamaterial, which has two remarkable properties, as follows: switchable rigidity and shape shifting with multiple degrees of freedom; hierarchical reconfigurability of rhombic cells, polyhedra and more complex assemblages. To make this point more understandable, let us look back the original intent of the term metamaterial, coined by Walser [43]: macroscopic materials having a human-made, 3D, periodic cellular architecture and exhibiting remarkable properties not available in nature. Academically, more and more novel metamaterials or metastructures have been put forward that blur the boundaries between material, structure, mechanism and even multifunctional materials [44]. For instance, Correll and Voyles [45] presented a new type of robotic material or computational metamaterial that tightly integrated sensing, actuation, computation, communication and power routing in a periodic fashion. As another example, Ion et al. [46] demonstrated the concept of metamaterial mechanisms by constructing 3D cell grid structures to transform input forces and movement into the desired outputs of force and movement. As mentioned in Section 1, these are all efforts to advance human long-standing dreams.
3. Magnetically Driven In-Pipe Robot Inspired by Origami Flexiball
3.1. Digital Fabrication of Origami Flexiball Metamaterial
Although the intrinsic metamaterial mechanisms of origami flexiballs have been demonstrated through the abovementioned analysis, this new type of origami metamaterial still encounters a practical application obstacle: manufacturability. Folding and assembling modular, unit-based thin sheets with negligible or zero thickness require a complex and tedious sequences of dexterous hand manipulations, and current manufacturing technologies cannot imitate this process automatically. In the past few years, harnessing the power of 3D printing technology to manufacture various soft robots has become an important trend [47]. Therefore, considering that 3D printing technology has strong adaptability to direct fabrications of complex geometries, we attempted to explore the digital fabrication approach of this origami flexiball metamaterial using the popular fused deposition modeling (FDM) method. Before 3D printing, the modular thin sheet structure needs to be redesigned to have a good trade-off between its 3D printability and foldability with high elasticity and damage tolerance. After many experiments, we designed the printable thin sheet units as shown in Figure 5.
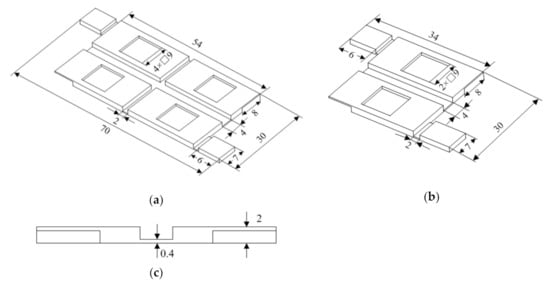
Figure 5.
Redesign of thin sheet units: (a) schematic of the thin sheet unit with one hinge, (b) schematic of the thin sheet unit with two hinges, (c) connecting schematic.
Considering the actual capability of our own 3D printer, we employed flexible 1.75 mm polylactic acid (PLA) filaments and a 0.3 mm diameter extruder nozzle. The infill density of the grid pattern was set as 50%. The printing speed was at 50 mm/s and the layer height was 0.2 mm. As illustrated in Figure 6, we then snapped the printed thin sheet units into the finalized origami flexiball using strong glue. Figure 7 demonstrates the multiple shape-shifting patterns of the finalized origami flexiball.

Figure 6.
Fabrication of origami flexiball: (a) 3D printed thin sheet units; (b) bonding thin sheet units together; (c) a bonded module; (d) the finalized origami flexiball.

Figure 7.
Shape-shifting patterns of 3D printed origami flexiball metamaterial: (a) freely expanded pattern; (b) fully compressed pattern; (c) fully compressed pattern at symmetric points; (d) fully compressed pattern at symmetric faces; (e) fully compressed pattern at symmetric edges.
3.2. Actuation of Origami Flexiball Metamaterial Actuator
Thus far, we have shown that the shape and volume of the origami flexiball can be altered by manually dexterous operations. It still cannot be actuated through various external stimuli, such as light, heat and magnetic and electric fields. Perhaps the most easy way to make it active is to use pneumatics to drive the motions of crease opening angles. However, this actuation method needs many flexible tethers to transfer the gas. In addition, we also forsake centering on the locally actuating concepts of hinge type or bending type active folds [48], and turn to a new actuation strategy.
Noting that the most basic deformation of the origami flexiball metamaterial is the rhombic cells opening and shutting, in this work, we present a magnetically driven soft actuator with rhombic motion, as shown in Figure 8. First, we used silicone as the medium to incorporate 5-micron magnetic powder particles of 30 wt.%, and achieved magneto-active elastomer (MAE) after drying and curing [49]. Then, we bonded the MAEs on the rhombic faces. In the experiments, the external magnetic field was a NdFeB permanent magnet with a magnetic field intensity of 2 T. Clearly, it can be seen that the rhombic unit cell with MAEs is quickly actuated to open or shut with the adjusting of the magnetic induction distance. The advantages of this actuation not only depend on the ease of quickly and accurately controlling the magnetic field direction and magnitude, but also on its ability to penetrate most materials without tethers. To our best knowledge, a soft actuator with rhombic deformations was created for the first time, which is distinctly different from the most current deformations of soft actuators, such as bending, twisting, stretching, compressing, buckling, wrinkling, etc.

Figure 8.
Magnetically driven rhombic deformations of soft actuator.
Next, we deployed MAEs onto the whole origami flexiball, as shown in Figure 9, according to the magnetic field simulation and actuation experiments. Similarly, under the stimulation of a NdFeB permanent magnet with a magnetic field intensity of 3 T, when the operating distance ranges from 140 mm to 10 mm, the origami flexiball can freely switch between the fully expanded pattern and the fully compressed pattern. This is very exciting and inspires us to wonder that how it can change into a kind of robot, after all, we have come a long way from the origami art, to metamaterial properties, and to this new type of soft actuator.

Figure 9.
Magnetically driven shape shifting of the origami flexiball.
3.3. An In-Pipe Robot Prototype
For a very long time, many types of in-pipe robots have been developed by different enabling technologies to adapt to certain complicated pipe structures [50]. The importance of the regular inspection and maintenance of pipelines in various industries and hydraulic or pneumatic equipment cannot be overemphasized. Working in constrained pipeline environments (e.g., variable pipe diameter, partial clogging, fragile pipe wall and low stiffness) is always a great challenge for this research community [51]. So, can the origami flexiball with MAEs move in an in-pipe scene like a robot? Next, our experiments try to give an answer.
Firstly, we put the origami flexiball with MAEs into a polycarbonate pipe with a diameter of 71 mm, as shown in Figure 10a. Obviously, if there is no external magnetic field, the origami flexiball actuator would relax naturally. When the NdFeB permanent magnet approaches the pipe from below, the origami flexiball actuator would compress in a radial direction and elongate in an axial direction. Additionally, when the permanent magnet leaves from the top with a relatively lower speed than approaching, the origami flexiball actuator would spring back, and, meanwhile, the origami flexiball actuator would move forward about 23 mm. Being very similar to earthworm crawling [52], this locomotion is caused by two concurrent factors, the first of which is the wave effects along the origami flexiball actuator originating from the velocity difference of elongation and contraction deformations during the reciprocating stroke. Additionally, the second factor is that the kinetic frictions between the origami flexiball and pipe walls vary with the changes of contact areas during the alternating deformations. When the static frictional force blocks the elongation from front to back, the overall actuator will move forward. As assembly errors in 3D printed thin sheet units are inevitable, it is easy to determine the front end of the moving origami flexiball after driving experiments. Maintaining the above alternating changes of external magnetic fields will achieve continuous locomotion. Further, we simulated an in-pipe cleaning task, and the origami flexiball robot successfully pushed out the foam-like rubbish, as shown in Figure 10b.

Figure 10.
In-pipe locomotion of the origami flexiball robot: (a) undulatory motion, (b) cleaning experiment.
Additionally, the ability of self-adaptive variable diameter has also been viewed as an important indicator to measure the performance of in-pipe robots. Therefore, we experimentally inspected the origami flexiball robot’s adaptability to pipes of variable diameters. As illustrated in Figure 11, the connected polycarbonate pipes include three different pieces with inner diameters of 57 mm, 67 mm and 71 mm. Our presented origami flexiball robot smoothly crawled through the pipes in sequence, and the locomotion speed was up to 6 mm/s. At the joins between different diameter pipes, no jam, stagnation or other problems were observed. This fully demonstrated that the controllable adaptive deformation of the origami flexiball robot has high compliance for various pipe sizes by adjusting the stimulation of the external magnetic field.

Figure 11.
The origami flexiball robot crawls through variable diameter pipes (the nested connections of variable diameter pipes are marked using red circles): (a) from mm pipe to mm pipe; (b) from mm pipe to mm pipe.
Obviously, although our origami flexiball-inspired in-pipe robot prototype looks a little simple, it provides a new alternative. Besides its good adaptability to various pipe sizes, it has many other potential advantages. For instance, due to its fully soft nature without any rigid parts, it can work in pipes with fragile walls. Further, it can be easily expanded to different scales, or reconfigured into many segments by assembly. Admittedly, there is much room for its full robotization, including self-sensing, long-range control strategy and a more complex deformation mechanism.
4. Conclusions
In recent years, origami-inspired structures, origami-inspired mechanisms, origami-inspired metamaterials and even origami-inspired robotics have primarily demonstrated their promising potential for innovative inspirations for engineering solutions. In this research, origami flexiballs configured with rhombic cells are investigated from underlying metamaterial mechanisms to robotized possibility.
In light of the definition of a mechanical metamaterial, and further referring to the similarly origami-inspired metamaterials, this type of origami flexiball could be exactly regarded as a shape-shifting metamaterial mechanism owing to multiple degrees of freedom, switchable rigidity and large volumetric deformations. Further, we redesigned and fabricated the soft origami structures considering 3D printability and foldability. Furthermore, we introduced a magnetically driven soft actuator with rhombic deformations different from soft bionic deformations like bending, stretching, twisting, spiraling, etc. Lastly, an applicable attempt was presented through robotizing the soft origami flexiball as an in-pipe crawling robot. Locomotion through variable diameter pipes and a cleaning task clearly suggested the presented origami flexiball robot has good adaptability to various pipe sizes, and can also be easily expanded to different scales, or reconfigured into more complex metastructures by assembly.
Although this exciting and illuminating research may contribute to the new soft robotics paradigm, admittedly, there is much room for the full robotization of origami metamaterial polyhedra, including self-sensing, long-range actuation methods and more controllable complex shape-shifting mechanisms like hopping, rolling and self-assembly. Besides robotic fields, many more applications in other interesting fields are expected, such as soft deformation sensors, transformable buildings, optical instruments with foldable long-focal-length and multiset lenses, reconfigurable dampers, lightweight haptic devices [53], constrained devices [54], etc.
Author Contributions
Conceptualization, F.H.; methodology, F.H.; software, T.L.; validation, F.H. and T.L.; formal analysis, T.L.; investigation, T.L.; resources, F.H.; data curation, T.L.; writing—original draft preparation, T.L., F.H.; writing—review and editing, F.H.; supervision, F.H.; project administration, F.H.; funding acquisition, F.H. All authors have read and agreed to the published version of the manuscript.
Funding
The project was supported by the Cooperation Project Between Industry and University approved by the Ministry of Education of China (No. 202002148005), and by the Planning Subject for the 13th Five Year Plan of Beijing Education Sciences (No. CDDB19163) and by the National Key Research and Development Program of China (No. 2017YFE0117400).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
All data generated or analyzed during this study are included in this article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| DOF | Degree of Freedom |
| FDM | Fused Deposition Modeling |
| MAE | Magnetoactive Elastomer |
| PLA | Polylactic Acid |
| RHD | Rhombic Hexahedron |
| RDD | Rhombic Dodecahedron |
| RTD | Rhombic Triacontahedron |
References
- Turner, N.; Goodwine, B.; Sen, M. A review of origami applications in mechanical engineering. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2345–2362. [Google Scholar] [CrossRef]
- Park, J.J.; Won, P.; Ko, S.H. A review on hierarchical origami and kirigami structure for engineering applications. Int. J. Precis. Eng. Manuf. Green Technol. 2019, 6, 147–161. [Google Scholar] [CrossRef]
- Zirbel, S.A.; Trease, B.P.; Thomson, M.W.; Lang, R.J.; Magleby, S.P.; Howell, L.H. Hanaflex: A large solar array for space applications. In Micro-and Nanotechnology Sensors, Systems, and Applications VII. Int. Soc. Opt. Photonics 2015, 9467, 94671C. [Google Scholar]
- Salazar, R.; Murthy, S.; Pellazar, C.; Stoica, A. TransFormers for lunar extreme environments: Large origami deployable solar reflectors. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–7. [Google Scholar]
- Lv, C.; Krishnaraju, D.; Konjevod, G.; Yu, H.; Jiang, H. Origami based mechanical metamaterials. Sci. Rep. 2014, 4, 5979. [Google Scholar] [CrossRef] [PubMed]
- Florijn, B.; Coulais, C.; van Hecke, M. Programmable mechanical metamaterials. Phys. Rev. Lett. 2014, 113, 175503. [Google Scholar] [CrossRef] [PubMed]
- Silverberg, J.L.; Evans, A.A.; McLeod, L.; Hayward, R.C.; Hull, T.; Santangelo, C.D.; Cohen, I. Using origami design principles to fold reprogrammable mechanical metamaterials. Science 2014, 345, 647–650. [Google Scholar] [CrossRef]
- Shigemune, H.; Maeda, S.; Hara, Y.; Hosoya, N.; Hashimoto, S. Origami robot: A self-folding paper robot with an electrothermal actuator created by printing. IEEE/ASME Trans. Mechatron. 2016, 21, 2746–2754. [Google Scholar] [CrossRef]
- Hu, F.; Wang, W.; Cheng, J.; Bao, Y. Origami spring–inspired metamaterials and robots: An attempt at fully programmable robotics. Sci. Prog. 2020, 103. [Google Scholar] [CrossRef]
- Göttler, C.; Elflein, K.; Siegwart, R.; Sitti, M. Spider Origami: Folding Principle of Jumping Spider Leg Joints for Bioinspired Fluidic Actuators. Adv. Sci. 2021, 2003890. [Google Scholar] [CrossRef]
- Kim, T.; Lee, Y.G. Shape transformable bifurcated stents. Sci. Rep. 2018, 8, 13911. [Google Scholar] [CrossRef]
- du Plessis d’Argentré, A.; Perry, S.; Iwata, Y.; Iwasaki, H.; Iwase, E.; Fabozzo, A.; Will, I.; Rus, D.; Damian, D.D.; Miyashita, S. Programmable medicine: Autonomous, ingestible, deployable hydrogel patch and plug for stomach ulcer therapy. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1511–1518. [Google Scholar]
- Tao, K.; Yi, H.; Yang, Y.; Tang, L.; Yang, Z.; Wu, J.; Chang, H.; Yuan, W. Miura-origami-inspired electret/triboelectric power generator for wearable energy harvesting with water-proof capability. Microsyst. Nanoeng. 2020, 6, 56. [Google Scholar] [CrossRef]
- Ho, D.T.; Kim, S.Y.; Schwingenschlögl, U. Graphene origami structures with superflexibility and highly tunable auxeticity. Phys. Rev. B 2020, 102, 174106. [Google Scholar] [CrossRef]
- Lee, H.; Choi, S. An origami paper-based bacteria-powered battery. Nano Energy 2015, 15, 549–557. [Google Scholar] [CrossRef]
- Cunha, F.; Mota, C.; Reis, A.; Marques, P.; Pinto, R.; Fangueiro, R. Development of a flexible, light weight structure, adaptable to any space through a shape shifting feature. Procedia Eng. 2016, 155, 426–441. [Google Scholar] [CrossRef]
- Yasuda, H.; Tachi, T.; Lee, M.; Yang, J. Origami-based tunable truss structures for non-volatile mechanical memory operation. Nat. Commun. 2017, 8, 962. [Google Scholar] [CrossRef]
- Yasuda, H.; Yang, J. Reentrant origami-based metamaterials with negative Poisson’s ratio and bistability. Phys. Rev. Lett. 2015, 114, 185502. [Google Scholar] [CrossRef] [PubMed]
- Zhai, Z.; Wang, Y.; Jiang, H. Origami-Inspired, On-Demand Deployable and Collapsible Mechanical Metamaterials with Tunable Stiffness. Proc. Natl. Acad. Sci. USA 2018, 115, 2032–2037. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, S.; Li, S. Harnessing the Anisotropic Multistability of Stacked-Origami Mechanical Metamaterials for Effective Modulus Programming. J. Intell. Mater. Syst. Struct. 2018, 29, 2933–2945. [Google Scholar] [CrossRef]
- Fang, H.B.; Chu, S.; Xia, Y.T.; Wang, K.W. Programmable Self-Locking Origami Mechanical Metamaterials. Adv. Mater. 2018, 30, 1706311. [Google Scholar] [CrossRef]
- Mu, J.; Hou, C.; Wang, H.; Li, Y.; Zhang, Q.; Zhu, M. Origami-inspired active graphene-based paper for programmable instant self-folding walking devices. Sci. Adv. 2015, 1, e1500533. [Google Scholar] [CrossRef]
- Deshpande, A.R.; Tse, Z.T.H.; Ren, H. Origami-inspired bi-directional soft pneumatic actuator with integrated variable stiffness mechanism. In Proceedings of the 2017 18th International Conference on Advanced Robotics (ICAR), Hong Kong, China, 10–12 July 2017; pp. 417–421. [Google Scholar]
- Lee, K.; Wang, Y.; Zheng, C. Twister hand: Underactuated robotic gripper inspired by origami twisted tower. IEEE Trans. Robot. 2020, 36, 488–500. [Google Scholar] [CrossRef]
- Li, S.; Stampfli, J.J.; Xu, H.J.; Malkin, E.; Diaz, E.V.; Rus, D.; Wood, R.J. A vacuum-driven origami “magic-ball” soft gripper. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 7401–7408. [Google Scholar]
- Zhou, X.; Zang, S.; You, Z. Origami Mechanical Metamaterials Based on the Miura-Derivative Fold Patterns. Proc. Math. Phys. Eng. Sci. 2016, 2191, 20160361. [Google Scholar] [CrossRef] [PubMed]
- Paez, L.; Agarwal, G.; Paik, J. Design and analysis of a soft pneumatic actuator with origami shell reinforcement. Soft Robot. 2016, 3, 109–119. [Google Scholar] [CrossRef]
- Tachi, T. Designing freeform origami tessellations by generalizing Resch’s patterns. J. Mech. Des. 2013, 135, 111006. [Google Scholar] [CrossRef]
- Kshad, M.A.E.; Popinigis, C.; Naguib, H.E. 3D Printing of Ron-Resch-Like Origami Cores for Compression and Impact Load Damping. Smart Mater. Struct. 2019, 28, 015027. [Google Scholar] [CrossRef]
- Yamada, T. Superstructure formation in a ternary Yb-Cd-Mg 1/1 quasicrystal approximant. Philos. Mag. 2021, 101, 257–275. [Google Scholar] [CrossRef]
- Taylor, W.R. Exploring protein fold space. Biomolecules 2020, 10, 193. [Google Scholar] [CrossRef]
- Janner, A. Towards a classification of icosahedral viruses in terms of indexed polyhedra. Acta Crystallogr. Sect. A Found. Crystallogr. 2006, 62, 319–330. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Latteur, P.; Mueller, C. Grammar-based Rhombic Polyhedral Multi-Directional Joints and Corresponding Lattices. In Proceedings of the IASS Annual Symposia—International Association for Shell and Spatial Structures (IASS), Tokyo, Japan, 26–30 September 2016; Volume 2016, pp. 1–10. [Google Scholar]
- Fras, J.; Macias, M.; Noh, Y.; Althoefer, K. Fluidical bending actuator designed for soft octopus robot tentacle. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 253–257. [Google Scholar]
- Kim, W.; Byun, J.; Kim, J.K.; Choi, W.Y.; Jakobsen, K.; Jakobsen, J.; Lee, D.Y.; Cho, K.J. Bioinspired dual-morphing stretchable origami. Sci. Robot. 2019, 4. [Google Scholar] [CrossRef]
- Wang, T.; Ge, L.; Gu, G. Programmable design of soft pneu-net actuators with oblique chambers can generate coupled bending and twisting motions. Sens. Actuators A Phys. 2018, 271, 131–138. [Google Scholar] [CrossRef]
- Uppalapati, N.K.; Krishnan, G. Towards pneumatic spiral grippers: Modeling and design considerations. Soft Robot. 2018, 5, 695–709. [Google Scholar] [CrossRef]
- Mersch, J.; Koenigsdorff, M.; Nocke, A.; Cherif, C.; Gerlach, G. High-Speed, Helical and Self-Coiled Dielectric Polymer Actuator. Actuators 2021, 10, 15. [Google Scholar] [CrossRef]
- Laliberté, T.; Gosselin, C.M. Polyhedra with articulated faces. In Proceedings of the 12th IFToMM World Congress, Besançon, France, 17–20 June 2007. [Google Scholar]
- Waitukaitis, S.; Menaut, R.; Chen, G.; Van Hecke, M. Origami multistability: From single vertices to metasheets. Phys. Rev. Lett. 2015, 114, 055503. [Google Scholar] [CrossRef]
- Overvelde, J.T.B.; de Jong, T.A.; Shevchenko, Y.; Becerra, S.A.; Whitesides, G.M.; Weaver, J.C.; Hoberman, C.; Bertoldi, K. A Three-Dimensional Actuated Origami-Inspired Transformable Metamaterial with Multiple Degrees of Freedom. Nat. Commun. 2016, 7, 10929. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Kuang, X.; Wu, J.; Zhang, Q.; Paulino, G.H.; Qi, H.J.; Fang, D. 3D Printing of Complex Origami Assemblages for Reconfigurable Structures. Soft Matter 2018, 14, 8051–8059. [Google Scholar] [CrossRef] [PubMed]
- Walser, R.M. Metamaterials: What are they? What are they good for? In Proceedings of the APS March Meeting Abstracts, Minneapolis, MN, USA, 20–24 March 2000; p. Z5-001. [Google Scholar]
- Wu, W.; Hu, W.; Qian, G.; Liao, H.; Xu, X.; Berto, F. Mechanical design and multifunctional applications of chiral mechanical metamaterials: A review. Mater. Des. 2019, 180, 107950. [Google Scholar] [CrossRef]
- Correll, N.; Voyles, R. Robotic materials: From smart polymers to computational metamaterials. In Proceedings of the Robot Makers Workshop, Robotics: Science Systems Conference, Berkeley, CA, USA, 12–16 July 2014. [Google Scholar]
- Ion, A.; Frohnhofen, J.; Wall, L.; Kovacs, R.; Alistar, M.; Lindsay, J.; Lopes, P.; Chen, H.T.; Baudisch, P. Metamaterial mechanisms. In Proceedings of the 29th Annual Symposium on User Interface Software and Technology, Tokyo, Japan, 16–19 October 2016; pp. 529–539. [Google Scholar]
- Gul, J.Z.; Sajid, M.; Rehman, M.M.; Siddiqui, G.U.; Shah, I.; Kim, K.H.; Lee, J.W.; Choi, K.H. 3D printing for soft robotics—A review. Sci. Technol. Adv. Mater. 2018, 19, 243–262. [Google Scholar] [CrossRef]
- Peraza-Hernandez, E.A.; Hartl, D.J.; Malak, R.J., Jr.; Lagoudas, D.C. Origami-inspired active structures: A synthesis and review. Smart Mater. Struct. 2014, 23, 094001. [Google Scholar] [CrossRef]
- Bowen, L.; Springsteen, K.; Feldstein, H.; Frecker, M.; Simpson, T.W.; von Lockette, P. Development and Validation of a Dynamic Model of Magneto-Active Elastomer Actuation of the Origami Waterbomb Base. J. Mech. Robot. 2015, 7, 011010. [Google Scholar] [CrossRef]
- Shao, L.; Wang, Y.; Guo, B.; Chen, X. A review over state of the art of in-pipe robot. In Proceedings of the 2015 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 2–5 August 2015; pp. 2180–2185. [Google Scholar]
- Wang, Z.; Gu, H. A bristle-based pipeline robot for ill-constraint pipes. IEEE/ASME Trans. Mechatron. 2008, 13, 383–392. [Google Scholar] [CrossRef]
- Dorgan, K.M. Environmental constraints on the mechanics of crawling and burrowing using hydrostatic skeletons. Exp. Mech. 2010, 50, 1373–1381. [Google Scholar] [CrossRef]
- Wang, P.; Conn, A.T. Elastic cube actuator with six degrees of freedom output. Actuators 2015, 4, 203–216. [Google Scholar] [CrossRef]
- Yan, H.; Tong, Z.; Park, D.; Lu, H. A Reconfigurable Joint Based on Extruded Polyhedrons. In Proceedings of the 25th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA), Bangkok, Thailand, 5–6 August 2020; Volume 1, pp. 455–464. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).