Tracking Control of Pneumatic Artificial Muscle-Activated Robot Arm Based on Sliding-Mode Control
Abstract
1. Introduction
2. Materials and Methods
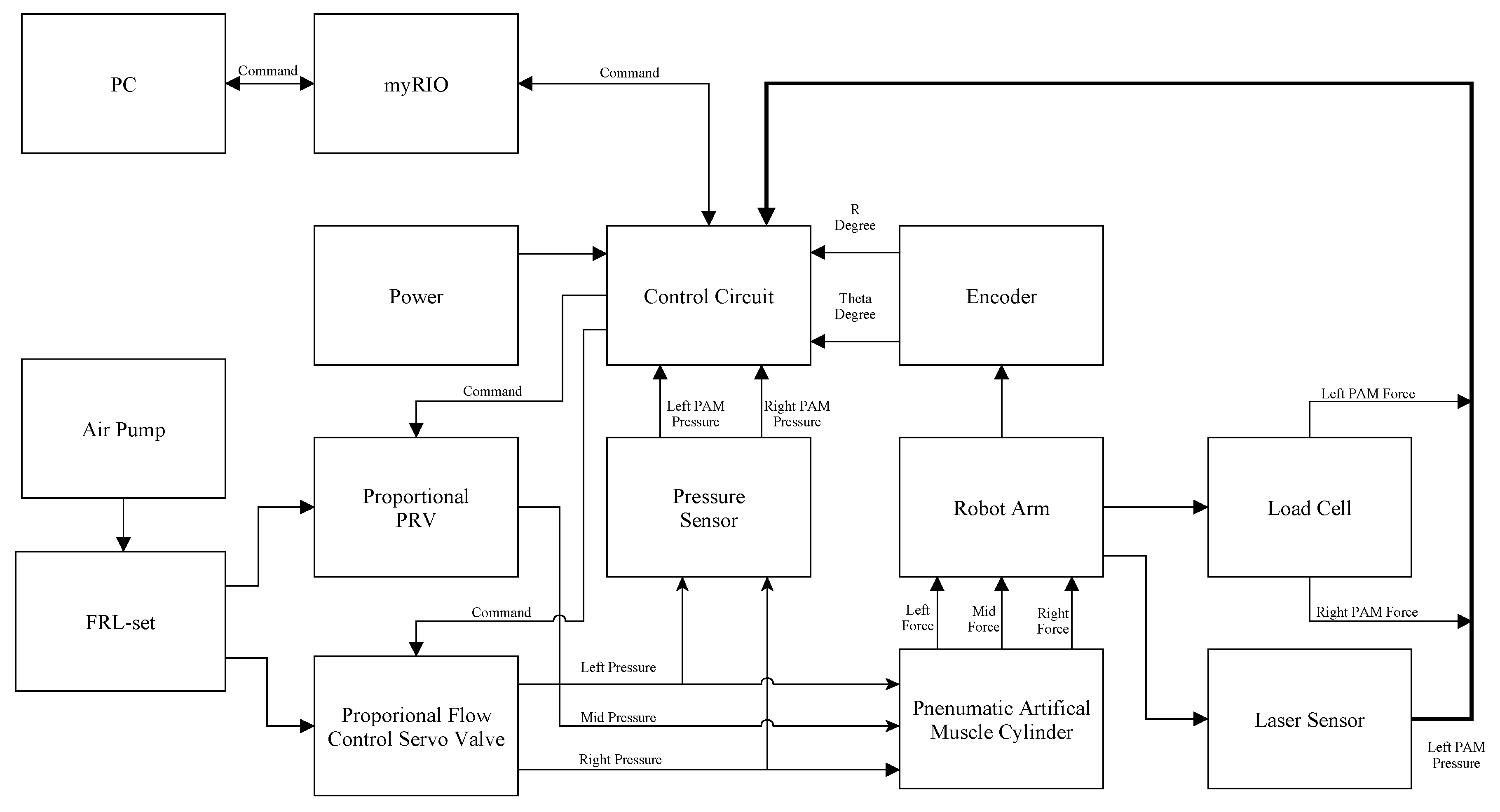
2.1. Materials and Experimental Setup
2.2. Introduction of a Dynamic Model
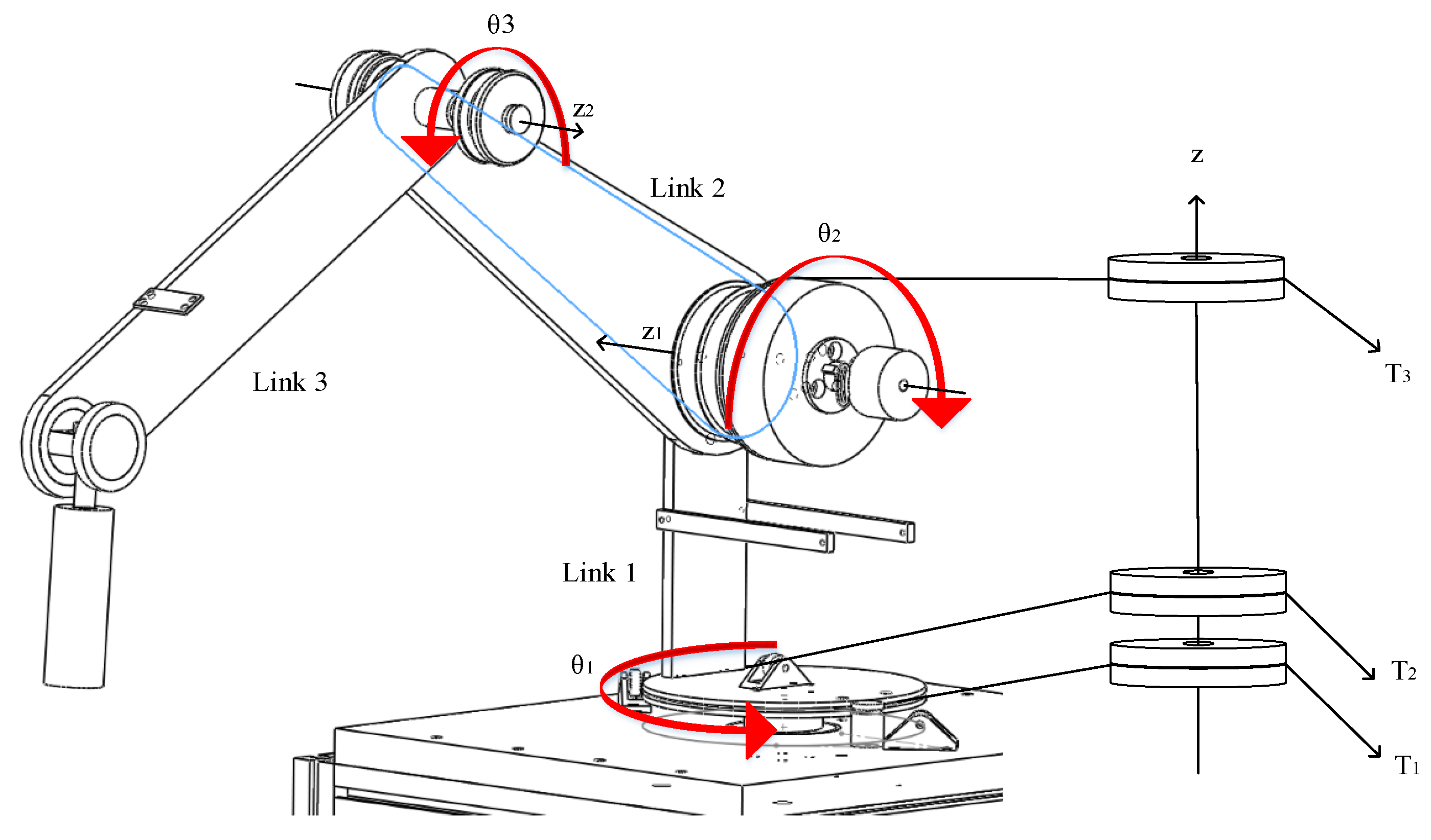
2.2.1. Analysis of Motion of Joint Angle and Terminal Point of a Robot Arm System
2.2.2. Dynamic Math and Model of Proportional Flow Control Servo Valve of PAM Cylinder
2.3. Parameter Identification of the Dynamic Model
2.3.1. Parameter Identification of the Model of the Proportional Flow Control Servo Valve
2.3.2. Using a Genetic Algorithm to Find the Optimum Parameters for a Dynamic Model
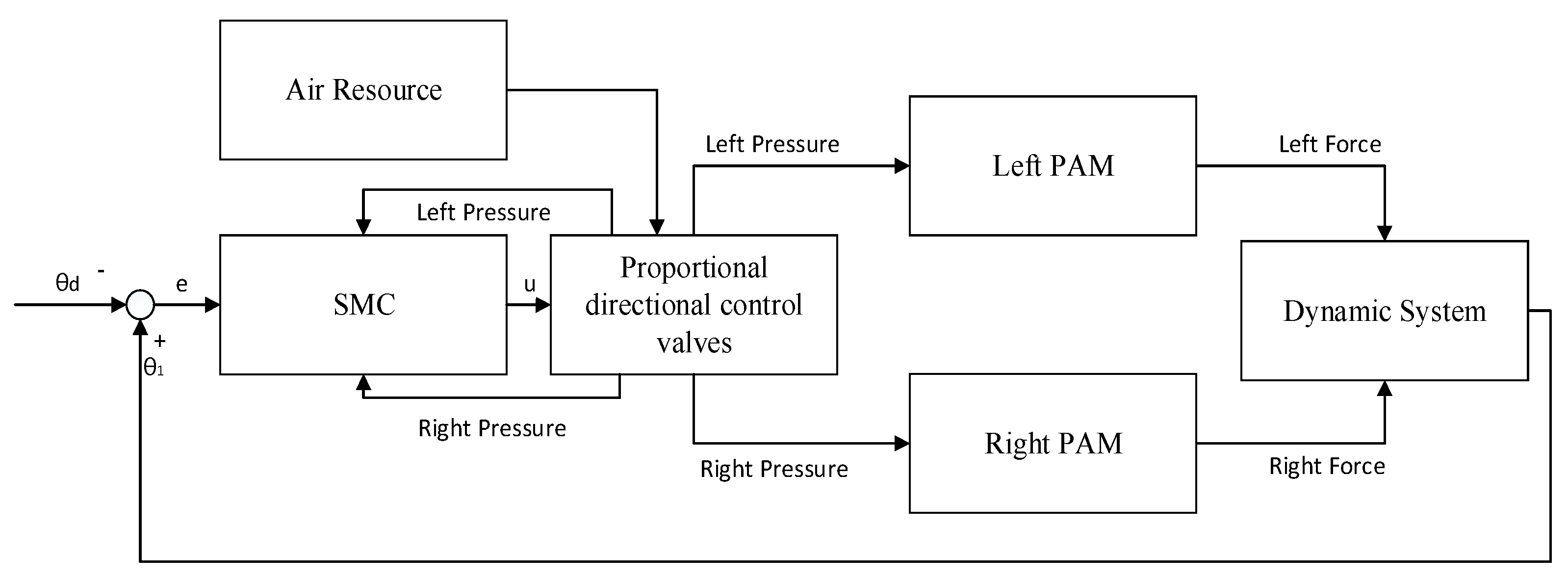
2.4. Extended Sliding-Mode Feedback Controller and Parameter Identification
3. Results and Discussion
3.1. Experiment and Discussion on the Fixed Moment of Inertia of a Robot Arm
3.1.1. Configuration of Sampling Time
3.1.2. Investigation on the Fixed Moment of Inertia of a Robot Arm Controller
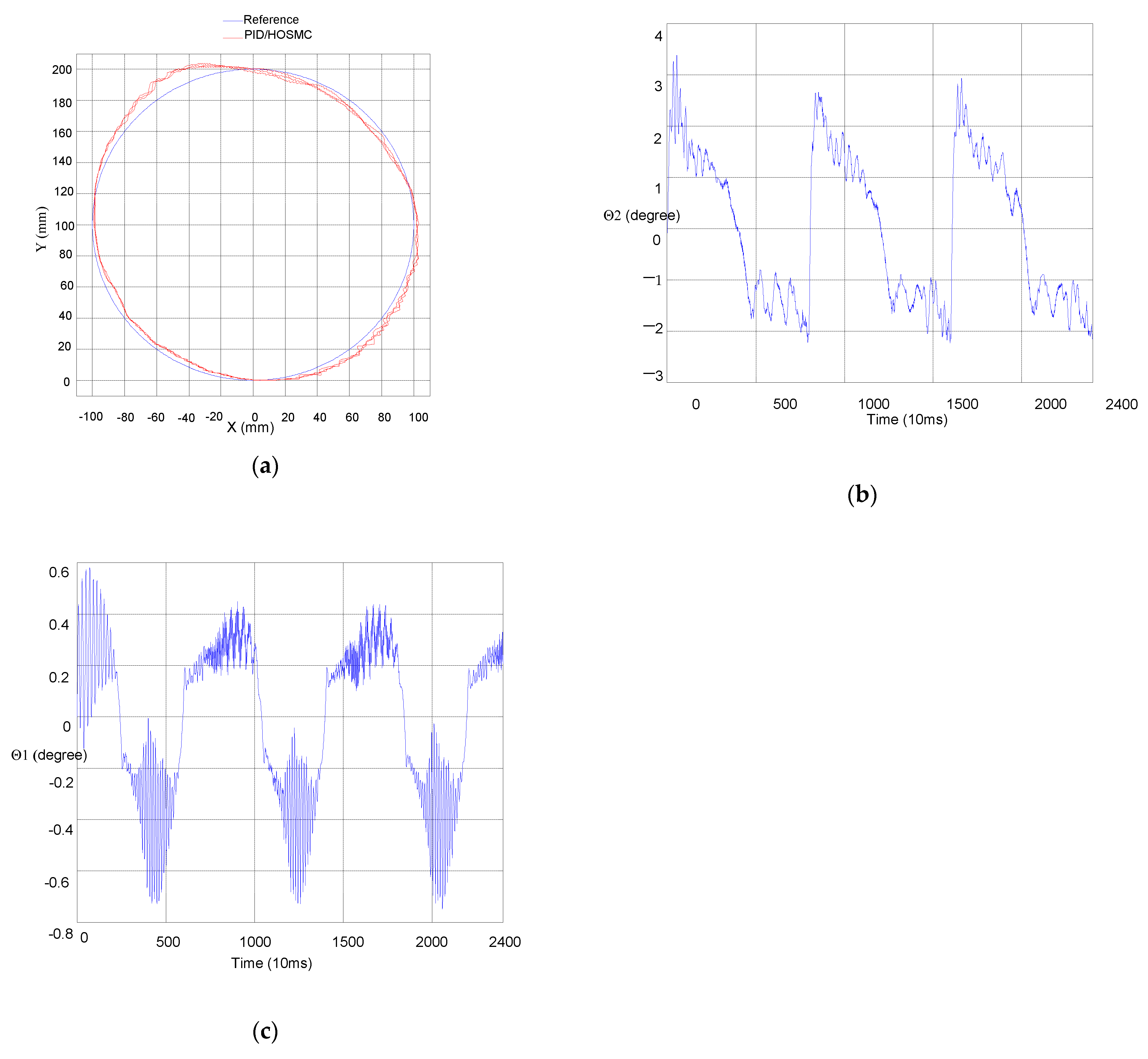
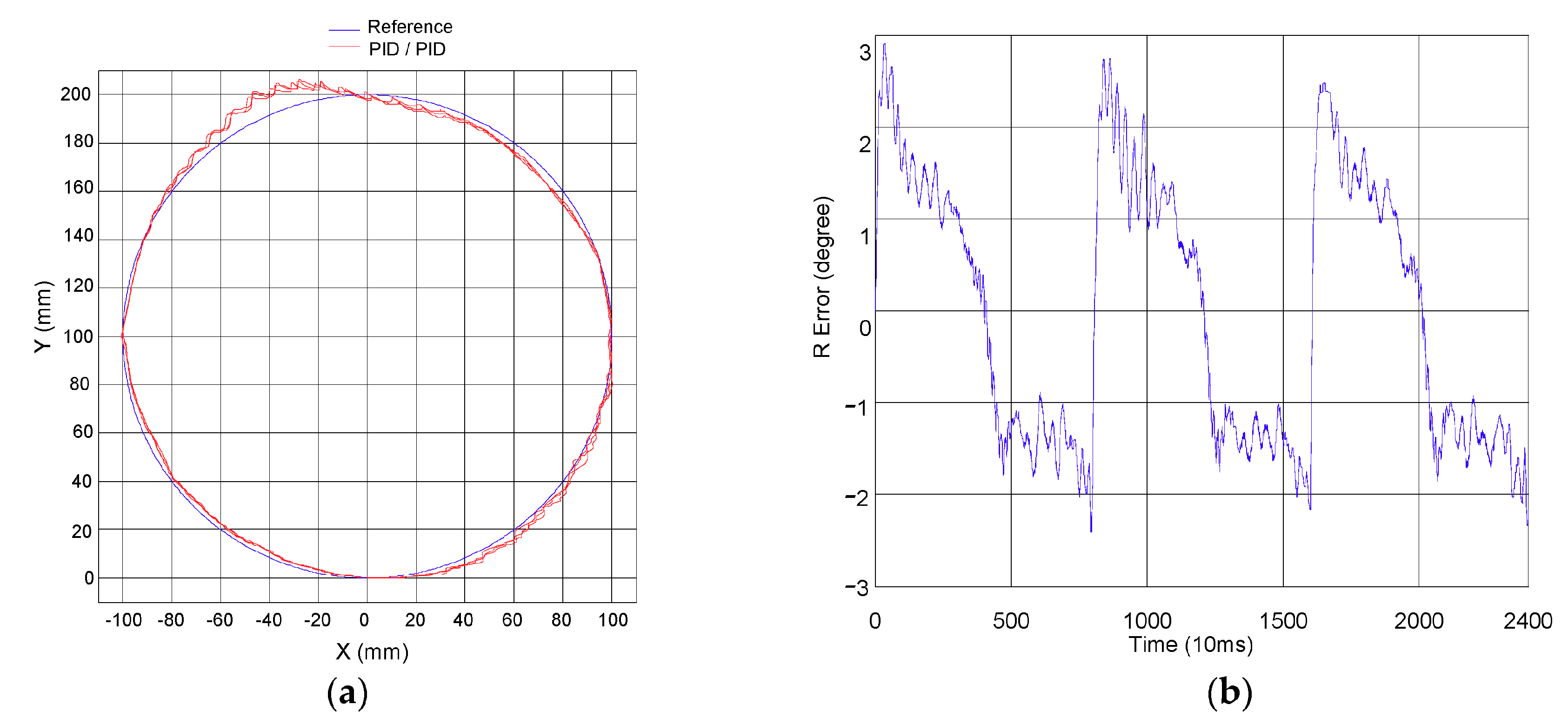
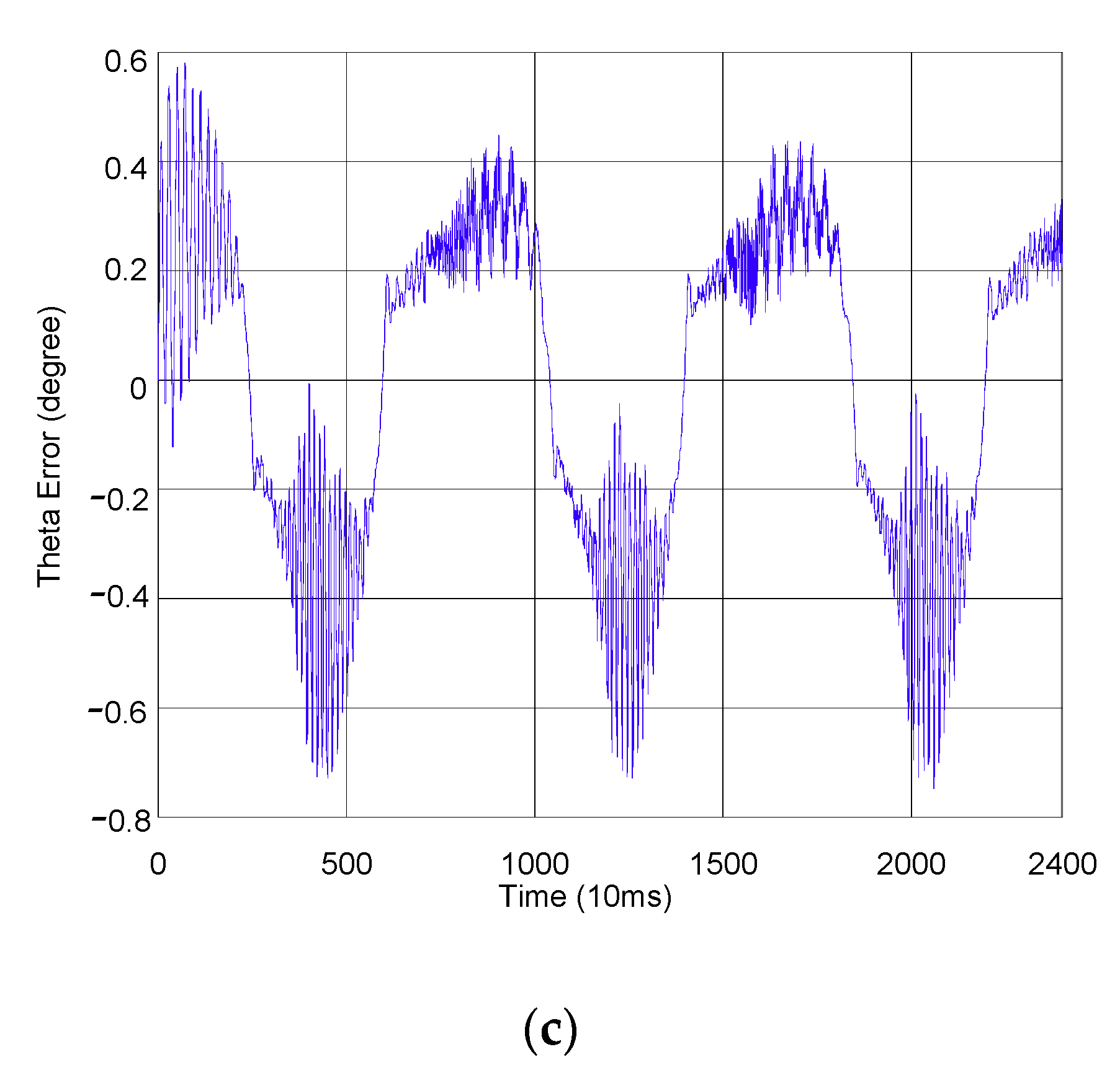
3.2. Circular Trajectory Tracking Based on Robot Arm Control
3.2.1. Outcomes at Zero Load
3.2.2. Outcomes at a Lower Load
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brahmi, B.; Saad, M.; Rahman, M.H.; Ochoa-Luna, C. Cartesian trajectory tracking of a 7-DOF exoskeleton robot based on human inverse kinematics. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 600–611. [Google Scholar] [CrossRef]
- Kubota, S.; Abe, T.; Kadone, H.; Fujii, K.; Shimizu, Y.; Marushima, A.; Ueno, T.; Kawamoto, H.; Hada, Y.; Matsumura, A.; et al. Walking ability following hybrid assistive limb treatment for a patient with chronic myelopathy after surgery for cervical ossification of the posterior longitudinal ligament. J. Spinal Cord Med. 2019, 42, 128–136. [Google Scholar] [CrossRef] [PubMed]
- Kwakkel, G.; Kollen, B.J.; Krebs, H.I. Effects of robot-assisted therapy on upper limb recovery after stroke: A systematic review. Neurorehabil. Neural Repair 2008, 22, 111–121. [Google Scholar] [CrossRef]
- Riener, R.; Nef, T.; Colombo, G. Robot-aided neurorehabilitation of the upper extremities. Med. Biol. Eng. Comput. 2005, 43, 2–10. [Google Scholar] [CrossRef] [PubMed]
- Veerbeek, J.M.; van Wegen, E.; van Peppen, R.; van der Wees, P.J.; Hendriks, E.; Rietberg, M.; Kwakkel, G. What is the evidence for physical therapy poststroke? A systematic review and meta-analysis. PLoS ONE 2014, 9, e87987. [Google Scholar] [CrossRef] [PubMed]
- Pollock, A.; Farmer, S.E.; Brady, M.C.; Langhorne, P.; Mead, G.E.; Mehrholz, J.; van Wijck, F. Interventions for improving upper limb function after stroke. Cochrane Database Syst. Rev. 2014, CD010820. [Google Scholar] [CrossRef] [PubMed]
- Daerden, F.; Lefeber, D.; Verrelst, B.; Van Ham, R. Pleated pneumatic artificial muscles: Actuators for automation and robotics. In Proceedings of the 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Como, Italy, 8–12 July 2001; pp. 738–743. [Google Scholar]
- Chou, C.P.; Hannaford, B. Measurement and modeling of McKibben pneumatic artificial muscles. IEEE Trans. Robot. Autom. 1996, 12, 90–102. [Google Scholar] [CrossRef]
- Huang, J.; Cao, Y.; Xiong, C.H.; Zhang, H.T. An echo state gaussian process-based nonlinear model predictive control for pneumatic muscle actuators. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1071–1084. [Google Scholar] [CrossRef]
- Xie, S.-L.; Liu, H.-T.; Mei, J.-P.; Gu, G.-Y. Modeling and compensation of asymmetric hysteresis for pneumatic artificial muscles with a modified generalized Prandtl–Ishlinskii model. Mechatronics 2018, 52, 49–57. [Google Scholar] [CrossRef]
- Yang, H.; Chen, Y.; Sun, Y.; Hao, L. A novel Kriging-median inverse compensator for modeling and compensating asymmetric hysteresis of pneumatic artificial muscle. Smart Mater. Struct. 2018, 27, 115019. [Google Scholar] [CrossRef]
- Cveticanin, L.; Zukovic, M.; Biro, I.; Sarosi, J. Mathematical investigation of the stability condition and steady state position of a pneumatic artificial muscle-Mass system. Mech. Mach. Theory 2018, 125, 196–206. [Google Scholar] [CrossRef]
- Kalita, B.; Dwivedy, S.K. Nonlinear dynamics of a parametrically excited pneumatic artificial muscle (PAM) actuator with simultaneous resonance condition. Mech. Mach. Theory 2019, 135, 281–297. [Google Scholar] [CrossRef]
- Chen, Y.L.; Zhang, J.H.; Gong, Y.J. Novel design and modeling of a soft pneumatic actuator based on antagonism mechanism. Actuators 2020, 9, 107. [Google Scholar] [CrossRef]
- Martens, M.; Boblan, I. Modeling the static force of a festo pneumatic muscle actuator: A new approach and a comparison to existing models. Actuators 2017, 6, 33. [Google Scholar] [CrossRef]
- Anh, H.P.H.; Son, N.N.; Kien, C.V. Adaptive neural compliant force-position control of serial PAM robot. J. Intell. Robot. Syst. 2018, 89, 351–369. [Google Scholar] [CrossRef]
- Anh, H.P.H.; Kien, C.V.; Son, N.N.; Nam, N.T. New approach of sliding mode control for nonlinear uncertain pneumatic artificial muscle manipulator enhanced with adaptive fuzzy estimator. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418773204. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Trinh, V.C.; Le, T.D. An adaptive fast terminal sliding mode controller of exercise-assisted robotic arm for elbow joint rehabilitation featuring pneumatic artificial muscle actuator. Actuators 2020, 9, 118. [Google Scholar] [CrossRef]
- Minh, T.V.; Tjahjowidodo, T.; Ramon, H.; Van Brussel, H. Cascade position control of a single pneumatic artificial muscle-mass system with hysteresis compensation. Mechatronics 2010, 20, 402–414. [Google Scholar] [CrossRef]
- Luk’yanov, A.; Dodds, S.; Vittek, J. Observer-based attitude control in the sliding mode. Trans. Built Environ. 1970, 22. [Google Scholar] [CrossRef]
- Sárosi, J.; Gyeviki, J.; Véha, A.; Toman, P. Accurate position control of PAM actuator in Lab VIEW environment. In Proceedings of the 2009 7th International Symposium on Intelligent Systems and Informatics, Subotica, Serbia, 25–26 September 2009; pp. 301–305. [Google Scholar]
- Shen, X.R. Nonlinear model-based control of pneumatic artificial muscle servo systems. Control Eng. Pract. 2010, 18, 311–317. [Google Scholar] [CrossRef]
- Furat, M.; Eker, I. Second-order integral sliding-mode control with experimental application. ISA Trans. 2014, 53, 1661–1669. [Google Scholar] [CrossRef] [PubMed]


| Item | Type | Specifications |
|---|---|---|
| Proportional flow control servo valve | Developed by Festo (MPYE-5-M5-010-B) | Standard nominal flow rate (L/min): 100 Product weight (g): 290 (not containing connectors) |
| PRV | Developed by Festo (VPPM-6L-L-1-G18-0L10H-V1N) | Pressure range: 0 to 10 bar Input voltage range: 0 to 10 V Feedback voltage by pressure range: 0 to 10 V |
| PAM cylinder | Developed by Festo (MAS-20-300N-AA-MC-O-ER-BG) | The structure includes a contractile system and a connector of two ends, where the inside of the contractile system is a hose, and the outside is covered by a fabric mesh with high intensity. |
| Power sensor | Developed by VPG load cell | A correspondent voltage generated by deformation due to the extension of the load cell can be obtained, where the force measure range is from 0 to 100 kg, and the feedback voltage signal is from 0 to 10 V. |
| Pressure sensor | Developed by Festo (SPAB-P10R-G18-NB-K1) | Pressure measure range: 0 to 10 bar Feedback voltage signal: 1 to 5 V |
| Optical encoder | Developed by QPhase (TSD-HB-8-1000A-H) | Can be utilized for the analysis of frequency quadruple, where the resolution of one cycle is 8000 Hz. |
| Laser rangefinder | Developed by Keyence Type of IL-300 | Measure distance: 300 mm Measure range: 160 to 450 mm Precision of measure repeatability: 30 µm Output voltage range: 0 to 5 V |
| θ | d | a | α |
|---|---|---|---|
| 0 | 0 | 90° | |
| 0 | 0° | ||
| 0 | 0° |
| Parameter | Units | Value | Range |
|---|---|---|---|
| 101.3 | – | ||
| 707 | – | ||
| γ | – | 1.4 | – |
| R | 0.287 | – | |
| T | 293 | – | |
| – | 0–30,000 | ||
| – | 200,000–400,000 | ||
| B | – | 0–10,000 | |
| Gain | – | – | 0.8–1.2 |
| – | 250–255 | ||
| D | – | 20–40 | |
| b | – | 250–441.673 | |
| – | – | 0–1 | |
| – | – | 0.143–1 |
| Gene | Range | Optimum Parameter |
|---|---|---|
| 0 to 30,000 | 15,960.7 | |
| 200,000 to 400,000 | 267,077 | |
| B | 0 to 10,000 | 7042.55 |
| 250 to 255 | 252.446 | |
| D | 20 to 40 | 35.406 |
| b | 250 to 441.673 | 385.02 |
| 0 to 1 | 0.0889213 | |
| 0.14268 to 1 | 0.538054 | |
| 0.8 to 1.2 | 0.988137 |
| Parameter | Range | Optimum Parameter |
|---|---|---|
| Λ | 0 to 100 | 17.6953 |
| G | 0 to 10,000 | 384.302 |
| 0 to 10,000 | 776.93 |
| Sampling Time | Max Error (Degree) | RMSE (Degree) |
|---|---|---|
| 20 ms | 2.089 | 0.51468 |
| 10 ms | 0.402 | 0.12895 |
| Controller | Controller Parameters |
|---|---|
| HOSMC | , , |
| PID | , , |
| Controller | State | Max Error (Degree) | RMSE (Degree) |
|---|---|---|---|
| HOSMC | Short | 0.448 | 0.11126 |
| Long | 0.381 | 0.090299 | |
| PID | Short | 0.523 | 0.25232 |
| Long | 0.706 | 0.289 |
| Controller | Controller Parameters |
|---|---|
| HOSMC | , , |
| 2-SMC | , , , |
| TSMC | , , , , , |
| PID | , , |
| Controller | Part | Max Error | RMSE |
|---|---|---|---|
| PID/HOSMC | (degree) | 0.524 | 0.14781 |
| Contour (mm) | 10.2528 | 3.6808 | |
| PID/PID | (degree) | 0.768 | 0.30876 |
| Contour (mm) | 10.0909 | 2.9096 |
| Controller | Part | Max Error | RMSE |
|---|---|---|---|
| PID/HOSMC | (degree) | 0.524 | 0.14781 |
| Contour (mm) | 10.2528 | 3.6808 | |
| PID/PID | (degree) | 0.768 | 0.30876 |
| Contour (mm) | 10.0909 | 2.9096 |
| Controller | Max Error (Degree) | RMSE (Degree) |
|---|---|---|
| HOSMC | 0.399 | 0.10167 |
| PID | 4.086 | 1.6673 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-J.; Sie, T.-Y.; Chu, W.-L.; Yau, H.-T.; Ding, C.-H. Tracking Control of Pneumatic Artificial Muscle-Activated Robot Arm Based on Sliding-Mode Control. Actuators 2021, 10, 66. https://doi.org/10.3390/act10030066
Lin C-J, Sie T-Y, Chu W-L, Yau H-T, Ding C-H. Tracking Control of Pneumatic Artificial Muscle-Activated Robot Arm Based on Sliding-Mode Control. Actuators. 2021; 10(3):66. https://doi.org/10.3390/act10030066
Chicago/Turabian StyleLin, Chih-Jer, Ting-Yi Sie, Wen-Lin Chu, Her-Terng Yau, and Chih-Hao Ding. 2021. "Tracking Control of Pneumatic Artificial Muscle-Activated Robot Arm Based on Sliding-Mode Control" Actuators 10, no. 3: 66. https://doi.org/10.3390/act10030066
APA StyleLin, C.-J., Sie, T.-Y., Chu, W.-L., Yau, H.-T., & Ding, C.-H. (2021). Tracking Control of Pneumatic Artificial Muscle-Activated Robot Arm Based on Sliding-Mode Control. Actuators, 10(3), 66. https://doi.org/10.3390/act10030066







