High Precision Motion Control of Electro-Mechanical Launching Platform with Modeling Uncertainties: A New Integrated Error Constraint Asymptotic Design
Abstract
:1. Introduction
2. System Mathematic Models
3. Design of Motion Controller
3.1. Model Transformation
- (1)
- The uncertain parameters satisfywhere θmin = [θ1min, θ2min, θ3min, θ4min, θ5min, θ6min]T and θmax = [θ1max, θ2max, θ3max, θ4max, θ5max, θ6max]T, ϑmax and ϑmin are known constant bounds of ϑ.
- (2)
- The un-periodic disturbance satisfies , where δ denotes unknown constant.
3.2. Final Controller Derivation
3.3. Main Results
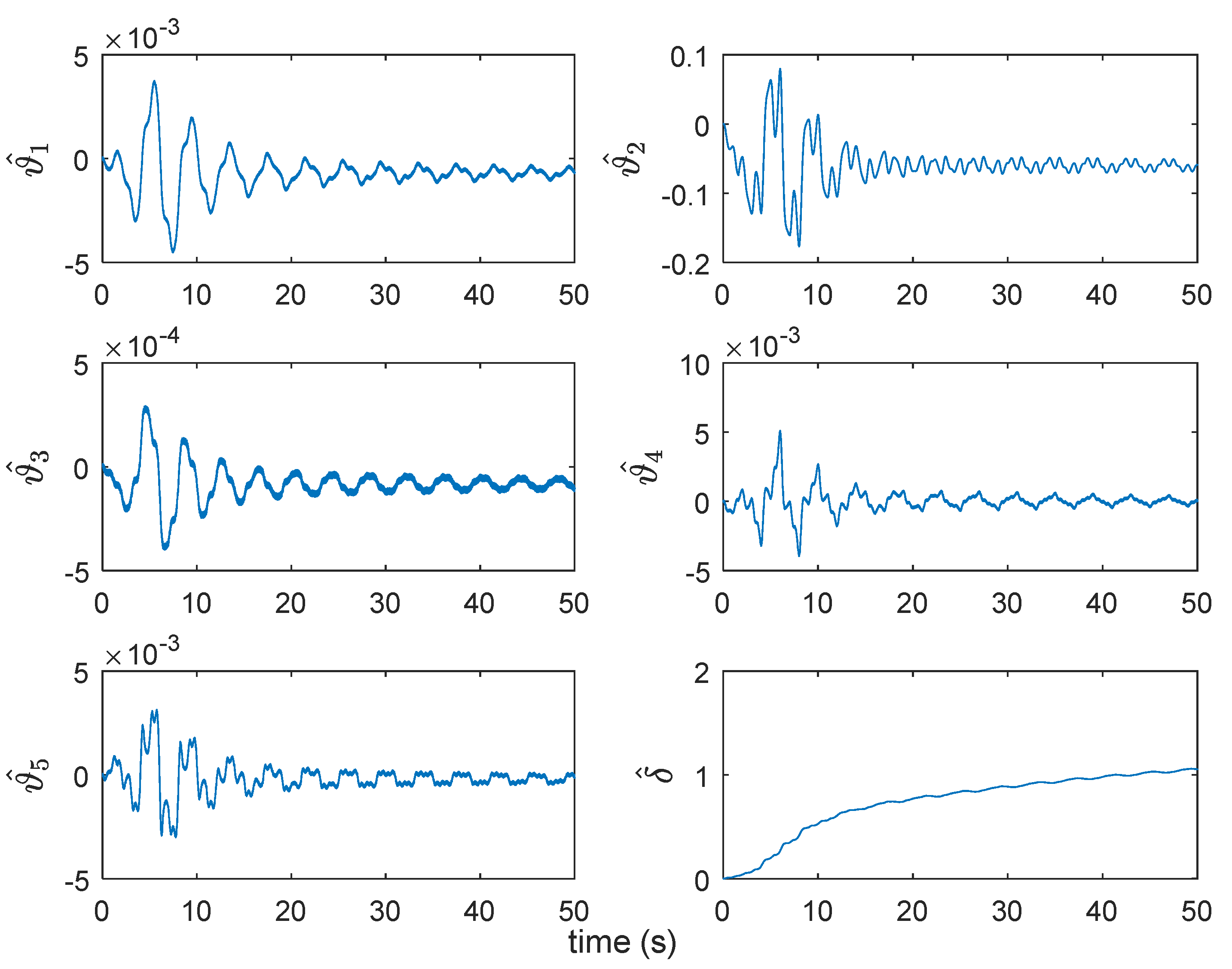
4. Comparative Experimental Verification
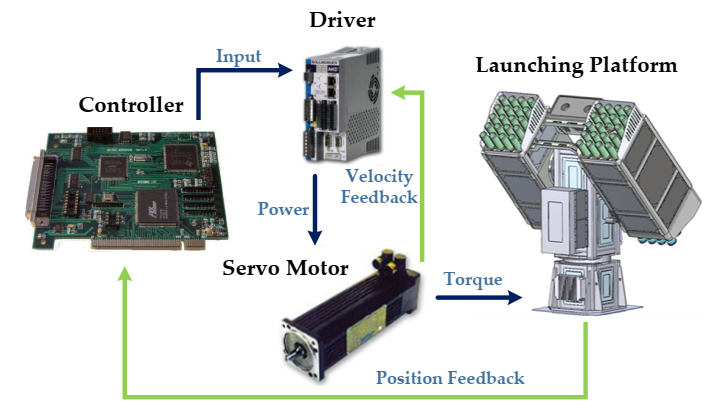
4.1. Experimental Platform
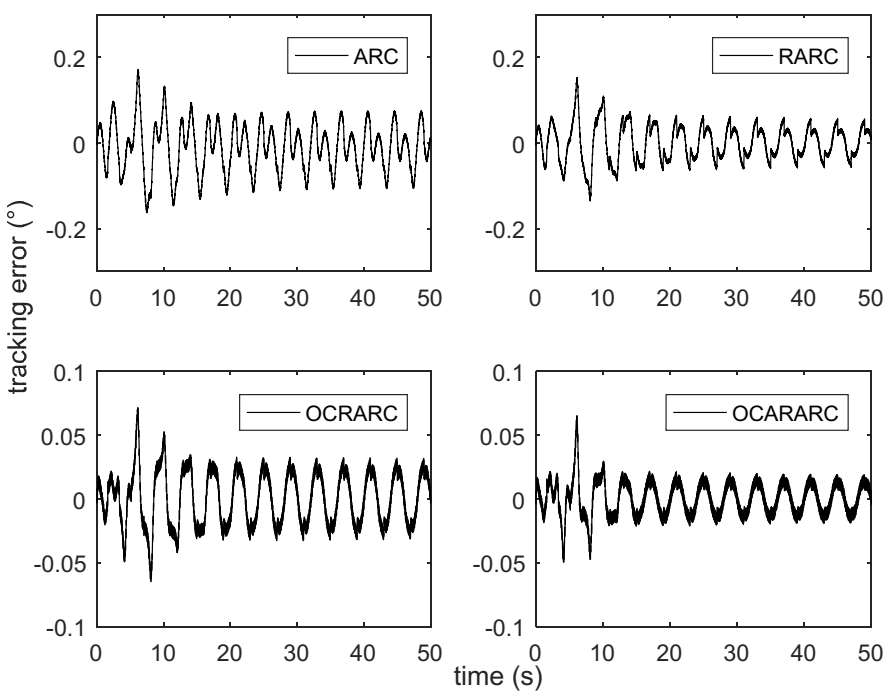
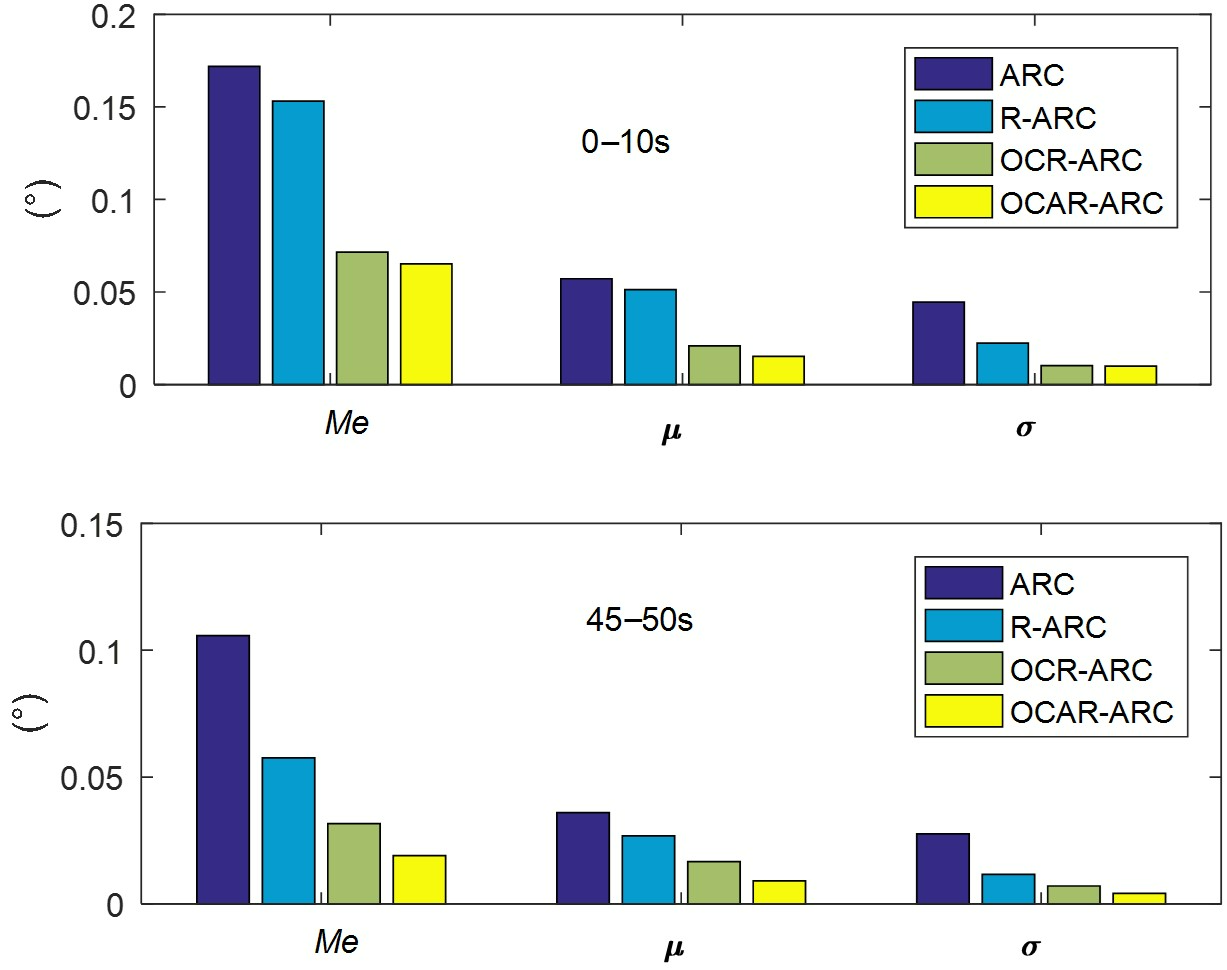
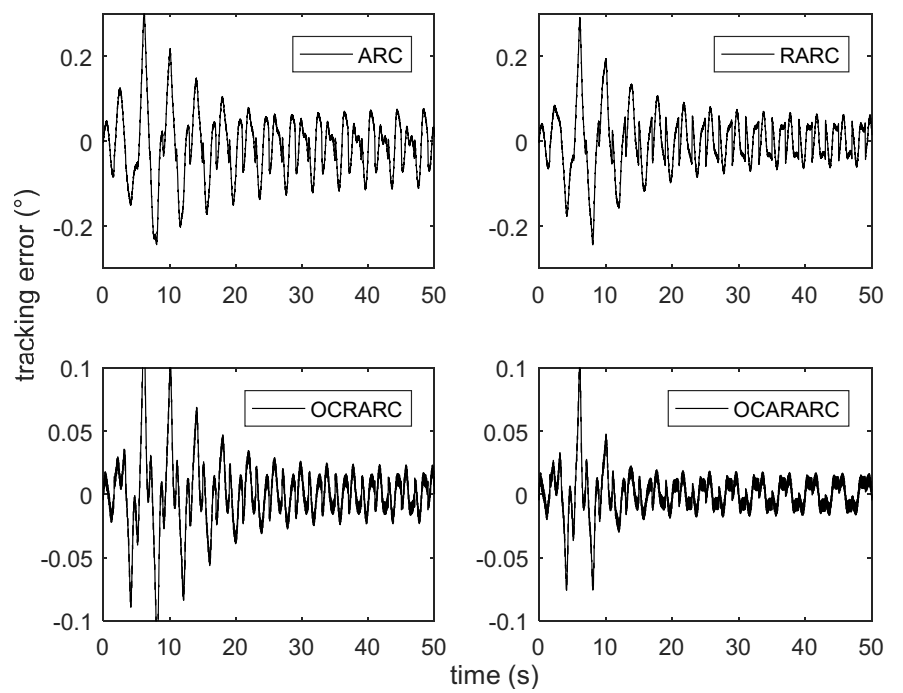
4.2. Comparative Verification Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Li, Y.; Yan, Y.; Cai, L. Study of electro-optical measuring system for measuring the swaying of rocket launcher and artillery systems. Def. Technol. 2008, 4, 247–249. [Google Scholar]
- Hu, J.; Qiu, Y.; Liu, L. High-order sliding-mode observer based output feedback adaptive robust control of a launching platform with backstepping. Int. J. Control 2016, 89, 2029–2039. [Google Scholar] [CrossRef]
- Hu, J.; Liu, L.; Wang, Y.; Xie, Z. Precision motion control of a small launching platform with disturbance compensation using neural networks. Int. J. Adapt. Control Signal Process. 2017, 31, 971–984. [Google Scholar] [CrossRef]
- Chiasson, J. A new approach to dynamic feedback linearization control of an induction motor. IEEE Trans. Autom. Control 1998, 43, 391–397. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T.; Dybkowski, M. Indirect adaptive control of induction motor drive system w an elastic coupling. IEEE Trans. Ind. Electron. 2009, 56, 4038–4042. [Google Scholar] [CrossRef]
- Underwood, S.; Husain, I. Online parameter estimation and adaptive control of permanent-magnet synchronous machines. IEEE Trans. Ind. Electron. 2010, 57, 4038–4042. [Google Scholar] [CrossRef]
- Yao, B.; Xu, L. Adaptive robust precision motion control of linear motors with negligible electrical dynamics: Theory and experiments. IEEE-ASME Trans. Mechatron. 2001, 6, 444–452. [Google Scholar]
- Dong, Z.; Ma, D.; Liu, Q.; Yue, X. Motion control of valve-controlled hydraulic actuators with input saturation and modelling uncertainties. Adv. Mech. Eng. 2018, 10, 1687814018812273. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, H.; Lu, W. Chattering-suppressed sliding mode control for flexible-joint robot manipulators. Actuators 2021, 10, 288. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, L.; Zhang, C.; Wang, C.; Xiao, K. Prescribed performance control with sliding-mode dynamic surface for a glue pump motor based on extended state observers. Actuators 2021, 10, 282. [Google Scholar] [CrossRef]
- Chen, M.; Ge, S.; How, B. Robust adaptive neural network control for a class of uncertain MIMO nonlinear systems with input nonlinearities. IEEE Trans. Neural Netw. 2010, 21, 796–812. [Google Scholar] [CrossRef]
- Yao, Z.; Yao, J.; Sun, W. Adaptive RISE control of hydraulic systems with multilayer neural-networks. IEEE Trans. Ind. Electron. 2019, 66, 8638–8647. [Google Scholar] [CrossRef]
- Xian, B.; Dawson, D.M.; de Queiroz, M.S.; Chen, J. A continuous asymptotic tracking control strategy for uncertain nonlinear systems. IEEE Trans. Autom. Control 2004, 49, 1206–1211. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D. RISE-based precision motion control of DC motors with continuous friction compensation. IEEE Trans. Ind. Electron. 2014, 61, 7067–7075. [Google Scholar] [CrossRef]
- Wang, Y.; Xiong, Z.; Ding, H. Robust controller based on friction compensation and disturbance observer for a motion platform driven by a linear motor. Proc. Inst. Mech. Eng. Part I-J Syst Control Eng. 2006, 220, 33–39. [Google Scholar] [CrossRef]
- Deng, W.; Yao, J. Extended-state-observer-based adaptive control of electrohydraulic servomechanisms without velocity measurement. IEEE-ASME Trans. Mechatron. 2020, 25, 1151–1161. [Google Scholar] [CrossRef]
- Xu, L.; Yao, B. Adaptive robust repetitive control of a class of nonlinear systems in normal form with applications to motion control of linear motors. In Proceedings of the 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Como, Italy, 8–12 July 2001. [Google Scholar]
- Yao, J.; Jiao, Z.; Ma, D. A practical nonlinear adaptive control of hydraulic servomechanisms with periodic-like disturbances. IEEE-ASME Trans. Mechatron. 2015, 20, 2752–2760. [Google Scholar] [CrossRef]
- Dong, Z.; Ma, J.; Yao, J. Barrier function-based asymptotic tracking control of uncertain nonlinear systems with multiple states constraints. IEEE Access 2020, 8, 14917–14927. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, S.; Zhang, B. Asymptotic tracking control of uncertain nonlinear systems with unknown actuator nonlinearity. IEEE Trans. Autom. Control 2014, 59, 1336–1341. [Google Scholar] [CrossRef]
- Bechlioulis, C.; Rovithakis, G. Robust Adaptive Control of Feedback Linearizable MIMO Nonlinear Systems with Prescribed Performance. IEEE Trans. Autom. Control 2008, 53, 1336–1341. [Google Scholar] [CrossRef]
- Tee, K.; Ge, T. Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica 2009, 45, 918–927. [Google Scholar] [CrossRef]
- Makkar, C.; Dixon, W.; Sawyer, W.; Hu, G. A new continuously differentiable friction model for control systems design. In Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005. [Google Scholar]
- Borello, L.; Dalla Vedova, M.D.L. Dry friction discontinuous computational algorithms. Int. J. Eng. Innovative Technol. 2014, 3, 1–8. [Google Scholar]
- Dong, Z.; Yao, J.; Ma, D. Asymptotic tracking control of motor servo system with input constraint. Acta Armamentarii 2015, 36, 1405–1410. [Google Scholar]
- Khalil, H. Nonlinear Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Yang, Y.; Li, G.; Zhang, Z. High Precision Motion Control of Electro-Mechanical Launching Platform with Modeling Uncertainties: A New Integrated Error Constraint Asymptotic Design. Actuators 2021, 10, 331. https://doi.org/10.3390/act10120331
Dong Z, Yang Y, Li G, Zhang Z. High Precision Motion Control of Electro-Mechanical Launching Platform with Modeling Uncertainties: A New Integrated Error Constraint Asymptotic Design. Actuators. 2021; 10(12):331. https://doi.org/10.3390/act10120331
Chicago/Turabian StyleDong, Zhenle, Yinghao Yang, Geqiang Li, and Zheng Zhang. 2021. "High Precision Motion Control of Electro-Mechanical Launching Platform with Modeling Uncertainties: A New Integrated Error Constraint Asymptotic Design" Actuators 10, no. 12: 331. https://doi.org/10.3390/act10120331
APA StyleDong, Z., Yang, Y., Li, G., & Zhang, Z. (2021). High Precision Motion Control of Electro-Mechanical Launching Platform with Modeling Uncertainties: A New Integrated Error Constraint Asymptotic Design. Actuators, 10(12), 331. https://doi.org/10.3390/act10120331





