Multiparameter Optimization Framework of Cyberphysical Systems: A Case Study on Energy Saving of the Automotive Engine

Abstract

Multiparameter optimization of complex electromechanical systems in a physical space is a challenging task. CPS (Cyberphysical system) technology can speed up the solution of the problem based on data interaction and collaborative optimization of physical space and cyberspace. This paper proposed a general multiparameter optimization framework by combining physical process simulation and clustering genetic algorithm for the CPS application. The utility of this approach is demonstrated in the instance of automobile engine energy-saving in this paper. A 1.8-L turbocharged GDI (gasoline direct injection) engine model was established and calibrated according to the test data and physical entity. A joint simulation program combining CGA (Clustering Genetic Algorithm) with the GDI engine simulation model was set up for the engine multiparameter optimization and performance prediction in cyberspace; then, the influential mechanism of multiple factors on engine energy-saving optimization was analyzed at 2000 RPM (Revolutions Per Minute) working condition. A multiparameter optimization with clustering genetic algorithm was introduced for multiparameter optimization among physical and digital data. The trade-off between fuel efficiency, dynamic performance, and knock risk was discussed. The results demonstrated the effectiveness of the proposed method and that it can contribute to develop a novel automotive engine control strategy in the future.

1. Introduction

The CPS (Cyberphysical system) is a multidimensional complex system integrating computation, communication, control, and physical elements that has become a cutting-edge technology for the next generation of industrial applications [1]. It has become a research hotspot in recent years for its explosive growth in the potential of numerous application areas including agriculture, energy, healthcare, manufacturing transportation, and smart environment. Plakhotnikov et al. applied the CPS to an automobile gas-filling compressor station to improve their work and take advantage of all the capabilities of cyberphysical systems [2]. Guo et al. proposed a systematic assessment of cyberphysical security on the energy management system for connected and automated electric vehicles [3]. How to integrate the information of physical space and cyberspace to achieve an overall objective optimization is important to the CPS applications in the future. The CPS theory and technology can improve complex systems’ operation performance such as adaptability, autonomy, efficiency, functionality, reliability, and safety. For the automotive industry, ICV (Intelligent and Connected Vehicle) has become an important development trend. ICV is equipped with advanced on-board sensors, controllers, actuators, and other devices. Integrating modern communication and network technologies can realize intelligent information exchange among passengers, vehicles, and roads. ICV has provided an important platform for the application of CPS. Existing research has shown that the concept of vehicular CPS has been circulating for some time but the studies of vehicular CPS still need further refinement at the subsystems and components level. As early as 2010, Wang et al. made a conclusion that CPS will be the key to any successful construction and deployment of AI (Artificial Intelligence)-based intelligent systems [4] and they have taken almost 5 years to establish the parallel driving theory of intelligent cars based on CPS [5]. In 2010, Fallah introduced the CPS named the cooperative vehicle safety system, coupling the computing and communications aspects of the vehicular system with its physical dynamics [6]. Wan et al. first proposed a multilayered context-aware architecture based on CPS leading to an increasing evolutionary tendency in vehicular social network developments [7]. With the development of V2X technology, the road traffic environment has gradually become a larger cyberphysical world. Some new technologies based on vehicular CPS also obtain the innovation breakthrough accordingly [8]. The above CPS theoretical application research was aimed at the whole vehicle and even more macroscopic dimensions of the intervehicle communication network. Referring to CPS theory, the vehicle or its subsystems can also be essentially described as a complex CPS system that uses digital and physical hybrid data for design, production, operation, and maintenance. Some researchers have realized that CPS can be used to guide more studies in-depth at the automotive subsystem level. For example, a CPS-based framework was proposed for co-design-optimization of the physical plant parameters and controller variables for an electric powertrain [9,10]. However, the automobile structure composed of thousands of parts obtains a large number of complex data from physical space and information space, which brings many challenges to the application of CPS. At present, CPS in the automotive field has not been refined at the subsystem level, and often works in combination with the whole vehicle and transportation system. This paper took the automobile engine as a research object and attempted to provide a general CPS framework to solve its problems, such as fuel efficiency, dynamic performance, and knock risk.

The paper is structured as follows: (1) The related works are introduced in Section 2. The technical route of engine energy saving and the difficulty of multiparameter optimization is discussed based on the related works. The significance of using multiparameter optimization method based on CPS theory in the engine energy-saving field is described briefly. (2) The multiparameter optimization framework of cyberphysical systems is expounded in Section 3. Referring to gasoline engine multiparameter optimization, we propose an improved clustering genetic algorithm for multiparameter optimization among physical and digital data. (3) The systematic optimization of full loads at an engine speed of 2000 rpm is selected as a validation case and the results are discussed in Section 4. At last, the conclusions are drawn in Section 5.

2. Related Works

Recently, air pollution reduction, energy conservation, and climate change mitigation have been issues of global concern. More strict fuel consumption and emission control policies will be enforced to internal combustion engine vehicles [11]. The CAFC (Corporate Average Fuel Consumption) was limited to 5 L/100 km in 2020 and will be even lower in the future. Turbocharged GDI (Gasoline Direct Injection) engines have become increasingly popular in the used engines markets recently [12,13]. However, the compression ratios of the turbocharged GDI engines are smaller than those of naturally aspirated engines, which are penalized by knock risks [14]. Increasing the compression ratio of gasoline engines has been considered as a way to obtain high combustion efficiency in the future. EGR (Exhaust Gas Recirculation) is a promoting way not only for suppressing engine knock but also for high efficiency and clean combustion. The potential has been shown in the latest study of energy conservation and emission reduction with EGR in gasoline engines. For example, the EGR-diluted clean combustion technology, named HEDGE (High Efficiency Dilute Gasoline Engine), has been under continuous research for 10 years so far. The long-term project indicates that high EGR rate has great potential to increase fuel efficiency and reduce emissions of spark ignition engines [15,16]. In China, Gong et al. presented the experimental results of a GDI engine that showed the positive effects of EGR on combustion and emission characteristics at low load and with different spark timings [17]. Shen et al. conducted an experimental investigation for comparing low- and high-pressure exhaust gas recirculation fixed on a turbocharged GDI engine and their impacts on fuel consumption, the combustion process, and pollutant emissions [18]. EGR reduces the combustion rate, which makes stable combustion more difficult to achieve. Moreover, with the fast development of EGR technology, EGR systems have been widely used in gasoline engines, such as hot EGR and cold EGR, high-pressure loop EGR, and low-pressure loop EGR; these EGR systems are commonly used by combining other technologies, leading to more complicated issues and challenges for academic studies [19]. Besides, EGR has potential for fuel consumption improvements of high-expansion-ratio cycle engines. The pumping loss reduced for low-load condition and effective compression ratio increased for high-load condition with the introduction of EGR gas were verified in a Toyota Atkinson engine [20] and Miller engine [21]. However, both EGR and LIVC (Late Intake Valve Closing) application need throttle valve, air fuel ratio, ignition timing, and other parameters matching. It will cost a lot of manpower, material resources, and time if the traditional method is applied to conduct bench testing and calibrate the complex parameters for introducing new engine technology. Developing a multiparameter optimization method based on CPS theory is meaningful for the EGR and LIVC strategy’s widespread application. A new approach for GDI fuel economy improvement with EGR dilution and LIVC strategy was expounded. The effects of EGR and LIVC on high GCR (Geometric compression ratio) GDI engine fuel economy were studied, and a multiparameter optimization with clustering genetic algorithm was introduced for automotive engine multiparameter optimization among physical and digital data.

3. Methodology

The development of CPS is facing great challenges from the theories and technologies of network and physical systems. As the CPS system must be designed and integrated based on existing physical system structures, no general theoretical framework has been proposed, especially for the joint optimization of virtual and real interaction data in multicomponent systems [22,23]. We attempt to propose a general CPS optimization framework based on the complementarity of physical space and cyber space in Section 3.1. Then, multiparameter optimization algorithm based on the framework for energy-saving of the automotive engine is introduced in Section 3.2. The optimization objectives and the algorithm verification combining the digital model and physical test are given in Section 3.3 and Section 3.4, respectively.

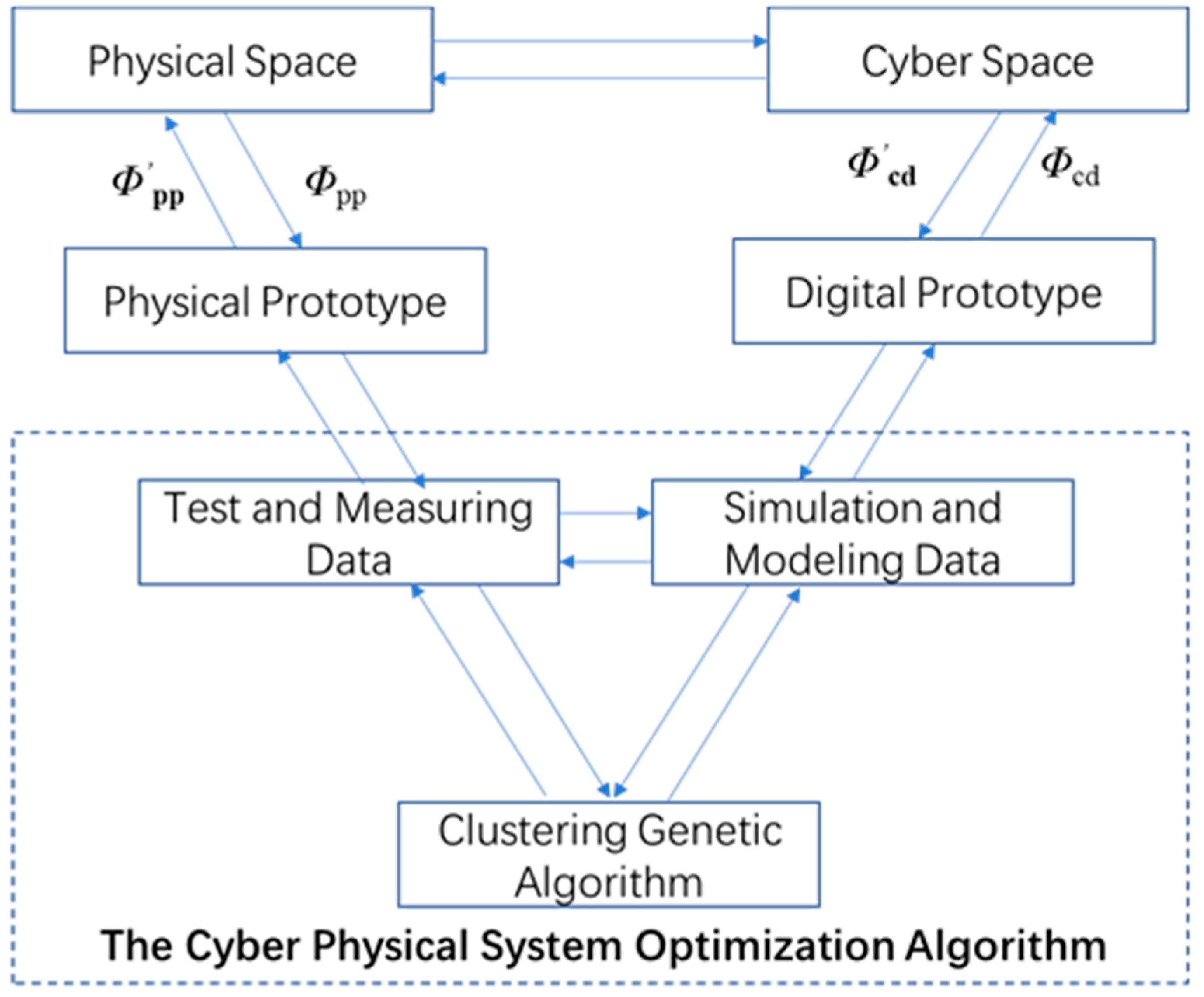
3.1. Framework

A general CPS framework combined with a multiparameter optimization algorithm was established. The data flow chart of the CPS framework is shown in Figure 1.

In this paper, the physical prototype was defined as the study subject and the physical space was defined as the surrounding environments and working conditions of the study object. Digital prototype and cyberspace that exist on a computer and communication network are the mapping and modeling of physical prototype and perceptual information in physical space, respectively. In the process of the interaction between the study object and the surrounding environment, Φ_pp represents the interface information set of the physical space acting on the physical prototype and Φ’_pp represents the interface information set that the physical prototype feeds back to the physical space. Φ_cd and Φ’_cd represent the interactive information sets between digital prototype and cyberspace. The core problem in our work is how to build the bridge between the physical prototype and digital prototype, and how to use the interactive data between them and the cyberphysical space to establish the optimization algorithm and improve the performance of the study object. The problem can be expressed as follows:

$$f\to f\left(A,B,C,D\right),A\subset {\Phi }_{\mathrm{pp}},B\subset {\Phi }_{\mathrm{pp}}^{\prime },C\subset {\Phi }_{\mathrm{cd}},D\subset {\Phi }_{\mathrm{cd}}^{\prime }$$

(1)

As f is a complex function of multidimensional variable spaces, it is necessary to convert it into a series of modeling solutions based on concrete cases. A 1.8-L turbocharged GDI engine was chosen as the study object in the case studied in this paper. The indoor engine bench is selected as the physical space that includes an electrical dynamometer system, fuel consumption measurement system, exhaust analyzer, and ECU of engine, which is combined with ETAS ES690 equipment and a combustion analyzer developed based on NI Compact-RIO system. The subset data of Φ_pp and Φ’_pp were gathered by the above equipment. The cyberspace and digital prototype engines were investigated preliminarily by engine bench test data measuring and 1-D (1-Dimensional) simulation modeling [24]. Then, the subset data of Φ_cd and Φ’_cd were calculated.

In this case study, the function f can be introduced for energy saving. We aim to increase the geometric compression ratio of the former engine from 9.6 to 11 by using the multiparameter optimization framework of CPS. The comprehensive fuel economic improvement strategy was drawn by the BSFC (Brake Specific Fuel Consumption) map data and its control parameters analysis, such as ignition time, throttle percentage, knock detection, and fuel enrichments. In the lower engine load conditions, the throttle percentage was set below 5%, which leads to great pumping loss. The high engine loads under both low and high speeds are detected as the knock-prone areas that have to be prevented by spark retard and fuel enrichment to decrease combustion velocity and temperature. Hence, the fuel consumptions in the knock areas are relatively high. Besides, the fuel enrichment strategy was widely used in the upper-right region of the entire map, where it will lead to high fuel consumption. In the medium speed and load area, the BSFC is relatively low but the BSFC varying gradient is large. The pumping loss and combustion need to be improved for better fuel economy. Based on the above analysis, the strategy to improve fuel economy of the engine can be drawn from the BSFC map, as shown in Figure 2. The methods for improving fuel consumption are reducing pumping loss, fuel enrichment, and knock.

The engine map in Figure 2 is based on the original engine test, and further analyzes the performance improvement direction in combination with the basic theory of the engine. In this paper, we select different loads of 2000 rpm for research, which is the most frequently working speed of the engine. This method can obtain all optimization results, from low load to high load, at one time. It can also be used for reference to other speeds, so similar optimization work is not repeated.

EGR technology and LIVC for low effective compression ratio are two promising ways for detonation suppression instead of fuel enrichment and ignition timing retards. In order to study the combined effects of EGR and LIVC on energy-saving of the automotive engine, the engine was studied as a typical calculation of the function f. The detail of the CPS optimization algorithm will be expounded later.

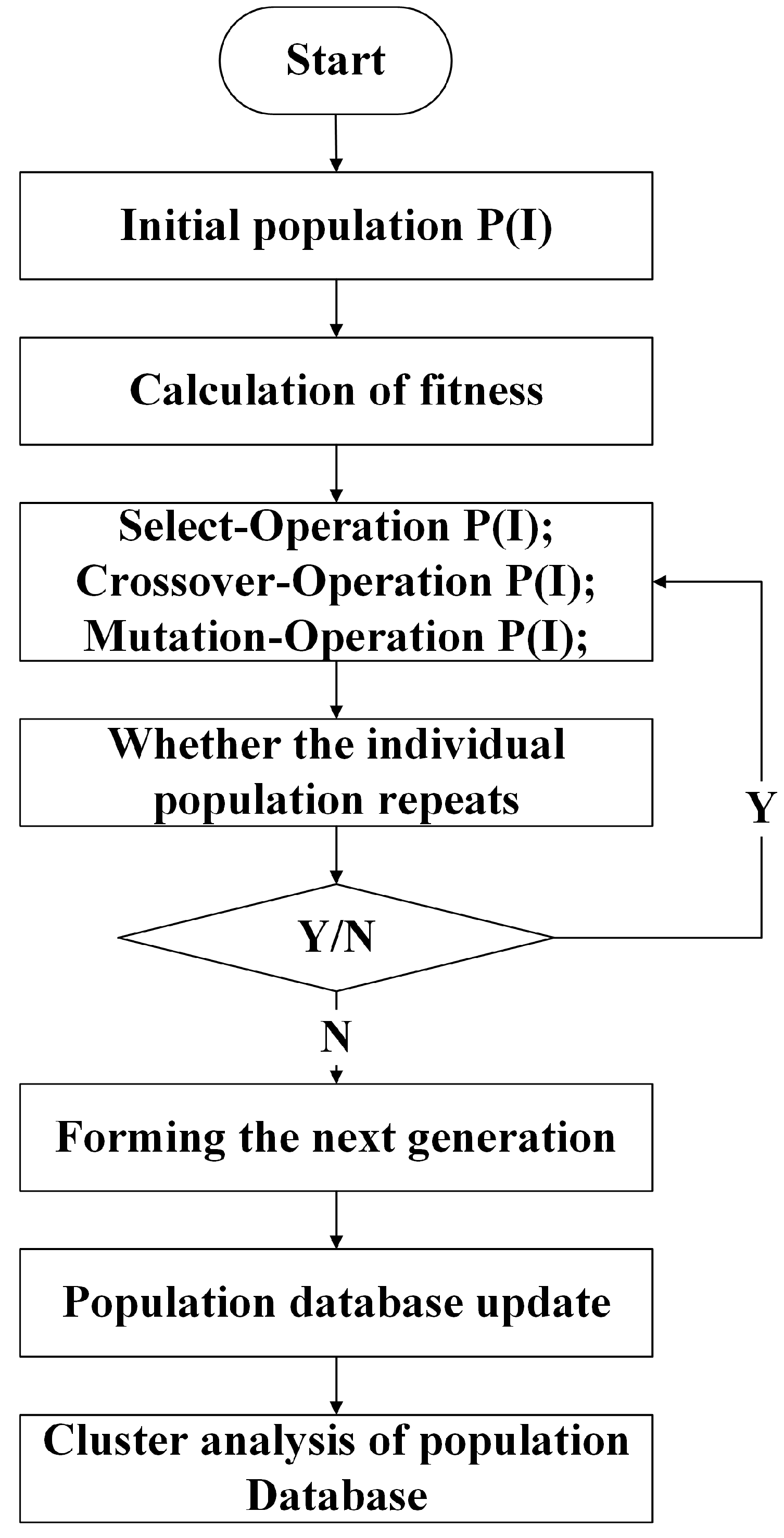
3.2. Optimization Algorithm

Genetic algorithm (GA) is an adaptive global random search optimization algorithm proposed by John Holland of the University of Michigan to simulate the process of natural selection, genetic variation, and population evolution in the biological world. The algorithm puts forward the concepts of population, individual, fitness, and chromosome; classifies and divides the data attributes of the research object; simulates Darwin evolution theory and Mendel genetics theory; and puts forward the basic optimization method of selection crossover mutation [25].

K-means algorithm is a clustering algorithm proposed in the 1950s, which is based on the similarity criterion of the minimum square sum of the distance between sample data points and clustering center points. With the rapid development of big data technology and machine learning technology, the clustering algorithm has become an important algorithm of machine learning and is widely used in the field of data mining and data analysis [26,27,28].

The genetic optimization is a widely used algorithm that applies the basic laws of genetic inheritance of nature’s evolution processes in computer programming and computational calculation. The clustering algorithm is an essential data mining and machine learning method that plays an important role in analyzing big data. In this paper, the clustering algorithm is integrated to analyze the producing data in the process of the genetic optimization. Compared with the traditional genetic algorithms, the CGA (clustering genetic algorithm) can obtain unsupervised classification optimum value for different engine loads. The general process of optimization algorithm is shown in Figure 3.

The idea of the CGA optimization procedure is as follows. There are four chromosomes denoted according to parameters X₁, X₂, X₃, X₄. Together, they constitute the genome of an individual that corresponds to the engine performance of different input parameters. The population is represented as a set of individuals. When initializing a population for CGA starting, 20 individuals are randomly generated, and each of them has different value combinations of chromosomes. Each chromosome is encoded in 8-bit binary. Then, the fitness function f of all the individuals is calculated by the engine model simulation, which is covered in more detail in Section 3.3. The fitness value will be a judgment for the next-generation population evolution. After comparing the effects of the active archive nondominated sorting genetic algorithm adopted by Salata F. [29], we combined the three types of operators named selection operator, crossover operator, and mutation operator with different random sampling rates for new individuals’ evolution. For the execution process of selection operator, the combined method of roulette selection with elite ranking that ensures the selection probability of the excellent individuals and the diversity of population, is used to select the individual for the next generation. In this regard, the individuals are randomly selected as members of the next-generation population and the individuals with bigger fitness function values are more prone to be selected as the member of the next-generation populations. The individuals that do not meet the limits of KI = 0 will be eliminated and do not participate in the formation of the next generation of the population. Secondly, some of the selected individuals will act as the parents and produce new individuals by crossover operator that uses a probability method to select chromosomes for binary bit-swapping. Thirdly, some of the selected individuals will act as the mutants for mutation operator that uses randomizing methods to select chromosomes variation. Then, the new generation population is eventually produced for population evolution. In addition, as the MATLAB and GT-Power cosimulation takes a long time for fitness value calculation, the unique method of MATLAB is used to eliminate the duplicated individuals after mutation, which avoids repetitive calculation and has strong ability to find the global optimization solution. New randomly generated individuals are added to the next-generation populations for the duplicated individuals. The iteration times of population evolution are set in 50 generations. During the iteration, the population base consisting of historical populations is stored, and finally, the global optimization and analysis are carried out by clustering analysis. The k-means clustering algorithm is considered one of the most powerful and popular data mining algorithms [30]. Aiming at the multidimensional data of the population database in this paper, we adopted the k-means clustering algorithm for studying the distribution of population, which aims to learn the influence of different parameters on the optimization goal under different condition grouping at one time.

The comparison between the improved CGA and the traditional genetic algorithm is as follows:

(1)

Traditional genetic algorithm requires a strict fitness function to limit the population range. The precise data label is required to classify the data. CGA has no limitation of strict population range definition.

(2)

Traditional genetic algorithm is an optimization method that only focuses on the final results but lacks the analysis and statistics of data changes in the iterative process. CGA facilitates the independent optimization analysis of the population and explores the iterative rule.

(3)

The fitness function of traditional genetic algorithm often has a significant impact on the optimization results. For example, in the process of energy-saving optimization of EGR, LIVC, ignition advance angle, and other parameters, a multiparameter design will not only affect the fuel consumption but also affect the torque. If the torque is limited to a wide range in the fitness function, it will result in a comparison of BSFC of different loads, which will affect the judgment of the optimal value. However, if the torque is limited to a narrow range in the fitness function, the optimization of the different torques requires repeated genetic algorithm calculations, which increases the amount of calculation. CGA can realize the energy-saving optimization of different loads and improve optimization efficiency in the process of continuous iterative optimization. The optimization objective of CGA is to automatically obtain the lowest BSFC under different loads by optimizing engine control parameters such as LIVC angle, EGR, ignition advance angle, and air–fuel ratio, and avoid engine knocking. If the traditional genetic algorithm is used, the fitness function should consider the torque changes, and the BSFC for different torques has to be optimized for its own genetic algorithm. The CGA optimization costs less time.

3.3. Optimization Objectives

The function f related to the model optimization objective can be changed into the fitness function of genetic algorithm and the constraint conditions of the fitness function according to the study object.

$$f=\min \left[\frac{1}{F\left(X_1,X_2,X_3,X_4\right)}\right]$$

(2)

$$\{\begin{array}{c}{\alpha }_{min}\le X_1\le {\alpha }_{max}\\ r_{min}\le X_2\le r_{max}\\ {\theta }_{min}\le X_3\le {\theta }_{max}\\ {\varphi }_{min}\le X_4\le {\varphi }_{max}\\ KI=0\end{array}$$

(3)

where the function F (X₁, X₂, X₃, X₄) is inversely related to the BSFC of the engine. X₁ is the value of LIVC angle that is among 16–66°ABDC (After Bottom Dead Center) according to the VVT (Variable Valve Timing) technology of the original engine. X₂ is the value of EGR rate r that is among 0–15% supported by LP-EGR (Low-Pressure Exhaust Gas Recirculation) technology; X₃ is the ignition advance angle and its range is −24–4 crank angle ATDC (After Top Dead Centre). X₄ is the air–fuel ratio and its optimization range is 12–15.7. The minimum target of the BSFC is the maximum value of the fitness function. The value of the fitness function F can be calculated by the 1-D simulation engine code modeled in GT-Power that will be introduced later. Besides, another variable named KI is the knock index, which is proposed to characterize knock of gasoline engine. According to the Kinetics-fit detonation model in GT-power, when the engine does not knock, the index KI = 0.

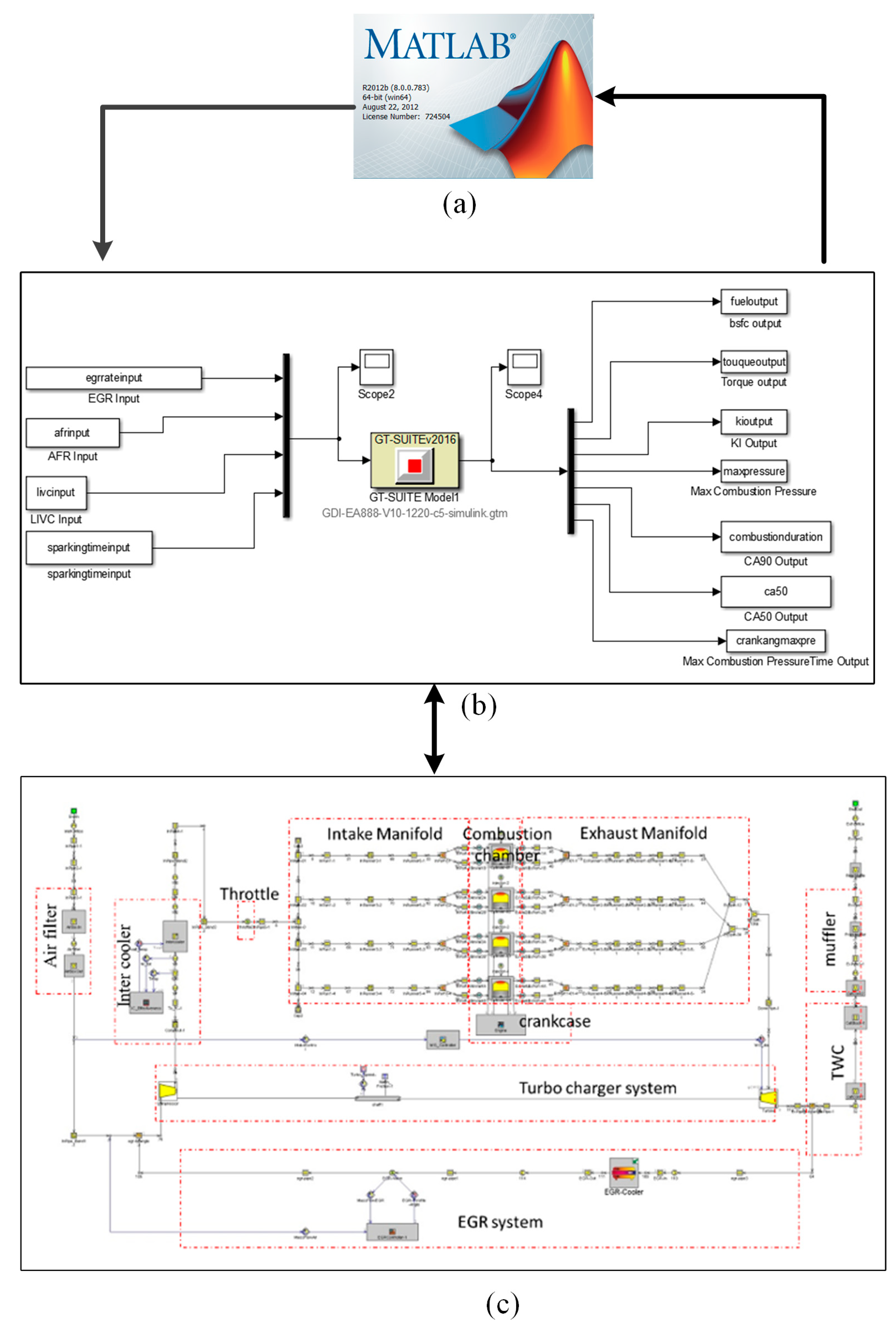
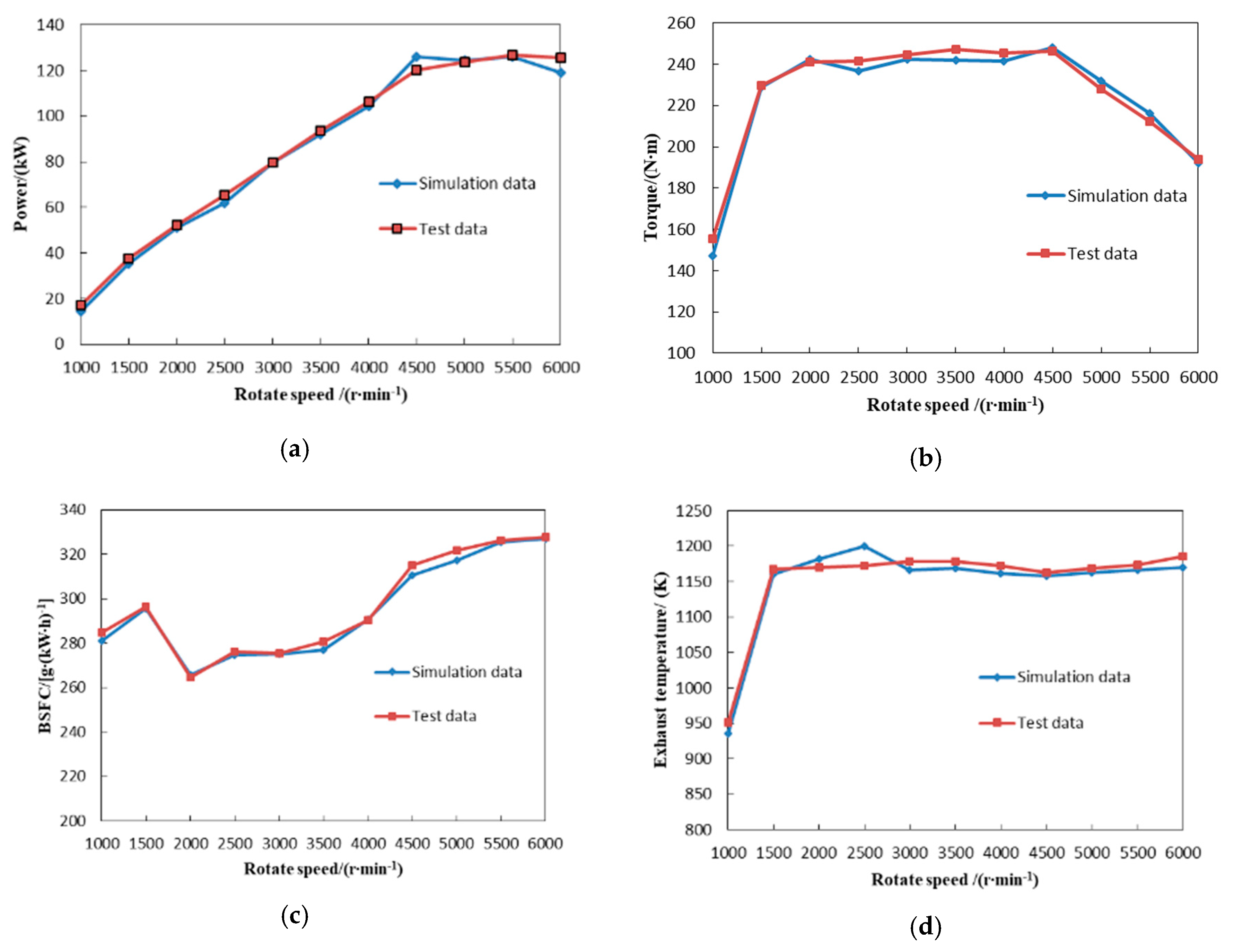
3.4. Digital Model and Physical Test Verification

As shown in Figure 4, the whole architecture of the simulation and optimization model consists of three parts: the CGA programmed in Matlab software, the interface between Simulink software and GT-Power software, and the 1-D simulation model of the engine coding in GT-Power. The model simulation working flow starts with the CGA as the main program, the main program will call the Simulink interface to transfer EGR rate, LIVC angles, air–fuel ratio and ignition advance angle to the 1-D simulation engine model of GT-power for engine performance simulation. The Simulink interface returns the results such as the BSFC and brake torque to the main program for fitness function calculation. Finally, the Matlab program, Simulink interface, and GT-Power software run in a closed cycle as an integrated simulation and optimization model.

The parameters of the engine are shown in

Table 1. Parameters of engine.

Engine Parameters	Value
Displayed volume	1.8 L
Stroke	84.1 mm
Bore	82.5 mm
Connecting Rod	146 mm
Compression ratio	9.6
Power Max. (kW/rpm)	118/5000
Torque Max. (N·m/rpm)	250/2000
Number of valves	4 (2 intake, 2 exhaust)
Injection	GDI
Fuel	Gasoline #96 of Chinese Standard

.

The 1-D simulation engine model mainly includes the air intake system, turbocharge system, throttle valve, intake manifold, combustion chamber, crankcase, exhaust manifold, EGR system, TWC (Three Way Catalysts), exhaust muffler, etc. All of the geometry parameters of the components are measured from the engine, such as the intake and exhaust pipe length and diameter, the piston stroke, the cylinder diameter, and the throttle valve length. The EGR system model was set up according to a real EGR assembly of Borg warner, shown in Figure 5. The EGR rate was controlled by PID (Proportion Integration Differentiation) module in the base of mass-throttle percentage curves.

The other boundary parameters for different engine speeds were set up according to the bench test data that are shown in

Table 2. The boundary parameters for different engine speeds.

Speed/rpm	1000	1500	2000	2500	3000	3500	4000	4500	5000	5500	6000
A/F	15.2	14.5	14.3	14.0	13.4	13.0	12.4	11.9	11.9	11.9	12.1
Atmospheric pressure/MPa	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1
Temperature/°C	20	20	20	20	20	20	20	20	20	20	20
Ignition angle/°CA	−7.5	−13.3	−4	−1	6.2	9.2	10.8	13.0	15.5	18.6	23.7
Intake mass/g/s	19.0	41.9	65.0	65.7	79.3	91.6	103.3	120.	126.7	131.8	130.9
IVO/°CA	−22	−22	−15.7	−12.5	−12	−9	−0.3	4.5	8.3	9.5	9.7
Throttle percentage/%	100	100	100	100	100	100	100	100	100	100	100

.

A heat transfer model named WoschniGT that closely emulates the classical Woschni correlation without swirl was included to calculate the heat transfer coefficient for the heat exchange of the cylinder wall. A predictive combustion model named SITurb was chosen to simulate the combustion process. SITurb takes into account the cylinder’s geometry, spark-timing, air motion, and fuel properties. The mass entrainment rate into the flame front and the burn rate are governed by the following three equations:

$$\{\begin{array}{l}\frac{d{M}_e}{dt}={\rho }_u{A}_e\left(S_T+S_L\right)\\ \frac{d{M}_b}{dt}=\frac{\left(M_e-M_b\right)}{\tau }\\ \tau =\frac{\lambda }{S_L}\end{array}$$

(4)

where $M_e$ = entrained mass of the unburned mixture, t = time, ${\rho }_u$ = unburned density, $A_e$ = entrainment surface area at the edge of the flame front, $S_T$ = turbulent flame speed, $S_L$ = laminar flame speed, $M_b$ = burned mass, τ = time constant, λ = Taylor microscale length. The model will be calibrated by adjusting FGWM (Flame Kernel Growth Multiplier) for the effects of turbulence intensity, TFSM (Turbulent Flame Speed Multiplier) for the calculation of turbulent flame speed, and TLSM (Taylor Length Scale Multiplier) for the Taylor microscale length. Besides, a knock model named Kinetics-Fit was added to SITurb model for knock intensity prediction. The knock model was calibrated by the ignition timing retard for full loads. The total engine mode of GT-Power was calibrated and verified by the engine bench test data at WOT (Wide Open Throttle) of various engine speeds. The bench test rigs including electrical dynamometer system, fuel consumption measurement system, exhaust analyzer, engine ECU combined with ETAS ES690 equipment, and combustion analyzer developed based on the NI CompactRIO system was introduced in our previous conference paper [22]. The errors of air mass flow, BSFC, brake torque, brake power, and exhaust temperature are less than 5%, as shown in Figure 6. Hence, the calibrated simulation model of the engine can used as the digital prototype for producing cyberspace data.

4. Results

After 50 genetic algorithm iterations, a population base of 1000 individuals including different LIVC, EGR rate, ignition timing, and air–fuel ratio chromosomes was generated. The distribution of the population against the BSFC and torque are shown in Figure 7. The band of BSFC changes widely for different LIVC, EGR rate, ignition timing, and air–fuel ratio parameters, which shows the necessity of multiparameter optimization, and the individuals gathering towards the low BSFC direction indicate that GA has a good convergence for fuel economy optimization. The band of torque also changes widely for different chromosome parameters, which indicates that the engine load can be controlled by EGR and LIVC strategy. However, the conclusion cannot be made that the EGR and LIVC strategy can replace throttle valve control entirely; at least, the BSFC outcome by the two-load control methods should be compared. Besides, it is not fair for the BSFC comparison among different loads; so, the clustering algorithm was used for further BSFC analysis.

In order to further analyze the optimal BSFC of different loads, eight different load conditions were classified automatically by clustering algorithm. The clustering centers correspond to the different torque levels that represent different loads. As shown in

Table 3. The clustering table of iteratively optimized population by genetic algorithm.

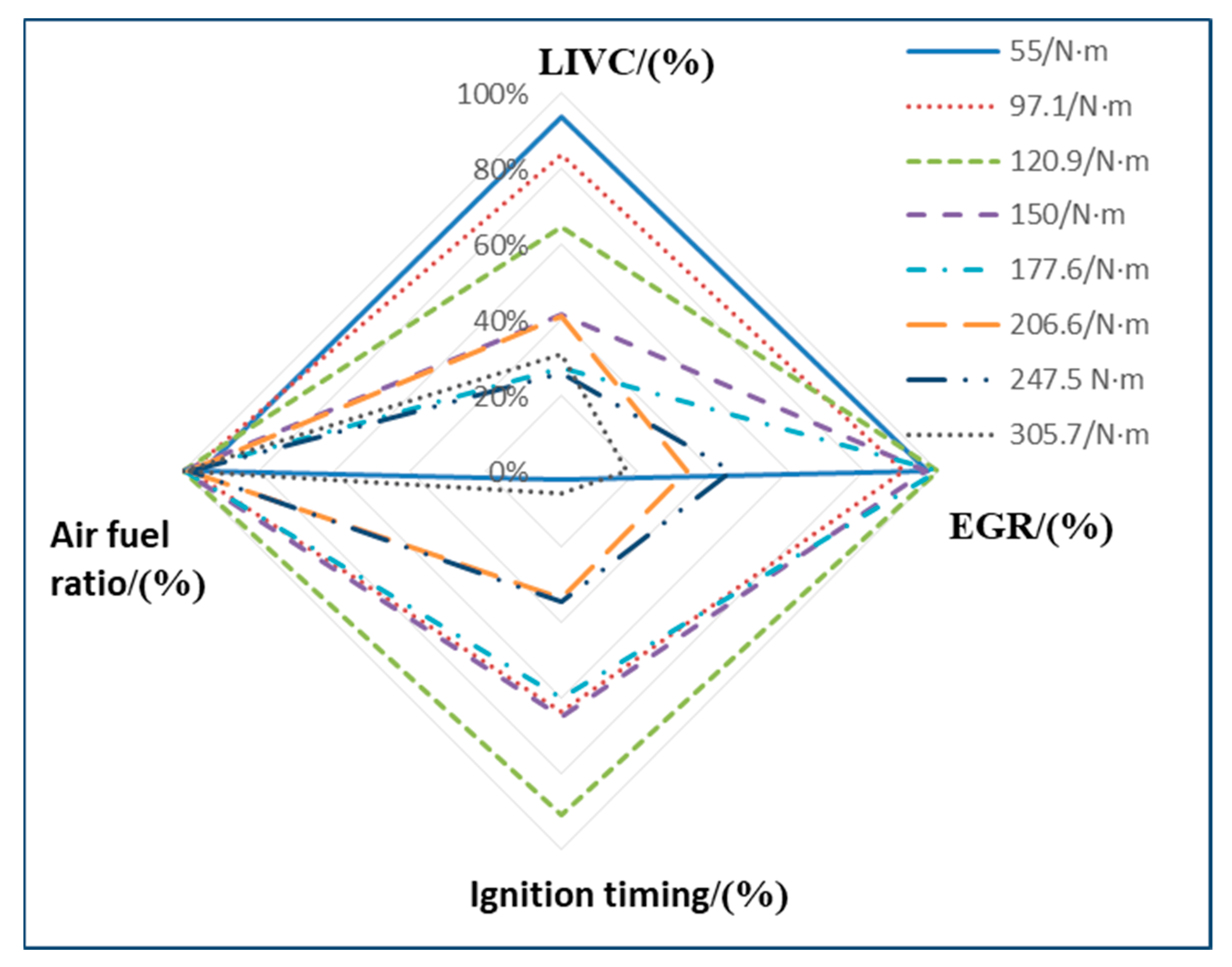
Operating Point	Statistical Number	The Clustering Center/N·m	EGR Rate
1	91	55	14.6%
2	253	97.1	13.6%
3	190	120.9	15%
4	158	150	14.5%
5	166	177.6	15%
6	69	206.6	5%
7	33	247.5	7%
8	45	305.7	2.6%

, the individuals were classified for each different torque level. The statistical numbers for different loads show that the individuals were mainly distributed in the medium loads. Too low or too high load clusters contain fewer individuals. The effects of the individual distribution on BSFC are discussed in next step.

Figure 8 shows the BSFC distribution of the corresponding populations at each torque level. As the torque increases, the distribution bandwidth of BSFC becomes narrower. At the same time, the population of each torque level are globally optimization-sequenced, the lowest BSFC points can be obtained, and the curve of lowest BSFC can be obtained by polynomial fitting. The curve indicates that the BSFC decreases with the increase in torque.

The optimum chromosomes for the lowest BSFC at different loads are shown in Figure 9. The percentage values in the figure are the values of the optimum chromosomes divided by the maximum value of the chromosomes, excepting an ignition timing of 24. The EGR rates corresponding to the lowest BSFC at different loads are 14.6%, 13.6%, 15%, 14.5%, 15%, 5%, 7%, 2.6%. The LIVC angles corresponding to the lowest BSFC at different loads are 61.9°CA, 55.4°CA, 42.6°CA, 27.3°CA, 17.9°CA, 27.1°CA, 17.1°CA, and 20.5°CA ABDC. The basic rule can be drawn that the optimal EGR rates and LIVC angles decrease as the torque increases. The air–fuel ratio corresponding to the lowest BSFC at different loads are getting near to theoretical air–fuel ratio of 14.7. However, the ignition timing retards closely to TDC time in high or low loads, and the ignition timing is advanced in medium loads.

Figure 10 is a comparison of the engine load characteristics curves at 2000 rpm between the original GDI engine and EHGE (EGR dilution coupled with high-expansion-ratio GDI engine) optimum result. The BSFC of EHGE was higher than the BSFC of the original engine at the working conditions below 150 N·m. However, the BSFC of EHGE at the working conditions above 150 N·m dropped significantly below the BSFC of the original engine. A maximum decline point leads to a 13% improvement to the BSFC of the original engine. The results indicated that EGR coupled with LIVC can be used to improve fuel economy at medium and high loads.

An ideal high-expansion-ratio thermodynamic cycle (Atkinson cycle) realized by LIVC strategy in this paper is compared with the traditional Otto cycle, as shown in Figure 11. As shown in the figure, 1–2–3–4–1 is Atkinson cycle and 1–2–3–4–1 is Otto cycle, where 1–2 is adiabatic compression process, 2–3 is constant volume heating process, 3–4 is adiabatic expansion process, 4–1 is constant pressure exothermic process, 1–2 is adiabatic compression process, and 4–1 is constant volume exothermic process in Otto cycle.

The theoretical thermal efficiency of the high-expansion-ratio gasoline engine derived from the first law of thermodynamics is calculated as follows:

$${\eta }_i=\frac{q_1-q_2}{q_1}$$

(5)

where q₁ is the circulating heat absorption, corresponding to the constant volume heating process 2–3, and q₂ is the circulating heat release, corresponding to the constant pressure heat release process 4–1. The calculation formulas for these are as follows:

$$\{\begin{array}{c}{q}_1=C_v\left(T_3-T_2\right)\\ q_2=C_p\left(T_4-T_1\right)\end{array}$$

(6)

where C_v is the specific heat capacity at constant volume; C_p is the specific heat capacity at constant pressure; T₁, T₂, T₃, and T₄ are the temperatures of corresponding points 1–2–3–4; and the following relationship is satisfied.

$$\{\begin{array}{l}\frac{T_2}{T_1}={\left(\frac{V_1}{V_2}\right)}^{K-1}={\epsilon }^{K-1}\\ \frac{T_3}{T_4}={\left(\frac{V_4}{V_3}\right)}^{K-1}={\rho }^{K-1}\\ \frac{T_1}{T_4}=\frac{V_1}{V_4}=\frac{\epsilon }{\rho }\end{array}$$

(7)

where K is the adiabatic index; ε is the actual compression ratio; ρ is the actual expansion ratio; and V₁, V₂, V₃, and V₄ are the volumes of corresponding points 1–2–3–4, where V₂ = V₃.

Substituting into Equation (5), we can obtain the following equation:

$$\begin{gathered} {\eta }_i=1-\frac{C_p}{C_v}.\left[1-\frac{T_1(\frac{T_4}{T_1}-1)}{T_2(\frac{T_3}{T_2}-1)}\right]=1-\gamma \frac{\rho -\epsilon }{{\rho }^K-{\epsilon }^K} \\ =1-\gamma \frac{1}{{\epsilon }^{K-1}}\left(\frac{\lambda -1}{{\lambda }^K-1}\right) \end{gathered}$$

(8)

where γ is adiabatic index or specific heat ratio, $\gamma =\frac{C_p}{C_v}$ and λ is the ratio of actual expansion ratio to actual compression ratio, $\lambda =\frac{\rho }{\epsilon }=\frac{V_4}{V_1}$.

The introduction of EGR is conducive to improving the specific heat capacity and the thermal efficiency, while LIVC is conducive to improving the actual expansion ratio (realized by increasing the geometric compression ratio) and reduce the actual compression ratio so as to improve the compression ratio. However, the introduction of EGR will prolong the combustion duration and affect the combustion stability. LIVC leads to intake backflow and intake efficiency reduction. This will affect the fuel economy in the actual engine working process. Therefore, it is also necessary to calibrate and correct the control parameters such as air–fuel ratio and ignition time. EGR, LIVC, ignition time, and air–fuel ratio are nonlinear, complex relationships that restrict each other, which is why the cluster genetic algorithm is introduced to carry out multiparameter optimization.

Results indicated that the multiparameter optimization including the ignition timing, air–fuel ratio, EGR, and LIVC has a very important effect on engine fuel economic performance. Using CGA and engine model simulation can determine the optimum combination of parameters for different loads efficiently and explain the conflicting results of different studies of EGR and LIVC strategy. The comparison of the minimum BSFC at different torque level shows that EGR rate and LIVC for the optimal BSFC decrease as the torque increases. EGR and LIVC strategy has potential to control the engine load instead of throttle valve. The comparison of the engine load characteristics curves between the original GDI engine and EHGE shows that EGR coupled with LIVC can be used to improve the fuel economy at medium and high loads. The maximum reduction in BSFC is almost 13% in contrast with the original engine. However, the BSFC at low loads controlled by EGR and LIVC are higher than that being controlled by throttle valve. Future work will be considered to study joint control by EGR, LIVC, and throttle valve.

5. Conclusions

In this paper, a general CPS framework combined with a multiparameter optimization algorithm was established. A multiparameter optimization simulation model combined with CGA programming and 1D engine simulation model were set up for improving the energy conservation potential of EGR gasoline engine.

The energy conservation effects of EGR dilution coupled with high-expansion-ratio thermodynamic cycle were investigated in virtual space. Thereafter, 1000 individuals with different chromosomes were iteratively optimized and automatically classified. The best individuals at different loads were screened. The optimal BSFC and corresponding control parameters were obtained for real, physical engine performance improvement and control optimization. The results demonstrated the effectiveness of the proposed method and can contribute to develop a novel automotive engine control strategy in the future.

The case study gives the research direction of CPS application at the vehicle subsystem level. In the future, high-performance computers may be used as CPS controllers in automobiles for subsystem components dynamic control based on the digital data and physical data of the vehicle Cyberphysical system.