Abstract
In this paper, an adaptive sliding mode fault-tolerant control scheme based on prescribed performance control and neural networks is developed for an Unmanned Aerial Vehicle (UAV) quadrotor carrying a load to deal with actuator faults. First, a nonsingular fast terminal sliding mode (NFTSM) control strategy is presented. In virtue of the proposed strategy, fast convergence and high robustness can be guaranteed without stimulating chattering. Secondly, to obtain correct fault magnitudes and compensate the failures actively, a radial basis function neural network-based fault estimation scheme is proposed. By combining the proposed fault estimation strategy and the NFTSM controller, an active fault-tolerant control algorithm is established. Then, the uncertainties caused by load variation are explicitly considered and compensated by the presented adaptive laws. Moreover, by synthesizing the proposed sliding mode control and prescribed performance control (PPC), an output error transformation is defined to deal with state constraints and provide better tracking performance. From the Lyapunov stability analysis, the overall system is proven to be uniformly asymptotically stable. Finally, numerical simulation based on a quadrotor helicopter is carried out to validate the effectiveness and superiority of the proposed algorithm.
1. Introduction
With the rapid development of onboard computer technology, communications and microelectronics systems, multi-rotor unmanned aerial vehicles (MUAVs) are increasingly popularized in the market [1]. UAVs can be widely used in military and civil fields by loading robot arms, cameras or other equipment, such as agricultural pesticide spraying, parcel delivery, and surface exploration [2].
Therefore, the control system of UAVs for load transportation is a topic of current interest [3]. Since UAV systems are susceptible to interference, the complex flight environment and long-term high-load operation may lead to faults. When faults occur, they may influence the stability of the whole control system and even lead to a catastrophic crash [4]. To save on costs and ensure safety, keeping the stability of UAV systems with the occurrence of faults is becoming increasingly important [5].
In [6], a general survey was presented on fault-tolerant control (FTC), and the authors categorized it into two types in a general framework: passive FTC (PFTC) and active FTC (AFTC). PFTC is designed aiming at a class of presumed faults [7]. This can stabilize the system by relying on robustness and does not need to adjust the structure of the controller [8]. Since PFTC would sacrifice nominal control performance, the research of AFTC has been explored to meet the high-performance requirements [9]. In contrast to PFTC, AFTC was designed based on online detection of faults and controller reconfiguration [10,11]. With the help of the FDD module, an AFTC can deal with faults by adjusting the control law [12].
In terms of fault diagnosis, a sliding mode observer was proposed in [13] for quadrotor actuator faults estimation. Moreover, reference [14] further proved that the system using the certain observer could be globally stable. In [15] a finite-time extended state observer was presented to obtain the state information of spacecraft. With the advent of the big data era, some data-driven diagnosis methods have been raised. In [16], by using an RBFNN-based estimation observer, the parameters of the sliding mode can be adjusted adaptively so that the tracking trajectory is more effective. A parallel bank of recurrent neural networks with an extended Kalman filter was designed to improve the reliability and accuracy of fault severity estimation in [17].
As for the control scheme, SMC has the advantage of strong robustness against uncertainties and disturbances; therefore, it is widely used in fault-tolerant control for quadrotor UAVs [18]. By combining SMC and back-stepping method, the authors in [19] proposed a fault-tolerant controller for a quadrotor. In [20], a scheme to deal with the sinusoidal wind model was designed based on the integral adaptive sliding mode control method.
A comparative survey study was presented in [21], and the authors elaborated both the advantages and disadvantages of each technique used for the controller to drive a QUAV. According to the survey results, the terminal sliding mode was considered as the most suitable method for quadrotor systems. In [22], a nonlinear terminal sliding mode controller was proposed for the attitude loop of a quadrotor. The authors in [23] designed a time-varying combinational terminal SMC method and expanded it to an adaptive fuzzy time-varying fast terminal SMC scheme for a quadrotor flight control.
To ensure fast convergence of the whole process, the authors in [24] proposed a global fast terminal sliding mode controller for second-order systems. Moreover, an adaptive nonsingular fast terminal sliding-mode tracking control algorithm is presented in [25] for a QUAV with modeling uncertainties, and a switching function was introduced to reduce the chattering.
From the model point of view, most of the existing studies for UAVs are based on the assumption that the mass and inertia of the system is time-invariant. However, this assumption ignores the effects of various loads. For example, some loads, such as robot arms, may change their shapes during flight, which will lead to changes in the momentum of inertia. The weight of the load is time-varying when quadrotors are applied for aerial refueling and pesticide seeding, so that both the mass and inertia are unknown.
In [26], a nonlinear dynamic inversion method was proposed to deal with the problem of a UAV with a suspended load. To deal with the influence of time-varying loads, an adaptive correcting coefficient is designed to estimate the amount of load in [27]. The researchers in [28] established a precise model for UAVs with time-varying load and proposed a compensation control law.
In this paper, inspired by the aforementioned practical problems, an adaptive robust flight fault-tolerant controller based on NFTSM control and prescribed performance function is developed for a quadrotor. The objective of this flight control algorithm is to stabilize the system and to track the flight path in the presence of actuator loss of effectiveness fault and effects of time-varying payloads. The main novelties and the critical features of this work are summarized as follows:
- (1)
- A new nonsingular fast terminal sliding mode is designed to deal with the quadrotor trajectory tracking problem and load disturbances. Strong robustness and fixed-time convergence are achieved by this algorithm.
- (2)
- To compensate for the uncertainty of mass and inertia caused by the loads, adaptive laws are designed to estimate the corresponding parameters online.
- (3)
- An RBFNN-based fault estimation observer is designed, so that we can obtain an accurate value of the actuator failure rate and disturbances.
- (4)
- A prescribed performance function is proposed and incorporated into the position control algorithm, which optimizes the dynamic performance to be more practical for real applications.
The remainder of this paper is organized as follows: the system model of the quadrotor UAV is given in Section 2. Section 3 presents an RBFNN-based fault estimation algorithm. In Section 4, the detailed design procedures of the proposed active NFSTM controller are addressed. The corresponding experimental results are given in Section 5 to show the effectiveness of the proposed control scheme. Finally, our general conclusions of this subject are summarized in the last section.
2. The Model Description
As shown in Figure 1, the quadrotor UAV is an underactuated vehicle with two pairs of propellers driven through four motors . By adjusting the speed of propellers, we can adjust the attitude angle and horizontal position of the UAV. In order to analyze the dynamics and kinematics of the system, position, and attitude equations for a quadrotor are described in two frameworks: the internal framework (B) located at the center mass of quadrotor and external framework (E), which is fixed with respect to the ground [29].
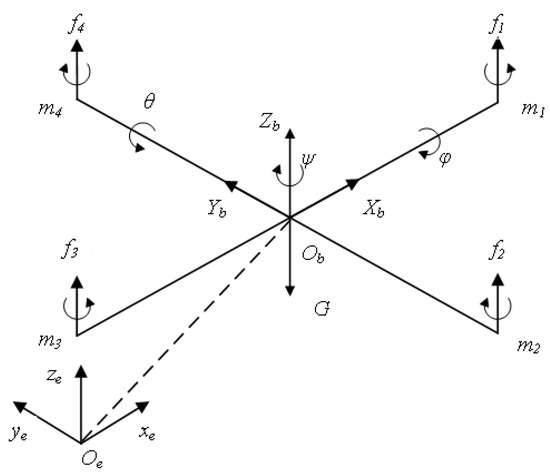
Figure 1.
Model of the quadrotor UAV.
2.1. Quadrotor Kinematics
Euler angles are used to describe the quadrotor attitude dynamics: represent the roll, pitch and yaw respectively. represents the relative position in the inertia system. The angular velocity and linear velocity are described by and . m and g are the mass of UAV and the acceleration of gravity. The main input is defined as:
where l is the distance from the center of mass of the aircraft to the propellers, is the thrust generated by the corresponding propeller. b is a constant coefficient and presents the torque generated by propellers. Neglecting the shape and the rotation of the Earth, then the kinematic and the dynamic equations can be established as:
where M, H, , and J stand for the linear momentum, angular momentum, torque, and inertia. Due to the time-varying payload of UAVs, m and J are time-varying. Therefore, we can obtain the following formulas by combining Newton’s second law [30]:
where , , are drag coefficients. is the translational matrix, which can be given as [31]:
Remark 1.
In this paper, and in Equation (3) are additional terms of time-varying loads, which are merged with external disturbances. m and are variables.
2.2. Problem Formulation
For the quadrotor system, the occurrence of actuator faults is inevitable. The faults discussed in this paper are modeled as loss of control effectiveness. Then, the system subject to actuator faults can be described as follows:
where , . is used to represent for simplification, is the sum of external disturbance and load disturbance, which would be called by disturbance term in the following, is virtual control quantity:
represents the actuator effectiveness of ith actuator. When , it shows that the ith actuator works properly. If , it means that the ith actuator partially loses its effectiveness but still works.
The purpose of this paper is to design an active fault-tolerant controller against actuator faults and the variation of the payload so that the safety and stability of the system can be guaranteed. To increase the trajectory tracking performance, the position state constraints are taken into consideration. In order to achieve the goal, certain lemmas and assumptions are used in this paper:
Assumption 1.
The disturbance term is bounded, and the upper bound is denoted by known constants: , therefore, , .
Lemma 1.
Based on RBFNN technology, a nonlinear function can be approximated in a compact set as [32]: with any designated precision, where denotes the ideal weight matrix whose Euclidean norm is bounded. represents the basis function and m is the number of implicit layer. ε is the approximation error of network, which satisfies .
Lemma 2.
Consider a ‘constrained’ system with the prescribed error performance:
where and are positive constants and is a positive decreasing smooth function, which satisfies: . If there is a smooth, strictly increasing function, satisfies [33]:
- (1)
- .
- (2)
- .Define transformed error as , where is the inverse function of . The inequality holds when the transformed error is convergent.
3. Estimation Observer DESIGN
In this section, an RBFNN-based fault estimate observer is designed to obtain the failure rate of actuators and the value of the disturbance term. First, Equations (6) and (7) can be manipulated into a state-space form:
where and represent the state variables, U is the control input vector, and B is the control effectiveness matrix, represents the failure rate of actuators, D is the disturbance term.
Then, a novel fault estimation observer is designed for the Equation (11) as follows:
where and are the estimated values of and respectively. L is a Hurwitz matrix. The adaptive updated laws are designed as:
The compensation of disturbance term is designed as:
where , and . are positive constants indicating gains; is the upper bound of the norm of and . P is an unknown positive definite matrix to be select. After simple calculation, the error dynamics equation is given by:
According to Equations (6) and (7), it is easy to obtain that there exist a positive constant makes the following inequality hold:
4. Fault Tolerant Controller Design
After fault diagnosis, the next problem is to construct fault-tolerant controllers for the UAV system with actuator faults and parametric uncertainties. The control block model and flowchart of the proposed control method are illustrated in Figure 2 and Figure 3. In this section, the overall UAV system is decoupled into the position subsystem and attitude subsystem as shown in Figure 2.
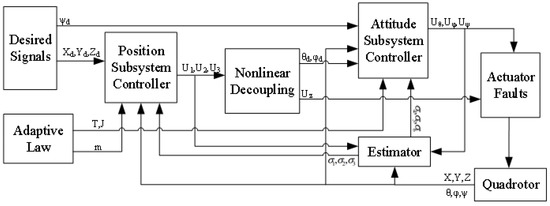
Figure 2.
The general control scheme of the quadrotor.
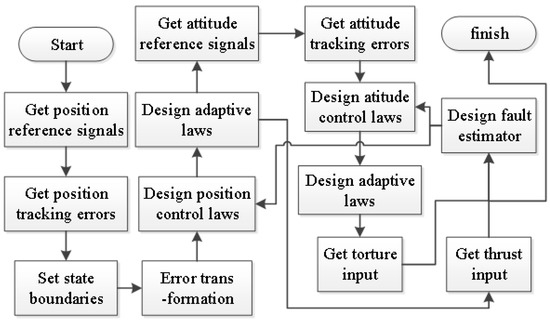
Figure 3.
The flowchart of the control system.
With the fault magnitudes and disturbance value obtained in Section 3, an adaptive NFTSMC scheme is presented for the corresponding subsystem to track the desired trajectory. It can be seen in Figure 2 that the algorithm is composed of an inner loop and an outer loop. The outer loop that gives the desired angles, and the total thrust is applied to perform robust path tracking. The inner loop is used to maintain the UAV attitude stabilization.
With the desired angles, this loop generates the yawing, pitching, and rolling torques to control the angular and the velocity of the attitude subsystem. The proposed scheme is not only able to handle the faults and disturbance term but also able to guesstimate the unknown mass and inertia caused by time-varying payloads. Additionally, for better dynamic performance, an error transformation based on the PPF method is designed on the position subsystem.
4.1. Position Subsystem
Considering Equation (6), the tracking error is defined as:
where is the desired trajectory.
4.1.1. Prescribed Performance
To avoid collision and optimize the control performance, we designed Prescribed Performance Functions (PPF) to ensure a maximum overshoot less than a prescribed value. An error transformed system is derived from the original system so that the stability of the transformed system can ensure that the tracking error of the original system is within the prescribed bounds. The constraints of error variables are set as:
The prescribed performance functions are set as , (), where and are positive constants.
Remark 2.
In (18), we can see that and define the upper bound and lower bound of error variables separately. The decreasing rate represents the lower bound of convergence speed, confines the steady-state tracking error. Therefore, the transient performance can be designed by turning corresponding parameters.
According to Lemma 2, we set the following transform to guarantee that the tracking errors remain within the prescribed performance bounds:
Since is strictly monotonic increasing, we can obtain its inverse function:
4.1.2. Position Control Design
In this part, controllers based on NFTSMC are proposed for the output error transformed system. The main advantage of this kind of algorithms is fast convergence and strong robustness under the effect of model uncertainties and disturbance terms. Two different controllers are discussed in this section. The first one is an NFTSMC algorithm developed for the position control subsystem without the uncertainty terms. Since the time-varying loads are considered in this paper, the adaptive method is introduced aiming at the uncertainty of mass, which can improve the control performance.
Without loss of generality, we take as an example to show the detailed design procedures. First, an NFTSM surface is introduced as follows:
where , . To avoid singularity, and .
By setting , the equivalent term in control signal is derived as:
To achieve strong robustness to deal with disturbance terms, the switching control law is designed as:
Finally, the complete control law is defined as:
where and are positive constants, and are obtained from the observer proposed in Section 3, .
The stability of this controller is proved with following Lyapunov function:
Therefore, according to the Lyapunov theory, the NFTSM surface would converge to zero with respect to disturbance terms. Due to the time-varying load, the mass m is unknown. Now, adaptive laws are designed to approximate the value of mass. The control law can be modified as:
where is the estimate of m. By defining , the corresponding adaptive law is designed as:
where is a positive constant. Moreover, the controllers for and can be designed in the same way.
Theorem 2.
For system with time-varying load described in Equation (6) with controllers , , and adaptive laws , we can conclude that the system states converge to the sliding surface in a finite and the constraints will never be violated.
Proof of Theorem 2.
A Lyapunov function for is defined as:
Combing Equations (6) and (26)–(28), the time derivative is given as:
According to the Lyapunov stability theory, subsystem is stable. By the same principle, we can conclude that and are stable too. The NFSTM can track the trajectory well, and the adaptive laws can accurately approximate the unknown mass. Moreover, we can conclude that the tracking errors remain within the prescribed performance bounds by combining Equations (23)–(34) and Lemma 2. This completes the proof. □
4.2. Attitude Subsystem
In this part, an NFSTM tracking control strategy is proposed for the attitude subsystem. First, we propose a robust NFSTM controller under the assumption that the inertia of UAV is exactly known. Then, adaptive laws are designed to compensate for the system uncertainties. According to Equation (8) the desired trajectories and are derived from the position subsystem. Considering Equation (7) the tracking error is defined as:
Similar to Equation (21) in Section 4.1.2, the sliding mode surfaces are proposed as:
where i = 1,2,3, , . To avoid singularity, and .
Without loss of generality, is taken as an example. First, a NFSTM algorithm for attitude subsystem without the uncertainty terms is designed. By the same processes, the control law is given as:
where and are positive constants.
The stability of this controller is proven with following Lyapunov function:
Therefore, according to the Lyapunov theory, the NFTSM surface would converge to zero with respect to the disturbance terms.
To compensate the uncertainties of inertia, the control law can be modified as:
where and are the estimated value of and . By defining , the corresponding adaptive laws are designed as:
where and are positive constants. Moreover, the controllers and adaptive laws for and can be designed in the same way.
Theorem 3.
For the system described in Equation (7) with controllers and adaptive laws designed as Equations (36) and (37), respectively, we can conclude that the system states converge to the sliding surface, and the constraints will never be violated.
Proof of Theorem 3.
A Lyapunov function for is defined as:
Combing Equations (7) and (33)–(37), the time derivative is given as:
According to the Lyapunov stability theory, subsystem is stable. By the same principle, we can conclude that and are stable too. This completes the Proof. □
Remark 3.
The control law of the NFTSM controller includes two parts: the equivalent term and the switching term. The equivalent term is adopted to construct a reaching law, which ensures fast convergence when the system states are not on the sliding surface. The other part makes the system more robust against the disturbance terms and uncertainties. This controller can make the tracking error converge to zero when the system uncertainties are known. However, this assumption is not satisfied due to the time-varying load. With the help of adaptive laws, the ANFTSMC scheme can eliminate the effects of system uncertainty. Moreover, the ANFTSM controller still has the advantage of high precision, strong robustness, and fast convergence.
5. Simulation
In this section, numerical simulations of the UAV control system are conducted to show the efficiency of the designed control strategy using the RBFNN-based observer and ANFTSMC technology with time-varying loads and actuator faults. Referring to the relevant data of Qdrone quadrotor designed by the Canadian Quanser company, the main parameters of UAV are chosen as: , , the air drag coefficient are given as .
Considering the real situation, white noise with upper bound is given as the external disturbances. The initial position and Euler angle are set as: , , and the desired trajectory is set as: .
Finally, considering the effects of time-varying loads, we simulate the scene where the UAV is used for pesticide spraying. The mass variation of the load is set as:
Thus, the total mass of UAV and load is , and the total momentum of inertia are given as . The variation of the total mass is shown in Figure 4.
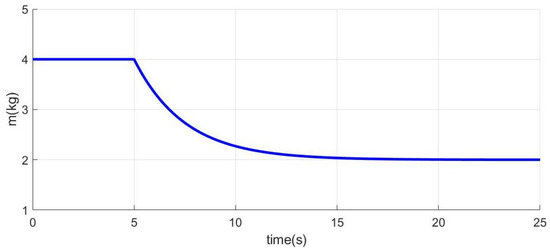
Figure 4.
The mass variation.
5.1. Fault Diagnosis
The efficiency of the fault observer is the first to be examined. Without loss of generality, we set a time-varying fault in both the attitude subsystem and position subsystem. The actuator control effectiveness fault scenario is given as:
The parameters of the observer are set as: . In order to validate the superiority of the proposed schedule, a two-stage extended Kalman filter (TSEKF) fault estimator [35] is utilized for the sake of comparative study. The comparison curves of fault estimation between the proposed method and TSEKF-based observer are shown in Figure 5.
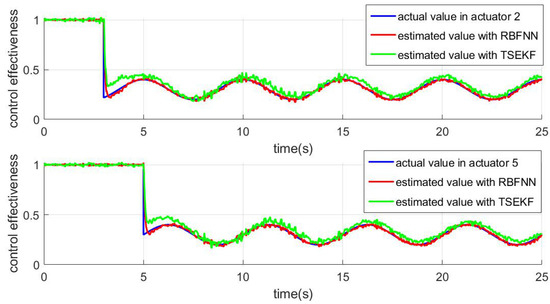
Figure 5.
Fault estimation performance.
According to Figure 5, the proposed fault observer can accurately and instantaneously recognize the fault severity. However, due to the model uncertainties caused by time-varying loads, the TSEKF estimator has a minor fault estimation error. TSEKF is a model-based method that relies on a detailed mathematical model and is sensitive to the changes in certain model parameters. The RBFNN-based observer presented in this work could tolerate influences of model uncertainties. Therefore, the proposed fault observer can accurately approximate the control effectiveness in about 2 s when dealing with actuator loss of effectiveness faults.
5.2. Trajectory Tracking in Presence of Actuator Fault
In this section, the performance of the proposed controller under the disturbance of faults with loss of control effectiveness in the actuator is studied. In order to validate the superiority of the ANFTSMC algorithm, a conventional adaptive SMC similar to [36] is introduced for comparison. To achieve better performance of the UAV system, the toolbox of optimization in MATLAB software and an optimization method proposed in [37] are utilized to obtain the gains of the controllers.
According to Equation (36), the parameters should make the control laws consistent with the performance of the motors. The parameters of the proposed control law are chosen as: , and the gains in the adaptive laws are given as .
Considering the working environment and performance requirements of the aircraft, the parameters of prescribed performance functions are given as: . To demonstrate the robustness of the proposed method, a loss of control effectiveness fault occurs in the fourth actuator at 12s. The purpose of the control schemes is to achieve trajectory tracking in a short time and overcome the influence of time-varying load and actuator failure.
Figure 6, Figure 7 and Figure 8 show the tracking errors of position variables(i.e., x, y, z respectively) under the designed scheme and a conventional sliding mode controller in the presence of time-varying load and actuator faults. Furthermore, the tracking errors of the attitude angles and inputs are shown in Figure 9 and Figure 10 separately. The simulation results show that the proposed method can make the attitude tracking curves converge in about 1 s, and the position tracking curves converge in about 1.7 s.
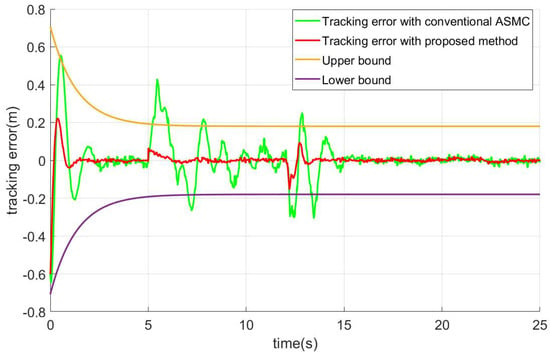
Figure 6.
Tracking error plot of position x.
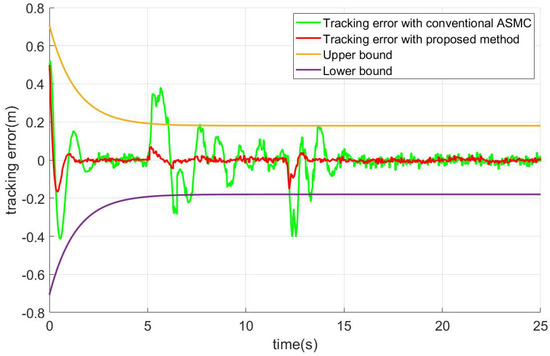
Figure 7.
Tracking error plot of position y.
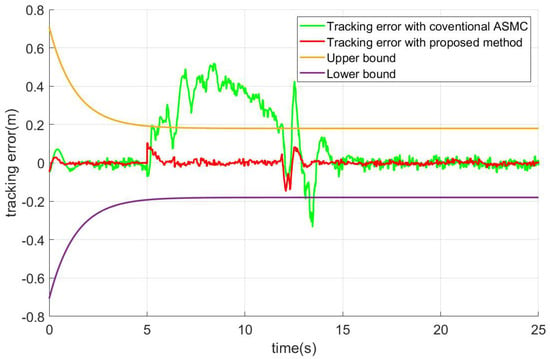
Figure 8.
Tracking error plot of position z.
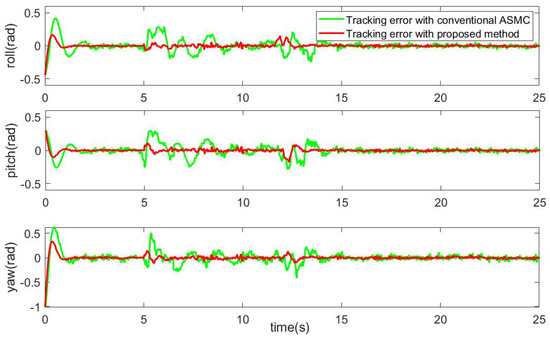
Figure 9.
Tracking error plot of attitude angles.
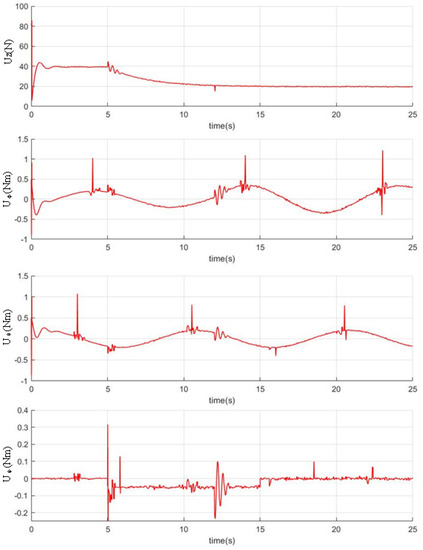
Figure 10.
The inputs of UAV.
The position subsystem can deal with the disturbance of time-varying load in about 1.2 s, and the error tracking curves would converge to zero in 1.5 s. Moreover, these disturbances can not make the curves out of the range of constraints. As for the attitude subsystem, the algorithm can dispose of the disturbance caused by the changes of the mass in 1 s, and the maximum oscillation amplitude of the curves is within 0.1. After the faults occur, the curves can converge within 1.2 s and the maximum amplitude is within 0.2.
As shown in Figure 6, Figure 7 and Figure 8, when the mass of load changes at 5 s, the conventional ASMC can hardly compensate for it. After 10 s, when the mass of the load tends to be constant, the system gradually stabilized. As gravity acts directly on the vertical, the variation of the load has a significant impact on the altitude of the UAV. From Figure 9, we can see that under the effect of time-varying load, the attitude curves of the quadrotor would fluctuate violently too.
It is difficult for the controller to deal with the problem of time-varying load only by the robustness of sliding mode. Compared to the conventional ASMC, the proposed method can effectively weaken the influence. With the help of RBFNN-based fault estimate observer and the strong robustness of NFTSM controller, the external disturbance and the influence caused by time-varying loads can be effectively disposed of. Benefiting from the adaptive law, the uncertainty terms can be estimated immediately. The error curves of the proposed scheme fluctuated only slightly.
It can be concluded from Figure 6, Figure 7, Figure 8 and Figure 9 that the curves fluctuated when the faults occurred after 12 s. Both controllers can deal with the actuator failures and achieve the convergence of system errors. With the information obtained by the proposed estimator integrated into the fault-tolerant controller, the proposed active fault-tolerant algorithm is more targeted. Therefore, once faults occur, the proposed active FTC scheme can instantly reduce the impact of faults and maintain the system stability in contrast to the compared ASMC without the FDD module.
Moreover, because the terminal sliding mode surface presented in this work is fast convergence, compared with the scheme in [36], the system response is faster, and the trajectory can be tracked more quickly and more accurately, which can be seen in Figure 6, Figure 7, Figure 8 and Figure 9. Moreover, it can be seen in Figure 10 and Equations (24), (27), (28), (36) and (37) the control torques generated by the proposed algorithm meet the characteristics of UAV.
In addition, from Figure 6, Figure 7 and Figure 8, it can be seen that the proposed active FTC method has less overshoot than conventional SMC when tracking the position signal. Due to the introduction of the prescribed performance function and the transformed system, it can be guaranteed that all the variables in the position subsystem are bounded, and the prescribed performance constraints are not transgressed. Finally, by comparing the simulation results, we can obtain that the proposed active fault-tolerant has better tracking performance and higher steady precision than conventional ASMC.
6. Conclusions and Future Works
In this paper, an active fault-tolerant control strategy based on NFTSM and RBFNN was proposed for a quadrotor UAV to accommodate actuator faults and time-varying payloads. With the help of the developed strategy, the fault value and the disturbance term can be precisely estimated online to reconfigure the controller to deal with actuator faults. First, the whole system was decoupled into the position and attitude subsystem.
By designing a prescribed performance function that characterizes the maximum overshoot, the position state of the UAV was limited within the prescribed performance bounds. Then, an adaptive nonsingular fast terminal sliding mode control scheme that could make system states converge within a finite time was presented to stabilize the system.
Moreover, a practical engineering problem about time-varying loads was considered, and the effect of load variations was attenuated by suggesting corresponding adaptive laws. Finally, simulation results validated the effectiveness of the control scheme proposed in this paper by comparing it with a two-stage extended Kalman filter (TSEKF) fault estimator and a conventional sliding mode controller.
The proposed method has the advantages of strong robustness. The estimator and adaptive laws can precisely and reliably compensate for the actuator faults and mode uncertainties. Furthermore, the overshoot can be effectively suppressed. However, the proposed method also has some disadvantages. The PPFs were designed to constrain the states of UAV, which makes the initial values of the state variables constrained as well. In future work, the constraints on the initial value will be removed, and the proposed algorithm will be tested on a real UAV system.
Author Contributions
All authors designed this work; Z.W. and P.Y. prepared an initial draft and overall structure of this research paper and invited other authors to contribute and expand the research scope. Z.Z. and X.H. supervised the research and edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by Key Laboratories for National Defense Science and Technology (6142605200402), the Aeronautical Science Foundation of China (20200007018001), the National Natural Science Foundation of China (61922042), the Aero Engine Corporation of China Industry-university-research cooperation project (HFZL2020CXY011) and the Research Fund of State Key Laboratory of Mechanics and Control of Mechanical Structures( MCMS-I-0121G03). Any opinions, findings, and conclusions, or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the sponsoring agency.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable to privacy and ethical restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hochstenbach, M.; Notteboom, C.; Theys, B.; De Schutter, J. Design and control of an unmanned aerial vehicle for autonomous parcel delivery with transition from vertical take-off to forward flight. Int. J. Micro Air Veh. 2015, 7, 395–405. [Google Scholar] [CrossRef] [Green Version]
- Abdessameud, A.; Tayebi, A. Global trajectory tracking control of VTOL–UA Vs without linear velocity measurements. Automatica 2010, 46, 1053–1059. [Google Scholar] [CrossRef]
- Zhou, B.; Satyavada, H.; Baldi, S. Adaptive path following for unmanned aerial vehicles in time-varying unknown wind environments. In Proceedings of the American Control Conference IEEE, Seattle, WA, USA, 24–26 May 2017; pp. 1127–1132. [Google Scholar]
- Wang, B.; Zhang, Y.M. An adaptive fault-tolerant sliding mode control allocation scheme for multirotor helicopter subject to simultaneous actuator faults. IEEE Trans. Ind. Electron. 2018, 65, 4227–4236. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Jiang, J. A survey of fault-tolerant controllers based on safety-related issues. Annu. Rev. Control 2015, 39, 46–57. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Jiang, J. Bibliographical review on reconfigurable fault-tolerant control systems. Annu. Rev. Control 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Avram, R.C.; Zhang, X.D.; Muse, J. Nonlinear adaptive fault-tolerant quadrotor altitude and attitude tracking with multiple actuator faults. IEEE Trans. Control Syst. Technol. 2018, 26, 701–707. [Google Scholar] [CrossRef]
- Merheb, A.R.; Noura, H.; Bateman, F. Design of passive fault-tolerant controllers of a quadrotor based on sliding mode theory. Int. J. Appl. Math. Comput. Sci. 2015, 25, 561–576. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.F.; Jiang, B.; Shi, P.; Qian, M.; Lin, J. Active fault tolerant control design for reusable launch vehicle using adaptive sliding mode technique. J. Frankl. Inst. 2012, 349, 1543–1560. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, X. Sliding mode control design for uncertain delay systems with partial actuator degradation. Int. J. Syst. Sci. 2009, 40, 403–409. [Google Scholar] [CrossRef]
- Hu, Q.L.; Shao, X.D.; Guo, L. Adaptive fault-tolerant attitude tracking control of spacecraft with prescribed performance. IEEE/ASME Trans. Mechatron. 2018, 23, 331–341. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Q.; Li, S. Adaptive integral-type terminal sliding mode fault tolerant control for spacecraft attitude tracking. IEEE Access 2019, 7, 195–207. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S. A new disturbance attenuation control scheme for quadrotor unmanned aerial vehicles. IEEE Trans. Ind. Inform. 2017, 13, 2922–2932. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S. Exponential tracking control of robotic manipulators with uncertain kinematics and dynamics. IEEE Trans. Ind. Inform. 2019, 15, 689–698. [Google Scholar] [CrossRef]
- Li, B.; Qin, K.; Xiao, B.; Yang, Y.S. Finite-time extended state observer based fault tolerant output feedback control for attitude stabilization. ISA Trans. 2019, 91, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Razmi, H.; Afshinfar, S. Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV. Aerosp. Sci. Technol. 2019, 91, 12–27. [Google Scholar] [CrossRef]
- Wang, B.; Shen, Y.; Zhang, Y. Active fault-tolerant control for a quadrotor helicopter against actuator faults and model uncertainties. Aerosp. Sci. Technol. 2020, 99, 105745. [Google Scholar] [CrossRef]
- Gong, W.; Li, B.; Yang, Y.; Ban, H.; Xiao, B. Fixed-time integral-type sliding mode control for the quadrotor UAV attitude stabilization under actuator failures. Aerosp. Sci. Technol. 2019, 95, 105444. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, R.; Zhang, K. Robust backstepping sliding-mode control and observer-based fault estimation for a quadrotor UAV. IEEE Ind. Electron. Soc. Newsl. 2016, 63, 5044–5056. [Google Scholar] [CrossRef]
- Escareno, J.; Salazar, S.; Romero, H.; Lozano, R. Trajectory control of a quadrotor subject to 2d wind disturbances. J. Intell. Robot. Syst. 2013, 70, 51–63. [Google Scholar] [CrossRef] [Green Version]
- Mo, H.; Farid, G. Nonlinear and adaptive intelligent control techniques for quadrotor UAV—A survey. Asian J. Control 2018, 21, 989–1008. [Google Scholar] [CrossRef]
- Ansari, U.; Bajodah, A.H.; Hamayun, M.T. Quadrotor control via robust generalized dynamic inversion and adaptive non-singular terminal sliding mode. Asian J. Control 2016, 21, 1237–1249. [Google Scholar] [CrossRef]
- Jie, G.; Yong, Z.S. Time-varying nonsingular terminal sliding mode control for robot manipulators. Trans. Inst. Meas. Control 2014, 36, 604–617. [Google Scholar]
- Pan, H.; Zhang, G.; Ouyang, H.; Mei, L. A novel global fast terminal sliding mode control scheme for second-order systems. IEEE Access 2020, 8, 22758–22769. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive nonsingular fast terminal sliding-mode tracking control for an uncertain quadrotor UAV subjected to disturbances. ISA Trans. 2020, 99, 290–304. [Google Scholar] [CrossRef] [PubMed]
- Das, H. Dynamic Inversion Control of Quadrotor with a Suspended Load. IFAC-PapersOnLine 2018, 51, 172–177. [Google Scholar] [CrossRef]
- Vandanipour, M.; Khodabandeh, M. Adaptive Fractional Order Sliding Mode Control for a Quadrotor with a Varying Load. Aerosp. Sci. Technol. 2019, 86, 737–747. [Google Scholar] [CrossRef]
- Wu, X.; Xiao, B.; Qu, Y. Modeling and sliding mode-based attitude tracking control of a quadrotor UAV with time-varying mass. ISA Trans. 2019, in press. [Google Scholar] [CrossRef]
- Kendoul, F. Survey of advances in guidance, navigation, and control of unmanned rotorcraft systems. J. Field Robot. 2012, 29, 315–378. [Google Scholar] [CrossRef]
- Jia, Z.; Yu, J.; Mei, Y.; Chen, Y.; Shen, Y.; Ai, X. Integral backstepping sliding mode control for quadrotor helicopter under external uncertain disturbances. Aerosp. Sci. Technol. 2017, 68, 299–307. [Google Scholar] [CrossRef]
- Raffo, G.V.; Ortega, M.G.; Rubio, F.R. An integral predictive/nonlinear H control structure for a quadrotor helicopter. Automatica 2010, 46, 29–39. [Google Scholar] [CrossRef]
- Gao, Z.; Cheng, P.; Qian, M.; Jiang, G.; Lin, J. Active faulttolerant control approach design for rigid spacecraft with multiple actuator faults. J. Syst. Control. Eng. 2018, 232, 1365–1378. [Google Scholar]
- Na, J.; Chen, Q.; Ren, X.; Guo, Y. Adaptive Prescribed Performance Motion Control of Servo Mechanisms with Friction Compensation. IEEE Trans. Ind. Electron. 2013, 61, 486–494. [Google Scholar] [CrossRef]
- Cheng, P.; Cai, C.; Zou, Y. Finite Time Fault Tolerant Control Design for UAV Attitude Control Systems with Actuator Fault and Actuator Saturation. IFAC-PapersOnLine 2019, 52, 53–58. [Google Scholar] [CrossRef]
- Chen, X.; Sun, R.; Jiang, W.; Jia, Q.; Zhang, J. A novel two-stage extended Kalman filter algorithm for reaction flywheels fault estimation. Chin. J. Aeronaut. 2016, 29, 462–469. [Google Scholar] [CrossRef] [Green Version]
- Tao, W.; Xie, W.; Zhang, Y. Sliding mode fault tolerant control dealing with modeling uncertainties and actuator faults. ISA Trans. 2012, 51, 386–392. [Google Scholar]
- Freire, F.P.; Martins, N.A.; Splendor, F. A simple optimization method for tuning the gains of PID controllers for the autopilot of cessna 182 aircraft using model-in-the-loop platform. Control Autom. Electr. Syst. 2018, 29, 441–450. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).