Position Soft-Sensing of Direct-Driven Hydraulic System Based on Back Propagation Neural Network
Abstract
:1. Introduction
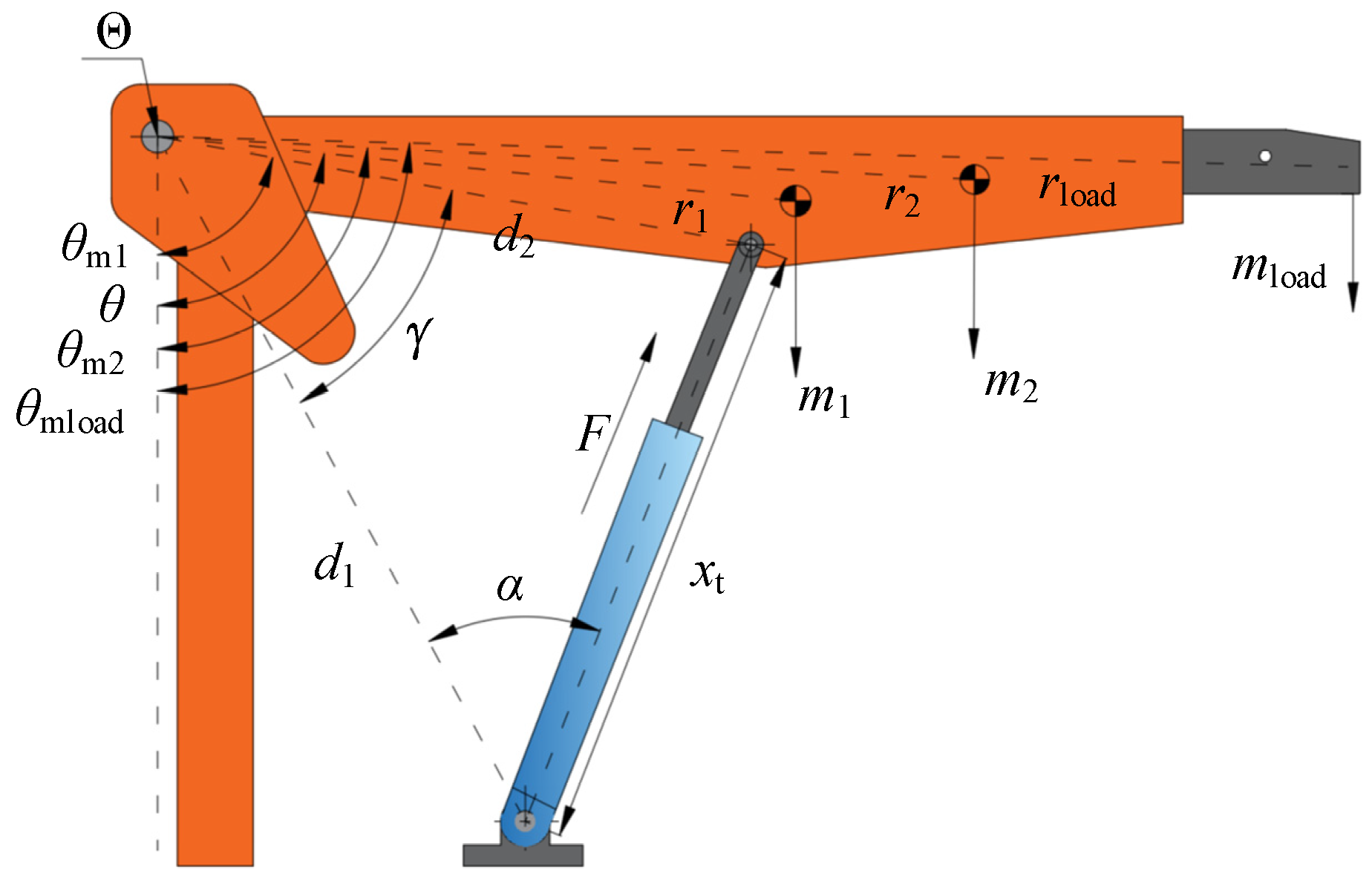
2. Modelling and Verification of a Crane with DDH
2.1. Modeling
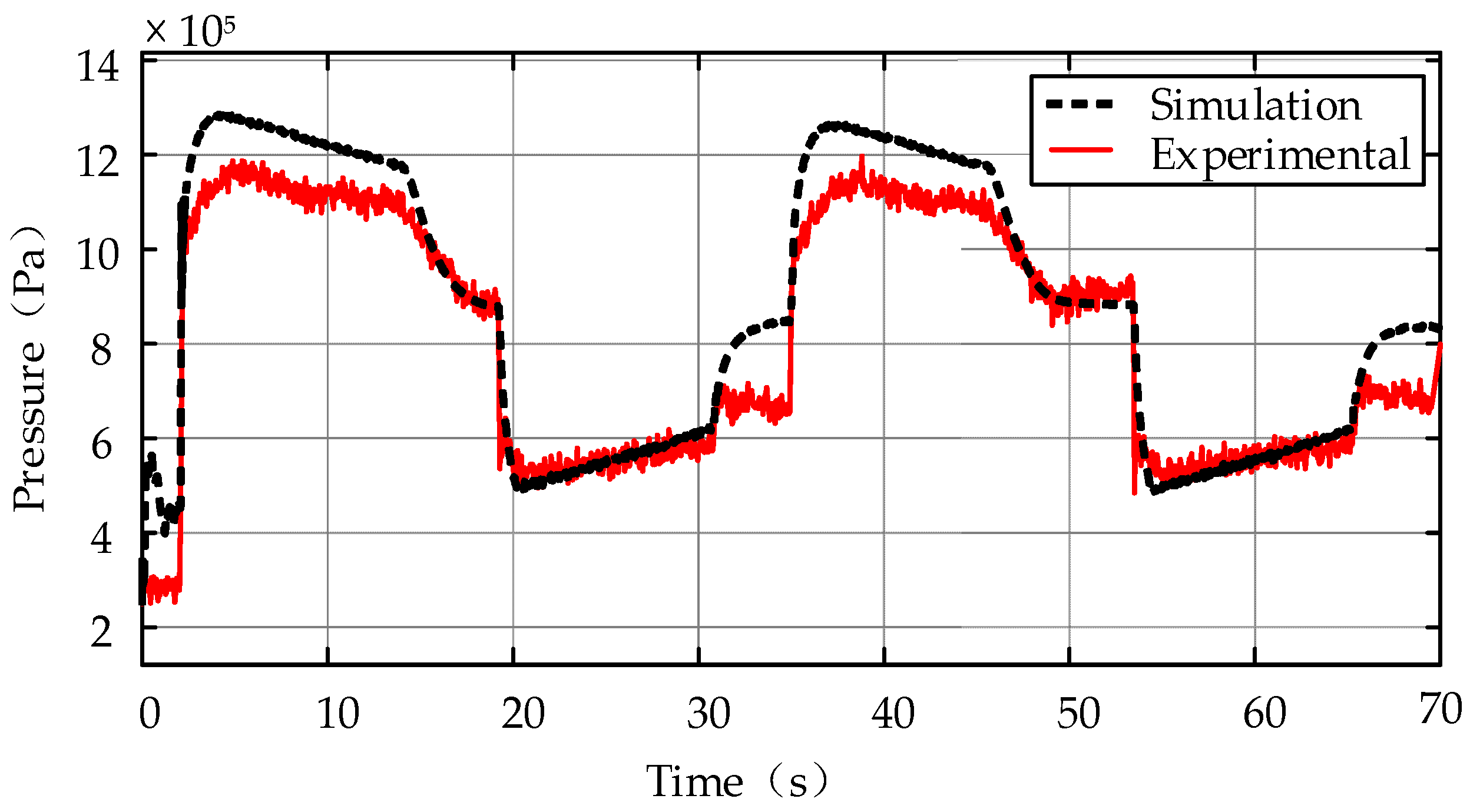
2.2. Model Verification
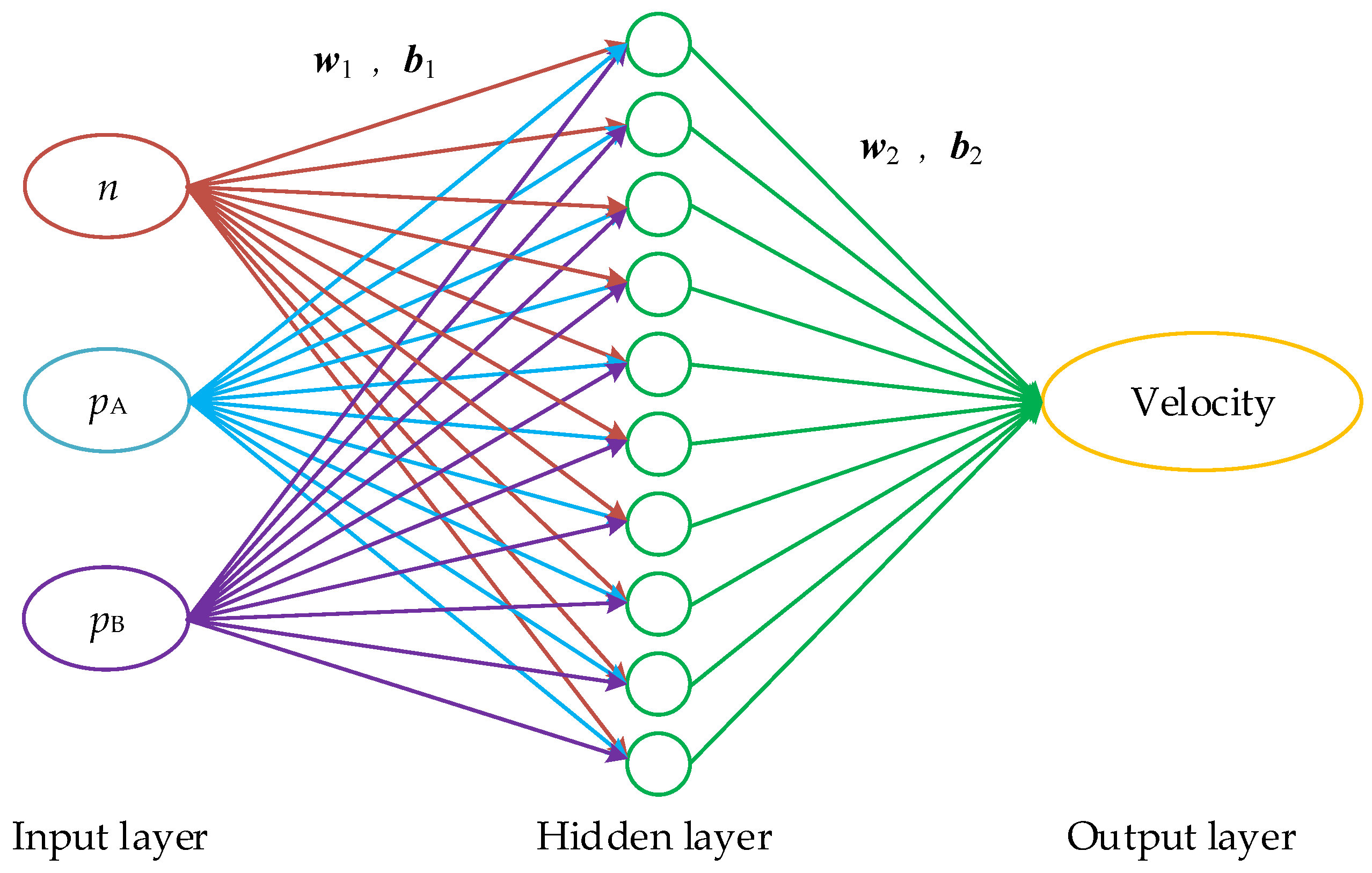
3. Position Soft-Sensing Model Based on BP Neural Network
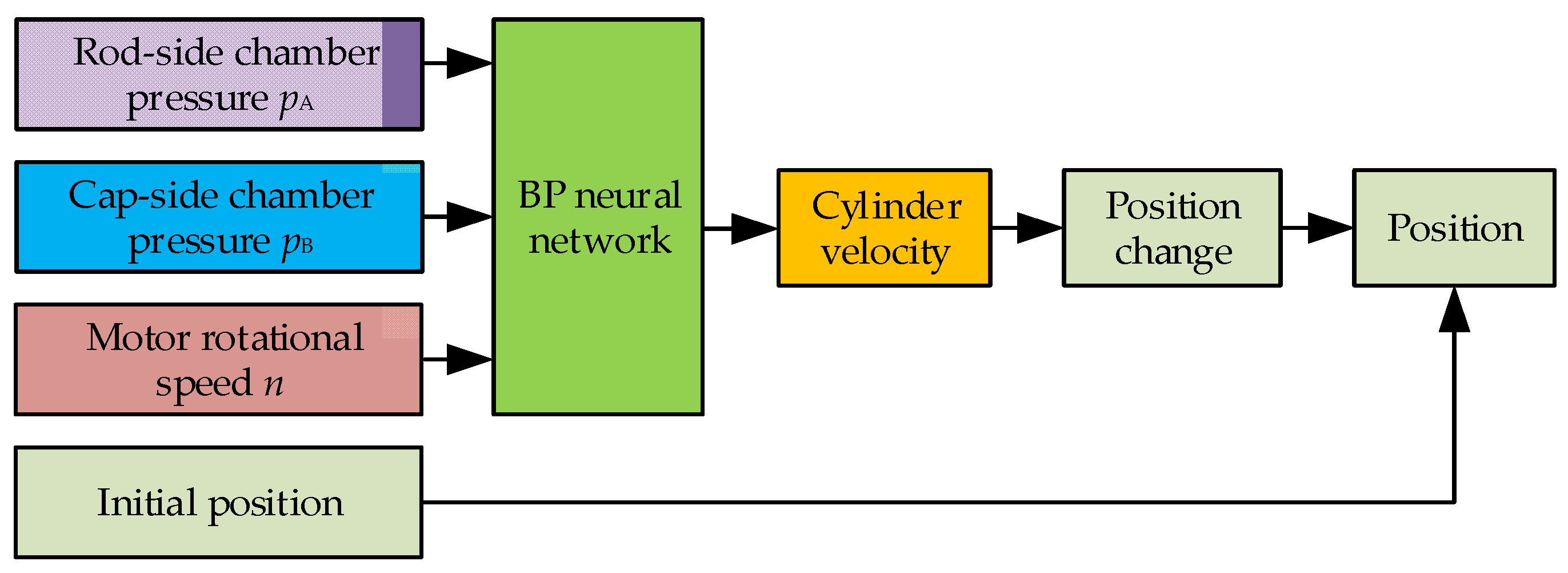
3.1. Principle of Position Soft-Sensing
3.2. Training and Testing Data Preparation
3.3. Training and Testing the BP Neural Network
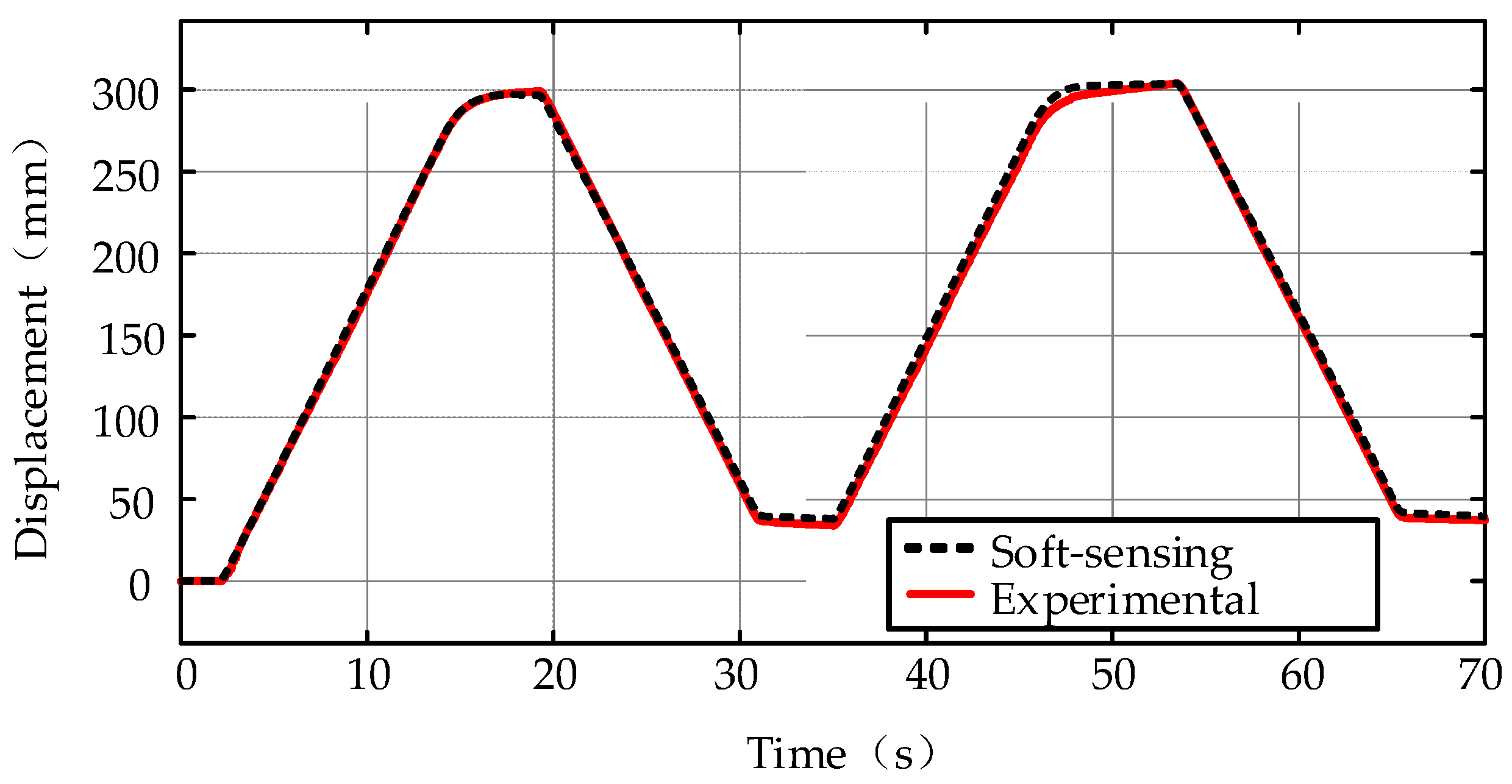
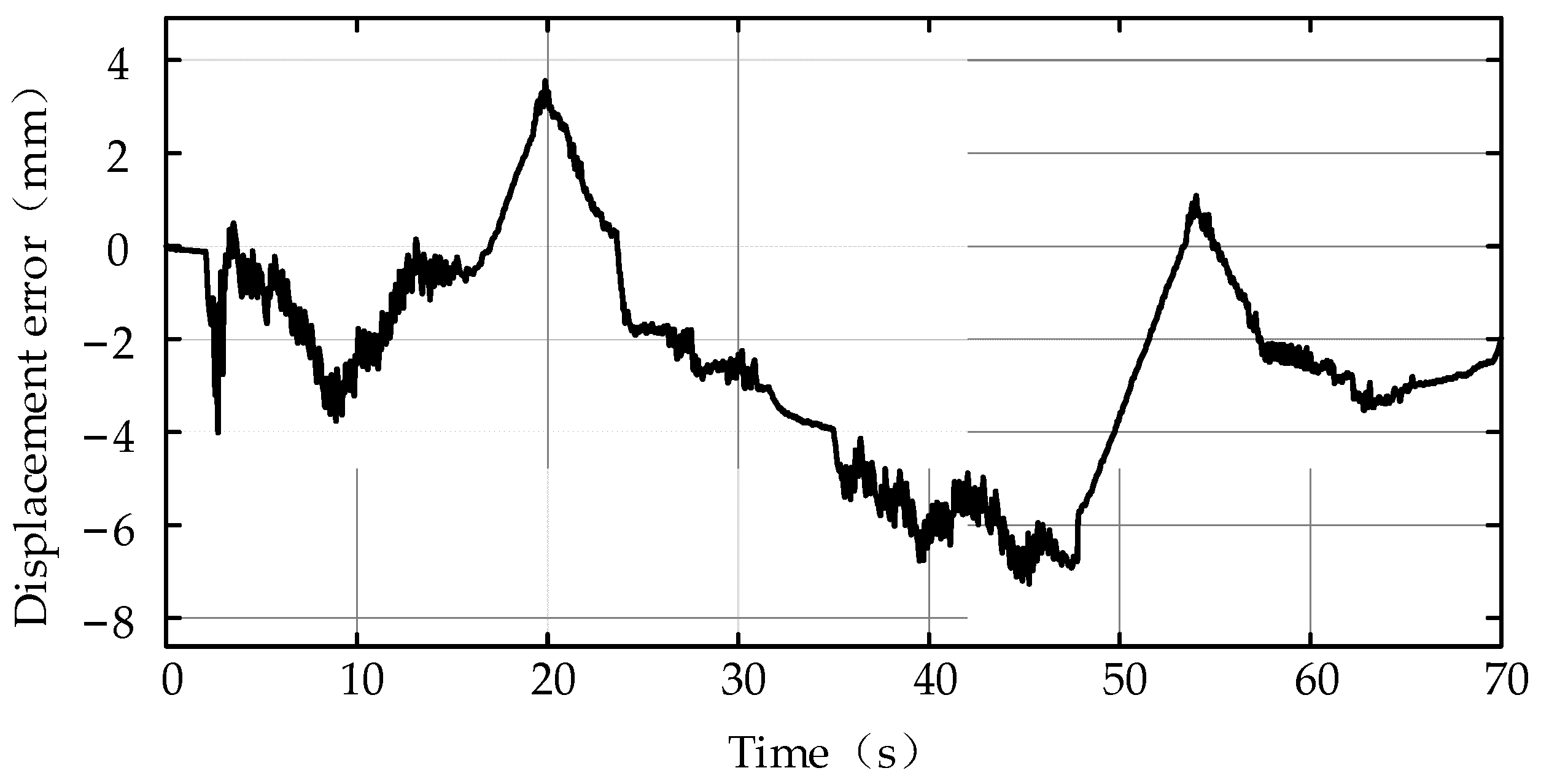
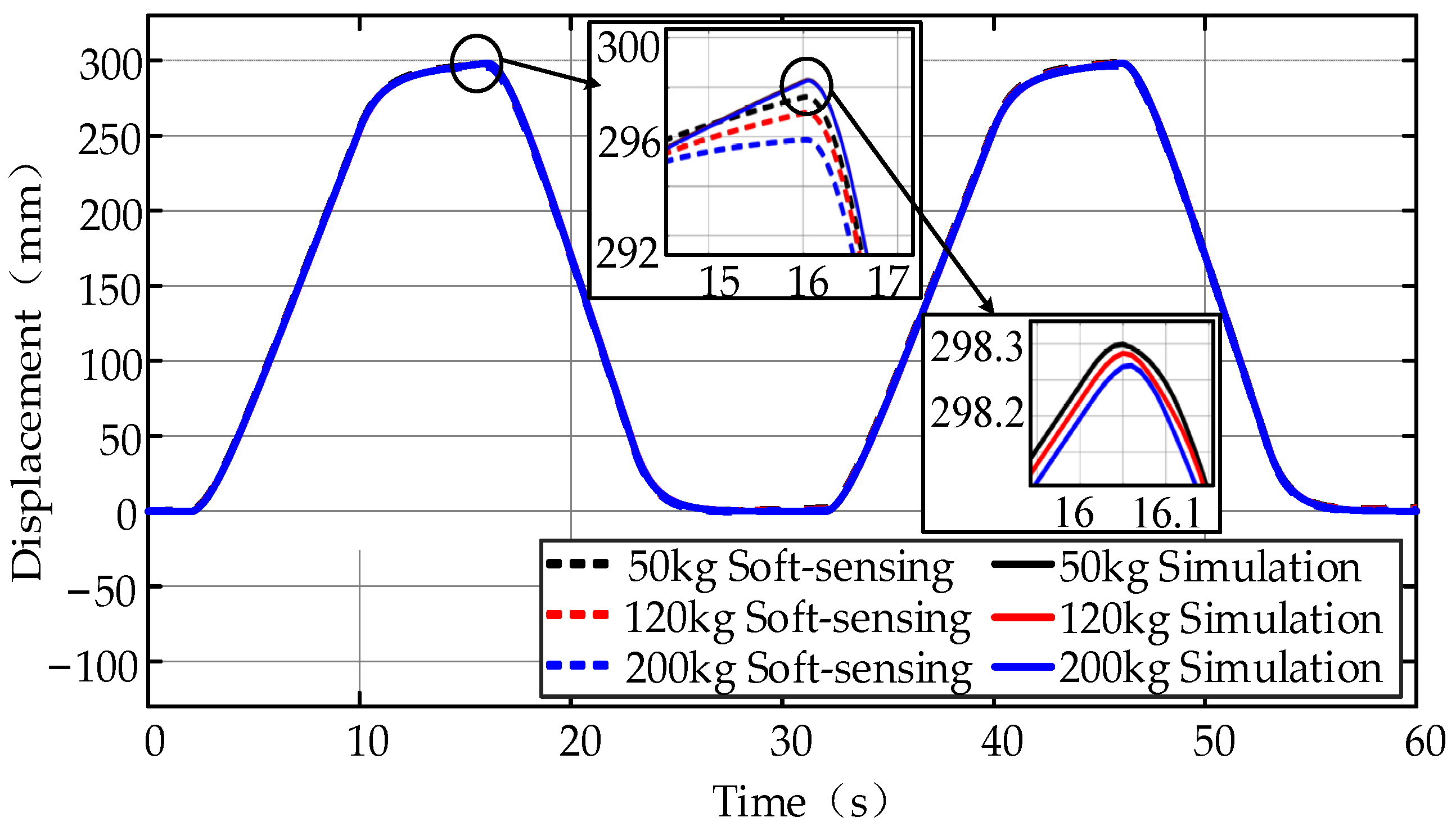
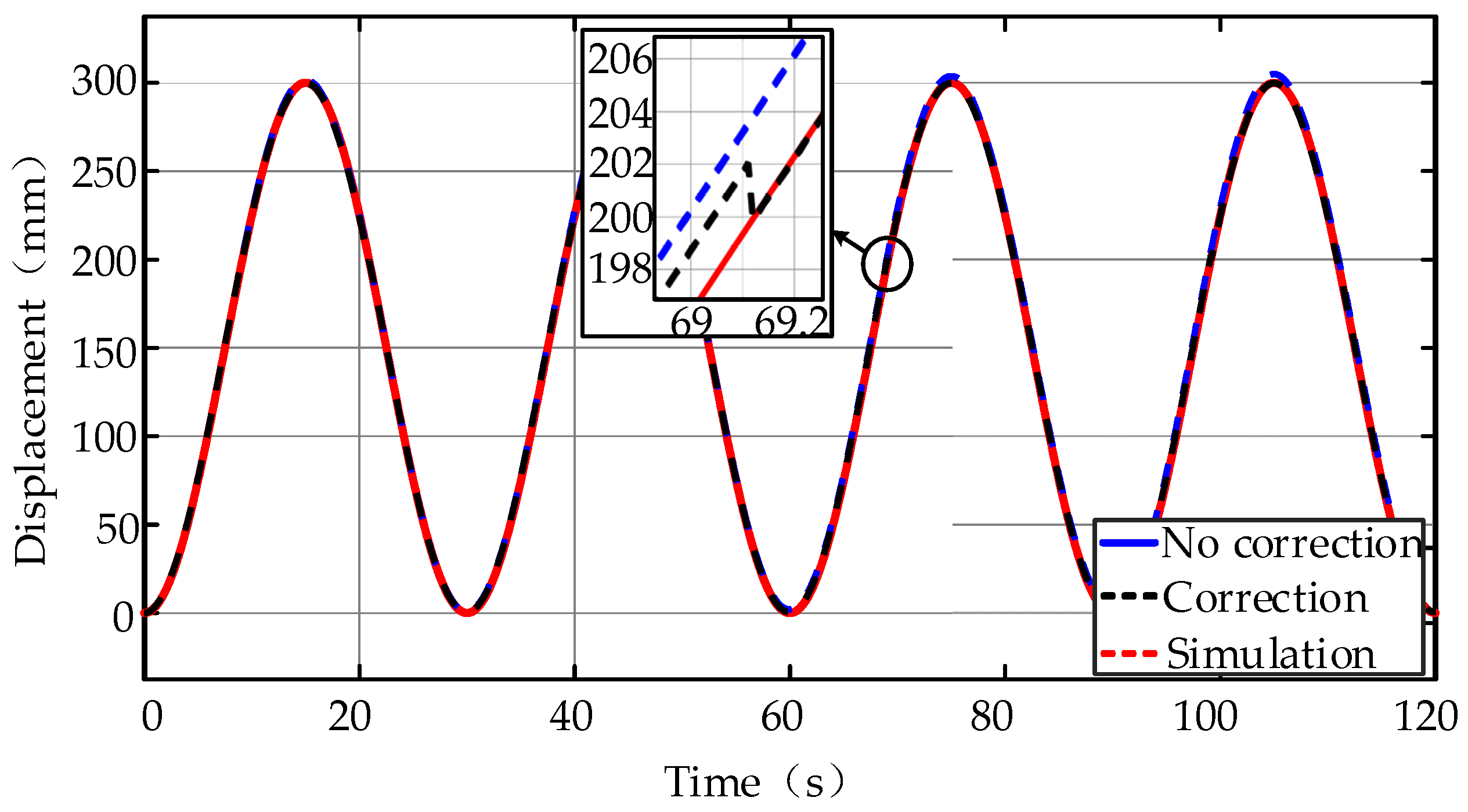
4. Verification of Position Soft-Sensing Model
5. Simulation and Accumulative Error Correction
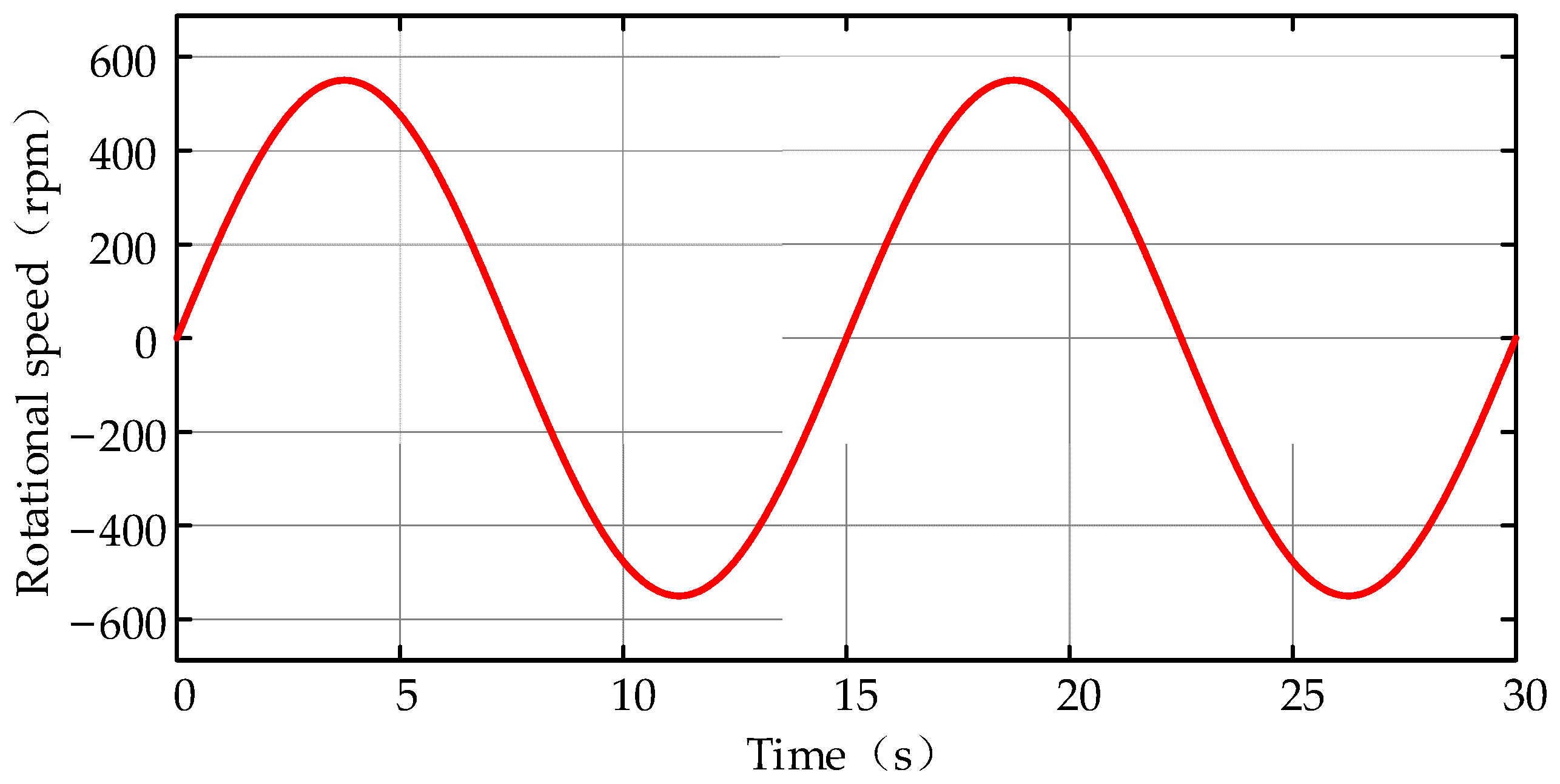
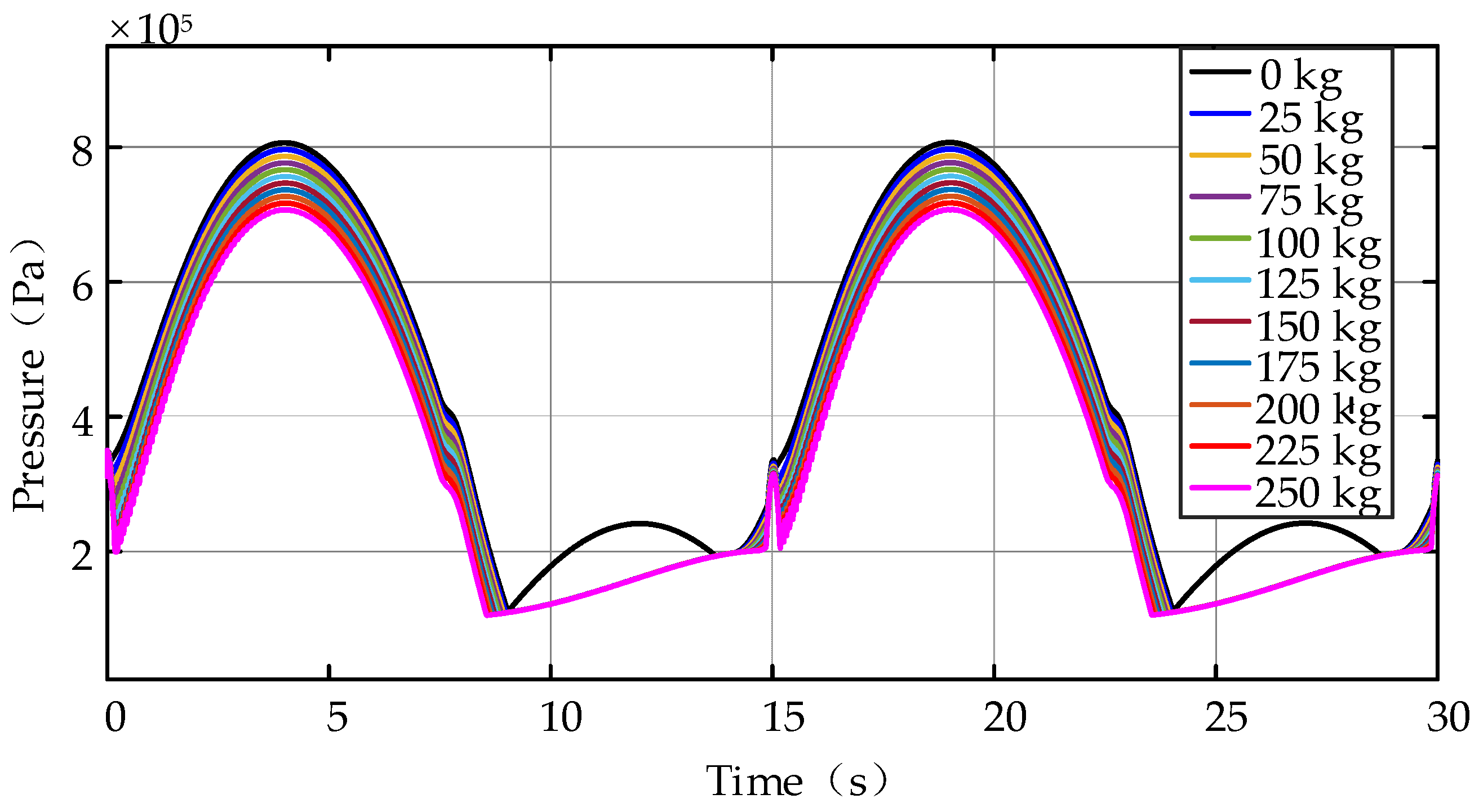
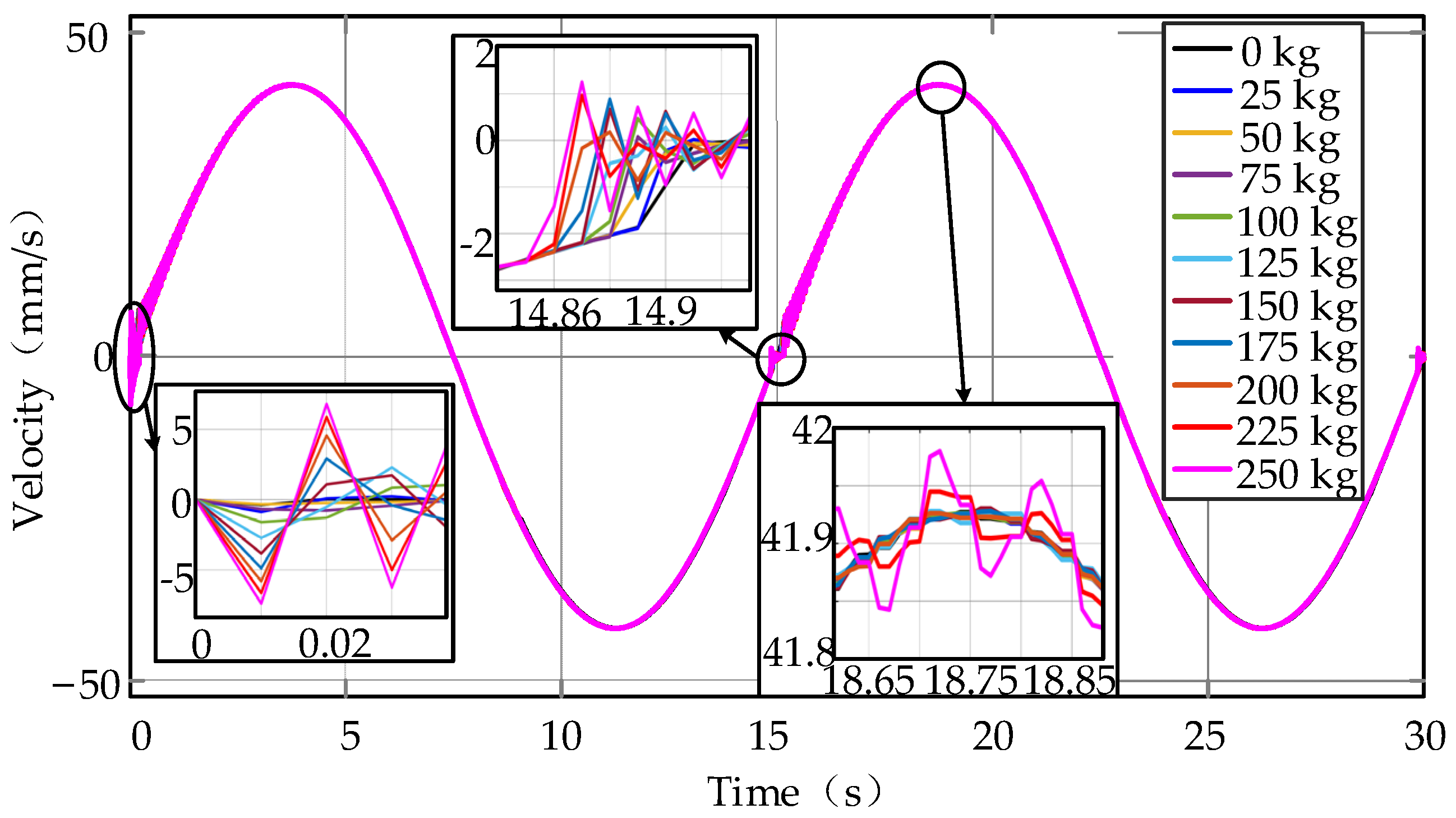
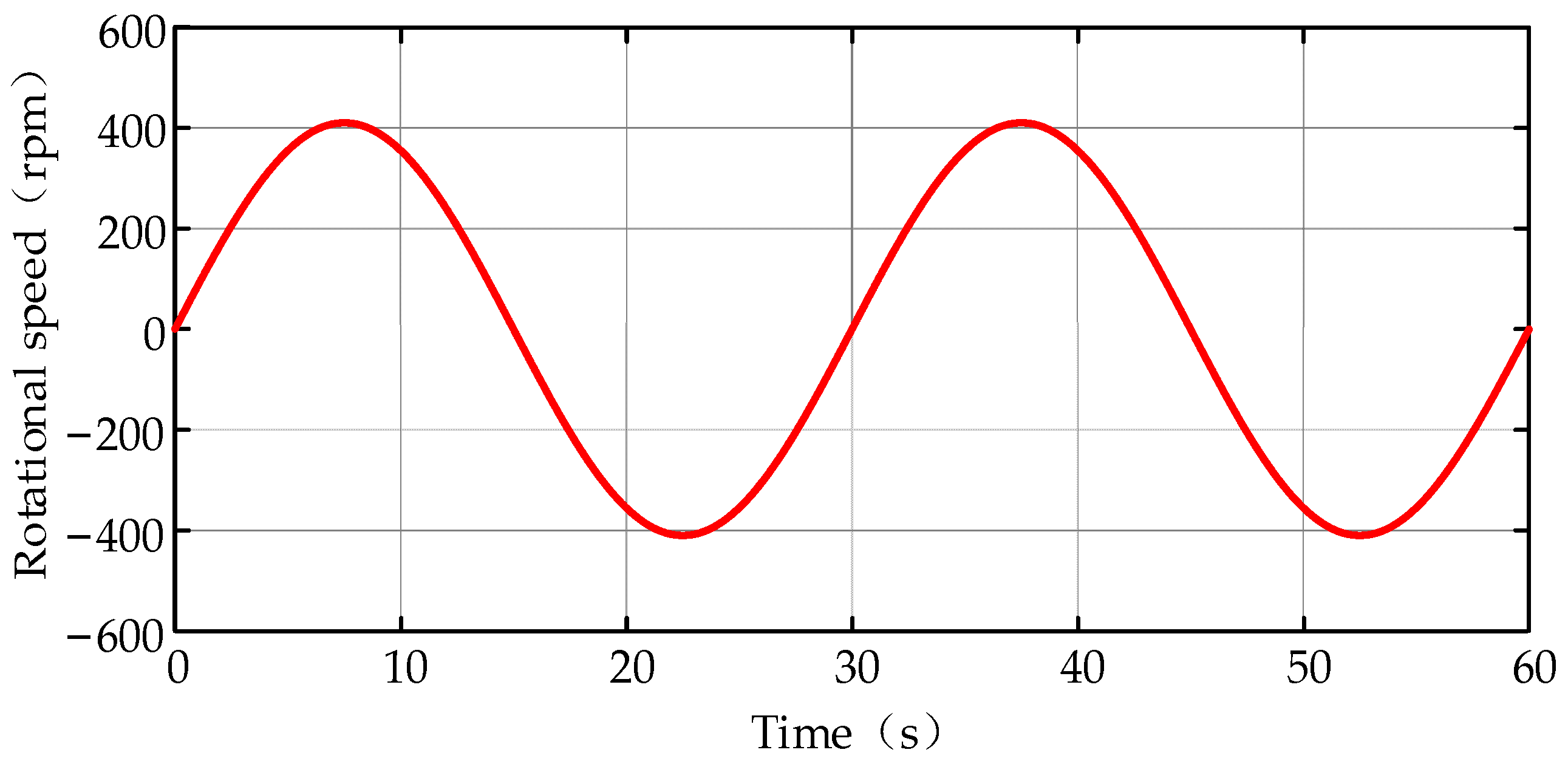
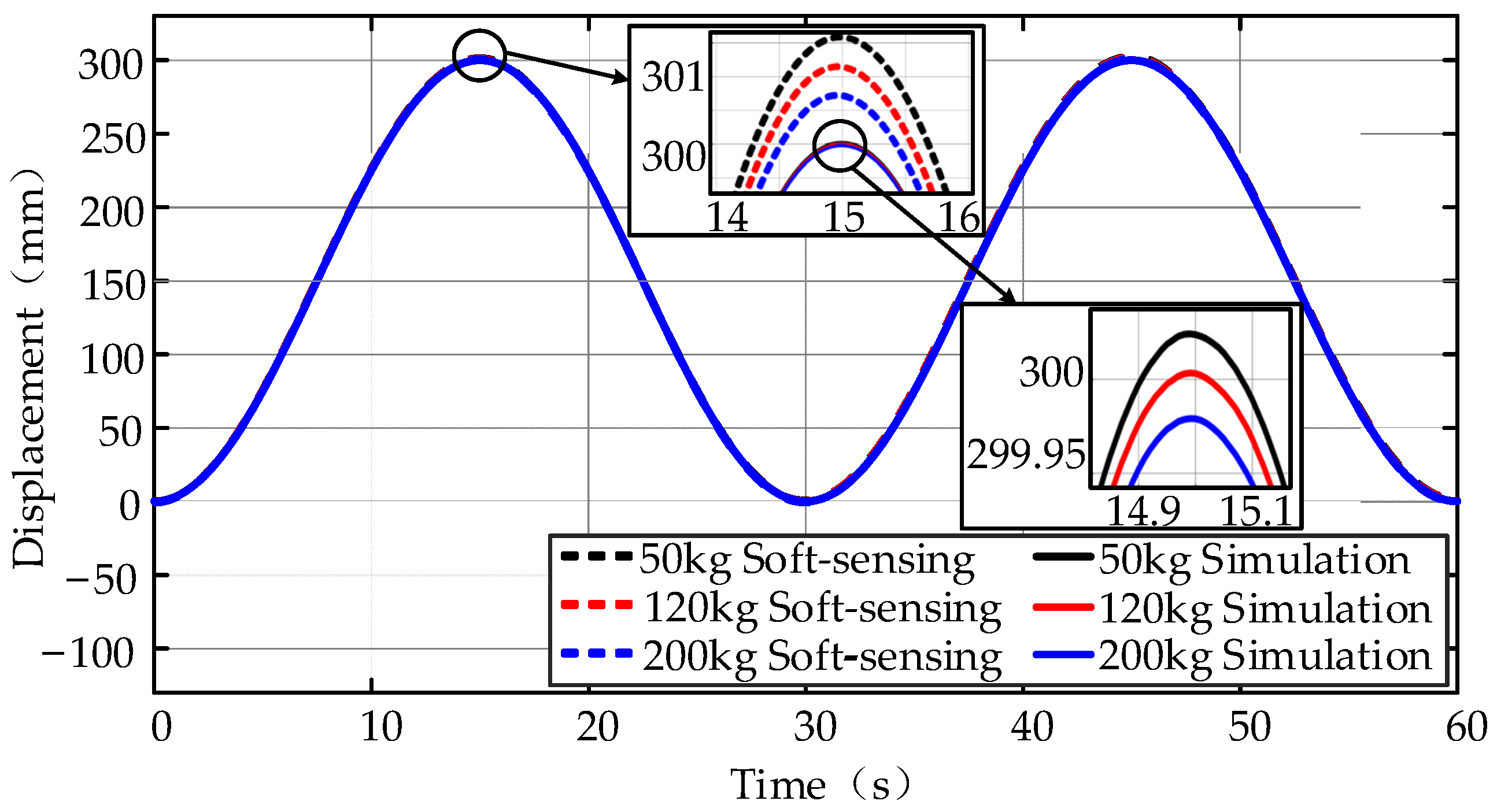
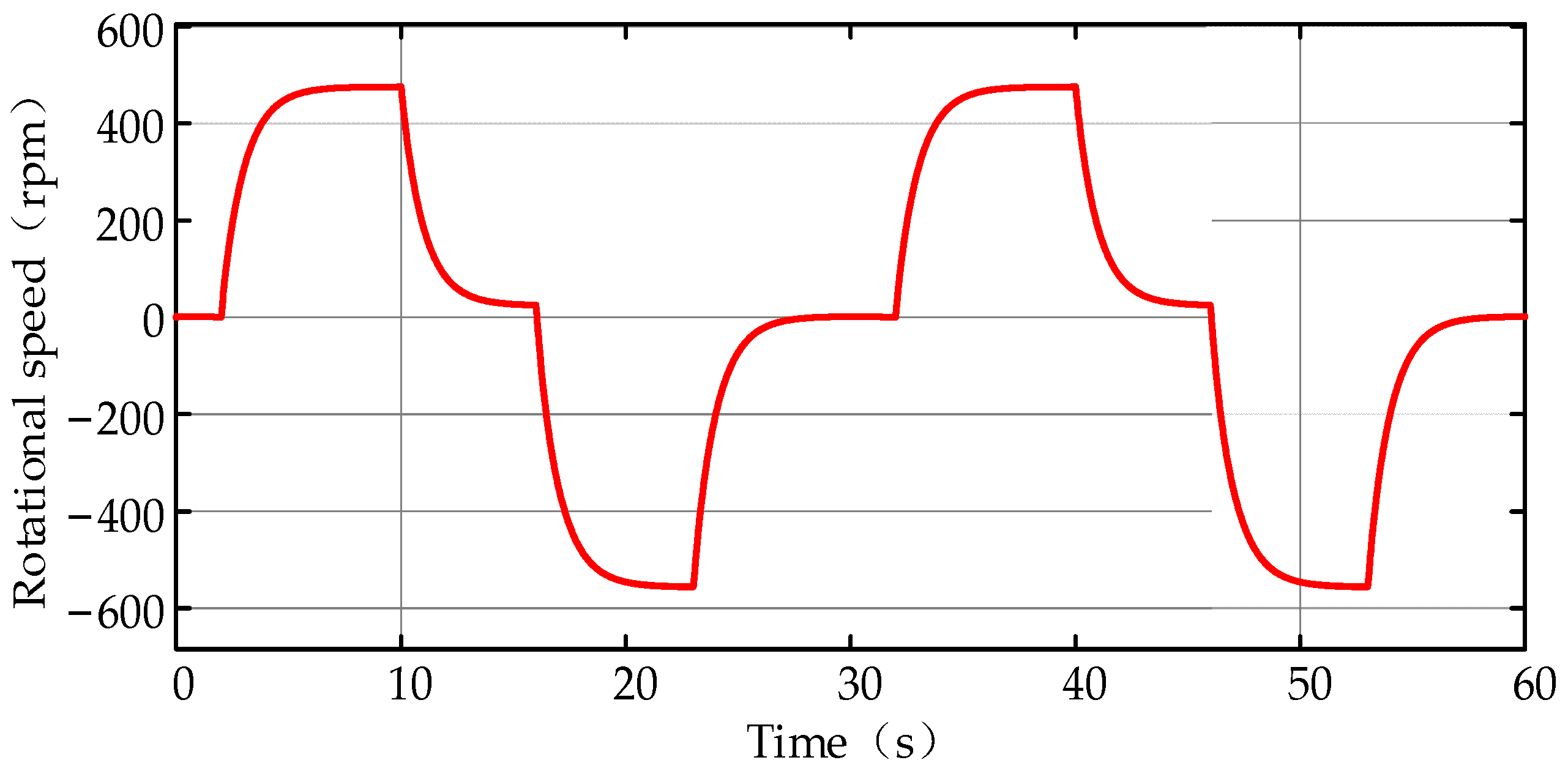
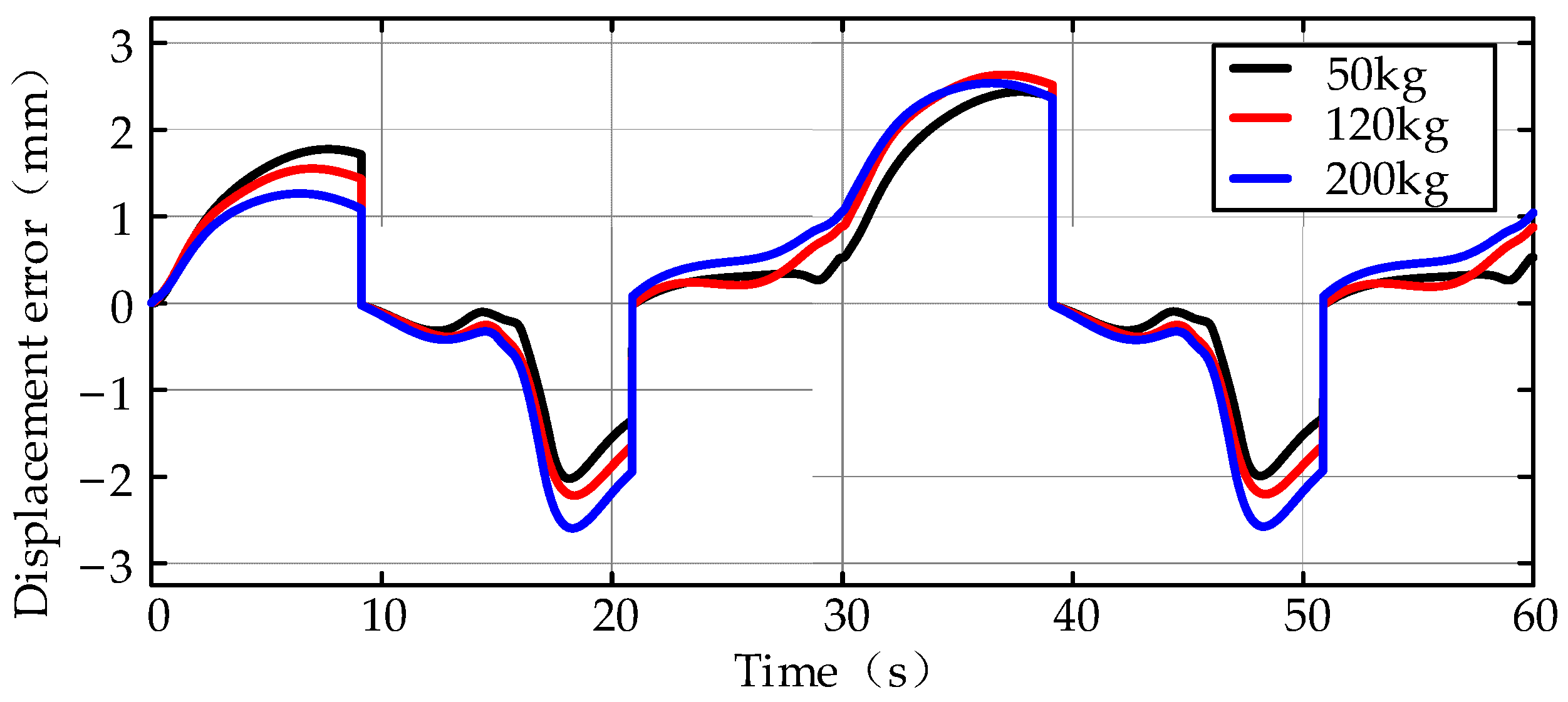
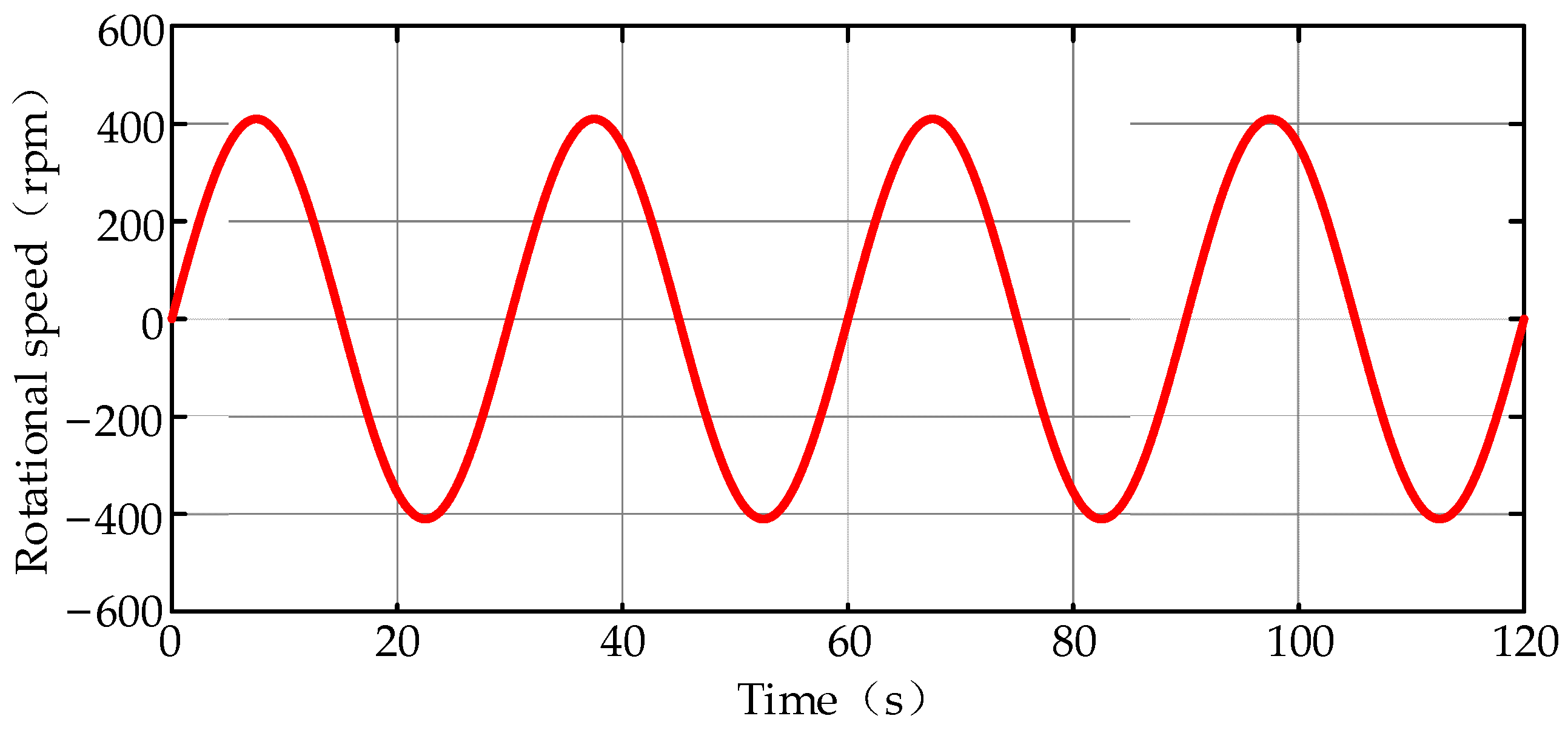
5.1. Sinusoidal Working Cycle with Varying Loads
5.2. Typical Cycle with Varying Loads
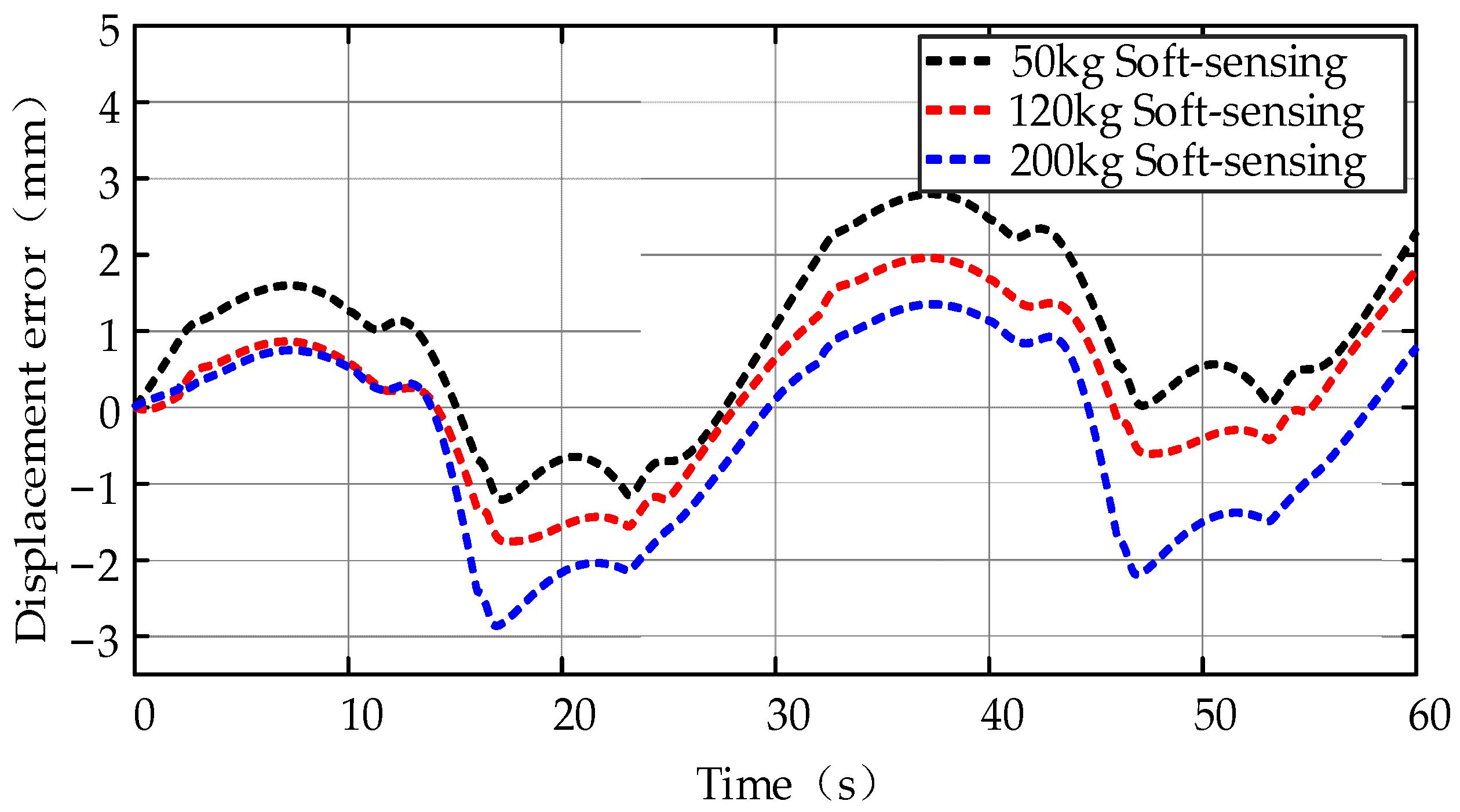
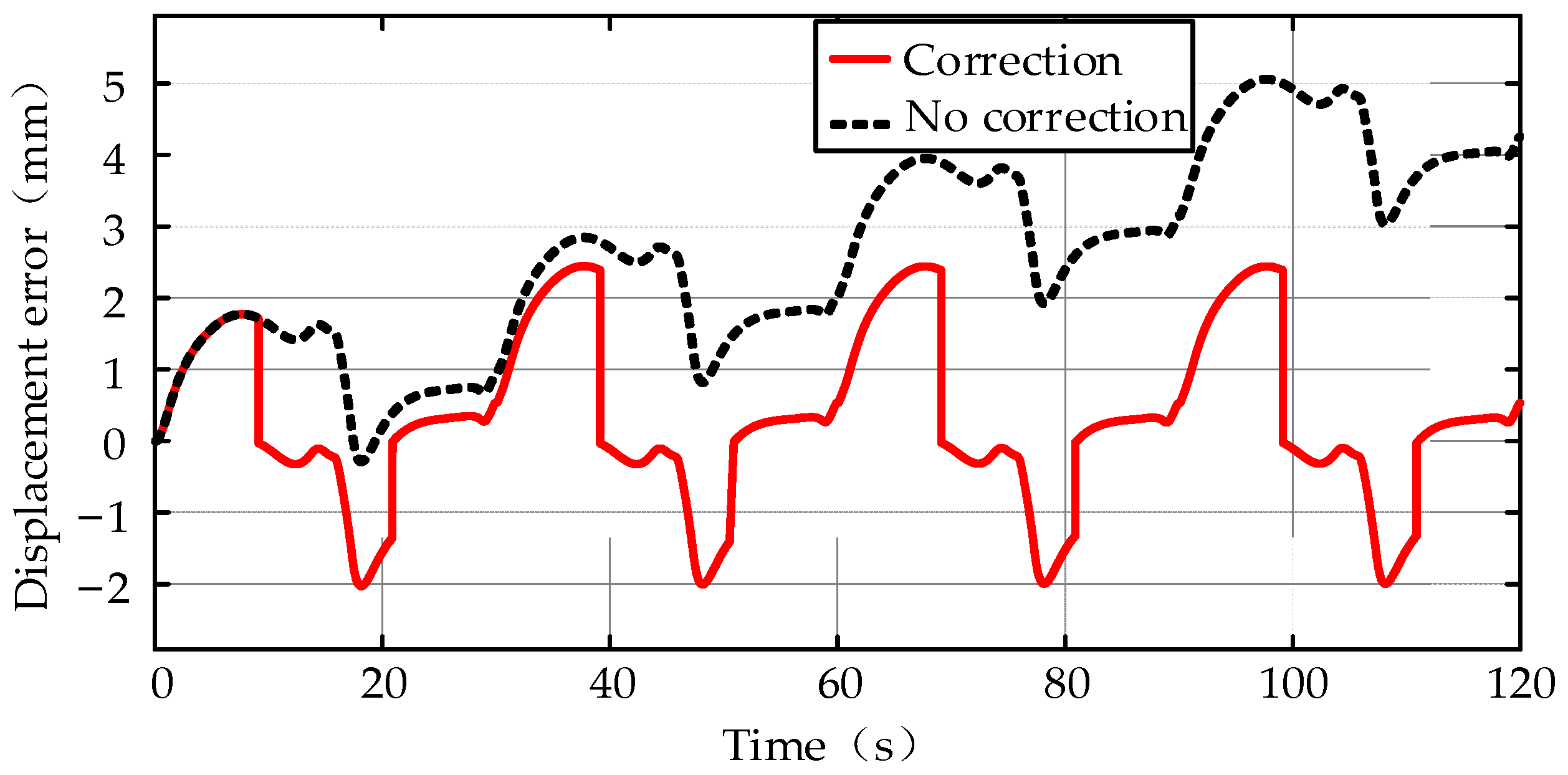
5.3. Accumulative Error Correction
6. Conclusions
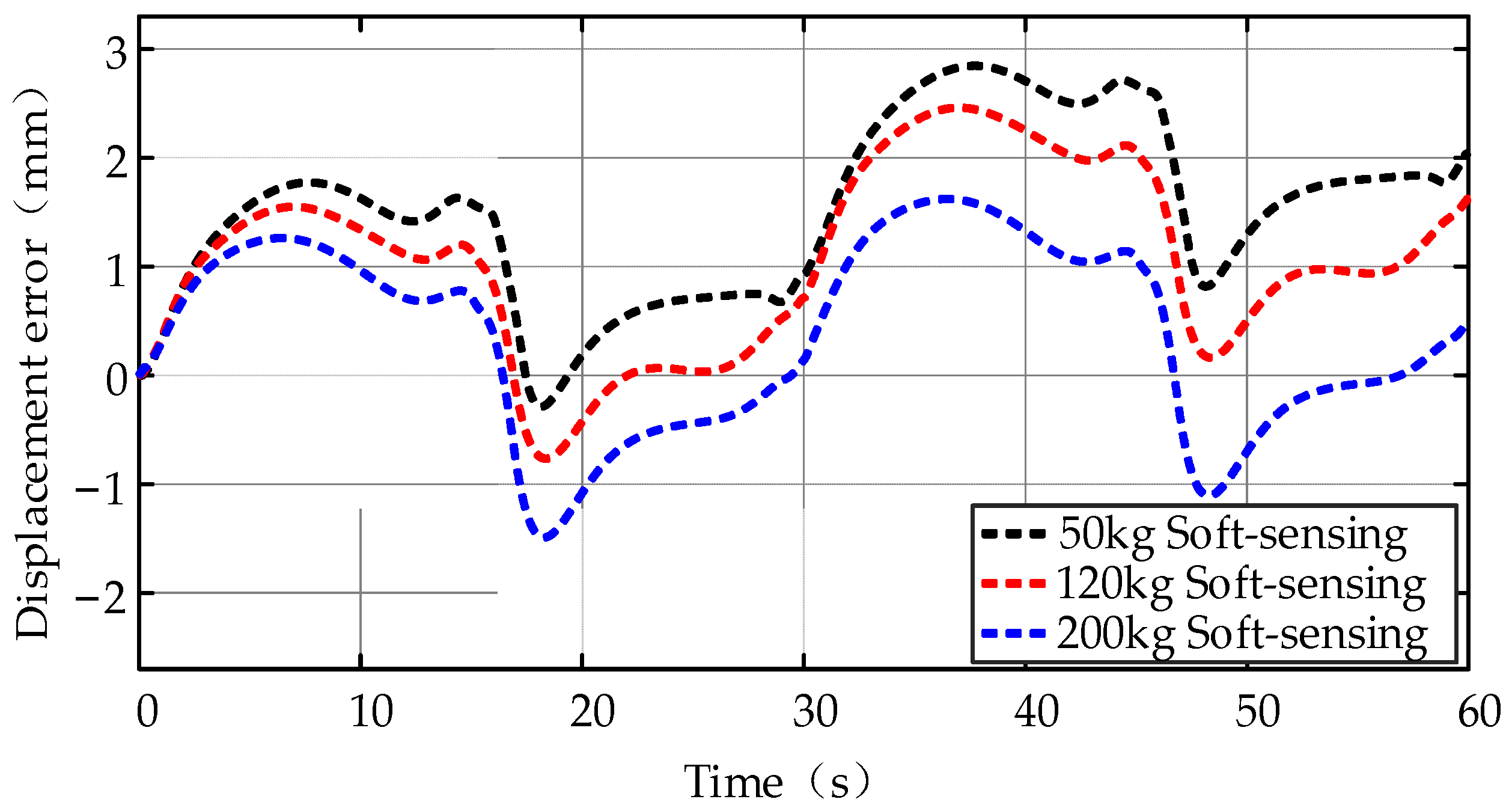
- The verification and simulations results show that the proposed position soft-sensing model for DDH had an accuracy within 7 mm and 4 mm, respectively, and the error rate was within 2.5%.
- Due to the notable accumulative error under multi-cycle, setting reference points can minimize the error accumulation. For example, when applying a middle reference point, the max error rate drops to 1%.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, H. Progress and Trend of Construction Machinery Intelligence. Constr. Mach. Technol. Manag. 2018, 31, 36–37. [Google Scholar]
- Zhang, S.; Minav, T.; Matti, P.; Huang, H. Performance Comparison between Single and Double Pump Controlled Asymmetric Cylinder under Four-quadrant Operation. Trans. Chin. Soc. Agric. Mach. 2018, 49, 409–419. [Google Scholar]
- Lee, S.; Hong, Y. A dual EHA system for the improvement of position control performance via active load compensation. Int. J. Precis. Eng. Manuf. 2017, 18, 937–944. [Google Scholar] [CrossRef]
- Tom, S.; Matti, P.; Minav, T.; Henri, H. Sensorless position estimation of simulated direct driven hydraulic actuators. In Proceedings of the 15th Scandinavian International Conference on Fluid Power, SICFP’17, Linköping, Sweden, 7–9 June 2017. [Google Scholar]
- Li, Y.; Fan, R.; Yang, L.; Zhao, B.; Quan, L. Research Status and Development Trend of Intelligent Excavators. J. Mech. Eng. 2020, 56, 165–178. [Google Scholar]
- Herceg, E.E. Taking a position on hydraulic cylinder sensors. Hydraul. Pneum. 2015, 68, 24. [Google Scholar]
- Lagozzino, S.; Simic, M.; Dudkiewicz, D. Development of a novel system for linear displacement sensor calibration. Energy Procedia 2019, 160, 519–525. [Google Scholar] [CrossRef]
- Staff, D.W. Magnetostrictive Sensor: Sizing and Applying. Available online: https://www.designworldonline.com/magnetostrictive-sensor/ (accessed on 30 September 2021).
- Hua, H.; Liao, Z.; Wu, X.; Chen, Y. A Bezier-based state calibrating method for the low-cost potentiometer with inherent nonlinearity. Measurement 2021, 178, 109325. [Google Scholar] [CrossRef]
- Danaee, S.; Nurmi, J.; Minav, T.; Mattila, J.; Pietola, M. Direct Position Control of Electro-Hydraulic Excavator. In Proceedings of the BATH/ASME 2018 Symposium on Fluid Power and Motion Control, Bath, UK, 27 July 2018. [Google Scholar]
- Wang, T.; Wang, Q.; Chen, Z. Sensorless Speed Tracking Control of PMSG Applied in Hydraulic Power Regeneration; IEEE: Budapest, Hungary, 2011; pp. 832–837. [Google Scholar]
- Rybarczyk, D. Application of the MEMS Accelerometer as the Position Sensor in Linear Electrohydraulic Drive. Sensors 2021, 21, 1479. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.J.; Lundeen, K.M.; McGee, W.; Menassa, C.C.; Lee, S.; Kamat, V.R. A vision-based marker-less pose estimation system for articulated construction robots. Autom. Constr. 2019, 104, 80–94. [Google Scholar] [CrossRef]
- Xu, J.; Yoon, H. Vision-based estimation of excavator manipulator pose for automated grading control. Autom. Constr. 2019, 98, 122–131. [Google Scholar] [CrossRef]
- Park, J.; Moon, D.; Yoon, H.; Gomez, F.; Spencer, B.F., Jr.; Kim, J.R. Visual-inertial displacement sensing using data fusion of vision-based displacement with acceleration. Struct. Control Health Monit. 2018, 25, e2122. [Google Scholar] [CrossRef]
- Minav, T.A.; Laurila, L.I.E.; Pyrhønen, J.J. Relative position control in an electro-hydraulic forklift. Int. Rev. Autom. Control 2013, 1, 54–61. [Google Scholar]
- Minav, T.; Bonato, C.; Sainio, P.; Pietola, M. Direct Driven Hydraulic Drive. In Proceedings of the 9th International Fluid Power Conference, Aachen, Germany, 24–26 March 2014. [Google Scholar]
- Danaee, S.; Minav, T.; Pietola, M. Sensorless Position Control For Electro-Hydraulic System—A technological status review. In 2018 Global Fluid Power Society PhD Symposium (GFPS); IEEE: Samara, Russia, 2018; pp. 1–6. [Google Scholar]
- Plöckinger, A.; Gradl, C.; Scheidl, R. High Accuracy Sensorless Hydraulic Stepping Actuator. In Proceedings of the Eighth Workshop on Digital Fluid Power (DFP 2016), Tampere, Finland, 24–25 May 2016. [Google Scholar]
- Gradl, C.; Plöckinger, A.; Scheidl, R. Sensorless position control with a hydraulic stepper drive—Concept, compression modeling and experimental investigation. Mechatronics 2016, 35, 91–101. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, L.; Liu, X.; Zhang, X. Soft-sensing Method for Cylinder Position of Pump-controlled System. Chin. Hydraul. Pneum. 2021, 45, 116–120. [Google Scholar]
- Zhu, H.; Lei, Y.; Xiaoyan, D. Displacement Sensorless Operation Control of Bearingless Permanent Magnet Synchronous Motor Based on BP Neural Network Left Inverse. Proc. CSEE 2020, 40, 3673–3681. [Google Scholar]
- Sun, X.; Chen, L.; Jiang, H.; Yang, Z.; Chen, J.; Zhang, W. High-Performance Control for a Bearingless Permanent-Magnet Synchronous Motor Using Neural Network Inverse Scheme Plus Internal Model Controllers. IEEE Trans. Ind. Electron. 2016, 63, 3479–3488. [Google Scholar] [CrossRef]
- Xiao, J.F.; Xiao, Q.M. Control of Switched Reluctance Motors based on Improved BP Neural Networks. Recent Adv. Electr. Electron. Eng. 2018, 11, 97–102. [Google Scholar]
- Agostini, T.; De Negri, V.; Minav, T.; Pietola, M. Effect of Energy Recovery on Efficiency in Electro-Hydrostatic Closed System for Differential Actuator. Actuators 2020, 9, 12. [Google Scholar] [CrossRef] [Green Version]
- Järf, A. Flow Compensation Using Hydraulic Accumulator in Direct Driven Hydraulic Differential Cylinder Application and Effects on Energy Efficiency. Master Thesis, Aalto University, Helsinki, Finland, 2016. [Google Scholar]
- Pourmovahed, A.; Beachley, N.H.; Fronczak, F.J. Modeling of a Hydraulic Energy Regeneration System: Part I—Analytical Treatment. J. Dyn. Syst. Meas. Control 1992, 114, 155–159. [Google Scholar] [CrossRef]
- Guo, Y.; Xiong, G.; Zeng, L.; Li, Q. Modeling and Predictive Analysis of Small Internal Leakage of Hydraulic Cylinder Based on Neural Network. Energies 2021, 14, 2456. [Google Scholar] [CrossRef]
- Alhanjouri, M. Speed Control of DC Motor Using Artificial Neural Network. Int. J. Sci. Res. (IJSR) 2017, 7, 2140–2148. [Google Scholar] [CrossRef]
- Johan, J.K.; Ebbesen, M.K.; Hansen, M.R. Novel Concept for Electro-Hydrostatic Actuators for Motion Control of Hydraulic Manipulators. Energies 2021, 20, 6566. [Google Scholar]

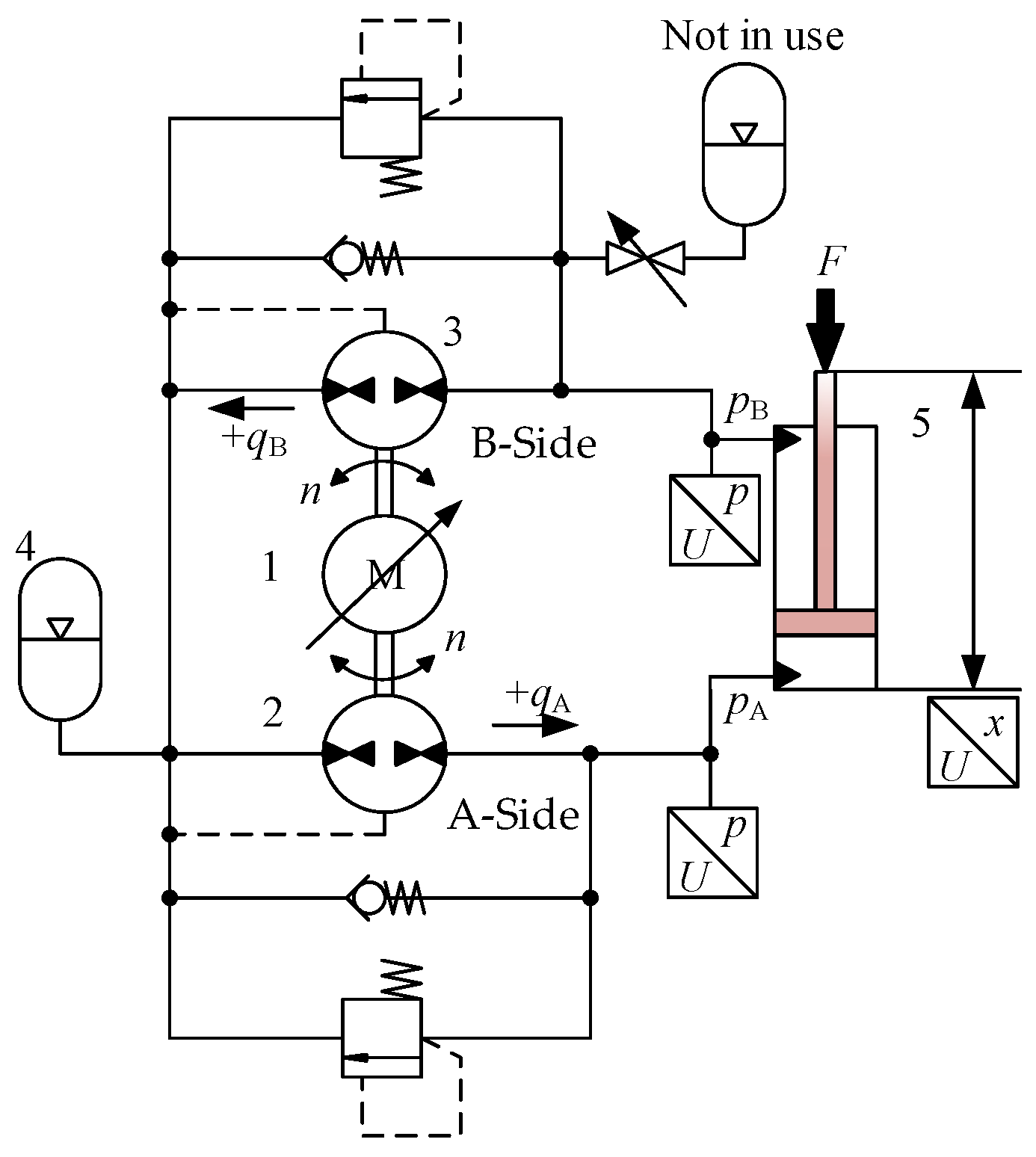












| NO. | Component | Parameters | Value | Description |
|---|---|---|---|---|
| 1 | Synchronous Motor | Rated Torque [N·m] Rated Speed [rpm] | 4.5 2500 | Rexroth IndraDyn T Synchronous Torque Motor |
| 2 | A-Side Pump/Motor | Volumetric Displacement [cm3/rev] | 13.03 | Rexroth External Gear motor AZMF Series |
| 3 | B-Side Pump/Motor | 9.35 | ||
| 4 | Hydraulic Accumulator | Rated Volume [L] | 0.7 | Rexroth Diaphragm Type |
| 5 | Cylinder | Dimensions [mm] Rated Pressure [MPa] | 60/30 × 40,019.0 | MIRO C-10 |
| 6 | Pressure Sensor | Pressure Range [MPa] Accuracy | 0–20 0.25% FS | GEMS 3100 Series |
| 7 | Position Sensor | Resolution [mm] | 0.1 | SIKO SGI Wire Incremental Encoder |
| Parameters | Value | Unit |
|---|---|---|
| d1 | 0.983 | m |
| d2 | 0.637 | m |
| m1 | 25.11 | kg |
| m2 | 21.40 | kg |
| mload | 50 | kg |
| r1 | 0.693 | m |
| r2 | 0.977 | m |
| rload | 1.674 | m |
| γ0 | 80 | degree |
| θm10 | 0.1169 | rad |
| θm20 | 0.1572 | rad |
| θmload | 0.1775 | rad |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Chen, T.; Minav, T.; Cao, X.; Wu, A.; Liu, Y.; Zhang, X. Position Soft-Sensing of Direct-Driven Hydraulic System Based on Back Propagation Neural Network. Actuators 2021, 10, 322. https://doi.org/10.3390/act10120322
Zhang S, Chen T, Minav T, Cao X, Wu A, Liu Y, Zhang X. Position Soft-Sensing of Direct-Driven Hydraulic System Based on Back Propagation Neural Network. Actuators. 2021; 10(12):322. https://doi.org/10.3390/act10120322
Chicago/Turabian StyleZhang, Shuzhong, Tianyi Chen, Tatiana Minav, Xuepeng Cao, Angeng Wu, Yi Liu, and Xuefeng Zhang. 2021. "Position Soft-Sensing of Direct-Driven Hydraulic System Based on Back Propagation Neural Network" Actuators 10, no. 12: 322. https://doi.org/10.3390/act10120322
APA StyleZhang, S., Chen, T., Minav, T., Cao, X., Wu, A., Liu, Y., & Zhang, X. (2021). Position Soft-Sensing of Direct-Driven Hydraulic System Based on Back Propagation Neural Network. Actuators, 10(12), 322. https://doi.org/10.3390/act10120322







