Abstract
A cascade proportional integral control method with back-electro motive force compensation has been widely used for permanent magnet synchronous motors. In the permanent magnet synchronous motor control, it is important to accurately know the back-electro motive force constant for torque generation as well as back-electro motive force compensation. In this study, a real-time back-electro motive force constant estimation algorithm is developed to improve the velocity tracking control performance. The proposed method consists of a proportional integral controller and a back-electro motive force constant estimator. The proportional integral controller is designed to reduce the velocity tracking error. The back-electro motive force constant estimator is designed to estimate the back-electro motive force constant. It was verified that the estimated back-electro motive force constant converges to the actual back-electro motive force constant. The estimated back-electro motive force constant is applied to the cascade proportional integral controller. To verify the effectiveness of the proposed method, the performance of the proposed method is validated experimentally.
1. Introduction
Permanent magnet synchronous motors (PMSMs) have been widely used in high-performance applications because of their significant advantages, such as high power density, high efficiency, and good dynamic performance [1]. Various control methods have been examined to improve the control performance of PMSMs [2,3,4,5,6]. LPV H control with disturbance estimation was proposed in [2]. Velocity control for sideband harmonics compensation was developed in [3]. To reduce torque oscillation, a model predictive direct speed control was utilized in [4]. An adaptive second-order sliding-mode observer was used for sensorless control considering the inverter nonlinearity in [5]. A robust speed regulation technique was designed to estimate the disturbances in [6].
Although these methods improve the control performance of PMSMs, they are complex in terms of implementation and gain tuning in industrial applications. Thus, cascade PI control with back-electro motive force (EMF) compensation has been widely used for industrial applications because it is simple to implement [7,8]. In this method, it is important to know the back-EMF constant for back-EMF compensation. Furthermore, the back-EMF constant is also used for torque generation as well as back-EMF compensation. In general, the flux linkage by the back-EMF in the PMSM model is presented as follows [9]:
where , P, and are the back-EMF constant, pole pair, and flux linkage, respectively. Unfortunately, the flux linkage may vary according to the variations of temperature, load torque [10,11,12,13]. For example, when using a neodymium magnet, NdFeB, the temperature increase reduces the magnetic flux density, which leads to a decrease in the control performance. Furthermore, estimating the nominal value of the model parameters in a static condition has limitations in enhancing the control performance because the flux linkage can change depending on velocity or current [14]. Thus, it is important to design the parameter identification method for the estimation of the back-EMF constant. There are two major approaches for parameter identification: off-line estimation and online estimation. Because the off-line estimation method does not reflect the effect on model parameters that change according to the environment, such as temperature variation and magnetic flux saturation. Various real-time online estimation approaches have been recently utilized in practical applications to determine model parameters. In [15], model reference adaptive PID controller was presented for CNC machine. Novel adaptive control of PMSM was proposed for electric vehicle in [16] A model reference adaptive system was developed for electrical parameter estimation to enhance the tracking performance in [17,18]. Online identification based on an extended Kalman filter was designed for interior PMSMs in [19]. An impedance-model-based multiparameter identification method was developed to identify flux linkage and resistance under various operation conditions in [20]. To estimate the flux linkage, different types of flux observers were designed in [9,14,21,22]. However, in these methods, the performance may degrade due to the load torque injection and/or the variation of the mechanical parameter.Furthermore, the estimation or adaptation methods for the whole back-EMF may result in the lag of the back-EMF estimation.
Against this background, this study proposes a real-time back-EMF constant estimation algorithm to improve the velocity tracking control performance of the PMSM. The performance of the cascade PI control method (where the dual PI controllers are used for both mechanical and electrical subsystems) according to the variation in the back-EMF constant is studied. The back-EMF constant estimator is designed to estimate the back-EMF constant. It is mathematically proven that the estimated back-EMF constant converges to the actual back-EMF constant. In the proposed method, only back-EMF constant is estimated so that the lag of the back-EMF estimation can be avoided. The estimated back-EMF constant is applied to the cascade PI control method for back-EMF compensation and torque generation. The performance of the proposed method was validated experimentally.
The remainder of this paper is organized as follows. Based on PMSM dynamics, the PI controller with back-EMF compensation is described in Section II. Section III introduces the design and analysis of the back-EMF constant estimator. The experimental results to demonstrate the effectiveness of the proposed estimator are provided in Section IV. Section V presents the conclusions.
2. Mathematical Modeling and Controller Design
2.1. PMSM Modeling
In this section, we describe the dynamic model of a three-phase synchronous motor with permanent magnets in , , coordinates as follows [2,3]:
where , and , are the current [A] and voltage [V] of phases and , respectively. In addition, is the rotor (angular) position [rad], is the rotor (angular) velocity [rad/s], B is the viscous friction coefficient [N·m·s/rad], J is the inertia of the motor [kg·m2/rad], R is the phase resistance of the phase winding [], and L is the phase inductance of the phase winding [H].
In this PMSM model, since the torque can be defined as
The back-EMF constant is used to generate the torque as well as back-EMF compensation.
2.2. PI Controller with Back-EMF Compensation
In several industrial applications, the cascade PI control method, where the dual PI controllers are used for both mechanical and electrical subsystems, has been widely applied for PMSM. To design a tracking controller, it is preferable to define the tracking errors as follows:
where is the desired velocity, and are the desired currents of phases and , respectively. First, the desired torque for velocity tracking is designed using the PI control as follows:
where and are the proportional and integral gains of velocity controller, respectively. From (2), the desired currents and for generating the desired torque (4) are derived using the commutation scheme as follows:
For the current tracking, and are obtained using the PI control and the back-EMF compensation as follows:
where and are the proportional and integral gains of current controller, respectively. The block diagram of the cascade PI control method with the back-EMF compensation is shown in Figure 1.
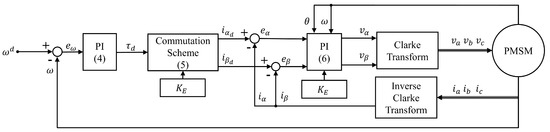
Figure 1.
Block diagram of the cascade PI control method with the back-EMF compensation.
3. Design and Analysis of Back-EMF Constant Estimator
3.1. Performance Analysis of Back-EMF Compensation
In this section, we analyze how the back-EMF constant affects the control performance using the following three cases:
- Case S.1: Cascade PI control without back-EMF compensation
- Case S.2: Cascade PI control with back-EMF compensation by 50% of the back-EMFswhere
- Case S.3: Cascade PI control with back-EMF compensation
The simulations were performed using MATLAB/Simulink for the performance analysis. Figure 2 shows the current tracking performance. In Case S.1, the magnitudes of the currents were reduced owing to the back-EMF in the current tracking. In Case S.2, although the 50% of the back-EMFs were rejected, the magnitudes of the currents were reduced because of inaccurate compensation of the back-EMFs. In Case S.3, the current tracking performance was the best among the three cases because the back-EMFs were rejected. These current tracking performances affect the velocity tracking performance, as shown in Figure 3. Similar to the current tracking performances, the velocity tracking performance of Case S.3 was the best among the three cases. From these simulation analyses, we observe that the accurate back-EMF compensation is important for the control performance of the PMSM.
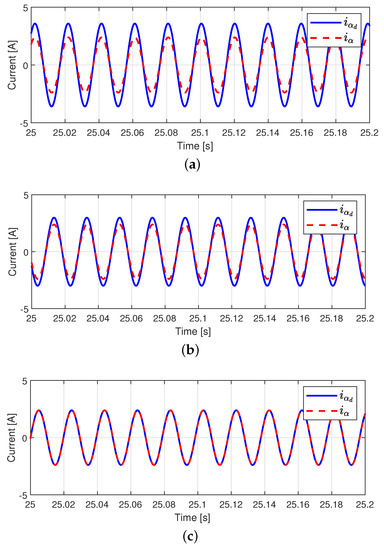
Figure 2.
Current tracking performance in simulation. (a) Case S.1. (b) Case S.2. (c) Case S.3.
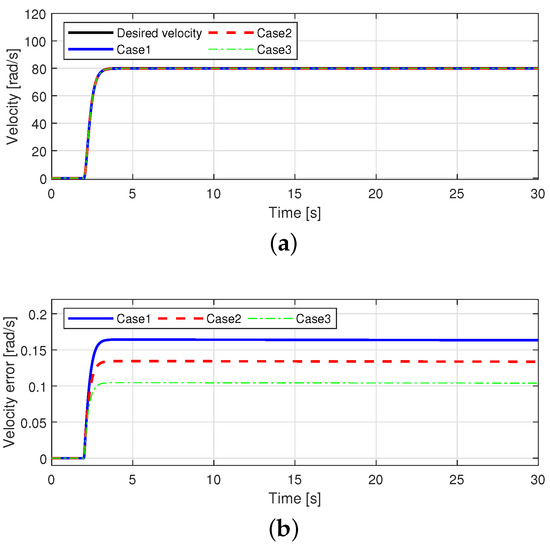
Figure 3.
Velocity tracking performance in simulation. (a) Velocity tracking performance. (b) Velocity tracking error.
3.2. Back-EMF Constant Estimator Design
The effect on the back-EMF constant has been investigated in the previous subsection. In this section, we develop the back-EMF constant estimator to avoid the lag of the back-EMF estimation. For the back-EMF constant , we develop the back-EMF constant estimator as follows: The magnetic flux varies for various reasons such as temperature, current, and velocity conditions. The back-EMF constant is derived as . The back-EMF constant may vary owing to the temperature changes, but it varies slowly [10]. Thus it is assumed that . The estimation algorithm for the back-EMF constant is designed as follows:
where is a positive constant, and is a positive odd integer. The estimation error is defined as follows:
Theorem 1.
Proof.
The estimation error dynamics are
During PMSM operation, locally and asymptotically converges to zero. □
Therefore, the control inputs can be represented as
The block diagram of the proposed method, including the cascade PI controller with back-EMF compensation and the back-EMF constant estimator, is shown in Figure 4.
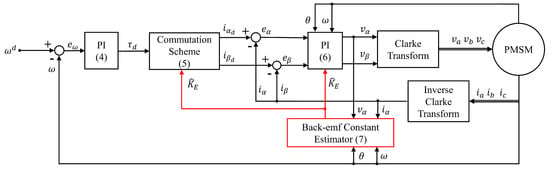
Figure 4.
Control block diagram of the proposed PI controller with the back-EMF constant estimator.
3.3. Tuning Guideline
In this section, we provide the procedure for the estimator gain tuning in order to replicate the proposed method under a different setup, which is as follows:
- Step 1: μ selectionSince operating frequency and electrical parameters are invariable in constant velocity range, estimation performance will be decided by choosing and . By (12), homogenous solution of differential equation can be represented aswhere t goes to infinity. is initial value of . .If magnitude of is relatively large, then is also large. So the convergence rate of is more faster. And if magnitude of is relatively small, then is also small. So the convergence rate of is more slower. Therefore, should be determined by the magnitude of the phase currents because there is a tradeoff relationship between and the phase currents.
- Step 2: selectionIn many industrial applications, it is common for measurement noise to be present in the signal measured from the sensor. Suppose that the measured angular velocity can be rewritten aswhere and are fundamental frequency and noise frequency obtained from the sensor, respectively. By this definition, the convergence rate, is redefined asIt means that high results in amplification of the measurement noise. Therefore, should be determined within a range that does not amplify the frequency of the measurement noise.
From the aforementioned procedure, we can analytically determine the back-EMF constant estimator gains and .
4. Experimental Results
Experiments were tested to validate the performance of the proposed method. Figure 5 shows the hardware configuration of the PMSM driver set. Experiments were performed using ControlDesk software, two RapidPro, and a SCALEXIO real-time system. We generated a real-time control code in MATLAB/Simulink to apply ControlDesk. SCALEXIO supported a sample rate of 40 kHz. Each RapidPro unit consisted of three half-bridge power stage modules. The two switches of each half-bridge were driven by complementary signals with dead time to prevent feed-through faults. Surface mounted PMSM (APM-SB03ADK-9, Kwapil & Co, Wien, Austria) was directly connected to an encoder (2500 pulses per revolution). The parameters used in the experiments and simulations were determined by referring to the data sheet. Powder brake was used to generate load torque. A personal computer was used to implement the control program in C language, compile the program, and upload executable output code to the SCALEXIO real-time system. The switching frequency was set to be 20 kHz. To evaluate the performance of the proposed estimator, we assume there is a control situation in which the nominal value of the back-EMF constant is not accurately known. Two cases were tested as follows:
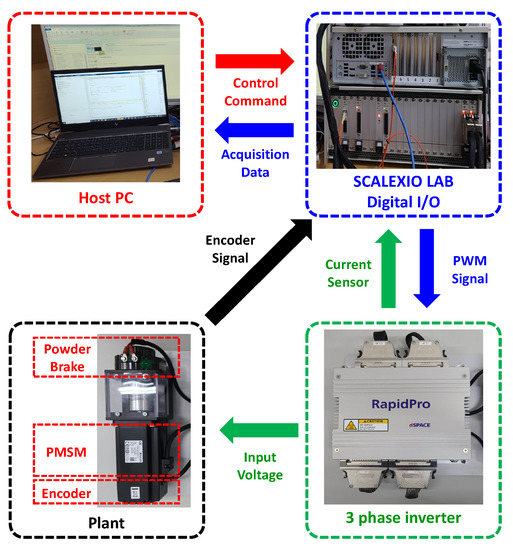
Figure 5.
PMSM experiments setup.
- Case 1: PI controller with = 0.105 (70% of nominal back-emf constant),
- Case 2: PI controller with (proposed back-EMF estimator).
The experimental setup parameters for PMSM and gains are listed in Table 1. For fair comparison, we use same control gains for two cases. The different three cases with two desired velocities (30 rad/s and 80 rad/s) were examined in the experiments.

Table 1.
PMSM parameters and gains.
4.1. 30 rad/s Operation
Figure 6 shows the desired velocity for 30 rad/s operation. Figure 7 shows the back-EMF constant estimation performance in Case 2. In the constant velocity region, the estimated back-EMF constant tracked the nominal back-EMF constant (=0.15) well. Figure 8 shows the velocity tracking performance for both cases. In Figure 8b, the velocity tracking error of Case 2 was relatively smaller than that of Case 1 because the back-EMF constant was accurately estimated by the proposed back-EMF estimator as shown in Figure 7.
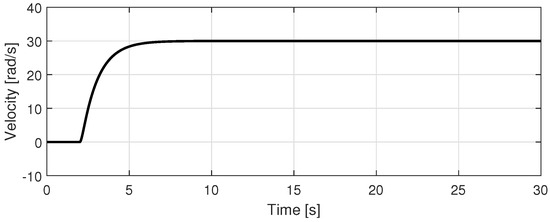
Figure 6.
Desired velocity ( = 30 rad/s).
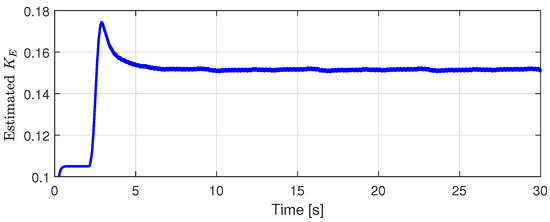
Figure 7.
Back-EMF estimation performance ( = 30 rad/s).
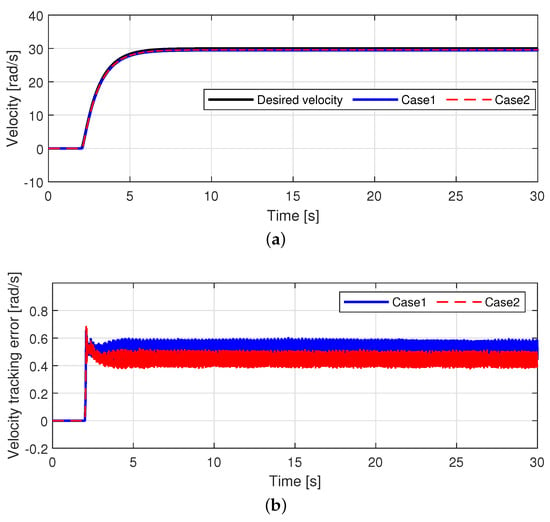
Figure 8.
Velocity tracking performance ( = 30 rad/s). (a) Velocity tracking performance. (b) Velocity tracking errors.
Figure 9 shows the current tracking performance and current tracking errors for both cases. In Figure 9a,b, even the phase delays of both methods are almost same, and the tracking performance of Case 2 is more close to the desired phase current compared to the phase current of Case 1. Therefore, in Case 2, the peak of the current tracking error decreased by approximately 10% from 1.37 A to 1.23 A.
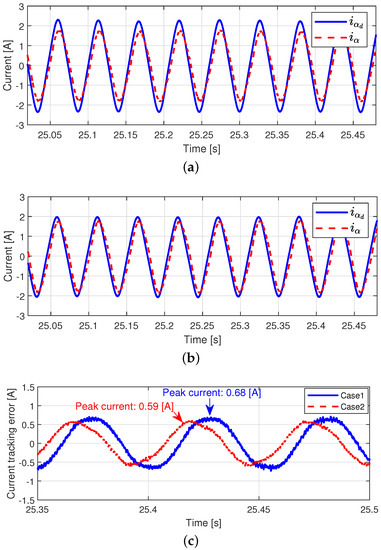
Figure 9.
Current tracking performances (30 rad/s Operation). (a) Current tracking performance (Case 1). (b) Current tracking performance (Case 2). (c) Current tracking errors.
4.2. 80 rad/s Operation
We conducted another experiment with 80 rad/s operation to evaluate the performance based on the presence of a load torque. Figure 10 shows the desired velocity for the 80 rad/s operation. A step load torque (=0.45 Nm) was injected after 16 s, as shown in Figure 11. Because the rated torque of the PMSM is 1.9 Nm, the injected load torque is approximately 23% of the rated torque.
Figure 10.
Desired velocity (80 rad/s Operation).
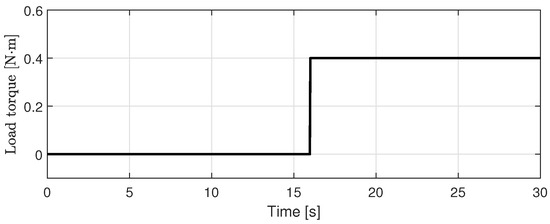
Figure 11.
Injected load torque (80 rad/s Operation).
Figure 12 shows the back-EMF constant estimation performance for Case 3. When the load torque was injected at 16 s, the estimated back-EMF constant was changed from 0.15 to 0.155. As mentioned in the introduction, the estimated back-EMF constant depends on the variation in the flux linkage. We can also observe fluctuations with a low frequency of the estimated back-EMF constant caused by structural vibration, such as the alignment of the mechanical coupler between the PMSM and the powder brake.
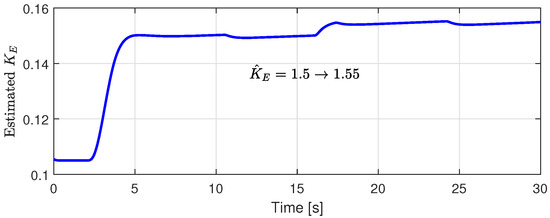
Figure 12.
Back-EMF estimation performance (80 rad/s Operation).
Figure 13 shows the velocity tracking performance for all cases. Before the load torque was injected, the velocity tracking errors of Case 2 were smaller than those of Case 1. After the load torque was applied, the velocity tracking error increased in both cases; however, it can be seen that the difference in velocity tracking error between Case 1 and Case 2 is relatively larger than before load torque application. In Case 2, the back-EMF constant according to the change in the experimental environment was well estimated, whereas the same back-EMF constant was still applied to the control input in Case 1; hence, this difference occurred after the load torque was injected. In contrast, the velocity tracking error of Case 2 was smaller than that of Case 2 after the load torque was injected at 16 s. After the load torque was injected, even if the flux linkage and the back-EMF constant were changed, the changed back-EMF constant was well estimated by the proposed estimator.
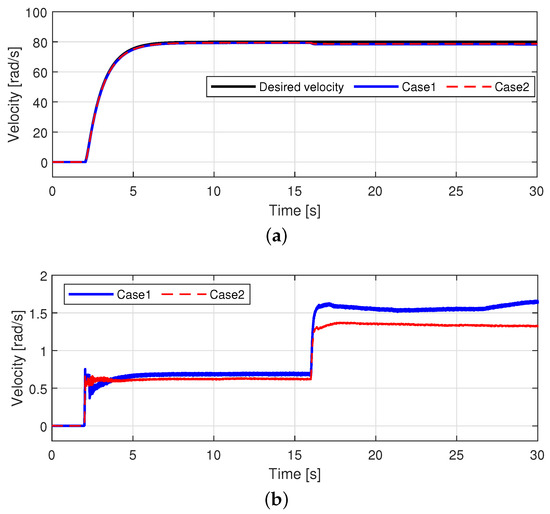
Figure 13.
Velocity tracking performance (80 rad/s Operation). (a) Velocity tracking performance. (b) Velocity tracking errors.
Figure 14 shows the current tracking performance and current tracking errors for both cases, respectively. Similar phase delay are observed in both cases, while the phase current well tracked the desired phase current in case 2. After the load torque injection, the peak of the current tracking error in case 2 was decreased by about 15 % from 1.95 A to 1.66 A compared with that of case 1, because current tracking performance was improved by designing the back-EMF constant estimator in case 2.
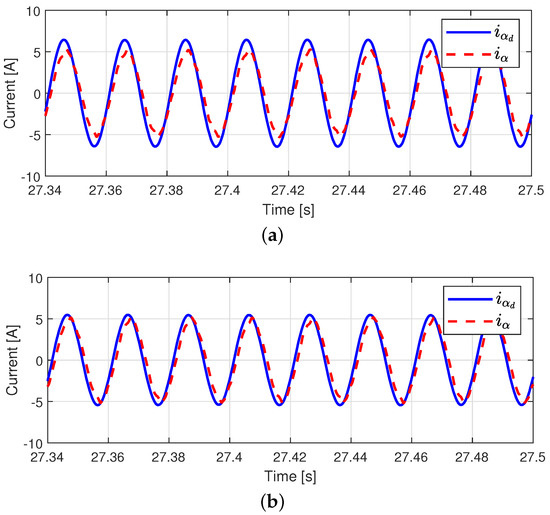
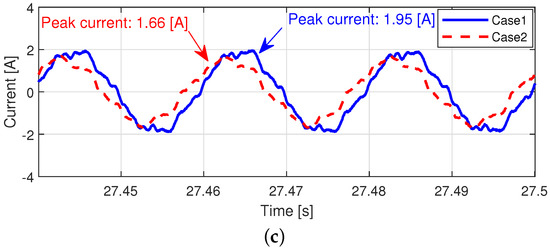
Figure 14.
Current tracking performance after load torque injection (80 rad/s Operation). (a) Current tracking performance (Case 1). (b) Current tracking performance (Case 2). (c) Current tracking errors.
4.3. Step Response
In this subsection, we conducted experiment with existing method [23] using step function as the desired velocity. Step time and final value of step function are 1 second and 40 rad/s, respectively. For fair comparison, the PI controller gains were determined with same gains used in the proposed method.
The velocity tracking performances are shown in Figure 15. Both methods have similar rising time (=0.065 s), whereas settling time of case 2 is faster than that of case 3. We can observe that the velocity tracking error of case 2 is smaller even though the same control gains were used in steady-state response. The velocity tracking errors were not zero, because an objective is not to optimize control performance in this paper.
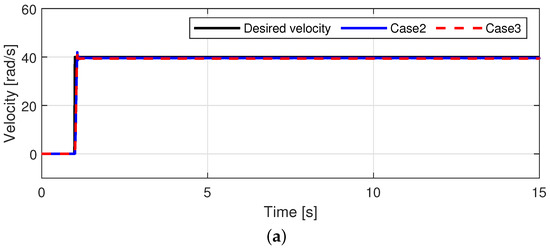
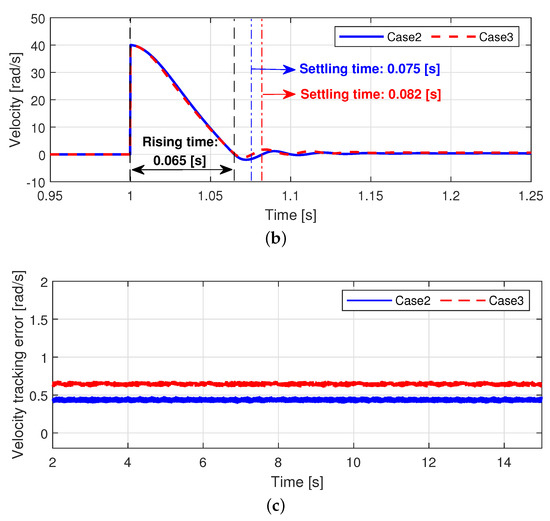
Figure 15.
Velocity tracking performance (Step response). (a) Velocity tracking performance. (b) Velocity tracking errors in transient region. (c) Velocity tracking errors in steady-state region.
Figure 16 shows the back-emf estimation performance. In the existing technique [23], since a nominal back-EMF signal, , was estimated, was estimated in both methods. The phase of the nominal back-EMF signal and the estimated back-EMF signal in case 2 are almost in-phase, whereas the phase delay was observed in case 3. This back-EMF estimation performance can affect the velocity tracking performance because the control input was designed by using the estimated back-EMF constant.
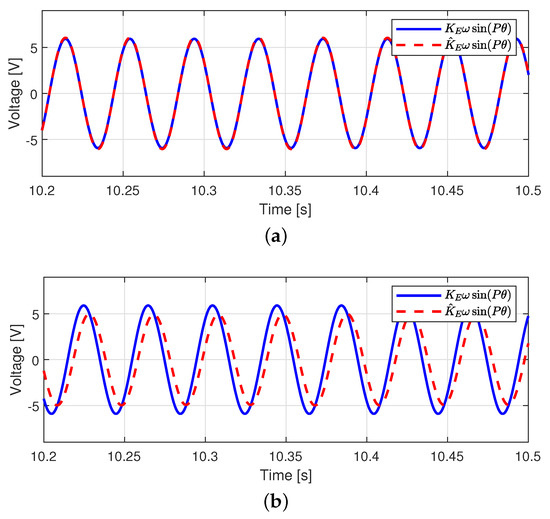
Figure 16.
Back-EMF estimation performance (Step response). (a) Case 2. (b) Case 3.
Figure 17 shows the current tracking performance. The estimated back-EMF constant, , was used in denominator of the desired phase current, magnitude of the desired current in case 3 is larger than that in case 2. However, we can observe that the both methods have different current tracking performance due to the difference in the back-EMF estimation performance. Therefore, the peak of the current tracking error in case 2 was smaller than that of case 3.
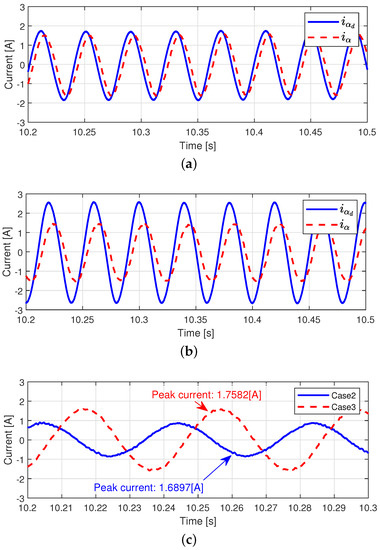
Figure 17.
Current tracking performance (Step response). (a) Current tracking performance (Case 2). (b) Current tracking performance (Case 3). (c) Current tracking errors.
5. Conclusions
In this paper, a real-time back-EMF constant estimation algorithm is proposed to enhance the velocity tracking control performance. The PI controller with the back-EMF constant estimator was designed to reduce the velocity tracking error. Using inaccurate back-EMF constants, an analysis was performed to find how the back-EMF constant affects the control performance. The back-EMF constant estimator is designed to estimate the back-EMF constant. Through experimental validation, it was observed that the back-EMF constant can be changed by the operating conditions such as the velocity, current, and load torque. The back-EMF constant was well estimated by the proposed real-time estimation algorithm under various operating conditions. We intend to estimate the back-EMF constant considering operating conditions such as the temperature and 3-phase unbalanced current in the future.
Author Contributions
J.G. and W.K. designed the algorithm and developed the simulation; S.Y. and Y.L. provided guidance in designing the algorithm; W.K. and Y.L. verified the simulation model and results; and all authors reviewed and approved the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Research Grant from DAWONSYS through the Korea Agency for Infrastructure Technology Advancement funded by the Ministry of Land, Infrastructure and Transport of the Korean Government under Project 21TBIP-C143153-04, in part by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2020R1I1A3073378).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no conflict of interest.
Abbreviations
| PI | Proportional integral |
| PID | Proportional integral differential |
| EMF | Electro motive force |
| PMSMs | Permanent magnet synchronous motors |
| LPV | Linear parameter varying |
| Nomenclature | |
| Rotor angular position [rad] | |
| Rotor angular velocity [rad/s] | |
| Mechanical torque [N· m] | |
| Current of phase [A] | |
| Current of phase [A] | |
| Voltage of phase [V] | |
| Voltage of phase [V] | |
| Desired rotor angular velocity [rad/s] | |
| Desired current of phase [A] | |
| Desired current of phase [A] | |
| Desired mechanical torque [N· m] | |
| Back-EMF constant [V·s/rad] | |
| P | Pole pair |
| Flux linkage [Wb] | |
| B | viscous friction of the motor [N·m·s/rad] |
| J | Inertia of the motor [kg·m2/rad] |
| R | Resistance of the phase winding [] |
| L | Inductance of the phase winding [H] |
| Estimation error of back-EMF constant [V·s/rad] | |
| Estimation state of back-EMF constant [V·s/rad] | |
| Proportional gain of velocity control loop | |
| Integral gain of velocity control loop | |
| Proportional gain of current control loop | |
| Integral gain of current control loop | |
| Estimator gains |
References
- Li, X.; Kennel, R. General formulation of Kalman-filter-based online parameter identification methods for VSI-fed PMSM. IEEE Trans. Ind. Electron. 2021, 58, 2856–2864. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.-H.; Chung, C.C. LPV H∞ control with disturbance estimation for permanent magnet synchronous motors. IEEE Trans. Ind. Electron. 2018, 65, 488–497. [Google Scholar] [CrossRef]
- Lee, Y.; Gil, J.; Kim, W. Velocity control for sideband harmonics compensation in permanent magnet synchronous motors with low switching frequency inverter. IEEE Trans. Ind. Electron. 2021, 68, 3434–3444. [Google Scholar] [CrossRef]
- Liu, M.; Chan, K.W.; Hu, J.; Xu, W.; Rodriguez, J. Model predictive direct speed control with torque oscillation reduction for PMSM drives. IEEE Trans. Ind. Inform. 2019, 15, 4944–4956. [Google Scholar] [CrossRef]
- Liang, D.; Li, J.; Qu, R.; Kong, W. Adaptive second-order sliding-mode observer for PMSM sensorless control considering VSI nonlinearity. IEEE Trans. Power Electron. 2018, 33, 8994–9004. [Google Scholar] [CrossRef]
- Yan, Y.; Yang, J.; Sun, Z.; Zhang, C.; Li, S.; Yu, H. Robust Speed Regulation for PMSM Servo System with multiple sources of disturbances via an augmented disturbance observer. IEEE/ASME Trans. Mechatron. 2018, 23, 769–780. [Google Scholar] [CrossRef]
- Choi, J.-W.; Sul, S.-K. Generalized solution of minimum time current control in three-phase balanced systems. IEEE Trans. Ind. Electron. 1998, 45, 738–744. [Google Scholar] [CrossRef]
- Kong, W.Y.; Holmes, D.G.; McGrath, B.P. Enhanced three phase ac stationary frame PI current regulators. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 91–98. [Google Scholar]
- Xu, W.; Jiang, Y.; Mu, C.; Blaabjerg, F. Improved nonlinear flux observer-based second-order SOIFO for PMSM sensorless control. IEEE Trans. Power Electron. 2019, 34, 565–579. [Google Scholar] [CrossRef] [Green Version]
- Hanselman, D. Brushless Permanent Magnet Motor Design; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Liu, K.; Zhu, Z.Q.; Stone, D.A. Parameter estimation for condition monitoring of PMSM stator winding and rotor permanent magnets. IEEE Trans. Ind. Electron. 2013, 60, 5902–5913. [Google Scholar] [CrossRef] [Green Version]
- Milanfar, P.; Lang, J.H. Monitoring the thermal condition of permanent-magnet synchronous motors. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1421–1429. [Google Scholar] [CrossRef]
- Fernandez, D.; Reigosa, D.; Tanimoto, T.; Kato, T.; Briz, F. Wireless permanent magnet temperature & field distribution measurement system for IPMSMs. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3996–4003. [Google Scholar]
- Pulvirenti, M.; Scarcella, G.; Scelba, G.; Testa, A.; Harbaugh, M.M. On-line stator resistance and permanent magnet flux linkage identification on open-end winding PMSM drives. IEEE Trans. Ind. Appl. 2019, 55, 504–515. [Google Scholar] [CrossRef]
- Gai, H.; Li, X.; Jiao, F.; Cheng, X.; Yang, X.; Zheng, G. Application of a New Model Reference Adaptive Control Based on PID Control in CNC Machine Tools. Machines 2021, 9, 274. [Google Scholar] [CrossRef]
- Xiao, R.; Wang, Z.; Zhang, H.; Shen, J.; Chen, Z. A Novel Adaptive Control of PMSM for Electric Vehicle. In Proceedings of the 2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 11–14 December 2017; pp. 1–8. [Google Scholar]
- Piippo, A.; Hinkkanen, M.; Luomi, J. Adaptation of motor parameters in sensorless PMSM drives. IEEE Trans. Ind. Appl. 2009, 45, 203–212. [Google Scholar] [CrossRef] [Green Version]
- Cao, P.; Zhang, X.; Yang, S. A unified-model-based analysis of MRAS for online rotor time constant estimation in an induction motor drive. IEEE Trans. Ind. Electron. 2017, 64, 4361–4371. [Google Scholar] [CrossRef]
- Shi, Y.; Sun, K.; Huang, L.; Li, Y. Online identification of permanent magnet flux based on extended Kalman filter for IPMSM drive with position sensorless control. IEEE Trans. Ind. Electron. 2012, 59, 4169–4178. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, G.; Zhao, N.; Zhang, G.; Cui, Q.; Xu, D. An impedance model-based multiparameter identification method of PMSM for both offline and online conditions. IEEE Trans. Power Electron. 2021, 36, 727–738. [Google Scholar] [CrossRef]
- Jang, M.; Akatsu, K. Magnet operating point estimation using flux linkage observer and magnetic and thermal equivalent circuit in PMSM. IEEJ J. Ind. Appl. 2021, 21006173. [Google Scholar] [CrossRef]
- Zhu, X.; Hua, W.; Wang, W.; Huang, W. Analysis of back-EMF in flux-reversal permanent magnet machines by air gap field modulation theory. IEEE Trans. Ind. Electron. 2019, 66, 3344–3355. [Google Scholar] [CrossRef]
- Park, J.S.; Lee, S.H.; Moon, C.; Kwon, Y.A. State observer with stator resistance and back-EMF constant estimation for sensorless PMSM. In Proceedings of the TENCON 2010—2010 IEEE Region 10 Conference, Fukuoka, Japan, 21–24 November 2010; pp. 31–36. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).