RETRACTED: A Closed-Loop Control Mathematical Model for Photovoltaic-Electrostatic Hybrid Actuator with a Slant Lower Electrode Based on PLZT Ceramic
Abstract
:1. Introduction
2. Mathematical Modeling of Photovoltaic-Electrostatic Hybrid Actuator with a Slant Lower Electrode
2.1. Photovoltaic-Electrostatic Hybrid Actuator
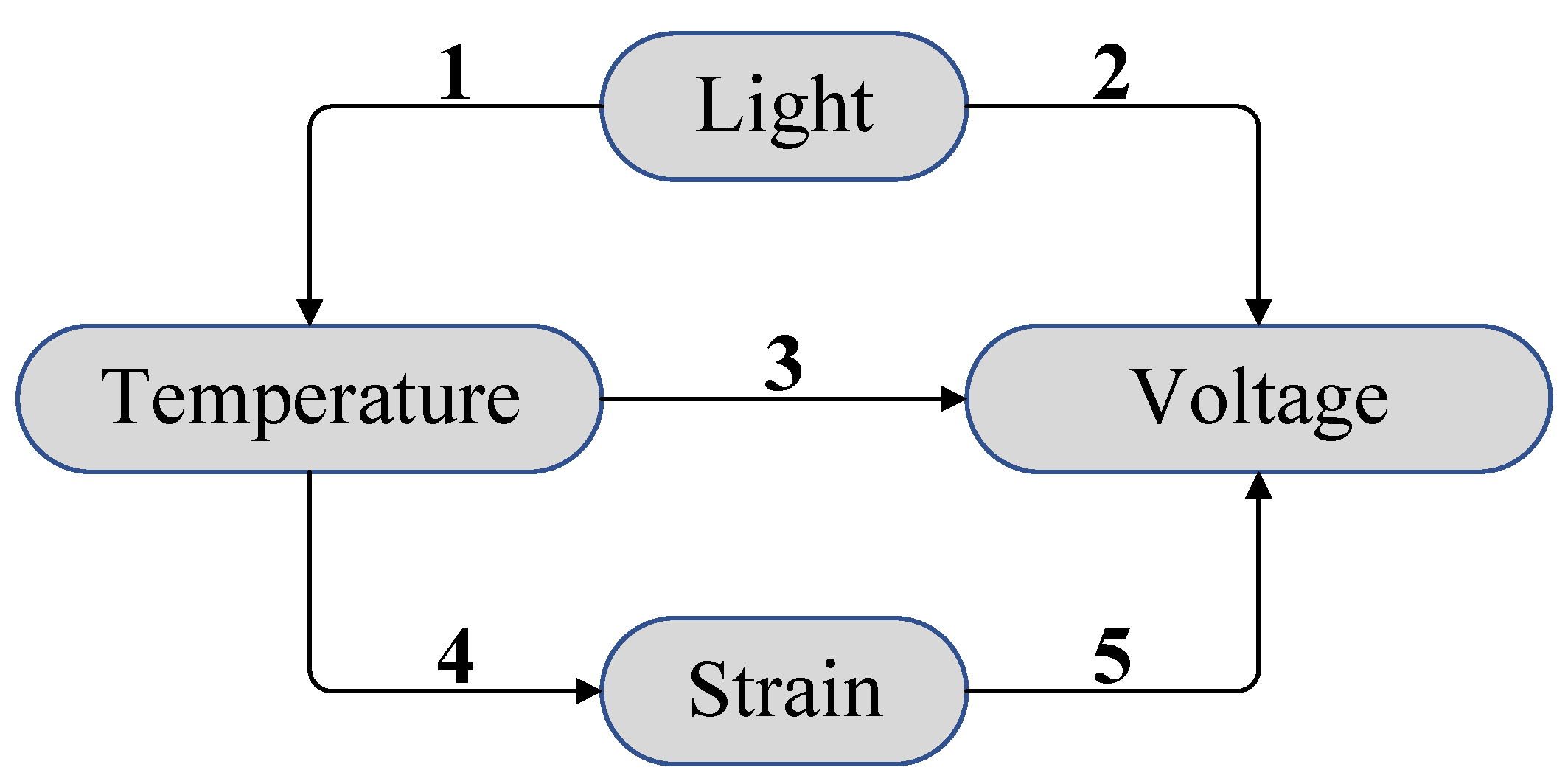
2.2. Mathematical Modeling of Photovoltage of PLZT Ceramic
2.3. Mechanical Modeling of Photovoltaic-Electrostatic Hybrid Actuator
3. Closed-Loop Control Method of Photovoltaic-Electrostatic Hybrid Actuator with a Slant Lower Electrode
3.1. Parameters Identification
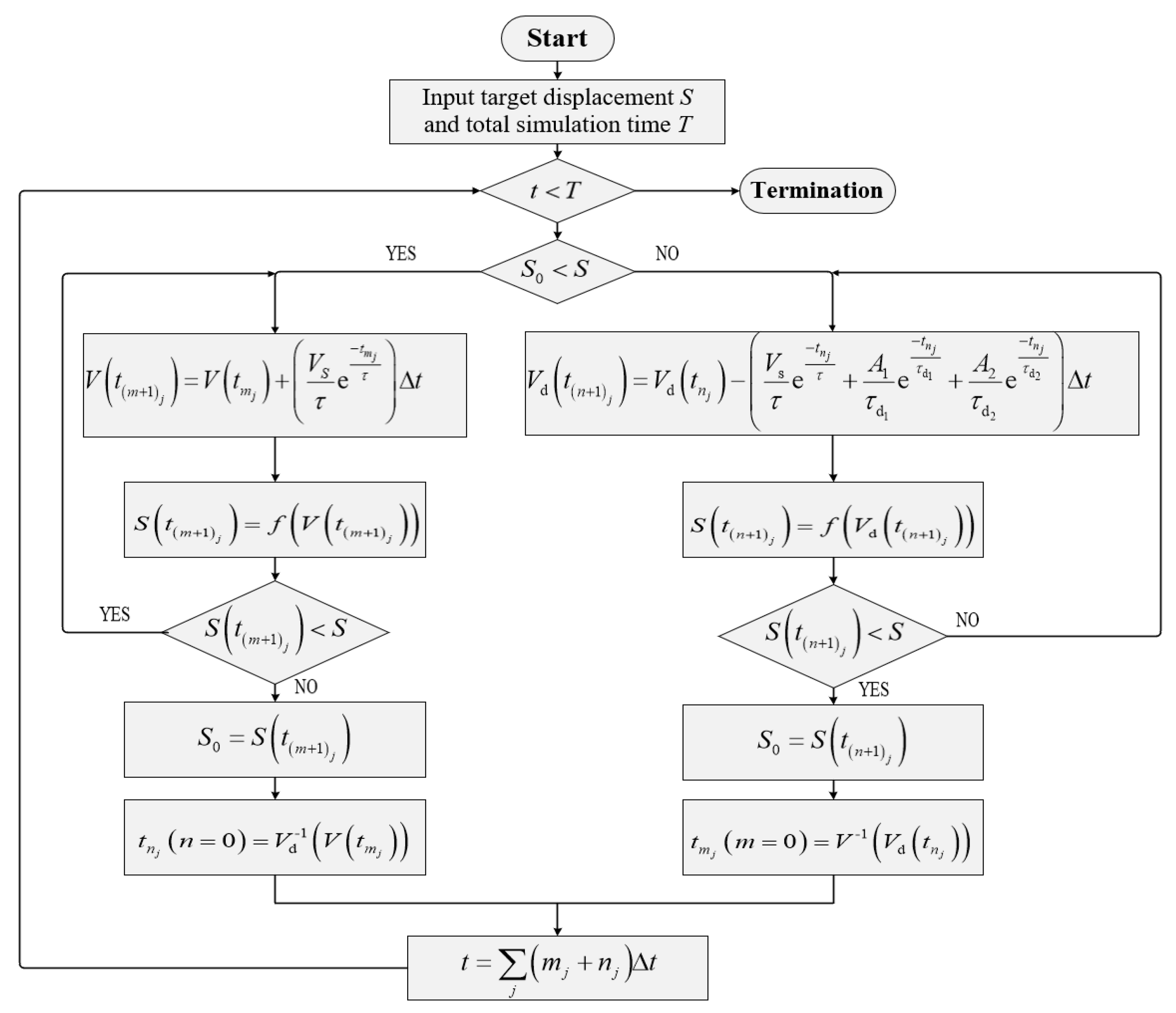
3.2. Closed-Loop Control Equations
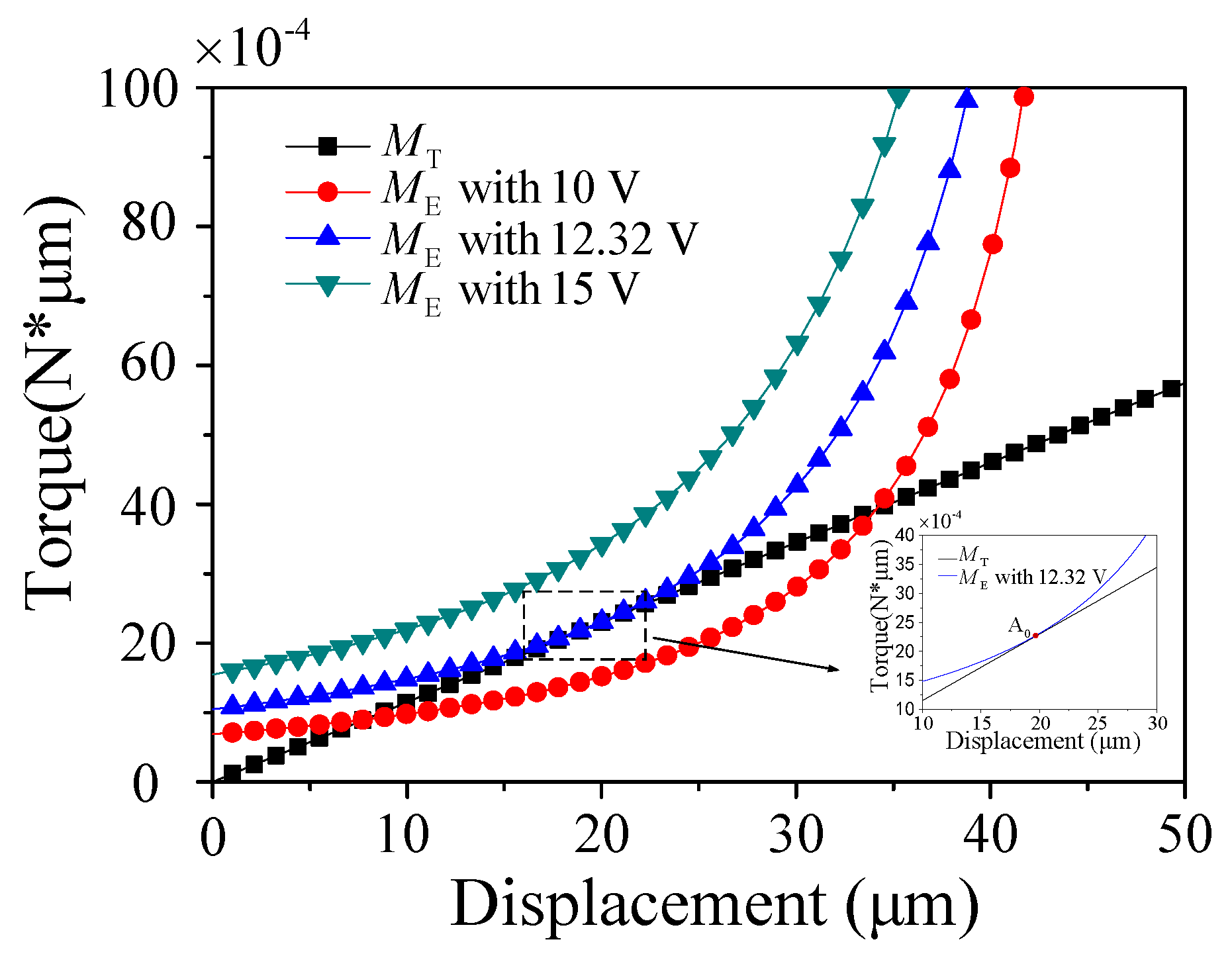
4. Results and Discussions
- (1)
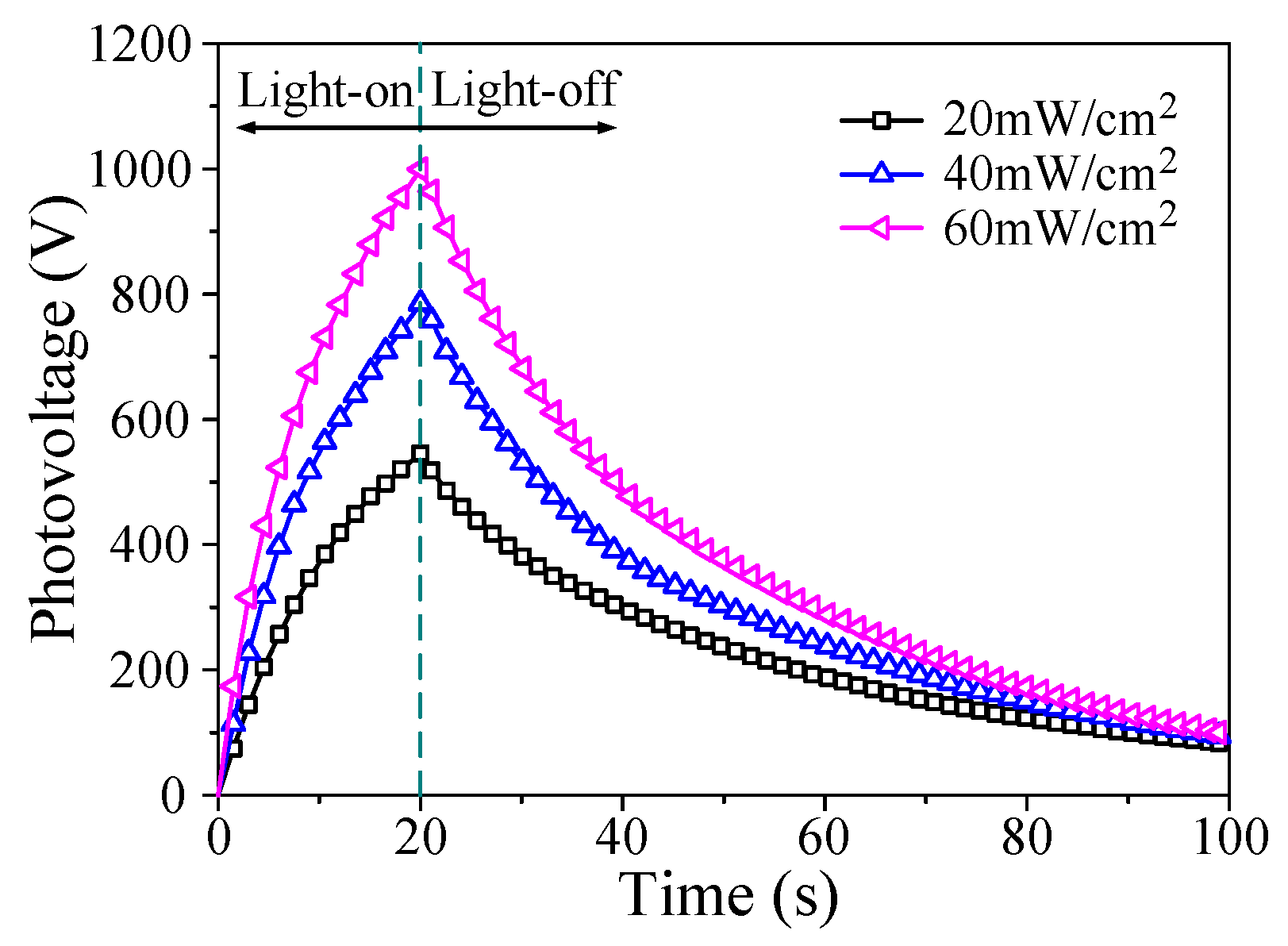
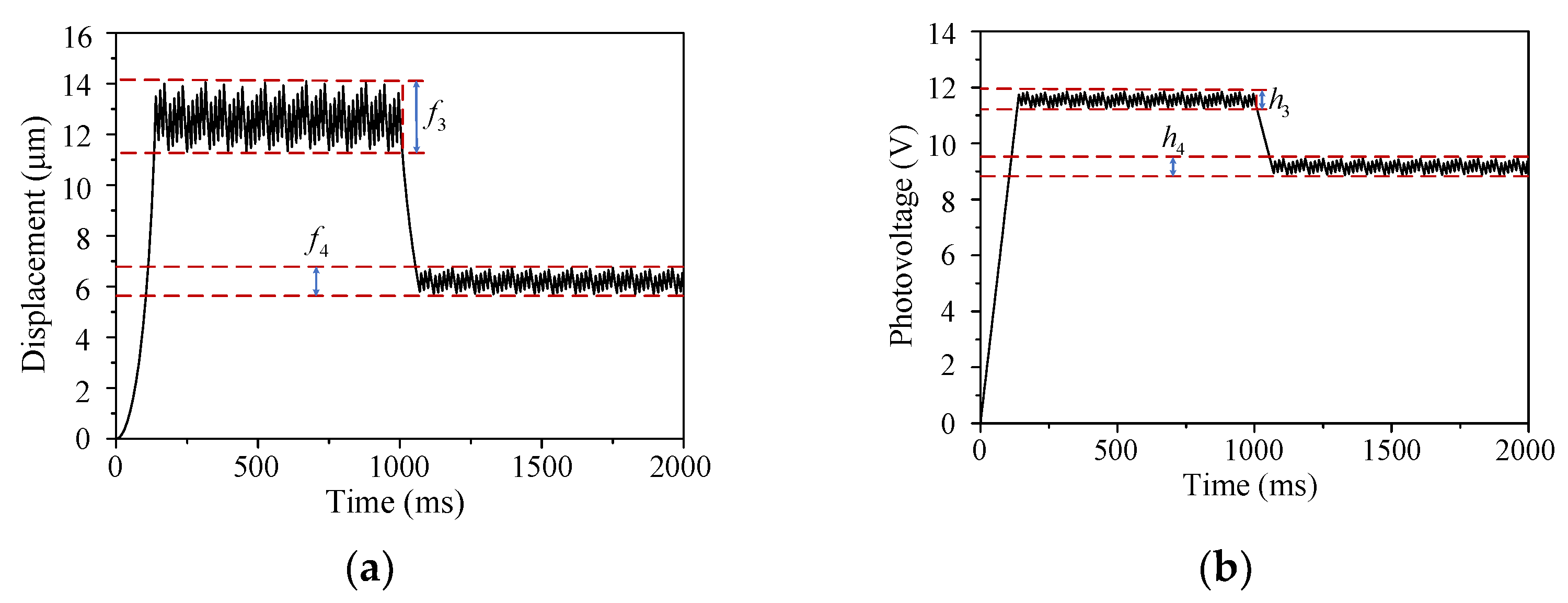
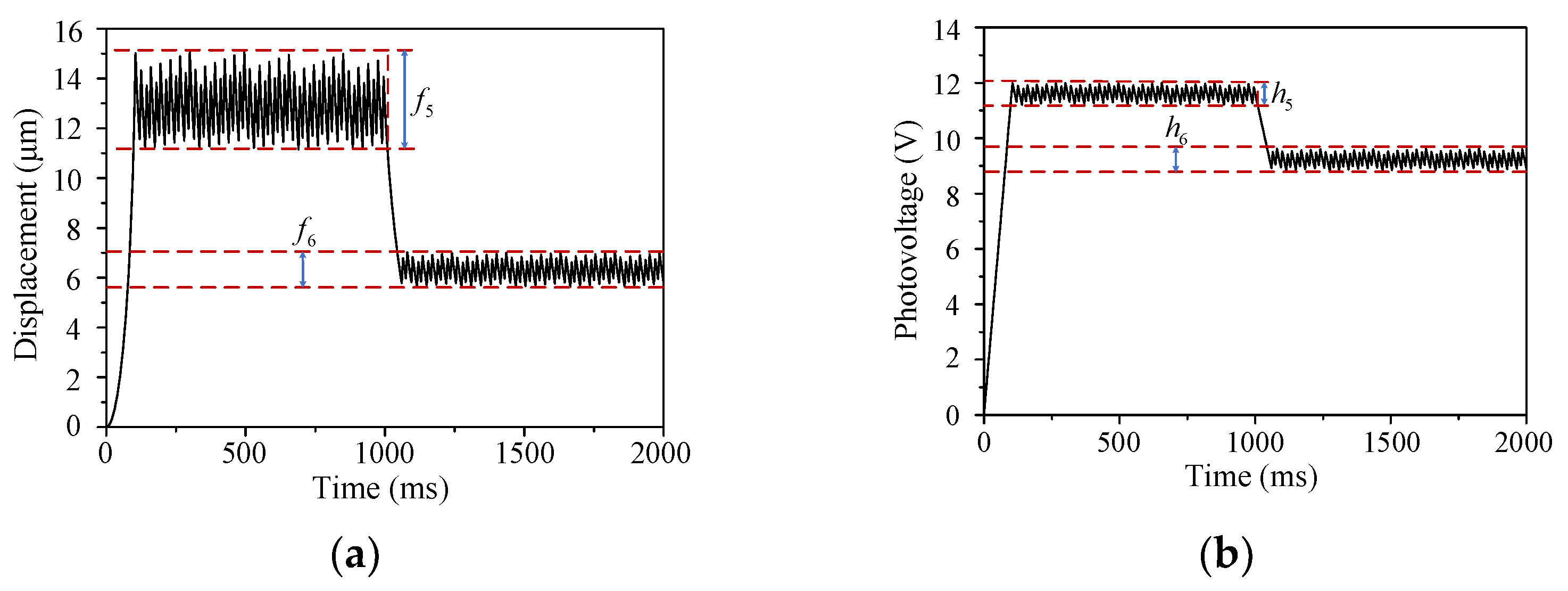
- The greater the light intensity, the shorter the response time to the target displacement for the upper electrode tip can be obtained. When the light intensity is 60 mW/cm2, the response time is only about 45% of that under 20 mW/cm2.
- (2)
- The maximal fluctuation heights around target displacement increase with the increase of the light intensity.
- (3)
- Under the same light intensity, the maximal fluctuation height around 12 μm is larger than around 6 μm. That is to say, the closer the output displacement is to the pull-in point, the more sensitive the displacement is to the change of driving voltage.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hubbard, N.B.; Culpepper, M.L.; Howell, L.L. Actuators for Micropositioners and Nanopositioners. Appl. Mech. Rev. 2006, 59, 324–334. [Google Scholar] [CrossRef]
- Mozhdehi, R.J.; Ghafari, A.S.; Khayyat, A.A.A. Design of electrostatic actuators for suppressing vertical disturbances of CMOS-MEMS capacitive force sensors in bio applications. Mech. Ind. 2015, 16, 306. [Google Scholar] [CrossRef]
- Brody, P.S. Optomechanical bimorph actuator. Ferroelectrics 1983, 50, 27–32. [Google Scholar] [CrossRef]
- Yue, H.H.; Sun, G.L.; Deng, Z.Q. Distributed shell control with a new multi-DOF photostrictive actuator design. J. Sound Vib. 2010, 329, 3647–3659. [Google Scholar] [CrossRef]
- Jiang, J.; Yue, H.H.; Deng, Z.Q. Active vibration control of an open cylindrical shell based on a 0-3 polarized PLZT photostrictive actuator. J. Vib. Shock. 2013, 32, 106–111. [Google Scholar]
- Zheng, S.J.; Lian, J.J.; Wang, H.T. Genetic algorithm based wireless vibration control of multiple modal for a beam by using photostrictive actuators. Appl. Math. Model. 2014, 38, 437–450. [Google Scholar]
- He, R.; Zheng, S.; Tong, L. Multimodal vibration control of photo-electric laminated thin cylindrical shells via self-organizing fuzzy sliding mode control. J. Vib. Acoust. 2016, 138, 041003. [Google Scholar] [CrossRef]
- Kikuchi, S.; Takagi, K.; Watanabe, R. Photostrictive characteristics of fine-grained plzt ceramics derived from mechanically alloyed powder. J. Jpn. Soc. Powder Powder Metall. 2004, 50, 572–576. [Google Scholar] [CrossRef]
- Lu, F.; Wang, X.J.; Huang, J.H. Theoretical and experimental analysis of an optical driven servo system. Smart Mater. Struct. 2016, 25, 095054. [Google Scholar] [CrossRef]
- Wang, X.J.; Huang, J.H.; Wang, J. Experimental research on the response characteristics of PLZT ceramics. Smart Mater. Struct. 2015, 24, 75017. [Google Scholar] [CrossRef]
- Huang, J.H.; Wang, X.J.; Wang, J. A mathematical model for predicting photo-induced voltage and photostriction of PLZT with coupled multi-physics fields and its application. Smart Mater. Struct. 2016, 25, 025002. [Google Scholar] [CrossRef]
- Jiang, J.; Li, X.; Ding, J. Mathematical model and characteristic analysis of hybrid photovoltaic/piezoelectric actuation mechanism. Smart Mater. Struct. 2016, 25, 125021. [Google Scholar] [CrossRef]
- Wang, X.J.; Lu, F.; Qiao, K. Closed-loop control for deflection of cantilever beam based on hybrid photovoltaic/piezoelectric actuation mechanism. Int. J. Appl. Electromagn. Mech. 2016, 53, 1–13. [Google Scholar] [CrossRef]
- Liu, Y.F.; Wang, X.J.; Wang, J. Investigation on influence factors of opto-electrostatic hybrid driving torsion actuator based on PLZT ceramic. Mater. Sci. Eng. B 2021, 263, 114798. [Google Scholar] [CrossRef]
- Wang, X.J.; Lu, F.; Huang, J.H. Closed-loop photovoltage control of lead lanthanum zirconate titanate ceramic for photovoltaic-electrostatic-driven servo system. J. Intell. Mater. Syst. Struct. 2017, 28, 2572–2578. [Google Scholar] [CrossRef]
- Huang, J.H.; Wang, X.J.; Wang, J. A study on residual photovoltage and photo-induced strain in plzt ceramic with coupled multi-physics fields. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13 November 2015. [Google Scholar]
- Fridkin, V.M. Photoferroelectrics; Springer: New York, NY, USA, 1979. [Google Scholar]
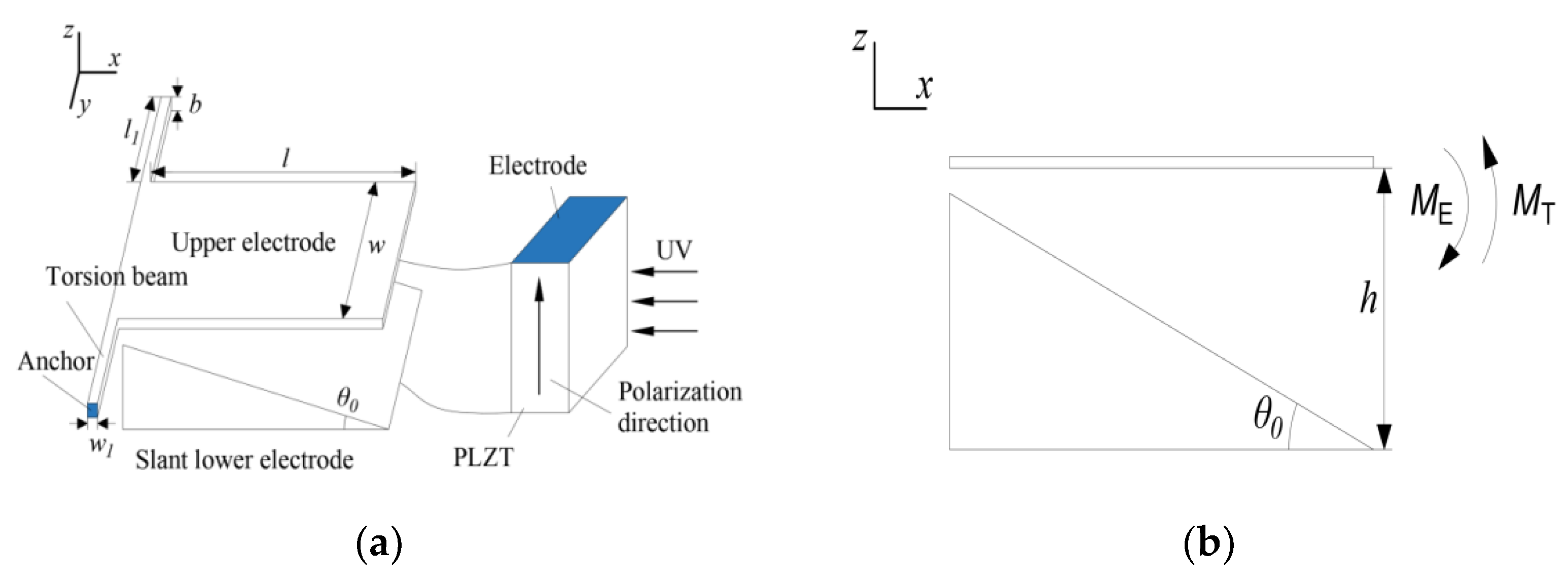


| Parameters | Value |
|---|---|
| Width of the torsion beam (w1) | 10 μm |
| Thickness of the torsion beam (b) | 10 μm |
| Length of the upper electrode (l) | 1600 μm |
| Width of the upper electrode (w) | 900 μm |
| Maximum distance between the two electrodes (h) | 50 μm |
| Length of the torsion beam (l1) | 800 μm |
| Slant angle of the lower electrode (θ0) | 1.6° |
| Light Intensity (mW/cm2) | Parameter | ||||||
|---|---|---|---|---|---|---|---|
| VS | τ | V0 | A1 | A2 | τd1 | τd2 | |
| 20 | 694.3520 | 13.0634 | 9.0043 | 1522.1006 | 684.5588 | 7.1986 | 44.8564 |
| 40 | 908.3209 | 10.7538 | 0.0266 | 2140.1163 | 919.9657 | 8.6733 | 43.7224 |
| 60 | 1127.7553 | 9.8232 | −18.3623 | 1239.8818 | 2096.6772 | 42.4285 | 9.4857 |
| Light Intensity | Response Time | Maximal Fluctuation Height around 12 μm | Maximal Fluctuation Height around 12 μm |
|---|---|---|---|
| 20 (mW/cm2) | 220 ms | 1.6 μm | 0.8 μm |
| 40 (mW/cm2) | 140 ms | 2.9 μm | 1.1 μm |
| 60 (mW/cm2) | 100 ms | 4 μm | 1.5 μm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Z.; Uzair, M.; Wang, X.; Liu, Y. RETRACTED: A Closed-Loop Control Mathematical Model for Photovoltaic-Electrostatic Hybrid Actuator with a Slant Lower Electrode Based on PLZT Ceramic. Actuators 2021, 10, 285. https://doi.org/10.3390/act10110285
Lv Z, Uzair M, Wang X, Liu Y. RETRACTED: A Closed-Loop Control Mathematical Model for Photovoltaic-Electrostatic Hybrid Actuator with a Slant Lower Electrode Based on PLZT Ceramic. Actuators. 2021; 10(11):285. https://doi.org/10.3390/act10110285
Chicago/Turabian StyleLv, Zhen, Muhammad Uzair, Xinjie Wang, and Yafeng Liu. 2021. "RETRACTED: A Closed-Loop Control Mathematical Model for Photovoltaic-Electrostatic Hybrid Actuator with a Slant Lower Electrode Based on PLZT Ceramic" Actuators 10, no. 11: 285. https://doi.org/10.3390/act10110285
APA StyleLv, Z., Uzair, M., Wang, X., & Liu, Y. (2021). RETRACTED: A Closed-Loop Control Mathematical Model for Photovoltaic-Electrostatic Hybrid Actuator with a Slant Lower Electrode Based on PLZT Ceramic. Actuators, 10(11), 285. https://doi.org/10.3390/act10110285







