Optimal Design of Magneto-Force-Thermal Parameters for Electromagnetic Actuators with Halbach Array
Abstract
:1. Introduction
2. Modeling of the Magnetic Field of a Non-Equal-Size Halbach Array
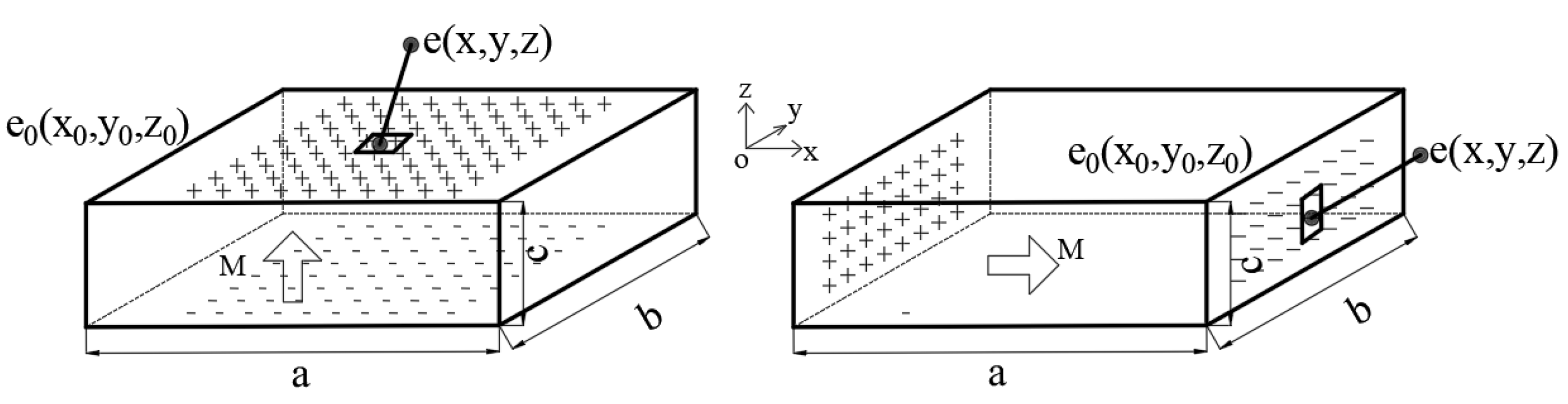
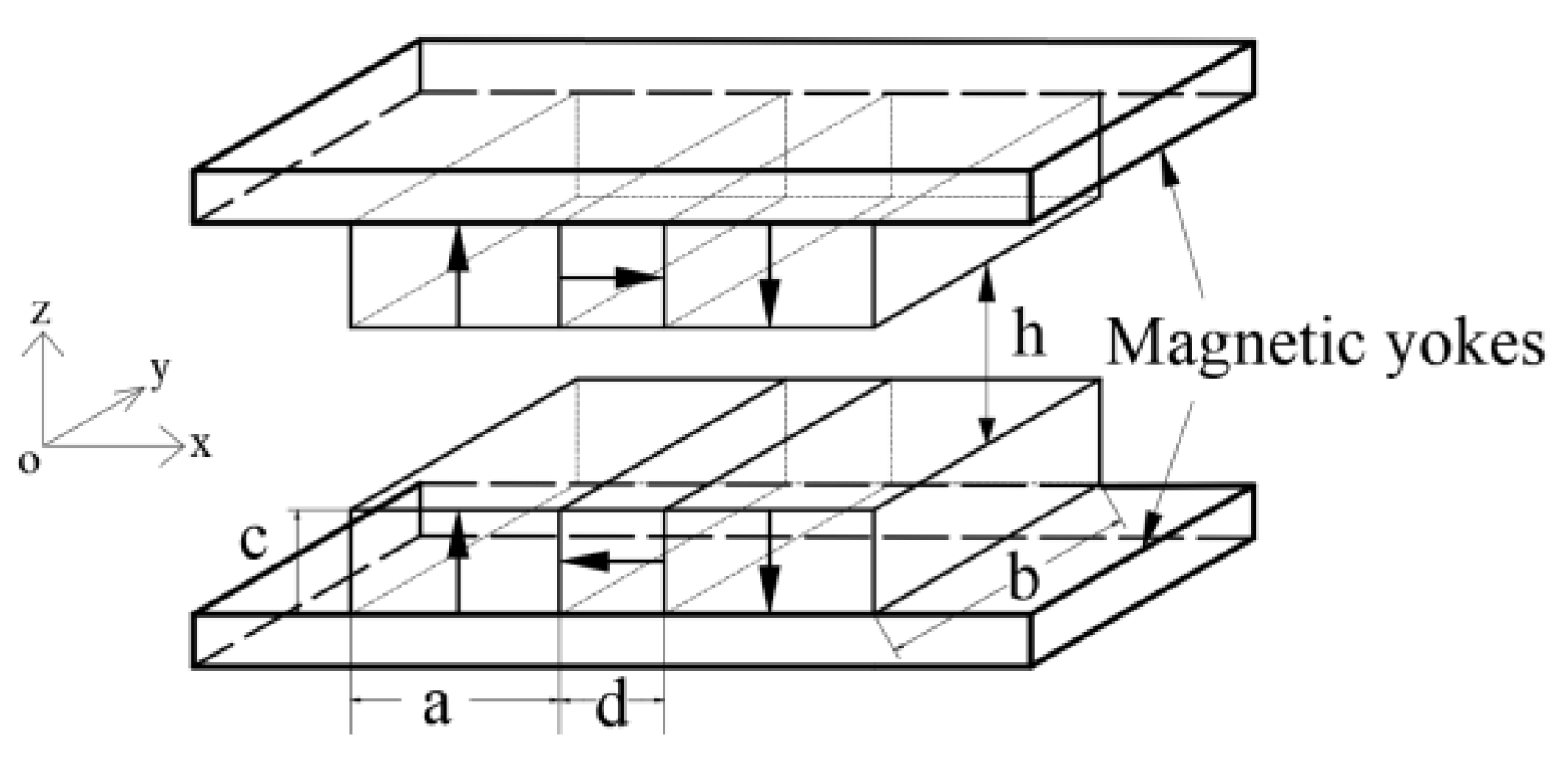
2.1. Spatial Magnetic Field Analytical Model of Rectangular Permanent Magnets
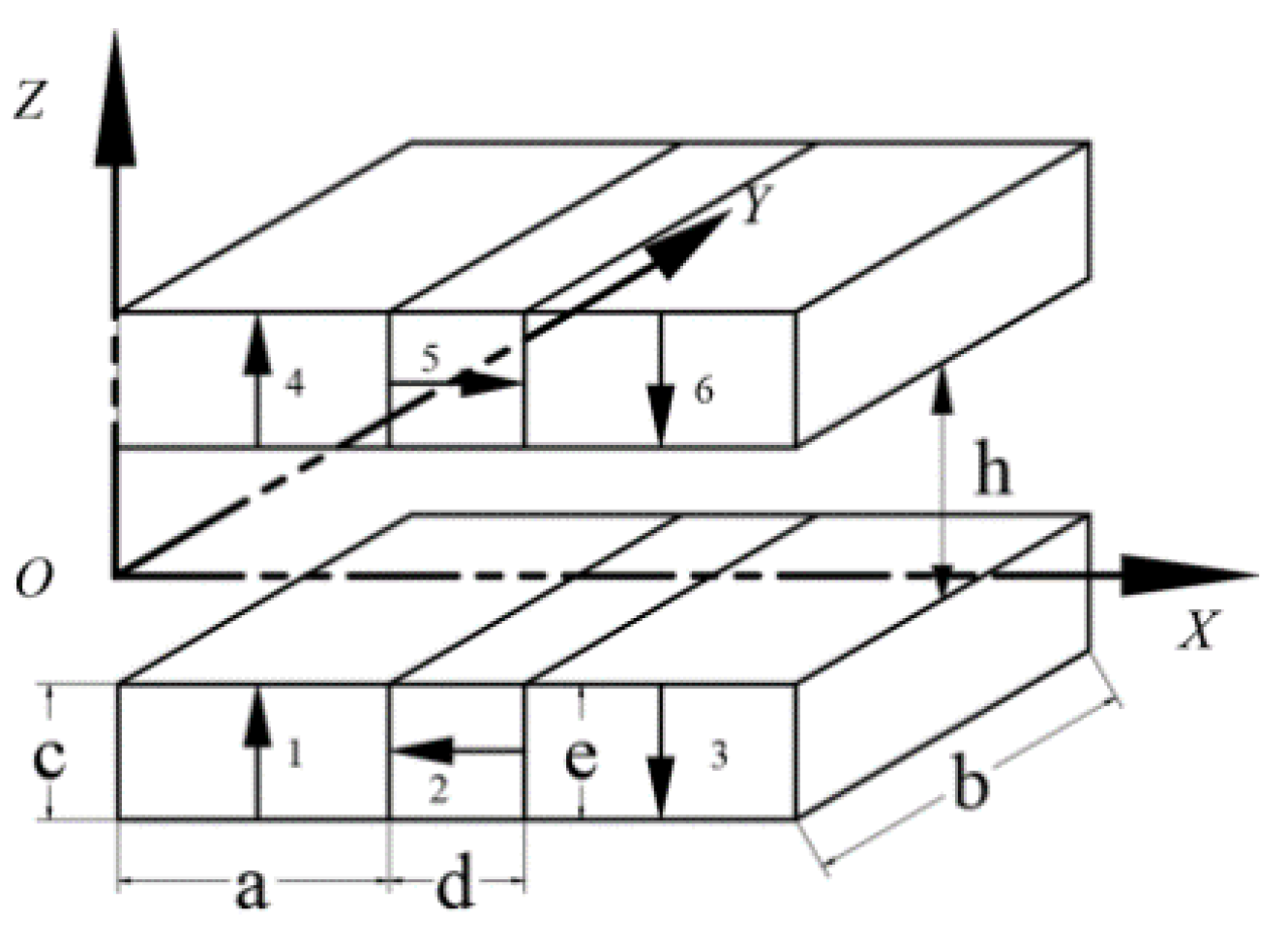
2.2. Parameterized Magnetic Field Model
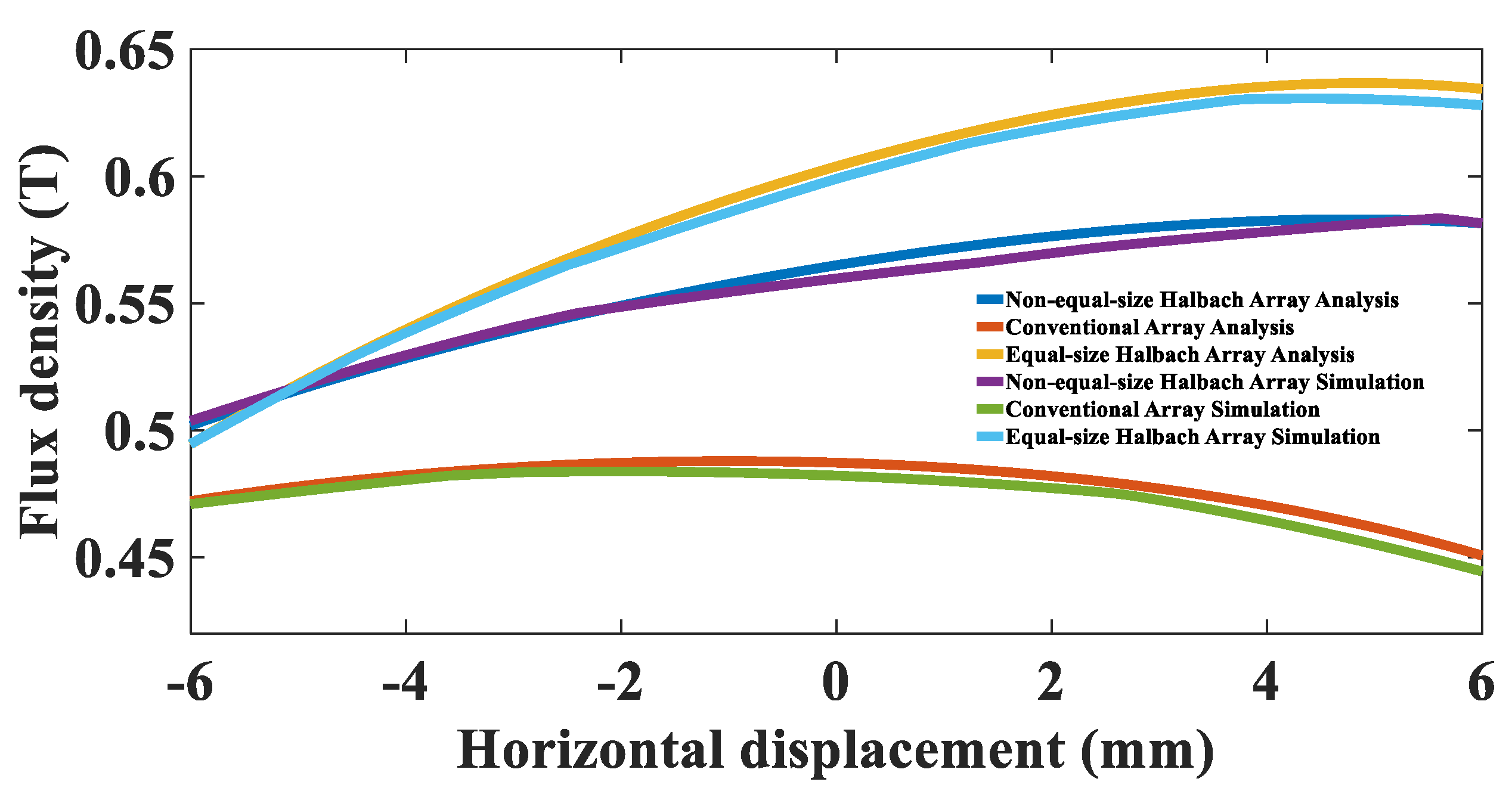
2.3. Comparison of Magnetic Flux Density between the Non-Equal-Size Halbach Array, Equal-Size Halbach Array and Conventional Magnet Groups
3. Effect of the Dimensional Parameters of the Halbach Array
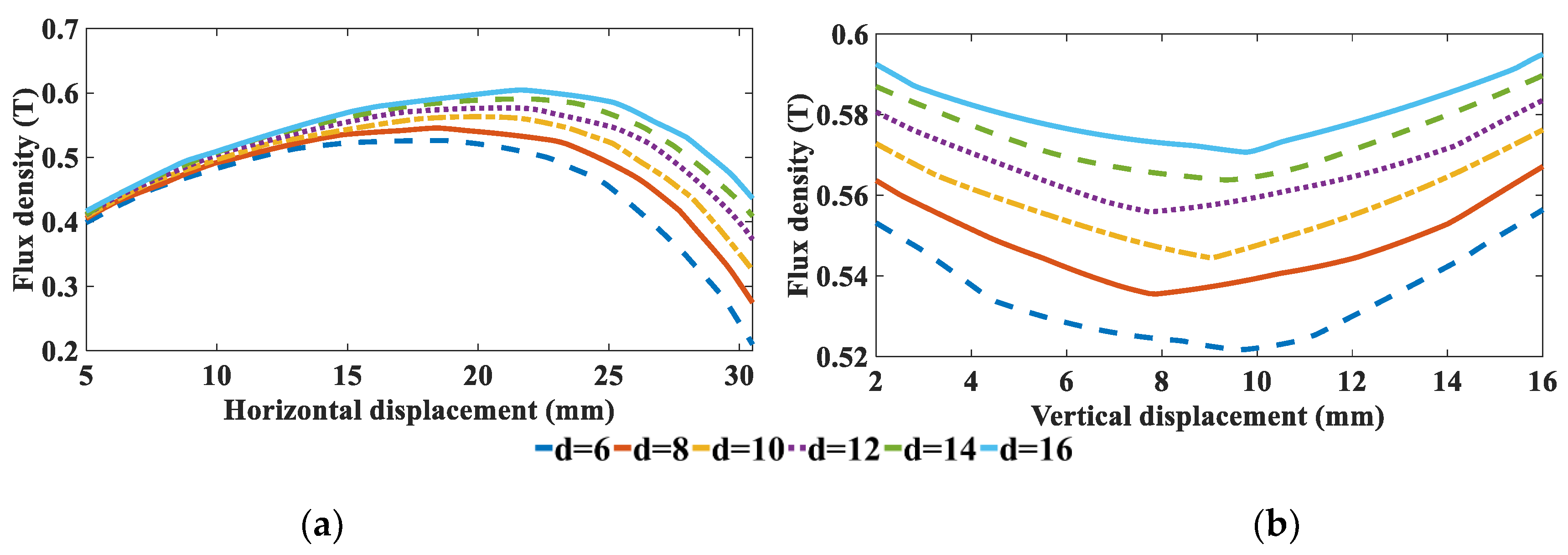
3.1. Effect of the Width of the Horizontal Magnetized Permanent Magnet
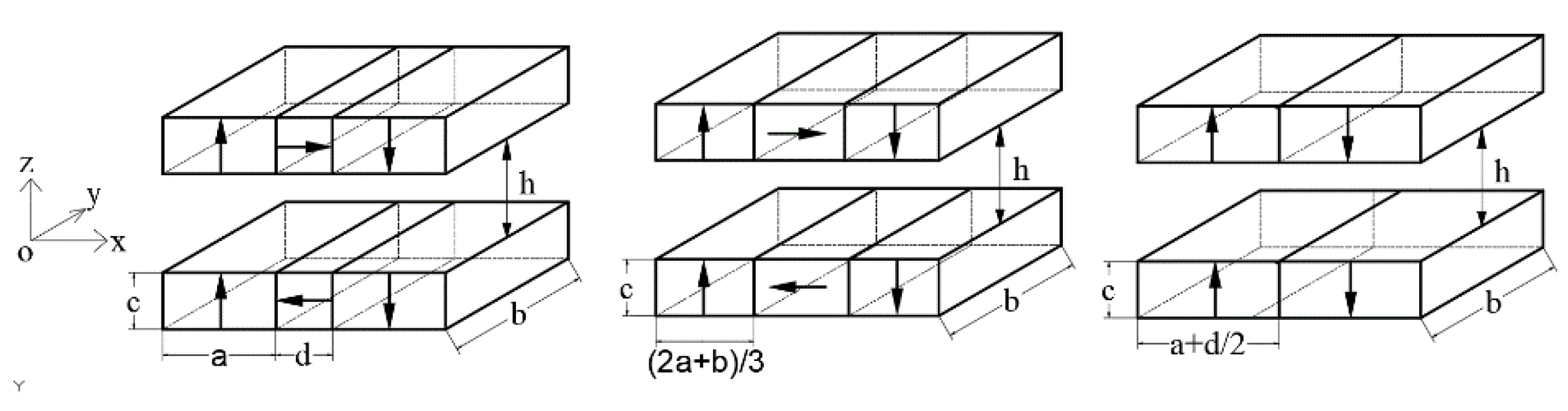
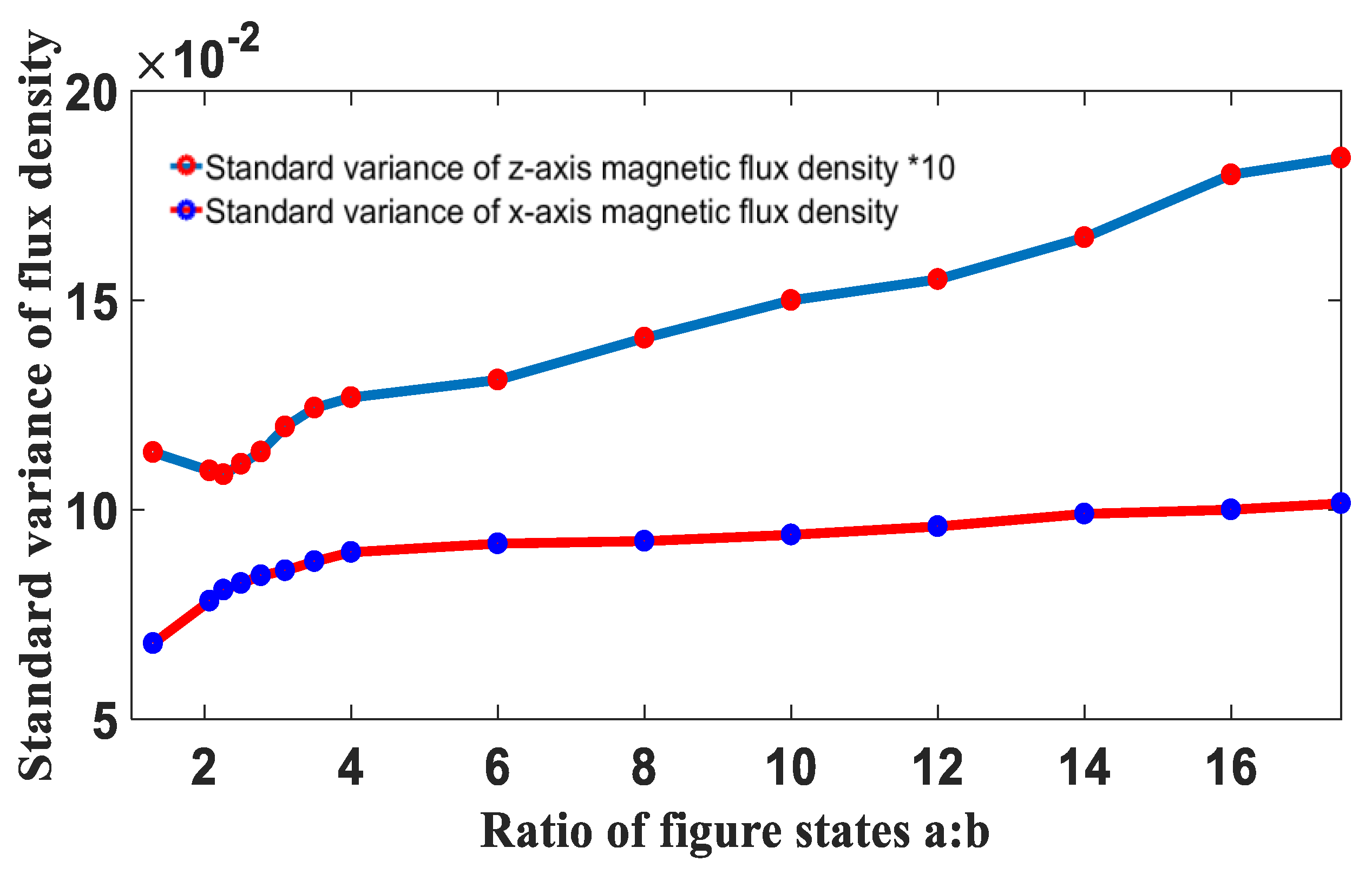
3.2. Effect of Width Ratio of the Vertically and Horizontally Magnetized Permanent Magnets
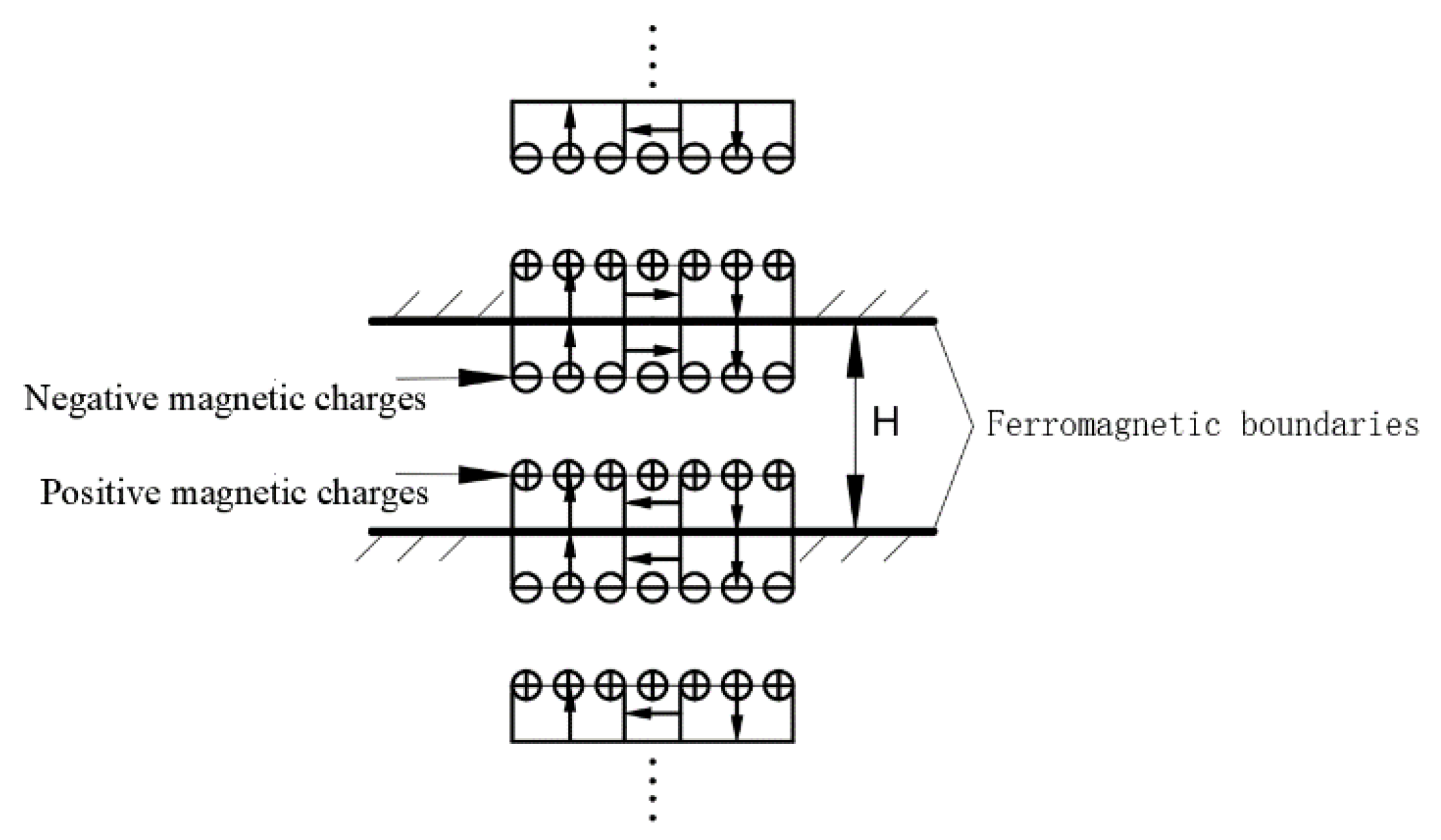
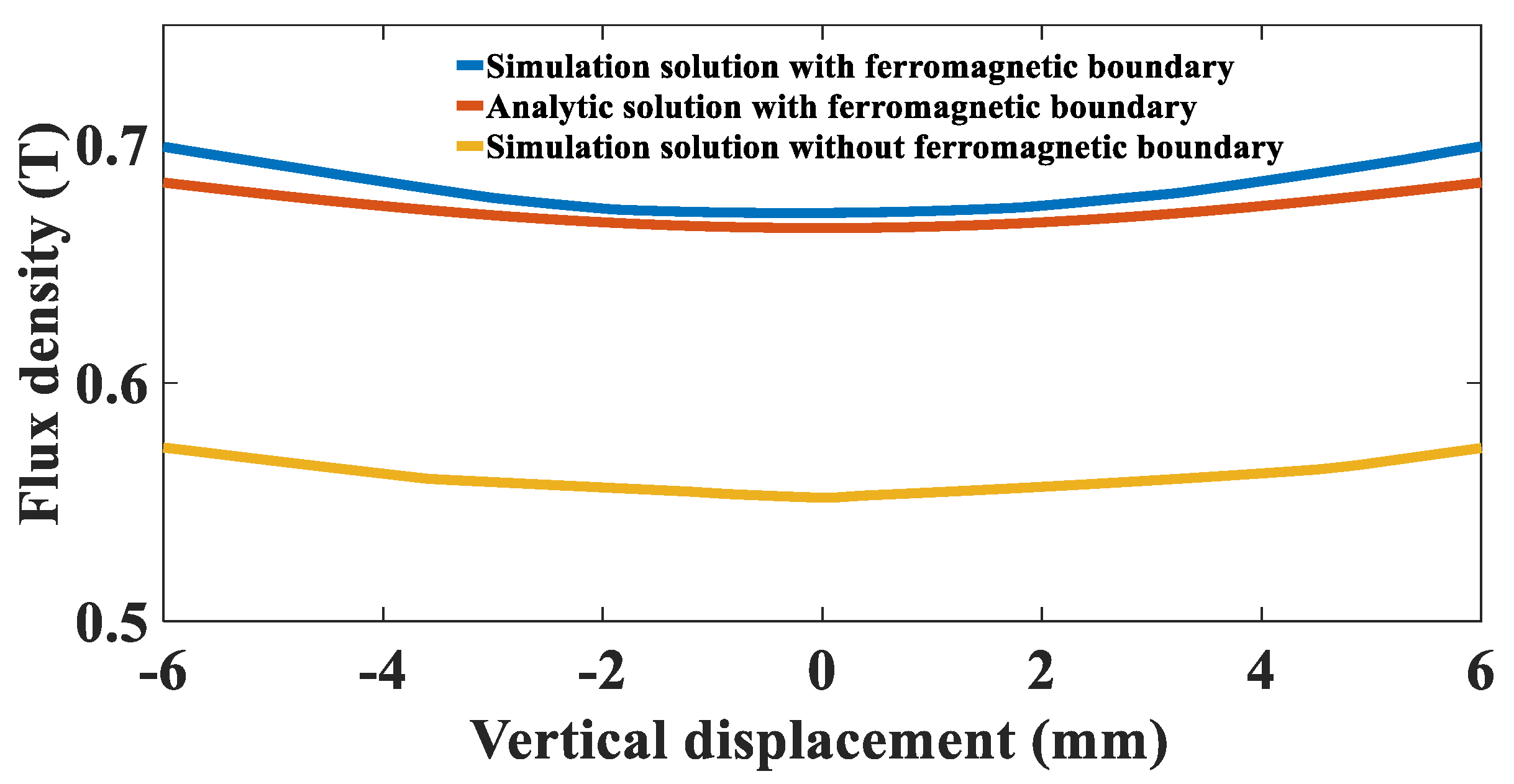
4. Effect of Ferromagnetic Boundary
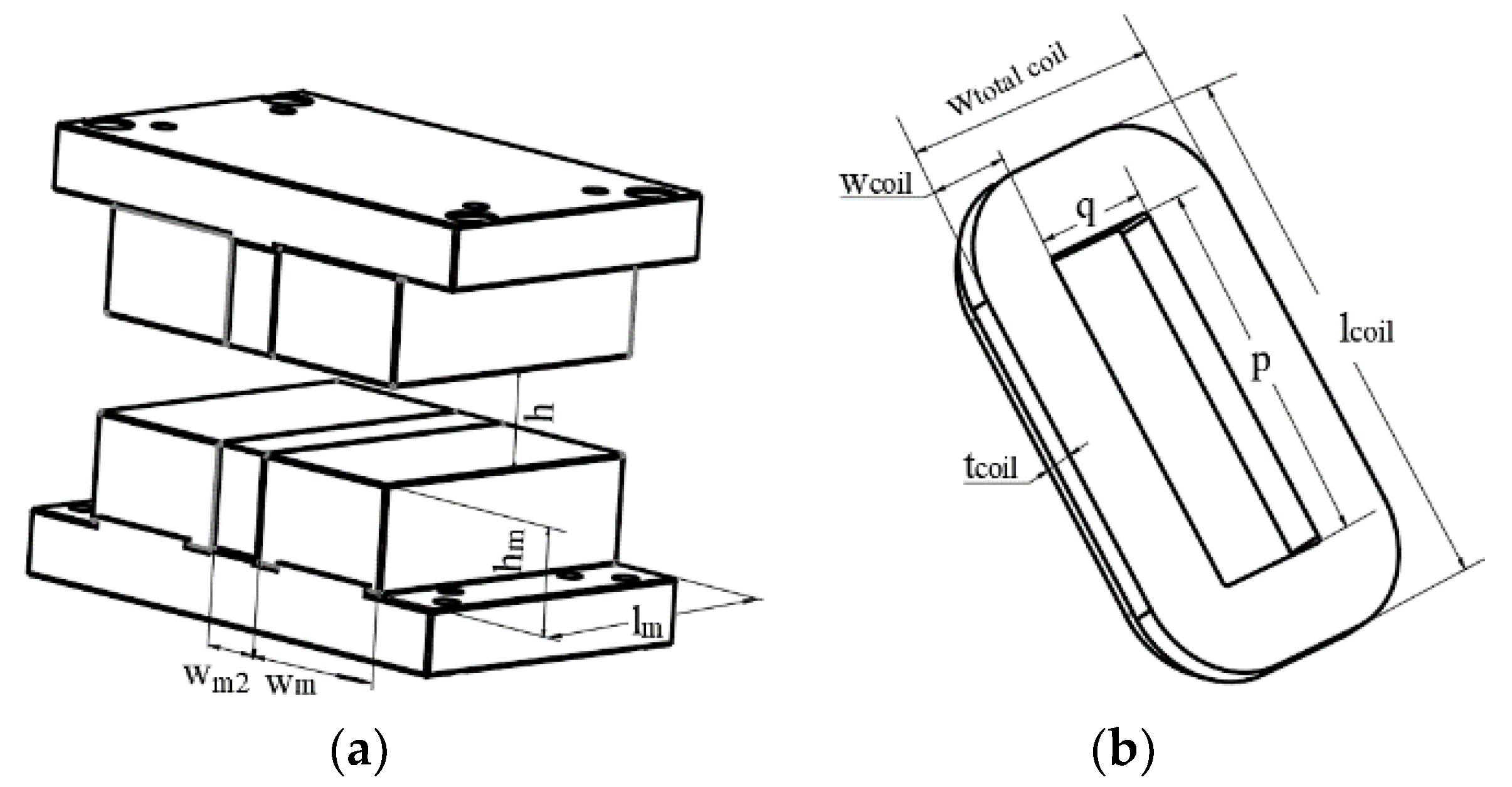
5. Optimized Design
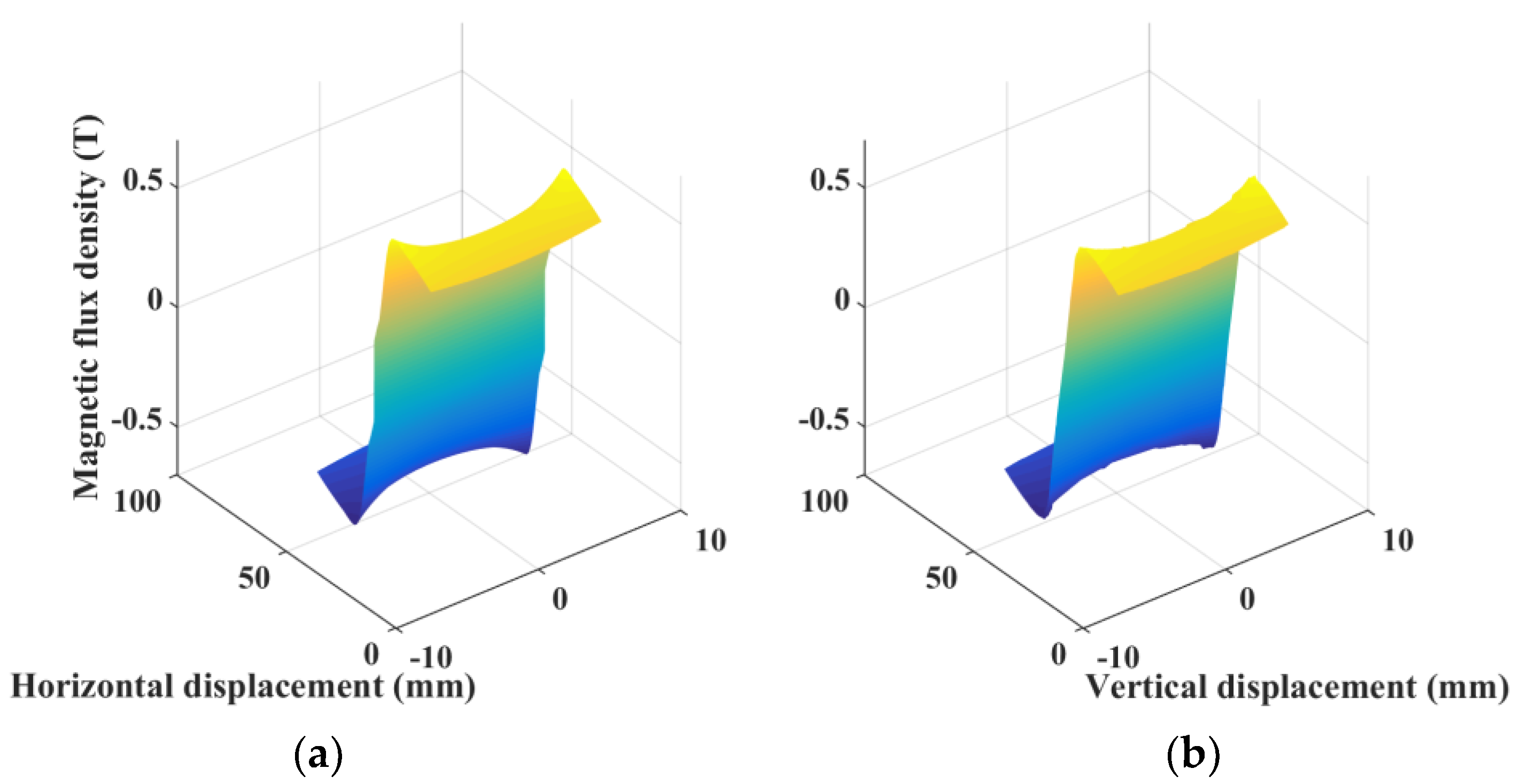
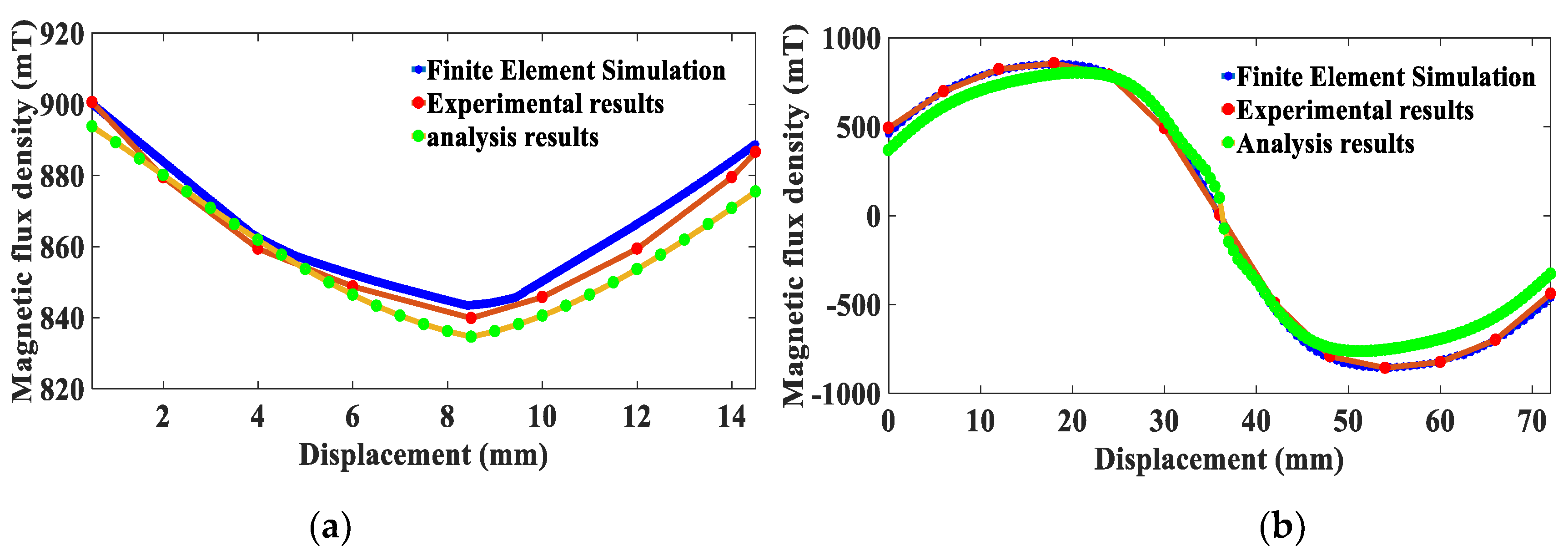
6. Experimental Section
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Poletkin, K.V.; Asadollahbaik, A.; Kampmann, R.; Korvink, J. Levitating Micro-Actuators: A Review. Actuators 2018, 7, 17. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Cui, N.; Zhao, S.; Zhang, H.; Liu, B. Modeling and Control of a Six Degrees of Freedom Maglev Vibration Isolation System. Sensors 2019, 19, 3608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jansen, J.H.; Van Lierop, C.N.; Lomonova, E.; Vandenput, A.J.A. Magnetically Levitated Planar Actuator with Moving Magnets. IEEE Trans. Ind. Appl. 2008, 44, 1108–1115. [Google Scholar] [CrossRef] [Green Version]
- Kamesh, D.; Pandiyan, R.; Ghosal, A. Modeling, design and analysis of low frequency platform for attenuating micro-vibration in spacecraft. J. Sound Vib. 2010, 329, 3431–3450. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.; Teo, T.J.; Pang, C.K. Design and Modeling of a Six-Degree-of-Freedom Magnetically Levitated Positioner Using Square Coils and 1-D Halbach Arrays. IEEE Trans. Ind. Electron. 2016, 64, 440–450. [Google Scholar] [CrossRef]
- Meng, B.; Zhu, C.; Xu, H.; Dai, M.; Li, S. Analytical and Experimental Investigations of Novel Maglev Coupling Based on Opposed Halbach Array for a 2D Valve. Actuators 2021, 10, 61. [Google Scholar] [CrossRef]
- Ham, C.; Ko, W.; Lin, K.-C.; Joo, Y. Study of a Hybrid Magnet Array for an Electrodynamic Maglev Control. J. Magn. 2013, 18, 370–374. [Google Scholar] [CrossRef] [Green Version]
- Chai, J.W.; Gui, X. Review of voice coil motor structure optimization and application. Trans. China Electrotech. Soc. 2021, 36, 1113–1125. [Google Scholar] [CrossRef]
- Kou, B.; Zhou, Y.; Yang, X.; Xing, F.; Zhang, H. Electromagnetic and Mechanical Characteristics Analysis of a Flat-Type Vertical-Gap Passive Magnetic Levitation Vibration Isolator. Shock. Vib. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Ahn, D. Analysis of High Force Voice Coil Motors for Magnetic Levitation. Actuators 2020, 9, 133. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Liu, C.-S.; Yeh, C.-N. Design and Simulation of Novel 3-DOF Spherical Voice Coil Motor. Actuators 2021, 10, 155. [Google Scholar] [CrossRef]
- Wei, W.; Li, Q.; Xu, F.; Zhang, X.; Jin, J.; Jin, J.; Sun, F. Research on an Electromagnetic Actuator for Vibration Suppression and Energy Regeneration. Actuators 2020, 9, 42. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, J.B.; Wang, L. Active control mechanism of vibration isolation foundation for very large optical instruments with differential electromagnetic actuators. Opt. Precis. Eng. 2007, 15, 1602–1608. [Google Scholar] [CrossRef]
- Han, B.C.; Peng, S.; He, Z.; Liu, X.; Zhang, X. Calculation and thermal analysis of eddy current losses in the windings of magnetic levitation controlled torque gyro high-speed motors. Opt. Precis. Eng. 2020, 28, 130–140. [Google Scholar] [CrossRef]
- Zhang, H.; Kou, B.Q.; Zhang, H.L.; Jin, Y.X.; Zhang, C.N.; Li, L.Y. Structural Optimization of an Integrated Winding Structure Short-Stroke Planar Motor Driven by Square DC Coils and Permanent Magnets. Appl. Mech. Mater. 2013, 416–417, 221–226. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, M.; Zhu, Y.; Yang, J.; Chen, B. Optimization of Voice Coil Motor to Enhance Dynamic Response Based on an Improved Magnetic Equivalent Circuit Model. IEEE Trans. Magn. 2011, 47, 2247–2251. [Google Scholar] [CrossRef]
- Smith, K.J.; Graham, D.; Neasham, J.A. Design and Optimization of a Voice Coil Motor with a Rotary Actuator for an Ultrasound Scanner. IEEE Trans. Ind. Electron. 2015, 62, 7073–7078. [Google Scholar] [CrossRef]
- He, Z.B.; Rong, C.; Li, D.W.; Xue, G.M.; Zheng, J.W. Modeling and analysis of magnetic field distribution of stacked super magnetostrictive actuators. Opt. Precis. Eng. 2017, 25, 2347–2358. [Google Scholar] [CrossRef]
- Kim, M.H.; Kim, H.Y.; Kim, H.C.; Ahn, D.; Gweon, D.-G. Design and Control of a 6-DOF Active Vibration Isolation System Using a Halbach Magnet Array. IEEE/ASME Trans. Mechatron. 2016, 21, 2185–2196. [Google Scholar] [CrossRef]
- Gou, X.F.; Yang, Y.; Zheng, X.J. Analytic expression of magnetic field distribution of rectangular permanent magnets. Appl. Math. Mech. 2004, 25, 297–306. [Google Scholar] [CrossRef]
- Zhang, H. Basic Research on Multi-Degree-of-Freedom Magnetic Levitation Micro-Motion Table. Ph.D. Dissertation, Harbin Institute of Technology, Harbin, China, 2014. [Google Scholar]
- Kou, B.; Zhang, H.; Li, L. Analysis and Design of a Novel 3-DOF Lorentz-Force-Driven DC Planar Motor. IEEE Trans. Magn. 2011, 47, 2118–2126. [Google Scholar] [CrossRef]


| Non-Equal-Size | Equal-Size | |
|---|---|---|
| Simulation result | 13.67% | 21.57% |
| Analysis result | 13.94% | 22.35% |
| Parameters | Numerical Value | Unit |
|---|---|---|
| a | 30 | mm |
| b | 60 | mm |
| c | 20 | mm |
| d | 11 | mm |
| e | 20 | mm |
| h | 16 | mm |
| 1.1 | T | |
| H/m |
| Actuator Parameters | Before Optimization | After Optimization | Unit | |
|---|---|---|---|---|
| Halbach array | Total length | 58 | 60 | mm |
| Total width | 70 | 72 | mm | |
| Height | 18 | 20 | mm | |
| Width of vertical permanent magnet | 25 | 30.5 | mm | |
| Width of horizontal permanent magnet | 20 | 11 | mm | |
| Air gap length | 20 | 15 | mm | |
| Coil | Total length | 105.6 | 99 | mm |
| Total width | 46 | 56 | mm | |
| Number of turns | 88 | 63 | turn | |
| Actuator | Effective stroke | ± 3 | ± 3 | mm |
| Force constants | 5.33 | 6.98 | N/A | |
| Continuous thrust | 42.68 | 56.5 | N | |
| Mass of the coil | 380 | 323.04 | g | |
| Consumption of the coil | 17.9 | 16.32 | W |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wu, Q.; Liu, B.; Gong, Z. Optimal Design of Magneto-Force-Thermal Parameters for Electromagnetic Actuators with Halbach Array. Actuators 2021, 10, 231. https://doi.org/10.3390/act10090231
Li Z, Wu Q, Liu B, Gong Z. Optimal Design of Magneto-Force-Thermal Parameters for Electromagnetic Actuators with Halbach Array. Actuators. 2021; 10(9):231. https://doi.org/10.3390/act10090231
Chicago/Turabian StyleLi, Zhihao, Qianqian Wu, Bilong Liu, and Zhaopei Gong. 2021. "Optimal Design of Magneto-Force-Thermal Parameters for Electromagnetic Actuators with Halbach Array" Actuators 10, no. 9: 231. https://doi.org/10.3390/act10090231
APA StyleLi, Z., Wu, Q., Liu, B., & Gong, Z. (2021). Optimal Design of Magneto-Force-Thermal Parameters for Electromagnetic Actuators with Halbach Array. Actuators, 10(9), 231. https://doi.org/10.3390/act10090231





