Abstract
In 10th-century Córdoba, mathematics—and particularly geometry—was applied to architectural design in new ways, constituting a “mathematical turn” of Islamic architecture. In the mosque of Córdoba and in the palaces of Madīnat al-Zahrāʾ, geometry was employed in the design of ground plans, elevations, decorative patterns, and even to measure the human view. While Roman architects like Vitruvius had used mathematics to place each element of a building in its appropriate relation to all other elements of a building, the architects at Córdoba employed geometry to create a spatial web in which all parts are equal to each other and part of a single, unified space. The architects of Córdoba thus pointed the way to new possibilities of designing architecture, possibilities which were to be tested further by architects of Gothic and Renaissance architecture, though to different ends.
1. Introduction
The proclamation of the caliphate at Córdoba in 929 CE marked a turning point not only in political and ideological terms but also in the history of art and architecture. With the foundation of a new capital city—Madīnat al-Zahrāʾ—in 936 CE, the architects of the caliphate initiated the creation of a novel way of designing, constructing, and decorating buildings. Among the signature elements to come out of this new “style” of designing architecture are the interlocking arch and the ribbed vault. An innovation of even greater consequence was the way mathematics was applied to the design of architecture. Mathematics had been an integral element of architectural design since ancient times. The architects of the caliphate applied mathematics—and geometry in particular—to architecture in new ways, however, which signified a mathematical turn in architectural design. The following paper focuses on how geometry was applied in different ways to the design of architecture in 10th-century Córdoba and what was achieved by doing so. Taken together, these innovative ways of applying mathematics to the design of architecture came to influence not only the further development of Islamic architecture in the region but also European architecture in general.
Since the 8th century, crucial advances had been made in the field of mathematics at the court of the Abbasid caliphs in Bagdad by combining the knowledge of Classical Greek mathematicians like Euclid with innovations made in India in the 6th and 7th century.1 Among these was the use of a decimal numeral system with zero as a digit, the foundations of algebra by al-Ḫwārizmī (Latinized Algoritmi, ca. 780–846) and the use of the trigonometric functions sine and cosine. These advances quickly reached the farthest ends of the Islamic world, including Córdoba.2 The Arabic-Indian numeral system was introduced to Córdoba already by the inventor Ibn Firnās (810–887/888). At the court of the caliph, the mathematician Maslama al-Maǧrītī (ca. 950–1007/1008) edited the astronomic tables of al-Ḫwārizmī, translated Ptolemy’s star chart and improved the translation of his Almagest (Arabic al-Maǧisṭī). He also worked on techniques of surveying and triangulation. The astronomer Ibn al-Ṣaffār (d. 1035) wrote a commentary on the astronomic tables of al-Ḫwārizmī and composed a treatise on the astrolabe, used until the 15th century to determine a geographic location based on the position of stars. The application of mathematics to architecture thus took place at a time and in a place where all the most recent advances in this field were known, read, and elaborated on.
2. From Arithmetic to Geometric Design
When ʿAbd al-Raḥmān I (r. 756–788) established himself as the Islamic ruler of the Iberian Peninsula, he ordered the construction of a congregational mosque in Córdoba, his capital city.3 His architects laid out the plan of the mosque as a perfect square, 150 cubits wide and 150 cubits long (Figure 1). The surface area was divided into two parts: the northern half (75 × 150 cubits) was to be left open as a courtyard, and the southern half (75 × 150 cubits) was roofed over in order to serve as a prayer hall. The hall was to be divided into 11 naves (10 naves + 1 central nave). Dividing 150 cubits by 11 would have made each nave 13 cubits wide. To avoid such an awkward number, each nave was designed to be 14 cubits wide, the two outermost naves 11 cubits, and the central nave 16 cubits (8 × 14 + 16 + 2 × 11 = 150). The design of the entire mosque was thus based on simple arithmetic. The same is true for most ancient Roman buildings, and for the churches that were built in Asturias at the time the mosque was constructed at Córdoba.4
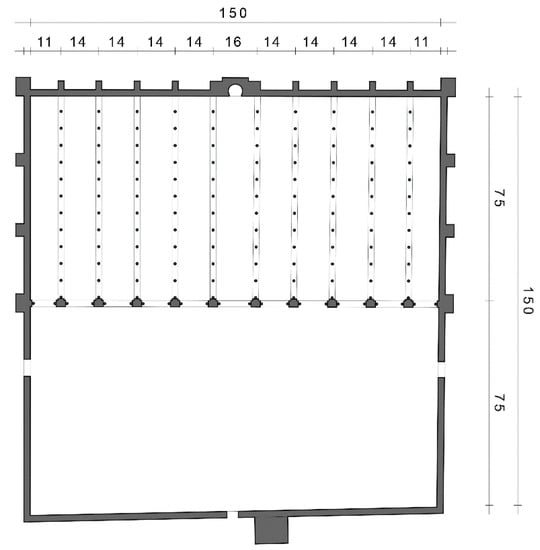
Figure 1.
Ground plan of the initial phase of the mosque of Córdoba, with measurements in cubits (1 cubits = 49.5 cm). Drawing by Felix Arnold, based on the plan of Félix Hernández.
In the 10th century, architects began to use geometry in addition to arithmetic to design buildings. An early example is the so called Salón basilical in the caliphal residence Madīnat al-Zahrāʾ, identified by some as the Dār al-Ǧund “House of the Army” and dated to ca. 950 CE. The building comprises a three-aisled hall with side chambers as well as a courtyard with porticos on three sides5. The width of the hall was again set out to measure an even number: 50 cubits of 46.3 cm each (23.12–23.16 m). The hall was divided into three naves, each 16⅔ cubits wide (7.76 m). The hall is not square, however (Figure 2). The depth measures only 20.03–20.07 m, or about 43.3 cubits. The design of the floor plan was in fact based on an equilateral triangle, 50 cubits wide on each side.6 The base of the triangle equals the width of the hall (50 cubits), the height of the triangle its depth—25√3 cubits (≈43.3 cubits), an irrational number. The design of the hall is thus based not on simple arithmetic, but on geometry. The same is true for another famous hall of Madīnat al-Zahrāʾ—the Salón Rico, which is 44 cubits (20.26–20.31 m) wide and 22√3 cubits (17.53 m) deep.7
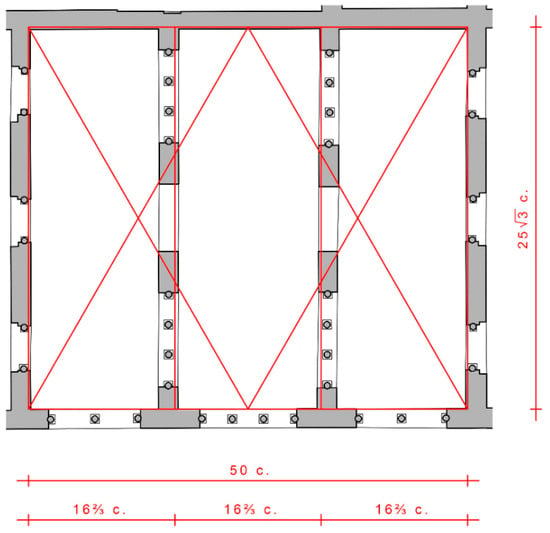
Figure 2.
Application of equilateral triangles in the design of the hall of the Dār al-Ǧund at Madīnat al-Zahrāʾ, with measurements in cubits (1 cubit = 46.3 cm). Drawing by Felix Arnold, based on the plan by Ana Zamorano.
The use of equilateral triangles had a practical advantage. One of the challenges in setting out a floor plan at the building site is establishing right angles. In order to set out a right angle Roman architects—and the builders of 9th- and 10th-century Asturias—made use of a Pythagorean triangle (known as norma) with sides measuring 3, 4, and 5 units.8 Such a triangle can be set out easily using sticks or ropes marked in corresponding units. This procedure has two disadvantages, however. The triangle has to be set out at each corner of the building, thus increasing potential inaccuracies. A Pythagorean triangle that is 3 units wide and 4 units long furthermore often does not coincide with the proportions of the whole floor plan and the directions gained thus need to be extrapolated to greater distances, creating an additional potential source of error. Equilateral triangles can be set out on the building site even more easily than a Pythagorean triangle by stretching out three ropes of equal length. If the midpoints of two sides are marked and a triangle of equal kind is flipped around these points, each corner marks the limits of a prefect rectangle. The only disadvantage is that the width of the rectangle is not equal to its length, but measures only (about 0.866) of the length. The architects of Madīnat al-Zahrāʾ appear to have accepted this disadvantage, as the hall of the Dār al-Ǧund shows.9
The architect of the Dār al-Ǧund applied the equilateral triangle to other parts of the building as well (Figure 3). The hall, including its side chambers, its vestibule and the platform in front of the vestibule also occupies a surface area with the proportion of 1: . The same holds true for the surface area of the adjoining courtyard. The sizes of the three areas are in fact related to each other and are all based on an overarching design. The architect apparently first set out a large equilateral triangle, each side measuring 200 cubits, its height 100√3 cubits. The base length was then divided arithmetically into 12 units (12a), each 16⅔ cubits wide. The naves of the hall and its side chambers each occupy one such unit (1a = 16⅔ cubits). The hall at the tip of the triangle occupies an area that is three units wide (3a = 50 cubits), the hall including its side chambers, its vestibule, and the platform in front of the vestibule an area that is five units wide (5a = 83⅓ cubits). The courtyard occupies an area that is seven units wide (7a = 116⅔ cubits).
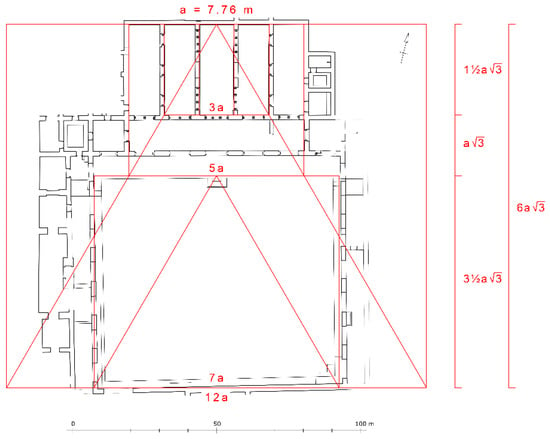
Figure 3.
Design scheme of the Dār al-Ǧund, based on the use of equilateral triangles. Drawing by Felix Arnold, based on the plan by Ana Zamorano.
The design of the Dār al-Ǧund is remarkable not only for the use of geometry but also for the way geometry is used in the design process. The Romans had established the proportions of spaces using arithmetic and at times geometric means for aesthetic purposes (what Vitruvius called symmetria and eurythmia)—calculating the proportion of each individual space at a time.10 In the Dār al-Ǧund, the proportion resulting from the use of equilateral triangles apply not only to individual spaces or structures but to the building complex as a whole. The architect applied the proportions to spaces that can hardly be appreciated by the user of the building—the equilateral triangles on which the design is based are not recognizable once the building has been constructed. Geometry was neither used for an aesthetic purpose nor with regard to construction but to create order in the ground plan. The order was applied to spaces that Vitruvius would have treated as separate entities—an interior hall and a courtyard. The architect of the Dār al-Ǧund not only treated these two spatial elements as one single space, but used geometry to bind them together, and in a way overcoming the difference between interior and exterior space—the approach that would become of particular importance in the architecture of the subsequent 11th century.11
3. Toward an Abstract Notion of Space
In the Dār al-Ǧund, equilateral triangles were applied also to the design of arcades, and this is where the difference with Roman design methods becomes most apparent. At Madīnat al-Zahrāʾ, the design of the columns themselves actually adheres rather closely to Roman prototypes.12 The columns are composed of a base, a shaft and a capital, and the capital is either of Corinthian or Composite type, though executed in a contemporary, often highly intricate style. The proportions of the columns and their parts furthermore often resemble those of the Corinthian order of Roman architecture. Thus, the height of the capital usually equals the width of the abacus, like in Roman prototypes. The ratio between the height of the column and that of its shaft is about 6:5 (1.2:1). And the columns are usually 9.5 times as high as they are thick (see Table 1). The architects of Madīnat al-Zahrāʾ may either have copied these proportions from examples of the Roman period preserved in the city of Córdoba or may actually have read the text of Vitruvius regarding the classic orders13. The general characteristics of columns remained the same throughout the 10th century and were changed only gradually in the ensuing 11th century, with capitals becoming twice as high, and columns more slender, with a ratio between thickness and height of 1:11–12 instead of 1:9.5.

Table 1.
Measurements and proportions of columns of the 10th and 11th century.14
In contrast to the principles expounded by Vitruvius, the design of the arcades of the Dār al-Ǧund was not derived from the proportions of columns but from overarching considerations (Figure 4). The opening to the lateral naves of the hall is 10 cubits wide and is divided by columns into two bays, each 5 cubits wide. The height of the arcade was determined by an equilateral triangle laid on its side: the center of the triangle marks the height of the columns including base, shaft, capital, and impost ( cubits), the tip the height of the alfiz—the rectangle surrounding the arches ( cubits). The entrance to the central nave of the hall is divided into three bays. The columns have the same height as in the lateral arcades: cubits. The spacing of the columns is determined by an equilateral triangle whose height corresponds to the height of the columns ( cubits) and whose base spans two bays (6⅔ cubits). Each bay is thus 3⅓ cubits wide instead of 5 cubits, although the column height is the same in both arcades.
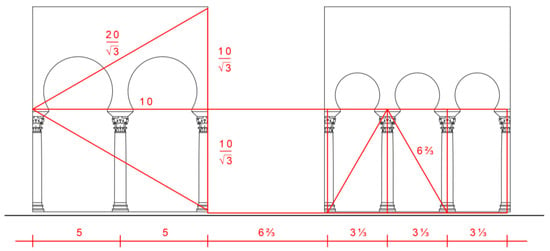
Figure 4.
Design scheme of the arcades at the entrance to the hall of the Dār al-Ǧund at Madīnat al-Zahrāʾ, with measurements in cubits (1 cubit = 46.3 cm). Drawings by Felix Arnold.
The spacing of the columns was thus established by geometric means on the basis of the overall proportions of the arcades. Such a procedure would have been unthinkable for Roman architects. For Vitruvius, the proportional relationship of each element of a building to the building as a whole was fixed and could not be changed. In his treaties De architectura (), he used the analogy of the human body, in which the size of each limb has a specific relation to the size of the whole body15. Vitruvius insisted on the use of a basic unit (modulus) for designing buildings, equivalent to the thickness of a column at its lower end. He thus proceeded from the individual element—the column—to the design of the whole building. This is not the case in the Dār al-Ǧund: the architect started from the design of the complete building complex, subdividing it by geometric means until he arrived at the dimensions of smaller elements (Figure 4). The size and proportion of individual columns was thus not related in a fixed way to the design of the whole building and not even to the design of the arcade of which it was part.
Vitruvius worked from the premise of the dignity of each individual element, which was to be achieved by keeping all other parts of the building in proportion. The architect of the Dār al-Ǧund had a more abstract approach to architecture and architectural space. In an innovative way, he proceeded from the idea of the unity of space, to which he subordinated the role of individual parts.16 The way the Dār al-Ǧund was designed liberated the architect from the constraints of Roman architecture as defined by Vitruvius and pointed the way to how architectural space could be organized by geometric means, going beyond the concept of the module as the basic element of design.
4. Mathematics of Vision
The arcades of the Dār al-Ǧund differ from Roman architecture in another important aspect. The size of the columns is much smaller compared to the height of the opening than in any Roman building (Figure 5). Placing arches instead of horizontal architraves above columns had already reduced the height of columns significantly—the first example being the church of Santa Costanza in Rome (ca. 340–345 CE). The use of horseshoe-shaped arches, introduced to the architecture of the Iberian Peninsula in the Visigothic period, reduced the height of the columns further. In the 6th century horseshoe arches were about 133% higher than regular arches, in the late 10th century 150% higher, and in the 11th century even 175% higher—an increase to be surpassed only by pointed arches.17 As a result, columns were only about two-thirds as high as the opening of the arcade, eventually even only half as high (see Table 2).
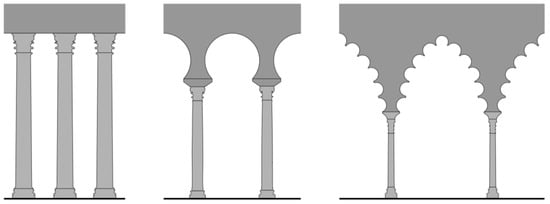
Figure 5.
Schematic comparison of the design of arcades: Corinthian order of Roman architecture; arcade of horseshoe-shaped arches at Madīnat al-Zahrāʾ (mid-10th century); arcade of multi-foil, pointed arches at the Aljafería (11th century). Drawing by Felix Arnold.

Table 2.
Measurements and proportions of arcades of the 10th and 11th century.18
These changes not only reduced significantly the size of the column shafts—a concern for builders trying to secure suitable materials of hard stone. They reduced the thickness of the columns needed to support an arcade. The ratio between bay width and column width was increased from 3:1 in the Corinthian order up to 8:1 in the 10th century, and even to 14:1 in the 11th century (see Table 2). The change becomes apparent also when the ratio between the thickness of the columns and the total height of the opening of the arcade is compared. In the Corinthian order, this ratio had been 1:10. In the 10th century, the ratio was increased to 1:11–15, in the 11th century up to 1:16–25. In other words, the thickness of the supports needed to carry an arcade was eventually cut in half compared to the Roman period.
The aim of the architects at Córdoba appears to have been to reduce the physical impact of the arcade on the ground. The reduction of the column thickness reduced how much they impeded visibility across a space and increased the potential use of the floor surface. This was a major concern especially in mosque architecture, in which the surface area available for prayer needed to be maximized. Though the faithful direct their prayers toward Mecca (qibla), it would have been an added value to see the prayer leader (imām). Particularly during the sermon, the columned prayer hall of the mosque was viewed by the congregation not only in the direction of the naves, but also in a concentric manner, in the direction of the preacher on his pulpit (minbar). In the extension of the mosque of Córdoba executed by al-Ḥakam II in 961–971, diagonal views across the prayer hall were highlighted by the distribution of gray and pink column shafts along diagonal lines, directed toward the central axis of the mosque (Figure 6).19 The same attention to concentric views was also paid to the throne halls of Madīnat al-Zahrāʾ, in which a large number of people gathered to greet the caliph.
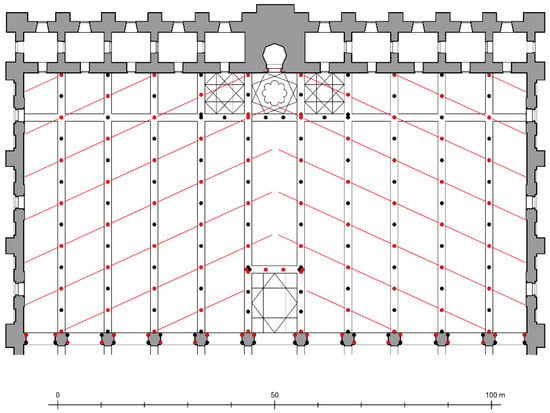
Figure 6.
Reconstructed ground plan of the extension of the mosque of Córdoba executed by al-Ḥakam II in 961–971, with distribution of column shafts in reddish-pink breccia (indicated in red) and in dark gray limestone (indicated in black). Drawing by Felix Arnold, based on the plan of Christian Ewert.
Visibility became a major concern to architects of Islamic Córdoba. Literary descriptions of garden mansions (munya) in the suburbs of Córdoba show that the view (nāẓir) onto the landscape was appreciated already in the 8th century.20 By the late 10th century, the framing of the view from palatial halls became an important motive in palace design. The earliest example is the garden hall of al-Rummānīya, a palace built by the finance minister of al-Ḥakam II in 965/966 CE.21 The hall was built on a dam that separated a large water reservoir from an extensive garden. Arcades opened in both directions, thus giving the hall a transparency not found in other buildings of the time. The width of the arcades was additionally determined by equilateral triangles whose base corresponded to the base of the triangle and whose tip was located in the center of the opposite back side of the hall (Figure 7). The angle of an equilateral triangle—60°—corresponds roughly to the angle of the human field of view. While the human eye is able to perceive a much wider angle—almost 180°—only a part of that is generally regarded as the field of view. Ordinary camera lenses thus have a field of 57° while artists frame their picture based on a field of view of 50–60°.22 A person sitting below the southern arcade of the hall and looking across the hall had his view of the water basin beyond framed by the outline of the northern arcade. In the same way a person sitting below the opposite, northern arcade of the hall and looking across the hall had his view of the garden framed by the outline of the southern arcade. At al-Rummānīya, vision became a subject of mathematics—an integral concept not found in any known building before and not applied as a common principle until the Italian Renaissance. The design of the hall of al-Rummānīya became the prototype of several later palatial halls, including one in the Alcázar of Córdoba, two on the Alcazaba of Almería and one in the Aljafería of Zaragoza, all dating to the 11th century.23
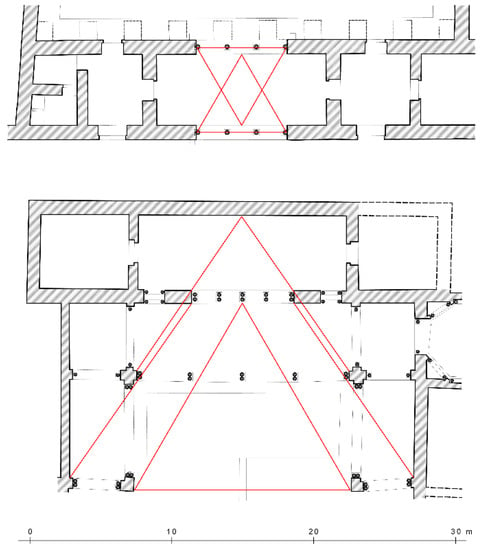
Figure 7.
Application of equilateral triangles to the design of arcade openings: western hall of al-Rummānīya in Córdoba (top); northern hall of the Aljafería in Zaragoza (bottom). Drawings by Felix Arnold.
A precondition for measuring the human view was an appreciation for the optic characteristics of the human eye. Ground breaking studies in this regard were being made at this time by Ibn Haiṯam (Latinized as “Alhacen”, 965–1040) at the Fatimid court in Cairo24. His treatise Kitāb al-Manāzir “Book of Optics“, written in 1028 and translated into Latin under the title De Aspectibus or Perspectiva, would become a reference work for Renaissance artists, including Filippo Brunelleschi and Leon Battista Alberti. It is rather unlikely that the architects at Córdoba were already aware of the scientific advanced made by Ibn Haiṯam. Both the works of Ibn Haiṯam and the architects at Córdoba are an expression for a new attitude toward man and space, however, an attitude based on a new mathematical concept of space.
5. Geometric Pattern as Structure
At Córdoba, the application of mathematics to architecture is most visible in the use of geometric motives and patterns for decorative purposes. Geometric motives are already found in the Late Antique and Visigothic period but become especially prevalent in the 10th century. At Madīnat al-Zahrāʾ frames of doors and arcades are frequently decorated by patterns of squares, hexagons, octagons, 6- and 8-pointed stars, swastikas, meanders, and other geometric motives.25 Sometimes geometric motives are interwoven with plant decoration, including circles, squares and triangles.
Usually decoration was applied to the architectural structure as a separate layer, with no correlation between decorative pattern and architectural form. In Islamic architecture, this distinction between architecture and decoration was increasingly blurred. Early examples are window grills, which are regularly decorated with geometric patterns from the Visigoth period onward.26 The grills are perforated according to a geometric pattern, decoration, and structure, thus becoming a unity. In the 10th century, the geometry of window grill patterns becomes ever more elaborate, incorporating octagons, stars, and other geometric motives.
This equation of geometric pattern and architectural structure was eventually applied to the building as a whole. A first step was taken in the first phase of the mosque of Córdoba, where the arcades were composed of two levels of arches. In the Roman and Late Antique Period arches were always understood as semicircular perforations of walls. Arcades could be superimposed one above the other—for example in the aqueducts of Segovia and Mérida—but each arcade always received a horizontal top. In the mosque of Córdoba, the lower level of arcades received free standing arches—a first step toward the isolation of the pure geometric shape from the wall plane.
A high point in the equation of geometric pattern and architectural structure was reached in the reign of al-Ḥakam II with the extension of the mosque in 961–971.27 The arcades of the maqṣūra area were designed as a complex superposition of different arches, including regular half-circle arches, some of horseshoe shape and some multi-foil—a shape first introduced at the Salón Rico a decade earlier. The arches span either a single bay or several bays at once, thus crossing each other (Figure 8). A common motive is the interlocking arch, in which arches span two bays at once. In this way, the role of the arch as an element spanning from one support to the next was abandoned in a strict sense, the arch now playing more a decorative role than serving a structural purpose. At the same time, decoration and structure now became identical, much like in the window grills before.

Figure 8.
The Capilla de Villaviciosa in the mosque of Córdoba, part of the extension executed by al-Ḥakam II. Photograph by R. Friedrich, German Archaeological Institute.
In the extension of al-Ḥakam II, this play between decoration patterns and structural elements was applied also to the design of vaults.28 In a structural sense, domes were deconstructed into arches, each spanning from one side of the vaulted space to another (Figure 8). The dome could be composed of four or more such arches, arranged according to different geometric patterns. The end result was the evolution of the ribbed vault, in which ribs highlight the structural composition of the vault. In contrast to later examples the ribs of the vaults of the mosque of Córdoba serve a decorative purpose more than a structural one and are the result of the application of geometry to decoration, and in this case to architectural design.
Eventually the equation between decoration and architectural structure led to the evolution of the muqarnaṣ decoration, a form of three-dimensional, geometric ornamentation in which a vaulting is fractionized into a large number of miniature squinches or corbles. The origins of the muqarnaṣ decoration are still being debated, some favoring an origin in the east, others in the west29. Among the earliest examples in the west are the ceiling of the palace of Muʿtaṣim in Almería and the ceiling of the palaces of Qalʿat Banī Ḥammād in Algeria, both dating to the 11th century.30 Whatever the actual origin of the idea, muqarnaṣ decoration is the most definitive expression of the application of mathematics to architectural design.
Interlocking arches, ribbed vaulting, and muqarnaṣ decoration all formed an integral part of the subsequent development of Islamic architecture in the western Mediterranean region, including the Nasrid architecture of Granada and the Marinid architecture of Morocco. Both the interlocking arches and the ribbed vaulting as first developed in the extension of the mosque of Córdoba also played a crucial role in the evolution of Gothic architecture, though the route from Córdoba to the Île-de-France cannot be traced with certainty. Early cases for the use of interlocking arches in church architecture are the transept of Ste.-Honorine in Graville and a church tower in Allemagne near Caen (both built in Normandy around 1070), early examples for the use of ribbed vaults the Cathedral of Durham (England, begun in 1093), all constructed by Normans, who may well have been acquainted with Islamic architecture, either on the Iberian Peninsula or in Sicily.31
The Islamic architecture of the Iberian Peninsula and the Gothic architecture of the Île-de-France both employed pointed arches and ribbed domes. The way these elements were used is quite different, however. Gothic architecture employs pointed arches and ribbed vaults as a way of clarifying the hierarchy of spatial elements. Ribbed vaults allow the architects of a Gothic church to divide the roof of the central nave into segments that are equal in width to the naves of the side aisles. Pointed arches offer the possibility of creating a hierarchy of arches of different widths, independent of their height. Pointed arches and ribbed vaults become part of a logical system.
In Islamic architecture, the same elements are employed to a very different end. The architects of Córdoba did not attempt to create a hierarchy but a web in which all parts would be equal to each other. The interlocking arch as employed in Islamic architecture does not create order but rather ambiguity, weaving together elements in a way that is beyond structural logic or even comprehension (cf. Figure 8 again). The ideal was the suspension of differences in space, the ultimate aim the blurring of the distinction between interior and exterior space.
6. Conclusions
In 10th-century Córdoba, mathematics—and geometry in particular—was applied to the design of architecture in different ways and at different levels—to organize ground plans and elevations, as a way to measure the human field of view, and as a means of decoration. In all cases, the use of geometry was based on a specific, novel concept of space. Architectural space was conceived in an abstract way as a holistic unity. The difference to how Roman architects had employed mathematics in architecture highlights how revolutionary this new attitude toward architectural design truly was. In Roman architecture mathematics—in the form of arithmetic and more rarely geometric ratios—was employed to place each element in its appropriate relation to all other elements of the building and thus to achieve what Vitruvius called simmetria, or aesthetic harmony. The architects of Islamic Córdoba instead employed geometry to create a spatial web, in which all parts are equal to each other, and part of a single unified space.
Both the advances made in the field of mathematics since the 9th century and the application of mathematics to architecture in the 10th century can be viewed as the result of what might be termed a “mathematical turn” of Islamic culture. The universe was considered in a new, abstract way, as governed by abstract rules and, in the case of art and architecture, by a web of regulating lines. This new world view pointed the way toward new possibilities of designing architecture, possibilities that were to be tested further by the architects of Gothic architecture and eventually the Renaissance, though in different ways.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Al-ʿUdrī, Aḥmad ibn ʿUmar. 1965. Fragmentos Geográfico-Histórico de al-Masālik ilā Ğamīʿ al-Mamālik. Edited by ʿAbd al-ʿAzīz al-Ahwānī. Madrid: Instituto de Estudios Islámicos. [Google Scholar]
- Arias Páramo, Lorenzo. 2008. Geometría y Proporción en la Arquitectura Prerománica Asturiana. Anejos de Archivo Español de Arqueología 49. Madrid: Consejo Superior de Investigaciones Científicas. [Google Scholar]
- Arnold, Felix. 2012. Architektur als kulturgeschichtliche Quelle. In Politische Räume in Vormodernen Gesellschaften: Gestaltung, Wahrnehmung, Funktion. Edited by Ortwin Dally, Friedericke Fless and Rudolf Haensch. Rahden: Leidorf, pp. 291–300. [Google Scholar]
- Arnold, Felix. 2017. Islamic Palace Architecture in the Western Mediterranean: A History. New York: Oxford University Press. [Google Scholar]
- Arnold, Felix, Alberto Canto García, and Antonio Vallejo Triano. 2015. Munyat ar-Rummaniya: Ein Islamischer Landsitz bei Córdoba. 1. Palastanlagen. Madrider Beitrage 34. Mainz: Reichert. [Google Scholar]
- Arnold, Felix. Forthcoming. Félix Hernández y el codo islámico. Cuadernos de Madinat al-Zahra 8.
- Belting, Hans. 2008. Florenz und Bagdad: Eine Westöstliche Geschichte des Blicks. Munich: C. H. Beck. [Google Scholar]
- Binding, Günther. 1993. Baubetrieb im Mittelalter. Darmstadt: Primus. [Google Scholar]
- Bischoff, Bernhard. 1981. Mittelalterliche Studien. Ausgewählte Aufsätze zur Schriftkunde und Literaturgeschichte 3. Stuttgart: Hiersemann. [Google Scholar]
- Brisch, Klaus. 1966. Die Fenstergitter und Verwandte Ornamente der Hauptmoschee von Córdoba. Madrider Forschungen 4. Berlin: Walter de Gruyter. [Google Scholar]
- Camps Cazorla, Emilio. 1953. Módulo, Proporciones y Composición en la Arquitectura Califal Cordobesa. Madrid: Instituto Diego Velázquez. [Google Scholar]
- Carrillo, Alicia. 2014. Architectural Exchanges between North Africa and the Iberian Peninsula: Muqarnas in al-Andalus. The Journal of North African Studies 19: 68–82. [Google Scholar] [CrossRef]
- Ewert, Christian. 1968. Spanisch-Islamische Systeme Sich Kreuzender Bögen I. Die Senkrechten Ebenen Systeme Sich Kreuzender Bögen als Stützkonstruktion der Vier Rippenkuppeln in der Ehemaligen Hauptmoschee von Córdoba. Madrider Forschungen 2. Berlin: Walter de Gruyter. [Google Scholar]
- Ewert, Christian. 1978. Spanisch-Islamische Systeme Sich Kreuzender Bögen III. Die Aljafería in Zaragoza. 1. Madrider Forschungen 12.2. Berlin: Walter de Gruyter. [Google Scholar]
- Ewert, Christian, and Jens-Peter Wisshak. 1981. Forschungen zur Almohadischen Moschee. I. Vorstufen. Madrider Beiträge 9. Mainz: Philipp von Zabern. [Google Scholar]
- Fernández-Puertas, Antonio. 2000. Mezquita de Córdoba. Trazado proporcional de su planta general (siglos VIII-X). Archivo Espanol de Arte 73: 217–48. [Google Scholar] [CrossRef]
- Fernández-Puertas, Antonio. 2008. Mezquita de Córdoba. ‘Abd al-Rahmān I (169/785–786). El trazado proporcional de la planta y alzado de las arquerías del oratorio. La qibla y el mihrāb del siglo VIII. Archivo Espanol de Arte 81: 333–56. [Google Scholar] [CrossRef]
- Giese-Vögeli, Francine. 2007. Das islamische Rippengewölbe: Ursprung, Form, Verbreitung. Berlin: Gebrüder Mann. [Google Scholar]
- Golvin, Lucien. 1974. Les plafonds à Muqarnas de la Qal’a des Banû Hammâd et leur influence possible sur l’art de la Sicile à la période normande. Revue des Mondes Musulmans et de la Méditerranée 17: 63–69. [Google Scholar] [CrossRef]
- Hecht, Konrad. 1969. Maß und Zahl in der Gotischen Baukunst. Abhandlungen der Braunschweigischen Wissenschaftlichen Gesellschaft 21. Hildesheim: Georg Olms. [Google Scholar]
- Hernández Giménez, Félix. 1961. El codo en la Historiografía Árabe de la Mezquita Mayor de Córdoba: Contribución al Estudio del Monumento. Madrid: Maestre. [Google Scholar]
- Hogendijk, Jan P. 1995. Al-Mu’taman ibn Hūd. 11th-century king of Saragossa and brilliant mathematician. Historia Mathematica 22: 1–18. [Google Scholar] [CrossRef]
- Kubisch, Natascha. 1997. Der geometrische Dekor des Reichen Saales von Madīnat az-Zahrāʾ. Madrider Mitteilungen 38: 300–65. [Google Scholar]
- Kubisch, Natascha. 1999. Die Fenstergitter von Madīnat az-Zahrāʾ. Madrider Mitteilungen 40: 290–307. [Google Scholar]
- Lindberg, David C. 1976. Theories of Vision from al-Kindi to Kepler. Chicago and London: University of Chicago Press. [Google Scholar]
- Marfil Ruiz, Pedro. 2004. Estudio de las linternas y extradós de las cúpulas de la maqsura de la Catedral de Córdoba, antigua mezquita aljama. Arqueología de la Arquitectura 3: 91–107. [Google Scholar] [CrossRef]
- Moreno Castillo, Ricardo. 2007. Alhacen. El Arquimedes Árabe. Madrid: Nivola. [Google Scholar]
- Rashed, Roshdi. 1984. Entre Arithmétique et Algèbre: Recherches sur l’Histoire des Mathématiques Arabes. Paris: Société d’Edition Les Belles Lettres. [Google Scholar]
- Riobóo Camacho, Francisco. 2015. La qubba no cuadrada: Influencias y repercusiones en la arquitectura hispanomusulmana. Al-Mulk 13: 75–101. [Google Scholar]
- Riobóo Camacho, Francisco. 2016. La geometría en el Salón Rico de Madinat al-Zahra. Al-Mulk 14: 51–81. [Google Scholar]
- Ruggles, D. Fairchild. 2000. Gardens, Landscape and Vision in the Palaces of Islamic Spain. University Park: Penn State Press. [Google Scholar]
- Sánchez Velasco, Jerónimo. 2006. Elementos Arquitectónicos de Época Visigoda en el Museo Arqueológico de Córdoba. Monografías del Museo Arqueológico de Córdoba 1. Córdoba: Junta de Andalucía. [Google Scholar]
- Vallejo Triano, Antonio. 2010. La Ciudad Califal de Madīnat al-Zahrāʾ: Arqueología de su Arquitectura. Jaén: Almuzara. [Google Scholar]
- Velázquez Bosco, Ricardo. 1923. Excavaciones en Medina Azahara. Junta Superior de Excavaciones y Antigüedades 54. Madrid: Junta Superior del Tesoro Artístico. [Google Scholar]
- Vitruvius. ca.25 BCE. De architectura: Libri decem.
- Wilson Jones, Mark. 2000. Principles of Roman Architecture. New Haven and London: Yale Univesrity Press. [Google Scholar]
- Wu, Nancy Y. 2002. Ad Quadratum: The Practical Application of Geometry in Medieval Architecture. Avista Studies in the History of Medieval Science, Technology and Art 1. London: Routledge. [Google Scholar]
| 1 | For an overview see (). |
| 2 | A detailed study of the mathematical knowledge in al-Andalus is still outstanding. |
| 3 | (); (). (Cf. ). () has suggested that the design of the original phase was based on the numbers √2 and √5. The use of a square—and dividing the square in two equal halves—will always lead to diagonals measuring √2 and √5, but this does not mean that these geometric properties were taken into consideration (at least in the original phase). () observed additional geometric relationships in the design of the original phase of the mosque. If true, they would suggest that geometry was applied already two centuries earlier than suggested here. |
| 4 | (). |
| 5 | (; ; ). |
| 6 | () correctly points out that the proportions are equal to those of a hexagon. |
| 7 | (; ; . Cf. ; ). The equilateral triangle also became important in Romanesque and Gothic architecture, though how far it was used for determining the proportion of buildings (ad triangulum)—particularly in the elevation of churches—is still being debated. (Cf. ; ). |
| 8 | Vitruvius IX, prologue; (; ). |
| 9 | The examples given here were all set out on the horizontal surface of a terrace. On a slope the architects would have had additional problems. |
| 10 | Vitruvius I, 2 and III, 1; (). For the use of the geometric proportion 1:√2 (diagonal of a square) see Vitruvius VI, 3. |
| 11 | For example in the design of the Aljafería (; ). |
| 12 | For the Roman prototypes see (). |
| 13 | Vitruvius was known and read already at the court of Charlemagne (r. 768–814). (). |
| 14 | Based on measurements made by Mark Hofmann, Ana Zamorano, and myself at the site in 2018. |
| 15 | Vitruvius III, 1. |
| 16 | The difference between the design methods of Vitruvius and the architect of the Dār al-Ǧund may reflect to some degree basic differences in how the role of the individual within society was conceived—an aspect that would warrant further study. |
| 17 | (). Pointed arches are first found in the extension of the mosque of Córdoba by al-Hakam II and become more and more frequent in the 11th century. |
| 18 | Based on measurements made by Mark Hofmann, Ana Zamorano and myself in 2018. |
| 19 | (). |
| 20 | (; ). |
| 21 | (; ). |
| 22 | (). |
| 23 | (). |
| 24 | (; ; ). The book was known in 11th-century Zaragoza. (). |
| 25 | (). |
| 26 | (; ). Fragments of the Visigoth period from Córdoba are published in (). |
| 27 | (). |
| 28 | (; ). |
| 29 | For a recent study see (). |
| 30 | (; ; ). |
| 31 | Cf. (), p. 176 deals with the question whether the transmission of architectural forms from Islamic to Late Romanesque architecture went hand in hand with the ideas and concepts behind these forms, specifically whether the association between Islamic philosophy and Scholasticism on the one hand and between Gothic architecture and Islamic architecture on the other was related in some way. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).