Prediction of the Maximum Seismic Member Force in a Superstructure of a Base-Isolated Frame Building by Using Pushover Analysis
Abstract
:1. Introduction
2. Building and Ground Motion Data
2.1. Building Data
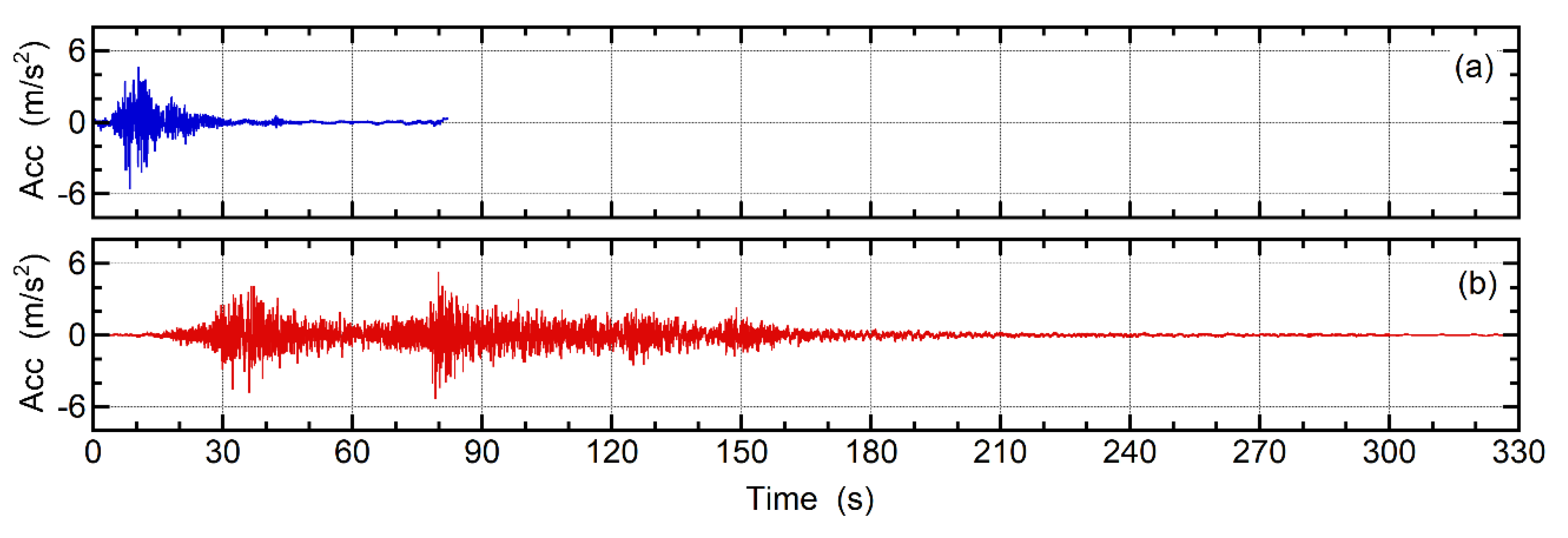
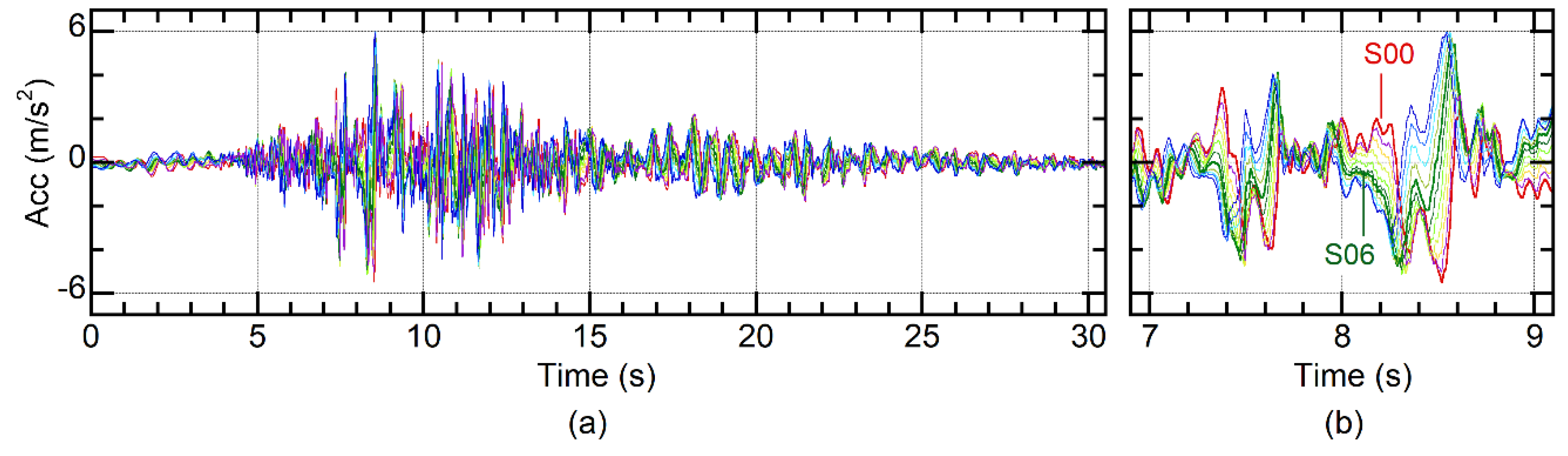
2.2. Ground Motion Data
2.3. Cases of Nonlinear Time-history Analysis
3. Nonlinear Modal Response
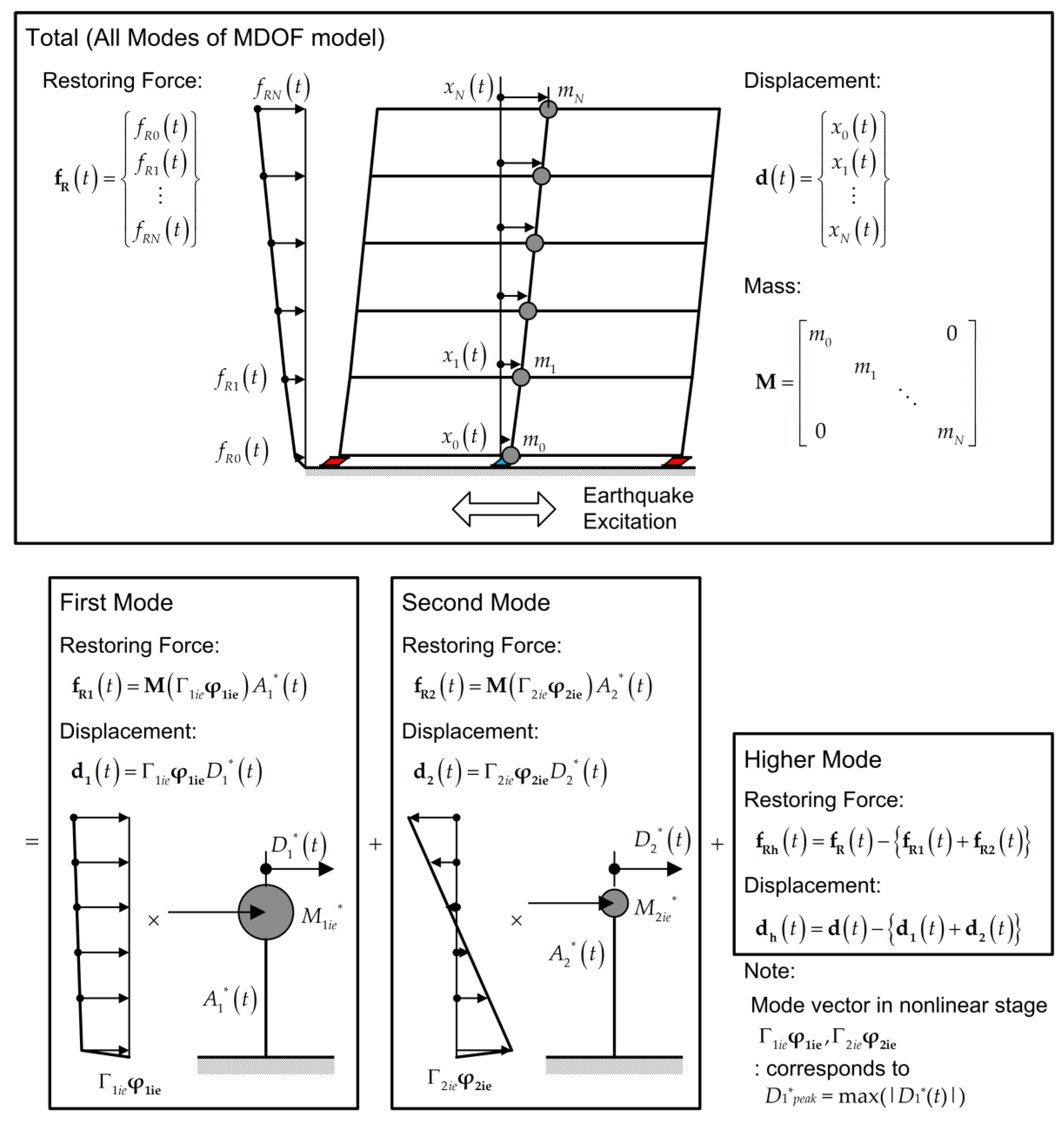
3.1. Procedure for Calculating the Modal Response
- Carry out the nonlinear time-history analysis of an N-story base-isolated frame building model to obtain the displacement vector d(t) and the restoring force vector fR(t).
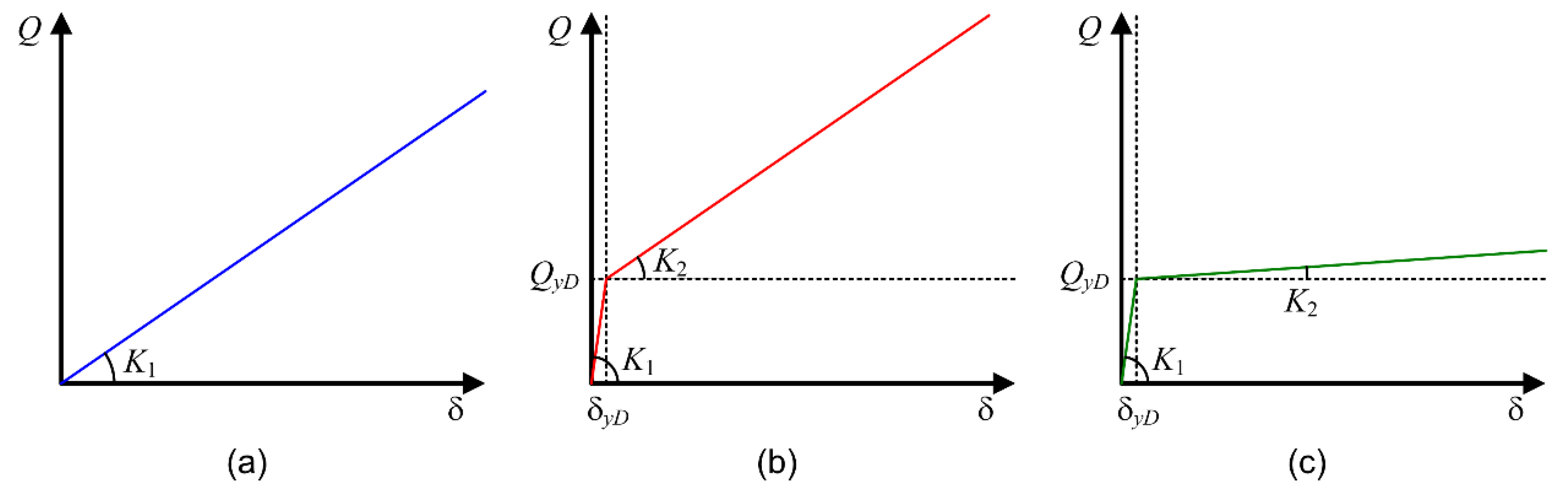
- Carry out the pushover analysis of the base-isolated frame building model considering the change in the first mode’s shape at each nonlinear stage. Displacement-based mode-adaptive pushover (DB-MAP) analysis [24,29] is adopted. The first mode vector at each loading step n, , is calculated assuming that the displacement vector at each loading step, nd, is proportional to the first-mode vector at each loading step:In Equations (3) to (5), nxj is the relative displacement of the jth floor at step n.
- Assume the first mode vector as that in the elastic stage and set D1*push = 1D1*.
- Calculate the time-history response of the equivalent displacement of the first mode, D1*(t), using the displacement vector d(t). Then find D1*peak as the largest value of |D1*(t)|:In Equation (6), M1* is the effective first modal mass calculated in terms of .
- Determine the first mode vector from the pushover analysis results corresponding to D1*peak.
- If D1*peak equals D1*push, go to the next step. Otherwise, update and D1*push = D1*peak. Then repeat steps 4 to 6 until the difference between D1*push and D1*peak is within the allowable band.
- Calculate the time-history response of the equivalent acceleration of the first mode, A1*(t), using the restoring force vector fR(t):In Equation (8), M1ie* is the effective first modal mass in terms of .
- Determine the second mode vector from Equations (10) and (11) in terms of and the second-mode vector in the elastic stage (), with consideration given to the orthogonality of the mode vectors, to satisfy the orthogonal condition of the two mode vectors:
- Calculate the time history of the equivalent displacement and acceleration of the second mode, D2*(t) and A2*(t), respectively:In Equation (12), M2ie* is the effective first modal mass in terms of .
- Calculate the relative displacement and restoring force vector of the ith mode (i = 1, 2), di(t) and fRi(t) respectively, and then calculate the relative displacement and restoring vector of the higher mode, dh(t) and fRh(t), respectively:
3.2. Calculation Results
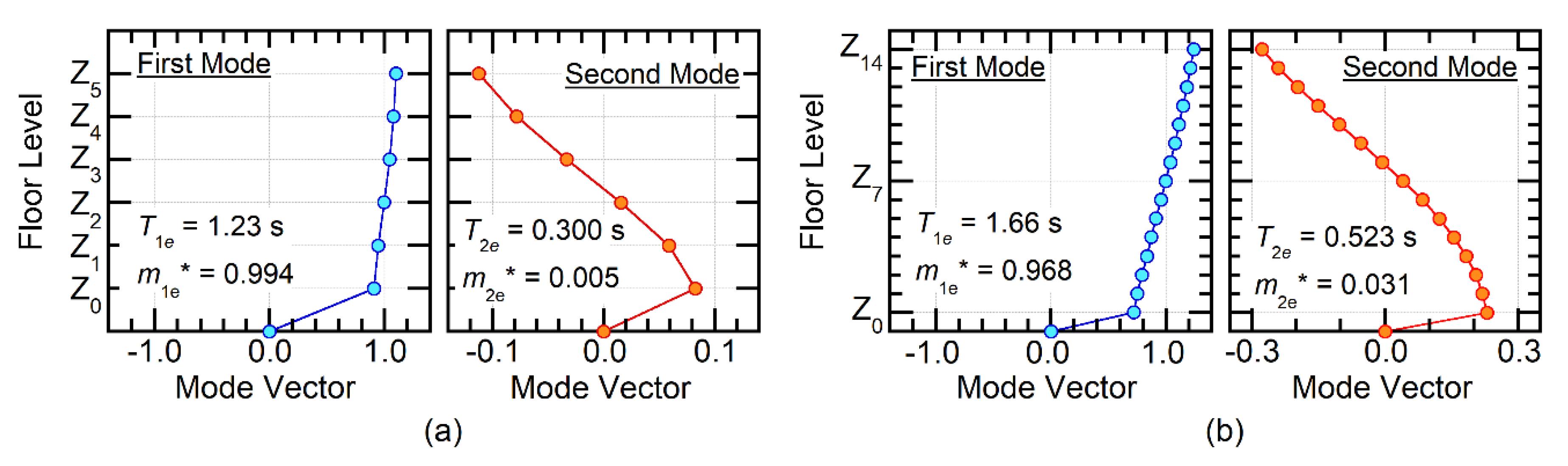
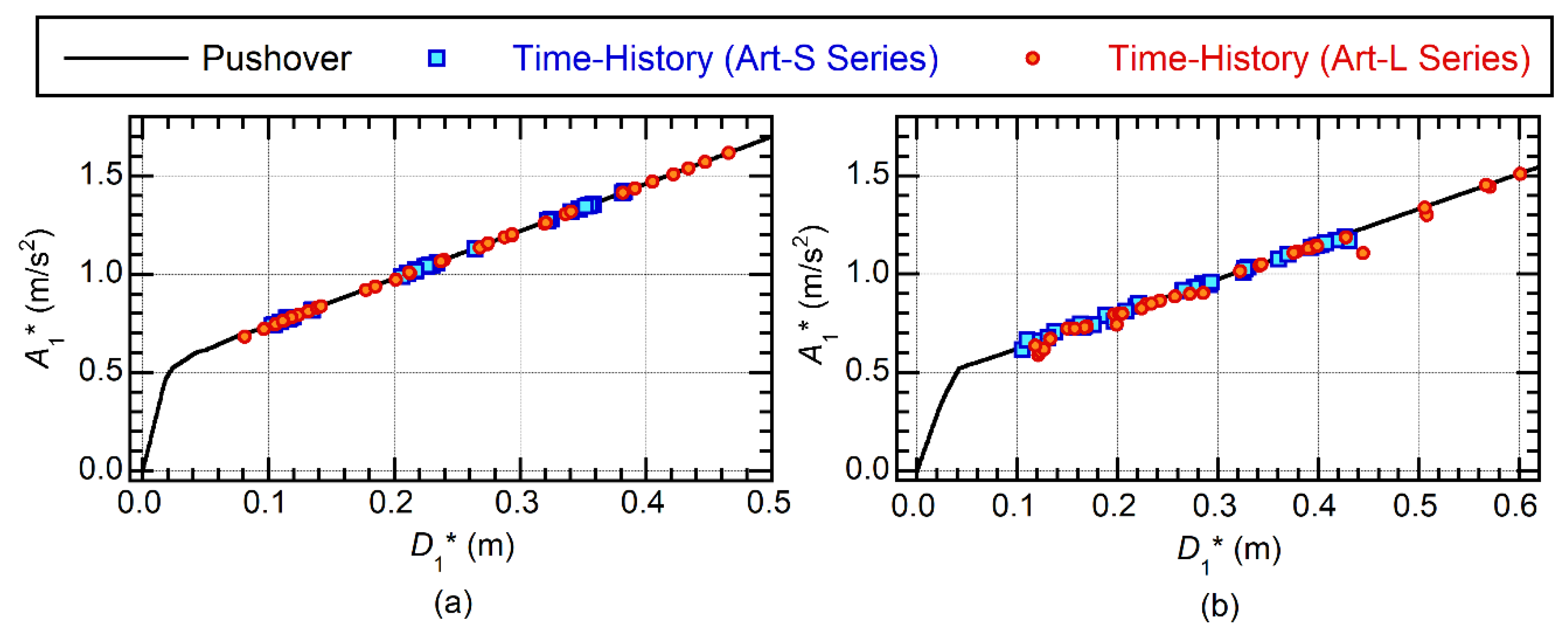
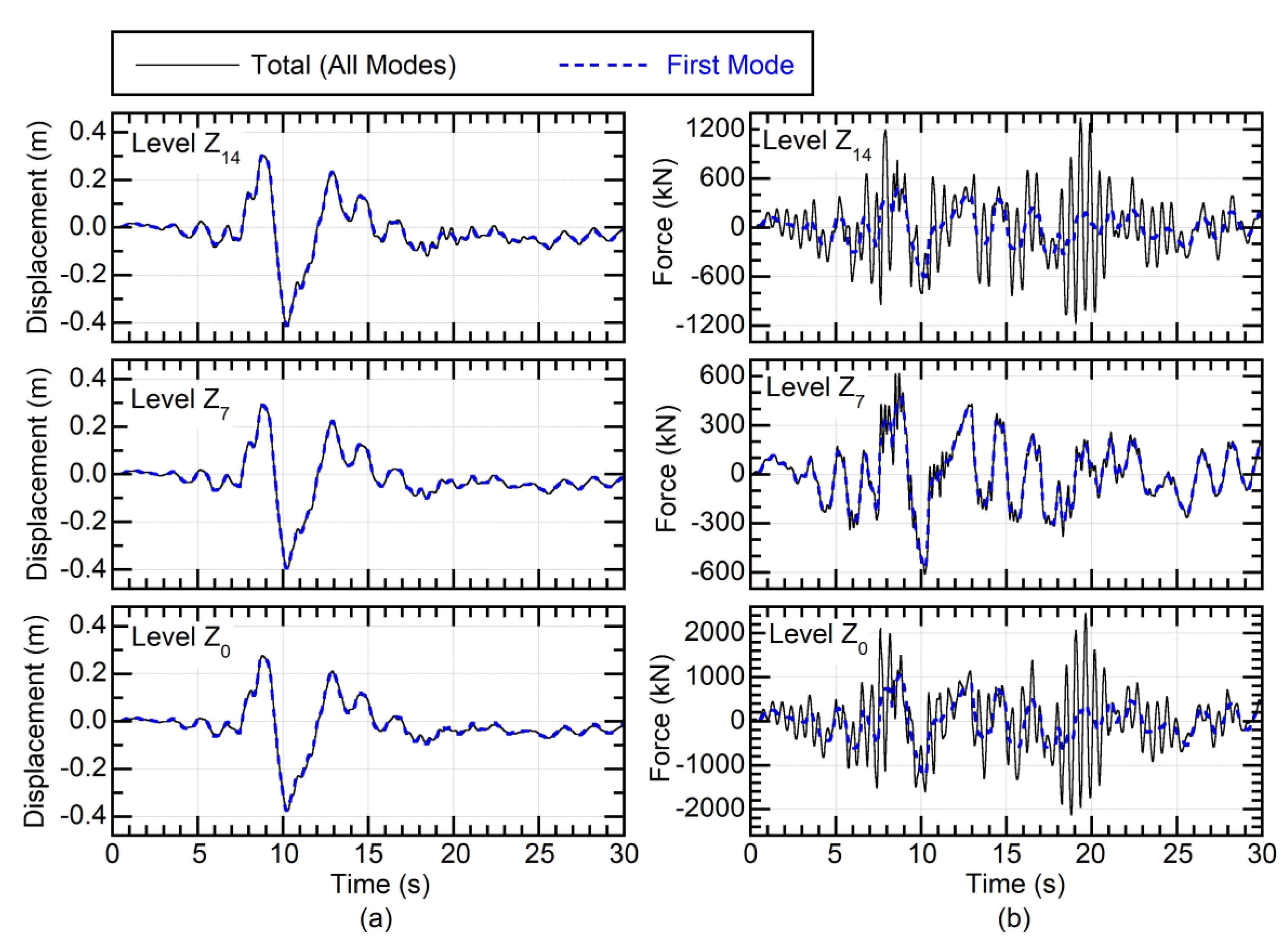
3.2.1. Validation for Modal Response Calculations
3.2.2. Comparison of the Modal Response
3.2.3. Simultaneity of the Peak Modal Response
4. Prediction of the Maximum Seismic Member Force in a Superstructure
4.1. Proposal of a Set of Pushover Analyses
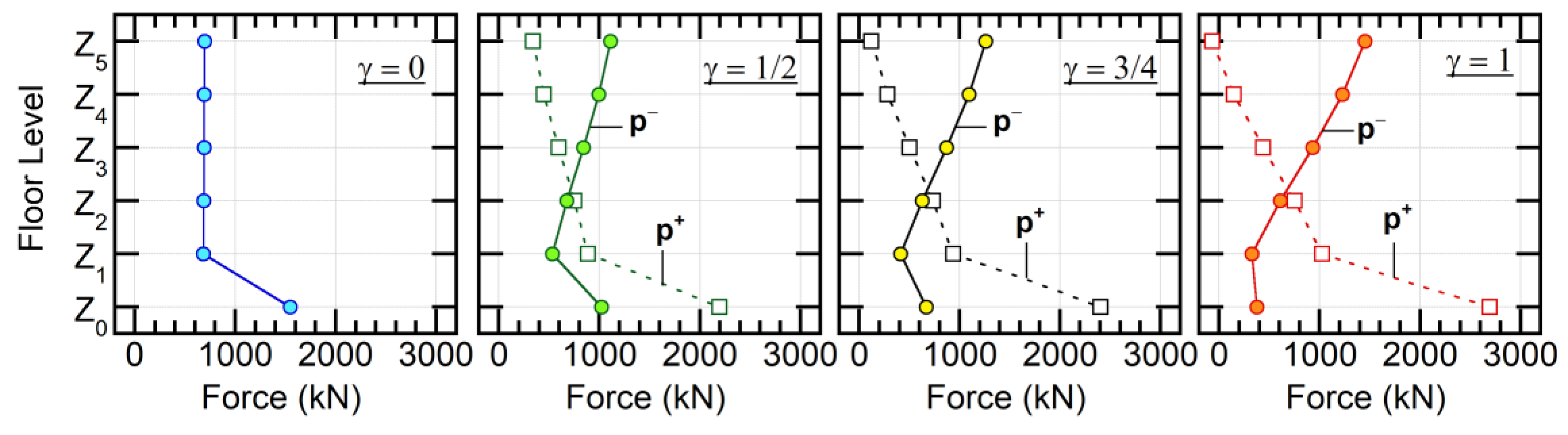
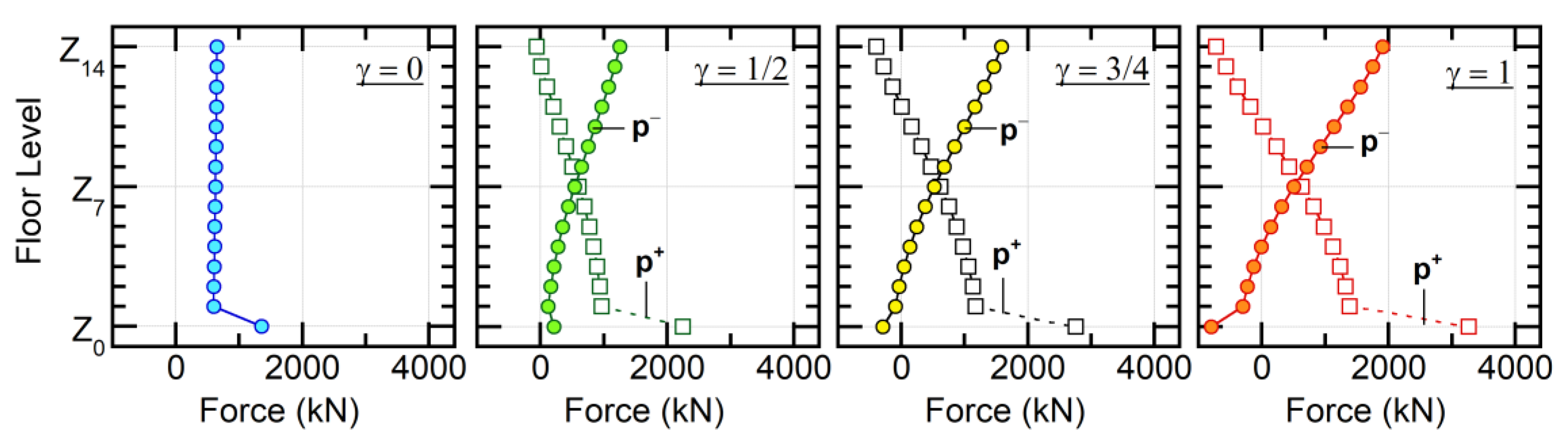
- Calculate a set of horizontal-force distributions p+ and p− in terms of the first- and second-mode vectors at D1*max:
- Perform the pushover analysis using the invariant force distributions p+ and p− (termed Pushover 1 and 2, respectively) until the equivalent displacement nD* calculated as:reaches D1*max.
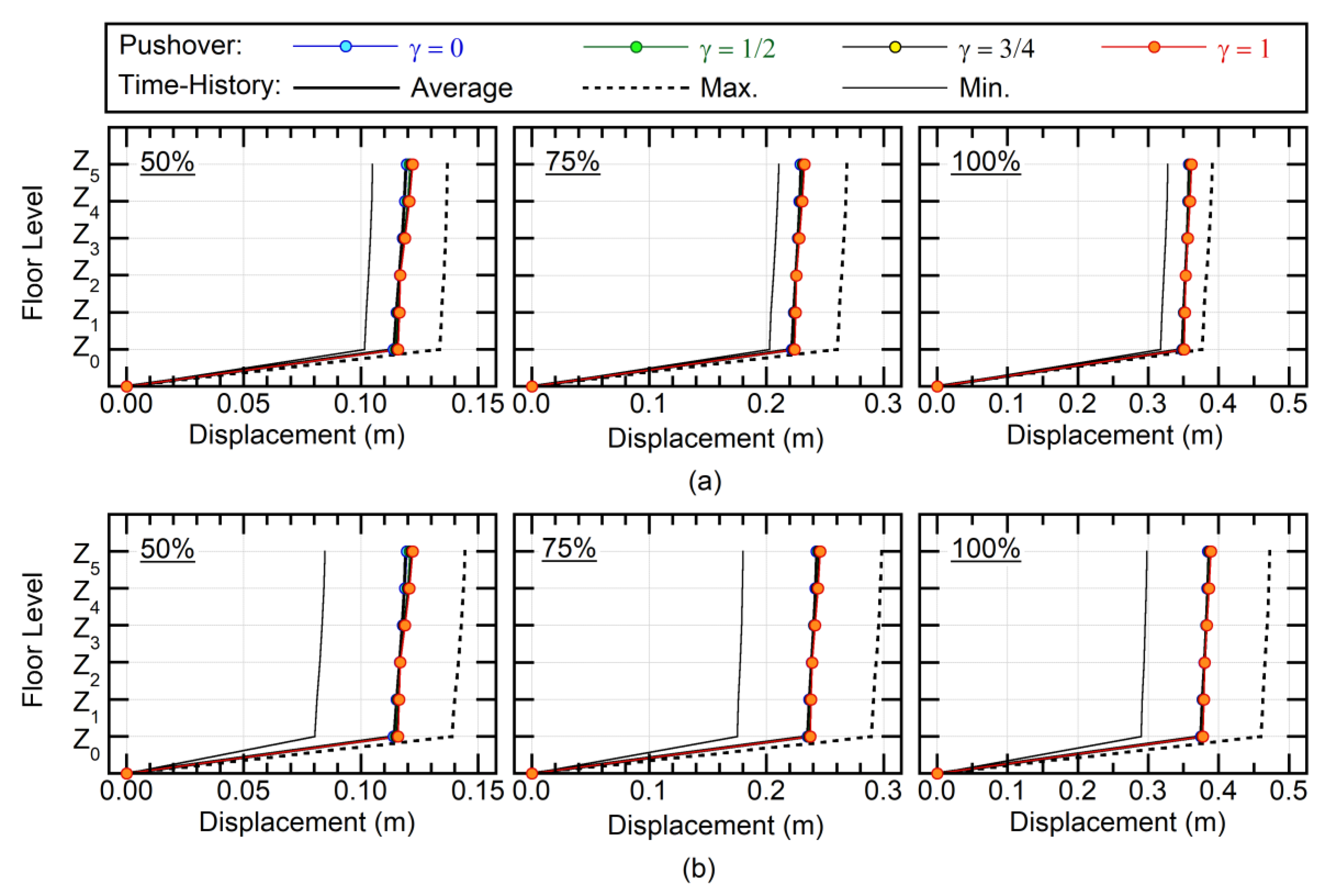
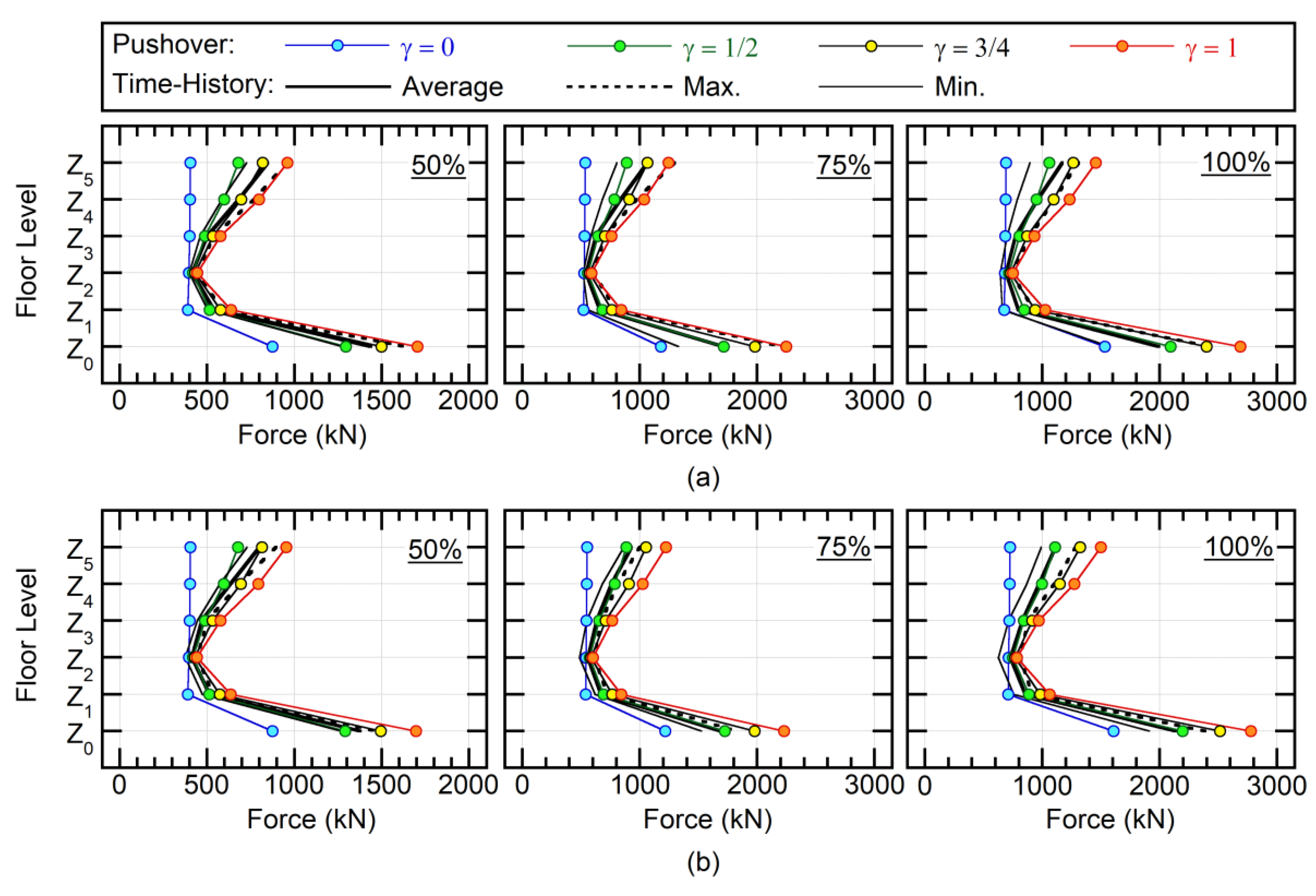
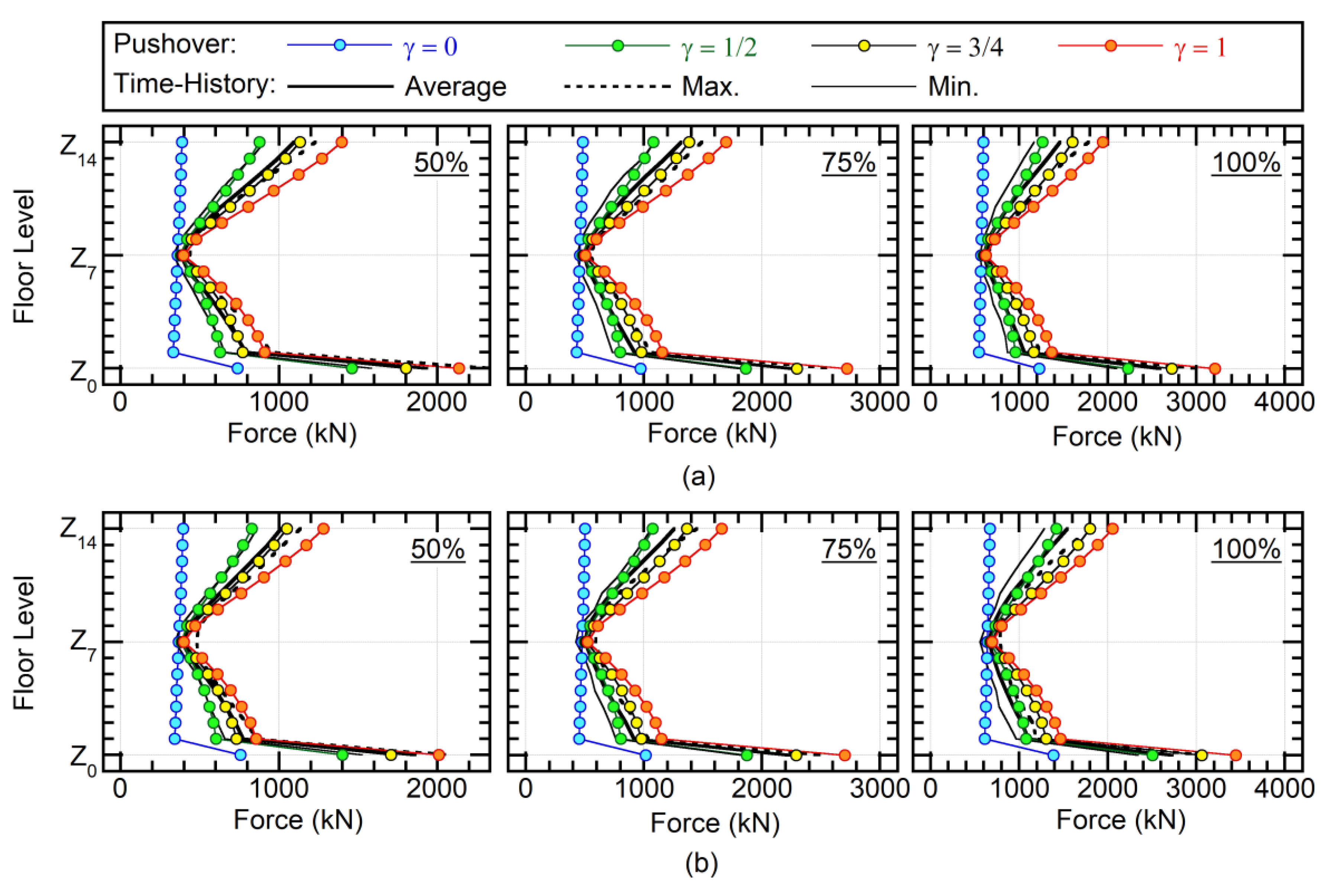
- Determine the maximum response from the envelope of Pushover 1 and 2, i.e., the maximum relative displacement, the maximum restoring force, and the maximum member forces are obtained as the maximum value of the results of Pushover 1 and 2.
4.2. Predicted Results and Comparison
4.2.1. Calculated Force Distribution
4.2.2. Relative Displacement at Each Floor
4.2.3. Restoring Force at Each Floor
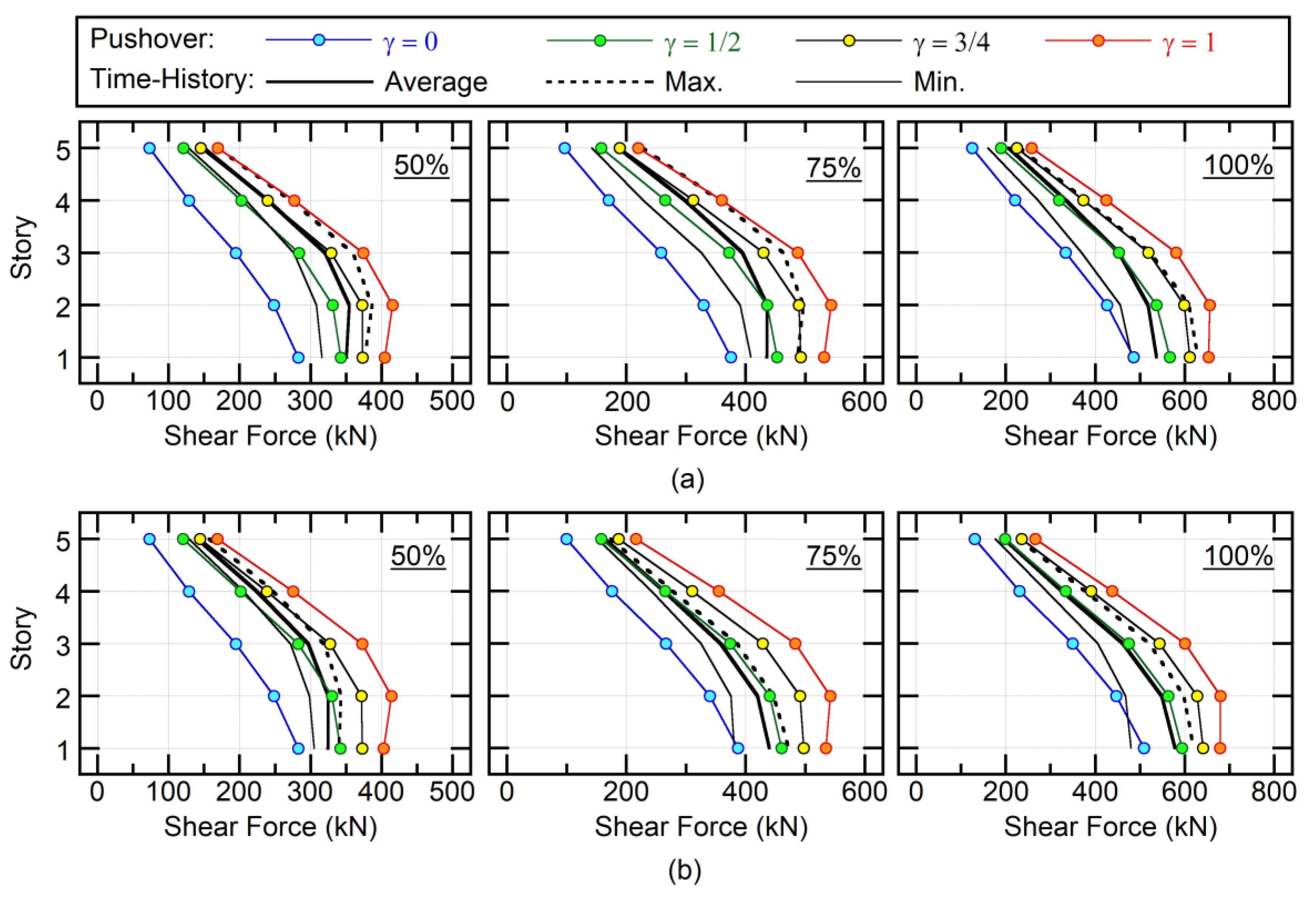
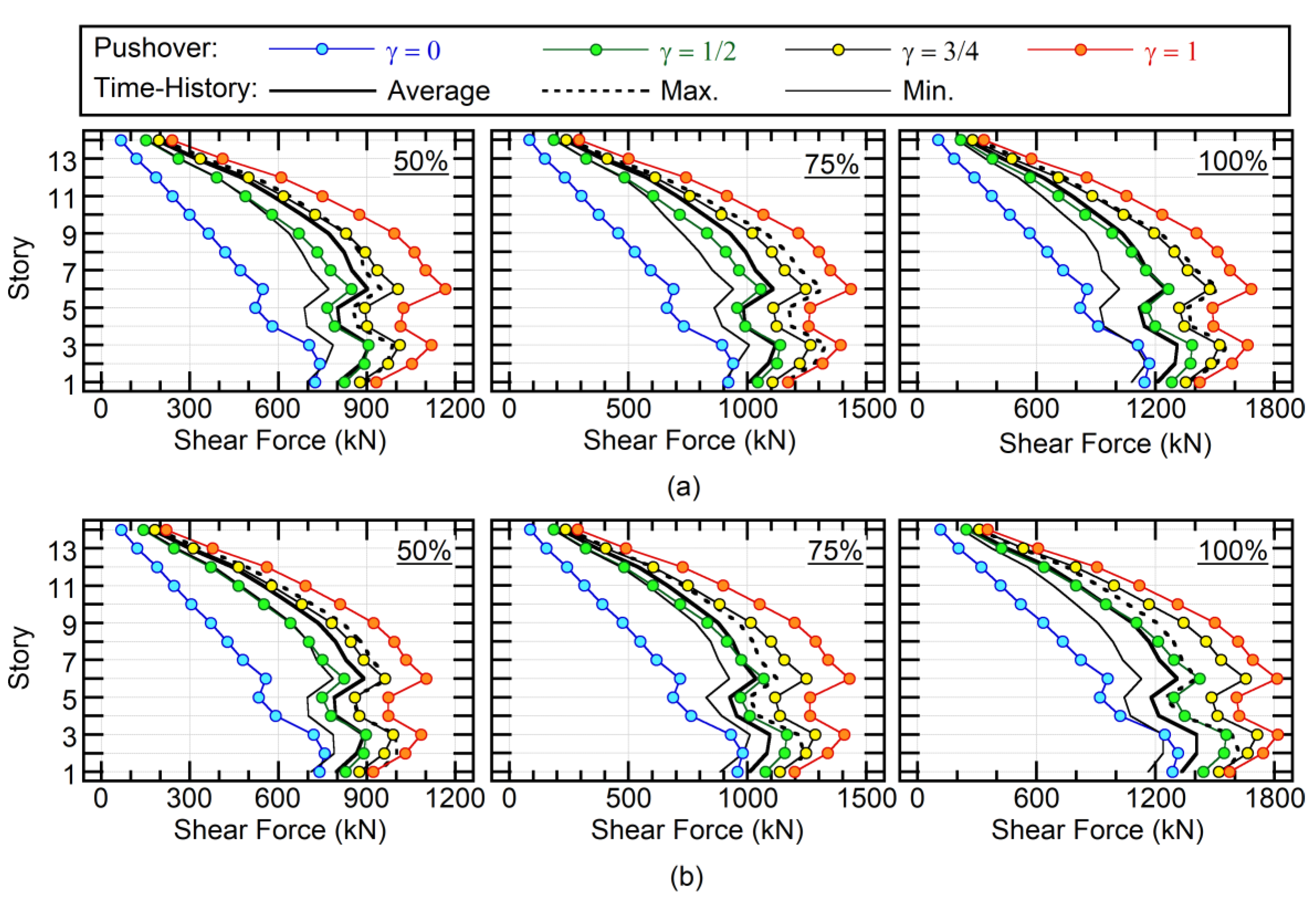
4.2.4. Shear Force of Column
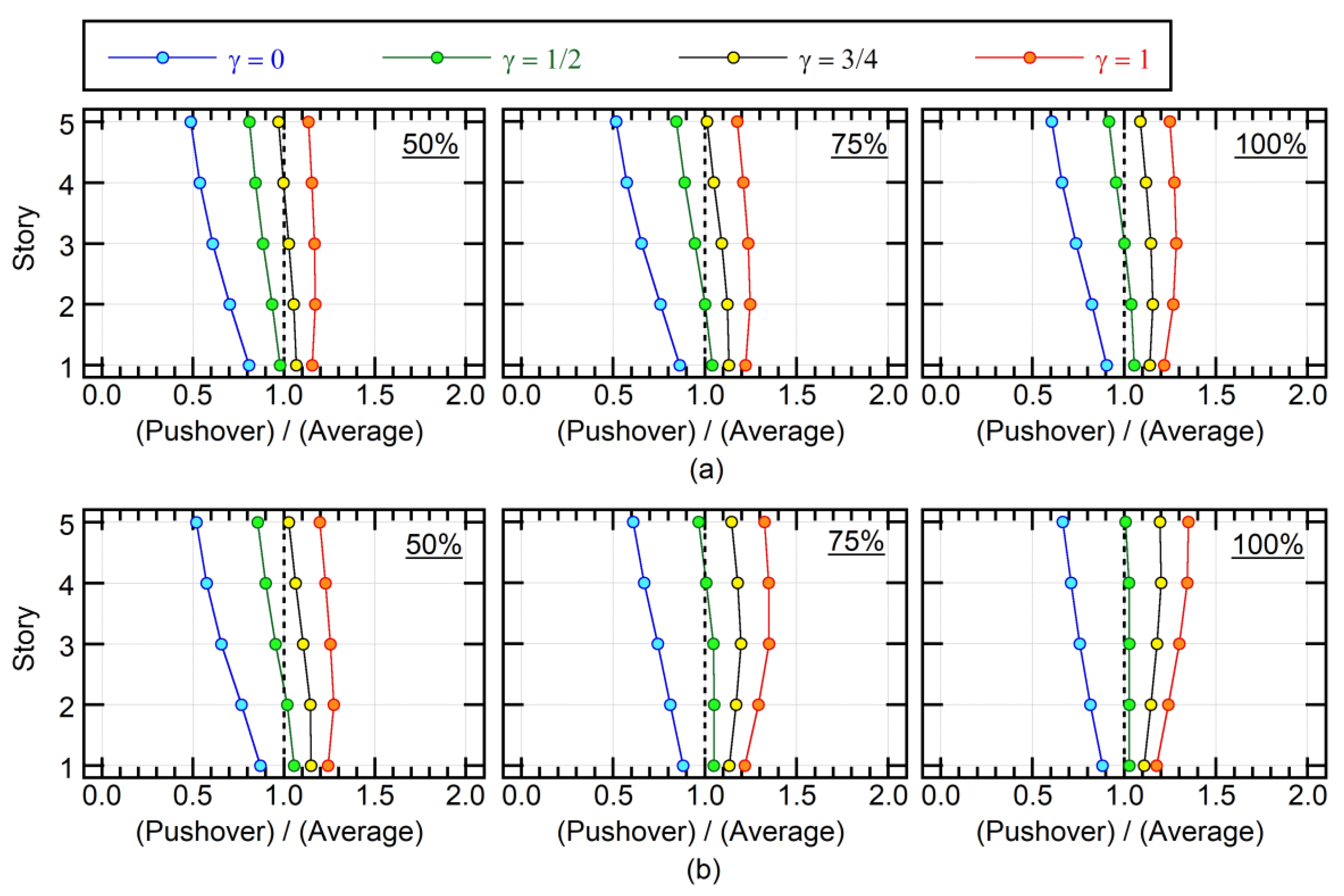
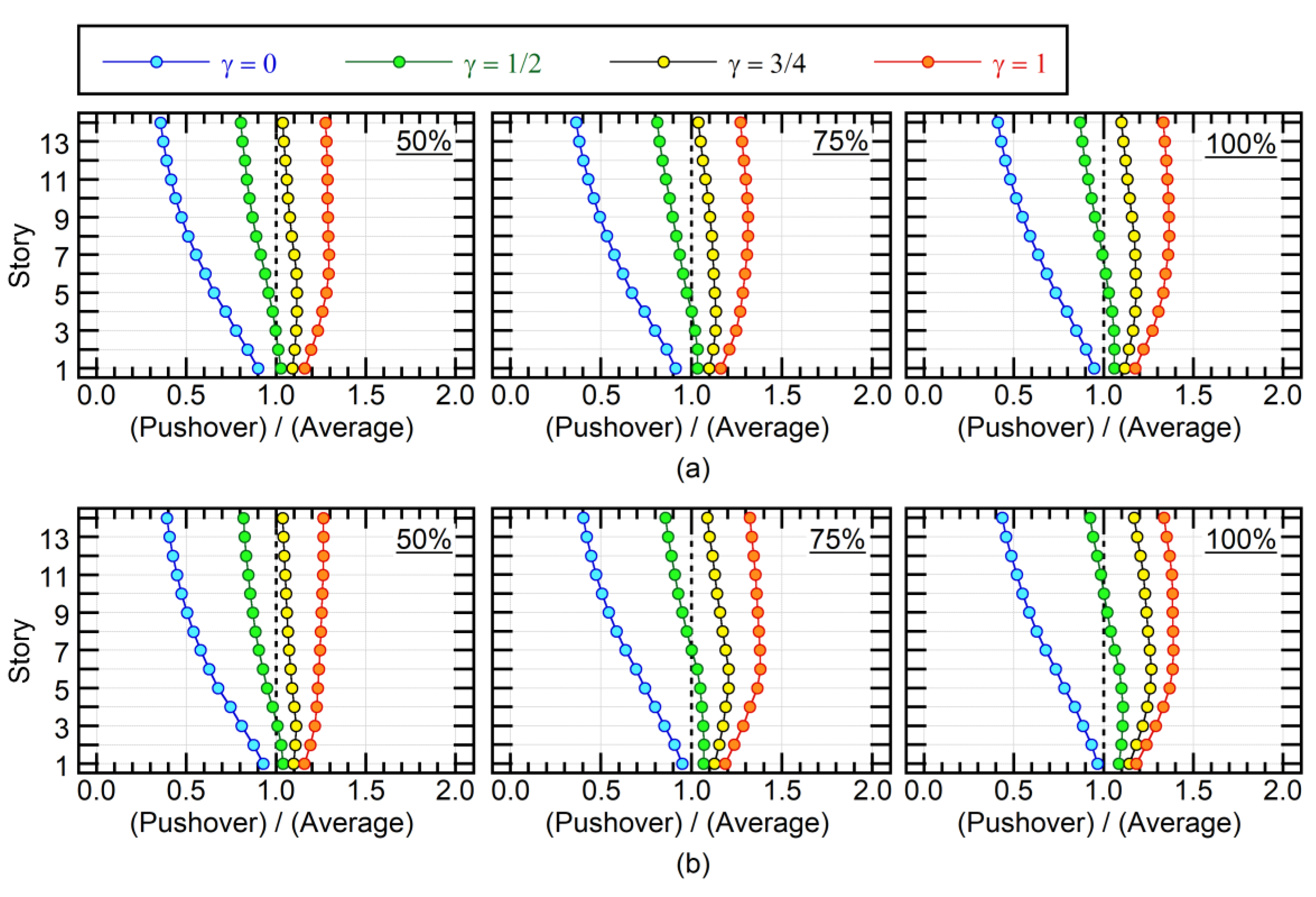
4.3. Accuracy of the Proposed Procedure
5. Discussions and Conclusions
- The calculation procedure for the nonlinear modal response was applied to the base-isolated frame buildings studied herein. Results show that the procedure works well for base-isolated buildings, i.e., the peak response of the first modal response agrees well with the results of pushover analysis, and the hysteresis rule of the first modal response is well regular and similar to normal bilinear behavior.
- The first modal response is predominant in the relative displacement responses of the base-isolated building models at all floor levels. In contrast, the contribution of the second modal response is important in the restoring force responses at the top and bottom floors of the base-isolated building models. Therefore, to determine the proper horizontal force distribution used in the pushover analysis, the combination of the first and second modal responses is an important issue.
- The peaks of the first and second modal responses rarely occur simultaneously, although there is a certain level of contribution of the second modal response when the maximum first modal response occurs. The factor of the simultaneity of the two modal responses, γ, approximately ranges between −1/2 and 1/2, however, there are cases that the absolute value of γ exceeds 1/2.
- The accuracy of the proposed set of pushover analyses for the prediction of the maximum member force was verified by nonlinear time-history analysis. Results show that the maximum member force can be satisfactorily predicted by considering the combination of the first and second modal responses properly. The limited numerical investigation herein revealed that the case γ = 3/4 provides reasonably conservative estimations. The case γ = 1/2 may provide the closest estimation to the average of nonlinear time-history analysis results, however, it may underestimate results in upper stories.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Charleson, A.; Guisasola, A. Seismic Isolation for Architects; Routledge: London, UK; New York, NY, USA, 2017. [Google Scholar]
- Architectural Institute of JAPAN (AIJ). Design Recommendations for Seismically Isolated Buildings; Architectural Institute of Japan: Tokyo, Japan, 2016. [Google Scholar]
- Lee, D.G.; Hong, J.M.; Kim, J. Vertical distribution of equivalent static loads for base isolated building structures. Eng. Struct. 2001, 23, 1293–1306. [Google Scholar] [CrossRef]
- York, K.; Ryan, K.L. Distribution of lateral forces in base-isolated buildings considering isolation system nonlinearity. J. Eqrthq. Eng. 2008, 12, 1185–1204. [Google Scholar] [CrossRef]
- American Society of Civil Engineering (ASCE). Seismic Evaluation and Retrofit of Existing Buildings: ASCE Standard, ASCE/SEI41-17; American Society of Civil Engineering: Reston, VA, USA, 2017. [Google Scholar]
- Ordoñez, D.; Foti, D.; Bozzo, L. Comparative study of the inelastic response of base isolated buildings. Earthq. Eng. Struct. Dyn. 2003, 32, 151–164. [Google Scholar] [CrossRef]
- Kikuchi, M.; Black, C.J.; Aiken, I.D. On the response of yielding seismically isolated structures. Earthq. Eng. Struct. Dyn. 2008, 37, 659–679. [Google Scholar] [CrossRef]
- Cardone, D.; Flora, A.; Gesualdi, G. Inelastic response of RC frame buildings with seismic isolation. Earthq. Eng. Struct. Dyn. 2013, 42, 871–889. [Google Scholar] [CrossRef]
- Mazza, F.; Vulcano, A. Effects of near-fault ground motions on the nonlinear dynamic response of base-isolated r.c. framed buildings. Earthq. Eng. Struct. Dyn. 2012, 41, 211–232. [Google Scholar] [CrossRef]
- Fajfar, P. A nonlinear analysis method for performance-based seismic design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Kreslin, M.; Fajfar, P. The extended N2 method considering higher mode effects in both plan and elevation. Bull. Earthq. Eng. 2002, 10, 561–582. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2013, 42, 871–889. [Google Scholar]
- Kilar, V.; Koren, D. Usage of Simplified N2 Method for Analysis of Base Isolated Structures. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Kilar, V.; Koren, D. Simplified inelastic seismic analysis of base-isolated structures using N2 method. Earthq. Eng. Struct. Dyn. 2010, 39, 967–989. [Google Scholar] [CrossRef]
- Kilar, V.; Koren, D. Seismic behaviour of asymmetric base isolated structures with various distributions of isolators. Eng. Struct. 2009, 31, 910–921. [Google Scholar] [CrossRef]
- Koren, D.; Kilar, V. The applicability of the N2 method to the estimation of torsional effects in asymmetric base-isolated buildings. Earthq. Eng. Struct. Dyn. 2011, 40, 867–886. [Google Scholar] [CrossRef]
- Providakis, C.P. Pushover analysis of base-isolated steel–concrete composite structures under near-fault excitations. Soil Dyn. Earthq. Eng. 2008, 28, 293–304. [Google Scholar] [CrossRef]
- Faal, H.N.; Poursha, M. Applicability of the N2, extended N2 and modal pushover analysis methods for the seismic evaluation of base-isolated building frames with lead rubber bearings (LRBs). Soil Dyn. Earthq. Eng. 2017, 98, 84–100. [Google Scholar] [CrossRef]
- Bhandari, M.; Bharti, S.D.; Shrimali, M.K.; Datta, T.K. Assessment of proposed lateral load patterns in pushover analysis for base-isolated frames. Eng. Struct. 2018, 175, 531–548. [Google Scholar] [CrossRef]
- Bhandari, M.; Bharti, S.D.; Shrimali, M.K.; Datta, T.K. Applicability of capacity spectrum method for base-isolated building frames at different performance points. J. Eqrthq. Eng. 2018, 1–30. Available online: www.tandfonline.com (accessed on 30 June 2019). [CrossRef]
- Japan Building Disaster Prevention Association (JBDPA). Kozo-Sekkei Buzai-Damnen Jirei-Shu (Structural Design Examples of Member Sections of Buildings); Japan Building Disaster Prevention Association: Tokyo, Japan, 2007. (in Japanese) [Google Scholar]
- Bridgestone Corporation. Seismic Isolation Product Line-Up Version 2017. Volume 1. Available online: https://www.bridgestone.com/products/diversified/antiseismic_rubber/pdf/catalog_201710.pdf (accessed on 3 August 2019).
- Nippon Steel Engineering Co. Ltd. Men-shin NSU Damper Line-Up. Available online: https://www.eng.nipponsteel.com/steelstructures/product/base_isolation/damper_u/lineup_du/ (accessed on 3 August 2019).
- Fujii, K. Pushover-based seismic capacity evaluation of Uto city hall damaged by the 2016 Kumamoto earthquake. Buildings 2019, 9, 140. [Google Scholar] [CrossRef]
- Wada, A.; Hirose, K. Elasto-plastic dynamic behaviors of the building frames subjected to bi-directional earthquake motions. J. Struct. Const. Eng. AIJ 1989, 399, 37–47. (In Japanese) [Google Scholar]
- Building Research Institute (BRI). BRI Strong Motion Network, Strong Motion Report, 2011/03/11 14:46 off Sanriku (M = 9.0, h = 24 km). Available online: http://smo.kenken.go.jp/index.php/report/201103111446 (accessed on 4 August 2019).
- Fujii, K.; Miyagawa, K. Nonlinear Seismic Response of A Seven-Story Steel Reinforced Concrete Condominium Retrofitted with Low-Yield-Strength-Steel Damper Columns. In Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018. [Google Scholar]
- Kuramoto, H. Earthquake response characteristics of equivalent SDOF system reduced from multi-story buildings and prediction of higher mode responses. J. Struct. Const. Eng. 2004, 580, 61–68. (in Japanese). [Google Scholar] [CrossRef]
- Fujii, K. Prediction of the largest peak nonlinear seismic response of asymmetric buildings under bi-directional excitation using pushover analyses. Bull. Earthq. Eng. 2014, 12, 909–938. [Google Scholar] [CrossRef]
- Rahmani, A.Y.; Bourahla, N.; Bento, R.; Badaoui, M. An improved upper-bound pushover procedure for seismic assessment of high-rise moment resisting steel frames. Bull. Earthq. Eng. 2018, 16, 315–339. [Google Scholar] [CrossRef]
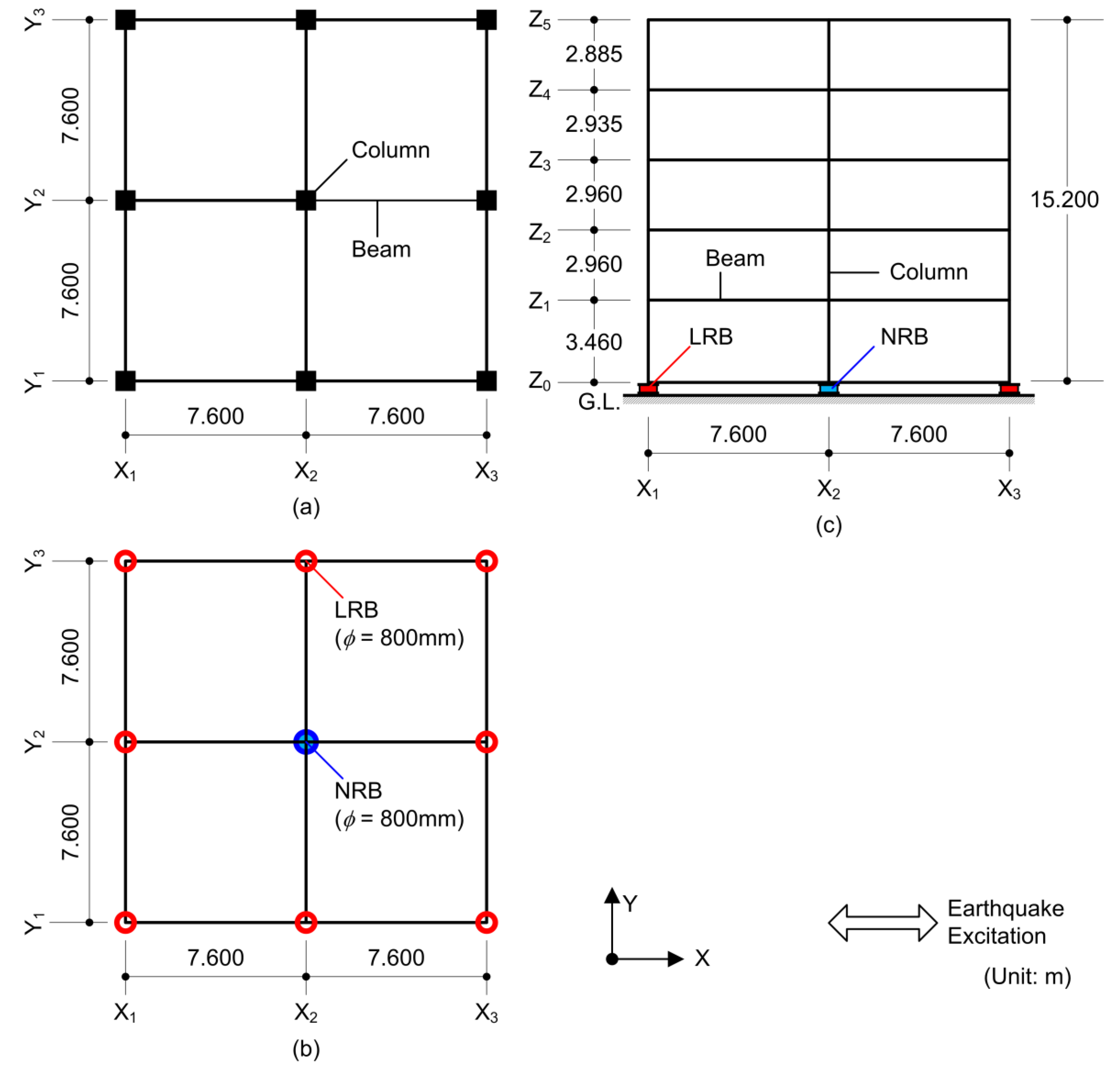
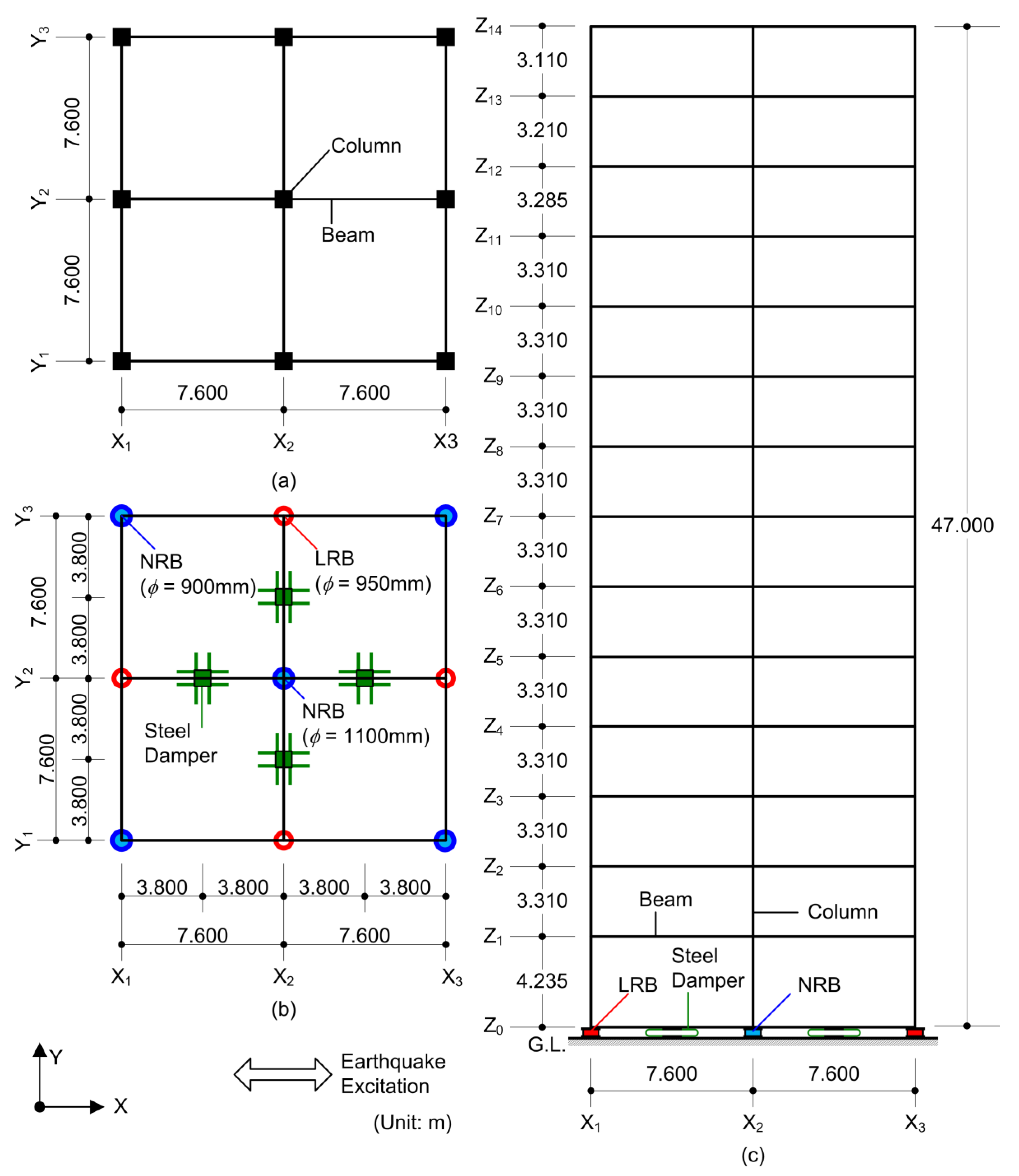




| Member | Section | Compressive Strength (MPa) | Young’s Modulus (MPa) |
|---|---|---|---|
| Beam (Z5) | 500 mm × 700 mm | 24 | 2.27 × 104 |
| Beam (Z4) | 500 mm × 750 mm | ||
| Beam (Z1 to Z3) | 550 mm × 800 mm | ||
| Beam (Z0) | 750 mm × 1800 mm | ||
| Column (All) | 850 mm × 850 mm | 24 | 2.27 × 104 |
| Member | Section | Compressive Strength (MPa) | Young’s Modulus (MPa) |
|---|---|---|---|
| Beam (Z14) | 550 mm × 900 mm | 24 | 2.27 × 104 |
| Beam (Z13) | 550 mm × 1000 mm | ||
| Beam (Z12) | 600 mm × 1100 mm | 27 | 2.35 × 104 |
| Beam (Z11) | 700 mm × 1150 mm | ||
| Beam (Z7 to Z10) | 700 mm × 1150 mm | 33 | 2.52 × 104 |
| Beam (Z1 to Z6) | 700 mm × 1150 mm | 36 | 2.59 × 104 |
| Beam (Z0) | 850 mm × 3000 mm | ||
| Column (13th to 14th Story) | 950 mm × 950 mm | 24 | 2.27 × 104 |
| Column (11th to 12th Story) | 1000 mm × 1000 mm | 27 | 2.35 × 104 |
| Column (7th to 10th Story) | 1050 mm × 1050 mm | 33 | 2.52 × 104 |
| Column (1st to 6th Story) | 1100 mm × 1100 mm | 36 | 2.59 × 104 |
| Type | Amount | Outer Diameter (mm) | Lead Plug Diameter (mm) | Shear Modulus (MPa) | Initial Stiffness K1 (MN/m) | Yield Strength QyD (kN) | Post Yield Stiffness K2 (MN/m) | Vertical Stiffness KV (MN/m) |
|---|---|---|---|---|---|---|---|---|
| NRB | 1 | 800 | − | 0.294 | 0.912 | − | − | 2800 |
| LRB | 8 | 800 | 200 | 0.385 | 13.0 | 250 | 1.00 | 2960 |
| Type | Amount | Outer Diameter (mm) | Lead Plug Diameter (mm) | Shear Modulus (MPa) | Initial Stiffness K1 (MN/m) | Yield Strength QyD (kN) | Post Yield Stiffness K2 (MN/m) | Vertical Stiffness KV (MN/m) |
|---|---|---|---|---|---|---|---|---|
| NRB | 4 | 900 | − | 0.441 | 1.56 | − | − | 3730 |
| NRB | 1 | 1100 | − | 0.441 | 1.89 | − | − | 4510 |
| LRB | 4 | 950 | 240 | 0.385 | 18.5 | 360 | 1.42 | 4210 |
| Amount | Initial Stiffness K1 (MN/m) | Yield Strength QyD (kN) | Post Yield Stiffness K2 (MN/m) |
|---|---|---|---|
| 4 | 19.2 | 608 | 0.32 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujii, K. Prediction of the Maximum Seismic Member Force in a Superstructure of a Base-Isolated Frame Building by Using Pushover Analysis. Buildings 2019, 9, 201. https://doi.org/10.3390/buildings9090201
Fujii K. Prediction of the Maximum Seismic Member Force in a Superstructure of a Base-Isolated Frame Building by Using Pushover Analysis. Buildings. 2019; 9(9):201. https://doi.org/10.3390/buildings9090201
Chicago/Turabian StyleFujii, Kenji. 2019. "Prediction of the Maximum Seismic Member Force in a Superstructure of a Base-Isolated Frame Building by Using Pushover Analysis" Buildings 9, no. 9: 201. https://doi.org/10.3390/buildings9090201





