1. Introduction
Green building notions [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11] and energy autonomy are becoming increasingly important in the last decades, especially in the industrial sector, where energy costs from machinery in the past used to overshadow other aspects of energy consumption. As progressively traditional approaches of manufacturing have yielded to leaner methods of production and management systems, there has been an increased pressure on architecture to focus and address other aspects of energy “waste”. Nowadays there is a worldwide interest, together with a considerable financial expenditure, in the quest for a better utilisation of available resources and a reduction in reliance on traditional “wasteful” techniques of operation. Furthermore, there is an increased demand for solutions that can also be applied in the form of retrofits to existing building structures as well. This signifies the need for an in-depth study of the interrelation between architectural characteristics and daylight [
12,
13,
14,
15]. While the selections of the luminaires [
16,
17,
18] and the corresponding lighting control [
19,
20,
21,
22,
23,
24,
25] are crucial for the calculation of energy consumption, the building form and the corresponding impact of the daylight [
26,
27] determines the energy savings potential, and is still an important issue at the initial design stage of a building. Therefore, the need to create an accurate mathematical model is apparent. This work investigates the influence of different opening types and their arrangements in the overall daylight provision in an industrial building.
There have been several studies in daylighting [
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37]. Tsangrassoulis et al. [
38] examined the hybrid daylighting system, Doulos et al. [
39,
40,
41] investigated the relationship between dimming and daylighting. Kontadakis et al. [
42] examined an active sunlight redirection system for daylight, with various studies investigating the effect of daylight driven from daylight systems and devices inside various types of buildings [
43,
44]. Huang et al. [
45] utilized statistic tools and symmetry properties to determine an exponential relationship between luminosity and CCT in red-green-blue (RGB) LED and OLED light sources. Such a relationship presents an option to remove the effects of CCT in colour evaluation standards, as well as to provide a guideline for adjusting visual experiences solely by adjusting the luminosity when creating a lighting system [
45].
Many studies have investigated the relationship between daylighting and the particular geometry of industrial buildings. Chena et al. [
46] showed that more than 33.3% of the factory area could meet the standard requirements for work spaces on the sunny day, as the heating energy consumption increased with the reduction of artificial lighting. Asdrubali [
47] examined the evaluation of the influence of the characteristics of 11 different sawtooth roofs. Bellia et al. [
48] investigated a lighting retrofit intervention for energy savings and comfort optimisation in an industrial building in Nola, Italy. Paule et al. [
49] examined a daylighting optimisation method in a new factory in Bordes, France. Wang et al. [
50] examined the energy consumption and overheating in a UK industrial building with rooflights. Stojkovic et al. [
51] investigated how the daylighting performance of an historic industrial building can be adapted into an office building. Katunsky et al. [
52] dealt with a daytime lighting assessment in Textile Factories. Acosta et al. [
53,
54,
55] dealt with the investigation of top lighting systems. The studies examined the daylighting design with light scoop skylights and presented the performance of lightwell skylights and monitor skylights.
The majority of the studies on industrial buildings concerning lighting is focused on to efficient artificial/daylight systems, rather than on the effect of the architectural structural shell to the lighting performance. The main scopes of this paper are: (a) The examination of how different roof openings affect the daylight performance of the building according to their type, shape, geometric orientation of the structure for a given geographical area during the design phase, and (b) how these factors can be optimised according to daylight. In more detail, this work identifies the effects of different roof types and opening geometries to the overall ingress indices of natural light and their effectiveness as complementary or exclusive light sources in an industrial environment in the Athens, Greece region (37°59′02.3″ N 23°43′40.1″ E). Three types of roof openings, which are quite common in Greece, the sawtooth roof, the skylight and the monitor, were tested, using a number of daylight metrics and LEED protocol. As already mentioned, an optimisation method was used in order to find the optimum distance between the openings, counterbalancing all of the factors involved. As the distance between the roof openings is increased, the construction cost is minimised while the lighting adequacy is deteriorated.
2. Materials and Methods
To apply the multiparametric approach three different roof opening types were used (i.e., saw tooth roof, skylight and monitor,
Figure 1) with various geometrical characteristics (width and height) and orientation, representing the most common construction types of industrial buildings in Greece.
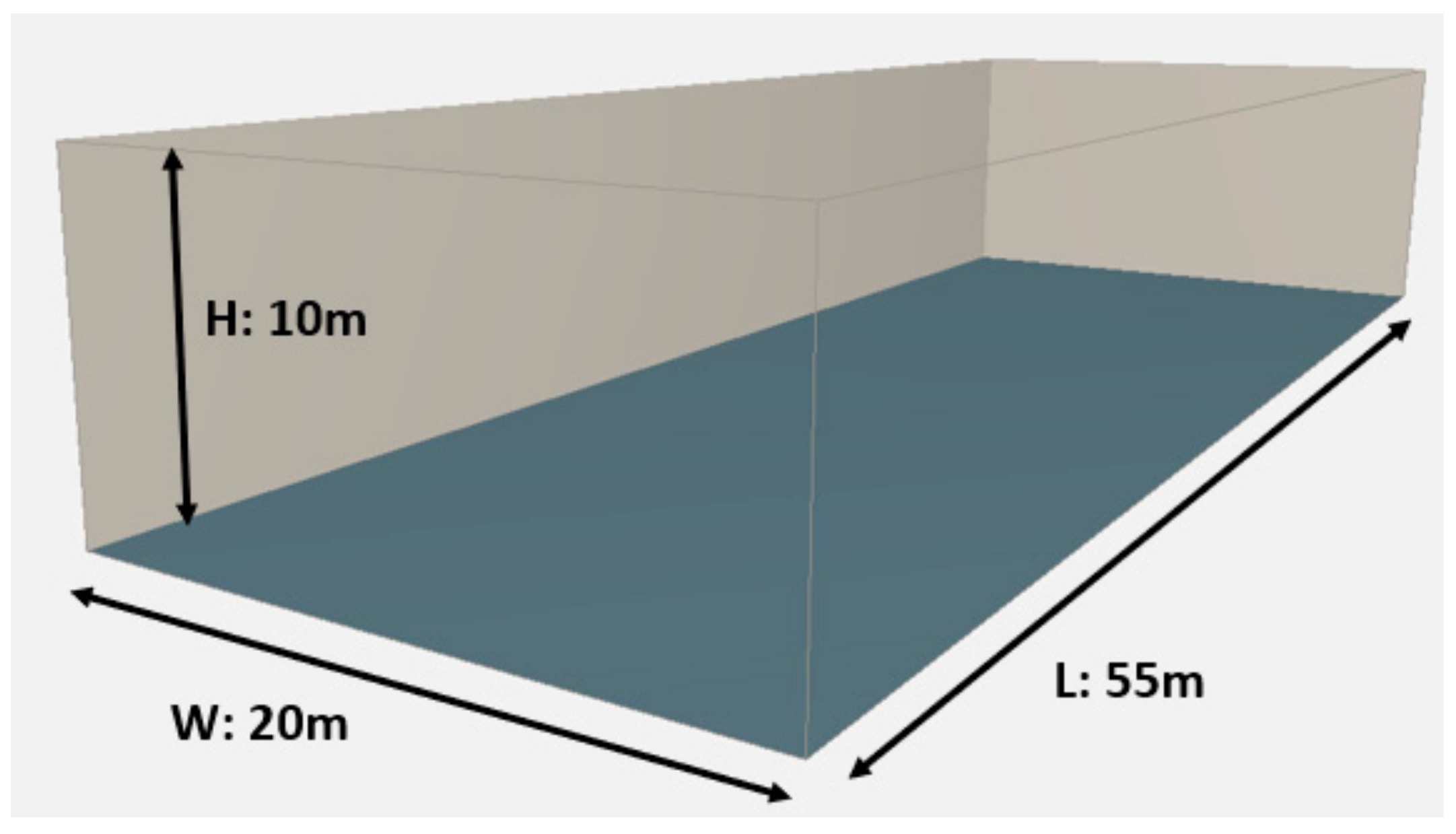
Using the aforementioned geometries, a series of simulations were performed. A number of different daylight indices have been calculated (i.e., Daylight Area 300 lx, Mean Daylight Factor, Daylight Factor >2%, Mean Daylight Autonomy, Mean Continuous Daylight Autonomy, Maximum Daylight Autonomy >5%, Uniform Daylight Index and Annual Sunlight Exposure). All indices were calculated using the Diva for Rhinoceros plugin. The typical industrial building (20 m × 55 m footprint, 10 m height) in Greece was selected for the case study (
Figure 2). The glazing height of each of the roof apertures was considered at 10 m above the reference plane (0 m).
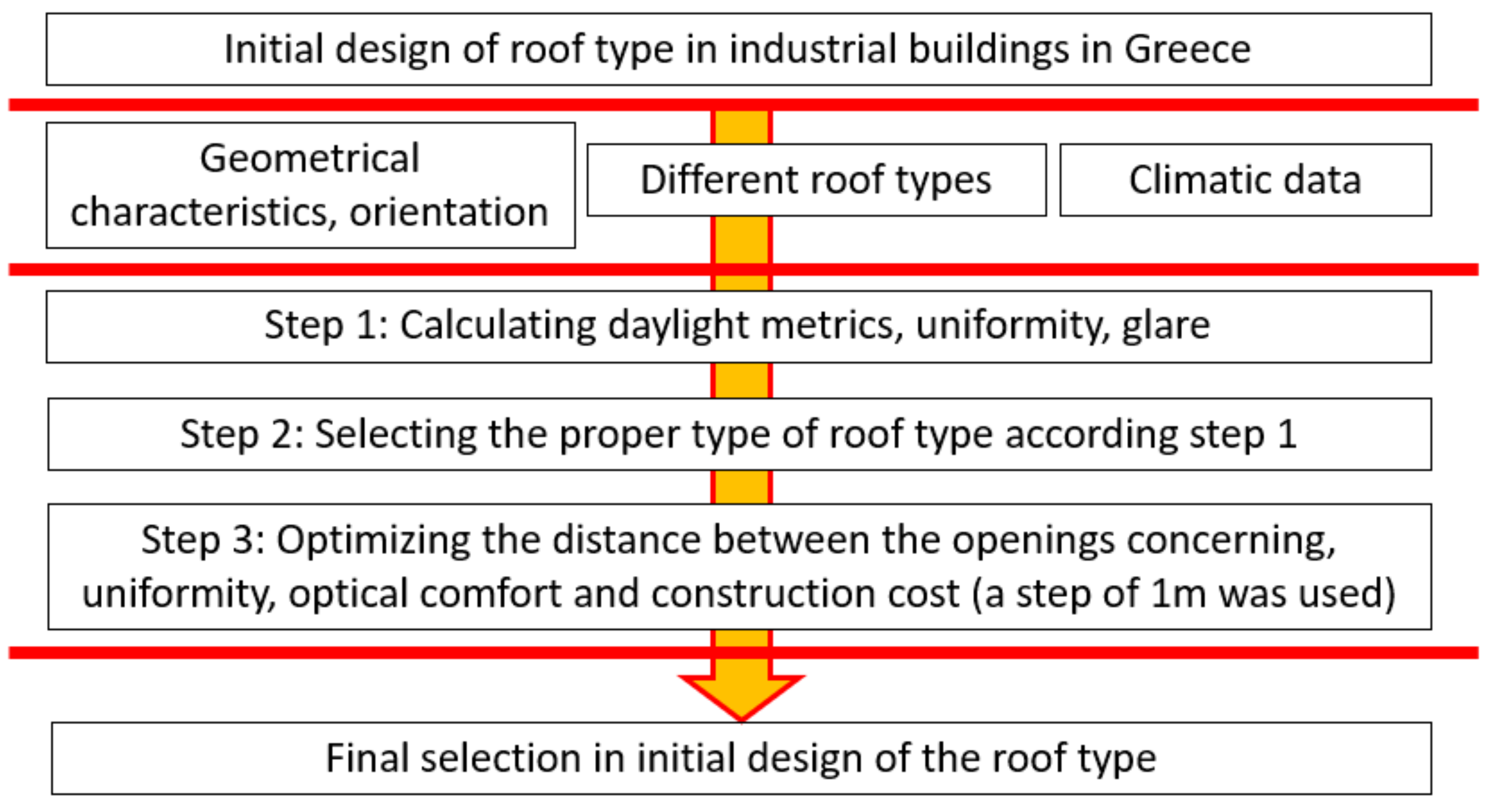
Figure 3 presents the overall steps used for the identification of the optimum design solution, balancing both structural characteristics and daylight metrics.
Three different models were used, carrying out the same building shell, but different geometrical characteristics of their roof apertures (
Figure 4,
Figure 5 and
Figure 6).
Table 1 provides the breakdown of the case studies selected, and presents the parameters examined, resulting in 72 scenarios.
Table 2 presents the construction properties of the model.
In each case, autonomy control of the daylight was performed for the monitor, skylight and sawtooth Roof ceiling aperture models, in order to extract the relevant daylight indicators. The percentage of the surface that receives sufficient illumination (>300 lx) for more than 50% of the hours under investigation was selected as the initial criterion of acceptability. The definitions of the rest of the factors used in the investigation are given in
Table 3.
2.1. Opening Types and Arrangements
All of the parameters examined are presented in the
Table 4.
2.2. Geometrical and Climatic Data Information
In the next step the latitude and surface materials of the industrial building were selected. The city of Athens (37.90 N/23.73 W), Greece, was used in order to obtain the corresponding climatic data [
56]. Due to the industrial use of the building, the basic working hours of industry in Greece were considered (07.00 LT–17.00 LT).
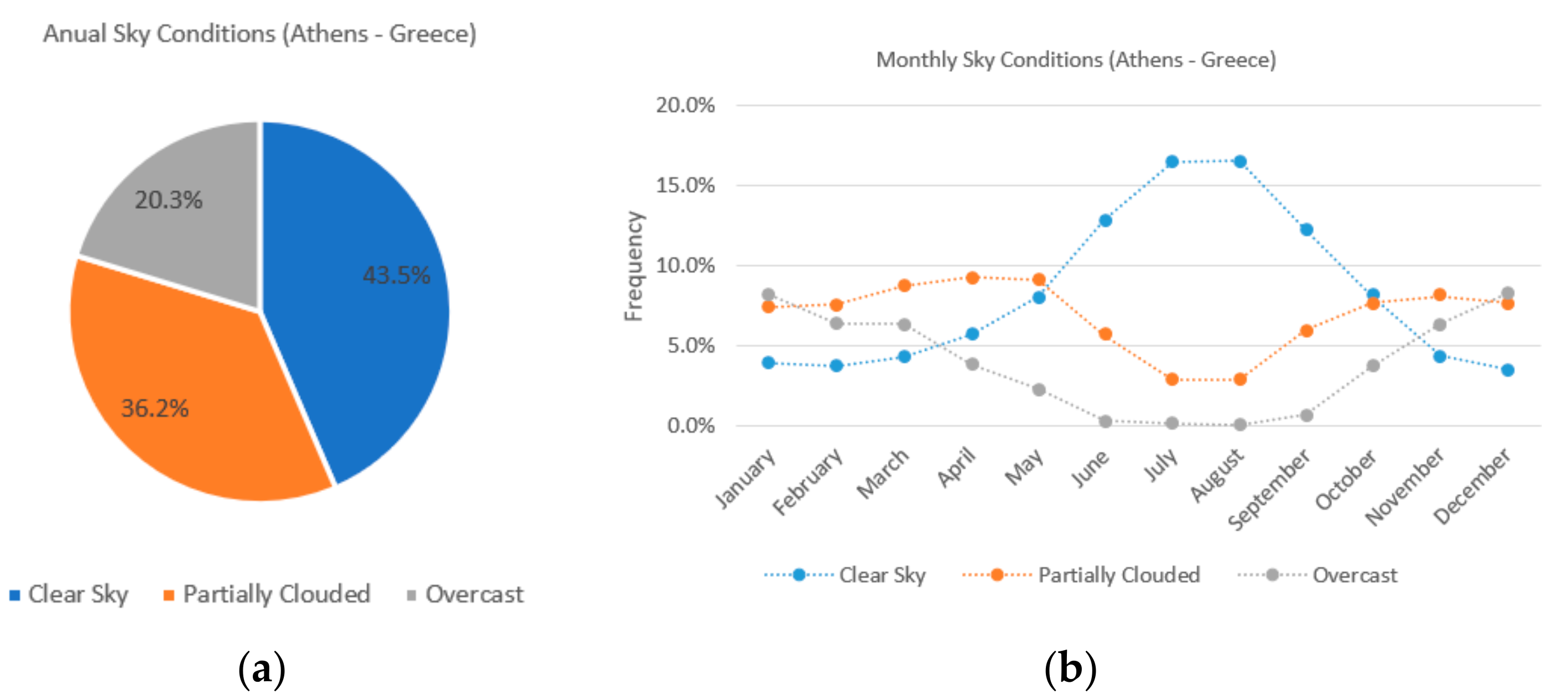
Athens presents climatic characteristics that are encountered in Mediterranean climates with relatively small rainfall and intense sunshine. The periods of sunshine, as well as the knowledge of weather data, were taken into account and were statistically processed (
www.meteoblue.com) in order to be used in the simulation procedure. Therefore, the selected dates (Summer Solstice, Winter Solstice and Spring Equinox) have been chosen as being the typical days covering the whole spectrum of expected sunshine duration over the year (
Figure 7).
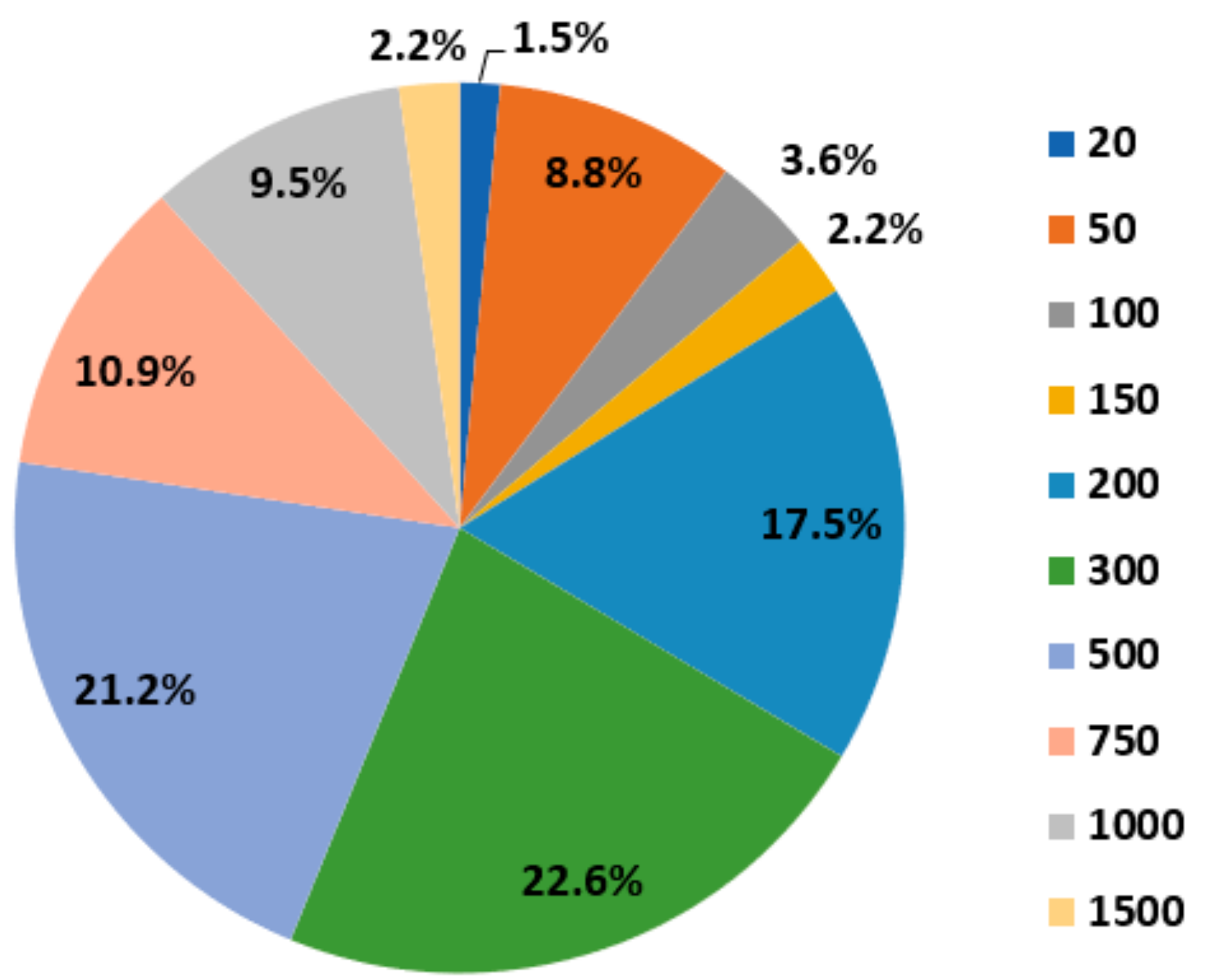
One of the key controls is the degree of daylight autonomy. The value of 300 lx was chosen as it was the most frequent target value in EN12464-1 [
57] for industrial buildings. Analysing these data, it was found that most of the working places in an industrial building require 300 lx. These operations represent more than 66% of industrial activities (EN 12464-1,
Figure 8).
3. Results
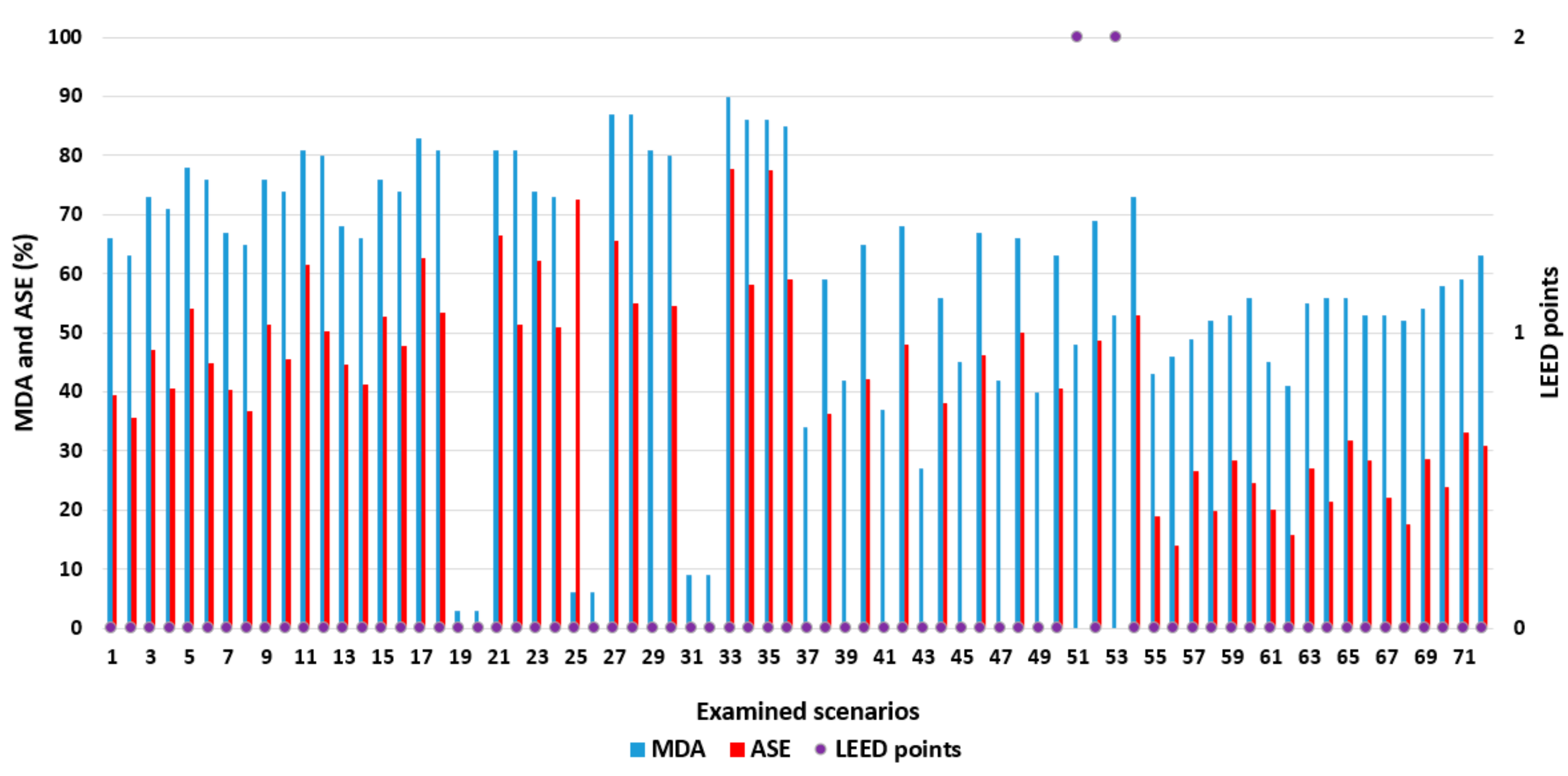
The metrics examined were DA, SDA, ASE and the LEEDv4 daylight requirement. The corresponding results are summarized in
Table 5,
Table 6 and
Table 7 for all of the 72 examined scenarios. The main goal of a successful design paradigm was to design and develop a best-case scenario that combines the appropriate daylight values (high values of DA and low ASE values) with the least amount of roof openings. Despite the lack of available LEED v4 values for industrial buildings, this research used the available LEED v4 criterion in order to assign the relevant points and identify its relevance with other parameters. A parametric analysis was performed based on and using the aforementioned factors, with
Table 5,
Table 6 and
Table 7 summarising thee results for each of the three different types of roof apertures.
Monitor roof openings have MeanDA values ranging from 82% to 93%, indicating the superiority of this case study against the others. In that regard, sawtooth roof openings provided lower values ranging from 56–74% for North (N) orientation openings, 73–85% for South (S) orientation openings and 65–79% for Eastern (E) and West (W) orientation. Finally, skylight roof openings exhibit the largest variation, which is strongly dependent upon the glass visible transmittance (Tvis). When glazing with Tvis 0.8 is used, MeanDA values are >91%. When the Tvis is reduced, MeanDA values are reduced as well. For example, when Tvis = 0.7, MeanDA varies between 87–93%, while when Tvis is 0.2, MeanDA < 30%. It is therefore evident that, according to the MeanDA metric, monitor roofs do present a consistently better performance, in terms of Daylight Autonomy behaviour, than the other types of openings.
Monitor roof openings have values ranging from 12–49%, while sawtooth roof openings have zero (0%) values for North Oriental (N) apertures, ~60% for South (S) orientation openings and 14–33% for Eastern (E) and West (W) orientation. Skylight roof openings exhibit the largest variations, which are also depended on the type of glazing visible transmittance, with a permeability of 0.8 and values >91%, with a permeability of 0.7 and 87–93%, and finally a low permeability 0.2 with values <30%, providing the highest values of all types.
In order to determine the degree of interdependence between the different results as presented in the above tables, the Kendal [
58] and Spearman [
59] correlation coefficients were calculated, both declaring the degree of hierarchical covariance between the two different parameters. It should be noted that the correlation coefficients with absolute values up to 0.5 indicate little interdependence between the tested variables, values ranging from 0.5 to 0.8 indicate moderate correlation, and those of 0.8 to 1.0 indicate strong interdependence of the size.
Table 8 and
Table 9 present the best correlating values (Mean DA and ASE) for both Kendal and Spearman correlation coefficients.
It is obvious that the correlation of the height of the opening with the target daylight illuminance was very small. Thus, there is no significant effect on the increase of this geometric feature, or a significant interrelationship between the width of the aperture and the daylight illuminance levels. It has therefore been decided to choose the Mean Daylight Autonomy (MDA), along with the Annual Solar Exposure (ASE), as the main variables for the comparison of daylight performance. The results show that the orientation affects the various scenarios as follows. For monitors, the variance of MeanDA values for the two available orientations (N-S, E-W) was small, and did not exceed 2–5%, while for our skylight, the variations were in the range of ±10%. Finally, in the case of the sawtooth roof, the differences were significantly greater, revealing the sensitivity to this parameter.
4. Optimisation and Discussion
As the overall performance of the saw-tooth type was better than the other types (
Figure 9), it was selected for the final step of the optimisation methodology. The proposed methodology involves the employment of a penalty function algorithm. For the equinoctial day in spring, a number of hourly simulations were performed. The hourly illuminance values and the corresponding uniformity values were calculated for a grid located between two consecutive openings. Nineteen grids were examined, with the distance varying from 5 m to 23 m (using a 1 m step between two consecutive openings). The examined counterbalancing parameters for the cross correlation of the optimisation methodology were: (a) The average illuminance (ranging from 300 lx, set as the target illuminance to 500 lx, which was set as a value for over illumination), (b) the uniformity defined as the ratio between minimum to average (up to 0.4) and (c) the number of openings in the examined space (the smaller the better, in an effort to reduce construction costs). As the number of openings is increased, the distance of the consecutive openings becomes smaller, while the illuminance and uniformity values are increased. On the other hand, as the number of the openings is reduced, the distance of the consecutively spaced openings is increased. Thus, the illuminance and uniformity values are decreasing considerably, resulting in daylight inadequacy, as the values are below the target values.
The results are presented in
Table 10. The values are highlighted according to whether they fully (Green) or partially (Orange) conform to the aforementioned target. In more detail, orange colour corresponds to a uniformity index (min/average) above 0.4, with average illuminance values above 300 lx.
Selection of Optimum Solution
A simple inverted penalty function algorithm has been proposed for the identification of the optimum distance value between two consecutively spaced openings. The form of a Boolean algebraic summation of the values was used, where the optimum case study was in conformance with the selected design criteria. Each solution has been valuated with 1 point for every fully fulfilled criterion (Green), 0.5 points for a partially fulfilled criterion (Orange) and 0 for failing to conform with all of the criteria.
Table 11 presents the final results, while a simple colouring scheme has been employed for quick visual inspection. As such, the top quartile solutions have been highlighted with Green, while all above average solutions have been highlighted Orange. The identification of the optimum solution in terms of distance values between two consecutive openings has led to the conclusion that the optimum distance should be in the range of 10 m to 13 m (
Table 11, top quartile values).
5. Conclusions
The results indicate the significant contribution of the roof opening type in the overall ability of daylight to act as a complementary or exclusive workbench light source in an industrial building. Moreover, the results showed the superiority of the north opening orientations combined with the partially indirect light ingress (i.e., sawtooth and monitor roof opening arrangements). In these case studies the high ASE values are avoided, while the daylight uniformity is high with reduced illuminance spikes. On the other hand, skylights have been deemed quite an inadequate arrangement, yielding highly concentrated illuminance levels. For monitor roofs a reduction of 55% (max) was observed between the E-W and N-S orientations; For sawtooth there was an increase of 22% (max) between N and S and 2% (max) between the E and W orientations; while skylights presented a rather erratic behaviour (ASE values ranged from 2% to more than 90%). Overall, it seems that a sawtooth roof represents the best choice for a source of daylight in industrial buildings at the examined geographic location. Despite the lack of available LEED v4 values for industrial building types, the examined case studies were investigated using LEED v4 as a criterion in order to assign the relevant points. Sawtooth was the only roof type with case studies resulting in 2 points. Both cases had ASE values equal to 0%. The selected one with the larger MDA value was chosen as the best performing one.
Above a certain threshold, daylight is no longer useful, as the space is “saturated” with light. The large number of openings can contribute to higher construction costs. Up to now, constructors in Greece use rules of a thumb for determining the type of the horizontal openings or the number of the openings at the initial design phase, except the minimum surface of the external opening. It is therefore expected that the designer will endeavour to make use of the minimum number of openings for a given solution that fulfils the daylight criteria. An optimisation tool was proposed in order to investigate the optimum distance between the openings. A penalty function algorithm was developed, taking into account the target illuminance values (from 300 lx to 500 lx), uniformity (>0.4 minimum to average illuminance) and the overall number of roof openings in a given space (the small number of roof openings reduces the construction costs). This resulted in an optimum range from 10 m and 13 m. With the addition of the constructability and maintenance, the optimum solution could be the one in which the distance between two consecutive openings can vary between 10 m and 11 m.