Abstract
The insurance market deliberately excludes the buildings’ envelope from their insurance policies, neglecting all the damage that can be caused by the degradation process or ageing of the materials. This stance is mainly due to the lack of knowledge in terms of risk and costs associated to the failure of these elements. Even though the building and its elements are the most valuable asset of any owner, most often homeowners do not adopt effective preventive measures to mitigate the deterioration and obsolescence of their assets. This study proposes an innovative methodology for the design of insurance policies for buildings’ envelopes, applied to natural stone facade claddings. The insurance product is defined based on deterministic and stochastic service life prediction models, established through the past degradation history of 142 natural stone claddings analyzed in service conditions in Portugal. Single-parameter (only analyzing the cladding’s age) and multiparameter (encompassing the relevant variables) models are applied in the calculation of the insurance premium. The expected claims are related with the performance of maintenance actions and established according to three degradation levels. The results obtained reveal that an increased knowledge about the insured cladding leads to a reduction of the risk margin and consequently, to a lower annual value of commercial premium paid by a household. This study proposes an innovative solution for tailoring the insurance products, in terms of the risk of failure of the buildings components, as well as the financial charges related with the maintenance of these elements, channeling the risks to the market.
1. Introduction
An insurance policy is a classical management tool to mitigate the risks of a given event, redistributing the costs of unexpected losses. Generally, by using the law of large numbers, the insurance policy reallocates the cost of losses from the few members experiencing them to all the insured members who paid the insurance premiums [1]. The theory reveals that, from the perspective of risk aversion, individuals are willing to buy an insurance product if the premium is actuarially reasonable, i.e., the insured is willing to spend a small amount in the present to be protected against the risk of a large monetary loss in the future [2,3].
In the housing sector, the insurance market presents different solutions and products to protect the client from unexpected losses in their dwellings. Most of the insurance market is focused on the construction stage and a posteriori periods of guarantee, given that this is the most challenging stage in terms of risk exposure. Concerning the use stage, the most common housing insurance policies are fire and multihazard, which intend to cover the damages for both interior/filling and property damage when subjected to accidents of various natures according to the insured’s concerns. These insurances are often mandatory in many countries, imposed by creditors under real estate mortgage.
In the case of failure of a building component, the first and most important question that arises is “who pays?”. Blong [4] states that the insured always intends to know whether building damage is covered under normal household insurance policies. According to this author, the answer would appear to be ‘yes, but not always’. A study performed by the Building Research Establishment (BRE) in England reveals that buildings’ owners are responsible for ensure the safety of buildings and their components, being also responsible for all the damages inflicted by any accident to third parties. The insurance companies are not legally responsible for the financial losses caused by the failure of the construction elements, when it is proved that the owners do not perform adequate maintenance actions [5].
Common housing insurance policies are based on past statistical standards and are usually too simplistic and generalist. Rarely in the past have actuarial data been collected regarding other crucial aspects concerning the specificity of the different building components, such as characteristics of the materials applied, design and execution processes, building’s environmental exposure, use and maintenance conditions, among other parameters. Although the existing actuarial models present an overall picture of losses, they are incapable of offering a view of the losses in terms of specific building components [6]. Therefore, the insurance sector is in transformation and is rapidly moving towards to a deeper segmentation and specification.
In this sense, new methodological approaches for the design of building components’ insurance products must be developed. Currently, the insurance market for losses regarding the natural degradation of buildings and components is practically nil. In fact, there are many imponderables involved in defining the vulnerability of the building component to the degradation agents and mechanisms. Moreover, the financial costs associated with the deterioration of the built park are difficult to measure. Nevertheless, building components, and in particular external claddings, can be seen as an insurable asset at risk of failure. For instance, internationally, there are some unfortunate news, with huge human losses, concerning the insurers facing increased risk of claims on covering high-rises with combustible cladding solutions (e.g., Grenfell Tower fire in London, UK).
Therefore, this study intends to propose an innovative approach for the design of an insurance policy model, applied to natural stone claddings. This study intends to identify the insurable risk of degradation of these claddings, examining how these risks are managed through the insurance method, thus analyzing different insurance premiums according to the expected claims and to the risk load. In the proposed model, the insurance premiums are established according to the knowledge concerning the loss of performance of natural stone claddings over time and according to their characteristics. For that purpose, deterministic and stochastic service life prediction models are used, which allow evaluating the likelihood of failure of the claddings. The service life prediction models used are defined through the knowledge of the degradation history of 142 natural stone claddings analyzed in service conditions, in Portugal.
The methodology proposed in this study allows establishing a system in which the insurance rates are scientifically and effectively determined, depending on more detailed risk categories, established based on technical knowledge related with the degradation of the building component under analysis. Moreover, it allows expanding and improving the scope of compensation of the insurance policies within the coverage of buildings’ claddings, adopting service life prediction methods to improve the risk assessment, thus reducing the risk of failure of the elements. This methodology, allied to the understanding of the decision processes of the property owner and insurer, allows providing some guidance for developing a set of strategies to reduce losses from future natural degradation of buildings’ facades.
The availability of realistic risk-based priced insurance policies can boost responsible behavior by owners, encouraging them to adopt cost-effective measures to reduce their potential losses from future degradation of buildings’ components. An insurance for the buildings’ facades can be an effective tool in assisting the restoration of damaged property and in the preservation of the built park, and can be seen as a means to fulfil governmental standards regarding the maintenance and conservation of buildings and components.
2. Background
The process of an insurance subscription encompasses five main stages [7]: (i) the first stage is the application, in which the customer contacts an insurance company to inquire about the types of coverage and related-costs; the customer fills out an application, which is sent to the insurance company underwriter; (ii) the second stage, when the insurance company performs a risk assessment, based on the amount of coverage requested, the policyholder’s insurance history, and other objective actuarial factors, and decides to accept or reject the application and the associated premium; (iii) in the third stage, the establishment of the policy contract, which includes a declaration page, an insurance agreement, modifications, and endorsements, is sent to the policyholder; (iv) the next stage corresponds to the claims; most policyholders do not suffer losses that lead them to submit claims (which does not occur in most cases) during the term of their insurance policy. In the event of a loss, the policyholder calls the company claims department to file a claim. The insurer investigates the loss, verifying the coverage for a particular risk, determining whether a policy is in force and, if so, estimates the related-costs; and (v) finally, the last stage is the renewal; most policies run for 12 months and are renewed at the end of that period. However, the policyholder can choose to cancel the policy during this period or move to another insurer at the end of the policy period.
Therefore, the definition of any insurance policy requires accurate knowledge regarding the: (i) insured, which is the party receiving a benefit on the occurrence of a specified event; (ii) the period of insurance, during which the policy covers a specific risk; and (iii) the indemnity, which is the total amount payable by the insurance company on each accepted claim.
A premium is the payment made by the policyholder for a partial or total coverage of a certain risk. In a simple actuarial perspective, the fair premium for a generic risk, for a specific insured, is estimated by the expected value of the claim (cost and probability of occurrence), when that risk occurs. However, in actuarial practice, a solidarity principle is usually applied, and the premium is estimated by evaluating the total damage of a specific risk in all the individuals belonging to the same risk class and equally dividing the costs among them [3].
There are no standardized principles or procedures to be used by insurers in the determination of insurance premiums, as this constitutes a typical managerial and commercial strategy of each insurance company. As mentioned by Ewald [8], insurance institutions are not repetitions of a single formula applied to different objects; instead, each insurance company presents different purposes, customers and legal basis. Since there is no legislation on the definition of premiums, each insurer is free to set its own prices in any of the insurance modalities according to its cost structure and the customer’s claims history.
The premium charged by the insurer is calculated based on the coverage, the exemption imposed, and other criteria considered as relevant for the insurer. In practice, insurers must account not only for the characteristics of the risks they have to insure, but also for other factors such as premiums charged by competing companies [9]. The premiums are estimated mainly based on the expected costs of claims and the legal and administrative costs [10]. Operating expenses, although variable across firms, are relatively predictable. Claim costs, on the other hand, are not.
3. Materials and Methods
Currently, insurers use the claims’ history data to develop an estimate of the amount of damages to be paid in the future. The accuracy of the estimations depends on the type of risk, the number and the characteristics of policyholders, as well as the number and value of accepted claims. The definition of the premium rate of a building is usually carried out by observing the risk inherent to its characteristics and based on an analysis of the historical data concerning the losses for similar types of buildings in the same risk situation. However, each building and component is a unique prototype subjected to unrepeatable conditions [5]. Therefore, the definition of insurance policies to cover the risk of failure of external claddings must consider the specificities of the insured object.
The methodology adopted in this study intends to define an expected rate of return for the investor, based on the age and estimated service life of the insured object, to determine the rates of degradation to be applied and to calculate the cost of the insurance policy, discounting the indemnity and adding the various administrative costs. In this study, the definition of an insurance premium for natural stone claddings encompasses three main steps:
- Risk assessment, in which service life prediction models are used to estimate the risk of failure of stone claddings over time and according to their characteristics. These models allow identifying the claddings’ expected condition in each instant, as well as the instant after which they present any given probability of reaching the end of their service life;
- The definition of the claims; in this case, the claims are related with the need of performing different maintenance actions according to the cladding’s degradation during the period of insurance;
- The estimation of the annual premium; the insurer reserves a monetary amount (provision) for the eventuality of the occurrence of the worst-case scenario to its customer portfolio and the respective indemnity payment. This amount depends on three factors: (a) number of subscribers; (b) cost of replacing the cladding (€/m2); (c) area of the facade in inadequate conditions (m2).
The insurer should validate the conditions of underwriting described by the policyholder, through an in situ inspection, carried out by an expert in this field. The inspection must be aided by an inspection and diagnostic data sheet, to systematize the data collected during the inspection. This file includes the characterization of the building and of the natural stone cladding, its maintenance history, and the surrounding environmental condition; moreover, the degradation condition of the cladding must be accurately described, through the identification of the anomalies observed, as well as their degradation level, the location of the anomalies in the stone plates, the determination of the probable causes, and the extent of the anomalies, as a percentage of cladding area. The information concerning the degradation condition of the cladding is essential to validate the insurance premium.
3.1. Proposal of Deterministic and Stochastic Actuarial Models
3.1.1. Overall Approach
One of the main challenges of actuarial science is to predict the costs of a future event (usually relying on past statistics) before the losses occur [1]. Inaccurate estimations could be dangerous, in two ways: if the insurance premium is underestimated, in the event of an accident, the losses may be too high to be borne by the insurer, but in the opposite sense, the lack of knowledge about the risk and costs of loss may lead to the premium being over evaluated, leading the potential consumers to choose another insurance company, or simply not subscribe at all.
In this sense, the service life prediction models applied in this study allow defining deterministic and stochastic actuarial models based on the analysis of the actual degradation condition of 142 stone claddings (located in Portugal) analyzed in situ and subjected to real exposure conditions and real degradation agents and mechanisms. The actuarial models proposed in this study adopt four different service life prediction models, of increasing complexity: (i) single-parameter deterministic model; (ii) multiparameter deterministic model; (iii) single-parameter stochastic model; and (iv) multiparameter stochastic model.
These models are based on the evaluation of the physical degradation condition of the stone claddings. For that purpose, a numerical index, called severity of degradation (Sw), is used [11], which evaluates the extent, condition, and cost of repair of the anomalies observed in a natural stone cladding (Equation (1)).
where Sw represents the severity of degradation of the building component, expressed as a percentage, kn is the multiplying factor of anomaly “n”, as a function of their degradation level, within the range K = {0, 1, 2, 3, 4} (Table 1), ka,n is the weighting factor corresponding to the relative weight of the anomaly detected (Table 2), An is the area of cladding affected by an anomaly “n”, in m2, A is the facade area, in m2, and k is the multiplying factor corresponding to the highest degradation level of a coating of area A.

Table 1.
Degradation levels for natural stone claddings (data sourced from Silva et al. [12]; Mousavi et al. [13]).

Table 2.
Weighting coefficients corresponding to the relative weight of the anomaly detected in natural stone claddings (data sourced from Silva et al. [12]).
In the single-parameter deterministic model, the evolution of the degradation condition of stone claddings over time (the only parameter analyzed) is defined based on the analysis of a degradation curve. Figure 1 shows an illustrative example of the degradation curve obtained for natural stone claddings, with three different Sw thresholds, in which a third-degree polynomial curve is adjusted to the scatter of points corresponding to the severity of degradation (obtained through a fieldwork survey) and the ages of a set of 142 case studies analyzed.
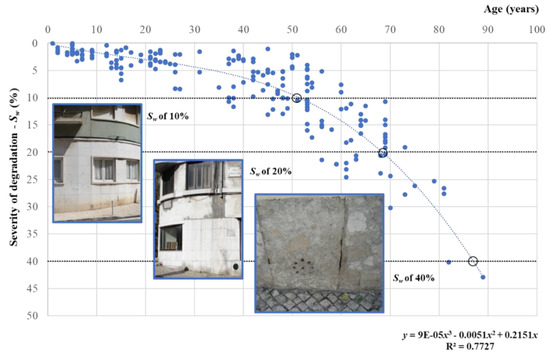
Figure 1.
Degradation’s evolution using the severity of degradation level for the 142 stone claddings inspected (data sourced from Silva et al. [12]).
The three Sw thresholds considered in this study correspond to different levels of claims for the insurance company. The first level, corresponding to a Sw of 10%, reveals a stone cladding with visual anomalies and slight cracking in the cladding, thus requiring a simple cleaning action. The second level, corresponding to a Sw of 20%, reveals a stone cladding with more serious defects, requiring a major intervention and partial replacement of the cladding. The third level, corresponding to a Sw of 40%, requires the replacement of the stone cladding.
According to the ISO 15686 [14], the service life of a building component can be defined as the period of time during which the element meets or exceeds the performance requirements. In this sense, the service life of a natural stone cladding can be predicted by determining the instant after which the cladding presents a degradation condition that it is no longer acceptable for the owners. The limit that establishes the end of service life (or the maximum acceptable degradation level) is not easy to define, and depends on the building context, social and legal requirements, as well as the funds available for maintenance actions [5]. Using the degradation curve, it is possible to obtain the estimated age of the natural stone claddings through the intersection of the degradation curve with a given degradation level. Table 3 shows the estimated age of the claddings obtained with the first model for three different Sw values. In this model, the of estimated values are independent of the cladding’s characteristics, since the model only encompasses the age of the building as explanatory variable of the stone claddings’ degradation phenomenon.

Table 3.
Estimated age of natural stone claddings for three different Sw values (single-parameter deterministic model).
This model presents accurate results but could be too simplistic to portray a complex phenomenon such as the degradation of natural stone claddings. In fact, the degradation of these claddings occurs due to a synergetic and simultaneous action of degradation agents and mechanisms, and the specific characteristics of the claddings must be considered, to obtain more reliable information. Therefore, this methodology can be used to disaggregate a generic vulnerability curve into several curves representing the vulnerability of specific building classes.
In this sense, a multiparameter deterministic model is also proposed, which allows encompassing different factors (e.g., environmental, design and type of materials, among others) in the determination of the estimated service life of stone claddings. Silva et al. [5,15] proposed different linear and nonlinear multiple regression models to estimate the severity of degradation of stone claddings. Among these, the generic exponential model, as shown in Equation (2), is the one with the best overall performance to describe the degradation of stone claddings; therefore, it is applied in this study.
where Sw represents the claddings’ severity of degradation, I their age, M distance from the sea, A area of the cladding, H exposure to damp, and TP type of stone. To apply the model shown in Equation (2), the variables M, A, H, and TP should be replaced by their numerical quantification, presented in Table 4 [15].

Table 4.
Numerical quantification of the variables of the multiparameter deterministic model.
The deterministic models provide accurate results and allow obtaining an average value of the instant after which it is necessary to intervene (the instant in which the insured makes the claim). However, more than an average estimated service life, the insurance company should know the probability of a stone cladding reaching the end of its service life, i.e., the probability of failure of the cladding over time and according to its characteristics. This information is crucial to convert those probabilities into costs, to predict unexpected situations during the claddings’ service life, whatever the origin of the unforeseen events [16].
In this sense, two stochastic models are proposed, both based on a logistic regression analysis. In the first model, a single-parameter stochastic model, it is possible to estimate the probability of the stone claddings reaching the end of their service life over time. Figure 2 shows the cumulative distribution functions concerning the probability of 142 stone claddings reaching the end of their service life, considering three Sw levels. For a Sw of 40%, a discrete cumulative distribution function is obtained, due to the small number of case studies with this degradation level. With this information, it is possible to define, for different risk thresholds, the probability of a given cladding reaching the specific degradation values (Table 5).
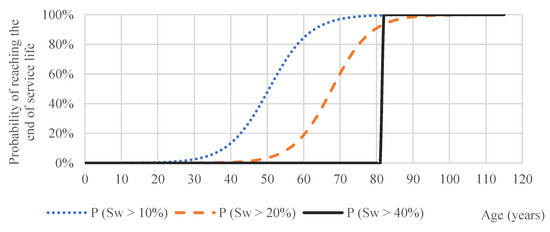
Figure 2.
Cumulative distribution functions concerning the probability of 142 stone claddings reaching the end of their service life, considering three risk thresholds.

Table 5.
Estimated claddings age obtained by the single-parameter stochastic model for different Sw values and risk margins.
In the multiparameter stochastic model, it is possible to include all the relevant variables to the explanation of the severity of degradation of stone claddings, allowing estimating the probability of the cladding reaching the end of its service life according to its characteristics. In the case of natural stone claddings, the variables considered as statistically relevant are the distance from the sea, size of the stone plates, exposure to damp and type of stone. The multiparameter stochastic model adopts a similar approach of the single-parameter model, but the determination of the estimated service life requires the application to a specific case study, since it requires the quantification of the explanatory variables included in the model.
3.1.2. Models’ Assumptions Concerning the Coverage of the Insurance Policy
The main coverage of the proposed insurance policy is related with the performance of three maintenance actions, when a specific degradation level is reached. The degradation levels that imply the performance of a specific action are intrinsically related with the owners’ levels of demand, and the cost that the owners are willing to pay to reduce the likelihood or magnitude of failure of the claddings [17]. In this study, the claims occur for three different Sw thresholds, including the following maintenance actions: (i) for Sw of 10% (slight degradation), a cleaning action is performed; (ii) for Sw of 20% (moderate degradation), a major intervention is performed; and iii) for Sw of 40% (generalised degradation), a replacement of the cladding is required.
The insurance company must perform periodic inspections, to estimate the Sw value. Based on the results obtained, the insurer decides to claim maintenance actions and the related budget, or not. The different levels of maintenance include the following actions:
- Cleaning: includes scaffolding installation, cleaning with water jet and brushing [18], repair of cracking with a width ≤ 1 mm and replacement of 20% of joints;
- Major intervention: includes all the previous actions but with the replacement of 30% of joints. Additionally, it includes the cleaning of the remainder 70% joints and the replacement of 20% of the stone plates;
- Replacement: includes scaffolding installation and the complete replacement of the cladding, with the application of the new cladding and the transportation to a landfill of the old cladding.
The costs of these actions are presented in Table 6 and are based on the most recent values of each operation found in the literature and from specialized companies.

Table 6.
Fixed costs of the maintenance actions (data sourced from CYPE [19] and Mousavi et al. [13]).
The insurance policy proposed presents some limitations regarding the claims:
- During the duration of the policy, the claim of each maintenance action occurs only once, i.e., after a cleaning action, the insurer will only intervene when the next degradation level is reached, thus performing a major intervention;
- It is considered, as a simplification, that the maintenance actions have no effect on the cladding’s degradation condition (in terms of the Sw value), i.e., the age in which the next maintenance action occurs is the same before and after the maintenance action;
- It is assumed there are no periodic maintenance actions by the insured;
- In the case of a condominium, the insurance is equally shared by the individual unit owners that pay the same premium;
- An annual policy with renewal option is adopted. The premium is fixed during the period of subscription, independently of the rate’s volatility, which is beneficial for the insured, since he/she knows the total cost of the insurance policy, without surprises, hassles, or extra calculations.
3.1.3. Determination of the Annual Premium for the Insurance Policy
This study establishes a calculation method for an insurance policy to cover the natural degradation of buildings’ components. According to the methodology proposed, the total present value of the insurance policy is given by Equation (3).
Ct, nom(C), Ct, nom(MI), and Ct,nom(R) correspond to the nominal costs of the maintenance actions of the different degradation thresholds, tC, tMI, and tR, indicating the year in which those costs occur and rnom represents the nominal discount rate, which includes the global inflation risk, opportunity costs, and other costs. The Ct,nom terms include the effect of inflation, which affects the nominal discount rate, as explained by Fisher’s theory [20], as shown in Equation (4).
The use of nominal or real values must be consistent, when the calculations are made with cash flows and discount rates. To work in nominal terms, the trends in equipment, labor, and material costs must be contemplated. In this study, an inflation rate (is) of 3% and a global inflation rate (ig) of 2% are adopted, in accordance with the Portuguese context. To simplify the presentation of this study results, real values are used. Equation (3) can be used to determine the expected costs and premiums, as shown in Equations (5) and (7), respectively.
Ct,real(10), Ct,real(20), and Ct,real(40) are the real costs of the maintenance actions of the different degradation thresholds, which are the same for all the proposed models; t10, t20 and t40 are the years in which those costs occur; rreal,cost is the real discount rate, equal for all the models and obtained through Equation (4). Equation (6) presents the discount rate applied to the cost, only considering rate is.
Equation (7) presents the present value of the premium, in which Ct,premium is the annual premium in €/m2, whose definition is the main objective of applying the proposed models.
The rreal,premium is the real discount rate, equal for all the models, considering not only rate is but also rate ig, as shown in Equation (8).
The premium value (Ct,prémio) is obtained by equalling Equations (5) and (7). The value obtained is converted to Euros paid per household by multiplying the premium by the cladding’s area and then dividing by the number of individual apartments. The final definition of the premium value should also consider the insurance company’s profit margin. The different models proposed allow transforming the probability of the claddings reaching the end of their service life into profit margins.
4. Application of the Methodology to a Real Case Study
One of the most important aspects in the insurance premium calculation is price discrimination. A bonus-malus premium calculation principle must be used, ensuring that not all the individual policies in the portfolio present the same premium, because the level of risk is distinct [21,22]. This concept is widely adopted in car insurance, in which a series of variables affecting the risk level are analyzed to establish the premium, e.g., the age and the gender of the driver, his/her living address, time since the driving licence was issued, among others. A similar principle should apply to insurance policies for claddings, in which the characteristics of these elements should be contemplated when the premium is determined.
For that purpose, the proposed models are analyzed using a real building as a case study. The first step was the visual inspection of the cladding in situ, collecting the relevant information to apply the service life prediction models. This inspection was complemented by an interview with the building’s architect. This case study is in Lisbon, Portugal, and has 15 apartments and 606 square meters of stone cladding. The cladding is 14 years old, presents medium-sized limestone plates (0.24 m2), is located less than 5 km from the sea, and has a high exposure to damp.
With the building’s characteristics, the application of the multiparameter models for the case study is feasible and the comparison between the resulting cladding age values and the ones obtained through the single-parameter models. That knowledge, paired with the costs previously presented, allows calculating the risk premium for each model.
Table 7 presents the case study’s remaining years until the proposed maintenance actions, for each model, and considering four insurance risks for which different premiums must be designed.

Table 7.
Case study’s remaining time (in years) before action for the defined degradation levels, by model.
The values were obtained by subtracting from the different estimated cladding age values the present age of the cladding (14 years). Table 6 typifies some aspects deemed important:
- The cladding’s characteristics do not produce significant deviations between the remaining time before action obtained by the deterministic models. The comparison between the remaining time before action obtained by the single-parameter stochastic model and multiparameter stochastic model, for the threshold Sw = 10%, for any risk margin is also inconclusive;
- In the multiparameter stochastic model, the risk’s reduction is equivalent to an anticipation of the maintenance action’s schedule. This effect is less noticeable in the second and third degradation levels;
- For the thresholds Sw = 20% and Sw = 40%, in both stochastic models, when a lower level of risk is assumed, naturally a lower remaining time before action is obtained. This conclusion is more evident for the single-parameter stochastic model, for replacement actions (Sw = 40%);
- For a fixed risk margin, in both the second and third degradation thresholds, the expected remaining time before action is higher in the multiparameter stochastic model than in the single-parameter one. The difference is substantial for lower risk margins (5%) and for more profound maintenance actions, such as the replacement.
Based on these values, the premium for each model is determined. The method is the same for every model, only changing the years in which the maintenance actions occur and the maximum duration of the policy until renewal. This duration corresponds to the period until the materialization of the last maintenance action associated with a Sw = 40%. The procedure will be exemplified with the single-parameter deterministic model, as shown in Equation (9).
Equation (10) presents the present value of the future payment.
Finally, it is possible to obtain the annual premium in €/m2, as shown in Equation (11).
This result is the risk premium rate for this case study, when the insurance is subscribed in 2017 based on this model. The risk premium by household is obtained through Equation (12).
The commercial premium is obtained by multiplying the result of Equation (10) by some coefficients that represent the margins for administrative expenses and expected profit. In this methodology, a fixed coefficient of 1.3 universal to all models is considered first, intending to cover the fixed costs present in any financial institution. A safety margin of 1.2 for the single-parameter and 1.1 for the multiparameter models is also applied, accounting for the estimation errors of the models. The commercial premium by household of the case study analyzed, for the single-parameter deterministic model, is 33.47€. Table 8 summarizes the same calculations for the remaining models.

Table 8.
Summary table with estimated times before action, costs, risk premium rates, risk premiums, risk coefficients, and commercial premiums per household for the different models.
Table 8 shows the relation between the estimated service lives related with each maintenance action and the resulting insurance’s premium. The deterministic model, although simpler, has the same probability of not estimating correctly the service life as the stochastic model for a risk margin of 50%. The simplification of using the average values leads to a slightly higher risk premium.
5. Results
In this study, the knowledge of the loss of performance of stone claddings, based on the evolution of degradation of these elements in real exposure conditions, is used to develop an insurance product. According to the results obtained, the following main conclusions can be drawn:
- An insurance product based on a deterministic model will not be able to compete against an insurance based on a stochastic model with a 50% risk margin, because it provides the same coverage and risk charging, with a higher premium;
- In the deterministic approach, the commercial premium’s difference between single-parameter and multiparameter is below 2€, which reveals the lack of preponderance of the discrimination of the cladding’s characteristics in these models;
- In the stochastic models, the lesser the assumed risk margin, the greater the premium. This aspect is more evident in the single-parameter model;
- For a fixed risk margin, the premium is lower in the multiparameter stochastic model than in the single-parameter one. The difference is more expressive for smaller risk margins (5%);
- These results reveal that the design of an insurance product knowing the characteristics of the insured object allows reducing the costs for the policyholder, which also increases the possibility of acquiring this insurance policy.
The risk premium is higher for an insurance product that predicts with greater prudence the expected intervention periods because the cost’s increase is passed on to the client. During the subscription to the product “multiparameter stochastic 5%”, the insurance company considers that the client belongs to the 5% whose cladding will need a cleaning at year 19, a major intervention at year 50 and a total replacement at year 70. In reality, 95% of the clients will have those maintenance needs at a later stage of the cladding’s life, which results in lower costs for the insurer.
In the real world, it is well-known that the prices reflect elasticities of demand just as much as costs [23]. If the premium prices are not well-adjusted to the market and to the insured object, customers will naturally choose competing companies with a better, risk adjusted pricing system [24]. Therefore, in this study, in order to provide a greater equilibrium to the commercial premiums, increasing their competitiveness and motivating a risk reduction, the final premium is adjusted. The insurer obtains some advantages through the application of the service life prediction models, i.e., knows, for a given cladding, the risk of failure with a known margin of risk. This knowledge must beneficiate not only the insurer, but also the policyholder. For that, the premium calculations must be made with the stochastic model’s results, and for models with risk margins lower than 50%, the insurance company can decrease up to 90% of the difference between the premium of the considered model and the premium of the 50% risk margin model, in order to make the product more competitive. Equation (13) presents an example of the determination of the final premium, adopting the multiparameter stochastic model with 5% risk margin.
The commercial premium for the policyholders of the case study varies between 25€ and 35€ per year. Considering the average apartment’s real estate value, the yearly premium corresponds to less than 0.1% of the cost of an apartment. The same cannot be said about vehicle insurance, the most popular nonlife insurance branch, where it is unexpected that the premium equals 0.1% the value of the vehicle. This difference shows the asymmetry in the way society values the building stock compared to other tangible assets.
6. Discussion
As mentioned by Kunreuther et al. [25], consumers and landlords usually misperceive the insurance products, mainly because of their feelings about losses they may or may not experience. The consumers usually want to pay low premiums, which do not cover all the possible losses, and feel disappointed when they suffer a loss; on the other hand, consumers see the insurance product as an unwise investment when they pay an insurance premium for several years and the loss does not occur. The authors [25] refer that when purchasing an insurance product, a costumer’s mantra should be the best return is no return at all, i.e., the insurance product should protect the costumer from potential losses, at an acceptable premium, while it is expected that the loss or an extreme event would never occur.
The potential losses due to the future degradation of buildings’ components are usually neglected by insurance companies, and most homeowners do not voluntarily adopt cost-effective measures to reduce the impact and costs of those losses [26]. These attitudes led to a built park with clear signs of degradation and a high economic burden associated with their maintenance and repair. In this sense, the role of the insurance companies is extremely important, since the policyholders can transfer the risk of degradation of the construction elements to insurance companies, which will defray the cost of maintenance and replacement of the buildings’ components in case of failure [27].
Currently, insurers do not have enough information to propose realistic risk-based pricing, incorporating mitigation activities [28,29]. The insurance business is highly dynamic and competitive and the clients’ majority is driven by basic insurance products with the lowest premium possible. However, the insurer must ensure the definition of well-designed insurance products, even if it costs more. In this sense, it is extremely important to have accurate knowledge regarding the object insured and the risk and cost of losses if a given event occurs.
Past studies [27,30] have discussed the benefits of using insurance as a mechanism for risk mitigation. In fact, several studies [31,32,33,34] discuss how insurance can be efficiently used to decrease litigation for defective construction. Moreover, some studies [35] also analyze the risks associated with the serviceability of the building and its components. However, the literature does not provide much evidence or insights on the particular design of such insurance policies for a specific maintenance/performance risk. This study has an innovative character, providing the methodological basis for the design of such insurance policies. It follows the standard approach for designing insurance (probability analysis, incident cost, and risk premium calculation), but specifically adapted to natural stone facade claddings.
More studies are needed in order to properly evaluate the aging and deterioration, and the consequent probability of failure of the facade elements. Some standard methods can be found in the literature, addressing the analysis of accelerated climate aging of building materials under different laboratory conditions [36,37]. These methods are extremely relevant for a deeper knowledge of the materials characteristics and their behaviour under different exposure conditions, allowing predicting an expected lifetime for a specific building material under a specific set of conditions. Accelerated artificial aging exposure experiments, such as the methods proposed by [36,37], save both time and cost; nevertheless, the extrapolation of these analyses to the real degradation processes can be a challenging task since the deterioration process in-service conditions is ruled by the simultaneous and synergic occurrence of several degradation factors. As mentioned by Silva et al. [15], each facade is a unique prototype subjected to unrepeatable conditions. In this sense, this study suggests the adoption of the analysis of real case studies, under natural exposure conditions, to evaluate the future trend of degradation of stone claddings.
Currently, there is an urgent demand for methodologies to evaluate the probability of failure of buildings and their components. Some probabilistic-based methodologies have been proposed for the evaluation of the degradation of building materials [38]. Structural approaches to evaluate the risk of failure can also be applied for modelling the deterioration of facade claddings. For example, Silva et al. [15] proposed the adoption of artificial neural networks, fuzzy systems, and Markov chains to model the deterioration and service life of external claddings. Markov chains are usually adopted for the stochastic analysis of the performance prediction, service life, and maintenance management of bridges. This model was successfully adopted for modelling the transition between degradation condition of facades’ claddings, and as well, other similar structural approaches can be used to model the service life prediction of facades’ claddings, thus providing extremely useful information related with the risk of failure of a given cladding, according to its age and specific conditions of exposure and use. In this study, a probabilistic approach is also proposed for the definition of the insurance policy, revealing that a better knowledge of the risk of failure of the cladding benefits not only the insurer, but also the policyholder.
The methodology for the premium’s valuation presented in this study needs to be adjusted based on the insurer’s portfolio and on the market conditions. In this study, a proposal that fits the observed context was presented, although it needs to be readjusted over time.
In future research, it would be relevant to evaluate similar insurance products covering different facade materials, such as ceramic cladding or renderings, and other coverings of building components, such as roofs and structure. Other aspects should also be analyzed in the future and adapted to each specific context, such as variation in the type, periodicity and effects of the maintenance actions, flexible scheduling of the maintenance actions in accordance with the owners’ needs and expectations, and the measurement of the severity of degradation of the cladding before defining the insurance policy and estimating the premium cost. Finally, future research should also include an analysis of the transaction and administrative costs associated with this methodology, considering that they will be higher for insurers when compared with the “business as usual” approach.
7. Conclusions
In this study, an innovative approach for the design of an insurance policy model, applied to natural stone facade claddings, is proposed. In this model, the insurance rates are scientifically and effectively determined, based on technical knowledge related with the real loss of performance of the stone claddings over time and according to their characteristics (collected through an extensive fieldwork). The insurance premiums are thus designed based on the information obtained by deterministic and stochastic service life prediction models. The service life prediction models allow estimating, in a more precise and scientific manner, the expected claims and the related risk load.
The results obtained reveal that stochastic models produce more relevant information for the definition of the insurance policies. The knowledge of the probability of failure of the building’s components over time and according to their characteristics is a very useful information to calculate the fair price of an insurance contract. Therefore, the stochastic models allow reducing the risk assumed by the insurance company by evaluating whether the planned maintenance activities must be anticipated or delayed, according to the corresponding degradation thresholds and the risk of the cladding reaching those thresholds.
The segmentation of the claddings’ characteristics allows discriminating the price of the insurance policy for different policyholders. In this sense, multiparameter models are more precise and useful. For an equal risk margin, and for more intrusive maintenance actions (also more expensive), such as the cladding’s replacement, a more accurate knowledge regarding the cladding’s characteristics leads to a postponement of the claims (i.e., the execution of the maintenance actions). An increased knowledge of the insured object allows decreasing the insurance premiums paid by the policyholders, as well as increasing the insurer’s safety margins.
Therefore, the use of multiparameter stochastic models in the design of the insurance premium is beneficial for both parties. The application of the insurance policy proposed in this study presents several advantages. For the policyholder, it allows altering the nature of the risk and its allocation, shifting increased risks to the insurance company. Moreover, this insurance product promotes the conservation of the built heritage, increasing the patrimonial value of the asset (which is beneficial for the image of the cities), reducing the risk of failure and the uncertainty of the cost of maintenance over time. For residential condominiums, this type of insurance can be very profitable, since the risks are shared by the households, resulting in a lower price for the insurance premium. For the insurance company, the adoption of accurate information regarding the probability of the claims and the related risks allows reducing the premium. On one hand, in the long-term, a lower insurance premium can affect the profits per insured. However, lower premium prices, once well-adjusted as described in this study, with safe and well-known risk margins, will expectedly lead to a greater number of clients in the portfolio, thus leading to a global reduction of the risks assumed by the insurance company.
Author Contributions
Data curation, A.S.; Formal analysis, C.O.C.; Investigation, M.M.; Methodology, J.d.B.; Writing—original draft, M.M.; Writing—review & editing, J.d.B., A.S. and C.O.C.
Funding
This research was funded by the FCT (Foundation for Science and Technology) through the projects SLPforBMS (PTDC/ECM-COM/5772/2014) and BestMaintenance-LowerRisks (PTDC/ECI-CON/29286/2017).
Acknowledgments
The authors gratefully acknowledge the support of the CERIS Research Institute, Instituto Superior Técnico (IST), University of Lisbon.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dorfman, M.S. Introduction to risk management and insurance, 6th ed.; Prentice Hall International, Inc.: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Mossin, J. Aspects of rational insurance purchasing. J. Political Economy 1968, 76, 553–569. [Google Scholar] [CrossRef]
- Bruno, M.G.; Grande, A.; Oliva, C.F. Anomalous demand and supply in cat risks insurance market. Annali del dipartimento di metodi e modelli per l’economia il territorio e la finanza 2015, 1, 51–62. [Google Scholar]
- Blong, R. Residential building damage and natural perils: Australian examples and issues. Build. Res. Inf. 2004, 32, 379–390. [Google Scholar] [CrossRef]
- Silva, A.; de Brito, J.; Gaspar, P. Methodologies for service life prediction of buildings: With a focus on facade claddings; Springer International Publishing: Zurich, Switzerland, 2016. [Google Scholar]
- Khanduri, A.C.; Morrow, G.C. Vulnerability of buildings to windstorms and insurance loss estimation. J. Wind Eng. Ind. Aerodyn. 2003, 91, 455–467. [Google Scholar] [CrossRef]
- American Insurance Association—Property-Casualty Insurance Basics: A Look inside the Fundamentals and Finance of Property & Casualty Insurance. Available online: http://www.aiadc.org/File%20Library/Resources/Industry%20Resources/Insurance%20101/Ins_101.pdf (accessed on 2 May 2017).
- Ewald, F. Insurance and risk. In The Foucault Effect: Studies in Governmentality; Burchell, G., Gordon, C., Miller, P., Eds.; University of Chicago Press: Chicago, IL, USA, 1991; Chapter 10; pp. 197–210. [Google Scholar]
- Dickson, D. Insurance risk and ruin; International Series on Actuarial Science, Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Pollner, J.D. Managing catastrophic Disaster Risks Using Alternative Risk Financing and Pooled Insurance Structures; Volumes 23-495, World Bank Technical Paper no. 495; The International Bank for Reconstruction and Development, The World Bank: Washington, DC, USA, 2001. [Google Scholar]
- Gaspar, P.; de Brito, J. Limit states and service life of cement renders on facades. J. Mater. Civ. Eng. 2011, 23, 1396–1404. [Google Scholar] [CrossRef]
- Silva, A.; de Brito, J.; Gaspar, P. Service life prediction model applied to natural stone wall claddings (directly adhered to the substrate). Constr. Build. Mater. 2011, 25, 3674–3684. [Google Scholar] [CrossRef]
- Mousavi, S.H.; Silva, A.; Brito, J.; Ekhlassi, A. Service life prediction of natural stone claddings with an indirect fastening system. J. Perform. Constr. Facil 2017, 31, 04017014. [Google Scholar] [CrossRef]
- ISO 15686-1. Building and constructed assets: Service life planning—Part 1: General principles; International Standard Organization: Geneva, Switzerland, 2011. [Google Scholar]
- Silva, A.; Gaspar, P.L.; de Brito, J. Comparative analysis of service life prediction methods applied to rendered facades. Mater. Struct. 2016, 49, 4893–4910. [Google Scholar] [CrossRef]
- Macedo, M.; de Brito, J.; Cruz, C.; Silva, A. Methodological proposal for the development of insurance policies for building components. J. Build. Eng. 2018. under review. [Google Scholar]
- MacDonald, D.N.; Murdoch, J.C.; White, H.L. Uncertain hazards, insurance, and consumer choice: Evidence from housing markets. Land Econ. 1987, 63, 361–371. [Google Scholar] [CrossRef]
- Madureira, S.; Flores-Colen, I.; de Brito, J.; Pereira, C. Maintenance planning of facades in current buildings. Constr. Build. Mater. 2017, 147, 790–802. [Google Scholar] [CrossRef]
- CYPE® Price Generator. Available online: http://www.geradordeprecos.info/ (accessed on 9 November 2016).
- Brealey, R.A.; Myers, S.C.; Allen, F. Principles of corporate finances; McGraw-Hill Publishers: New York, NY, USA, 2011; ISBN 9788580552386. [Google Scholar]
- Rolski, T.; Schmidli, H.; Schmidt, V.; Teugels, J.L. Stochastic processes for insurance and finance. In Wiley Series in Probability and Statistics; John Wiley & Sons Ltd.: Chichester, UK, 1999. [Google Scholar]
- Denuit, M.; Marechal, X.; Pitrebois, S.; Walhin, J.F. Actuarial Modelling of Claim Counts: Risk Classification, Credibility and Bonus-Malus Systems; John Wiley & Sons, Ltd.: Chichester, UK, 2007. [Google Scholar]
- Ungern-Sternberg, T. The limits of competition: Housing insurance in Switzerland. Eur. Econ. Rev. 1996, 40, 1111–1121. [Google Scholar] [CrossRef]
- Mahmoudvand, R.; Aziznasiri, S. Bonus-malus systems in open and closed portfolios. In Modern Problems in Insurance Mathematics; Silvestrov, D., Matin-Löf, Eds.; Springer: Cham, Switzerland, 2014; Chapter 16; pp. 261–271. [Google Scholar]
- Kunreuther, H.C.; Pauly, M.V.; McMorrow, S. Insurance & behavioral economics. Improving decisions in the most misunderstood industry; Cambridge University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Kleindorfer, P.R.; Kunreuther, H. The complementary roles of mitigation and insurance in managing catastrophic risks. Risk Anal. 1999, 19, 727–738. [Google Scholar] [CrossRef]
- Odeyinka, H.A. An evaluation of the use of insurance in managing construction risks. Constr. Manage. Econ. 2000, 18, 519–524. [Google Scholar] [CrossRef]
- Arnell, N.W.; Clark, M.J.; Gurnell, A.M. Flood insurance and extreme events: The role of crisis in prompting changes in British institutional response to flood hazard. Appl. Geogr. 1984, 4, 167–181. [Google Scholar] [CrossRef]
- Lamond, J.E.; Proverbs, D.G.; Hammond, F.N. Accessibility of flood risk insurance in the UK: Confusion, competition and complacency. J. Risk Res. 2009, 12, 825–841. [Google Scholar] [CrossRef]
- El-Adaway, I.H.; Kandil, A.A. Construction risks: Single versus portfolio insurance. J. Manag. Eng. 2009, 26, 2–8. [Google Scholar] [CrossRef]
- Dekker, D.; Green, D.; Palley, S. The expansion of insurance coverage for defective construction. Constr. Law 2008, 28, 19. [Google Scholar]
- National Association of Home Builders (NAHB). Insurance Coverage for Claims of Latent Defects: What Protection Is a Builder Buying? Available online: file:///C:/Users/Ana/Downloads/INSURANCE-COVERAGE-FOR-CLAIMS-OF-LATENT-DEFECTS-2015.pdf (accessed on 28 April 2019).
- Ostrager, B.R.; Newman, T.R. Handbook on insurance coverage disputes, 19th ed.; Wolters Kluwer: New York, NY, USA, 2019. [Google Scholar]
- Tronquet, M.C. There’s no place like home—Until you discover defects: Do prelitigation statutes relating to construction defect cases really protect the needs of homeowners and developers. Santa Clara Law Rev. 2004, 44, 4. [Google Scholar]
- Bunni, N.G. Risk and insurance in construction; Taylor & Francis Group: London, UK, 2003. [Google Scholar]
- Jelle, B.P.; Nilsen, T.N.; Hovde, P.J.; Gustavsen, A. Accelerated climate aging of building materials and their characterization by Fourier transform infrared radiation analysis. J. Build. Phys. 2011, 36, 99–112. [Google Scholar] [CrossRef]
- Nosrati, R.; Berardi, U. Long-term performance of aerogel-enhanced materials. Energy Procedia 2017, 132, 303–308. [Google Scholar] [CrossRef]
- Gradeci, K.; Berardi, U.; Time, B.; Köhler, J. Evaluating highly insulated walls to withstand biodeterioration: A probabilistic-based methodology. Energy Build. 2018, 177, 112–124. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).