Incremental Dynamic Analysis for Estimating Seismic Performance of Multi-Story Buildings with Butterfly-Shaped Structural Dampers
Abstract
:1. Introduction
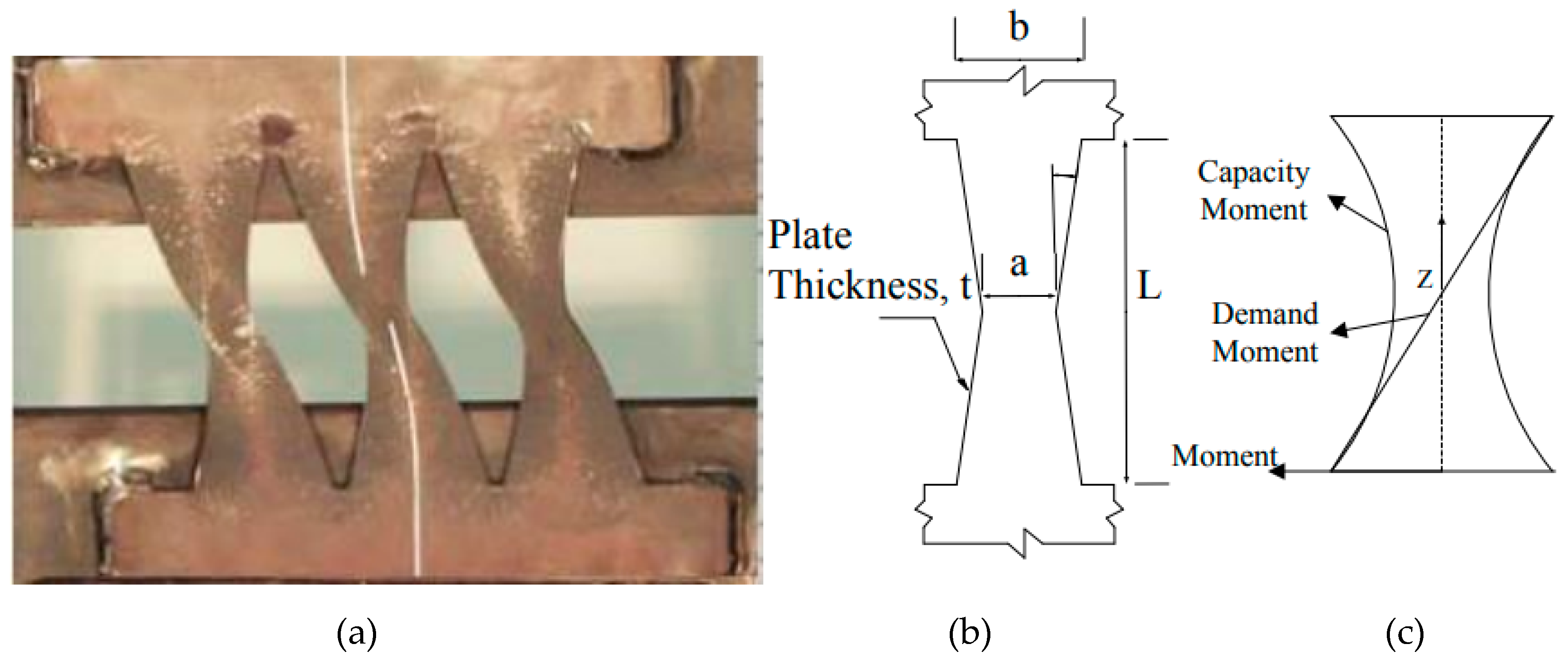
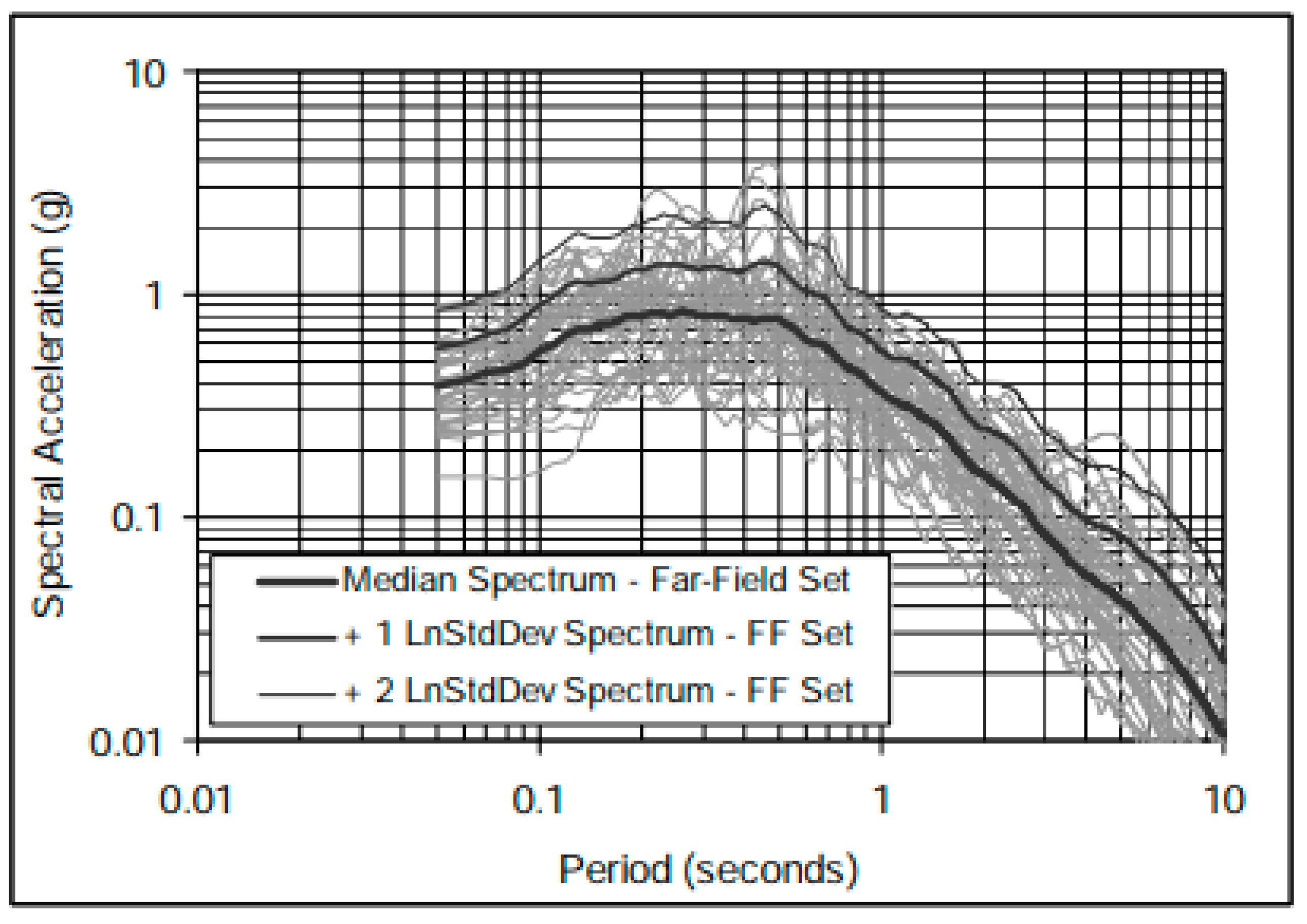
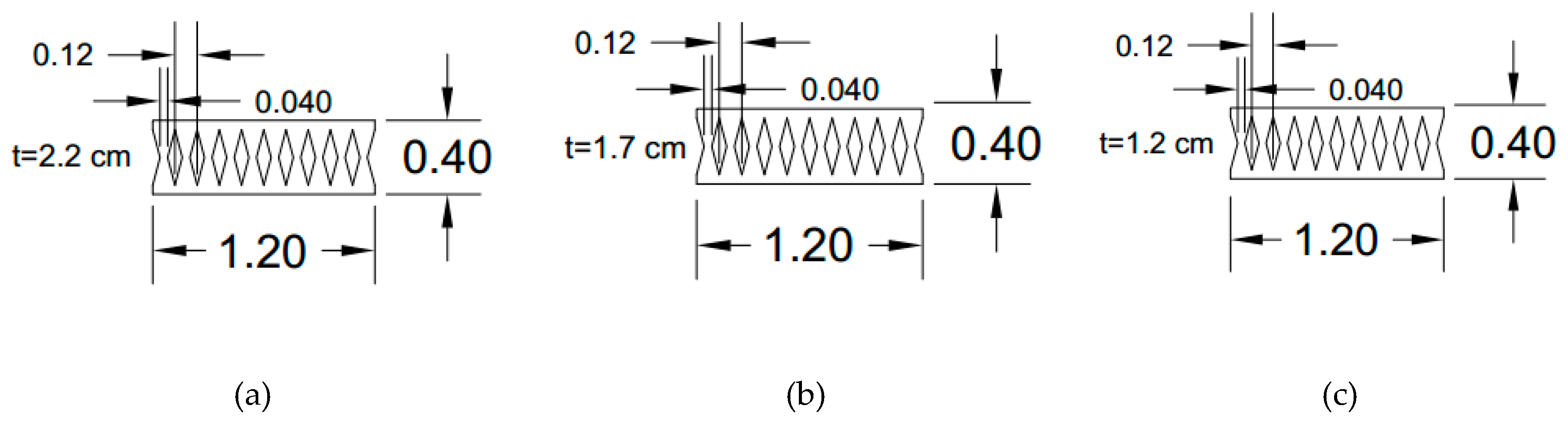
2. Design and Verification of the Modeling Methodology
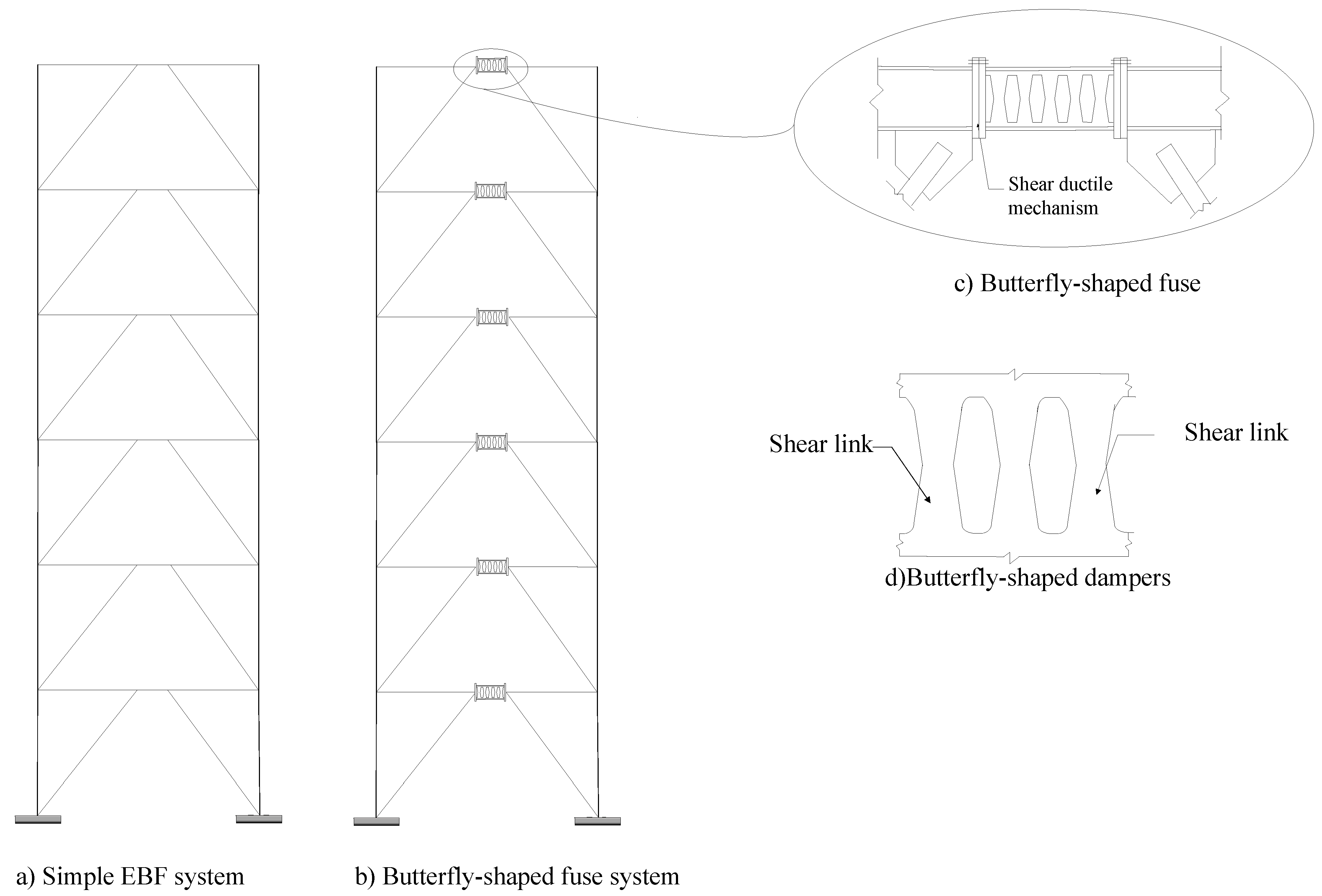
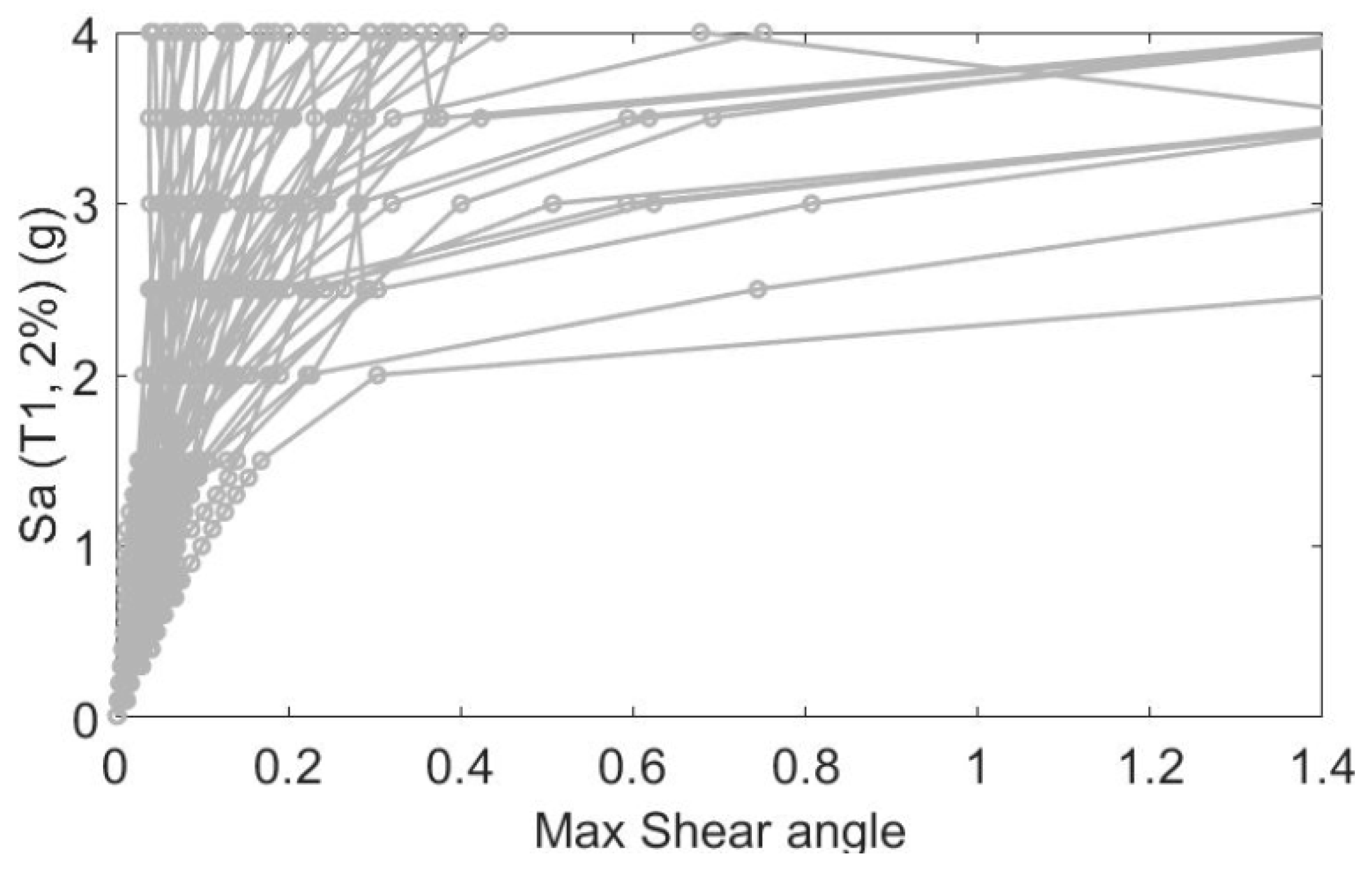
3. Comparison of the Seismic Behavior of the EBF Conventional and Butterfly-Shaped Systems
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- El Ouni, M.H.; Laissy, M.Y.; Ismaeil, M.; Kahla, N.B. Effect of shear walls on the active vibration control of buildings. Buildings 2018, 8. [Google Scholar] [CrossRef]
- Palazzo, B.; Castaldo, P.; Marino, I. The dissipative column: A new hysteretic damper. Buildings 2015, 5, 163–178. [Google Scholar] [CrossRef]
- Farzampour, A. Evaluating Shear links for Use in Seismic Structural Fuses. Ph.D. Thesis, Virginia Tech, Blacksburg, VA, USA, November 2019. [Google Scholar]
- Kazemzadeh, A.; Topkaya, C. A review of research on steel eccentrically braced frames. J. Constr. Steel Res. 2017, 128, 53–73. [Google Scholar] [CrossRef]
- Farzampour, A.; Eatherton, M.R. Yielding and lateral torsional buckling limit states for butterfly-shaped shear links. Eng. Struct. 2019, 180, 442–451. [Google Scholar] [CrossRef]
- Hitaka, T.; Matsui, C. Seismic performance of Steel Shear Wall with Slits integrated with multi story composite moment frame. In Proceedings of the 5th International Conference on Behaviour of Steel Structures in Seismic Areas, STESSA 2006, Yokohama, Japan, 14–17 August 2006; pp. 241–246. [Google Scholar]
- Mirzai, N.M.; Attarnejad, R.; Hu, J.W. Enhancing the seismic performance of EBFs with vertical shear link using a new self-centering damper. Ing. Sismica 2018, 35, 57–76. [Google Scholar]
- Luth, G.; Krawinkler, H.; McDonald, B. USC School of Cinema: An example of reparable performance based design. In Proceedings of the 77th Annual Structural Engineers Association of California (SEAOC) Convention, Sacramento, CA, USA, 23–27 September 2008. [Google Scholar]
- Lee, C.H.; Ju, Y.K.; Min, J.K.; Lho, S.H.; Kim, S.D. Non-uniform steel strip dampers subjected to cyclic loadings. Eng. Struct. 2015, 99, 192–204. [Google Scholar] [CrossRef]
- Martínez-Rueda, J.E. On the evolution of energy dissipation devices for seismic design. Earthq. Spectra 2002, 18, 309–346. [Google Scholar] [CrossRef]
- Farzampour, A.; Eatherton, M.R. Lateral torsional buckling of butterfly-shaped shear links. In Proceedings of the SSRC Annual Stability Conference Structural Stability Research Council, San Antonio, TX, USA, 21–24 March 2017. [Google Scholar]
- Farzampour, A.; Eatherton, M.R. Parametric study on butterfly-shaped shear links with various geometries. In Proceedings of the 11th National Conference on Earthquake Engineering, 11NCEE, Los Angeles, CA, USA, 25–29 June 2018. [Google Scholar]
- Farzampour, A.; Eatherton, M.R. Investigating limit states for butterfly-shaped and straight shear links. In Proceedings of the 16th European Conference on Earthquake Engineering, 16ECEE, Thessaloniki, Greece, 18–21 June 2018. [Google Scholar]
- Daie, M.; Jalali, A.; Suhatril, M.; Shariati, M.; Arabnejad Khanouki, M.M.; Shariati, A.; Kazemi-Arbat, P. A new finite element investigation on pre-bent steel strips as damper for vibration control. Int. J. Phys. Sci. 2011, 6, 8044–8050. [Google Scholar] [CrossRef]
- Mansouri, I.; Safa, M.; Ibrahim, Z.; Kisi, O.; Tahir, M.M.; Baharom, S.; Azimi, M. Strength prediction of rotary brace damper using MLR and MARS. Struct. Eng. Mech. 2016, 60, 471–488. [Google Scholar] [CrossRef]
- Oh, S.H.; Kim, Y.J.; Ryu, H.S. Seismic performance of steel structures with slit dampers. Eng. Struct. 2009, 31, 1997–2008. [Google Scholar] [CrossRef]
- Aschheim, M.; Halterman, A. Reduced web section beams, Phase one: Experimental findings and design implications. In Proceedings of the 7th US National Conference on Earthquake Engineering, Boston, MA, USA, 21–25 July 2002. [Google Scholar]
- ICC Staff; SEAOC Staff. 2012 IBC SEAOC Structural/Seismic Design Manual Vol. 4: Examples for Steel-Framed Buildings; International Code Council: San Francisco, CA, USA, 2012. [Google Scholar]
- ICC Staff; SEAOC Staff. 2012 IBC SEAOC Structural Seismic Design Manual Vol. 3: Examples for Concrete Buildings; International Code Council: San Francisco, CA, USA, 2012. [Google Scholar]
- FEMA, P. 2009 NEHRP Recommended Seismic Provisions: Design Examples; Building Seismic Safety Council of the National Institute of Building Sciences: Washington, DC, USA, 2012. [Google Scholar]
- Montuori, R.; Nastri, E.; Piluso, V. Theory of Plastic Mechanism Control for MRF-EBF dual systems: Closed form solution. Eng. Struct. 2016, 118, 287–306. [Google Scholar] [CrossRef]
- Montuori, R.; Nastri, E.; Piluso, V. Influence of the bracing scheme on seismic performances of MRF-EBF dual systems. J. Constr. Steel Res. 2017, 132, 179–190. [Google Scholar] [CrossRef]
- Nastri, E.; Montuori, R.; Piluso, V. Seismic design of MRF-EBF dual systems with vertical links: EC8 vs plastic design. J. Earthq. Eng. 2015, 19, 480–504. [Google Scholar] [CrossRef]
- Montuori, R.; Nastri, E.; Piluso, V. Preliminary analysis on the influence of the link configuration on seismic performances of MRF-EBF dual systems designed by TPMC. Ing. Sismica 2016, 33, 52–64. [Google Scholar]
- Zeynali, K.; Saeed Monir, H.; Mirzai, N.M.; Hu, J.W. Experimental and numerical investigation of lead-rubber dampers in chevron concentrically braced frames. Arch. Civ. Mech. Eng. 2018, 18, 162–178. [Google Scholar] [CrossRef]
- Prinz, G.S.; Richards, P.W. Eccentrically braced frame links with reduced web sections. J. Constr. Steel Res. 2009, 65, 1971–1978. [Google Scholar] [CrossRef]
- AISC-341-16. Seismic Provisions for Structural Steel Buildings. American Institute of Steel Construction: Chicago, IL, USA, 2016. Available online: https://www.aisc.org/globalassets/aisc/publications/standards/seismic-provisions-for-structural-steel-buildings-ansi-aisc-341-16.pdf (accessed on 1 March 2019).
- ASCE-7-05. Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers: Washington, DC, USA, 2005. Available online: https://law.resource.org/pub/us/cfr/ibr/003/asce.7.2002.pdf (accessed on 1 March 2019).[Green Version]


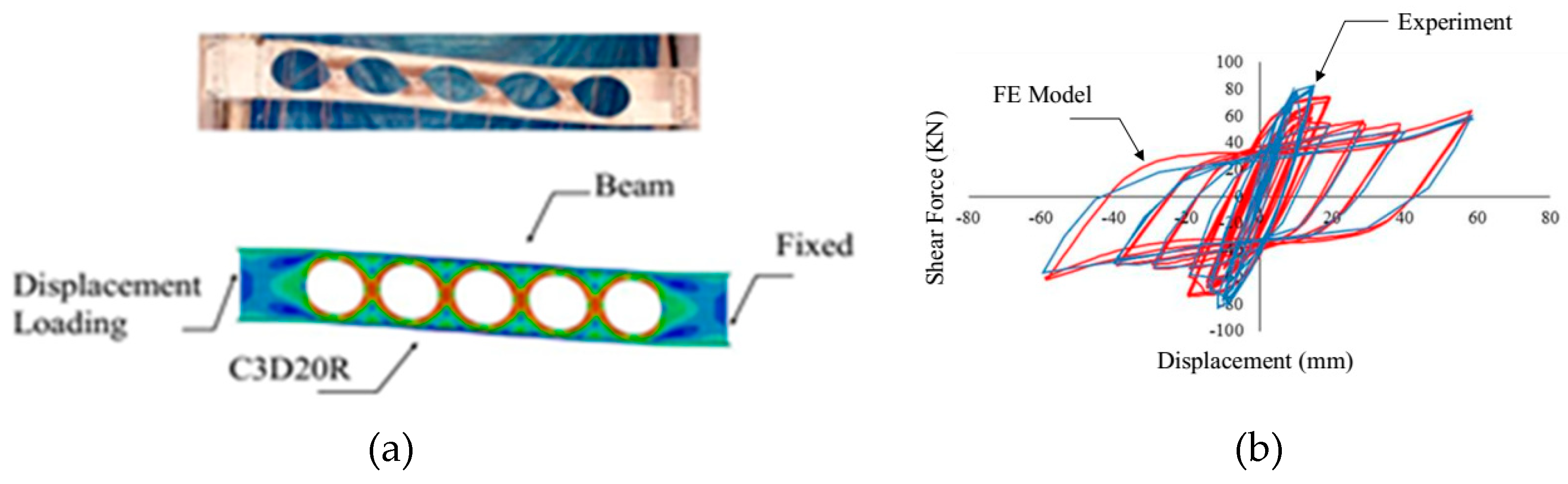
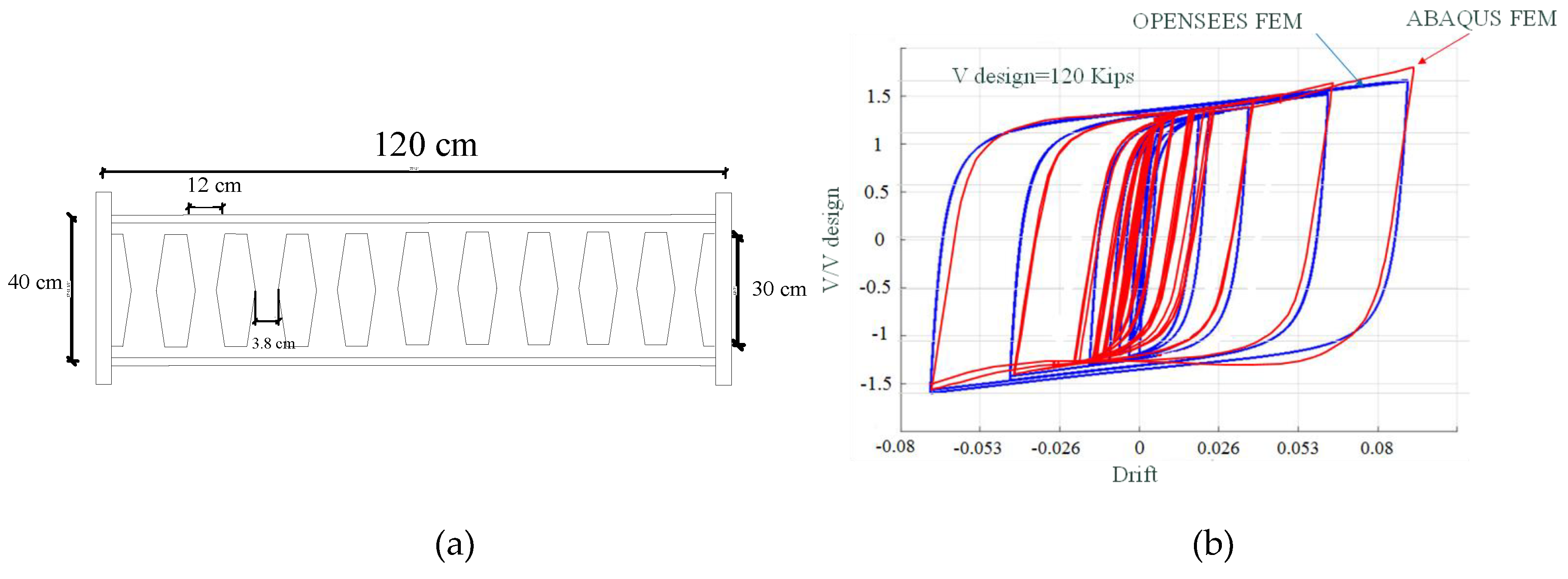
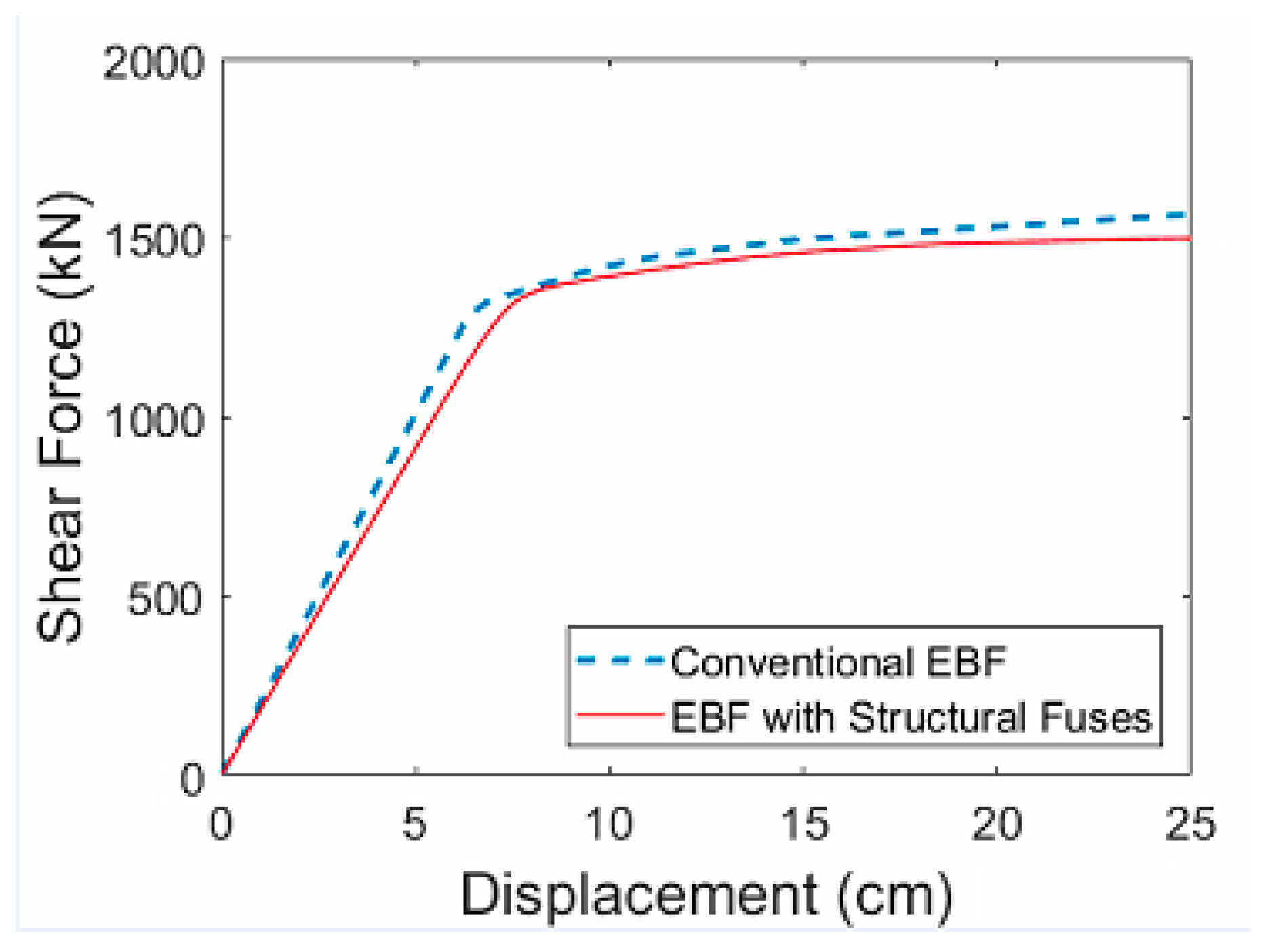
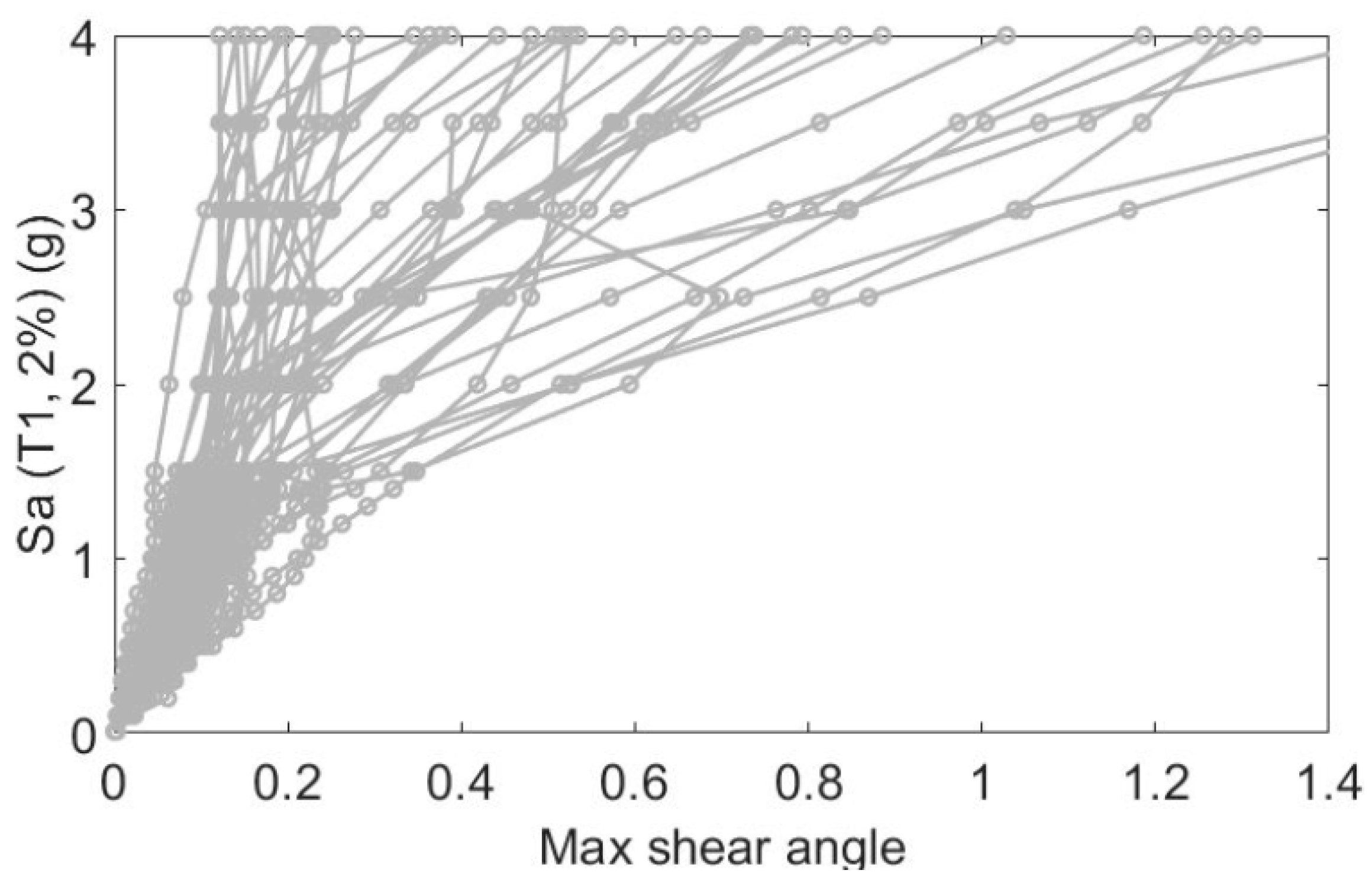
| Level | Shear (kips) | Cumulative Force (kips) | Design Section for EBF | Design Force for the BF Links | Design Groups for BF System | |
|---|---|---|---|---|---|---|
| Roof | 60 | 60 | BU 13 × 53 | 244 | 244 | III |
| 6th | 60 | 120 | BU 13 × 53 | 244 | ||
| 5th | 88 | 208 | BU13 × 53 | 358 | 358 | II |
| 4th | 125 | 333 | W 10 × 68 | 508 | 508 | I |
| 3rd | 125 | 458 | W 10 × 68 | 508 | ||
| 2nd | 125 | 583 | W 10 × 68 | 508 | ||
| Mode No. | BF Fuse System | Conventional System |
|---|---|---|
| 1 | 1.332 | 1.283 |
| 2 | 0.518 | 0.482 |
| 3 | 0.299 | 0.289 |
| 4 | 0.243 | 0.227 |
| 5 | 0.192 | 0.18 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farzampour, A.; Mansouri, I.; Dehghani, H. Incremental Dynamic Analysis for Estimating Seismic Performance of Multi-Story Buildings with Butterfly-Shaped Structural Dampers. Buildings 2019, 9, 78. https://doi.org/10.3390/buildings9040078
Farzampour A, Mansouri I, Dehghani H. Incremental Dynamic Analysis for Estimating Seismic Performance of Multi-Story Buildings with Butterfly-Shaped Structural Dampers. Buildings. 2019; 9(4):78. https://doi.org/10.3390/buildings9040078
Chicago/Turabian StyleFarzampour, Alireza, Iman Mansouri, and Hamzeh Dehghani. 2019. "Incremental Dynamic Analysis for Estimating Seismic Performance of Multi-Story Buildings with Butterfly-Shaped Structural Dampers" Buildings 9, no. 4: 78. https://doi.org/10.3390/buildings9040078
APA StyleFarzampour, A., Mansouri, I., & Dehghani, H. (2019). Incremental Dynamic Analysis for Estimating Seismic Performance of Multi-Story Buildings with Butterfly-Shaped Structural Dampers. Buildings, 9(4), 78. https://doi.org/10.3390/buildings9040078





