Next Article in Journal
Metaphors as Discourse Interaction Devices in Architectural Design
Previous Article in Journal
Rheological and Strength Behavior of Binary Blended SCC Replacing Partial Fine Aggregate with Plastic E-Waste as High Impact Polystyrene
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 9
Issue 2
10.3390/buildings9020051
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Thermal Performance of Hollow-Core Slab Ventilation System with Macro-Encapsulated Phase-Change Materials in Supply Air Duct

by
Hasnat Jamil
,
Morshed Alam
* and
Jay Sanjayan
Centre for Sustainable Infrastructure, Department of Civil and Construction Engineering, Faculty of Science, Engineering and Technology, Swinburne University of Technology, Hawthorn, VIC 3122, Australia
*
Author to whom correspondence should be addressed.
Buildings 2019, 9(2), 51; https://doi.org/10.3390/buildings9020051
Submission received: 8 January 2019 / Revised: 9 February 2019 / Accepted: 18 February 2019 / Published: 22 February 2019
(This article belongs to the Section Building Materials, and Repair & Renovation)
Browse Figures
Versions Notes

Abstract

:
The aim of this research was to evaluate the effectiveness of phase-change materials (PCMs) incorporated into the supply air duct of a hollow-core slab ventilation system. Both experimental and numerical approaches were adopted in this investigation. In the experimental work, the air was passed through a PCM-incorporated aluminum air duct, and the temperature at various points of the duct was recorded. Computational fluid dynamics models of the PCM-incorporated supply air duct and the hollow-core slab were developed and validated with the respective experimental data. The validated models were used to simulate the performance of PCM-incorporated hollow-core slabs during summer in Melbourne, Australia. The results showed that the reduction in temperature fluctuation varied with the way the PCM was incorporated inside the supply air duct. The temperature difference was maximum and was maintained for a longer period when the PCM was spread to all four internal surfaces of the supply air duct. The results also showed that the effectiveness of the combined PCM–air duct–hollow-core slab system in reducing the temperature fluctuation was lower than the individual performance of the PCM–air duct and hollow-core concrete slab for a given inlet temperature condition during the simulated period. This was because the integration of PCMs in the supply air duct resulted in a precooling effect which reduced the difference between the amplitude of slab inlet temperature swing and average slab temperature. As a result, the reduction in temperature fluctuation due to the thermal mass of the hollow-core slab was 21% lower in the presence of PCMs compared to the no-PCM case.

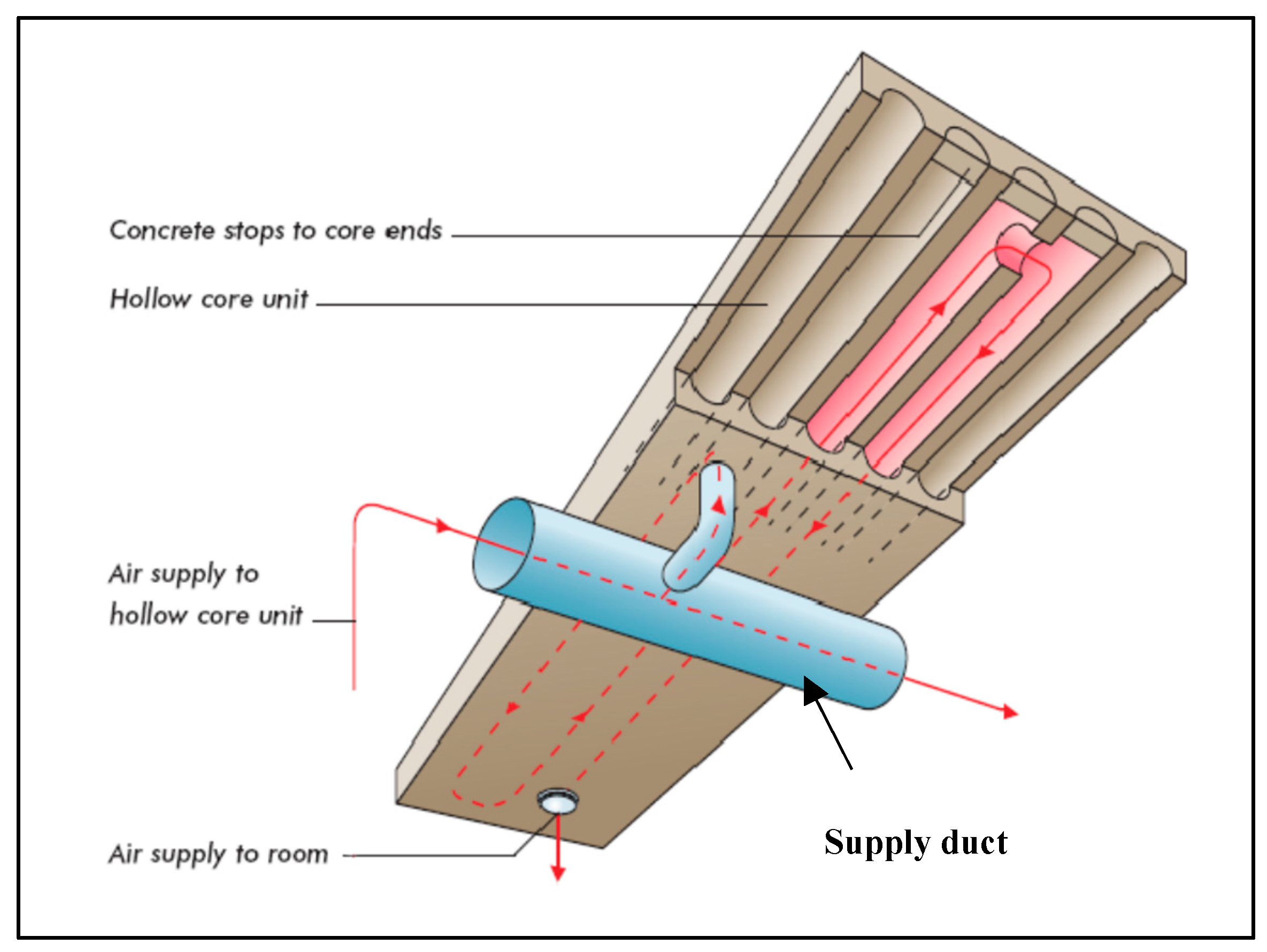
1. Introduction

Buildings are one of the largest users of energy, accounting for 32% of total global final energy use and 19% of total energy-related greenhouse gas (GHG) emissions [1]. Due to population growth, increase in building stock, and lifestyle changes, the energy consumption and GHG emissions in this sector are increasing continuously, which contributes to global average temperature increase and may lead to harmful climate change impact [2]. Improving energy efficiency in buildings encompasses the most cost-effective energy usage and GHG mitigation opportunities. Use of thermal energy storage (TES) systems in buildings is an attractive option to reduce the building energy use and to improve indoor thermal comfort.
A TES system in a building can store thermal energy using the sensible and latent heat thermal energy storage methods [3]. In the sensible heat storage method, the energy is stored by changing the temperature of the storage mediums (e.g., masonry walls, concrete, rock beds, etc.). On the other hand, in the latent heat storage method, the material stores heat by changing its phase. The material is known as phase-change material (PCM).
One of the ways to use the building fabric as sensible thermal storage is to pass the cold/hot heat transfer fluid through precast hollow cores in the hollow-core slabs. The earliest development of the hollow-core slab was reported in Sweden in the late 1970s which was later commercialized in the UK as the “TermoDeck®” System [5]. It consists of a patented arrangement of interconnected hollow cores making an air passage within a precast concrete plank as shown in Figure 1. In the hollow-core concrete slab system, air is used as a heat transfer fluid. The air passes through the several cores back and forth utilizing the increased heat transfer area of the inside surface of the cores. During the summer nights, the cool ambient air removes the heat from the slab as it passes through the hollow cores, lowering its temperature for the daytime use. During the day, warmer outside air is cooled down as it circulates through the cores of the slab before entering the occupied space. The supply air is distributed to the hollow-core slabs with a central distribution air duct which runs perpendicular to the slabs as shown in Figure 1. Each slab is connected to this air duct. The supply air, either from outside or the HVAC system, is sent through the distribution duct and then through the hollow-core slabs to the conditioned space.
Various studies have been carried out regarding the design, modeling, and application of hollow-core slabs [6,7]. Winwood et al. [8] performed a three-dimensional (3D) Computational Fluid Dynamics (CFD) analysis of a hollow-core slab in PHONICS using a simplified geometry. The effects of various parameters (e.g., insulation on the surface, a variation of thermal conductivity of the slab, air flow rate, etc.) on the heat transfer of the hollow-core slab were investigated. The results showed that the model could reproduce the pattern of the heat transfer in the hollow-core slab similar to the experimental data with 2.0% accuracy. In another study, Winwood et al. [9] reported an application of the TermoDeck® slab in a real office building (Weidmuller Building) in the UK which suggested that with better control, efficient fans, and improved night ventilation, the building could reach the energy target of 50 to 70 kWh/m2. Zmeureanu and Fazio [10] showed that the hollow-core slab can save average cooling load from 28.4 W/m2 to 44.2 W/m2 and can provide thermal comfort without the mechanical system in an office building in Montréal, Canada. Similar observations were reported by Willis and Wilkins [11] based on their experimental study.
Russell and Surendran [12] established a correlation between the air temperature through the slab, slab surface temperature, and the cooling potential for different configurations of the slab (e.g., number of cores, position of cores in the slab, etc.). Knowledge of the correlation can be useful in understanding the influence of core air temperature on cooling potential, the likelihood of surface condensation, and the obvious implication on thermal comfort. Corgnati and Kindinis [13] coupled the hollow-core slab with the night ventilation and the results showed that night ventilation coupled with thermal mass activation can reduce the average operative temperature and improve the thermal comfort. Chae et al. [14] developed a computational model of the hollow-core slab using Energy Plus and investigated its influence on the whole building operation. The model included an auxiliary air-handling unit, radiant slab with hollow cores, and various control options to provide conditioned air when desired.
On the other hand, the use of phase-change materials (PCMs) has received considerable attention in recent decades due to its potential benefits of high volumetric heat capacity and small temperature variation during the phase transition process. The use of PCMs in buildings can be categorized into three methods: passive, active, and free cooling. In the passive application method, PCM can be incorporated in brick walls [15,16], wall plasterboards [17,18,19,20], concrete floors [21,22,23,24,25], and ceilings [26,27,28,29]. These studies have reported varying degrees of energy savings and thermal comfort improvement depending on thermophysical properties of PCM used, application location, and local climatic conditions.
In the case of active methods, PCM can be integrated into HVAC (heating, ventilation, and air conditioning) systems [30], floor heating systems [31], and heat pumps [32,33] to improve the energy efficiency of the unit. Real et al. [33] studied the performance enhancement of a heat-pump-based HVAC system with two thermal storage tanks using PCM. One tank utilizes the cool nighttime outside air temperature to solidify the PCM and uses it later to cool the building. The second tank acts as an alternative hot reservoir providing the system with the flexibility to dissipate heat at constant temperature ensuring the Coefficient of Performance (COP) value remains over a minimum limit. Chaiyat [30] used PCM to reduce the air temperature entering the evaporative coil of an air-conditioning unit in Thailand. The results showed that electrical consumption of the modified air conditioner could be decreased to 3.09 kWh/day which is equivalent to the cost savings of 170 USD/year. The calculated payback period was around 4.12 years.
The free-cooling method stores the coldness of night ambient temperature and extracts it during daytime by supplying the indoor/outdoor air through the PCM storage unit [34]. The PCM storage unit is placed between the suspended ceiling and the floor/roof above [35,36]. During the day, the room air is circulated through the unit to reduce the temperature, and cool outside air is used during the night to regenerate the PCM. The free-cooling method can overcome the melting and solidification problems experienced in the passive application method and can increase the effectiveness of PCM [34]. However, the design of the heat storage unit plays a vital role in the effective utilization of the PCM storage unit.
Realizing the potential of both PCM and hollow-core system in improving building energy efficiency and thermal comfort, several studies have investigated the combination of these two technologies to further improve the energy efficiency. Whiffen et al. [37] worked on a prototype of hollow-core slab with PCM enhancement and investigated energy savings and comfort benefits under laboratory conditions. Due to the PCM incorporation, additional 0.1 kWh energy was saved per day, with 1.2 h thermal delay and 1.0 °C reduction of room temperature reported compared to the original hollow-core slab. Pomianowski et al. [38] carried out a full-scale experimental study where a microencapsulated PCM layer was applied on the surface of a hollow-core slab. The results indicated that the incorporation of the PCM layer in the hollow-core slab reduced its cooling capacity, which was attributed to the low thermal conductivity of the PCM or the experimental error. Faheem et al. [39] studied the effects of incorporating microencapsulated PCM in hollow-core slabs on cooling energy savings of an office building. Their results showed that the PCM-incorporated hollow-core system exhibited much higher cooling potential when placed in low-thermal-mass buildings compared to high-thermal-mass buildings. The cooling also depends on ventilation rate and PCM content. Navarro et al. [40,41] incorporated PCM, macro-encapsulated in aluminum tubes, inside the concrete slab hollows. The prefabricated prototype was tested in a house-like, two-story cubicle where the system was used as an internal slab to store thermal energy in order to minimize or eliminate the use of HVAC systems. The cool nighttime air was used to solidify the PCM and prepare it for the next day cooling operation. The results showed significant HVAC energy savings ranging from 30% to 55% under mild conditions and 15% to 20% under severe conditions with the application of PCM. In terms of heating, the application of PCM reduced heat pump energy consumptions by 25% under severe conditions and 40% under mild conditions.
The previous studies on PCM-integrated hollow-core systems either applied microencapsulated PCM in the concrete slab or macroencapsulated PCM in the hollows. Mixing of microencapsulated PCM with concrete can result in leakage issues [42]. On the other hand, insertion of macroencapsulated PCM in the hollow may increase the resistance to air flow and generate unwanted noise. Hence, to overcome the resistance and maintain the same air flow rate, one may need to increase the fan pressure, which may further increase the noise as well as fan energy consumption [40]. Also, application of microencapsulated PCM in concrete, as well as insertion of macroencapsulated PCM in the hollows, are not practical in existing buildings with the hollow-core system. To address the factors mentioned above, this study aimed to explore the effectiveness of macro-encapsulated PCM integrated into the supply air duct of a hollow-core system. The supply air duct of a hollow-core system is easily accessible, and the PCM can be applied in both new and existing buildings. The effect of different PCM arrangements inside the supply air duct was investigated.

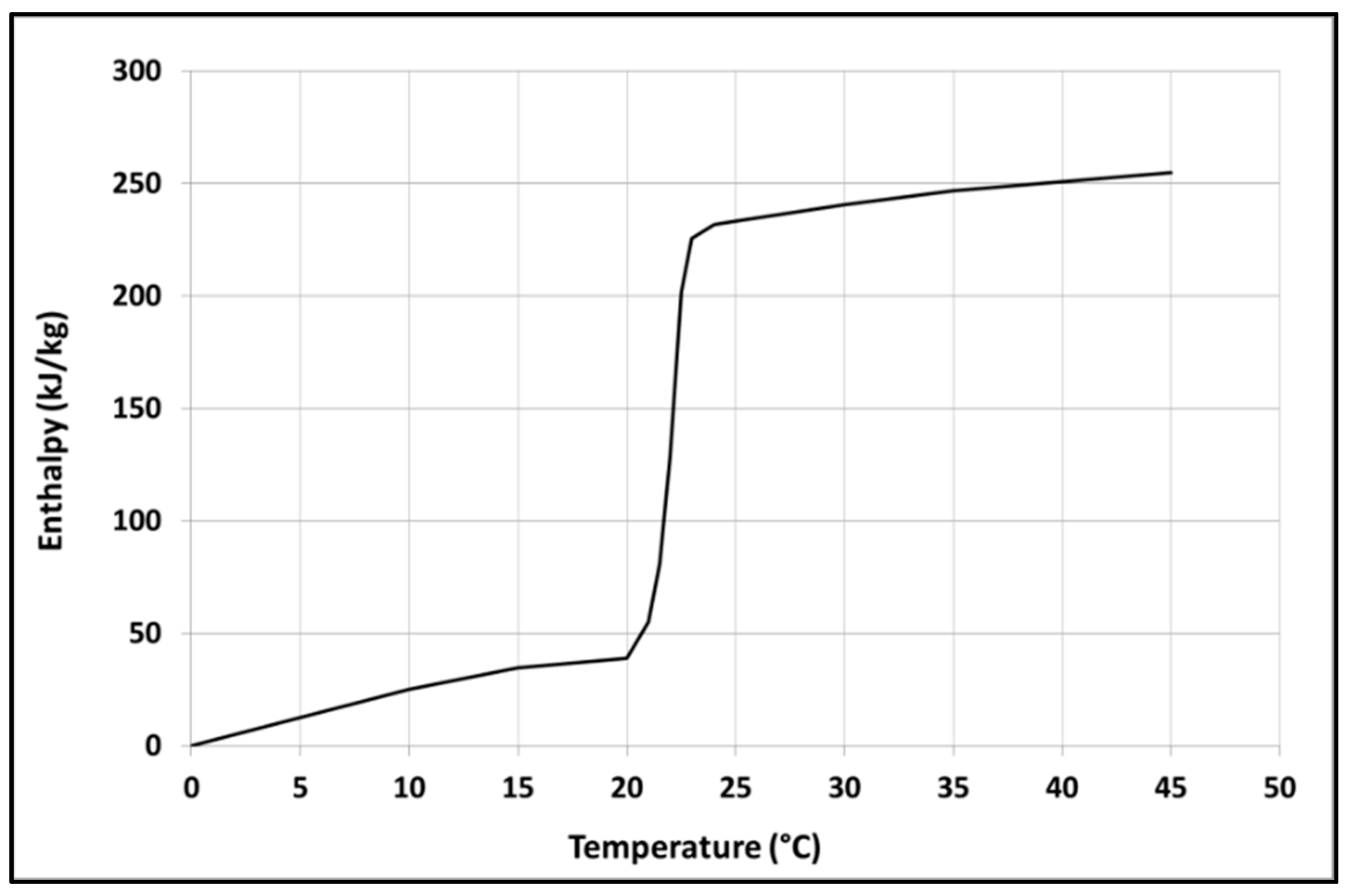
2. Methodology

This study adopted both an experimental and numerical approach to investigate the effectiveness of PCM as shown in Figure 2. The experimental study investigated the heat transfer and interactions between air and PCM in a supply air duct without any hollow-core slab. The experimental data was used to validate the developed CFD model of a PCM-incorporated supply air duct. A second CFD model for the hollow-core slab system was developed and validated against experimental measurements available in the literature. Finally, the validated CFD models of supply air duct and hollow-core slab were used together to investigate the effectiveness of PCM on the thermal performance of the hollow-core system during summer in Melbourne, Australia.

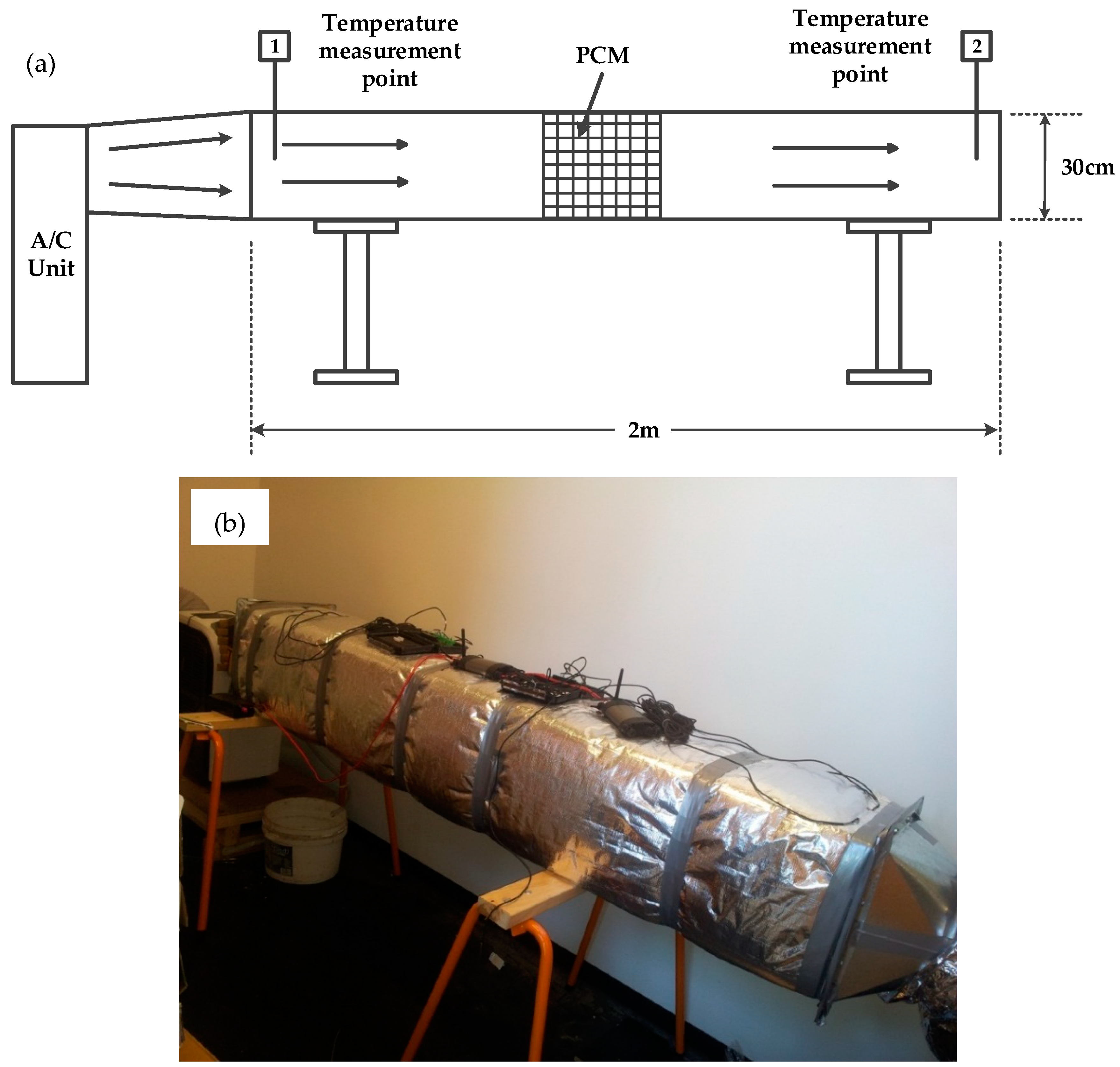
2.1. Experimental Study with PCM-Incorporated Supply Air Duct

The experimental test setup is shown in Figure 3. A 2 m long rectangular-shaped (300 mm × 300 mm) aluminum air duct was used in the experiment to represent the supply air duct of a hollow-core slab system. A 300 mm wide and 1200 mm long BioPCM mat with an area density of 1.5 kg/m2 was used. The BioPCM with 21 °C was selected in this study because it was found to be the optimum PCM temperature for Melbourne weather [27]. The phase change of this 21 °C BioPCM occurs in the temperature range from 18 °C (melting starts) to 23 °C (freezing starts) as shown in the enthalpy–temperature curve of the BioPCM in Figure 4.
The Dimplex DC10RC portable reverse-cycle air-conditioning (A/C) unit was used in the experiment to supply conditioned air through the duct. This unit can provide air with temperatures ranging from 10 °C to 45 °C. The air duct was covered by R 1.8 reflective earthwool insulation to minimize the heat transfer through its wall. Air temperature at the inlet and outlet of the air duct was recorded at one-second intervals by using thermistors (accuracy ± 0.1 °C). Three thermistors were installed at each of the positions 1 and 2. The temperature data recorded by these three thermistors at each position were averaged to calculate the inlet and outlet air temperature. The velocity of the supplied air flow through the duct was measured by using a hot-wire anemometer (accuracy ± 0.1 m/s). Three sets of experiments were performed:
(i)
Without PCM (No-PCM),
(ii)
PCM on single surface arrangement (PCM-SSA) as shown in Figure 5a
(iii)
PCM on all surfaces arrangement (PCM-ASA) as shown in Figure 5b
In case of PCM-SSA and PCM-ASA, the total volumetric capacity of PCM was kept the same. All experiments were carried out for 2 h (120 min).
To study the influence of PCM on inlet air temperature, the experiment was carried out in two modes: cooling mode and heating mode. Figure 6 shows typical inlet temperature profiles for the two modes. In the cooling mode, at first, the inlet air was supplied at 27 °C for 1 h at high flow rate to ensure that the PCM was completely melted (data from this step is not shown in Figure 6). Then, the cooling mode experiment was started and the inlet air temperature was decreased to 10 °C as shown in Figure 6. Similarly, in the heating mode, the inlet temperature was kept around 12 °C to ensure that the PCM was solidified before the start of the experiment. Then, the temperature was increased to 32 °C at the start of the heating mode experiment. In both cooling and heating modes, the inlet and outlet temperatures were recorded, and the difference between them was calculated to evaluate the effectiveness of the PCM.

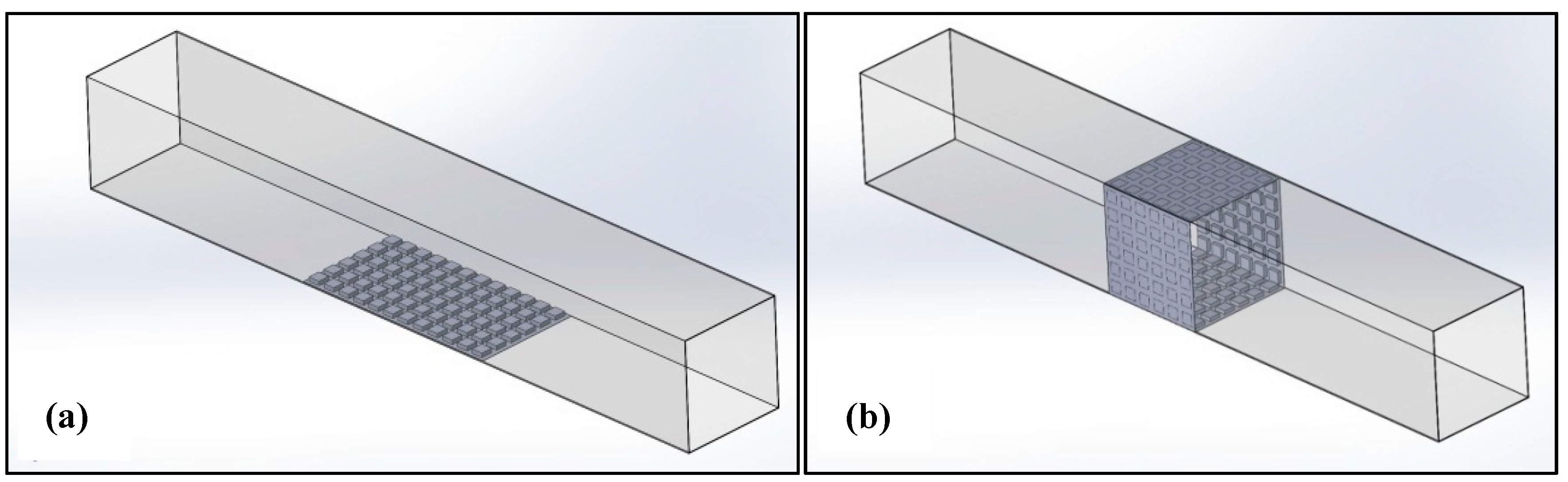
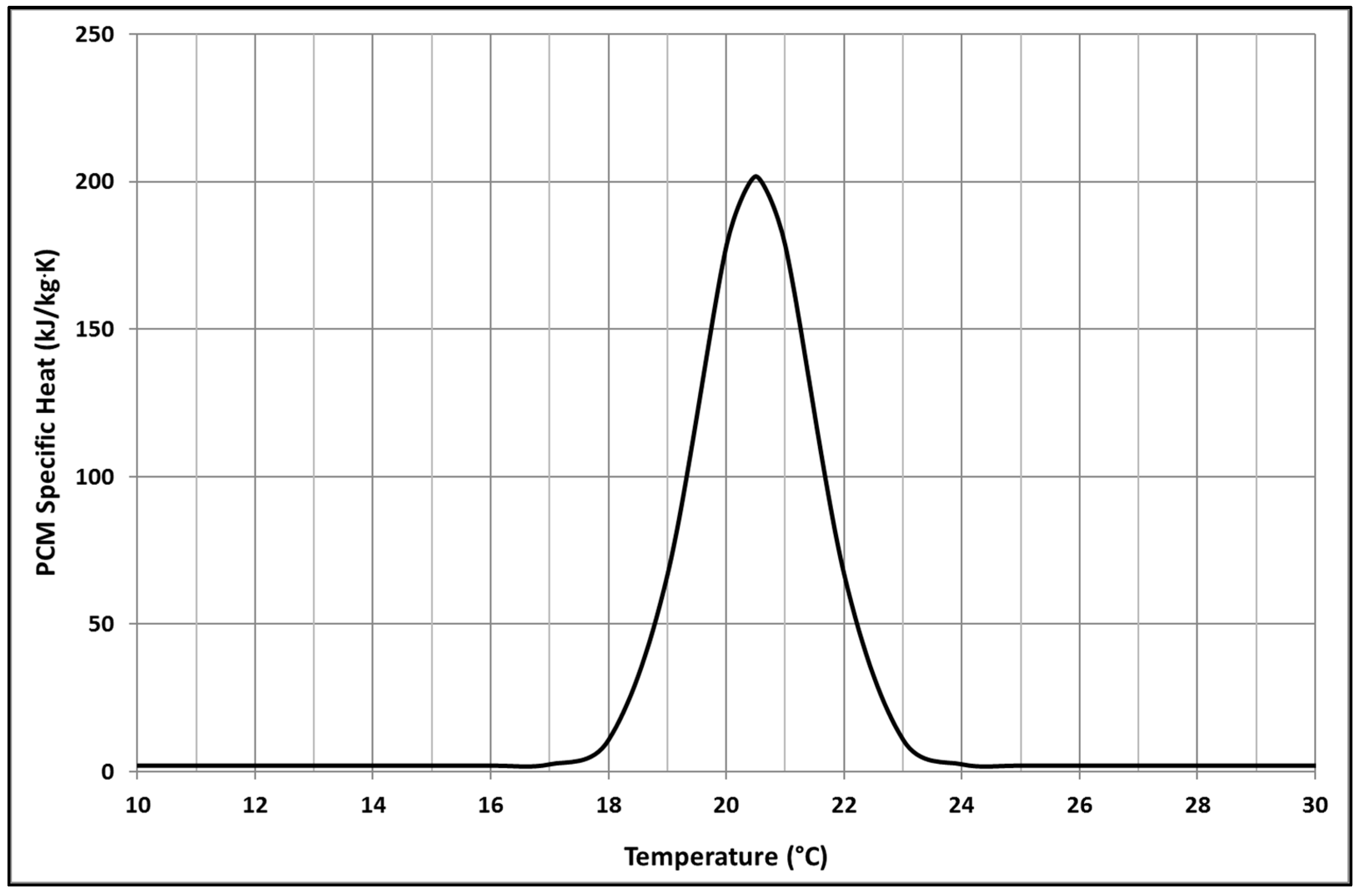
2.2. Development of Computational Fluid Dynamics Model

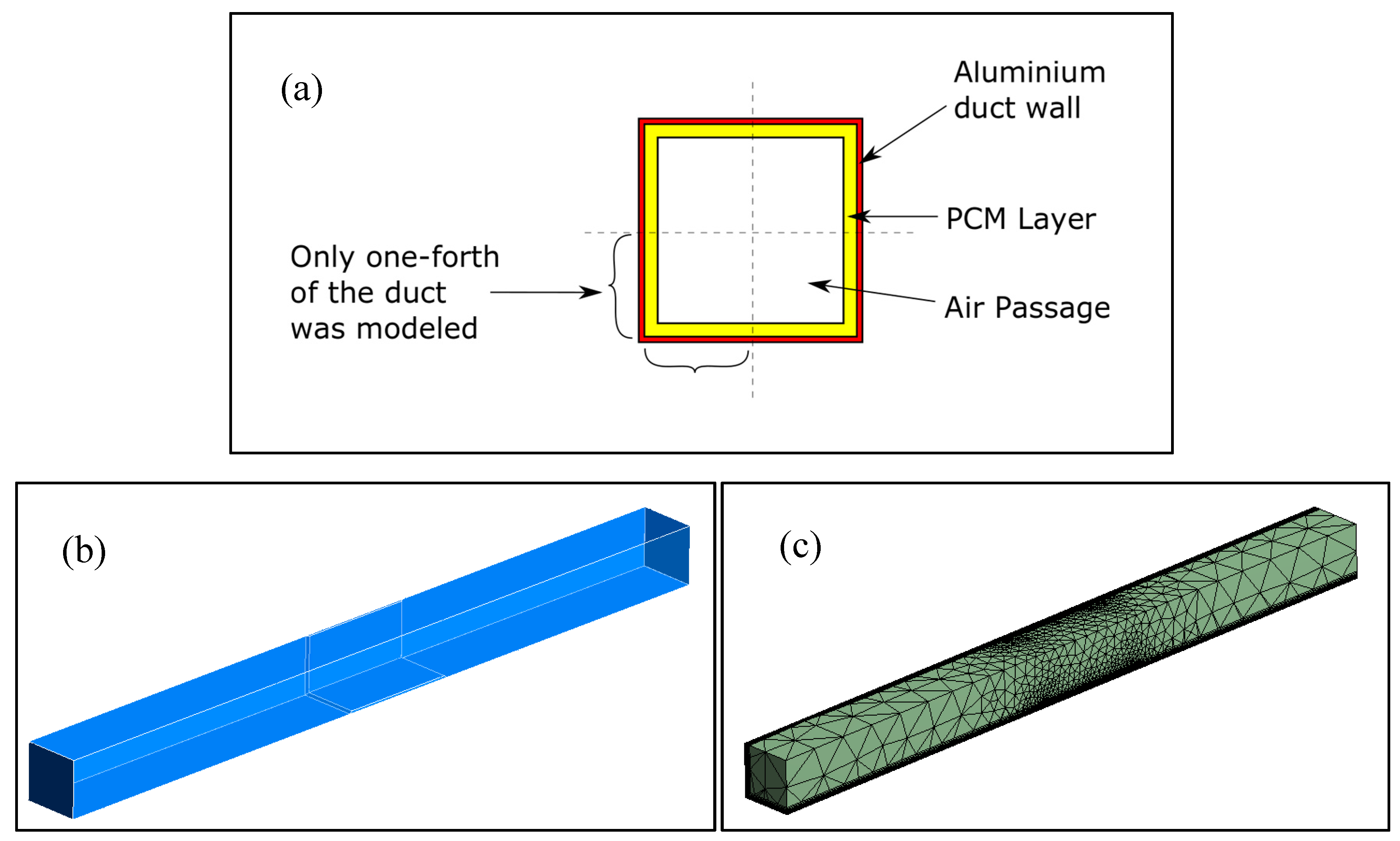
2.2.1. Computational Fluid Dynamics Model of the Air Duct

Computational Fluid Dynamics model (CFD) of the experimental air duct was developed using the ANSYS® CFX software. Due to the axisymmetric nature of the air flow through the air duct, a one-fourth section (150 mm × 150 mm) of the duct was considered in the model with symmetric boundary (Figure 7a,b). This made the flow domain smaller (i.e., a smaller number of cells), which required less simulation time. The length of the air duct was 2 m, which is similar to the experimental. The model included three domains: air flow domain (fluid region), aluminum body (solid region), and PCM (in PCM-ASA case) domain (solid region). The mesh of the modeled region is shown in Figure 7c. The number of cells in the mesh were 20,000 and 75,000 for No PCM and PCM-ASA cases, respectively. It should be noted that the CFD model of PCM-SSA was not developed because the experimental study showed that the PCM-ASA case was more effective than the PCM-SSA case. The details of the experimental results are shown in Section 3.1.
The thickness of the aluminum shell was 0.4 mm. The PCM layer was considered as a flat layer as used by Muruganantham [43] rather than a sheet of square pouches, to make a smoother and more convenient mesh generation. The area of the PCM layer was kept the same as the area of the BioPCM™ mat used in the experiment (300 mm × 1200 mm for PCM-ASA). The thickness of the PCM layer used in the simulation was 6.4 mm, which was calculated using the area density 1.5 kg/m2 and material density 235 kg/m3 of BioPCM™. The phase-change process of the PCM was modeled in ANSYS® CFX software using specific heat capacity curve as shown in Figure 8.
The outside wall of the air duct was set as an adiabatic wall to assume zero heat transfer through the wall. Velocity boundary condition was applied at the inlet of the domain. The air inlet velocity was 0.5 m/s, which was determined from the experimental measurement. The recorded time series data of inlet temperature from the experiment was applied as the inlet temperature profile of the air in the CFD model. The outlet boundary condition was set as an outlet to atmospheric pressure (zero relative pressure). The k-epsilon turbulence model was used in the simulation to model the turbulent flow.
In this study, the air flow profile through the air duct did not change with time. Only the temperature changed with time. Also, the heat transfer occurred with few degrees Celsius temperature difference, and hence the effect of convection heat transfer on air flow field can be assumed negligible. That is why the simulation was done in two steps. In the first step, the fluid flow was solved in a steady-state condition. Once the fluid flow was established, the transient heat transfer equation was solved with 1-min time step to calculate the temperature distribution with time. This approach greatly reduced the computational time and facilitated the simulation of a longer period.

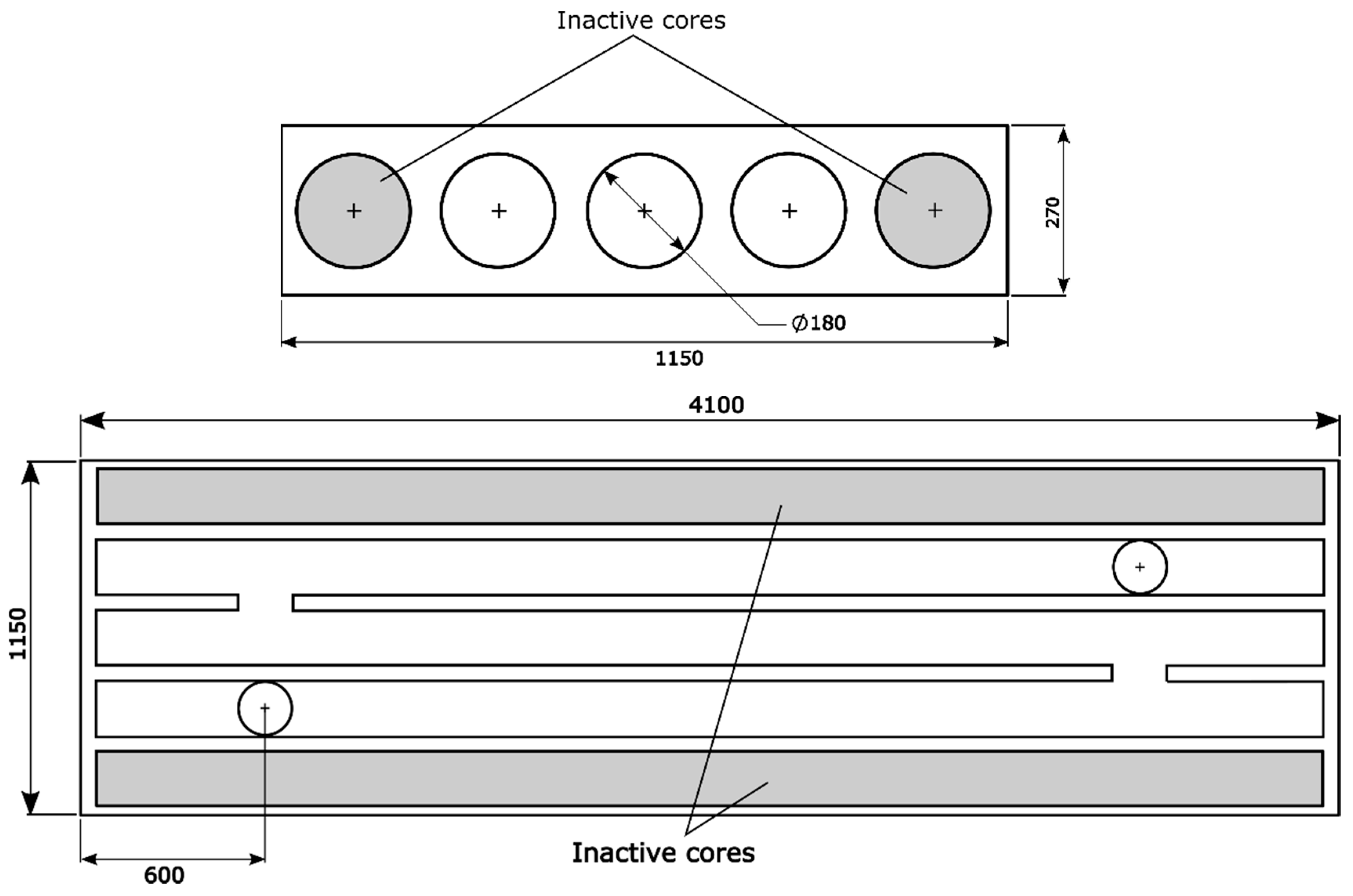
2.2.2. Computational Fluid Dynamics Model of the Hollow-Core Concrete Slab

A second CFD model of the hollow-core concrete slab was developed using the ANSYS® CFX model. There are many different sizes of the precast hollow-core slab. In this study, the geometry of the hollow-core concrete slab was built similar to the dimensions used in the experimental study of Winwood et al. [44]. In this hollow-core slab, three middle cores were active cores (i.e., air flowed only through three middle cores). They were interconnected sideways as shown in Figure 9. The two side cores were disconnected and remained idle. They were not used for the air flow. All the cores were closed at both ends.
The model was divided into two regions: the solid region (concrete) and the fluid region (air passage or cores). The mesh of these two regions is shown in Figure 10. The mesh consisted of 640,000 elements. The slab surface which contained the inlet and outlet boundary was assumed to interact with the conditioned room. In this CFD model, no indoor zone was considered. Instead, the surface was exposed to the same ambient temperature as the outlet temperature assuming that the room temperature would be the same as the outlet shortly. The convection heat transfer coefficient of the exposed surface was calculated using the equations of free convection from heated and cooled plate facing downward [45]. The calculated average value of the convection heat transfer coefficient was 1 W/m.K. because limited convection heat transfer was expected from the downward-facing surface due to the smaller temperature differences. The other surfaces of the slab were modeled as an adiabatic wall to limit the heat transfer in those directions.
The velocity of air at the inlet boundary was set to 1 m/s as suggested by Winwood et al. [8] for the hollow-core system. For the validation case, the temperature profile at inlet boundary was taken similar to the experimental inlet temperature of Winwood et al. [44]. Similar to the PCM–air duct model, the hollow-core slab model was solved in two steps. The first step was to solve the fluid dynamics problem in a steady-state simulation. Then, the transient heat transfer problem was solved in the second step. The time-step was set to 5 min, which is higher than the PCM–air duct model because there is no PCM in the slab. The k-epsilon model was used for turbulence modeling.

3. Results and Discussion

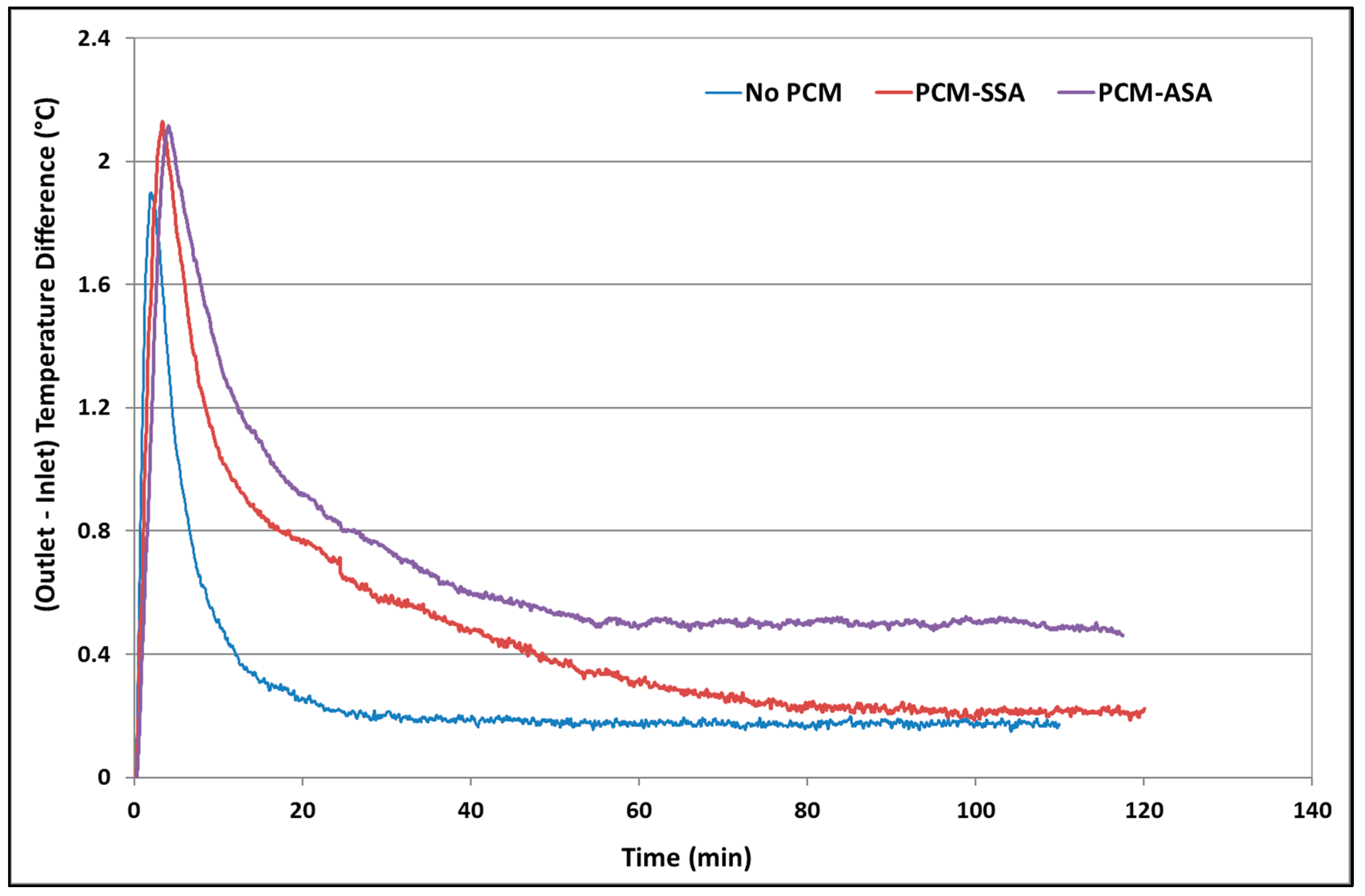
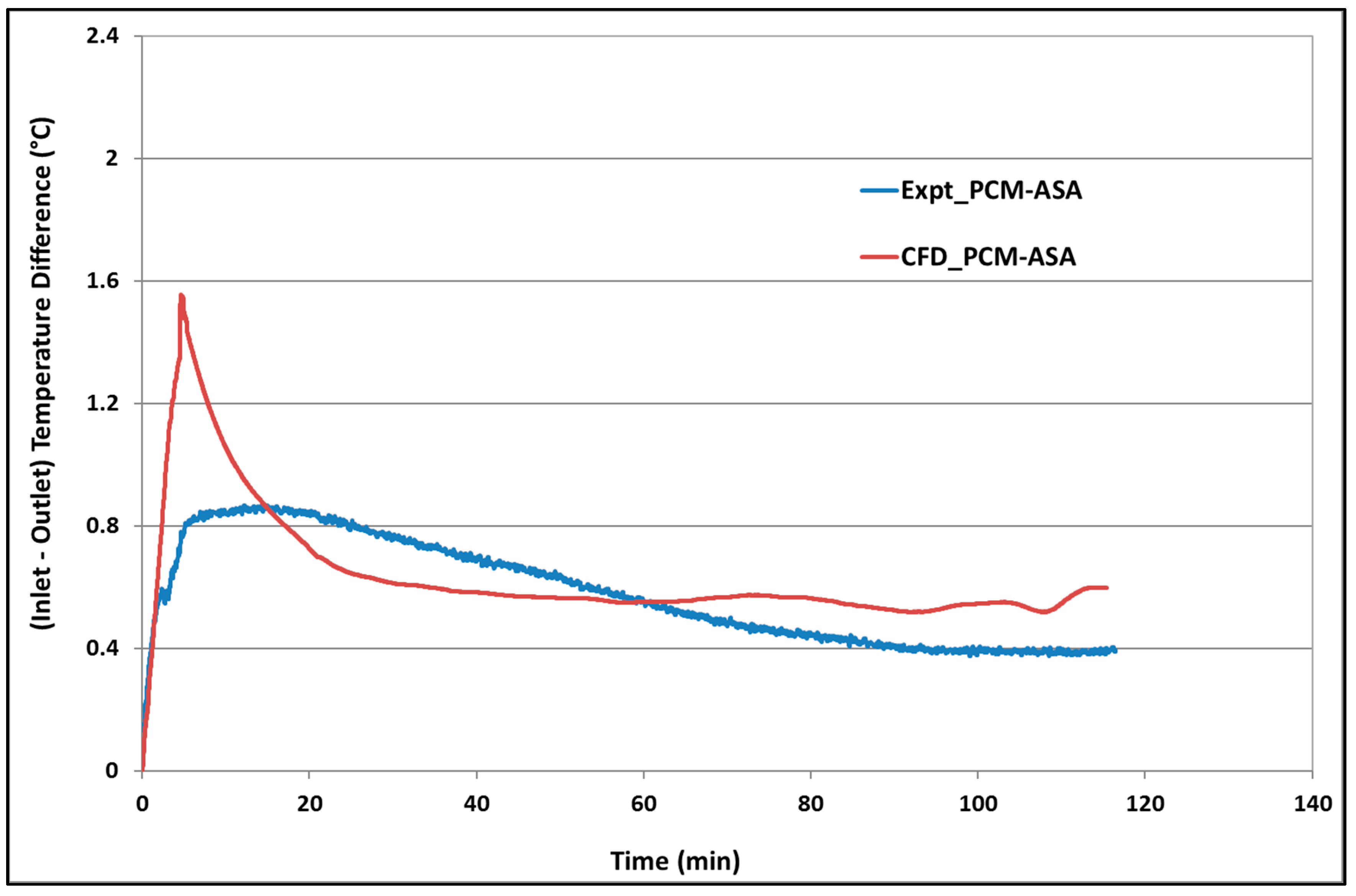
3.1. Experimental Results of PCM-Integrated Supply Air Duct

Figure 11 shows the difference between outlet and inlet temperatures for the three different PCM arrangements in cooling mode. In this mode, the inlet temperature was dropped from 27 °C to approximately 10 °C. In the beginning, there was a peak in the temperature difference for all three cases which represents the initial delay in outlet temperature in response to the inlet temperature. Afterward, the temperature difference dropped sharply in the No-PCM case, that is, outlet temperature closely followed the inlet temperature because there was no thermal storage or thermal mass in the air duct. In this case, ideally, the temperature difference should be zero. However, 0.18 °C difference was observed which might be due to some experimental noises (e.g., leakage, sensor accuracy, etc.).
Figure 11 shows that the temperature difference was higher than 0.5 °C for 10 min, 38 min, and 54 min for no PCM, PCM-SSA, and PCM-ASA cases, respectively. The PCM-SSA and PCM-ASA cases exhibited slower descent in the temperature difference plot due to the presence of PCM. In the cooling mode, when inlet temperature of the air dropped from 27 °C to 10 °C, the PCM changed its phase from liquid to solid. During this phase change, it released heat and warmed the flowing air, which resulted in an outlet air temperature higher than the inlet temperature. Although the volumetric capacity of PCM was the same in both PCM-SSA and PCM-ASA cases, the temperature difference was higher and was maintained for a longer period in the PCM-ASA case. This occurred due to the difference in PCM application methods in those two cases. In the PCM-SSA case, the BioPCM™ sheet was placed on the bottom surface of the air duct (Figure 5a). This arrangement allowed PCM to interact with the air only from one side. On the other hand, in the PCM-ASA case, the PCM was laid out on all the four surfaces (Figure 5b) which increased interaction of PCM with the air in all four directions. That is why this arrangement maintained higher temperature difference for a longer period compared to the PCM-SSA case.
In the heating mode, the inlet temperature was raised from 12 °C to 32 °C, and the corresponding outlet temperature was recorded. Figure 12 shows the temperature difference between inlet and outlet for the three cases in heating mode. The inlet temperature was higher than that of the outlet, and that is why “inlet–outlet” difference is shown in Figure 12. After the peak of the initial delay, the temperature difference of the No-PCM case fell sharply to approximately 0.2 °C as there was no PCM material to keep the difference. The temperature difference was higher than 0.5 °C for 9 min, 36 min, and 69 min for no PCM, PCM-SSA, and PCM-ASA cases, respectively. Similar to the cooling mode, PCM-ASA demonstrated higher temperature difference for a longer period compared to the PCM-SSA case. In this case, PCM changed from solid to liquid by taking the heat from the flowing air which eventually lowered the temperature at the outlet.

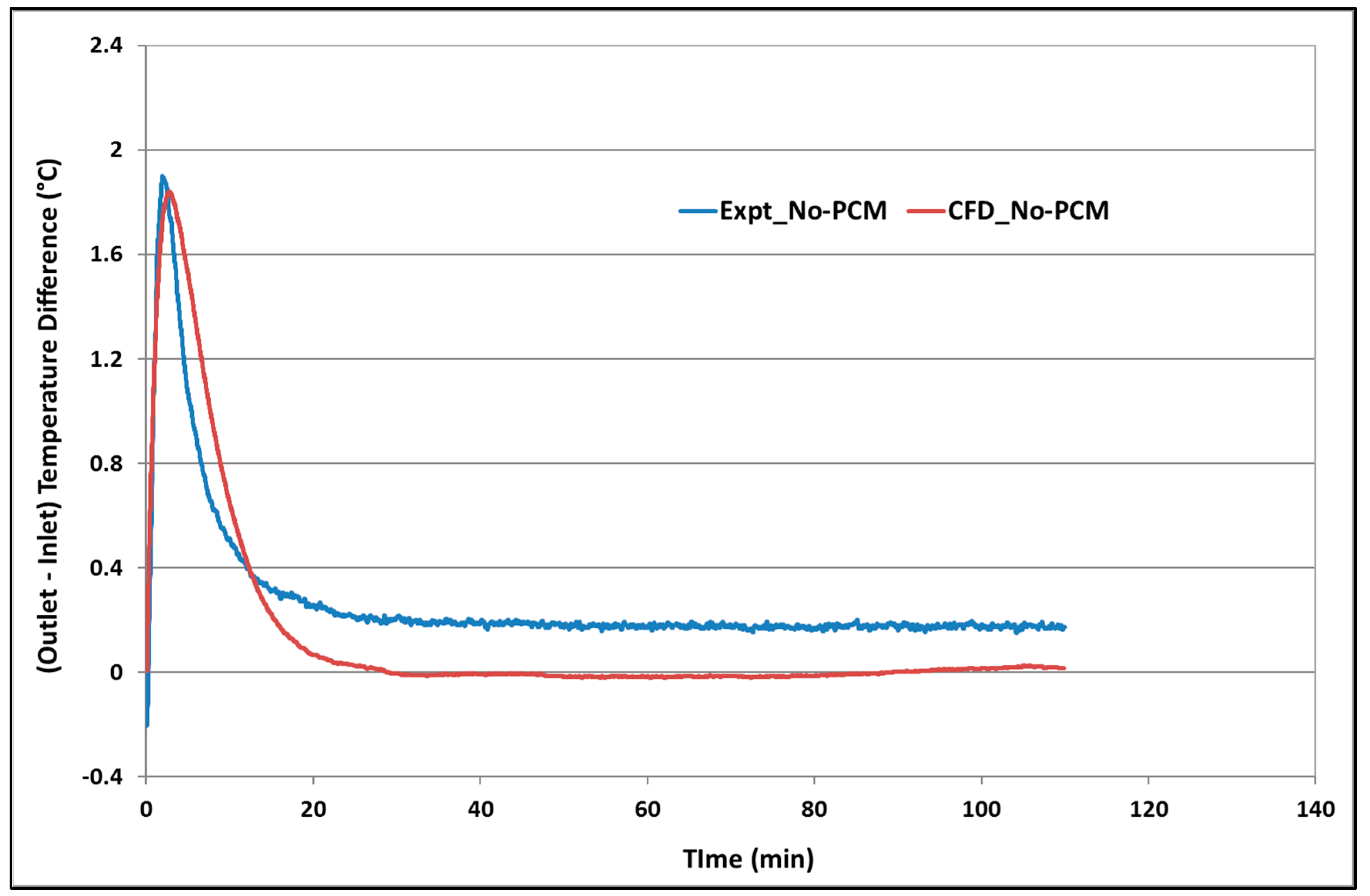
3.2. Validation of CFD Model of PCM–Air Duct

The developed CFD model of the PCM–air duct was validated by comparing the simulation results with the experimental data. The PCM-ASA was observed to be performing better in the experimental study than the PCM-SSA case. That is why CFD models for No-PCM and PCM-ASA cases were developed and validated here. Figure 13 shows the comparison of experimental and simulation temperature difference for the No-PCM case in cooling mode. The simulation profile captured the initial delay (up to 13 min) very close to the experimental one. Afterward, the simulation temperature difference dropped to zero, which is more reasonable as there was no PCM to influence the air temperature. On the other hand, the experimental profile stayed at 0.18 °C, keeping this difference with the simulation all the way. This might be due to some experimental noises coming from the sensors, leakage, and so forth, as explained in the previous section. The overall RMS error between experimental result and simulation was 0.195 °C. Figure 14 shows the comparison of experimental and simulation temperature difference for the No-PCM case in heating mode. The initial delay (up to 15 min) was sharper in the experiment than the simulation and the difference between them was slightly higher than the cooling mode. The average error was 0.4 °C with maximum 0.8 °C in this range. As expected, after the delay, the simulation gradually dropped to zero. The RMS error between simulation and experiment data was 0.24 °C.
The experimental and simulation results of PCM-ASA configuration in cooling mode are presented in Figure 15. From the figure, it is apparent that both the experiment and the simulation profiles followed a similar trend. The initial delay in the simulation showed a lower peak than that of the experimental result. After this, both experimental and simulation profiles of temperature difference gradually dropped to around 0.5 °C and maintained it until the end. The average error in simulation results was about 0.09 °C, although the maximum error was about 0.5 °C, which was near the peak of the delay period. The overall RMS error was 0.14 °C.
Figure 16 shows the comparison of results for the same configuration in heating mode. Although the peak of the initial delay was missing in the experimental result, it is present in the simulation temperature difference profile. After the peak, the simulation profile gradually reduced to around 0.5 °C, where the experimental result further dropped to 0.4 °C. The average disagreement between the experiment and the simulation results was 0.13 °C with the maximum of 0.8 °C, which was near the initial delay period. The overall RMS error was 0.17 °C.
From the above discussion, it is evident that the developed CFD model can be used to evaluate the performance of PCM-integrated air ducts at various inlet air conditions with good accuracy.

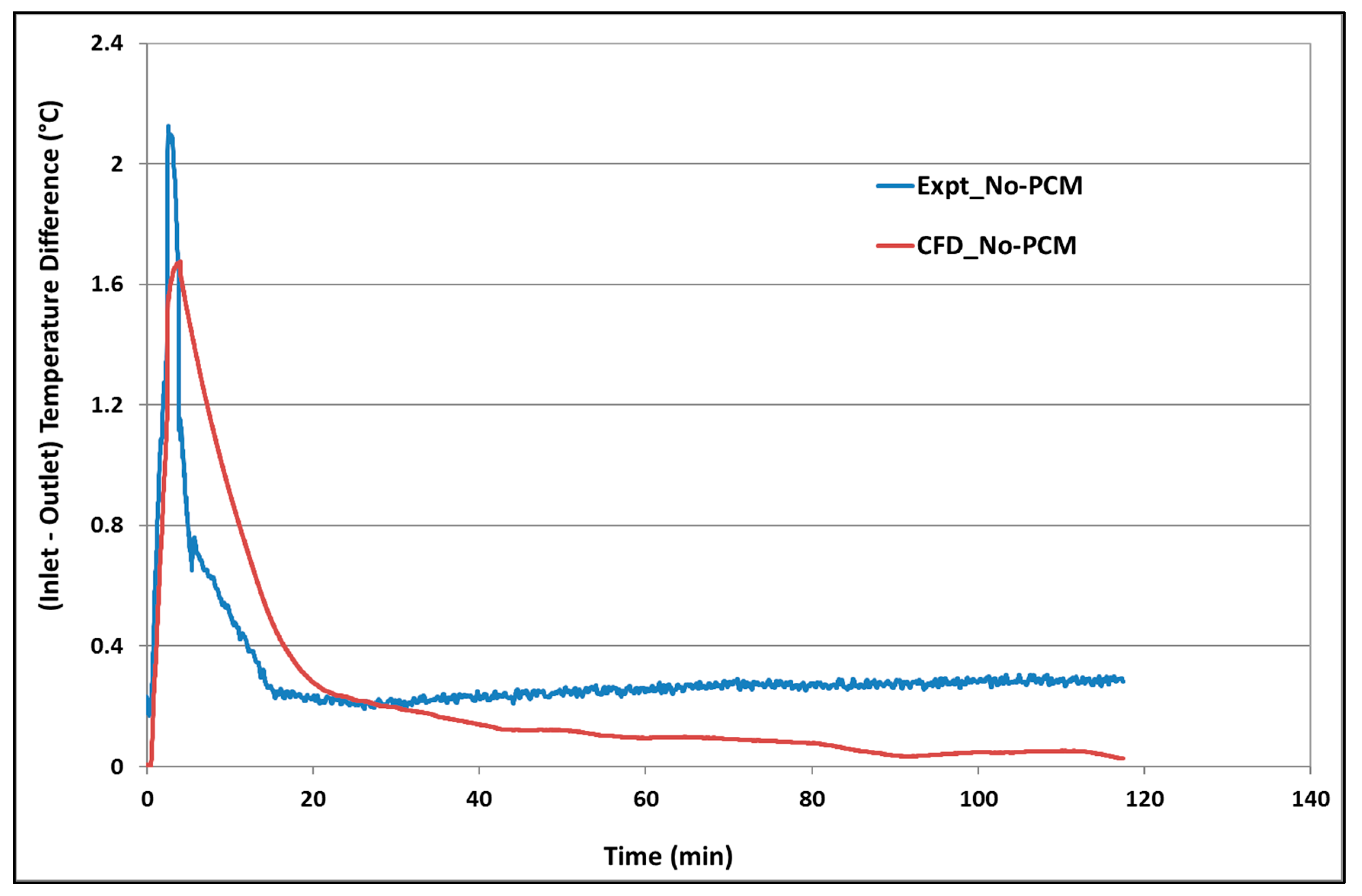
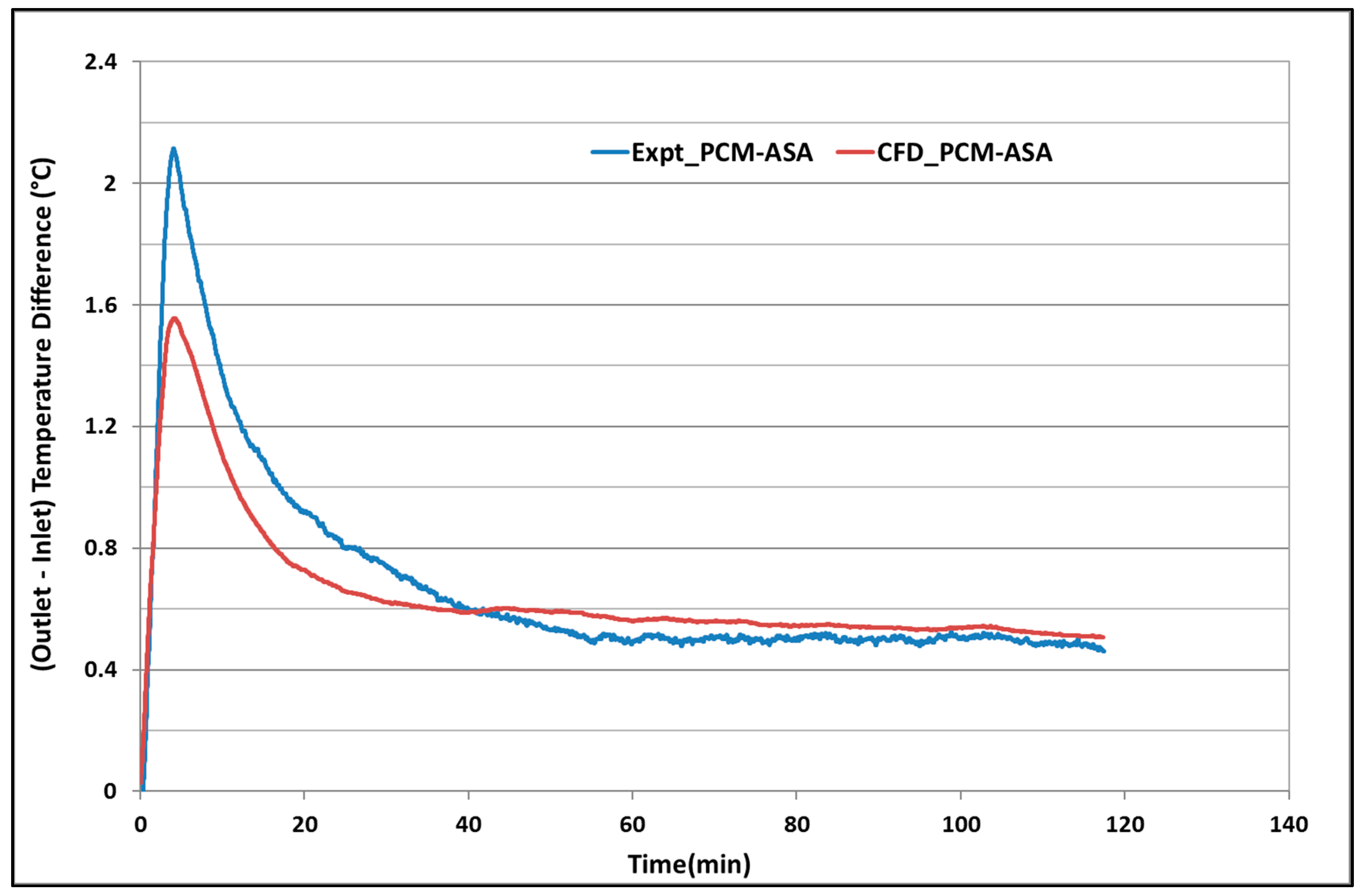
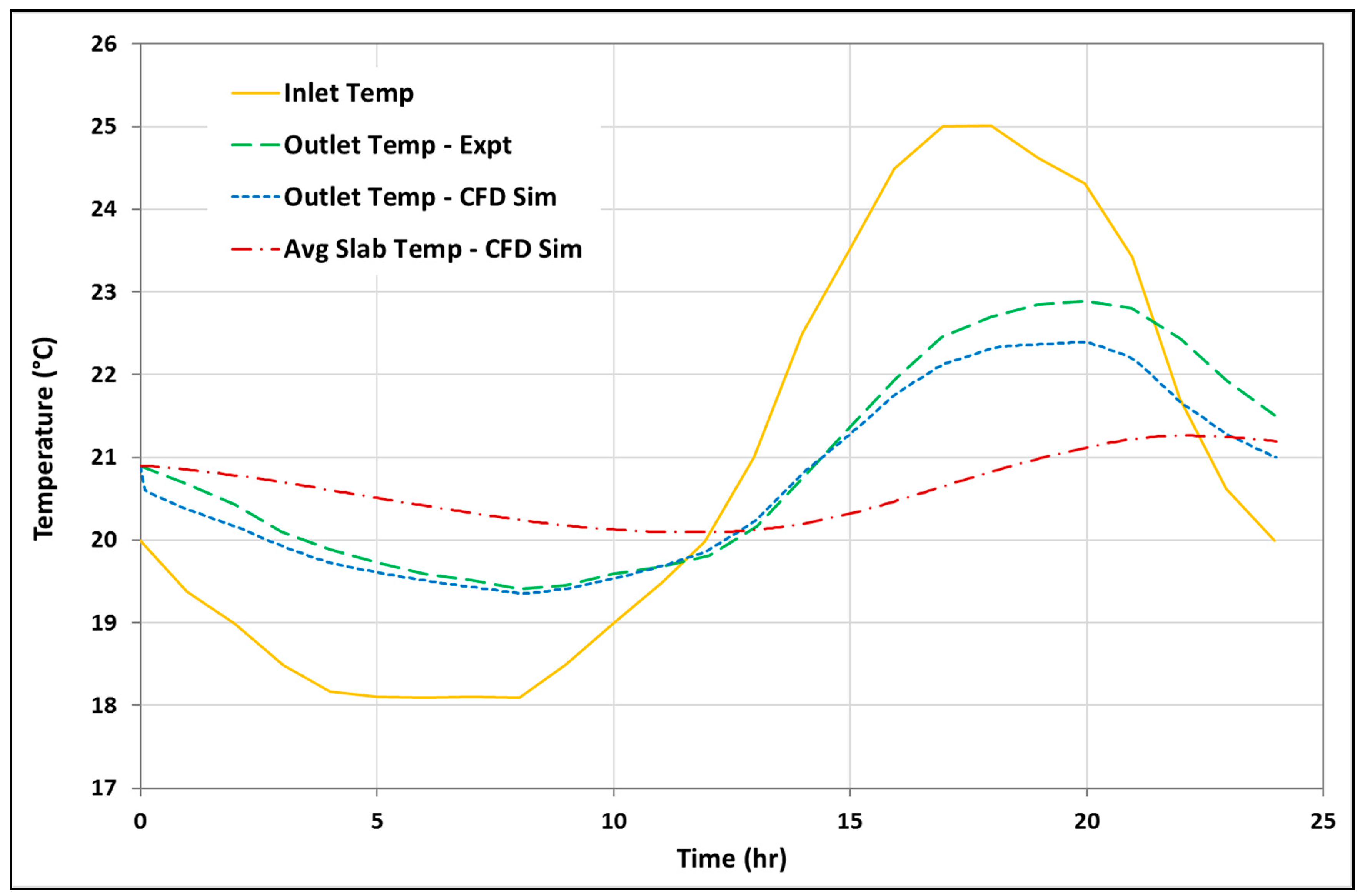
3.3. Validation of Hollow-Core Slab CFD Model

The developed CFD model of the hollow-core slab was validated by using the experimental data from Winwood et al. [44]. The slab outlet temperatures from experiment and simulation are presented in Figure 17. The outlet temperature was calculated by taking a surface average of temperatures at the simulated outlet surface. Figure 17 shows that the simulated outlet temperature agreed well with the experimental outlet temperature profile. The average difference in temperature of simulation and experiment was 0.24 °C with the maximum difference of 0.77 °C. The RMS error was 0.32 °C.

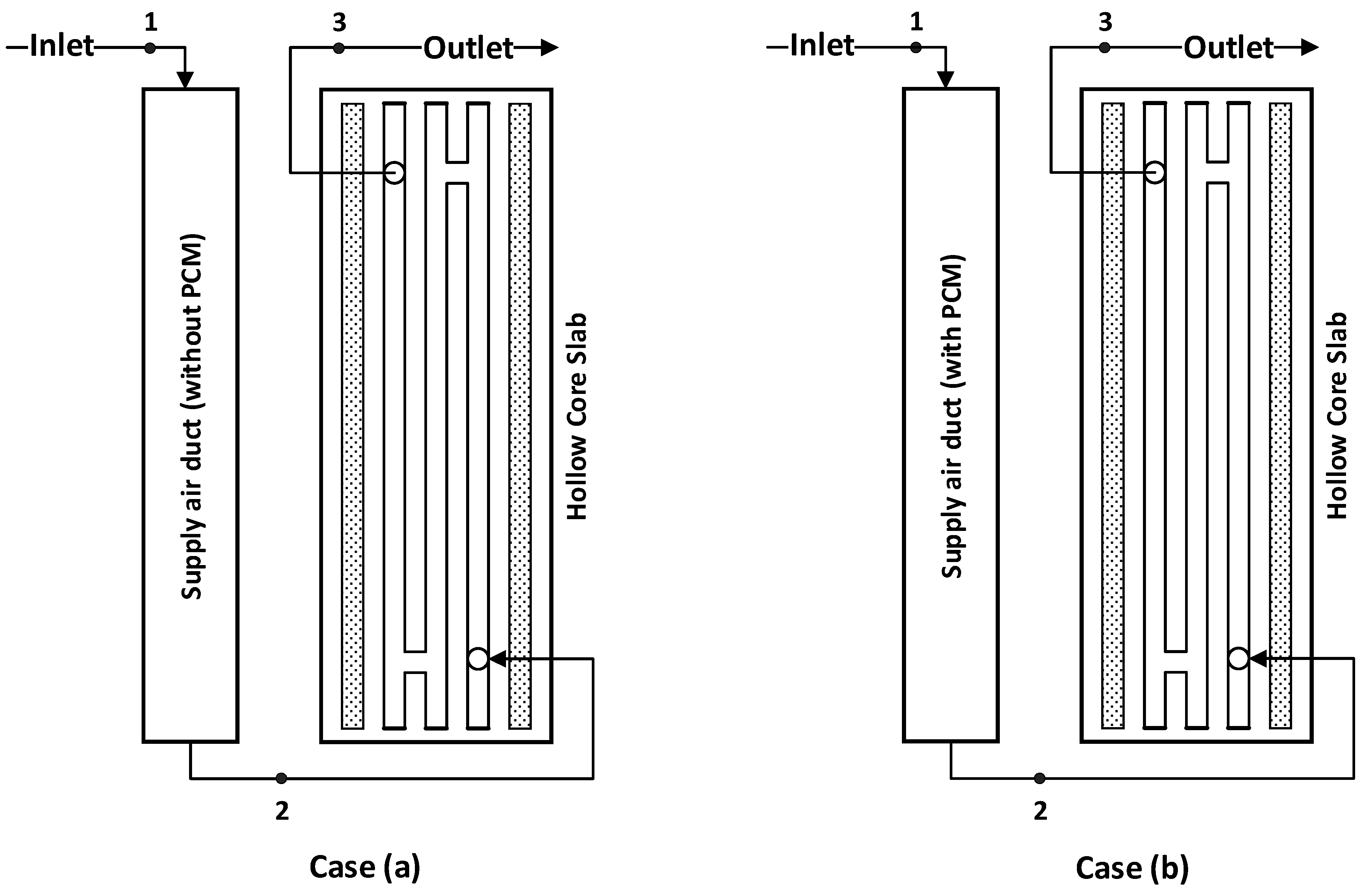
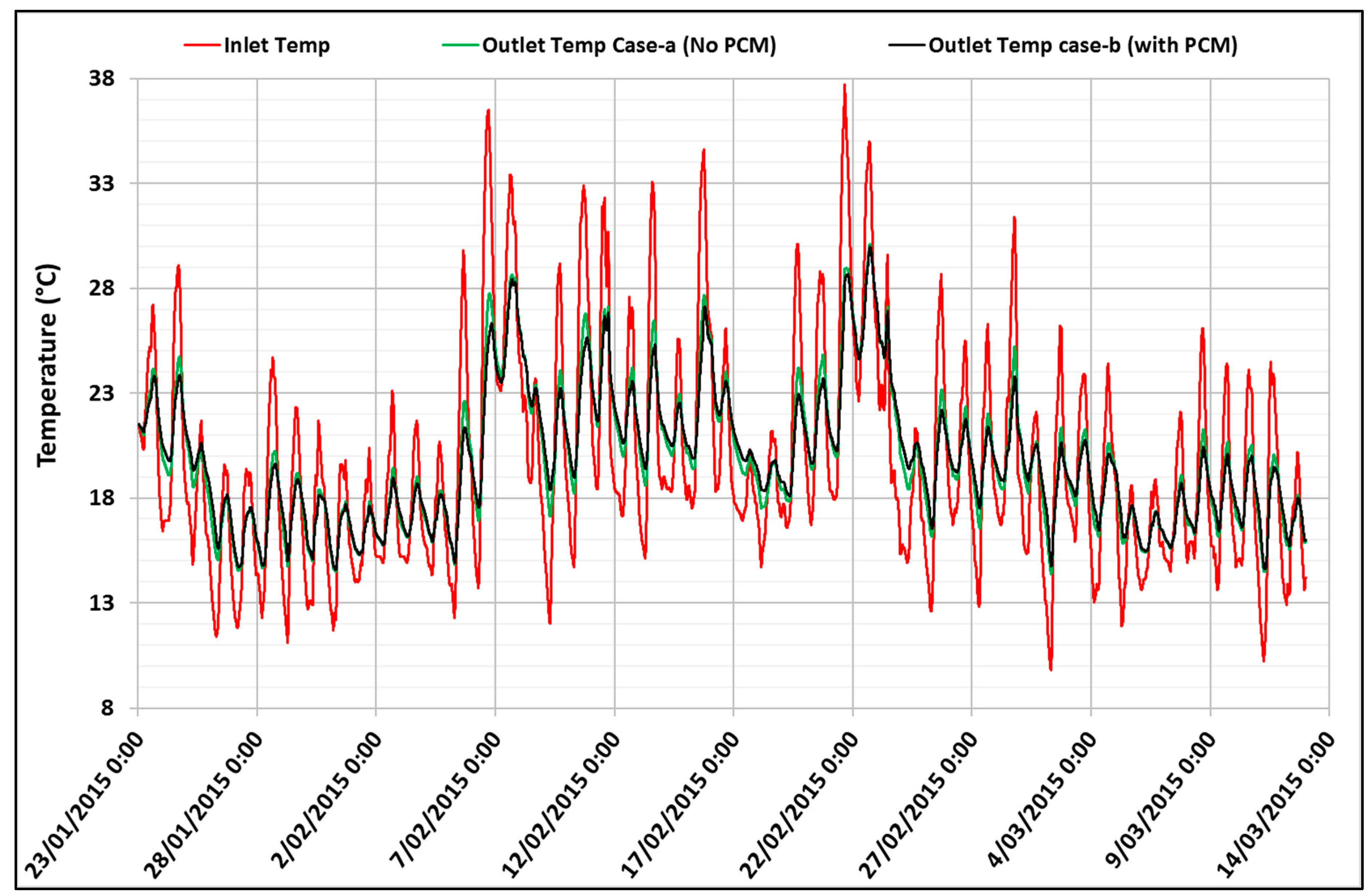
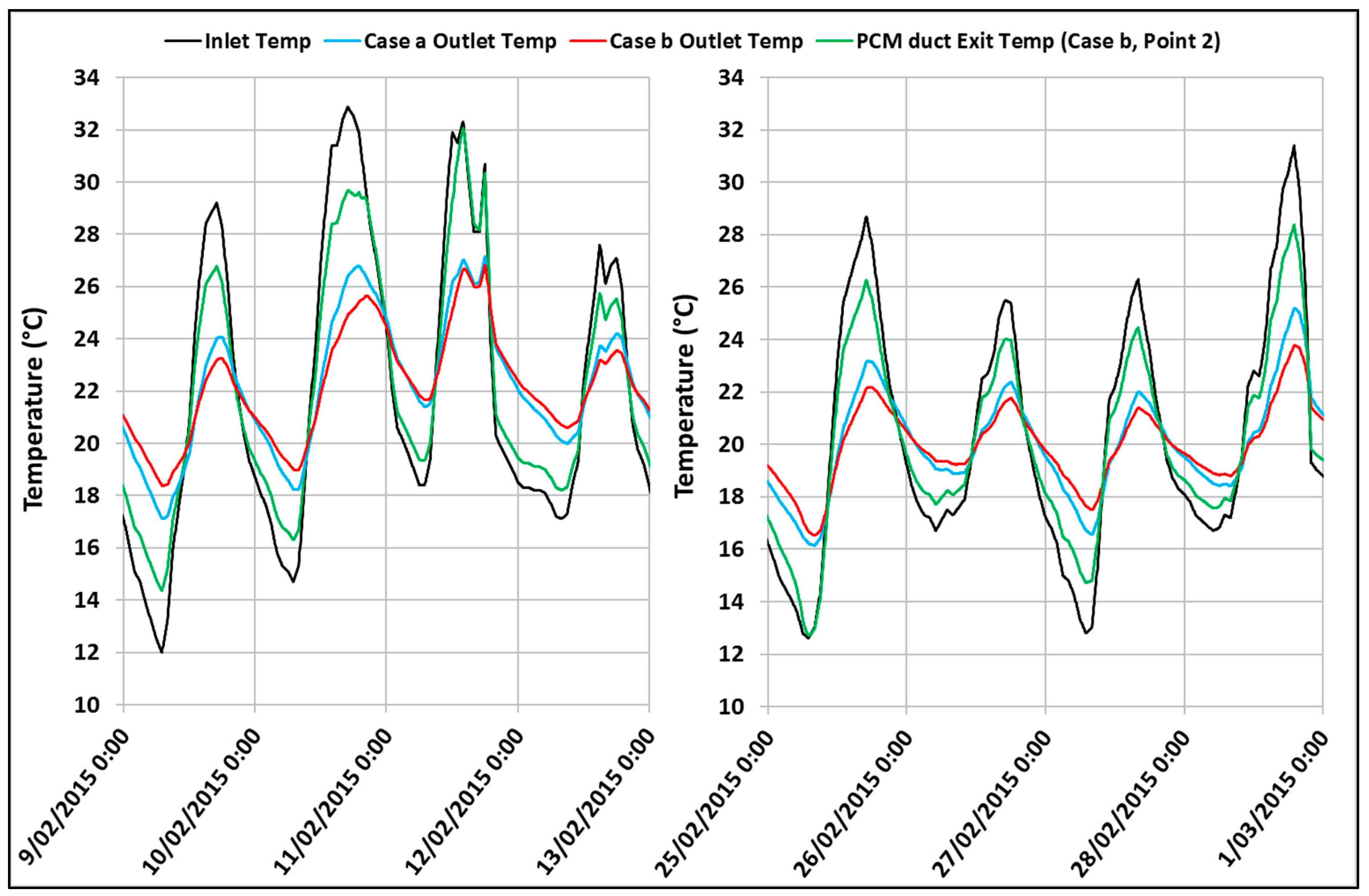
3.4. Scenario Analysis Using Different Weather Conditions

After validation, the CFD models were used to evaluate the effectiveness of PCM in a hollow-core system under Melbourne weather conditions. Simulations were carried out for 49 days using Melbourne summer weather from 25 January to 13 March 2015. In this simulation, a 0.3 m × 0.3 m × 6 m supply air duct was used to supply air through a hollow-core slab. The length of the supply air duct was taken as 6 m which is sufficient to supply air in the hollow-core slabs of a medium-size office room. PCM was applied to all surfaces of the supply air duct at 1.5 kg/m2. Two different configurations were simulated and compared as shown in Figure 18:
  • Case-a (No PCM): Outdoor air passes through the air duct and then the hollow-core system into the room. The outlet temperature profile from the supply air duct simulation was used as the inlet temperature of the hollow-core slab simulation model.
  • Case-b (With PCM): Outdoor air passes through the PCM-incorporated supply air duct and then the hollow-core system into the room. The outlet temperature profile from the PCM-incorporated supply air duct simulation was used as the inlet temperature of the hollow-core slab simulation model. In the simulation of the PCM-incorporated supply air duct, the PCM-ASA configuration was chosen as PCM effectiveness was maximum in this arrangement.
Outdoor air temperature of the simulated period was applied at the inlet of Case-a and Case-b. Figure 19 presents the simulated outlet temperatures of the two cases. It is evident from this figure that integration of PCM in the hollow-core system can result in a higher reduction of supply air temperature. To describe the results clearly and in detail, simulation results of 10 days have been seperately presented in Figure 20. The figure also shows the temperature at the outlet of PCM-incorporated supply air duct (point 2 in Figure 18) for Case-b.
Figure 20 shows that on 10th of February, the reduction of maximum air temperature was 1.15 °C higher in Case-b compared to Case-a. In Case-a and Case-b, the maximum air temperature was reduced by 6.1 °C and 7.25 °C, respectively. A similar trend was observed for all simulated days. However, the effectiveness of PCM in reducing the maximum daytime air temperature depends on the previous night’s minimum air temperature. Figure 20 shows that on 11 February, the difference in maximum air temperature for Case-a and Case-b was only 0.32 °C, which means PCM was not effective on that day. The exit temperature of the PCM-incorporated supply air duct (Case-b, point 1) closely followed the outdoor air temperature at the inlet. This occurred due to the fact that the minimum night air temperature on 11 February was higher than 18 °C (solidification point of PCM) which inhibited complete solidification of PCM. As a result, the PCM could not effectively contribute to the reduction of supply air temperature.
Table 1 presents a summary of the effectiveness of the hollow-core system in reducing indoor temperature fluctuations (reducing maximum temperature and increasing minimum temperature) with and without the application of PCM. The table shows that integration of PCM resulted in an increase of number of days with maximum temperature reduction greater than 4 °C. In Case-b, the maximum temperature reduced by 4 °C for 51% of the simulated days compared to 38.8% in Case-a. The minimum temperature also increased by 4 °C for 20.4% of the simulated days in Case-b compared to only 8.2% in Case-a. Understandably, the reduction in maximum temperature in other temperature ranges below 4 °C was higher in Case-a compared to Case-b. The integration of PCM resulted in more days with higher temperature reductions which caused a shift in “% of days” from lower range to higher range.
Moreover, in Case-a, the reduction in air temperature fluctuation occurred due to the heat transfer between hollow-core concrete slab and supply air, whereas in Case-b, both the PCM and hollow-core slab contributed to the reduction of supply air temperature fluctuation. Figure 21 shows that the effectiveness of the combined PCM–air duct–hollow-core slab system was not equal to the individual performance of the PCM–air duct and hollow-core concrete slab for a given inlet temperature swing (point 1 in both Case-a and Case-b as shown in Figure 18). The reduction in peak air temperature in Case-b was lower than the summation of peak temperature reduction in Case-a and PCM-incorporated supply air duct only (Case-b, T2 – T1 as shown in Figure 18). This finding suggests that the reduction in temperature swing due to the thermal mass of the slab was not the same for the two cases. For example, on 13 February, the PCM-incorporated air duct alone reduced the peak temperature by 3.28 °C. However, the difference between the peak outlet air temperatures of Case-a and Case-b was only 1.12 °C, which is 2.16 °C lower than the peak air temperature reduction by PCM only. In Case-b, the combination of PCM-incorporated air duct and hollow-core slab reduced the peak air temperature by 7.77 °C, which means the hollow-core slab reduced the peak air temperature by (7.77 °C–3.28 °C) 4.49 °C in this case. On the other hand, in Case-a, the hollow-core slab reduced the peak air temperature by 6.65 °C. This means that the slab in Case-b was less efficient.
During the simulated period, the average peak air temperature reduction by PCM air duct only was 1.21 °C. The average reduction of peak air temperature by the combination of PCM-incorporated air duct and hollow-core slab (Case-b) was 4.07 °C, which means, on average, the hollow-core slab (in Case-b) reduced the peak air temperature by (4.07 °C–1.21 °C) 2.86 °C. On the other hand, the average reduction of peak air temperature by hollow-core slab in Case-a was 3.62 °C. Hence, on average, the hollow-core slab was 21% less efficient in reducing peak air temperature with the presence of PCM. This may have occurred due to the difference between the average slab temperature and the corresponding slab inlet temperature swing. The higher the difference, the more would be the heat transfer between the slab and the air passing through it. The presence of PCM in the supply air duct resulted in a precooling effect which reduced the amplitude of slab inlet temperature swing in Case-b. Hence, the difference between the average slab temperature and the slab inlet temperature swing was lower in Case-b, which reduced the functionality of the hollow-core slab in Case-b. From the simulation, the calculated daytime average slab temperatures on 13th February were 22.09 °C and 22.03 °C for Case-a and Case-b, respectively. However, the difference between the peak slab inlet air temperature and average hollow-core slab temperature (point 2 in Case-a and Case-b) during the daytime were 11.1 °C and 7.77 °C for Case-a and Case-b, respectively. In Case-b, the integration of PCM resulted in a precooling effect which reduced the peak slab inlet air temperature by 3.28 °C. Hence, due to lower temperature difference, the hollow-core slab was less effective in reducing the air temperature in Case-b compared to Case-a.

4. Conclusions

This study explored the effectiveness of PCM when applied in the supply air duct of a hollow-core ventilation system. Validated computational fluid dynamic models of a PCM-incorporated supply air duct and hollow-core slab were used in the investigation.
This study showed that integration of PCM in the supply air duct of a hollow-core system reduced diurnal (day–night) temperature extremes. The magnitude of diurnal temperature fluctuation reduction depends on PCM configuration inside the air duct. The reduction was higher and was maintained for a longer period in PCM-ASA (PCM applied to all four sides) case compared to PCM-SSA case (PCM applied to the single surface). In cooling mode, the difference between inlet and outlet temperature was higher than 0.5 °C for 10 min, 38 min, and 54 min for no-PCM, PCM-SSA, and PCM-ASA cases, respectively. In heating mode, the temperature difference was higher than 0.5 °C for 9 min, 36 min, and 69 min for no-PCM, PCM-SSA, and PCM-ASA cases, respectively. This occurred due to the difference in interaction mechanism between the air and the PCM in these two cases. Although the surface area and the amount of the PCM for both cases were the same, the interaction between the PCM and the air in PCM-ASA takes place in all four directions, which allows more air particles to interact with PCM than the PCM-SSA case in a given volume of air.
The integration of PCM resulted in an increase of number of days with maximum temperature reduction greater than 4 °C during the simulated period. In the combined PCM–air duct–hollow-core slab system, the maximum temperature reduced by 4 °C for 51% of the simulated days compared to 38.8% in the hollow-core slab only case. The minimum temperature also increased by 4 °C for 20.4% of the simulated days in combined PCM–air duct–hollow-core slab system compared to only 8.2% in hollow-core slab only case.
The effectiveness of the combined PCM–air duct–hollow-core slab system was not equal to the individual performance of the PCM–air duct and hollow-core concrete slab for a given inlet temperature fluctuation. Although the PCM-incorporated supply air duct significantly reduced the air temperature fluctuation, it was not realized fully in the PCM-integrated hollow-core slab system. During the simulated period, the average peak air temperature reduction by PCM air duct only was 1.21 °C. However, the average reduction of peak air temperature by the combination of PCM-incorporated air duct and hollow-core slab was 4.07 °C, which means, on average, the hollow-core slab (in Case-b) reduced the peak air temperature by (4.07 °C–1.21 °C) 2.86 °C. On the other hand, the average reduction of peak air temperature by hollow-core slab only case was 3.62 °C. Hence, on average, the hollow-core slab was 21% less efficient in reducing peak air temperature with the presence of PCM. The reduction of temperature fluctuation by the hollow-core slab depends on the difference between the amplitude of inlet temperature swing and the average hollow-core slab temperature. The higher the difference, the more would be the heat transfer between the slab and the air passing through it. The presence of PCM in the supply air duct resulted in a precooling effect which reduced the amplitude of slab inlet temperature swing. Hence, the difference between the average slab temperature and the slab inlet temperature swing was lower, which reduced the functionality of the hollow-core slab in the presence of PCM.
Future study is recommended to explore the optimum PCM temperature for hollow-core slab ventilation systems as well as optimize the hollow-core system so that the thermal mass of PCM and hollow-core slabs can be utilized more efficiently to reduce the temperature fluctuations further.

Author Contributions

H.J. conceptualized the paper and developed simulation models using CFD and EnergyPlus and validated it. M.A. designed the experimental setup and conducted the experimental studies. J.S. supervised the whole work, reviewed and edited the draft.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lucon, O.; Ürge-Vorsatz, D.; Zain Ahmed, A.; Akbari, H.; Bertoldi, P.; Cabeza, L.F.; Eyre, N.; Gadgil, A.; Harvey, L.D.D.; Jiang, Y.; et al. Buildings. In Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Brunner, P.E., Kriemann, B., Savolainen, J., et al., Eds.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
  2. Levine, M.; Ürge-Vorsatz, D.; Blok, K.; Geng, L.; Harvey, D.; Lang, S.; Levermore, G.; Mongameli Mehlwana, A.; Mirasgedis, S.; Novikova, A.; et al. Residential and commercial buildings. In Climate Change 2007: Mitigation. Contribution of Working Group III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
  3. Navarro, L.; de Gracia, A.; Colclough, S.; Browne, M.; McCormack, S.J.; Griffiths, P.; Cabeza, L.F. Thermal energy storage in building integrated thermal systems: A review. Part 1. active storage systems. Renew. Energy 2016, 88, 526–547. [Google Scholar] [CrossRef] [Green Version]
  4. Rinaldi, N. Thermal Mass, Night Cooling and Hollow Core Ventilation System as Energy Saving Strategies in Buildings. In KTH Architecture and The Built Environment; KTH Royal Institute of Technology: Stockholm, Sweden, 2009. [Google Scholar]
  5. Winwood, R.; Benstead, R.; Edwards, R. Advanced Fabric Energy Storage I: Review. Build. Serv. Eng. Res. Technol. 1997, 18, 1–6. [Google Scholar] [CrossRef]
  6. Xu, X.; Yu, J.; Wang, S.; Wang, J. Research and application of active hollow core slabs in building systems for utilizing low energy sources. Appl. Energy 2014, 116, 424–435. [Google Scholar] [CrossRef]
  7. Ren, M.J.; Wright, J.A. A ventilated slab thermal storage system model. Build. Environ. 1998, 33, 43–52. [Google Scholar] [CrossRef]
  8. Winwood, R.; Benstead, R.; Edwards, R. Advanced fabric energy storage II: Computational fluid dynamics modelling. Build. Serv. Eng. Res. Technol. 1997, 18, 7–16. [Google Scholar] [CrossRef]
  9. Winwood, R.; Benstead, R.; Edwards, R. Advanced fabric energy storage IV: Experimental monitoring. Build. Serv. Eng. Res. Technol. 1997, 18, 25–30. [Google Scholar] [CrossRef]
  10. Zmeureanu, R.; Fazio, P. Thermal performance of a hollow core concrete floor system for passive cooling. Build. Environ. 1988, 23, 243–252. [Google Scholar] [CrossRef]
  11. Willis, S.; Wilkins, J. Mass Appeal. Build. Serv. J. 1993, 15, 25–28. [Google Scholar]
  12. Russell, M.B.; Surendran, P.N. Influence of active heat sinks on fabric thermal storage in building mass. Appl. Energy 2001, 70, 17–33. [Google Scholar] [CrossRef]
  13. Corgnati, S.P.; Kindinis, A. Thermal mass activation by hollow core slab coupled with night ventilation to reduce summer cooling loads. Build. Environ. 2007, 42, 3285–3297. [Google Scholar] [CrossRef]
  14. Chae, Y.T.; Strand, R.K. Modeling ventilated slab systems using a hollow core slab: Implementation in a whole building energy simulation program. Energy Build. 2013, 57, 165–175. [Google Scholar] [CrossRef]
  15. Castell, A.; Martorell, I.; Medrano, M.; Pérez, G.; Cabeza, L.F. Experimental study of using PCM in brick constructive solutions for passive cooling. Energy Build. 2010, 42, 534–540. [Google Scholar] [CrossRef]
  16. Silva, T.; Vicente, R.; Soares, N.; Ferreira, V. Experimental testing and numerical modelling of masonry wall solution with PCM incorporation: A passive construction solution. Energy Build. 2012, 49, 235–245. [Google Scholar] [CrossRef]
  17. Athienitis, A.K.; Liu, C.; Hawes, D.; Banu, D.; Feldman, D. Investigation of the thermal performance of a passive solar test-room with wall latent heat storage. Build. Environ. 1997, 32, 405–410. [Google Scholar] [CrossRef]
  18. Behzadi, S.; Farid, M.M. Experimental and numerical investigations on the effect of using phase change materials for energy conservation in residential buildings. HVAC&R Res. 2011, 17, 366–376. [Google Scholar]
  19. Ahmad, M.; Bontemps, A.; Sallée, H.; Quenard, D. Thermal testing and numerical simulation of a prototype cell using light wallboards coupling vacuum isolation panels and phase change material. Energy Build. 2006, 38, 673–681. [Google Scholar] [CrossRef]
  20. Ascione, F.; Bianco, N.; De Masi, R.F.; de’ Rossi, F.; Vanoli, G.P. Energy refurbishment of existing buildings through the use of phase change materials: Energy savings and indoor comfort in the cooling season. Appl. Energy 2014, 113, 990–1007. [Google Scholar] [CrossRef]
  21. Ramakrishnan, S.; Wang, X.; Sanjayan, J.; Wilson, J. Thermal performance assessment of phase change material integrated cementitious composites in buildings: Experimental and numerical approach. Appl. Energy 2017, 207, 654–664. [Google Scholar] [CrossRef]
  22. Ramakrishnan, S.; Wang, X.; Sanjayan, J.; Petinakis, E.; Wilson, J. Development of thermal energy storage cementitious composites (TESC) containing a novel paraffin/hydrophobic expanded perlite composite phase change material. Sol. Energy 2017, 158, 626–635. [Google Scholar] [CrossRef]
  23. Ramakrishnan, S.; Sanjayan, J.; Wang, X.; Alam, M.; Wilson, J. A novel paraffin/expanded perlite composite phase change material for prevention of PCM leakage in cementitious composites. Appl. Energy 2015, 157, 85–94. [Google Scholar] [CrossRef]
  24. Entrop, A.G.; Brouwers, H.J.H.; Reinders, A.H.M.E. Experimental research on the use of micro-encapsulated Phase Change Materials to store solar energy in concrete floors and to save energy in Dutch houses. Sol. Energy 2011, 85, 1007–1020. [Google Scholar] [CrossRef]
  25. Hunger, M.; Entrop, A.G.; Mandilaras, I.; Brouwers, H.J.H.; Founti, M. The behavior of self-compacting concrete containing micro-encapsulated Phase Change Materials. Cem. Concr. Compos. 2009, 31, 731–743. [Google Scholar] [CrossRef]
  26. Jamil, H.; Alam, M.; Sanjayan, J.; Wilson, J. Investigation of PCM as retrofitting option to enhance occupant thermal comfort in a modern residential building. Energy Build. 2016, 133, 217–229. [Google Scholar] [CrossRef]
  27. Alam, M.; Jamil, H.; Sanjayan, J.; Wilson, J. Energy saving potential of phase change materials in major Australian cities. Energy Build. 2014, 78, 192–201. [Google Scholar] [CrossRef]
  28. Sage-Lauck, J.S.; Sailor, D.J. Evaluation of phase change materials for improving thermal comfort in a super-insulated residential building. Energy Build. 2014, 79, 32–40. [Google Scholar] [CrossRef]
  29. Ramakrishnan, S.; Wang, X.; Sanjayan, J.; Wilson, J. Thermal performance of buildings integrated with phase change materials to reduce heat stress risks during extreme heatwave events. Appl. Energy 2017, 194, 410–421. [Google Scholar] [CrossRef]
  30. Chaiyat, N. Energy and economic analysis of a building air-conditioner with a phase change material (PCM). Energy Convers. Manag. 2015, 94, 150–158. [Google Scholar] [CrossRef]
  31. Mazo, J.; Delgado, M.; Marin, J.M.; Zalba, B. Modeling a radiant floor system with Phase Change Material (PCM) integrated into a building simulation tool: Analysis of a case study of a floor heating system coupled to a heat pump. Energy Build. 2012, 47, 458–466. [Google Scholar] [CrossRef]
  32. Moreno, P.; Solé, C.; Castell, A.; Cabeza, L.F. The use of phase change materials in domestic heat pump and air-conditioning systems for short term storage: A review. Renew. Sustain. Energy Rev. 2014, 39, 1–13. [Google Scholar] [CrossRef]
  33. Real, A.; García, V.; Domenech, L.; Renau, J.; Montés, N.; Sánchez, F. Improvement of a heat pump based HVAC system with PCM thermal storage for cold accumulation and heat dissipation. Energy Build. 2014, 83, 108–116. [Google Scholar] [CrossRef]
  34. Alam, M.; Sanjayan, J.; Zou, P.X.W.; Ramakrishnan, S.; Wilson, J. Evaluating the passive and free cooling application methods of phase change materials in residential buildings: A comparative study. Energy Build. 2017, 148, 238–256. [Google Scholar] [CrossRef]
  35. Weinläder, H.; Körner, W.; Strieder, B. A ventilated cooling ceiling with integrated latent heat storage—Monitoring results. Energy Build. 2014, 82, 65–72. [Google Scholar] [CrossRef]
  36. Osterman, E.; Butala, V.; Stritih, U. PCM thermal storage system for ‘free’ heating and cooling of buildings. Energy Build. 2015, 106, 125–133. [Google Scholar] [CrossRef]
  37. Whiffen, T.R.; Russell-Smith, G.; Riffat, S.B. Active thermal mass enhancement using phase change materials. Energy Build. 2016, 111, 1–11. [Google Scholar] [CrossRef] [Green Version]
  38. Pomianowski, M.; Heiselberg, P.; Jensen, R.L. Full-scale investigation of the dynamic heat storage of concrete decks with PCM and enhanced heat transfer surface area. Energy Build. 2013, 59, 287–300. [Google Scholar] [CrossRef]
  39. Faheem, A.; Ranzi, G.; Fiorito, F.; Lei, C. A numerical study on the thermal performance of night ventilated hollow core slabs cast with micro-encapsulated PCM concrete. Energy Build. 2016, 127, 892–906. [Google Scholar] [CrossRef]
  40. Navarro, L.; de Gracia, A.; Castell, A.; Cabeza, L.F. Experimental evaluation of a concrete core slab with phase change materials for cooling purposes. Energy Build. 2016, 116, 411–419. [Google Scholar] [CrossRef] [Green Version]
  41. Navarro, L.; de Gracia, A.; Castell, A.; Cabeza, L.F. Experimental study of an active slab with PCM coupled to a solar air collector for heating purposes. Energy Build. 2016, 128, 12–21. [Google Scholar] [CrossRef]
  42. Li, X.; Sanjayan, J.G.; Wilson, J.L. Fabrication and stability of form-stable diatomite/paraffin phase change material composites. Energy Build. 2014, 76, 284–294. [Google Scholar] [CrossRef]
  43. Muruganantham, K. Application of Phase Change Material in Buildings: Field Data vs. EnergyPlus Simulation. Master’s Thesis, Arizona State University, Tempe, AZ, USA, 2010. [Google Scholar]
  44. Winwood, R.; Benstead, R.; Edwards, R.; Letherman, K.M. Building fabric thermal storage: Use of computational fluid dynamics for modelling. Build. Serv. Eng. Res. Technol. 1994, 15, 171–178. [Google Scholar] [CrossRef]
  45. Holman, J.P. Heat Transfer, 10th ed.; Mcgraw-Hill: New York, NY, USA, 2010. [Google Scholar]
Buildings 09 00051 g001 550
Figure 1. Schematic of TermoDeck® hollow-core slab system reproduced from [4].
Figure 1. Schematic of TermoDeck® hollow-core slab system reproduced from [4].
Buildings 09 00051 g001
Buildings 09 00051 g002 550
Figure 2. Research methods and process.
Figure 2. Research methods and process.
Buildings 09 00051 g002
Buildings 09 00051 g003 550
Figure 3. (a) Schematic and (b) the picture of the experimental setup.
Figure 3. (a) Schematic and (b) the picture of the experimental setup.
Buildings 09 00051 g003
Buildings 09 00051 g004 550
Figure 4. The Enthalpy–Temperature curve for BioPCM™ Q21 supplied by the manufacturer.
Figure 4. The Enthalpy–Temperature curve for BioPCM™ Q21 supplied by the manufacturer.
Buildings 09 00051 g004
Buildings 09 00051 g005 550
Figure 5. Schematic of BioPCM™ arrangement inside the air duct: (a) PCM-SSA, (b) PCM-ASA.
Figure 5. Schematic of BioPCM™ arrangement inside the air duct: (a) PCM-SSA, (b) PCM-ASA.
Buildings 09 00051 g005
Buildings 09 00051 g006 550
Figure 6. Typical inlet temperature profile for cooling and heating mode.
Figure 6. Typical inlet temperature profile for cooling and heating mode.
Buildings 09 00051 g006
Buildings 09 00051 g007 550
Figure 7. The PCM–Air Duct (a) cross-section (schematic), (b) full-length duct (2 m long), and (c) the mesh.
Figure 7. The PCM–Air Duct (a) cross-section (schematic), (b) full-length duct (2 m long), and (c) the mesh.
Buildings 09 00051 g007
Buildings 09 00051 g008 550
Figure 8. Specific heat capacity curve for BioPCM™ (Q21).
Figure 8. Specific heat capacity curve for BioPCM™ (Q21).
Buildings 09 00051 g008
Buildings 09 00051 g009 550
Figure 9. The geometry of the hollow-core slab.
Figure 9. The geometry of the hollow-core slab.
Buildings 09 00051 g009
Buildings 09 00051 g010 550
Figure 10. The mesh of (a) solid region and (b) fluid region of the hollow-core slab model.
Figure 10. The mesh of (a) solid region and (b) fluid region of the hollow-core slab model.
Buildings 09 00051 g010
Buildings 09 00051 g011 550
Figure 11. Outlet–inlet air temperature difference in case of cooling mode.
Figure 11. Outlet–inlet air temperature difference in case of cooling mode.
Buildings 09 00051 g011
Buildings 09 00051 g012 550
Figure 12. Inlet–outlet air temperature difference in case of heating mode.
Figure 12. Inlet–outlet air temperature difference in case of heating mode.
Buildings 09 00051 g012
Buildings 09 00051 g013 550
Figure 13. Comparison of experimental and simulation temperature difference for No-PCM configuration in cooling mode.
Figure 13. Comparison of experimental and simulation temperature difference for No-PCM configuration in cooling mode.
Buildings 09 00051 g013
Buildings 09 00051 g014 550
Figure 14. Comparison of experimental and simulation temperature difference for No-PCM configuration in heating mode.
Figure 14. Comparison of experimental and simulation temperature difference for No-PCM configuration in heating mode.
Buildings 09 00051 g014
Buildings 09 00051 g015 550
Figure 15. Comparison of experimental and simulation temperature difference for PCM-ASA configuration in cooling mode.
Figure 15. Comparison of experimental and simulation temperature difference for PCM-ASA configuration in cooling mode.
Buildings 09 00051 g015
Buildings 09 00051 g016 550
Figure 16. Comparison of experimental and simulation temperature difference for PCM-ASA configuration in heating mode.
Figure 16. Comparison of experimental and simulation temperature difference for PCM-ASA configuration in heating mode.
Buildings 09 00051 g016
Buildings 09 00051 g017 550
Figure 17. Transient inlet and outlet temperature profile of the simulated hollow-core slab compared with the experimental data reported in Winwood et al. [44].
Figure 17. Transient inlet and outlet temperature profile of the simulated hollow-core slab compared with the experimental data reported in Winwood et al. [44].
Buildings 09 00051 g017
Buildings 09 00051 g018 550
Figure 18. Schematics of simulated cases in scenario analysis. Case (a) No PCM, Case (b) With PCM.
Figure 18. Schematics of simulated cases in scenario analysis. Case (a) No PCM, Case (b) With PCM.
Buildings 09 00051 g018
Buildings 09 00051 g019 550
Figure 19. Comparison of outlet temperatures with and without PCM under real summer weather in Melbourne.
Figure 19. Comparison of outlet temperatures with and without PCM under real summer weather in Melbourne.
Buildings 09 00051 g019
Buildings 09 00051 g020 550
Figure 20. Comparison of outlet temperatures of the hollow-core system with and without PCM during summer in Melbourne.
Figure 20. Comparison of outlet temperatures of the hollow-core system with and without PCM during summer in Melbourne.
Buildings 09 00051 g020
Buildings 09 00051 g021 550
Figure 21. Comparison of peak temperature reduction by hollow-core system for PCM and no-PCM cases.
Figure 21. Comparison of peak temperature reduction by hollow-core system for PCM and no-PCM cases.
Buildings 09 00051 g021
Table
Table 1. The difference in inlet and outlet temperatures of hollow-core system without (Case-a) and with (Case-b) PCM.
Table 1. The difference in inlet and outlet temperatures of hollow-core system without (Case-a) and with (Case-b) PCM.
|Inlet − Outlet|
Without PCM (Case a)With PCM (Case b)
MinMaxMinMax
ΔT (°C)% of days% of days% of days% of days
ΔT ≤ 1 °C4.1%12.2%4.1%12.2%
1 °C < ΔT ≤ 2 °C26.5%12.2%16.3%10.2%
2 °C < ΔT ≤ 3 °C32.7%14.3%32.7%10.2%
3 °C < ΔT ≤ 4 °C28.6%22.4%26.5%16.3%
ΔT > 4 °C8.2%38.8%20.4%51.0%

Share and Cite

MDPI and ACS Style

Jamil, H.; Alam, M.; Sanjayan, J. Thermal Performance of Hollow-Core Slab Ventilation System with Macro-Encapsulated Phase-Change Materials in Supply Air Duct. Buildings 2019, 9, 51. https://doi.org/10.3390/buildings9020051

AMA Style

Jamil H, Alam M, Sanjayan J. Thermal Performance of Hollow-Core Slab Ventilation System with Macro-Encapsulated Phase-Change Materials in Supply Air Duct. Buildings. 2019; 9(2):51. https://doi.org/10.3390/buildings9020051

Chicago/Turabian Style

Jamil, Hasnat, Morshed Alam, and Jay Sanjayan. 2019. "Thermal Performance of Hollow-Core Slab Ventilation System with Macro-Encapsulated Phase-Change Materials in Supply Air Duct" Buildings 9, no. 2: 51. https://doi.org/10.3390/buildings9020051

APA Style

Jamil, H., Alam, M., & Sanjayan, J. (2019). Thermal Performance of Hollow-Core Slab Ventilation System with Macro-Encapsulated Phase-Change Materials in Supply Air Duct. Buildings, 9(2), 51. https://doi.org/10.3390/buildings9020051

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop