Decoupling and Enhanced-Synergy Based Optimization for Multi-Fan Power Allocation in Highway Tunnel Ventilation

Abstract

Energy-efficient operation of highway tunnel ventilation systems remains challenging, and optimal power allocation among multiple fans is essential for reducing overall energy consumption. This study begins with a quantitative analysis of multi-fan synergistic effects, decoupling the interactions into sequential transverse and longitudinal superpositions. An equivalent predictive model is then established for rapid and accurate calculation of the overall ventilation supply, where a neural-network surrogate model is integrated to predict the superposition effects. Building on this model, an improved particle swarm optimization (PSO) algorithm is applied to determine the optimal power allocation, demonstrating robust applicability across tunnels of different lengths and fan configurations. Validation against CFD simulations shows that the predictive model yields an error of about 3%. By enhancing both transverse and longitudinal synergies, the optimized power allocation scheme can reduce ventilation energy consumption by 36%. Thus, the proposed framework provides a practical and scalable solution for multi-fan power allocation in highway tunnel ventilation systems.

1. Introduction

With the continuous expansion of highway tunnel mileage, both the installed capacity and operational energy consumption of ventilation systems have increased significantly [1,2,3]. Long-term high-load ventilation exacerbates operational and maintenance costs [4,5]. Consequently, for existing tunnels, optimizing fan-power allocation to reduce energy consumption while satisfying ventilation requirements has been recognized as crucial for energy-efficient operation [6,7,8,9].

Tunnel ventilation supply and demand fluctuate in real time, driven by variables such as traffic volume, atmospheric conditions and pollutant concentrations [10,11,12,13,14]. Through real-time monitoring and demand forecasting, fan operations can be dynamically adjusted [8,15,16,17,18], yielding substantial energy savings while maintaining safety and air quality [19,20,21]. In practice, multiple jet fans are typically arranged in series or parallel to meet tunnel ventilation requirements [22,23]. However, the accurate prediction of ventilation performance under these multi-fan synergistic conditions remains challenging, often resulting in insufficient airflow, energy wastage or suboptimal power distribution.

It has been demonstrated that full exploitation of fan synergistic effects can greatly enhance ventilation efficiency [24,25]. However, as the number of concurrently operating fans increases, tunnel-ventilation energy optimization has become a typical high-dimensional nonlinear problem. To address this, ventilation optimization models aimed at minimizing overall energy consumption have been developed [26,27,28], and methods such as genetic algorithms [29], grey wolf optimization [30], and particle swarm optimization (PSO) [31,32] have been applied. Dimensionality reduction has been attempted by simplifying decision variables. For example, Li et al. [33] proposed an improved bare-bones PSO algorithm and simplified decision variables, and Wang et al. [34] applied a minimum spanning-tree method to select the most influential variables, which both enhanced the optimization efficiency and accuracy in ventilation control. Despite these advances, most studies constrain only flow conservation, pressure balance and fan states [35,36] and largely neglects coupling effects among fans [37,38], which limits optimization in multi-fan scenarios.

To characterize multi-fan synergistic effects more accurately, detailed flow-field investigations have been undertaken. Dong and Jiang [39] demonstrated that series or parallel configurations shift fan operating points and yield a nonlinear superposition of individual airflow contributions. Guo et al. [40] pointed out that similar power (with a relative ratio below 5.3) should be allocated in parallel-fan configurations to enhance synergy and avoid surge and stall. Pei et al. [41] found that 100 m downstream of a single fan, the velocity profile remains essentially unchanged, whereas under parallel operation, the two jets are merged within the same distance, yielding a flow distribution identical to the single-jet case. However, these findings remain largely qualitative and are not readily integrated into optimization frameworks.

To address these gaps, in this work, a flow-field analysis of multi-fan synergy in highway tunnels is conducted, a predictive model for ventilation supply is developed, and an optimization method for multi-fan power allocation is established. First, transverse and longitudinal interactions are decoupled and quantified, enabling a streamlined calculation method for the overall airflow supply. Leveraging this predictive method, a power-minimization model is then formulated and an improved PSO algorithm is applied for an efficient solution. Finally, the optimization results are validated against CFD simulations, and the applicability of the proposed method is discussed for tunnels of varying lengths and fan configurations.

2. Synergy Analysis of Multiple Fans

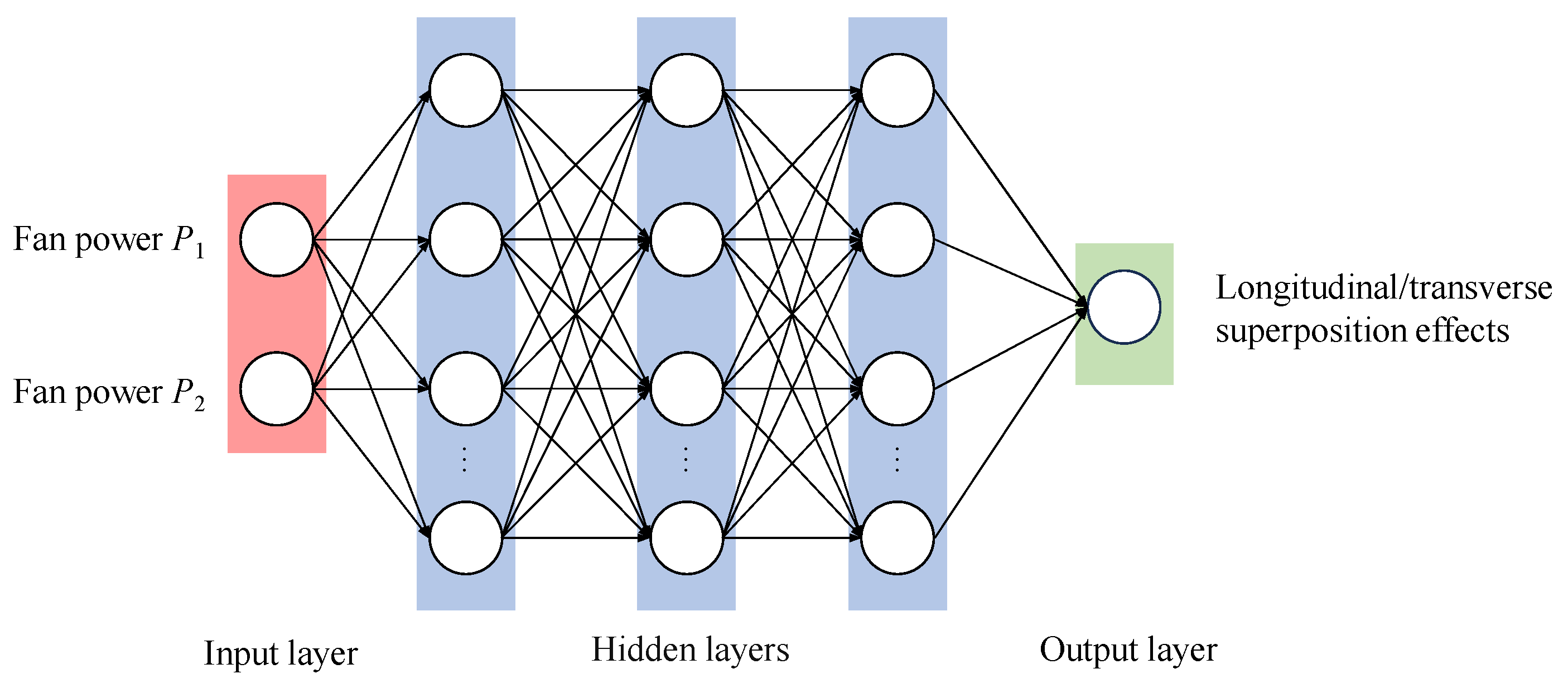
2.1. Tunnel Ventilation Model and CFD Simulation Method

A 500 m-long, two-lane, single-bore highway tunnel is focused on in this work, representing a single ventilation section employing longitudinal mechanical ventilation. The arrangement of these jet fans is shown in Figure 1a. Three pairs of jet fans are installed on the tunnel crown, located at 15 m, 165 m, and 315 m from the tunnel entrance. The cross-section features a 2 m transverse spacing between fans and an installation height of 6 m, as illustrated in Figure 1b. The cross-sectional area of the tunnel is 65.4 m².

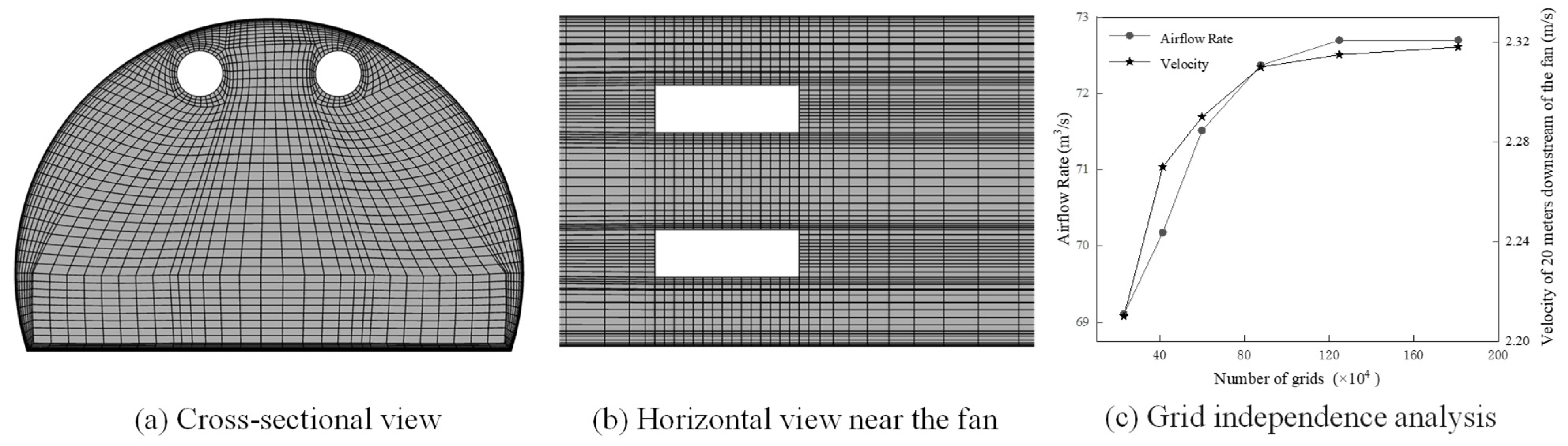
To simulate the airflow field in the tunnel ventilation system, a computational fluid dynamics (CFD) model is established using the ANSYS Fluent 2022 R1. The Reynolds-Averaged Navier–Stokes (RANS) method is applied in the CFD simulations. Referring to common CFD studies [22,42,43,44] the standard k-ε turbulence model exhibits high robustness and has been fully validated by experiments; it is employed in this work. Six sets of grids for the simulation with the same topology but different densities are selected for the grid independence analysis. The structure of the grid and the calculation results are presented in Figure 2. It is shown that, when the grid density exceeds that of Grid 4 (the fourth from the left in Figure 2c), the numerical error of total airflow rate in the tunnel and the velocity at 20 m downstream of the fan caused by the variance of grid density is about 1%, which can meet the precision requirement. Therefore, Grid 4 is selected in the work, and the total grid number is 8.76 × 10⁵. Regarding boundary conditions, both the inlet and outlet of the fans are defined as velocity inlets, the inlet and outlet velocities of the fan are equal in magnitude but opposite in direction; the tunnel entrance is set as a pressure inlet; and the tunnel exit is set as a pressure outlet.

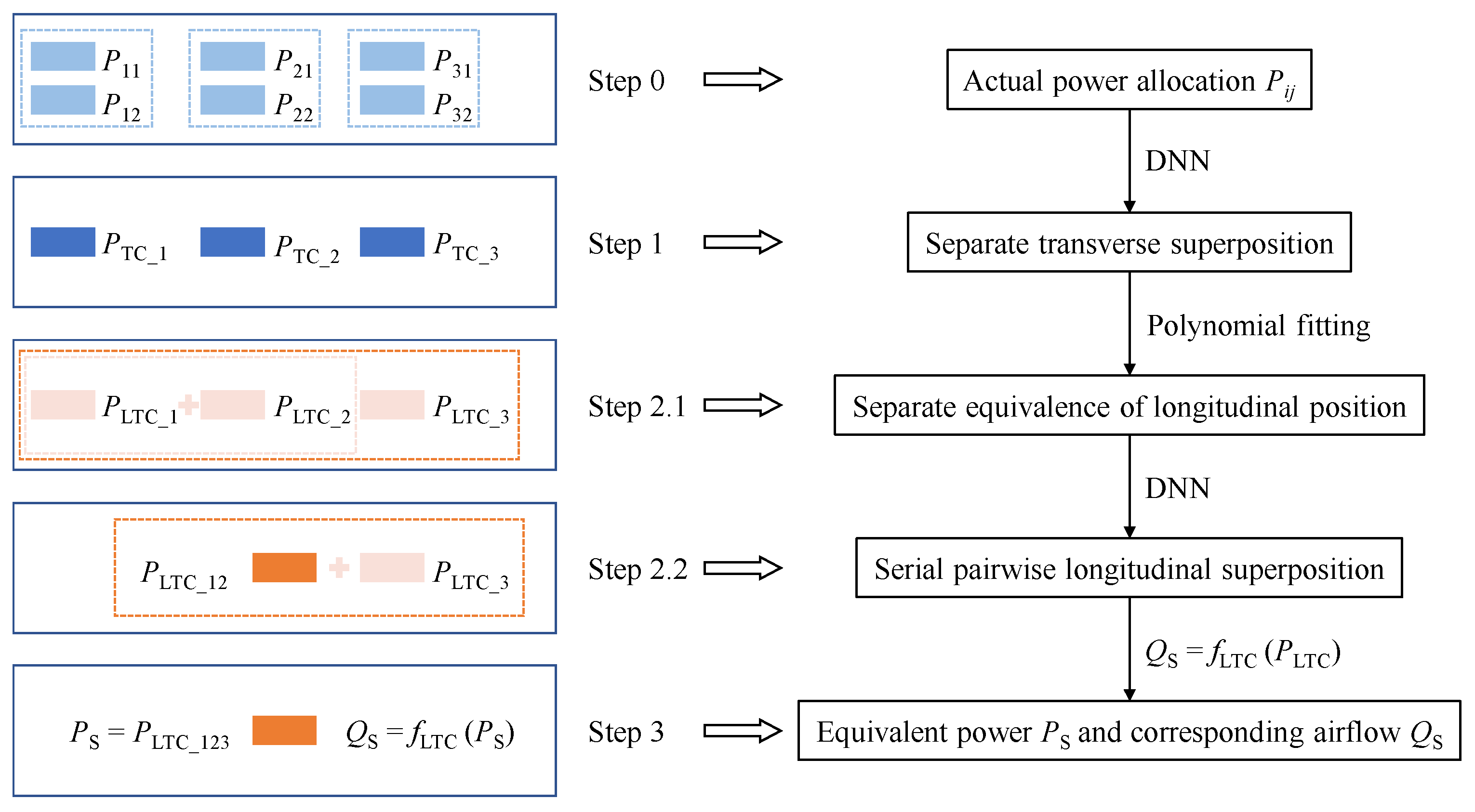
The multi-fan configuration in actual ventilation poses significant challenges for accurately predicting the total airflow rate. To address this, a simplification strategy is proposed, as illustrated in Figure 3. The nonlinear superposition of the multi-fan ventilation effects is decoupled into longitudinal and transverse components. Through sequential transverse and longitudinal superposition, the equivalent power P_S corresponding to f_LTC with equal ventilation supply Q_S is obtained. The equivalent object is a virtual scenario where tunnel ventilation is solely provided by a single fan (denoted f_LTC) centred in both the longitudinal and transverse directions, and its power P_LTC is assumed to be infinitely and continuously adjusted. Through the fitting of CFD results, a one-to-one correspondence is established between P_LTC and the resulting airflow rate Q_S, as expressed in Equation (1). Based on this strategy, a simplified predictive model for the total tunnel airflow rate is developed, laying the groundwork for subsequent optimization. The physical basis, training, and usage of this model are as follows.

$$Q_S=f_{LTC}(P_{LTC})$$

(1)

2.2. Analysis and Quantification of Transverse Synergy

In tunnel ventilation systems, jet fans are typically installed in parallel pairs, symmetrically positioned about the longitudinal axis. However, aerodynamic coupling between fans makes airflow calculations for such layouts computationally intensive. In this study, a transverse synergy-equivalence method is introduced, wherein the combined effect of paired fans is modelled as a single equivalent fan. This equivalent fan retains the original longitudinal position but is placed at the tunnel’s transverse centreline (denoted F_TC).

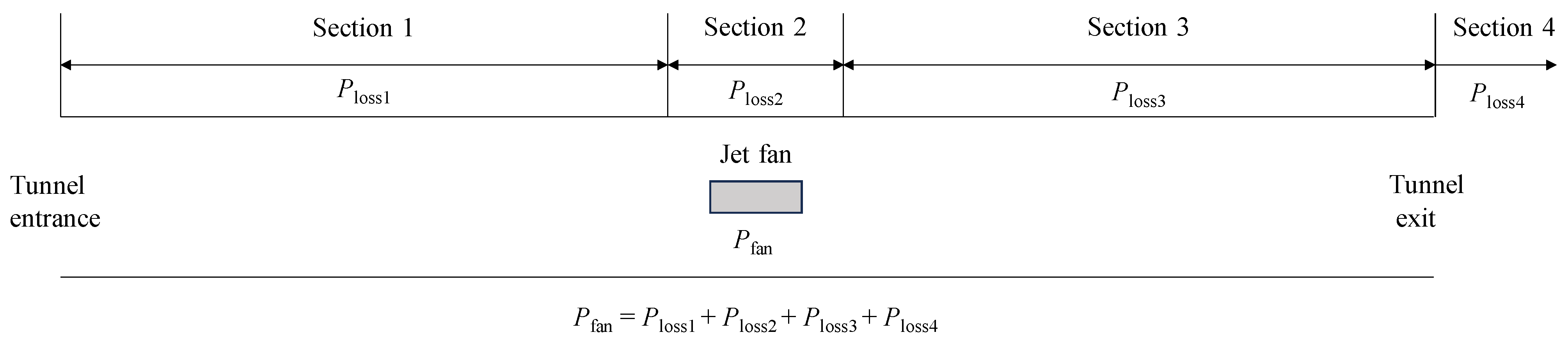
When the same ventilation effect is achieved, parallel fans operating in synergy consume less energy than the equivalent F_TC fan. For detailed analysis, the overall energy loss of tunnel airflow is divided into four segments, and their sum equals the fan power P_fan according to the energy conservation principle, as shown in Figure 4. Section 1 covers from the tunnel entrance to 1 m upstream of the fan inlet, with energy loss P_loss1 and specific loss ΔP_loss1. Section 2 spans from 1 m upstream of the fan inlet to 1 m downstream of the fan outlet, incurring with loss P_loss2. Section 3 runs from 1 m downstream of the fan outlet to the tunnel exit, with loss P_loss3 and specific loss ΔP_loss3. Section 4 accounts for loss beyond the tunnel exit (P_loss4).

Table 1. Total simulated fan power and sectional energy losses for single and parallel fan arrangements.

Fan Arrangement	Pfan (kW)	Ploss1 (kW)	Ploss2 (kW)	Ploss3 (kW)	Ploss4 (kW)
Single fan FTC	15.82	0.28	5.71	8.46	1.37
Parallel fans	11.20	0.29	3.67	5.88	1.37
Difference	4.62	−0.06	2.04	2.58	0.00

compares fan power and energy losses for each segment under the same tunnel airflow rate (200 m³/s). The combined power of the parallel fans is 4.62 kW lower than that of a single fan. Sections 1 and 4 show negligible differences, whereas Section 2 contributes 2.04 kW (44.2%) and Section 3 contributes 2.58 kW (56.0%) of the total savings. Consequently, Sections 2 and 3 are identified as the primary focus.

To examine the loss in Section 2 in detail, the local distributions of longitudinal velocity (hereafter referred to simply as velocity) and entropy generation near the fans for single-fan and parallel-fan arrangements are compared in Figure 5 and Figure 6, respectively. At equal tunnel airflow rates, the single fan produces higher inlet and outlet velocities, steep velocity gradients, and greater frictional loss—resulting in increased energy dissipation. By contrast, the parallel-fan arrangement uses lower power per fan and yields reduced inlet and outlet velocities, producing a more uniform velocity field and lower frictional loss. This difference continues downstream until the tunnel exit. The global distributions of velocity for both arrangements are presented in Figure 7. It is revealed that in the extended downstream region, the airflow in the parallel-fan case is more evenly distributed, with lower velocity gradients. The reduced shear minimizes frictional energy loss in Section 3. Overall, the parallel-fan arrangement achieves superior aerodynamic synergy, reduces velocity gradients, and consequently cuts total frictional losses and energy consumption.

In the transverse equivalence calculation, under identical ventilation conditions, the combined power of two parallel fans is mapped to the power of a single equivalent fan F_TC (Equation (2)). Here, P_{TC_i} (i = 1, 2, 3) denotes the equivalent fan power resulting from transverse superposition, while P_i1 and P_i2 represent the actual powers of the two parallel fans at the ith longitudinal station. This nonlinear mapping is modelled using data from multiple representative operating conditions. Equation (1) is subsequently applied to calculate the equivalent ventilation effect. 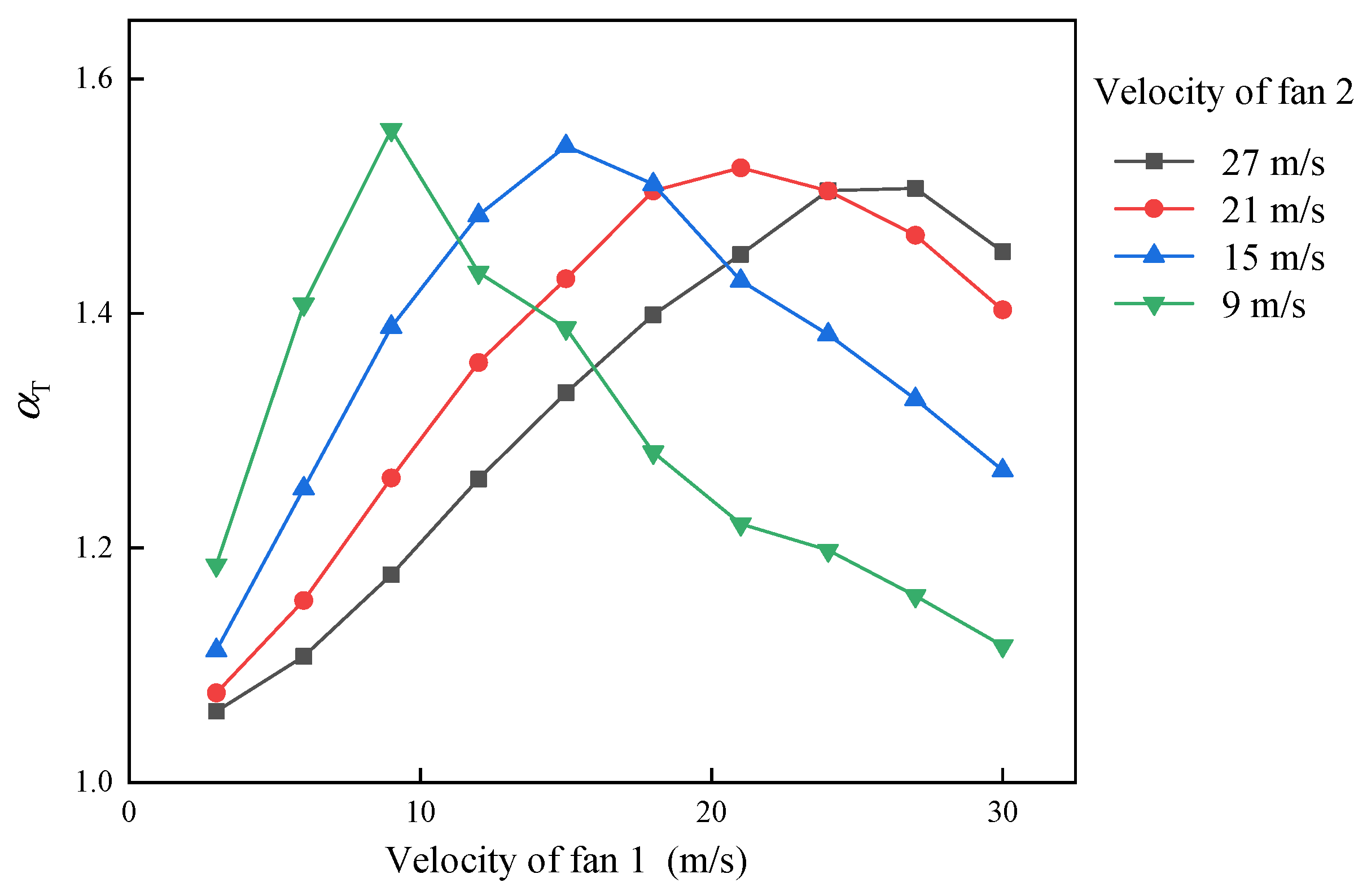To quantify this synergy, the transverse superposition factor α_T is introduced (Equation (3)), defined as the ratio of the equivalent single-fan power to the sum of the two fans’ powers at equal airflow. The relationship between α_T and the outlet-velocity difference is shown in Figure 8: When velocities match closely, shear is minimal, frictional loss is low, yielding a high α_T; as the velocity gap widens, shear and loss increase, and α_T decreases.

$$P_{TC\_i}=g_T(P_{i1},P_{i2}),i=1,2,3$$

(2)

$${\alpha }_T={\displaystyle \frac{P_{TC\_i}}{P_{i1}+P_{i2}}}$$

(3)

To validate decoupling local transverse superposition from global longitudinal superposition, the influence of transverse superposition on longitudinal effects is first examined, to ensure the applicability of the decoupling effect. It is demonstrated in Figure 7 that two parallel jets diffuse and merge within a short distance, producing a flow field equivalent to a single fan. As a result, the perceived background flow around downstream fans is consistent with the single-fan conditions. The same applies to the upstream flow field. Thus, under identical ventilation conditions, the local transverse arrangement does not alter the background flow perceived by upstream or downstream fans. That is, the transverse arrangement of fans has no substantial effect on the longitudinal superposition within downstream ventilation systems. Next, the influence of longitudinal superposition on transverse superposition is analyzed. To assess whether upstream jets influence downstream transverse synergy, two scenarios are established: identical downstream ventilation is provided either by a single fan or parallel fans. An upstream fan is introduced with adjustable outlet velocity. As shown in Figure 9, the total tunnel airflow remains unchanged across a range of background velocities, confirming that the transverse superposition effect is invariant with respect to longitudinal flow variations. In summary, when enough longitudinal spacing exists between fan groups, longitudinal and transverse superposition operate independently, allowing us to decouple them and simplify the multi-fan ventilation model.

2.3. Analysis and Quantification of Longitudinal Synergy

(1)

Influence of longitudinal positions

Although the downstream diffusion of fan jets is fundamentally similar across longitudinal positions, ventilation performance varies with distance from the tunnel entrance. It is therefore necessary to compare the ventilation performance of fans at different longitudinal positions after applying the equivalent treatment of transverse synergistic effects described in the previous subsection. Fan powers and sectional energy losses of the fans located at 15 m, 165 m, and 315 m (Cases 15, 165, and 315) under the same tunnel airflow rate (200 m³/s) are compared in

Table 2. Total simulated fan power and sectional energy losses at different longitudinal locations in the tunnel.

Fan Location	Pfan (kW)	Ploss1 (kW)	ΔPloss1 (W/m)	Ploss2 (kW)	Ploss3 (kW)	ΔPloss3 (W/m)	Ploss4 (kW)
Case 15	15.94	0.03	1.73	5.78	8.85	18.4	1.29
Case 165	16.27	0.22	1.36	5.65	9.07	27.3	1.33
Case 315	17.55	0.44	1.40	6.48	9.08	56.0	1.54
Difference between Cases 315 and 15	1.61	0.42	0.33	0.71	0.23	37.6	0.25

. The power difference between Cases 15 and 315 is 1.61 kW. Section 1 shows only minor variation in specific loss. Section 2 contributes a loss differential of 0.71 kW (44% of the overall difference), and Section 3 also exhibits a notable disparity. Section 4 adds 0.25 kW (15.6%). Accordingly, the losses in Sections 2 and 4 are first targeted, with the specific loss discrepancy in Section 3 examined next.

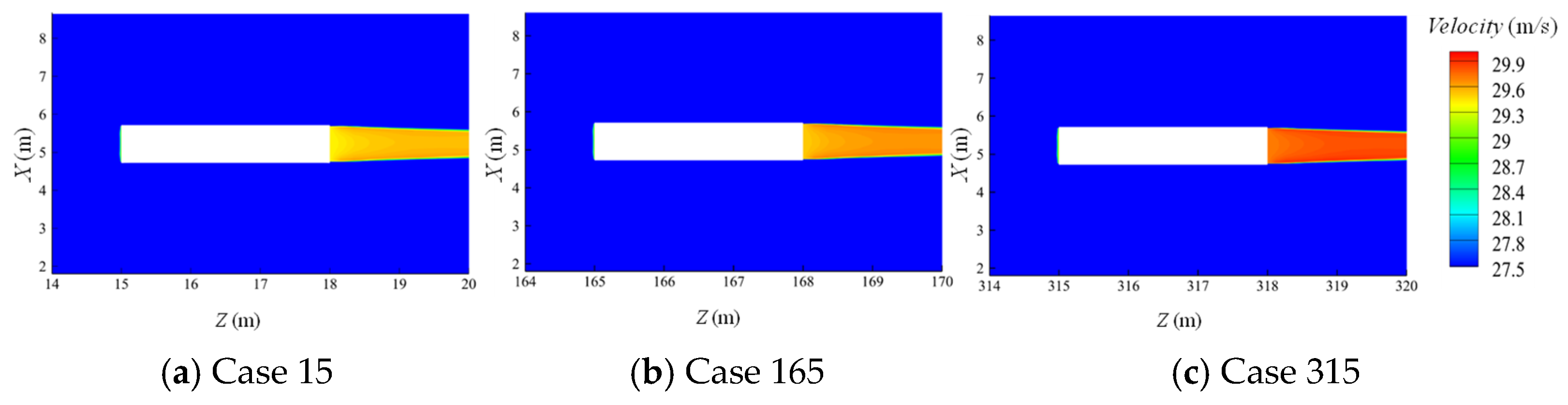
Regarding the energy loss in Section 4, velocity distributions at the tunnel exit for fans at three longitudinal positions are displayed in Figure 10. Compared to the fan outlet, the velocity distribution at the tunnel exit is essentially uniform after long-distance mixing. However, this quantitative difference still results in a significant energy difference. In Case 315, due to relatively insufficient mixing, the larger velocity differences lead to greater total kinetic energy, increasing external dissipation. In comparison, as the mixing distance increases, the total kinetic energy in Case 165 and Case 15 decreases. The elevated residual kinetic energy (energy dissipation after exiting the tunnel) in Case 315 forces the upstream fan to inject more power, reflected in higher inlet and outlet velocities and highlighting notable local flow loss differences.

Local distributions of velocity are then compared in Figure 11. In Case 315, the higher inlet and outlet velocities create steep velocity gradients and increased frictional loss, especially in high-shear zones near the fan. This raises local energy dissipation. By contrast, Cases 15 and 165 maintain gentler velocity gradients and lower frictional loss. This disparity in velocity gradients persists downstream from the fan outlets to the tunnel exit, driving proportionally larger specific loss in Section 3. On the other hand, at a tunnel flow rate of 200 m³/s, the average velocity is about 3 m/s. Thus, the flow is considered uniform when the maximum cross-sectional velocity reaches 5 m/s. This occurs at 97 m, 100 m, and 101 m downstream of the fan for case15, case165, and case315, respectively. Case315 has the longest diffusion distance and the highest energy loss, while case15 has the shortest and lowest energy loss.

Fan power differentials across longitudinal arrangement positions, under identical ventilation conditions, are quantified. Equation (4) is applied to calculate the equivalent power P_{LTC_i} of f_LTC corresponding to the actual power at the ith longitudinal position, and the relative ratio is defined as the longitudinal position coefficient lp (Equation (5)). It is found that the relative ratio of power among the three positions remains essentially unchanged across a range of airflow rates. Based on this near-invariance, polynomial regression is applied to fit lp as a function of fan power over the operational range at a given longitudinal position. The prediction of lp is much easier than that of transverse and longitudinal superposition effects, which can also be approximated by interpolation according to the longitudinal position. Therefore, by equivalently treating the effect of different longitudinal positions in advance, there is no need to consider this effect in the subsequent longitudinal superimposition, further simplifying the prediction process.

$$P_{LTC\_i}=g_{LP\_i}(P_{TC\_i}),i=1,2,3$$

(4)

$$l{p}_i={\displaystyle \frac{P_{LTC\_i}}{P_{TC\_i}}},i=1,2,3$$

(5)

(2)

Longitudinal superposition

Under identical ventilation requirements, lower energy consumption is observed for serially configured fans compared to single-fan systems. A synergistic equivalence method is proposed to quantify longitudinal synergistic effects. For the same ventilation airflow supply (200 m³/s), a single fan installed in the longitudinal centre and a series of fans installed at 15 m and 165 m, respectively, are used for comparison. It is found that 3.59 kW more power is required by the single-fan configuration than by the serial-fan one, of which 1.86 kW is attributed to increased longitudinal distributed losses (51.8% of the total difference) and 1.75 kW to increased local losses (48.8%) near the fans.

Energy loss is analyzed based on local distributions of velocity for the single-fan and serial-fan arrangements (Figure 12), respectively. The single-fan configuration exhibits significantly higher inlet and outlet velocities, resulting in larger velocity gradients and frictional losses that elevate overall energy dissipation. By contrast, in the serial-fan case, the upstream-generated jet is fully mixed before encountering the downstream fan, establishing a nearly uniform background flow field. At this time, the downstream fan generates a weaker jet. Consequently, the velocity difference between the fan inlet/outlet and the surrounding airflow is significantly reduced, and total frictional loss is markedly lowered. The global distributions of velocity in Figure 13 further illustrate that the reduced velocity differentials are maintained over a long downstream distance, decreasing the frictional loss. A similar influence is observed for the downstream fan on the upstream unit. In summary, by providing a uniform background flow, the two fans in series minimize local velocity gradients and frictional loss, thereby reducing overall energy consumption.

Based on the above analysis, the ventilation effect resulting from longitudinal superposition is solely determined by the equivalent ventilation powers P_LTC of the upstream and downstream fans (rows), and is independent of their specific allocations. This demonstrates that upstream longitudinal superposition does not influence subsequent downstream superposition. Consequently, through successive pairwise superpositions, multiple fans can ultimately be represented by a single equivalent fan f_LTC situated at the longitudinal and transverse midpoint, thereby quantifying the coupling effect among multiple fans (rows). An illustrative example for three fans in series is given in Equation (6), in which the subscript L2 denotes longitudinal pairwise superposition.

$$\begin{array}{cc}\hfill P_{LTC\_total}& =g_L(P_{LTC\_1},P_{LTC\_2},P_{LTC\_3})\hfill \\ & =g_{L2}(P_{LTC\_12},P_{LTC\_3})\hfill \\ & =g_{L2}(g_{L2}(P_{LTC\_1},P_{LTC\_2}),P_{LTC\_3})\hfill \end{array}$$

(6)

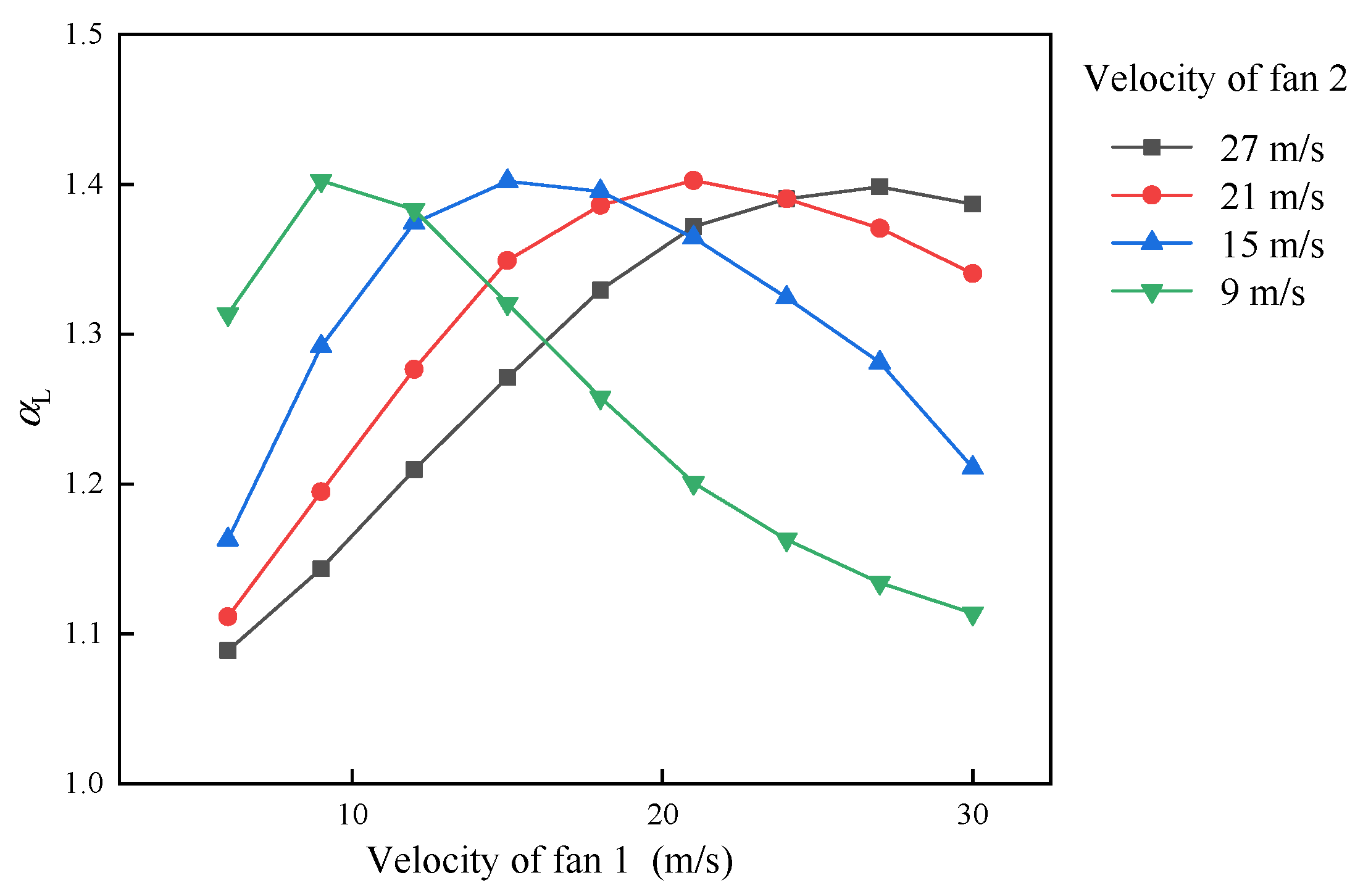
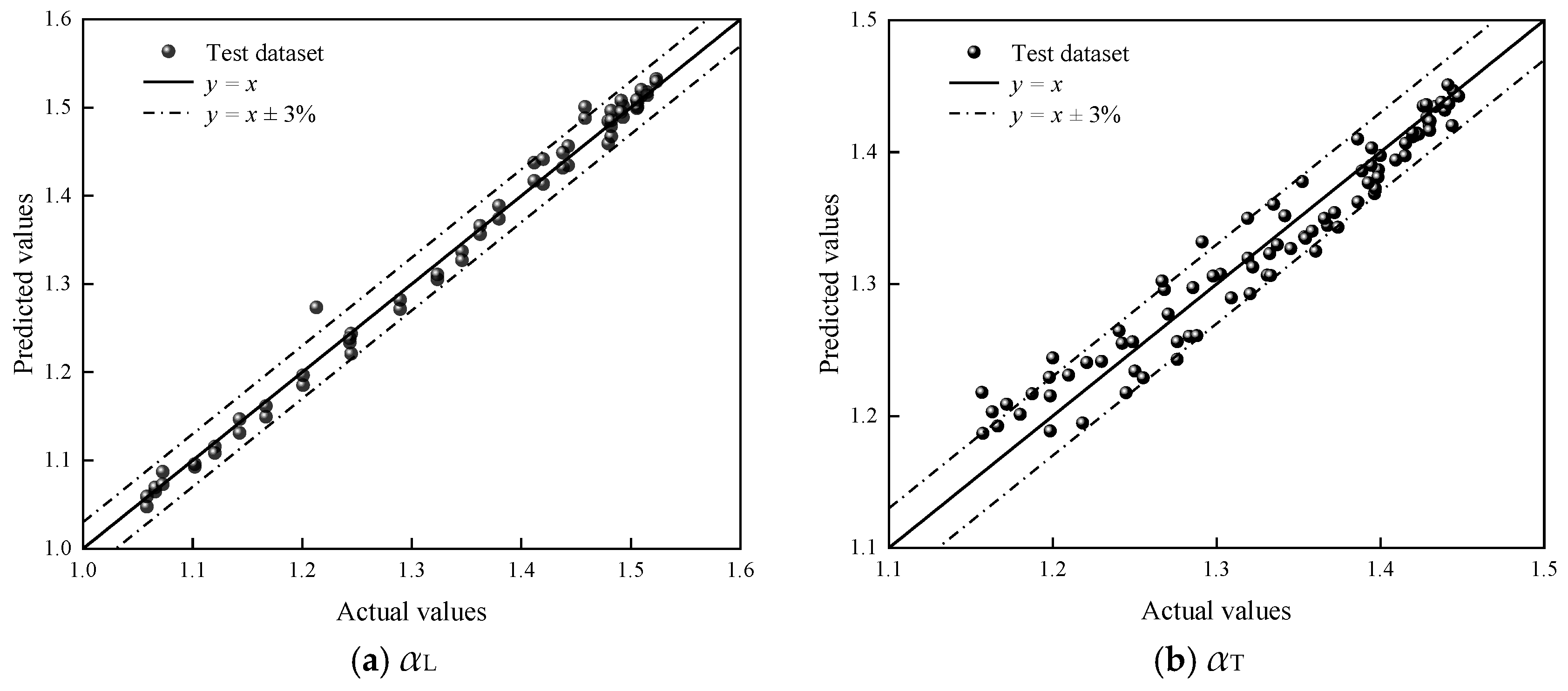
To quantify the synergistic effect of serial-fan operation, the longitudinal superposition factor α_L is defined as the ratio of the power of an equivalent single fan to the total power of all serially arranged fans achieving the same airflow rate. An example of two serial fans is shown in Equation (7). The relationship between α_L and the outlet velocity of each fan is presented in Figure 14. When the outlet velocities are close, the velocity gradients in the surrounding flow field decrease, and the shear effect in the flow is weakened, resulting in an enhanced synergy (larger α_L). In contrast, when the velocity difference is large, the airflow becomes less uniform, leading to stronger friction and a reduced synergy.

$${\alpha }_L={\displaystyle \frac{P_{LTC\_12}}{P_{LTC\_1}+P_{LTC\_2}}}$$

(7)

3. Optimization of Multi-Fan Power Allocation

3.1. Prediction of Superposition Effects Based on Surrogate Model

Based on the flow analysis, the superposition among multiple fans can be decoupled into longitudinal and transverse components. Thus, the prediction of the total ventilation airflow is decomposed into two-dimensional longitudinal and transverse superposition effects, as well as the longitudinal position coefficient. This physics-based decoupling significantly simplifies the prediction task and expands the applicability to different ventilation systems, which will be discussed in Section 4.3.

A surrogate model is trained to predict superposition effects from fan power inputs. CFD simulation results are applied for the training, and the dataset covers various power allocations, ensuring strong representativeness and broad coverage. Given the wide range of fan powers, logarithmic normalization is first applied. To capture the nonlinear superposition relationships, several machine-learning models are employed, including Deep Neural Networks (DNN), Random Forests (RF), Support Vector Regression (SVR), and Gaussian Process Regression (GPR). All the above methods were implemented using MATLAB R2023b.

The predictive performance of these models for the longitudinal superposition effect (represented by α_L) is evaluated in Figure 15 and

Table 3. Comparison of predictive performance using different methods.

Method	R2	MSE	RMSE
DNN	0.96	0.001	0.036
GPR	0.89	0.004	0.063
RF	0.73	0.010	0.101
SVR	0.90	0.004	0.061

, using R², MSE and RMSE as metrics. The scatter plot in Figure 15a indicates that only the DNN predictions fall entirely within the ±3% error band. Moreover, the DNN yields median and mean errors closest to zero, with a narrower error band than those of the other models (Figure 15b). Consistent findings are shown in Table 3, confirming the superior accuracy of the DNN surrogate in this prediction task.

Based on these results, a DNN-based surrogate model is adopted to predict both longitudinal and transverse superposition effects. The network architecture (Figure 16) consists of input, hidden, and output layers of interconnected neurons. By training on preprocessed fan power data, this model bypasses the high computational cost of CFD simulations while meeting real-time optimization requirements.

The predictive performance of the DNN model for longitudinal and transverse superposition effects (represented by α_L and α_T) is shown in Figure 17. The solid line denotes the ideal y = x reference, and the dashed lines mark a ±3% error margin. In Figure 17a, most points cluster symmetrically around the y = x line, demonstrating excellent predictive accuracy, with the majority falling within the ±3% band. This confirms low errors and strong robustness. Overall, the DNN model generalizes well for both superposition effects, consistently delivering high accuracy and effectively standing in for CFD simulations.

3.2. Calculation Method for Total Ventilation Airflow Supply

The equivalent power P_S and the resulting tunnel airflow Q_S are obtained by sequential transverse and longitudinal superposition of the actual fan powers, as illustrated in Figure 3 and given in Equation (8). In this calculation, the aforementioned DNN surrogate model is used for longitudinal and transverse superpositions, and the effect of longitudinal position is predicted through polynomial fitting.

$$\begin{array}{cc}\hfill P_S& =g_L(P_{LTC\_1},P_{LTC\_2},P_{LTC\_3})\hfill \\ & =g_L\left(g_{LP\_1}\left(P_{LTC\_1}\right),g_{LP\_2}\left(P_{LTC\_2}\right),g_{LP\_3}\left(P_{LTC\_3}\right)\right)\hfill \\ & =g_L\left(g_{LP\_1}\left(g_T\left(P_{11},P_{12}\right)\right),g_{LP\_2}\left(g_T\left(P_{21},P_{22}\right)\right),g_{LP\_3}\left(g_T\left(P_{31},P_{32}\right)\right)\right)\hfill \end{array}$$

(8)

To validate this predictive method, P_S and corresponding Q_S are calculated for various equal-power allocations and are compared against CFD-derived airflow, as presented in

Table 4. Comparison between predicted and CFD-simulated tunnel airflow.

Power of Each Fan (kW)	Predicted		CFD-Simulated
	PS (kW)	QS (m3/s)	QS (m3/s)	Relative Error of QS
2 kW	32.9	251	259	3.1%
5 kW	79.9	341	349	2.3%
8 kW	125.1	397	409	2.9%

. Across different allocations, the predicted airflow agrees with the CFD results within approximately 3%, confirming the method’s accuracy. The prediction error of the model originates from error amplification during the stepwise superposition process. In practical applications, additional data is required to modify the model and ensure the robustness of the model. Therefore, this predictive method has the advantages of high precision and low training cost, and is applied for the subsequent optimization of fan-power allocation.

3.3. Improved Particle Swarm Optimization Algorithm

To minimize the energy consumption of tunnel ventilation, the total power of fans, P_T, is adopted as the objective function (Equation (9)). The power of each fan is taken as the decision variable, assumed to be continuously adjustable between 0% and 100% of its rated capacity. The constraint is that the supplied ventilation rate Q_S should be greater than or equal to the required tunnel ventilation rate Q_R (Equation (10)).

$$\min P_T={\displaystyle \sum _{i=1}^n{P}_{ij}}$$

(9)

$$Q_S=f_{LTC}(P_S)\ge Q_R$$

(10)

An optimization method assisted by a DNN surrogate model is proposed, comprising two principal stages. First, a DNN surrogate model is established for the rapid prediction of longitudinal and transverse synergistic effects between fans (Equations (2) and (6)), thereby supporting the computation of the constraint in Equation (10) and accelerating the optimization process. Second, a particle swarm optimization (PSO) algorithm is employed to solve the optimization problem. While PSO demonstrates strengths in global search capability and convergence efficiency, its performance may be constrained by premature convergence to local optima when dealing with complex, nonlinear problems. To mitigate this issue, three enhancement measures are introduced as follows:

(1)

Latin hypercube sampling initialization

Latin hypercube sampling (LHS) is a stratified random sampling method for generating near-uniform samples in a multidimensional space [45,46]. In this method, each dimension of the sampling space is first divided into N non-overlapping intervals, with one sample point randomly selected from each interval to eliminate duplication. Subsequently, these single-dimensional sample points are randomly combined across all dimensions to construct an N × d sample matrix, where d denotes the dimensionality. Compared with simple random sampling, LHS-based initialization ensures more uniform coverage of the search space.

(2)

Adaptive learning factors

Asymmetric learning factors facilitate particles’ adaptive learning during optimization [47,48], as defined in Equations (11) and (12), where Iter and Iter_max denote the current and maximum iterations. In the early search phase, a higher individual learning factor C₁ promotes exploration of each particle’s historical best, reducing local–optima entrapment; in the later phase, a higher social learning factor C₂ drives convergence toward the global optimum.

$$C_1=\cos ({\displaystyle \frac{\pi }{2}}\cdot {\displaystyle \frac{Iter}{Ite{r}_{\max }}})\cdot \cos (\pi \cdot {\displaystyle \frac{Iter}{Ite{r}_{\max }}})+1.5$$

(11)

$$C_2=\sin ({\displaystyle \frac{\pi }{2}}\cdot {\displaystyle \frac{Iter}{Ite{r}_{\max }}})\cdot \sin (\pi \cdot ({\displaystyle \frac{Iter}{Ite{r}_{\max }}}+1.5))+1.5$$

(12)

(3)

Adaptive inertia weight

An adaptive inertia-weight coefficient strategy [48] is adopted, in which the inertia weight w is dynamically adjusted to balance global exploration and local exploitation (Equation (13)). During initial iterations, a larger w is employed to sustain higher search momentum and thus enhance global exploration; in later stages, a reduced w is applied to facilitate local convergence and improve search precision.

$$w=w_{\min }+(w_{\max }-w_{\min }){\displaystyle \frac{e^{-0.1l}-e^{-0.1Ite{r}_{\max }}}{1-e^{-0.1Ite{r}_{\max }}}}$$

(13)

The improved PSO algorithm is implemented in MATLAB, with initial parameters presented in

Table 5. Initial parameters of the improved particle swarm optimization algorithm.

Parameter	Setting
Number of particles	500
Maximum iterations	2000
Learning factor	C1 = 2.5, C2 = 1.5
Inertia weight	wmax = 0.9, wmin = 0.5

. Given the wide adjustable range of fan power, population size has a critical influence on optimization: an appropriate population size influences global search capability, convergence speed and solution quality. Convergence curves for populations of 100, 200, 300, 500 and 1000 particles are compared in Figure 18a. Convergence is not achieved within 2000 iterations for 100–300 particles, whereas 500 and 1000 particles converge by 1000 iterations with similar results. The computation time for 1000 particles is approximately 1.6 times that for 500 particles, and therefore a swarm size of 500 particles is adopted for subsequent calculations. Convergence curves with baseline PSO, adaptive-weight PSO (AWPSO), and the improved PSO for a target ventilation rate of 200 m³/s are presented in Figure 18b. The improved PSO yields a lower initial fitness value, reducing unproductive search, and converges within 500 iterations—exhibiting faster convergence than the other two methods.

4. Results and Discussion

4.1. Optimization Results and Validation

Tunnel ventilation demand is determined according to Guidelines for Design of Ventilation of Highway Tunnels (Ministry of Communications of PRC [49]), and the air-change velocity in longitudinal ventilation tunnels should not be less than 1.5 m/s. The required ventilation airflow rates are set to 200 m³/s, 250 m³/s, and 300 m³/s, respectively. The improved PSO algorithm is employed to determine the minimum energy consumption that meets these requirements. The convergence curves are shown in Figure 19, and the resulting fan power allocations for each ventilation rate are listed in

Table 6. Optimized fan power allocations under different ventilation requirements.

Fan	Fan Power at 200 m3/s (kW)	Fan Power at 250 m3/s (kW)	Fan Power at 300 m3/s (kW)
Fan 11	1.29	2.25	3.73
Fan 12	1.26	2.22	3.76
Fan 21	1.22	2.41	3.93
Fan 22	1.19	2.24	3.86
Fan 31	0.56	1.23	2.40
Fan 32	0.51	1.19	2.46
Total	6.03	11.67	20.15

.

The optimization results are validated through CFD simulations, where the simulated P_T and simulated Q_S for each allocation are compared in

Table 7. CFD-simulated versus required airflow rates under optimized fan power allocations.

QR (m3/s)	Simulated PT (kW)	Simulated QS (m3/s)
200	6.03	205.8
250	11.70	256.7
300	20.20	309.2

. The simulation results demonstrate that the airflow delivered by the fans under all optimized allocations meets or exceeds the required rates, confirming the effectiveness and reliability of the method. In summary, the developed approach enables the optimal allocation of fan power while satisfying the ventilation demand, providing a practical solution for energy-efficient tunnel ventilation control.

4.2. Comparison of Energy-Saving Effect

It can be observed from Table 6 that under the optimized fan power allocation schemes, each pair of parallel fans exhibits closely matched power in the transverse direction. This matching results in minimal outlet velocity gradients, reduces frictional losses and enhances transverse synergy. In the longitudinal direction, fan powers vary by position: upstream fans provide the primary airflow acceleration, while fans near the tunnel exit are allocated lower power, which minimizes the kinetic energy dissipation after exiting the tunnel. This approach ensures the required ventilation airflow while fully exploiting multi-fan synergy, thereby achieving energy-efficient and optimal fan power allocation.

To verify the energy-saving benefits of the proposed method, it is compared against a conventional binary on–off strategy in which all fans operate at equal, constant power. As shown in

Table 8. Comparative energy-saving efficacy under ventilation demands.

QR (m3/s)	Before Optimization			After Optimization			Difference
	Airflow (m3/s)	Power (kW)	Specific Airflow (m3/s·kW)	Airflow (m3/s)	Power (kW)	Specific Airflow (m3/s·kW)	Power (kW)	Specific Airflow (m3/s·kW)
200	199.7	9.56	20.9	205.8	6.03	34.1	−36.9%	+63.2%
250	250.1	18.47	13.5	256.7	11.67	22.0	−36.8%	+63.0%
300	300.2	31.67	9.5	309.2	20.15	15.3	−36.4%	+61.1%

, the optimized power allocation reduces tunnel ventilation energy consumption by approximately 36% and increases the specific airflow by over 60%. The result suggests that compared with the traditional scheme, the proposed optimization method substantially mitigates energy losses arising from inadequate fan synergy and enhances overall energy efficiency.

4.3. Applicability for Varying Tunnel Lengths and Fan Configurations

To further validate the applicability and scalability of the proposed optimization method across tunnel scales, three representative ventilation systems are selected for comparative analysis. Tunnel lengths are set to 500 m, 1000 m, and 1500 m, with corresponding numbers of fans of 6, 10, and 16, respectively. The transverse arrangement and longitudinal spacing (150 m) remain consistent. In the ventilation prediction for new tunnels, only the predictive model for the longitudinal position coefficient lp is retrained based on a small set of CFD results. The models for transverse and longitudinal superposition effects remain unchanged, that is, the previously trained DNN models. As a result, the optimization cost for each new tunnel is significantly reduced, demonstrating excellent transferability.

Optimization, along with CFD verification are conducted, and the resulting tunnel airflow rates are compared with the required rate of 200 m³/s. The results in

Table 9. Applicability of the proposed method to tunnels with different lengths.

Tunnel Length (m)	Number of Fans	QR (m3/s)	Simulated QS (m3/s)	Simulated PT (kW)
500	6	200	205.8	6.03
1000	10		202.4	9.55
1500	16		205.7	10.40

demonstrate that the proposed method satisfies all ventilation demands and exhibits strong applicability across varying tunnel lengths and fan counts. In summary, for diverse tunnel ventilation systems, this approach enables optimal multi-fan power allocation while meeting the ventilation requirements, enhancing ventilation efficiency and reducing energy consumption.

4.4. Limitations and Future Work

This study is based on a straight tunnel model with a constant cross-section, without considering the complex geometry of real tunnels or the effects of natural and traffic-induced winds, which will be studied in further work. Building on the decoupling and equivalent superposition principle, the natural ventilation and traffic-induced airflow can be treated as the background flow field. The comprehensive ventilation airflow is then calculated through an additional longitudinal superposition process. In addition, for tunnels with non-straight alignments or variable cross-sections, the longitudinal position coefficient needs to be appropriately corrected. With these supplementary adjustments, the predictive model can be applied to a practical tunnel ventilation scenario.

5. Conclusions

Focusing on longitudinally ventilated highway tunnels, multi-fan synergistic effects within the flow field are quantified in this work. By decoupling longitudinal and transverse interactions, a rapid predictive model and optimization method for multi-fan ventilation performance is established. Combined with an improved PSO algorithm, the proposed framework determines optimal power allocations under varying ventilation demands. The key conclusions are as follows:

(1)

The synergistic operation of fans in both transverse and longitudinal directions significantly reduces local velocity gradients, lowering frictional loss and enhancing ventilation efficiency. The transverse fan arrangement exerts minimal influence on upstream and downstream velocity distributions, and the background airflow generated by upstream and downstream fans does not substantially affect local transverse synergy. These findings support the decoupling of transverse and longitudinal interactions.

(2)

The prediction of overall ventilation supply by multiple fans is simplified as sequential transverse and longitudinal superpositions, as well as the equivalence of longitudinal positions. Integrating neural-network surrogate models for these superposition effects, the proposed predictive model enables reliable and rapid calculation of ventilation supply. This model exhibits errors of about 3% relative to CFD simulations, thereby facilitating a dynamic supply–demand balance of ventilation rates.

(3)

The proposed optimization method achieves optimal multi-fan power allocation under specific ventilation demands, reducing energy consumption by up to 36% in test scenarios compared with conventional strategies. This improvement arises from enhanced synergistic effects in both transverse and longitudinal directions. Furthermore, the method demonstrates robust applicability across tunnels of different lengths and fan configurations.