Durability Assessment of Marine Steel-Reinforced Concrete Using Machine Vision: A Case Study on Corrosion Damage and Geometric Deformation in Shield Tunnels

Abstract

The rapid urbanization of coastal regions has intensified the demand for durable underground infrastructure like shield tunnels, where reinforced concrete (RC) structures are critical yet susceptible to long-term degradation in marine environments. This study develops an integrated machine vision-based framework for assessing the long-term durability of RC in marine shield tunnels by synergistically combining point cloud analysis and deep learning-based damage recognition. The methodology involves preprocessing tunnel point clouds to extract the centerline and cross-sections, enabling the quantification of geometric deformations, including segment misalignment and elliptical distortion. Concurrently, an advanced YOLOv8 model is employed to automatically identify and classify surface corrosion damages—specifically water leakage, cracks, and spalling—from images, achieving high detection accuracies (e.g., 95.6% for leakage). By fusing the geometric indicators with damage metrics, a quantitative risk scoring system is established to evaluate structural durability. Experimental results on a real-world tunnel segment demonstrate the framework’s effectiveness in correlating surface defects with underlying geometric irregularities. This integrated approach offers a data-driven solution for the continuous health monitoring and residual life prediction of RC tunnel linings in marine conditions, bridging the gap between visual inspection and structural performance assessment.

1. Introduction

The rapid urbanization of coastal and offshore regions has driven an increasing demand for durable and resilient underground infrastructure such as shield tunnels, ports, and subsea transportation systems. Among these, reinforced concrete (RC) structures play a pivotal role due to their high load-bearing capacity and adaptability to complex marine geotechnical conditions [1]. However, under long-term exposure to marine environments, RC structures face severe durability challenges. Ensuring the long-term durability of RC structures in marine conditions is therefore essential for the sustainability and resilience of coastal and offshore infrastructure [2].

The lining structure used in submarine shield tunnels is made of reinforced concrete or steel-fiber-reinforced concrete segments. During its service life, it is corroded by seawater and suffers from water leakage, concrete cracks and other damages. Traditional durability assessment methods, such as manual inspection, destructive testing, or local instrumentation, are often time-consuming and labor-intensive, while lacking the spatial continuity and temporal resolution required for effective long-term monitoring [3]. Furthermore, the degradation of reinforced concrete structures in marine environments is highly nonlinear and spatially heterogeneous, making early detection and quantification particularly challenging using traditional techniques [4]. Therefore, non-contact and data-driven methods are urgently needed to comprehensively and continuously assess the health of structures under harsh service conditions [5,6].

Recent advances in machine vision, 3D sensing, and artificial intelligence (AI) have opened new avenues for intelligent monitoring and durability evaluation of steel-reinforced concrete structures. Specifically, the 3D point cloud-based identification of segment dislocation and cross-sectional deformation in shield tunnels provides a precise and holistic means of quantifying geometric irregularities associated with stress redistribution and material degradation [7,8,9]. By acquiring dense point cloud data through terrestrial laser scanning or structured-light imaging, it is possible to measure segmental misalignment, convergence, and ovalization with millimeter-level accuracy [10,11,12]. These deformation indicators often serve as early manifestations of corrosion-induced cracking or mechanical fatigue, providing a geometric basis for understanding the deterioration process and evaluating the residual mechanical capacity of tunnel linings in marine settings.

When applying machine vision to identify corrosion damage, end-to-end convolutional neural networks (CNNs) are usually used for learning to generate a defect recognition model [13,14]. The more nodes and hidden layers a CNN has, the easier it is to achieve parameter approximation [15]. To further improve recognition efficiency and accuracy, researchers have proposed regional convolutional neural networks (RCNNs), which divide the detection task into three stages: feature pre-training, classification prediction, and bounding box regression [16]. However, these algorithms are currently mainly targeted at single damage detection. Compared with traditional RCNN detection algorithms, YOLO (You Only Look Once) [17] further transforms the target detection task into a unified regression problem. It can predict the position and category of the target in a single forward propagation of the image, thereby facilitating continuous monitoring of corrosion progression in marine RC structures.

The objective of this study is to develop an integrated machine vision-based framework for assessing the long-term durability of reinforced concrete in marine shield tunnels. The integration of visual and geometric information provides a more comprehensive understanding of deterioration mechanisms. Leveraging high-resolution 3D point clouds and advanced deep learning algorithms YOLO-v8, the proposed approach establishes an evaluation process encompassing corrosion recognition, geometric deformation quantification, and mechanical degradation assessment. The general flowchart of the proposed framework is demonstrated in Figure 1.

2. Methodologies

2.1. 3D Point Cloud Preprocessing for Shield Tunnels

2.1.1. Point Cloud Registration and Downsampling

In this section, point cloud registration is employed to merge point clouds from multiple scenes and achieve three-dimensional modeling of the tunnel segment. The registration process consists of two main stages: coarse registration and fine registration. In the coarse registration stage, correspondences between point clouds are established based on the morphological characteristics of the measured objects in different scenes. Subsequently, fine registration is performed to minimize the spatial positional discrepancies between the point clouds obtained from coarse alignment. Since the tunnel lining consists predominantly of curved surfaces, this study adopts the point-to-plane Iterative Closest Point (ICP) fine registration algorithm [18], which offers faster convergence. The objective function of the algorithm minimizes the squared distance from each source vertex to the corresponding target plane, as expressed below:

$$M=\arg {\min }_M{\displaystyle \sum ((M\cdot s_i-d_i)•n_i)}$$

(1)

where M is a 3D rigid transformation matrix composed of rotation and translation, s denotes the source vertex, d represents the target vertex, and n is the normal vector of the target vertex.

$$M=T(t_x,t_y,t_z)\cdot R(\alpha ,\beta ,\gamma )$$

(2)

$$T(t_x,t_y,t_z)=\left(\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right)$$

(3)

$$R(\alpha ,\beta ,\gamma )=\left(\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& 0\\ r_{21}& r_{22}& r_{23}& 0\\ r_{31}& r_{32}& r_{33}& 0\\ 0& 0& 0& 1\end{array}\right)$$

(4)

where r₁₁ = cos γcos β, r₁₂ = −sin γcos α + cos γsin βsin α, r₁₃ = sin γsin α + cos γsin βcos α, r₂₁ = sin γcos β, r₂₂ = cos γcos α + sin γsin βsin α, r₂₃ = −cos γsin α + sin γsin βcos α, r₃₁ = −sin β, r₃₂ = cos βsin α, and r₃₃ = cos βcos α.

Therefore, the minimization of the objective function involves 6 parameters in total. To accelerate the computation, when the relative rotation between the two point clouds is less than 30°, the rotation matrix is linearized by replacing sin θ with θ and cos θ with 1, thereby approximating the nonlinear least-squares optimization problem with a linear model.

After registration, the tunnel point cloud model typically contains a large amount of data, and direct processing requires high computational cost. Therefore, in the preprocessing stage, this study applies voxel grid downsampling [19] to reduce computational complexity by transforming all point cloud operations onto key points while effectively preserving the three-dimensional structural information. Voxel grid downsampling works by voxelizing the 3D space and selecting one representative point from each voxel. The representative point can be the centroid of all points within the voxel or the point closest to the centroid. This method ensures a more uniform distribution of sampled points and provides high computational efficiency. The spacing between sampled points can be controlled by adjusting the voxel size, which is determined by the number of grid divisions along the three coordinate directions of the bounding box or set according to practical requirements. Each voxel contains several original points, and one point—either the centroid or the point nearest to it—is selected as the representative. After processing all voxels, a downsampled point cloud is obtained. The schematic diagram of the voxel downsampling process is shown in Figure 2, and the registered tunnel section after downsampling is illustrated in Figure 3.

2.1.2. Calculation of Tunnel Centerline and Mileage

The extraction of tunnel cross-sections from point cloud data is essential for analyzing structural deformation. The key challenge in cross-section extraction lies in ensuring that the sections are precisely orthogonal to the tunnel’s longitudinal axis. In practice, this process primarily involves several steps: obtaining the projected curve of the tunnel’s centerline on the horizontal plane, rotating the tunnel point cloud so that its alignment coincides with one of the coordinate axes, and then slicing cross-sections perpendicular to that axis. In three-dimensional space, the tunnel centerline is generally represented in a discrete form, expressed as a polyline composed of a sequence of measured points {P₀, P₁, P₂, …, P_n}. For computational convenience, it is assumed that the sampling interval along the x-direction is Δx (in millimeters). The spatial position of the tunnel centerline can then be described as a continuous function through polynomial fitting based on the discrete measurement points. Taking the x-direction as the independent variable, the mathematical expression of the tunnel centerline can be written as:

$$\mathrm{\Theta }=\{(x_i,y_i,z_i)|x_i,a_1\cdot x_i^2+b_1\cdot x_i+c_1,a_2\cdot x_i^2+b_2\cdot x_i+c_2\}(x_i=x_0+i\cdot \Delta x)$$

(5)

where a₁, b₁, c₁, a₂, b₂, and c₂ are the fitting parameters of the tunnel centerline, representing its planar geometry in the y and z directions, respectively. x₀ denotes the x-coordinate of the starting point of the centerline. This formulation enables the conversion of a discrete set of centerline points into a continuous curve, thereby facilitating subsequent chainage calculation and spatial positioning.

In tunnel construction monitoring and data analysis, if the chainage value corresponding to the spatial coordinates (x, y, z) of any measured point inside the tunnel is known, a chainage computation model can be established based on the spatial model of the tunnel centerline, using the chainage information as a reference (as shown in Figure 4). Assume that the chainage at a known point P(x, y, z) is K₀ + 0. By applying the Nearest Point Search [20], the corresponding point p_i(x_i, y_i, z_i) on the tunnel centerline can be determined. This point is considered the projection of the measured point P onto the centerline. Since P and p_i are spatially closest to each other, it can be assumed that they share the same chainage value, that is:

$$p_i(x_i,y_i,z_i)=\min ({(x-x_i)}^2+{(y-y_i)}^2+{(z-z_i)}^2)i=0,1,2,\dots ,n$$

(6)

After determining the chainage value of the reference point p_i, the Cumulative Chord Length Method [21] can be applied to calculate the chainage of any point along the tunnel centerline. For instance, for an arbitrary point p_n(x_n, y_n, z_n) on the centerline, its chainage value can be obtained by sequentially accumulating the spatial distances between adjacent discrete points along the centerline, starting from the reference point p_i, as expressed by the following equation:

$$K(p_n)=K_0+{\displaystyle \sum _{j=i}^{n-1}\sqrt{{(x_{j+1}-x_j)}^2+{(y_{j+1}-y_j)}^2+{(z_{j+1}-z_j)}^2}}$$

(7)

By employing this method, the discretized nature of the tunnel centerline can be effectively utilized to achieve rapid chainage computation at any position along the tunnel axis, while maintaining high accuracy and avoiding complex integral operations.

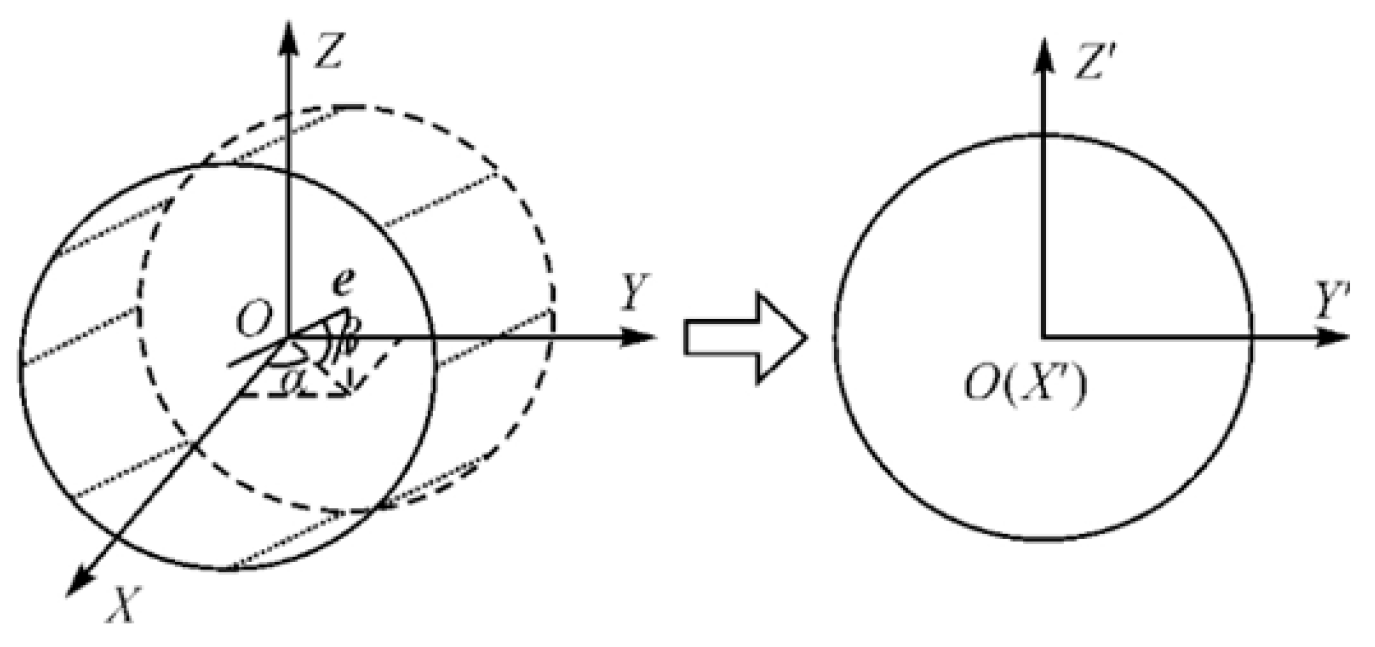
2.1.3. Tunnel Point Cloud Rotation

The tunnel is segmented along the centerline at an interval of d, where the chainage at point O_i(x_i, y_i, z_i) is defined as K₀ + 0. Based on Equation (8), the coordinates of the next point O_i+1(x_i+1, y_i+1, z_i+1) corresponding to the chainage K₀ + d can be calculated. The normal planes passing through points O_i and O_i+1 can be expressed, respectively, as:

$$\left\{\begin{array}{c}x-x_i+y_i^{\prime }(y-y_i)+z_i^{\prime }(z-z_i)=0\\ x-x_{i+1}+y_{i+1}^{\prime }(y-y_{i+1})+z_i^{\prime }(z-z_{i+1})=0\end{array}\right.$$

(8)

where $y_i^{\prime }=2a_1\cdot x_i+b_1$, $z_i^{\prime }=2a_2\cdot x_i+b_2$, $y_{i+1}^{\prime }=2a_1\cdot x_{i+1}+b_1$, ${\mathrm{z}}_{i+1}^{\prime }=2a_2\cdot x_{i+1}+b_2$.

According to Equation (8), the set of scanned points whose chainage values fall within the range of K₀ + 0 to K₀ + d can be obtained as:

$$\begin{array}{l}{\mathbf{\Phi }}_i=\{x,y,z||l_i\ge 0\mathrm{and}{l}_{i+1}\le 0,\\ l_k={\displaystyle \frac{x-x_k+y_k^{\prime }(y-y_i)+z_k^{\prime }(z-z_k)}{\sqrt{1+{y_k^{\prime }}^2+{z_k^{\prime }}^2}}}\}\end{array}$$

(9)

As shown in Figure 5, the discrete point set extracted at point O_i(x_i, y_i, z_i) is rotated around the Z-axis and Y-axis according to the tangent vector at O_i, so that the transformed X-axis becomes parallel to the tunnel centerline:

$$\alpha =\arctan (y^{\prime }),\beta =\arctan ({\displaystyle \frac{z^{\prime }}{\sqrt{1+{y^{\prime }}^2}}})$$

(10)

The coordinate transformation formula is:

$$\left.\begin{array}{c}\begin{array}{l}{[XYZ]}_2^T=R_{\beta }{R}_{\alpha }{[XYZ]}_1^T\\ \end{array}\\ R_{\alpha }=\left[\begin{array}{ccc}\cos \alpha & \sin \alpha & 0\\ \sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]\\ R_{\beta }=\left[\begin{array}{ccc}\cos \beta & 0& \sin \beta \\ 0& 1& 0\\ -\sin \beta & 0& \cos \beta \end{array}\right]\end{array}\right\}$$

(11)

Taking O_i+1 as the new starting point, the point set corresponding to the chainage range of K₀ + 0 to K₀ + 2d is calculated in the same manner, and the process is repeated accordingly.

2.1.4. Tunnel Cross-Section Extraction and Point Cloud Noise Filtering

For any given cross-section of a shield tunnel, its geometric shape can be described by the point cloud data on that section. However, during actual point cloud measurement and processing, the collected data are not continuous data precisely located on a single geometric plane, but rather a series of spatially discrete points distributed along the tunnel’s central axis. To extract the data of a specific cross-section from the 3D point cloud, a sectional slicing thickness d is introduced, and the slicing range is defined with respect to a point on the tunnel’s central axis.

Assuming that the tunnel’s central axis uses the X-axis as the mileage direction, when extracting a given cross-section, all point clouds within the range of d/2 before and after that point on the X-axis are included within the section. That is, the point set Φ(x_i,y_i,z_i) of the point cloud in that section satisfies the following equation, where (x_p,y_p,z_p) is a point on the tunnel’s central axis:

$${\displaystyle \frac{|y_i-y_p+x^{\prime }(x_i-x_p)+z^{\prime }(z_i-z_p)|}{\sqrt{1+{x^{\prime }}^2+{z^{\prime }}^2}}}$$

(12)

Therefore, the section slicing thickness d significantly affects the results of cross-sectional extraction. If the value of d is too small, it may lead to an incomplete description of the cross-sectional geometry, especially causing the loss of detailed features on the tunnel’s inner wall. This, in turn, affects subsequent processes such as cross-section fitting, feature point extraction, and deformation analysis. On the other hand, if d is too large, although the number of point clouds within the slice increases, it introduces a large number of “interference points” that do not lie on the target cross-sectional plane. These may include irrelevant structural features around the tunnel, or even reflections from construction equipment or temporary facilities, all of which can affect the accuracy of the extracted information.

By comparing cross-sectional views of the tunnel obtained with slice thicknesses of 4 cm, 3 cm, 2 cm, and 1 cm, as shown in Figure 6, it can be seen that the smaller the value of d, the fewer point cloud data are included in the section. When d = 1, the cross-sectional point cloud is significantly sparse, with few feature points, which is insufficient for deformation monitoring. When the slicing thickness is 3 cm, the cross-sectional features are clearly visible and the data volume is manageable for subsequent processing (Figure 7).

Point cloud denoising is performed by evaluating the difference between the distance from points within each segmented region of the tunnel to the corresponding division point on the central axis, and the designed tunnel radius r. After denoising the point set Φ_i, the resulting filtered point set Φ_i^′ can be expressed as:

$${\mathbf{\Phi }}_i^{\prime }=\{x,y,z||\left|\sqrt{{(x-x_i)}^2+{(y-y_i)}^2+{(z-z_i)}^2-r}\right|\le \gamma \}$$

(13)

where δ is the denoising threshold, representing the maximum displacement of the tunnel.

2.2. Corrosion Damage Identification for Shield Tunnels

The YOLO series of object detection algorithms have gained widespread attention due to their high efficiency and accuracy [22,23,24]. Among them, YOLO-v8 has been optimized and improved based on previous versions, making the model more flexible in predicting target locations [25]. In this study, the YOLO-v8 deep learning algorithm is utilized to detect bounding boxes of various defects in shield tunnel damage images and to perform classification predictions. The overall workflow of the algorithm is shown in Figure 8, which illustrates the main execution steps and data flow involved in using the improved YOLO-v8 model for tunnel defect detection tasks. In the detection process, the raw tunnel corrosion image, which may contain multiple types of damages such as cracks, spalling, or water leakage, is first used as input. Before being fed into the model, the image undergoes preprocessing operations such as resizing, normalization, and denoising to meet the input size and numerical distribution requirements of the network structure.

Next, the image is passed into a pretrained backbone network for multi-scale feature extraction. During this stage, a series of convolution, activation, and pooling operations are applied to progressively extract low-level texture information and high-level semantic information, generating multiple feature maps that accurately represent the spatial distribution and structural characteristics of different defect regions. After feature extraction, the algorithm proceeds to the bounding box prediction stage. Based on the extracted features, the network’s detection head generates a set of candidate bounding boxes and performs object classification and bounding box regression for each. Each bounding box contains four location coordinates (x, y, w, h) and a classification confidence score corresponding to a defect type, indicating the likelihood that the region contains a specific defect and its type.

As defect regions may produce overlapping detections or redundant predictions, non-maximum suppression (NMS) [26] is applied after the bounding box generation to improve accuracy and clarity. By setting a threshold, the algorithm automatically removes redundant bounding boxes with high overlap and low confidence, retaining only the highest-scoring and most optimal candidate regions, thus preventing multiple detections of the same defect. Finally, the remaining optimal bounding boxes are mapped back to the original image coordinates and visualized as rectangular annotations on the original image, along with the corresponding defect class labels and confidence scores. The output image intuitively displays the spatial distribution and classification of tunnel defects, enabling synchronous recognition and automated annotation of multiple structural defects.

2.2.1. Pre-Trained Network

In the improved YOLOv8 network architecture used in this study, the core feature extraction component is constructed using the deep convolutional neural network Darknet-53 [27]. Structurally, Darknet-53 consists of 53 convolutional layers and incorporates a large number of residual connections to enhance cross-layer information flow and stabilize gradient propagation. This effectively alleviates potential issues such as gradient vanishing and degradation during the training of deep networks. The network is divided into five main stages, each composed of multiple convolutional layers and residual blocks. At the beginning of each stage, downsampling of the feature map is performed using stride-2 convolution operations or pooling operations to extract deeper, more abstract features. Meanwhile, the number of channels doubles progressively with each downsampling operation to ensure that the network captures multi-scale targets and complex structural information.

To further improve the model’s training stability, a batch normalization layer is added after each convolutional layer. By normalizing the activation distribution of each batch of samples, batch normalization helps suppress overfitting and significantly accelerates network convergence. Additionally, global average pooling (GAP) [28] is used before the final classification and regression outputs, instead of traditional fully connected layers. This reduces the number of parameters and computational complexity while enhancing the model’s ability to capture the global semantic context of the image. This architectural design not only improves training efficiency but also enhances the model’s robustness when performing defect detection tasks in the complex environments of tunnel structures.

The convolution module consists of convolution operations, batch normalization, and the SiLU activation function. After the initial features are extracted by the backbone network from the input tunnel damage images, they are further passed to the Feature Pyramid Network (FPN) [29] for multi-scale semantic enhancement. The FPN architecture starts from the top-level feature map, progressively transmitting features with strong semantic information down to lower-level feature maps, while fusing them at each stage. This feature fusion strategy allows shallow feature maps, which retain high resolution, to acquire richer semantic information, thereby facilitating the detection of fine defects such as cracks and spalling. The multi-level feature maps P3, P4, and P5 correspond to different image regions at varying scales to accommodate targets of different sizes.

Although the FPN improves the transmission of high-level semantic information into lower-level feature maps, it remains focused primarily on semantic enhancement and does not fully account for spatial localization information. This limitation can result in localization errors when dealing with defects that have blurred edges, small sizes, or irregular shapes. To overcome this structural limitation, the Path Aggregation Network (PAN) [30] is introduced, constructing a bottom-up feature path to enhance the model’s sensitivity to spatial location. PAN passes the spatial detail information from lower-level features upward to higher-level semantic feature maps, achieving bidirectional fusion of semantics and localization cues. The network also adopts cross-layer connections, combining high-resolution shallow feature maps with deep abstract features—preserving clear target edges and shape details while maintaining strong semantic discrimination. The resulting fused feature maps are finally passed to the detection head for precise localization and classification of defects such as water leakage.

The combined operation of FPN and PAN significantly enhances the model’s ability to perceive targets of various scales and shapes. This is particularly valuable when detecting tunnel defects that vary greatly in size and morphology, such as cracks, leaks, and spalling. With this architecture, the model maintains computational efficiency while gaining a stronger expressive capability—improving the detection accuracy of small-scale defects and enhancing the robustness in locating large-scale structural faults.

The operation layer is the final layer of the algorithm, where a decoupled structure is used to separate classification and bounding box regression. The classifier employs a VariFocal Loss (VFL) based on cross entropy for measurement, which is defined as follows:

$$L_{cls}=VFL(p,q)=\left\{\begin{array}{c}-q(q(\log (p)+(1-q)\log (1-p)),q>0\\ -\alpha p^{\gamma }\log (1-p),q=0\end{array}\right.$$

(14)

where q represents the Intersection over Union (IoU) between the predicted bounding box and the ground truth box, where IoU is calculated as the area of overlap between the two boxes divided by the area of their union. p denotes the score, i.e., the probability.

2.2.2. Bounding Box Prediction

In bounding box prediction, the Anchor-Free mechanism from YOLOv8 is adopted. This approach directly predicts the bounding box by regressing the distances from the object’s center point to its four boundaries (left, top, right, bottom), improving the model’s flexibility and adaptability to varying object scales. In the output layer, the network predicts bounding boxes at three different scales using feature maps of different resolutions. Each candidate region includes four regression coordinates, an object confidence score, and multiple class probabilities for classification tasks. The predicted box positions are obtained by applying offset regression on the feature map grid, which enhances localization accuracy while maintaining detection speed.

Two types of loss functions are used during regression: Distribution Focal Loss (DFL) and CIoU Loss. These enhance the optimization capability for bounding box overlap, center distance, and aspect ratio. DFL converts the boundary box regression problem into a distribution modeling problem, where each coordinate value is modeled as a probability distribution over a discrete interval. Instead of predicting a single coordinate value directly, the network outputs a probability distribution over discrete positions representing possible coordinate values. The cross-entropy loss is then used to optimize the probability distribution around the label y, so that the output distribution is concentrated near the target value:

$$DFL(S_i,S_{i+1})=-((y_{i+1}-y)\log (S_i)+(y-y_i)\log (S_{i+1}))$$

(15)

CIoU Loss not only considers the overlap area between the predicted box and the ground truth box, but also takes into account the distance between their center points and the differences in width and height ratios. Its value is calculated as follows:

$$L_{CIoU}=1-IoU+{\displaystyle \frac{{\rho }^2(b,b^{gt})}{c^2}}+\alpha \upsilon$$

(16)

where b and b^gt represent the centroids of the predicted box and the ground truth box, respectively; ρ denotes the Euclidean distance between the two boxes; c is the diagonal distance of the smallest enclosing box covering both boxes; α is a weighting factor; and v represents the aspect ratio (w/h) similarity, defined as:

$$v={\displaystyle \frac{4}{{\pi }^2}}{(\arctan {\displaystyle \frac{w^{gt}}{h^{gt}}}-\arctan {\displaystyle \frac{w}{h}})}^2$$

(17)

2.2.3. Non-Maximum Suppression

During the adjustment of training hyperparameters, to improve the accuracy and clarity of detection results, this study employs the Non-maximum suppression strategy to ensure that only a single optimal bounding box is retained for each detected corrosion damage. During the forward inference phase, object detection models often predict multiple high-confidence bounding boxes for the same target or region, resulting in overlapping boxes. This phenomenon, known as bounding box redundancy or stacking, significantly reduces the readability of the detection results and the effectiveness of subsequent processing.

To remove these redundant boxes and improve the uniqueness and localization quality of detected bounding boxes, the NMS algorithm is introduced for post-processing the model outputs. In each iteration, the box with the highest confidence (i.e., the model’s most certain prediction of a target) is selected as the current optimal box. Then, all other candidate boxes whose overlap (IoU) with this box exceeds a preset threshold are eliminated, as these highly overlapping boxes are likely duplicate predictions of the same target. In each round, only the highest-confidence box is retained, and the remaining redundant boxes are discarded. This process is iterated until all candidate boxes have been processed.

3. Experimental Procedures

3.1. Geometric Deformation in Reinforced-Concrete Tunnels

Relying on a section of a shield tunnel under construction in a cross-river tunnel project in Ningbo, the tunnel structure after completion is selected as the research subject. The shield tunnel in this section adopts standard segmental assembly, with a single ring width of 1.5 m, and each ring is composed of four segments. Starting from the first wedge-shaped segment and following the counterclockwise direction of assembly, the four segments are numbered sequentially as 1, 2, 3, and 4. In the obtained 3D point cloud model, the positions and structural forms of the circumferential joints between the rings can be clearly identified. To visually represent the geometric characteristics of the inspection target, a 3D point cloud schematic of the segment joint misalignment is drawn (Figure 9). As shown in the locally enlarged details in the figure, there exists a certain height difference between adjacent segments, i.e., a misalignment phenomenon. This is manifested as a significant discontinuity in the normal height between the surfaces on both sides of the joint, with noticeable local bulges or depressions. Such irregularities not only affect the overall smoothness of the structure but may also adversely impact the durability of the reinforced concrete structure during long-term operation.

Figure 10 illustrates the schematic principle of the segment misalignment detection method adopted in this study. By analyzing the local 3D geometric shapes of the two segment surfaces on either side of the assembly joint, the central axis of the joint is extracted, which serves as a baseline for subsequent misalignment calculation. The point cloud data of the two adjacent segments near the assembly joint is unfolded and transformed into coordinates, and then projected onto the yoz plane, allowing the geometric features along the joint direction to be intuitively represented in 2D space. The parametric equation of the central axis of the joint on the projection plane along the y-axis is given by:

$$a_j={\displaystyle \frac{1}{n+1}}{\displaystyle \sum _{i=0}^n{a}_{kj}},b_j={\displaystyle \frac{1}{n+1}}{\displaystyle \sum _{i=0}^n{a}_{bj}}$$

(18)

where a_j and b_j are the parameters of the j-th term of the central axis equation, and n represents the total number of coordinate rotation transformations.

After the above processing, the final equation of the central axis can be obtained as:

$$x={\displaystyle \sum _{j=0}^2{a}_j{y}^j,z=}{\displaystyle \sum _{j=0}^2{b}_j{y}^j}$$

(19)

Following the method described earlier, the 3D unfolded point cloud within each ring is obtained based on the central axis. From the unfolded point cloud, a tunnel slice with a thickness of 3 mm along the y-axis is extracted. The location of the segment joint is determined by identifying variations in point cloud spacing combined with the designed assembly values of the tunnel segments. Based on the location of the assembly joint, the unfolded point clouds of the two segments at the joint are extracted. Since each tunnel ring is assembled from 4 segments, there are 3 joints within each ring. Taking the joint between segments 2 and 3 as an example, the misalignment at the joint within the ring is detected and analyzed. The point cloud at the 2–3 segment joint is projected onto the yoz plane to extract the boundary points. The misalignment is then calculated from the two segment boundary lines. On the yoz projection plane, the relative misalignment of segment 2 with respect to segment 3 ranges from −3.5 mm to 1.7 mm. At the beginning of the joint, segment 2 is recessed by 3.5 mm compared to segment 3, while at the end of the joint, segment 2 protrudes by 1.7 mm compared to segment 3. The average misalignment is −0.9 mm, indicating that segment 2 is, on average, recessed by 0.9 mm compared to segment 3 at the joint.

The range and average values of the misalignment at each joint are calculated from the point cloud data, and the results are shown in

Table 1. Ring segment misalignment measurement table.

Segment No.	Misalignment/mm
	Range of Misalignment	Average Value	Measured Value	Error
1–2	0.2~0.8	0.5	1	0.5
2–3	−3.5~1.7	−0.9	1	0.1
3–4	0.4~2.0	1.2	2	0.8

. Misalignment refers to the relative displacement between two adjacent segments at the joint: a misalignment greater than 0 indicates that the first segment protrudes relative to the second, while a misalignment less than 0 indicates that the second segment is recessed relative to the first. From Table 1, it can be seen that the maximum misalignment occurs at the 3–4 joint, with an average value of 1.2 mm, meaning segment 4 protrudes 1.2 mm more than segment 3. The minimum misalignment occurs at the 1–2 joint, with a value of 0.5 mm, indicating that segment 2 protrudes 0.5 mm more than segment 1. Comparing the misalignment values detected by the method in this paper with field measurements using calipers and feeler gauges, the maximum error is 0.8 mm and the average error is 0.5 mm, which meets the detection requirements. Previous studies and engineering practice suggest that misalignment values below 2–3 mm are typically acceptable for shield tunnel linings. The maximum average misalignment detected in this study is 1.2 mm, with a maximum measurement error of 0.8 mm compared to field measurements, indicating that the segment joints are generally well aligned and within acceptable tolerance limits.

The test area selected for the cross-sectional deformation detection is a circular shield tunnel section, approximately 36 m in length, with an inner lining diameter of 5.5 m. The lining consists of precast reinforced concrete segments. The point spacing is less than 1 cm, and the data acquisition accuracy is 2 mm. A total of 185,142,624 points were collected, which were then downsampled to 41,246 points. The tunnel’s central axis was first extracted using the method described previously, and the resulting equation of the central axis is as follows:

$$\left.\begin{array}{c}x=-0.0005121y^2+1.502y+7.258\\ z=-0.0000696y^2+0.023y-1.623\end{array}\right\}$$

(20)

On this basis, the automatic extraction of tunnel cross-sectional point sets is carried out. The starting point for section extraction along the central axis is set at 2 m from the tunnel entrance, with an extraction interval of 2 m. An appropriate slice thickness is also specified—in this experiment, the slice thickness d is set to 3 cm for tunnel cross-section extraction. For each cross-section, a noise filtering threshold γ of 2 mm is applied, and points within the threshold γ are projected onto the section plane. Ultimately, 18 cross-sectional point sets are obtained, as shown in Figure 11a. To more accurately analyze both local and overall deformation of the tunnel, noise removal is performed on the cross-sectional data following the method described previously. Figure 11b shows the result of noise removal for the cross-sectional point sets (S12 represents the 12th cross-section).

The tunnel in the test area adopts a segmental lining, with a designed inner diameter of 5.5 m. Due to the high precision of segment assembly, the alignment tolerance can be neglected. Therefore, the theoretical radius of the tunnel inner wall, 2.75 m, is taken as the reference value. Based on the 18 fitted elliptical cross-sections, the major and minor axes were statistically analyzed, subtracting the theoretical radius to obtain the maximum deformation distribution curves in the transverse and longitudinal directions.

The results show that the maximum transverse deformation ranges from 0 to 12 mm, indicating that the major axes of all cross-sections are larger than the theoretical radius, and the tunnel exhibits slight stretching in the horizontal direction, with the most significant stretching occurring at the 10th cross-section. The maximum longitudinal deformation ranges from −22 to 0 mm, indicating that the minor axes of all cross-sections are smaller than the theoretical radius, and the tunnel generally shows a contraction trend in the vertical direction, with the most pronounced contraction at the 6th cross-section. To better evaluate the engineering significance of the detected deformation, the measured diameter variation, ellipticity, and segment misalignment are interpreted in relation to commonly reported tolerance ranges and maintenance thresholds in shield tunnel engineering practice. For circular shield tunnels with an inner diameter of approximately 5–6 m, horizontal or vertical diameter variations within ±25–30 mm (5%) are generally regarded as serviceable deformation levels, while larger deviations may require detailed structural assessment or corrective measures. In this study, the maximum detected horizontal deformation is 12 mm, and the maximum vertical contraction is 22 mm, both of which remain within the commonly reported serviceability range, indicating that no immediate structural intervention is required.

Since each cross-sectional curve is fitted using an elliptical model, the ellipticity indicates how closely the cross-section conforms to an ellipse. A larger ellipticity value signifies greater overall deformation of the tunnel cross-section. According to Equation (21), the ellipticity of each cross-section can be calculated. The calculation results are shown in

Table 2. Ellipticity of each section.

Section No.	Ellipticity	Section No.	Ellipticity	Section No.	Ellipticity
S1	0.0084	S7	0.0087	S13	0.0083
S2	0.0107	S8	0.0104	S14	0.0062
S3	0.0082	S9	0.0098	S15	0.0108
S4	0.0090	S10	0.0112	S16	0.0067
S5	0.0082	S11	0.0097	S17	0.0074
S6	0.0103	S12	0.0099	S18	0.0071

, where the maximum ellipticity is 0.0112, occurring at the 10th cross-section. Additionally, ellipticity values exceeding approximately 0.01 are often considered indicative of noticeable cross-sectional deformation and may warrant closer inspection or monitoring. The results in Table 2 show that the ellipticity values of the 2nd, 6th, 8th, and 15th cross-sections all exceed 0.01, indicating that these locations exhibit relatively large overall deformation. These findings suggest localized deformation concentration rather than global structural instability. Overall, the combined analysis indicates that the investigated tunnel section is currently in a mild deformation state. While the detected deformation and misalignment levels do not pose an immediate threat to structural safety, the presence of locally elevated ellipticity and repeated deformation peaks suggests the need for targeted inspection and long-term monitoring to prevent potential progression that could affect durability and service performance.

$$\mathrm{Ellipticity}={\displaystyle \frac{\mathrm{Maximum}\mathrm{outer}\mathrm{diameter}-\mathrm{Minimum}\mathrm{outer}\mathrm{diameter}}{\mathrm{Theoretical}\mathrm{radius}}}$$

(21)

3.2. Corrosion Damage Detection in Reinforced-Concrete Tunnels

3.2.1. Dataset Creation and Training Parameter Configuration

Image data acquisition was primarily accomplished in two ways: first, maintenance personnel used high-resolution smart terminals to capture raw photos of tunnel internal structural damage during routine inspections, as shown in Figure 12a; second, orthophotos were generated from point cloud data collected by equipment equipped with a laser scanning system, as shown in Figure 12b. This ensured both image quality and data authenticity and engineering applicability. To enhance the model’s ability to identify tunnel damage features under different working conditions, increase the diversity of training samples, and effectively mitigate the risk of model overfitting, data augmentation was performed on the original image samples. The main methods employed were: translation transformation, which enhanced the model’s robustness to target position shifts through random horizontal and vertical displacements; Gaussian noise addition, which simulated photosensitive noise that might occur during image acquisition, improving the model’s ability to recognize low signal-to-noise ratio images; mirror flipping, including horizontal and vertical flipping, which expanded the coverage of image orientation changes; and angular rotation, which enhanced the model’s adaptability to changes in image viewing angle.

Table 3. Data augmentation strategies and parameters.

Augmentation Method	Description	Parameter Range	Application Probability
Translation	Random horizontal and vertical shifting	±10% of image width/height	0.3
Gaussian noise	Addition of Gaussian noise to simulate sensor noise	Mean = 0, Variance = 0.01	0.2
Mirror flipping	Horizontal and vertical flipping	Horizontal/Vertical	0.5
Rotation	Random angular rotation	−15° to +15°	0.3

shows the applied transformations, including translation, Gaussian noise addition, mirror flipping, and rotation, together with their parameter ranges and probabilities. A total of 5700 tunnel corrosion damage images were obtained, and they were divided into training, validation and test sets in a ratio of 7:2:1, with 3990 images in the training set, 1140 images in the validation set and 570 images in the test set.

The open-source image annotation tool LabelImg was used to finely label the tunnel images in the training set, ensuring consistent labeling quality and category uniformity for the defect targets. Based on the classification standards for common structural defects in tunnels, three typical types of corrosion damage were labeled in the dataset: “water leakage”, “crack” and “spalling”. All annotations were performed using rectangular bounding boxes, and a secondary review was conducted to avoid missed or incorrect labels, providing accurate training labels for subsequent supervised learning.

The training experiments were conducted on a computer equipped with a Core i9-9900k @3.60 GHz CPU and an 11 GB NVIDIA GeForce RTX 2080Ti GPU, using a deep learning environment configured with Python 3.8, Cudatoolkit 11.3.1, Cudnn 8.2.1, and Pytorch 1.12.1. Before training, all model parameters were randomly initialized to prevent the model from falling into local minima. Additionally, pixel-level normalization was applied to the input images, mapping each pixel value into a unified numerical range to accelerate model convergence. The optimizer used was Stochastic Gradient Descent (SGD), with an initial learning rate of 0.01 and a momentum coefficient of 0.937 to enhance parameter updates between iterations. To prevent overfitting and gradient explosion caused by excessively large weight values, a weight decay coefficient of 0.0005 was set. The batch size for the experiment was 8, with each iteration including multiple regions of interest to compute loss gradients and update the weights. The entire training process ran for 150 epochs, and the loss gains for bounding boxes, classes, and DFL (Distribution Focal Loss) were set to 7.5, 0.5, and 1.5, respectively—this hyperparameter combination was validated as optimal in preliminary experiments. Under these configurations and parameter settings, the training process for the tunnel defect recognition model took approximately 5 h in total.

3.2.2. Model Evaluation Index Analysis

During the model training process, several visualization charts are automatically generated, including a label heatmap and a label distribution chart, which are used to inspect and analyze the quality and distribution of the dataset labels. As shown in Figure 13, the first chart shows the number of samples for each damage category in the training set; the second chart displays the sizes and counts of the detection bounding boxes; the third chart shows the relative positions of the object centers within the image; and the fourth chart illustrates the height-width proportions of the target objects relative to the entire image. The label heatmap visualizes the distribution of bounding box center points across all training images, with the color intensity reflecting target density. This helps reveal whether the objects in the dataset are evenly distributed or if issues such as positional bias, occlusion, or concentration in specific image regions exist.

In the label heatmap of this experiment, the category distribution bar chart (top left) shows the instance count for each of the three target categories: approximately 1500+ instances of “water leakage,” about 700 instances of “spalling,” and around 400 instances of “cracks.” A clear class imbalance is observed, with “water leakage” being the dominant category. Such imbalance may result in poorer recognition performance for the “crack” class, so techniques like downsampling or focal loss adjustment could be considered in future work to mitigate this issue. The bounding box schematic (top right) shows the outlines of all bounding boxes in red, overlaid in a unified coordinate system. This helps visualize the overall distribution and sizes of the boxes. Most bounding boxes are small and concentrated in specific areas, indicating a consistent target location pattern across samples, which is beneficial for faster model convergence.

The target center point distribution heatmap (bottom left) shows the distribution of all bounding box centers within the images (normalized x-y coordinates). The centers are concentrated in the middle-lower region, indicating that most structural damage occurs near the midsection of the tunnel segments. Overall, the distribution is relatively uniform, with no noticeable bias or missing regions. The target bounding box size distribution chart (bottom right) displays the width and height of each bounding box. Most bounding box widths fall within the range of 0.02 to 0.05, and heights are mostly within 0.05 to 0.15. This indicates that the model needs to be capable of effectively detecting small-scale damage targets.

The bounding box size and position distribution diagrams illustrate the relationships among the center point coordinates (x and y) and the box dimensions (width and height). The x-y center point distribution map shows where target centers are located within the images, while the w-h size distribution map displays the spread of target widths and heights within the dataset. These diagrams help analyze the spatial distribution and size variation in targets, providing guidance for designing the model’s receptive field or setting anchor box priors. As shown in Figure 14, the horizontal (x) distribution of target centers is approximately uniform across the 0 to 1 range, with a slight concentration in the middle, showing no significant positional bias. The vertical (y) distribution is concentrated between 0.3 and 0.7, indicating that most targets are located in the mid-to-lower region of the images. This suggests that the sampling coverage is adequate and reflects that defects frequently occur near segment edges or joints, areas that require attention during maintenance.

The distribution of bounding box widths peaks between 0.02 and 0.05, indicating that the widths of most targets are relatively small; a few widths exceed 0.1, which may correspond to more severe spalling areas. The heights are mainly distributed between 0.05 and 0.15, with a few values above 0.2. Overall, the bounding boxes are small, with heights slightly larger than widths, indicating that the targets generally exhibit a “vertically elongated” structure, consistent with the appearance of cracks or spalling streaks. The x-y joint distribution plot shows that the center points are concentrated in the central region of the images. In the width-height plot, data points cluster in the lower-left corner, confirming that targets are small in size with modest variation. No strong correlation is observed between x and width or between y and height, suggesting that target position and size are largely independent.

Figure 15 presents several examples of defect detection performed on images from the test set. As shown in the figure, the proposed model can accurately identify and localize multiple types of typical tunnel defects, including water leakage, cracks, and concrete spalling. The predicted bounding boxes effectively cover the defect regions, with few false positives or missed detections, demonstrating reliable localization performance. To provide a more comprehensive evaluation of the detection performance, multiple quantitative metrics were adopted, including Precision, Recall, F1-score, mAP@50, and mAP@50–95, as summarized in

Table 4. Quantitative performance metrics of defect detection on the test set.

Defect Type	Precision (%)	Recall (%)	F1-Score (%)	mAP@50 (%)	mAP@50–95 (%)
Water leakage	95.6	100.0	97.8	99.0	91.2
Crack	88.5	86.7	87.6	88.2	72.6
Concrete spalling	93.2	92.4	92.8	95.0	85.8

. mAP@50 denotes the mean Average Precision at an IoU threshold of 0.5, while mAP@50–95 represents the averaged mAP over IoU thresholds from 0.5 to 0.95 with a step size of 0.05. The results demonstrate that the model achieves a high average prediction accuracy across different defect categories. Specifically, for water leakage detection, the model performs particularly well, achieving an average prediction accuracy of 95.6%, indicating strong capability in feature extraction and classification for this defect type. The average prediction accuracy for crack detection is 88.5%, which, while slightly lower than the other two categories, is still at a high level, showing that the model is well-suited for fine-grained structural damage identification. For concrete spalling detection, the average prediction accuracy reaches 93.2%, demonstrating the robustness of the model. Crack detection shows slightly lower but still competitive performance, which is mainly attributed to the fine-scale and irregular morphology of crack features. Concrete spalling detection demonstrates robust accuracy and localization performance.

4. Risk Scoring-Based Durability Assessment

The durability of tunnel structures is critically influenced by the presence and development of surface defects such as water leakage, cracking, and concrete spalling. Based on the analysis of the test dataset and the performance of the defect detection model, a comprehensive assessment of the tunnel’s durability was conducted. The spatial distribution of damages—as visualized through heatmaps and bounding box analyses—reveals that most anomalies are concentrated in the lower-mid regions of the tunnel lining. This clustering is consistent with typical wear mechanisms caused by groundwater infiltration, joint degradation, and sustained mechanical stress. Crack damages often appear as vertically elongated thin structures, reflecting tensile stress concentrations along structural joints. Spalling tends to present as larger but localized surface damage, indicating potential loss of protective concrete cover and exposure of reinforcement. Given the frequency and distribution of the detected defects, the evaluated tunnel section exhibits early-stage durability concerns, particularly in regions with repeated leakage and spalling. Therefore, geometric deformation metrics and corrosion damage metrics are quantified into terms that can be directly calculated:

Maximum Deformation ${∆}_r$:

$${\Delta }_r=r_{meas}(\theta )-r_{theo}$$

(22)

Ellipticity E:

$$E={\displaystyle \frac{a-b}{r_{theo}}}$$

(23)

where a is major axes, and b is minor axes.

Leakage Intensity L:

$$L={\displaystyle \frac{S_{\mathrm{water}\text{\_}\mathrm{leakage}}}{S_{\mathrm{pixel}\text{\_}\mathrm{area}}}}$$

(24)

Crack Index C:

$$C={\displaystyle {\sum }_i{l}_i\cdot w_i}$$

(25)

where ${\displaystyle {\sum }_i{l}_i}$ is cumulative crack length, $w_i$ refers to mean width.

Spalling Area Ratio S:

$$S={\displaystyle \frac{S_{\mathrm{spalling}}}{S_{\mathrm{total}\text{\_}\mathrm{lining}\text{\_}\mathrm{area}\text{\_}\mathrm{per}\text{\_}\mathrm{ring}}}}$$

(26)

and Multi-defect Overlap Index O, which is the frequency of spatial overlap between damaged regions.

To obtain a comparable risk score R, each indicator M can first be linearly normalized to [0, 1] as following:

$$\tilde{M}={\displaystyle \frac{M-M_{\min }}{M_{\max }-M_{\min }}}$$

(27)

Then risk scores can be calculated using a weighted composite method based on the project weights:

$$R=w_1\widetilde{{\Delta }_r}+w_2\tilde{E}+w_3\tilde{C}+w_4\tilde{S}+w_5\tilde{L}+w_6\tilde{O}$$

(28)

where ${\displaystyle \sum w_i=1}$.

The weight coefficients w₁–w₆ reflect the relative contribution of geometric deformation indicators and corrosion-related damage indicators to tunnel durability. In this study, the weights were determined based on expert knowledge and engineering experience reported in existing tunnel inspection and durability assessment literature, with greater emphasis placed on indicators directly associated with structural safety and corrosion progression. Specifically, deformation-related metrics and surface deterioration indicators such as leakage intensity, crack index, and spalling area ratio were assigned higher weights due to their strong correlation with long-term durability degradation. It should be noted that the objective of this work is to establish a unified and extensible risk evaluation framework rather than to derive optimal weights for a specific tunnel case. More rigorous weighting strategies, such as Analytic Hierarchy Process (AHP), Fuzzy AHP (FAHP), or sensitivity analysis, will be adopted in future studies when sufficient expert survey data and long-term monitoring records become available.

To ensure comparability among different indicators, each metric is linearly normalized to the range [0, 1]. The minimum and maximum values used in the normalization process are determined based on the observed value range of the test dataset, supplemented by reference thresholds reported in relevant engineering specifications and previous studies. This approach allows the normalized indicators to reflect both actual measured conditions and practical engineering limits. The risk scores are divided into four levels: 0.0–0.2: Normal, routine inspection; 0.2–0.5: Attention, schedule short-term reinspection or local health monitoring; 0.5–0.8: Repair needed, develop maintenance plan and intensify monitoring; 0.8–1.0: Emergency, immediate onsite measures or traffic closure (depending on structural criticality). These risk classes are adapted from commonly adopted engineering risk classification practices in tunnel inspection and maintenance management, providing a practical and interpretable basis for durability evaluation. In this experiment, w₁ = 0.2, w₂ = 0.15, w₃ = 0.2, w₄ = 0.2, w₅ = 0.15, w₆ = 0.1, and the risk level is calculated as the first level.

In order to assess the risk of corrosion and estimate the service life of marine steel-reinforced concrete structures, leakage intensity L, spalling area ratio S and crack index C are combined to infer the concrete cover deterioration and moisture ingress. If S > threshold or persistent L > 0, the likelihood of carbonation or chloride ingress increases. The probability of rebar exposure can be calculated using the spalling area ratio S and crack index C as indicators of cover integrity:

$$P_{ex}=1-\exp (-{\alpha }_{1}S-{\alpha }_{2}C)$$

(29)

where parameters α₁, α₂ calibrated via sample tests or historical data.

The corrosion rate of reinforced steel can be simplified by the following formula:

$${\upsilon }_{\mathrm{corr}}\propto {\beta }_1{P}_{ex}+{\beta }_{2}L+{\beta }_3$$

(30)

where β₃ are environment factors.

Given allowable steel loss ΔA_allow, the remaining service life estimation can be obtained as follow:

$$T_{\mathrm{rem}}\approx {\displaystyle \frac{\Delta A_{\mathrm{allow}}}{{\nu }_{\mathrm{corr}}}}$$

(31)

5. Conclusions

This study proposes an integrated approach for the durability assessment of reinforced concrete tunnel structures by combining geometric deformation analysis based on point cloud data and corrosion damage recognition driven by deep learning. Through extraction of tunnel centerlines and cross-sectional profiles, the geometric parameters such as radial deformation and ellipticity were quantitatively evaluated, enabling the characterization of the tunnel’s spatial and temporal deformation patterns. Meanwhile, a YOLOv8-based detection model was developed for the automatic identification of typical structural damages, including water leakage, cracks, and concrete spalling, achieving high detection accuracy: 95.6% for water leakage, 88.5% for cracks, and 93.2% for spalling, demonstrating robust localization performance across diverse scenarios.

By integrating the 2D detection results with the 3D geometric information, the study establishes a multi-dimensional fusion framework that correlates visible surface damages with underlying structural deformations. This integration allows for a comprehensive understanding of both surface deterioration and internal mechanical distortion, effectively bridging the gap between visual inspection and structural health assessment. Furthermore, a quantitative durability evaluation model was developed by normalizing and weighting multiple geometric and defect indicators, yielding a unified risk index R capable of ranking sections by their deterioration severity and maintenance priority. Experimental results demonstrate that the proposed method can accurately locate deformation-prone and defect-concentrated regions. The high correspondence between areas of severe deformation and concentrated surface damage suggests that combined monitoring of geometry and visual defects provides a more reliable basis for predicting corrosion progression and residual service life of reinforced concrete linings.

Future research will focus on enhancing the coupling between geometric deformation analysis and surface defect recognition to achieve a more comprehensive evaluation of the structural health of tunnel linings. In particular, the durability assessment model can be further improved through on-site sampling and laboratory calibration, including measurements of concrete chloride content, cover thickness, and steel corrosion rate tests, as well as by leveraging historical databases from similar tunnel environments. These data sources will be used to calibrate and validate the empirical parameters in the proposed models, thereby improving the accuracy, adaptability, and predictive reliability of the durability evaluation framework.