Research on the Shear Performance of Concrete Beams Strengthened with Lateral External Prestressing
Abstract
1. Introduction
2. Experimental Design
2.1. Materials and Their Properties
2.2. Experimental Design and Parameters
2.3. Reinforcement Scheme for the Beam
2.4. Test Equipment and Loading Scheme
3. Test Result Analysis
3.1. Summary of Failure Process and Results of Specimens
3.2. Stress Analysis of Specimens
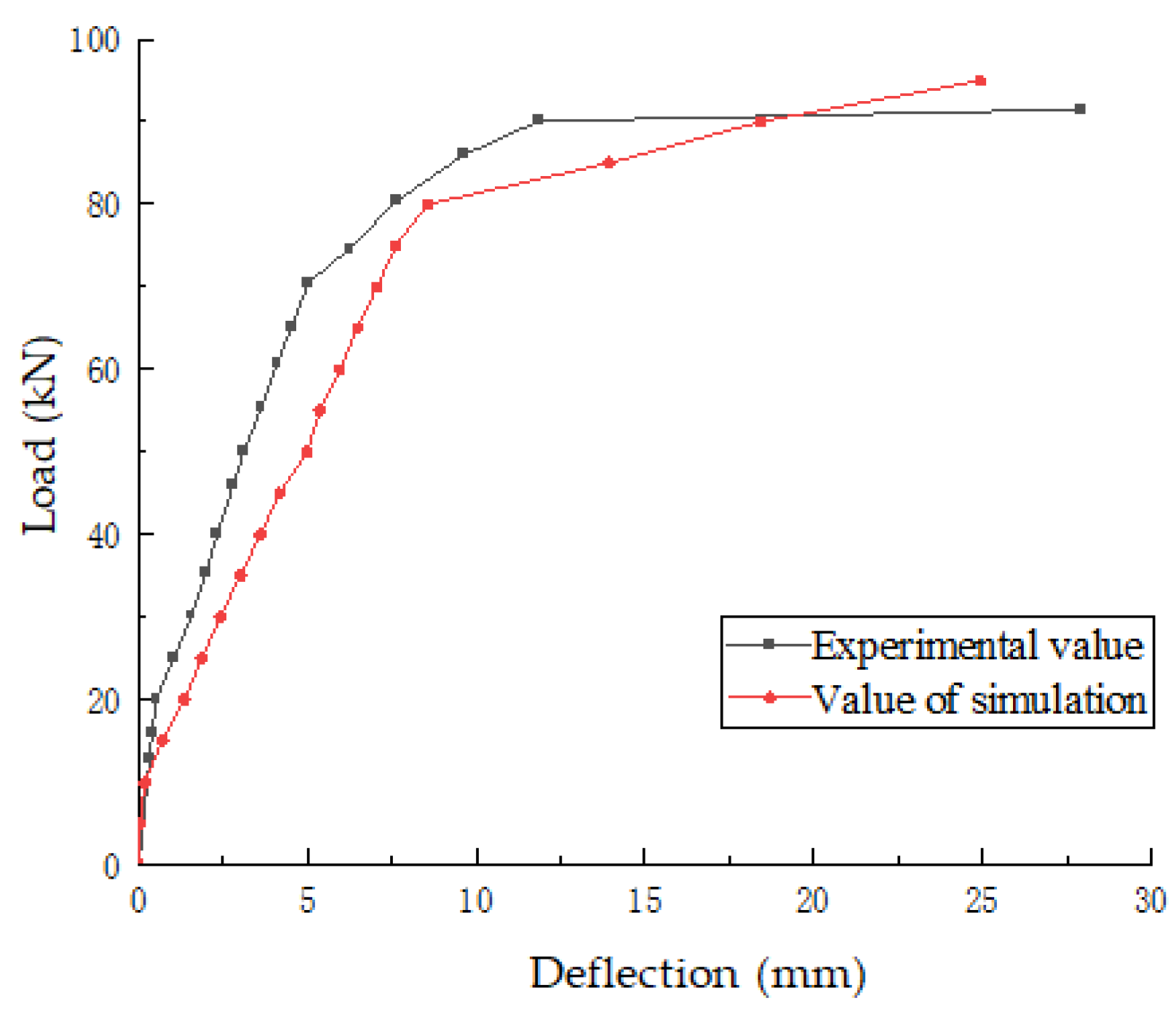
3.2.1. Analysis of Load–Deflection Curves
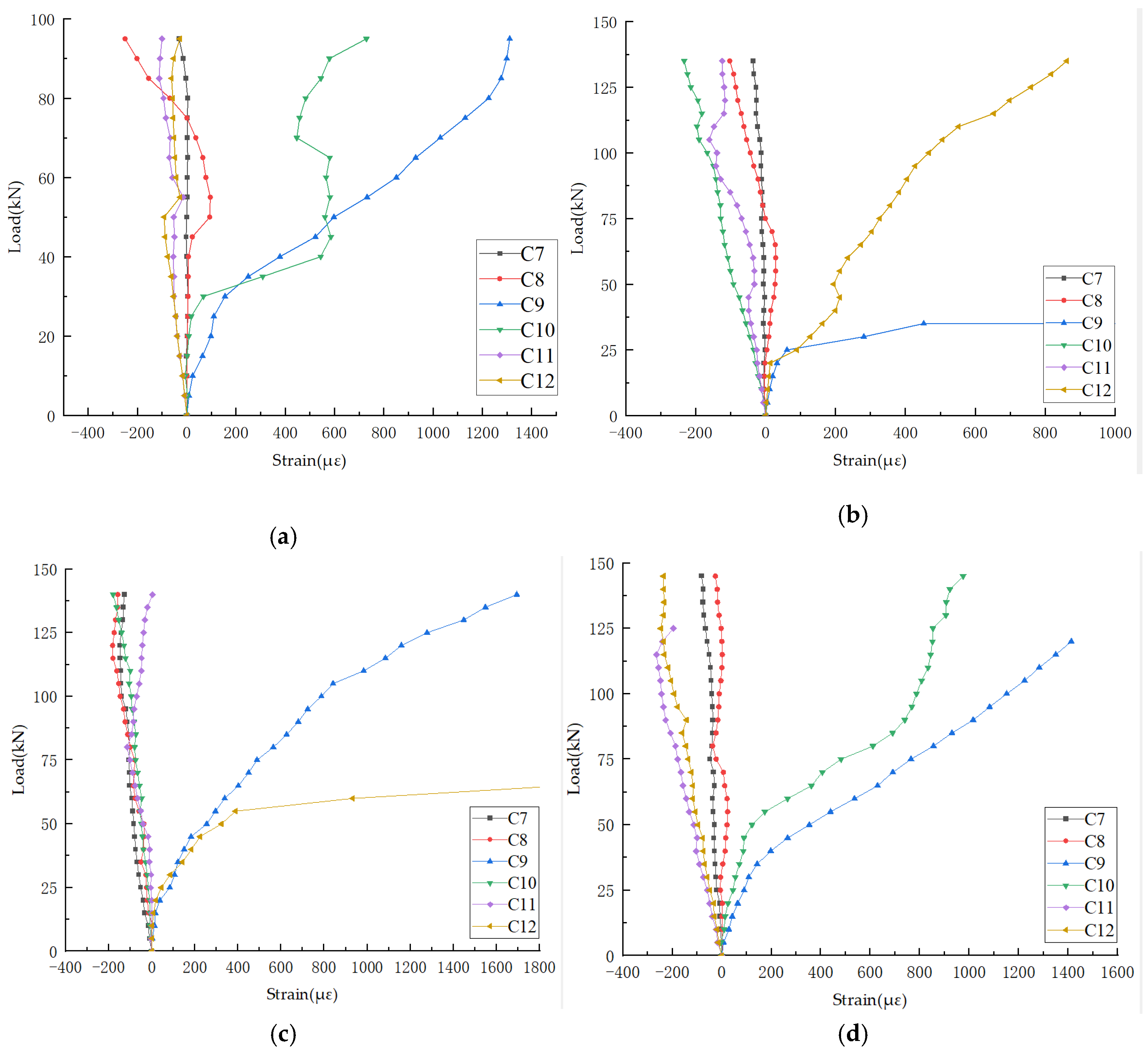
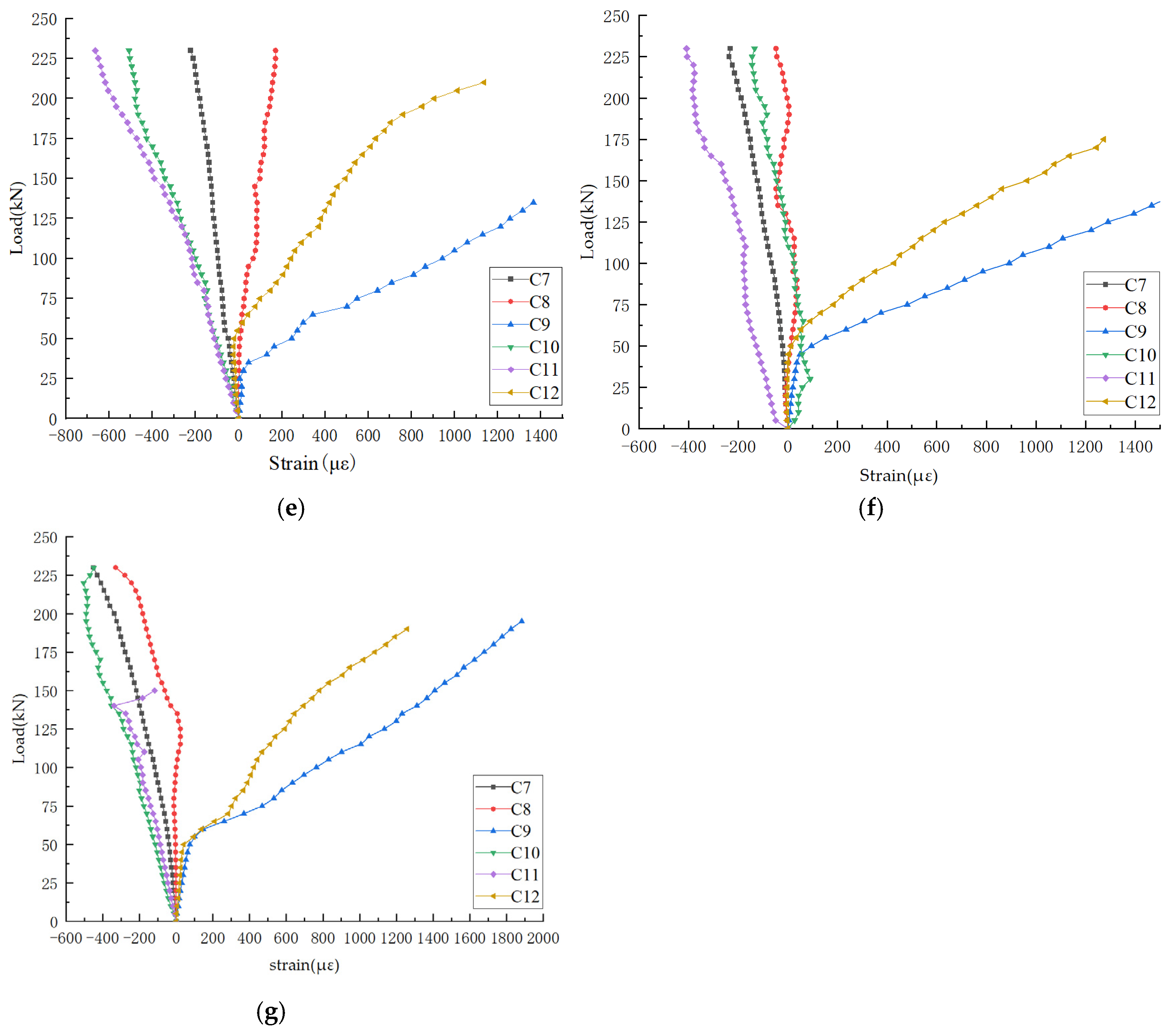
3.2.2. Stirrup Strain Responses
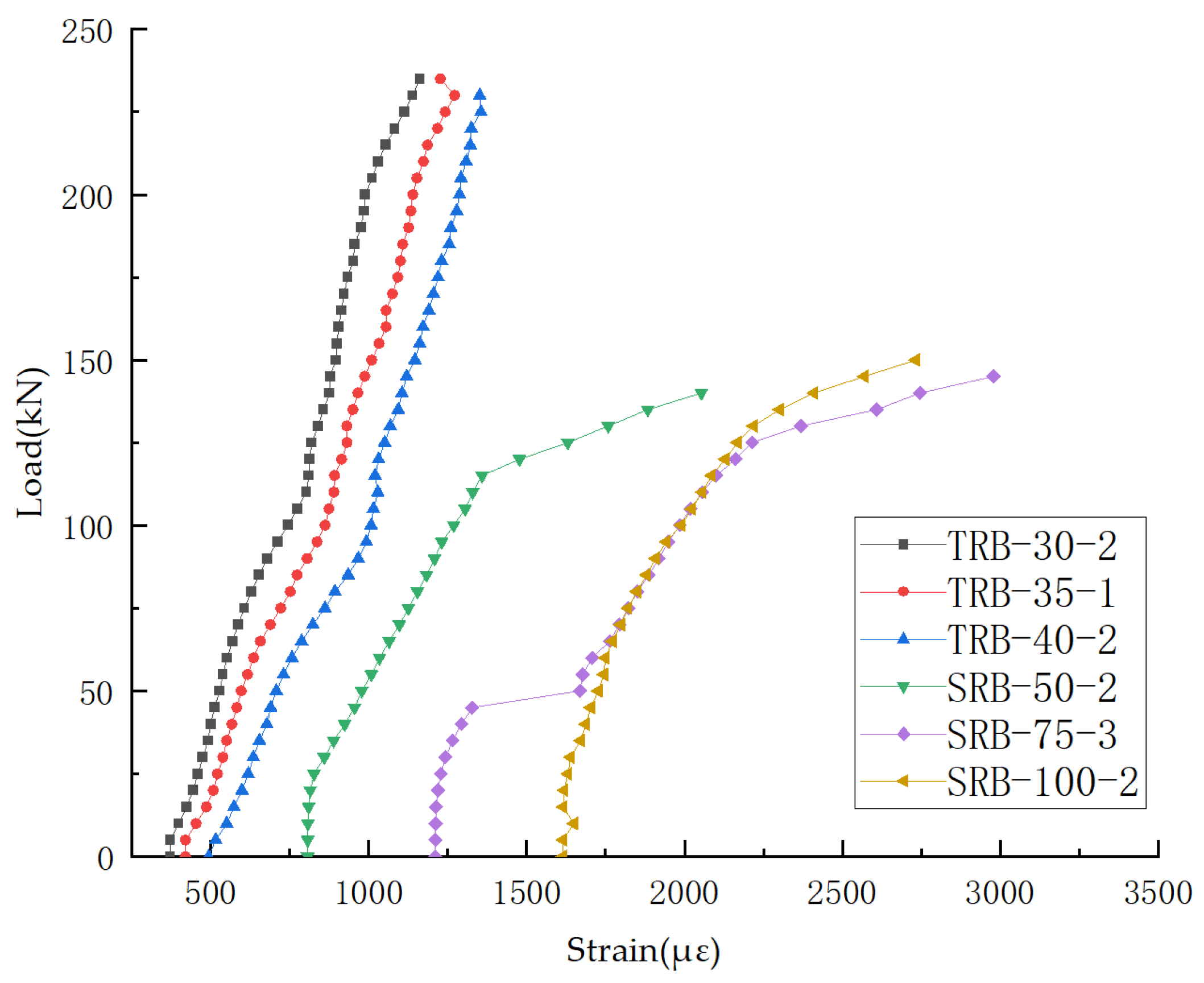
3.2.3. Stress Analysis of Prestressing Steel Bars
3.2.4. Analysis of Concrete Stresses
4. Finite Element Analysis of External Prestressed Reinforced Concrete Beams
4.1. Establishment of ABAQUS Finite Element Model
4.1.1. Steel Constitutive Model
4.1.2. Constitutive Model of Long Bolts
4.1.3. Concrete Constitutive Model
- (1)
- Under a uniaxial tensile load:
- (2)
- Under uniaxial pressure:
4.1.4. Establish Model and Mesh Division
4.1.5. Verification of Software Analysis Results
5. Suggested Formula for Shear Capacity
5.1. Analysis of Influencing Factors on Shear Performance
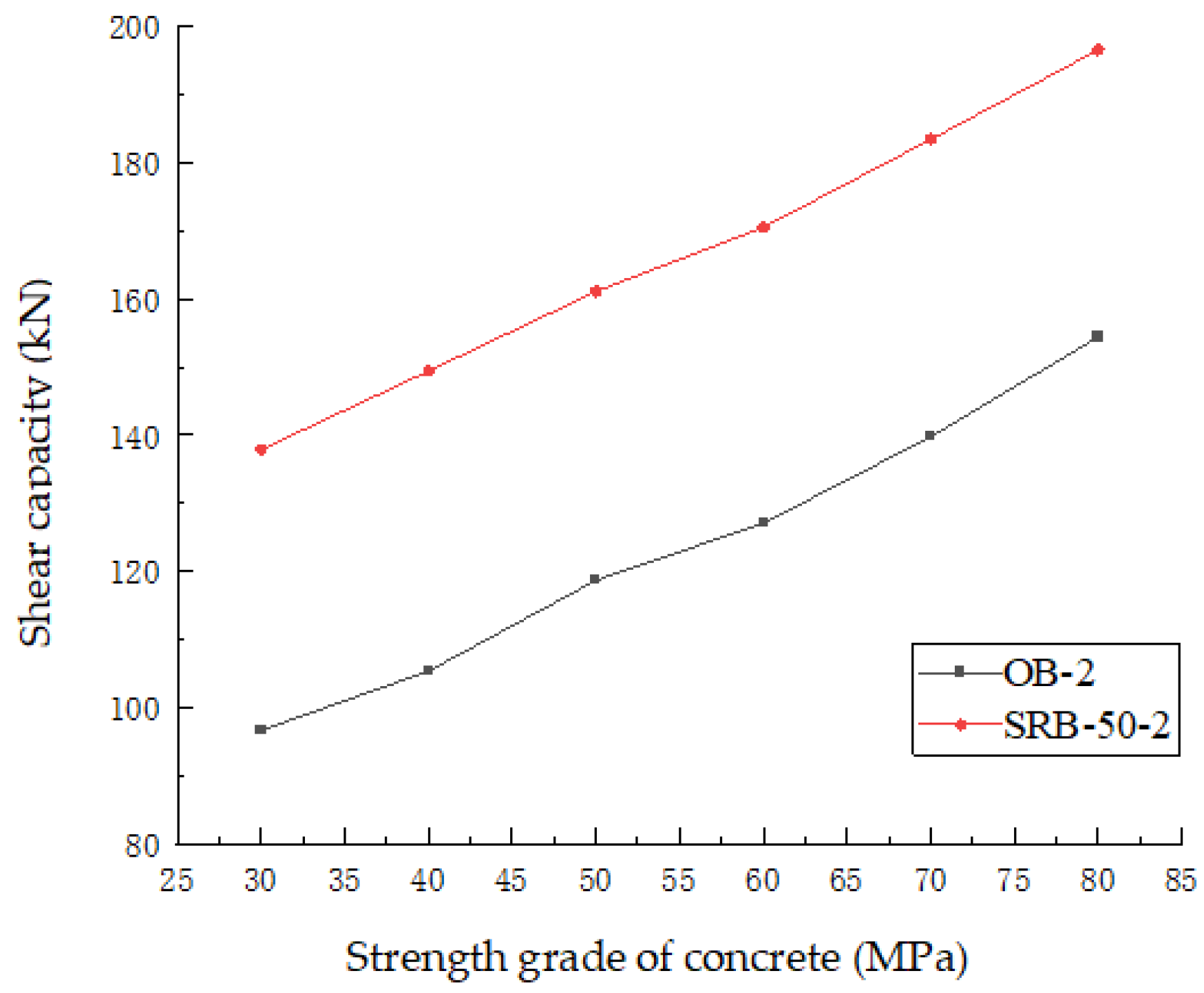
5.1.1. Concrete Strength
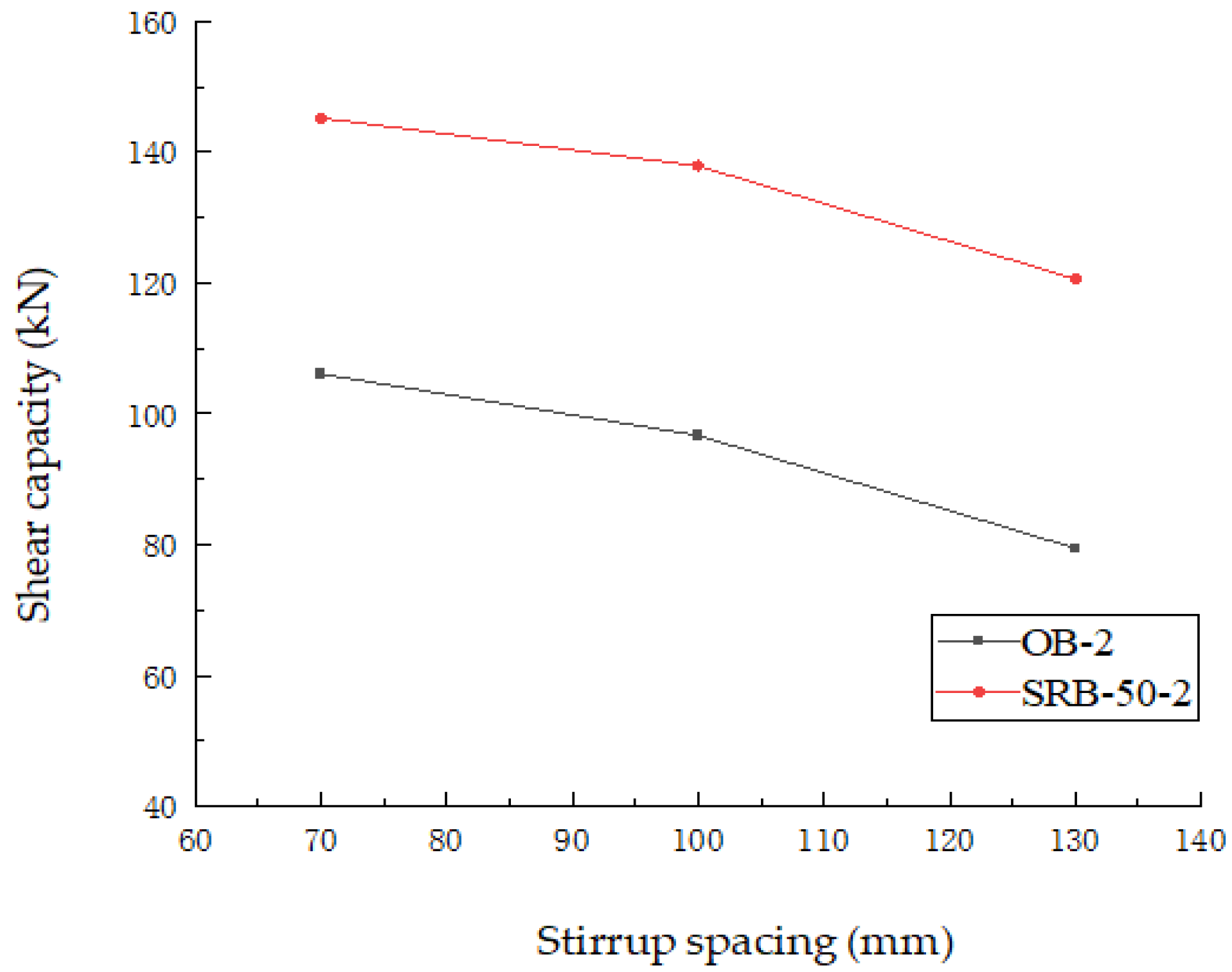
5.1.2. Stirrup Spacing
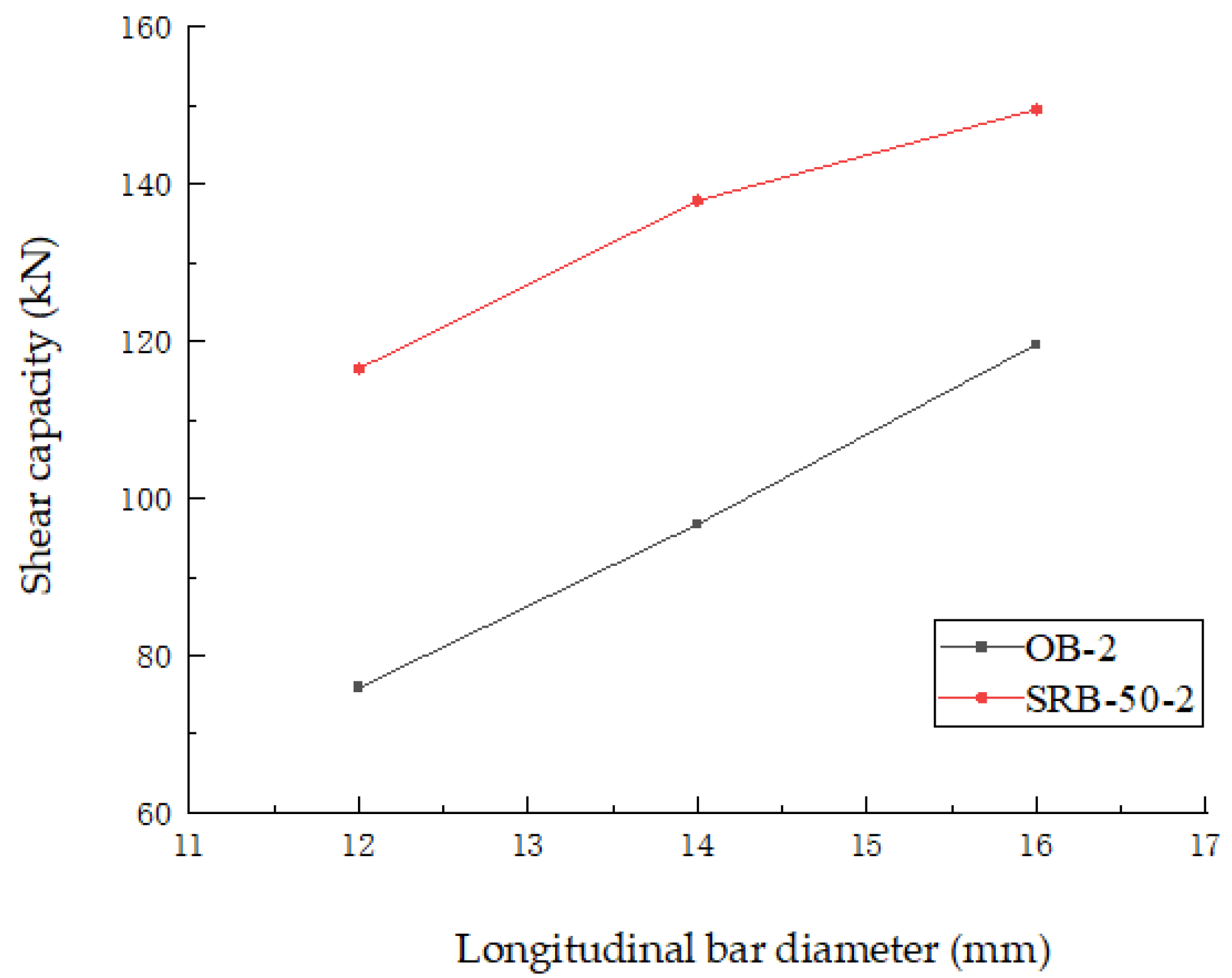
5.1.3. Diameter of Longitudinal Reinforcement
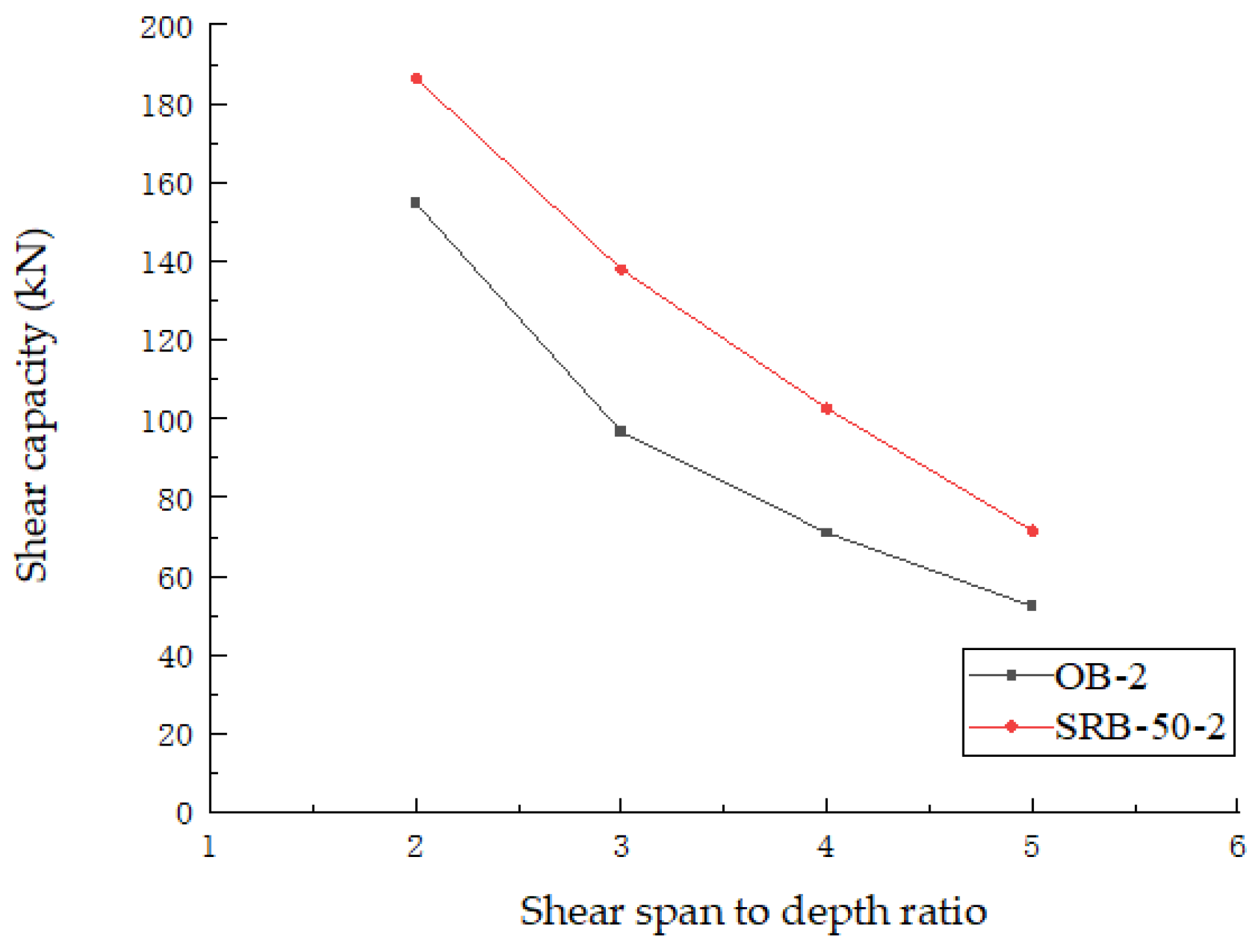
5.1.4. Ratio of Shear Span to Depth
5.2. Shear Resistance Provided by Concrete
5.3. Shear Resistance Provided by Stirrups and Prestressing Tendons
5.4. Proposed Formula
6. Conclusions
- (1)
- The external prestressing reinforcement method on the side face can effectively enhance the shear bearing capacity of concrete beams and improve their working performance. Compared with the OB, the cracking loads of the side face external prestressing reinforced beams SRB-50-2, SRB-75-3 and SRB-100-2 increased by 71.5%, 103.1% and 130.1%, respectively, but the cracking loads of their oblique cracks decreased by 9.4%, 5.1% and 2.5%, respectively. The external prestressing on the side face has a certain inhibitory effect on the initial cracking of concrete beams.
- (2)
- The reinforcing effect of traditional external prestressing on concrete beams is superior to that of side façade external prestressing. Specifically, the oblique crack loads of the TRB-30-2, TRB-35-1 and TRB-40-2 beams increased by 68.9%, 74.6% and 65.2%, respectively. This improvement can be attributed to the fact that in the traditional prestressed reinforcement method, the axis of the prestressed tendons is positioned outside the edge of the concrete beam and at a considerable distance from the neutral axis of the concrete. Conversely, the axis of the external prestressing tendons on the side façade is closer to the neutral axis, which has a limited influence on crack control in the concrete beam. Furthermore, once the crack tip development surpasses the axis of the prestressed tendons, it may adversely affect crack propagation. Therefore, when arranging prestressing tendons, their axis should ideally be as far from the neutral axis as possible to enhance the reinforcement efficiency.
- (3)
- Parameters such as the concrete strength, stirrup spacing, shear span to depth ratio, and reinforcement ratio of longitudinal reinforcement exert varying degrees of influence on the shear capacity of reinforced concrete beams. The numerical simulation results indicate that the shear capacity of the concrete beams exhibited a slight increase with enhanced concrete strength, a significant increase with a reduced shear span to depth ratio, and an increase associated with both a higher longitudinal reinforcement ratio and decreased stirrup spacing.
- (4)
- The formula for calculating the shear capacity of externally prestressed reinforced concrete beams with side façades was derived through a systematic and rigorous methodology that integrated test data, simulation outcomes, and advanced numerical analysis. The accuracy of this formula has been thoroughly validated by comparing it with the experimental results, revealing a maximum deviation of only 3%. This substantiates the formula’s reliability as a critical reference for practical engineering design and construction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeng, X.T.; Zeng, Y.X.; Ren, Z.H. Research on the rigidity of wide gap concrete beams strengthened with externally bonded CFRP plates based on the quasi plane assumption. J. Railw. Sci. Eng. 2021, 18, 1846–1851. [Google Scholar]
- Ren, Z.H.; Zeng, X.T. Cracks of wide-notch concrete beams strengthened with near-surface mounted CFRP bars based on quasi-plane assumption. J. Build. Struct. 2019, 40, 88–95. [Google Scholar]
- Yang, Y.Z. Research on External Prestressing Reinforcement Technology of Long-Span PC Continuous Rigid Frame Bridge. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2020. [Google Scholar]
- Zhang, S.Y. Research on Technology and Engineering Application of External Prestressing Strengthening Continuous Rigid Frame Bridge. Master’s Thesis, Anhui University of Science and Technology, Huainan, China, 2022. [Google Scholar]
- Ren, Z.H.; Zeng, X.T.; Yan, Q. Calculation method for interface slip of wide-notch concrete beam strengthened with carbon fiber reinforced plastics plate. J. Build. Struct. 2018, 39, 119–128. [Google Scholar]
- Huang, Z.; Shen, J.; Lin, B.; Miao, X.; Cheng, Z.H. Experimental and numerical investigation on shear behavior of concrete beams reinforced with CFRP grid shear reinforcements. J. Compos. Struct. 2024, 349–350, 118552. [Google Scholar] [CrossRef]
- Li, W.; Din, E.B.A.; Mansour, W.; Fayed, S. Improving shear performance of regular web openings concrete beams using steel mesh reinforced strain hardening cementitious composites: An experimental and numerical study. J. Eng. Struct. 2024, 314, 118344. [Google Scholar] [CrossRef]
- Fan, T. Calculation and Finite Element Analysis of Steel-Encased Reinforced Concrete Members. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2006. [Google Scholar]
- Ren, H.T. Study on the Basic Mechanical Properties and Long-Term Mechanical Properties of Concrete Structures Strengthened with Fiber Reinforced Composite Materials. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2003. [Google Scholar]
- Ibrahim, K.S.; Rad, M.M. Optimal elasto-plastic analysis of prestressed concrete beams by applying residual plastic deformation limitations. J. Sustain. 2023, 15, 5742. [Google Scholar]
- Ren, Z.H.; Zeng, X.T.; Chi, Q.H.; Zeng, Y.X. An External Prestressed Loading Structure on the Side Facade of a Concrete Beam. CN201921264085.9, 9 June 2020. Available online: https://pss-system.cponline.cnipa.gov.cn/conventionalSearch (accessed on 3 April 2025).
- Zhang, X.Y. Design method of reinforced concrete beams with post-tensioned external tendons. J. Build. Struct. 1985, 3, 44–57. [Google Scholar]
- Zhang, S.D. Development of post-tensioned prestressed concrete without bonding in vitro. J. Highw. 1988, 5, 11–14. [Google Scholar]
- Qian, Z.S. Design and calculation of external prestressed composite beams of reinforced concrete. J. Archit. Anhui 1994, S1, 46–50. [Google Scholar]
- Xu, M.H.; Wang, X.J.; Zhang, G.M.; Chen, J.W.; Zhang, Z.Y. Experimental investigation on the dynamic compression properties of Kevlar fiber-reinforced composite laminates. J. Exp. Mech. 2001, 1, 26–33. [Google Scholar]
- Niu, J. Experimental Study and Finite Element Analysis of Reinforced Concrete T-Shaped Column with Bonded Steel Plate and Carbon Fiber Sheet. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2011. [Google Scholar]
- Xing, L.Y. Experimental Study on Axial Compression of Damaged RC Short Columns Reinforced by GFRP and Steel Fiber Mortar. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2020. [Google Scholar]
- Wang, X.; Shi, J.; Wu, G.; Yang, L.; Wu, Z. Effectiveness of basalt FRP tendons for strengthening of RC beams through the external prestressing technique. J. Eng. Struct. 2015, 101, 34–44. [Google Scholar] [CrossRef]
- Wan, Z.W. Theoretical Study of External Prestressing Technology in Bridge Reinforcement. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2011. [Google Scholar]
- Gao, X.L.; Yin, C.L.; Guo, J.Y.; Chen, G.X.; Huang, H.R. Experimental and theoretical study on the shear behaviors of an innovative precast UHPC composite beams reinforced with inverted T-shaped steel. J. Build. Eng. 2024, 96, 110504. [Google Scholar] [CrossRef]
- Liao, B.Q.; Du, Y.X.; Ma, G.; Zhou, R.; Zhu, D.J. Shear behavior of seawater sea-sand concrete beams reinforced with BFRP bars after seawater dry-wet cycling. J. Eng. Struct. 2024, 316, 118573. [Google Scholar] [CrossRef]
- Liu, C.W.; Yang, M.; Wang, P.F.; Ba, G.Z.; Miao, J.J. Effects of stirrup corrosion on the shear performance of reinforced concrete beams after fire exposure. J. Struct. Eng. 2024, 150, 04024093. [Google Scholar] [CrossRef]
- Moubarak, A.M.R.; Ibrahim, A.; Farouk, M.A.; Elwardany, H. Shear performance of glass fiber reinforced concrete beams with diverse embedded GFRP trusses. J. Case Stud. Constr. Mater. 2023, 18, e02195. [Google Scholar] [CrossRef]
- ACI 318-02/ACI 318R-02; Building Code Requirements for Structural Concrete (and Commentary). American Concrete Institute: Farmington Hills, MI, USA, 2002.
- Shu, C.Q.; Wei, M.H. Discussion on shear strength of reinforced concrete cantilever beam under indirect loading. J. Guizhou Inst. Technol. 1985, 03, 74–85. [Google Scholar]
- Su, X.Z.; Haldance, D.; Kutab, A.S. A mechanism of shear resistance of reinforced concrete beams. J. Fuzhou Univ. (Nat. Sci. Ed.) 1996, S1, 99–103. [Google Scholar]
- Zeng, Q.X.; He, G.M.; Yu, J.H. Shear Strength of concrete bidirectional flexural members. In Proceedings of the 5th National Conference on Structural Engineering, Haikou, China, 25 November 1996; Volume 2. [Google Scholar]
- Jiang, H.B.; Che, H.M.; Zhang, K.J. Application of classical truss model to fatigue shear analysis of reinforced concrete and prestressed concrete beams. J. Bridge Constr. 1996, 2, 71–73. [Google Scholar]
- GB/T21839-2008; Test Method for Steel Used in Prestressed Concrete. National Standard of the People’s Republic of China: Beijing, China, 2008.
- GB/T50081-2019; Standard for Test Methods of Physical and Mechanical Properties of Concrete. National Standard of the People’s Republic of China: Beijing, China, 2019.
- GB/T28900-2012; Steel Test Method for Reinforced Concrete. National Standard of the People’s Republic of China: Beijing, China, 2012.
- Wang, Y.Y.; Gu, Y.; Liu, J.L. A domain-decomposition generalized finite difference method for stress analysis in three-dimensional composite materials. Appl. Math. Lett. 2020, 104, 106226. [Google Scholar] [CrossRef]
- Kabir, H.; Aghdam, M.M. A robust Bézier based solution for nonlinear vibration and post-buckling of random checkerboard graphene nano-platelets reinforced composite beams. Compos. Struct. 2019, 212, 184–198. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Shafighfard, T.; Jankowski, R.; Yoo, D.-Y. Machine-learning methods for estimating performance of structural concrete members reinforced with fiber-reinforced polymers. Arch. Comput. Methods Eng. 2024, 32, 1–33. [Google Scholar] [CrossRef]
- GB 50010-2010; The Ministry of Housing and Urban-Rural Development of the People’s Republic of China—Code for Design of Concrete Structures. China Construction Industry Press: Beijing, China, 2014.
- Chen, B. Study on Shear Behavior of Prestressed RPC Beams. Master’s Thesis, Hunan University, Changsha, China, 2007. [Google Scholar]
- Zheng, S.B. Experimental Study on Shear Behavior of Transversely Tensioned Prestressed Concrete Beams. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2003. [Google Scholar]
- Zhao, S.B.; Zhao, G.F.; Huang, C.K. Test and calculation method of bearing capacity of oblique section of prestressed steel fiber reinforced concrete beams. J. Civ. Eng. 1999, 32, 28–33. [Google Scholar]
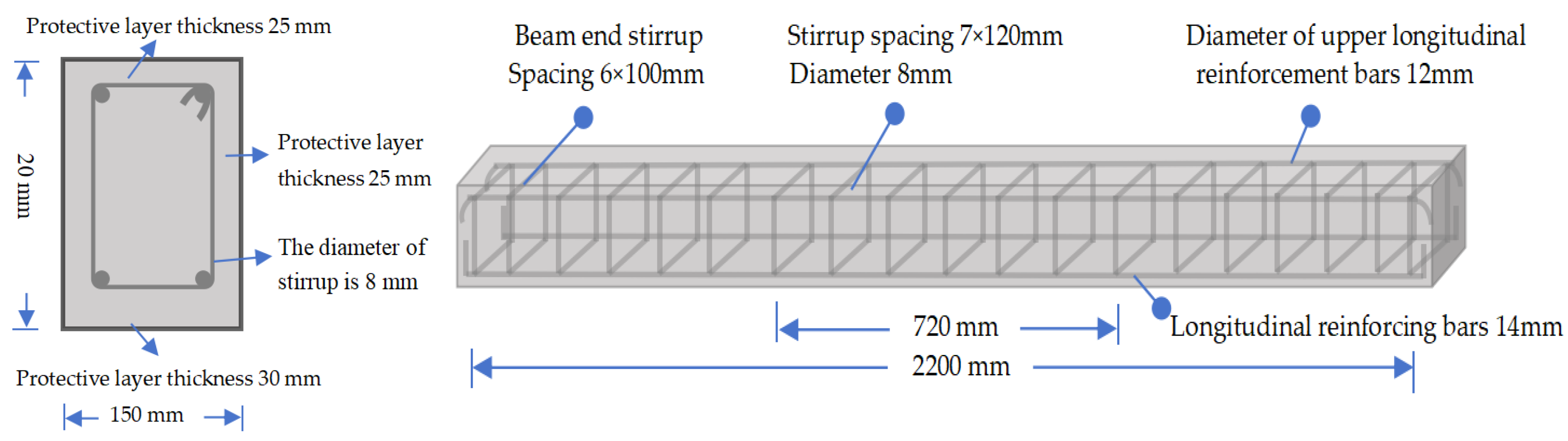
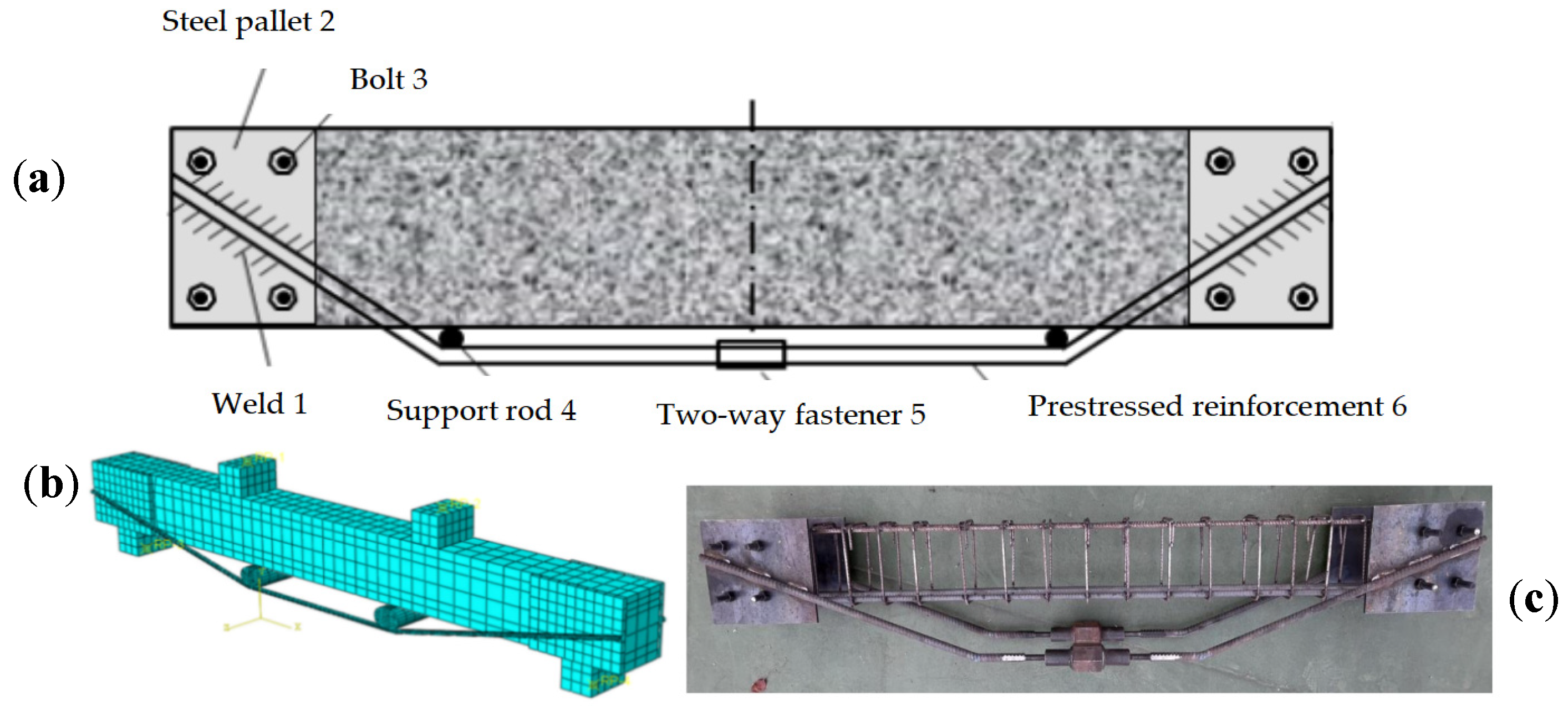
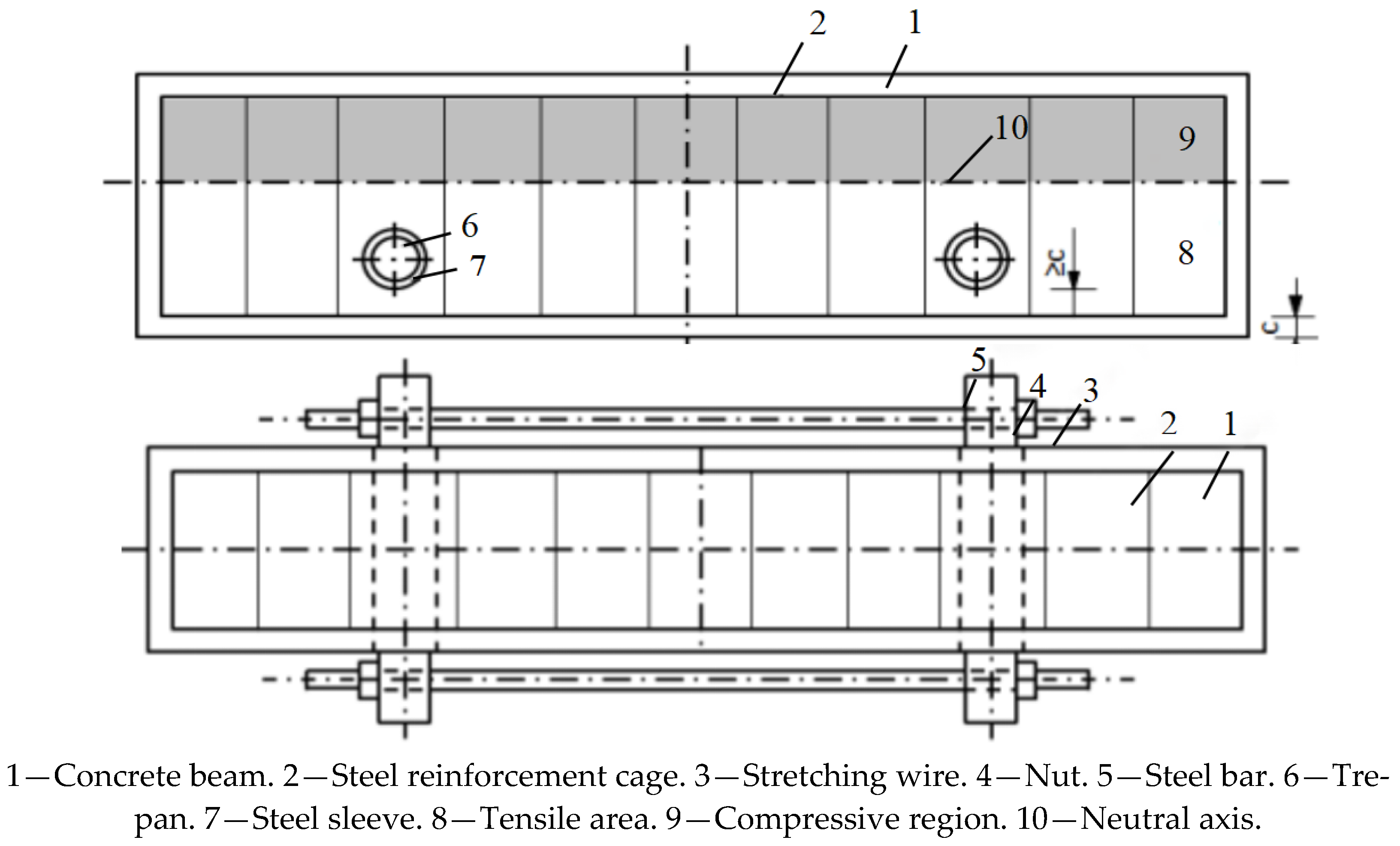




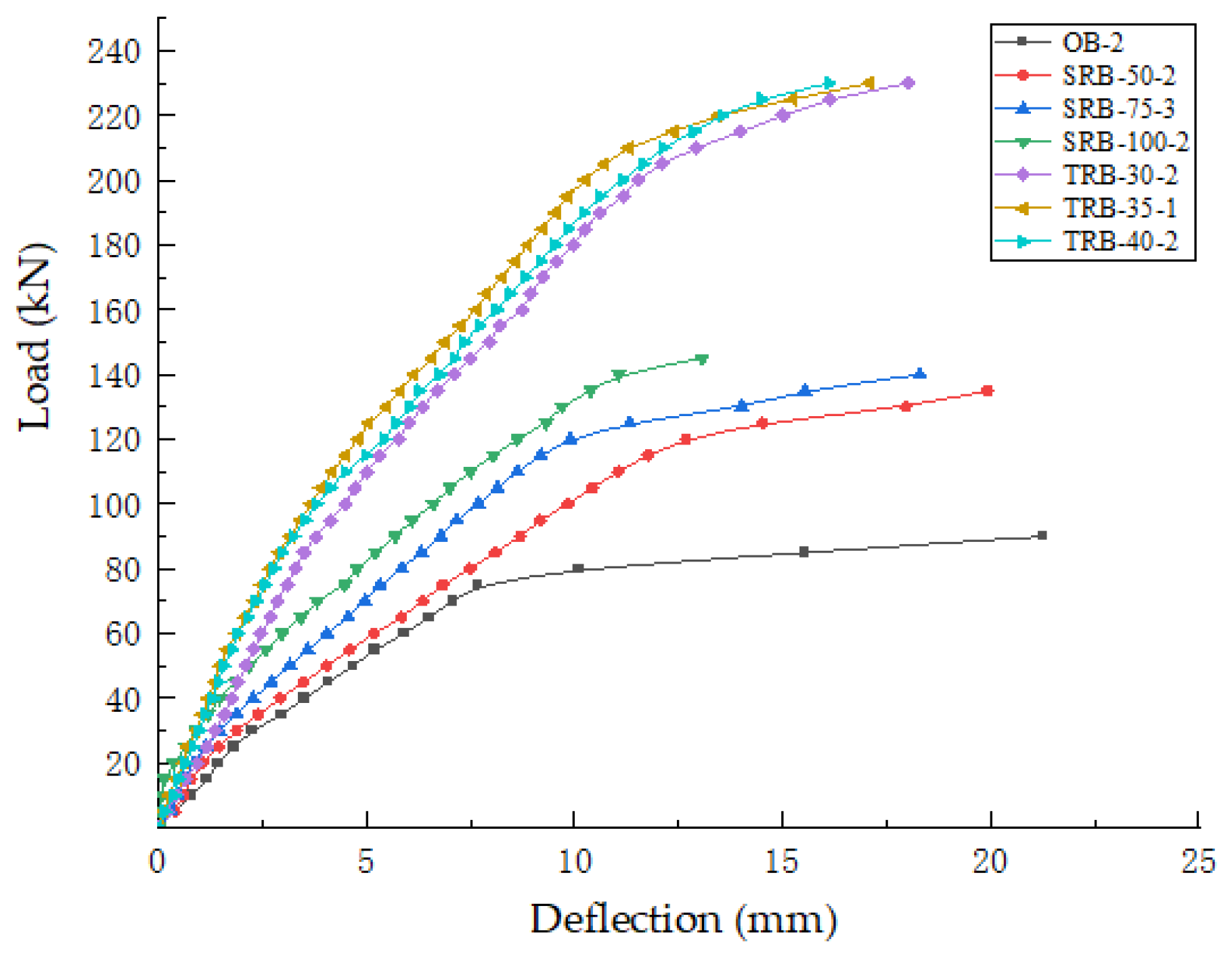


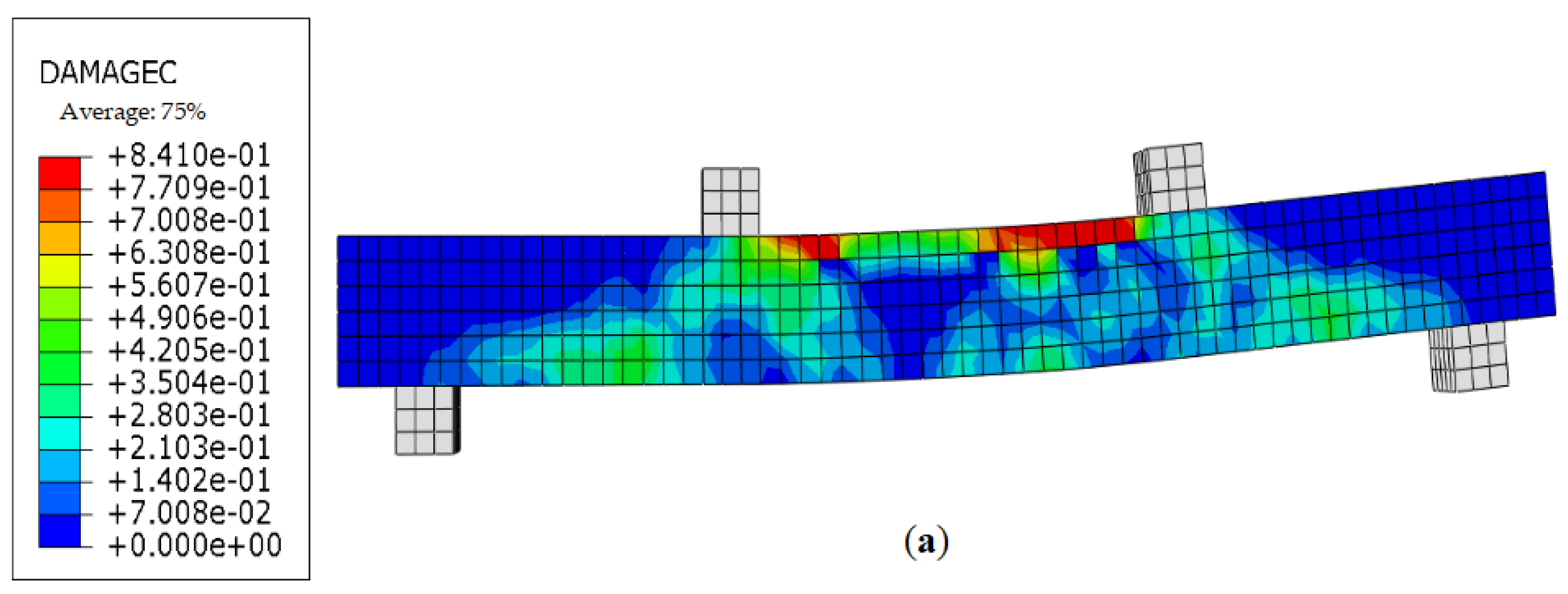


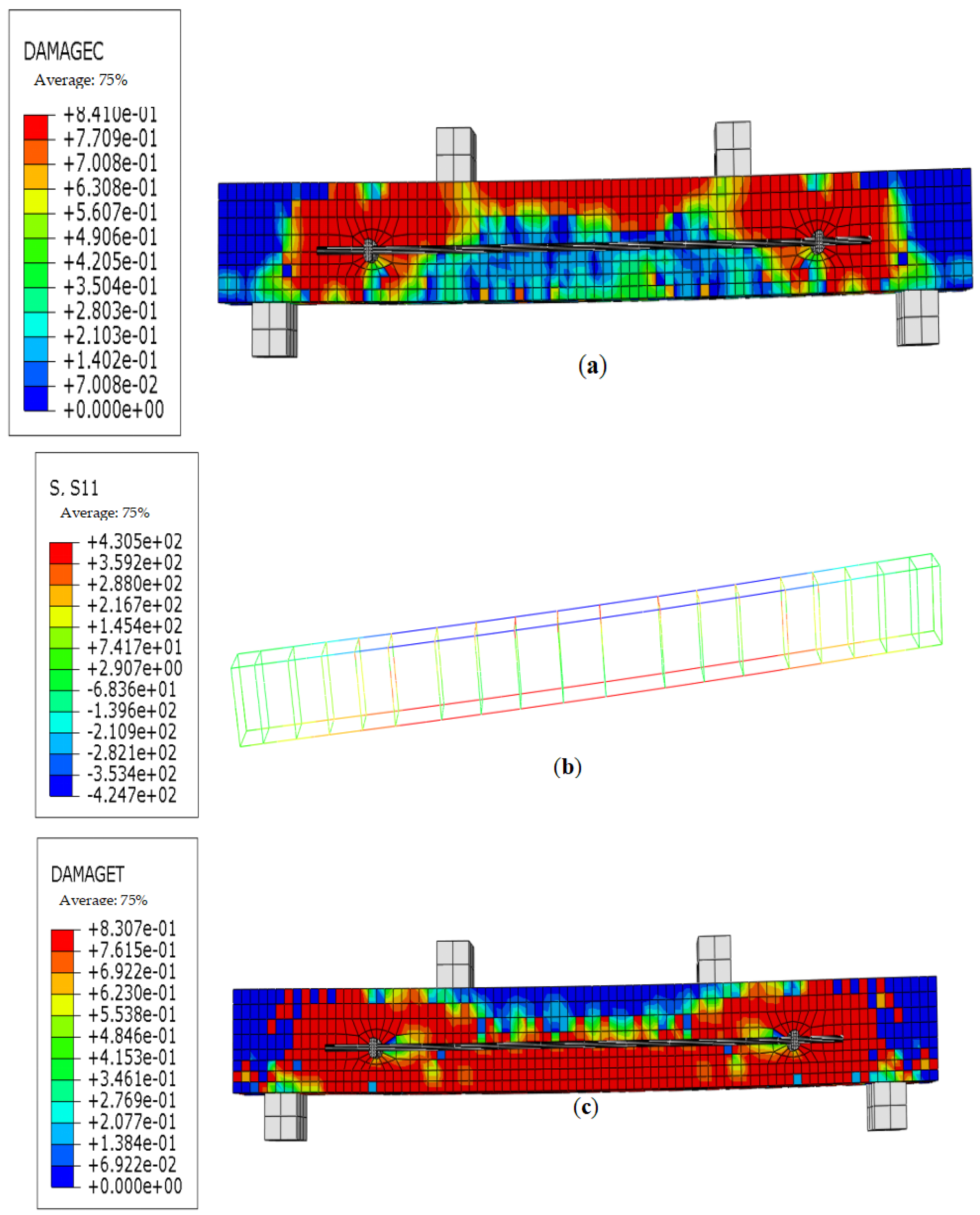
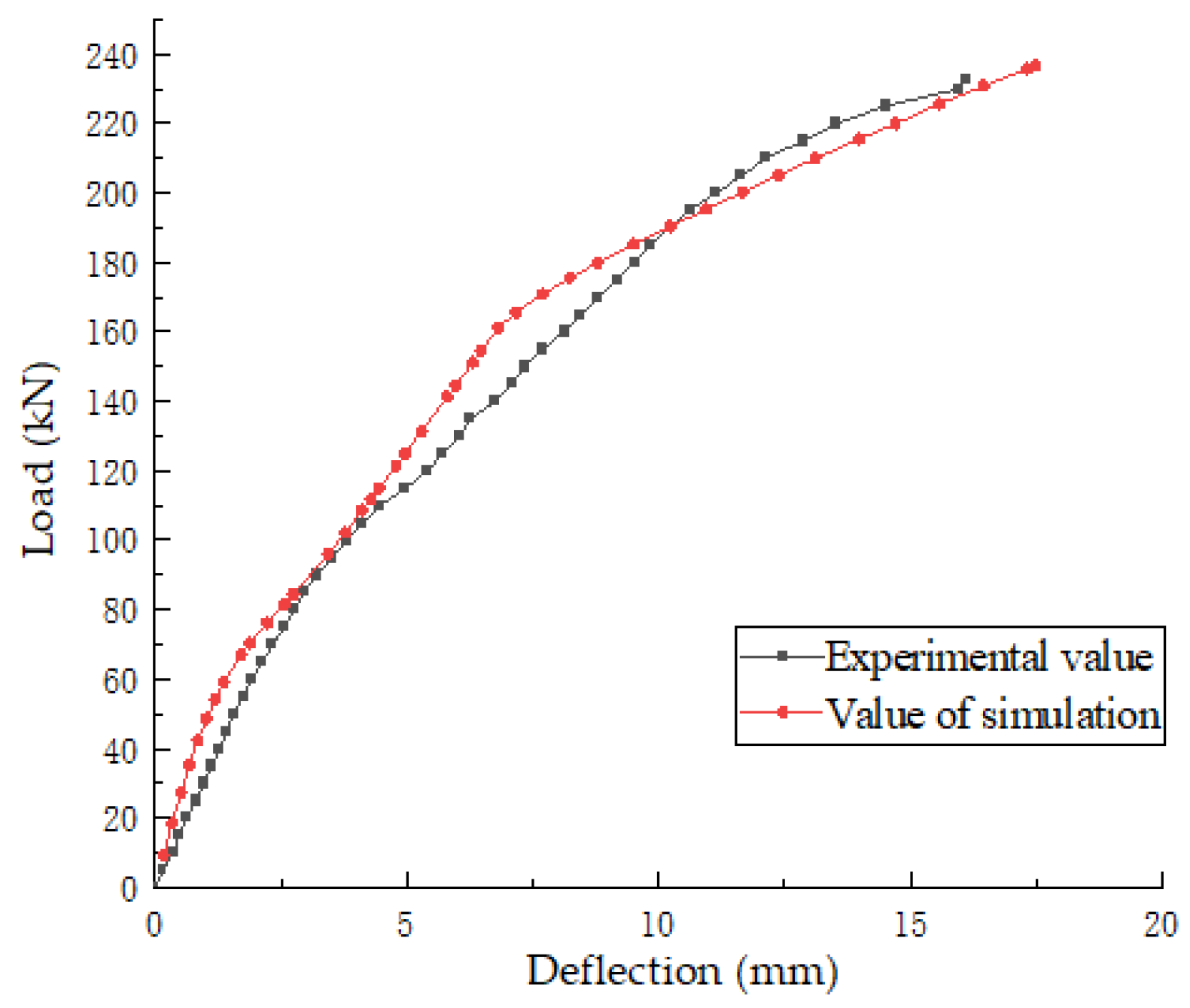

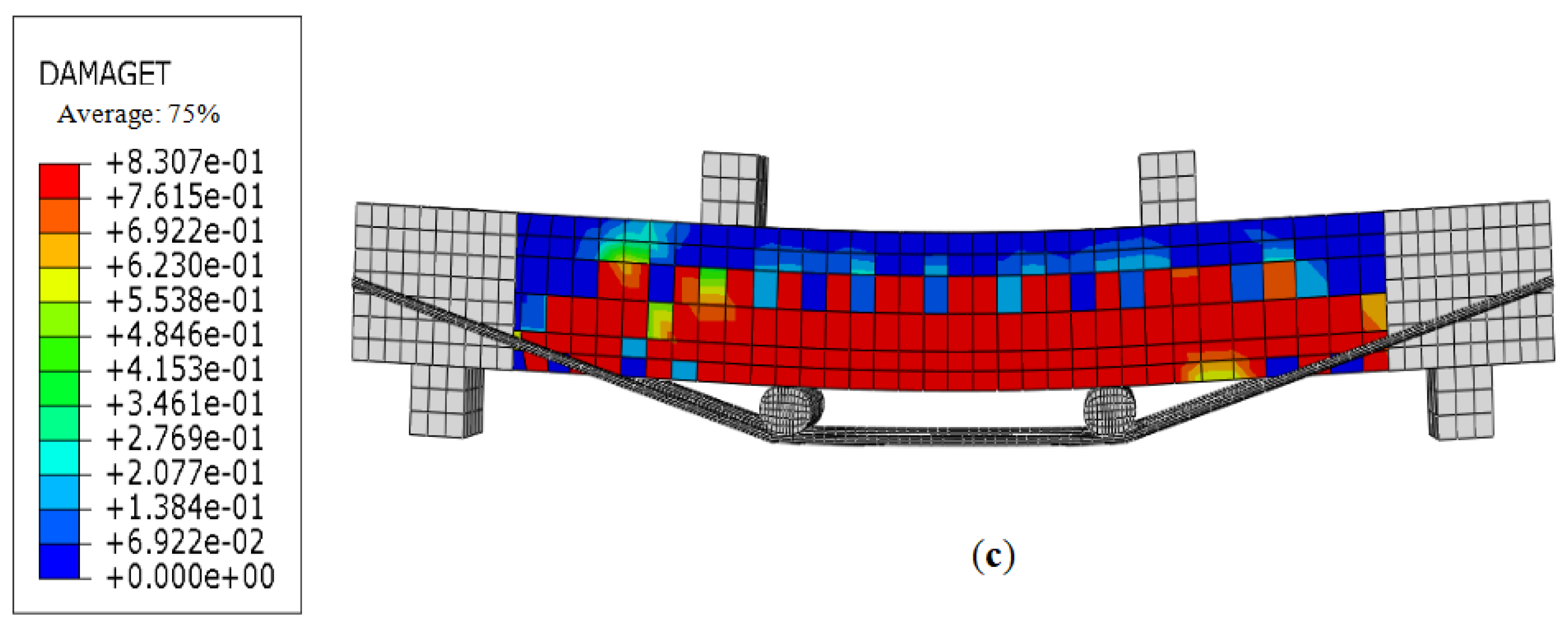
| Materials | Ultimate Strength/MPa | Yield Strength/MPa | Elasticity Modulus/MPa | Type | Remarks |
|---|---|---|---|---|---|
| Concrete | 35.97 (Compressive) | — | — | C30 | Actual measurement |
| RebarΦ8 | 435.8 (Tensile) | 381.6 | 2.05 × 105 | HRB400 | |
| RebarΦ10 | 443.5 (Tensile) | 389.7 | 2.02 × 105 | HRB400 | |
| RebarΦ14 | 469.6 (Tensile) | 401.2 | 2.0 × 105 | HRB400 | |
| Rebar14 | 903.6 (Tensile) | 693.4 | 1.98 × 105 | 8.8 Long bolts | Actual measurement Prestressed bar [29] |
| No. | Stirrup Diameter | Diameter of Prestressed Bar | Diameter of Upper Longitudinal Bar | Diameter of Lower Longitudinal Bar | Ratio of Reinforcement | Numbers |
|---|---|---|---|---|---|---|
| OB | 8 | — | 10 | 14 | 1.4% | 3 |
| TRB | 8 | 14 | 10 | 14 | 1.4% | 9 |
| SRB | 8 | 14 | 10 | 14 | 1.4% | 9 |
| No. | ||||||
|---|---|---|---|---|---|---|
| OB-2 | 19.3 | 65.0 | 70.6 | 83.9 | 96.7 | 24.9 |
| SRB-50-2 | 33.1 | 58.9 | 70.8 | 113.9 | 137.9 | 19.6 |
| SRB-75-3 | 39.2 | 61.7 | 72.6 | 116.1 | 142.3 | 17.9 |
| SRB-100-2 | 44.4 | 63.4 | 75.1 | 119.6 | 147.0 | 13.1 |
| TRB-30-2 | 70.2 | 107.4 | 175.6 | 210.5 | 230.0 | 18.0 |
| TRB-35-1 | 72.0 | 109.8 | 176.9 | 212.5 | 231.2 | 17.1 |
| TRB-40-2 | 78.9 | 113.5 | 179.6 | 218.1 | 232.9 | 16.1 |
| No. | Experimental Value (kN) | Calculated Value (kN) | Simulated Value (kN) | Simulated Value/ Calculated Value | Experimental Value/ Calculated Value |
|---|---|---|---|---|---|
| SRB-50-2 | 68.50 | 66.66 | 62.54 | 0.94 | 1.03 |
| SRB-75-3 | 71.15 | 68.94 | 65.68 | 0.95 | 1.03 |
| SRB-100-2 | 73.50 | 71.21 | 68.48 | 0.96 | 1.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; Wang, Y.; Chen, W.; Zeng, X.; Ding, X. Research on the Shear Performance of Concrete Beams Strengthened with Lateral External Prestressing. Buildings 2025, 15, 1482. https://doi.org/10.3390/buildings15091482
Ren Z, Wang Y, Chen W, Zeng X, Ding X. Research on the Shear Performance of Concrete Beams Strengthened with Lateral External Prestressing. Buildings. 2025; 15(9):1482. https://doi.org/10.3390/buildings15091482
Chicago/Turabian StyleRen, Zhenhua, Yuzhu Wang, Wei Chen, Xiantao Zeng, and Xuanming Ding. 2025. "Research on the Shear Performance of Concrete Beams Strengthened with Lateral External Prestressing" Buildings 15, no. 9: 1482. https://doi.org/10.3390/buildings15091482
APA StyleRen, Z., Wang, Y., Chen, W., Zeng, X., & Ding, X. (2025). Research on the Shear Performance of Concrete Beams Strengthened with Lateral External Prestressing. Buildings, 15(9), 1482. https://doi.org/10.3390/buildings15091482







