Evaluation of the Buttress System of a Great Ottoman Mosque Against Gravity Loads and Horizontal Seismic Forces: The Case of the Istanbul Süleymaniye Mosque
Abstract
1. Introduction
2. Previous Studies on the Süleymaniye
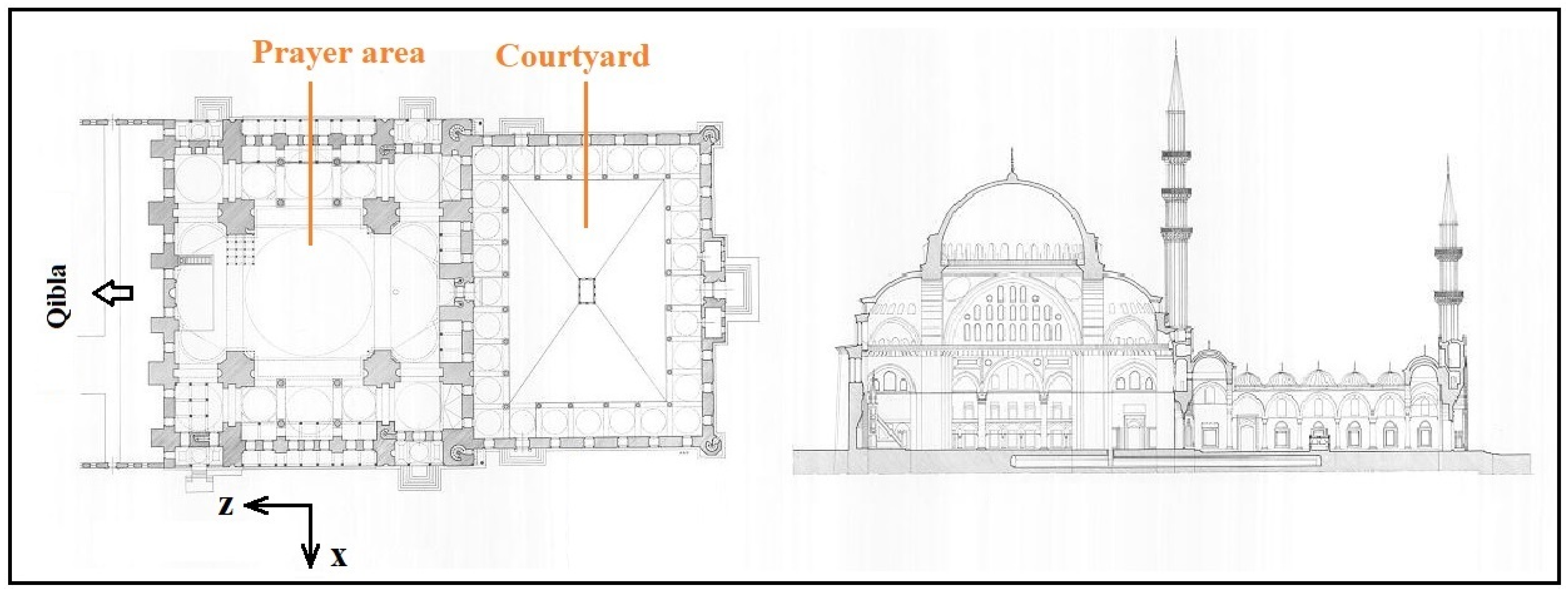
3. Main Structural Features of the Mosque and Its Buttress System
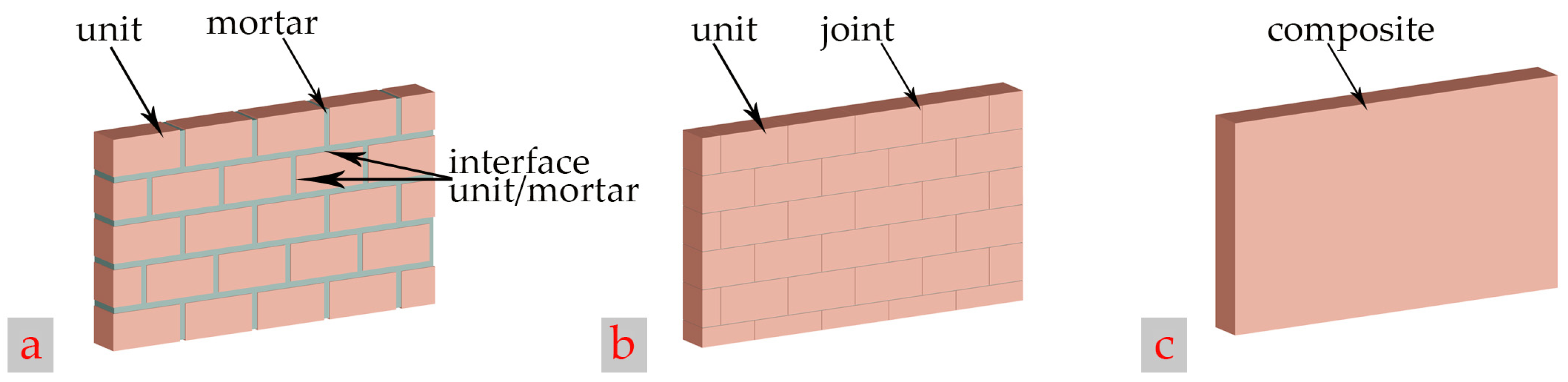
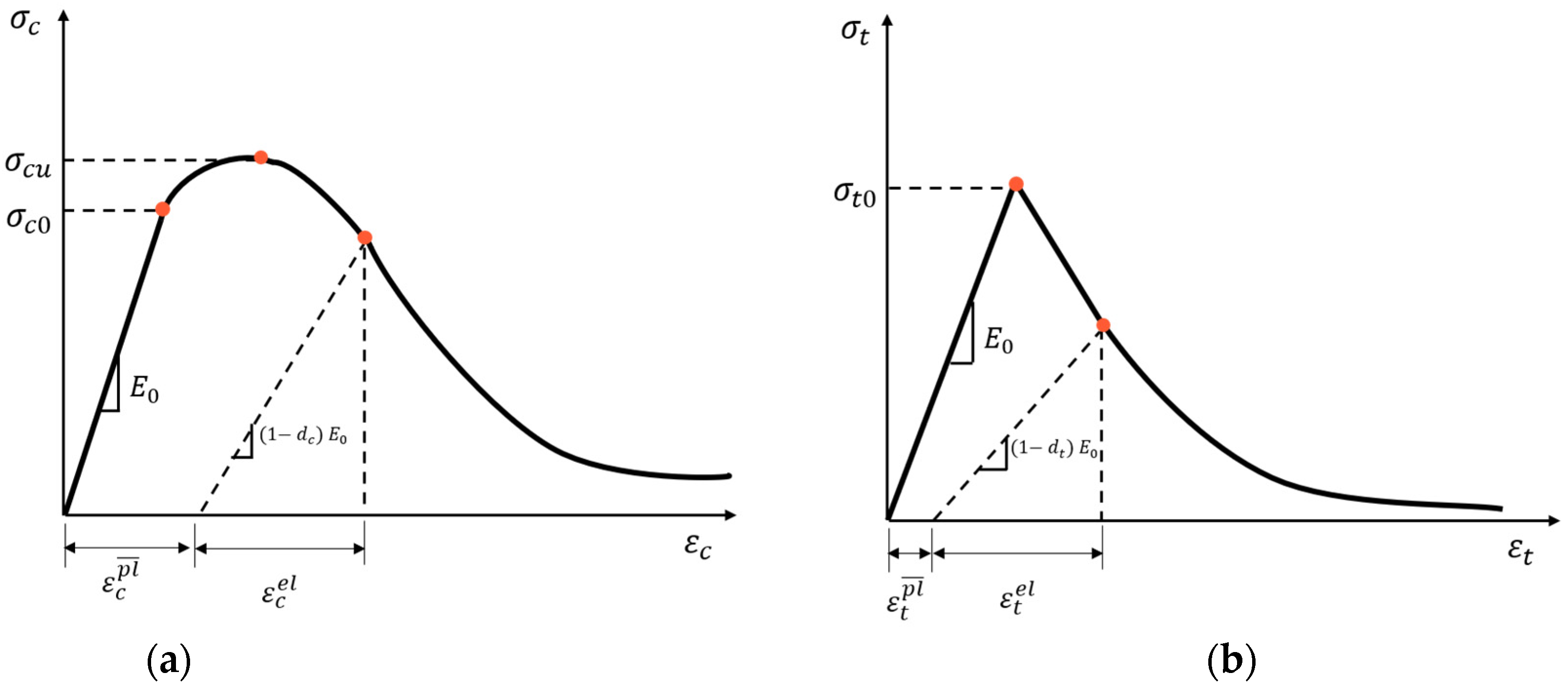
4. The Material Model Used and Material Properties of the Structure
5. Finite Element Model of the Structure
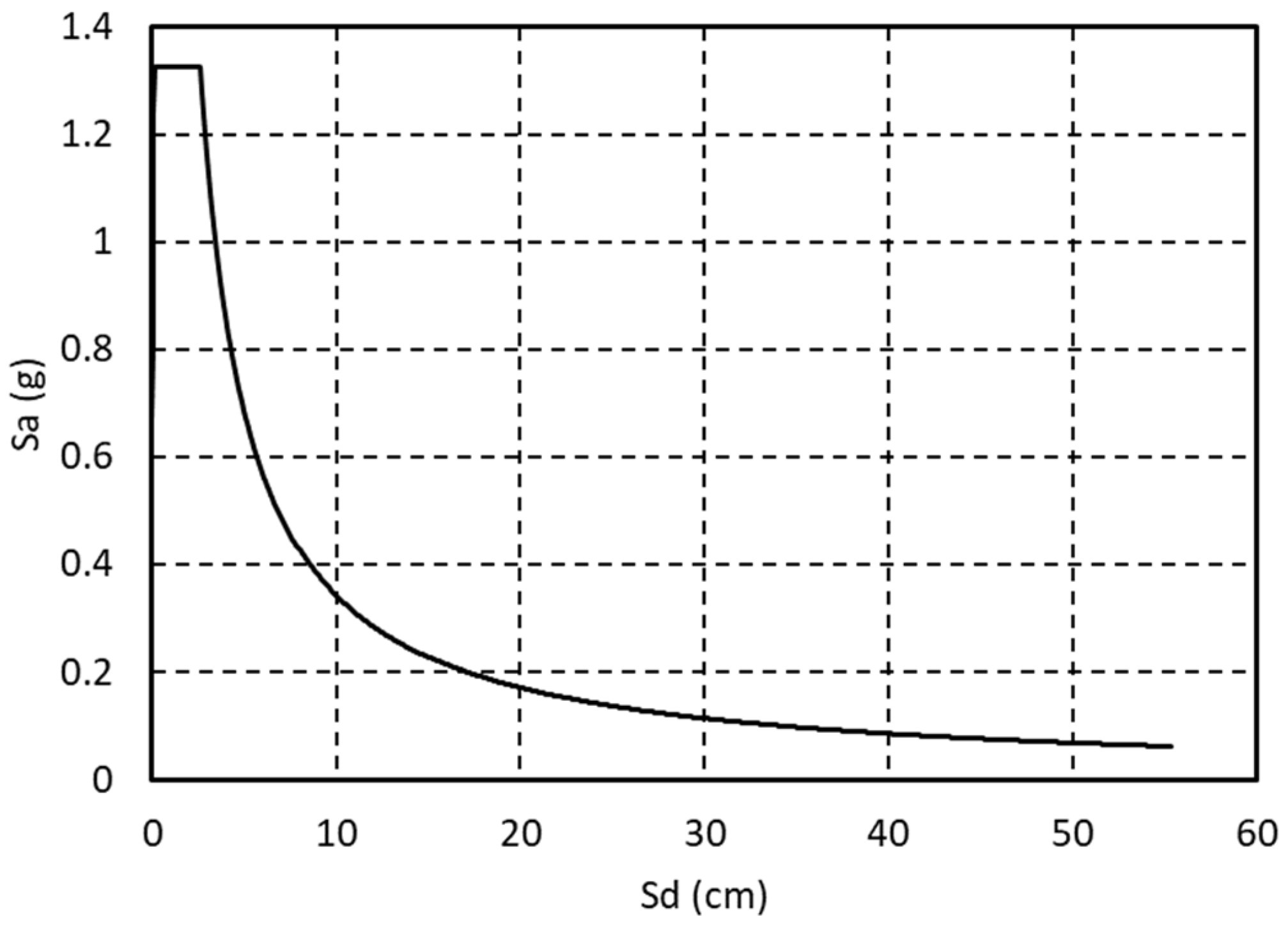
6. Analysis Method and Computational Procedure
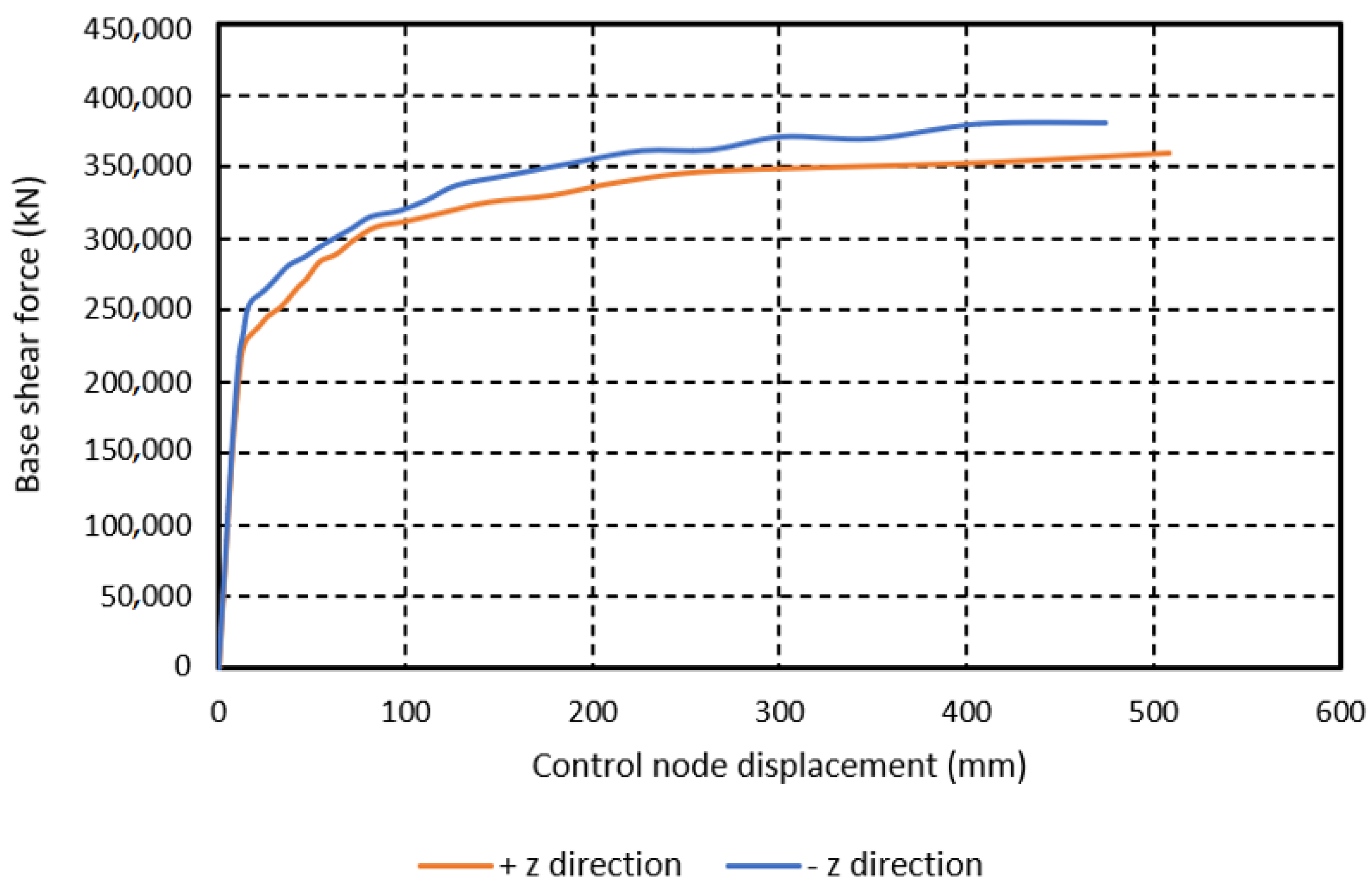
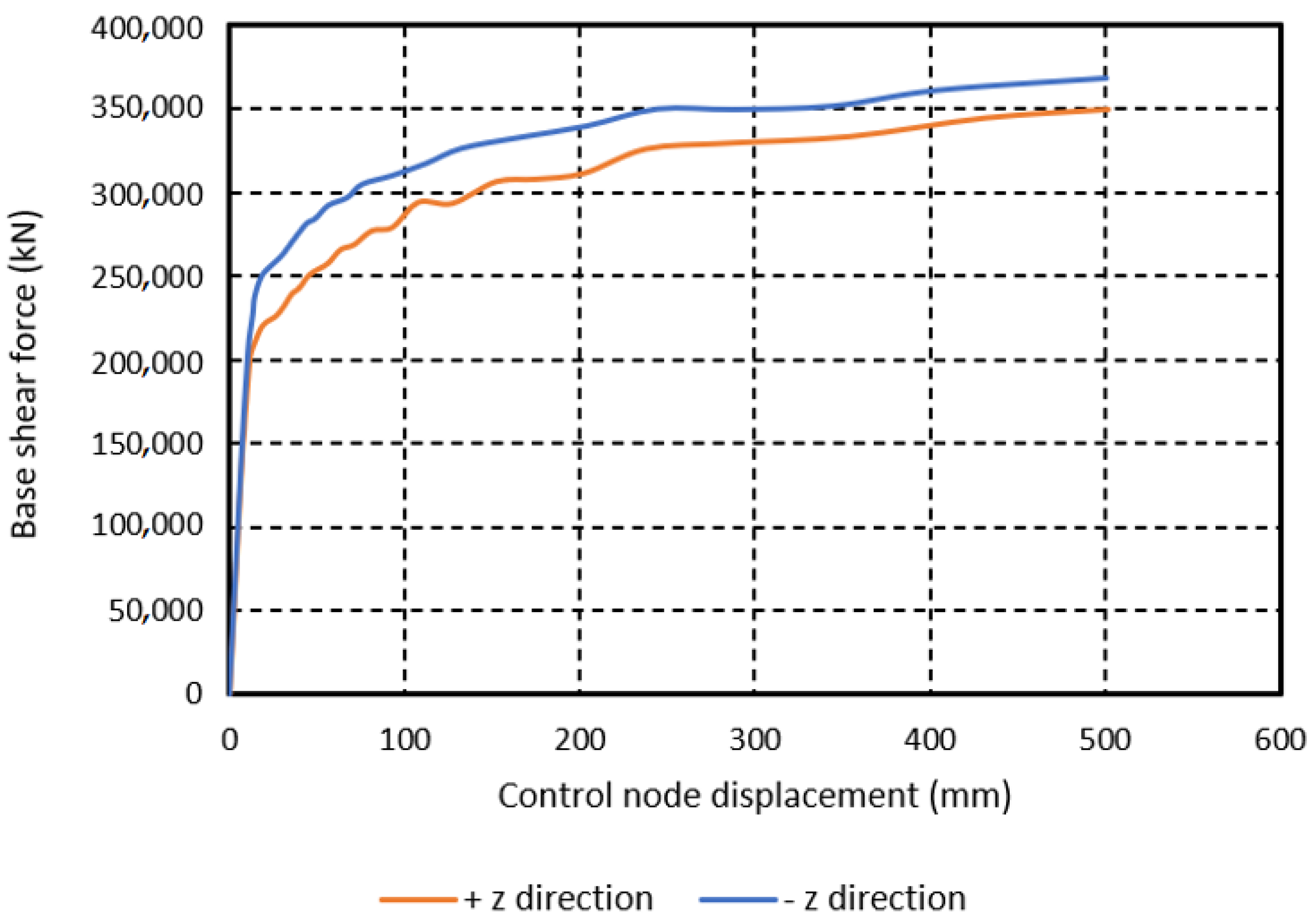
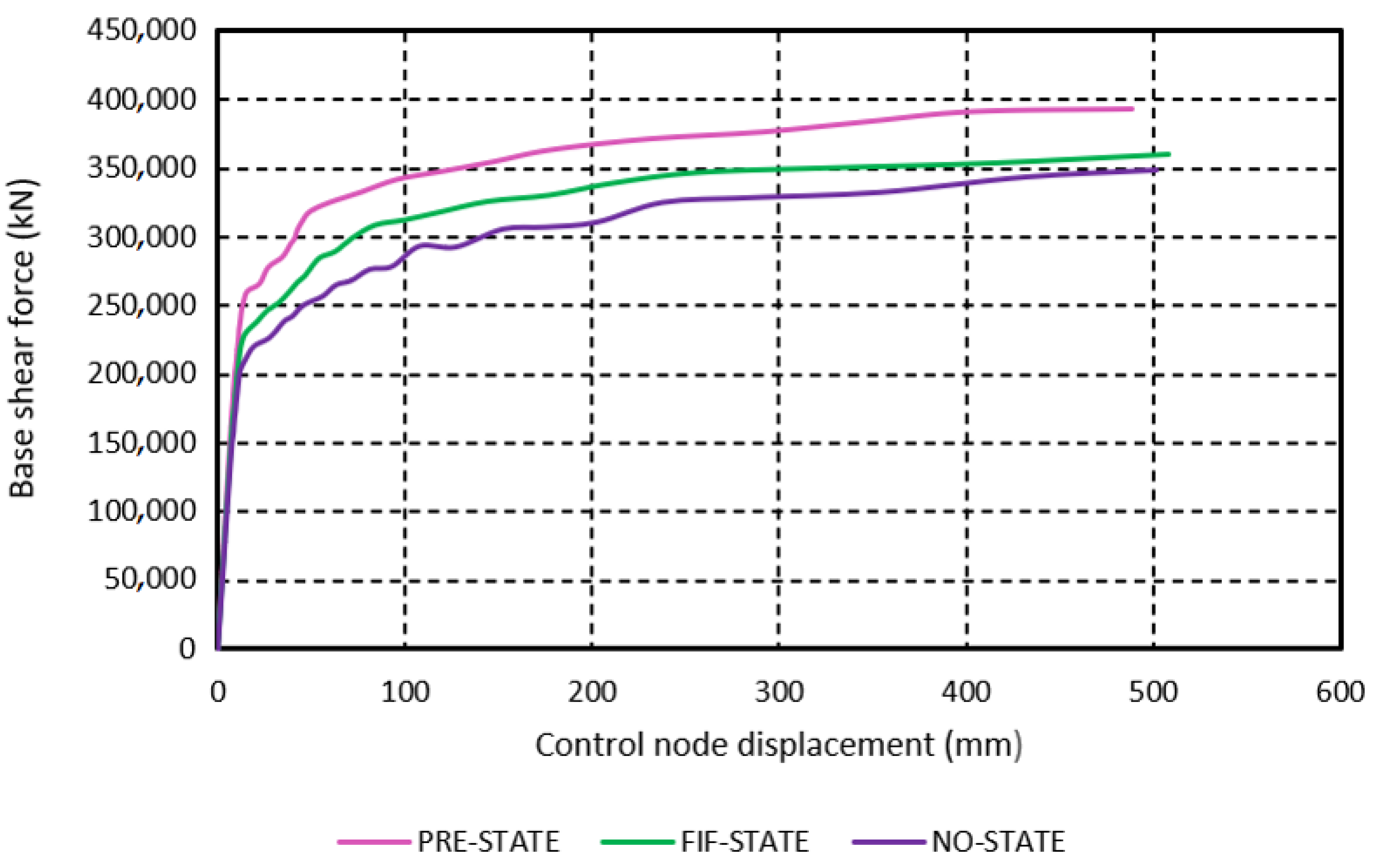
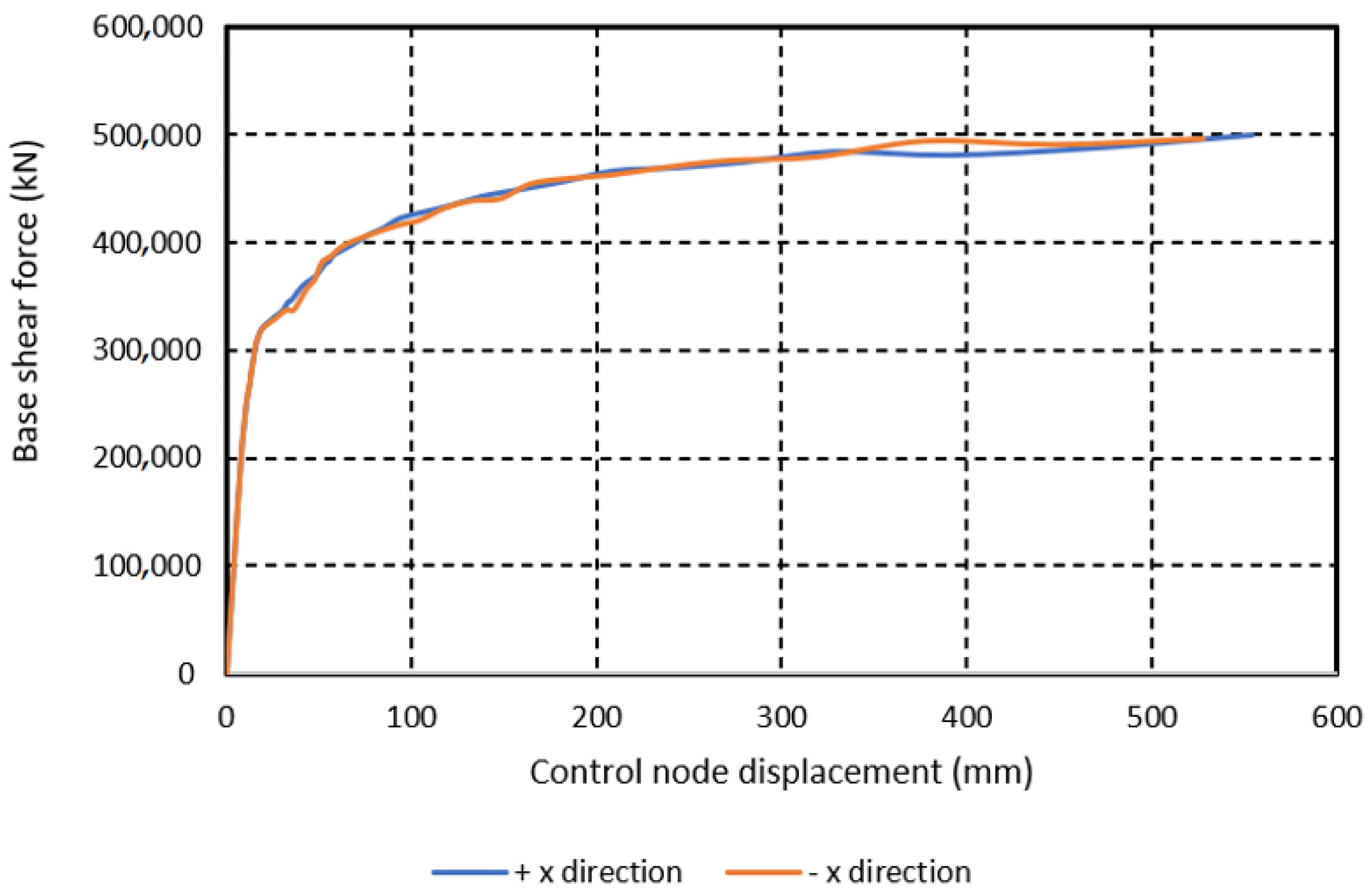
7. Analyses and Interpretation of Results
7.1. Modal Analysis
7.2. Linear Static Analysis Under Gravity Loads
7.3. Nonlinear Static Analyses
7.4. Performance Evaluation of the Mosque
8. Conclusions
- The mosque does not have any problems in terms of stresses and displacements under gravity loads.
- The structure has high horizontal earthquake resistance in both main axis directions in its present state. With the present buttress dimensions, the structure has a horizontal load-carrying capacity of around 70% of self-weight on the Qibla axis and around 90% on the axis perpendicular to the Qibla. These resistance values decrease to about 66% and 78%, respectively, if the buttress outer depths are completely eliminated. It should be noted that these capacity values were obtained by using the material values in Table 3. In addition, some inevitable simplifications, albeit small, were made in the modeling of the structure. Therefore, these values should not be regarded as absolute values for the structure. However, since we tried to use as consistent values as possible for the materials and were meticulous in modeling the structure, of course, it can be said that the results obtained are values that give a good idea about the horizontal load capacities of the structure.
- Horizontal load-carrying capacities can be maintained to a large extent even when the outer depths of the buttresses are reduced by fifty percent or even completely eliminated.
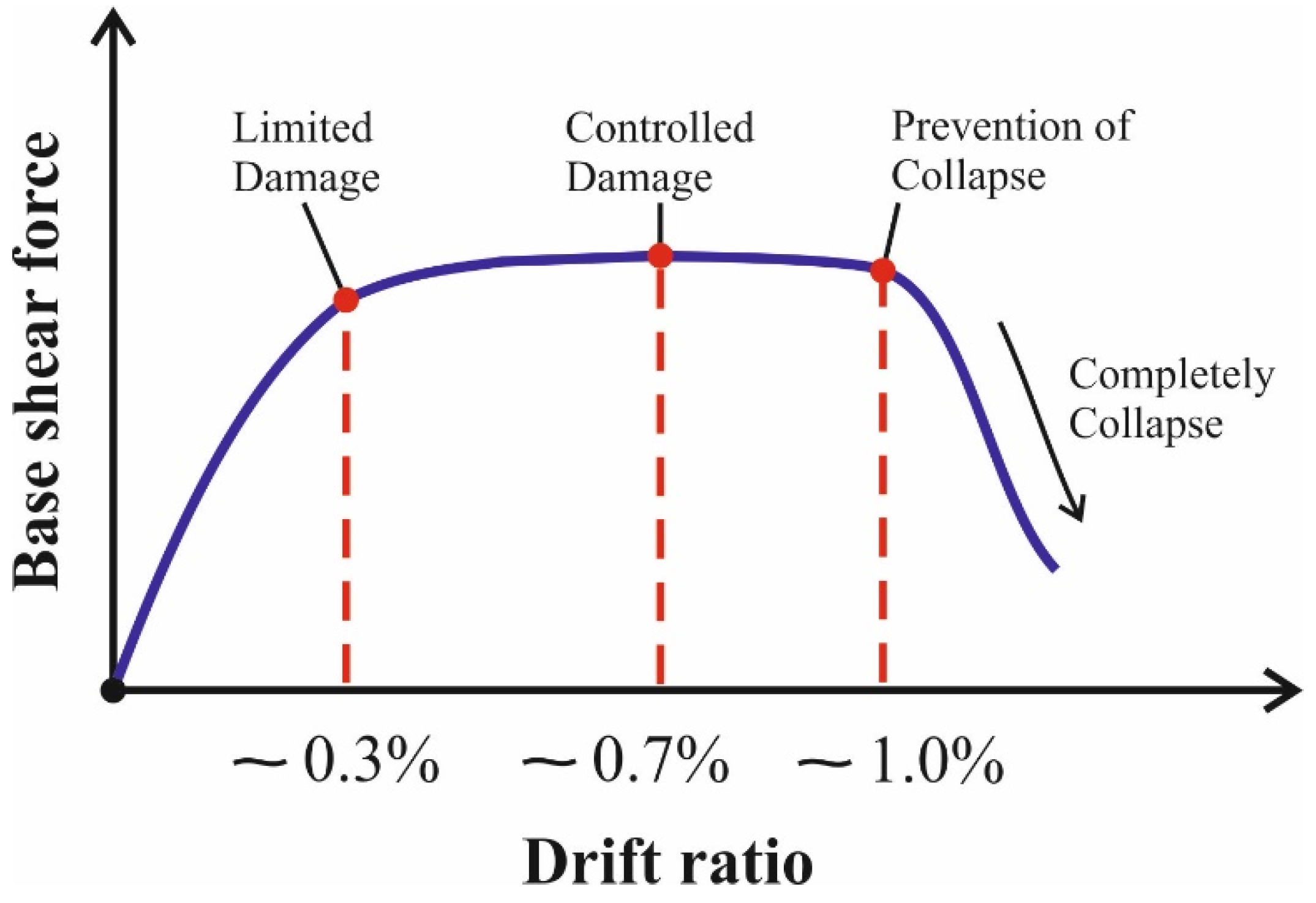
- The structure can ensure the limited damage performance level condition under the design earthquake only with the existing buttress dimensions. In cases where the outer depths of the buttresses are halved or completely removed, the structure enters the controlled damage performance region. However, the structure is still far from the collapse prevention limit even without the outer depths of the buttresses.
- The good behavior of the mosque under horizontal earthquake loads, even without the outer parts of its buttresses, is attributed to its balanced structural system, generously sized walls and piers, and well-sized buttress system.
- As a result, the study revealed that the buttress system of the Süleymaniye Mosque has high adequacy against seismic transverse forces and that it was designed not only with experience but also with a sound knowledge of structural behavior because it was seen that this support system of the structure was neither weak nor oversized.
- The first two authors of this study have initiated and are continuing a second study on the Süleymaniye Mosque, in which the time-history analysis method is used, soil-structure interaction is considered, and the minarets and courtyard of the structure are included in the models. Additionally, they examine the vertical component of the earthquake effect in a section of this new study. Thanks to this new study, the adequacy of the structure’s buttress system for real earthquakes and their scaled versions will be understood more comprehensively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aslanapa, O. Osmanlı Devri Mimarisi. In İnkılap Kitabevi; Sayfa sayısı: Istanbul, Turkey, 1986; p. 568. (In Turkish) [Google Scholar]
- Çelik, S. The Construction Process of the Süleymaniye Complex Within the Light of Available Documents. Ph.D. Thesis, Institute of Science, Istanbul Technical University, Istanbul, Turkey, 2001; 322p. (In Turkish). [Google Scholar]
- Necipoğlu, G. The Age of Sinan: Architectural Culture in the Ottoman Empire; Reaktion Books Ltd.: London, UK, 2005; 592p. [Google Scholar]
- Kuban, D. Osmanlı Mimarisi; Yapı–Endüstri Merkezi Yayınları, Yayın no: 134; Sayfa sayısı: Istanbul, Turkey, 2007; p. 719. (In Turkish) [Google Scholar]
- Günay, R. Sinan: The Architect and His Works; YEM Yayın; Milet Publishing Ltd.: Istanbul, Turkey, 2016; 234p. [Google Scholar]
- Taken from the Video: Kubbe-i Mina, Chapter 11-Süleymaniye Camii. Available online: https://www.youtube.com/watch?v=jQeYWIvciME (accessed on 23 March 2023).
- Ochsendorf, J.A. Collapse of Masonry Structures. Ph.D. Thesis, King’s College, University of Cambridge, Cambridge, UK, 2002; 185p. [Google Scholar]
- Huerta, S. The safety of masonry buttresses. Proc. Inst. Civ. Eng. Eng. Hist. Herit. 2010, 163, 3–24. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Dimitri, R.; Ochsendorf, J. Structural study of masonry buttresses: The trapezoidal form. Proc. Inst. Civ. Eng.–Struct. Build. 2012, 165, 483–498. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Dimitri, R.; Ochsendorf, J. Structural study of masonry buttresses: The stepped form. Proc. Inst. Civ. Eng.–Struct. Build. 2012, 165, 499–521. [Google Scholar] [CrossRef]
- İzol, R. The Effect of Buttress Form on Seismic Resistance of Masonry Buildings and Examination of the Buttress System of the Süleymaniye Mosque. Ph.D. Thesis, Graduate School of Natural and Applied Sciences, Harran University, Şanlıurfa, Turkey, 2022; 123p. (In Turkish). [Google Scholar]
- İzol, R.; Gürel, M.A.; Buyuktaskin, H.A.A. Investigation of the effectiveness of nature-inspired buttress forms in supporting masonry structures. Građevinar 2022, 74, 573–586. [Google Scholar] [CrossRef]
- Karaesmen, E. Variations on the Theme of Sinan; Chamber of Civil Engineers: Ankara, Turkey, 2008; 296p. (In Turkish) [Google Scholar]
- Ierimonti, L.; Cavalagli, N.; Venanzi, I.; García-Macías, E.; Ubertini, F. A Bayesian-based inspection-monitoring data fusion approach for historical buildings and its post-earthquake application to a monumental masonry palace. Bull. Earthq. Eng. 2023, 21, 1139–1172. [Google Scholar] [CrossRef]
- Gara, F.; Nicoletti, V.; Arezzo, D.; Cipriani, L.; Leoni, G. Model Updating of Cultural Heritage Buildings Through Swarm Intelligence Algorithms. Int. J. Archit. Herit. 2023, 19, 259–275. [Google Scholar] [CrossRef]
- Onat, O.; Toy, A.T.; Özdemir, E. Block masonry equation-based model updating of a masonry minaret and seismic performance evaluation. J Civ. Struct. Health Monit. 2023, 13, 1221–1241. [Google Scholar] [CrossRef]
- Shehu, R. Static and Seismic Safety of the Inclined Tower of Portogruaro: A Preliminary Numerical Approach. Buildings 2024, 14, 2611. [Google Scholar] [CrossRef]
- Pouraminian, M. Multi-hazard reliability assessment of historical brick minarets. J. Build. Pathol. Rehabil. 2022, 7, 10. [Google Scholar] [CrossRef]
- Jadallah, M.; Almustafa, M.K.; Doğangün, A.; Nehdi, M.L. Nonlinear analysis of historical Toptaş minaret and FRP strengthening for sequence earthquake events. J. Build. Pathol. Rehabil. 2025, 10, 57. [Google Scholar] [CrossRef]
- Kaya, S.M.; Yuzugullu, O.; Erdik, M.; Aydinoglu, N. Earthquake performance of Süleymaniye Mosque. In Structural Analysis of Historical Constructions–Possibilities of Numerical and Experimental Techniques, Proceedings of the IVth International Seminar on Structural Analysis of Historical Constructions, Padova, Italy, 10–13 November 2004; Modena, C., Lourenço, P.B., Roca, P., Eds.; CRC Press: London, UK, 2005. [Google Scholar] [CrossRef]
- Erdik, M. Earthquake Performance of Hagia Sophia. In Seismic Isolation, Structural Health Monitoring, and Performance Based Seismic Design in Earthquake Engineering; Kasimzade, A., Şafak, E., Ventura, C., Naeim, F., Mukai, Y., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Arıoğlu, E.; Anadol, K. On the Earthquake Resistance of the Süleymaniye Mosque (Istanbul) in the Historical Perspective (1557–1973). In Proceedings of the 5th World Conference on Earthquake Engineering, Rome, Italy, 25–29 June 1973. [Google Scholar]
- Aksoy, İ.H. Foundation Systems Applied in Historical Buildings in Istanbul. Ph.D. Thesis, Istanbul Technical University, Istanbul, Turkey, 1982. (In Turkish). [Google Scholar]
- Selahiye, A.; Aydınoglu, M.N.; Erdik, M. Determination of Dynamic Characteristics of Süleymaniye Mosque by Analitical and Experimental methods. In Proceeding of the Third National Conference on Earthquake Engineering, Tokyo, Japan, 14–16 November 1995; pp. 284–293. (In Turkish). [Google Scholar]
- Kaya, S.M. Determination of Earthquake Performance of Süleymaniye Mosque. Master’s Thesis, Department of Civil Engineering, Boğaziçi University, Istanbul, Turkey, 1999; 121p. [Google Scholar]
- Fahjan, Y.M.; Keypour, H. Effects of dome system on the seismic behaviour of Ottomans historical structure. In Structural Analysis of Historical Constructions; MacMillan: New Delhi, India, 2006; pp. 1617–1624. [Google Scholar]
- Şeker, B.Ş. Investigation of Behaviour of Architect Sinan’s Mosques Under Static and Dynamic Loads. Ph.D. Thesis, Department of Civil Engineering, Karadeniz Technical University, Trabzon, Turkey, 2011; 373p. [Google Scholar]
- Aslan, A. Evaluation of the Earthquake Performance of the Süleymaniye Mosque Depending on Local Soil Conditions. Master’s Thesis, Department of Civil Engineering, Graduate School of Natural and Applied Sciences, Yıldız Technical University, Istanbul, Turkey, 2016; 130p. (In Turkish). [Google Scholar]
- Akyürek, M.E.; Kahraman, G. Structural art in Sinan’s mosques. J. Art Hist. 2021, 30, 255–283. (In Turkish) [Google Scholar] [CrossRef]
- Ural, A. 19th May 2011 Simav (Kütahya) earthquake and response of masonry Halil Aga Mosque. Earthq. Struct. 2013, 4, 671–683. [Google Scholar] [CrossRef]
- Çavuşlu, M. Assessing Seismic Crack Performance of Diyarbakır Çüngüş Masonry Stone Bridge Considering 2023 Kahramanmaraş, Hatay, Malatya, Gaziantep Earthquakes. Bitlis Eren Üniversitesi Fen Bilim. Derg. 2023, 12, 544–556. [Google Scholar] [CrossRef]
- Erkek, H.; Yetkin, M. Assessment of the performance of a historic minaret during the Kahramanmaraş earthquakes (Mw 7.7 and Mw 7.6). In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 58, p. 105620. [Google Scholar]
- Kocaman, İ. The effect of the Kahramanmaraş earthquakes (Mw 7.7 and Mw 7.6) on historical masonry mosques and minarets. Eng. Fail. Anal. 2023, 149, 107225. [Google Scholar] [CrossRef]
- Kocaman, İ.; Mercimek, Ö.; Gürbüz, M.; Erbaş, Y.; Anıl, Ö. The effect of Kahramanmaraş earthquakes on historical Malatya Yeni Mosque. Eng. Fail. Anal. 2024, 161, 108310. [Google Scholar] [CrossRef]
- Dogangun, A.; Sezen, H. Seismic vulnerability and preservation of historical masonry monumental structures. Earthq. Struct. 2012, 3, 83–95. [Google Scholar] [CrossRef]
- Pouraminian, M.; Didevar, E. Performance of Gaskar Historical Minaret against natural wind and earthquake hazards. Anal. Struct. Earthq. 2021, 18, 47–58. [Google Scholar]
- Işık, E.; Harirchian, E.; Arkan, E.; Avcil, F.; Günay, M. Structural analysis of five historical minarets in Bitlis (Turkey). Buildings 2022, 12, 159. [Google Scholar] [CrossRef]
- Scamardo, M.; Zucca, M.; Crespi, P.; Longarini, N.; Cattaneo, S. Seismic vulnerability evaluation of a historical masonry tower: Comparison between different approaches. Appl. Sci. 2022, 12, 11254. [Google Scholar] [CrossRef]
- Avcil, F.; Işık, E.; Bilgin, H.; Özmen, H.B. Tbdy-2018’de verilen tasarım spektrumlarının anıtsal yığma yapı sismik davranışına etkisi. Adıyaman Üniversitesi Mühendislik Bilim. Derg. 2022, 9, 165–177. [Google Scholar] [CrossRef]
- Cavuslu, M. 3D seismic assessment of historical stone arch bridges considering effects of normal-shear directions of stiffness parameters between discrete stone elements. Struct. Eng. Mech. Int. J. 2022, 83, 207–227. [Google Scholar]
- Bahreini, V.; Pouraminian, M.; Tabaroei, A. Seismic sensitivity analysis of Musa Palas historic masonry arch bridge by Tornado diagram. J. Build. Pathol. Rehabil. 2022, 7, 71. [Google Scholar] [CrossRef]
- Trešnjo, F.; Humo, M.; Casarin, F.; Ademović, N. Experimental investigations and seismic assessment of a historical stone minaret in Mostar. Buildings 2023, 13, 536. [Google Scholar] [CrossRef]
- Restoration, Yearbook. In General Directorate of Foundations; Istanbul I. Regional Directorate: Istanbul, Turkey, 2011; 172p. (In Turkish)
- Available online: https://archives.saltresearch.org/handle/123456789/70567 (accessed on 23 March 2023).
- Available online: https://archives.saltresearch.org/handle/123456789/75733 (accessed on 23 March 2023).
- Özgüleş, M. Innovation in Sinan’s Art. In Bilim ve Teknik; TÜBİTAK: Ankara, Turkey, 2008; Issue 492; pp. 54–67. (In Turkish) [Google Scholar]
- Lourenço, P.B. Computational Strategies for Masonry Structures. Ph.D. Thesis, University of Porto, Porto, Portugal, 1996. [Google Scholar]
- Işık, E.; Ademović, N.; Harirchian, E.; Avcil, F.; Büyüksaraç, A.; Hadzima-Nyarko, M.; Akif Bülbül, M.; Işık, M.F.; Antep, B. Determination of Natural Fundamental Period of Minarets by Using Artificial Neural Network and Assess the Impact of Different Materials on Their Seismic Vulnerability. Appl. Sci. 2023, 13, 809. [Google Scholar] [CrossRef]
- Işık, E.; Avcil, F.; Harirchian, E.; Arkan, E.; Bilgin, H.; Özmen, H.B. Architectural Characteristics and Seismic Vulnerability Assessment of a Historical Masonry Minaret under Different Seismic Risks and Probabilities of Exceedance. Buildings 2022, 12, 1200. [Google Scholar] [CrossRef]
- Illampas, R. Experimental and Computational Invrstigation of the Structural Response of Adobe Structure. Ph.D. Thesis, Department of Civil and Environmental Engineering, University of Cyprus, Nicosia, Cyprus, 2013; 225p. [Google Scholar]
- Giordano, A.; Mele, E.; De Luca, A. Modelling of historical masonry structures: Comparison of different approaches through a case study. Eng. Struct. 2002, 24, 1057–1069. [Google Scholar] [CrossRef]
- Angelillo, M. (Ed.) Mechanics of Masonry Structures; CISM International Centre for Mechanical Sciences; Springer: Vienna, Austria, 2014. [Google Scholar] [CrossRef]
- Illampas, R.; Ioannou, I.; Lourenço, P.B. Seismic appraisal of heritage ruins: The case study of the St. Mary of Carmel church in Cyprus. Eng. Struct. 2020, 224, 111209. [Google Scholar] [CrossRef]
- Tomaževič, M. Earthquake-Resistant Design of Masonry Buildings; Imperial College Press: London, UK, 1999; 268p. [Google Scholar]
- Çelik, S. Süleymaniye Complex, Material, Technique and Process; Atatürk Cultural Center Publications: Istanbul, Turkey, 2008; 328p. (In Turkish) [Google Scholar]
- Ahunbay, Z. Construction techniques and materials used in Mimar Sinan structures. In Mimarbaşı Koca Sinan: His Age and Works; T. C. General Directorate of Foundations: Istanbul, Turkey, 1988. (In Turkish) [Google Scholar]
- Arioğlu, N.; Arioğlu, E. Engineering Mystery of Master Architect Sinan’s “Küfeki” Shell Limestone. Archit. Sci. Rev. 2005, 48, 163–171. [Google Scholar] [CrossRef]
- Korkmaz, Ş. Determination of Thermal Conductivity, Physical and Mechanical Properties of Brick Materials Used in Historical Buildings. Master’s Thesis, Department of Civil Engineering, Graduate School of Natural and Applied Sciences, Süleyman Demirel University, Isparta, Turkey, 2019. [Google Scholar]
- ABAQUS. Theory Manual, version 6.14; Simulia place: Providence, RI, USA, 2014.
- Tiberti, S.; Acito, M.; Milani, G. Comprehensive FE numerical insight into Finale Emilia Castle behavior under 2012 Emilia Romagna seismic sequence: Damage causes and seismic vulnerability mitigation hypothesis. Eng. Struct. 2016, 117, 397–421. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G. Effects of Geometrical Features on the Seismic Response of Historical Masonry Towers. J. Earthq. Eng. 2017, 22, 2–34. [Google Scholar] [CrossRef]
- Massicotte, B.; Elwi, A.E.; Macgregor, J.G. Tension-stiffening model for planar reinforced concrete members. J. Struct. Eng. 1990, 116, 3039–3058. [Google Scholar] [CrossRef]
- Hognestad, E. A Study of Combined Bending and Axial Load in Reinforced Concrete Members; University of Illinois Bulletin: Champaign, IL, USA, 1951; p. 49, 128s. [Google Scholar]
- Valente, M.; Milani, G. Non-linear dynamic and static analyses on eight historical masonry towers in the North-East of Italy. Eng. Struct. 2016, 114, 241–270. [Google Scholar] [CrossRef]
- Demir, A.; Altıok, T.Y. Numerical assessment of a slender structure damaged during 30 October 2020, İzmir earthquake in Turkey. Bull. Earthq. Eng. 2021, 19, 5871–5896. [Google Scholar] [CrossRef]
- Müdürlüğü, V.G. Archives guide of the General Directorate of Foundations [Vakıflar Genel Müdürlüğü Arşiv Rehberi] Ankara: Vakıflar Genel Müdürlüğü Yayınları. 2020. Available online: https://www.academia.edu/44253905/VAKIFLAR_GENEL_M%C3%9CD%C3%9CRL%C3%9C%C4%9E%C3%9C_AR%C5%9E%C4%B0V_REHBER%C4%B0 (accessed on 10 December 2024).
- Dejong, M.J. Seismic Assessment Strategies for Masonry Structures. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Endo, Y.; Pelà, L.; Roca, P. Review of different pushover analysis methods applied to masonry buildings and comparison with nonlinear dynamic analysis. J. Earthq. Eng. 2016, 21, 1234–1255. [Google Scholar] [CrossRef]
- Gürel, M.A.; İzol, R.; Mollamahmutoğlu, Ç.; Pekgökgöz, R.K.; Yüksel, F.Ş.K.; Özeren, M. Effect of Buttress Form on Transverse Seismic Resistance of Masonry Buildings. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023, 48, 185–210. [Google Scholar] [CrossRef]
- SRMGHS-2017; Seismic Risks Management Guide for Historical Structures. General Directorate of Foundations: Ankara, Turkey, 2017. (In Turkish)
- Fajfar, P. A nonlinear analysis method for performance-based seismic design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Cattari, S. PERPETUATE guidelines for seismic performance-based assessment of cultural heritage masonry structures. Bull. Earthq. Eng. 2015, 13, 13–47. [Google Scholar] [CrossRef]
- Turkish Building Seismic Code. In Official Gazette; Disaster and Emergency Management Presidency (AFAD): Ankara, Türkiye, 2018. (In Turkish)


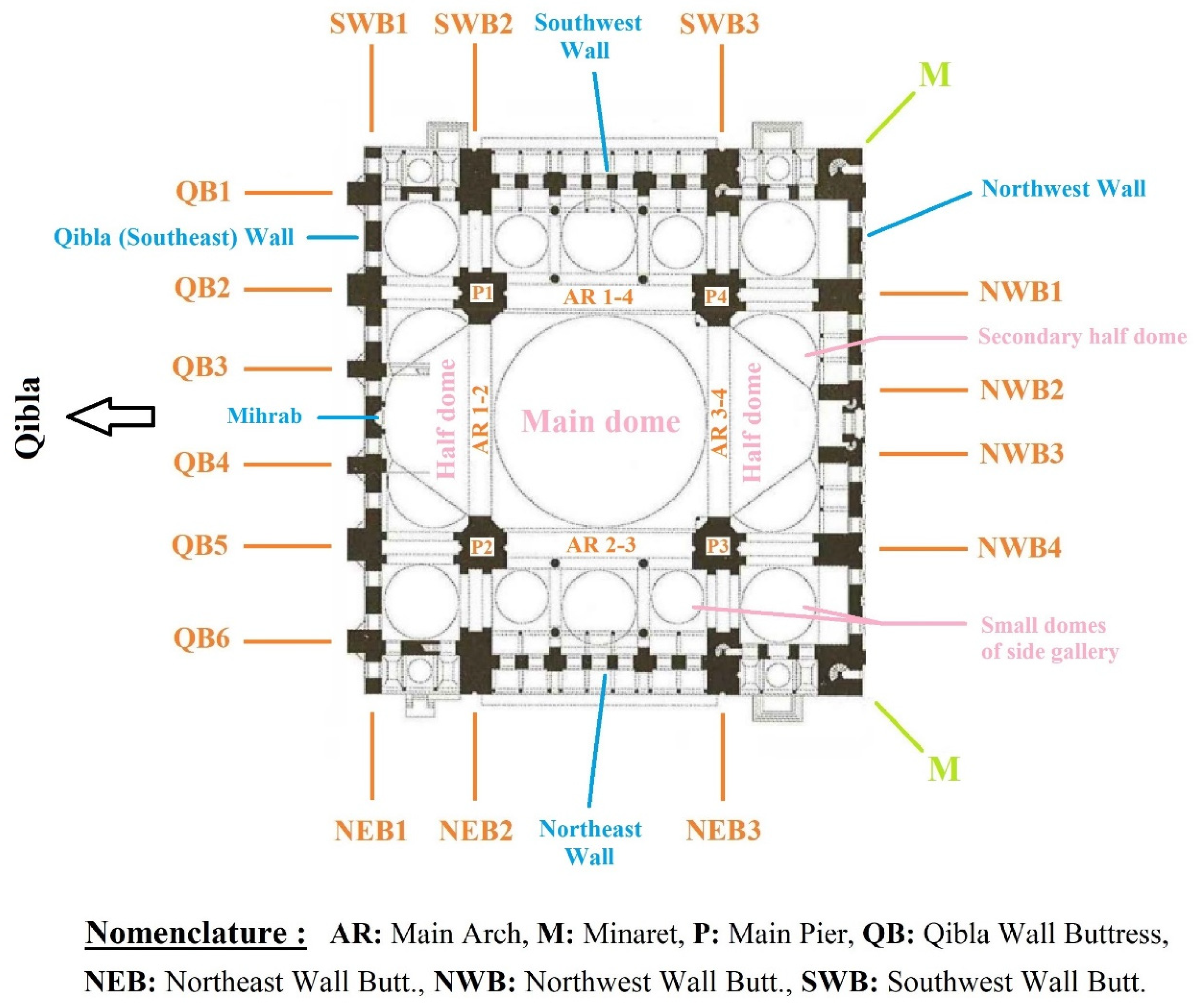
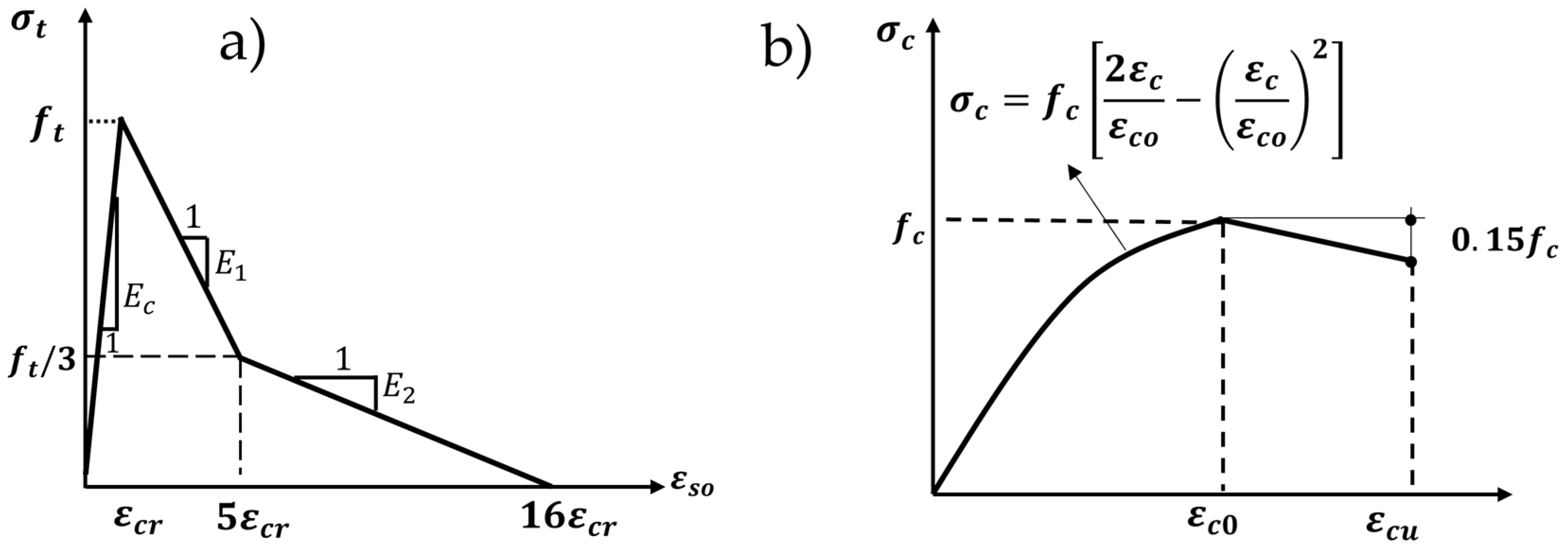






| Qibla Wall Buttresses | PRE-STATE | FIF-STATE | ||
|---|---|---|---|---|
| Top | Bottom | Top | Bottom | |
| Side buttresses (QB1 and QB6) | 1.36 | 1.56 | 0.68 | 0.78 |
| Buttresses on the same axes as the piers (QB2 and QB5) | 2.60 | 2.85 | 1.30 | 1.43 |
| Buttresses next to the mihrab (QB3 and QB4) | 2.18 | 2.40 | 1.09 | 1.20 |
| Buttresses on the Northeast and Southwest Walls | PRE-STATE | FIF-STATE | ||
| Buttresses on the same axes as the piers (NEB2, NEB3, SWB2, SWB3) | 3.21 | 1.62 | ||
| Stepped buttresses (NEB1, SWB1) | 4.00 (Lower part) 1.55 (Upper part) | 2.00 (Lower part) 0.78 (Upper part) | ||
| Material | Unit Volume Weight, γ (kN/m3) | Compressive Strength, fc (MPa) |
|---|---|---|
| Stone (Küfeki) | 21.48 | 33.20 |
| Khorasan mortar | 17.95 | 7.59 |
| Khorasan brick | 17.60 | 5.50 |
| Materials | Unit Vol. Weight, γ (kN/m3) | Elastic Modulus, E (MPa) | Compressive Strength, fc (MPa) | Tensile Strength, ft (MPa) | Poisson’s Ratio, ν |
|---|---|---|---|---|---|
| Küfeki stone + Khorasan mortar | 19.70 | 8875 | 8.87 | 0.887 | 0.20 |
| Khorasan brick + Khorasan mortar | 16.79 | 2800 | 2.78 | 0.280 | 0.20 |
| Parameter | Value Used in the Study |
|---|---|
| ψ | 36° |
| ϵ | 0.1 |
| fb0/fc0 | 1.16 |
| Kc | 0.667 |
| μ | 0.002 |
| Mode | Amb. Vibr. Tests Results—Accelero. Results Belonging to A Quake [24] | ABAQUS | Difference * |
|---|---|---|---|
| 1 | 3.38—3.38 | 3.98 | 17.7% |
| 2 | 3.44—3.42 | 4.17 | 21.2% |
| 3 | 4.26—4.3 | 5.12 | 17% |
| 4 | 4.71—** | 5.13 | 6% |
| Mode | PRE-STATE | FIF-STATE | NO-STATE |
|---|---|---|---|
| 1 | 3.98 | 3.90 | 3.83 |
| 2 | 4.17 | 3.99 | 3.91 |
| 3 | 5.12 | 5.01 | 4.94 |
| 4 | 5.13 | 5.02 | 4.95 |
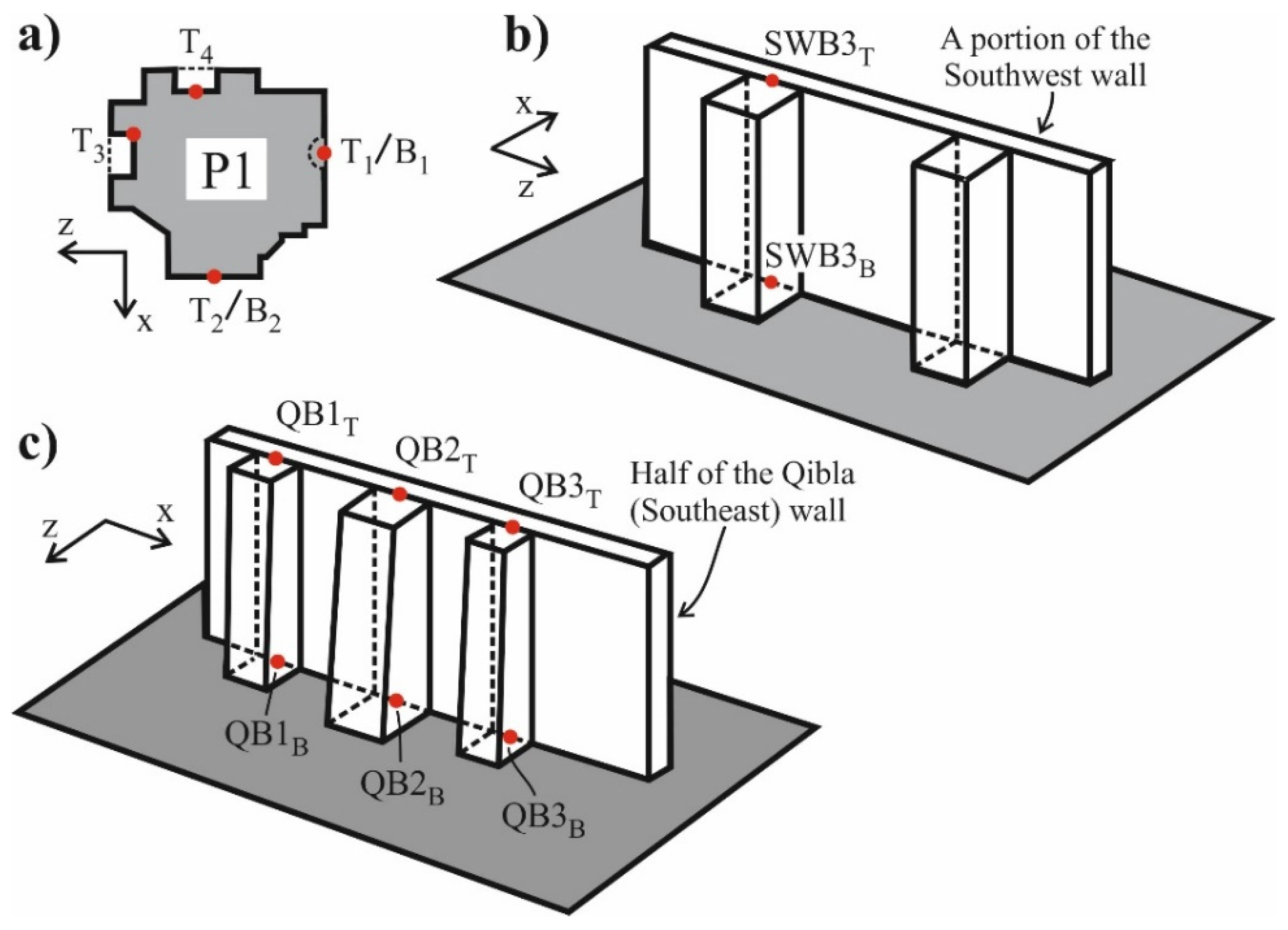
| Point | Location of the Point in the Structure |
|---|---|
| DT | Top of the main dome |
| (AR 1-2)T | Top of the AR 1-2 |
| (AR 1-4)T | Top of the AR 1-4 |
| T1 | Point 1 on the top section of the pier P1 |
| T2 | Point 2 on the top section of the pier P1 |
| T3 | Point 3 on the top section of the pier P1 |
| T4 | Point 4 on the top section of the pier P1 |
| B1 | Point 1 on the bottom section of the pier P1 |
| B2 | Point 2 on the bottom section of the pier P1 |
| SWB3T | The buttress–wall outer interface midpoint of the SWB3 buttress at the level of the wall top section |
| SWB3B | The buttress–wall outer interface midpoint of the SWB3 buttress at the level of the wall bottom section |
| (QB1-2-3)T | The buttress–wall outer interface midpoints of the QB1, QB2, and QB3 buttresses at the level of the wall top section |
| (QB1-2-3)B | The buttress–wall outer interface midpoints of the QB1, QB2, and QB3 buttresses at the level of the wall bottom section |
| Point | PRE-STATE | FIF-STATE | NO-STATE |
|---|---|---|---|
| B1 | 0.83 | 0.80 | 0.79 |
| B2 | 0.94 | 0.93 | 0.92 |
| T3 | 1.14 | 1.18 | 1.20 |
| T4 | 1.18 | 1.20 | 1.23 |
| SWB3B | 0.66 | 0.72 | 0.83 |
| QB1B | 0.47 | 0.57 | 0.61 |
| QB2B | 0.48 | 0.59 | 0.77 |
| QB3B | 0.49 | 0.61 | 0.66 |
| Point | PRE-STATE | FIF-STATE | NO-STATE |
|---|---|---|---|
| DT (Vertical displacement) | 6.0 | 6.08 | 6.10 |
| (AR 1–2)T (Ver. displacemet) | 3.45 | 3.50 | 3.55 |
| (AR 1–4)T (Ver. displacement) | 4.17 | 4.30 | 4.38 |
| T1 (Hor. disp. in +z direction) | 0.29 | 0.38 | 0.44 |
| T2 (Hor. disp. in −x direction) | 0.38 | 0.45 | 0.50 |
| SWB3T (Hor. disp. in −x dir.) | 0.26 | 0.31 | 0.34 |
| QB1T (Hor. disp. in +z dir.) | 0.09 | 0.14 | 0.16 |
| QB2T (Hor. disp. in +z dir.) | 0.34 | 0.44 | 0.52 |
| QB3T (Hor. disp. in +z dir.) | 0.28 | 0.45 | 0.62 |
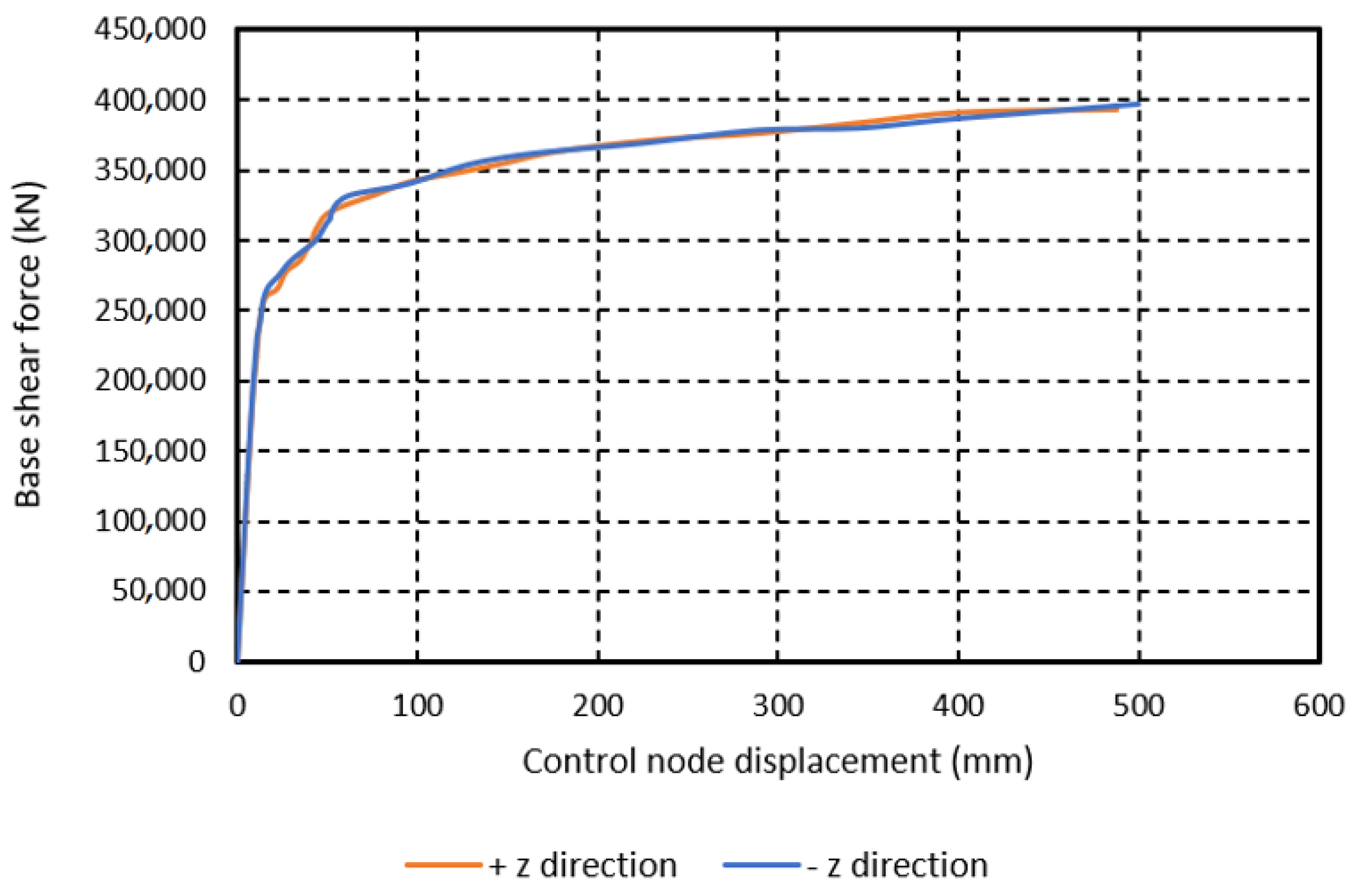
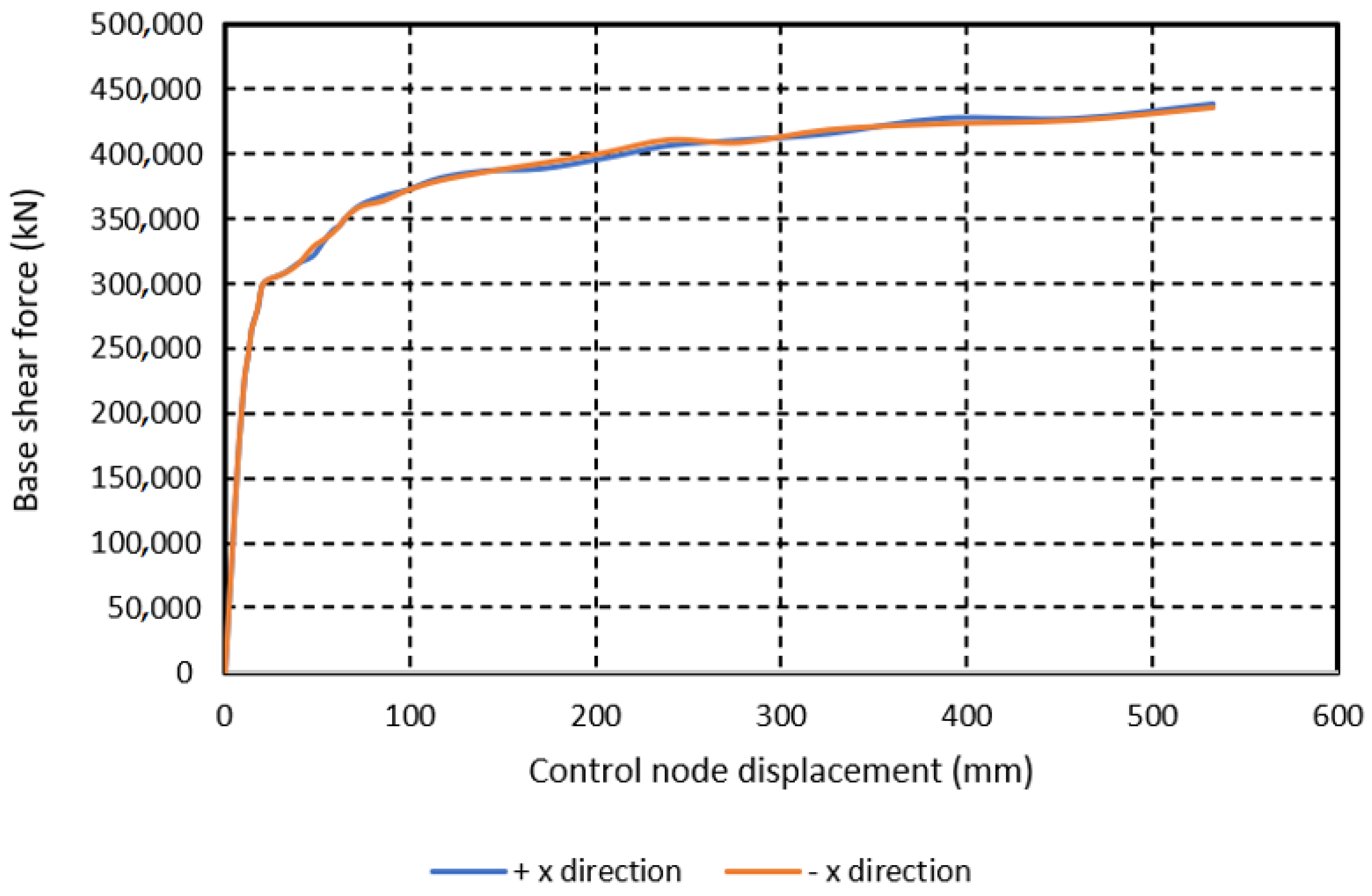
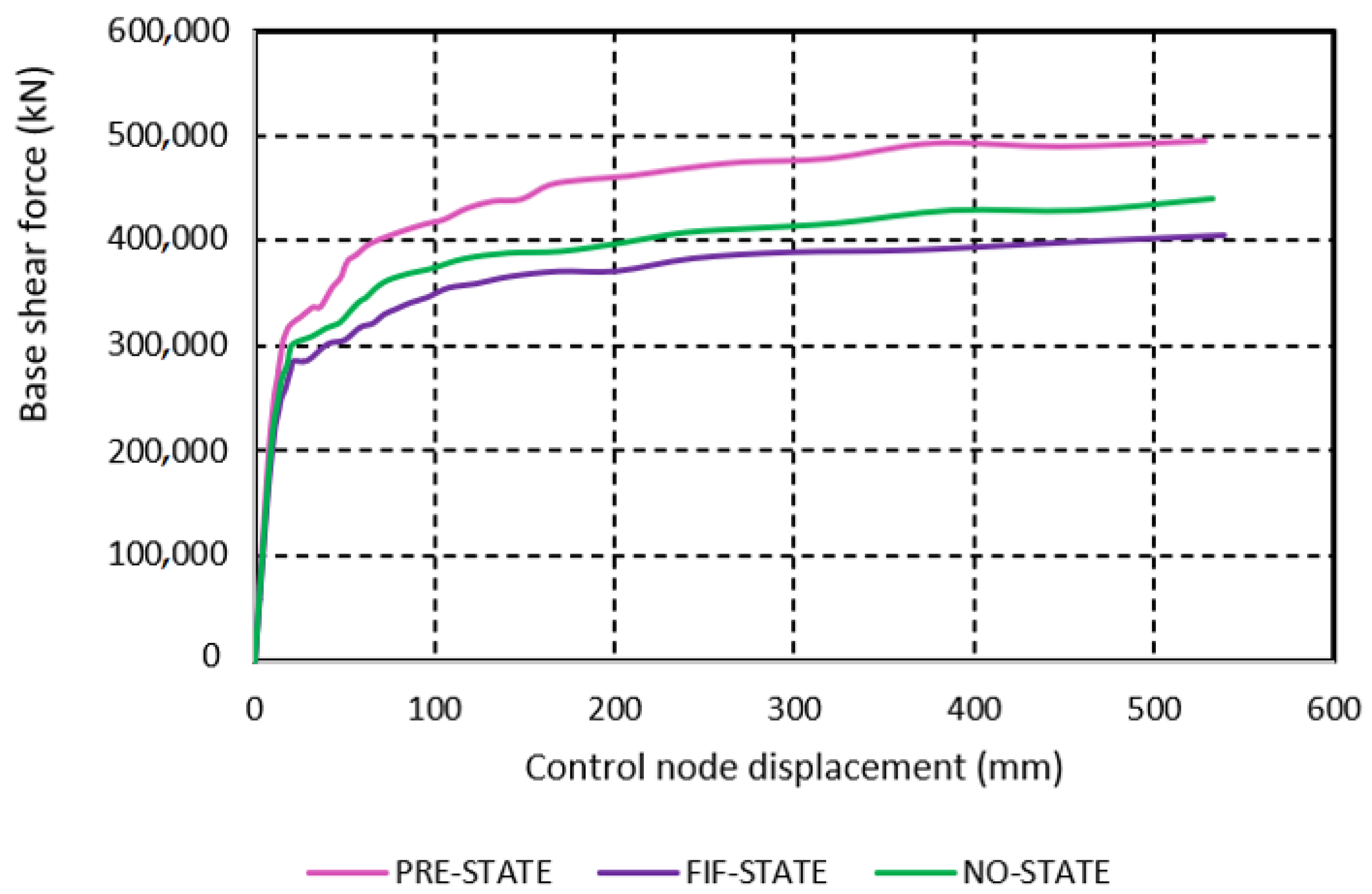
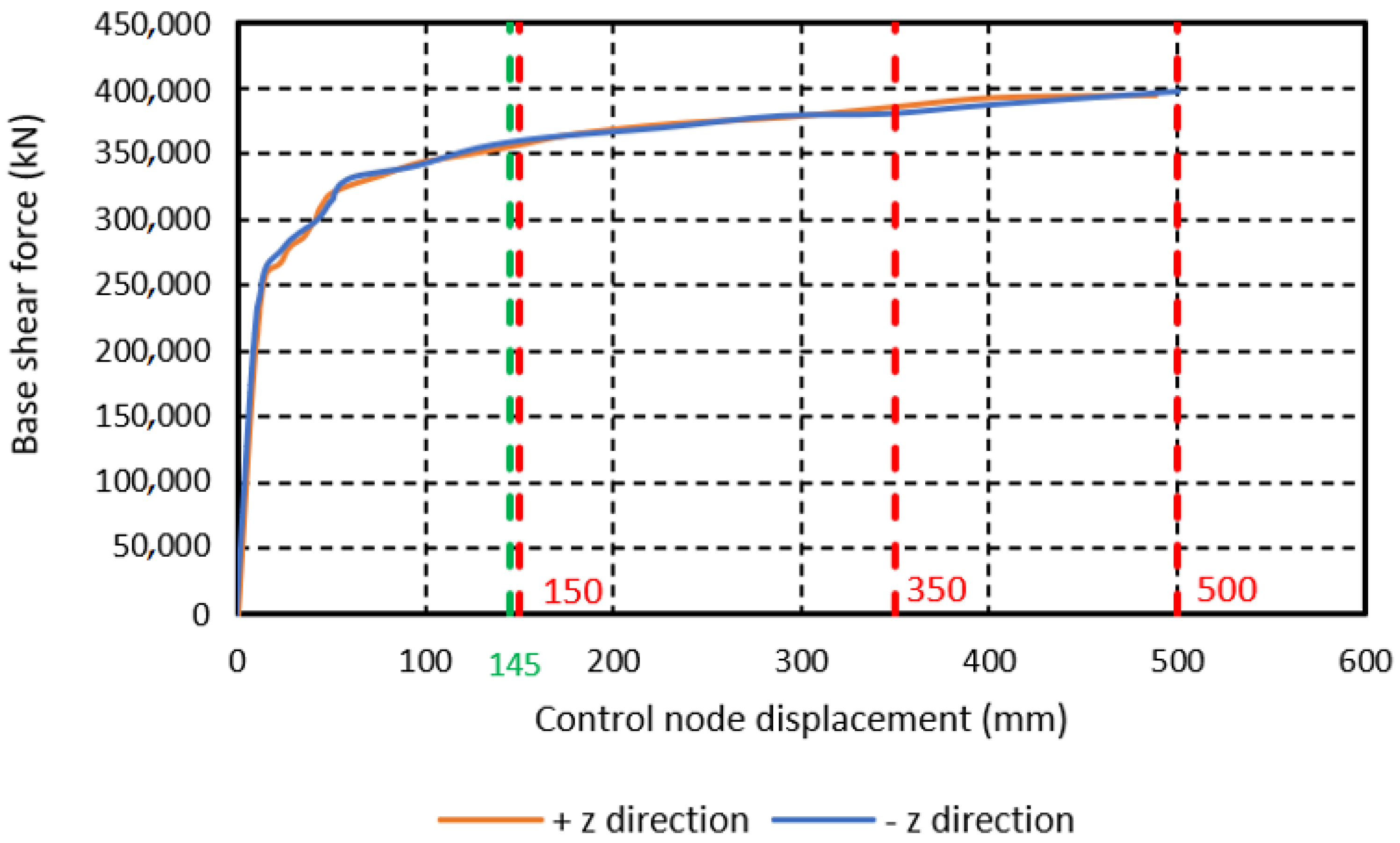
| Model | Max. Base Shear Force, Rmax (kN) | Wmodel (kN) | Max. Seis. Coeff., c = Rmax/Wmodel |
|---|---|---|---|
| PRE-STATE (Qibla axis, +z direction) | 393,755 | 564,784 | 0.70 |
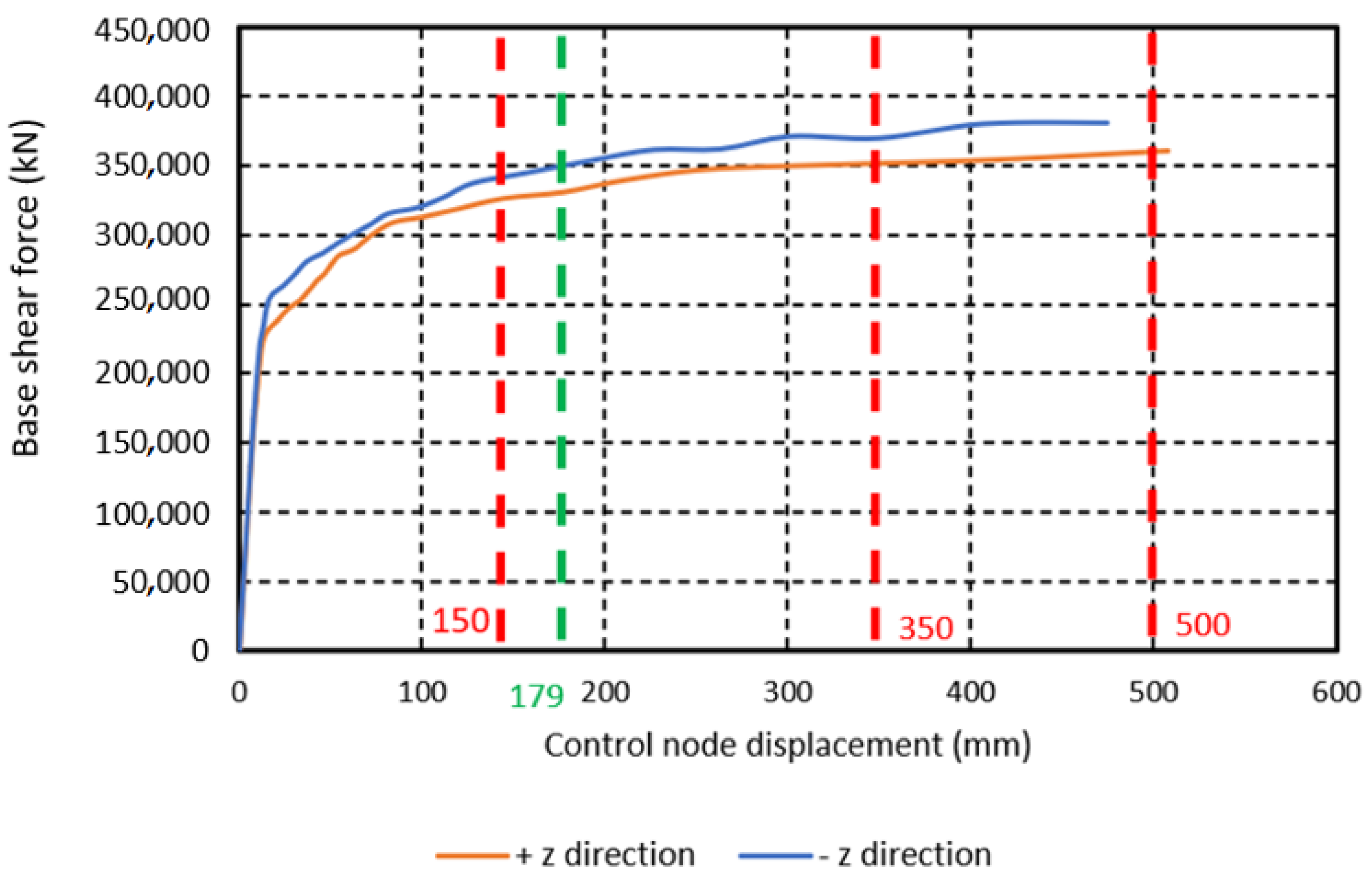
| FIF-STATE (Qibla axis, +z direction) | 360,407 | 542,888 | 0.66 |
| NO-STATE (Qibla axis, +z direction) | 349,283 | 527,656 | 0.66 |
| PRE-STATE (Per-Qibla axis, −x direction) | 500,223 | 564,784 | 0.89 |
| FIF-STATE (Per-Qibla axis, −x direction) | 439,331 | 542,888 | 0.81 |
| NO-STATE (Per-Qibla axis, −x direction) | 410,936 | 527,656 | 0.78 |
| Performance Level | Definition of Performance Level |
|---|---|
| Limited damage | It corresponds to the damage level at which limited damage occurs (limited nonlinear behavior) to the structural elements of the structure. |
| Controlled damage | This level corresponds to the level of controlled damage to the structural elements of the structure, which is mostly possible to repair. |
| Prevention of collapse | This level corresponds to the situation in which severe damage occurs in the structural elements of the building, the structure is close to partial or complete collapse, but the collapse is prevented. |
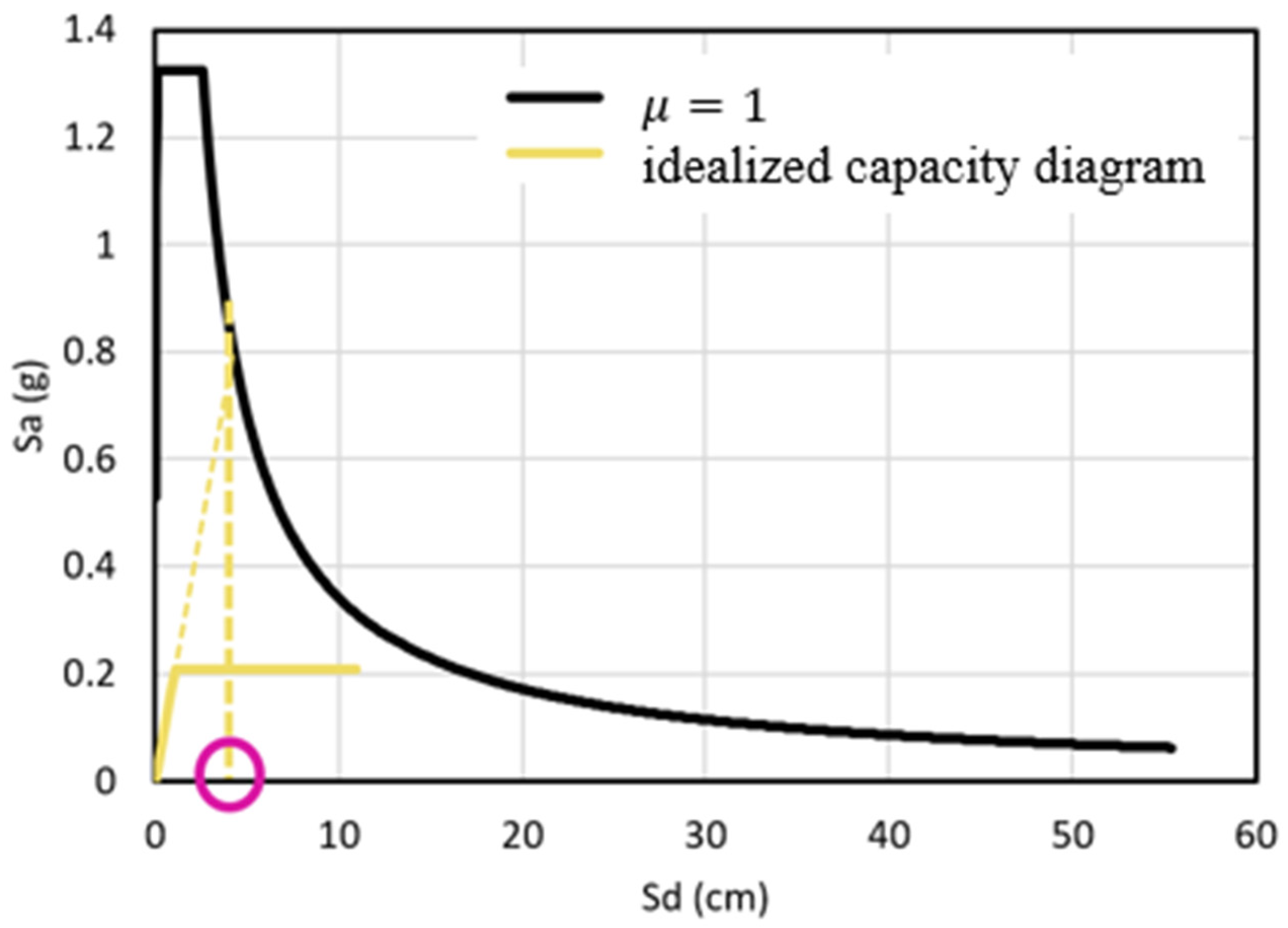
| m*(PRE-STATE) | 34,409 ton |
| (PRE-STATE) | 4.64 |
| m*(FIF-STATE) | 33,885 ton |
| (FIF-STATE) | 4.61 |
| m*(NO-STATE) | 33,370 ton |
| (NO-STATE) | 4.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
İzol, R.; Gürel, M.A.; Mollamahmutoğlu, Ç.; Avcil, F. Evaluation of the Buttress System of a Great Ottoman Mosque Against Gravity Loads and Horizontal Seismic Forces: The Case of the Istanbul Süleymaniye Mosque. Buildings 2025, 15, 1360. https://doi.org/10.3390/buildings15081360
İzol R, Gürel MA, Mollamahmutoğlu Ç, Avcil F. Evaluation of the Buttress System of a Great Ottoman Mosque Against Gravity Loads and Horizontal Seismic Forces: The Case of the Istanbul Süleymaniye Mosque. Buildings. 2025; 15(8):1360. https://doi.org/10.3390/buildings15081360
Chicago/Turabian Styleİzol, Rabia, Muhammet Arif Gürel, Çağrı Mollamahmutoğlu, and Fatih Avcil. 2025. "Evaluation of the Buttress System of a Great Ottoman Mosque Against Gravity Loads and Horizontal Seismic Forces: The Case of the Istanbul Süleymaniye Mosque" Buildings 15, no. 8: 1360. https://doi.org/10.3390/buildings15081360
APA Styleİzol, R., Gürel, M. A., Mollamahmutoğlu, Ç., & Avcil, F. (2025). Evaluation of the Buttress System of a Great Ottoman Mosque Against Gravity Loads and Horizontal Seismic Forces: The Case of the Istanbul Süleymaniye Mosque. Buildings, 15(8), 1360. https://doi.org/10.3390/buildings15081360









