Cutting Feature Extraction Method for Ultra-High Molecular Weight Polyethylene Fiber-Reinforced Concrete Based on Feature Classification and Improved Hilbert–Huang Transform
Abstract
1. Introduction
2. Experimental Methods
2.1. Concrete Specimen and Diamond Saw Blade
2.2. Experimental Equipment and Conditions
3. Experimental Results and Discussion
3.1. Mechanical Characteristics of Cutting UHMWPE-FRC
3.2. Cutting Feature Extraction for UHMWPE-FRC Based on Feature Classification and Improved Hilbert–Huang Transform (HHT)
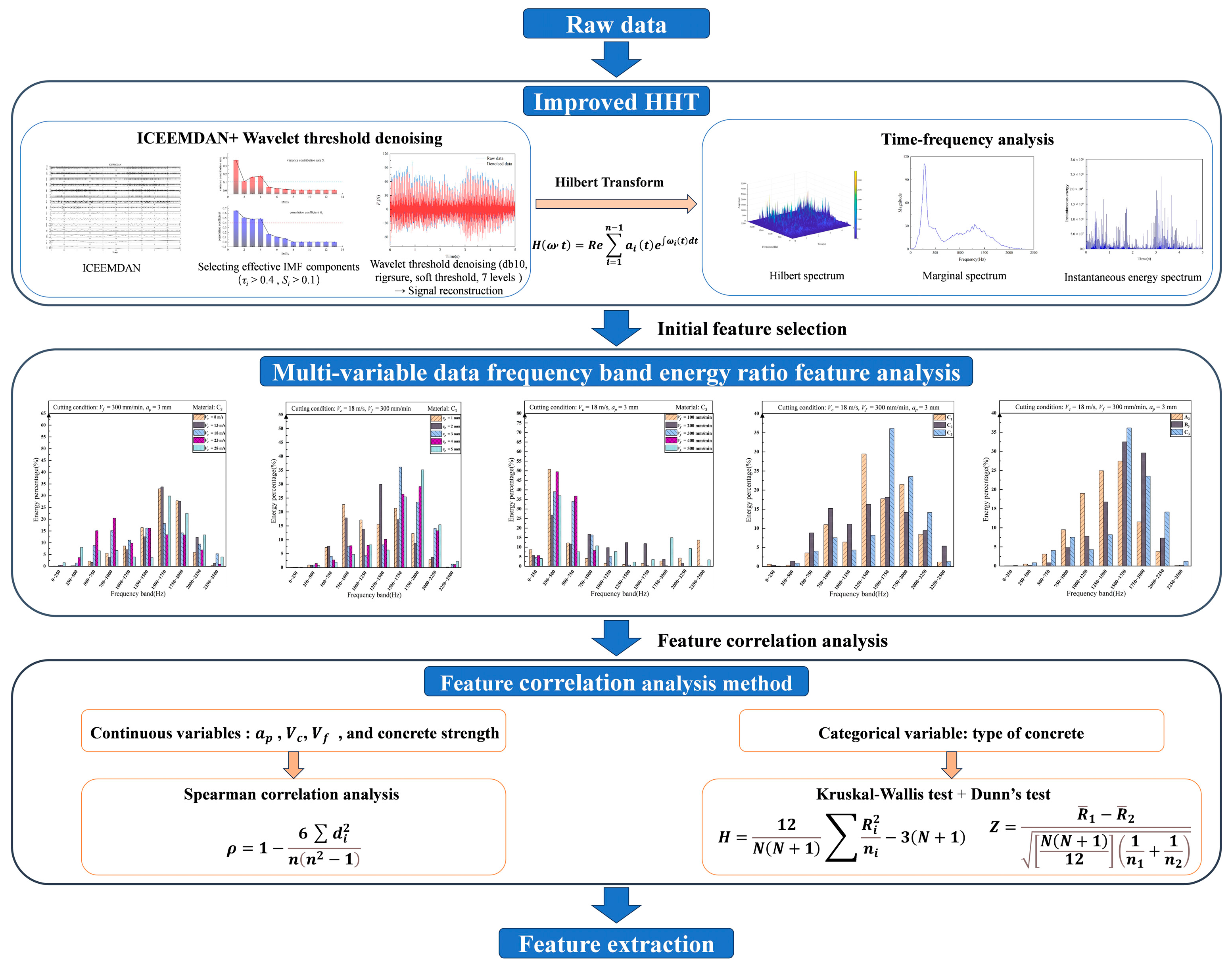
3.2.1. The Cutting Feature Extraction Method for UHMWPE-FRC Based on the Improved HHT
- 1.
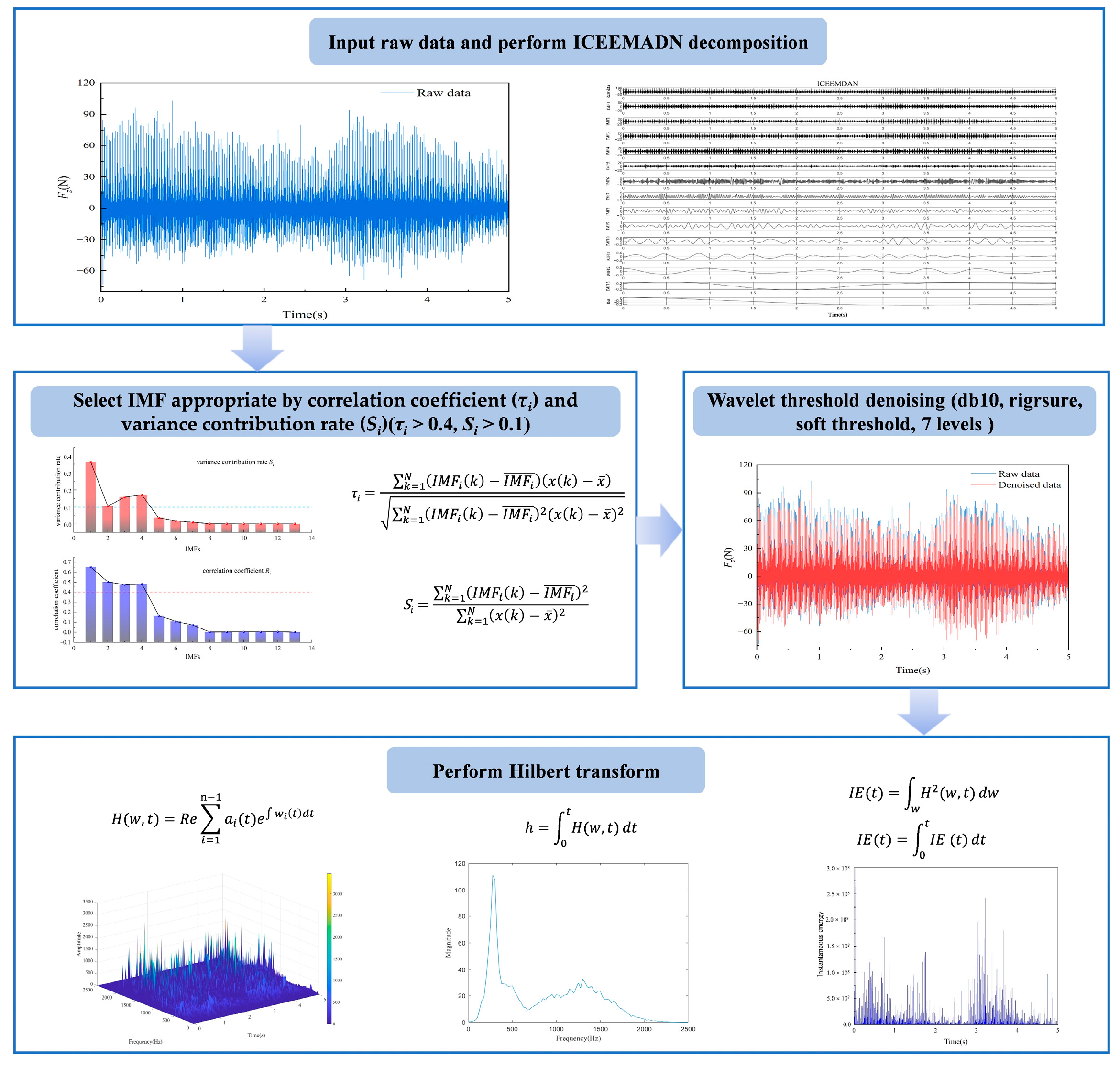
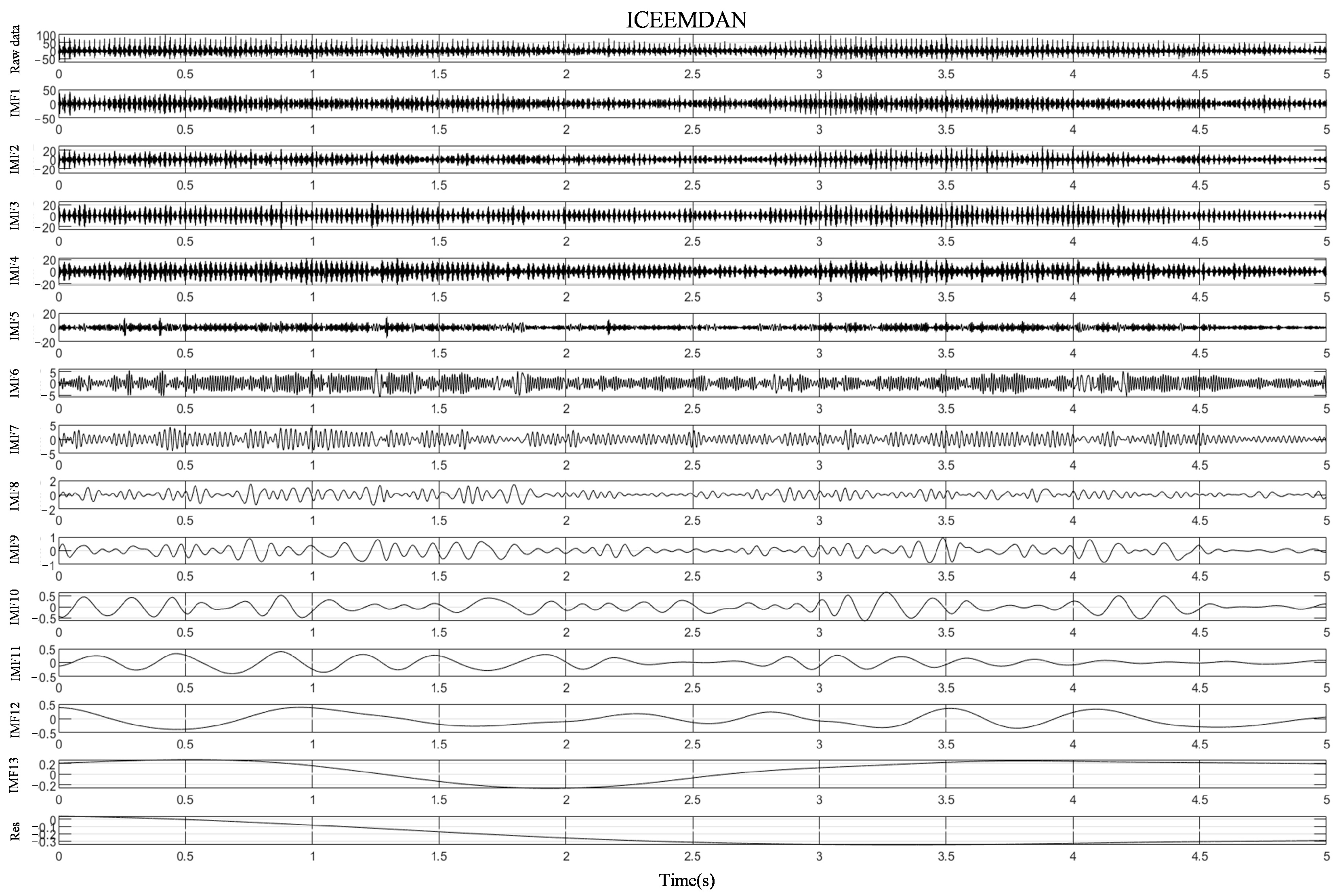
- The Improved HHT Considering ICEEMDAN and Wavelet Threshold De-Noising:
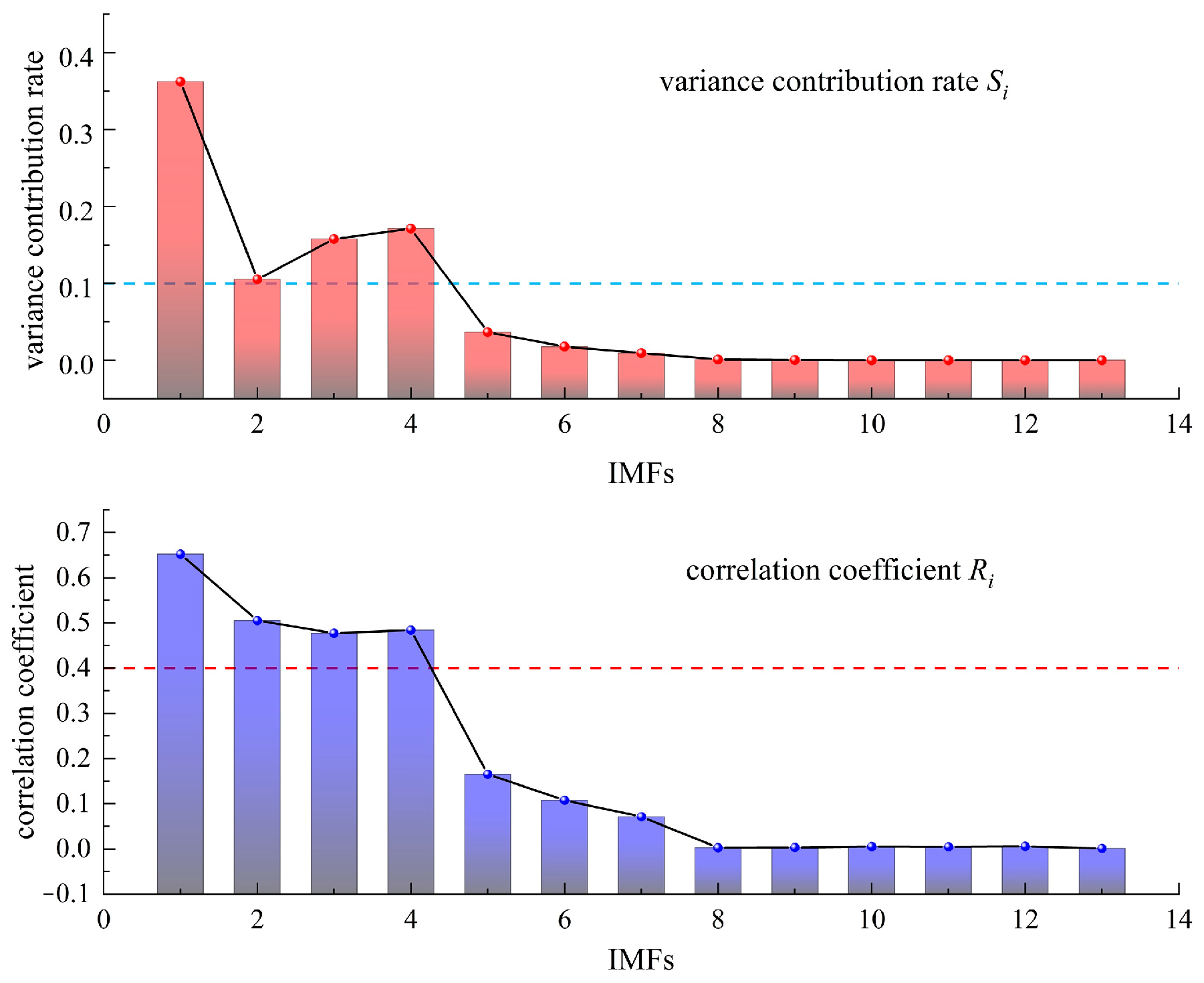
- 2.
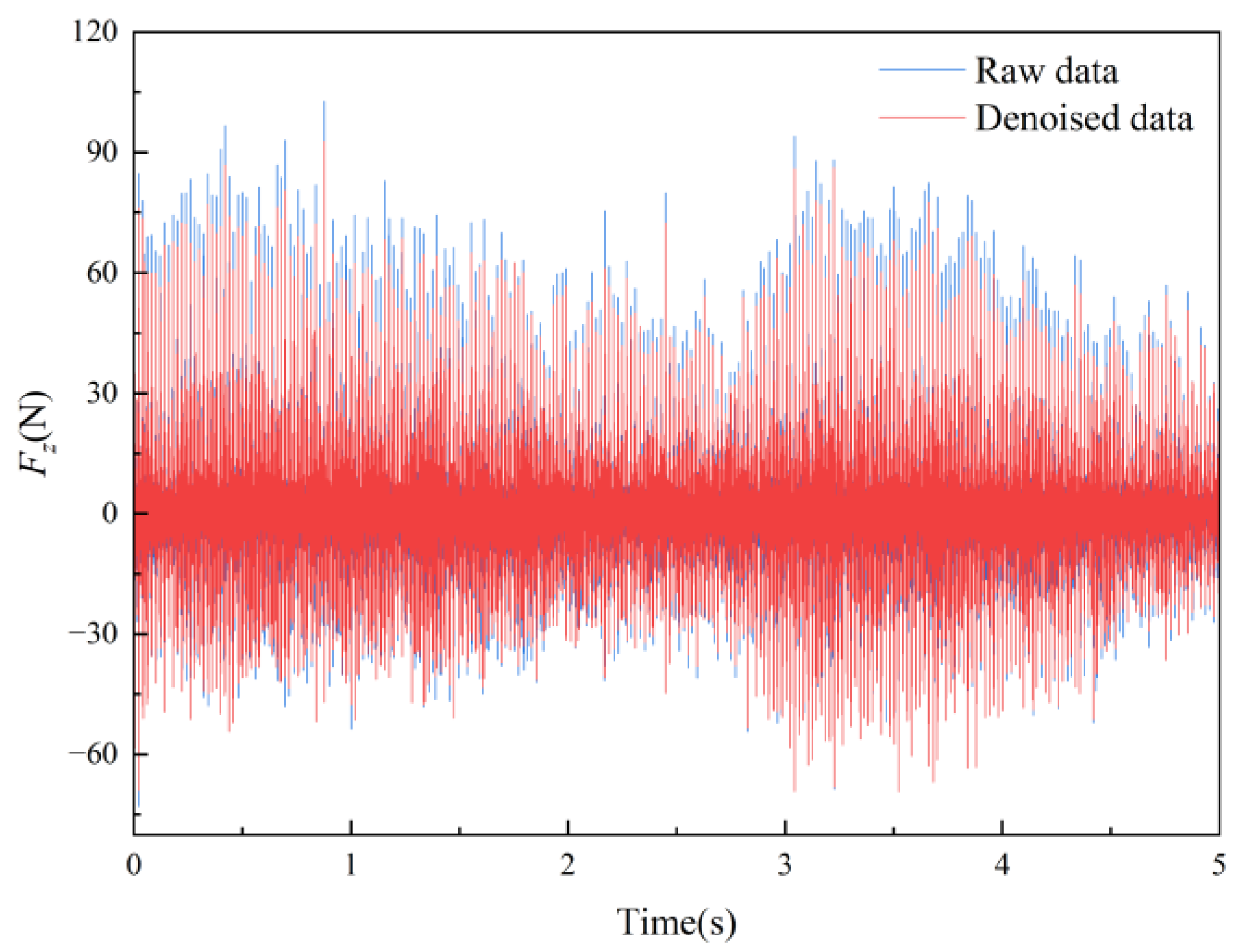
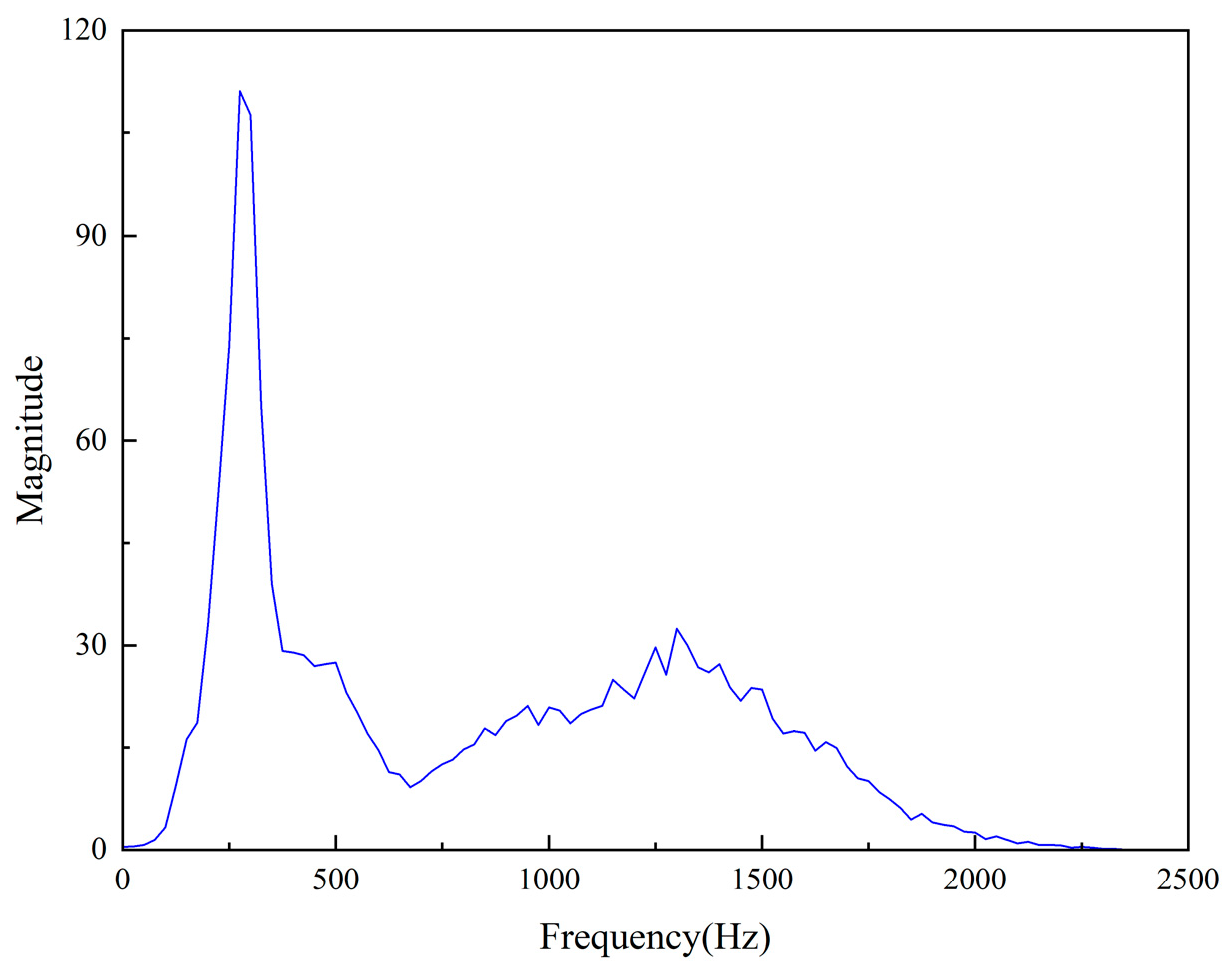
- An Example of Cutting Force De-Noising and Time-Frequency Analysis with Improved HHT:
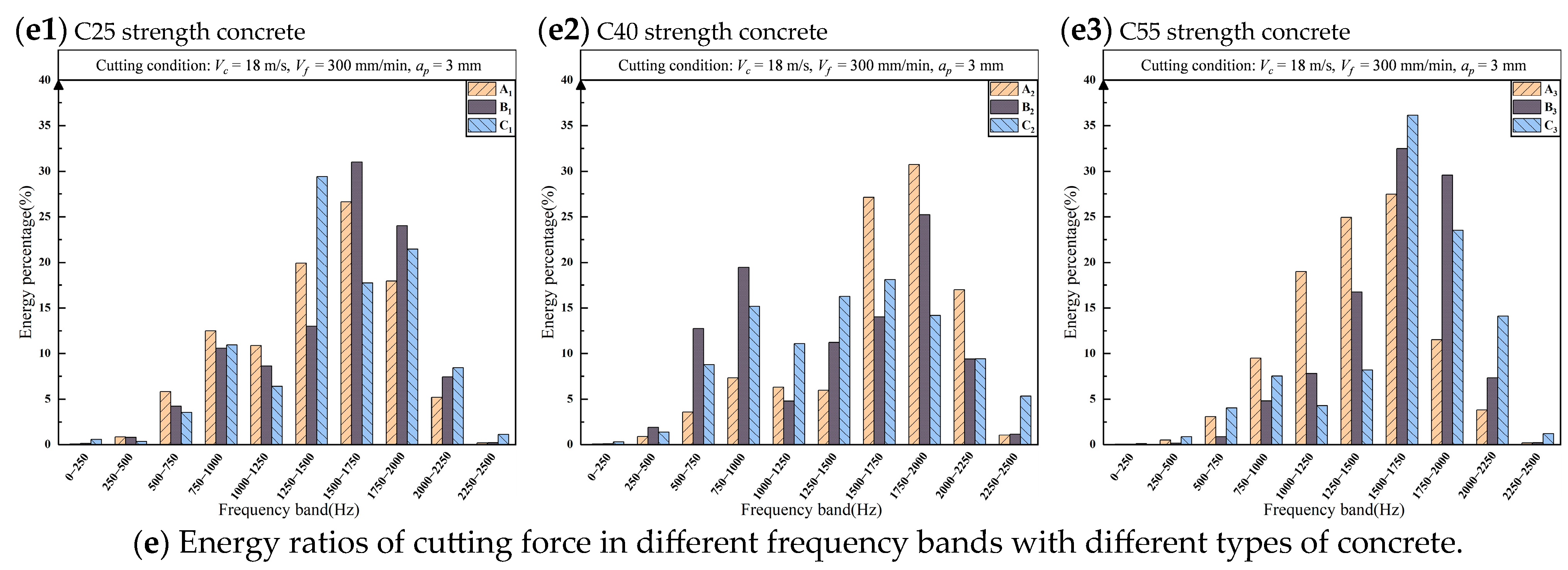
3.2.2. Feature Analysis and Preliminary Screening Based on Energy Ratios of Different Frequency Bands
3.2.3. Correlation Analysis for Feature Extraction of UHMWPE-FRC Based on Feature Classification
- 1.
- Correlation Analysis Methods for Continuous Variable Features:
- 2.
- Correlation Analysis Methods for Unordered Category of Variable Features:
3.2.4. Correlation Analysis Results and Feature Extraction
- 1.
- Correlation Analysis Results for Continuous Variable Features:
- 2.
- Correlation Analysis Results for Unordered Categorical Variable Features:
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Wu, C.; Liu, Z.-X. Comparative Evaluation of Steel Wire Mesh, Steel Fibre and High Performance Polyethylene Fibre Reinforced Concrete Slabs in Blast Tests. Thin Walled Struct. 2018, 126, 117–126. [Google Scholar] [CrossRef]
- Chen, L.; Chen, Z.; Xie, Z.; Wei, L.; Hua, J.; Huang, L.; Yap, P.S. Recent developments on natural fiber concrete: A review of properties, sustainability, applications, barriers, and opportunities. Dev. Built Environ. 2023, 16, 100255. [Google Scholar] [CrossRef]
- García, G.; Cabrera, R.; Rolón, J.; Pichardo, R.; Thomas, C. Natural Fibers as Reinforcement of Mortar and Concrete: A Systematic Review from Central and South American Regions. J. Build. Eng. 2024, 98, 111267. [Google Scholar] [CrossRef]
- Guo, Z.; Zhuang, C.; Li, Z.; Chen, Y. Mechanical Properties of Carbon Fiber Reinforced Concrete (CFRC) after Exposure to High Temperatures. Compos. Struct. 2021, 256, 113072. [Google Scholar] [CrossRef]
- Ivorra, S.; Garcés, P.; Catalá, G.; Andión, L.G.; Zornoza, E. Effect of Silica Fume Particle Size on Mechanical Properties of Short Carbon Fiber Reinforced Concrete. Mater. Des. 2010, 31, 1553–1558. [Google Scholar] [CrossRef]
- Spagnuolo, S.; Meda, A.; Rinaldi, Z.; Nanni, A. Precast Concrete Tunnel Segments with GFRP Reinforcement. J. Compos. Constr. 2017, 21, 04017020. [Google Scholar] [CrossRef]
- Song, P.S.; Hwang, S. Mechanical Properties of High-Strength Steel Fiber-Reinforced Concrete. Constr. Build. Mater. 2004, 18, 669–673. [Google Scholar] [CrossRef]
- Iqbal Khan, M.; Abbas, Y.M. Significance of Fiber Characteristics on the Mechanical Properties of Steel Fiber-Reinforced High-Strength Concrete at Different Water-Cement Ratios. Constr. Build. Mater. 2023, 408, 133742. [Google Scholar] [CrossRef]
- Yao, X.; Han, Y.; Shen, L.; Zhu, D. Experimental study on the effect of polypropylene fiber on compressive strength and fracture properties of high-strength concrete after elevated temperatures. J. Build. Eng. 2024, 86, 108860. [Google Scholar] [CrossRef]
- Yang, Y.B.; Chen, B.X.; Chen, Y.; Liu, F.C.; Xie, X.M.; Guo, W.Y.; Wang, H.C. Effect of admixtures and PVA fiber on the mechanical properties of high strength cementitious grout. Case Stud. Constr. Materials 2023, 18, e01884. [Google Scholar] [CrossRef]
- Zhen, G. Study on the failure effect of aramid reinforced concrete slab under localized blast loading. Structures 2024, 63, 106292. [Google Scholar] [CrossRef]
- Staniszewski, J.M.; Bogetti, T.A.; Wu, V.; Moy, P. Interfibrillar behavior in ultra-high molecular weight polyethylene (UHMWPE) single fibers subjected to tension. Int. J. Solids Struct. 2020, 206, 354–369. [Google Scholar] [CrossRef]
- Li, Y.-F.; Hsu, C.-F.; Syu, J.-Y.; Chen, F.-W.; Wu, J.-H. Experimental Investigation on the Mechanical Characteristics of Ultra-High-Molecular-Weight Polyethylene (UHMWPE) Based Fiber-Reinforced Concrete. Case Stud. Constr. Mater. 2024, 21, e03762. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, L.; Jin, W.; Jiang, L.; Guo, M. Effect of ultra-high molecular weight polyethylene fiber on the early mechanical strength and shrinkage crack resistance of concrete. Struct. Concr. 2022, 23, 412–422. [Google Scholar] [CrossRef]
- Ji, Y.; Pei, Z. Investigation of Mechanical Properties of Ultra-High-Performance Polyethylene-Fiber-Reinforced Recycled-Brick-Aggregate Concrete. Polymers 2023, 15, 4573. [Google Scholar] [CrossRef]
- Yan, L.H.; Zhang, Y.W.; Zhu, L. Basic mechanical properties of ultra high molecular weight polyethylene fiber concrete. J. Natl. Univ. Def. Technol. 2014, 36, 43–47. [Google Scholar]
- Chu, S. Strain-hardening ultra-high performance concrete (UHPC) with hybrid steel and ultra-high molecular weight polyethylene fibers. Constr. Build. Mater. 2024, 438, 136716. [Google Scholar] [CrossRef]
- Wu, J.Q.; Wang, Y.; Sun, P.; Sun, Z.S.; Shen, J.S. The complete chloroplast genome of Prunus phaeosticta(Hance) Maxim. (Rosaceae) and its phylogenetic implications. Mitochondrial DNA Part B 2023, 8, 136–140. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, M.; Chen, D.; Zhou, X.; He, J. Modification of ultra-high molecular weight polyethylene fiber to improve mechanical properties of foamed concrete. Constr. Build. Mater. 2024, 450, 138681. [Google Scholar] [CrossRef]
- Chun, B.; Lee, S.W.; Piao, R.; Kim, S.; Yoo, D.-Y. Enhanced Impact Resistance of RC Beams Using Various Types of High-Performance Fiber-Reinforced Cementitious Composites. Eng. Struct. 2024, 319, 118790. [Google Scholar] [CrossRef]
- Hajiesmaeili, A.; Denarié, E. Next Generation UHPFRC for Sustainable Structural Applications. In DSCS 2018: 2nd International Workshop on Durability and Sustainability of Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 2018. [Google Scholar]
- Osman, B.H.; Sun, X.; Tian, Z.; Lu, H.; Jiang, G. Dynamic Compressive and Tensile Characteristics of a New Type of Ultra-High-Molecular Weight Polyethylene (UHMWPE) and Polyvinyl Alcohol (PVA) Fibers Reinforced Concrete. Shock. Vib. 2019, 2019, 6382934. [Google Scholar] [CrossRef]
- Pan, Z.; Tuladhar, R.; Yin, S.; Shi, F.; Dang, F. Feasibility of Repairing Concrete with Ultra-High Molecular Weight Polyethylene Fiber Cloth: A Comprehensive Literature Review. Buildings 2024, 14, 1631. [Google Scholar] [CrossRef]
- Wei, X.; Du, H.W.; Wang, C.Y.; Fang, Y.L. Investigation of Cutting Forces in Concrete Sawing Process. Key Eng. Mater. 2003, 250, 181–186. [Google Scholar] [CrossRef]
- Wang, C.Y.; Hu, Y.N.; Ding, H.N. Cutting Forces in Sawing Process of Reinforced Concrete. Mater. Sci. Forum 2004, 471–472, 292–297. [Google Scholar] [CrossRef]
- Yuan, H.; Wang, C.Y.; Hu, S.S.; Hu, Y.N.; Wang, Z.W.; Ding, H.N. Characteristics of Concrete Sawing Process with Diamond Tools. Chin. J. Mech. Eng. 2007, 18, 1604–1609. [Google Scholar]
- Yang, Z.L.; Hu, S.S.; Wang, Y.; Wang, C.Y.; Chen, B. Machining State and Surface Quality Analysis of Diamond Saw Blade Sawing Concrete Based on Wavelet Analysis. Tool Eng. 2018, 52, 45–51. [Google Scholar]
- Zheng, D.R.; Hu, S.S.; Wang, C.Y.; Hu, Y.N.; Chen, B.D.; Qin, C.H. Multi-scale analysis on dynamic characteristics of dry cutting plain concrete with diamond saw blades. Diam. Abras. Eng. 2015, 35, 40–45+51. [Google Scholar]
- Hu, S.S.; Yang, F.; Yang, Z.L.; Xiong, F.X.; Shi, W.W.; Tang, H.Q. Sawing Status Prediction of Diamond Sawblade Sawing Concrete Based on the Characteristics of Material Composition. In Proceedings of the ASME 2018 International Mechanical Engineering Congress and Exposition. Volume 13: Design, Reliability, Safety, and Risk, Pittsburgh, PA, USA, 9–15 November 2018; p. V013T05A069. [Google Scholar] [CrossRef]
- Li, M.Y.; Liu, S.; Tian, S.; Xiao, G.F. Image feature extraction and recognition of milling chatter of thin walled parts. J. Jilin Univ. (Eng. Technol. Ed.) 2022, 52, 425–432. [Google Scholar]
- Guo, L.; Yan, F.; Li, T.; Yang, T.; Lu, Y. An Automatic Method for Constructing Machining Process Knowledge Base from Knowledge Graph. Robot. Comput. Integr. Manuf. 2022, 73, 102222. [Google Scholar] [CrossRef]
- Wu, Y.; Du, R. Feature extraction and assessment using wavelet packets for monitoring of machining processes. Mech. Syst. Signal Process. 1996, 10, 29–53. [Google Scholar] [CrossRef]
- Segreto, T.; Simeone, A.; Teti, R. Principal Component Analysis for Feature Extraction and NN Pattern Recognition in Sensor Monitoring of Chip Form during Turning. CIRP J. Manuf. Sci. Technol. 2014, 7, 202–209. [Google Scholar] [CrossRef]
- Caggiano, A.; Angelone, R.; Napolitano, F.; Nele, L.; Teti, R. Dimensionality Reduction of Sensorial Features by Principal Component Analysis for ANN Machine Learning in Tool Condition Monitoring of CFRP Drilling. Procedia CIRP 2018, 78, 307–312. [Google Scholar] [CrossRef]
- Liang, Y.; Hu, S.; Guo, W.; Tang, H. Abrasive Tool Wear Prediction Based on an Improved Hybrid Difference Grey Wolf Algorithm for Optimizing SVM. Measurement 2022, 187, 110247. [Google Scholar] [CrossRef]
- Wang, G.; Zhuang, Y.; Song, L.; He, Z.; Zhang, J.; Zhou, H. Mechanical Properties and Failure Mechanism of Fiber-Reinforced Concrete Materials: Effects of Fiber Type and Content. Constr. Build. Mater. 2025, 465, 140190. [Google Scholar] [CrossRef]
- Fadli, M.; Alhamli, B.; Aldosari, A.; Alajmi, N.; Alkhayat, Z.; Potams, A.; Salman, M. Q-State Versus FFT and WT for Stress Detection. In Recent Trends and Advances in Artificial Intelligence; Garcia, F.P., Jamil, A., Hameed, A.A., Ortis, A., Ramirez, I.S., Eds.; ICAETA: Catania, Italy; Springer: Cham, Switzerland, 2024; Volume 1138. [Google Scholar] [CrossRef]
- Lever, J.; Krzywinski, M.; Altman, N. Principal component analysis. Nat. Methods 2017, 14, 641–642. [Google Scholar] [CrossRef]
- Kariri, E.; Louati, H.; Louati, A.; Masmoudi, F. Exploring the Advancements and Future Research Directions of Artificial Neural Networks: A Text Mining Approach. Appl. Sci. 2023, 13, 3186. [Google Scholar] [CrossRef]
- Xu, J.; Du, J.; Yuan, C. An alternative 2D ICEEMDAN-based denoising method and its application in processing magnetic anomaly data. Geod. Geodyn. 2024, 15, 465–476. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control. 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Bai, Z.; Wei, J.; Chen, K.; Wang, K. ICEEMDAN and improved wavelet threshold for vibration signal joint denoising in OPAX. J. Mech. Sci. Technol. 2024, 38, 5841–5851. [Google Scholar] [CrossRef]
- Zhao, Y.; Shan, R.L.; Wang, H.L. Research on Vibration Effect of Tunnel Blasting Based on an Improved Hilbert–Huang Transform. Environ. Earth Sci. 2021, 80, 206. [Google Scholar] [CrossRef]
- Yang, C.; Wang, A.L.; Wang, J.H.; Cai, J. Hilbert-Huang Transfer Time-frequency Energy Analysis on Ultrasonic Signal of Detecting Lotus Root Based on ICEEMDAN. Chin. J. Mech. Eng. 2021, 10, 52–54+59. [Google Scholar]
- Cai, G.P.; Zhao, X.T.; Hu, X.N.; Huang, X.H.; Chen, H.M. Denoising Method of Vibration Signal of Ball Mill based on CEEMDAN-wavelet Threshold Combination. Mech. Sci. Technol. Aerosp. Eng. 2020, 39, 1077–1085. [Google Scholar]
- Zhang, J.; Li, S.; Liu, X.; Chen, H.; Zhou, Q. A WOA-ICEEMDAN joint wavelet threshold function based denoising method for ultrasound signals. Nondestruct. Test. Eval. 2025, 1–36. [Google Scholar] [CrossRef]
- Keppel, G.; Wickens, T.D. Design and Analysis: A Researcher’s Handbook. In Upper Saddle River, 4th ed.; Pearson: New York, NY, USA, 2004. [Google Scholar]





| Concrete Types | Compressive /MPa | Tensile /MPa | Flexural /MPa | Elastic Modulus /GPa | Impact Number of Times |
|---|---|---|---|---|---|
| Plain concrete (U-CTRL) ① [13] | 85.5 | 4.11 | 5.47 | / | / |
| Steel fiber-reinforced concrete (U-F2-1.5) ① [13] | 93.0 | 5.32 | 13.33 | / | / |
| Steel fiber-reinforced concrete (U-F1-1.5) ① [13] | 92.7 | 5.33 | 12.27 | / | / |
| Plain concrete ② [36] | 31.92 | / | / | 3.71 | / |
| Basalt fiber concrete ② [36] | 34.44 | / | / | 4.47 | / |
| Carbon fiber concrete ② [36] | 46.86 | / | / | 4.56 | / |
| Steel fiber concrete(0.2) ② [36] | 89.40 | / | / | 7.61 | / |
| Plain concrete ③ [15] | 22.09 | 3.01 (split tensile) | 5.04 | / | 15.7 |
| UHMWPE fiber concrete (C-T15-L12) ③ [15] | 33.55 | 5.43 (split tensile) | 5.82 | / | 866.0 |
| Concrete | No. | Concrete Strength | W/C Ratio | Portland Cement (P42.5) | River Sand (0.25 mm) | Fine Aggregate (≤10 mm) | Fiber Volume Fraction |
|---|---|---|---|---|---|---|---|
| Non-aggregate and non-fiber concrete (A) | A1 | C25 | 25% | 25% | 50% | 0 | 0 |
| A2 | C40 | 22% | |||||
| A3 | C55 | 20% | |||||
| Aggregate-free UHMWPE-FRC (B) | B1 | C25 | 25% | 50% | 50% | 0 | 1% |
| B2 | C40 | 22% | |||||
| B3 | C55 | 20% | |||||
| Aggregate-Containing UHMWPE-FRC (C) | C1 | C25 | 25% | 25% | 25% | 50 | 1% |
| C2 | C40 | 22% | |||||
| C3 | C55 | 20% |
| Category | Conditions |
|---|---|
| Concrete | A1, A2, A3, B1, B2, B3, C1, C2, C3 |
| Saw blade diameter (mm) | ∅160 |
| Cutting speed Vc (m/s) | 8, 13, 18, 23, 28 |
| Feed speed Vf (mm/min) | 100, 200, 300, 400, 500 |
| Depth of cut ap (mm) | 1, 2, 3, 4, 5 |
| Cutting method | Down cutting |
| Cooling method | Dry cut |
| Continuous Variable Features | n | di2 | ρ |
|---|---|---|---|
| ap | 5 | 2 | 0.9 |
| Vc | 5 | 34 | −0.7 |
| Vf | 5 | 14 | 0.3 |
| Concrete strength | 3 | 0 | 1.0 |
| Kruskal–Wallis Test | Post Hoc Dunn’s Test | |||||||
|---|---|---|---|---|---|---|---|---|
| Frequency Band | H | P | Significance (α = 0.1) | Pairwise Comparison | Z | P | Adjusted P | Significance (α = 0.1) |
| 0–250 Hz | 5.115 | 0.077 | Significant | A vs. B | 0.981 | 0.327 | 0.980 | |
| A vs. C | −1.275 | 0.202 | 0.607 | |||||
| B vs. C | −2.255 | 0.024 | 0.072 | Significant | ||||
| 250–500 Hz | 2.192 | 0.334 | Not significant | (The result of the Kruskal–Wallis test was not significant, therefore a post hoc Dunn’s test was not required) | ||||
| 500–750 Hz | 1.077 | 0.584 | Not significant | (The result of the Kruskal–Wallis test was not significant, therefore a post hoc Dunn’s test was not required) | ||||
| 750–1000 Hz | 7.731 | 0.021 | Significant | A vs. B | −2.059 | 0.039 | 0.118 | |
| A vs. C | 0.588 | 0.556 | 1.000 | |||||
| B vs. C | 2.648 | 0.008 | 0.024 | Significant | ||||
| 1000–1250 Hz | 4.885 | 0.087 | Significant | A vs. B | −1.961 | 0.050 | 0.150 | |
| A vs. C | −0.098 | 0.922 | 1.000 | |||||
| B vs. C | 1.863 | 0.062 | 0.187 | |||||
| 1250–1500 Hz | 6.000 | 0.050 | Significant | A vs. B | 1.765 | 0.078 | 0.233 | |
| A vs. C | −0.588 | 0.556 | 1.000 | |||||
| B vs. C | −2.353 | 0.019 | 0.056 | Significant | ||||
| 1500–1750 Hz | 7.654 | 0.022 | Significant | A vs. B | 2.746 | 0.006 | 0.018 | Significant |
| A vs. C | 1.079 | 0.281 | 0.842 | |||||
| B vs. C | −1.667 | 0.096 | 0.287 | |||||
| 1750–2000 Hz | 8.769 | 0.012 | Significant | A vs. B | 2.942 | 0.003 | 0.010 | Significant |
| A vs. C | 1.765 | 0.078 | 0.233 | |||||
| B vs. C | −1.177 | 0.239 | 0.718 | |||||
| 2000–2250 Hz | 8.346 | 0.015 | Significant | A vs. B | 2.844 | 0.004 | 0.013 | Significant |
| A vs. C | 1.863 | 0.062 | 0.187 | |||||
| B vs. C | −0.981 | 0.327 | 0.980 | |||||
| 2250–2500 Hz | 4.803 | 0.091 | Significant | A vs. B | 2.165 | 0.030 | 0.091 | Significant |
| A vs. C | 0.787 | 0.431 | 1.000 | |||||
| B vs. C | −1.378 | 0.168 | 0.505 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Feng, J.; Liu, H.; Tang, G.; Zhang, G.; Xiong, F.; Zhong, S.; Huang, Y. Cutting Feature Extraction Method for Ultra-High Molecular Weight Polyethylene Fiber-Reinforced Concrete Based on Feature Classification and Improved Hilbert–Huang Transform. Buildings 2025, 15, 1272. https://doi.org/10.3390/buildings15081272
Hu S, Feng J, Liu H, Tang G, Zhang G, Xiong F, Zhong S, Huang Y. Cutting Feature Extraction Method for Ultra-High Molecular Weight Polyethylene Fiber-Reinforced Concrete Based on Feature Classification and Improved Hilbert–Huang Transform. Buildings. 2025; 15(8):1272. https://doi.org/10.3390/buildings15081272
Chicago/Turabian StyleHu, Shanshan, Jinzhao Feng, Hui Liu, Guoxin Tang, Geng’e Zhang, Fali Xiong, Shirun Zhong, and Yilong Huang. 2025. "Cutting Feature Extraction Method for Ultra-High Molecular Weight Polyethylene Fiber-Reinforced Concrete Based on Feature Classification and Improved Hilbert–Huang Transform" Buildings 15, no. 8: 1272. https://doi.org/10.3390/buildings15081272
APA StyleHu, S., Feng, J., Liu, H., Tang, G., Zhang, G., Xiong, F., Zhong, S., & Huang, Y. (2025). Cutting Feature Extraction Method for Ultra-High Molecular Weight Polyethylene Fiber-Reinforced Concrete Based on Feature Classification and Improved Hilbert–Huang Transform. Buildings, 15(8), 1272. https://doi.org/10.3390/buildings15081272





