Prediction of Shear Strength of Steel Fiber-Reinforced Concrete Beams with Stirrups Using Hybrid Machine Learning and Deep Learning Models
Abstract
1. Introduction
2. Support Vector Regression (SVR)
3. Particle Swarm Optimization (PSO)
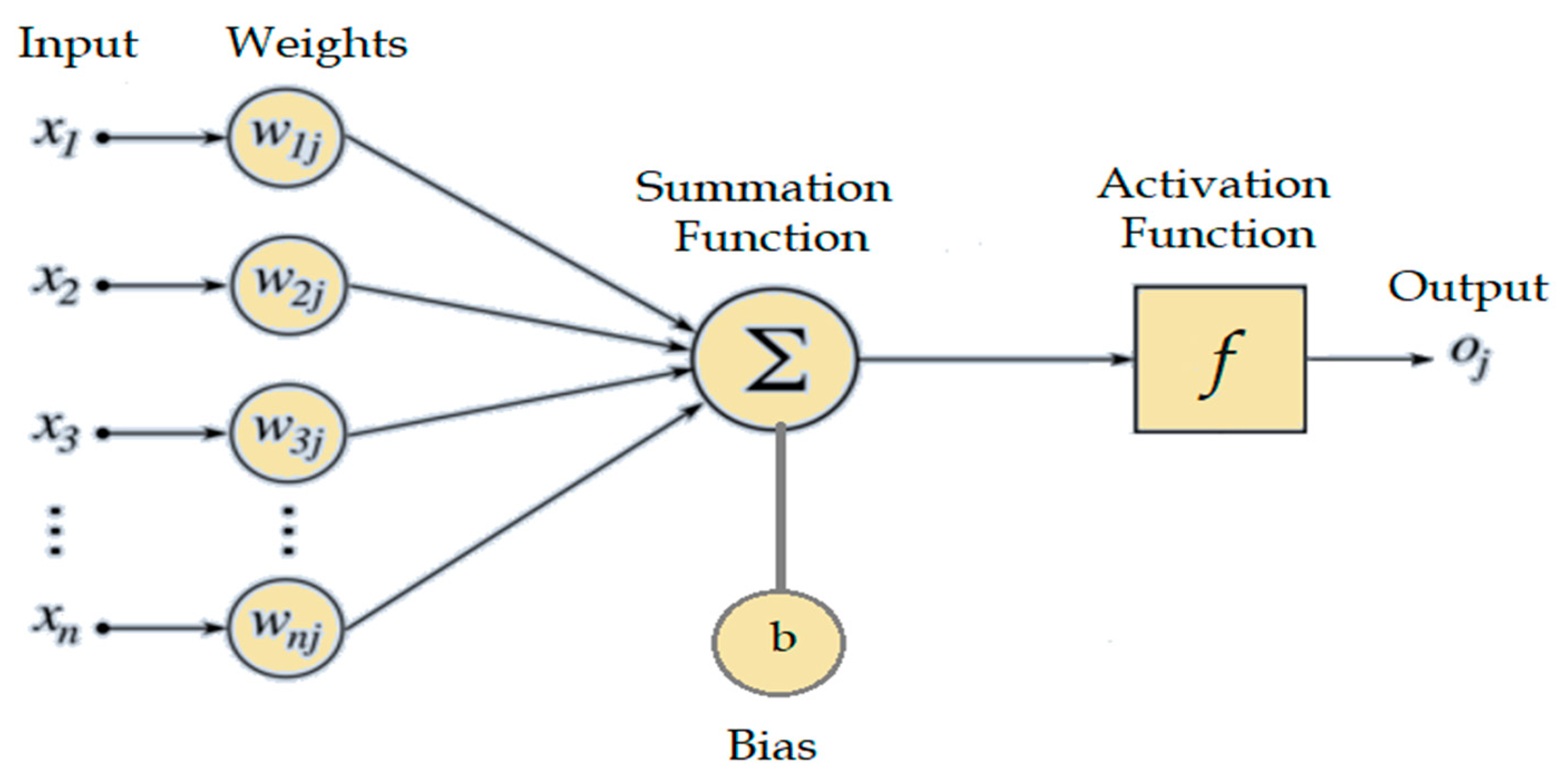
4. Artificial Neural Network
5. Convolutional Neural Network
6. Experimental Dataset
7. Performance Measure
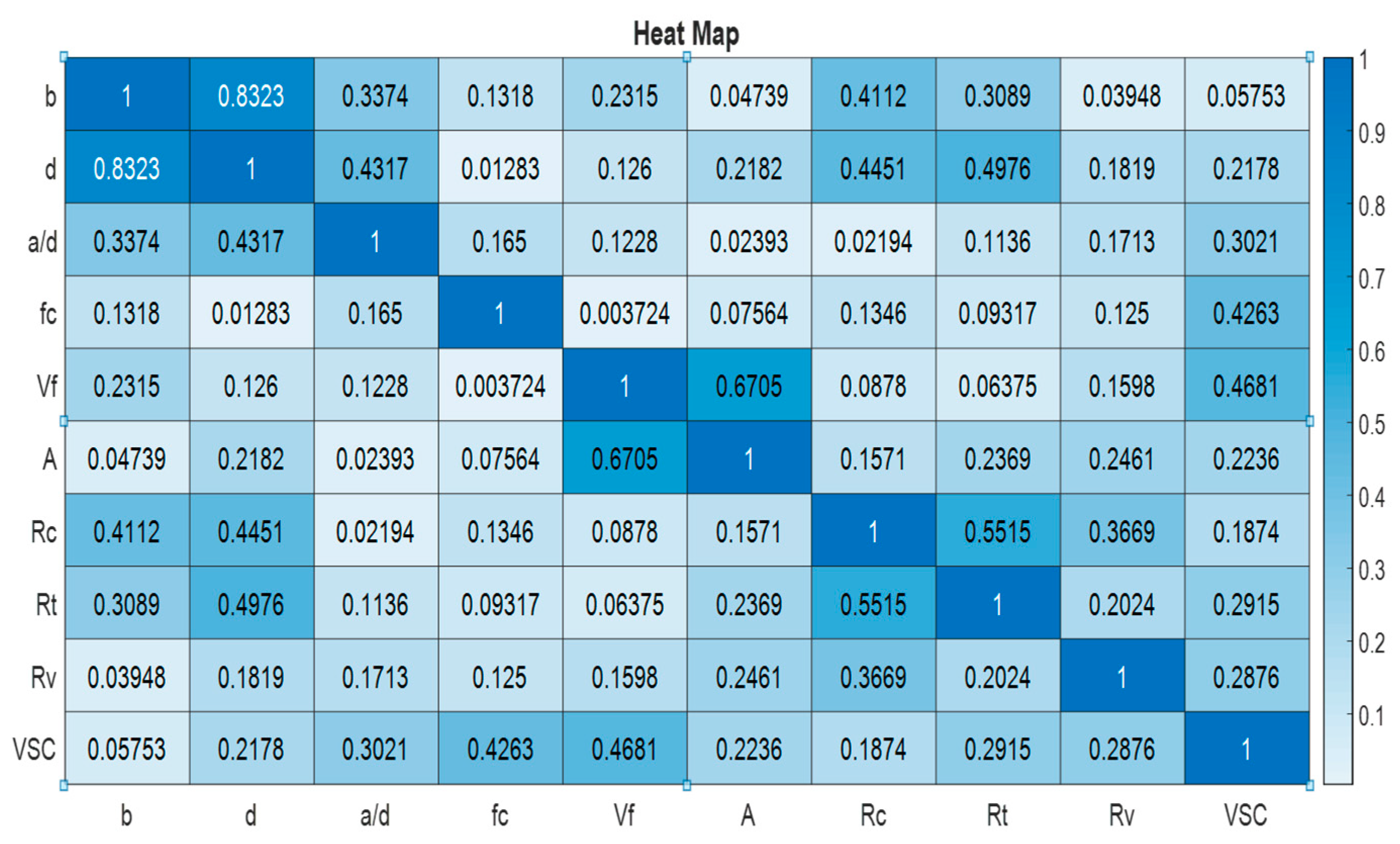
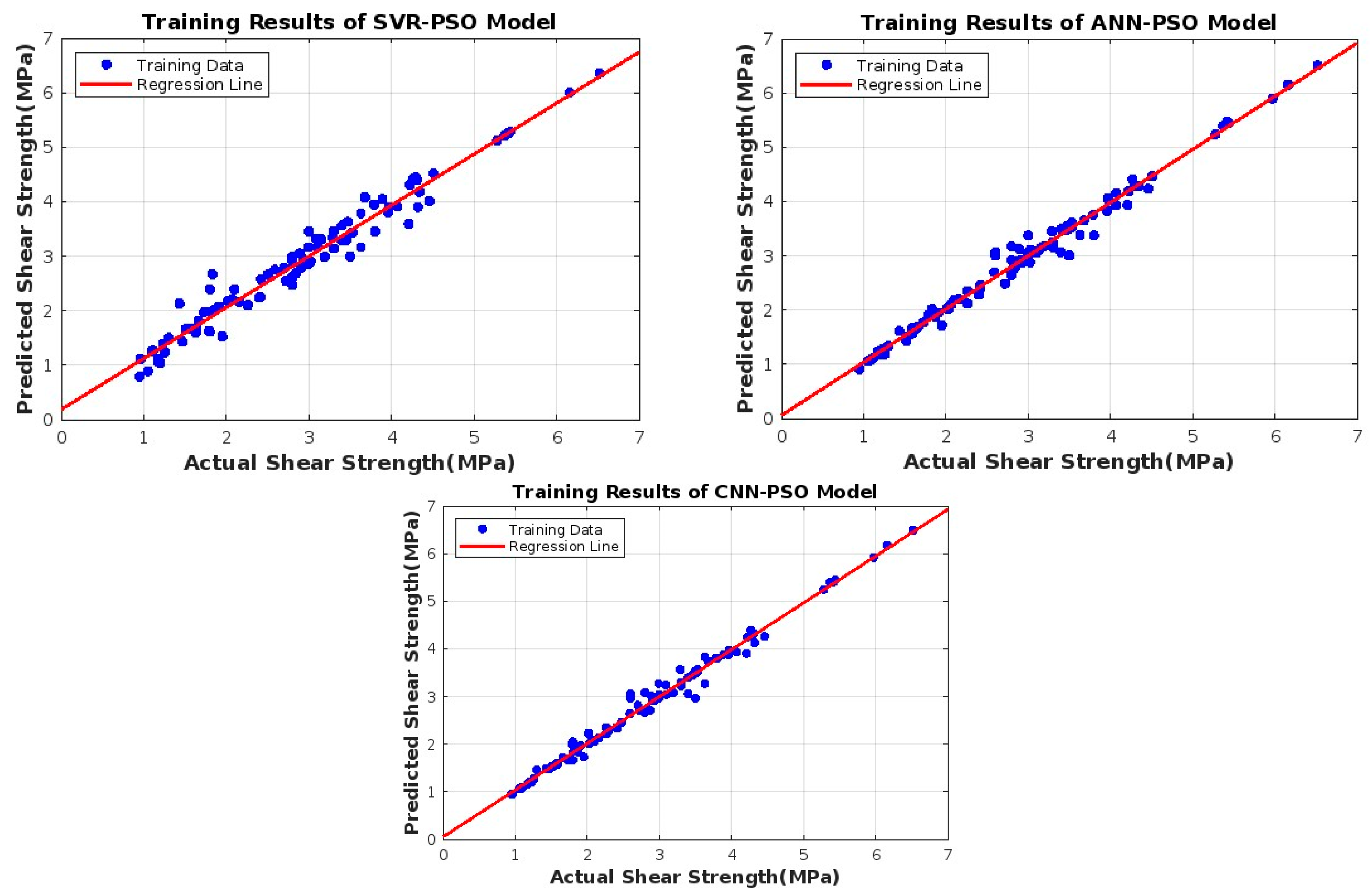
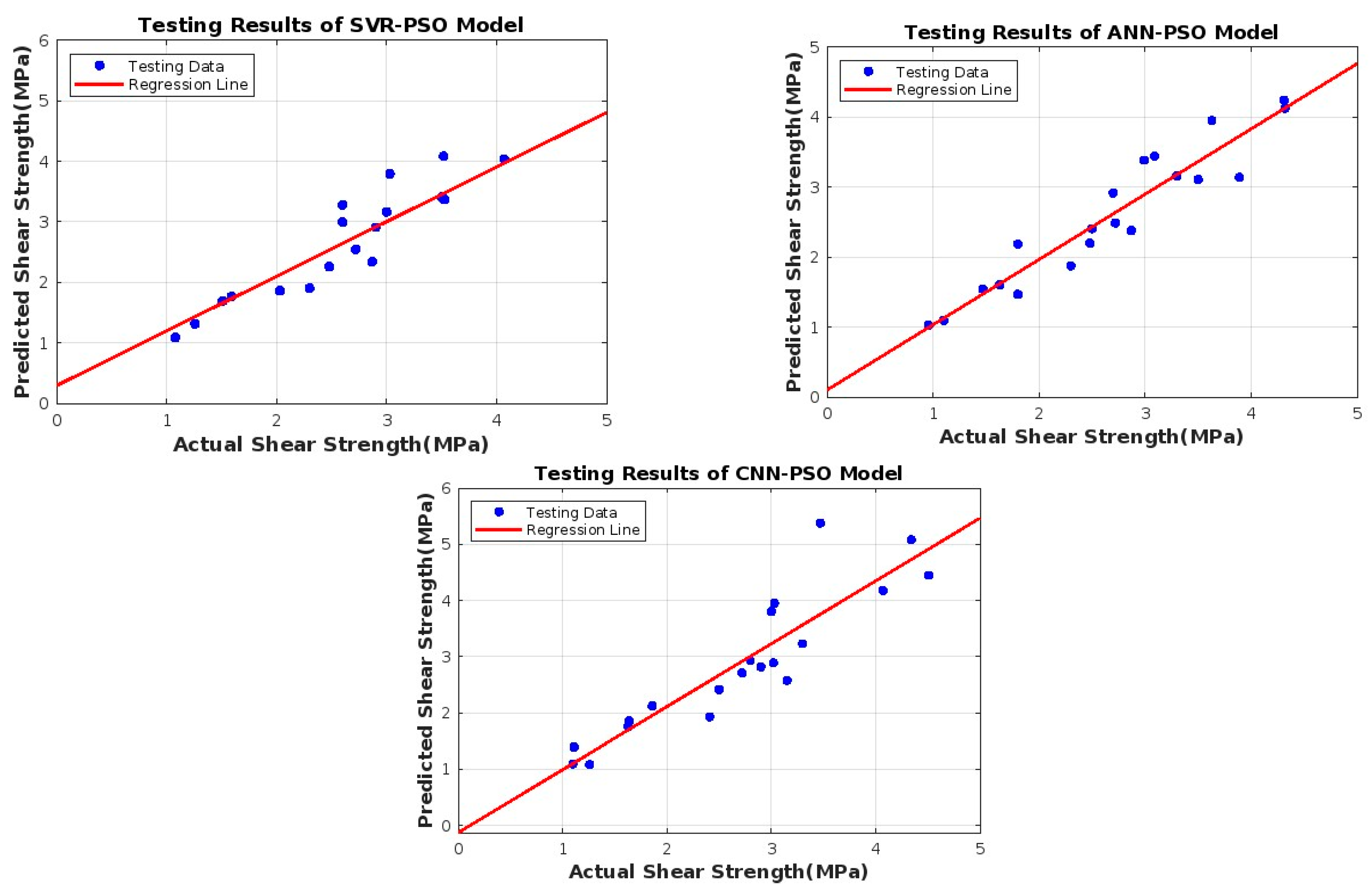
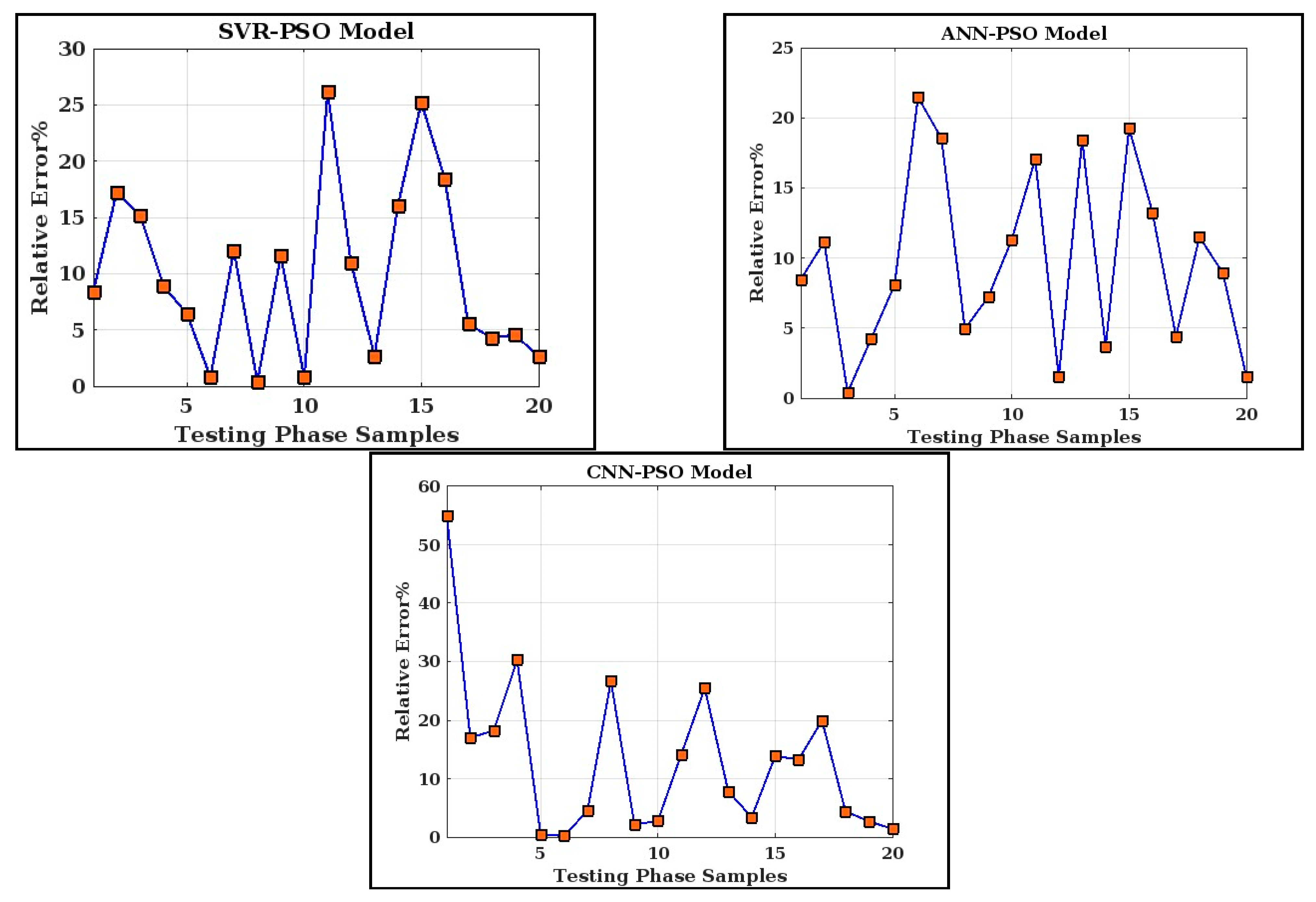
8. Analysis and Discussions
9. Conclusions
- ❖
- Overall, the proposed SVR-PSO model demonstrates superior performance over the analogous ANN-PSO and CNN-PSO models.
- ❖
- he accomplished results considered in the testing period demonstrate that the hybrid SVR-PSO model is a reliable and robust intelligent data model to predict the ultimate shear strength of steel fiber-reinforced concrete beams, showing the predictive model as a very useful decision-support tool for structural engineers.
- ❖
- Despite the present research supporting the superiority of the SVR-PSO model, the approach can be further explored with other nature-inspired evolutionary algorithms, where the influence of parameters on the shear strength helps preclude the manual trial-and-error processes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adhikary, B.B.; Mutsuyoshi, H. Prediction of shear strength of steel fiber RC beams using neural networks. Constr. Build. Mater. 2006, 20, 801–811. [Google Scholar] [CrossRef]
- Ahn, N.; Jang, H.; Park, D.K. Presumption of Shear Strength of Steel Fiber Reinforced Concrete Beam Using Artificial Neural Network Model. J. Appl. Polym. Sci. 2007, 103, 2351–2358. [Google Scholar] [CrossRef]
- Hossain, K.M.A.; Gladson, L.R.; Anwar, M.S. Modeling shear strength of medium to ultra-high-strength steel fiber-reinforced concrete beams using artificial neural network. Neural Comput. Appl. 2017, 28, 1119–1130. [Google Scholar] [CrossRef]
- Naik, U.; Kute, S. Span-to-depth ratio effect on shear strength of steel fiber-reinforced high-strength concrete deep beams using ANN model. Int. J. Adv. Struct. Eng. 2013, 5, 29. [Google Scholar] [CrossRef]
- Gandomi, A.; Alavi, A.; Yun, G. Nonlinear modeling of shear strength of SFRC beams using linear genetic programming. Struct. Eng. Mech. 2011, 38, 1–25. [Google Scholar] [CrossRef]
- Shahnewaz, M.; Alam, M.S.; Tannert, T. Shear strength prediction of steel fiber reinforced concrete beams from genetic programming and its sensitivity analysis. In Proceedings of the 9th RILEM International Symposium on Fiber Reinforced Concrete, Vancouver, BC, Canada, 19–21 September 2016; pp. 1183–1192. [Google Scholar] [CrossRef]
- Slater, E.; Moni, M.; Alam, M.S. Predicting the shear strength of steel fiber reinforced concrete beams. Constr. Build. Mater. 2012, 26, 423–436. [Google Scholar] [CrossRef]
- Kara, I.F. Empirical modeling of shear strength of steel fiber reinforced concrete beams by gene expression programming. Neural Comput. Appl. 2013, 23, 823–834. [Google Scholar] [CrossRef]
- Islam, M.S.; Alam, S. Principal Component and Multiple Regression Analysis for Steel Fiber Reinforced Concrete (SFRC) Beams. Int. J. Concr. Struct. Mater. 2013, 7, 303–317. [Google Scholar] [CrossRef]
- Sarveghadi, M.; Gandomi, A.H.; Bolandi, H.; Alavi, A.H. Development of prediction models for shear strength of SFRCB using a machine learning approach. Neural Comput. Appl. 2019, 31, 2085–2094. [Google Scholar] [CrossRef]
- Islam, M.S. Simplified shear-strength prediction models for steel-fibre-reinforced concrete beams. Constr. Mater. 2021, 174, 88–100. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Deo, R.C.; Hilal, A.; Abd, A.M.; Bueno, L.C.; Salcedo-Sanz, S.; Nehdi, M.L. Predicting compressive strength of lightweight foamed concrete using extreme learning machine model. Adv. Eng. Softw. 2018, 115, 112–125. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Yang, H.; Zhang, S.; Deng, K.; Du, P. Research into a Feature Selection Method for Hyperspectral Imagery Using PSO and SVM. J. China Univ. Min. Technol. 2007, 17, 473–478. [Google Scholar] [CrossRef]
- Cucchiara, C.; Mendola, L.L.; Papia, M. Effectiveness of stirrups and steel fibres as shear reinforcement. Cem. Concr. Compos. 2004, 26, 777–786. [Google Scholar] [CrossRef]
- Dinh, H.H.; Parra-montesinos, G.J.; Wight, J.K. Shear Strength Model for Steel Fiber Reinforced Concrete Beams without Stirrup Reinforcement. J. Struct. Eng. 2010, 137, 1039–1051. [Google Scholar] [CrossRef]
- Aoude, H.; Belghiti, M.; Cook, W.D.; Mitchell, D. Response of steel fiber-reinforced concrete beams with and without stirrups. Struct. J. 2012, 109, 359–367. [Google Scholar] [CrossRef]
- Spinella, N.; Colajanni, P.; Mendola, L.L. Nonlinear analysis of beams reinforced in shear with stirrups and steel fibers. Struct. J. 2012, 109, 53–64. [Google Scholar] [CrossRef]
- Amin, A.; Foster, S.J. Shear strength of steel fibre reinforced concrete beams with stirrups. Eng. Struct. 2016, 111, 323–332. [Google Scholar] [CrossRef]
- Navas, F.O.; Navarro-Gregori, J.; Herdocia, G.L.; Serna, P.; Cuenca, E. An experimental study on the shear behaviour of reinforced concrete beams with macro-synthetic fibres. Constr. Build. Mater. 2018, 169, 888–899. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Yang, J.M. Effects of stirrup, steel fiber, and beam size on shear behavior of high-strength concrete beams. Cem. Concr. Compos. 2018, 87, 137–148. [Google Scholar] [CrossRef]
- Gali, S.; Subramaniam, K.V.L. Efficiency of steel fibers in shear resistance of reinforced concrete beams without stirrups at different moment-to-shear ratios. Eng. Struct. 2018, 188, 249–260. [Google Scholar] [CrossRef]
- Moradi, M.; Aletaha, S.H.; Asadzadeh, E.; Qomzade, M.M. Shear Strength of Fiber-Reinforced Concrete Beams with Stirrups. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 865–888. [Google Scholar] [CrossRef]


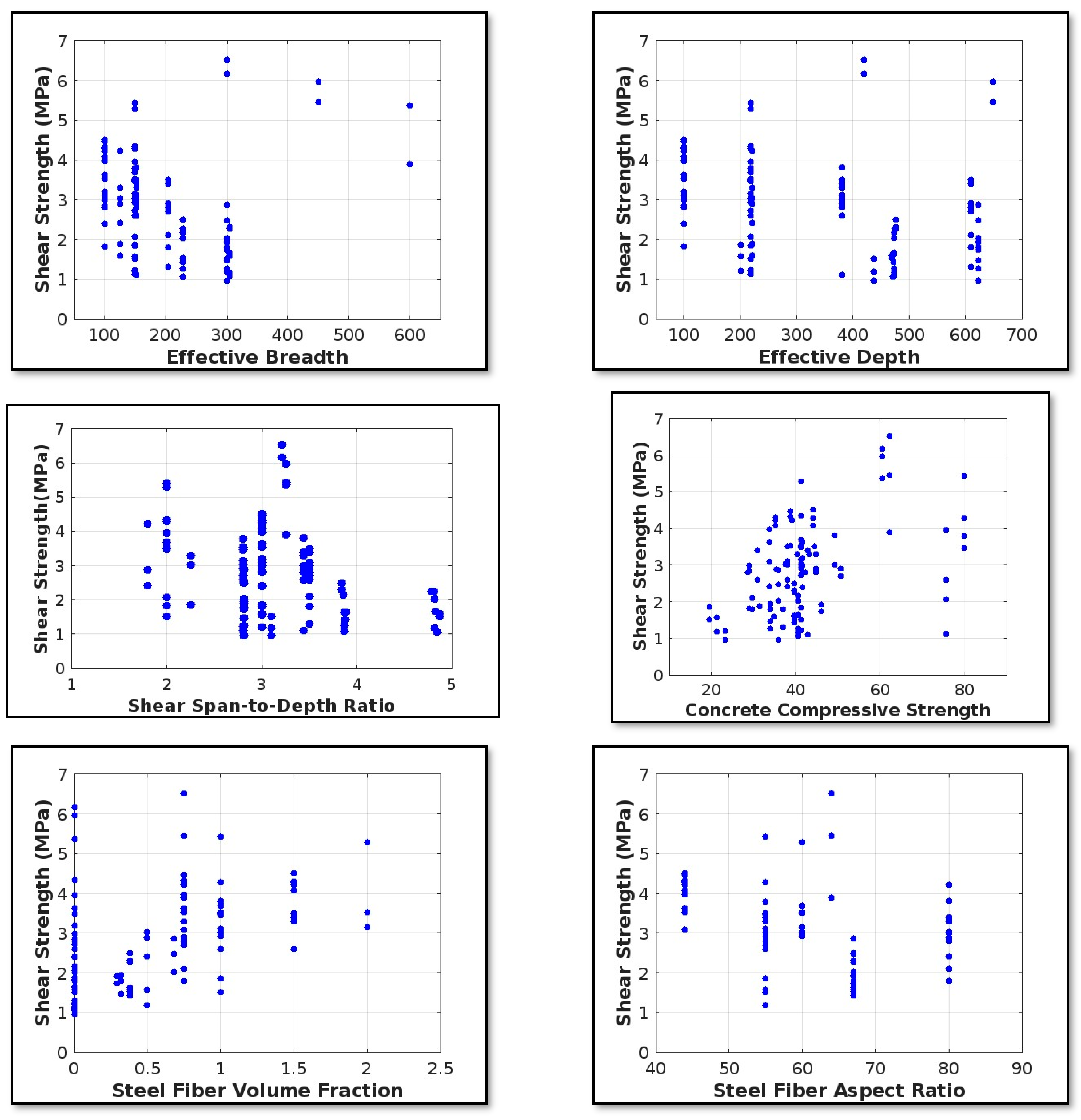


| SN | b | d | a/d | fc | Vf | A | Rc | Rt | Rv | VSC | Reference |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 150 | 219 | 2.80 | 41.2 | 0.00 | 00 | 0.00 | 11.66 | 0.00 | 1.23 | [15] |
| 2 | 150 | 219 | 2.80 | 41.2 | 0.00 | 00 | 2.92 | 11.66 | 0.48 | 2.72 | |
| 3 | 150 | 219 | 2.80 | 41.2 | 0.00 | 00 | 2.92 | 11.66 | 1.60 | 3.47 | |
| 4 | 150 | 219 | 2.00 | 41.2 | 0.00 | 00 | 0.00 | 11.66 | 0.00 | 1.51 | |
| 5 | 150 | 219 | 2.00 | 41.2 | 0.00 | 00 | 2.92 | 11.66 | 0.48 | 1.83 | |
| 6 | 150 | 219 | 2.00 | 41.2 | 0.00 | 00 | 2.92 | 11.66 | 1.60 | 4.34 | |
| 7 | 150 | 219 | 2.80 | 41.2 | 1.00 | 60 | 0.00 | 11.66 | 0.00 | 2.93 | |
| 8 | 150 | 219 | 2.80 | 41.2 | 2.00 | 60 | 0.00 | 11.66 | 0.00 | 3.15 | |
| 9 | 150 | 219 | 2.80 | 41.2 | 1.00 | 60 | 2.92 | 11.66 | 0.48 | 3.03 | |
| 10 | 150 | 219 | 2.80 | 41.2 | 1.00 | 60 | 2.92 | 11.66 | 1.60 | 3.53 | |
| 11 | 150 | 219 | 2.80 | 41.2 | 0.00 | 00 | 2.92 | 11.66 | 0.48 | 2.72 | |
| 12 | 150 | 219 | 2.00 | 41.2 | 1.00 | 60 | 0.00 | 11.66 | 0.00 | 3.50 | |
| 13 | 150 | 219 | 2.00 | 41.2 | 2.00 | 60 | 0.00 | 11.66 | 0.00 | 3.52 | |
| 14 | 150 | 219 | 2.00 | 41.2 | 1.00 | 60 | 2.92 | 11.66 | 0.48 | 3.68 | |
| 15 | 150 | 219 | 2.00 | 41.2 | 2.00 | 60 | 2.92 | 11.66 | 0.48 | 5.28 | |
| 16 | 152 | 381 | 3.44 | 42.8 | 0.00 | 00 | 2.00 | 12.32 | 0.00 | 1.10 | [16] |
| 17 | 152 | 381 | 3.44 | 42.8 | 0.00 | 00 | 2.00 | 12.32 | 0.00 | 1.10 | |
| 18 | 152 | 381 | 3.44 | 44.8 | 0.75 | 55 | 2.21 | 09.04 | 0.00 | 2.90 | |
| 19 | 152 | 381 | 3.44 | 44.8 | 0.75 | 55 | 2.21 | 09.04 | 0.00 | 2.80 | |
| 20 | 152 | 381 | 3.50 | 38.1 | 1.00 | 55 | 2.21 | 09.04 | 0.00 | 3.00 | |
| 21 | 152 | 381 | 3.50 | 38.1 | 1.00 | 55 | 2.21 | 09.04 | 0.00 | 3.10 | |
| 22 | 152 | 381 | 3.50 | 38.1 | 1.00 | 55 | 2.00 | 12.32 | 0.00 | 3.50 | |
| 23 | 152 | 381 | 3.50 | 38.1 | 1.00 | 55 | 2.00 | 12.32 | 0.00 | 2.60 | |
| 24 | 152 | 381 | 3.44 | 31.0 | 1.50 | 55 | 2.00 | 12.32 | 0.00 | 2.60 | |
| 25 | 152 | 381 | 3.44 | 31.0 | 1.50 | 55 | 2.00 | 12.32 | 0.00 | 3.40 | |
| 26 | 152 | 381 | 3.44 | 44.9 | 1.50 | 55 | 2.00 | 12.32 | 0.00 | 3.30 | |
| 27 | 152 | 381 | 3.44 | 44.9 | 1.50 | 55 | 2.00 | 12.32 | 0.00 | 3.30 | |
| 28 | 152 | 381 | 3.44 | 49.2 | 1.00 | 80 | 2.00 | 12.32 | 0.00 | 3.00 | |
| 29 | 152 | 381 | 3.44 | 49.2 | 1.00 | 80 | 2.00 | 12.32 | 0.00 | 3.80 | |
| 30 | 152 | 381 | 3.44 | 43.3 | 0.75 | 80 | 2.21 | 09.04 | 0.00 | 3.30 | |
| 31 | 152 | 381 | 3.44 | 43.3 | 0.75 | 80 | 2.21 | 09.04 | 0.00 | 3.30 | |
| 32 | 205 | 610 | 3.50 | 50.8 | 0.75 | 55 | 0.94 | 09.38 | 0.00 | 2.90 | |
| 33 | 205 | 610 | 3.50 | 50.8 | 0.75 | 55 | 0.94 | 09.38 | 0.00 | 2.70 | |
| 34 | 205 | 610 | 3.50 | 28.7 | 0.75 | 80 | 0.94 | 09.38 | 0.00 | 2.80 | |
| 35 | 205 | 610 | 3.50 | 28.7 | 0.75 | 80 | 0.94 | 09.38 | 0.00 | 2.80 | |
| 36 | 205 | 610 | 3.50 | 42.3 | 0.75 | 55 | 0.92 | 07.13 | 0.00 | 2.80 | |
| 37 | 205 | 610 | 3.50 | 29.6 | 0.75 | 80 | 0.92 | 07.13 | 0.00 | 2.10 | |
| 38 | 205 | 610 | 3.50 | 29.6 | 0.75 | 80 | 0.92 | 07.13 | 0.00 | 1.80 | |
| 39 | 205 | 610 | 3.50 | 44.4 | 1.50 | 55 | 0.94 | 09.38 | 0.00 | 3.50 | |
| 40 | 205 | 610 | 3.50 | 42.8 | 1.50 | 80 | 0.94 | 09.38 | 0.00 | 3.40 | |
| 41 | 205 | 610 | 3.50 | 37.0 | 0.00 | 00 | 0.92 | 07.13 | 0.00 | 1.30 | |
| 42 | 205 | 610 | 3.50 | 37.0 | 0.00 | 00 | 0.92 | 07.13 | 0.07 | 1.80 | |
| 43 | 150 | 202 | 3.00 | 23.3 | 0.00 | 00 | 0.00 | 12.62 | 0.00 | 1.20 | [17] |
| 44 | 150 | 202 | 3.00 | 21.3 | 0.50 | 55 | 0.00 | 12.62 | 0.00 | 1.57 | |
| 45 | 150 | 202 | 3.00 | 19.6 | 1.00 | 55 | 0.00 | 12.62 | 0.00 | 1.86 | |
| 46 | 300 | 437 | 3.10 | 23.3 | 0.00 | 0 | 2.00 | 06.54 | 0.00 | 0.95 | |
| 47 | 300 | 437 | 3.10 | 21.3 | 0.50 | 55 | 2.00 | 06.54 | 0.00 | 1.18 | |
| 48 | 300 | 437 | 3.10 | 19.6 | 1.00 | 55 | 2.00 | 06.54 | 0.00 | 1.51 | |
| 49 | 150 | 219 | 2.80 | 75.7 | 0.00 | 00 | 0.00 | 11.45 | 0.00 | 1.11 | |
| 50 | 150 | 219 | 2.80 | 75.7 | 0.00 | 00 | 2.86 | 11.45 | 0.45 | 2.59 | [18] |
| 51 | 150 | 219 | 2.80 | 80.0 | 1.00 | 55 | 0.00 | 11.45 | 0.00 | 3.46 | |
| 52 | 150 | 219 | 2.80 | 80.0 | 1.00 | 55 | 2.86 | 11.45 | 0.45 | 3.79 | |
| 53 | 150 | 219 | 2.00 | 75.7 | 0.00 | 00 | 0.00 | 11.45 | 0.00 | 2.07 | |
| 54 | 150 | 219 | 2.00 | 75.7 | 0.00 | 00 | 2.86 | 11.45 | 0.45 | 3.96 | |
| 55 | 150 | 219 | 2.00 | 80.0 | 1.00 | 55 | 0.00 | 11.45 | 0.00 | 4.29 | |
| 56 | 150 | 219 | 2.00 | 80.0 | 1.00 | 55 | 2.86 | 11.45 | 0.45 | 5.42 | |
| 57 | 300 | 622 | 2.81 | 34.0 | 0.00 | 00 | 1.88 | 10.69 | 0.26 | 1.26 | [19] |
| 58 | 300 | 622 | 2.81 | 34.0 | 0.32 | 67 | 1.88 | 10.69 | 0.00 | 1.47 | |
| 59 | 300 | 622 | 2.81 | 34.0 | 0.32 | 67 | 1.88 | 10.69 | 0.12 | 1.95 | |
| 60 | 300 | 622 | 2.81 | 34.0 | 0.32 | 67 | 1.88 | 10.69 | 0.26 | 1.79 | |
| 61 | 300 | 622 | 2.81 | 46.0 | 0.29 | 67 | 1.88 | 10.69 | 0.13 | 1.73 | |
| 62 | 300 | 622 | 2.81 | 46.0 | 0.29 | 67 | 1.88 | 10.69 | 0.24 | 1.91 | |
| 63 | 300 | 622 | 2.81 | 36.0 | 0.00 | 00 | 1.88 | 10.69 | 0.12 | 0.96 | |
| 64 | 300 | 622 | 2.81 | 36.0 | 0.68 | 67 | 1.88 | 10.69 | 0.00 | 2.02 | |
| 65 | 300 | 622 | 2.81 | 36.0 | 0.68 | 67 | 1.88 | 10.69 | 0.12 | 2.48 | |
| 66 | 300 | 622 | 2.81 | 36.0 | 0.68 | 67 | 1.88 | 10.69 | 0.26 | 2.87 | |
| 67 | 305 | 470 | 3.89 | 39.7 | 0.38 | 67 | 1.11 | 09.84 | 0.00 | 1.63 | [20] |
| 68 | 305 | 469 | 4.87 | 39.7 | 0.38 | 67 | 1.11 | 13.32 | 0.00 | 1.59 | |
| 69 | 229 | 472 | 3.88 | 39.7 | 0.38 | 67 | 1.48 | 12.74 | 0.00 | 1.43 | |
| 70 | 229 | 469 | 4.87 | 39.7 | 0.38 | 67 | 1.48 | 13.32 | 0.00 | 1.52 | |
| 71 | 305 | 477 | 3.84 | 39.7 | 0.38 | 67 | 1.11 | 09.84 | 0.26 | 2.30 | |
| 72 | 305 | 477 | 4.79 | 39.7 | 0.38 | 67 | 1.11 | 12.74 | 0.26 | 2.26 | |
| 73 | 229 | 477 | 3.84 | 39.7 | 0.38 | 67 | 1.48 | 12.74 | 0.38 | 2.50 | |
| 74 | 229 | 475 | 4.81 | 39.7 | 0.38 | 67 | 1.48 | 11.58 | 0.38 | 2.26 | |
| 75 | 305 | 473 | 3.87 | 40.6 | 0.00 | 00 | 1.11 | 09.84 | 0.00 | 1.08 | |
| 76 | 305 | 474 | 4.82 | 40.6 | 0.00 | 00 | 1.11 | 12.74 | 0.00 | 1.17 | |
| 77 | 229 | 473 | 3.87 | 40.6 | 0.00 | 00 | 1.48 | 12.74 | 0.00 | 1.26 | |
| 78 | 229 | 471 | 4.85 | 40.6 | 0.00 | 00 | 1.48 | 12.74 | 0.00 | 1.05 | |
| 79 | 305 | 473 | 3.87 | 40.6 | 0.00 | 00 | 1.11 | 09.84 | 0.28 | 1.64 | |
| 80 | 305 | 473 | 4.83 | 40.6 | 0.00 | 00 | 1.11 | 12.74 | 0.28 | 1.66 | |
| 81 | 229 | 474 | 3.86 | 40.6 | 0.00 | 00 | 1.48 | 12.74 | 0.38 | 2.16 | |
| 82 | 229 | 474 | 4.82 | 40.6 | 0.00 | 00 | 1.48 | 12.74 | 0.38 | 2.03 | |
| 83 | 300 | 420 | 3.21 | 60.5 | 0.00 | 00 | 0.45 | 16.02 | 0.45 | 6.16 | [21] |
| 84 | 300 | 420 | 3.21 | 62.3 | 0.75 | 64 | 0.00 | 16.02 | 0.00 | 6.52 | |
| 85 | 450 | 648 | 3.26 | 60.5 | 0.00 | 00 | 0.16 | 11.09 | 0.41 | 5.97 | |
| 86 | 450 | 648 | 3.26 | 62.3 | 0.75 | 64 | 0.00 | 11.09 | 0.00 | 5.44 | |
| 87 | 600 | 887 | 3.26 | 60.5 | 0.00 | 00 | 0.10 | 08.24 | 0.38 | 5.37 | |
| 88 | 600 | 887 | 3.26 | 62.3 | 0.75 | 64 | 0.00 | 08.24 | 0.00 | 3.89 | |
| 89 | 125 | 222 | 1.80 | 33.7 | 0.00 | 00 | 0.00 | 07.24 | 0.00 | 2.41 | [22] |
| 90 | 125 | 222 | 1.80 | 35.4 | 0.50 | 80 | 0.00 | 07.24 | 0.00 | 2.89 | |
| 91 | 125 | 222 | 1.80 | 39.1 | 0.75 | 80 | 0.00 | 07.24 | 0.00 | 4.21 | |
| 92 | 125 | 222 | 2.25 | 31.4 | 0.00 | 00 | 0.00 | 07.24 | 0.00 | 1.87 | |
| 93 | 125 | 222 | 2.25 | 37.6 | 0.50 | 80 | 0.00 | 07.24 | 0.00 | 3.02 | |
| 94 | 125 | 222 | 2.25 | 40.3 | 0.75 | 80 | 0.00 | 07.24 | 0.00 | 3.29 | |
| 95 | 125 | 222 | 3.00 | 34.9 | 0.00 | 00 | 0.00 | 07.24 | 0.00 | 1.59 | |
| 96 | 125 | 222 | 3.00 | 38.0 | 0.50 | 80 | 0.00 | 07.24 | 0.00 | 2.42 | |
| 97 | 100 | 100 | 3.00 | 41.7 | 0.00 | 00 | 3.78 | 14.80 | 0.00 | 2.40 | [23] |
| 98 | 100 | 100 | 3.00 | 41.7 | 0.00 | 00 | 3.78 | 14.80 | 0.24 | 3.19 | |
| 99 | 100 | 100 | 3.00 | 41.7 | 0.00 | 00 | 3.78 | 14.80 | 0.24 | 2.80 | |
| 100 | 100 | 100 | 3.00 | 41.7 | 0.00 | 00 | 3.78 | 14.80 | 0.30 | 2.99 | |
| 101 | 100 | 100 | 3.00 | 41.7 | 0.00 | 00 | 3.78 | 14.80 | 0.30 | 3.63 | |
| 102 | 100 | 100 | 3.00 | 28.9 | 0.00 | 00 | 3.78 | 14.80 | 0.00 | 1.81 | |
| 103 | 100 | 100 | 3.00 | 28.9 | 0.00 | 00 | 3.78 | 14.80 | 0.24 | 2.84 | |
| 104 | 100 | 100 | 3.00 | 28.9 | 0.00 | 00 | 3.78 | 14.80 | 0.30 | 2.99 | |
| 105 | 100 | 100 | 3.00 | 38.8 | 0.75 | 44 | 3.78 | 14.80 | 0.00 | 3.53 | |
| 106 | 100 | 100 | 3.00 | 38.8 | 0.75 | 44 | 3.78 | 14.80 | 0.24 | 4.32 | |
| 107 | 100 | 100 | 3.00 | 38.8 | 0.75 | 44 | 3.78 | 14.80 | 0.30 | 4.46 | |
| 108 | 100 | 100 | 3.00 | 33.7 | 0.75 | 44 | 3.78 | 14.80 | 0.00 | 3.09 | |
| 109 | 100 | 100 | 3.00 | 33.7 | 0.75 | 44 | 3.78 | 14.80 | 0.24 | 3.63 | |
| 110 | 100 | 100 | 3.00 | 33.7 | 0.75 | 44 | 3.78 | 14.80 | 0.30 | 3.97 | |
| 111 | 100 | 100 | 3.00 | 35.2 | 1.50 | 44 | 3.78 | 14.80 | 0.00 | 4.07 | |
| 112 | 100 | 100 | 3.00 | 35.2 | 1.50 | 44 | 3.78 | 14.80 | 0.24 | 4.22 | |
| 113 | 100 | 100 | 3.00 | 35.2 | 1.50 | 44 | 3.78 | 14.80 | 0.30 | 4.31 | |
| 114 | 100 | 100 | 3.00 | 44.1 | 1.50 | 44 | 3.78 | 14.80 | 0.00 | 4.07 | |
| 115 | 100 | 100 | 3.00 | 44.1 | 1.50 | 44 | 3.78 | 14.80 | 0.24 | 4.27 | |
| 116 | 100 | 100 | 3.00 | 44.1 | 1.50 | 44 | 3.78 | 14.80 | 0.30 | 4.51 |
| SC | B | d | a/d | fc | Vf | A | RC | Rt | Rv | VSC |
|---|---|---|---|---|---|---|---|---|---|---|
| Min. | 100 | 100 | 1.80 | 19.6 | 0.00 | 00 | 0.00 | 6.54 | 0.00 | 0.95 |
| Max. | 600 | 887 | 4.87 | 80.0 | 2.00 | 80 | 3.78 | 16.02 | 1.60 | 6.52 |
| µ | 194 | 355 | 3.13 | 42.1 | 0.57 | 40 | 1.75 | 11.35 | 0.16 | 2.82 |
| σ | 94.7 | 195 | 0.69 | 12.6 | 0.55 | 31 | 1.30 | 02.48 | 0.29 | 1.22 |
| Ku | 4.68 | −0.72 | 0.87 | 2.66 | −0.39 | −1.56 | −1.11 | −0.68 | 14.02 | 0.26 |
| Sk | 1.80 | 0.39 | 0.48 | 1.48 | 0.63 | −0.33 | 0.16 | −0.23 | 3.29 | 0.62 |
| Min. Relative Error (%) | Max. Relative Error (%) | MAPE (%) | MAE | RMSE | SI | ||
|---|---|---|---|---|---|---|---|
| SVR-PSO | 0.05 | 45.84 | 8.18 | 0.19 | 0.24 | 0.96 | 0.08 |
| ANN-PSO | 0.02 | 14.10 | 3.03 | 0.09 | 0.14 | 0.98 | 0.05 |
| CNN-PSO | 0.01 | 15.21 | 3.20 | 0.09 | 0.14 | 0.98 | 0.05 |
| Min. Relative Error (%) | Max. Relative Error (%) | MAPE (%) | MAE | RMSE | SI | ||
|---|---|---|---|---|---|---|---|
| SVR-PSO | 0.78 | 25.40 | 9.91 | 0.28 | 0.37 | 0.88 | 0.13 |
| ANN-PSO | 0.39 | 19.25 | 9.77 | 0.26 | 0.32 | 0.89 | 0.12 |
| CNN-PSO | 0.20 | 55.01 | 13.19 | 0.36 | 0.57 | 0.81 | 0.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kavya, B.R.; Shrikanth, A.S.; Sreekeshava, K.S. Prediction of Shear Strength of Steel Fiber-Reinforced Concrete Beams with Stirrups Using Hybrid Machine Learning and Deep Learning Models. Buildings 2025, 15, 1265. https://doi.org/10.3390/buildings15081265
Kavya BR, Shrikanth AS, Sreekeshava KS. Prediction of Shear Strength of Steel Fiber-Reinforced Concrete Beams with Stirrups Using Hybrid Machine Learning and Deep Learning Models. Buildings. 2025; 15(8):1265. https://doi.org/10.3390/buildings15081265
Chicago/Turabian StyleKavya, B. R., A. S. Shrikanth, and K. S. Sreekeshava. 2025. "Prediction of Shear Strength of Steel Fiber-Reinforced Concrete Beams with Stirrups Using Hybrid Machine Learning and Deep Learning Models" Buildings 15, no. 8: 1265. https://doi.org/10.3390/buildings15081265
APA StyleKavya, B. R., Shrikanth, A. S., & Sreekeshava, K. S. (2025). Prediction of Shear Strength of Steel Fiber-Reinforced Concrete Beams with Stirrups Using Hybrid Machine Learning and Deep Learning Models. Buildings, 15(8), 1265. https://doi.org/10.3390/buildings15081265





