Experimental Study on Axial Compression Behavior of Fiber-Reinforced Lightweight Aggregate Concrete Columns Confined by Grid Stirrups
Abstract
1. Introduction
2. Experimental Program
2.1. Raw Materials
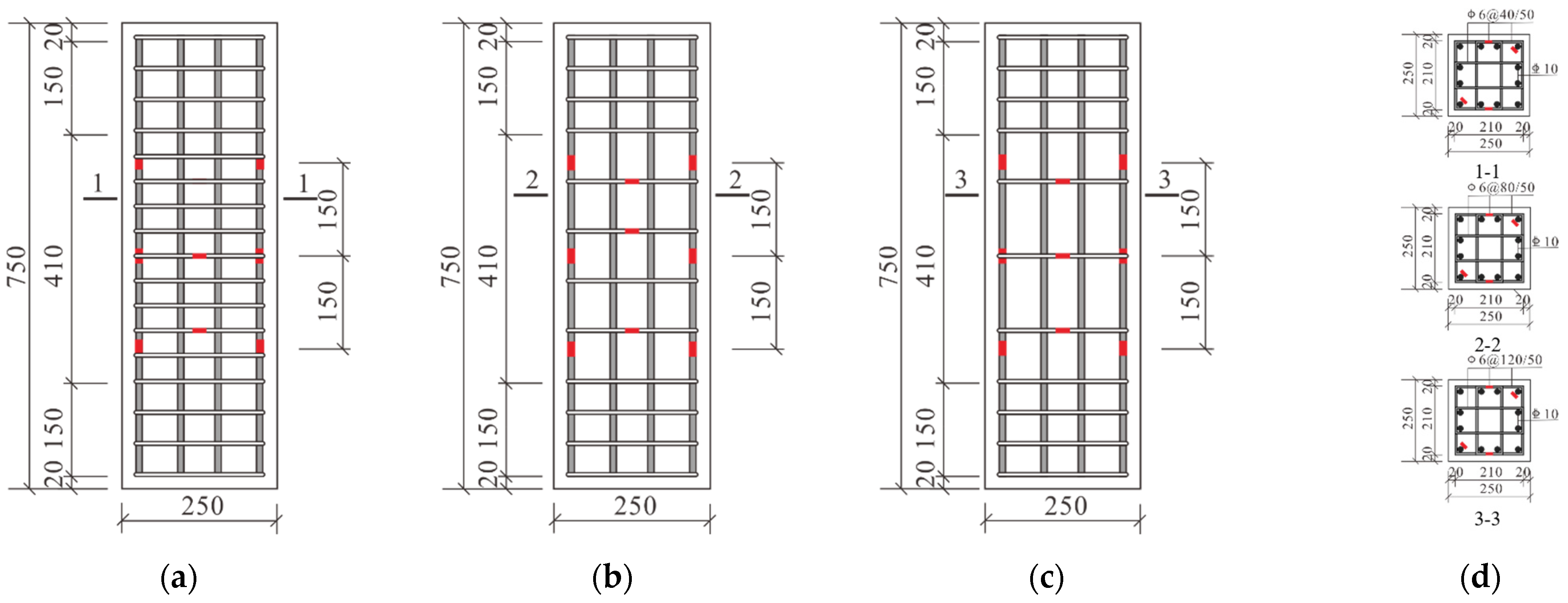
2.2. Specimen Design
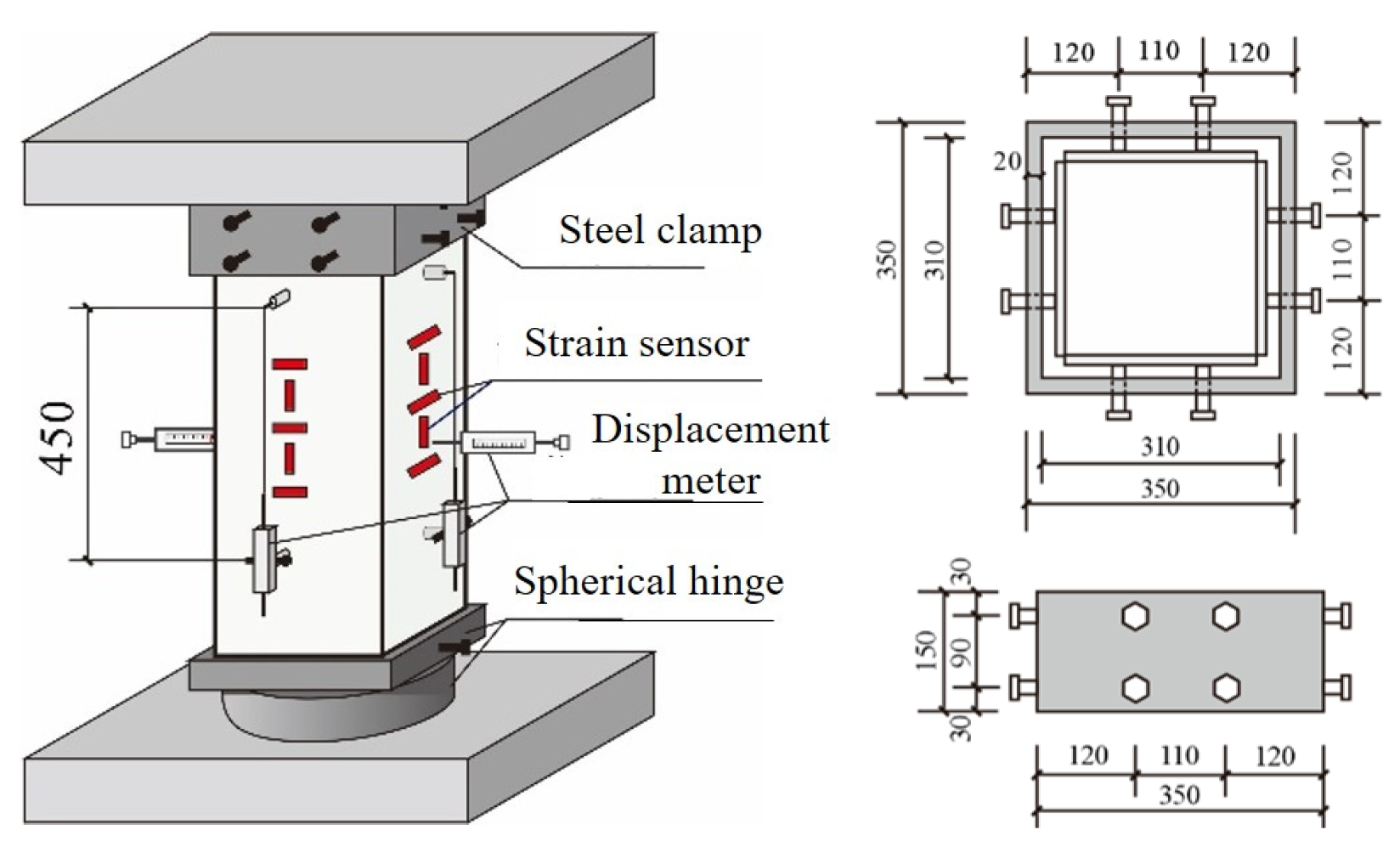
2.3. Test Loading and Measurement
3. Results and Discussion
3.1. Test Phenomenon and Failure Mode
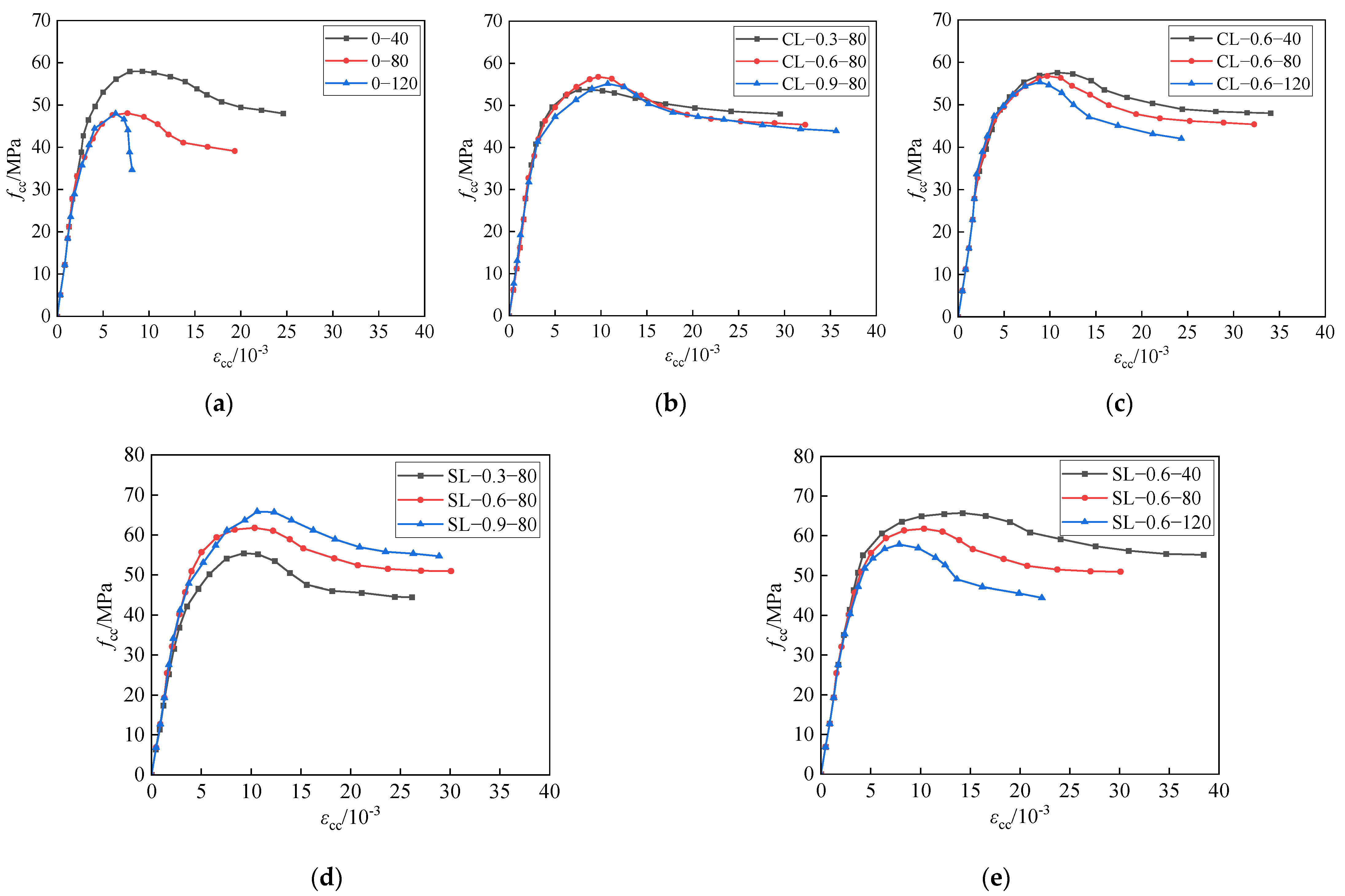
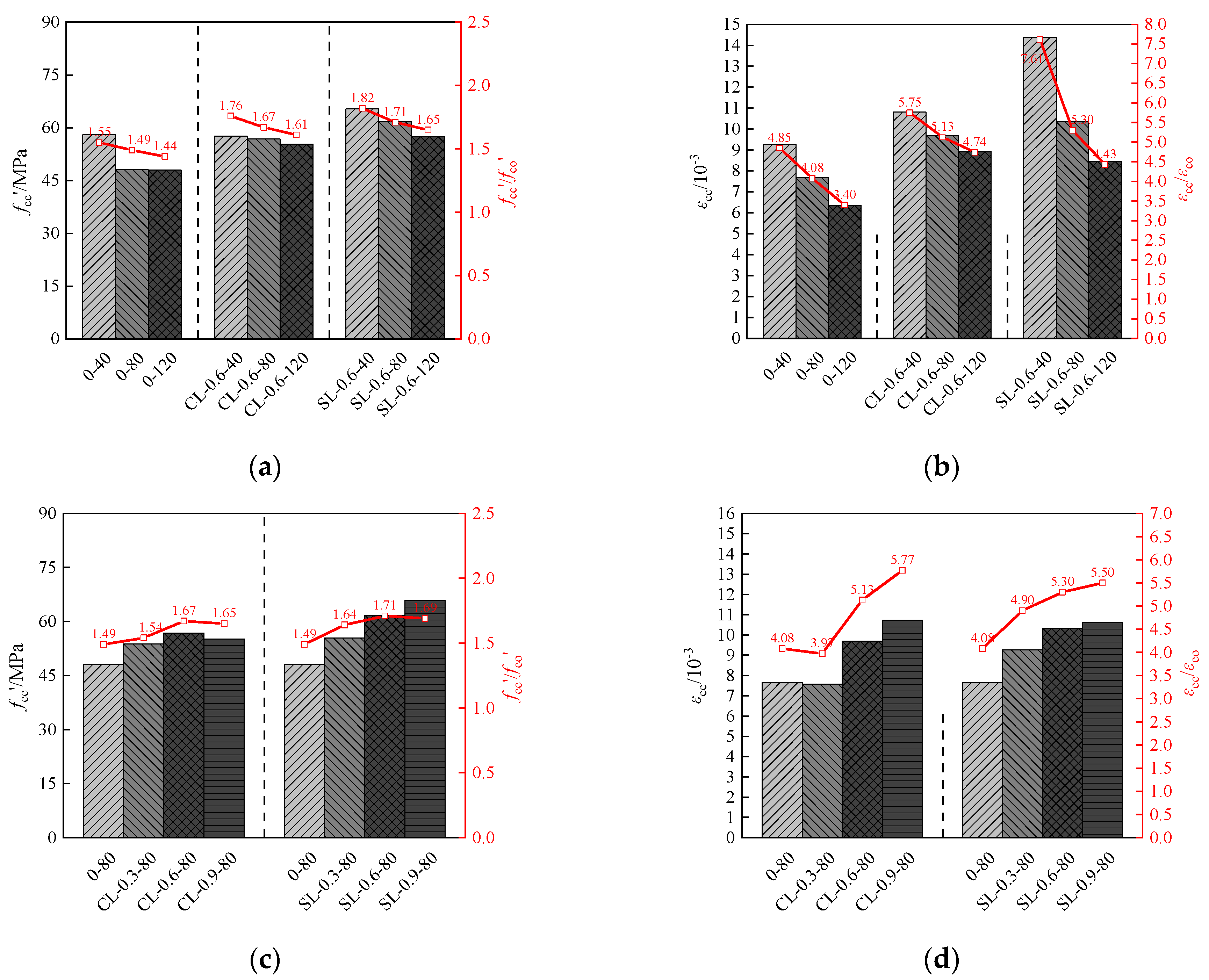
3.2. Major Experimental Results
3.3. Stress–Strain Curve of the Specimen
3.4. Analysis of Influencing Factors
3.4.1. Stirrup Spacing
3.4.2. Fiber Type and Fiber Content
4. Peek Stress and Strain Prediction Model
4.1. Stirrup Restraint Mechanism
4.2. Modified Model
4.2.1. Constraint on the Selection of Efficiency Indicators
4.2.2. Peak Stress and Peak Strain Calculation Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bian, Z.; Huang, Y.; Liu, Y.; Lu, J.-X.; Fan, D.; Wang, F.; Poon, C.S. A novel foaming-sintering technique for developing eco-friendly lightweight aggregates for high strength lightweight aggregate concrete. J. Cleaner Prod. 2024, 448, 141499. [Google Scholar]
- Gao, Y.; Liu, G.; Han, X.; Gao, Q.; Ren, J. Research on the design method of mix proportion of ceramsite lightweight aggregate concrete. Constr. Build. Mater. 2024, 433, 136665. [Google Scholar]
- Li, J.; Niu, J.; Wan, C.; Liu, X.; Jin, Z. Comparison of flexural property between high performance polypropylene fiber reinforced lightweight aggregate concrete and steel fiber reinforced lightweight aggregate concrete. Constr. Build. Mater. 2017, 157, 729–736. [Google Scholar]
- Ye, Y.; Liu, J.; Zhang, Z.; Wang, Z.; Peng, Q. Experimental Study of High-Strength Steel Fiber Lightweight Aggregate Concrete on Mechanical Properties and Toughness Index. Adv. Mater. Sci. Eng. 2020, 2020, 5915034. [Google Scholar]
- Ombres, L.; Mazzuca, P.; Verre, S. Effects of thermal conditioning at high temperatures on the response of concrete elements confined with a PBO-FRCM composite system. J. Mater. Civ. Eng. 2020, 34, 04021413. [Google Scholar] [CrossRef]
- Hassanpour, M.; Shafigh, P.; Mahmud, H.B. Mechanical properties of structural lightweight aggregate concrete containing low volume steel fiber. Arab. J. Sci. Eng. 2014, 39, 3579–3590. [Google Scholar]
- Divyah, N.; Thenmozhi, R.; Neelamegam, M.; Prakash, R. Characterization and behavior of basalt fiber-reinforced lightweight concrete. Struct. Concr. 2021, 22, 422–430. [Google Scholar]
- Ecemiş, A.S.; Madenci, E.; Karalar, M.; Fayed, S.; Althaqafi, E.; Özkılıç, Y.O. Bending Performance of Reinforced Concrete Beams with Rubber as Form of Fiber from Waste Tires. Materials 2024, 17, 4958. [Google Scholar] [CrossRef]
- Ecemiş, A.S.; Madenci, E.; Karalar, M.; Fayed, S.; Althaqafi, E.; Özkılıç, Y.O. Shear performance of reinforced concrete beams with rubber as form of fiber from waste tire. Steel Compos. Struct. 2024, 51, 337–349. [Google Scholar]
- Zivkovic, J.; Øverli, J.A. Confinement in bending of high-strength lightweight aggregate concrete beams. Structures 2022, 39, 419–433. [Google Scholar]
- Al-Eliwi, B.J.; Ekmekyapar, T.; Al-Samaraie, M.I.; Doğru, M.H. Behavior of reinforced lightweight aggregate concrete-filled circular steel tube columns under axial loading. Structures 2018, 16, 101–111. [Google Scholar] [CrossRef]
- Wei, H.; Wu, T.; Liu, X.; Zhang, R. Investigation of stress-strain relationship for confined lightweight aggregate concrete. Constr. Build. Mater. 2020, 256, 119432. [Google Scholar] [CrossRef]
- Qian, Z.; Wang, J.; Liu, Y.; Xu, Q. Axial compressive performance of partially encased steel-concrete composite stub columns filled with lightweight aggregate concrete. Eng. Struct. 2023, 291, 116422. [Google Scholar] [CrossRef]
- Campione, G.; La Mendola, L. Behavior in compression of lightweight fiber reinforced concrete confined with transverse steel reinforcement. Cem. Concr. Compos. 2004, 26, 645–656. [Google Scholar] [CrossRef]
- Haddad, R.H.; Ashour, D.M. Thermal performance of steel fibrous lightweight aggregate concrete short columns. J. Compos. Mater. 2013, 47, 2013–2025. [Google Scholar] [CrossRef]
- Wu, T.; Sun, L.; Wei, H.; Liu, X. Uniaxial performance of circular hybrid fibre-reinforced lightweight aggregate concrete columns. Eng. Struct. 2021, 238, 112263. [Google Scholar] [CrossRef]
- GB/T 14684-2022; Sand for Construction. China General Administration for Market Regulation: Beijing, China, 2022.
- GB/T 14685-2022; Pebble and Crushed Stone for Construction. China General Administration for Market Regulation: Beijing, China, 2022.
- GB/T 14337-2022; Man-Made Fibre-Test Method for Tensile Properties of Staple Fibre. China General Administration for Market Regulation: Beijing, China, 2022.
- Wei, H.; Wu, T.; Yang, X. Properties of lightweight aggregate concrete reinforced with carbon and/or poly-propylene fibers. Materials 2020, 13, 640. [Google Scholar] [CrossRef]
- Wu, T.; Wei, H.; Liu, X.; Liu, Q. Experimental study on axial compression performance of stirrup confined high-strength lightweight aggregate concrete columns. Eng. Mech. 2018, 35, 203–213. [Google Scholar]
- Hassanpour, M.; Shafigh, P.; Mahmud, H.B. Lightweight aggregate concrete fiber reinforcement–A review. Constr. Build. Mater. 2012, 37, 452–461. [Google Scholar] [CrossRef]
- Sheikh, S.; Uzumeri, S.M. Analytical model for concrete confinement in tied columns. ASCE J. Struct. Div. 1982, 108, 2703–2722. [Google Scholar] [CrossRef]
- Ahmad, S.H.; Shah, S.P. Complete triaxial stress-strain curves for concrete. ASCE J. Struct. Div. 1982, 108, 728–742. [Google Scholar] [CrossRef]
- Li, H. High Strength Concrete and Its Combined Structure; Science Press: Beijing, China, 2004. [Google Scholar]
- Bahn, B.Y.; Han, B.S.; Shin, S.W. A model of confined concrete in high-strength reinforced concrete tied columns. Mag. Concr. Res. 2003, 55, 203–214. [Google Scholar]
- Nielsen, C. Ultra High Strength Steel Fiber Reinforced Concrete; Technical University of Denmark: Copenhagen, Denmark, 1995. [Google Scholar]
- Aoude, H. Structural Behaviour of Steel Fiber Reinforced Concrete Members; McGill University: Montreal, QC, Canada, 2008. [Google Scholar]
- Paultre, P.; Eid, R.; Langlois, Y.; Lévesque, Y. Behavior of steel fiber-reinforced high-strength concrete columns under uniaxial compression. ASCE J. Struct. Eng. 2010, 136, 1225–1235. [Google Scholar] [CrossRef]
- Aveston, J.; Mercer, R.A.; Sillwood, J.M. Fiber reinforced cements-scientific foundation for specification. In: Compos.-Stand. Test. Des. Proc. Natl. Phys. Lab. Conf, UK. 1974; 93–103. [Google Scholar]
- Maage, M. Interaction between steel fibers and cement based matrixes. Mater. Constr. 1977, 10, 297–301. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. ASCE J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Cusson, D.; Paultre, P. Stress-strain model for confined high-strength concrete. ASCE J. Struct. Eng. 1995, 121, 468–477. [Google Scholar] [CrossRef]
- Légeron, F.; Paultre, P. Uniaxial confinement model for normal- and high-strength concrete columns. ASCE J. Struct. Eng. 2003, 129, 241–252. [Google Scholar] [CrossRef]
- Khaloo, A.R.; Eldash, K.; Ahmad, S.H. Model for lightweight concrete columns confined by either single hoops or interlocking double spirals. ACI Struct. J. 1999, 96, 883–890. [Google Scholar]
- Lim, J.C.; Ozbakkaloglu, T. Stress-strain model for normal-and light-weight concretes under uniaxial and triaxial compression. Constr. Build. Mater. 2014, 71, 492–509. [Google Scholar] [CrossRef]
- Manrique, M.A.; Bertero, V.V.; Popov, E.P. Mechanical Behavior of Lightweight Concrete Confined by Different Types of Lateral Reinforcement; College of Engineering University of California: Berkeley, CA, USA, 1979. [Google Scholar]
- Shah, S.P.; Naaman, A.E.; Moreno, J. Effect of confinement on the ductility of lightweight concrete. Int. J. Cem. Compos. Lightweight Concr. 1983, 5, 15–25. [Google Scholar] [CrossRef]
- Martinez, S.; Nilson, A.H.; Slate, F.O. Spirally reinforced high-strength concrete columns. ACI J. 1984, 81, 431–442. [Google Scholar]
- Hlaing, M.M.; Huan, W.T.; Thangayah, T. Response of spiral-reinforced lightweight concrete to short-term compression. J. Mater. Civ. Eng. ASCE 2010, 22, 1295–1303. [Google Scholar]
- Khaloo, A.R.; Bozorgzadeh, A. Influence of confining hoop flexural stiffness on behavior of high-strength lightweight concrete columns. ACI Struct. J. 2001, 98, 657–664. [Google Scholar]
- Basset, R.; Uzumeri, S.M. Effect of confinement on the behaviour of high-strength lightweight concrete columns. Can. J. Civ. Eng. 1986, 13, 741–751. [Google Scholar] [CrossRef]




| Material | Chemical Composition/% | Loss on Ignition /% | Fineness /m2/kg | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SiO2 | Al2O3 | Fe2O3 | CaO | MgO | SO3 | K2O | Na2O | |||
| Cement | 20.36 | 5.67 | 3.84 | 62.81 | 2.68 | 2.51 | 0.87 | 0.19 | 1.07 | 329 |
| Fly ash | 53.26 | 33.99 | 4.72 | 2.46 | 0.55 | 1.40 | 1.21 | 1.1 | 2.02 | 420 |
| Aggregate | PS/mm | ρ1/(kg·m3) | ρ2/(kg·m3) | W/% | f/MPa |
|---|---|---|---|---|---|
| Shale ceramsite | 5–16 | 870 | 1525 | 2.17 | 6.57 |
| Sand | 0.75–4.75 | 1400 | 2375 | - | - |
| Fiber | l/mm | d/μm | ρ/(kg·m3) | Es/GPa | fsf/MPa |
|---|---|---|---|---|---|
| CF | 8 | 6 | 1824 | 238 | 3800 |
| SF | 13 | 185 | 7800 | 195 | 3100 |
| Rebar | d/mm | fy/MPa | fu/MPa | Es × 105/MPa | εy × 10−3 |
|---|---|---|---|---|---|
| HRB400 | 10 mm | 454 | 558 | 2.0 | 2.270 |
| HPB300 | 6 mm | 523 | 617 | 2.1 | 2.490 |
| Cement | Fly Ash | Superplasticizer | Shale Ceramsite | Sand | Water |
|---|---|---|---|---|---|
| 539 | 73.5 | 3.5 | 537 | 540 | 214 |
| Specimen | Stirrup Parameters | Fiber Types | Fiber Content/vol% | |
|---|---|---|---|---|
| s/mm | ρv/% | |||
| 0–40 | 40 | 3.0 | - | - |
| 0–80 | 80 | 1.5 | - | - |
| 0–120 | 120 | 1.0 | - | - |
| CL-0.3–80 | 80 | 1.5 | CF | 0.3 |
| CL-0.6–40 | 40 | 3.0 | CF | 0.6 |
| CL-0.6–80 | 80 | 1.5 | CF | 0.6 |
| CL-0.6–120 | 120 | 1.0 | CF | 0.6 |
| CL-0.9–80 | 80 | 1.5 | CF | 0.9 |
| SL-0.3–80 | 80 | 1.5 | SF | 0.3 |
| SL-0.6–40 | 40 | 3.0 | SF | 0.6 |
| SL-0.6–80 | 80 | 1.5 | SF | 0.6 |
| SL-0.6–120 | 120 | 1.0 | SF | 0.6 |
| SL-0.9–80 | 80 | 1.5 | SF | 0.9 |
| LVDT | Test Accuracy | Variation of the Displayed Value | Basic Error | Correction Factor |
| 0.01 mm | <±3 με(8 h) | <±5 με | 0.003 με/mm | |
| Strain Gauge | Sensitivity factor | Measurement accuracy | Resistance accuracy | Strain limitation |
| 2.0 ± 0.01 | 0.1 με | 120 ± 0.3 Ω | 20,000 um/m |
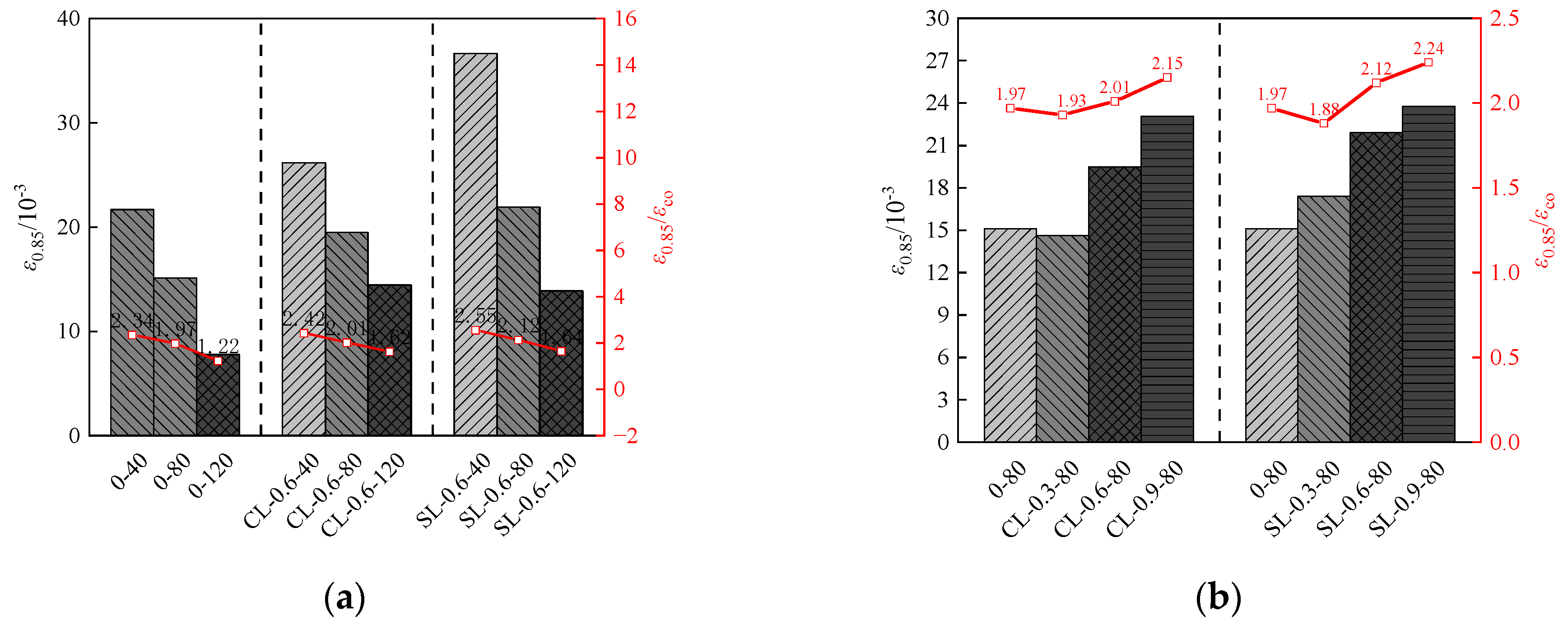
| Specimen | Pmax/kN | fcu/MPa | fc′/MPa | fco′/MPa | fcc′/MPa | εcc/10−3 | εco/10−3 | ε0.85/10−3 | fcc′/fco′ | εcc/εco | ε0.85/εcc |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0–40 | 2702.11 | 47.71 | 43.89 | 37.31 | 57.97 | 9.26 | 1.91 | 21.68 | 1.55 | 4.85 | 2.34 |
| 0–80 | 2273.13 | 41.22 | 37.92 | 32.23 | 48.05 | 7.67 | 1.88 | 15.11 | 1.49 | 4.08 | 1.97 |
| 0–120 | 2269.6 | 42.61 | 39.20 | 33.32 | 47.97 | 6.36 | 1.87 | 7.76 | 1.44 | 3.40 | 1.22 |
| CL-0.3–80 | 2519.49 | 44.68 | 41.11 | 34.94 | 53.75 | 7.58 | 1.91 | 14.63 | 1.54 | 3.97 | 1.93 |
| CL-0.6–40 | 2685.69 | 41.79 | 38.45 | 32.68 | 57.59 | 10.81 | 1.88 | 26.16 | 1.76 | 5.75 | 2.42 |
| CL-0.6–80 | 2649.69 | 43.58 | 40.09 | 34.08 | 56.76 | 9.70 | 1.89 | 19.49 | 1.67 | 5.13 | 2.01 |
| CL-0.6–120 | 2589.21 | 44 | 40.48 | 34.41 | 55.36 | 8.91 | 1.88 | 14.44 | 1.61 | 4.74 | 1.62 |
| CL-0.9–80 | 2579.41 | 42.81 | 39.39 | 33.48 | 55.13 | 10.73 | 1.86 | 23.07 | 1.65 | 5.77 | 2.15 |
| SL-0.3–80 | 2591.88 | 43.32 | 39.85 | 33.88 | 55.42 | 9.26 | 1.89 | 17.41 | 1.64 | 4.90 | 1.88 |
| SL-0.6–40 | 3020.97 | 46 | 42.32 | 35.97 | 65.34 | 14.38 | 1.89 | 36.68 | 1.82 | 7.61 | 2.55 |
| SL-0.6–80 | 2866 | 46.05 | 42.37 | 36.01 | 61.76 | 10.34 | 1.95 | 21.91 | 1.71 | 5.30 | 2.12 |
| SL-0.6–120 | 2681.3 | 44.56 | 41.00 | 34.85 | 57.49 | 8.46 | 1.91 | 13.88 | 1.65 | 4.43 | 1.64 |
| SL-0.9–80 | 3042.36 | 49.84 | 45.85 | 38.97 | 65.83 | 10.62 | 1.93 | 23.78 | 1.69 | 5.50 | 2.24 |
| Mean value | 2651.60 | 44.47 | 40.92 | 34.78 | 56.80 | 9.54 | 1.90 | 19.69 | 1.63 | 5.03 | 2.01 |
| Standard Deviation Values | 225.15 | 2.33 | 2.14 | 1.82 | 5.20 | 1.91 | 0.02 | 6.92 | 0.10 | 1.01 | 0.35 |
| Presented by | Peak Stress fcc′ | Peak Strain εcc |
|---|---|---|
| Mander [32] | ||
| Cusson [33] | ||
| Legeron and Paultre [34] | ||
| Khaloo [35] | ||
| Lim [36] | ||
| Aoude [28] |
| Specimen Number | Mander Model | Cusson Model | Legeron Model | Khaloo Model | Lim Model | Aoude Model | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fcc′ calc/test | εcc calc/test | fcc′ calc/test | εcc calc/test | fcc′ calc/test | εcc calc/test | fcc′ calc/test | εcc calc/test | fcc′ calc/test | εcc calc/test | fcc′ calc/test | εcc calc/test | |
| 0–40 | 0.77 | 0.77 | 0.76 | 0.21 | 0.68 | 0.32 | 0.72 | 0.21 | 0.79 | 0.21 | 0.78 | 0.21 |
| 0–80 | 0.75 | 0.85 | 0.75 | 0.25 | 0.69 | 0.31 | 0.71 | 0.25 | 0.77 | 0.25 | 0.77 | 0.25 |
| 0–120 | 0.75 | 0.94 | 0.76 | 0.29 | 0.71 | 0.34 | 0.72 | 0.29 | 0.76 | 0.29 | 0.77 | 0.29 |
| CL-0.3–80 | 0.72 | 0.93 | 0.73 | 0.25 | 0.67 | 0.31 | 0.69 | 0.25 | 0.74 | 0.25 | 1.47 | 0.25 |
| CL-0.6–40 | 0.69 | 0.83 | 0.68 | 0.17 | 0.60 | 0.28 | 0.64 | 0.17 | 0.71 | 0.17 | 2.01 | 0.17 |
| CL-0.6–80 | 0.67 | 0.85 | 0.67 | 0.19 | 0.62 | 0.24 | 0.64 | 0.19 | 0.68 | 0.19 | 2.05 | 0.19 |
| CL-0.6–120 | 0.67 | 0.85 | 0.68 | 0.21 | 0.63 | 0.24 | 0.65 | 0.21 | 0.68 | 0.21 | 2.09 | 0.21 |
| CL-0.9–80 | 0.68 | 0.74 | 0.68 | 0.17 | 0.62 | 0.22 | 0.65 | 0.17 | 0.69 | 0.17 | 2.78 | 0.17 |
| SL-0.3–80 | 0.68 | 0.86 | 0.68 | 0.20 | 0.63 | 0.26 | 0.65 | 0.20 | 0.70 | 0.20 | 0.73 | 0.20 |
| SL-0.6–40 | 0.66 | 0.67 | 0.65 | 0.13 | 0.58 | 0.20 | 0.61 | 0.13 | 0.68 | 0.13 | 0.73 | 0.13 |
| SL-0.6–80 | 0.64 | 0.86 | 0.65 | 0.19 | 0.60 | 0.23 | 0.62 | 0.19 | 0.66 | 0.19 | 0.73 | 0.19 |
| SL-0.6–120 | 0.65 | 0.96 | 0.66 | 0.23 | 0.62 | 0.26 | 0.63 | 0.23 | 0.66 | 0.23 | 0.74 | 0.23 |
| SL-0.9–80 | 0.65 | 0.81 | 0.66 | 0.18 | 0.61 | 0.22 | 0.62 | 0.18 | 0.67 | 0.18 | 0.77 | 0.18 |
| Mean value | 0.691 | 0.840 | 0.693 | 0.205 | 0.635 | 0.264 | 0.658 | 0.205 | 0.707 | 0.205 | 1.263 | 0.205 |
| Variance | 0.0018 | 0.0065 | 0.0017 | 0.0018 | 0.0016 | 0.0020 | 0.0015 | 0.0018 | 0.0019 | 0.0018 | 0.5245 | 0.0018 |
| Researchers | The Amount of Specimens | Peak Stress | Peak Stress Enhancement Ratio | Peak Strain Increase Ratio | ε0.85/εcc |
|---|---|---|---|---|---|
| Manrique [37] | 21 | 34.82~38.64 | 1.04~1.24 | 1.08~1.58 | 1.62~4.92 |
| Shah [38] | 4 | 33.64~49.21 | 1.01~1.56 | 1.34~1.46 | 1.12~1.84 |
| Martinez [39] | 41 | 25.67~59.17 | 1.41~1.76 | 1.23~4.50 | 1.16~6.78 |
| Hlaing [40] | 14 | 35.21~65.20 | 1.42~1.27 | 1.22~3.08 | 1.04~1.53 |
| Khaloo [35,41] | 24 | 52.49~70.52 | 1.01~1.88 | 1.10~4.43 | 1.15~1.73 |
| Wu [21] | 12 | 42.76~52.18 | 1.09~1.47 | 1.23~2.36 | 1.31~6.34 |
| Basset [42] | 15 | 33.43~38.52 | 1.08~1.58 | 1.07~1.43 | 2.01~8.43 |
| Wu [16] | 20 | 31.67~55.32 | 1.34~2.48 | 1.32~8.25 | 1.42~3.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Wu, T.; Huang, Y.; Sun, G. Experimental Study on Axial Compression Behavior of Fiber-Reinforced Lightweight Aggregate Concrete Columns Confined by Grid Stirrups. Buildings 2025, 15, 1206. https://doi.org/10.3390/buildings15071206
Chen S, Wu T, Huang Y, Sun G. Experimental Study on Axial Compression Behavior of Fiber-Reinforced Lightweight Aggregate Concrete Columns Confined by Grid Stirrups. Buildings. 2025; 15(7):1206. https://doi.org/10.3390/buildings15071206
Chicago/Turabian StyleChen, Shun, Tao Wu, Yujie Huang, and Guangyu Sun. 2025. "Experimental Study on Axial Compression Behavior of Fiber-Reinforced Lightweight Aggregate Concrete Columns Confined by Grid Stirrups" Buildings 15, no. 7: 1206. https://doi.org/10.3390/buildings15071206
APA StyleChen, S., Wu, T., Huang, Y., & Sun, G. (2025). Experimental Study on Axial Compression Behavior of Fiber-Reinforced Lightweight Aggregate Concrete Columns Confined by Grid Stirrups. Buildings, 15(7), 1206. https://doi.org/10.3390/buildings15071206






