Study on the Dynamic Deformation Characteristics of Artificial Structural Loess
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Materials
2.2. Sample Preparation
2.3. Test Method
3. Results
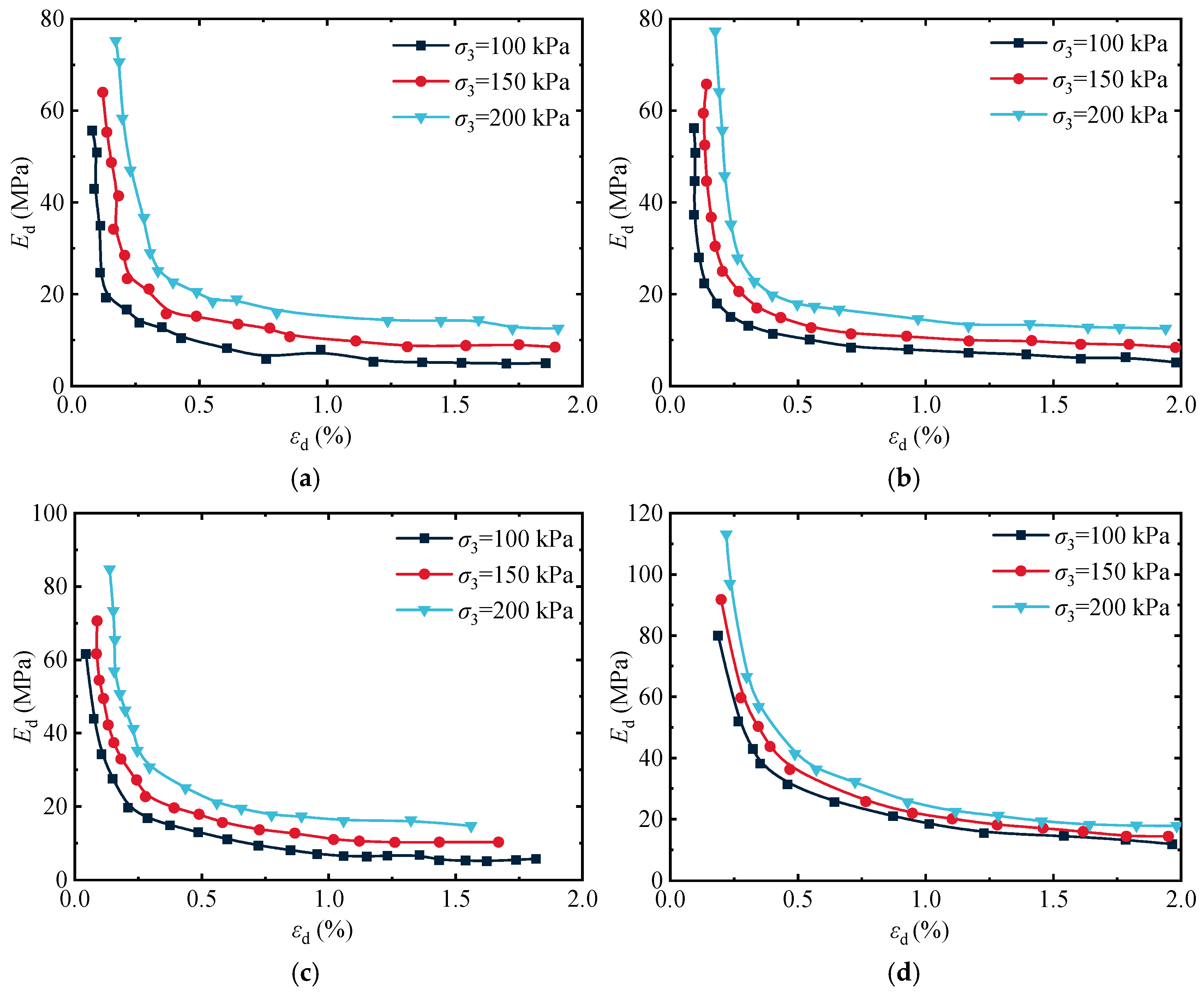
3.1. Analysis of the Influence of CP on the DM-E of Artificial Structural Loess
3.2. Analysis of the Influence of Dry Density on the DM-E of Artificial Structural Loess
3.3. Analysis of the Influence of Cement Content on the DM-E of Artificial Structural Loess
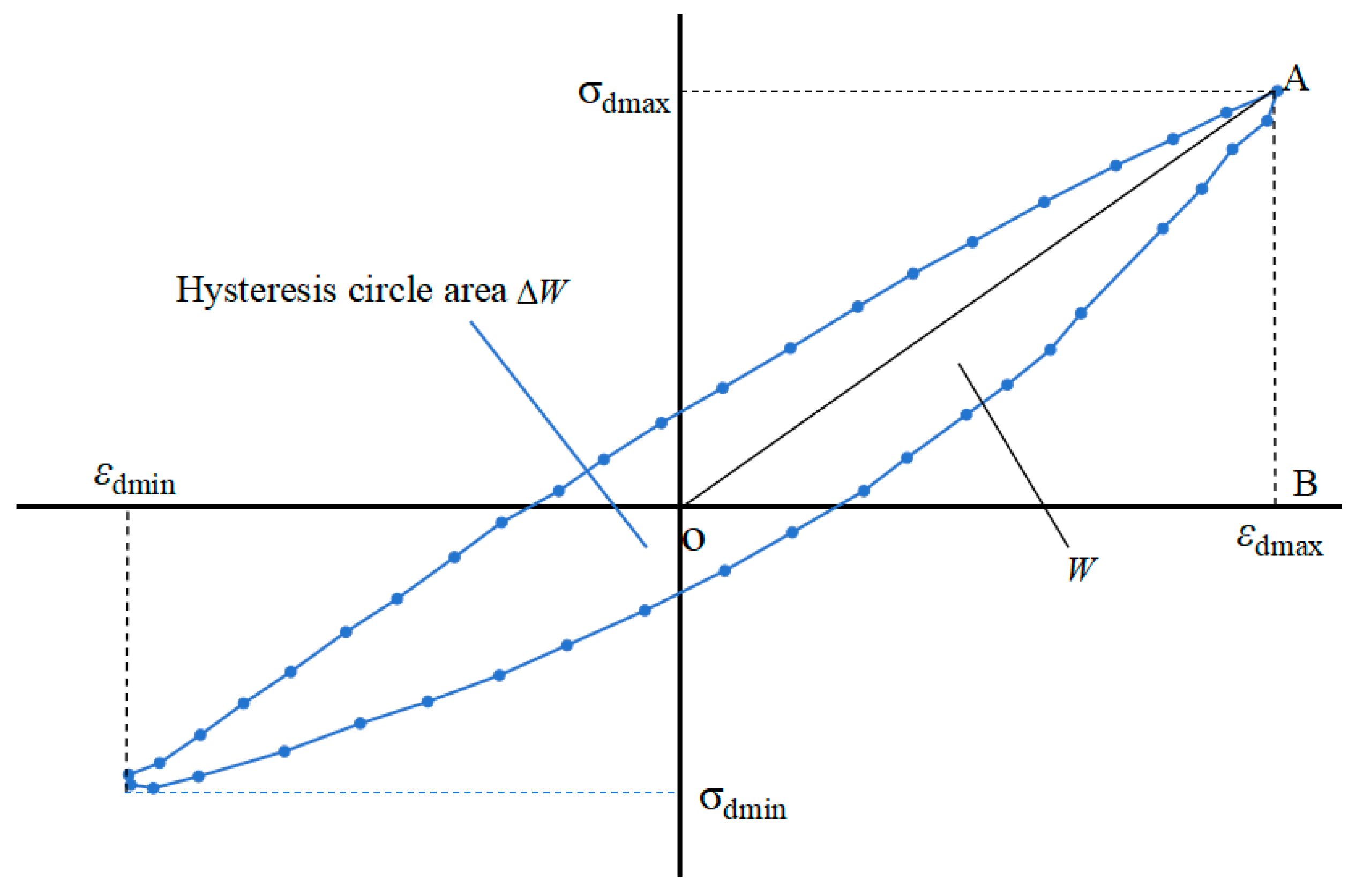
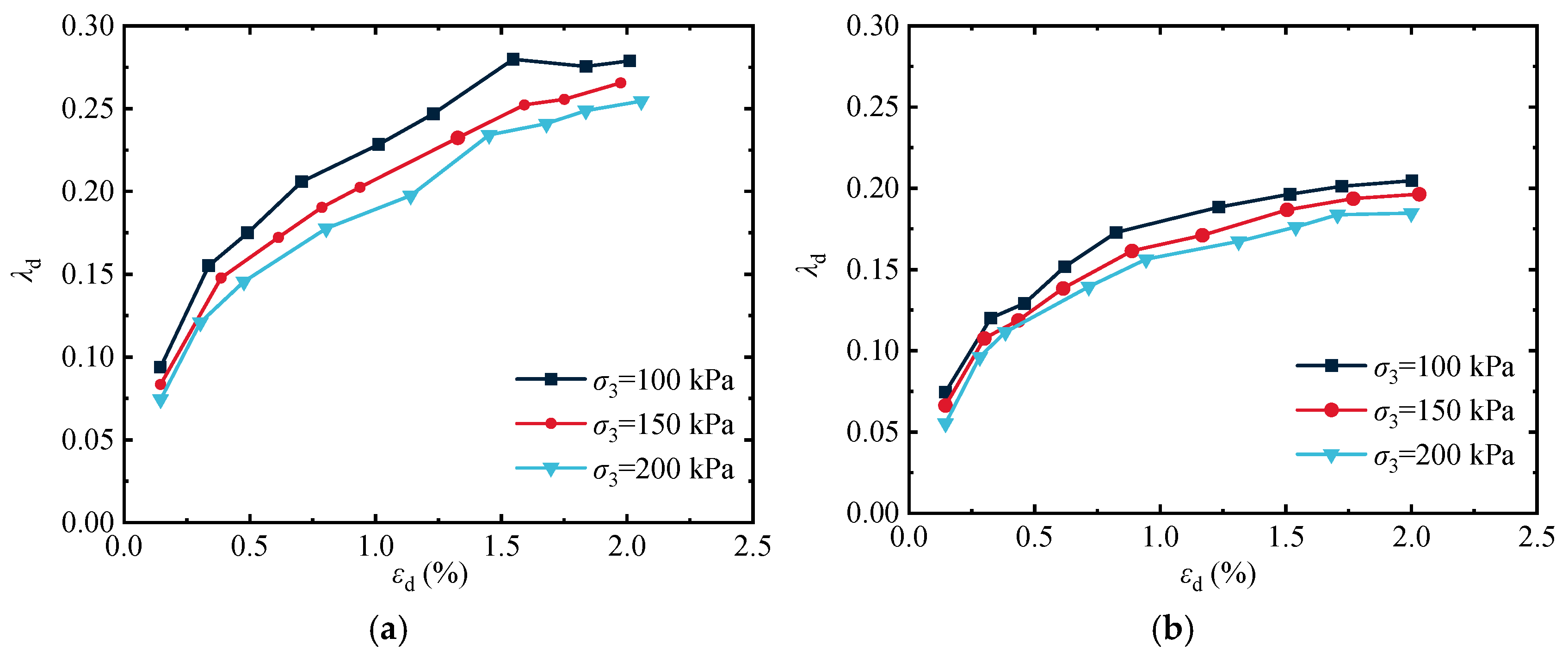
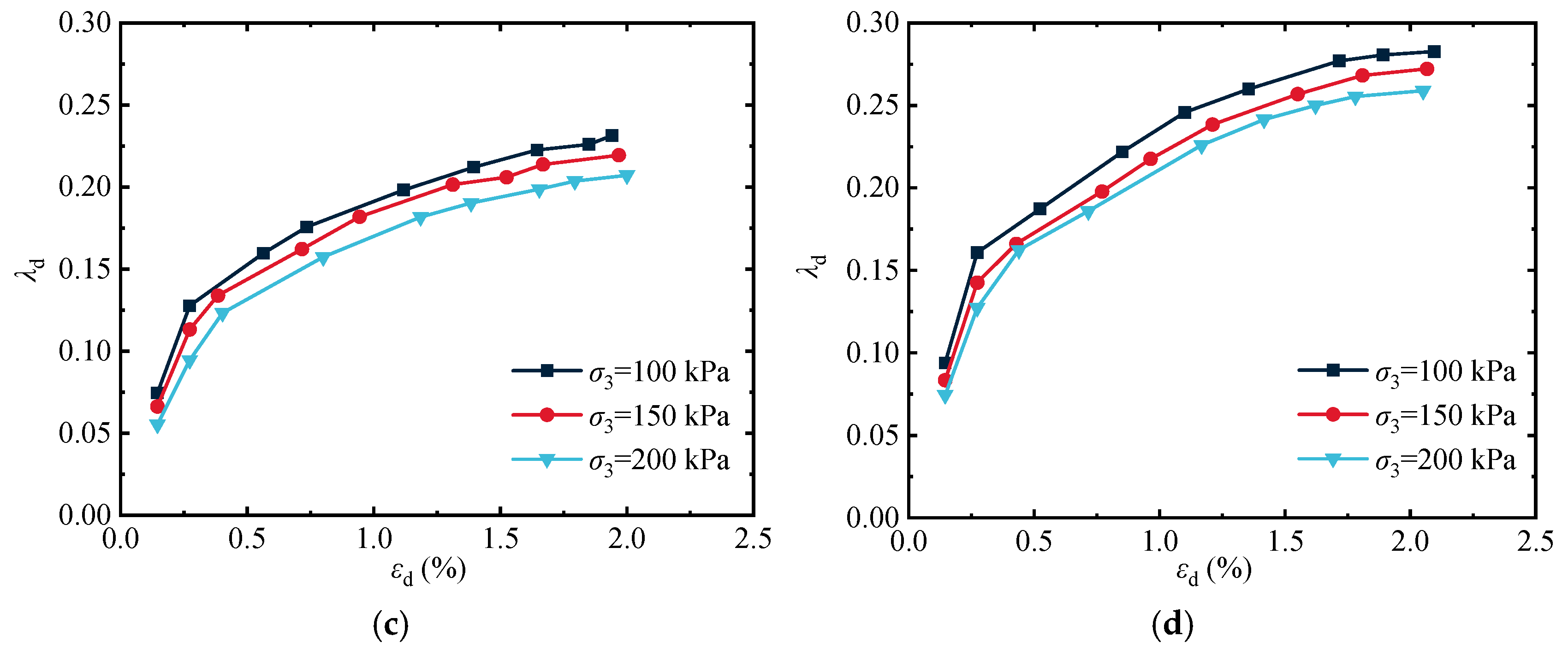
3.4. Analysis of the Influence of CP on the Damping Ratio of Artificial Structural Loess
4. Study on Dynamic Elastic Modulus Model of Artificial Structural Loess
4.1. Model Establishment
4.2. Model Parameter Acquisition
4.3. Model Verification
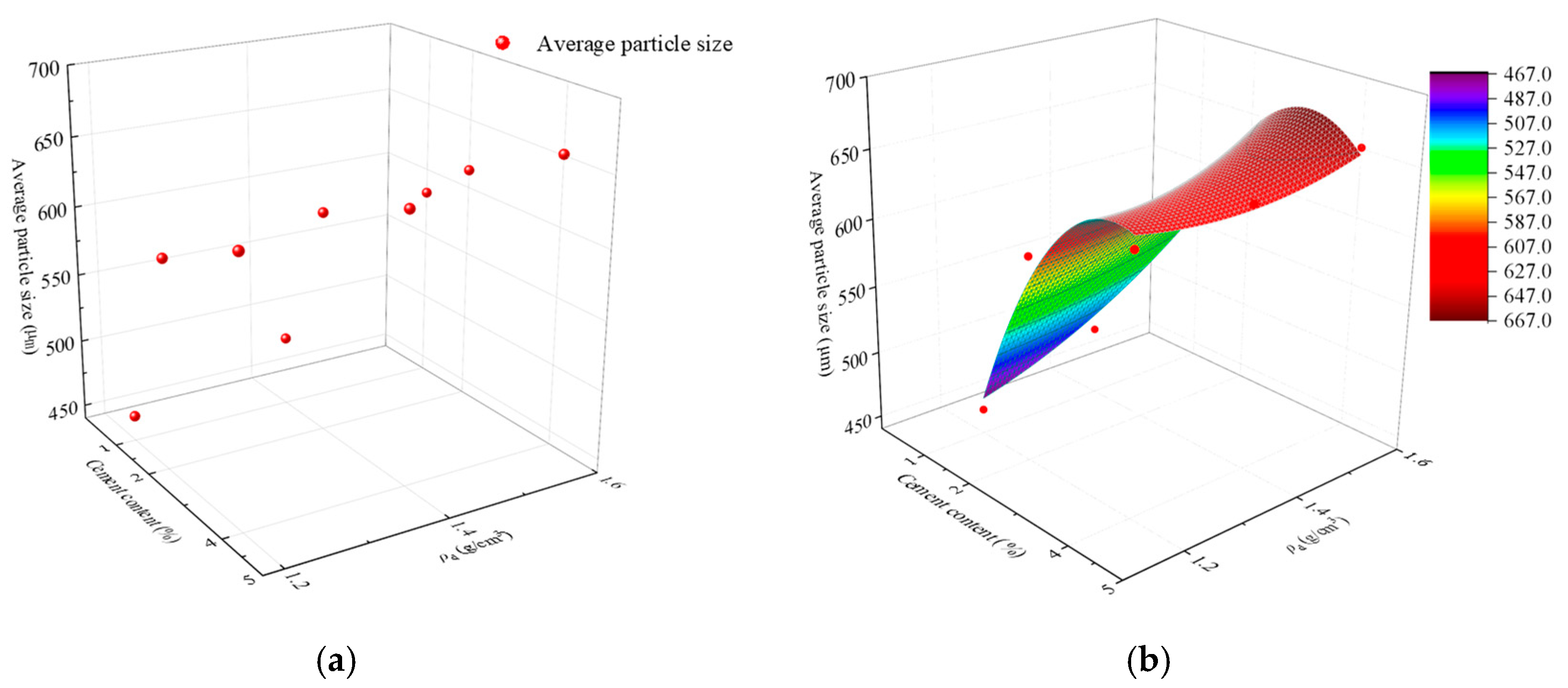
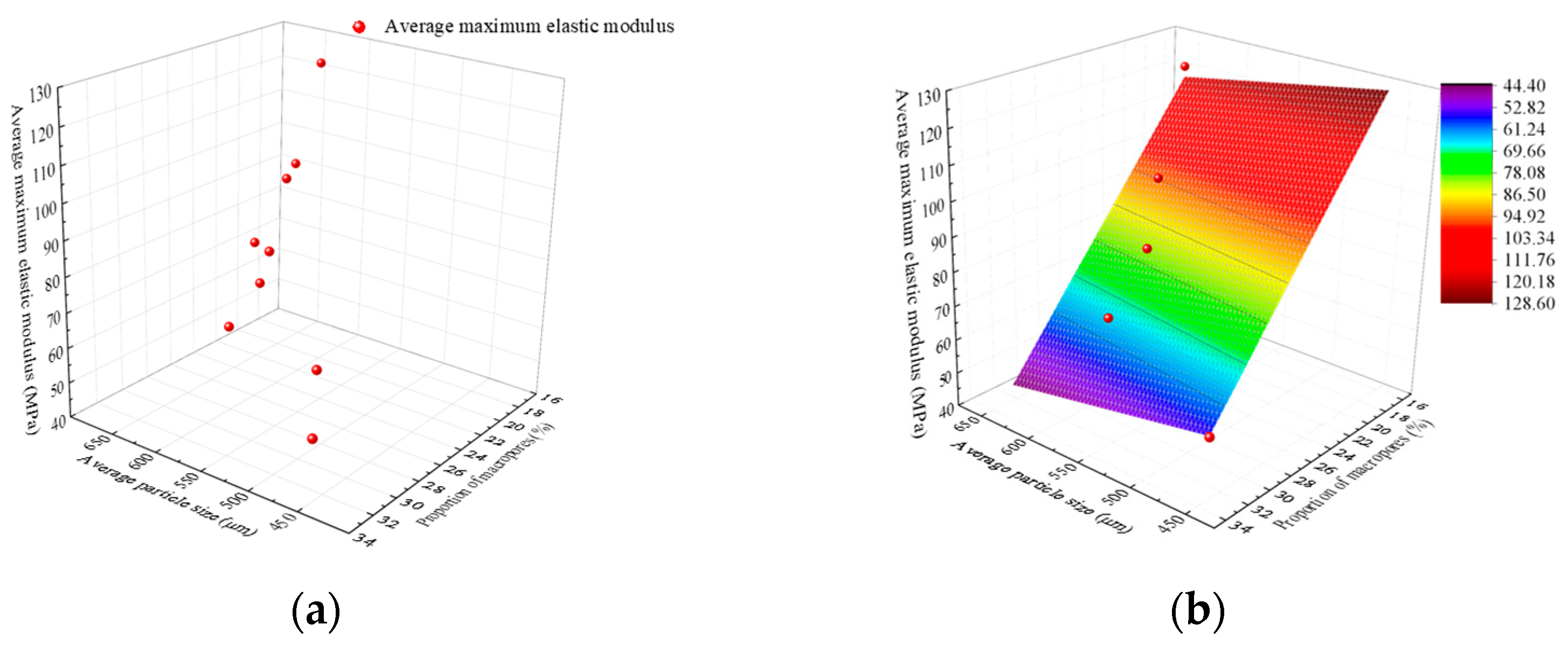
5. The Relationship Between Microstructure and Maximum Dynamic Modulus of Artificially Structured Loess
6. Conclusions
- (1)
- With the CP increasing, the DM-E of the soil gradually increases. As the dynamic strain rises, the DM-E of the soil gradually decreases. This is because, with the rise in CP, the contact between soil particles becomes tighter. Under a CP of 100 kPa, the dynamic elastic moduli of artificial structural loess with a cement content of 2% and dry densities of 1.20, 1.40, and 1.60 g/cm3 are 42.2, 52.7, and 66.1 MPa, respectively.
- (2)
- Under CP of 100 kPa and 200 kPa, the initial DM-E of soil with a dry density of 1.60 g/cm3 is 23.77 MPa and 35.66 MPa higher than that with a dry density of 1.20 g/cm3, indicating that the higher the dry density, the higher the DM-E of the soil and the more potent its ability to resist deformation.
- (3)
- When the dry density is 1.20 g/cm3, and the cement content is 1, 2, and 4%, the maximum dynamic elastic moduli under a CP of 150 kPa are 53.64, 65.30, and 80.42 MPa. With the increase in cement content, the bonding properties of the soil become better. As dynamic loading increases, the original balance between soil particles is broken, and the soil structure gradually becomes loose, unable to effectively resist stress so that the DM-E will decrease.
- (4)
- The damping fraction of loess generally shows an upward trend as the dynamic load increases. When the dynamic strain εd > 2%, the damping ratio stabilizes to a specific value, reaching the maximum damping ratio. Moreover, the impact of consolidation CP on the damping fraction also has a precise regularity, manifested as the more significant the CP, the smaller the damping ratio. Cement, as a bonding material, can absorb energy under dynamic loads, raise the damping fraction of the soil, and play a role in vibration reduction.
- (5)
- The relationship curve between the modulus of elasticity and dynamic strain of artificial structural loess conforms to the H-D hyperbolic model, and the fitting degree of parameters a and b is high. The average correlation coefficient is 0.955, indicating that the experimental and predicted results are promising. The proven model and parameter valuation method are appropriate for studying the DM-E of artificial structural loess.
- (6)
- Based on the results of macroscopic mechanics experiments and microscopic experiments, a surface model was established to describe the influence of different microscopic structure levels on the dynamic elastic modulus of artificial structural loess. The model is suitable for describing the impact of microscopic structure parameters on the dynamic elastic modulus of artificial structural loess.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Li, H.; Jiang, Y.; Yu, Q.; Yao, M.; Shan, W. Feasibility study on artificial preparation of structured loess. Geosci. Lett. 2022, 9, 21. [Google Scholar] [CrossRef]
- Pan, L.; Zhu, J.G.; Zhang, Y.F. Evaluation of structural strength and parameters of collapsible loess. Int. J. Geomech. 2021, 21, 04021066. [Google Scholar]
- Li, Y.; Wang, Y.; Aydin, A. Loess structure: Evolution and a scale-based classification. Earth Sci. Rev. 2024, 249, 104665. [Google Scholar] [CrossRef]
- Cui, C.; Xu, M.; Xu, C.; Zhang, P.; Zhao, J. An ontology-based probabilistic framework for comprehensive seismic risk evaluation of subway stations by combining Monte Carlo simulation. Tunn. Undergr. Space Technol. 2023, 135, 105055. [Google Scholar]
- Meng, K.; Cui, C.; Liang, Z.; Li, H.; Pei, H. A new approach for longitudinal vibration of a large-diameter floating pipe pile in visco-elastic soil considering the three-dimensional wave effects. Comput. Geotech. 2020, 128, 103840. [Google Scholar] [CrossRef]
- Qiao, F.; Chang, C.; Bo, J.; Wang, L.; Wang, J. Study on the dynamic characteristics of loess. Sustainability 2023, 15, 5428. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, D.; Wang, S.; Liang, C.; Zhao, D. Dynamic-response characteristics and deformation evolution of loess slopes under seismic loads. Eng. Geol. 2020, 267, 105507. [Google Scholar]
- Consoli, N.C.; da Silva, A.; Barcelos, A.M.; Festugato, L.; Favretto, F. Porosity/cement index controlling flexural tensile strength of artificially cemented soils in Brazil. Geotech. Geol. Eng. 2020, 38, 713–722. [Google Scholar]
- Zhang, X.; Li, Y.; Liu, Y.; Huang, Y.; Wang, Y.; Lu, Z. Characteristics and prevention mechanisms of artificial slope instability in the Chinese Loess Plateau. Catena 2021, 207, 105621. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, S.; Chen, D.; Zhao, D.; Zhang, D. An experimental study of the influence of structural parameters on dynamic characteristics of loess. Soil Dyn. Earthq. Eng. 2020, 132, 106067. [Google Scholar]
- Li, P.; Pan, Z.; Xiao, T.; Wang, J. Effects of molding water content and compaction degree on the microstructure and permeability of compacted loess. Acta Geotech. 2023, 18, 921–936. [Google Scholar] [CrossRef]
- Ni, W.; Nie, Y.; Lü, X.; Fan, M. Mechanical behavior and microstructure evolution of Malan loess under dynamic compaction. Environ. Earth Sci. 2024, 83, 76. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, Y.; Ma, Q.; Wang, J.; Li, L. Study of the law of strength attenuation and microstructure damage to cement improved loess under acid rain erosion. Environ. Earth Sci. 2024, 83, 555. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, Z.; Chen, H.; Ruan, L.; He, S. Experimental study on collapsible and structural characteristics of artificially prepared loess material. Sci. Rep. 2023, 13, 4113. [Google Scholar] [CrossRef]
- Axel, M.; Li, X.A.; Wen, F.; An, M.X. Microstructure and strength parameters of cement-stabilized loess. Geotechnics 2023, 3, 161–178. [Google Scholar] [CrossRef]
- Chen, R.; Cai, G.; Congress, S.S.C.; Dong, X.; Duan, W. Dynamic properties and environmental impact of waste red mud-treated loess under adverse conditions. Bull. Eng. Geol. Environ. 2021, 80, 93–113. [Google Scholar] [CrossRef]
- Yang, X.; Hu, Z.; Li, L.; Wang, X.; Zhou, X. Strength properties, microstructural evolution, and reinforcement mechanism for cement-stabilized loess with silica micro powder. Case Stud. Constr. Mater. 2024, 20, e02848. [Google Scholar] [CrossRef]
- Yuan, K.; Liu, K.; Yi, G.; Bowen, Y. Mechanical properties and evolution of microstructure of cement stabilized loess. J. Renew. Mater. 2022, 10, 3611. [Google Scholar] [CrossRef]
- G/BT 50123-2019; Standard for Geotechnical Testing Method. Construction Ministry of PRC: Beijing, China, 2019.
- Huang, C.X.; Wang, X.H.; Zhou, H.; Qin, D.C. Dynamic elastic modulus and damping ratio of unsaturated red clay. Geotech. Geol. Eng. 2020, 38, 873–881. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, M.J.; Zhang, J.Z.; Hao, Y.Z.; He, R.X. Effect of wetting and drying cycles on the dynamic properties of compacted loess. Adv. Civ. Eng. 2022, 8748109. [Google Scholar] [CrossRef]
- Liu, W.; Qu, S.; Nie, Z.; Zhang, J. Effects of density and moisture variation on dynamic deformation properties of compacted lateritic soil. Adv. Mater. Sci. Eng. 2016, 5951832. [Google Scholar] [CrossRef]

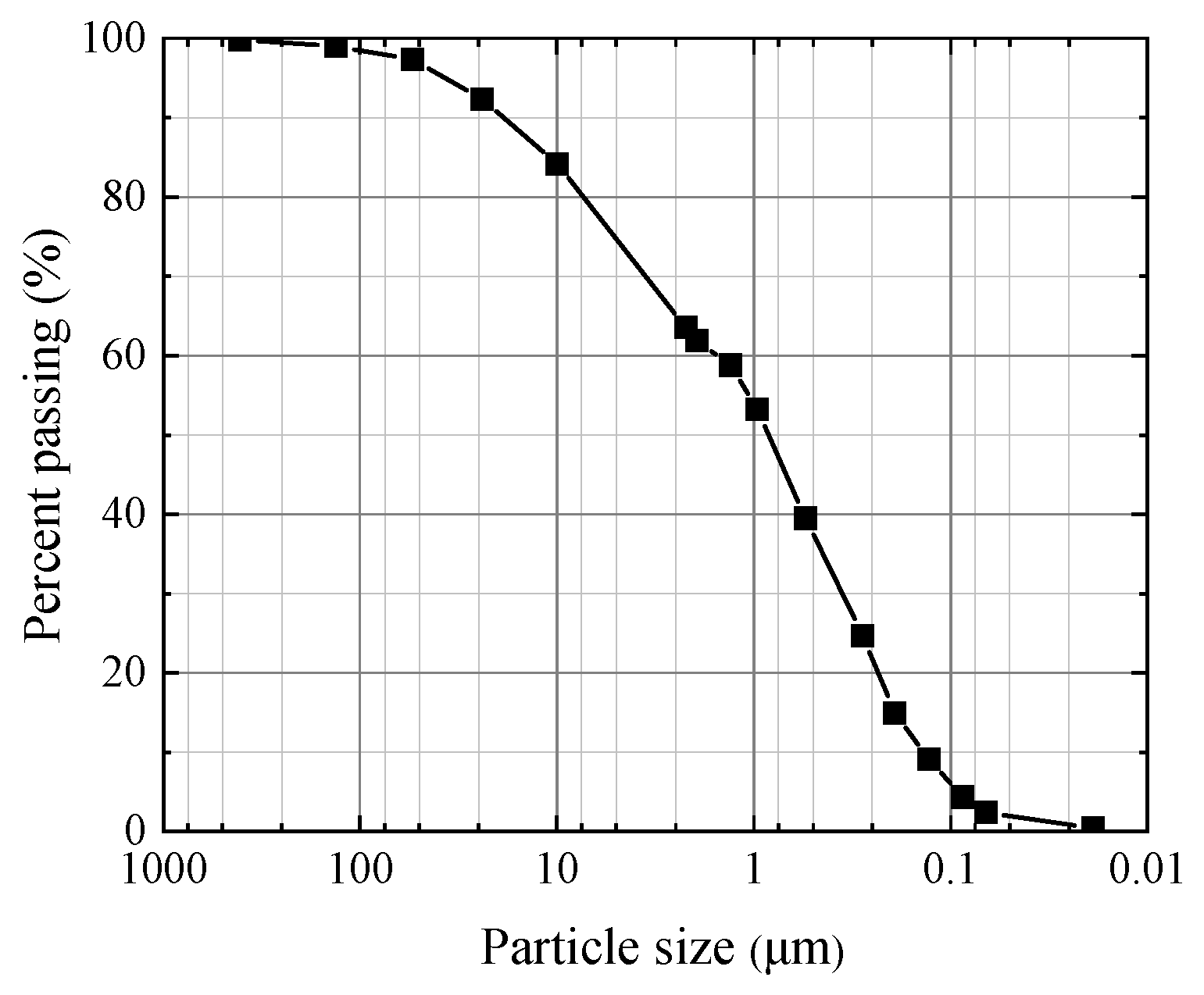





| Specific Gravity (Gs) | Water Content (%) | Dry Density (g/cm3) | Initial Porosity Ratio | Plasticity Limit (%) | Liquid Limit (%) | Plasticity Index |
|---|---|---|---|---|---|---|
| 2.71 | 12.64 | 1.52 | 0.97 | 20.54 | 35.78 | 15.24 |
| Density (g/cm3) | Fusion Point (°C) | Boiling Point (°C) | pH |
|---|---|---|---|
| 2.16 | 801 | 1465 | neutral |
| Density (g/cm3) | Fineness (μm) | Setting Time (min) | Water-Retaining Property | Compressive Strength (MPa) | Flexural Strength (MPa) |
|---|---|---|---|---|---|
| 3 | 801 | 5–10 | Good | 24 | 4 |
| Confining Pressure σ3 (kPa) | Dry Density ρ (g/cm3) | Saltiness (%) | Cement Content (%) |
|---|---|---|---|
| 100 | 1.52 | 0 | 0 |
| 1.20 | 2 | 1 | |
| 2 | 2 | ||
| 2 | 4 | ||
| 150 | 1.52 | 0 | 0 |
| 1.40 | 2 | 1 | |
| 2 | 2 | ||
| 2 | 4 | ||
| 200 | 1.52 | 0 | 0 |
| 1.60 | 2 | 1 | |
| 2 | 2 | ||
| 2 | 4 |
| Cement Content (%) | Dry Density (g/cm3) | Confining Pressure σ3 (kPa) | a | b | R2 | Edmax (MPa) |
|---|---|---|---|---|---|---|
| 0 | 1.52 | 100 | 0.0125 | 0.0415 | 0.9050 | 55.669 |
| 150 | 0.0101 | 0.0365 | 0.9526 | 64.016 | ||
| 200 | 0.0090 | 0.0298 | 0.9432 | 75.279 | ||
| 1 | 1.2 | 100 | 0.0280 | 0.0487 | 0.9726 | 42.299 |
| 150 | 0.0182 | 0.0427 | 0.9694 | 53.262 | ||
| 200 | 0.0126 | 0.0369 | 0.9785 | 69.557 | ||
| 1.4 | 100 | 0.0241 | 0.0426 | 0.8776 | 52.783 | |
| 150 | 0.0164 | 0.0337 | 0.9598 | 62.999 | ||
| 200 | 0.0166 | 0.0255 | 0.8867 | 78.051 | ||
| 1.6 | 100 | 0.0133 | 0.0312 | 0.9727 | 66.175 | |
| 150 | 0.0098 | 0.0272 | 0.9745 | 83.155 | ||
| 200 | 0.0062 | 0.0248 | 0.9892 | 103.344 | ||
| 2 | 1.2 | 100 | 0.0338 | 0.0832 | 0.9173 | 56.201 |
| 150 | 0.0205 | 0.0759 | 0.9441 | 65.800 | ||
| 200 | 0.0148 | 0.0634 | 0.9534 | 77.306 | ||
| 1.4 | 100 | 0.0169 | 0.0874 | 0.9669 | 61.580 | |
| 150 | 0.0147 | 0.0773 | 0.9735 | 70.628 | ||
| 200 | 0.0103 | 0.0576 | 0.9615 | 84.758 | ||
| 1.6 | 100 | 0.0119 | 0.0379 | 0.9763 | 79.980 | |
| 150 | 0.0097 | 0.0334 | 0.9649 | 97.794 | ||
| 200 | 0.0087 | 0.0277 | 0.9483 | 113.156 | ||
| 4 | 1.2 | 100 | 0.0203 | 0.0637 | 0.9656 | 67.642 |
| 150 | 0.0149 | 0.0498 | 0.9671 | 80.724 | ||
| 200 | 0.0086 | 0.0489 | 0.9530 | 90.493 | ||
| 1.4 | 100 | 0.0150 | 0.0382 | 0.9249 | 86.422 | |
| 150 | 0.0102 | 0.0324 | 0.9272 | 96.584 | ||
| 200 | 0.0083 | 0.0292 | 0.9463 | 106.773 | ||
| 1.6 | 100 | 0.0068 | 0.02685 | 0.9815 | 102.750 | |
| 150 | 0.0070 | 0.02254 | 0.9657 | 118.861 | ||
| 200 | 0.0045 | 0.02171 | 0.9865 | 140.775 |
| Cement Content (%) | Dry Density (g/cm3) | Average Particle Size (μm) | Proportion of Macropores (%) | Average Edmax (MPa) |
|---|---|---|---|---|
| 1 | 1.2 | 458.4 | 31.67 | 55.039 |
| 1.4 | 490.88 | 29.55 | 64.611 | |
| 1.6 | 582.00 | 27.45 | 84.224 | |
| 2 | 1.2 | 591.67 | 29.38 | 66.436 |
| 1.4 | 601.97 | 25.5 | 72.322 | |
| 1.6 | 612.92 | 23.9 | 96.977 | |
| 4 | 1.2 | 628.32 | 21.43 | 79.620 |
| 1.4 | 633.87 | 18.32 | 96.593 | |
| 1.6 | 650.803 | 16.17 | 120.795 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, Y.; Sun, M.; Hua, X.; Zhang, Y.; Yuan, Y. Study on the Dynamic Deformation Characteristics of Artificial Structural Loess. Buildings 2025, 15, 1198. https://doi.org/10.3390/buildings15071198
Xi Y, Sun M, Hua X, Zhang Y, Yuan Y. Study on the Dynamic Deformation Characteristics of Artificial Structural Loess. Buildings. 2025; 15(7):1198. https://doi.org/10.3390/buildings15071198
Chicago/Turabian StyleXi, Yu, Mingming Sun, Xueqing Hua, Yao Zhang, and Ye Yuan. 2025. "Study on the Dynamic Deformation Characteristics of Artificial Structural Loess" Buildings 15, no. 7: 1198. https://doi.org/10.3390/buildings15071198
APA StyleXi, Y., Sun, M., Hua, X., Zhang, Y., & Yuan, Y. (2025). Study on the Dynamic Deformation Characteristics of Artificial Structural Loess. Buildings, 15(7), 1198. https://doi.org/10.3390/buildings15071198





