From 2D to 3D Urban Analysis: An Adaptive Urban Zoning Framework That Takes Building Height into Account
Abstract
1. Introduction
2. Materials and Methods
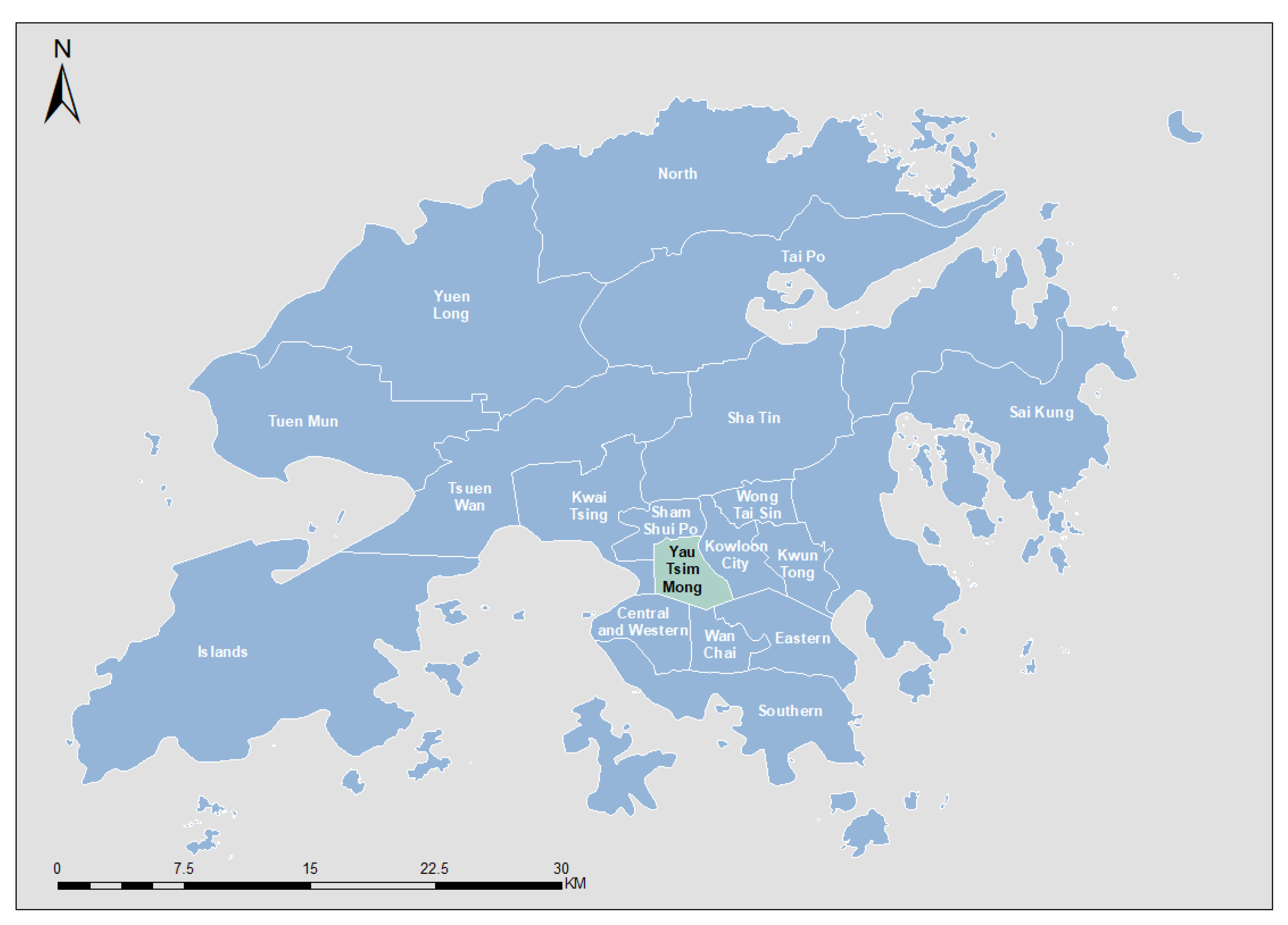
2.1. Study Area
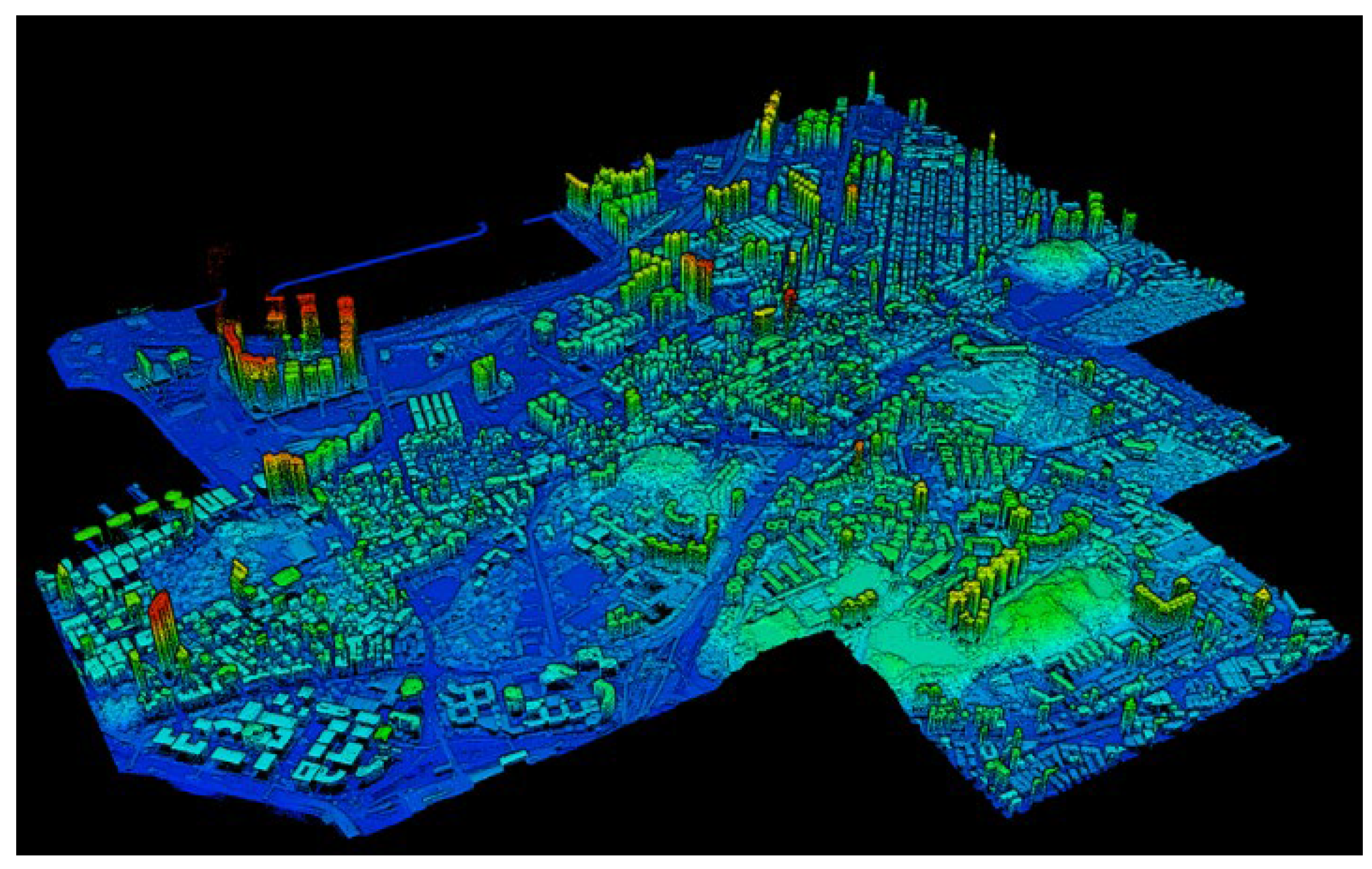
2.2. Data Preprocessing
2.3. DBSCAN Algorithm
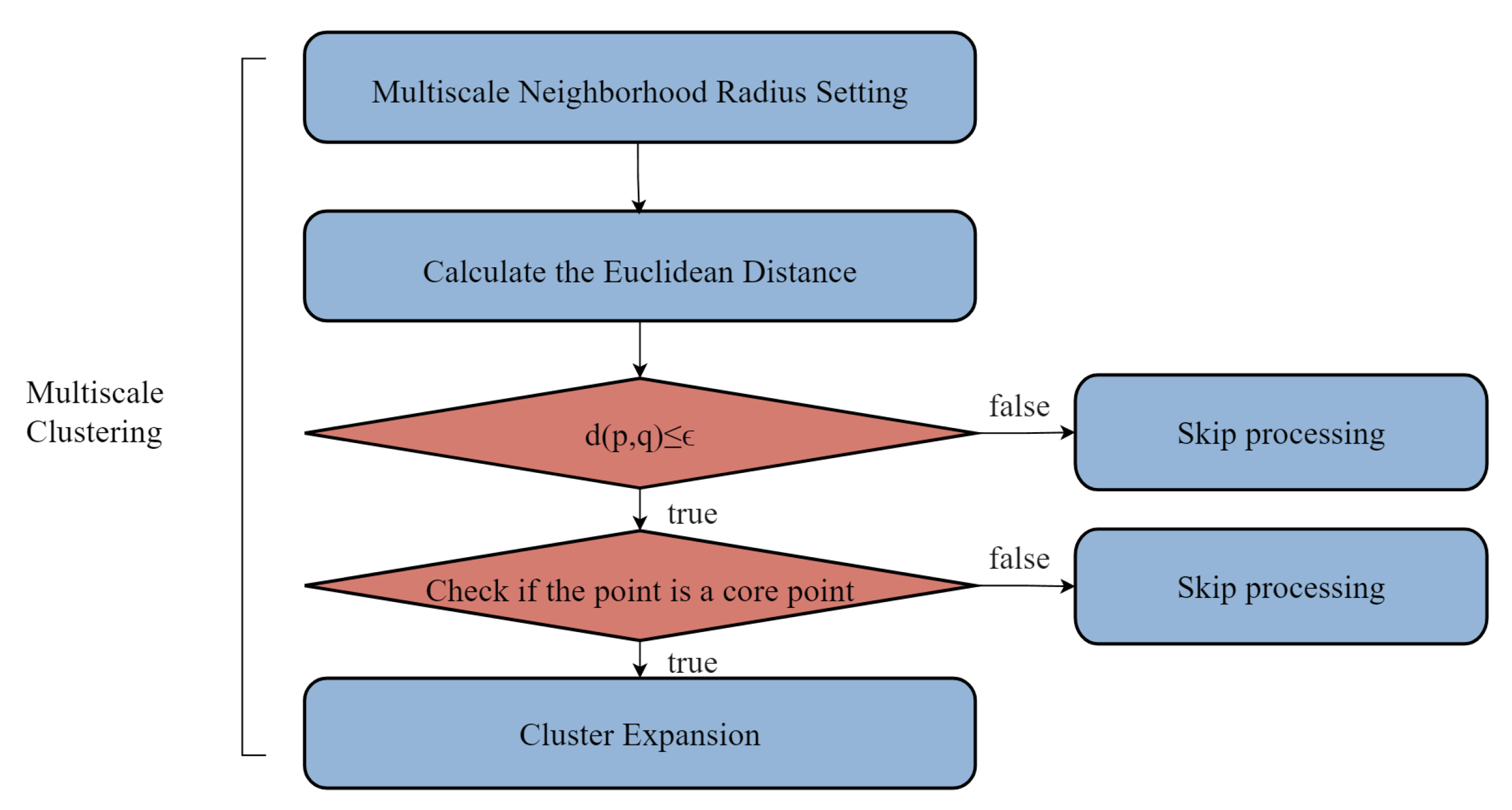
2.4. Three-Dimensional Multiscale Adaptive Clustering Framework
- Multiscale delineation:
- Dynamic parameter adaptation mechanism:
- Multiscale clustering:
2.4.1. Multiscale Partitioning
- Macro scale
- Meso scale
- Micro scale
2.4.2. Dynamic Parameter Adjustment
2.4.3. Multiscale Spatial Clustering
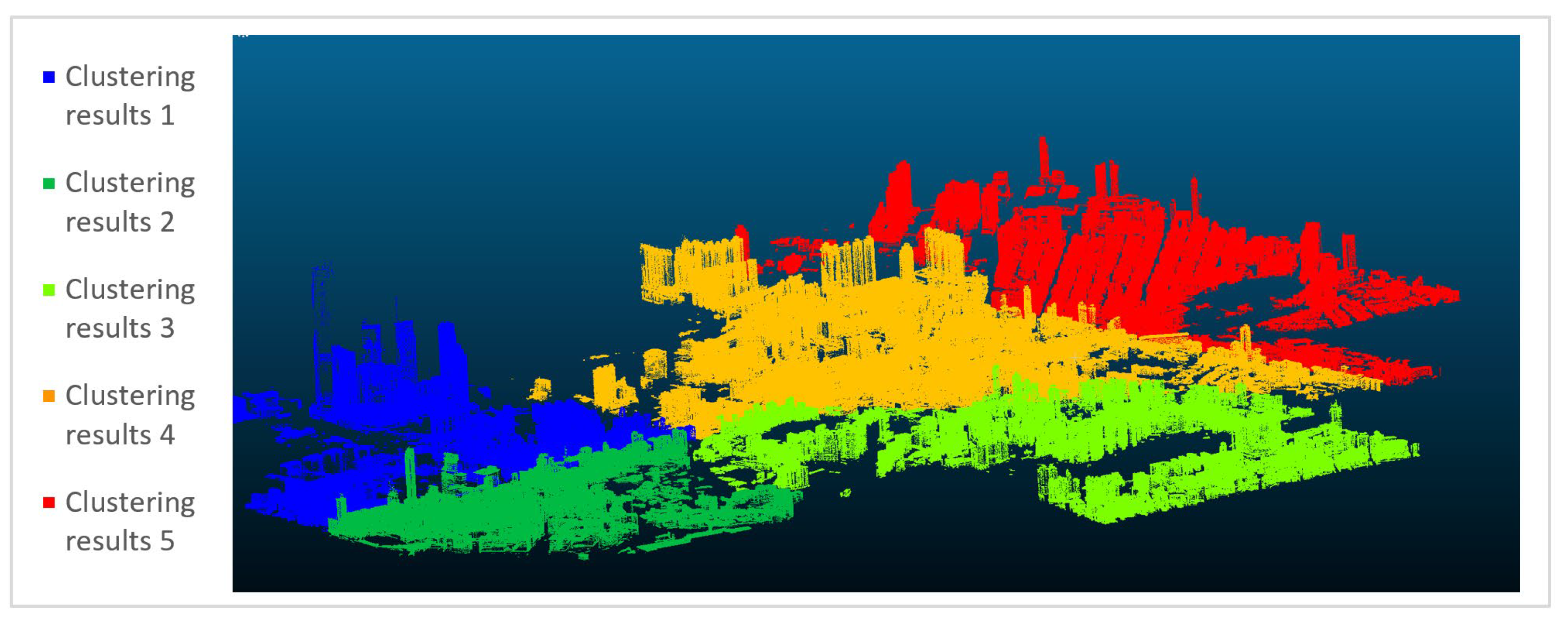
3. Results
4. Discussion
4.1. Research Results and Significance
4.2. Comparison with Existing Research
4.3. Future Research Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pelorosso, R. Modeling and urban planning: A systematic review of performance-based approaches. Sustain. Cities Soc. 2020, 52, 101867. [Google Scholar] [CrossRef]
- Anders, K.; Winiwarter, L.; Mara, H.; Lindenbergh, R.C.; Vos, S.E.; Höfle, B. Fully automatic spatiotemporal segmentation of 3D LiDAR time series for the extraction of natural surface changes. ISPRS J. Photogramm. Remote Sens. 2021, 173, 297–308. [Google Scholar] [CrossRef]
- Julin, A.; Jaalama, K.; Virtanen, J.; Pouke, M.; Ylipulli, J.; Vaaja, M.T.; Hyyppä, J.; Hyyppä, H. Characterizing 3D City Modeling Projects: Towards a Harmonized Interoperable System. ISPRS Int. J. Geo-Inf. 2018, 7, 55. [Google Scholar] [CrossRef]
- Rao, Y.; Zhou, J.; Zhou, M.; He, Q.; Wu, J. Comparisons of three-dimensional urban forms in different urban expansion types: 58 sample cities in China. Growth Change 2020, 51, 1766–1783. [Google Scholar] [CrossRef]
- Pepe, M.; Fregonese, L.; Crocetto, N. Use of SfM-MVS approach to nadir and oblique images generated throught aerial cameras to build 2.5D map and 3D models in urban areas. Geocarto Int. 2019, 37, 120–141. [Google Scholar] [CrossRef]
- Vartholomaios, A. A machine learning approach to modelling solar irradiation of urban and terrain 3D models. Comput. Environ. Urban Syst. 2019, 78, 101387. [Google Scholar] [CrossRef]
- Palliwal, A.; Song, S.; Tan, H.T.; Biljecki, F. 3D city models for urban farming site identification in buildings. arXiv 2020, arXiv:2007.14203. [Google Scholar] [CrossRef]
- Zuo, Z.; Xinhai, L.; Xiang, L.; Min, Z.; Gui, J. 3-D Visualization and Spatial Morphology Analysis of Urban Benchmark Land Prices for Residential Use: A Case Study of Wuhan, China. J. Tsinghua Univ. 2018, 58, 941–952. [Google Scholar] [CrossRef]
- Hu, D.; Minner, J.S. UAVs and 3D City Modeling to Aid Urban Planning and Historic Preservation: A Systematic Review. Remote Sens. 2023, 15, 5507. [Google Scholar] [CrossRef]
- Lu, H.; Li, F.; Yang, G.; Sun, W. Multi-scale impacts of 2D/3D urban building pattern in intra-annual thermal environment of Hangzhou, China. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102558. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, J.; Liu, H.; Lu, S. A systematic review of evidence of additional health benefits from forest exposure. Landsc. Urban Plan. 2021, 212, 104123. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, S.; Wang, H.; Ding, Y. Spatial Coupling Analysis of Urban Waterlogging Depth and Value Based on Land Use: Case Study of Beijing. Water 2025, 17, 529. [Google Scholar] [CrossRef]
- Xia, X.; Jian, L.; Ouyang, K.; Liu, X.; Liang, X.; Zhang, Y.; Li, B. Assessment of Ventilation Potential and Construction of Wind Corridors in Chengdu City Based on Multi-Source Data and Multi-Model Analysis. Land 2024, 13, 1671. [Google Scholar] [CrossRef]
- Sun, B.; Li, Y.; Zhang, Y.; Guo, T. Multi-source heterogeneous data fusion prediction technique for the utility tunnel fire detection. Reliab. Eng. Syst. Saf. 2024, 248, 110154. [Google Scholar] [CrossRef]
- Bi, Q.; Azman, A.S.; Satter, S.M.; Khan, A.I.; Ahmed, D.; Riaj, A.A.; Gurley, E.S.; Lessler, J. Micro-Scale Spatial Clustering of Cholera Risk Factors in Urban Bangladesh. PLoS Negl. Trop. Dis. 2016, 10, e0004400. [Google Scholar] [CrossRef]
- Franch-Pardo, I.; Napoletano, B.M.; Rosete-Vergés, F.A.; Billa, L. Spatial analysis and GIS in the study of COVID-19. A review. Sci. Total Environ. 2020, 739, 140033. [Google Scholar] [CrossRef]
- Wang, H.; Song, C.; Wang, J.; Gao, P. A raster-based spatial clustering method with robustness to spatial outliers. Sci. Rep. 2024, 14, 4103. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, Y.; Guan, Q.; Hong, Y.; Wang, R.; Wang, R.; Liang, X. Spatiotemporal distribution of human trafficking in China and predicting the locations of missing persons. Comput. Environ. Urban Syst. 2021, 85, 101567. [Google Scholar] [CrossRef]
- Ng, R.T.; Han, J. CLARANS: A Method for Clustering Objects for Spatial Data Mining. IEEE Trans. Knowl. Data Eng. 2002, 14, 1003–1016. [Google Scholar] [CrossRef]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Jia, H. K-Means Clustering Algorithms: A Comprehensive Review, Variants Analysis and Advances in the Era of Big Data. Inf. Sci. 2022, 622, 178–210. [Google Scholar] [CrossRef]
- Xia, Z.; Chen, Y.; Xu, C. Multiview PCA: A Methodology of Feature Extraction and Dimension Reduction for High-Order Data. IEEE Trans. Cybern. 2021, 52, 11068–11080. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, J.; Tao, D. Local Deep-Feature Alignment for Unsupervised Dimension Reduction. IEEE Trans. Image Process. 2018, 27, 2420–2432. [Google Scholar] [CrossRef]
- Du, H.; Zhao, S.; Zhang, D.; Wu, J. Novel clustering-based approach for Local Outlier Detection. In Proceedings of the 2016 IEEE Conference on Computer Communications Workshops, San Francisco, CA, USA, 10–14 April 2016; pp. 802–811. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Simoudis, E., Han, J.W., Fayyad, U.M., Eds.; AAAI Press: Portland, OR, USA, 1996; pp. 226–231. [Google Scholar]
- Gao, S.; Cheng, M.; Zhao, K.; Zhang, X.; Yang, M.; Torr, P.H. Res2Net: A New Multi-Scale Backbone Architecture. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 652–662. [Google Scholar] [CrossRef]
- Hausler, S.; Garg, S.; Xu, M.; Milford, M.; Fischer, T. Patch-NetVLAD: Multi-Scale Fusion of Locally-Global Descriptors for Place Recognition. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14136–14147. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, S. WOA-DBSCAN: Application of Whale Optimization Algorithm in DBSCAN Parameter Adaption. IEEE Access 2023, 11, 91861–91878. [Google Scholar] [CrossRef]
- Xiao, T.; Wan, Y.; Jin, R.; Qin, J.; Wu, T. Integrating Gaussian Mixture Dual-Clustering and DBSCAN for Exploring Heterogeneous Characteristics of Urban Spatial Agglomeration Areas. Remote Sens. 2022, 14, 5689. [Google Scholar] [CrossRef]
- Zhang, W.; Dong, X.; Cheng, J.; Wang, S. Advanced Point Cloud Techniques for Improved 3D Object Detection: A Study on DBSCAN, Attention, and Downsampling. World Electr. Veh. J. 2024, 15, 527. [Google Scholar] [CrossRef]
- Shao, J.; Wang, X.; Yang, Q.; Plant, C.; Böhm, C. Synchronization-based scalable subspace clustering of high-dimensional data. Knowl. Inf. Syst. 2016, 52, 83–111. [Google Scholar] [CrossRef]
- Zhang, Z.; Dou, Y.; Liu, X.; Gong, Z. Multi-Hierarchical Spatial Clustering for Characteristic Towns in China: An Orange-Based Framework to Integrate GIS and Geodetector. J. Geogr. Sci. 2023, 33, 618–638. [Google Scholar] [CrossRef]
- Lin, A.; Huang, B.; Wu, H.; Luo, W. An MIU-based deep embedded clustering model for urban functional zoning from remote sensing images and VGI data. Int. J. Appl. Earth Obs. Geoinf. 2024, 128, 103689. [Google Scholar] [CrossRef]
- Zhu, J.; Lang, Z.; Yang, J.; Wang, M.; Zheng, J.; Na, J. Integrating Spatial Heterogeneity to Identify the Urban Fringe Area Based on NPP/VIIRS Nighttime Light Data and Dual Spatial Clustering. Remote Sens. 2022, 14, 6126. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, H.; Pang, L.; Fang, L.; Dou, W. DBSCAN-based point cloud extraction for Tomographic synthetic aperture radar (TomoSAR) three-dimensional (3D) building reconstruction. Int. J. Remote Sens. 2020, 42, 2327–2349. [Google Scholar] [CrossRef]
- Liu, H.; Tong, Y.; Han, J.; Zhang, P.; Lu, X.; Xiong, H. Incorporating Multi-Source Urban Data for Personalized and Context-Aware Multi-Modal Transportation Recommendation. IEEE Trans. Knowl. Data Eng. 2022, 34, 723–735. [Google Scholar] [CrossRef]
- Wang, D.; Wang, X.; Liu, L.; Wang, D.; Zeng, Z. Urban Signatures in the Spatial Clustering of Precipitation Extremes over Mainland China. J. Hydrometeorol. 2021, 22, 639–656. [Google Scholar] [CrossRef]
- Fang, X.; Xu, Z.; Ji, H.; Wang, B.; Huang, Z. A Grid-Based Density Peaks Clustering Algorithm. IEEE Trans. Ind. Inform. 2023, 19, 5476–5484. [Google Scholar] [CrossRef]
- Yangtianzheng, Z.; Ying, G. Spatial Patterns and Trends of Inter-City Population Mobility in China—Based on Baidu Migration Big Data. Cities 2024, 151, 105124. [Google Scholar] [CrossRef]
- Chowdhury, S.; Helian, N.; de Amorim, R.C. Feature weighting in DBSCAN using reverse nearest neighbours. Pattern Recognit. 2023, 137, 109314. [Google Scholar] [CrossRef]
- He, Y.; Tan, H.; Luo, W.; Mao, H.; Ma, D.; Feng, S.; Fan, J. MR-DBSCAN: An Efficient Parallel Density-Based Clustering Algorithm Using MapReduce. In Proceedings of the 2011 IEEE 17th International Conference on Parallel and Distributed Systems, Tainan, Taiwan, 7–9 December 2011; pp. 473–480. [Google Scholar] [CrossRef]
- Lulli, A.; DellAmico, M.; Michiardi, P.; Ricci, L. NG-DBSCAN: Scalable Density-Based Clustering for Arbitrary Data. Proc. VLDB Endow. 2016, 10, 157–168. [Google Scholar] [CrossRef]
- Gulen, M.F.; Samson, N.; Keller, A.; Schwabenland, M.; Liu, C.; Glück, S.; Thacker, V.V.; Favre, L.; Mangeat, B.; Kroese, L.J.; et al. cGAS–STING Drives Ageing-Related Inflammation and Neurodegeneration. Nature 2023, 620, 374–380. [Google Scholar] [CrossRef]
- Miranda, F.; Ortner, T.; Moreira, G.; Hosseini, M.; Vuckovic, M.; Biljecki, F.; Silva, C.T.; Lage, M.; Ferreira, N. The State of the Art in Visual Analytics for 3D Urban Data. Comput. Graph. Forum 2024, 43, e15112. [Google Scholar] [CrossRef]
- Zheng, Y.; Lin, Y.; Zhao, L.; Wu, T.; Jin, D.; Li, Y. Spatial Planning of Urban Communities via Deep Reinforcement Learning. Nat. Comput. Sci. 2023, 3, 748–762. [Google Scholar] [CrossRef]
- Sander, J.; Ester, M.; Kriegel, H.; Xu, X. Density-Based Clustering in Spatial Databases: The Algorithm GDBSCAN and Its Applications. Data Min. Knowl. Discov. 1998, 2, 169–194. [Google Scholar]
- Liu, Z.; Wang, A.; Weber, K.; Chan, E.H.; Shi, W. Categorisation of Cultural Tourism Attractions by Tourist Preference Using Location-Based Social Network Data: The Case of Central, Hong Kong. Tour. Manag. 2022, 90, 104488. [Google Scholar] [CrossRef]
- Karunarathne, A.Y.; Lee, G. The Geographies of the Dynamic Evolution of Social Networks for the Flood Disaster Response and Recovery. Appl. Geogr. 2020, 125, 102274. [Google Scholar] [CrossRef]
- Tai, A.C.; Wong, D.W.; Lee, H.F.; Qiang, W. Tourism’s Long- and Short-Term Influence on Global Cities’ Economic Growth: The Case of Hong Kong. PLoS ONE 2022, 17, e0275152. [Google Scholar] [CrossRef]
- Liu, S.; Kwok, Y.T.; Ren, C. Investigating the Impact of Urban Microclimate on Building Thermal Performance: A Case Study of Dense Urban Areas in Hong Kong. Sustain. Cities Soc. 2023, 94, 104509. [Google Scholar] [CrossRef]
- Ye, X.; Wang, L.; Xiong, C.; Wang, X.; Wen, G.; Yu, D.; Guo, Z.; Wang, W.; Lv, Z.; Wu, H.; et al. Shallow 3D Structure Investigation of Some Cities in the Guangdong–Hong Kong–Macao Greater Bay Area. Seismol. Res. Lett. 2024, 95, 2000–2012. [Google Scholar] [CrossRef]
- Fan, D.; Zeng, X.; Wang, H.; Wang, M.; Li, Q.; Jiang, H.; Li, S. The Role of Ecological Space Structure Optimization in Synergetic Sustainable Development: Evidence from the Guangdong–Hong Kong–Macao Greater Bay Area. Forests 2024, 15, 2225. [Google Scholar] [CrossRef]
- Shen, T.; Zhou, W.; Yuan, S.; Huo, L. Spatiotemporal Characterization of the Three-Dimensional Morphology of Urban Buildings Based on Moran’s I. Sustainability 2024, 16, 6540. [Google Scholar] [CrossRef]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.; Xu, X. DBSCAN Revisited, Revisited. ACM Trans. Database Syst. 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Biljecki, F.; Ledoux, H.; Stoter, J. An Improved LOD Specification for 3D Building Models. Comput. Environ. Urban Syst. 2016, 59, 25–37. [Google Scholar] [CrossRef]
- Huang, X.; Cao, R.; Cao, Y. A Density-Based Clustering Method for the Segmentation of Individual Buildings from Filtered Airborne LiDAR Point Clouds. J. Indian Soc. Remote Sens. 2018, 47, 907–921. [Google Scholar] [CrossRef]
- Liu, M.; Yan, J.; Dai, T. A Multi-Scale Approach Mapping Spatial Equality of Urban Public Facilities for Urban Design. Heliyon 2023, 9, e18281. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Zhang, H.; Wong, C.U.; Chen, X.; Li, F.; Wei, X.; Shen, J. Research on the Spatial Distribution Characteristics and Influencing Factors of Educational Facilities Based on POI Data: A Case Study of the Guangdong-Hong Kong-Macao Greater Bay Area. ISPRS Int. J. Geo-Inf. 2024, 13, 225. [Google Scholar] [CrossRef]
- Tang, B.; Chen, Z.; Zhang, Y.; Sun, H. A Study on the Evolution of Economic Patterns and Urban Network System in Guangdong-Hong Kong-Macao Greater Bay Area. Front. Public Health 2022, 10, 973843. [Google Scholar] [CrossRef]
- Fu, J.; Jing, C.; Du, M.; Fu, Y.L.; Dai, P. Study on Adaptive Parameter Determination of Cluster Analysis in Urban Management Cases. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 1143–1150. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, J.L.; Yang, H.; Han, Y.J.; Li, F. Intersection and Passageway Designs of Urban Agglomeration Connection Road. Appl. Mech. Mater. 2013, 361–363, 2330–2338. [Google Scholar] [CrossRef]
- Li, N.; Quan, S. Identifying Urban Form Typologies in Seoul Using a New Gaussian Mixture Model-Based Clustering Framework. Environ. Plan. B Urban Anal. City Sci. 2023, 50, 2342–2358. [Google Scholar] [CrossRef]
- Kartal, S.; Inceoğlu, M. Evaluating Street Character Using the 3D Fractal Analysis Method: Lefkoşa. J. Des. Studio 2023, 5, 207–222. [Google Scholar] [CrossRef]
- Afrianto, F. Fractal Dimensions Analysis of Urban Agglomeration at Road Intersections in Metropolitan Malang Raya. IOP Conf. Ser. Earth Environ. Sci. 2023, 1186, 012010. [Google Scholar] [CrossRef]
- Esch, T.; Zeidler, J.; Palacios-Lopez, D.; Marconcini, M.; Roth, A.; Mönks, M.; Leutner, B.F.; Brzoska, E.; Metz-Marconcini, A.; Bachofer, F.; et al. Towards a Large-Scale 3D Modeling of the Built Environment: Joint Analysis of TanDEM-X, Sentinel-2 and Open Street Map Data. Remote Sens. 2020, 12, 2391. [Google Scholar] [CrossRef]
- Srinivasan, K.; Selvakumar, K. Comparative Study of Pre-Engineered Building and Space Truss Building with Different Span. Indian J. Eng. Mater. Sci. 2022, 29, 428–431. [Google Scholar] [CrossRef]
- Zhang, L.; Wan, W.; Lv, B.; Li, Q.; Sun, K.; Wan, Q. Identification of Urban Traffic Accident Hotspots Using Getis-Ord Gi and DBSCAN Algorithmsimes. In Proceedings of the 2024 3rd International Conference on Cloud Computing, Big Data Application and Software Engineering (CBASE), Hangzhou, China, 11–13 October 2024; pp. 93–99. [Google Scholar] [CrossRef]
- Caudillo-Cos, C.; Montejano-Escamilla, J.A.; Tapia-McClung, R.; Ávila-Jiménez, F.G.; Barrera-Alarcón, I. Defining Urban Boundaries Through DBSCAN and Shannon’s Entropy: The Case of the Mexican National Urban System. Cities 2024, 149, 104969. [Google Scholar] [CrossRef]
- Zou, Y.; Wang, Z.; Wang, X.; Lv, T. A Clustering Algorithm Based on Local Relative Density. Electronics 2025, 14, 481. [Google Scholar] [CrossRef]
- Zhang, X.; Lauber, L.; Liu, H.; Shi, J.; Wu, J.; Pan, Y. Research on the Method of Travel Area Clustering of Urban Public Transport Based on Sage-Husa Adaptive Filter and Improved DBSCAN Algorithm. PLoS ONE 2021, 16, e0259472. [Google Scholar] [CrossRef]



| Clustering Phase | ||
|---|---|---|
| Macro | 100 m | 800 m |
| Meso | 40 m | 400 m |
| Micro | 20 m | 200 m |
| Clustering Phase | ||
|---|---|---|
| Macro | 800 m | 55 |
| Meso | 400 m | 82 |
| Micro | 200 m | 101 |
| Model | Silhouette Coefficient | Davies–Bouldin Index | ||||
|---|---|---|---|---|---|---|
| Macro | Meso | Micro | Macro | Meso | Micro | |
| DBSCAN | 0.65 | 0.55 | 0.43 | 0.72 | 0.85 | 0.93 |
| HDBSCAN | 0.52 | 0.47 | 0.44 | 0.89 | 0.95 | 1.02 |
| Our | 0.71 | 0.63 | 0.50 | 0.65 | 0.81 | 0.84 |
| Metric | Clustering Phase | DBSCAN | Our |
|---|---|---|---|
| Times | Macro | 6 h25 min | 8 h 52 min |
| Meso | 7 h14 min | 9 h 03 min | |
| Micro | 8 h55 min | 10 h 35 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, T.; Kong, F.; Yuan, S.; Wang, X.; Sun, D.; Ren, Z. From 2D to 3D Urban Analysis: An Adaptive Urban Zoning Framework That Takes Building Height into Account. Buildings 2025, 15, 1182. https://doi.org/10.3390/buildings15071182
Shen T, Kong F, Yuan S, Wang X, Sun D, Ren Z. From 2D to 3D Urban Analysis: An Adaptive Urban Zoning Framework That Takes Building Height into Account. Buildings. 2025; 15(7):1182. https://doi.org/10.3390/buildings15071182
Chicago/Turabian StyleShen, Tao, Fulu Kong, Shuai Yuan, Xueying Wang, Di Sun, and Zongshuo Ren. 2025. "From 2D to 3D Urban Analysis: An Adaptive Urban Zoning Framework That Takes Building Height into Account" Buildings 15, no. 7: 1182. https://doi.org/10.3390/buildings15071182
APA StyleShen, T., Kong, F., Yuan, S., Wang, X., Sun, D., & Ren, Z. (2025). From 2D to 3D Urban Analysis: An Adaptive Urban Zoning Framework That Takes Building Height into Account. Buildings, 15(7), 1182. https://doi.org/10.3390/buildings15071182





