Study on the Vulnerability of Steel Frames Under Fire Smoke Propagation
Abstract
1. Introduction
2. Model Establishment and Analysis Methods
2.1. Material Model Parameters
2.2. Model Parameters
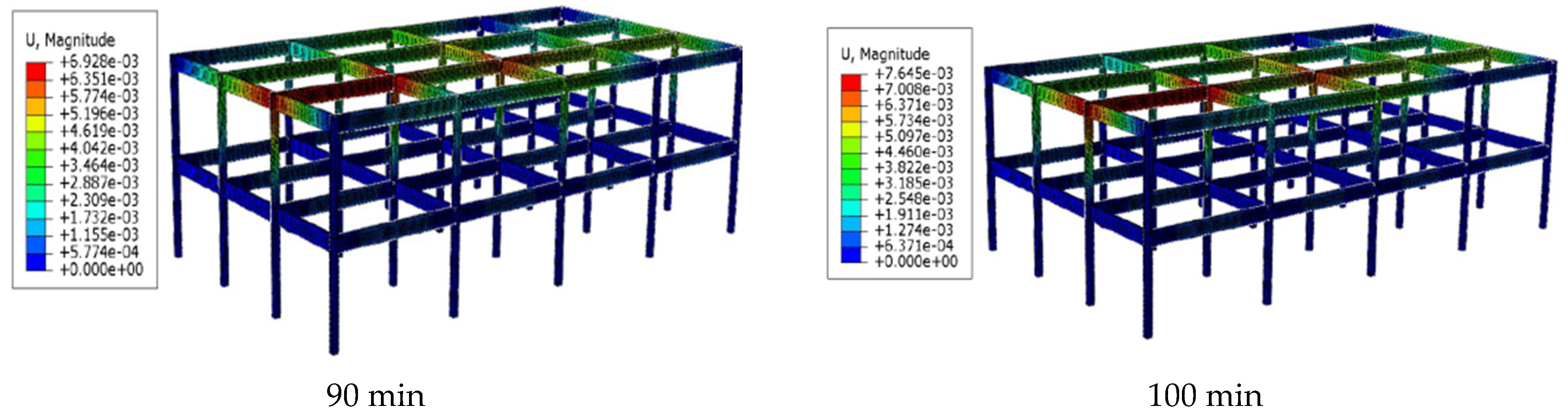
2.3. Finite Element Model Validation
2.4. Damageability Analysis Method
- t: time, min;
- h: cross-sectional height, mm;
- L: calculation span, mm;
- H: initial fire height of the component, mm;
- : the absolute value of the maximum displacement when the laterally bent member reaches the fire resistance limit;
- : the absolute value of the maximum displacement reached by the laterally bent member during a fire;
- : the absolute value of the maximum vertical displacement when vertical load-bearing components reach the fire resistance limit;
- the absolute value of the maximum vertical displacement reached by vertical load-bearing components during a fire;
- d/dt: the maximum deformation rate when the laterally bent member reaches its fire resistance limit;
- d/dt: the maximum deformation rate of a laterally loaded member during a fire.
- d/dt: the maximum vertical displacement deformation rate when the vertical load-bearing component reaches the fire resistance limit;
- d/dt: the maximum vertical displacement deformation rate when the vertical load-bearing component reaches the fire resistance limit;
- displacement correction factor,
- displacement rate correction factor;
- : displacement vulnerability,
- : repair displacement rate vulnerability;
- Ζ: the ultimate vulnerability of the Z steel structure.
3. Analysis Results
3.1. Fire Temperature Rise Without Considering the Spread of Hot Smoke
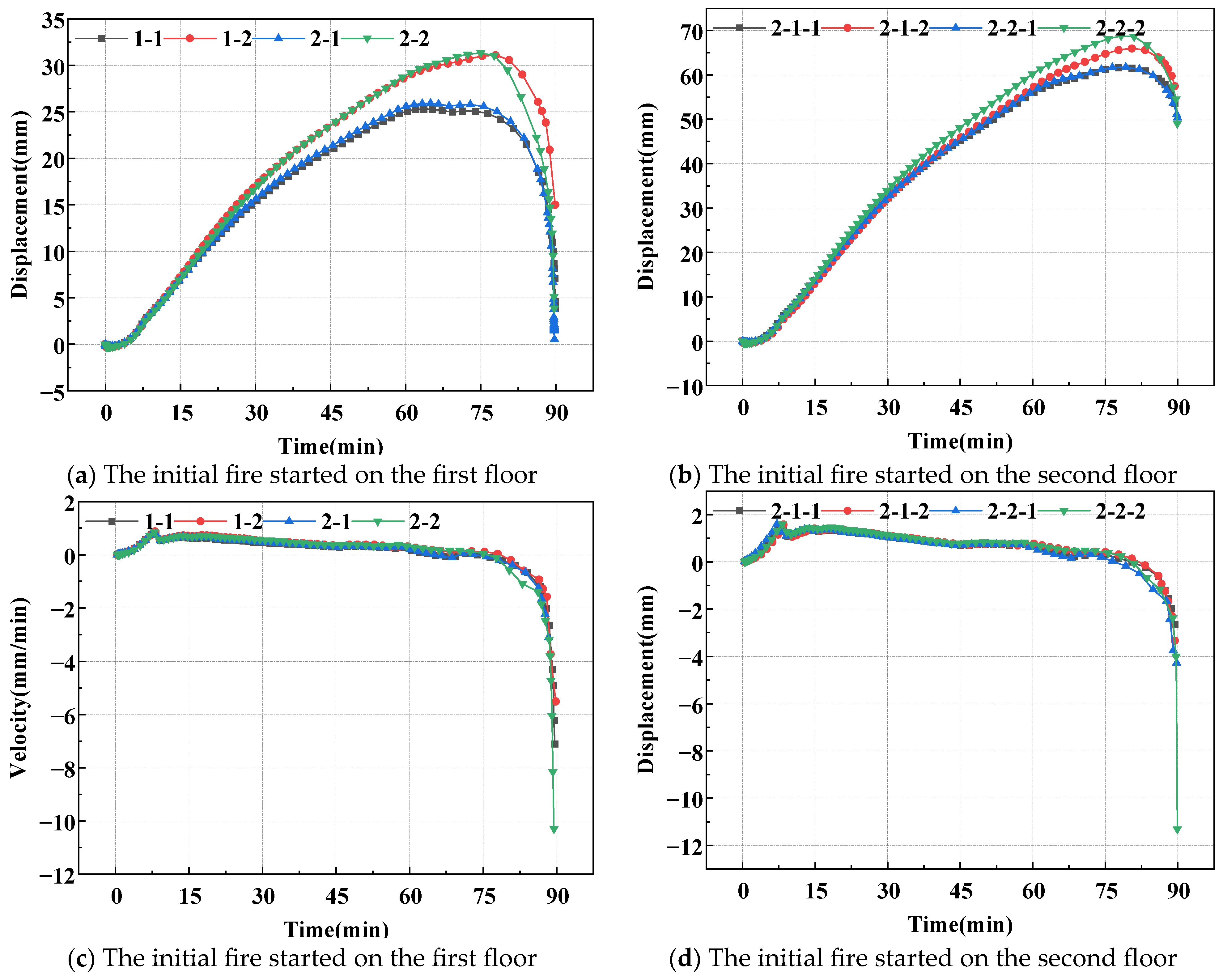
3.1.1. Displacements and Deformation Rates of Bending Components
3.1.2. Displacement and Deformation Rate of Load-Bearing Components
3.2. Fire Temperature Rise Considering the Steel Structure Under Hot Smoke Propagation
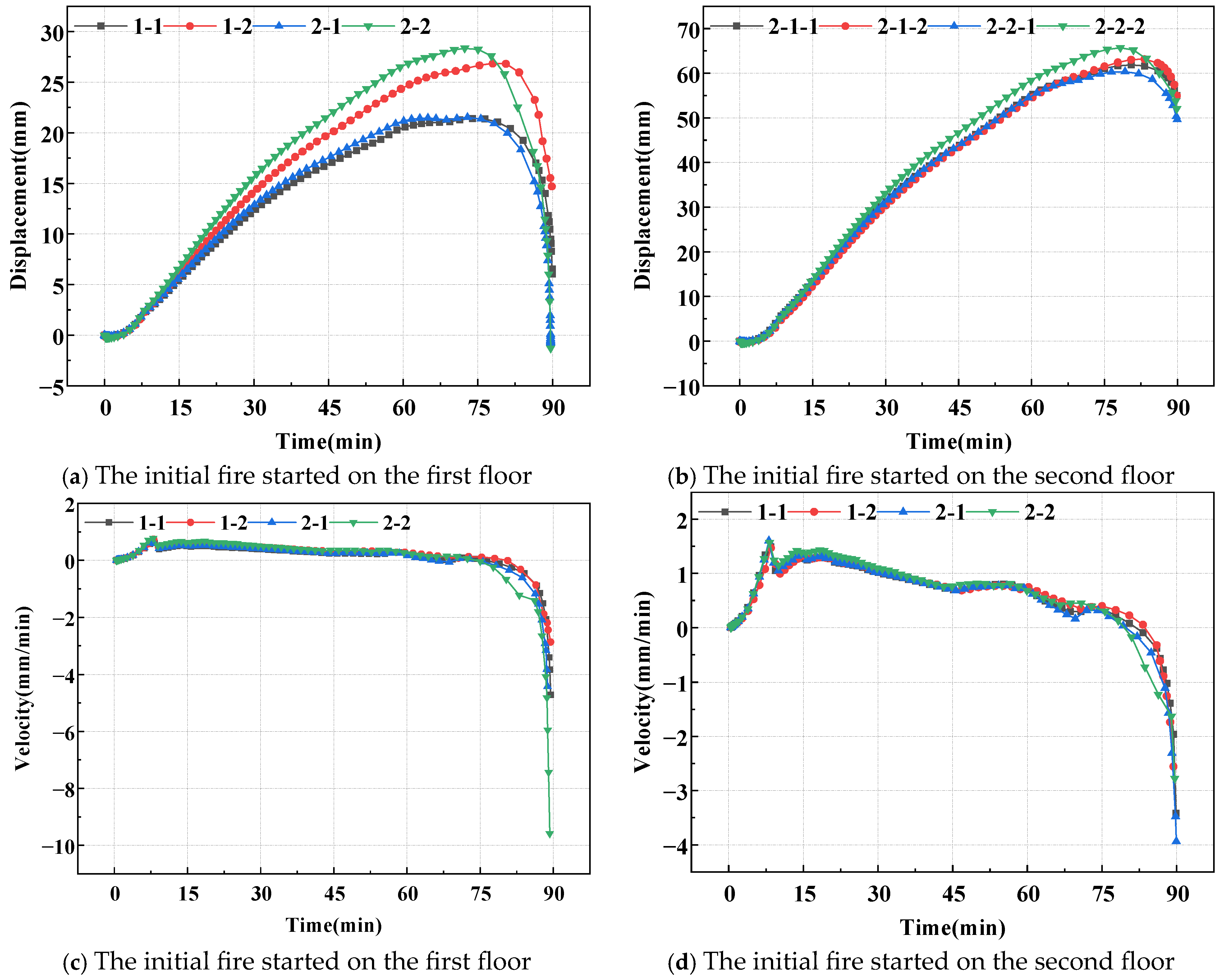
3.2.1. Displacements and Deformation Rates of Bending Components
3.2.2. Displacements and Deformation Rates of Load-Bearing Components
3.3. The Impact of Fireproof Coatings on Steel Structure
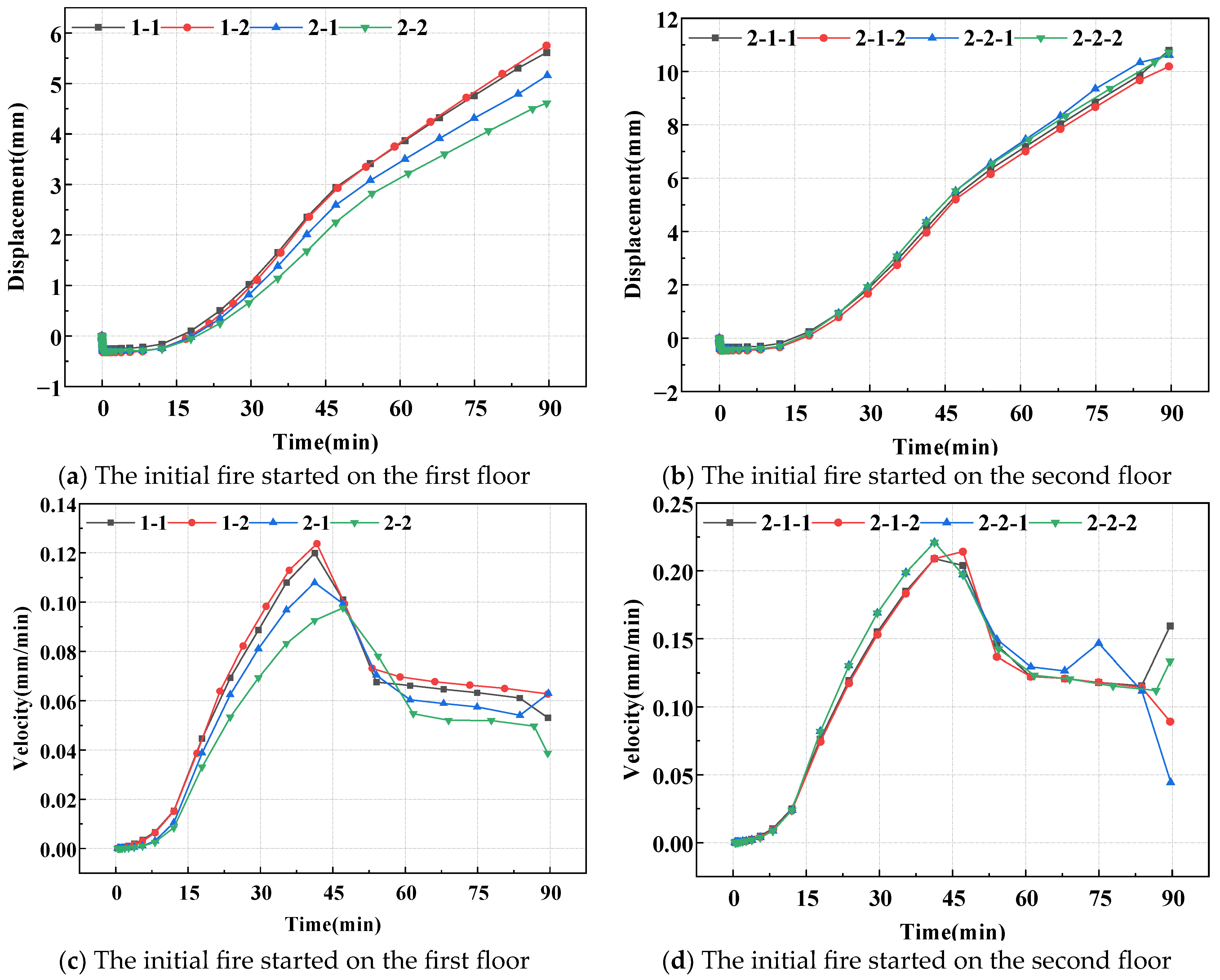
3.3.1. Displacements and Deformation Rates of Bending Components
3.3.2. Displacements and Deformation Rates of Load-Bearing Components
4. Verification of Vulnerability Formula Validity
5. Discussion
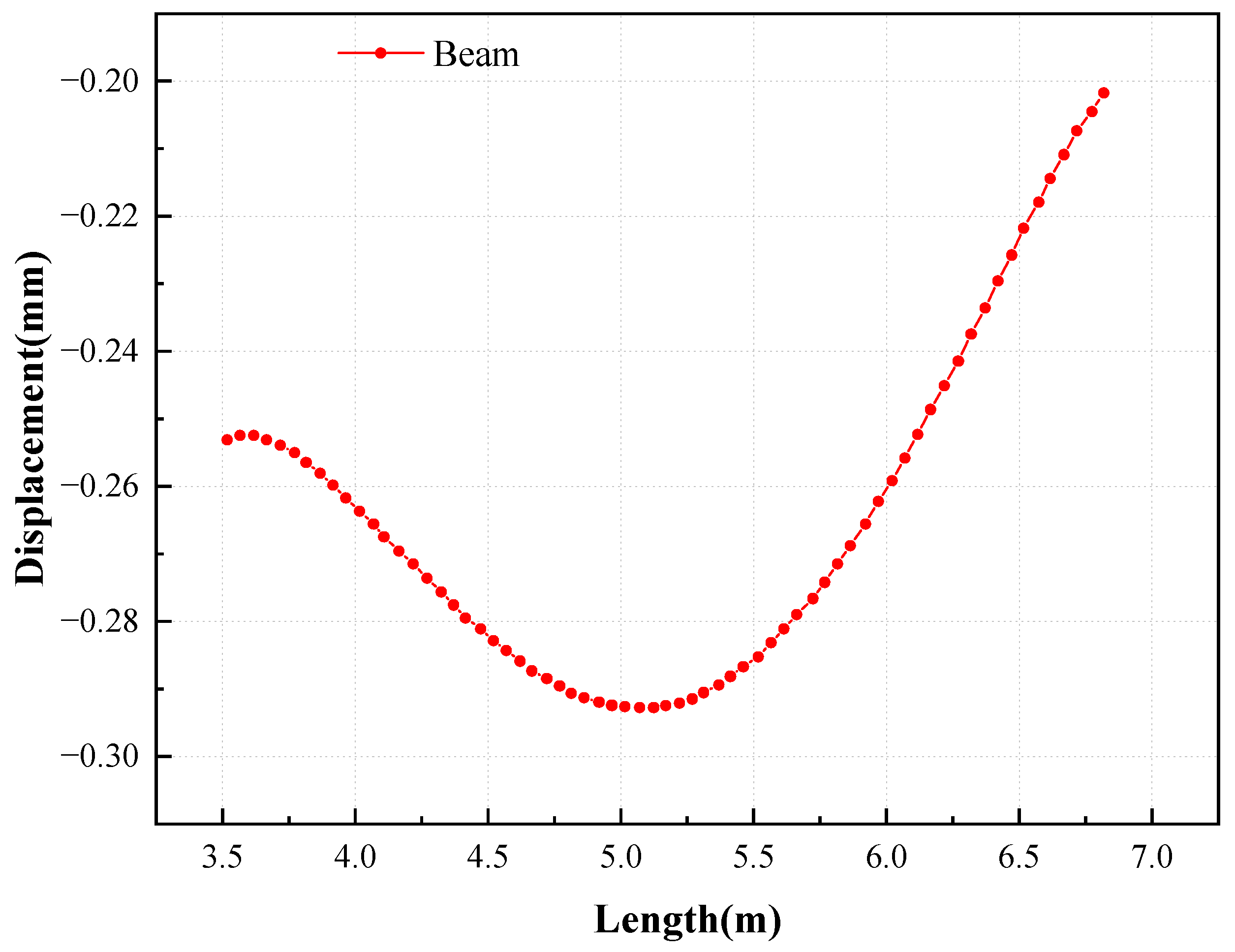
- Material thermodynamic reaction: In a fire, homogenous steel components heat up quickly but unevenly. The temperature differential of the beam web in the next fire compartment is between 180 and 250 °C. Asymmetric heating on both sides of the web results in increased deflection of the freely expanding beam and axial compressive stress of the restricted beam. According to the time-dependent study, beam deflection grows exponentially as the fire exposure time increases;
- Structural reaction in the absence of smoke propagation: Corner chambers reveal significant deformations in beams and columns. The longitudinal beam has a greater deflection than the transverse beam due to its longer span. Due to decreased limitations, the outer column deforms 23.6% more than the inner column. The firing interval has a substantial impact on the span along the short axis. When the deflection exceeds the allowed limit, the secondary beam firmly attached to the fire-damaged longitudinal beam would bend and collapse. Because of the reduced limitations, the center column deformation is less (58% of the corner column);
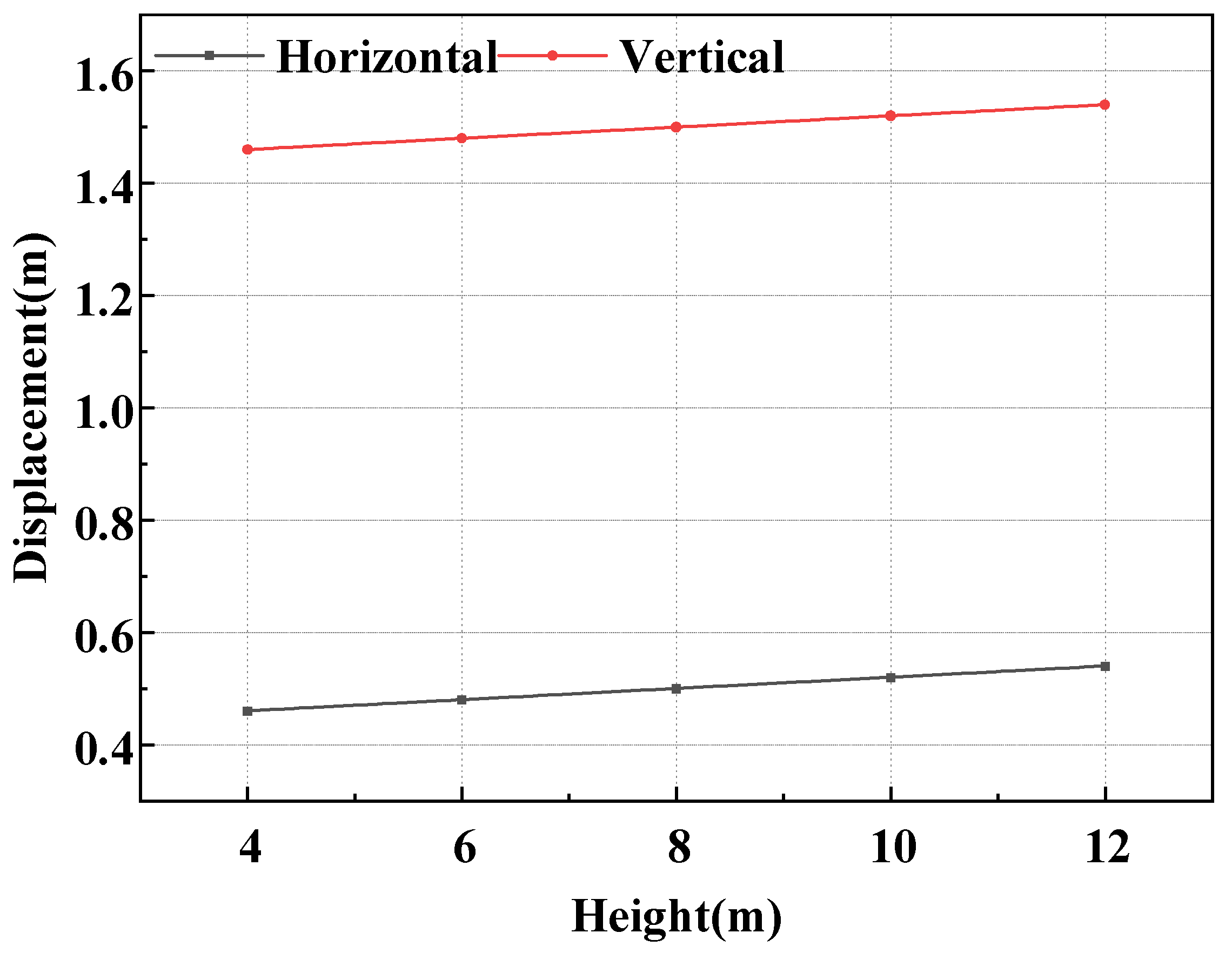
- Thermomechanical effects and smoke propagation: The center fireproof compartment transfers heat and smoke more quickly than the corner compartment, driving the total structure to the steel’s critical softening temperature. Because of the inter-story chimney effect, the buoyancy-driven air flow at the second-story fire source accelerated the smoke upward, resulting in a 96% higher column top displacement than the first-story fire scenario;
- Comparison of fire protection technology: The expanding covering is lightweight and adaptable to complicated geometry, but it requires rigorous environmental control. Fire panels provide more environmental compatibility, but they take up more area and impose structural pressures. Both approaches minimize deformation rate and peak value while increasing fire resistance;
- Smoke toxicity and occupant safety: Modern building fires emit poisonous vapors, including CO2, CO, H2O, SO2, CH4, CnHm, and other chemicals. Synthetic polymers in furniture and décor add to the complexity and toxicity of gasses. The enhanced smoke exhaust design can increase the safety evacuation time by 30 s while reducing casualties.
6. Conclusions
- The displacements of components fail to align with actual conditions when hot smoke propagation is disregarded. The consideration of hot smoke propagation resulted in a 342.3% increase in component displacement and a 561.4% increase in the displacement rate of components compared with scenarios where hot smoke propagation is not accounted for, aligning with real-world conditions;
- The spreads of fire and hot smoke indicate that varying initial fire locations will influence the degree of deformation of the overall structure. The displacement of components in the room with the initial fire as the center increased by 23.1% compared with the components in the corner room, while the displacement in the room on the second floor increased by 115.6% compared with the components on the first floor. Therefore, it is essential to enhance fire prevention measures in the central room;
- The application of fireproof coating markedly diminishes the displacement of components due to the spread of hot smoke, achieving a reduction of 82.8% in displacement for components located in the same position. Consequently, the use of fireproof coating mitigates structural deformation and lowers the risk of progressive collapse;
- The improved vulnerability quantification formula enhances the accuracy of predicting the continuous collapse of the steel frame by 29.1% compared with predictions based solely on the displacement of the component;
- The limitations of experimental conditions indicate that further exploration is required regarding the influence of hot smoke propagation on steel structures in fire scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Azim, I.; Yang, J.; Bhatta, S.; Wang, F.; Liu, Q.-f. Factors influencing the progressive collapse resistance of RC frame structures. J. Build. Eng. 2020, 27, 100986. [Google Scholar] [CrossRef]
- Wang, F.; Yang, J.; Wang, X.; Azim, I. Study on progressive collapse behaviour of steel-framed substructures with sheathed CFS stud infill walls. J. Build. Eng. 2021, 42, 102720. [Google Scholar] [CrossRef]
- Zhang, C.; Shu, J.; Zhang, H.; Ning, Y.; Yu, Y. Estimation of load-carrying capacity of cracked RC beams using 3D digital twin model integrated with point clouds and images. Eng. Struct. 2024, 310, 118126. [Google Scholar] [CrossRef]
- Yuan, X. Study on Smoke Transport and Dispersion Characteristics of Apartment Shaft Fire. Master’s Thesis, Liaoning Technical University, Liaoning, China, 2021. [Google Scholar]
- Sun, G.; Xiao, S.; Wu, J.; Xue, S. Study on mechanical properties of large-span spatial structures under large-space fire: Review and outlook. J. Build. Eng. 2024, 98, 111421. [Google Scholar]
- Chen, W.; Ye, J. The most adverse fire scenario research of steel frame structure fire-resistant design based on structural vulnerability analysis. Structures 2021, 34, 2861–2875. [Google Scholar]
- Zhai, C.; Li, J.; Xing, J.; An, X.; Zhang, W.; Yang, R. A promising strategy for enhancing fire resistance of steel structure: A composite thermoplastic polyurethane sheet adhered to steel plate. Chem. Eng. J. 2024, 488, 150689. [Google Scholar]
- Zhang, J.; Guo, Y.; Shao, W.; Xiao, F.J.C.; Materials, B. Benign design of intumescent fire protection coatings for steel structures containing biomass humic acid as carbon source. Constr. Build. Mater. 2023, 409, 134001. [Google Scholar] [CrossRef]
- Wang, G.; Yang, J. Influences of binder on fire protection and anticorrosion properties of intumescent fire resistive coating for steel structure. Surf. Coat. Technol. 2010, 204, 1186–1192. [Google Scholar] [CrossRef]
- Zhan, W.; Chen, L.; Gu, Z.Z.; Jiang, J.C. Influence of graphene on fire protection of intumescent fire retardant coating for steel structure. Energy Rep. 2020, 6, 693–697. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, R.; Fan, W. Experimental study on smoke diffusion from corridors to large open spaces. Fire Sci. 1995, (S1), 60–66. [Google Scholar]
- Tao, L.; Wu, H.; Wang, J.; Li, B.; Wang, X.; Ning, P. Bayer process red mud for flue gas desulfurization: Influencing factors and mechanism. J. Cent. South Univ. 2019, 26, 467–478. [Google Scholar] [CrossRef]
- Xie, M.; Xu, F.B.; Wang, Z.D.; Yin, L.E.; Wu, X.D.; Xu, M.Q.; Li, X. Investigating fire collapse early warning systems for portal frames. Buildings 2025, 15, 296. [Google Scholar] [CrossRef]
- ISO 834; Fire Resistance Tests—Elements of Building Construction. International Organization for Standardization: London, Britain, 2014.
- Cai, G.; Zheng, X.; Gao, W.; Guo, J. Self-extinction characteristics of fire extinguishing induced by nitrogen injection rescue in an enclosed urban utility tunnel. Case Stud. Therm. Eng. 2024, 59, 104478. [Google Scholar] [CrossRef]
- Wang, J.; Fan, W. Numerical simulation of the fire process in a multi-room building. J. Univ. Sci. Technol. China 1996, 2, 204–209. [Google Scholar]
- John, A.; Podila, K.; Chen, Q.; Rao, Y. Application of high-fidelity modelling approach to predict smoke and fire propagation in a nuclear fire scenario. Therm. Sci. Eng. Prog. 2021, 23, 100903. [Google Scholar] [CrossRef]
- Hou, S.; Zhang, B.; Xing, L.; Chen, T.; Klymenko, O.V. 3D modelling and turbulence analysis of multiple pool fires: Capturing synergistic effects and identifying optimal models. Int. J. Therm. Sci. 2025, 210, 109652. [Google Scholar] [CrossRef]
- Helfenstein, R.P.; Lemmertz, C.K.; Centeno, F.R. The impact of fire source location on hot gas layer temperature in multi-compartment pre-flashover fires: Analysis and semi-empirical model development. Int. J. Therm. Sci. 2025, 208, 109464. [Google Scholar] [CrossRef]
- Wei, X.; Liu, J.; Xu, L. Intelligent prediction method for the collapse time of steel frame structures under fire. J. Constr. Steel Res. 2024, 219, 108798. [Google Scholar]
- Argenti, F.; Landucci, G. Experimental and numerical methodology for the analysis of fireproofing materials. J. Loss Prev. Process Ind. 2014, 28, 60–71. [Google Scholar] [CrossRef]
- Ji, J.; Nie, J.K.; Zhu, H.; Han, Y.; Liu, H.; Wang, X.M. Experimental analysis of intumescence fireproofing coating on base material of substation frames. Case Stud. Therm. Eng. 2024, 64, 105478. [Google Scholar] [CrossRef]
- Ma, X.M.; Pan, J.L.; Cai, J.M.; Zhang, Z.Y.; Han, J.S. A review on cement-based materials used in steel structures as fireproof coating. Constr. Build. Mater. 2022, 315, 125623. [Google Scholar]
- GB 50017-2017; Code for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017.
- Li, W.C.; Ge, B.T.; Li, Z.P.; Xing, G.H.; Jing, Y. Post-fire mechanical properties and constitutive model of Q690 high-strength structural steel. Eng. Fail. Anal. 2024, 160, 108232. [Google Scholar] [CrossRef]
- Li, X.H.; Zhang, S.Y.; Yang, X.C.; Guo, Z.M.; Li, Z.J.; Xu, X.L. Air temperature characteristics of cable-girder pin joint node of suspension bridge under pool fire. Structures 2024, 69, 107354. [Google Scholar]
- EU3; Bijlaard, F. Eurocode 3: Design of steel structures–Present status and further developments. Steel Constr. Des. Res. 2008, 1, 16–23. [Google Scholar]
- GB50009-2012; Code for Load on Building Structures. China Architecture & Building Press: Beijing, China, 2012.
- Wang, H.; Yang, B.; Zhou, X.H.; Kang, S.B. Numerical analyses on steel beams with fin-plate connections subjected to impact loads. J. Constr. Steel Res. 2016, 124, 101–112. [Google Scholar]
- Sedaghatkish, A.; Pastore, C.; Doumenc, F.; Jeannin, P.Y.; Luetscher, M. Thermal modeling of caves ventilated by chimney effect. Int. J. Therm. Sci. 2025, 212, 109757. [Google Scholar]
- Choi, Y.; Yang, S.; Kim, S. The smoke control system to improve the possibility of evacuation from fire disasters in high-rise buildings. Therm. Sci. Eng. Prog. 2025, 59, 103269. [Google Scholar] [CrossRef]
- Xu, Z. Study on Somke Temperature and Velocity in the Stairwell with Differnent Opening Conditions. Master’s Thesis, University of Science and Technology of China, Hefei, China, 2010. [Google Scholar]
- Tian, X.M.; Chen, S.C. Numerical simulation of fire response and failure mechanism of multi-story steel structures. J. Disaster Prev. Mitig. Eng. 2012, 32, 59–63. [Google Scholar]
- ASCE 41-17; Seismic Evaluation and Retrofit of Existing Buildings. American Society of Civil Engineers: Reston, VA, USA, 2017.
- Jiang, J.; Cao, Y.F.; Zhang, Q.J. Research progress on quantitative evaluation methods for structural robustness. Prog. Steel Build. Struct. 2022, 24, 1–21. [Google Scholar]
- Huang, J.Z.; Wang, Z. Evaluation method for robustness of steel frame structures. J. Civ. Eng. 2012, 45, 46–54. [Google Scholar]
- Liu, Y.B.; Liu, J.B. Damageability analysis of steel-concrete composite frame structures. In Proceedings of the 17th National Conference on Structural Engineering; Tsinghua University Press: Beijing, China, 2008; Volume II. [Google Scholar]
- Cai, X.J.; Jiang, W.J.; Mao, X.Y.; Shi, Z.T. Damageability analysis of multi-story steel frames under post-earthquake fire based on fire load density. J. Disaster Prev. Mitig. Eng. 2022, 42, 269–275. [Google Scholar]
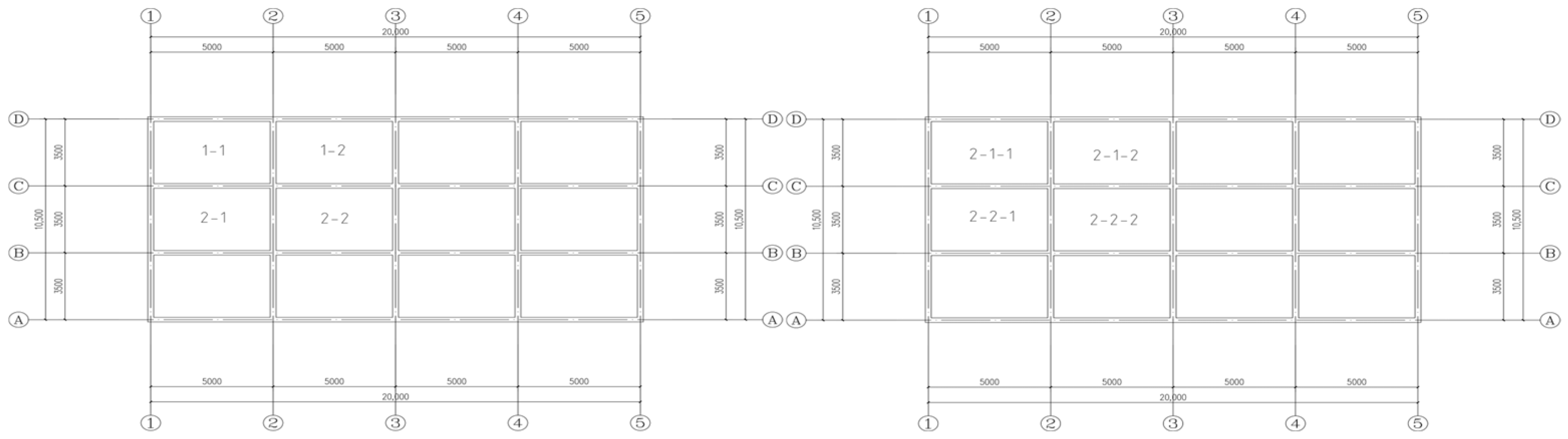

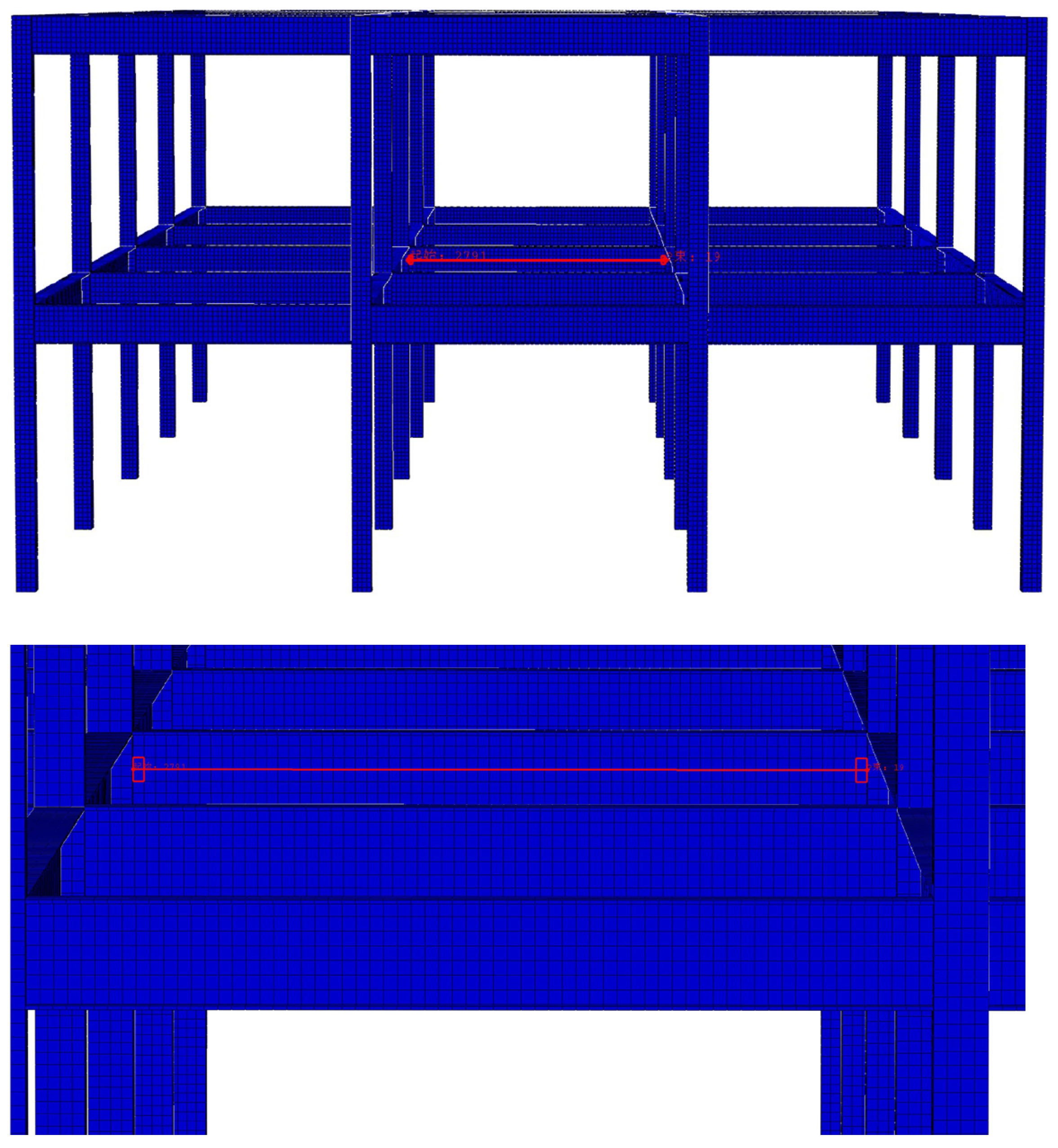





| Argument | Density ρs | Specific Heat Capacity Cs | Poisson’s Ratio Vs | Coefficient of Thermal Expansion ɑs | Coefficient of Heat Conduction λs |
|---|---|---|---|---|---|
| Unit | kg/m3 | J/(kg·°C) | - | m/(m·°C) | W/(m °C) |
| Data | 7850 | 600 | 0.3 | 1.4 × 10−5 | 45 |
| Strain Range | Stress: σ | Tangent Modulus |
|---|---|---|
| ε < | ε | |
| ε < | ||
| ε < | 0 | |
| ε < | [1 − (ε − )(−)] | - |
| ε = | 0 | - |
| Destruction Status | Maximum Displacement (mm) |
|---|---|
| Basically intact | 129 |
| Minor damage | 129 360 |
| Moderate damage | 590 |
| Severe damage | 947 |
| Complete destruction |
| The Possibility of a Continuous Collapse Occurring | Vulnerability Parameters |
|---|---|
| Basically impossible | 0 |
| Very small possibility | 1 |
| Smaller possibility | 10 |
| Higher possibility |
| Case | Peak Lateral Displacement/ 10−3 m | Peak Lateral Displacement Rate/ 10−3 m/min | Vertical Displacement Peak/ 10−3 m | Vertical Displacement Rate Peak/ 10−3 m/min | Ζ | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1-1 | 7.11 | 0.141 | 5.79 | 0.118 | 2.63 | −0.853 | 0.930 | −0.882 | −0.566 |
| 1-2 | 5.31 | 0.092 | 4.62 | 0.092 | 1.71 | −0.904 | 0.540 | −0.908 | −0.016 |
| 2-1 | 5.25 | 0.095 | 5.32 | 0.107 | 1.68 | −0.901 | 0.773 | −0.893 | −0.149 |
| 2-2 | 2.51 | 0.044 | 1.00 | 0.022 | 0.28 | −0.954 | −0.667 | −0.978 | −1.350 |
| 2-1-1 | 7.00 | 0.123 | 5.95 | 0.124 | 2.57 | −0.872 | 0.983 | −0.876 | 0.585 |
| 2-1-2 | 3.91 | 0.071 | 3.65 | 0.074 | 0.99 | −0.926 | 0.217 | −0.926 | −0.476 |
| 2-2-1 | 3.89 | 0.065 | 3.80 | 0.072 | 0.98 | −0.932 | 0.267 | −0.928 | −0.447 |
| 2-2-2 | 3.11 | 0.058 | 2.41 | 0.045 | 0.58 | −0.940 | −0.197 | −0.955 | −0.912 |
| Case | Peak Lateral Displacement/ 10−3 m | Peak Lateral Displacement Rate/ 10−3 m/min | Vertical Displacement Peak/ 10−3 m | Vertical Displacement Rate Peak/ 10−3 m/min | Ζ | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1-1 | 25.2 | −7.11 | 2.14 | −4.71 | 11.90 | −8.41 | 6.13 | −5.71 | 1.33 |
| 1-2 | 31.0 | −5.51 | 26.8 | −2.87 | 14.80 | −6.74 | 7.93 | −3.87 | 5.27 |
| 2-1 | 25.8 | −3.12 | 21.4 | 12.20 | 12.20 | −4.25 | 6.13 | 11.20 | 14.50 |
| 2-2 | 31.3 | −1.03 | 28.3 | 13.80 | 15.00 | −11.70 | 8.43 | 12.80 | 15.80 |
| 2-1-1 | 61.5 | −2.67 | 61.8 | 3.42 | 30.40 | −3.78 | 19.60 | 2.42 | 23.40 |
| 2-1-2 | 65.9 | −3.44 | 63.1 | 2.56 | 32.60 | −4.58 | 20.00 | 1.56 | 23.50 |
| 2-2-1 | 61.7 | −4.28 | 60.3 | 3.94 | 30.50 | −5.46 | 19.10 | 2.94 | 22.90 |
| 2-2-2 | 68.7 | −11.00 | 65.7 | 2.78 | 34.10 | −12.50 | 20.90 | 1.78 | 22.40 |
| Case | Peak Lateral Displacement/ 10−3 m | Peak Lateral Displacement Rate/ 10−3 m/s | Vertical Displacement Peak/ 10−3 m | Vertical Displacement Rate Peak/ 10−3 m/s | Ζ | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1-1 | 5.61 | 0.119 | 4.27 | 8.9 | 1.86 | −0.876 | 0.423 | −0.911 | −0.045 |
| 1-2 | 5.75 | 0.123 | 4.42 | 9.5 | 1.93 | −0.872 | 0.473 | −0.905 | −0.016 |
| 2-1 | 5.16 | 0.107 | 4.41 | 9.4 | 1.63 | −0.889 | 0.470 | −0.906 | −0.082 |
| 2-2 | 4.61 | 0.097 | 5.35 | 11.4 | 1.35 | −0.899 | 0.783 | −0.886 | −0.064 |
| 2-1-1 | 10.80 | 0.208 | 10.10 | 20.2 | 4.51 | −0.783 | 23.7 | −0.798 | 2.220 |
| 2-1-2 | 10.20 | 0.214 | 9.90 | 20.3 | 4.20 | −0.777 | 23.0 | −0.797 | 2.080 |
| 2-2-1 | 10.60 | 0.220 | 9.20 | 18.6 | 4.41 | −0.771 | 20.7 | −0.814 | 1.970 |
| 2-2-2 | 10.70 | 0.220 | 10.40 | 22.0 | 4.46 | −0.771 | 24.7 | −0.780 | 2.290 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Xiong, Y.; Ke, C. Study on the Vulnerability of Steel Frames Under Fire Smoke Propagation. Buildings 2025, 15, 1128. https://doi.org/10.3390/buildings15071128
Jiang J, Xiong Y, Ke C. Study on the Vulnerability of Steel Frames Under Fire Smoke Propagation. Buildings. 2025; 15(7):1128. https://doi.org/10.3390/buildings15071128
Chicago/Turabian StyleJiang, Junling, Yingchao Xiong, and Changren Ke. 2025. "Study on the Vulnerability of Steel Frames Under Fire Smoke Propagation" Buildings 15, no. 7: 1128. https://doi.org/10.3390/buildings15071128
APA StyleJiang, J., Xiong, Y., & Ke, C. (2025). Study on the Vulnerability of Steel Frames Under Fire Smoke Propagation. Buildings, 15(7), 1128. https://doi.org/10.3390/buildings15071128





