Research on Mechanical Properties of Non-Directly Welded Reinforced Casings Under High Stress Ratio
Abstract
1. Introduction
2. Experimental Scheme
2.1. Specimen Design
2.2. Material Property Test
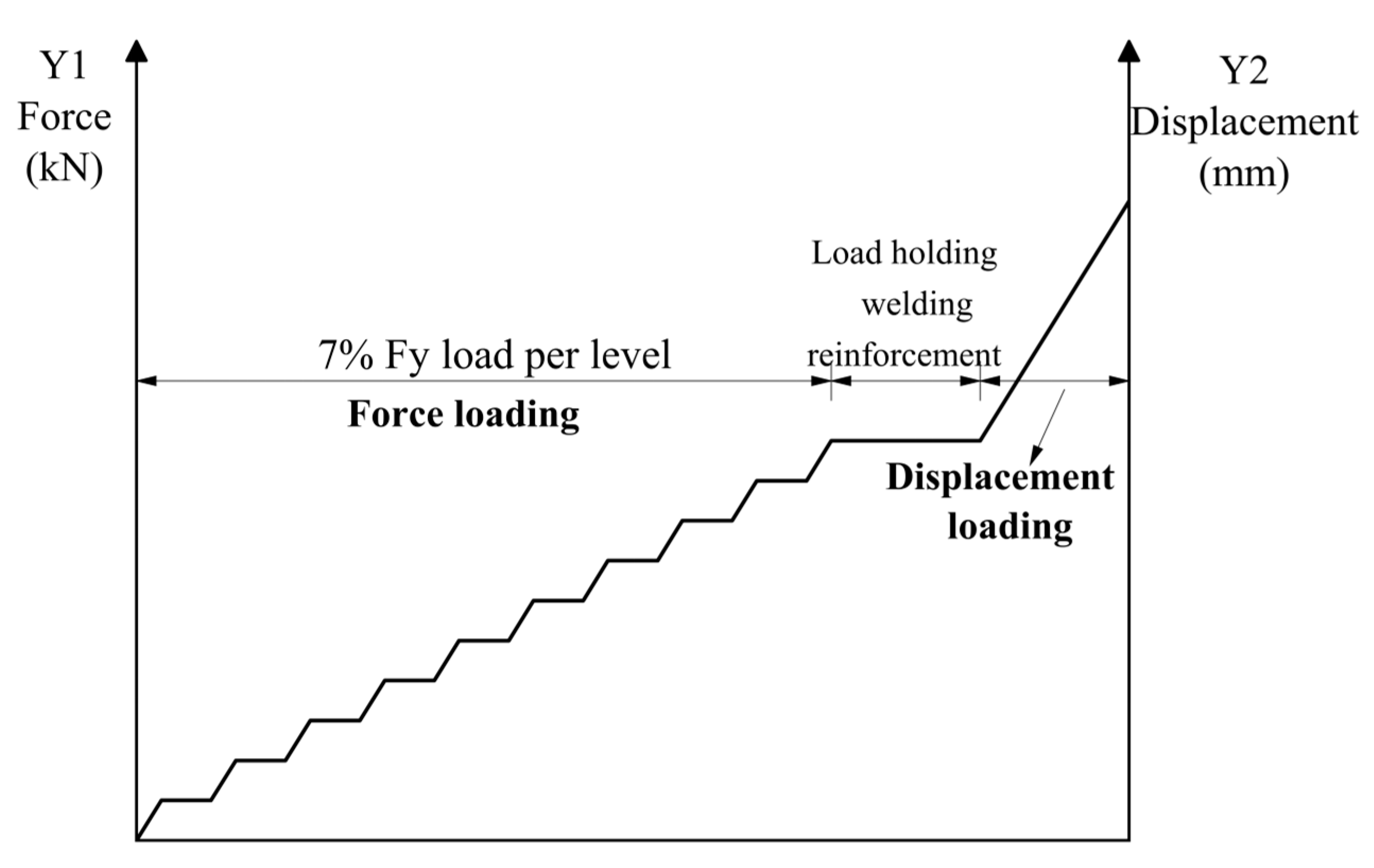
2.3. Loading Scheme
2.4. Test Point Arrangement
3. Test Results and Analysis
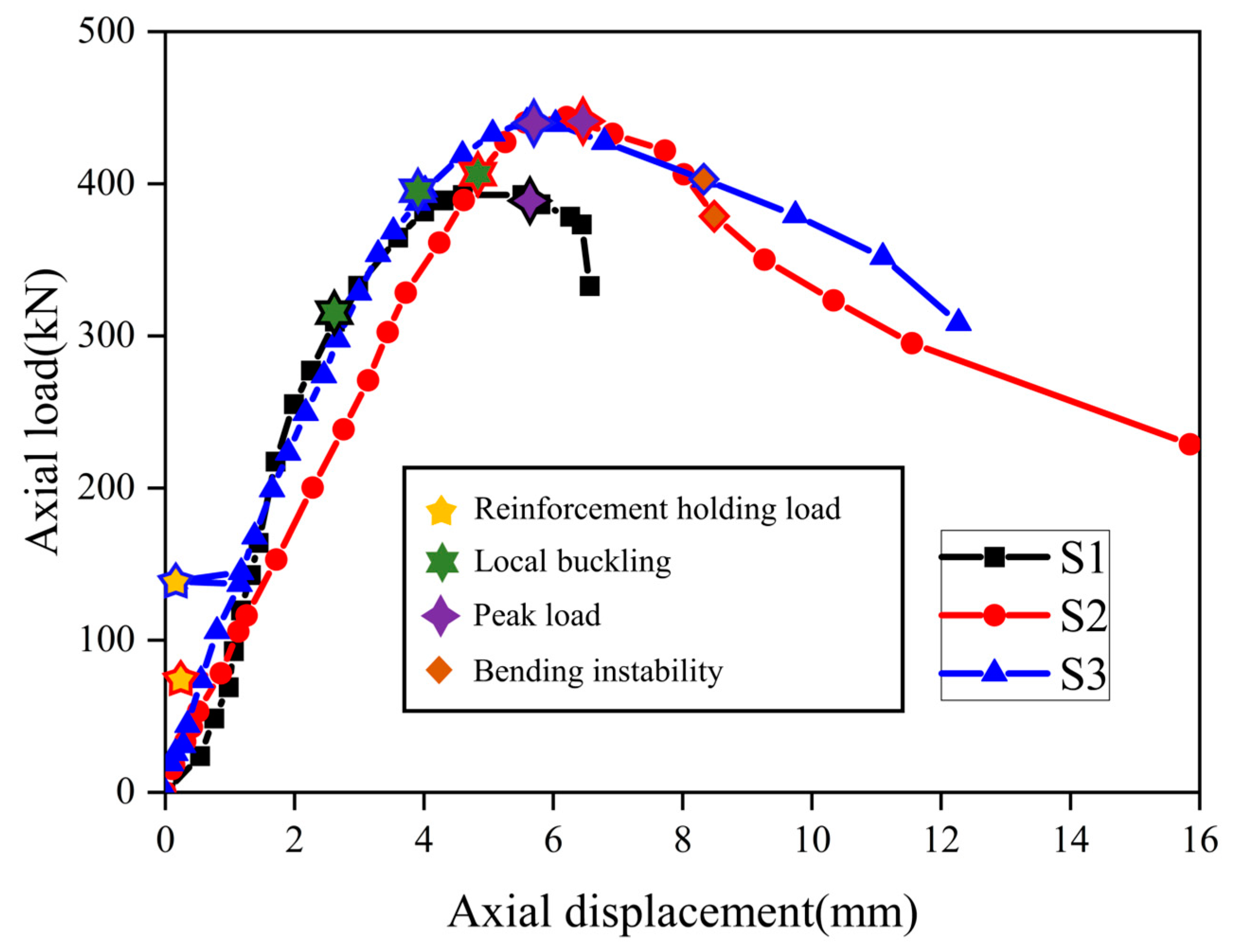
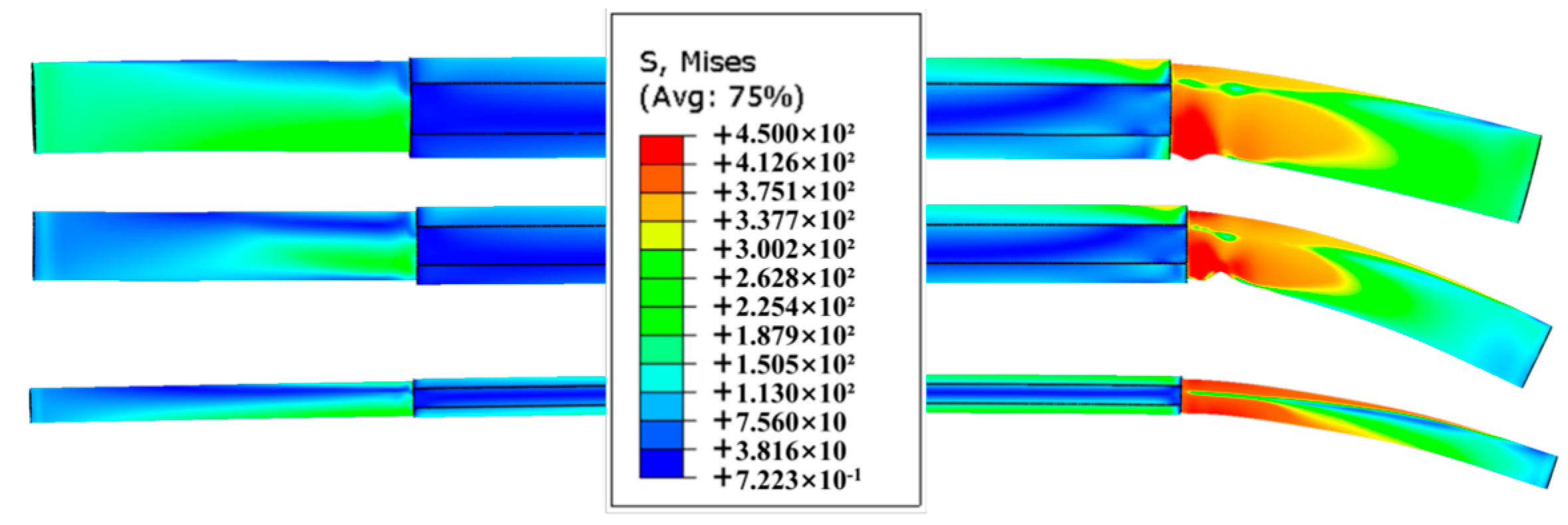
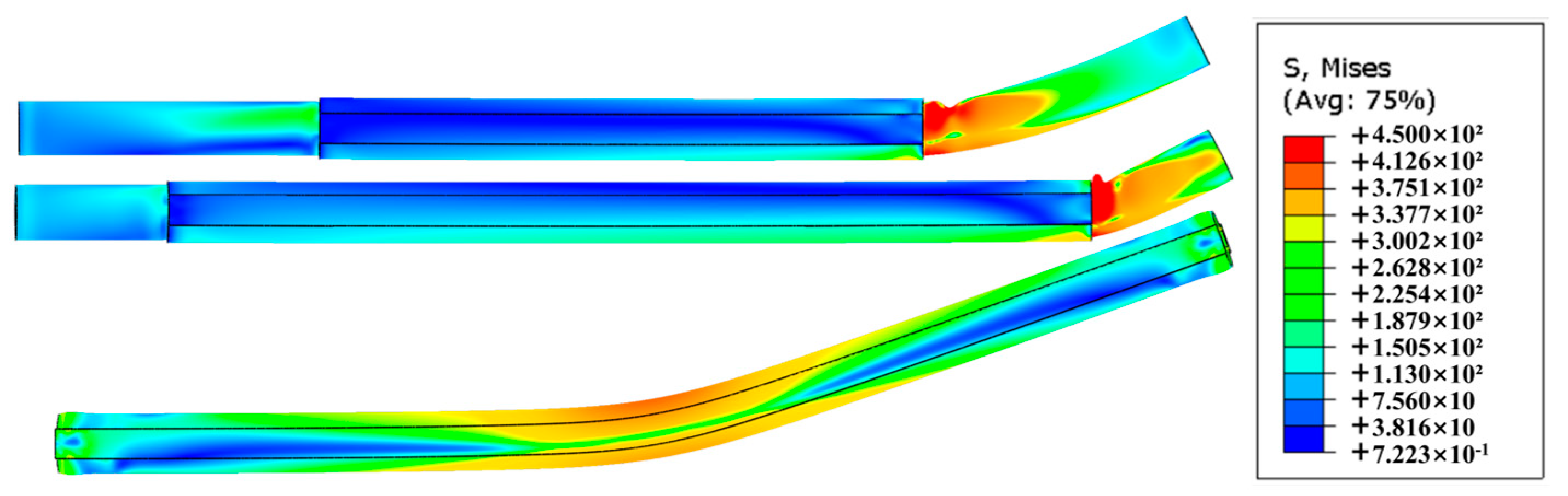
3.1. Phenomenon of Destruction
3.2. Carrying Capacity Analysis
3.3. Strain Variation Analysis
4. Numerical Simulation Analysis
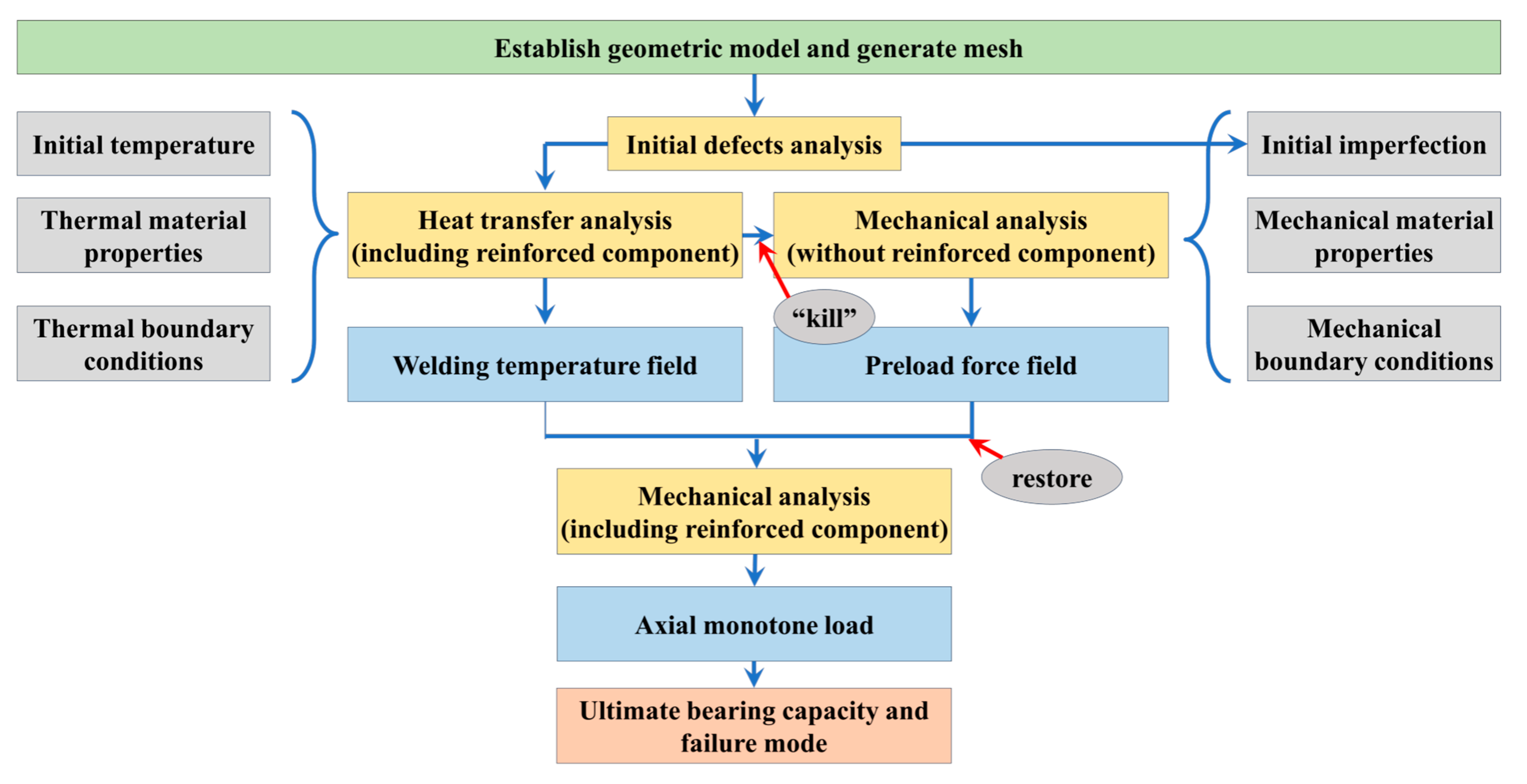
4.1. Finite Element Simulation Process
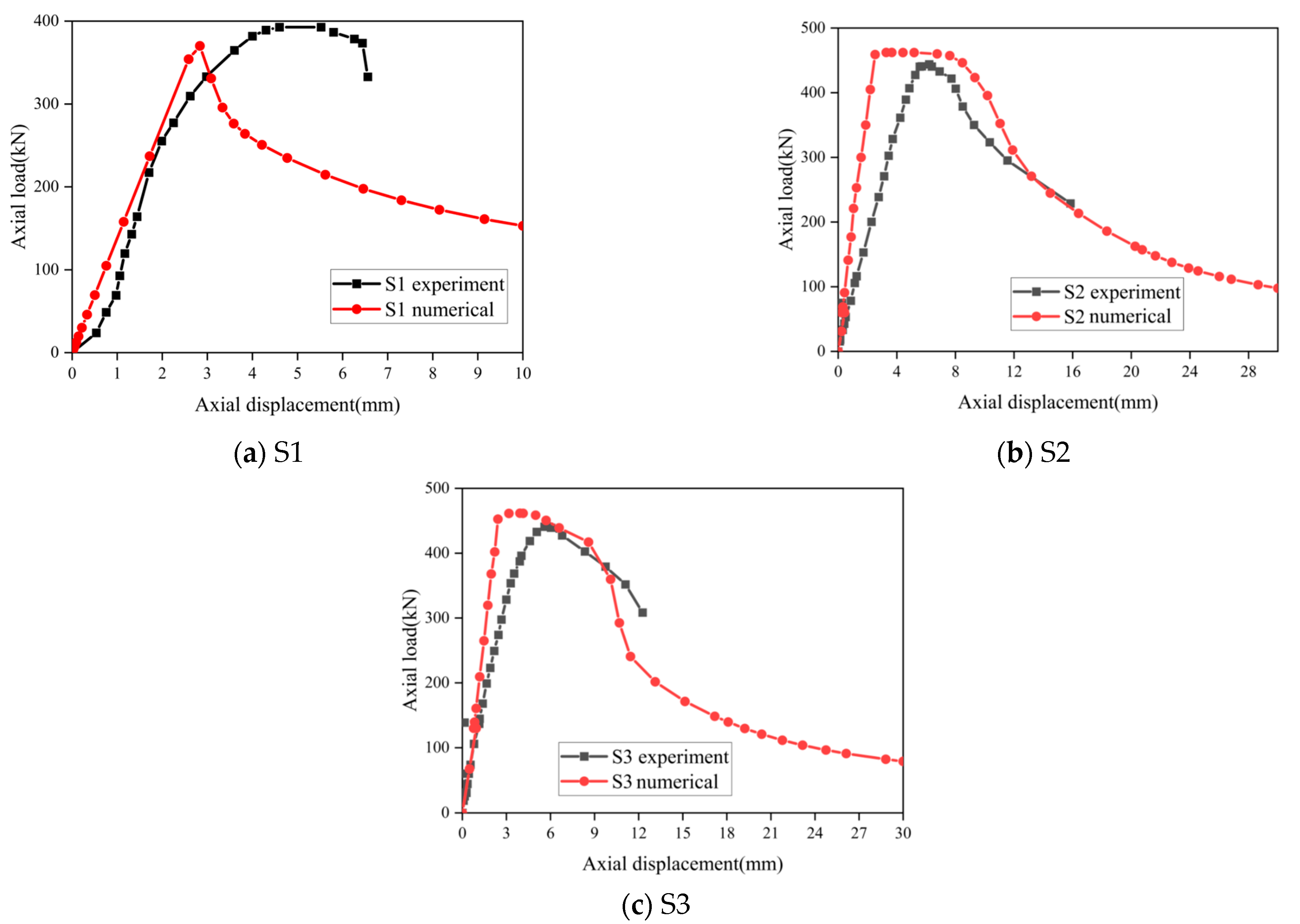
4.2. Finite Element Simulation Verification
4.3. Parametric Analysis
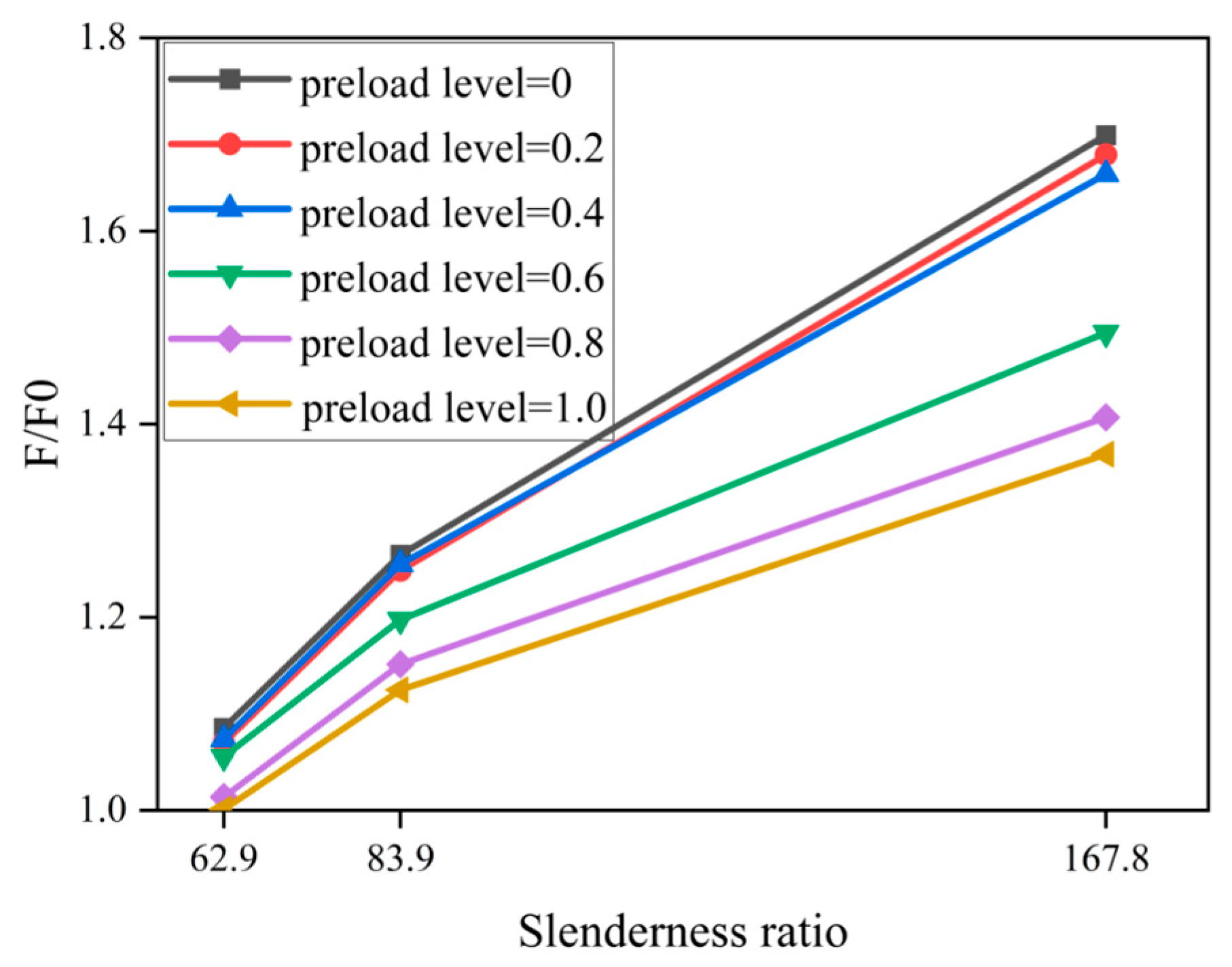
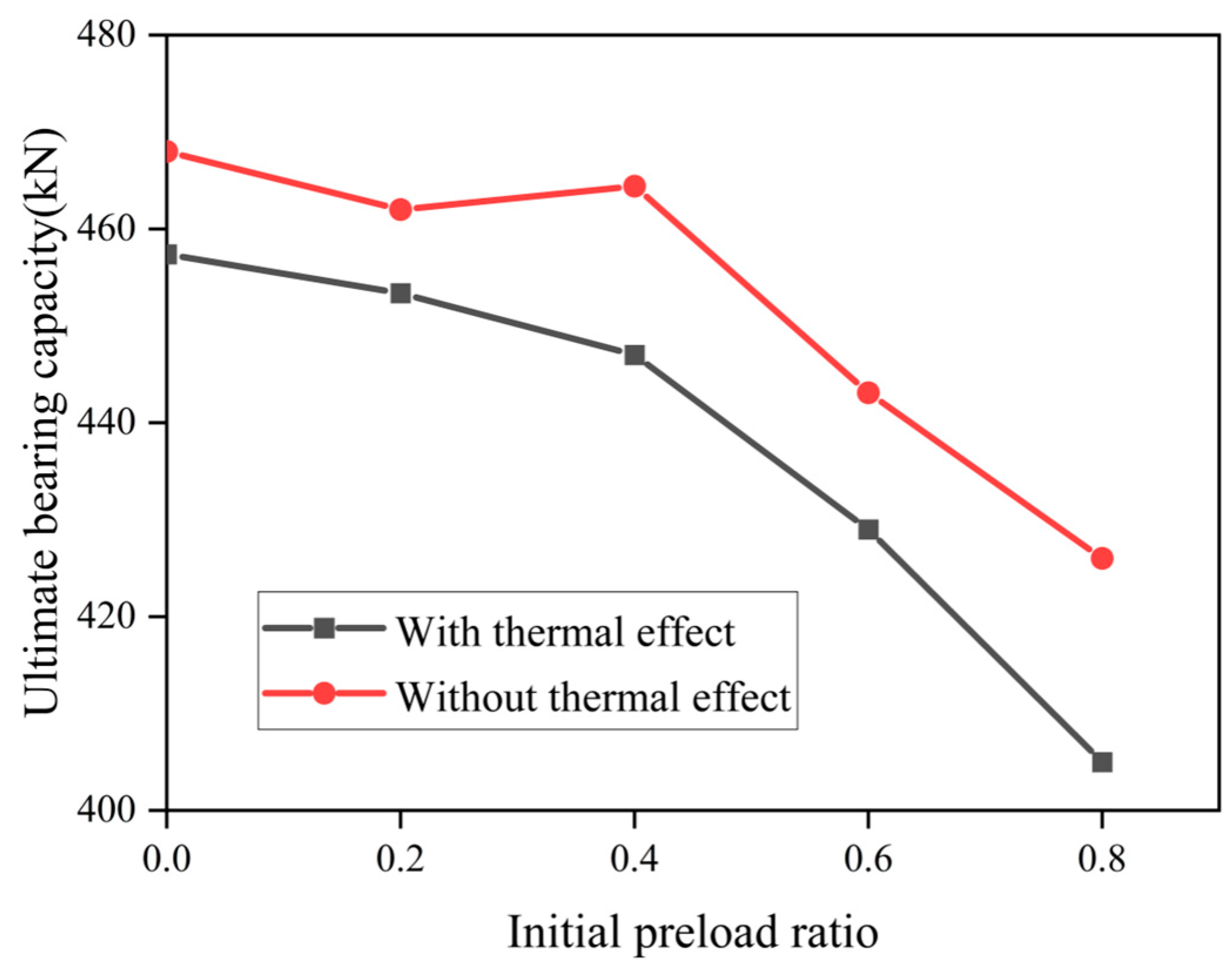
4.3.1. Initial Stress Ratio
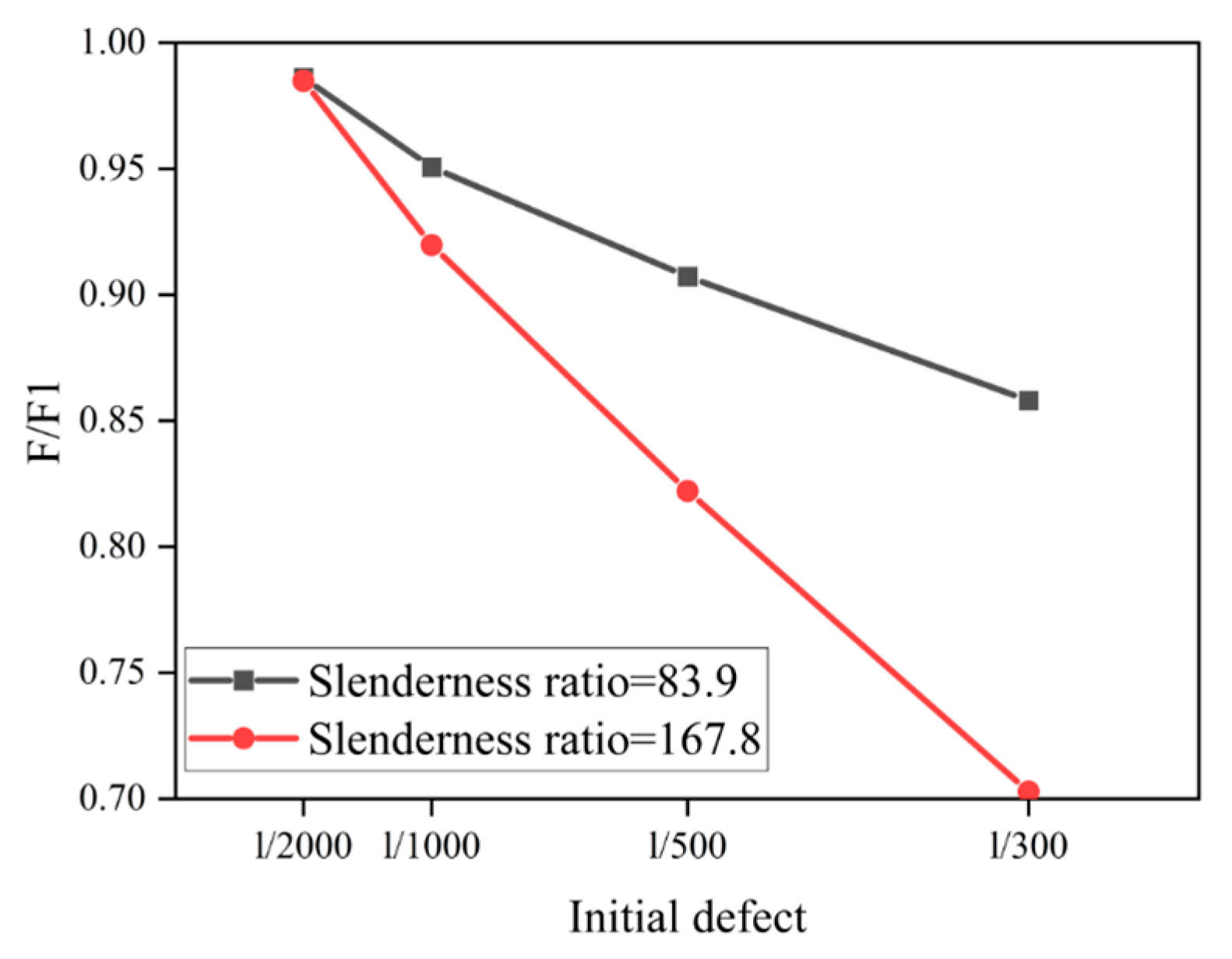
4.3.2. Initial Defects
4.3.3. Slenderness Ratio
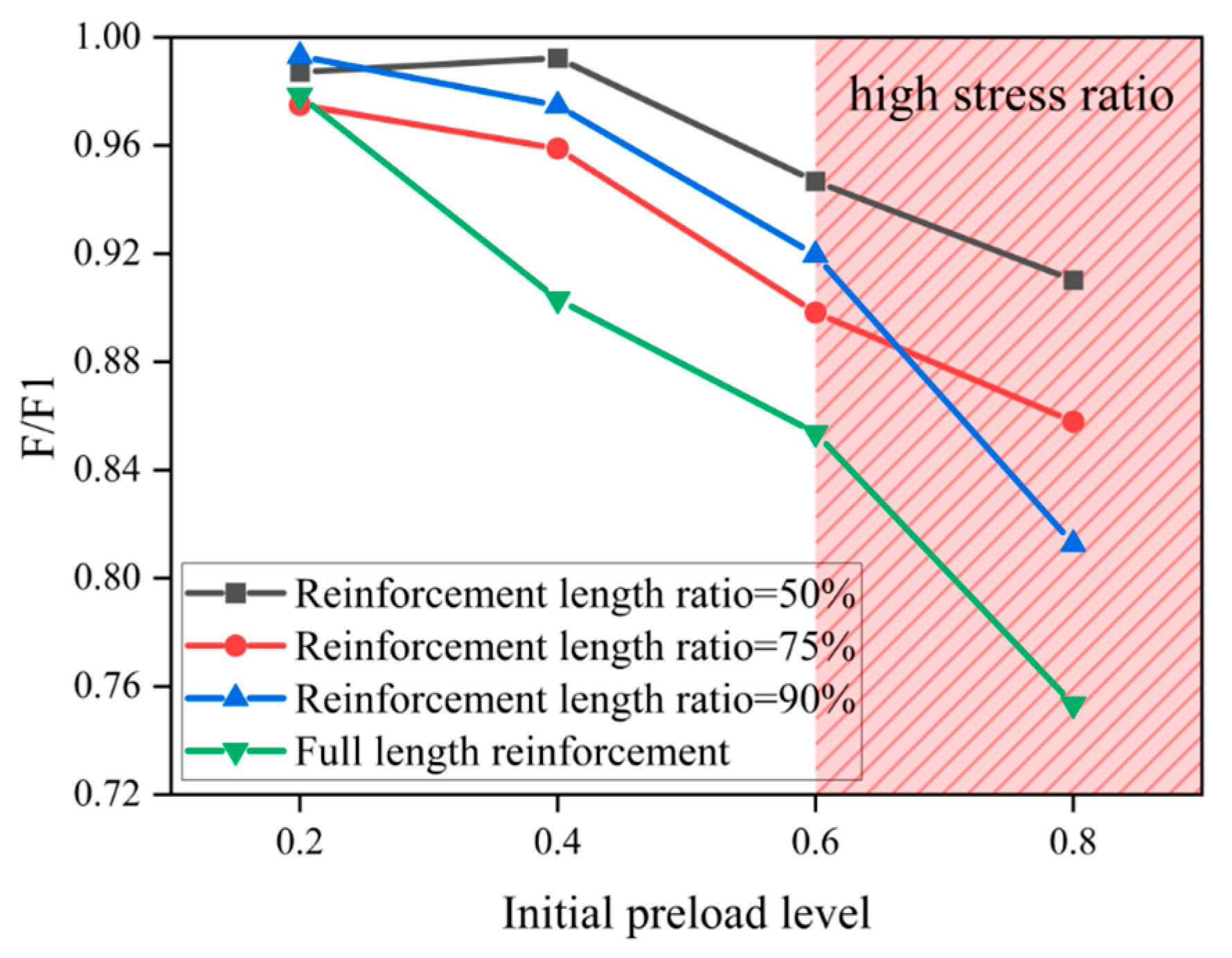
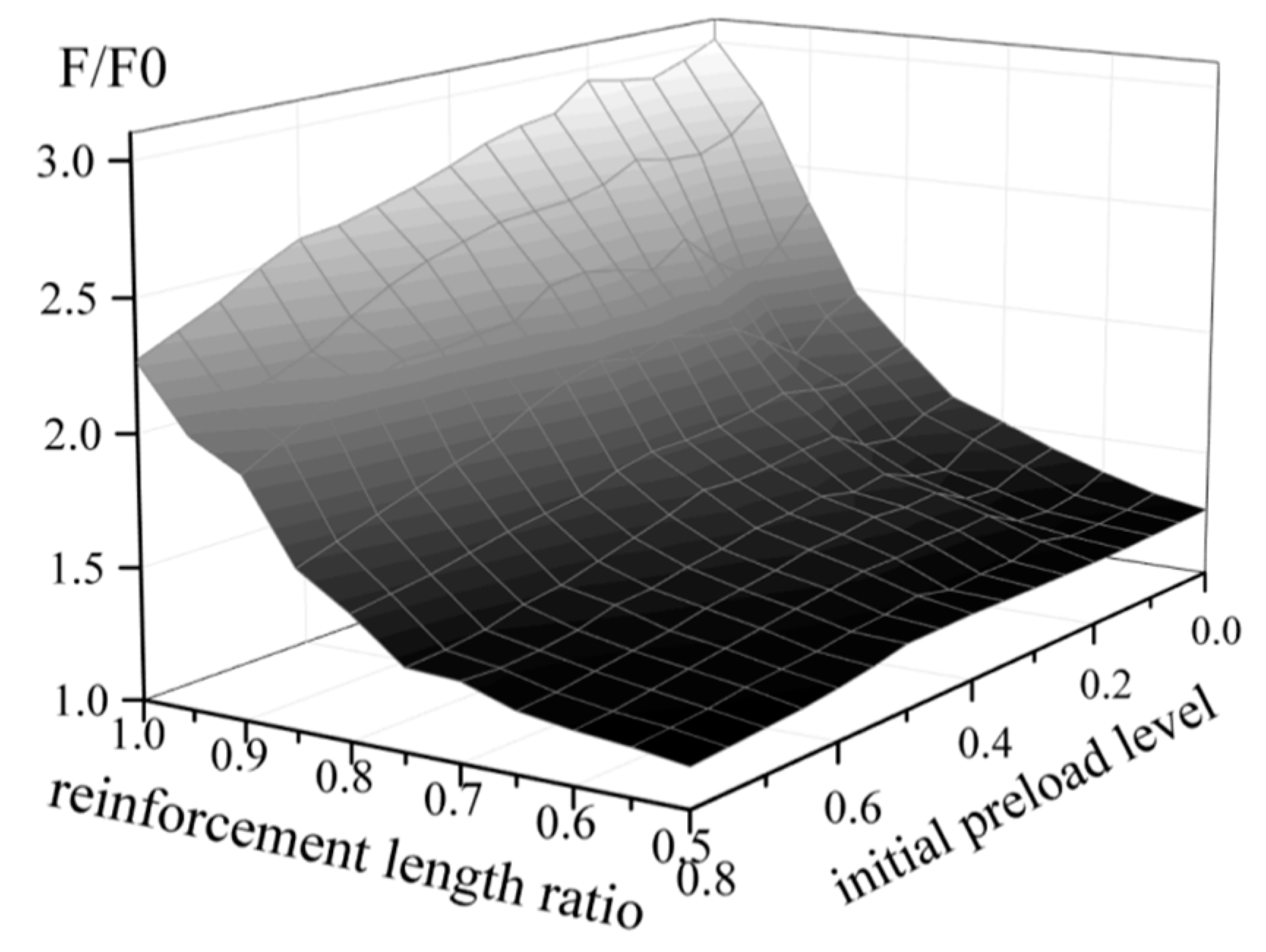
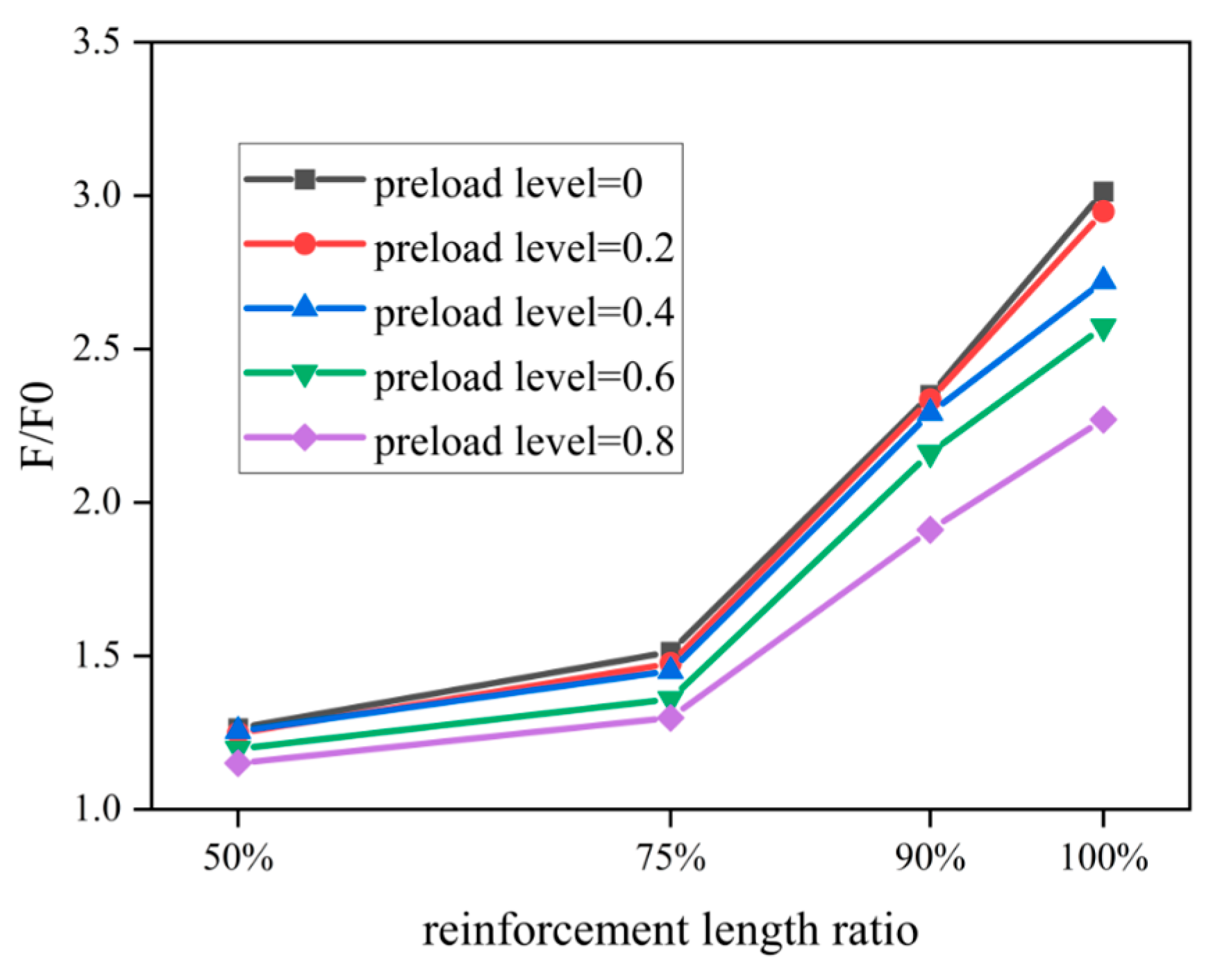
4.3.4. Reinforcement Length
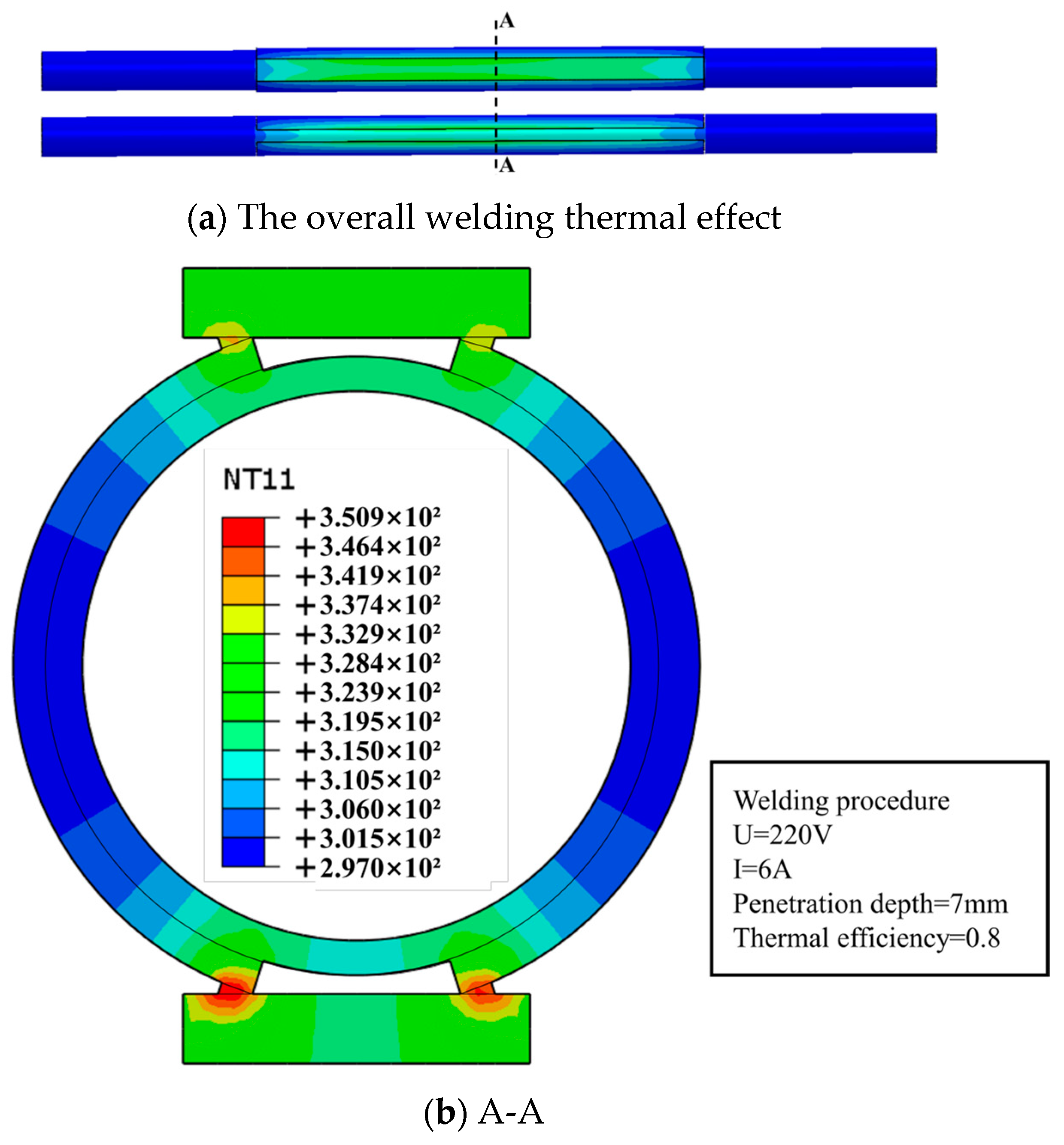
4.3.5. Welding Thermal Influence
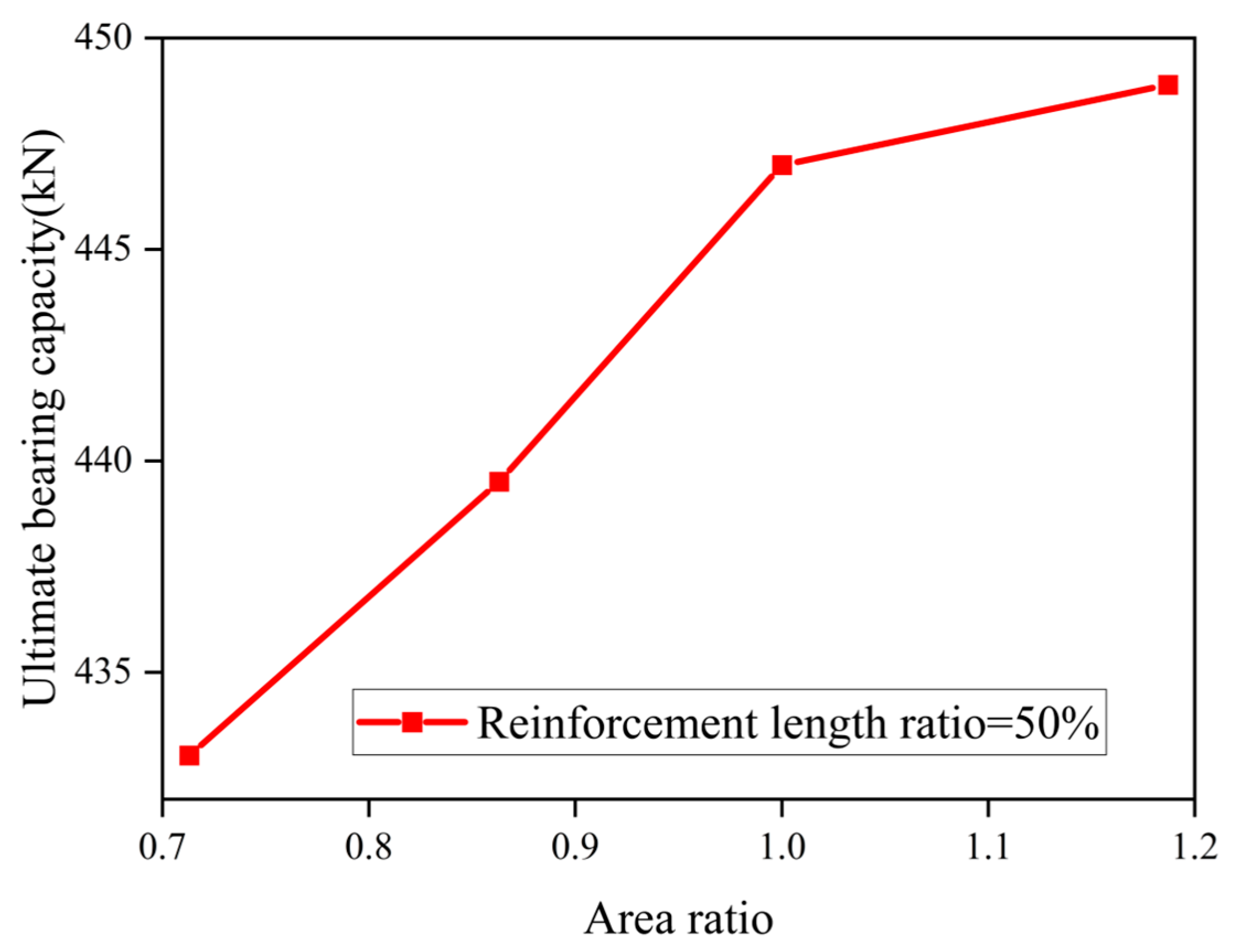
4.3.6. Reinforced Area Ratio
4.3.7. Weld Distribution
5. Calculation of the Ultimate Bearing Capacity
6. Conclusions
- In this paper, a new method for strengthening welded casings is proposed. Instead of direct welding, the reinforced part is attached using natural cooling and shrinkage after welding. This reduces residual stress and mechanical defects. The proposed method demonstrates competitive efficiency for steel pipes under high loads compared to the conventional welding techniques, with superior residual stress control and a shorter installation time. The finite element analysis shows the minimal impact of welding heat on the ultimate bearing capacity, providing an effective strengthening scheme for space steel structures. Compared to the traditional welding methods, the proposed method reduces the labor hours by 30% and lowers the labor costs.
- In this research, axial compression tests were conducted on welded pipe reinforcements under load. The results show that reinforcement significantly increases the bearing capacity. Before reinforcement, members fail due to instability; after reinforcement, they fail due to overall buckling after local buckling. The yield load of the reinforced members was increased by 30–40%, which verified the feasibility of this reinforcement method.
- In order to make the finite element simulation method more reliable, a combined method of live/dead elements and thermo-mechanical coupling was used for finite element simulations. By comparing the simulation results with the experimental data, the relative error of the ultimate bearing capacity of the two is less than 6%, which confirms the accuracy of the numerical simulation process.
- The test and simulation results were compared to study the ultimate bearing capacity of reinforced steel pipes under load. An improved formula for the local reinforcement length and axial compression force was derived. Recommendations for optimal reinforcement lengths for long and short columns are provided (50~65% for long columns and 75~90% for short columns).
- Finite element models were used to study the effects of preload level, initial defects, slenderness ratio, reinforcement length, area ratio, and welding thermal influence on the ultimate bearing capacity. Quantitative analysis provides a reference for reinforcing steel members under various loads.
- To further validate the practical application effectiveness of this reinforcement method, it is necessary to propose large-scale structural testing and long-term fatigue monitoring and evaluate the metallurgical defects, thereby optimizing the overall reinforcement process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al Ali, M.; Kvočák, V.; Platko, P. Stress State of Steel Column Strengthened Under Load. Procedia Eng. 2017, 190, 632–636. [Google Scholar] [CrossRef]
- Liu, Y.; Gannon, L. Experimental behavior and strength of steel beams strengthened while under load. J. Constr. Steel Res. 2009, 65, 1346–1354. [Google Scholar] [CrossRef]
- Erfani, S.; Naseri, M.; Akrami, V. Effect of in-service strengthening on the axial load carrying capacity of steel box columns. Int. J. Steel Struct. 2017, 17, 231–244. [Google Scholar] [CrossRef]
- Xiangyang, J.; Haiqing, L.; Zhongwei, Z.; Xiufeng, W.; Ming, L.; Zimu, C. A study of the mechanical behavior of rectangular steel tubular column strengthened using intermittent welding angle steel. Structures 2021, 33, 3298–3310. [Google Scholar]
- Zhongwei, Z.; Pingyi, Z.; Song, Z. Loading capacity of welded hollow spherical joints strengthened by cone member. Structures 2023, 58, 105634. [Google Scholar]
- Goldak, J.; Chakravarti, A.; Bibby, M. A new finite element model for welding heat sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Marzouk, H.; Mohan, S. Strengthening of wide-flange columns under load. Can. J. Civ. Eng. 1990, 17, 835–843. [Google Scholar] [CrossRef]
- O’Sullivan, T.P. Strengthening of steel structures under load. Proc. Inst. Civ. Eng. 1953, 2, 76–95. [Google Scholar]
- Tafsirojjaman, T.; Fawzia, S.; Thambiratnam, D. Investigation on the behaviour of CFRP strengthened CHS members under monotonic loading through finite element modelling. Structures 2020, 28, 297–308. [Google Scholar] [CrossRef]
- Tafsirojjaman, T.; Miri, A.; Khuda, E.N.S.; Ahmed, A.; Islam, A.S.; Khan, M. Structural performance of CFRP strengthened SHS beam-column connections subjected to monotonic loading: A numerical simulation. Structures 2024, 61, 106030. [Google Scholar] [CrossRef]
- Wei, J.; Ding, Z.; Shen, W.; Xiaoqin, L. Mechanical Characteristics of Cracked Lining Reinforced with Steel Plate–UHPC Subjected to Vertical Load. Buildings 2024, 14, 1515. [Google Scholar] [CrossRef]
- Açıkel, H.; Kaltakcı, M.Y.; Sönmez, A. Reinforcement of Steel Tubes with Rings under Compression. Mater. Test. 2013, 55, 772–780. [Google Scholar]
- Bingsheng, H.; Haitao, C.; Fang, Y. Experimental study on axial compressive behavior of circular steel tubes strengthened by sleeved pipe. J. Build. Struct. 2020, 41, 198–206. [Google Scholar]
- Yuanqing, W.; Ruixiang, Z.; Guoxin, D. Experimental study on load-carrying behavior of I section steel columns strengthened by welding with initial load. J. Build. Struct. 2014, 35, 78–86. [Google Scholar]
- Li, J.; Yuanqing, W.; Guoxin, D. Influence Factor Analysis of Mechanical Behavior of Compression-bending Member of Steel Structure Strengthened by Welding Under Load. J. Archit. Civ. Eng. 2016, 33, 120–126. [Google Scholar]
- Liu, H.; Hu, J.; Chen, Z.; Wang, L.; Mashrah, W.A.H. Reinforcement of Circular Steel Tubes Using Welded Casings Under Axial Compression Loading. Int. J. Steel Struct. 2022, 22, 894–912. [Google Scholar]
- Hongbo, L.; Jie, H.; Yuan, Y.; Zhihua, C.; Longxuan, W. Circular steel tubes strengthened by welding angle steel under preloading condition. J. Constr. Steel Res. 2021, 184, 106816. [Google Scholar]
- Zhao, X.; Lyu, J.; Yan, S.; Chen, X.; Wu, X.; Xu, X.; Gao, F. Performance evaluation of axial-loaded circular steel tubes strengthened by welding under service load. Eng. Struct. 2022, 271, 114948. [Google Scholar]
- Vild, M.; Bajer, M. Strengthening Under Load: Numerical Study of Flexural Buckling of Columns. Procedia Eng. 2017, 190, 118–125. [Google Scholar]
- Mourad, K.; Amar, K.; Marc, O. Modelling of Strengthened Steel Connections under Static and Cyclic Loading. Buildings 2022, 12, 1962. [Google Scholar] [CrossRef]
- Ji-hao, C.; Yu-xin, W.; Qian, Z.; Ming-zhen, G.; Bu-qiao, F. Mechanical properties and reinforcement technology of deep joints under static and fatigue loads. Structures 2023, 47, 1182–1195. [Google Scholar]
- Bibby, M.J.; Chong, L.M.; Goldak, J.A. Predicting Heat-affected Zone Hardness by the weld test method. J. Test. Eval. 1982, 11, 56–57. [Google Scholar]
- Weifeng, T.; Jialiang, S.; Jiping, H. Effective length factors of stepped columns considering interaction effect among columns. J. Build. Struct. 2021, 42, 159–171. [Google Scholar]
- Kyvelou, P.; Huang, C.; Li, J.; Gardner, L. Residual stresses in steel I-sections strengthened by wire arc additive manufacturing. Structures 2024, 60, 105828. [Google Scholar]
- Jaromir, M.; Jiri, S.; Pavel, S.; Robin, T. Heat Input Influence on the Fatigue Life of Welds from Steel S460MC. Metal 2020, 10, 1288. [Google Scholar]
- Zheng, X.; Li, D.; Liao, W.; He, Z. Residual Stress and Fatigue Strength Analysis of Stiffener Welds of Steel-Plate Composite Girder Bridge Considering Welding Sequence. Buildings 2024, 14, 1801. [Google Scholar] [CrossRef]
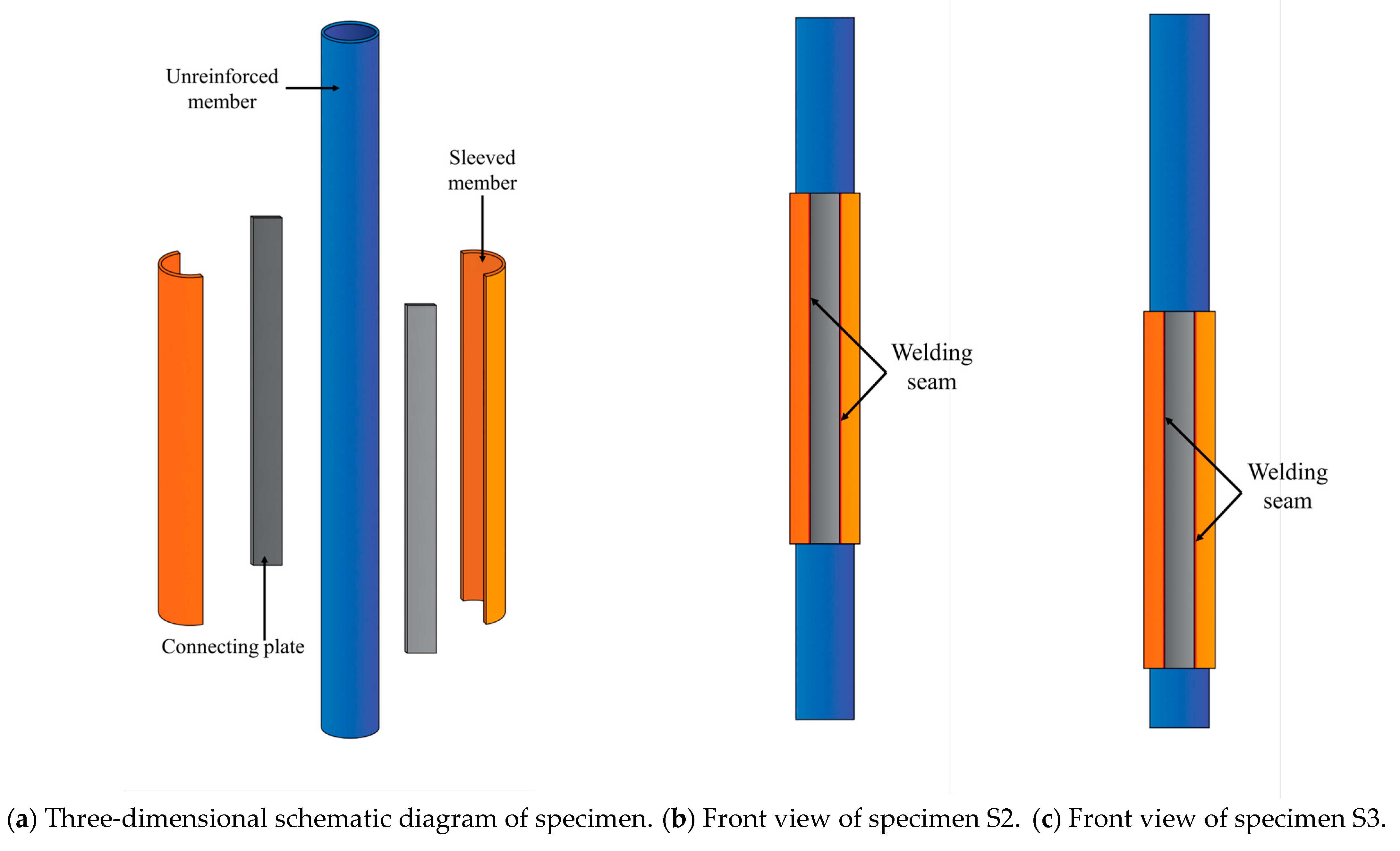
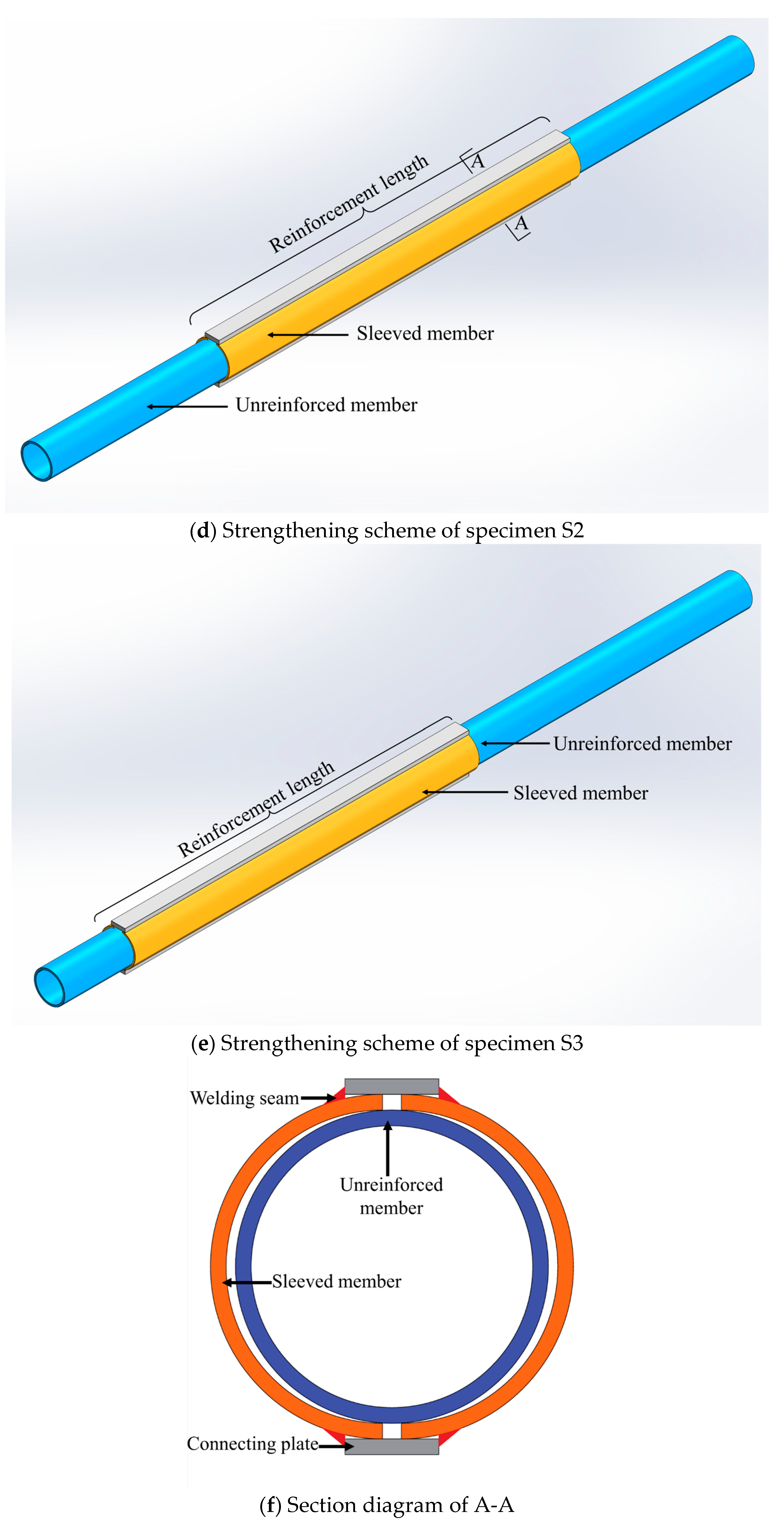










| Specimen | Diameter of the Circular Steel Tube (mm) | Reinforcement Positon | Diameter of the Casing (mm) | Method of Reinforcement | Slenderness Ratio of Steel Pipe |
|---|---|---|---|---|---|
| S-1 | Φ89 × 5 | / | / | Unreinforced | 83.9 |
| S-2 | Φ89 × 5 | Steel pipe midspan | Φ89 × 5 | Load-reinforced | 83.9 |
| S-3 | Φ89 × 5 | Stell pipe lower part | Φ89 × 5 | Load-reinforced | 83.9 |
| Specimen | fy (Mean ± SD) (N/mm2) | fu (Mean ± SD) (N/mm2) | Es (N/mm2) | εs (%) | εst (%) | εu (%) | COV (%) |
|---|---|---|---|---|---|---|---|
| Φ89 × 5 | 361.4 ± 2.7 | 515 ± 3.7 | 2.06 × 105 | 0.185 | 0.782 | 5.690 | 0.61 |
| Specimen | Ny (kN) | Yield Load (kN) | Pu (kN) | Preload (kN) | Preload Level |
|---|---|---|---|---|---|
| S-1 | 203.9 | 309.5 | 392.7 | - | - |
| S-2 | 203.9 | 406.9 | 443.9 | 78.3 | 0.384 |
| S-3 | 203.9 | 396.1 | 441.5 | 136.3 | 0.668 |
| Parameter | Reinforcement Length | Slenderness Ratio | Reinforced Area Ratio | Initial Stress Ratio | Initial Defect |
|---|---|---|---|---|---|
| 0.1985 | 0.2788 | 0.05887 | 0.2502 | 5.783 × 10−4 | |
| SRC | 0.78 | 0.36 | 0.02 | 0.28 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Li, Y.; Xing, K.; Liu, Z. Research on Mechanical Properties of Non-Directly Welded Reinforced Casings Under High Stress Ratio. Buildings 2025, 15, 1042. https://doi.org/10.3390/buildings15071042
Fang Y, Li Y, Xing K, Liu Z. Research on Mechanical Properties of Non-Directly Welded Reinforced Casings Under High Stress Ratio. Buildings. 2025; 15(7):1042. https://doi.org/10.3390/buildings15071042
Chicago/Turabian StyleFang, Yiwei, Yuming Li, Kuntao Xing, and Zhe Liu. 2025. "Research on Mechanical Properties of Non-Directly Welded Reinforced Casings Under High Stress Ratio" Buildings 15, no. 7: 1042. https://doi.org/10.3390/buildings15071042
APA StyleFang, Y., Li, Y., Xing, K., & Liu, Z. (2025). Research on Mechanical Properties of Non-Directly Welded Reinforced Casings Under High Stress Ratio. Buildings, 15(7), 1042. https://doi.org/10.3390/buildings15071042





