Effect of Density and Number of Layers of Fiber Sheets and End Anchors on the Flexural Capacity of SRG-Strengthened RC Beams
Abstract
1. Introduction
2. Experimental Campaign
2.1. Material Characterization
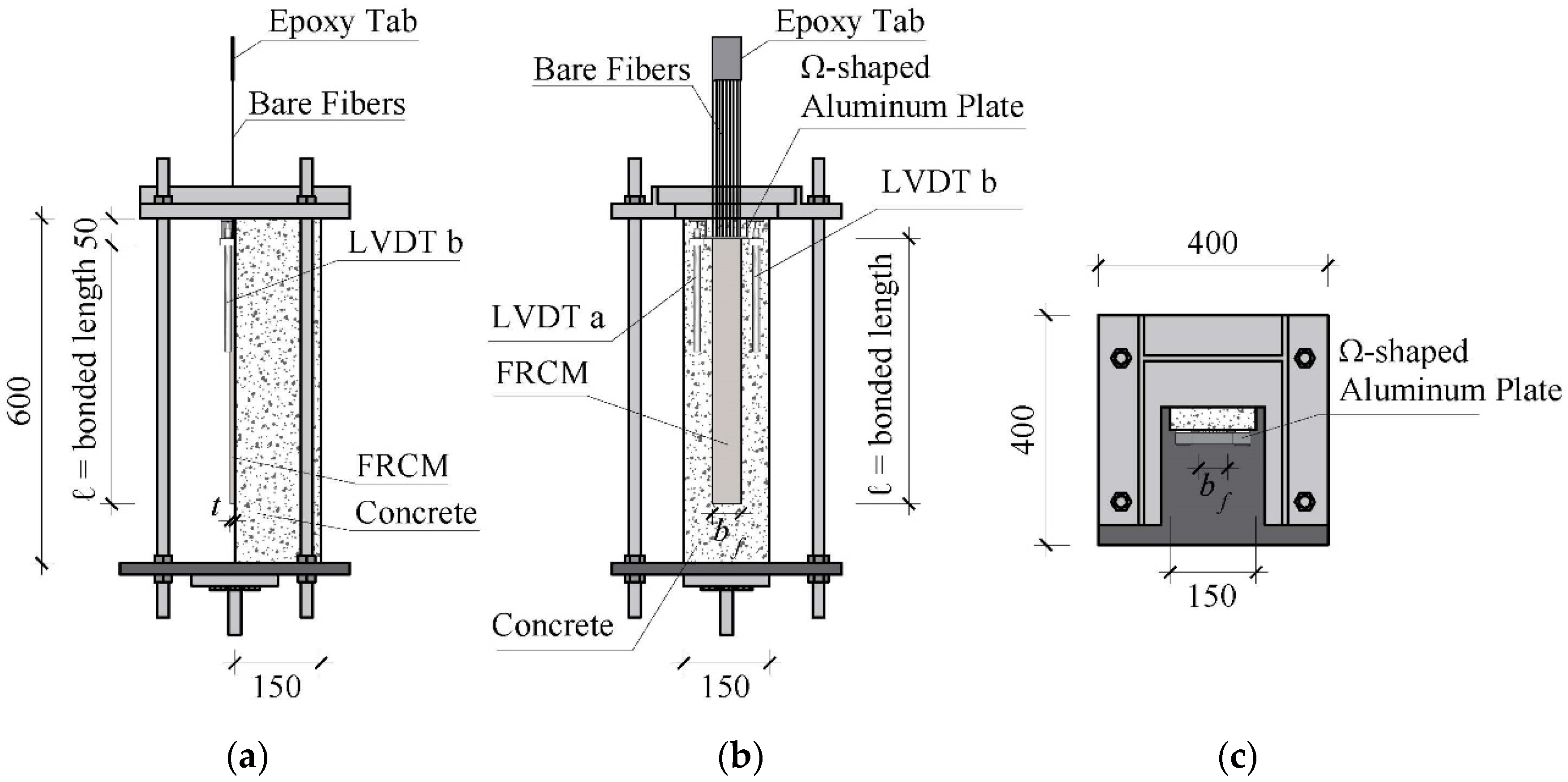
2.2. Direct Shear Tests
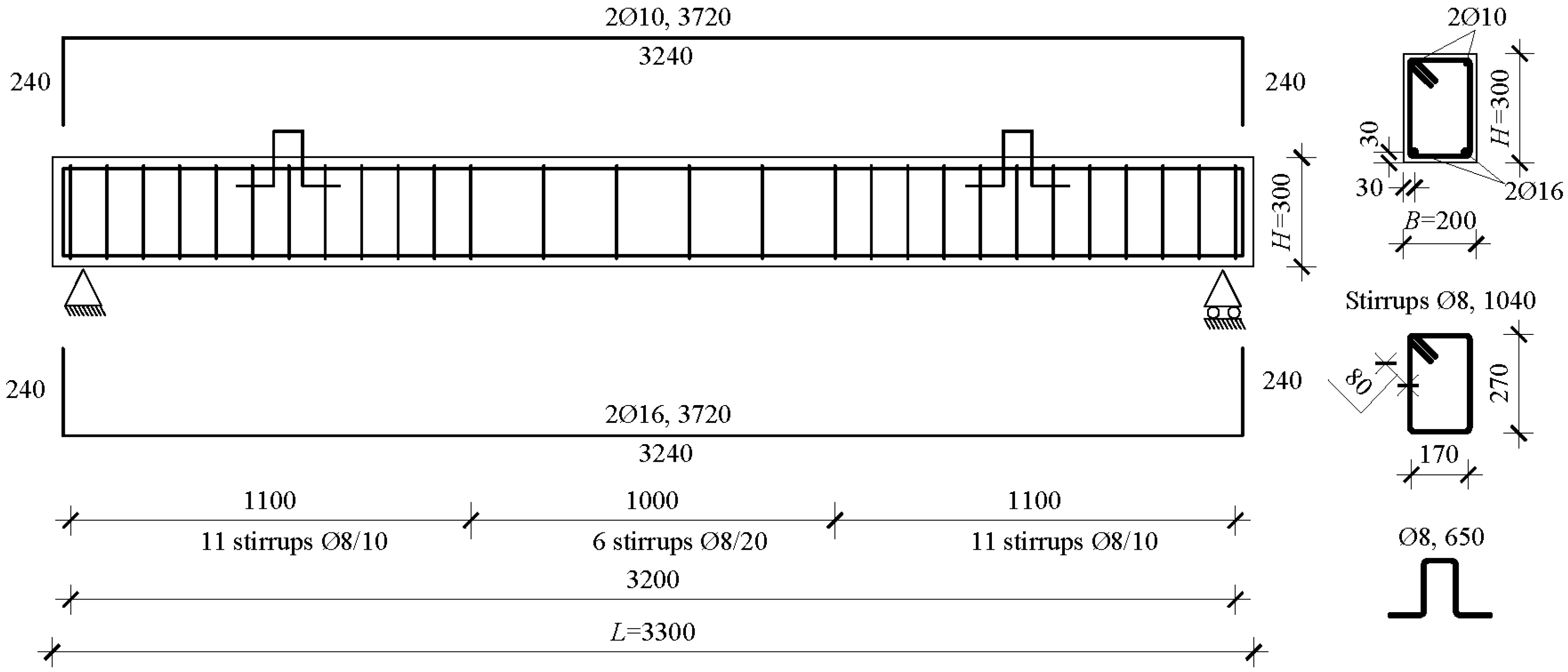
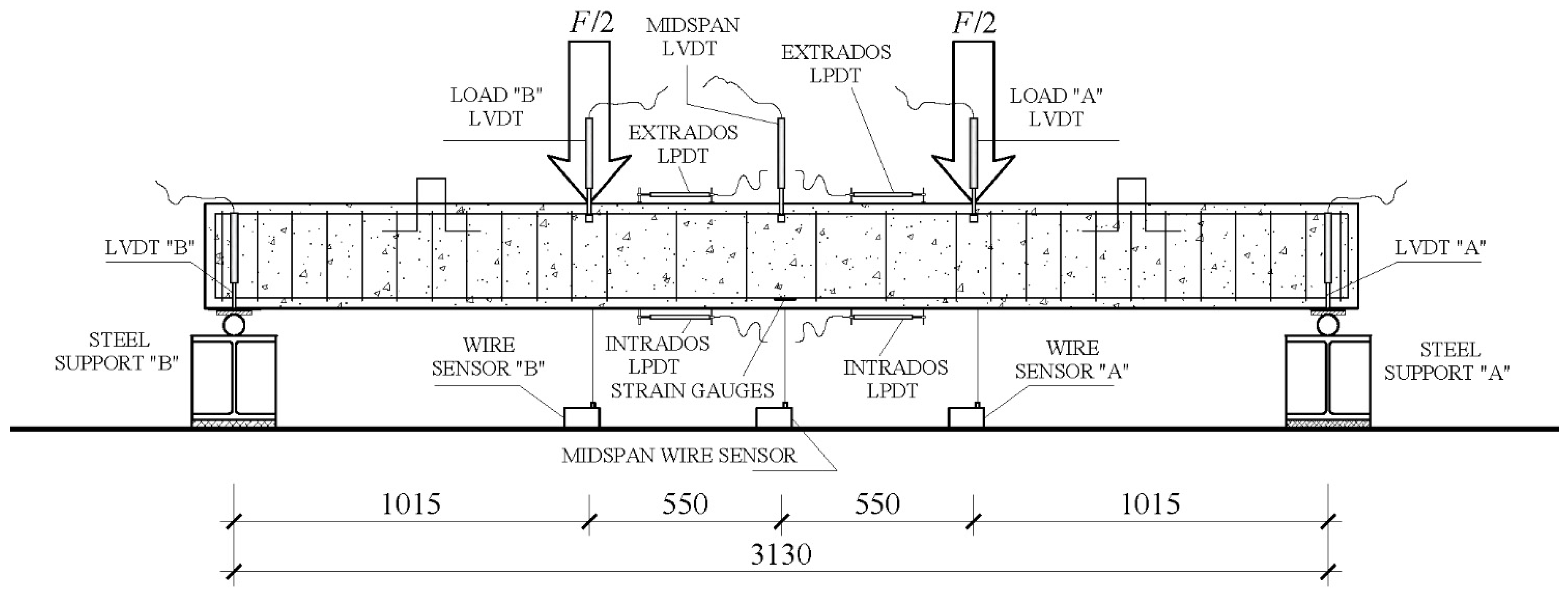
2.3. Beam Tests
3. Experimental Results
3.1. Direct Shear Test of SRG–Concrete Joints
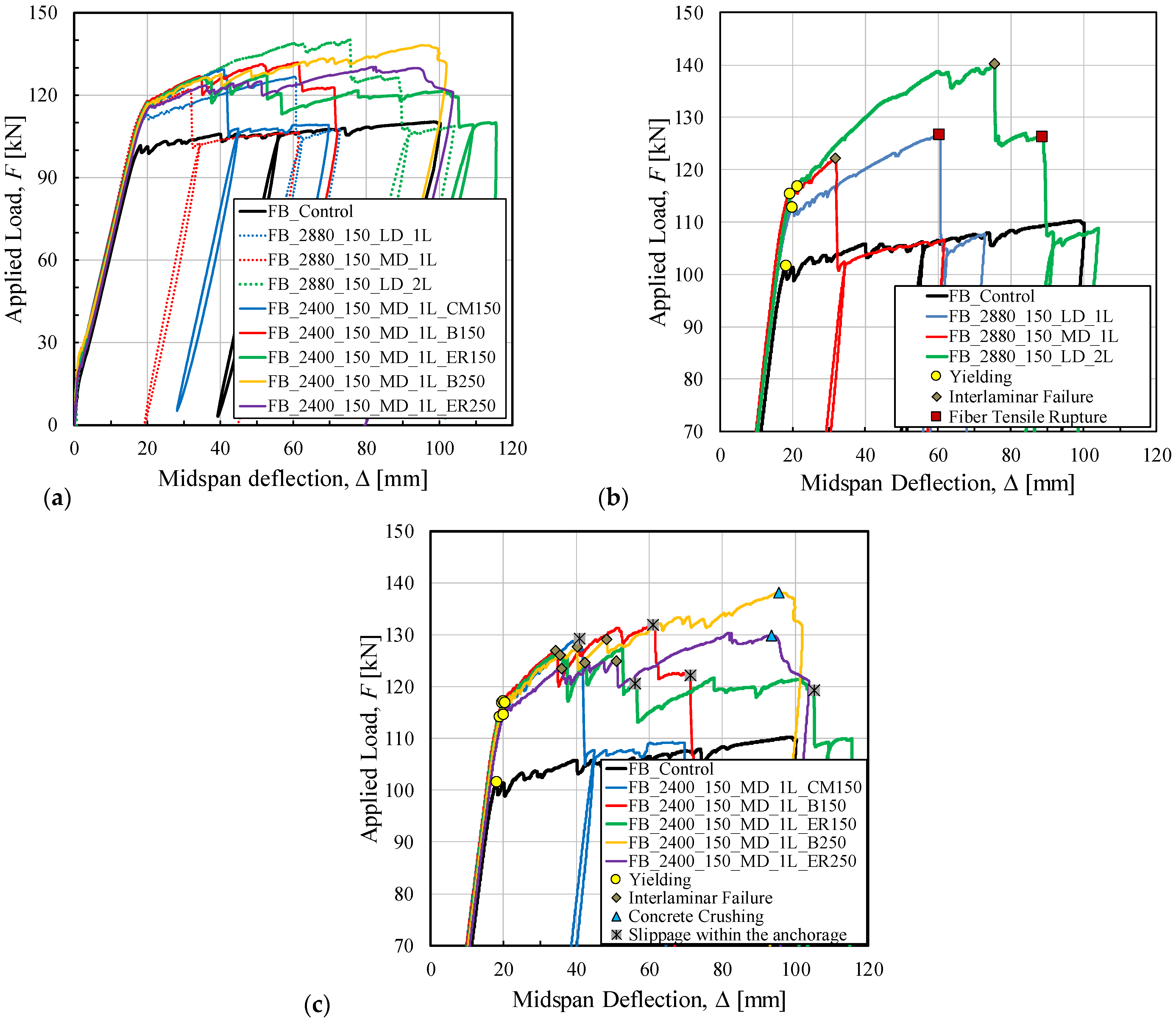
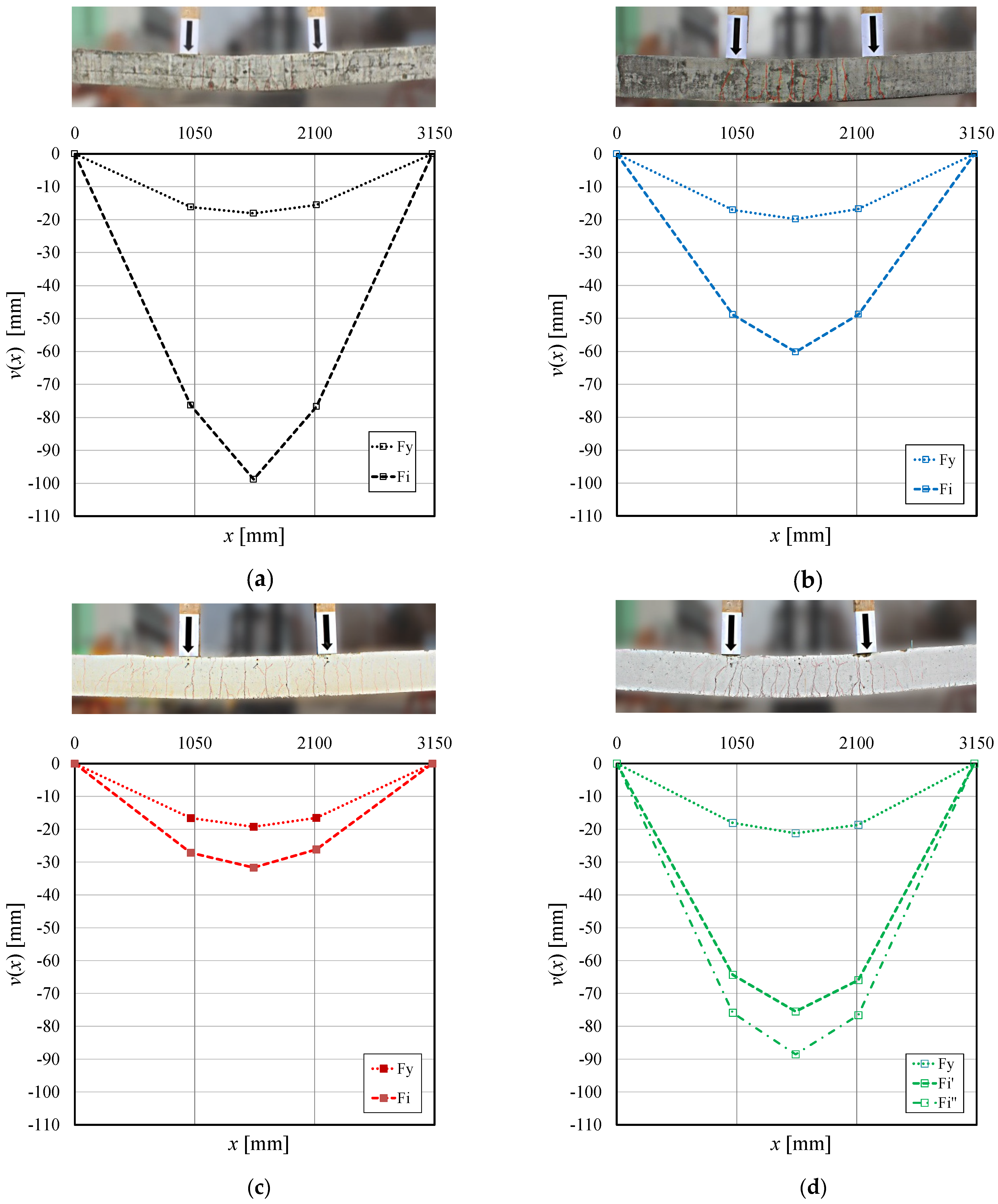
3.2. Four-Point Bending Tests on RC Beams
3.2.1. Control Beam
3.2.2. Specimens Strengthened Without Mechanical Anchors (Group A)
3.2.3. Specimens Strengthened with Mechanical Anchors (Group B)
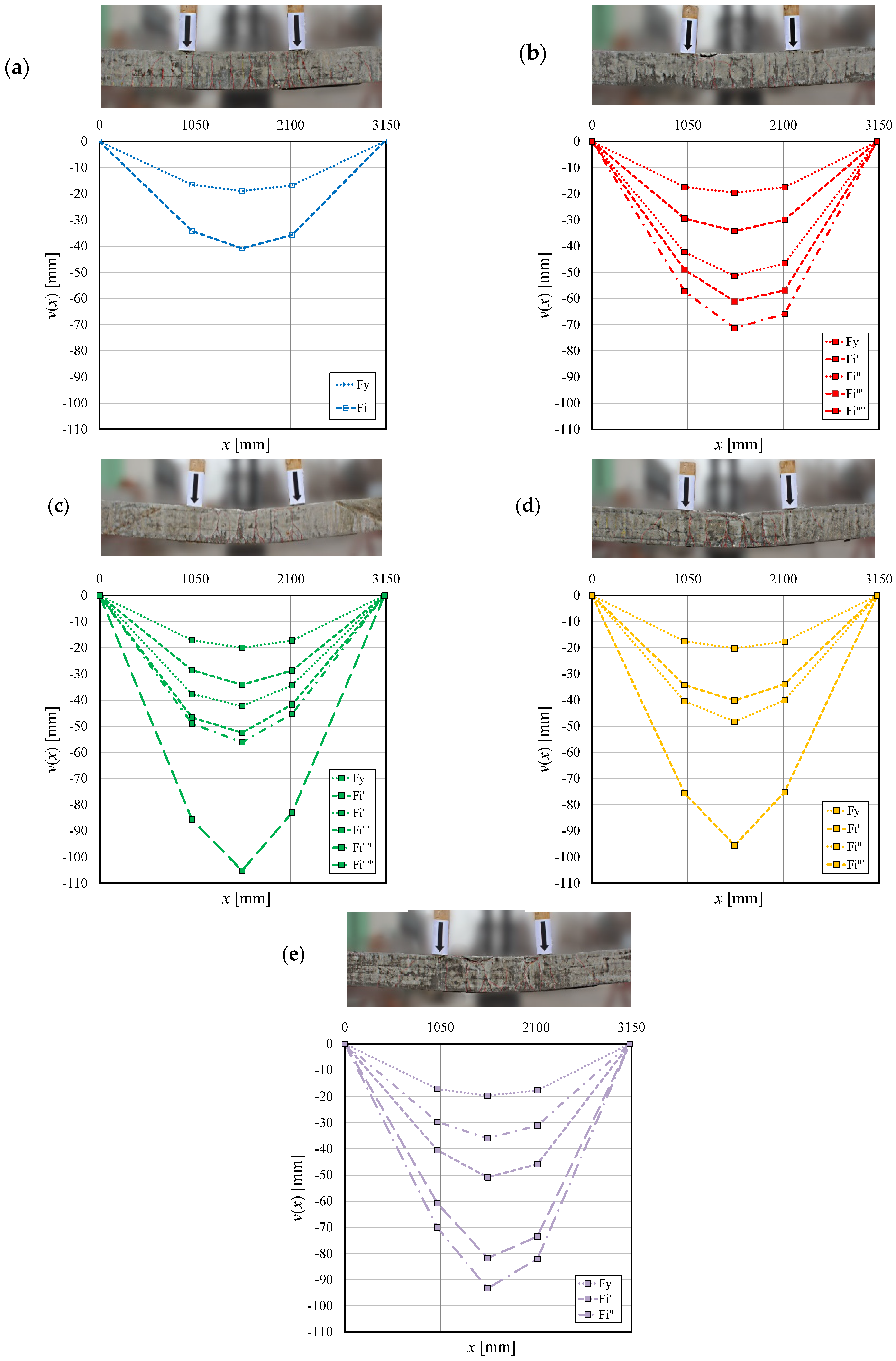
4. Discussion of the Results
4.1. Direct Shear Tests
4.2. Four-Point Bending Flexural Tests of RC Beams
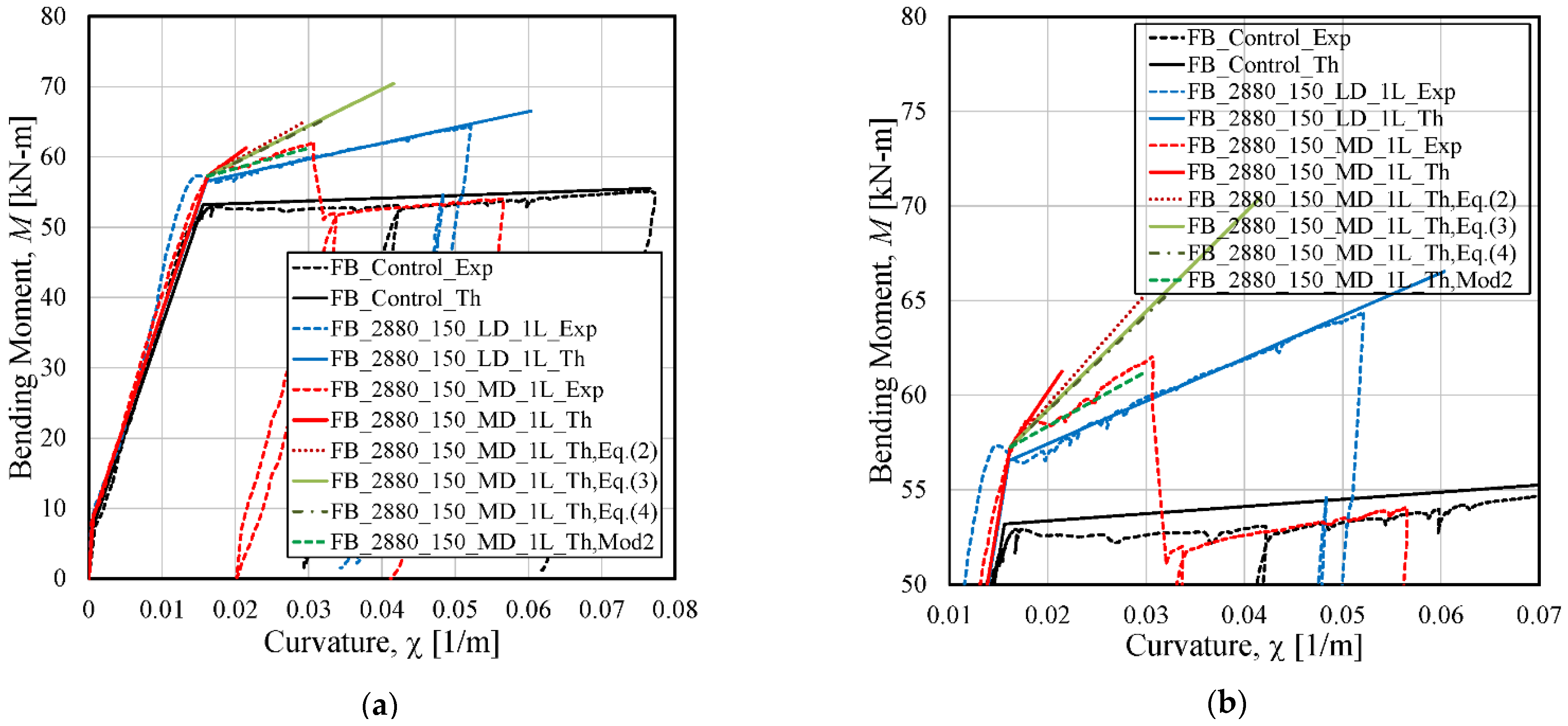
5. Analysis of Strain in the Fibers at Failure and Deformability of the Beams
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prota, A.; Manfredi, G.; Nanni, A.; Cosenza, E.; Pecce, M. Flexural strengthening of R/C beams using emerging materials: Ultimate behavior. In Proceedings of the CICE, Adelaide, Australia, 8–10 December 2004; pp. 163–170. [Google Scholar]
- Kim, J.Y.; Fam, A.; Kong, A.; El-Hacha, R. Flexural strengthening of RC beams using steel reinforced polymer (SRP) composites. In Proceedings of the 7th International Symposium FRP Reinforcement for Concrete Structures; ACI SP-230, 1, Paper #93; American Concrete Institute: Farmington Hills, MI, USA, 2005; pp. 1647–1664. [Google Scholar]
- Barton, B.; Wobbe, E.; Dharani, L.R.; Silva, P.; Birman, V.; Nanni, A.; Alkhrdaji, T.; Thomas, J.; Tunis, G. Characterization of reinforced concrete beams strengthened by steel reinforced polymer and grout (SRP and SRG) composites. Mater. Sci. Eng. A 2005, 412, 129–136. [Google Scholar]
- Prota, A.; Tan, K.Y.; Nanni, A.; Pecce, M.; Manfredi, G. Performance of shallow R/C beams with externally bonded steel-reinforced polymer. ACI Struct. J. 2006, 103, 163–170. [Google Scholar]
- Balsamo, A.; Nardone, F.; Iovinella, I.; Ceroni, F.; Pecce, M. Flexural strengthening of concrete beams with EB-FRP, SRP and SRCM: Experimental investigation. Compos. Part B 2013, 46, 91–101. [Google Scholar]
- Kalfat, R.; Al-Mahaidi, R.; Smith, S. Anchorage Devices Used to Improve the Performance of Reinforced Concrete Beams Retrofitted with FRP Composites: State-of-the-Art Review. J. Compos. Constr. 2013, 17, 14–33. [Google Scholar]
- Krevaikas, T.D.; Triantafillou, T.C. Masonry confinement with fibre-reinforced polymers. J. Compos. Constr. 2005, 9, 128–135. [Google Scholar]
- Corradi, M.; Grazini, A.; Borri, A. Confinement of brick masonry columns with CFRP materials. Compos. Sci. Technol. 2007, 67, 1772–1783. [Google Scholar]
- Aiello, M.A.; Micelli, F.; Valente, L. FRP confinement of square masonry columns. J. Compos. Constr. 2009, 13, 148–158. [Google Scholar]
- Di Ludovico, M.; D’Ambra, C.; Prota, A.; Manfredi, G. FRP Confinement of tuff and clay brick columns: Experimental study and assessment of analytical models. J. Compos. Constr. 2010, 14, 583–596. [Google Scholar]
- Incerti, A.; Vasiliu, A.; Ferracuti, B.; Mazzotti, C. Uni-Axial compressive tests on masonry columns confined by FRP and FRCM. In Proceedings of the 12th FRPRCS and 5th APFIS Conference, Nanjing, China, 14–16 December 2015. [Google Scholar]
- Mazzotti, C.; Sassoni, E.; Bellini, A.; Ferracuti, B.; Franzoni, E. Strengthening of masonry elements by FRP: Influence of brick mechanical and microstructural properties. Key Eng. Mater. 2015, 624, 330–337. [Google Scholar]
- Ferretti, F.; Incerti, A.; Ferracuti, B.; Mazzotti, C. Diagonal compression tests on masonry panels strengthened by FRP and FRCM. In Proceedings of the 10th SAHC Conference; Van Balen, K., Verstrynge, E., Eds.; Taylor & Francis Group: London, UK, 2016. [Google Scholar]
- Bencardino, F.; Spadea, G.; Swamy, R.N. Strength and ductility of reinforced concrete beams externally reinforced with carbon fiber fabric. ACI Struct. J. 2002, 99, 163–171. [Google Scholar]
- Wobbe, E.; Silva, P.; Barton, B.L.; Dharani, L.R.; Birman, V.; Nanni, A.; Alkhrdaji, T.; Thomas, J.; Tunis, T. Flexural capacity of R/C beams externally bonded with SRP and SRG. In Proceedings of the Society for the Advancement of Material and Process Engineering Symposium, Long Beach, CA, USA, 16–20 May 2004; pp. 20–27. [Google Scholar]
- Casadei, P.; Nanni, A.; Alkhrdaji, T.; Thomas, J. Performance of double-t prestressed concrete beams strengthened with steel reinforced polymer. Adv. Struct. Eng. 2005, 8, 427–442. [Google Scholar] [CrossRef]
- Babaeidarabad, S.; De Caso, F.; Nanni, A. URM walls strengthened with fabric-reinforced cementitious matrix composite subjected to diagonal compression. J. Compos. Constr. 2014, 18, 04013045. [Google Scholar] [CrossRef]
- De Felice, G.; De Santis, S.; Garmendia, L.; Ghiassi, B.; Larrinaga, P.; Lourenço, P.B.; Oliveira, D.V.; Paolacci, F.; Papanicolaou, C.G. Mortar-based systems for externally bonded strengthening of masonry. Mater. Struct. 2014, 47, 2021–2037. [Google Scholar] [CrossRef]
- D’Antino, T.; Carloni, C.; Sneed, L.H.; Pellegrino, C. Matrix-fiber bond behavior in PBO FRCM composites: A Fracture Mechanics Approach. Eng. Fract. Mech. 2014, 117, 94–111. [Google Scholar] [CrossRef]
- Hawileh, R.; Abdalla, J.; Nawaz, W.; Alzeer, A.; Muwafi, R.; Faridi, A. Strengthening reinforced concrete beams in flexure using hardwire steel fiber sheets. In Proceedings of the CICE, Vancouver, BC, Canada, 20–22 August 2014; p. 22. [Google Scholar]
- Napoli, A.; Realfonzo, R. Reinforced concrete beams strengthened with SRP/SRG systems: Experimental investigation. Constr. Build. Mater. 2015, 93, 654–677. [Google Scholar] [CrossRef]
- Sneed, L.H.; Verre, S.; Carloni, C.; Ombres, L. Flexural Behavior of RC Beams Strengthened with Steel-FRCM Composites. Eng. Struct. 2016, 127, 686–699. [Google Scholar] [CrossRef]
- Ferretti, F.; Incerti, A.; Ferracuti, B.; Mazzotti, C. FRCM strengthened masonry panels: The role of mechanical anchorages and symmetric layouts. Key Eng. Mater. 2017, 747, 334–341. [Google Scholar] [CrossRef]
- Incerti, A.; Ferretti, F.; Mazzotti, C. FRCM strengthening systems efficiency on the shear behavior of pre-damaged masonry panels: An experimental study. J. Build. Pathol. Rehabil. 2019, 4, 14. [Google Scholar] [CrossRef]
- Incerti, A.; Tilocca, A.R.; Ferretti, F.; Mazzotti, C. Influence of Masonry Texture on the Shear Strength of FRCM Reinforced Panels; RILEM Bookseries; Springer: Cham, Switzerland, 2019; Volume 18, pp. 1623–1631. [Google Scholar]
- Cascardi, A.; Longo, F.; Micelli, F.; Aiello, M.A. Compressive strength of confined column with Fiber Reinforced Mortar (FRM): New design-oriented-models. Constr. Build. Mater. 2017, 156, 387–401. [Google Scholar] [CrossRef]
- Carozzi, F.G.; Bellini, A.; D’Antino, T.; De Felice, G.; Focacci, F.; Hojdys, L.; Laghi, L.; Lanoye, E.; Micelli, F.; Panizza, M.; et al. Experimental investigation of tensile and bond properties of Carbon-FRCM composites for strengthening masonry elements. Compos. Part B 2017, 128, 100–119. [Google Scholar] [CrossRef]
- Incerti, A.; Santandrea, M.; Carloni, C.; Mazzotti, C. Destructive in situ tests on masonry arches strengthened with FRCM composite materials. Key Eng. Mater. 2017, 747, 567–573. [Google Scholar] [CrossRef]
- Bellini, A.; Incerti, A.; Bovo, M.; Mazzotti, C. Effectiveness of FRCM Reinforcement Applied to Masonry Walls Subject to Axial Force and Out-Of-Plane Loads Evaluated by Experimental and Numerical Studies. Int. J. Archit. Herit. 2018, 12, 376–394. [Google Scholar] [CrossRef]
- Kouris, L.A.S.; Triantafillou, T.C. State-of-the-art on strengthening of masonry structures with textile reinforced mortar (TRM). Constr. Build. Mater. 2018, 188, 1221–1233. [Google Scholar] [CrossRef]
- Bencardino, F.; Condello, A. Structural behaviour of RC beams externally strengthened in flexure with SRG and SRP systems. Int. J. Struct. Eng. 2014, 5, 346–368. [Google Scholar]
- Micelli, F.; Di Ludovico, M.; Balsamo, A.; Manfredi, G. Mechanical behaviour of FRP-confined masonry by testing of full-scalle columns. Mater. Struct. 2014, 47, 2081–2100. [Google Scholar] [CrossRef]
- Ebead, U.; El-Sherif, H. Near surface embedded-FRCM for flexural strengthening of reinforced concrete beams. Constr. Build. Mater. 2019, 204, 166–176. [Google Scholar]
- Aljazaeri, Z.R.; Janke, M.A.; Myers, J.J. A novel and effective anchorage system for enhancing the flexural capacity of RC beams strengthened with FRCM composite. Compos. Struct. 2019, 210, 20–28. [Google Scholar] [CrossRef]
- Spadea, G.; Bencardino, F.; Sorrenti, F.; Swamy, R.N. Structural effectiveness of FRP materials in strengthening RC beams. Eng. Struct. 2015, 99, 631–641. [Google Scholar]
- Raoof, S.M.; Koutas, L.N.; Bournas, D.A. Textile-reinforced mortar (TRM) versus fibre-reinforced polimer (FRP) in flexural strengthening of RC beams. Constr. Build. Mater. 2017, 151, 279–291. [Google Scholar]
- Bencardino, F.; Carloni, C.; Condello, A.; Focacci, F.; Napoli, A.; Realfonzo, R. Flexural behaviour of RC members strenghtened with FRCM: State-of-the-art and predictive formulas. Compos. Part B Eng. 2018, 148, 132–148. [Google Scholar]
- D’Antino, T.; Focacci, F.; Sneed, L.H.; Carloni, C. Relationship between the Effective Strain of PBO FRCM-Strengthened RC Beams and the Debonding Strain of Direct Shear Tests. Eng. Struct. 2020, 214, 110631. [Google Scholar] [CrossRef]
- BS EN 197-1:2019; Cement—Part 1: Composition, Specifications and Conformity Criteria for Common Cements. BSI Group: London, UK, 2019.
- BS EN 12390-3:2019; Testing Hardened Concrete—Compressive Strength of Test Specimens. BSI Group: London, UK, 2019.
- BS EN 12390-13:2013; Testing Hardened Concrete—Determination of Secant Modulus of Elasticity in Compression. BSI Group: London, UK, 2013.
- Carloni, C.; Santandrea, M.; Imohamed, A.O. Determination of the interfacial properties of SRP strips bonded to concrete and comparison between single-lap and notched beam tests. Eng. Fract. Mech. 2017, 186, 80–104. [Google Scholar]
- Carloni, C.; Santandrea, M.; Wendner, R. An investigation on the “width and size effect in the evaluation of the fracture energy of concrete”. Procedia Struct. Integr. 2017, 3, 450–458. [Google Scholar]
- Hillerborg, A. The theoretical basis of a method to determine the fracture energy GF of concrete. Mater. Struct. 1985, 18, 291–296. [Google Scholar] [CrossRef]
- Elices, M.; Guinea, V.G.; Planas, J. Measurement of the fracture energy using three-point bend tests: Part 3—Influence of cutting the P-δ tail. Mater. Struct. 1992, 25, 327–334. [Google Scholar]
- Hoover, C.G.; Bažant, Z.P. Comprehensive concrete fracture tests: Size effects of types 1 & 2, crack length effect and postpeak. Eng. Fract. Mech. 2013, 110, 281–289. [Google Scholar]
- ISO 15630-1:2010; Steel for the Reinforcement and Prestressing of Concrete—Test Methods–Part 1: Reinforcing Bars, Wire Rod and Wire. ISO: Geneva, Switzerland, 2010.
- Kerakoll Spa Website. Available online: https://products.kerakoll.com/en/c/repair-and-structural-strengthening-anti-seismic (accessed on 17 March 2025).
- De Santis, S.; Carozzi, F.G.; De Felice, G.; Poggi, C. Test methods for Textile Reinforced Mortar systems. Compos. Part B Eng. 2017, 127, 121–132. [Google Scholar]
- BS EN 1015-11:2019; Methods of Test for Mortar For Masonry Determination of Flexural and Compressive Strength of Hardened Mortar. BSI Group: London, UK, 2019.
- D’Antino, T.; Sneed, L.H.; Carloni, C.; Pellegrino, C. Effect of the Inherent Eccentricity in Single-Lap Direct Shear Tests of FRCM-Concrete Joints. Compos. Struct. 2016, 142, 117–129. [Google Scholar]
- Ascione, L.; Carozzi, F.G.; D’Antino, T.; Poggi, C. New Italian guidelines for design of externally bonded Fabric-Reinforced Cementitious Matrix (FRCM) systems for repair and strengthening of masonry and concrete structures. Procedia Struct. Integr. 2018, 11, 202–209. [Google Scholar]
- ASTM D8337; Standard Test Method for Evaluation of Bond Properties of FRP Composite Applied to Concrete Substrate Using Single-Lap Shear Test. ASTM: West Conshohocken, PA, USA, 2021.
- EN 1992-1-1; Eurocode 2—Design of Concrete Structures. European Committee for Standardization: Brussels, Belgium, 2004.







| fy,s (MPa) (CoV) | ft,s (MPa) (CoV) | εu,s (%) (CoV) | |
|---|---|---|---|
| Ø16 | 512.4 (0.01) | 636.1 (0.01) | 17.9 (0.06) |
| Ø10 | 584.1 (0.01) | 624.1 (0.02) | 6.7 (0.17) |
| Ø8 | 607.8 (0.02) | 637.2 (0.01) | 4.7 (0.08) |
| Specimen | Fiber Sheet Density | Number of Layer | Anchor Material | La (mm) |
|---|---|---|---|---|
| FB_Control | - | - | - | - |
| FB_2880_150_LD_1L | LD | 1 | - | - |
| FB_2880_150_MD_1L | MD | 1 | - | - |
| FB_2880_150_LD_2L | LD | 2 | - | - |
| FB_2400_150_MD_1L_CM150 | MD | 1 | Cementitious mortar | 150 |
| FB_2400_150_MD_1L_B150 | MD | 1 | Inorganic mortar | 150 |
| FB_2400_150_MD_1L_ER150 | MD | 1 | Epoxy resin | 150 |
| FB_2400_150_MD_1L_B250 | MD | 1 | Inorganic mortar | 250 |
| FB_2400_150_MD_1L_ER250 | MD | 1 | Epoxy resin | 250 |
| Specimen | Fy or Fy,control [kN] | Fi [kN] | Δy [mm] | Δi [mm] | Failure Mode | |||
|---|---|---|---|---|---|---|---|---|
| FB_Control | 101.7 | - | - | - | 18.1 | 100.1 | 5.53 (µc) | C |
| FB_2880_150_LD_1L | 112.9 | 1.11 | 126.7 | 1.12 | 19.9 | 60.2 | 3.03 (µc) | T |
| FB_2880_150_MD_1L | 115.5 | 1.14 | 122.2 | 1.06 | 19.2 | 31.7 | 1.65 (µc) | I |
| FB_2880_150_LD_2L | 116.9 | 1.15 | 140.2 126.4 | 1.20 1.08 | 21.2 | 75.5 88.6 | 3.56 4.17 (µc) | I T |
| FB_2400_150_MD_1L_CM150 | 114.3 | 1.12 | 129.4 | 1.13 | 18.9 | 40.9 | 2.16 (µc) | I/S |
| FB_2400_150_MD_1L_B150 | 117.0 | 1.15 | 126.9 131.3 131.9 122.1 | 1.08 1.12 1.13 1.04 | 19.6 | 34.2 51.5 61.1 71.3 | 1.75 2.63 3.12 3.64 (µc) | I C S S |
| FB_2400_150_MD_1L_ER150 | 117.3 | 1.15 | 126.1 124.7 127.5 120.7 119.2 | 1.08 1.06 1.09 1.03 1.02 | 20.0 | 35.5 42.3 52.4 56.1 105.2 | 1.71 2.12 2.62 2.81 5.27 (µc) | I I C S S |
| FB_2400_150_MD_1L_B250 | 116.9 | 1.15 | 127.7 129.1 138.2 | 1.09 1.10 1.18 | 20.3 | 40.2 48.3 95.6 | 1.99 2.38 4.72 (µc) | I I C |
| FB_2400_150_MD_1L_ER250 | 114.6 | 1.13 | 123.6 125.0 130.3 129.9 | 1.08 1.09 1.14 1.13 | 20.0 | 36.0 50.9 81.8 93.4 | 1.80 2.54 4.10 4.68 (µc) | I I C C |
| Specimen | Mcrack,Th (kNm) | χcrack,Th (1/m) | My,Th (kNm) | χy,Th (1/m) | Mu,Th (kNm) | χu,Th (1/m) | zu,Th (mm) |
|---|---|---|---|---|---|---|---|
| FB_Control | 7.3 | 0.00053 | 53.4 | 0.01532 | 55.8 | 0.08147 | - |
| FB_2880_150_LD_1L | 9.3 | 0.00065 | 56.7 | 0.01578 | 66.3 | 0.05939 | 54 |
| FB_2880_150_MD_1L | 9.3 | 0.00065 | 57.8 | 0.01618 | 61.2 | 0.02140 | 71 |
| Specimen | Mmax,Exp (kN-m) | (1/m) | zu,Exp (mm) | εu,FB,Exp (%) | (%) | (%) | εu,DS,Exp (%) |
|---|---|---|---|---|---|---|---|
| FB_2880_150_LD_1L | 64.3 | 0.053 | 67 | 1.257 | - | 1.656 | 1.594 |
| FB_2880_150_MD_1L | 62.0 | 0.031 | 71 | 0.722 | 1.050 | 0.792 | 0.499 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Incerti, A.; Rinaldini, V.; Santandrea, M.; Carloni, C.; Mazzotti, C. Effect of Density and Number of Layers of Fiber Sheets and End Anchors on the Flexural Capacity of SRG-Strengthened RC Beams. Buildings 2025, 15, 1005. https://doi.org/10.3390/buildings15071005
Incerti A, Rinaldini V, Santandrea M, Carloni C, Mazzotti C. Effect of Density and Number of Layers of Fiber Sheets and End Anchors on the Flexural Capacity of SRG-Strengthened RC Beams. Buildings. 2025; 15(7):1005. https://doi.org/10.3390/buildings15071005
Chicago/Turabian StyleIncerti, Andrea, Valentina Rinaldini, Mattia Santandrea, Christian Carloni, and Claudio Mazzotti. 2025. "Effect of Density and Number of Layers of Fiber Sheets and End Anchors on the Flexural Capacity of SRG-Strengthened RC Beams" Buildings 15, no. 7: 1005. https://doi.org/10.3390/buildings15071005
APA StyleIncerti, A., Rinaldini, V., Santandrea, M., Carloni, C., & Mazzotti, C. (2025). Effect of Density and Number of Layers of Fiber Sheets and End Anchors on the Flexural Capacity of SRG-Strengthened RC Beams. Buildings, 15(7), 1005. https://doi.org/10.3390/buildings15071005






