The Influence of the Construction of the Bridge Pile Foundation on the Adjacent Operating Subway Tunnel Considering the Creep Characteristics of the Stratum
Abstract
1. Introduction
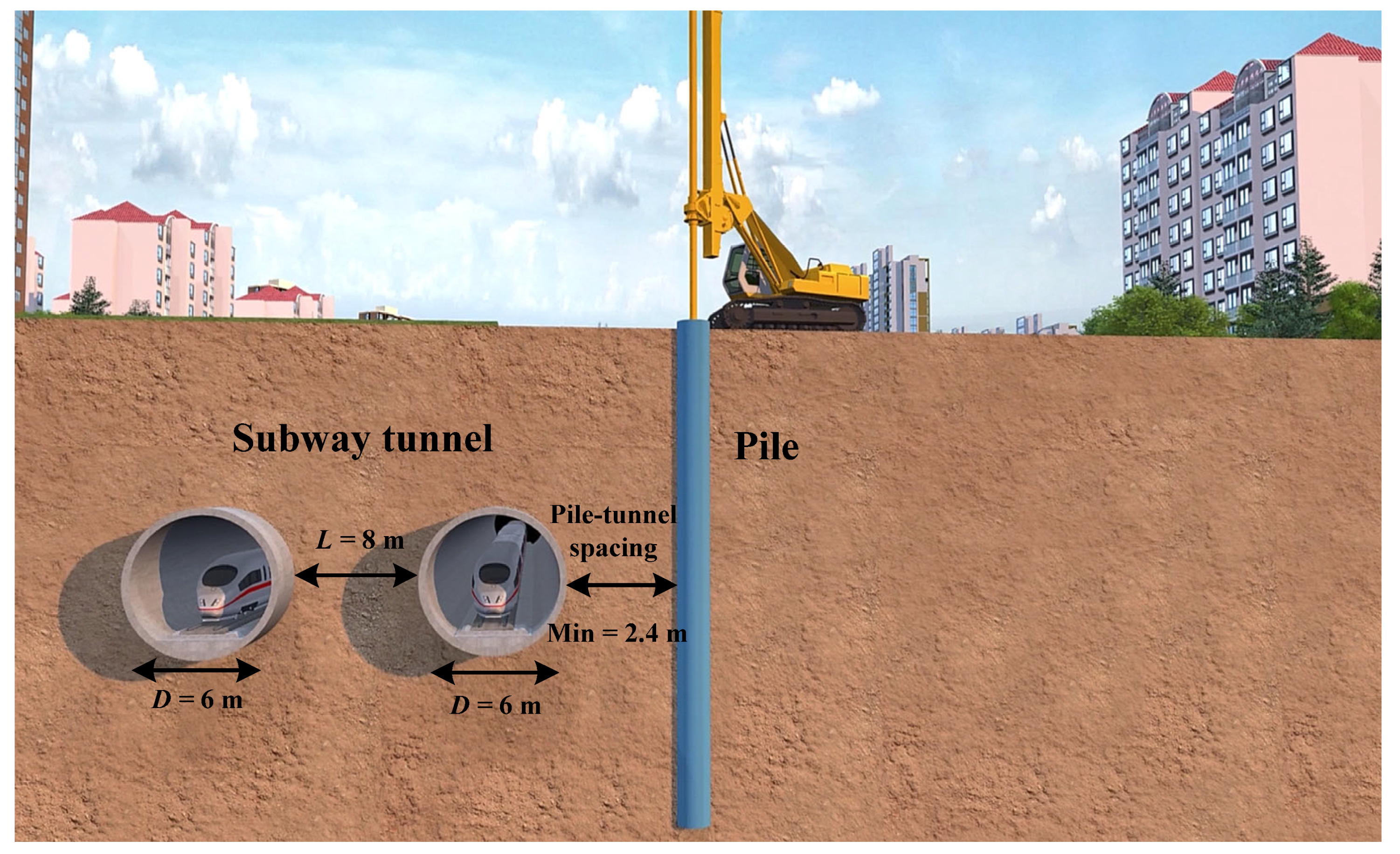
2. Engineering Background
2.1. Project Overview
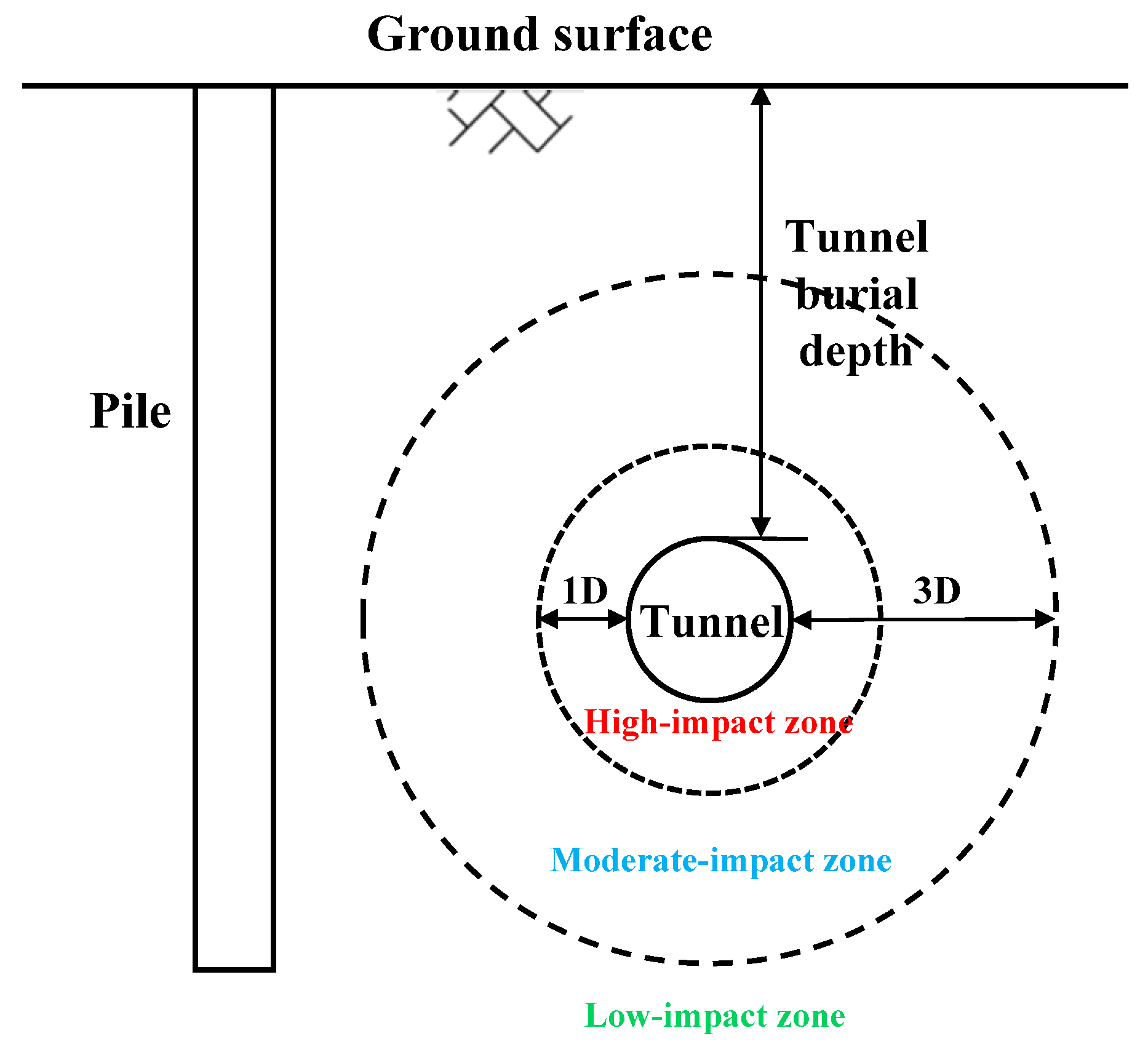
2.2. Tunnel Monitoring
3. Creep Test and Model Identification
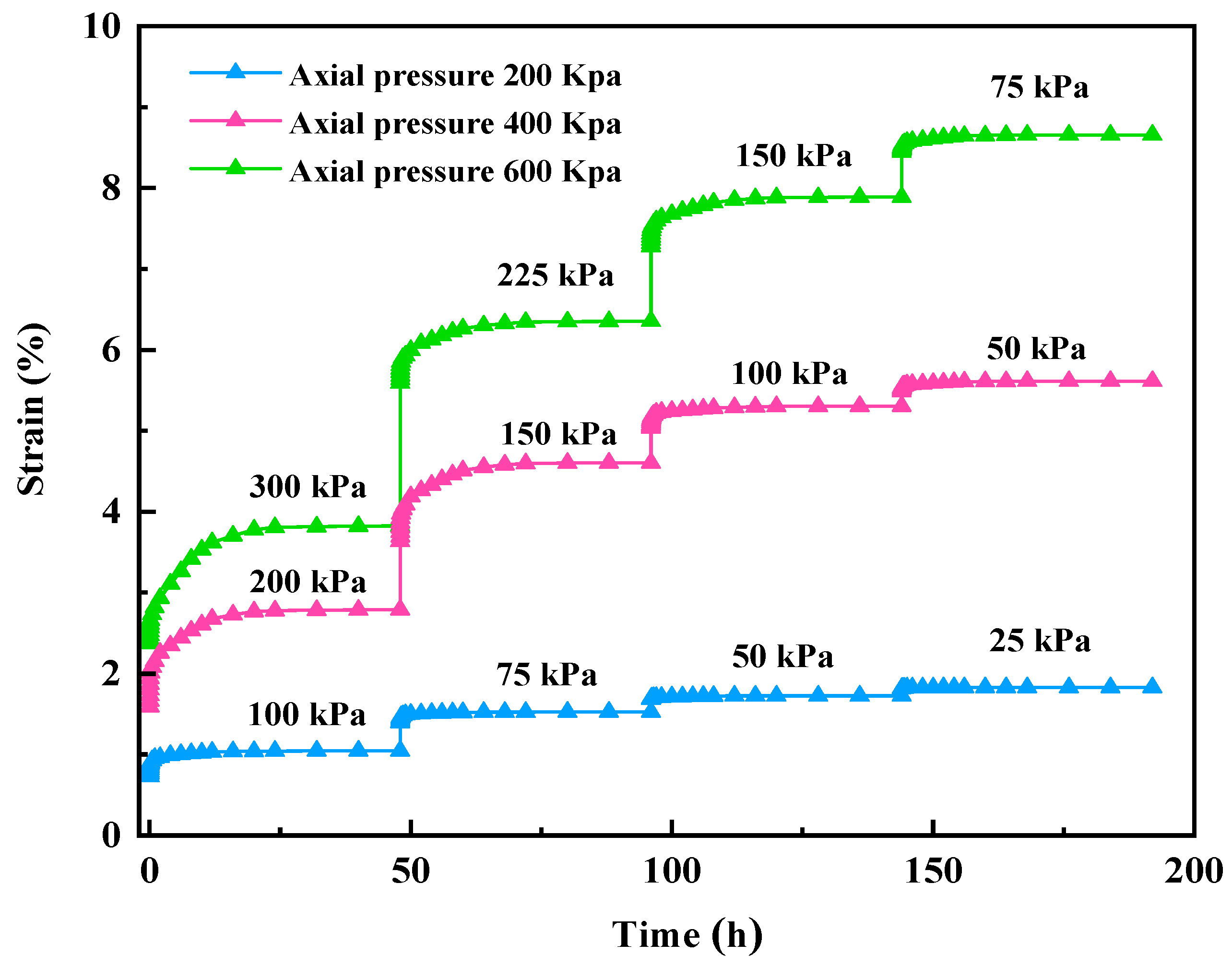
3.1. Graded Unloading Creep Test
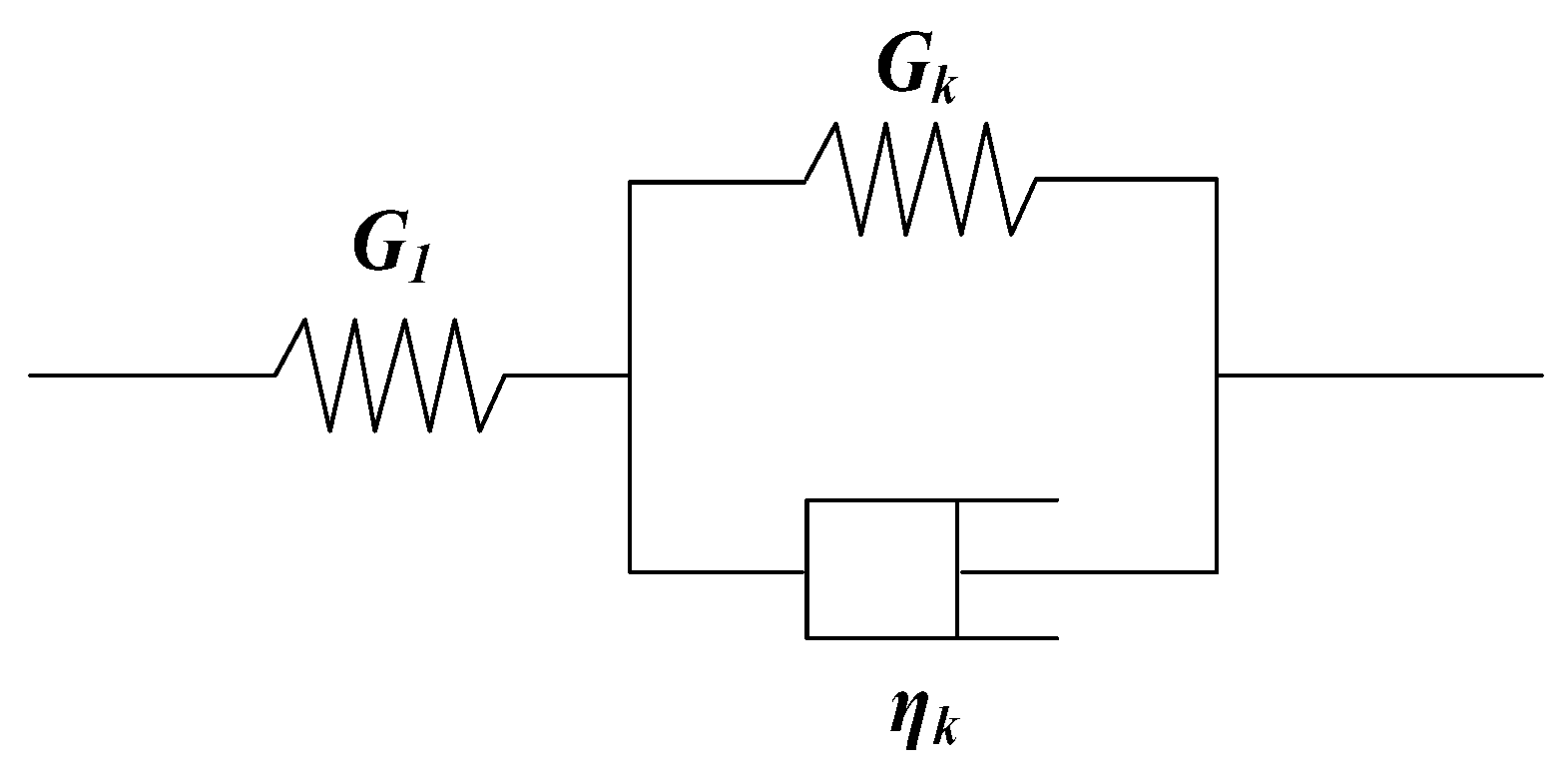
3.2. Creep Test Results and Identification of Creep Model
4. Theoretical Analysis and Numerical Simulation
4.1. Assumption and Soil Deformation
4.2. Calculation of Viscoelastic Solutions
4.3. Numerical Model and Parameter Determination
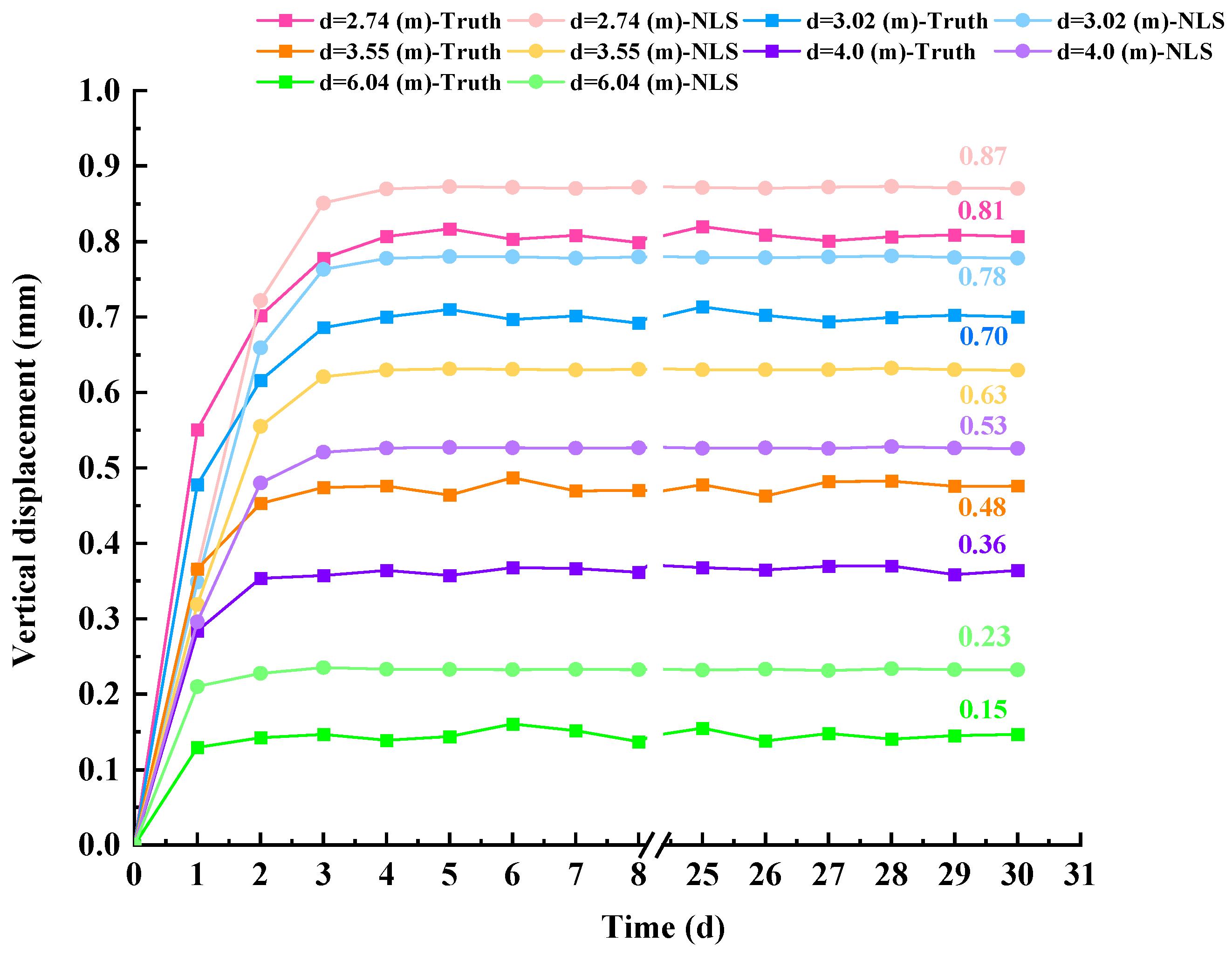
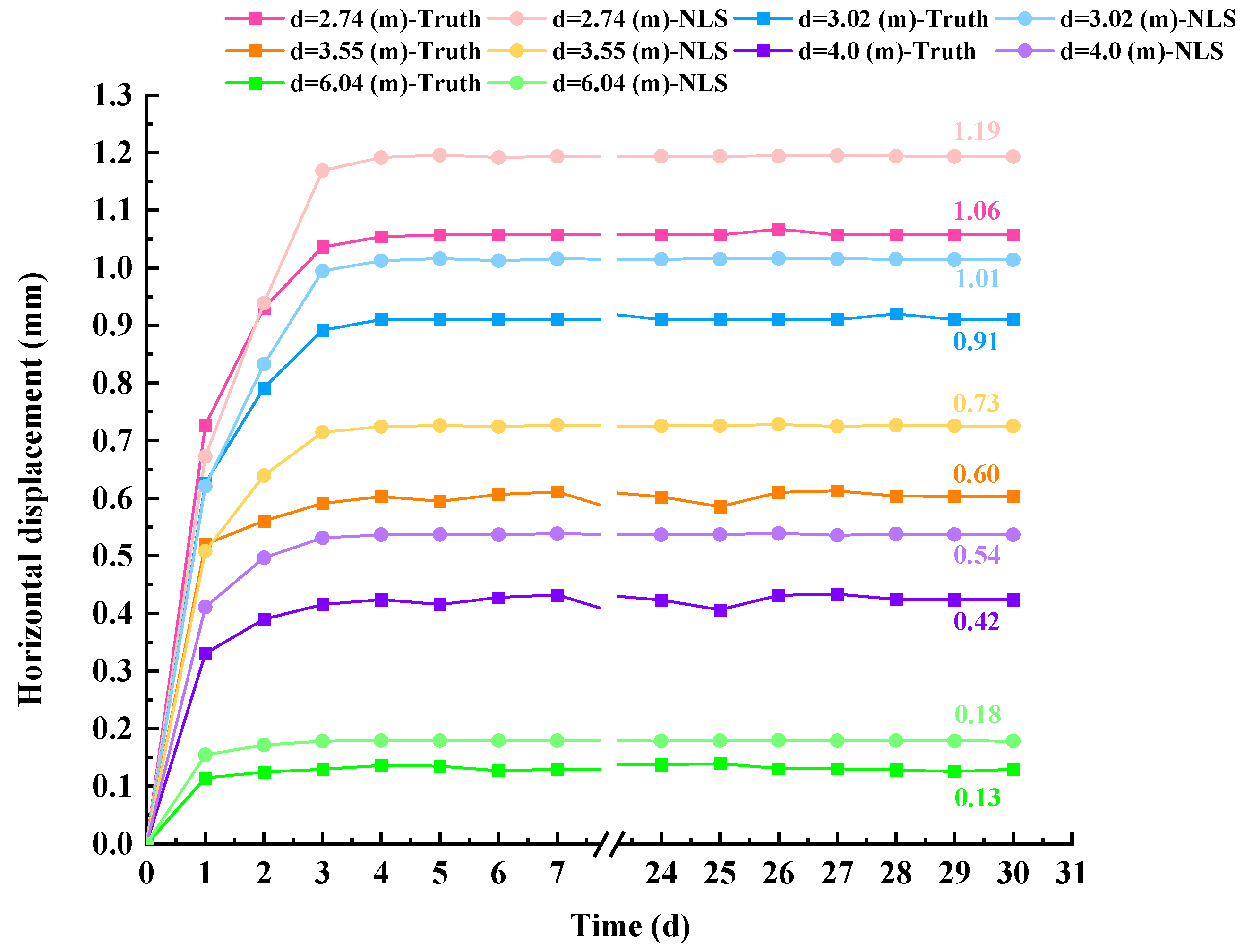
5. Comparative Analysis of Theoretical Models, Numerical Simulations, and Monitoring Data
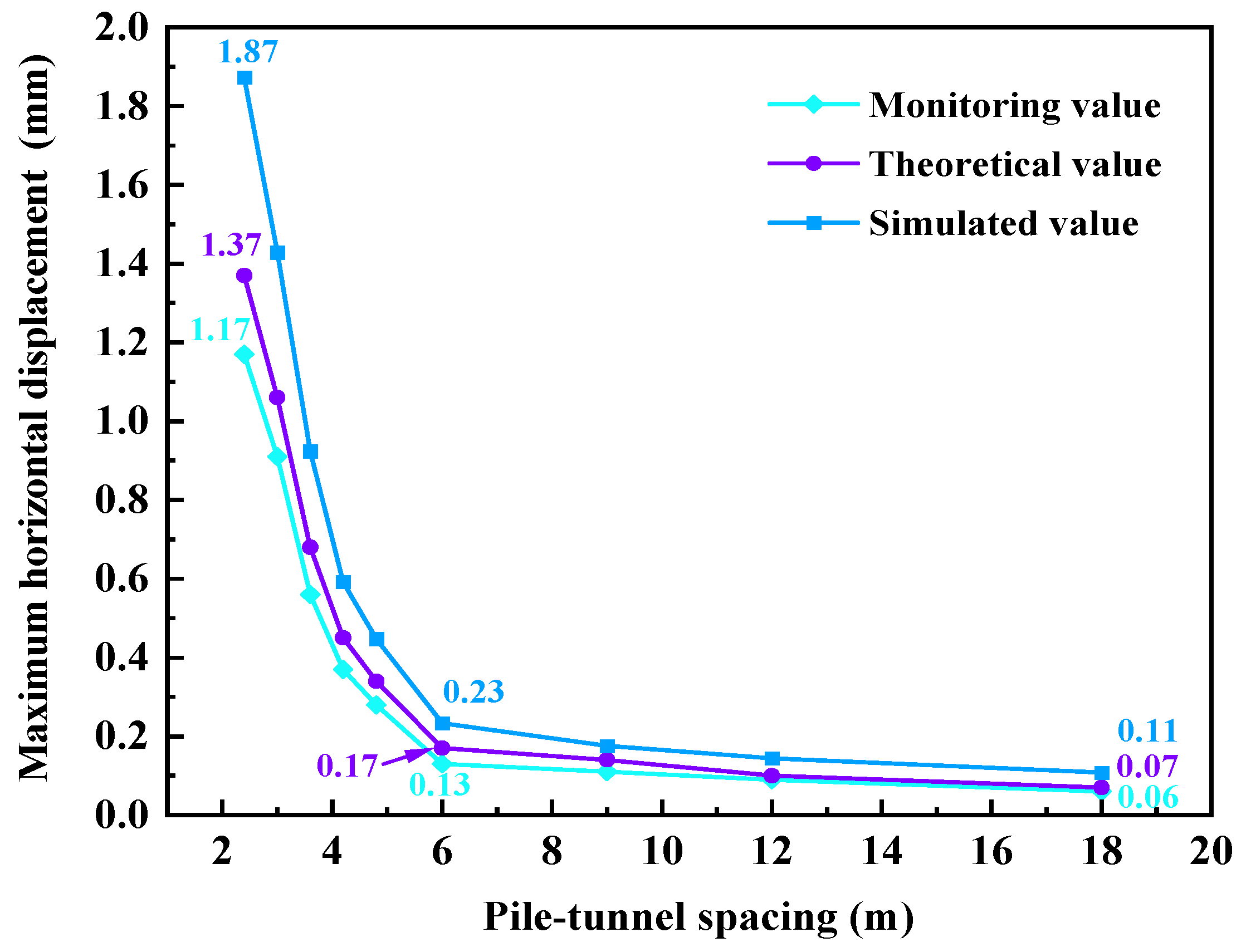
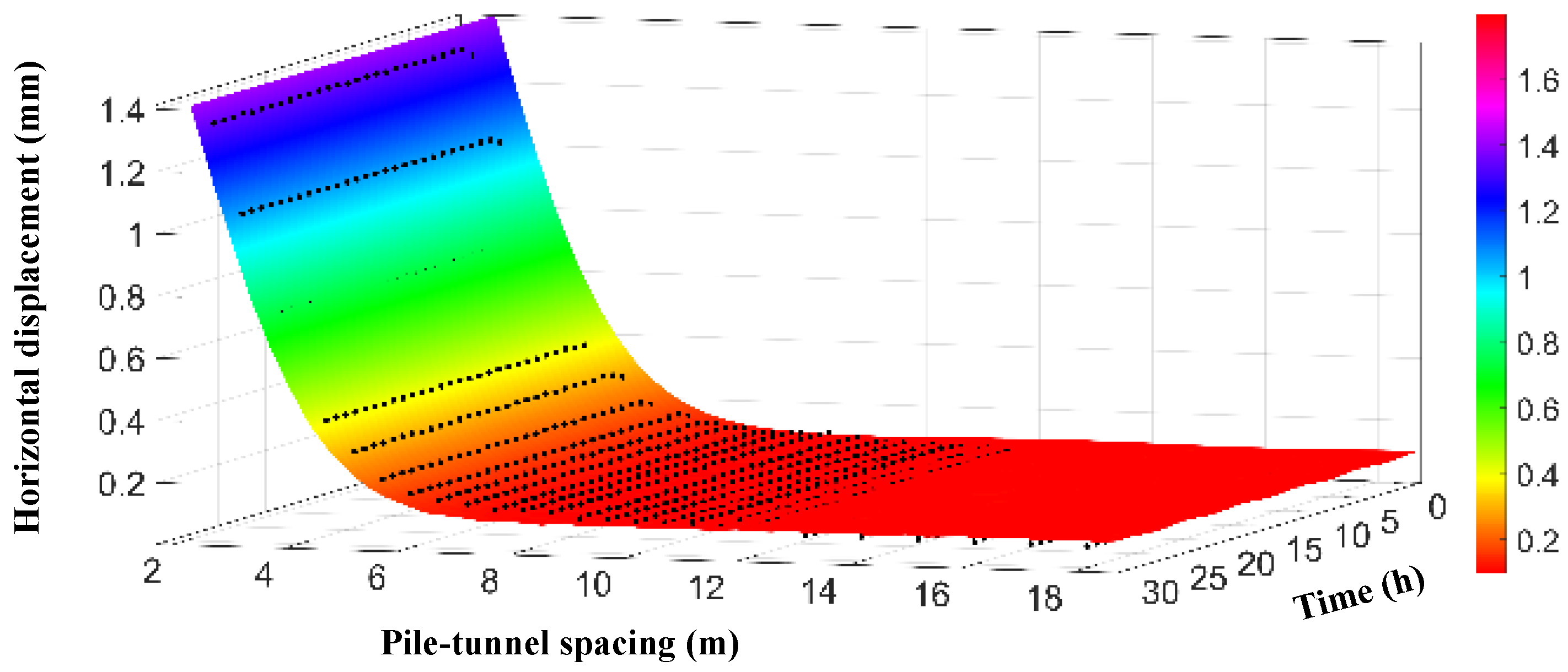
5.1. The Effect of Pile–Tunnel Spacing on Tunnel Deformation
5.2. Impact of Time Variations on Tunnel Deformation
5.3. Tunnel Deformation Prediction Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, L.; Xiang, P.; Qian, Y.; Yang, S.; Zhou, T.; Wang, F. Vulnerability Assessment of Urban Rail Transit Network—A Case Study of Chongqing. Buildings 2025, 15, 170. [Google Scholar] [CrossRef]
- Wei, Y.; Yang, X.; Xiao, X.; Ma, Z.; Zhu, T.; Dou, F.; Wu, J.; Chen, A.; Gao, Z. Understanding the Resilience of Urban Rail Transit: Concepts, Reviews, and Trends. Engineering 2024, 41, 7–18. [Google Scholar] [CrossRef]
- Wei, J.L.; Zhao, L.Y. Urban Road Network Vulnerability Assessment and Mitigation Strategies: A Case Study in Wuhan Main City. Mod. Urban Res. 2020, 35, 6. [Google Scholar]
- Zargarian, R. A new sustainability framework for urban underground space. Proc. Inst. Civ. Eng.-Eng. Sustain. 2016, 171, 238–253. [Google Scholar] [CrossRef]
- Li, X.; Liu, T.; Ju, S.; Guo, Y. Optimization and Impact Assessment of Excavation Sequence around Subway Stations from the Perspective of Sustainable Urban Development. Buildings 2024, 14, 1767. [Google Scholar] [CrossRef]
- Liu, B.; Yu, Z.; Yao, B.; Han, Y.; Liu, H.; Wang, S. Responses of the ground and adjacent pile to excavation of U-shaped tunnel. Comput. Geotech. 2021, 130, 103919. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, G.; Diao, Y.; Li, Z.; Peng, J.; Jia, J.; Li, K.; Huang, J. Effect of excavation on adjacent tunnel and performance of grouting-based active protective method in spatially variable soil. KSCE J. Civ. Eng. 2025, 29, 100053. [Google Scholar] [CrossRef]
- Lueprasert, P.; Jongpradist, P.; Jongpradist, P.; Suwansawat, S. Numerical investigation of tunnel deformation due to adjacent loaded pile and pile-soil-tunnel interaction. Tunn. Undergr. Space. Technol. 2017, 70, 166–181. [Google Scholar] [CrossRef]
- Lin, G.; Ke, W.; Guo, S.; Lin, Z.; Xu, C.; Chi, M.; Xiao, Y. Influence of pile foundation construction on existing tunnels in a Metro Protection Area: Field Test and Numerical Simulation. Buildings 2024, 14, 2280. [Google Scholar] [CrossRef]
- Tao, W.; Le, W.; Nan, C.L. The Influence of Bridge Construction and Operation on Adjacent Nanjing Yangtze River Tunnels. Adv. Mater. Res. 2013, 838–841, 1018–1023. [Google Scholar]
- Schroeder, F.C. The Influence of Bored Piles on Existing Tunnels. Ph.D. Thesis, Imperial College London, London, UK, 2003. [Google Scholar]
- Yoo, C. Three-dimensional numerical investigation on the effect of bridge construction on existing tunnel. KSCE J. Civ. Eng. 2014, 18, 794–802. [Google Scholar] [CrossRef]
- Lueprasertl, P.; Jongpradist, P.; Charoenpak, K. Three-dimensional finite element analysis for preliminary establishment of tunnel influence zone subject to pile loading. Maejo. Int. J. Sci. Tech. 2015, 9, 209–223. [Google Scholar]
- Li, T.; Chen, G.; Liu, Y.; Luo, B.; Zhu, B. Mechanical Characteristics of the Combination System of Medium-Diameter Anti-Slide Piles and Tunnel-Under-Landslide Loading. Sustainability 2022, 14, 12135. [Google Scholar] [CrossRef]
- Yao, J.; Taylor, R.N.; McNamara, A.M. The effects of loaded bored piles on existing tunnels. In Geotechnical Aspects of Underground Construction in Soft Ground; CRC Press: Boca Raton, FL, USA, 2009; pp. 751–754. [Google Scholar]
- Sadek, M.; Shahrour, I. Use of the Boussinesq solution in geotechnical and road engineering: Influence of plasticity. Comptes Rendus. Mécanique 2007, 335, 516–520. [Google Scholar]
- Mindlin, R.D. Force at a point in the interior of a semi-infinite solid. Physics 1936, 7, 195–202. [Google Scholar] [CrossRef]
- Liang, R.Z.; Xia, T.D.; Huang, M.S.; Lin, C.G. Simplified analytical method for evaluating the effects of adjacent excavation on shield tunnel considering the shearing effect. Comput. Geotech. 2017, 81, 167–187. [Google Scholar]
- Liang, R.Z.; Wu, W.B.; Yu, F.; Liu, J.W.; Jiang, G. Simplified method for evaluating shield tunnel deformation due to adjacent excavation. Tunn. Undergr. Space Technol. 2018, 71, 94–105. [Google Scholar] [CrossRef]
- Jia, R.; Zheng, G.; Jiang, Y. The effect of clay structure formed during deposition on the ground deformation induced by shield tunneling. Tunn. Undergr. Space Technol. 2024, 147, 105689. [Google Scholar]
- Zeng, G.; Wang, H.; Jiang, M. Analytical solutions of noncircular tunnels in viscoelastic semi-infinite ground subjected to surcharge loadings. Appl. Math. Model. 2022, 102, 492–510. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Y.; Han, Y.; Wei, G.; Pan, Y.; Sun, M. Mathematical modelling for interaction between soft ground and small curvature shield tunneling considering viscoelastic characteristics influences. Appl. Math. Model. 2024, 127, 607–639. [Google Scholar] [CrossRef]
- CJJT 202-2013; Technical Code for Protection Structures of Urban Rail Transit. China Architecture & Building Press: Beijing, China, 2013.
- GB 50911-2013; Code for Monitoring Measurement of Urban Rail Transit Engineering. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2013.
- Zhang, J.F.; Chen, J.J.; Wang, J.H.; Zhu, Y.F. Prediction of tunnel displacement induced by adjacent excavation in soft soil. Tunn. Undergr. Space Technol. 2013, 36, 24–33. [Google Scholar] [CrossRef]
- Zheng, W. Simplified method for evaluating mechanical interactions between tunnel and soil due to adjacent excavation. Tunn. Undergr. Space Technol. 2023, 139, 105205. [Google Scholar]
- Zhang, Z.; Zhang, M.; Zhao, Q. A simplified analysis for deformation behavior of buried pipelines considering disturbance effects of underground excavation in soft clays. Arab. J. Geosci. 2015, 8, 7771–7785. [Google Scholar] [CrossRef]
- Shi, X.; Rong, C.; Wang, H.; Cui, L.; Cai, H.; Wang, B. Analytical Study of Soil Displacement Induced by Twin Shield Tunneling in Semi-Infinite Viscoelastic Ground. Adv. Civ. Eng. 2020, 2020, 8839010. [Google Scholar]









| Density/(g·cm−3) | Porosity Ratio | Saturation/% | Internal Friction Angle φ/° | Cohesion c/kPa |
|---|---|---|---|---|
| 2.01 | 0.679 | 93.9 | 15.4 | 79.4 |
| Sample Name | Axial Pressure (kPa) | Confining Pressure (kPa) |
|---|---|---|
| 1 | 200 | 100 → 75 → 50 → 25 |
| 2 | 400 | 200 → 150 → 100 → 50 |
| 3 | 600 | 300 → 225 →150 → 75 |
| Material Name | ρ/(kg·m−3) | E/MPa | v | Internal Friction Angle φ/° | Cohesion c/kPa |
|---|---|---|---|---|---|
| Plain fill | 1860 | 10.8 | 0.35 | 11.8 | 35.8 |
| Clay | 2010 | 30.5 | 0.3 | 15.4 | 79.4 |
| Sandstone | 2230 | 28,000 | 0.18 | 35 | 240 |
| Tunnel | 2500 | 35,000 | 0.2 | - | - |
| Pile | 2500 | 30,000 | 0.3 | - | - |
| Model Parameter | K/MPa | Gk/MPa | ηk/MPa·h | G1/MPa |
|---|---|---|---|---|
| Clay | 24.75 | 12.70 | 334.7 | 9.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Cui, W. The Influence of the Construction of the Bridge Pile Foundation on the Adjacent Operating Subway Tunnel Considering the Creep Characteristics of the Stratum. Buildings 2025, 15, 1001. https://doi.org/10.3390/buildings15071001
Wu D, Cui W. The Influence of the Construction of the Bridge Pile Foundation on the Adjacent Operating Subway Tunnel Considering the Creep Characteristics of the Stratum. Buildings. 2025; 15(7):1001. https://doi.org/10.3390/buildings15071001
Chicago/Turabian StyleWu, Dandan, and Wentian Cui. 2025. "The Influence of the Construction of the Bridge Pile Foundation on the Adjacent Operating Subway Tunnel Considering the Creep Characteristics of the Stratum" Buildings 15, no. 7: 1001. https://doi.org/10.3390/buildings15071001
APA StyleWu, D., & Cui, W. (2025). The Influence of the Construction of the Bridge Pile Foundation on the Adjacent Operating Subway Tunnel Considering the Creep Characteristics of the Stratum. Buildings, 15(7), 1001. https://doi.org/10.3390/buildings15071001





