Deflection Predictions of Tapered Cellular Steel Beams Using Analytical Models and an Artificial Neural Network
Abstract
1. Introduction

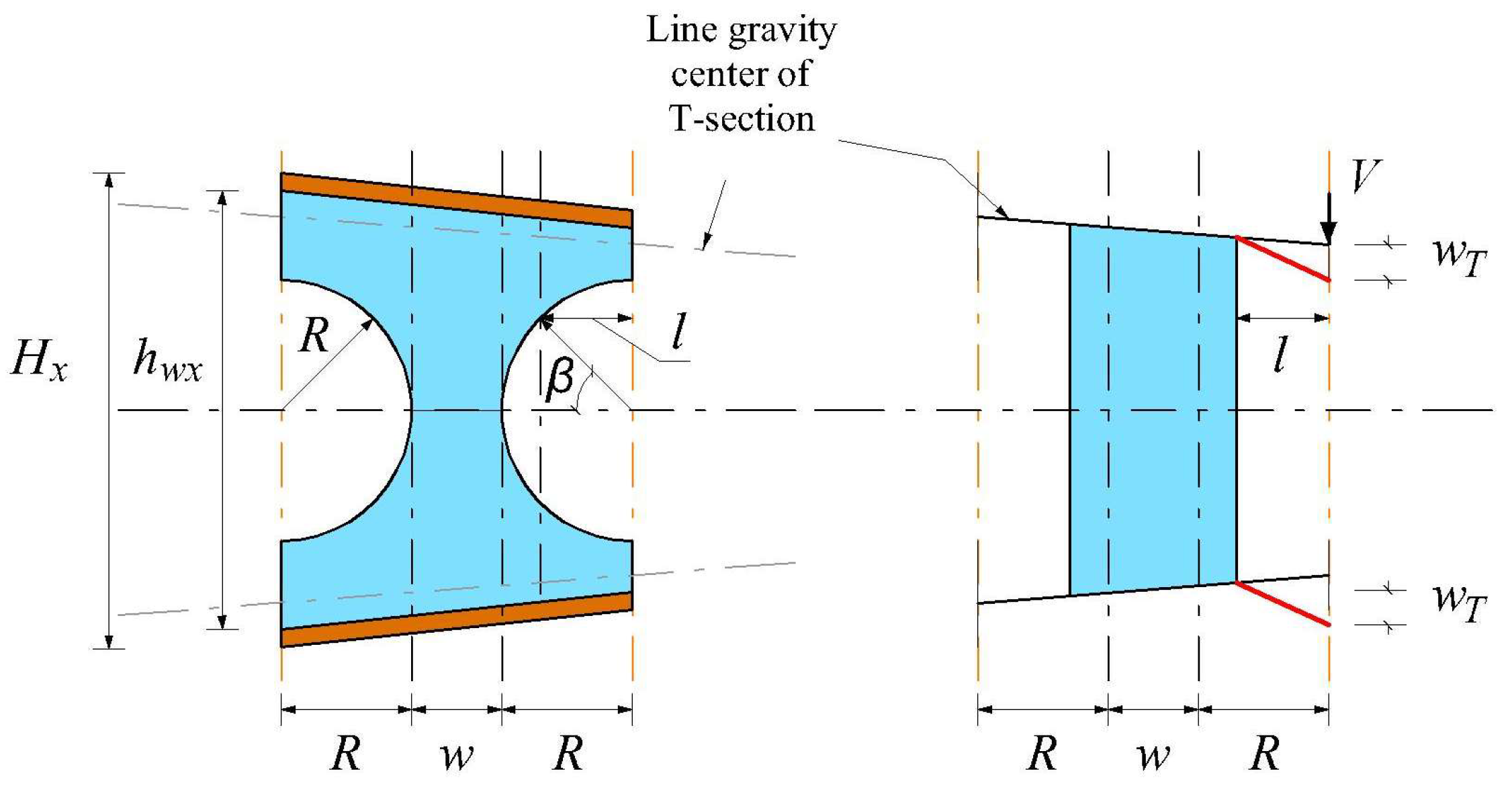
2. Prediction Models for Additional and Total Deflection
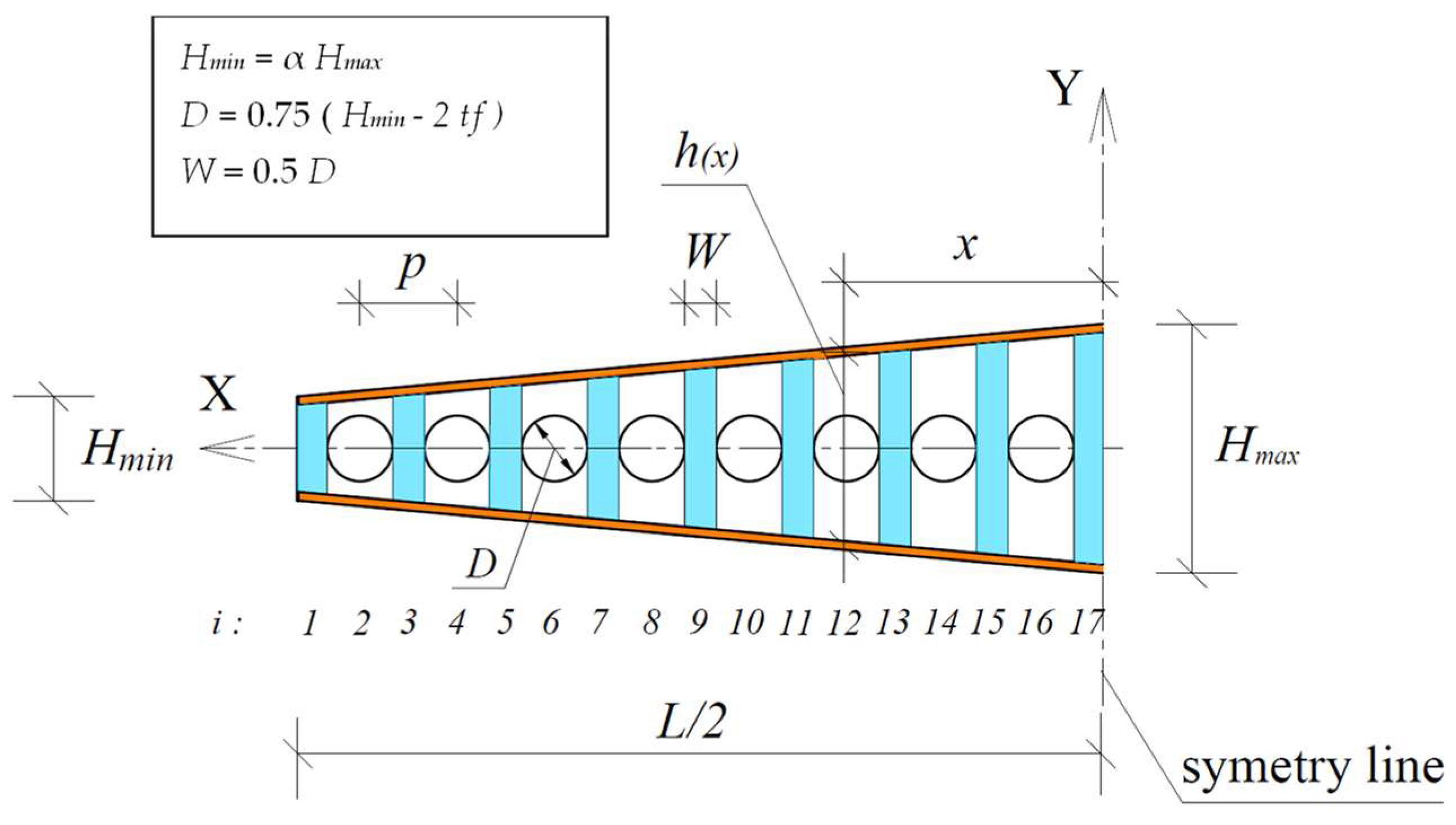
3. Proposed Model
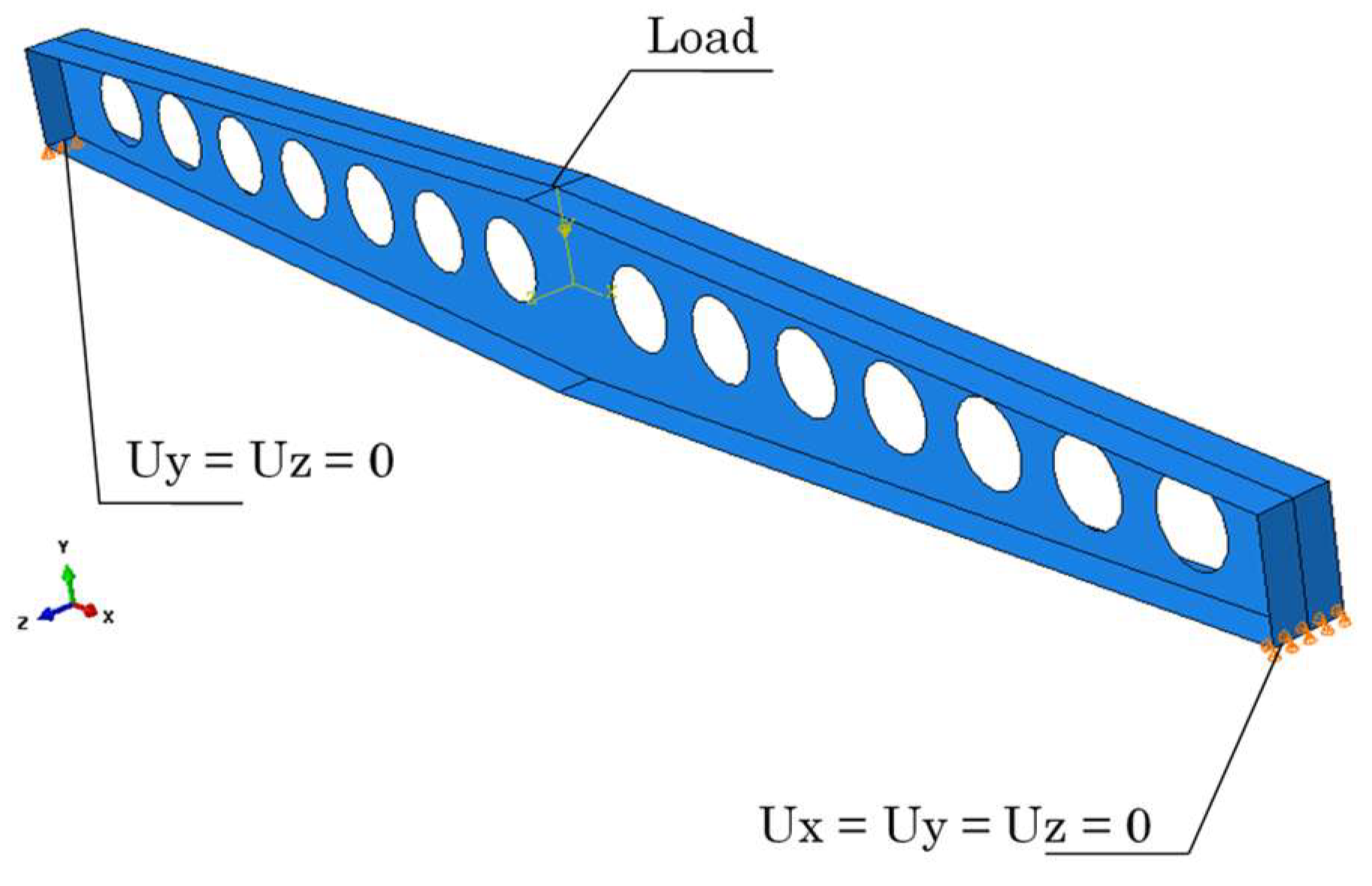
4. Finite Element Method
5. Artificial Neural Network
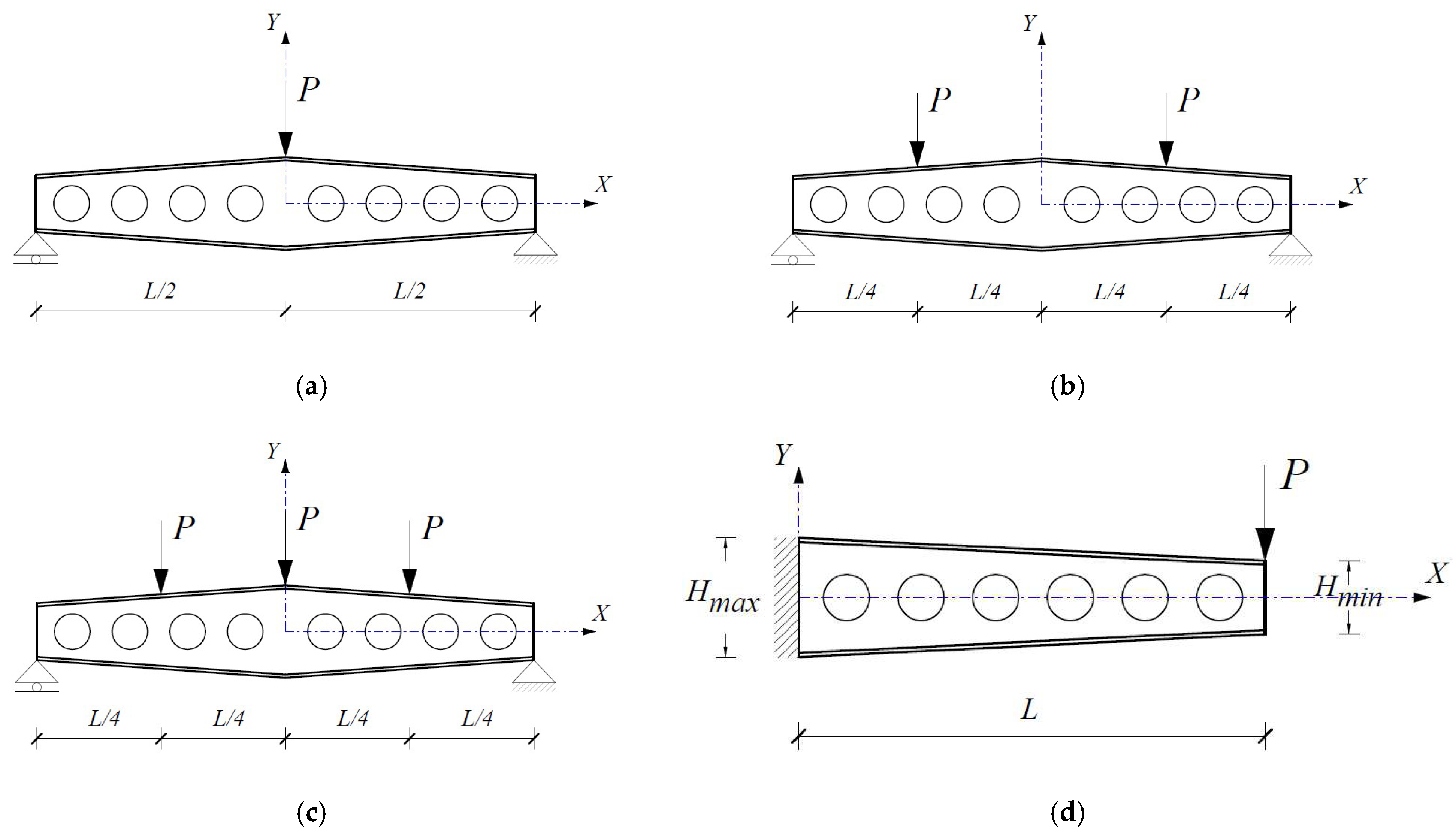
6. Results and Discussion
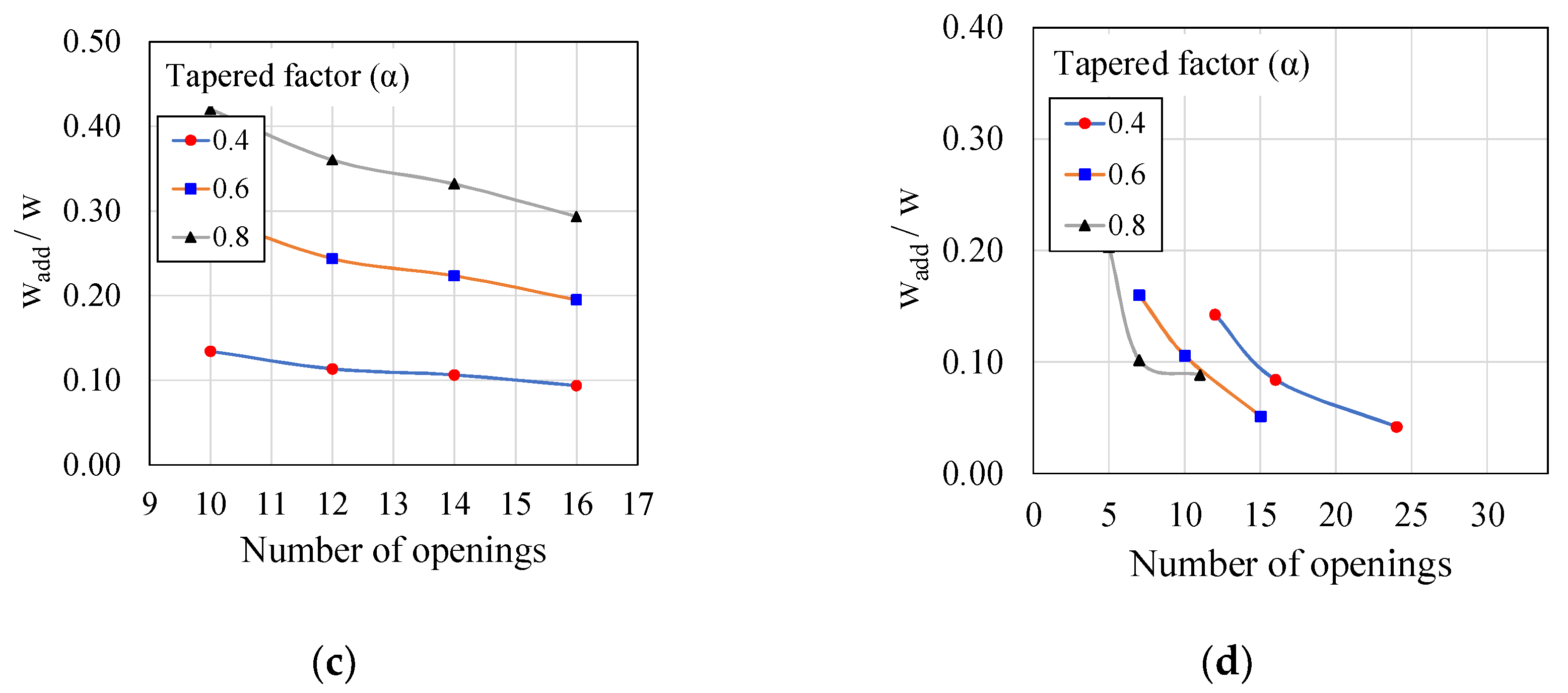
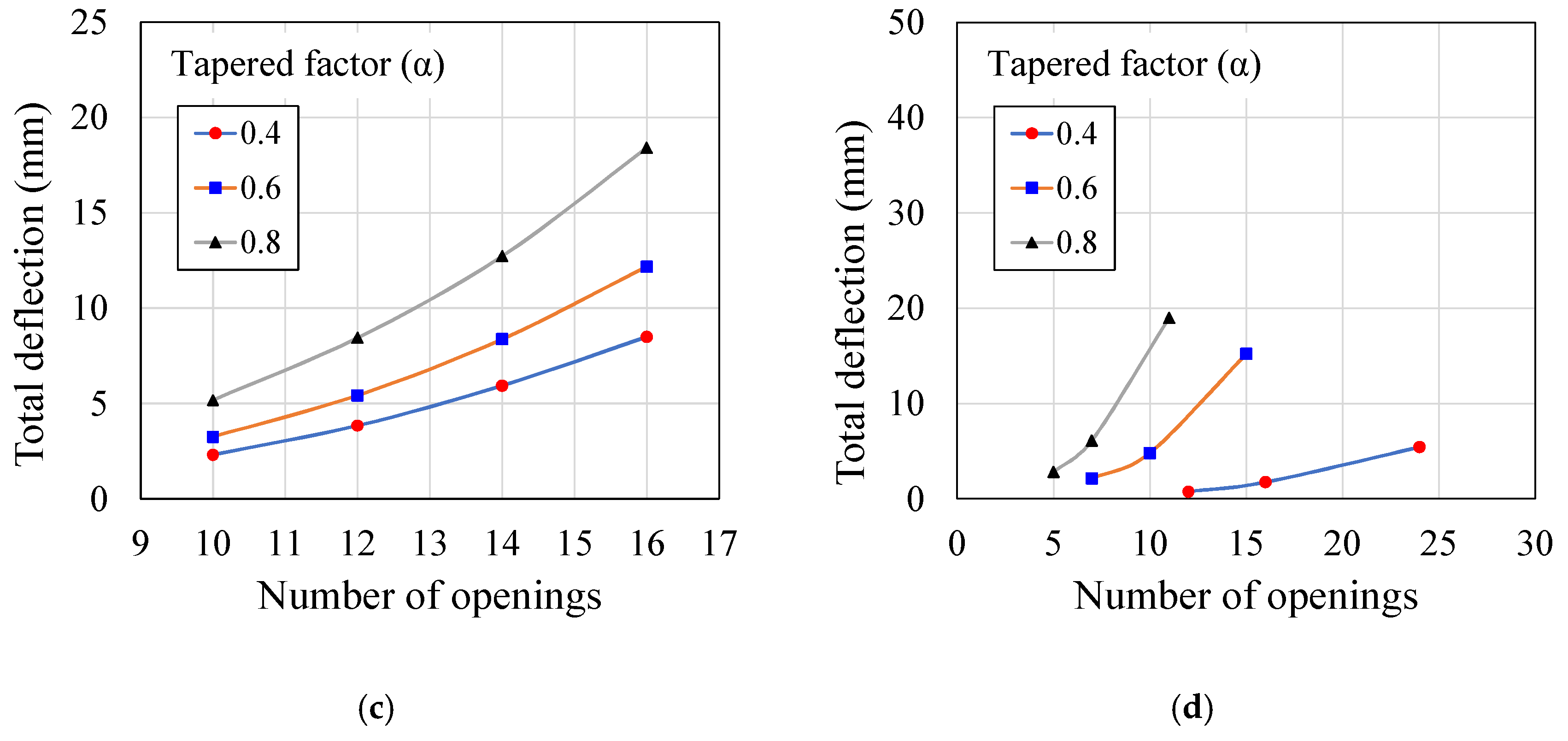
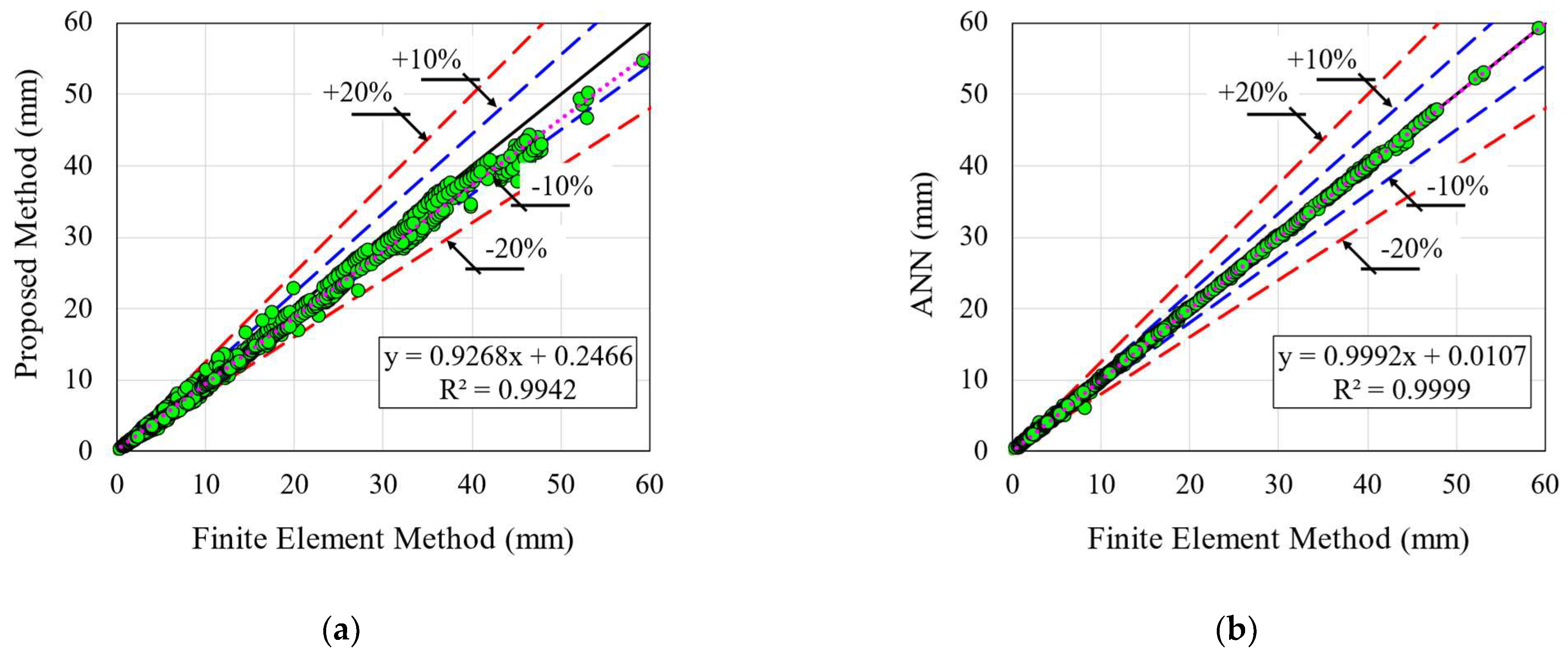
6.1. Additional Deflection
6.2. Total Deflection
6.3. Prediction-Based ANN
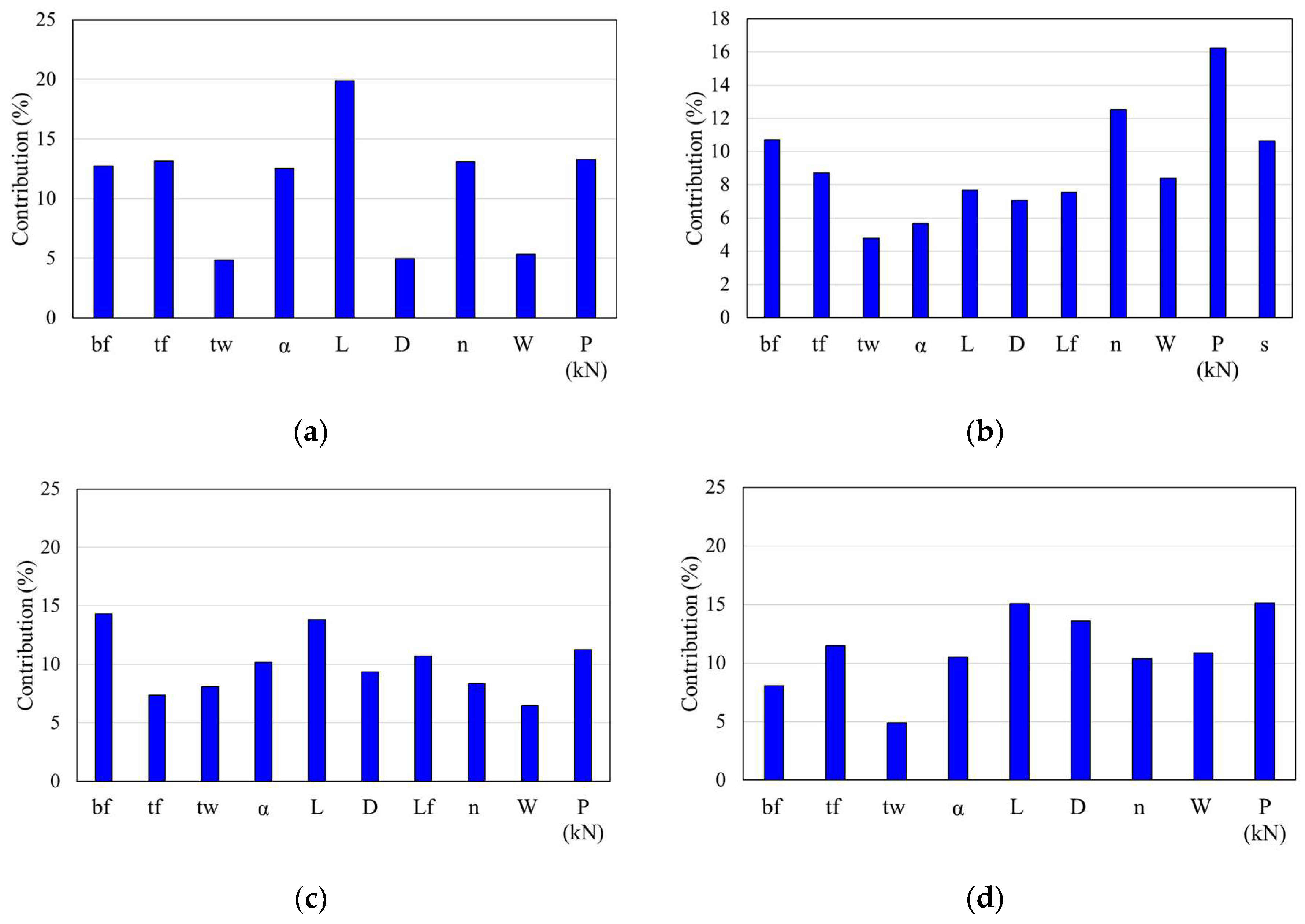
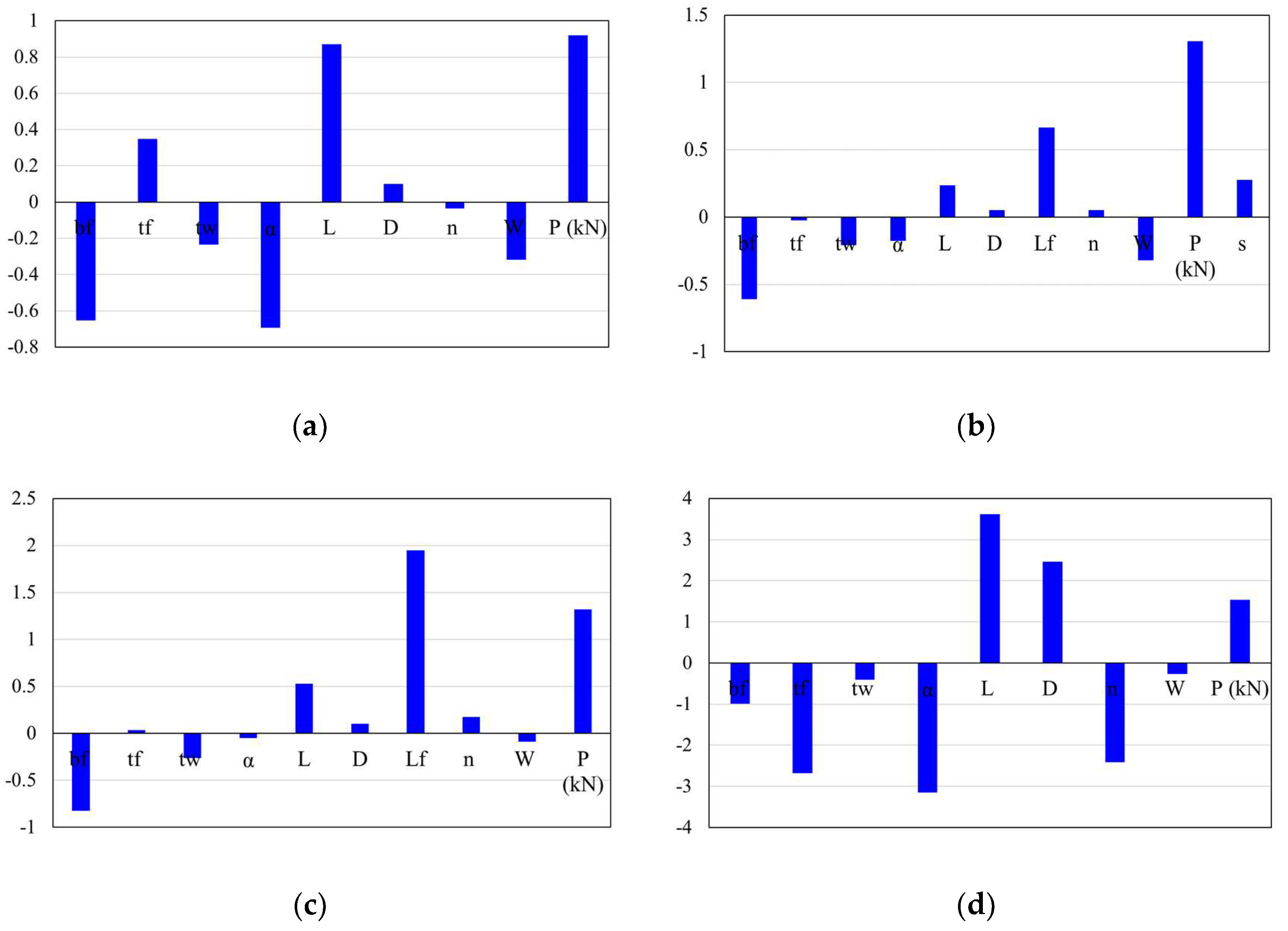
6.3.1. Variable Contribution
6.3.2. Impact of Input Parameters on Deflection
6.3.3. ANN-Based Formula
- Input Data Collection: Geometric and loading parameters such as flange width, web thickness, taper factor, beam span, and number of openings.
- ANN Model Execution: Normalised inputs are fed into the trained ANN model for deflection predictions.
7. Comparative Study
8. Benchmarking the Proposed Analytical Method Against SCI P355 and FEM
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Flange width | |
| Modulus of elasticity | |
| Force for four-point bending analysis | |
| Shear modulus | |
| Height of tapered web steel I-section without flanges | |
| Maximum height of tapered web steel I-section | |
| Minimum height of tapered web steel I-section | |
| Height of tapered web steel I-section | |
| Moment of inertia | |
| Moment of inertia of tapered steel I-section | |
| Index loop counter | |
| Moment of inertia of the flange | |
| Moment of inertia of the tee-section | |
| Moment of inertia of the tee-section tapered web | |
| Beam length | |
| Cantilever length at circular web opening | |
| Bending moment | |
| Index end-of-loop counter | |
| Number of openings | |
| Force for three-point bending analysis | |
| Circular opening radius | |
| Flange thickness | |
| Web thickness | |
| Displacement | |
| Global shear | |
| Distance between openings | |
| Distance between two circular openings at their centre | |
| Total deflection | |
| Total additional deflections for all openings | |
| Total additional deflections for i opening | |
| Finite element model deflection | |
| The deflection under bending effect | |
| Local additional deflections for i opening due to bending effect | |
| The deflection under shear effect | |
| Local additional deflections for i opening due to shear effect | |
| Local additional deflections for the upper tee-sections | |
| Local additional deflections for the lower tee-sections | |
| Total additional deflections for tee-section | |
| Deflection for solid tapered beam | |
| Position of openings | |
| Tapered factor section | |
| The angle of stress concentration | |
| Angular displacement | |
| Poisson’s ratio | |
| Web area at opening |
References
- Boissonnade, N.; Muzeau, J.-P. Mise au Point d’un Elément fini de Type Poutre à Section Variable et Autres Applications à la Construction Métallique. 2002. Available online: https://theses.fr/2002CLF21394 (accessed on 15 March 2025).
- Hosain, M.U.; Speirs, W.G. Experiments on Castellated Steel Beams; Welding Research Supplement; Department of Civil Engineering, University of Saskatchewan: Saskatoon, SK, Canada, 1973; pp. 329–342. [Google Scholar]
- Ferreira, F.P.V.; Rossi, A.; Martins, C.H. Lateral-torsional buckling of cellular beams according to the possible updating of EC3. J. Constr. Steel Res. 2019, 153, 222–242. [Google Scholar] [CrossRef]
- Ferreira, F.P.V.; Shamass, R.; Santos, L.F.P.; Tsavdaridis, K.D.; Limbachiya, V. Web-post buckling resistance calculation of perforated high-strength steel beams with elliptically-based web openings for EC3. Structures 2023, 55, 245–262. [Google Scholar] [CrossRef]
- BS EN 1993.1.1:2022; Eurocode 3—Design of Steel Structures. Part 1-1: General Rules and Rules for Buildings. British Standards: London, UK, 2022.
- BS EN 1993-1-13; Eurocode 3. Design of Steel Structures. Beams with Large Web Openings. British Standards: London, UK, 2024.
- Lawson, R.M.; Hicks, S.J. Design of Composite Beams with Large Web Openings, P355 ed.; The Steel Construction Institute: London, UK, 2011. [Google Scholar]
- Fares, S.S.; Coulson, J.; Dinehart, D.W. AISC Steel Design Guide 31: Castellated and Cellular Beam Design; American Institute of Steel Construction: Chicago, IL, USA, 2016. [Google Scholar]
- Thai, H.T. Machine learning for structural engineering: A state-of-the-art review. Structures 2022, 38, 448–491. [Google Scholar] [CrossRef]
- Shamass, R.; Ferreira, F.P.V.; Limbachiya, V.; Santos, L.F.P.; Tsavdaridis, K.D. Web-post buckling prediction resistance of steel beams with elliptically-based web openings using Artificial Neural Networks (ANN). Thin-Walled Struct. 2022, 180, 109959. [Google Scholar] [CrossRef]
- Gholizadeh, S.; Pirmoz, A.; Attarnejad, R. Assessment of load carrying capacity of castellated steel beams by neural networks. J. Constr. Steel Res. 2011, 67, 770–779. [Google Scholar] [CrossRef]
- Sharifi, Y.; Tohidi, S. Lateral-torsional buckling capacity assessment of web opening steel girders by artificial neural networks—Elastic investigation. Front. Struct. Civ. Eng. 2014, 8, 167–177. [Google Scholar] [CrossRef]
- Tohidi, S.; Sharifi, Y. Neural networks for inelastic distortional buckling capacity assessment of steel I-beams. Thin-Walled Struct. 2015, 94, 359–371. [Google Scholar] [CrossRef]
- Tohidi, S.; Sharifi, Y. Load-carrying capacity of locally corroded steel plate girder ends using artificial neural network. Thin-Walled Struct. 2016, 100, 48–61. [Google Scholar] [CrossRef]
- Hosseinpour, M.; Sharifi, Y.; Sharifi, H. Neural network application for distortional buckling capacity assessment of castellated steel beams. Structures 2020, 27, 1174–1183. [Google Scholar] [CrossRef]
- Nguyen, T.-A.; Ly, H.-B.; Tran, V.Q. Investigation of ANN Architecture for Predicting Load-Carrying Capacity of Castellated Steel Beams. Complexity 2021, 2021, 6697923. [Google Scholar] [CrossRef]
- Abambres, M.; Rajana, K.; Tsavdaridis, K.; Ribeiro, T. Neural Network-Based Formula for the Buckling Load Prediction of I-Section Cellular Steel Beams. Computers 2018, 8, 2. [Google Scholar] [CrossRef]
- Ferreira, F.P.V.; Shamass, R.; Limbachiya, V.; Tsavdaridis, K.D.; Martins, C.H. Lateral–torsional buckling resistance prediction model for steel cellular beams generated by Artificial Neural Networks (ANN). Thin-Walled Struct. 2022, 170, 108592. [Google Scholar] [CrossRef]
- Rabi, M.; Jweihan, Y.S.; Abarkan, I.; Ferreira, F.P.V.; Shamass, R.; Limbachiya, V.; Tsavdaridis, K.D.; Santos, L.F.P. Machine learning-driven web-post buckling resistance prediction for high-strength steel beams with elliptically-based web openings. Results Eng. 2024, 21, 101749. [Google Scholar] [CrossRef]
- Degtyarev, V.V.; Tsavdaridis, K.D. Buckling and ultimate load prediction models for perforated steel beams using machine learning algorithms. J. Build. Eng. 2022, 51, 104316. [Google Scholar] [CrossRef]
- Dassault Systèmes. ABAQUS 2017 Documentation. 2017. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/ (accessed on 15 March 2025).
- BS EN 1994-1-1:2004; Eurocode 4: Design of Steel and Concrete Composite Structures. Part 1.1: General Rules and Rules for Buildings. British Standards: London, UK, 2004.
- Lawson, R.M. Design for Openings in the Webs of Composite Beams; CIRIA: London, UK, 1987. [Google Scholar]
- Lawson, R.M.; Chung, K.F.; Price, A.M. Tests on composite beams with large web openings to justify existing design methods. Struct. Eng. Lond. 1992, 70, 1–7. [Google Scholar]
- Lawson, R.M.; Lim, J.; Hicks, S.J.; Simms, W.I. Design of composite asymmetric cellular beams and beams with large web openings. J. Constr. Steel Res. 2006, 62, 614–629. [Google Scholar] [CrossRef]
- Ward, J.K. Design of Composite and Non-Composite Cellular Beams. 1990. Available online: https://www.abebooks.com/9781870004510/Design-Composite-Non-composite-Cellular-Beams-1870004515/plp (accessed on 15 March 2025).
- Redwood, R.G. Design of Beams with Web Holes; Canadian Steel Industries Construction Council: Markham, ON, Canada, 1973. [Google Scholar]
- Tsavdaridis, K.D. Structural Performance of Perforated Steel Beams with Novel Web Openings and with Partial Concrete Encasement. Ph.D. Thesis, City University London, London, UK, 2010. [Google Scholar]
- MathWorks. MATLAB R2019a Documentation. 2019. Available online: https://www.mathworks.com (accessed on 15 March 2025).
- Osmani, A.; Meftah, S.A. Lateral buckling of tapered thin walled bi-symmetric beams under combined axial and bending loads with shear deformations allowed. Eng. Struct. 2018, 165, 76–87. [Google Scholar] [CrossRef]
- Saoula, A.; Meftah, S.A.; Mohri, F.; Daya, E.M. Lateral buckling of box beam elements under combined axial and bending loads. J. Constr. Steel Res. 2016, 116, 141–155. [Google Scholar] [CrossRef]
- Benyamina, A.B.; Meftah, S.A.; Mohri, F.; Daya, E.M. Analytical solutions attempt for lateral torsional buckling of doubly symmetric web-tapered I-beams. Eng. Struct. 2013, 56, 1207–1219. [Google Scholar] [CrossRef]
- Moradi, M.J.; Khaleghi, M.; Salimi, J.; Farhangi, V.; Ramezanianpour, A.M. Predicting the compressive strength of concrete containing metakaolin with different properties using ANN. Measurement 2021, 183, 109790. [Google Scholar] [CrossRef]
- Jin, J.; Li, M.; Jin, L. Data Normalization to Accelerate Training for Linear Neural Net to Predict Tropical Cyclone Tracks. Math. Probl. Eng. 2015, 2015, 931629. [Google Scholar] [CrossRef]
- Olden, J.D.; Jackson, D.A. Illuminating the “black box”: Understanding variable contributions in artificial neural networks. Ecol. Modell. 2002, 154, 135–150. [Google Scholar] [CrossRef]
- Limbachiya, V.; Shamass, R. Application of Artificial Neural Networks for web-post shear resistance of cellular steel beams. Thin-Walled Struct. 2021, 161, 107414. [Google Scholar] [CrossRef]
- Garson, D.G. Interpreting neural network connection weights. AI Expert 1991, 6, 46–51. [Google Scholar]
- Gupta, T.; Patel, K.A.; Siddique, S.; Sharma, R.K.; Chaudhary, S. Prediction of mechanical properties of rubberised concrete exposed to elevated temperature using ANN. Measurement 2019, 147, 106870. [Google Scholar] [CrossRef]
- Sharifi, Y.; Moghbeli, A. Shear capacity assessment of steel fiber reinforced concrete beams using artificial neural network. Innov. Infrastruct. Solut. 2021, 6, 89. [Google Scholar] [CrossRef]
- al-Swaidani, A.M.; Khwies, W.T. Applicability of Artificial Neural Networks to Predict Mechanical and Permeability Properties of Volcanic Scoria-Based Concrete. Adv. Civ. Eng. 2018, 2018, 5207962. [Google Scholar] [CrossRef]
- Tsavdaridis, K.D.; D’Mello, C. Web buckling study of the behaviour and strength of perforated steel beams with different novel web opening shapes. J. Constr. Steel Res. 2011, 67, 1605–1620. [Google Scholar] [CrossRef]
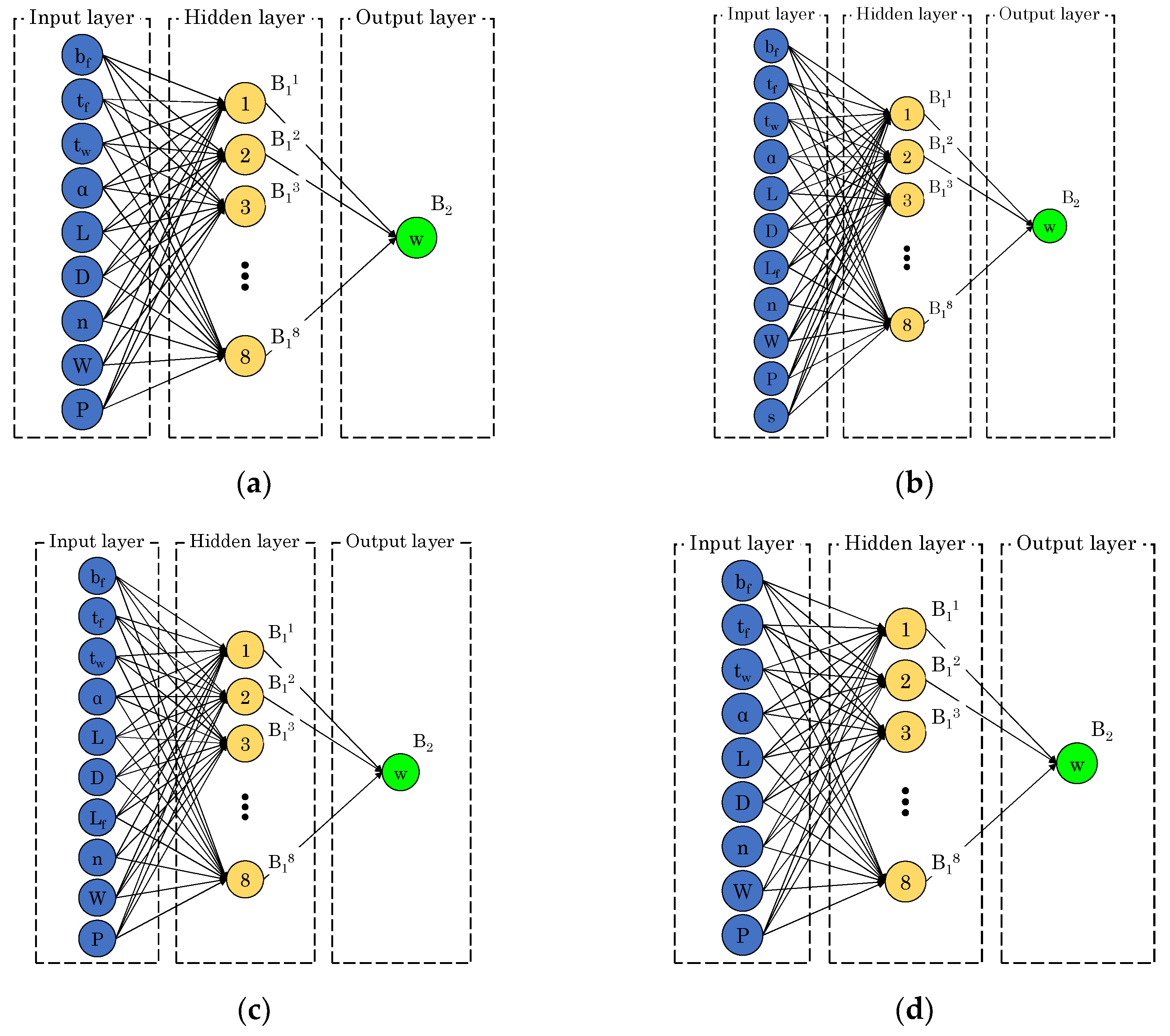


| α | L (m) | P (kN) | Section | n | Deflection (mm) | Δ (%) | CPU Run-Time (s) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mesh Size | Proposed Method | Mesh Size | ||||||||||||
| 10 | 20 | 40 | 10.00 | 20.00 | 40.00 | 10 | 20 | 40 | ||||||
| 0.4 | 6 | 100 | IPE600 | 24 | 4.43 | 4.42 | 4.39 | 4.183 | 5.58 | 5.36 | 4.72 | 29.4 | 5.7 | 1.3 |
| 8 | 100 | IPE600 | 32 | 9.85 | 9.83 | 9.79 | 9.094 | 7.68 | 7.49 | 7.11 | 48.2 | 10.8 | 2.1 | |
| 12 | 100 | IPE600 | 48 | 31.61 | 31.59 | 31.52 | 28.417 | 10.10 | 10.04 | 9.84 | 67.2 | 12.2 | 2.5 | |
| 0.6 | 6 | 100 | IPE600 | 14 | 4.05 | 4.04 | 4.02 | 3.905 | 3.58 | 3.34 | 2.86 | 38.7 | 7.7 | 1.3 |
| 8 | 100 | IPE600 | 20 | 8.69 | 8.69 | 8.66 | 8.471 | 2.52 | 2.52 | 2.18 | 40.3 | 10 | 1.9 | |
| 12 | 100 | IPE600 | 30 | 27.2 | 27.19 | 27.14 | 26.133 | 3.92 | 3.89 | 3.71 | 66 | 15.2 | 3.7 | |
| 0.8 | 6 | 100 | IPE600 | 10 | 3.93 | 3.93 | 3.91 | 3.878 | 1.32 | 1.32 | 0.82 | 33.6 | 9.6 | 2.4 |
| 8 | 100 | IPE600 | 14 | 8.2 | 8.2 | 8.18 | 8.053 | 1.79 | 1.79 | 1.55 | 50.3 | 12.7 | 2 | |
| 12 | 100 | IPE600 | 20 | 24.62 | 24.61 | 24.58 | 24.130 | 1.99 | 1.95 | 1.83 | 66 | 15.5 | 3.2 | |
| Input/Target Parameter | Xmin | Xmax | Ymin | Ymax |
|---|---|---|---|---|
| bf (mm) | 190 | 220 | −1 | 1 |
| tf (mm) | 14.6 | 19 | −1 | 1 |
| tw (mm) | 5 | 17.2 | −1 | 1 |
| α | 0.4 | 1 | −1 | 1 |
| L (mm) | 4702 | 12,000 | −1 | 1 |
| D (mm) | 130 | 353.6 | −1 | 1 |
| n | 10 | 58 | −1 | 1 |
| Lf (mm) | 1175.5 | 6000 | −1 | 1 |
| W (mm) | 66 | 450 | −1 | 1 |
| a P (kN) | 1.67 | 180 | −1 | 1 |
| a s (mm) | 1175.5 | 6000 | −1 | 1 |
| 3 Points | 4 Points | |||||
|---|---|---|---|---|---|---|
| Number of neurons | 4 | 6 | 8 | 4 | 6 | 8 |
| Max error | 36.41 | 26.28 | 68.52 | 29.91 | 33.26 | 12.21 |
| Min error | −24.48 | −24.86 | −28.64 | −56.84 | −22.13 | −68.88 |
| R2 | 0.99970 | 0.99993 | 0.99980 | 0.99940 | 0.9999 | 0.9999 |
| RMSE | 0.632 | 0.262 | 0.274 | 0.309 | 0.108 | 0.0997 |
| 5 points | Cantilever | |||||
| Number of neurons | 4 | 6 | 8 | 4 | 6 | 8 |
| Max error | 45.57 | 13.44 | 70.52 | 4.56 | 3.18 | 1.49 |
| Min error | −26.40 | −11.40 | −60.09 | −1.96 | −1.46 | −0.62 |
| R2 | 0.9995 | 0.9999 | 0.9995 | 0.99976 | 0.99993 | 0.99999 |
| RMSE | 0.288 | 0.121 | 0.627 | 0.0188 | 0.023 | 0.008 |
| Neuron | w1 (i,j) | w2 (i) | B1 (i) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| bf | tf | tw | α | L | D | n | W | P | |||
| 1 | −0.8323 | −0.2838 | 0.2185 | 0.6005 | 0.5157 | −0.0184 | −1.0640 | 0.2714 | 0.2282 | −0.009 | 1.9988 |
| 2 | −0.3009 | 0.5388 | 0.0270 | 0.2434 | −0.6898 | −0.4004 | −0.3283 | 0.0379 | 0.5404 | 1.1882 | 1.3659 |
| 3 | −0.4953 | 0.4739 | 0.2031 | −0.378 | −1.2543 | 0.0158 | −0.4703 | −0.0504 | −0.2901 | −0.0565 | −0.6044 |
| 4 | −0.1522 | −0.1612 | −0.0724 | −0.1355 | 0.6588 | 0.1919 | 0.2130 | 0.0137 | 0.2587 | 2.6628 | −1.1937 |
| 5 | 1.0733 | 1.3069 | 0.5113 | 0.3062 | 0.4176 | 0.0260 | −0.3167 | 0.2060 | 0.7646 | 0.0129 | 1.3511 |
| 6 | −0.0981 | −0.2377 | 0.1109 | 1.0537 | 0.2210 | 0.1974 | 0.4015 | 0.6608 | 0.7172 | −0.6093 | −1.7799 |
| Neuron | w1 (i,j) | w2 (i) | B1 (i) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bf | tf | tw | α | L | D | Lf | n | W | P | s | |||
| 1 | −0.252 | −0.011 | −0.017 | −0.158 | 0.392 | −0.091 | 0.562 | −0.390 | −0.019 | 0.445 | 0.468 | 0.184 | −0.285 |
| 2 | 0.309 | −0.133 | −0.317 | −0.337 | 0.877 | 0.357 | −0.055 | 0.584 | −0.815 | −1.120 | −0.298 | 0.225 | −1.722 |
| 3 | 1.314 | −1.483 | 0.156 | −0.238 | 0.275 | 0.932 | 0.191 | 1.490 | −0.279 | −0.401 | −0.266 | 0.352 | −0.741 |
| 4 | 0.194 | −0.611 | −0.870 | 0.023 | −0.276 | 0.039 | 0.528 | 0.123 | 1.204 | 0.705 | 0.230 | 0.140 | −0.840 |
| 5 | 0.147 | −0.296 | 0.022 | −0.444 | −0.084 | 0.634 | −0.115 | 0.947 | 0.059 | −0.985 | 0.620 | −0.791 | −1.000 |
| 6 | −0.900 | 0.339 | −0.047 | −0.305 | −0.140 | 0.138 | 0.304 | 0.177 | −0.141 | 0.660 | 0.721 | 1.121 | −1.642 |
| Neuron | w1 (i,j) | w2 (i) | B1 (i) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bf | tf | tw | α | L | D | Lf | n | W | P | |||
| 1 | −1.088 | 0.503 | −0.083 | 0.377 | 0.255 | −0.272 | 0.016 | −0.190 | 0.304 | −0.305 | −0.305 | 1.052 |
| 2 | 0.153 | 0.015 | 0.134 | −0.682 | −0.714 | 0.647 | 0.648 | 0.060 | −0.124 | 0.255 | −1.121 | −1.247 |
| 3 | −0.647 | 0.693 | 1.163 | −0.779 | 0.015 | 0.375 | −0.083 | −0.042 | 0.148 | −0.189 | 0.074 | −0.344 |
| 4 | −0.377 | 0.249 | 0.309 | 0.142 | −1.150 | −0.405 | −0.336 | 0.421 | 0.366 | 0.048 | −0.057 | −0.009 |
| 5 | −0.411 | 0.121 | −0.114 | −0.024 | 0.387 | 0.089 | 0.080 | 0.918 | 0.400 | −1.221 | −0.357 | −1.266 |
| 6 | 0.378 | −0.071 | 0.085 | 0.195 | 0.404 | −0.210 | −0.923 | −0.185 | −0.067 | −0.374 | −2.923 | 1.216 |
| Neuron | w1 (i,j) | w2 (i) | B1 (i) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| bf | tf | tw | α | L | D | n | W | P | |||
| 1 | −0.205 | 0.254 | 0.602 | 0.075 | −0.405 | 0.188 | 0.493 | −0.104 | −0.481 | −0.324 | 2.361 |
| 2 | −0.415 | −0.247 | −0.067 | 0.826 | −0.819 | 0.280 | −0.438 | 1.758 | 1.255 | −0.024 | −1.786 |
| 3 | 0.339 | −0.386 | 0.039 | −0.721 | −1.342 | 1.197 | 0.271 | 0.967 | −0.354 | −0.041 | 0.206 |
| 4 | 0.548 | 0.795 | 0.098 | −0.249 | −0.128 | −0.503 | −0.177 | −0.159 | −0.208 | 0.024 | 0.151 |
| 5 | 0.314 | 0.716 | 0.054 | 0.847 | −0.884 | −0.804 | 0.694 | −0.041 | −0.208 | −3.545 | 2.564 |
| 6 | −0.065 | 0.155 | 0.040 | 0.192 | −0.420 | 0.391 | −0.319 | −0.258 | −0.987 | −0.669 | 0.782 |
| Model | Proposed | ANN |
|---|---|---|
| Mean | 0.95 | 1.00 |
| S.D | 7.15% | 2.79% |
| R2 | 0.9942 | 0.9999 |
| MAE | 0.904 | 0.087 |
| RMSE | 1.550 | 0.154 |
| Minimum error (WPredicted/NFE − 1) | −30% | −25% |
| Maximum error (WPredicted/NFE − 1) | 16% | 33% |
| Beam | tf [mm] | tw [mm] | b [mm] | h [mm] | Openings | D [mm] | W [mm] | P [mm] | L [m] |
|---|---|---|---|---|---|---|---|---|---|
| B1 | 19 | 12 | 220 | 600 | 14 | 257.6 | 125 | 382.6 | 6 |
| B2 | 19 | 12 | 220 | 600 | 24 | 161.6 | 80 | 241.6 | 6 |
| B3 | 16 | 10.2 | 200 | 745 | 10 | 525 | 135 | 660 | 7 |
| B4 | 16 | 10.2 | 200 | 745 | 13 | 525 | 135 | 660 | 9 |
| B5 | 19 | 12 | 220 | 896 | 11 | 630 | 160 | 790 | 9 |
| Beam | Load case | P [kN] | [mm] | [mm] | [mm] | SCI P355 [mm] | [mm] | [mm] | (%) | (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| B1 | 3 pts | 100 | 0.50 | 2.43 | 2.92 | 0.129 | 2.74 | 3.33 | 12.25 | 17.71 |
| B2 | 3 pts | 100 | 0.37 | 2.43 | 2.79 | 0.087 | 2.64 | 3.14 | 11.08 | 15.99 |
| B3 | 3 pts | 100 | 2.886 | 2.937 | 5.82 | 0.260 | 3.70 | 5.78 | 0.76 | 35.98 |
| B4 | 3 pts | 100 | 3.464 | 6.242 | 9.71 | 0.262 | 7.88 | 10.12 | 4.09 | 22.13 |
| B5 | 3 pts | 100 | 2.43 | 3.230 | 5.66 | 0.266 | 4.09 | 6.14 | 7.88 | 33.47 |
| B1 | 4 pts | 50 | 0.28 | 1.67 | 1.95 | 0.129 | 1.88 | 2.16 | 9.68 | 12.78 |
| B2 | 4 pts | 50 | 0.18 | 1.67 | 1.85 | 0.087 | 1.81 | 2.04 | 9.27 | 11.10 |
| B3 | 4 pts | 50 | 1.732 | 2.019 | 3.75 | 0.260 | 2.54 | 3.39 | 10.66 | 24.97 |
| B4 | 4 pts | 50 | 1.732 | 4.292 | 6.02 | 0.262 | 5.42 | 6.21 | 2.98 | 12.74 |
| B5 | 4 pts | 50 | 1.458 | 2.220 | 3.68 | 0.266 | 2.81 | 3.74 | 1.54 | 24.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osmani, A.; Shamass, R.; Tsavdaridis, K.D.; Ferreira, F.P.V.; Khatir, A. Deflection Predictions of Tapered Cellular Steel Beams Using Analytical Models and an Artificial Neural Network. Buildings 2025, 15, 992. https://doi.org/10.3390/buildings15060992
Osmani A, Shamass R, Tsavdaridis KD, Ferreira FPV, Khatir A. Deflection Predictions of Tapered Cellular Steel Beams Using Analytical Models and an Artificial Neural Network. Buildings. 2025; 15(6):992. https://doi.org/10.3390/buildings15060992
Chicago/Turabian StyleOsmani, Amine, Rabee Shamass, Konstantinos Daniel Tsavdaridis, Felipe Piana Vendramell Ferreira, and Abdelwahhab Khatir. 2025. "Deflection Predictions of Tapered Cellular Steel Beams Using Analytical Models and an Artificial Neural Network" Buildings 15, no. 6: 992. https://doi.org/10.3390/buildings15060992
APA StyleOsmani, A., Shamass, R., Tsavdaridis, K. D., Ferreira, F. P. V., & Khatir, A. (2025). Deflection Predictions of Tapered Cellular Steel Beams Using Analytical Models and an Artificial Neural Network. Buildings, 15(6), 992. https://doi.org/10.3390/buildings15060992







