Hydro-Mechanical Numerical Analysis of a Double-Wall Deep Excavation in a Multi-Aquifer Strata Considering Soil–Structure Interaction
Abstract
1. Introduction
2. Project Description
2.1. Project Overview
2.2. Ground Condition
2.3. Design Scheme and Construction Sequence
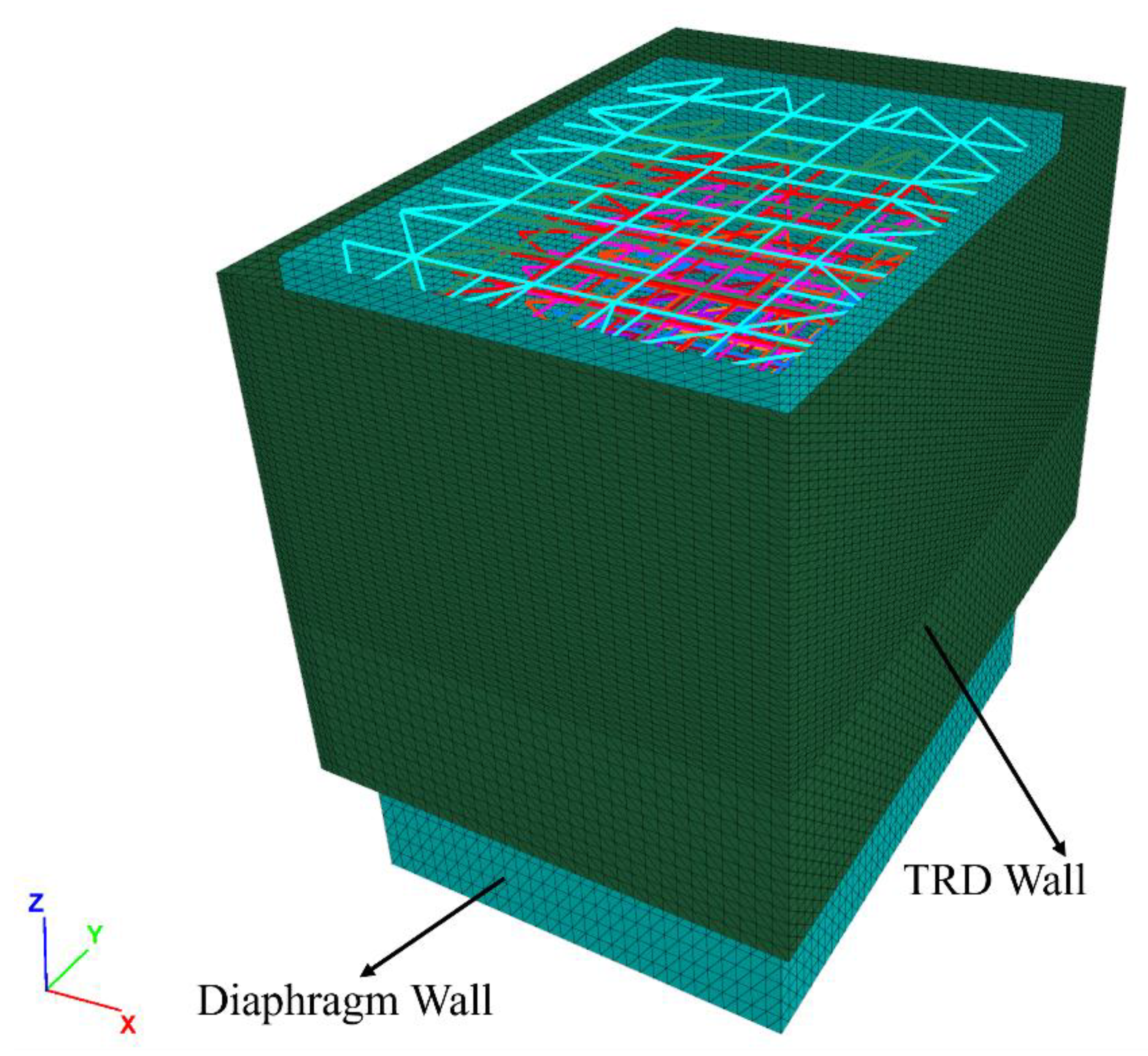
3. Numerical Modeling
3.1. General Description of the Numerical Model
3.2. Boundary Conditions
3.3. Constitutive Models and Parameters
3.4. Construction Stages in Simulation
3.5. Model Verification
4. Parametric Analysis
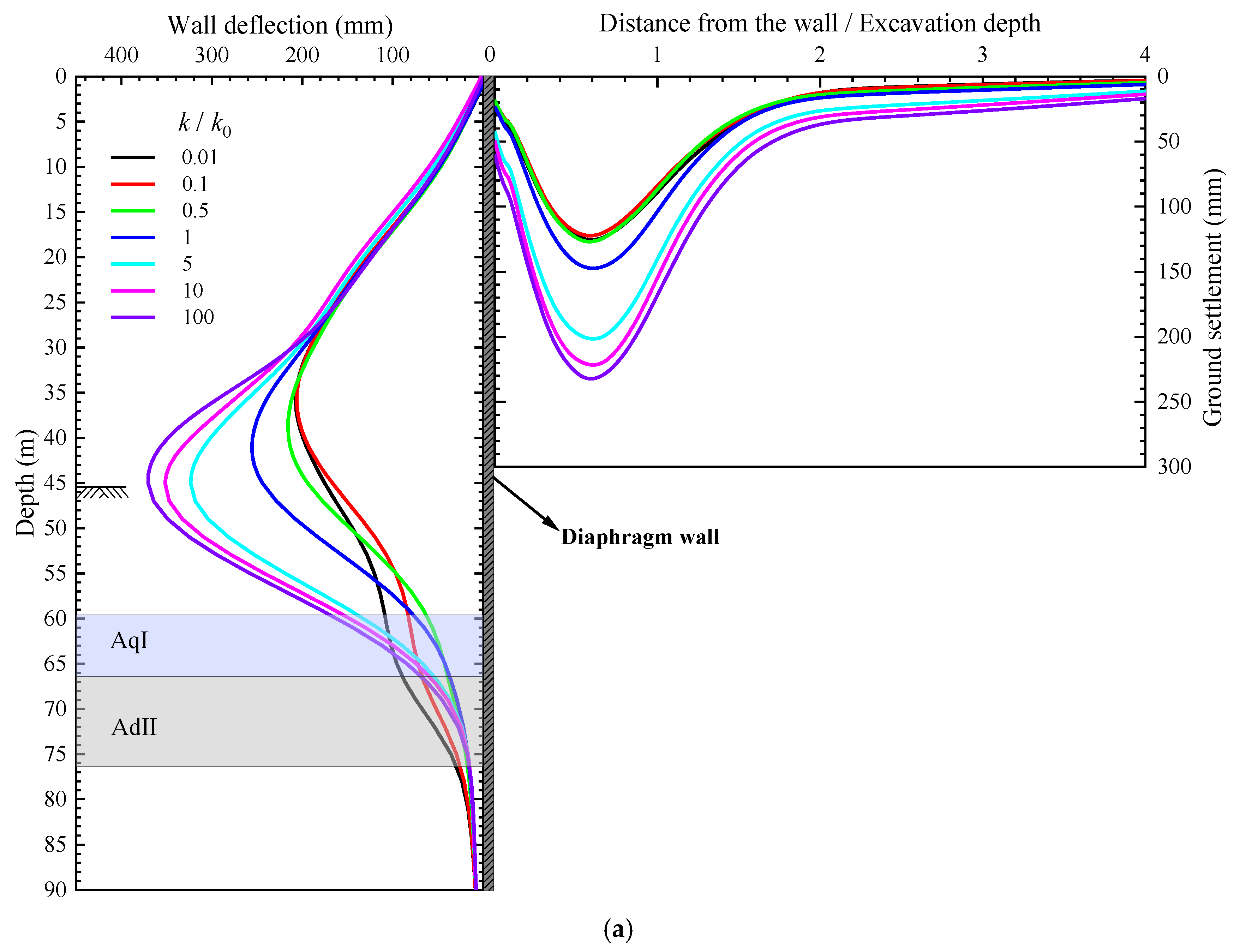
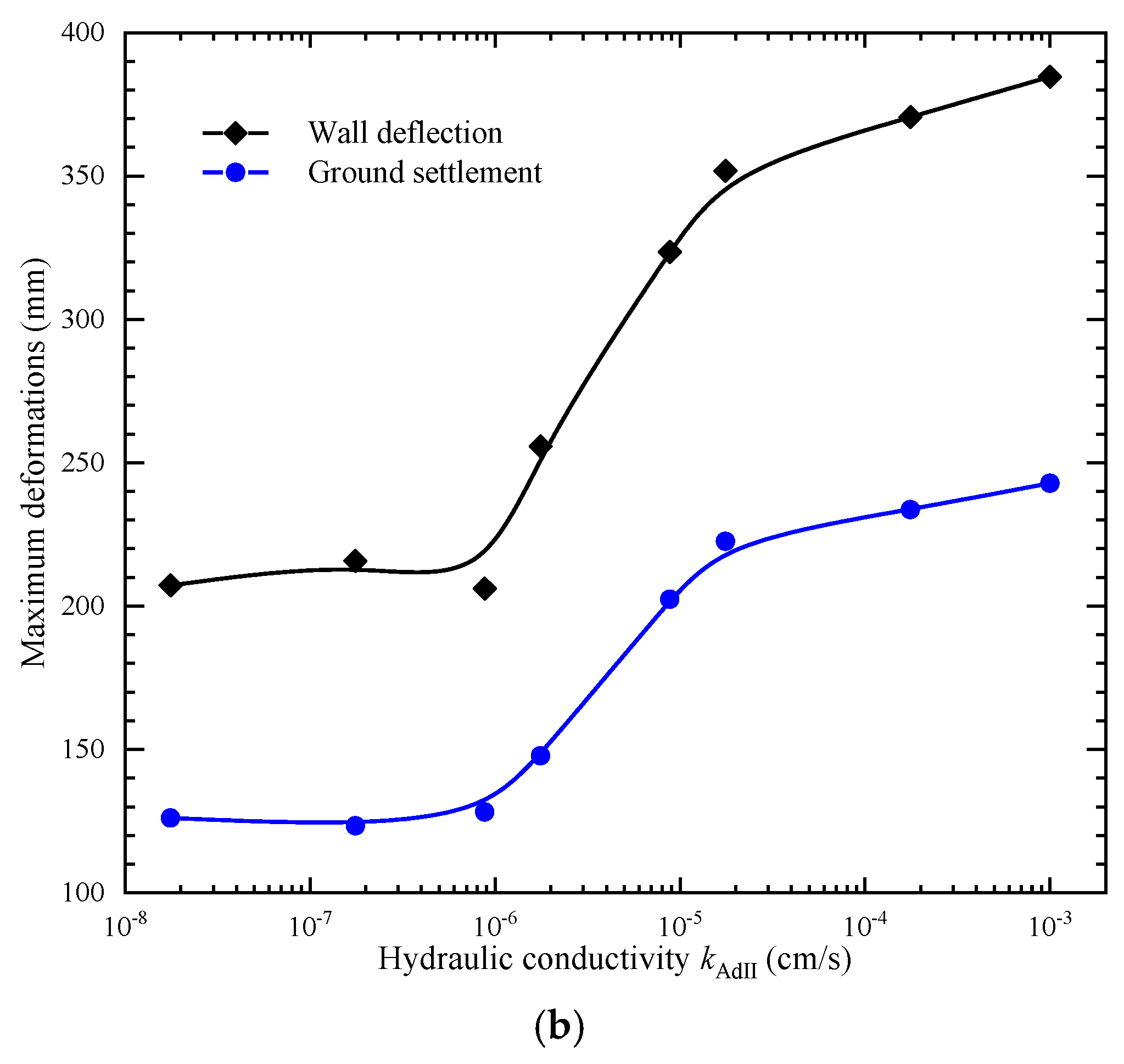
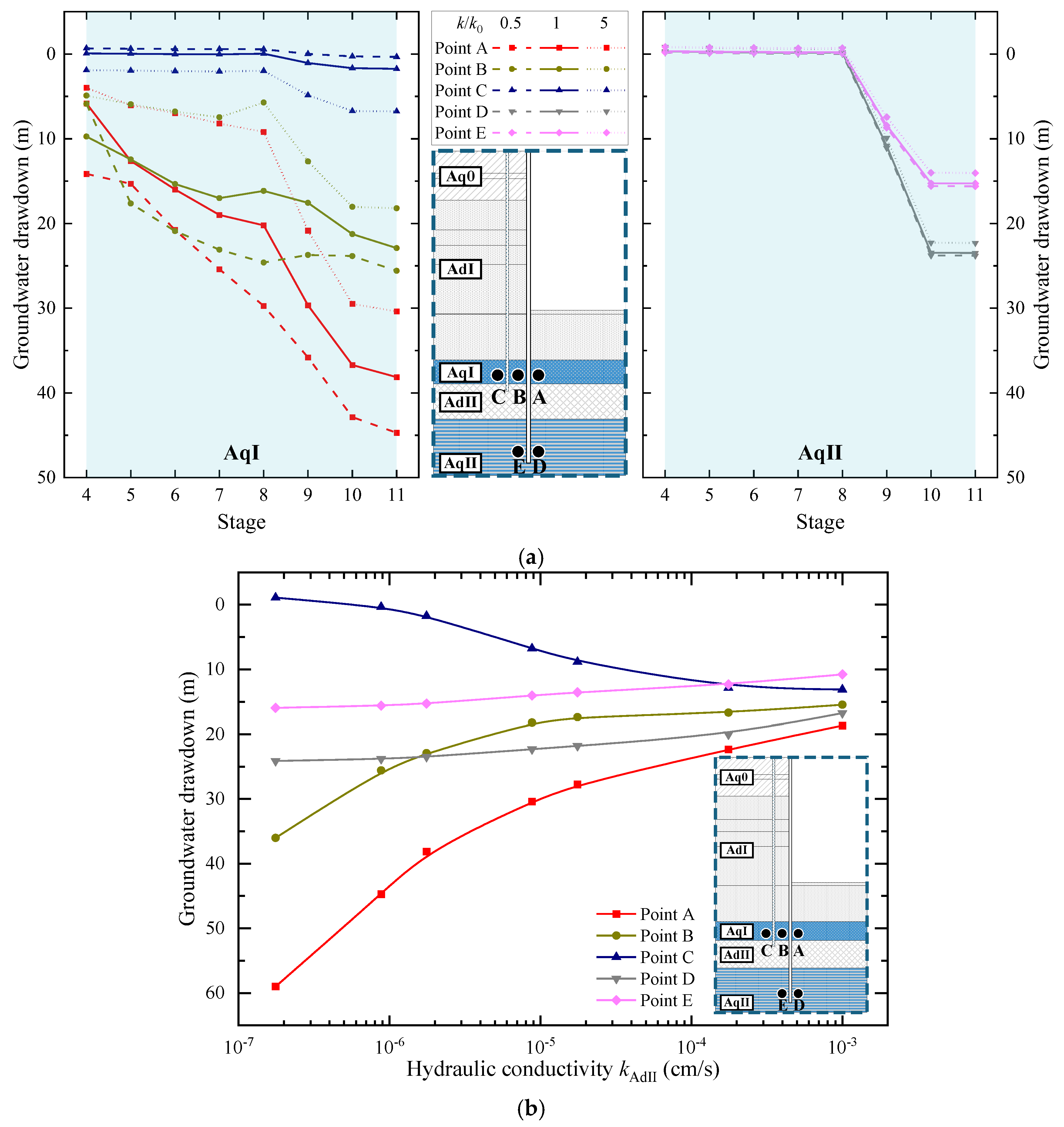
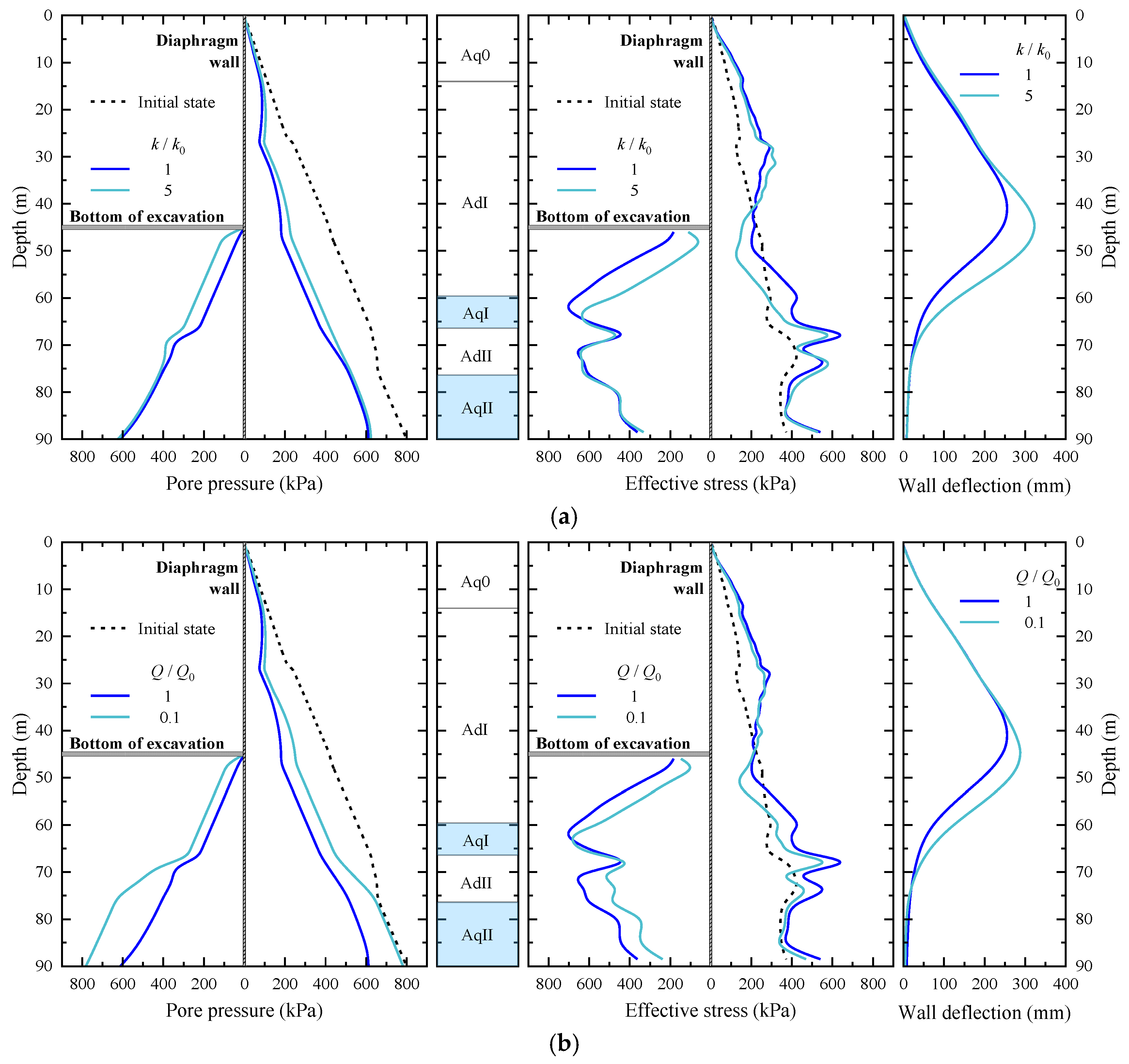
4.1. Aquitard Hydraulic Conductivity
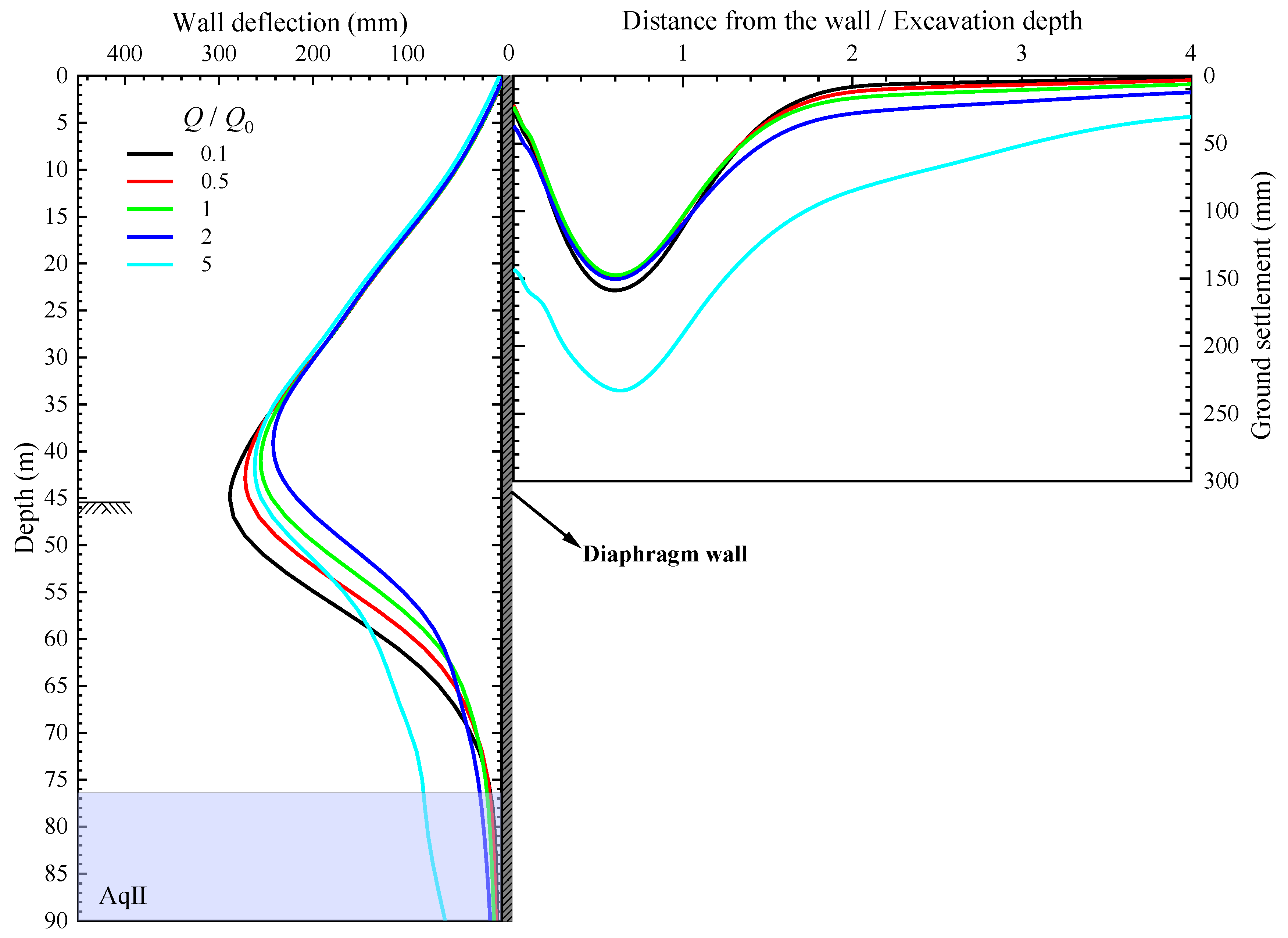
4.2. Pumping Rate in Aquifer
4.3. Presence of TRD Wall
5. Discussion
6. Conclusions
- (1)
- The calculated deflection pattern of the wall and groundwater drawdown basically matches the measured one, and the calculation error at the final stage is within millimeters at the monitoring point where maximum deflection occurred. It proves that the three-dimensional hydro-mechanical model can effectively simulate the excavation and dewatering process of the foundation pit.
- (2)
- The hydraulic conductivity of the aquitard AdII below the bottom of the pit directly affects the groundwater drawdown in the overlying aquifer AqI during the dewatering process. This, in turn, affects the effective stress in the soil in the passive zone and the consolidation of soils outside the pit, both of which play a crucial role in resisting wall deformation and preventing excessive ground settlement. As the kAdII increases from 10−6 to 10−3 cm/s, the final groundwater drawdown in AqI inside the pit reduces by about 50%, which reduces the effective stress in the passive zone, thereby increasing the wall deformation. Specifically, the wall deflection and ground settlement increase by about 80% under this condition.
- (3)
- The pumping in the second confined aquifer AqII can help to alleviate the deformation of the wall to some extent, as it is more of a measure to prevent hydraulic uplift at the bottom of the pit. When the ratio of pumping rate increases from 0.1 to 2.0, the maximum deflection decreases by about 16%. However, the pumping rate should not be too high, because it will induce excessive wall deflection and ground settlement. In engineering practices, dewatering tests are usually carried out to help determine the required pumping rate. Although the pumping rate is determined more empirically, numerical simulation can serve as a complimentary method to analyze the influence of different dewatering scenarios.
- (4)
- The TRD wall plays a good role in watertightness, although it has a limited capability in controlling the deformation of diaphragm wall. Only about 4% of the deformations can be reduced according to the case in this study. But the groundwater drawdown can be alleviated due to additionally induced seepage between the diaphragm wall and the TRD wall. Nonetheless, in ultra-deep excavations with abundant groundwater, the TRD wall is still recommended, because the quality of the diaphragm wall is more difficult to guarantee, and the risk of leakage and failure is greater with an increasing excavation depth.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, R.; Liu, S.; Xu, L.; Zhao, C.; Ni, P.; Zheng, W. Performance of a 56 m Deep Circular Excavation Supported by Diaphragm and Cut-off Double-Wall System in Shanghai Soft Ground. Can. Geotech. J. 2023, 60, 521–540. [Google Scholar] [CrossRef]
- Chu, Y.; Shi, J.; Ye, Z.; Liu, D. Dewatering Characteristics and Drawdown Prediction of Suspended Waterproof Curtain Foundation Pit in Soft Soil Areas. Buildings 2024, 14, 119. [Google Scholar] [CrossRef]
- Li, M.-G.; Chen, J.-J.; Xia, X.-H.; Zhang, Y.-Q.; Wang, D.-F. Statistical and Hydro-Mechanical Coupling Analyses on Groundwater Drawdown and Soil Deformation Caused by Dewatering in a Multi-Aquifer-Aquitard System. J. Hydrol. 2020, 589, 125365. [Google Scholar] [CrossRef]
- Hong, Y.; Ng, C.W.W. Base Stability of Multi-Propped Excavations in Soft Clay Subjected to Hydraulic Uplift. Can. Geotech. J. 2013, 50, 153–164. [Google Scholar] [CrossRef]
- Liu, J.; Hou, X.; Liu, G.; Wang, W. Excavation Engineering Manual; China Architecture & Building Press: Beijing, China, 2009. [Google Scholar]
- Ou, C.-Y.; Lai, C.-H. Finite-Element Analysis of Deep Excavation in Layered Sandy and Clayey Soil Deposits. Can. Geotech. J. 1994, 31, 204–214. [Google Scholar] [CrossRef]
- Uribe-Henao, A.F.; Arboleda-Monsalve, L.G.; Ballesteros, C.; Zapata-Medina, D.G. Method for Estimating Fully Coupled Response of Deep Excavations in Soft Clays. J. Geotech. Geoenviron. Eng. 2023, 149, 04023026. [Google Scholar] [CrossRef]
- Nogueira, C.D.L.; Azevedo, R.F.D.; Zornberg, J.G. Validation of Coupled Simulation of Excavations in Saturated Clay: Camboinhas Case History. Int. J. Geomech. 2011, 11, 202–210. [Google Scholar] [CrossRef]
- Liu, N.-W.; Peng, C.-X.; Li, M.-G.; Chen, J.-J. Hydro-Mechanical Behavior of a Deep Excavation with Dewatering and Recharge in Soft Deposits. Eng. Geol. 2022, 307, 106780. [Google Scholar] [CrossRef]
- Li, M.-G.; Li, J.-B.; Liu, N.-W.; Peng, C.-X.; Chen, J.-J. Numerical Investigation of the Effect of Stratum Hydraulic Conductivity on Performance of Deep Excavations in an Aquifer–Aquitard System. Int. J. Geomech. 2024, 24, 04024062. [Google Scholar] [CrossRef]
- Ha, D.; Zheng, G.; Zhou, H.; Zeng, C.; Zhang, H. Estimation of Hydraulic Parameters from Pumping Tests in a Multiaquifer System. Undergr. Space 2020, 5, 210–222. [Google Scholar] [CrossRef]
- Zheng, G.; Ha, D.; Loaiciga, H.; Zhou, H.; Zeng, C.; Zhang, H. Estimation of the Hydraulic Parameters of Leaky Aquifers Based on Pumping Tests and Coupled Simulation/Optimization: Verification Using a Layered Aquifer in Tianjin, China. Hydrol. J. 2019, 27, 3081–3095. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Shen, S.-L.; Lyu, H.-M.; Zhou, A. Analyses of Leakage Effect of Waterproof Curtain during Excavation Dewatering. J. Hydrol. 2020, 583, 124582. [Google Scholar] [CrossRef]
- Wu, Y.-X.; Lyu, H.-M.; Shen, S.-L.; Zhou, A. A Three-Dimensional Fluid-Solid Coupled Numerical Modeling of the Barrier Leakage below the Excavation Surface Due to Dewatering. Hydrol. J. 2020, 28, 1449–1463. [Google Scholar] [CrossRef]
- Zeng, C.-F.; Wang, S.; Xue, X.-L.; Zheng, G.; Mei, G.-X. Evolution of Deep Ground Settlement Subject to Groundwater Drawdown during Dewatering in a Multi-Layered Aquifer-Aquitard System: Insights from Numerical Modelling. J. Hydrol. 2021, 603, 127078. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Wang, J.-H.; Li, M.-G. Effect of Dewatering in a Confined Aquifer on Ground Settlement in Deep Excavations. Int. J. Geomech. 2018, 18, 04018120. [Google Scholar] [CrossRef]
- Zhao, C.; Lei, Q.; Zhang, Z.; Loew, S. Causal Mechanism of Gotthard Base Tunnel-Induced Ground Deformation: Insights from 3D Fully-Coupled Hydro-Mechanical Simulation and Comparison to Field Measurements. Int. J. Rock Mech. Min. Sci. 2023, 170, 105515. [Google Scholar] [CrossRef]
- Peng, C.-X.; Liu, N.-W.; Li, M.-G.; Zhen, L.; Chen, J.-J. Hydro-Mechanical Coupled Analyses on Wall Deformations Caused by Deep Excavations and Dewatering in a Confined Aquifer. Acta Geotech. 2022, 17, 2465–2479. [Google Scholar] [CrossRef]
- Li, M.-G.; Yan, Y.-H.; Xu, Z.-H.; Chen, H.-B.; Peng, C.-X.; Chen, J.-J. Fully Hydro-Mechanical Coupled Analyses of the Deep Excavation above a Multi-Aquifer-Aquitard System. Tunn. Undergr. Space Technol. 2025, 156, 106259. [Google Scholar] [CrossRef]
- Itasca Consulting Group, Inc. Itasca FLAC3D 7.0 Documentation; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2019. [Google Scholar]
- Wang, J.H.; Xu, Z.H.; Wang, W.D. Wall and Ground Movements Due to Deep Excavations in Shanghai Soft Soils. J. Geotech. Geoenviron. Eng. 2010, 136, 985–994. [Google Scholar] [CrossRef]
- Xu, Z.-H.; Wang, W.-D. Selection of soil constitutive models for numerical analysis of deep excavations in close proximity to sensitive properties. Rock Soil Mech. 2010, 31, 258–264+326. [Google Scholar] [CrossRef]
- Burland, J.B. Ninth Laurits Bjerrum Memorial Lecture: “Small Is Beautiful”—The Stiffness of Soils at Small Strains. Can. Geotech. J. 1989, 26, 499–516. [Google Scholar] [CrossRef]
- Benz, T. Small-Strain Stiffness of Soils and Its Numerical Consequences; Inst. für Geotechnik: Stuttgart, Germany, 2007. [Google Scholar]
- Carter, J.P. Constitutive Modelling in Computational Geomechanics—61st Rankine Lecture, British Geotechnical Association, 2023. Géotechnique 2024, 74, 1511–1535. [Google Scholar] [CrossRef]
- Bolton, M.D. The Strength and Dilatancy of Sands. Géotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.J.; Broere, W. Plaxis Material Models Manual; Delft University of Technology Press: Delft, The Netherlands, 2006. [Google Scholar]
- Gao, D.-Z.; Wei, D.-D.; Hu, Z.-X. Geotechnical Properties of Shanghai Soils and Engineering Applications. In Marine Geotechnology and Nearshore/Offshore Structures; Chaney, R., Fang, H., Eds.; ASTM International: West Conshohocken, PA, USA, 1986; pp. 161–177. ISBN 978-0-8031-0490-7. [Google Scholar]
- Janbu, N. Soil Compressibility as Determined by Oedometer and Triaxial Test. In Proceedings of the European Conference on Soil Mechanics and Foundation Engineering, Wiesbaden, Germany, 16–20 September 1963. [Google Scholar]
- Wang, W.-D.; Wang, H.-R.; Xu, Z.-H. Experimental study of parameters of hardening soil model for numerical analysis of excavations of foundation pits. Rock Soil Mech. 2012, 33, 2283–2290. (In Chinese) [Google Scholar] [CrossRef]
- DGJ08-37–2012; Code for Investigation of Geotechnical Engineering. Shanghai Municipal Commission of Housing and Urban-Rural Development: Shanghai, China, 2012.
- Ou, C.-Y.; Liao, J.-T.; Lin, H.-D. Performance of Diaphragm Wall Constructed Using Top-Down Method. J. Geotech. Geoenviron. Eng. 1998, 124, 798–808. [Google Scholar] [CrossRef]
- Abdi, A.S.; Ou, C.-Y. Evaluation of Cross Wall Performance on Restraining the Wall Displacement and Resisting the Basal Heave in Deep Excavations. Acta Geotech. 2024, 19, 4037–4053. [Google Scholar] [CrossRef]
- Lim, A.; Ou, C.-Y.; Hsieh, P.-G. A Novel Strut-Free Retaining Wall System for Deep Excavation in Soft Clay: Numerical Study. Acta Geotech. 2020, 15, 1557–1576. [Google Scholar] [CrossRef]
- Kung, G.T.; Juang, C.H.; Hsiao, E.C.; Hashash, Y.M. Simplified Model for Wall Deflection and Ground-Surface Settlement Caused by Braced Excavation in Clays. J. Geotech. Geoenviron. Eng. 2007, 133, 731–747. [Google Scholar] [CrossRef]
- Xu, Z.H. Deformation Behavior of Deep Excavations Supported by Permanent Structures in Shanghai Soft Deposit. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2007. [Google Scholar]
- Wang, Z.Z.; Whittle, A.J. Effects of Movement Induced by Ground Improvement on the Performance of an Excavation Support System in Underconsolidated Clay. J. Geotech. Geoenviron. Eng. 2024, 150, 05023008. [Google Scholar] [CrossRef]
- Lim, A.; Ou, C.-Y.; Hsieh, P.-G. Investigation of the Integrated Retaining System to Limit Deformations Induced by Deep Excavation. Acta Geotech. 2018, 13, 973–995. [Google Scholar] [CrossRef]
- Wang, X.-W.; Yang, T.-L.; Xu, Y.-S.; Shen, S.-L. Evaluation of Optimized Depth of Waterproof Curtain to Mitigate Negative Impacts during Dewatering. J. Hydrol. 2019, 577, 123969. [Google Scholar] [CrossRef]
- Yang, T.; Tong, L.; Hesham El Naggar, M.; Yan, X. Hydraulic Head Difference at Two Sides of Suspended Waterproof Curtain during Multi-Grade Dewatering of Excavation. Undergr. Space 2023, 10, 137–149. [Google Scholar] [CrossRef]
- Xu, X.B.; Hu, Q.; Huang, T.M.; Chen, Y.; Shen, W.M.; Hu, M.Y. Seepage Failure of a Foundation Pit with Confined Aquifer Layers and Its Reconstruction. Eng. Fail. Anal. 2022, 138, 106366. [Google Scholar] [CrossRef]
- Tan, Y.; Lu, Y.; Wang, D. Synchronous-Cross Zoned Excavation of the Oversized Basement of Shanghai International Financial Centre by Combination of Bottom-up and Top-down Methods: Structural and Geotechnical Behaviors. Tunn. Undergr. Space Technol. 2024, 153, 106023. [Google Scholar] [CrossRef]
- Zheng, G.; Li, Q.H.; Cheng, X.S.; Ha, D.; Shi, J.C.; Shi, X.R.; Lei, Y.W. Diaphragm Wall Deformation and Ground Settlement Caused by Dewatering before Excavation in Strata with Leaky Aquifers. Géotechnique 2022, 74, 1–17. [Google Scholar] [CrossRef]
- Zhang, J. Small Strain Stiffness Properties of Shanghai Soft Soils and Application in Deformation Analysis of Deep Excavations. Ph.D. Thesis, Tongji University, Shanghai, China, 2017. [Google Scholar]
- Li, M.; Chen, H.; Zhang, Z.; Chen, J.; Yang, Q. Numerical Analysis of a Deep and Oversized Group Excavation: A Case Study. Undergr. Space 2025, 21, 178–197. [Google Scholar] [CrossRef]
- Huynh, Q.T.; Lai, V.Q.; Boonyatee, T.; Keawsawasvong, S. Verification of Soil Parameters of Hardening Soil Model with Small-Strain Stiffness for Deep Excavations in Medium Dense Sand in Ho Chi Minh City, Vietnam. Innov. Infrastruct. Solut. 2022, 7, 15. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, J.; Zhan, H.; Wang, J.; Dou, Z.; Zhang, C.; Chen, C.; Fu, Y. Optimization Schemes for Deep Foundation Pit Dewatering under Complicated Hydrogeological Conditions Using MODFLOW-USG. Eng. Geol. 2022, 303, 106653. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, Z.; Tong, L.; Sun, J.; Cui, J.; Zhou, X.; Liu, S. Optimization of Confined Aquifer Dewatering for Long-Deep Excavation Using Simulation–Optimization Method. Undergr. Space 2024, 17, 246–266. [Google Scholar] [CrossRef]


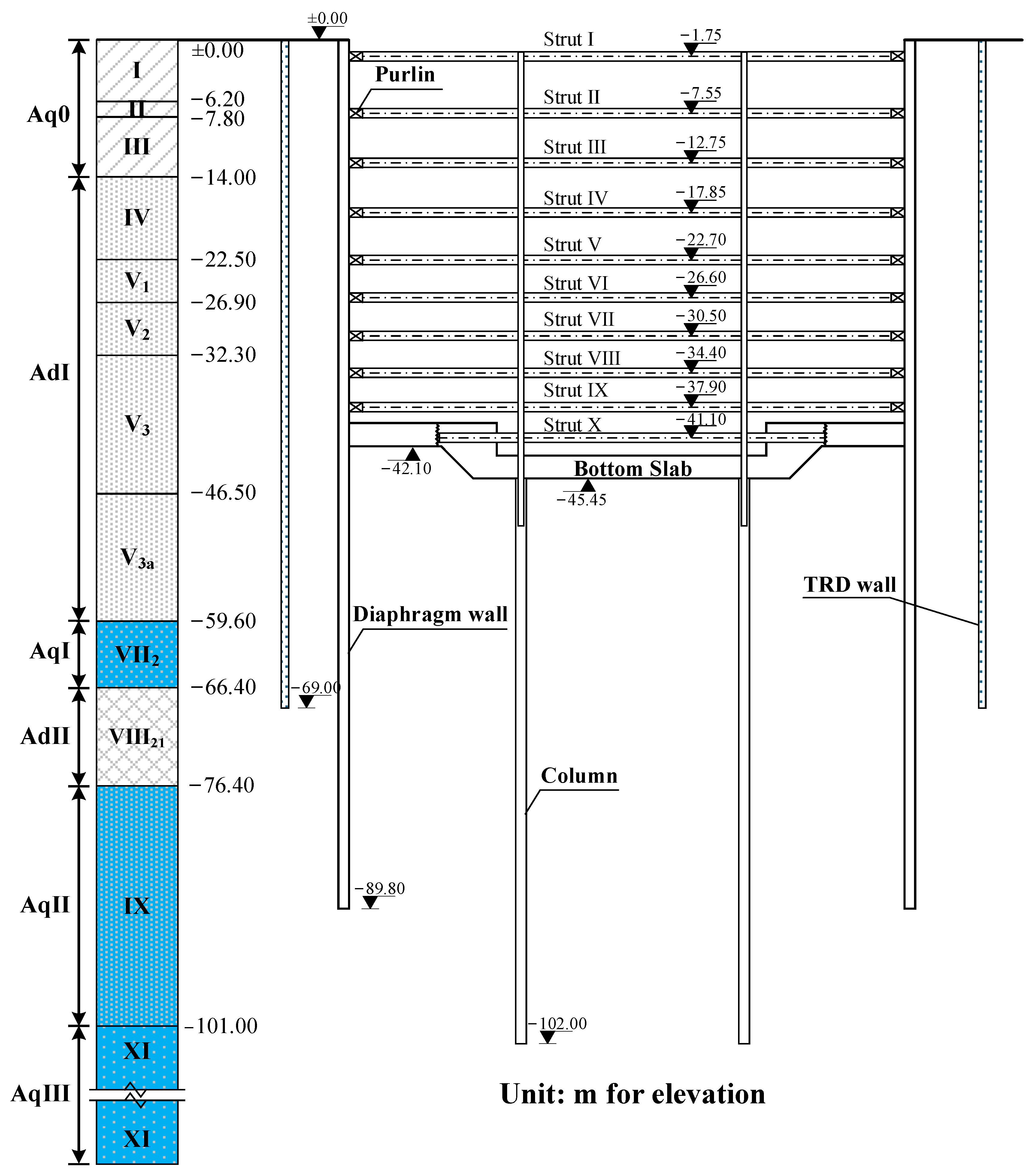





| Details of Construction | Date of Completion | |
|---|---|---|
| Stage 1 | Excavation to the depth of about 3.0 m BGS and installation of Strut I | 19 June 2020 |
| Stage 2 | Excavation to the depth of about 8.0 m BGS and installation of Strut II | 3 July 2020 |
| Stage 3 | Excavation to the depth of about 13.20 m BGS and installation of Strut III | 26 July 2020 |
| Stage 4 | Excavation to the depth of about 18.30 m BGS and installation of Strut IV | 7 August 2020 |
| Stage 5 | Excavation to the depth of about 23.15 m BGS and installation of Strut V | 25 August 2020 |
| Stage 6 | Excavation to the depth of about 27.05 m BGS and installation of Strut VI | 13 September 2020 |
| Stage 7 | Excavation to the depth of about 30.95 m BGS and installation of Strut VII | 2 October 2020 |
| Stage 8 | Excavation to the depth of about 34.85 m BGS and installation of Strut VIII | 17 October 2020 |
| Stage 9 | Excavation to the depth of about 38.35 m BGS and installation of Strut IX | 1 November 2020 |
| Stage 10 | Excavation to the depth of 42.10 m BGS, casting the first slab in the general area and installation of Strut X in the locally deepened area | 1 December 2020 |
| Stage 11 | Excavation to the depth of 45.45 m BGS locally and casting the second slab in the locally deepened area | 24 December 2020 |
| Soil Layer | γ | c′ | φ′ | ψ | k | E50 | Eoed | Eur | νur | m | Rf | γ0.7 | G0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| kN/m3 | kPa | ° | ° | cm/s | MPa | MPa | MPa | ×10−4 | MPa | ||||
| II clayey silt with silty clay | 18.5 | 6 | 27.1 | 0 | 2.74 × 10−7 | 5.0 | 4.2 | 25.1 | 0.2 | 0.8 | 0.9 | 2.7 | 87.70 |
| III mucky silty clay with clayey silt | 17.7 | 4 | 23.9 | 0 | 5.89 × 10−7 | 3.8 | 3.2 | 25.4 | 0.2 | 0.8 | 0.6 | 2.7 | 83.87 |
| IV mucky clay | 16.8 | 8 | 19.6 | 0 | 3.38 × 10−7 | 2.5 | 2.1 | 16.6 | 0.2 | 0.8 | 0.6 | 2.7 | 46.37 |
| V1 clay | 17.6 | 10 | 23.1 | 0 | 3.69 × 10−7 | 3.7 | 3.1 | 18.4 | 0.2 | 0.8 | 0.9 | 2.7 | 47.88 |
| V2 clayey silt with silty clay | 18.0 | 5 | 29.5 | 0 | 8.97 × 10−5 | 5.7 | 4.8 | 28.5 | 0.2 | 0.8 | 0.9 | 2.7 | 74.13 |
| V3 silty clay | 17.9 | 9 | 25.5 | 0 | 4.17 × 10−7 | 4.6 | 3.8 | 23.1 | 0.2 | 0.8 | 0.9 | 2.7 | 59.95 |
| V3a sandy silt with silty clay | 18.4 | 5 | 29.5 | 0 | 5.10 × 10−4 | 9.8 | 8.2 | 48.9 | 0.2 | 0.8 | 0.9 | 2.7 | 127.20 |
| VII2 fine sand | 19.2 | 1 | 34.5 | 4.5 | 1.02 × 10−3 | 14.1 | 14.1 | 56.2 | 0.2 | 0.5 | 0.9 | 2.7 | 281.00 |
| VIII21 silty clay with silty sand | 18.3 | 12 | 25.0 | 0 | 1.76 × 10−6 | 5.6 | 4.6 | 27.8 | 0.2 | 0.8 | 0.9 | 2.7 | 138.78 |
| IX fine sand | 19.7 | 0 | 36.0 | 6 | 1.18 × 10−3 | 13.4 | 13.4 | 53.5 | 0.2 | 0.5 | 0.9 | 2.7 | 267.60 |
| XI fine sand | 19.6 | 0 | 35.0 | 5 | 1.03 × 10−3 | 13.3 | 13.3 | 53.3 | 0.2 | 0.5 | 0.9 | 2.7 | 266.60 |
| Stages | Details of Construction | Duration |
|---|---|---|
| Stage 0 | Activation of initial stress field with installation of walls and piles | / |
| Stage 1 | Lowering groundwater to 3 m BGS and excavation of soil to 2 m BGS; | 3 days |
| installation of Strut I | ||
| Stage 2 | Lowering groundwater to 9 m BGS and excavation of soil to 8 m BGS; | 14 days |
| installation of Strut II | ||
| Stage 3 | Lowering groundwater to 14 m BGS and excavation of soil to 13 m BGS; | 23 days |
| installation of Strut III | ||
| Stage 4 | Lowering groundwater to 19 m BGS and excavation of soil to 18 m BGS; | 12 days |
| installation of Strut IV | ||
| Stage 5 | Lowering groundwater to 24 m BGS, dewatering in AqI and excavation of soil to 23 m BGS; | 18 days |
| installation of Strut V | ||
| Stage 6 | Lowering groundwater to 28 m BGS, dewatering in AqI and excavation of soil to 27 m BGS; | 19 days |
| installation of Strut VI | ||
| Stage 7 | Lowering groundwater to 32 m BGS, dewatering in AqI and excavation of soil to 31 m BGS; | 19 days |
| installation of Strut VII | ||
| Stage 8 | Lowering groundwater to 36 m BGS, dewatering in AqI and excavation of soil to 35 m BGS; | 15 days |
| installation of Strut VIII | ||
| Stage 9 | Lowering groundwater to 39.5 m BGS, dewatering in AqI and AqII and excavation of soil to 38.5 m BGS; | 15 days |
| installation of Strut IX | ||
| Stage 10 | Lowering groundwater to 43.1 m BGS, dewatering in AqI and AqII and excavation of soil to 42.1 m BGS; | 30 days |
| casting of bottom slab and installation of Strut X | ||
| Stage 11 | Lowering groundwater to 46.5 m BGS, dewatering in AqI and AqII and excavation of soil to 45.45 m BGS; | 23 days |
| casting of bottom slab in locally deepened area |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Wang, W.; Xu, Z.; Chen, J.; Zhang, J. Hydro-Mechanical Numerical Analysis of a Double-Wall Deep Excavation in a Multi-Aquifer Strata Considering Soil–Structure Interaction. Buildings 2025, 15, 989. https://doi.org/10.3390/buildings15060989
Zhu Y, Wang W, Xu Z, Chen J, Zhang J. Hydro-Mechanical Numerical Analysis of a Double-Wall Deep Excavation in a Multi-Aquifer Strata Considering Soil–Structure Interaction. Buildings. 2025; 15(6):989. https://doi.org/10.3390/buildings15060989
Chicago/Turabian StyleZhu, Yinhang, Weidong Wang, Zhonghua Xu, Jinjian Chen, and Ji Zhang. 2025. "Hydro-Mechanical Numerical Analysis of a Double-Wall Deep Excavation in a Multi-Aquifer Strata Considering Soil–Structure Interaction" Buildings 15, no. 6: 989. https://doi.org/10.3390/buildings15060989
APA StyleZhu, Y., Wang, W., Xu, Z., Chen, J., & Zhang, J. (2025). Hydro-Mechanical Numerical Analysis of a Double-Wall Deep Excavation in a Multi-Aquifer Strata Considering Soil–Structure Interaction. Buildings, 15(6), 989. https://doi.org/10.3390/buildings15060989





