Study on Eccentric Compression Behavior of Precast Stratified Concrete Composite Column with Inserted Steel Tube
Abstract
1. Introduction
2. Experimental Programs
2.1. Specimens and Material
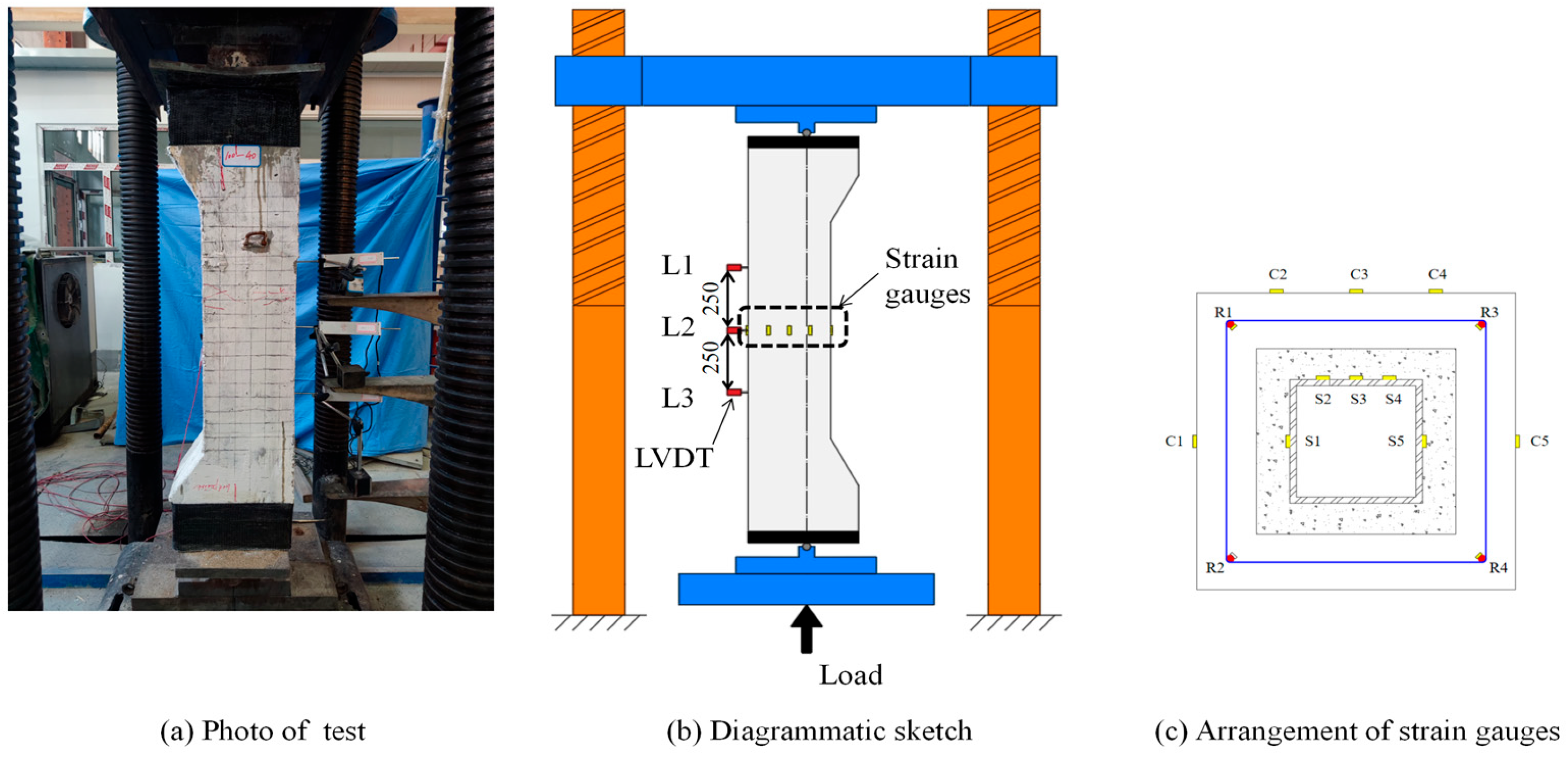
2.2. Test Setup and Measuring Instrumentation
3. Test Results and Discussion
3.1. Crack Propagation and Failure State
- PSCCST-80-20 specimen:
- 2.
- PSCCST-80-130 specimen:
- 3.
- PSCCST-80-200 specimen:
- 4.
- PSCCST-100-40 specimen:
- 5.
- PSCCST-100-150 specimen:
- 6.
- PSCCST-100-220 specimen:
3.2. Ultimate Bearing Capacity of Specimens
3.3. Load-Strain Relationships
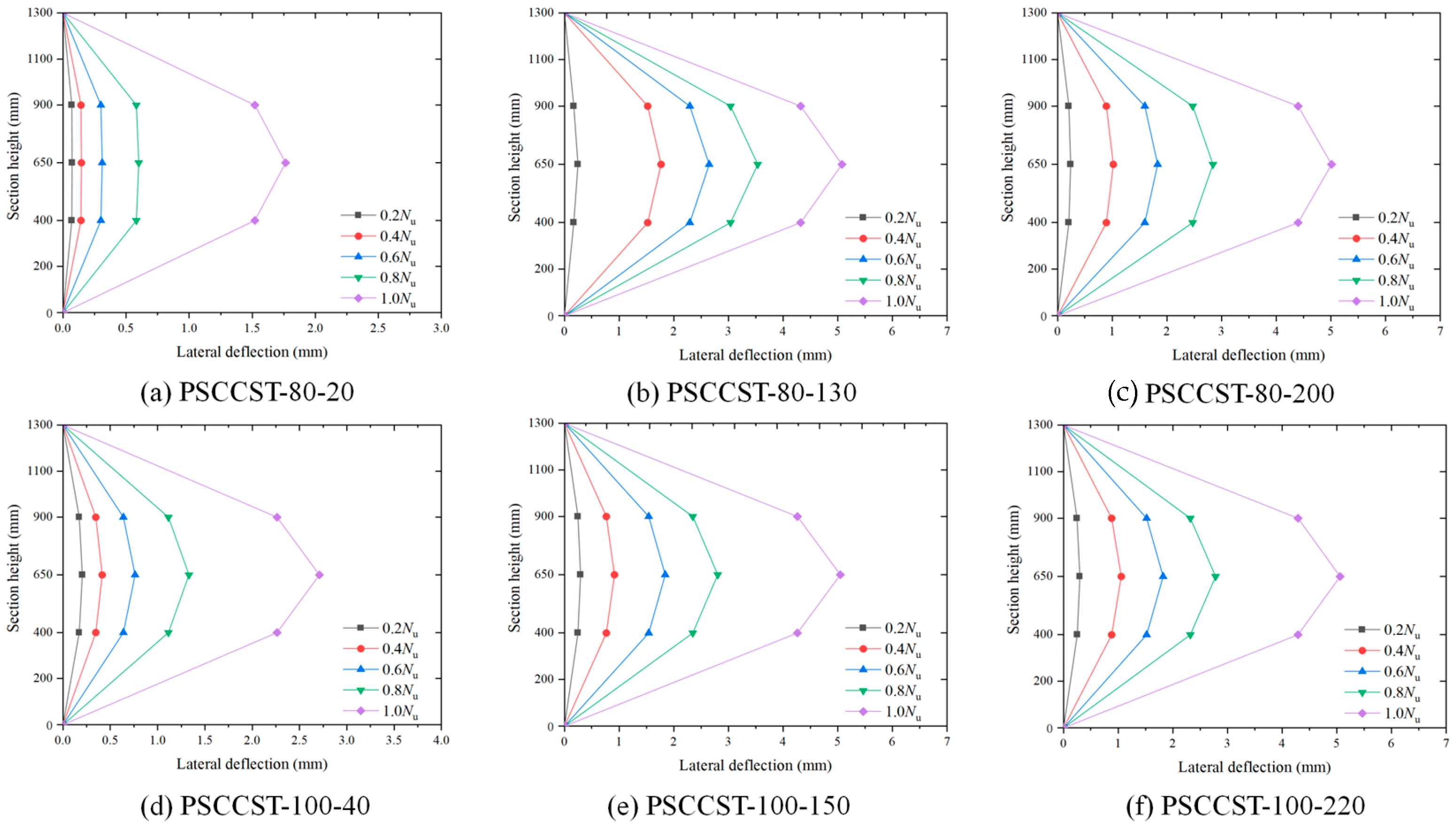
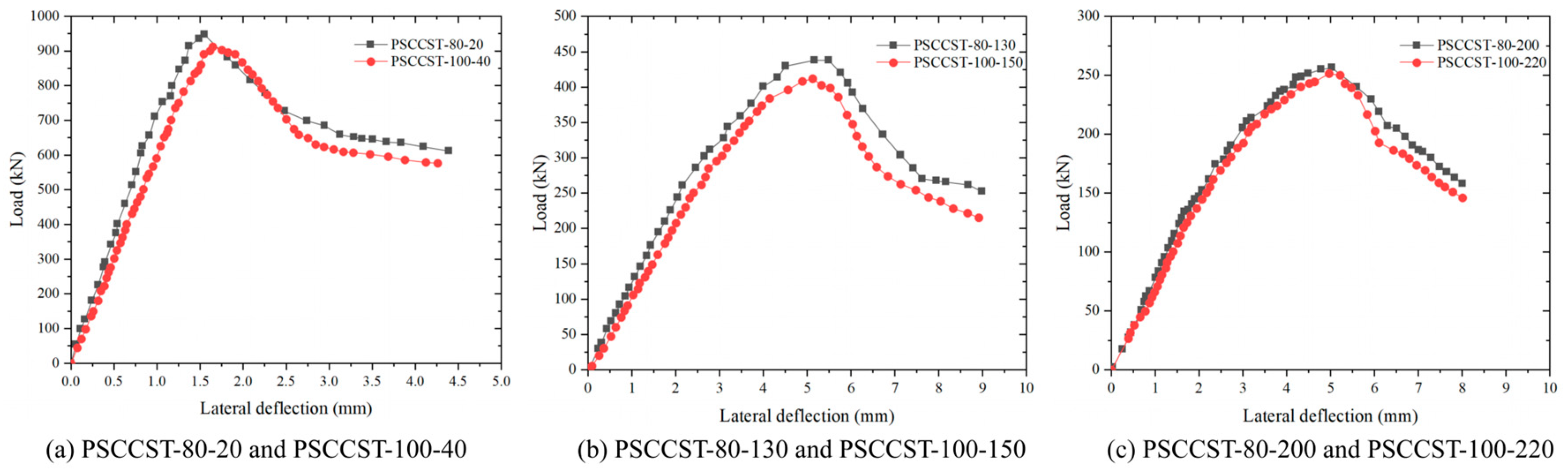
3.4. Load-Deflection Relationships
3.5. Summary of Failure Type
3.5.1. Failure Type 1
3.5.2. Failure Type 2
3.5.3. Failure Type 3
3.6. Failure Mode Deduction
3.6.1. Compressive-Type Failure Mode
- Further extended analysis based on failure type 1
- 2.
- Extended analysis of failure type 2
- 3.
- Further extended analysis based on failure type 1 and 2
- 4.
- Compressive-type failure mode deduction
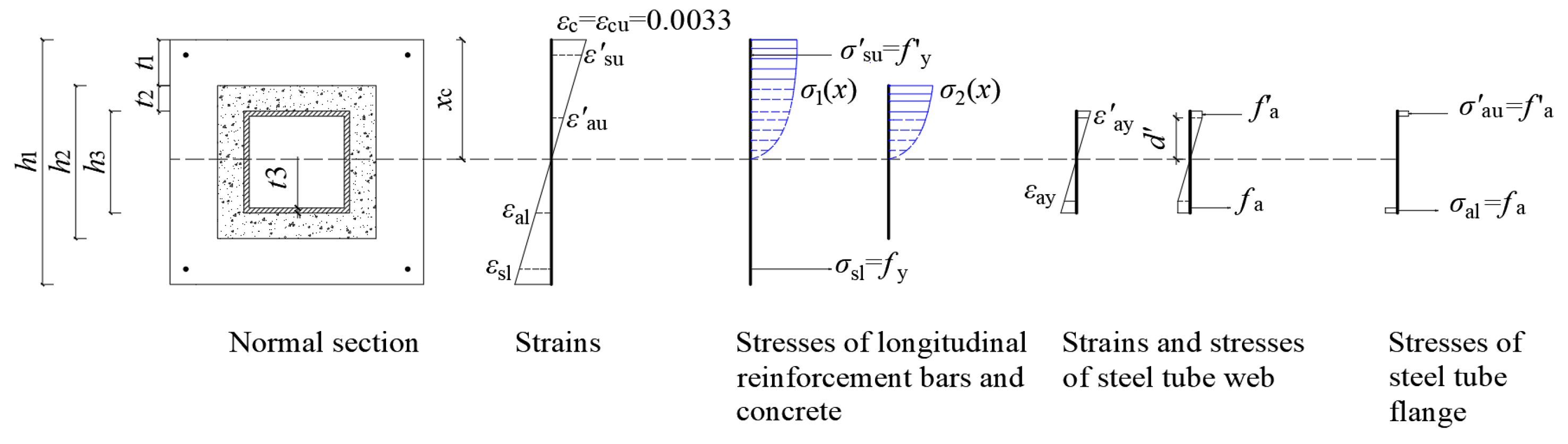
3.6.2. Total-Yield-Type Failure Mode
4. Calculation Methods of Eccentric Compression Bearing Capacity
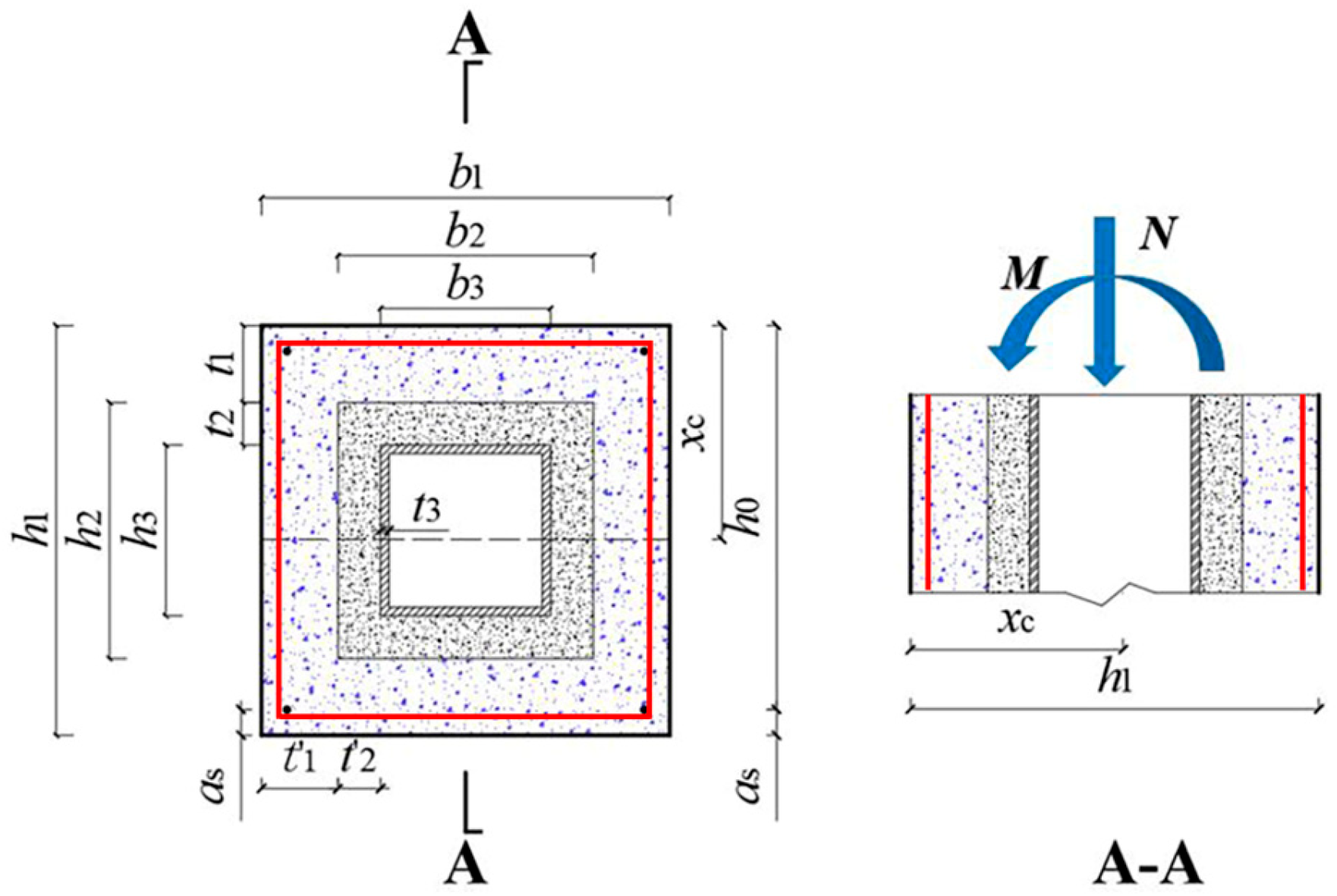
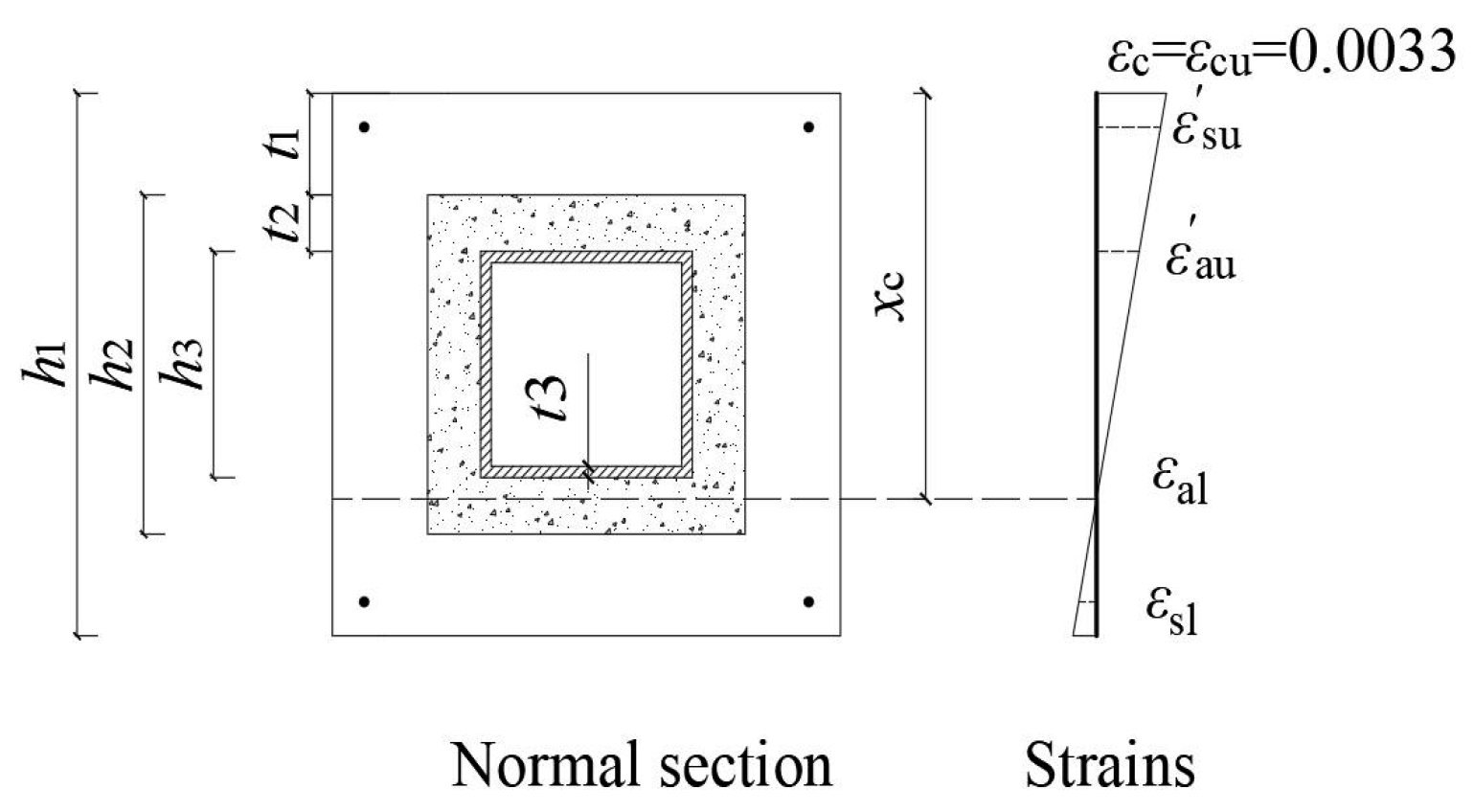
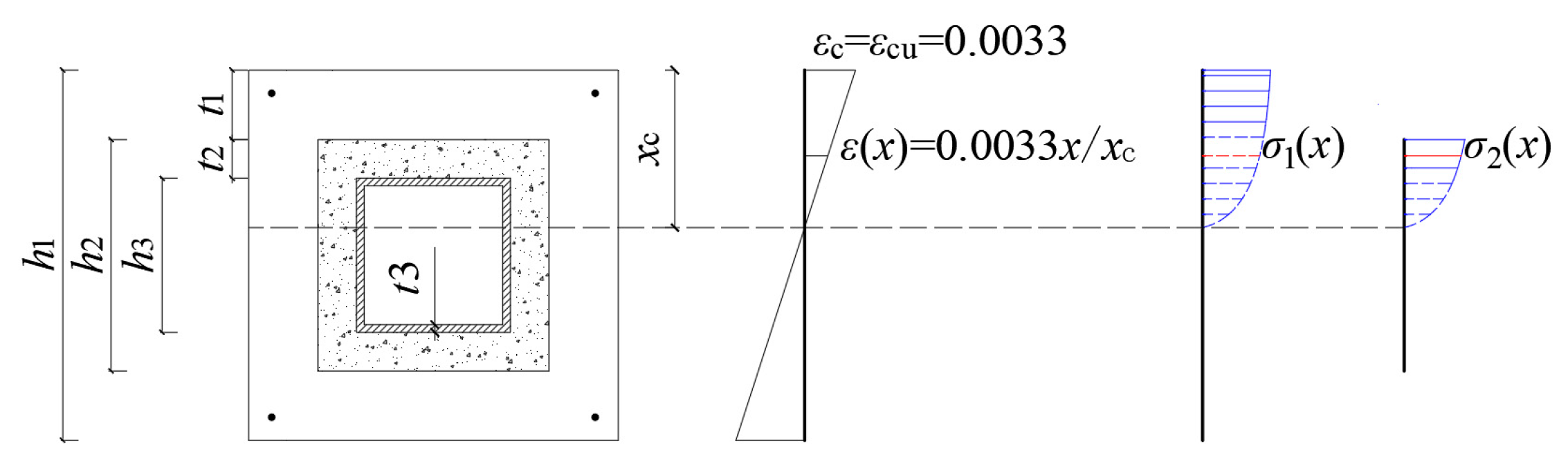
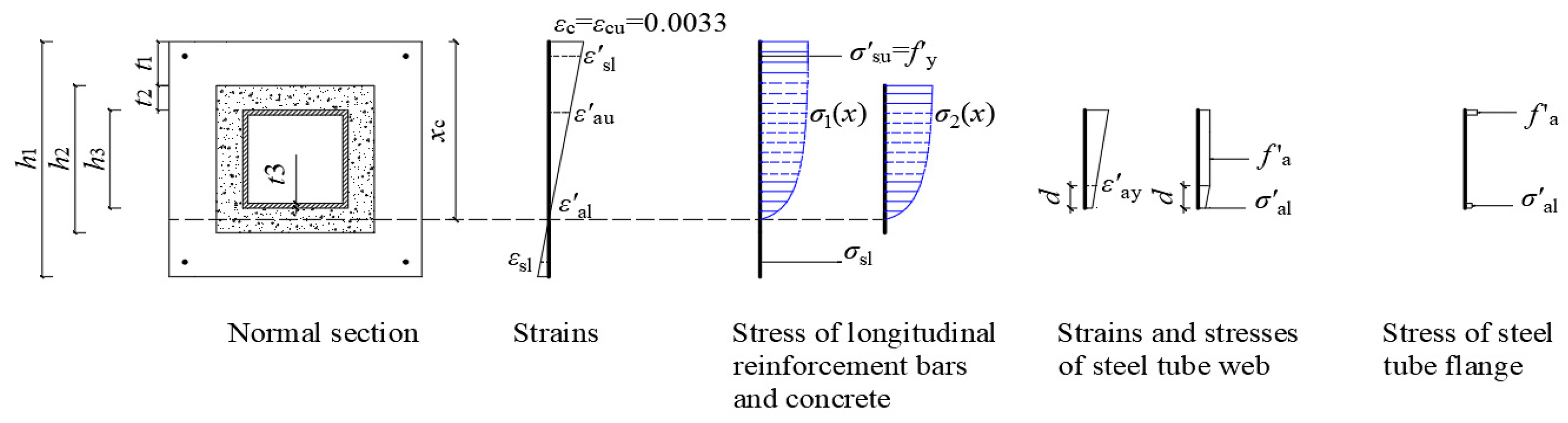
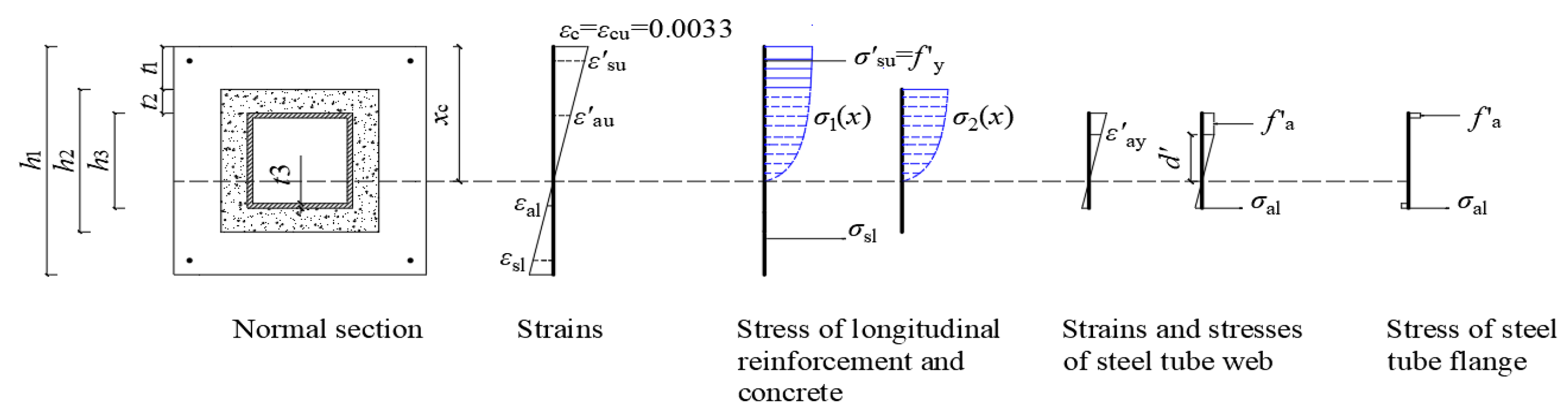
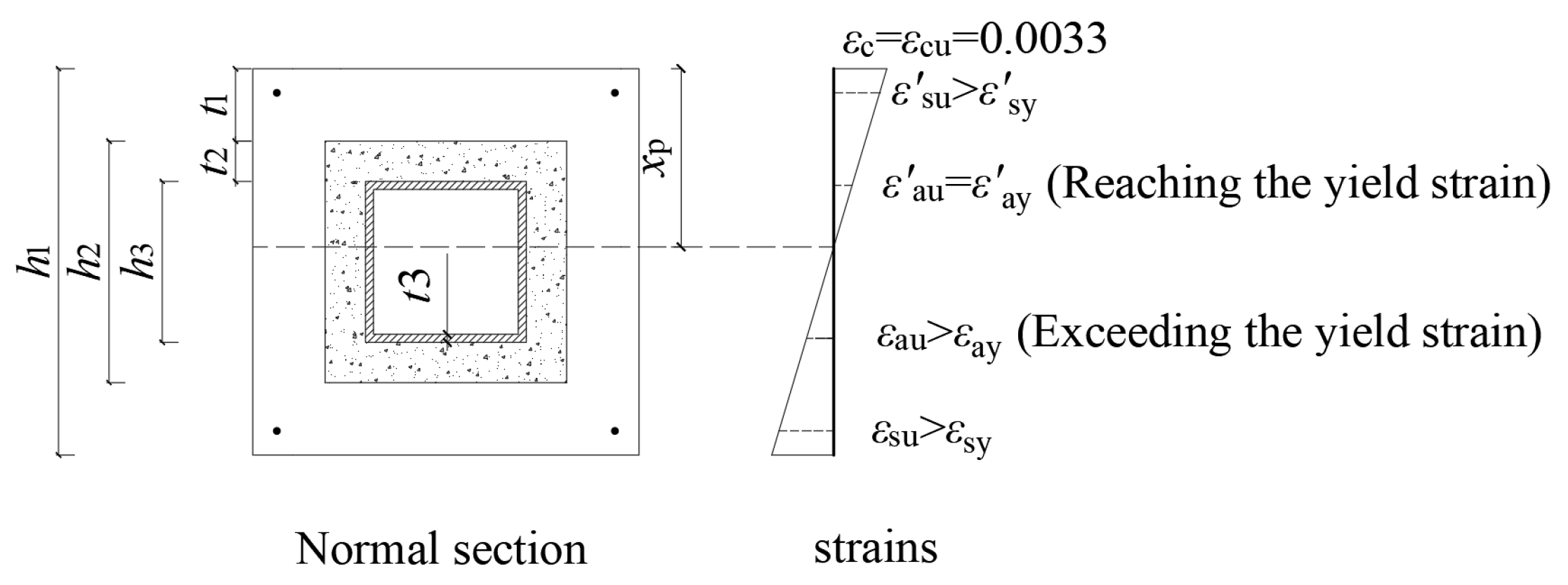
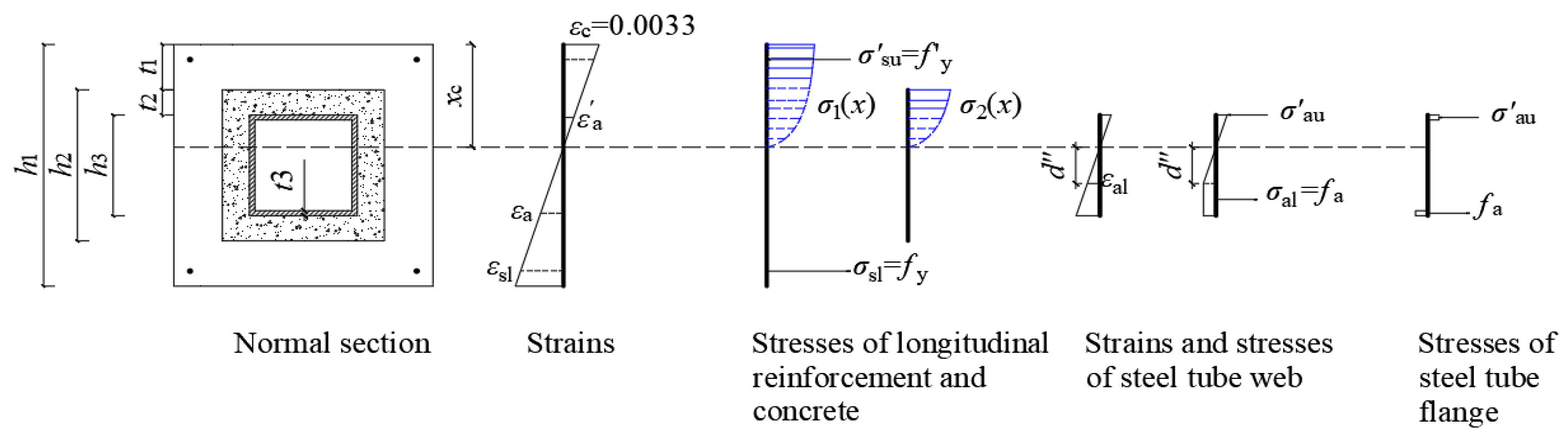
4.1. Basic Assumptions
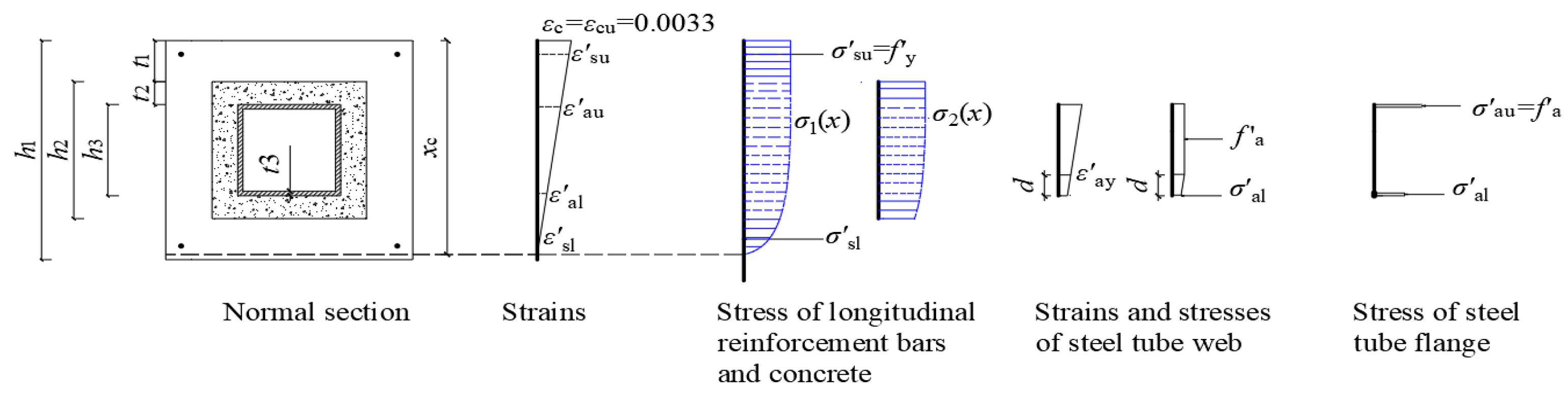
4.2. Establishment of Equations
4.2.1. Calculation Equations for Compressive-Type Failure Mode
- Case 1 (the neutral axis appears in the lower precast part, h2 + t1 ≤ xc < h1)
- (a)
- Sub-case 1 (h0 ≤ xc < h1):
- (b)
- Sub-case 2 (h2 + t1 ≤ xc < h0):
- 2.
- Case 2 (the neutral axis appears in the lower post-cast part, h3 + t1 + t2 ≤ xc < h2 + t1)
- 3.
- Case 3 (the neutral axis appears in the middle steel tube web, xt ≤ xc < h3 + t1 + t2)
4.2.2. Calculation Equations for Total-Yield-Type Failure Mode
4.3. Verification of Calculation Methods
4.3.1. PSCCST-100-X Specimens
4.3.2. PSCCST-80-X Specimens
4.4. Error Analysis Between Nc and Nt
4.5. Sensitivity Analysis of Calculation Methods
4.6. Comparison with Another Method
5. Further Expanded Analysis
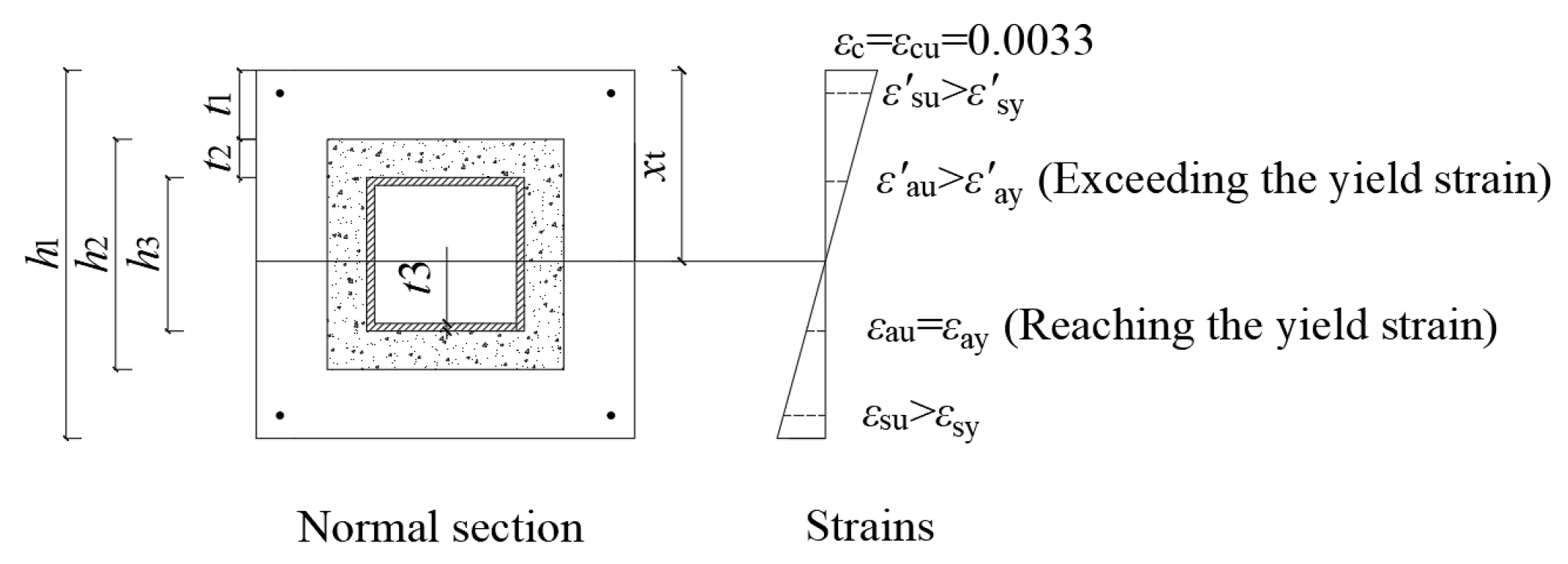
5.1. Tensile-Type Failure Mode
5.2. Calculation Equations for Tensile-Type Failure Mode
6. Conclusions
- There are three typical failure modes, including the compressive-type failure mode, total-yield-type failure mode, and tensile-type failure mode, which are primarily dependent on the eccentricity e. As e increased, there was a noticeable decrease in the ultimate eccentric compression capacity of the PSCCST column Nu.
- The PSCCST column has good ductility. With the increase of e, the horizontal lateral deflection corresponding to Nu increased, indicating that the deformation capacity increased.
- A set of calculation formulas for predicting Nu was proposed, which can serve as the design basis for the PSCCST column.
- PSCCST columns can be employed as new vertical load-bearing components in various structural systems, especially in prefabricated concrete structure systems.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chinnasamy, Y.; Joanna, P.S.; Kothanda, K.; Gurupatham, B.G.A.; Roy, K. Behavior of Pultruded Glass-Fiber-Reinforced Polymer Beam-Columns Infilled with Engineered Cementitious Composites under Cyclic Loading. J. Compos. Sci. 2022, 6, 338. [Google Scholar] [CrossRef]
- Samuel, J.; Nair, S.R.; Joanna, P.S.; Gurupatham, B.G.A.; Roy, K.; Lim, J.B.P. Composite Cold-Formed Steel Beams with Diagonal Rebars for Earthquake-Resistant Buildings. Materials 2023, 16, 3002. [Google Scholar] [CrossRef] [PubMed]
- Reena, G.C.; Gurupatham, A.G.B.; Tsavdaridis, D.K. Column Link Behavior in Eccentrically Braced Composite 3-Dimensional Frames. Buildings 2023, 13, 2970. [Google Scholar] [CrossRef]
- Wu, X.M.; Shi, Y.L.; Zheng, L.; Wang, W.D. Performance of rectangular SRCFST stub columns under long-term loading and preload on steel tube. Structures 2024, 61, 106110. [Google Scholar] [CrossRef]
- Ji, S.H.; Wang, W.D.; Shi, Y.L.; Zheng, L. Residual compressive behaviour and CFRP strengthening of SRCFST columns after combined damage of fire and lateral impact. Thin-Walled Struct. 2025, 207, 112756. [Google Scholar] [CrossRef]
- Wang, S.Y.; Wang, Y.L.; Sheng, D.P.; Wang, Y. Study on new prefabricated reinforced concrete structure technology based on fault-tolerant design. Buildings 2022, 12, 814. [Google Scholar] [CrossRef]
- Hwang, J.H.; Lee, D.H.; Oh, J.Y.; Choi, S.H.; Kim, K.S.; Seo, S.Y. Seismic performances of centrifugally-formed hollow-core precast columns with multi-interlocking spirals. Steel Compos. Struct. 2016, 20, 1259–1274. [Google Scholar] [CrossRef]
- Xue, Y.; Yang, Y.; Yu, Y. Cyclic behavior of partially precast steel reinforced concrete short columns: Experiment and theoretical analysis. Eng. Struct. 2019, 199, 109658. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y.; Zhang, J.T.; Xue, Y.C.; Liu, R.Y.; Yu, Y.L. Experimental investigation on shear capacity of partially prefabricated steel reinforced concrete columns. Steel Compos. Struct. 2018, 28, 73–82. [Google Scholar] [CrossRef]
- Zhang, B.J.; Xie, Y.T.; Wang, S.Y.; Feng, J.P.; Gao, Y.; Wang, Y. Eccentric bearing capacity of steel reinforced reactive powder concrete columns after high temperature exposure. Case Stud. Constr. Mat. 2023, 19, e02648. [Google Scholar] [CrossRef]
- Morteza, N.; Mohsen, A.; Mahdi, N. Effect of concrete confinement level on load-bearing capacity of steel-reinforced concrete (SRC) columns under eccentric loading: Experiment and FEA model. Structures 2022, 35, 202–213. [Google Scholar] [CrossRef]
- An, Y.; Han, L. Behaviour of concrete-encased CFST columns under combined compression and bending. J. Constr. Steel. Res. 2014, 101, 314–330. [Google Scholar] [CrossRef]
- Lai, B.; Liew, J.Y.R.; Li, S. Finite element analysis of concrete-encased steel composite columns with off-center steel section. In Proceedings of the 12th International Conference on ‘Advances in Steel-Concrete Composite Structures’, Valencia, Spain, 27–29 June 2018. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Y.; Zhang, W.; Feng, S.Q. Behavior of partially precast steel reinforced concrete columns under eccentric loading. Eng. Struct. 2019, 197, 109429. [Google Scholar] [CrossRef]
- Ren, Q.; Ding, J.; Wang, Q.; Lou, H.Q. Behavior of slender square hollow steel-reinforced concrete columns under eccentric compression. J. Build. Eng. 2021, 43, 103133. [Google Scholar] [CrossRef]
- Wang, R.; Han, L.H.; Lam, D. Behaviour of octagonal steel-reinforced concrete box columns under compressive load. Mag. Concr. Res. 2018, 70, 838–855. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Li, G.Q. Residual strength of L-shaped steel reinforced concrete columns after exposure to high temperatures. KSCE J. Civ. Eng. 2021, 25, 1369–1384. [Google Scholar] [CrossRef]
- ACI 318-19; Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- ASCE/SEI 41-17; Seismic Evaluation and Retrofit of Existing Buildings. Structural Engineering Institute: Reston, VA, USA; American Society of Civil Engineers: Reston, VA, USA, 2017.
- CEB-FIP Model Code 90; Design Code. Comité Euro-International du Béton (CEB): Lausanne, Switzerland; Fédération Internationale de la Précontrainte (FIP): Lausanne, Switzerland; Thomas Telford Services Ltd.: Westminster, UK, 1993.
- JGJ 138-2016; Code for Design of Composite Structures. Ministry of Housing and Urban-Rural Development (MOHURD): Beijing, China; China Architecture Publishing & Media Co., Ltd.: Beijing, China, 2016. (In Chinese)
- GB 50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development (MOHURD): Beijing, China; China Architecture Publishing & Media Co., Ltd.: Beijing, China, 2010. (In Chinese)
- GB 1499.2-2024; Steel for the Reinforcement of Concrete—Part 2: Hot Rolled Ribbed Bars. China Standards Press: Beijing, China, 2024. (In Chinese)
- GB/T 8162-2018; Seamless Steel Tubes for Structural Purposes. China Standards Press: Beijing, China, 2018. (In Chinese)
- Wang, F.; Young, B.; Gardner, L. Testing and numerical modelling of circular CFDST normal sections with stainless steel outer tubes in bending. Eng. Struct. 2021, 247, 113170. [Google Scholar] [CrossRef]
- Ahmed, M.; Liang, Q.Q.; Patel, V.I.; Hadi, M.N.S. Behavior of eccentrically loaded double circular steel tubular short columns filled with concrete. Eng. Struct. 2019, 201, 109790. [Google Scholar] [CrossRef]
- Cao, B.; Zhu, L.; Jiang, X.T.; Wang, C.S. An investigation of compression bearing capacity of concrete-filled rectangular stainless steel tubular columns under axial load and eccentric axial load. Sustainability 2022, 14, 8946. [Google Scholar] [CrossRef]
- Chen, Z.P.; Liao, H.; Zhou, J.; Ye, P. Eccentric compression behavior of reinforced recycled aggregate concrete columns after exposure to elevated temperatures: Experimental and numerical study. Structures 2022, 43, 959–976. [Google Scholar] [CrossRef]
- Ma, H.; Chen, Y.C.; Bai, H.Y.; Zhao, Y.L. Eccentric compression performance of composite columns composed of RAC-filled circular steel tube and profile steel. Eng. Struct. 2019, 201, 109778. [Google Scholar] [CrossRef]
- Zhu, X.H. Behavior of Hollow Steel Reinforced Concrete Columns Under Eccentric Compression. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2015. (In Chinese). [Google Scholar]
- T/CCES 30–2022; Standard for Tolerances for Precast Concrete Components. China Architecture Publishing & Media Co., Ltd.: Beijing, China, 2022. (In Chinese)
- GB 50204–2015; Code for Acceptance of Construction Quality of Concrete Structures. Ministry of Housing and Urban-Rural Development (MOHURD): Beijing, China; China Architecture Publishing & Media Co., Ltd.: Beijing, China, 2015. (In Chinese)

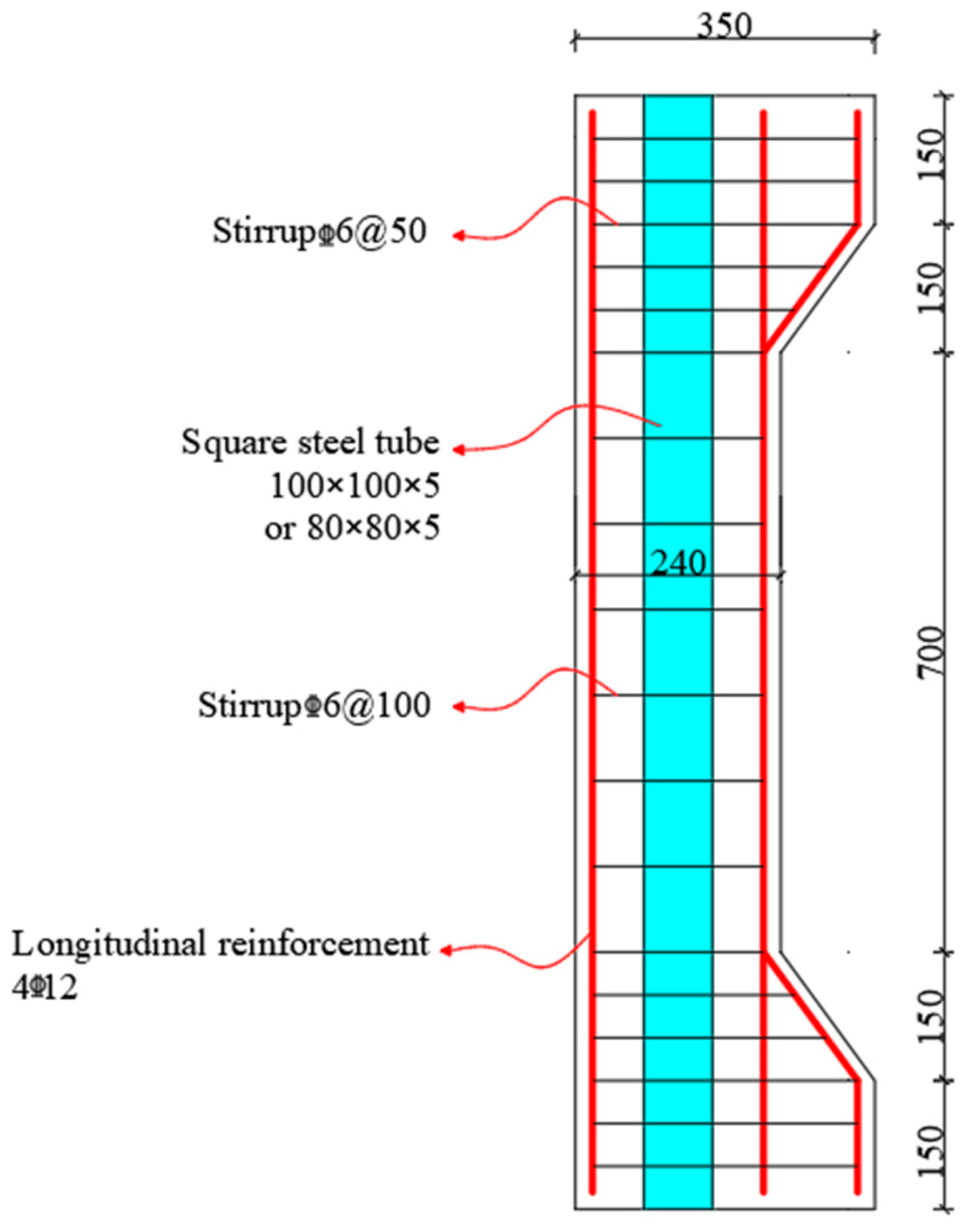










| Specimen No. | Size of Precast Concrete Part | Size of Post-Cast Concrete Part | Size of Steel Tube | Load Eccentricity e0 (mm) | ||||
|---|---|---|---|---|---|---|---|---|
| h1 × b1 (mm × mm) | t1 = t′1 (mm) | as (mm) | h2 × b2 (mm × mm) | t2 = t′2 (mm) | h3 × b3 (mm × mm) | t3 (mm) | ||
| PSCCST-80-20 | 240 × 240 | 45 | 27 | 150 × 150 | 35 | 80 × 80 | 5 | 20 |
| PSSCT-80-130 | 240 × 240 | 45 | 27 | 150 × 150 | 35 | 80 × 80 | 5 | 130 |
| PSCCST-80-200 | 240 × 240 | 45 | 27 | 150 × 150 | 35 | 80 × 80 | 5 | 200 |
| PSCCST-100-40 | 240 × 240 | 45 | 27 | 150 × 150 | 25 | 100 × 100 | 5 | 40 |
| PSCCST-100-150 | 240 × 240 | 45 | 27 | 150 × 150 | 25 | 100 × 100 | 5 | 150 |
| PSCCST-100-220 | 240 × 240 | 45 | 27 | 150 × 150 | 25 | 100 × 100 | 5 | 220 |
| Concrte Grade | Water | Cement | Fly Ash | Mineral Fines | Sand | Aggregate | Superplasticizer |
|---|---|---|---|---|---|---|---|
| C30 | 170 | 230 | 80 | 70 | 889 | 925 | 1.8 |
| C40 | 170 | 280 | 70 | 60 | 882 | 918 | 1.8 |
| Specimen | Eccentricity e0 (mm) | Test Value of Nt (kN) |
|---|---|---|
| PSCCST-80-20 | 20 mm | 947 |
| PSCCST-80-130 | 130 mm | 443 |
| PSCCST-80-200 | 200 mm | 258 |
| PSCCST-100-40 | 40 mm | 916 |
| PSCCST-100-150 | 150 mm | 410 |
| PSCCST-100-220 | 220 mm | 256 |
| Edge of Concrete Compression Zone | Lower Flange of Steel Tube | Upper Flange of Steel Tube | Web of Steel Tube | Longitudinal Reinforcement Bars | |
|---|---|---|---|---|---|
| In Tension Zone | In Compression Zone | ||||
| Crushed | Just yield under tension | Yield under compression | The webs contain compression and tension zones, with partial webs in the compression zone yield. | Yield | Yield |
| Specimen | Eccentricity e0 (mm) | η | Eccentricity e = ηe0 (mm) | Failure Mode | Calculated Value of Nc (kN) | Test Value of Nt (kN) | Nc/Nt |
|---|---|---|---|---|---|---|---|
| PSCCST-100-40 | 40 | 1.05 | 42 | compression failure (Case 1) | 871 | 916 | 0.95 |
| PSCCST-100-150 | 150 | 1.03 | 154 | compression failure (Case 3) | 393 | 410 | 0.96 |
| PSCCST-100-220 | 220 | 1.02 | 224 | total yield failure | 242 | 256 | 0.95 |
| Specimen No. | Eccentricity e0 (mm) | η | Eccentricity e = ηe0 (mm) | Failure Mode | Calculated Value of Nc (kN) | Test Value of Nt (kN) | Nc/Nt |
|---|---|---|---|---|---|---|---|
| PSCCST-80-20 | 20 mm | 1.05 | 21 | compression failure (Case 1) | 885 | 947 | 0.93 |
| PSCCST-80-130 | 130 mm | 1.03 | 144 | compression failure (Case 3) | 427 | 443 | 0.96 |
| PSCCST-80-200 | 200 mm | 1.02 | 204 | total yield failure | 246 | 258 | 0.95 |
| Parameter | Deviation Rate/Amount | Parameter Value (mm) | Nc′ (kN) | Nc′/Nt |
|---|---|---|---|---|
| b2 | −5% | 142.5 | 246.132 | 0.954 |
| b2 | +5% | 157.5 | 244.068 | 0.946 |
| t1 | −5% | 42.75 | 247.422 | 0.959 |
| t1 | +5% | 47.25 | 243.552 | 0.944 |
| t2 | −5% | 33.25 | 246.906 | 0.957 |
| t2 | +5% | 36.75 | 243.810 | 0.945 |
| as | −5 mm | 22 | 245.358 | 0.951 |
| as | +5 mm | 32 | 244.842 | 0.949 |
| Specimen | PSCCST-80-20 | PSCCST-100-40 | PSCCST-80-130 | PSCCST-100-150 | PSCCST-80-200 | PSCCST-100-220 |
|---|---|---|---|---|---|---|
| Nc | 885 | 871 | 427 | 393 | 246 | 242 |
| Nc2 | 821 | 824 | 405 | 371 | 230 | 222 |
| Nc2/Nc | 0.928 | 0.946 | 0.949 | 0.944 | 0.935 | 0.917 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ma, S.; Wang, S. Study on Eccentric Compression Behavior of Precast Stratified Concrete Composite Column with Inserted Steel Tube. Buildings 2025, 15, 826. https://doi.org/10.3390/buildings15050826
Wang Y, Ma S, Wang S. Study on Eccentric Compression Behavior of Precast Stratified Concrete Composite Column with Inserted Steel Tube. Buildings. 2025; 15(5):826. https://doi.org/10.3390/buildings15050826
Chicago/Turabian StyleWang, Yilin, Shikun Ma, and Shunyao Wang. 2025. "Study on Eccentric Compression Behavior of Precast Stratified Concrete Composite Column with Inserted Steel Tube" Buildings 15, no. 5: 826. https://doi.org/10.3390/buildings15050826
APA StyleWang, Y., Ma, S., & Wang, S. (2025). Study on Eccentric Compression Behavior of Precast Stratified Concrete Composite Column with Inserted Steel Tube. Buildings, 15(5), 826. https://doi.org/10.3390/buildings15050826






