Interfacial Bond Behavior of Clay Brick Masonry Strengthened with CFRP
Abstract
1. Introduction
2. Experimental
2.1. Material Properties
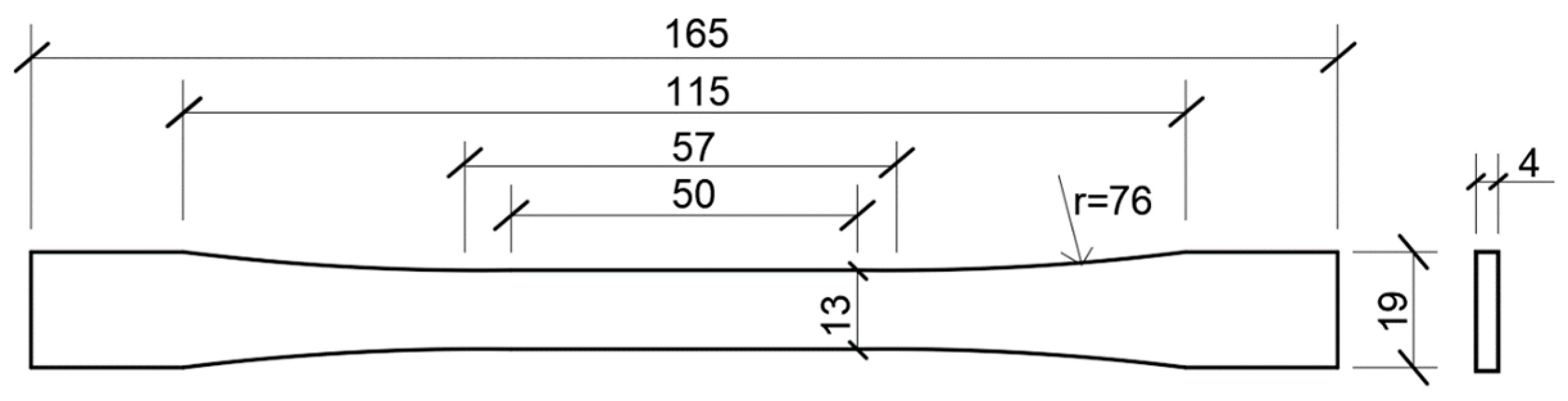
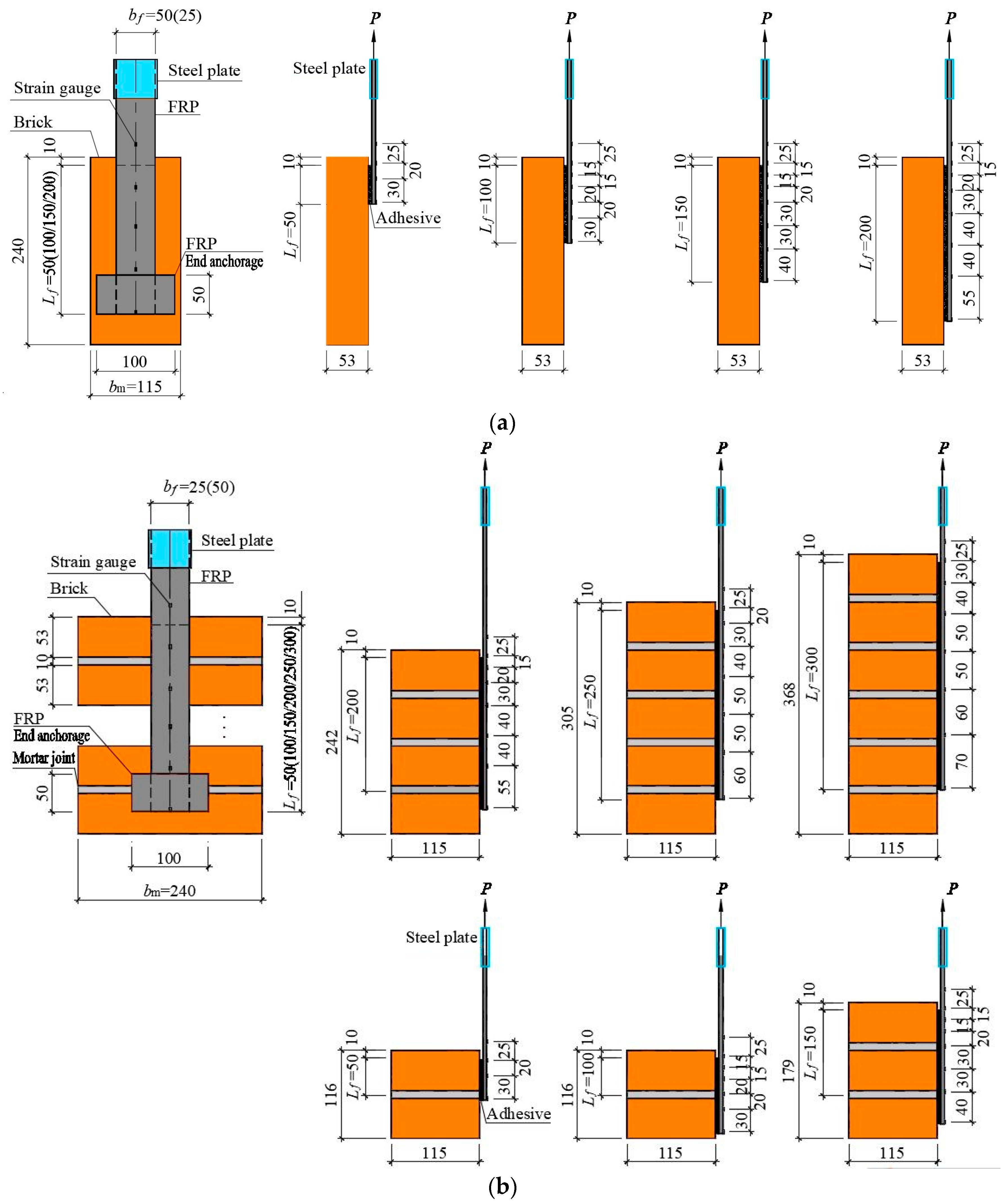
2.2. Specimen Fabrication
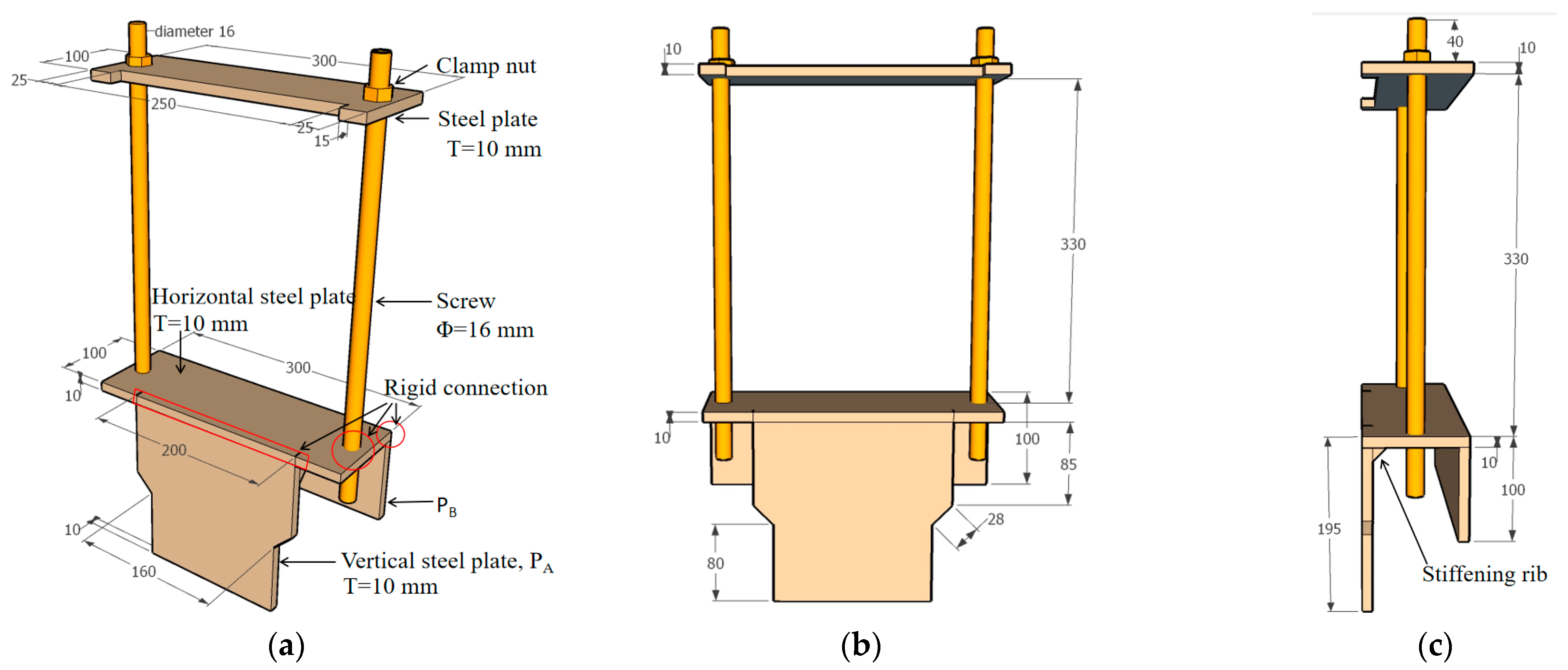
2.3. Loading System
3. Results and Discussion
3.1. Failure Modes
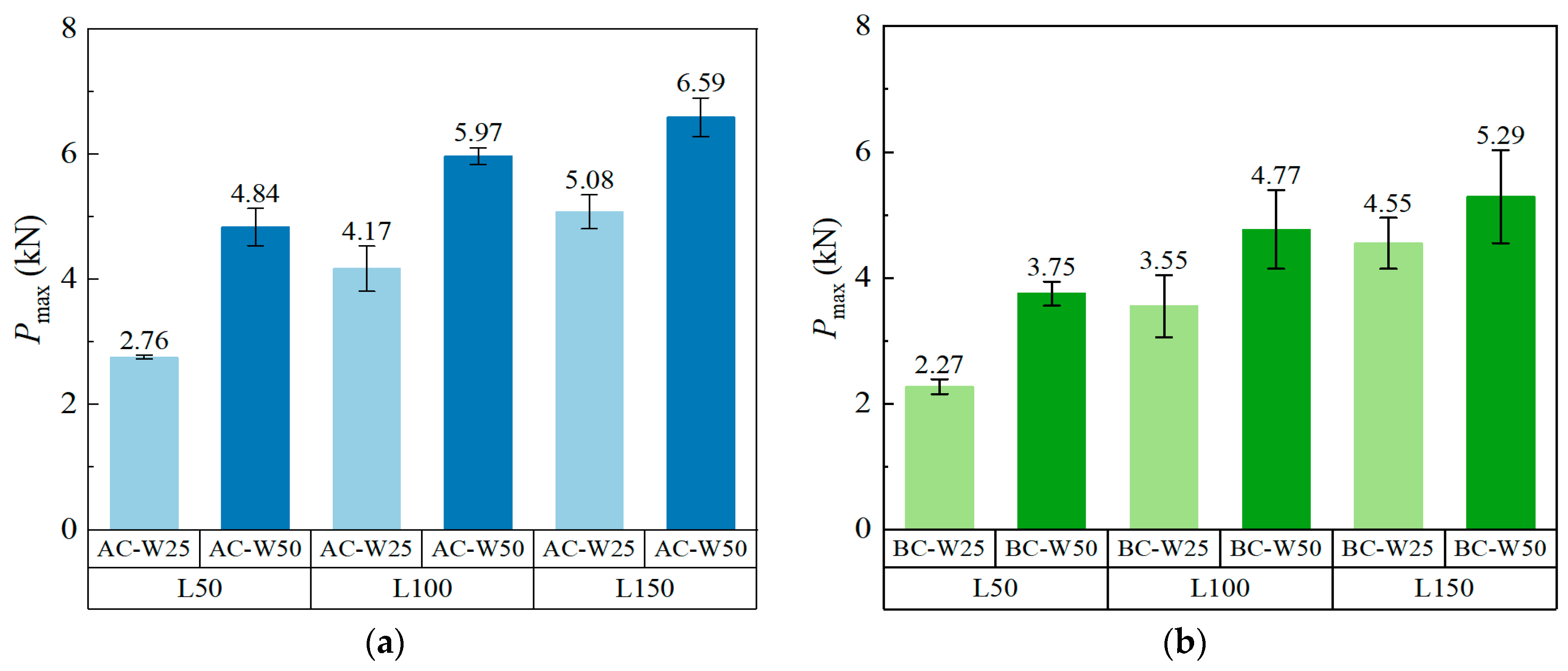
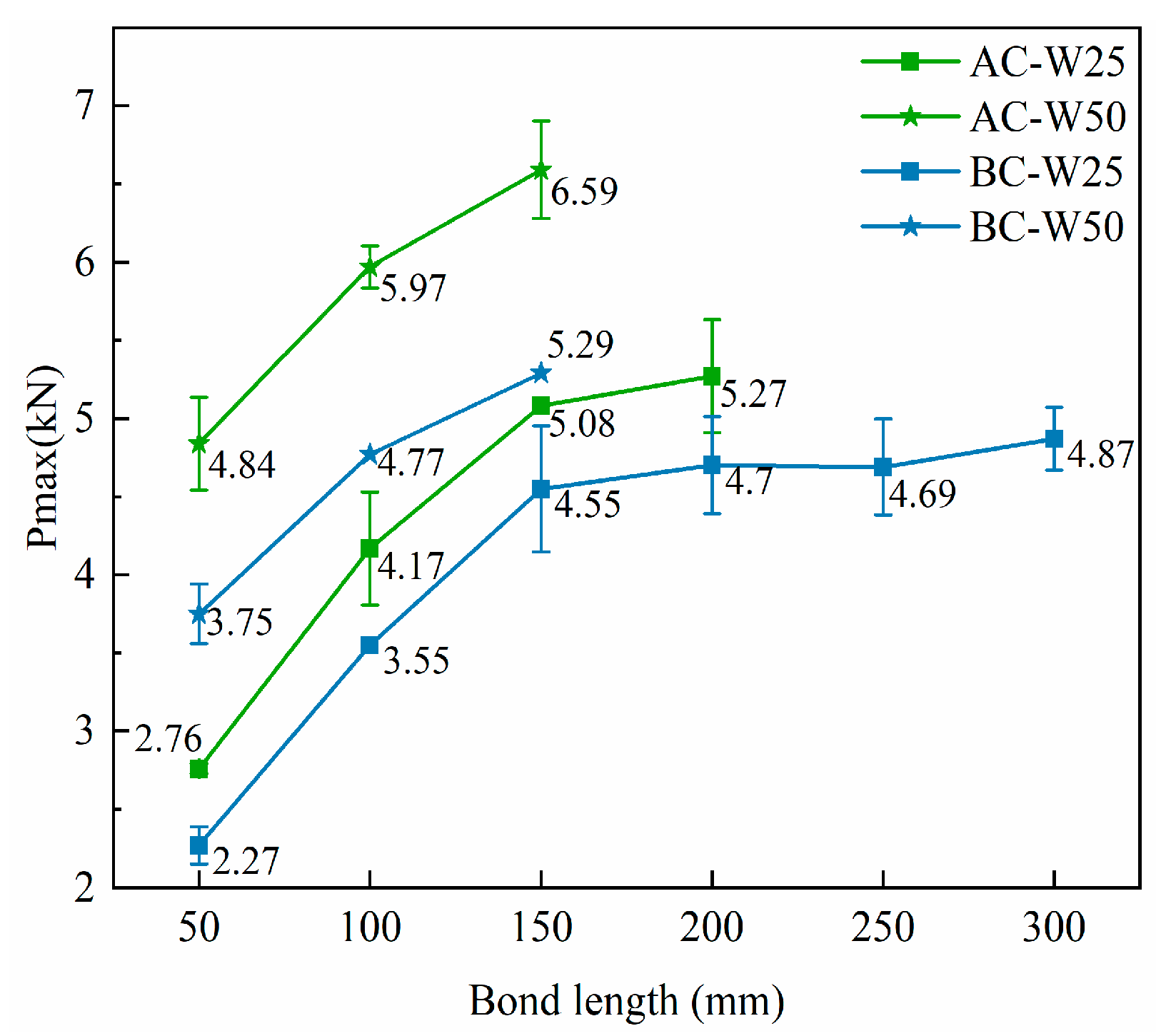
3.2. Bond Capacity
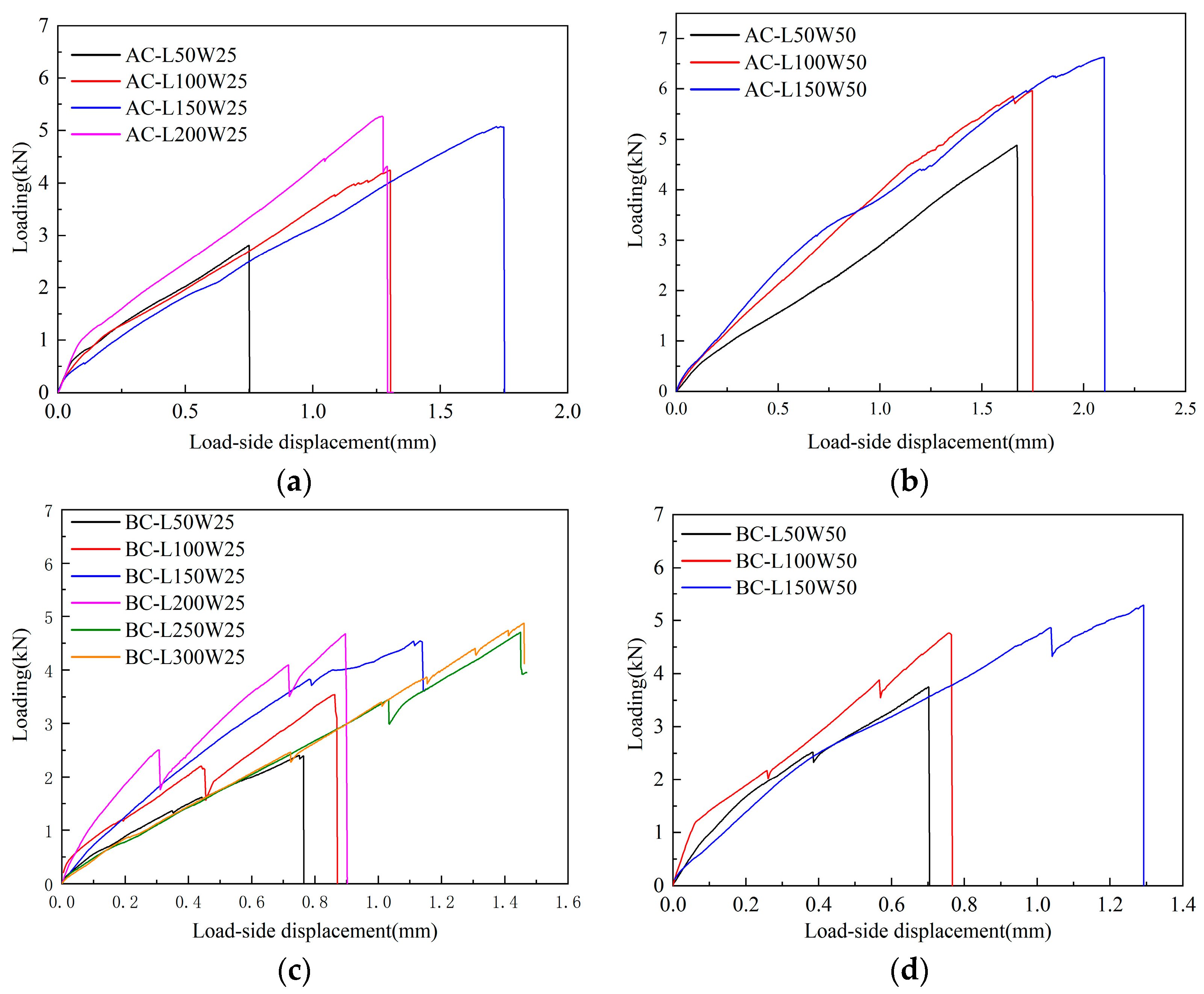
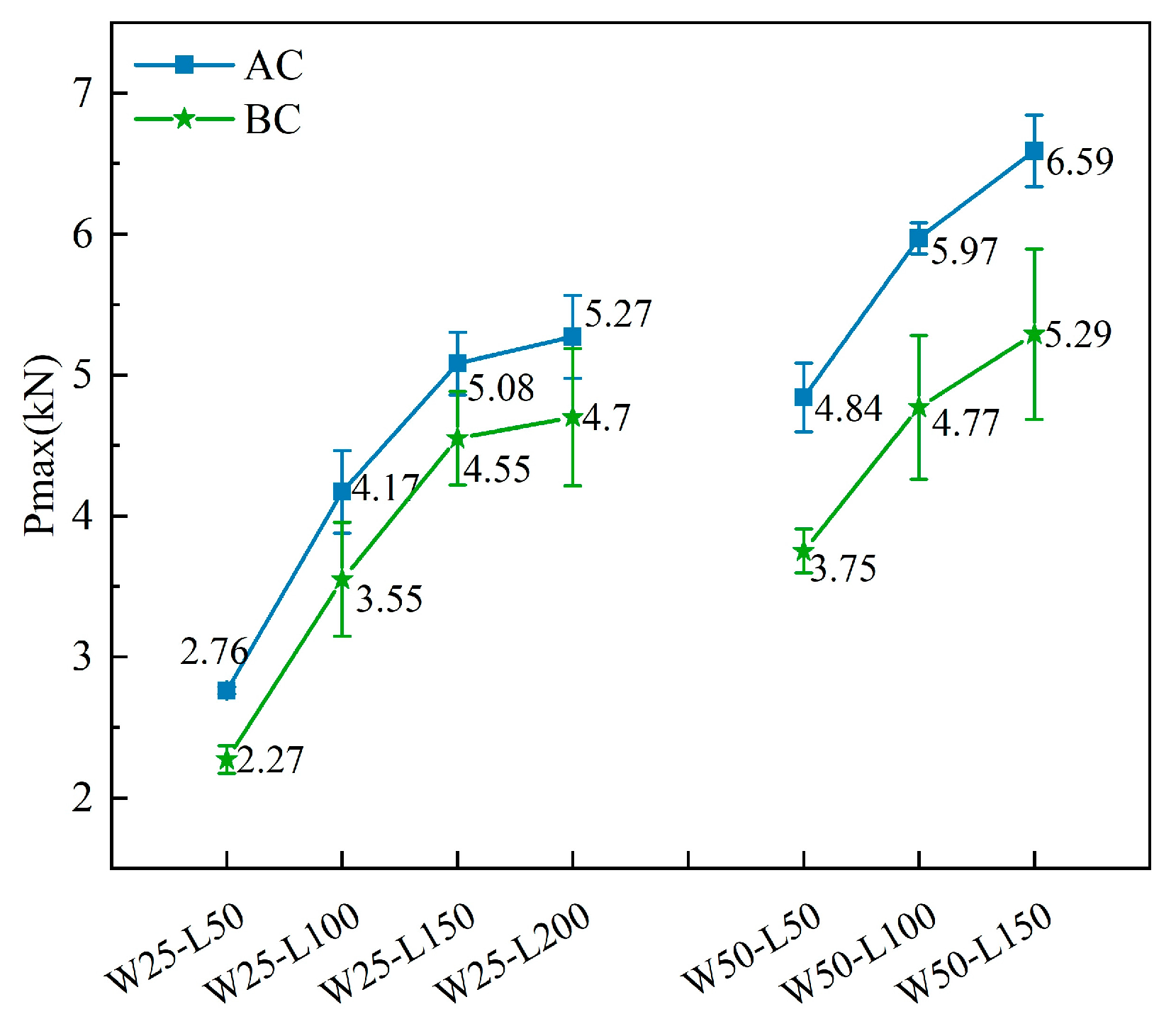
3.2.1. Influence of Bond Width on Bond Capacity
3.2.2. Influence of Bond Length on Bond Capacity
3.2.3. Influence of End Anchorage on Bond Capacity
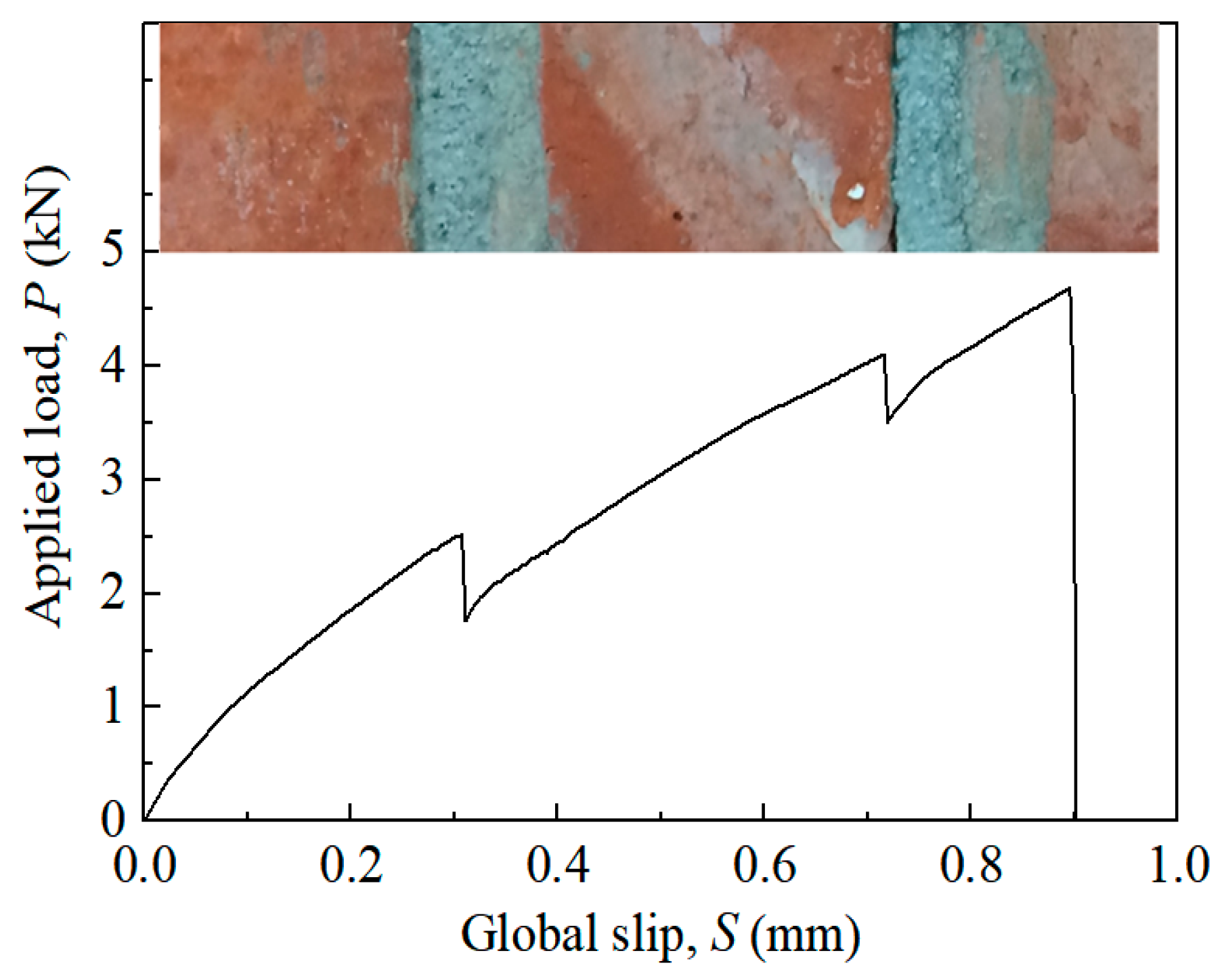
3.2.4. Influence of Mortar Joint on Bond Capacity
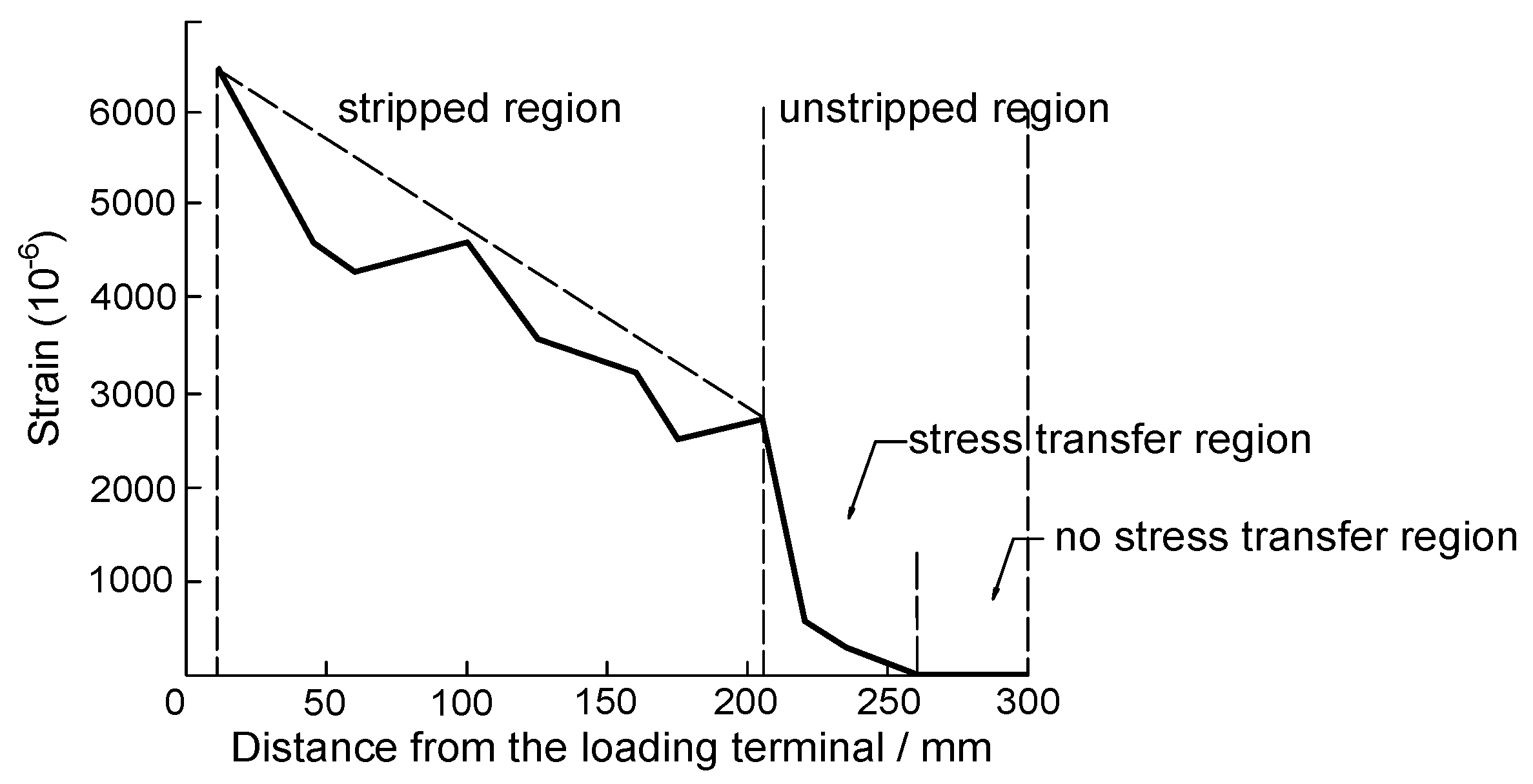
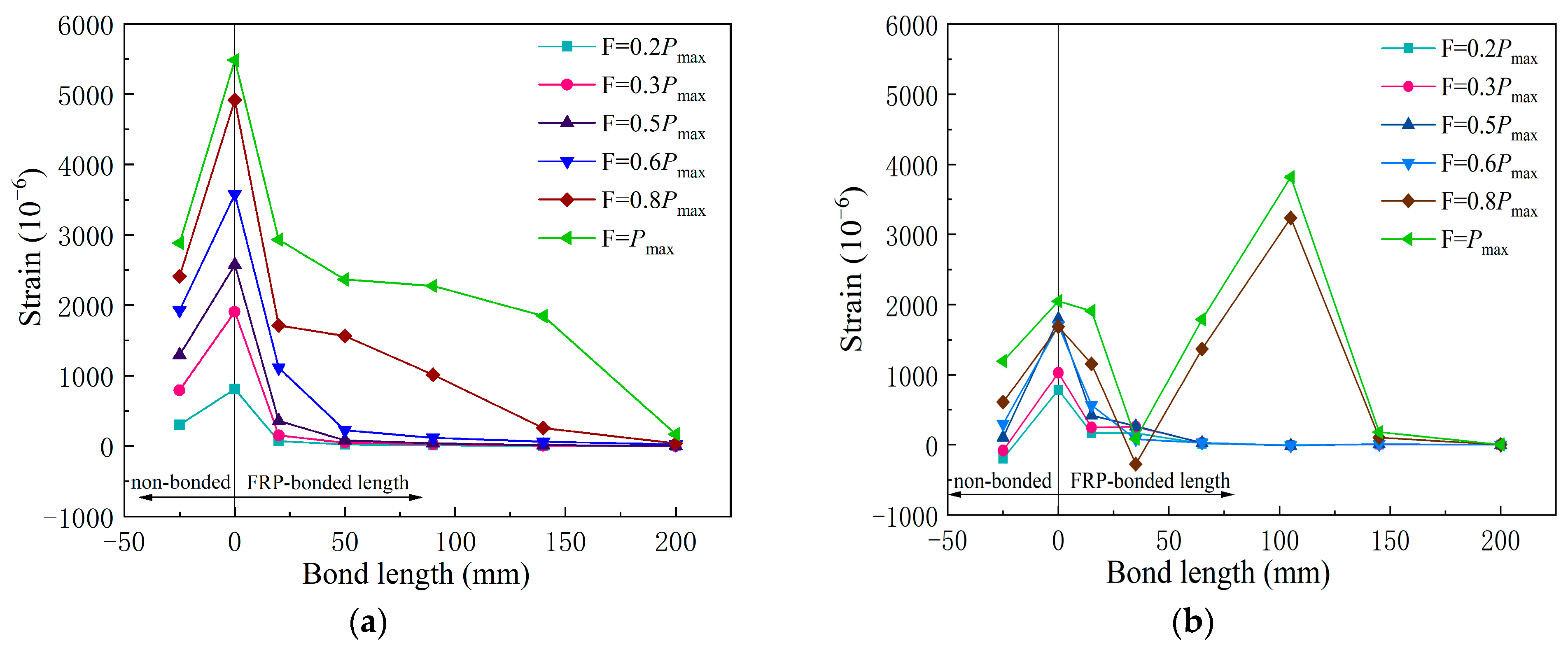
Shear Stress Analysis of Mortar Joint
Influence of Mortar Joint on the Bond Capacity
Influence of Mortar Joint on the FRP Deformation
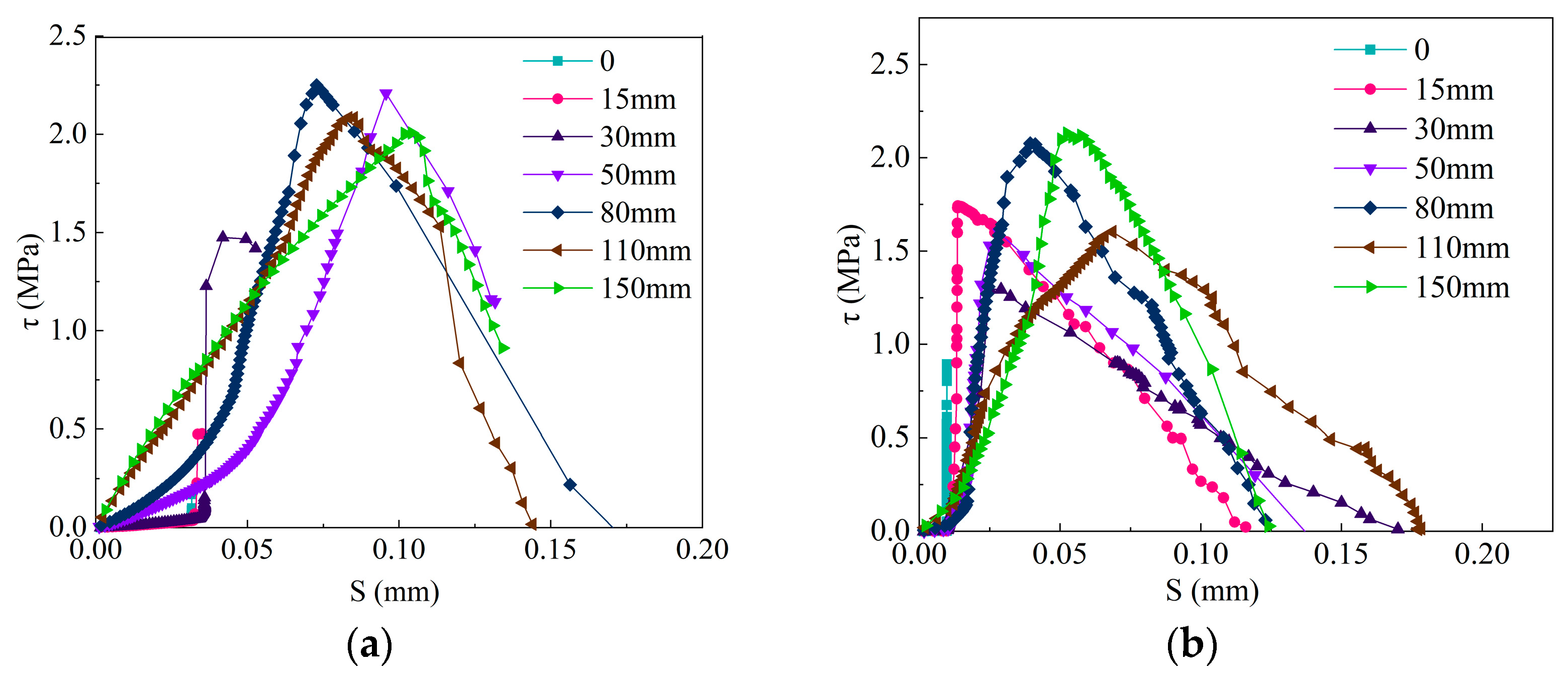
3.3. Effective Bond Length Le
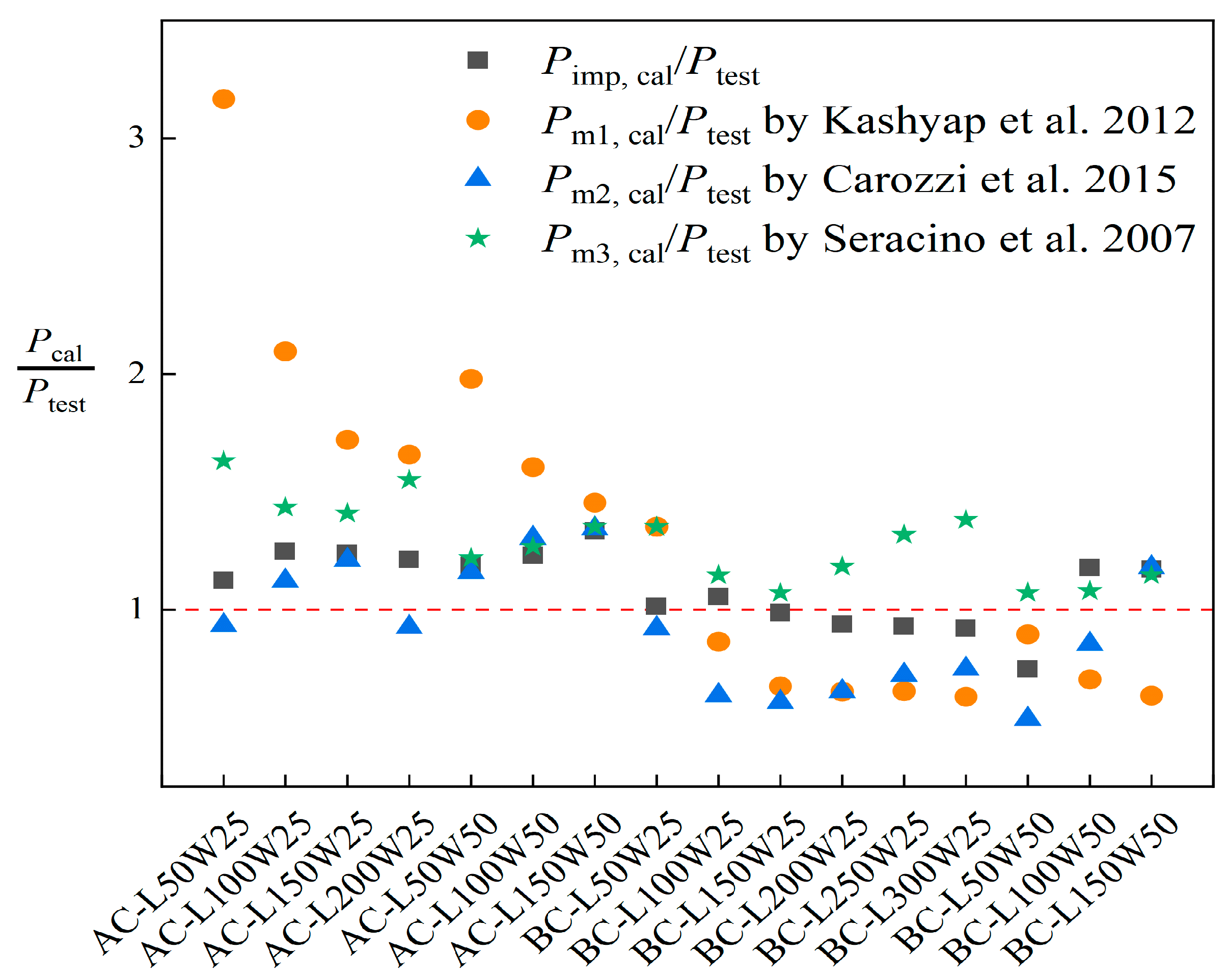
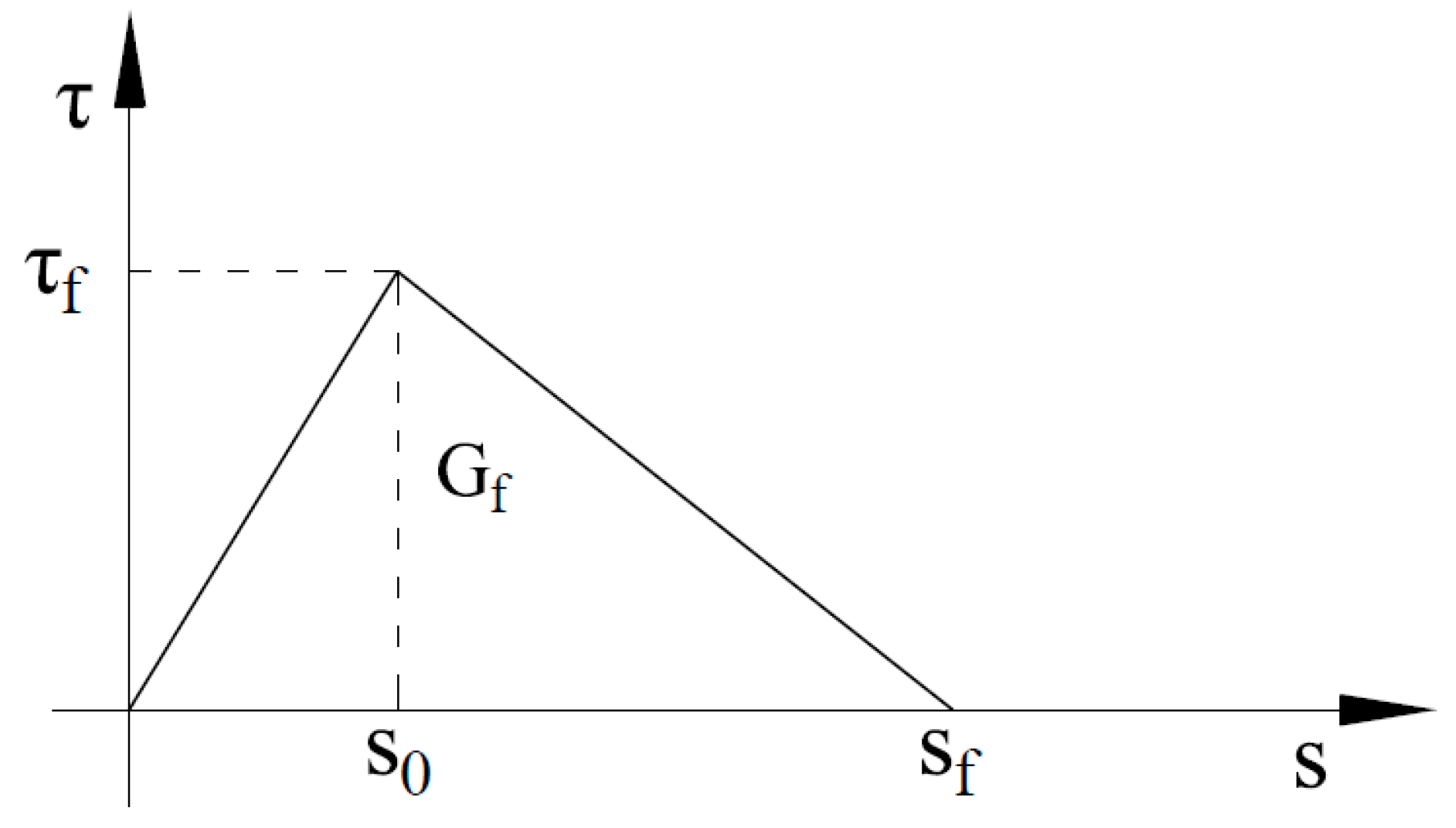
3.4. Interface Bond Strength Model
4. Conclusions and Future Outlook
- (1)
- Increasing the FRP bonding width can significantly enhance the bond strength of reinforced masonry structures by 16.3–75.4%. The displacement at the loading end of specimen AC increased as the bond width increased, while the effect on the displacement at the loading end of specimen BC was not significant. Within the effective bond length range, the interfacial bond capacity increased with longer FRP bonding lengths, although the rate of increase gradually decreased. The maximum displacement at the loading end also increased with longer bonding lengths; however, it decreased when the bond length in specimen AC exceeded 200 mm. Additionally, the end anchorage had a moderate impact on interface bond capacity, resulting in an increase ranging from 7.5% to 21.8%.
- (2)
- The shear stress at the mortar joint was lower than that at the brick base. The bond strength of specimen BC was 10.4–22.5% less than that of specimen AC, but its effective bond length was greater than that of specimen AC. The force vs. slip curves showed a discontinuous increase. When the load was transferred to the mortar joint, the load value continued to rise after decreasing by 7.5–30.0%. The FRP deformation limit in specimen AC occurred at only one location, while in specimen BC it occurred at multiple locations. Oblique cracks were visible in specimen BC but not in specimen AC.
- (3)
- The improved bond strength model, incorporating χ and energy release rate, represents a significant advancement over prior approaches by addressing the discontinuous load transfer caused by mortar joints. The calculated results showed good agreement with experimental data, with an average prediction error of 10%. This improved model is suitable for the reinforcement design of brick masonry using fiber-reinforced composite materials.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ElGawady, M.A.; Lestuzzi, P.; Badoux, M. Aseismic retrofitting of unreinforced masonry walls using FRP. Compos. Part B-Eng. 2005, 37, 148–162. [Google Scholar] [CrossRef]
- Lin, B.; Chun, Q.; Ma, Y. Seismic behavior of historical masonry arched walls reinforced with novel hybrid FRPs. Structures 2025, 71, 107987. [Google Scholar] [CrossRef]
- Akhtar, A.; Saleem, S.; Salman, M.; Noman, M.; Zulqarnain, M.; Jirawattanasomkul, T. Performance of square masonry columns retrofitted with NSM steel and GFRP reinforcement under axial compression. Constr. Build. Mater. 2025, 458, 139534. [Google Scholar] [CrossRef]
- ElGawady, M.A.; Lestuzzi, P.; Badoux, M. Static cyclic response of masonry walls retrofitted with fiber-reinforced polymers. J. Compos. Constr. 2007, 11, 50–61. [Google Scholar] [CrossRef]
- Oliveira, D.V.; Basilio, I.; Lourenço, P.B. Experimental behavior of FRP strengthened masonry arches. J. Compos. Constr. 2010, 14, 312–322. [Google Scholar] [CrossRef]
- Cascardi, A.; Dell’Anna, R.; Micelli, F.; Lionetto, F.; Aiello, M.A.; Maffezzoli, A. Reversible techniques for FRP-confinement of masonry columns. Constr. Build. Mater. 2019, 225, 415–428. [Google Scholar] [CrossRef]
- Zhou, D.; Zhou, S.; Lei, Z. In-plane shear behaviors of constrained masonry walls externally retrofitted with BFRP. J. Compos. Constr. 2016, 20, 04015059. [Google Scholar] [CrossRef]
- Zhou, D.; Lei, Z.; Wang, J. In-plane behavior of seismically damaged masonry walls repaired with external BFRP. Compos. Struct. 2013, 102, 9–19. [Google Scholar] [CrossRef]
- Ehsani, M.R.; Saadatmanesh, H.; Velazquez-Dimas, J.I. Behavior of retrofitted URM walls under simulated earthquake loading. J. Compos. Constr. 1999, 3, 134–142. [Google Scholar] [CrossRef]
- Corradi, M.; Borri, A.; Vignoli, A. Strengthening techniques tested on masonry structures struck by the Umbria-Marche earthquake of 1997–1998. Constr. Build. Mater. 2002, 16, 229–239. [Google Scholar] [CrossRef]
- ElGawady, M.A.; Lestuzzi, P.; Badoux, M. In-plane seismic response of URM walls upgraded with FRP. J. Compos. Constr. 2005, 9, 524–535. [Google Scholar] [CrossRef]
- Gattulli, V.; Lofrano, E.; Paolone, A.; Pirolli, G. Performances of FRP reinforcements on masonry buildings evaluated by fragility curves. Comput. Struct. 2017, 190, 150–161. [Google Scholar] [CrossRef]
- Corradi, M.; Borri, A.; Castori, G.; Coventry, K. Experimental analysis of dynamic effects of FRP reinforced masonry vaults. Materials 2015, 8, 8059–8071. [Google Scholar] [CrossRef]
- Al-Jaberi, Z.; Myers, J.J.; ElGawady, M.A. Experimental and analytical approach for prediction of out-of-plane capacity of reinforced masonry walls strengthened with externally bonded FRP laminate. J. Compos. Constr. 2019, 23, 04019026. [Google Scholar] [CrossRef]
- Kałuża, M. Experimental Analysis of surface application of fiber-Reinforced polymer composite on shear behavior of masonry walls made of autoclaved concrete blocks. Buildings 2022, 12, 2208. [Google Scholar] [CrossRef]
- Guo, Z.; Tang, L.; Zong, Z.; Xiong, Y.; Jiang, T.; Xu, H. Cyclic out-of-plane testing of clay brick masonry walls strengthened with glass fiber-reinforced polymer strips. ACI Struct. J. 2023, 120, 135–148. [Google Scholar] [CrossRef]
- Bellini, A.; Mazzotti, C. A review on the bond behavior of FRP composites applied on masonry substrates. RILEM Tech. Lett. 2017, 2, 74–82. [Google Scholar] [CrossRef]
- Vaculik, J.; Visintin, P.; Burton, N.G.; Griffith, M.C.; Seracino, R. State-of-the-art review and future research directions for FRP-to-masonry bond research: Test methods and techniques for extraction of bond-slip behaviour. Constr. Build. Mater. 2018, 183, 325–345. [Google Scholar] [CrossRef]
- Olivito, R.S.; Codispoti, R.; Cevallos, O.A. Bond behavior of Flax-FRCM and PBO-FRCM composites applied on clay bricks: Experimental and theoretical study. Compos. Struct. 2016, 146, 221–231. [Google Scholar] [CrossRef]
- Gentilini, C.; Carloni, C.; Santoro, R.; Franzoni, E. Characterization of FRCM- and FRP-Masonry Bond Behavior. In Proceedings of the XII International Conference on Structural Analysis of Historical Constructions–SAHC, Online, 29 September–1 October 2021; pp. 2451–2457. [Google Scholar]
- Ceroni, F.; Leone, M.; Rizzo, V.; Bellini, A.; Mazzotti, C. Influence of mortar joints on the behaviour of FRP materials bonded to different masonry substrates. Eng. Struct. 2017, 153, 550–568. [Google Scholar] [CrossRef]
- Du, H.; Xian, G.; Tian, J.; Ma, Z.; Li, C.; Xin, M.; Zhang, Y. Effect of fiber surface treatment with silane coupling agents and carbon nanotubes on mechanical properties of carbon fiber reinforced polyamide 6 composites. Polym. Compos. 2025, 46, 1267–1283. [Google Scholar] [CrossRef]
- Dong, Z.; Ji, J.; Liu, Z.; Wu, C.; Wu, G.; Zhu, H.; Zhang, P. I-shaped ECC/UHPC composite beams reinforced with steel bars and BFRP sheets. Sustain. Struct. 2023, 3, 000022. [Google Scholar] [CrossRef]
- Ma, P.; Xin, R.; Yao, J. An investigation of bond behavior between composite materials (CFRP, GWMM, KPGC) and substrates (Brick and Concrete) for strengthening existing masonry structures. Constr. Build. Mater. 2023, 409, 134019. [Google Scholar] [CrossRef]
- Reboul, N.; Saidi, M.; Mualla, S.; Homoro, O.; Amziane, S. Bond behaviour of fibre reinforced polymers applied on masonry substrate: Analysis based on acoustic emission, digital image correlation and analytical modelling. Constr. Build. Mater. 2023, 403, 132921. [Google Scholar] [CrossRef]
- Ghiassi, B.; Marcari, G.; Oliveira, D.V.; Lourenço, P.B.; Monti, G. Numerical analysis of bond behavior between masonry bricks and composite materials. Eng. Struct. 2012, 43, 210–220. [Google Scholar] [CrossRef]
- Maruccio, C.; Basilio, I.; Oliveira, D.V.; Lourenço, P.B.; Monti, G. Numerical modelling and parametric analysis of bond strength of masonry members retrofitted with FRP. Constr. Build. Mater. 2014, 73, 713–727. [Google Scholar] [CrossRef]
- Grande, E.; Milani, G.; Formisano, A.; Ghiassi, B.; Fabbrocinol, F. Bond behaviour of FRP strengthening applied on curved masonry substrates: Numerical study. Int. J. Mason. Res. Inno. 2020, 5, 303–320. [Google Scholar] [CrossRef]
- Toufigh, V.; Yarigarravesh, M.; Mofid, M. Environmental effects on the bond at the interface of fiber-reinforced polymer and masonry brick. J. Reinf. Plast. Comp. 2017, 36, 1355–1368. [Google Scholar] [CrossRef]
- Maljaee, H.; Ghiassi, B.; Lourenço, P.B.; Oliveira, D.V. FRP-brick masonry bond degradation under hygrothermal conditions. Compos. Struct. 2016, 147, 143–154. [Google Scholar] [CrossRef]
- Ramirez, R.; Ghiassi, B.; Oliveira, D.; Lourenço, P.B. Long-term behaviour of GFRP-reinforced masonry components under outdoor environmental conditions: Results after 5-Year ex-posure. In International Brick and Block Masonry Conference; Springer: Cham, Switzerland, 2025; pp. 833–844. [Google Scholar] [CrossRef]
- Li, C.; Xian, G. Novel wedge-shaped bond anchorage system for pultruded CFRP plates. Mater. Struct. 2018, 51, 1–14. [Google Scholar] [CrossRef]
- Mansouri, I.; Hu, J.W.; Kisi, O. Novel predictive model of the debonding strength for masonry members retrofitted with FRP. Compos. Struct. 2016, 6, 337. [Google Scholar] [CrossRef]
- Kashyap, J.; Willis, C.R.; Griffith, M.C.; Ingham, J.M.; Masia, M.J. Debonding resistance of FRP-to-clay brick masonry joints. Eng. Struct. 2012, 41, 186–198. [Google Scholar] [CrossRef]
- Carozzi, F.G.; Colombi, P.; Poggi, C. Calibration of end-debonding strength model for FRP-reinforced masonry. Compos. Struct. 2015, 120, 366–377. [Google Scholar] [CrossRef]
- Rabi, M.; Cashell, K.A.; Shamass, R.; Desnerck, P. Bond behaviour of austenitic stainless steel reinforced concrete. Eng. Struct. 2020, 221, 111027. [Google Scholar] [CrossRef]
- Rabi, M. Bond prediction of stainless-steel reinforcement using artificial neural networks. Proc. Inst. Civ. Eng. -Constr. Mater. 2023, 177, 87–97. [Google Scholar] [CrossRef]
- Rabi, M.; Shamass, R.; Cashell, K.A. Structural performance of stainless steel reinforced concrete members: A review. Constr. Build. Mater. 2022, 325, 126673. [Google Scholar] [CrossRef]
- Sassoni, E.; Sarti, V.; Bellini, A.; Mazzotti, C.; Franzoni, E. The role of mortar joints in FRP debonding from masonry. Compos. Part B-Eng. 2018, 135, 166–174. [Google Scholar] [CrossRef]
- Capozucca, R.; Ricci, V. Bond of GFRP strips on modern and historic brickwork masonry. Compos. Struct. 2016, 140, 540–555. [Google Scholar] [CrossRef]
- Freddi, F.; Sacco, E. Debonding Process of Masonry Element Strengthened with FRP. Procedia Eng. 2015, 109, 27–34. [Google Scholar] [CrossRef]
- Carloni, C.; Focacci, C. FRP-masonry interfacial debonding: An energy balance approach to determine the influence of the mortar joints. Eur. J. Mech. A Solids 2016, 55, 122–133. [Google Scholar] [CrossRef]
- Mazzotti, C.; Murgo, F.S. Numerical and experimental study of GFRP-masonry interface behavior: Bond evolution and role of the mortar layers. Compos. Part B-Eng. 2015, 75, 212–225. [Google Scholar] [CrossRef]
- Ghiassi, B.; Oliveira, D.V.; Lourenço, P.B.; Marcari, G. Numerical study of the role of mortar joints in the bond behavior of FRP-strengthened masonry. Compos. Part B-Eng. 2013, 46, 21–30. [Google Scholar] [CrossRef]
- Focacci, F.; Carloni, C. A study of the fracture process at the FRP-masonry interface: The role of the periodic pattern of bricks and mortar joints. Key Eng. Mater. 2014, 624, 611–618. [Google Scholar] [CrossRef]
- GB 50003-2011; Code for Design of Masonry Structures. Ministry of Construction of China: Beijing, China, 2011. (In Chinese)
- GB/T 2542-2012; Test Methods for Wall Bricks. National Standardization Administration of China: Beijing, China, 2012. (In Chinese)
- GB 175-2023; Common Portland Cement. National Standardization Administration of China: Beijing, China, 2023. (In Chinese)
- JGJ 52-2006; Standard for Technical Requirements and Test Method of Sand and Crushed Stone (or Gravel) for Ordinary Concrete. Ministry of Construction of China: Beijing, China, 2006.
- JGJ/T 70-2009; Standard for Test Method of Basic Properties of Construction Mortar. Ministry of Construction of China: Beijing, China, 2009.
- ASTM D3039/D3039M-17; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2017.
- ASTM D638-22; Standard Test Method for Tensile Properties of Plastics. ASTM: West Conshohocken, PA, USA, 2022.
- GB 50702-2011; Code for Design of Strengthening Masonry Structures. Ministry of Con-Struction of China: Beijing, China, 2011. (In Chinese)
- Leone, M.; Aiello, M.A. Bond tests on clay bricks and natural stone masonry externally bonded with FRP. Materials 2021, 14, 7439. [Google Scholar] [CrossRef] [PubMed]
- Sassoni, E.; Andreotti, S.; Bellini, A.; Mazzanti, B.; Bignozzi, M.C.; Mazzotti, C.; Franzoni, E. In-fluence of mechanical properties, anisotropy, surface roughness and porosity of brick on FRP debonding force. Compos. Part B-Eng. 2017, 108, 257–269. [Google Scholar] [CrossRef]
- Ceroni, F. Bond tests to evaluate the effectiveness of anchoring devices for CFRP sheets epoxy bonded over masonry elements. Compos. Part B-Eng. 2017, 113, 317–330. [Google Scholar] [CrossRef]
- CNR-DT 200/2004; Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures. CNR-Advisory Committee of Technical Recommen-Dations for Construction, National Research Council: Rome, Italy, 2004.
- Bertolesi, E.; Grande, E.; Fagone, M.; Milani, G.; Rotunno, T. Mechanical model based on a BVP for FRPs applied on flat and curved masonry pillars with anchor spikes. Compos. Struct. 2021, 273, 114251. [Google Scholar] [CrossRef]
- Malena, M.; Focacci, F.; Carloni, C.; De Felice, G. The effect of the shape of the cohesive material law on the stress transfer at the FRP-masonry interface. Compos. Part B-Eng. 2017, 110, 368–380. [Google Scholar] [CrossRef]
- Yun, Y.; Wu, Y.F. Durability of CFRP-concrete joints under freeze-thaw cycling. Cold. Reg. Sci. Technol. 2011, 65, 401–412. [Google Scholar] [CrossRef]
- Huang, T.L.; Huang, Y.H. Analysis of the effective bond length between fiber reinforced polymer and brick. Sichuan Build. Sci. 2015, 41, 195–198. (In Chinese) [Google Scholar]
- Lu, X.; Ye, L.; Teng, J.; Zhuang, J. Bond-slip model for FRP-to-concrete interface. J. Build. Struct. 2005, 26, 10–18. (In Chinese) [Google Scholar] [CrossRef]
- Seracino, R.; Raizal Saifulnaz, M.R.; Oehlers, D.J. Generic debonding resistance of EB and NSM plate-to-concrete joints. J. Compos. Constr. 2007, 11, 62–70. [Google Scholar] [CrossRef]
- Rabi, M.; Shamass, R.; Cashell, K.A. Experimental investigation on the flexural behaviour of stainless steel reinforced concrete beams. Struct. Infrastruct. E 2023, 19, 1847–1859. [Google Scholar] [CrossRef]
- Rabi, M.; Cashell, K.A.; Shamass, R. Flexural analysis and design of stainless steel reinforced concrete beams. Eng. Struct. 2019, 198, 109432. [Google Scholar] [CrossRef]
- Rabi, M.; Cashell, K.A.; Shamass, R. Ultimate behaviour and serviceability analysis of stainless steel reinforced concrete beams. Eng. Struct. 2021, 248, 113259. [Google Scholar] [CrossRef]
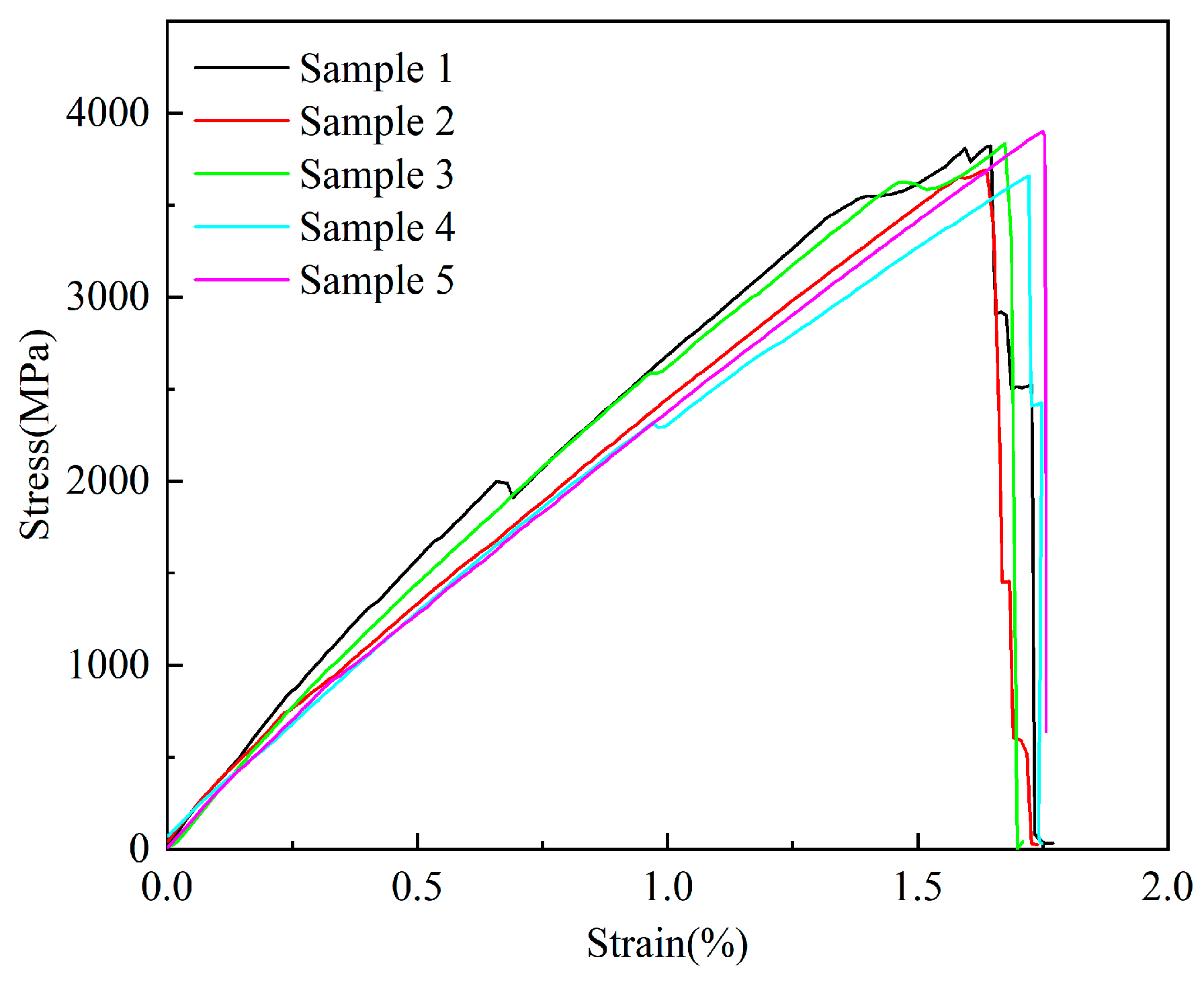


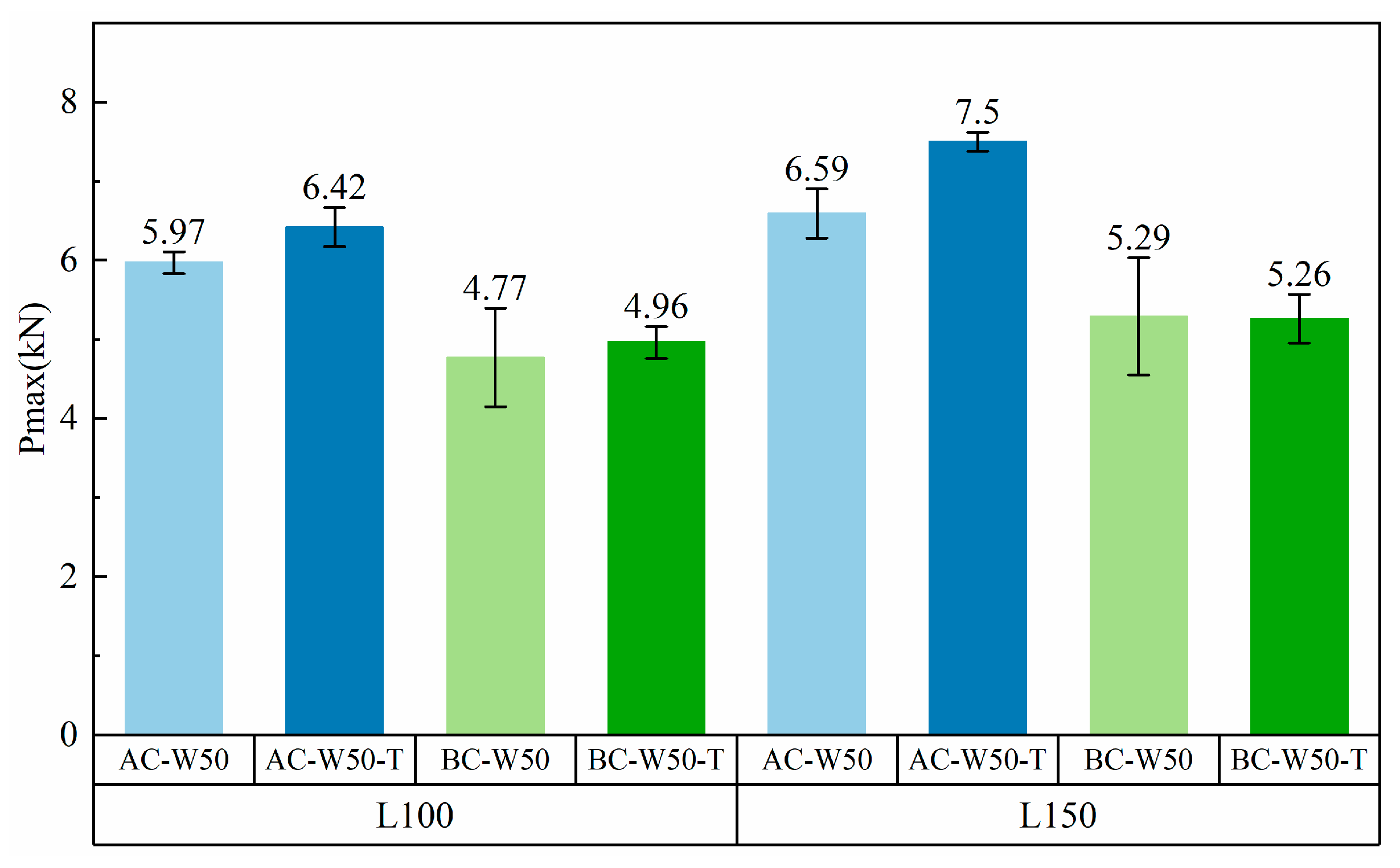
| Material | /GPa | /MPa | Ultimate Strain/% | ||||
|---|---|---|---|---|---|---|---|
| Average | Standard Deviation | Average | Standard Deviation | Average | Standard Deviation | ||
| CFRP | Manufacturer | 241 | / | 3710 | / | 1.70 | / |
| Sample test | 247 | 2.83 | 3780 | 7.07 | 1.74 | 0.04 | |
| Adhesive | Manufacturer | 2.69 | / | 51.5 | / | 2.51 | / |
| Sample test | 2.73 | 0.06 | 52.1 | 0.14 | 2.59 | 0.02 | |
| Specimen | Type | Bond Length/mm | Bond Width/mm | Number | End Anchorage |
|---|---|---|---|---|---|
| AC-L50W25 | Single brick | 50 | 25 | 3 | × |
| AC-L100W25 | 100 | 25 | 3 | × | |
| AC-L150W25 | 150 | 25 | 3 | × | |
| AC-L200W25 | 200 | 25 | 3 | × | |
| BC-L50W25 | Masonry prism | 50 | 25 | 3 | × |
| BC-L100W25 | 100 | 25 | 3 | × | |
| BC-L150W25 | 150 | 25 | 3 | × | |
| BC-L200W25 | 200 | 25 | 3 | × | |
| BC-L250W25 | 250 | 25 | 3 | × | |
| BC-L300W25 | 300 | 25 | 3 | × | |
| AC-L50W50 | Single brick | 50 | 50 | 3 | × |
| AC-L100W50 | 100 | 50 | 3 | × | |
| AC-L150W50 | 150 | 50 | 3 | × | |
| BC-L50W50 | Masonry prism | 50 | 50 | 3 | × |
| BC-L100W50 | 100 | 50 | 3 | × | |
| BC-L150W50 | 150 | 50 | 3 | × | |
| AC-L100W50T | Single brick | 100 | 50 | 3 | √ |
| AC-L150W50T | 150 | 50 | 3 | √ | |
| BC-L100W50T | Masonry prism | 100 | 50 | 3 | √ |
| BC-L150W50T | 150 | 50 | 3 | √ |
| Specimen | Failure Mode | Pmax/kN | Pmax,avg /kN | Pmax,COV | Send/mm | Send,avg /mm | Send,COV | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. 1 | No. 2 | No. 3 | No. 1 | No. 2 | No. 3 | No. 1 | No. 2 | No. 3 | |||||
| AC-L50W25 | II | II | I | 2.80 | 2.74 | 2.75 | 2.76 | 1.2 | 0.76 | 0.79 | 0.68 | 0.74 | 7.6 |
| AC-L100W25 | I | I | I | 3.75 | 4.38 | 4.37 | 4.17 | 8.7 | 1.05 | 1.59 | 1.35 | 1.33 | 20.3 |
| AC-L150W25 | IV | I | II | 4.82 | 5.05 | 5.36 | 5.08 | 5.3 | 1.75 | 1.40 | 2.30 | 1.82 | 25.0 |
| AC-L200W25 | II | II | I | 4.90 | 5.62 | 5.29 | 5.27 | 6.8 | 1.74 | 1.29 | 1.32 | 1.45 | 17.4 |
| BC-L50W25 | I | II | II | 2.22 | 2.19 | 2.41 | 2.27 | 5.2 | 0.69 | 0.77 | 0.73 | 0.73 | 5.5 |
| BC-L100W25 | II | I | I | 3.16 | 3.39 | 4.11 | 3.55 | 13.9 | 1.05 | 0.96 | 1.30 | 1.10 | 16.0 |
| BC-L150W25 | I | II | II | 4.69 | 4.09 | 4.86 | 4.55 | 8.9 | 1.43 | 1.07 | 0.89 | 1.13 | 24.3 |
| BC-L200W25 | II | I | I | 4.06 | 4.80 | 5.24 | 4.7 | 12.7 | 1.43 | 0.94 | 1.58 | 1.32 | 25.4 |
| BC-L250W25 | I | I | I | 4.77 | 4.95 | 4.35 | 4.69 | 6.6 | 1.57 | 1.79 | 1.47 | 1.61 | 10.2 |
| BC-L300W25 | I | I | I | 4.85 | 5.08 | 4.68 | 4.87 | 4.1 | 1.96 | 1.90 | 1.73 | 1.86 | 6.4 |
| AC-L50W50 | I | II | IV | 4.92 | 4.51 | 5.09 | 4.84 | 6.2 | 1.68 | 1.62 | 1.40 | 1.57 | 9.4 |
| AC-L100W50 | I; III | I | I | 5.84 | 6.11 | 5.96 | 5.97 | 2.3 | 1.85 | 1.90 | 1.83 | 1.86 | 1.9 |
| AC-L150W50 | III | I | III | 6.93 | 6.52 | 6.32 | 6.59 | 4.7 | 1.96 | 2.05 | 1.82 | 1.94 | 6.0 |
| BC-L50W50 | II | I | I | 3.59 | 3.69 | 3.96 | 3.75 | 5.1 | 0.72 | 0.71 | 0.67 | 0.70 | 3.8 |
| BC-L100W50 | I | II | II | 4.95 | 4.08 | 5.29 | 4.77 | 13.1 | 0.94 | 1.09 | 1.03 | 1.02 | 7.4 |
| BC-L150W50 | II | I | II | 6.02 | 5.30 | 4.54 | 5.29 | 14.0 | 1.67 | 1.67 | 1.56 | 1.63 | 3.9 |
| AC-L100W50T | IV | II | I | 6.20 | 6.69 | 6.37 | 6.42 | 3.9 | 1.67 | 1.64 | 1.49 | 1.60 | 6.0 |
| AC-L150W50T | IV | I | II | 7.63 | 7.46 | 7.40 | 7.50 | 1.6 | 4.15 | 3.65 | 2.40 | 3.40 | 26.5 |
| BC-L100W50T | II | I; II | I; II | 4.81 | 4.88 | 5.19 | 4.96 | 4.1 | 1.72 | 1.72 | 1.83 | 1.76 | 3.6 |
| BC-L150W50T | I; II | I; II | II | 5.59 | 4.98 | 5.20 | 5.26 | 5.9 | 1.34 | 1.18 | 1.06 | 1.19 | 11.8 |
| Specimen | εmax | Specimen | εmax | Specimen | εmax | Specimen | εmax |
|---|---|---|---|---|---|---|---|
| AC-L50W25 | 3823 | AC-L50W50 | 3083 | BC-L100W25 | 3472 | BC-L300W25 | 8702 |
| AC-L100W25 | 3675 | AC-L100W50 | 2494 | BC-L150W25 | 3514 | BC-L50W50 | 2006 |
| AC-L150W25 | 4116 | AC-L150W50 | 3351 | BC-L200W25 | 3967 | BC-L100W50 | 2292 |
| AC-L200W25 | 5820 | BC-L50W25 | 3206 | BC-L250W25 | 6558 | BC-L150W50 | 3462 |
| Specimen | Le,mea/mm | Le,cal/mm | Le,mea/Le,cal |
|---|---|---|---|
| AC-L50W25 | 41.6 | 69.2 | 0.60 |
| AC-L100W25 | 75.0 | 69.2 | 1.08 |
| AC-L150W25 | 100.7 | 69.2 | 1.45 |
| AC-L200W25 | 136.6 | 69.2 | 1.97 |
| AC-L50W50 | 41.8 | 69.2 | 0.60 |
| AC-L100W50 | 62.4 | 69.2 | 0.90 |
| AC-L150W50 | 87.3 | 69.2 | 1.26 |
| BC-L50W25 | 41.9 | 120.3 | 0.35 |
| BC-L100W25 | 85.0 | 107.0 | 0.79 |
| BC-L150W25 | 106.3 | 110.7 | 0.96 |
| BC-L200W25 | 161.8 | 113.3 | 1.43 |
| BC-L250W25 | 165.9 | 114.6 | 1.45 |
| BC-L300W25 | 207.3 | 110.7 | 1.87 |
| BC-L50W50 | 46.8 | 120.3 | 0.39 |
| BC-L100W50 | 79.4 | 107.0 | 0.74 |
| BC-L150W50 | 90.7 | 110.7 | 0.82 |
| Specimen | /mm | /MPa | /(N/mm) |
|---|---|---|---|
| AC-L50W25 | 0.039 | 0.500 | 0.085 |
| AC-L100W25 | 0.035 | 0.697 | 0.028 |
| AC-L150W25 | 0.101 | 1.801 | 0.218 |
| AC-L200W25 | 0.048 | 1.671 | 0.105 |
| AC-L50W50 | 0.023 | 0.464 | 0.011 |
| AC-L100W50 | 0.040 | 1.601 | 0.092 |
| AC-L150W50 | 0.099 | 1.642 | 0.163 |
| BC-L50W25 | 0.010 | 1.615 | 0.016 |
| BC-L100W25 | 0.051 | 1.379 | 0.083 |
| BC-L150W25 | 0.047 | 1.443 | 0.099 |
| BC-L200W25 | 0.044 | 1.092 | 0.074 |
| BC-L250W25 | 0.053 | 1.770 | 0.102 |
| BC-L300W25 | 0.069 | 1.487 | 0.186 |
| BC-L50W50 | 0.017 | 1.250 | 0.023 |
| BC-L100W50 | 0.013 | 0.550 | 0.015 |
| BC-L150W50 | 0.016 | 0.640 | 0.016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Z.; Ma, H.; Luo, Y.; Wang, E.; Huang, H.; Zhang, L. Interfacial Bond Behavior of Clay Brick Masonry Strengthened with CFRP. Buildings 2025, 15, 809. https://doi.org/10.3390/buildings15050809
Lei Z, Ma H, Luo Y, Wang E, Huang H, Zhang L. Interfacial Bond Behavior of Clay Brick Masonry Strengthened with CFRP. Buildings. 2025; 15(5):809. https://doi.org/10.3390/buildings15050809
Chicago/Turabian StyleLei, Zhen, Hui Ma, Yumin Luo, Enmao Wang, Haiyan Huang, and Li Zhang. 2025. "Interfacial Bond Behavior of Clay Brick Masonry Strengthened with CFRP" Buildings 15, no. 5: 809. https://doi.org/10.3390/buildings15050809
APA StyleLei, Z., Ma, H., Luo, Y., Wang, E., Huang, H., & Zhang, L. (2025). Interfacial Bond Behavior of Clay Brick Masonry Strengthened with CFRP. Buildings, 15(5), 809. https://doi.org/10.3390/buildings15050809