A Deformation Prediction Model for Concrete Dams Based on RSA-VMD-AttLSTM
Abstract
1. Introduction
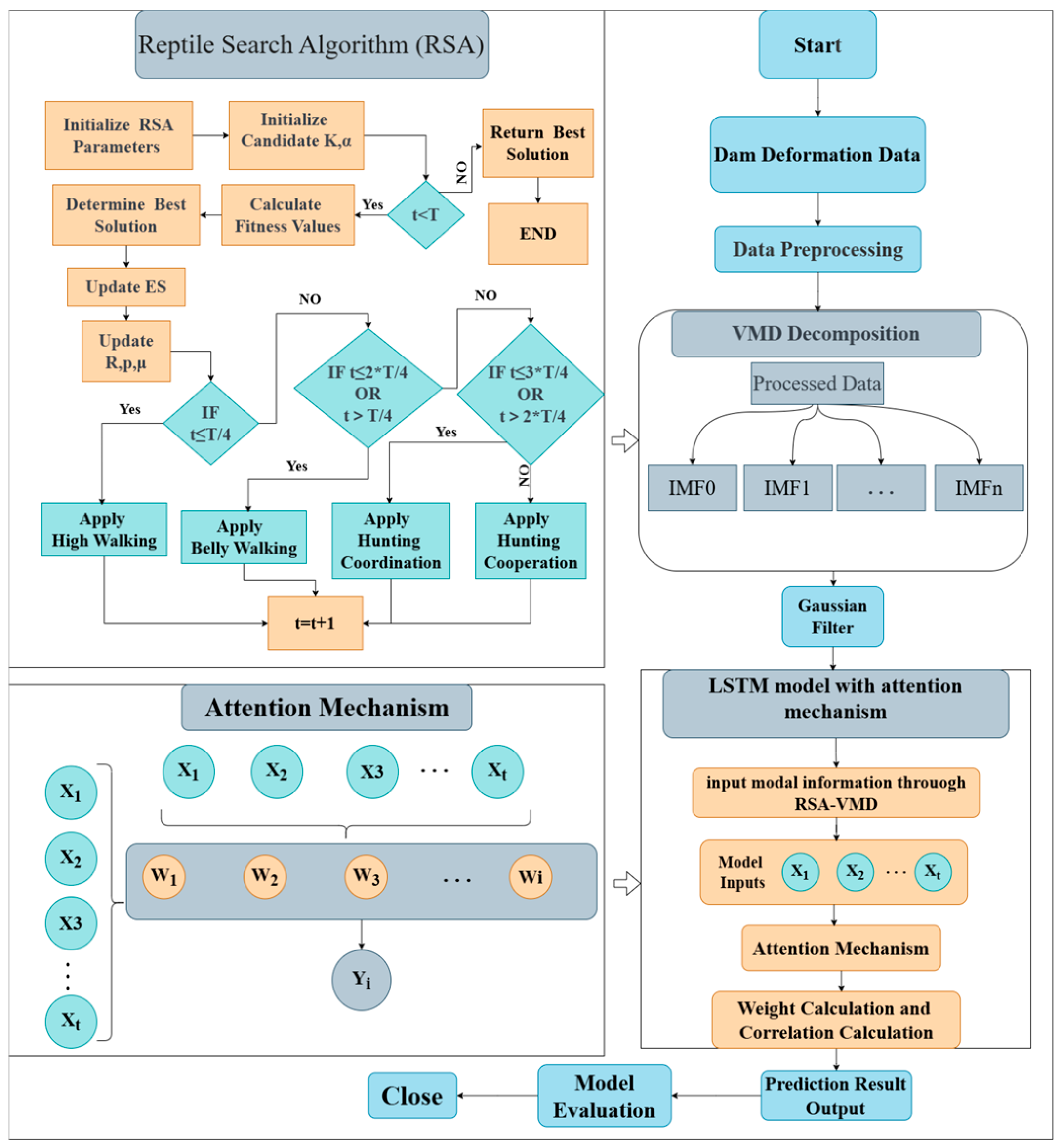
2. Fundamentals of a Deformation Prediction Model for Concrete Dams Based on RSA-VMD-AttLSTM
2.1. VMD Metamodal Decomposition
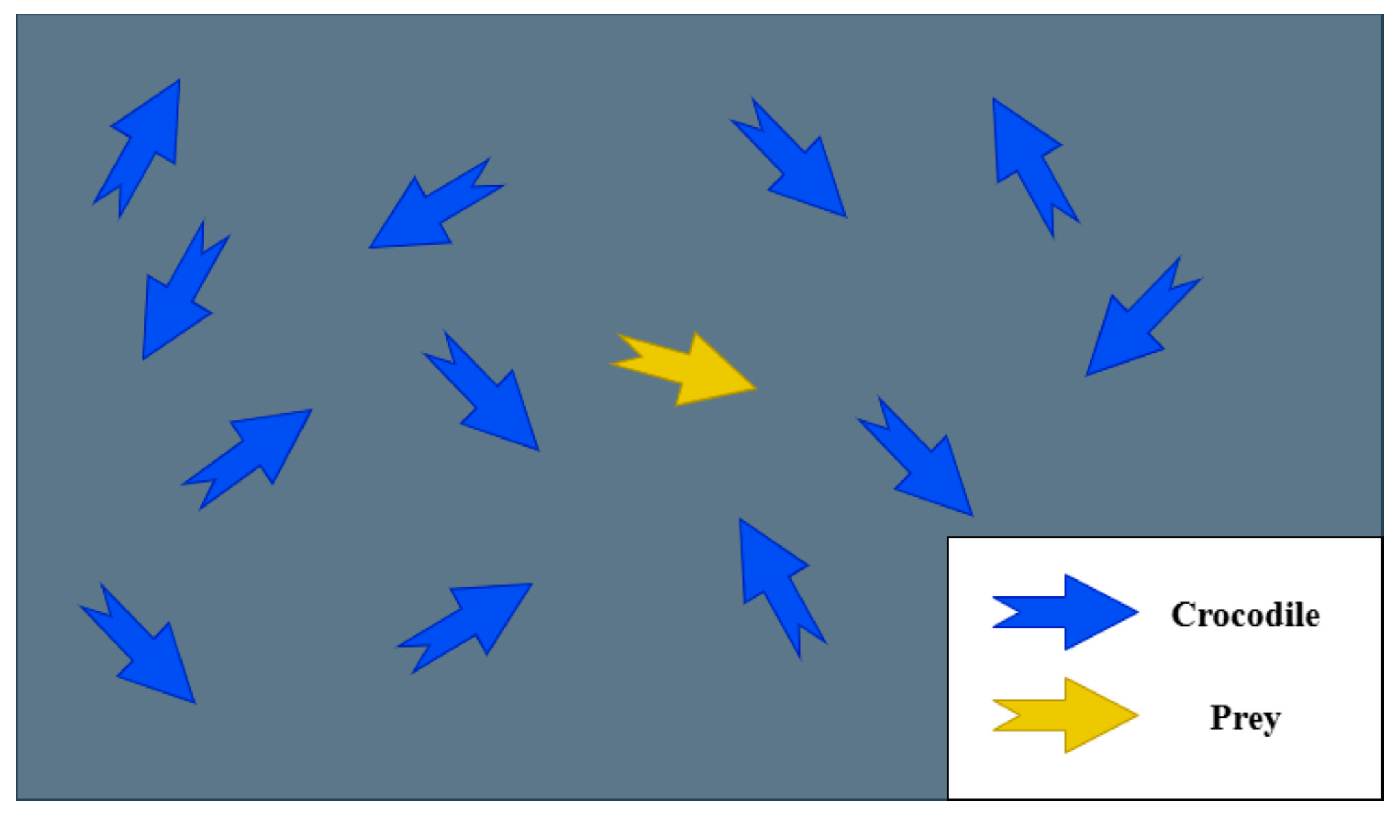
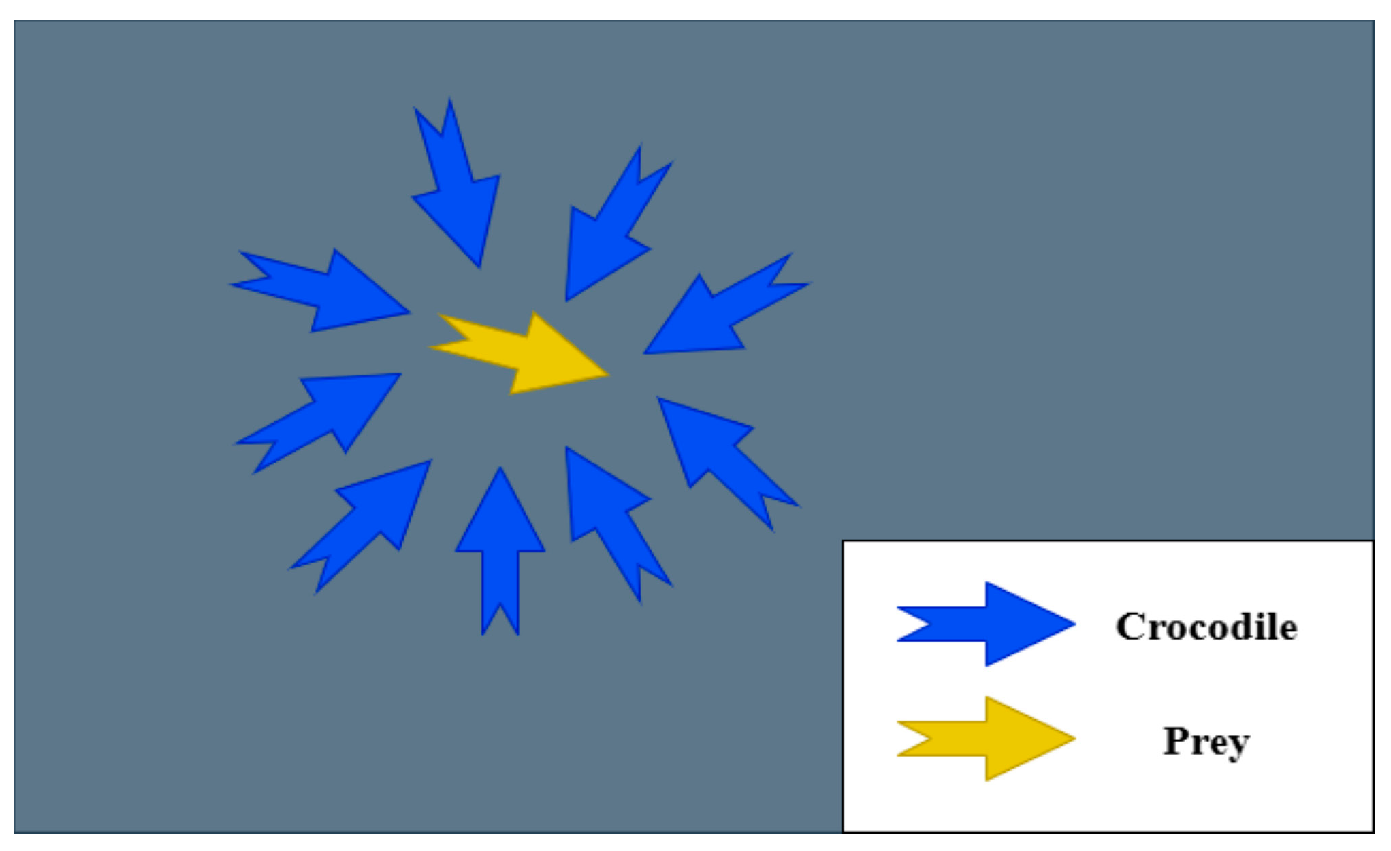
2.2. Reptile Search Optimization Algorithm
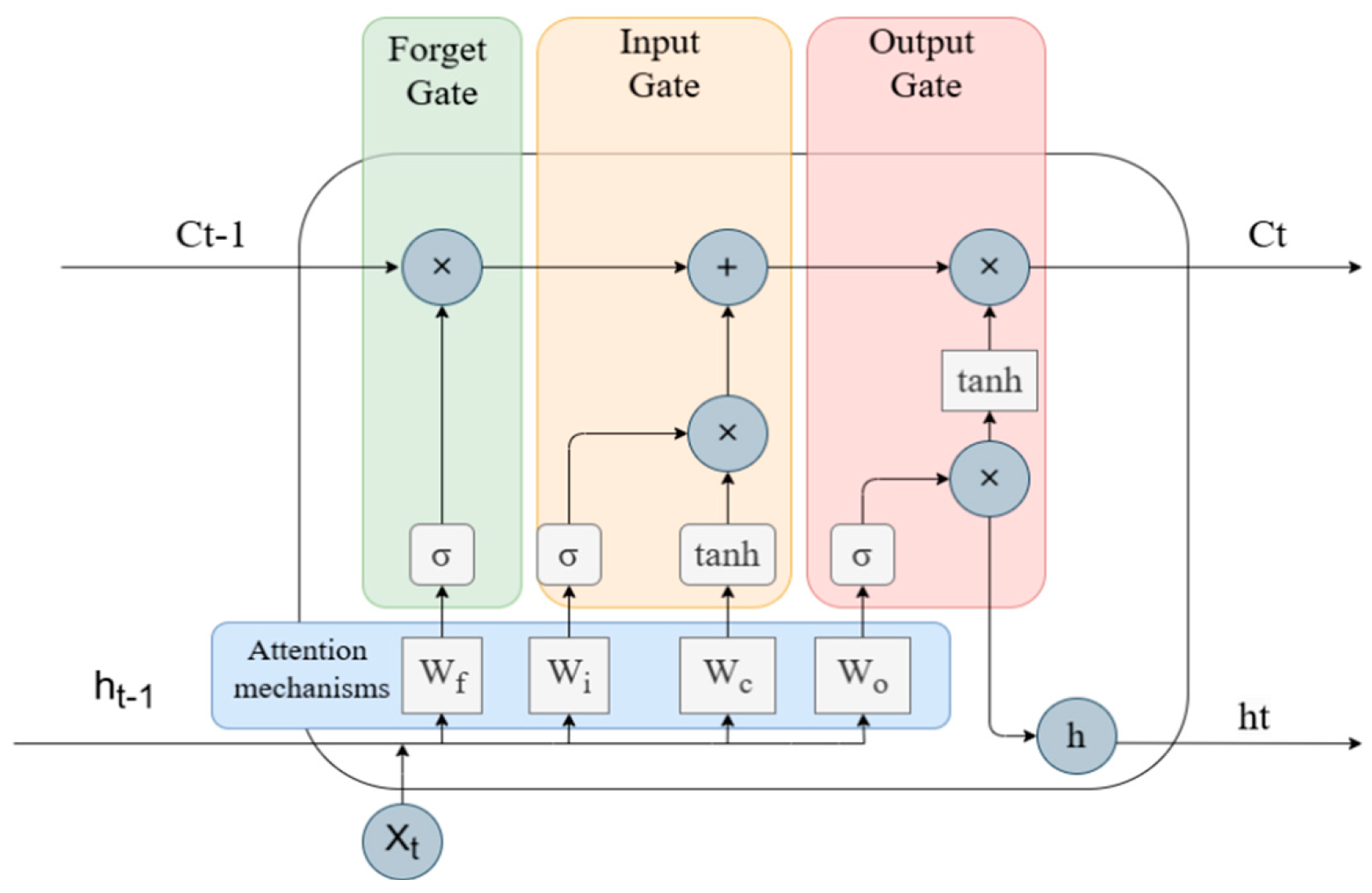
2.3. AttLSTM Prediction Model
3. Model Establishment
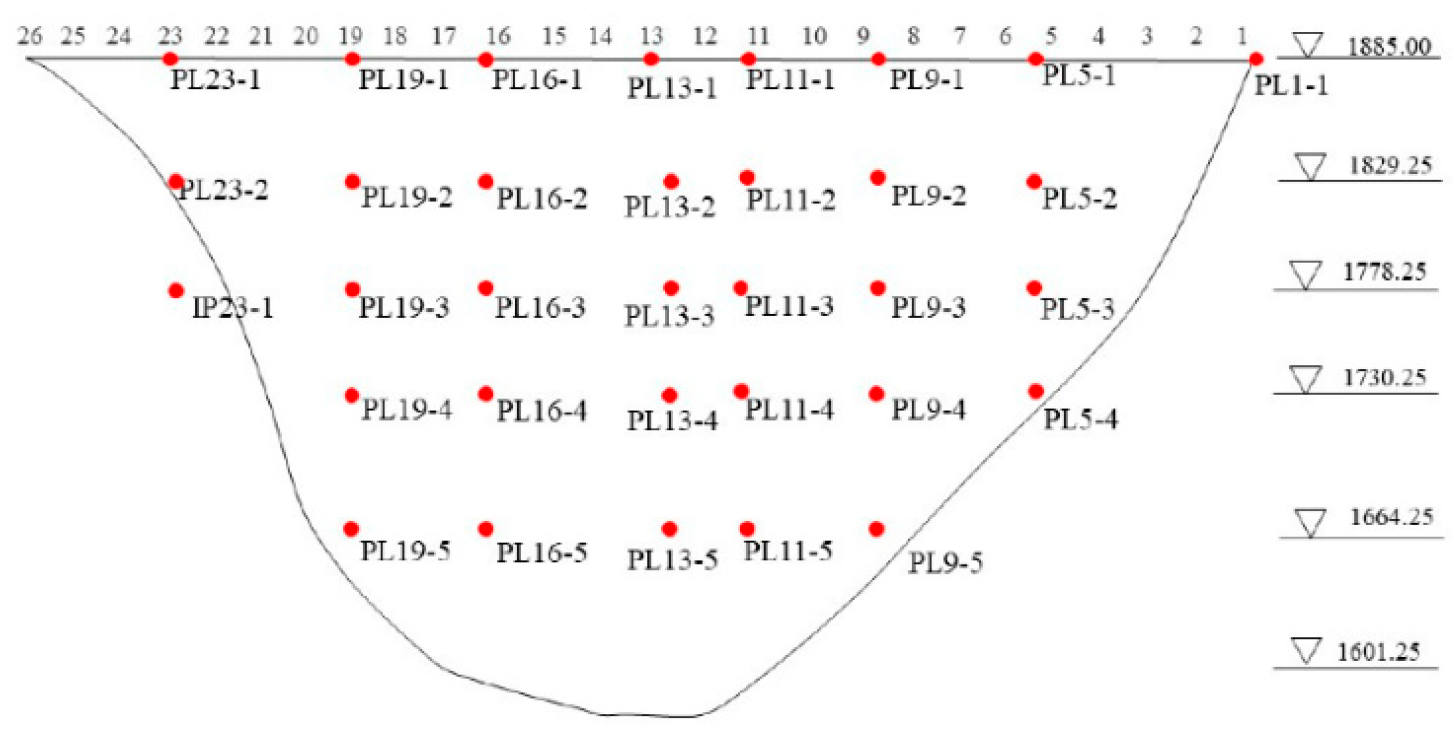
4. Case Studies
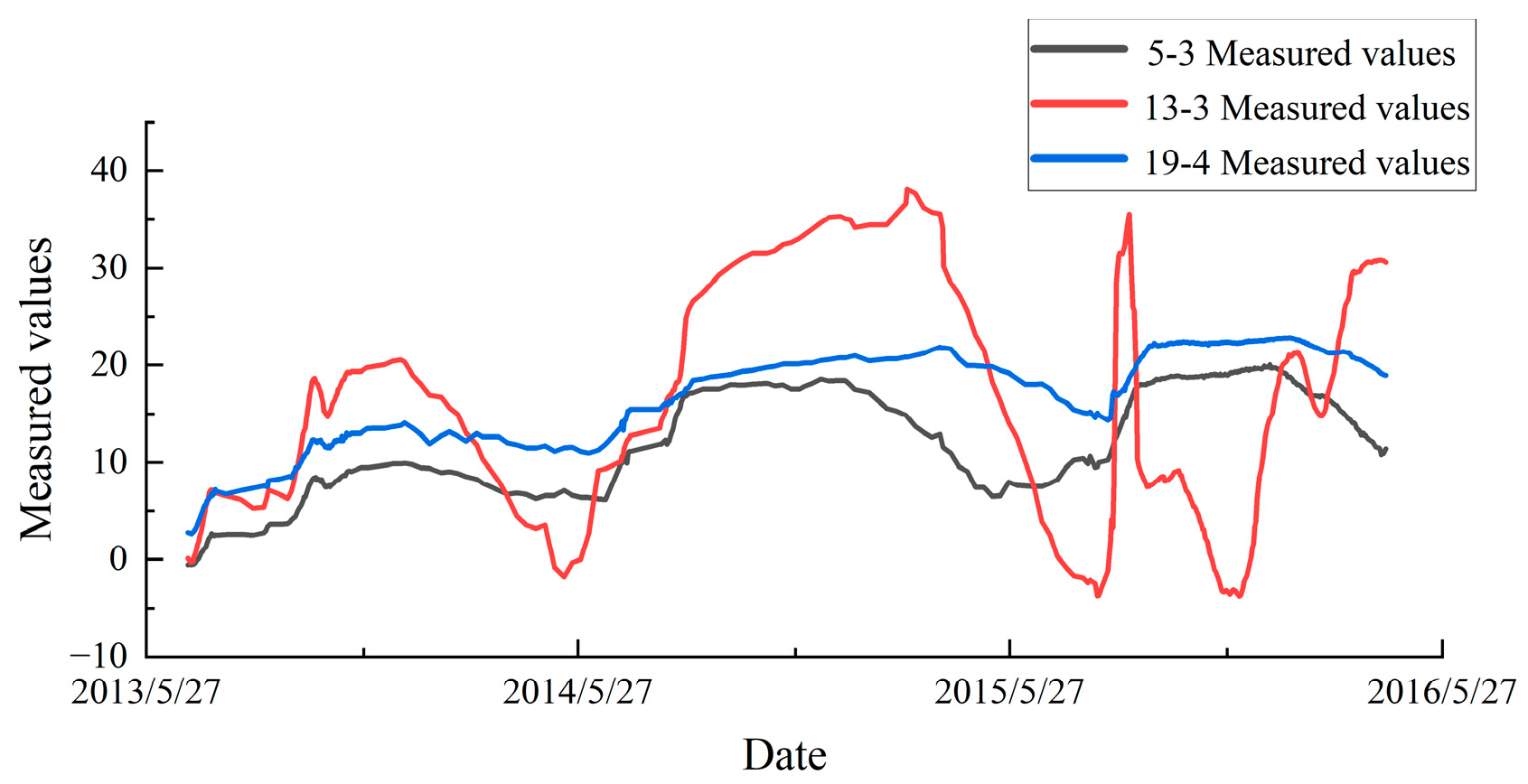
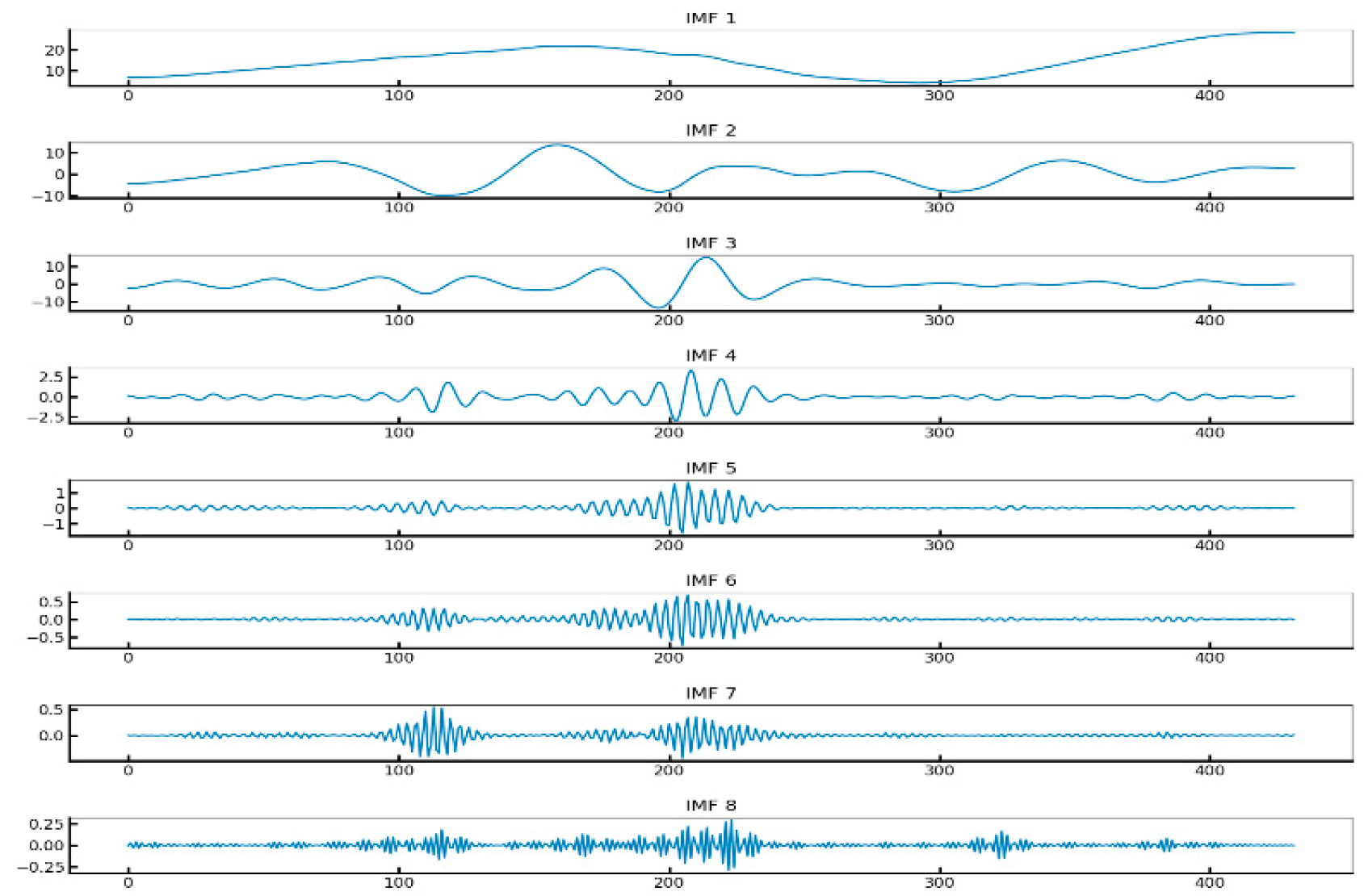
4.1. Optimized VMD for Noise Decomposition and Data Feature Preservation
4.2. Prediction Using the AttLSTM Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, C.S.; Su, H.Z.; Wang, S.W. Advances in calculation models and monitoring methods for long-term deformation behavior of concrete dams. J. Hydroelectr. Eng. 2016, 35, 1–14. [Google Scholar]
- Gu, C.; Cui, X.; Gu, H.; Yang, M. A New Hybrid Monitoring Model for Displacement of the Concrete Dam. Sustainability 2023, 15, 9609. [Google Scholar] [CrossRef]
- Chen, S.; Gu, C.; Lin, C.; Zhang, K.; Zhu, Y. Multi-kernel optimized relevance vector machine for probabilistic prediction of concrete dam displacement. Eng. Comput. 2021, 37, 1943–1959. [Google Scholar] [CrossRef]
- Wei, B.; Yuan, D.; Xu, Z.; Li, L. Modified hybrid forecast model considering chaotic residual errors for dam deformation. Struct. Control. Health Monit. 2018, 25, e2188. [Google Scholar] [CrossRef]
- Gu, C.; Wu, B.; Chen, Y. A High-Robust Displacement Prediction Model for Super-High Arch Dams Integrating Wavelet De-Noising and Improved Random Forest. Water 2023, 15, 1271. [Google Scholar] [CrossRef]
- Shao, C.; Zheng, S.; Gu, C.; Hu, Y.; Qin, X. A novel outlier detection method for monitoring data in dam engineering. Expert Syst. Appl. 2022, 193, 116476. [Google Scholar] [CrossRef]
- Salazar, F.; Morán, R.; Toledo, M.; Oñate, E. Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations. Arch. Comput. Methods Eng. 2015, 24, 1–21. [Google Scholar] [CrossRef]
- Belmokre, A.; Santillan, D.; Mihoubi, M.K. Improved Hydrostatic-Season-Time Model for Dam Monitoring: Inclusion of a Thermal Analytical Solution. In Proceedings of the 1st International Conference on Structural Damage Modelling and Assessment, Ghent, Belgium, 4–5 August 2020; pp. 67–78. [Google Scholar]
- Ran, L.; Yang, J.; Zhang, P.; Wang, J.; Ma, C.; Cui, C.; Cheng, L.; Wang, J.; Zhou, M. A hybrid monitoring model of rockfill dams considering the spatial variability of rockfill materials and a method for determining the monitoring indexes. J. Civ. Struct. Health Monit. 2022, 12, 817–832. [Google Scholar]
- Wei, B.; Chen, L.; Li, H.; Yuan, D.; Wang, G. Optimized prediction model for concrete dam displacement based on signal residual amendment. Appl. Math. Model. 2020, 78, 20–36. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Shu, X.; Chen, Z.; Gao, Z.; Zhang, K. A Hybrid Model Integrating Principal Component Analysis, Fuzzy C-Means, and Gaussian Process Regression for Dam Deformation Prediction. Arab. J. Sci. Eng. 2020, 46, 4293–4306. [Google Scholar] [CrossRef]
- Gu, H.; Yang, M.; Gu, C.-S.; Huang, X.-F. A factor mining model with optimized random forest for concrete dam deformation monitoring. Water Sci. Eng. 2021, 14, 330–336. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Li, Y.; Wen, L.; Sun, X. AF-OS-ELM-MVE: A new online sequential extreme learning machine of dam safety monitoring model for structure deformation estimation. Adv. Eng. Inform. 2024, 60, 102345. [Google Scholar] [CrossRef]
- Song, S.; Zhou, Q.; Zhang, T.; Hu, Y. Automatic Concrete Dam Deformation Prediction Model Based on TPE-STL-LSTM. Water 2023, 15, 2090. [Google Scholar] [CrossRef]
- Pan, J.; Liu, W.; Liu, C.; Wang, J. Convolutional neural network-based spatiotemporal prediction for deformation behavior of arch dams. Expert Syst. Appl. 2023, 232, 120835. [Google Scholar] [CrossRef]
- Lu, Z.; Ding, Y.; Li, D. Coupling VMD and MSSA denoising for dam deformation prediction. Structures 2023, 58, 105503. [Google Scholar]
- Fang, W.; Liu, Y.; Hu, L.; Hu, H.; Tian, J. Intelligent deformation prediction model for concrete dams based on VMD-ResNetPlus-BiLSTM. In Proceedings of the 2024 International Academic Conference on Edge Computing, Parallel and Distributed Computing, Xi’an, China, 19–21 April 2024; pp. 258–264. [Google Scholar]
- Yang, J.; Lv, Z. Research on dam foundation deformation prediction based on VMD optimized temporal convolutional network. In Proceedings of the 2021 7th International Conference on Hydraulic and Civil Engineering & Smart Water Conservancy and Intelligent Disaster Reduction Forum (ICHCE & SWIDR), Nanjing, China, 6–8 November 2021; pp. 232–238. [Google Scholar]
- Cao, E.; Bao, T.; Gu, C.; Li, H.; Liu, Y.; Hu, S. A Novel Hybrid Decomposition—Ensemble Prediction Model for Dam Deformation. Appl. Sci. 2020, 10, 5700. [Google Scholar] [CrossRef]
- Kumar, A.; Zhou, Y.; Xiang, J.J.M. Optimization of VMD using kernel-based mutual information for the extraction of weak features to detect bearing defects. Measurement 2021, 168, 108402. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Xie, Y.; Meng, X.; Wang, J.; Li, H.; Lu, X.; Ding, J.; Jia, Y.; Yang, Y. Enhancing GNSS Deformation Monitoring Forecasting with a Combined VMD-CNN-LSTM Deep Learning Model. Remote. Sens. 2024, 16, 1767. [Google Scholar] [CrossRef]
- Ahmadi, F.; Tohidi, M.; Sadrianzade, M. Streamflow prediction using a hybrid methodology based on variational mode decomposition (VMD) and machine learning approaches. Appl. Water Sci. 2023, 13, 135. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Sasmal, B.; Hussien, A.G.; Das, A.; Dhal, K.G.; Saha, R. Reptile Search Algorithm: Theory, Variants, Applications, and Performance Evaluation. Arch. Comput. Methods Eng. 2023, 31, 521–549. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Gu, C.; Zhu, Y.; Dai, B.; Zhang, K.; Zhang, Z.; Li, B. A Concrete Dam Deformation Prediction Method Based on LSTM with Attention Mechanism. IEEE Access 2020, 8, 185177–185186. [Google Scholar] [CrossRef]
- Cao, W.; Wen, Z.; Su, H. Spatiotemporal clustering analysis and zonal prediction model for deformation behavior of super-high arch dams. Expert Syst. Appl. 2023, 216, 119439. [Google Scholar] [CrossRef]
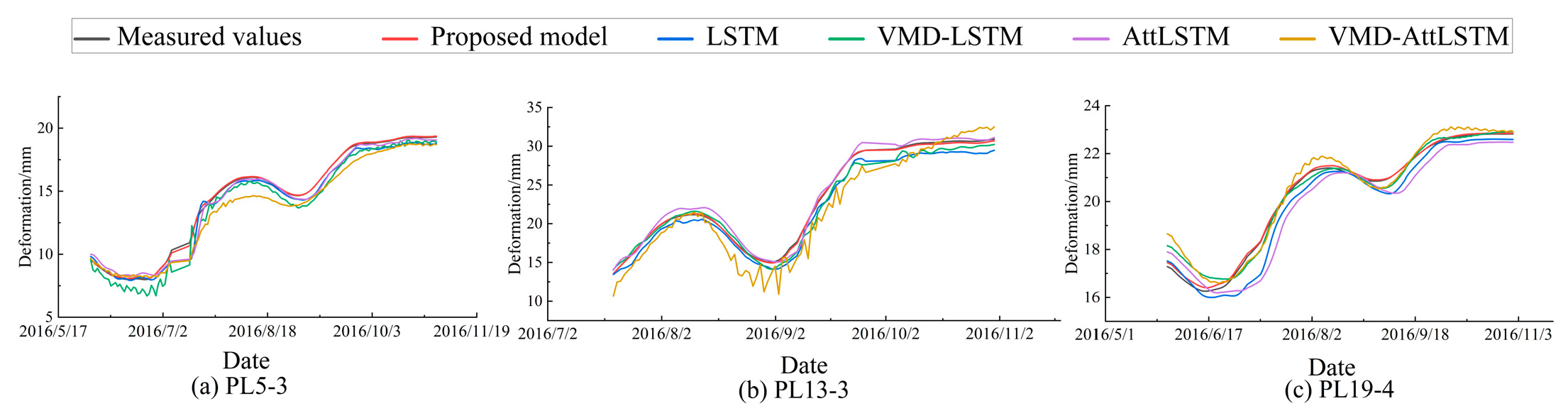
| Measuring Points | Model | R2 | MAE/mm | MSE/mm2 | RMSE/mm | MAPE/% |
|---|---|---|---|---|---|---|
| PL5-3 | Proposed model | 0.9997 | 0.0469 | 0.0476 | 0.069 | 0.54 |
| LSTM | 0.9843 | 0.3832 | 0.1880 | 0.5027 | 2.56 | |
| VMD-LSTM | 0.9879 | 0.3869 | 0.2903 | 0.4336 | 5.34 | |
| AttLSTM | 0.9820 | 0.3560 | 0.2903 | 0.5388 | 2.66 | |
| VMD-AttLSTM | 0.9830 | 0.8463 | 0.9600 | 0.9798 | 5.69 | |
| PL19-4 | Proposed model | 0.9951 | 0.0923 | 0.0099 | 0.0996 | 0.42 |
| LSTM | 0.9565 | 0.4140 | 0.2644 | 0.5142 | 1.89 | |
| VMD-LSTM | 0.9682 | 0.3132 | 0.1914 | 0.4375 | 1.23 | |
| AttLSTM | 0.9878 | 0.6460 | 0.6216 | 0.7884 | 2.81 | |
| VMD-AttLSTM | 0.9629 | 0.3079 | 0.2222 | 0.4713 | 1.74 | |
| PL13-3 | Proposed model | 0.9998 | 0.0587 | 0.0052 | 0.0720 | 0.50 |
| LSTM | 0.9958 | 0.3098 | 0.1540 | 0.3924 | 4.34 | |
| VMD-LSTM | 0.9801 | 0.6948 | 0.7034 | 0.8387 | 3.26 | |
| AttLSTM | 0.9904 | 0.4646 | 0.3550 | 0.5958 | 2.59 | |
| VMD-AttLSTM | 0.9865 | 0.5267 | 0.3198 | 0.8220 | 8.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Gu, H.; Gu, C.; Wang, Y. A Deformation Prediction Model for Concrete Dams Based on RSA-VMD-AttLSTM. Buildings 2025, 15, 357. https://doi.org/10.3390/buildings15030357
Liu P, Gu H, Gu C, Wang Y. A Deformation Prediction Model for Concrete Dams Based on RSA-VMD-AttLSTM. Buildings. 2025; 15(3):357. https://doi.org/10.3390/buildings15030357
Chicago/Turabian StyleLiu, Pei, Hao Gu, Chongshi Gu, and Yanbo Wang. 2025. "A Deformation Prediction Model for Concrete Dams Based on RSA-VMD-AttLSTM" Buildings 15, no. 3: 357. https://doi.org/10.3390/buildings15030357
APA StyleLiu, P., Gu, H., Gu, C., & Wang, Y. (2025). A Deformation Prediction Model for Concrete Dams Based on RSA-VMD-AttLSTM. Buildings, 15(3), 357. https://doi.org/10.3390/buildings15030357







