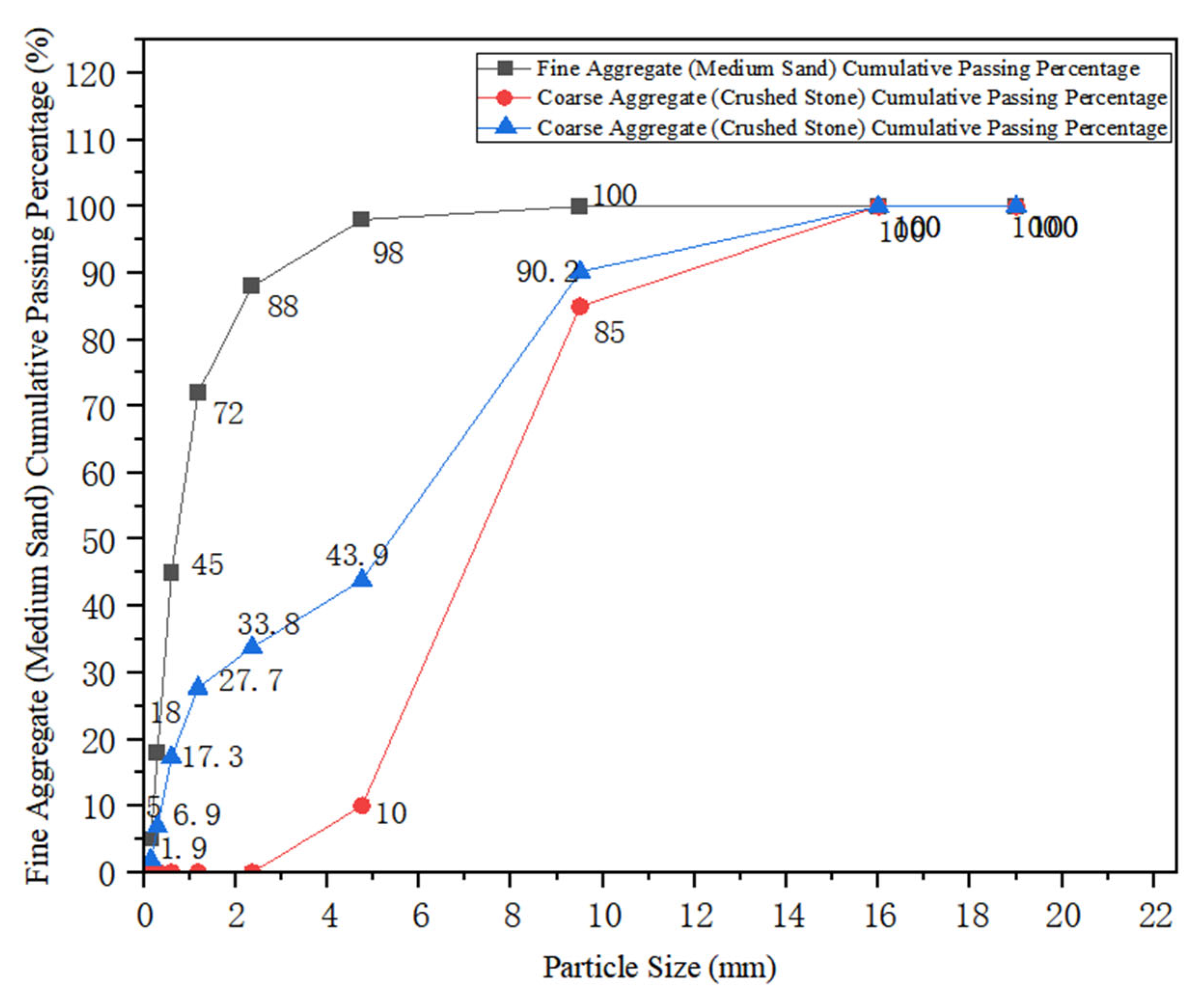
Figure 1.
Aggregate gradation curve.
Figure 1.
Aggregate gradation curve.
Figure 2.
Images of graphene oxide (GO) used in this study.
Figure 2.
Images of graphene oxide (GO) used in this study.
Figure 3.
Photograph of a copper mesh electrode used for conductivity measurements.
Figure 3.
Photograph of a copper mesh electrode used for conductivity measurements.
Figure 4.
Demolded concrete specimens after curing.
Figure 4.
Demolded concrete specimens after curing.
Figure 5.
Concrete specimen with copper mesh electrodes installed for electrical testing.
Figure 5.
Concrete specimen with copper mesh electrodes installed for electrical testing.
Figure 6.
Specimen loading setup.
Figure 6.
Specimen loading setup.
Figure 7.
Typical failure mode of an ordinary concrete specimen.
Figure 7.
Typical failure mode of an ordinary concrete specimen.
Figure 8.
Typical failure mode of GO-modified concrete specimens.
Figure 8.
Typical failure mode of GO-modified concrete specimens.
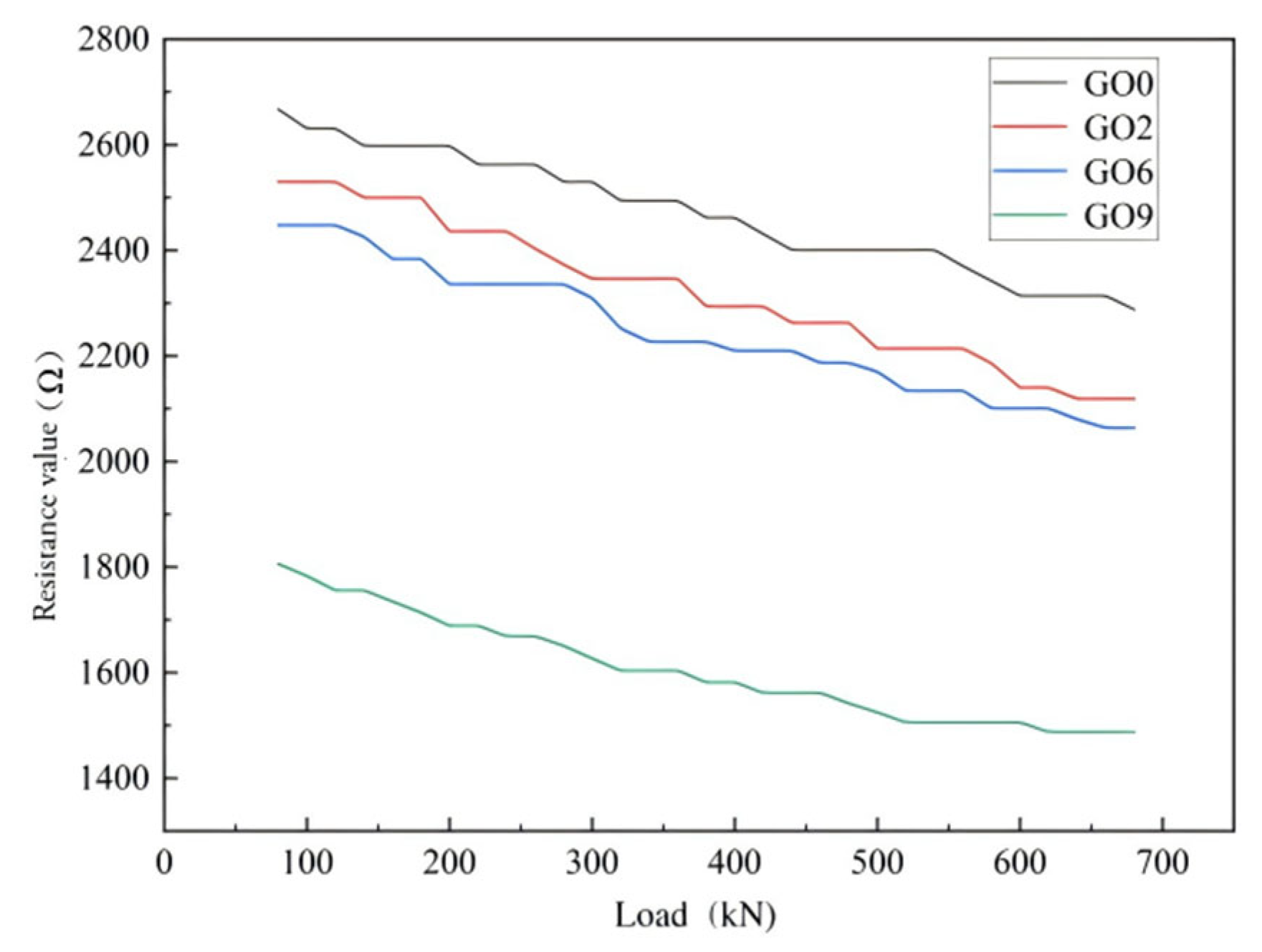
Figure 9.
Load–resistance relationships of concrete specimens with varying GO dosages.
Figure 9.
Load–resistance relationships of concrete specimens with varying GO dosages.
Figure 10.
Load–resistivity relationships of concrete specimens with varying GO dosages.
Figure 10.
Load–resistivity relationships of concrete specimens with varying GO dosages.
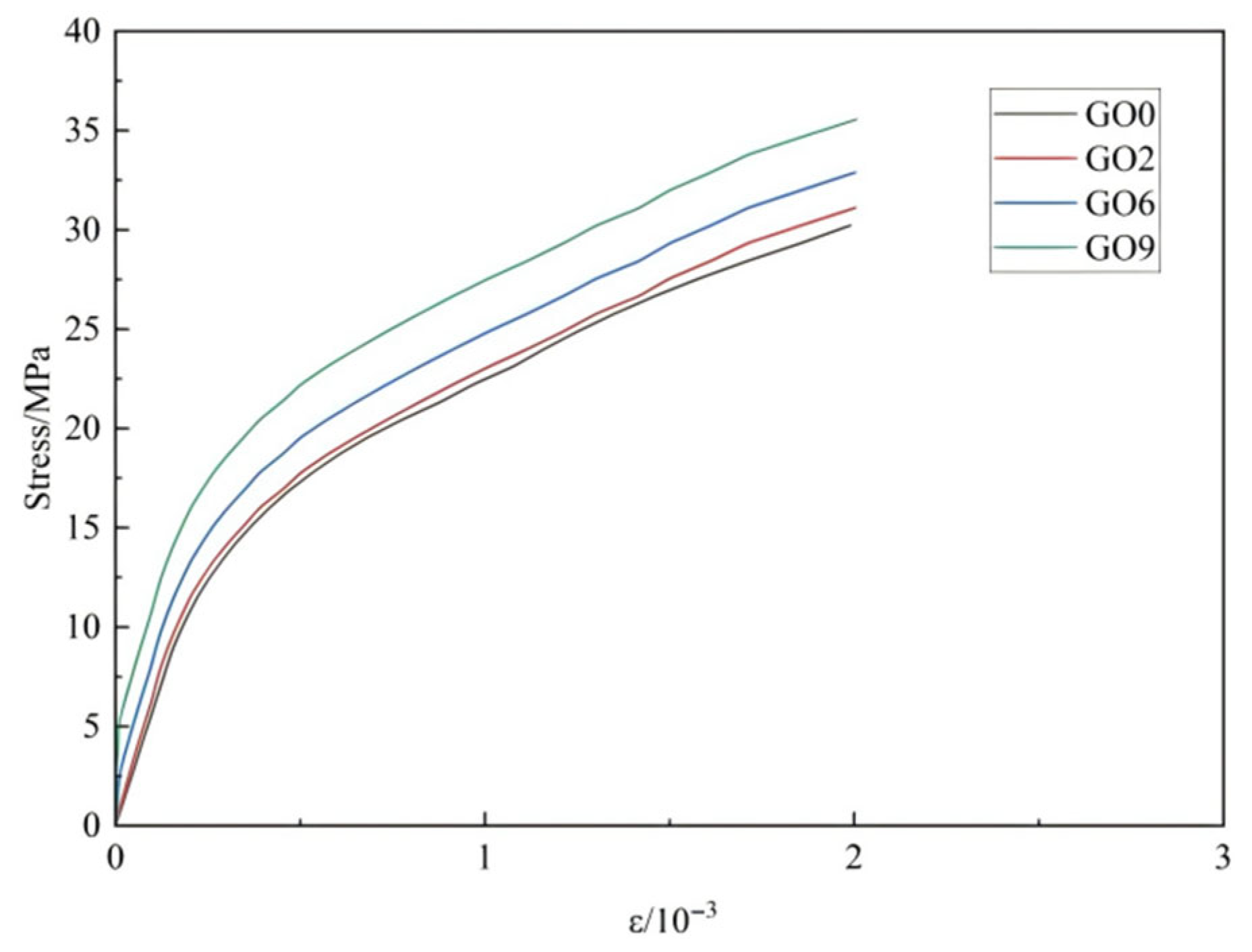
Figure 11.
Stress–strain curves of concrete specimens with different GO dosages.
Figure 11.
Stress–strain curves of concrete specimens with different GO dosages.
Figure 12.
S-3400N scanning electron microscope (SEM) used for microstructural analysis.
Figure 12.
S-3400N scanning electron microscope (SEM) used for microstructural analysis.
Figure 13.
Ion sputter coater employed for SEM sample preparation.
Figure 13.
Ion sputter coater employed for SEM sample preparation.
Figure 14.
SEM test specimens prepared from concrete samples.
Figure 14.
SEM test specimens prepared from concrete samples.
Figure 15.
Micromorphology of a concrete specimen containing 0% GO (ordinary concrete).
Figure 15.
Micromorphology of a concrete specimen containing 0% GO (ordinary concrete).
Figure 16.
Micromorphology of a concrete specimen containing 0.02% GO.
Figure 16.
Micromorphology of a concrete specimen containing 0.02% GO.
Figure 17.
Micromorphology of a concrete specimen containing 0.06% GO.
Figure 17.
Micromorphology of a concrete specimen containing 0.06% GO.
Figure 18.
Micromorphology of a concrete specimen containing 0.09% GO.
Figure 18.
Micromorphology of a concrete specimen containing 0.09% GO.
Figure 19.
Operation diagram used for rebar tensile testing.
Figure 19.
Operation diagram used for rebar tensile testing.
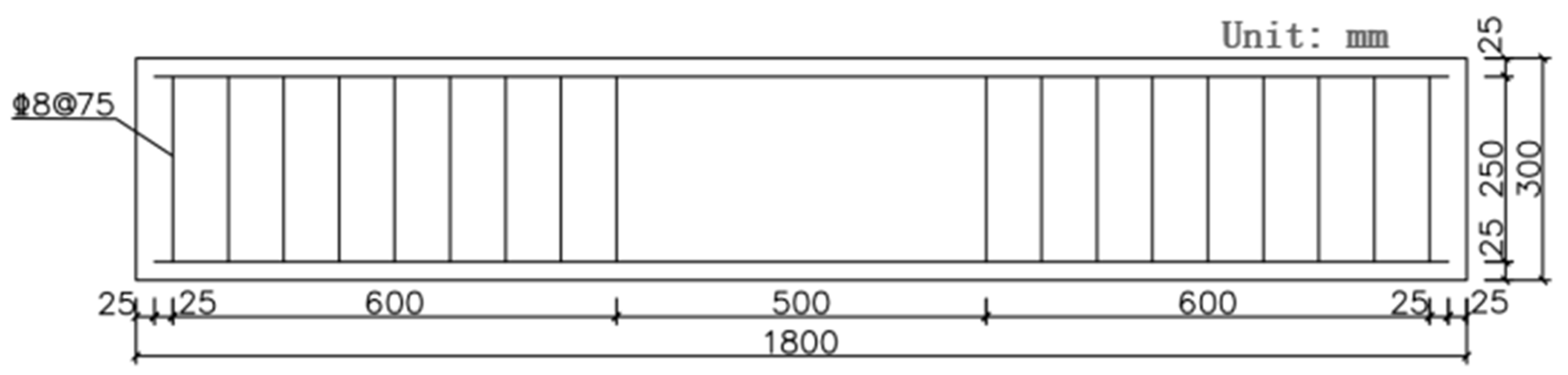
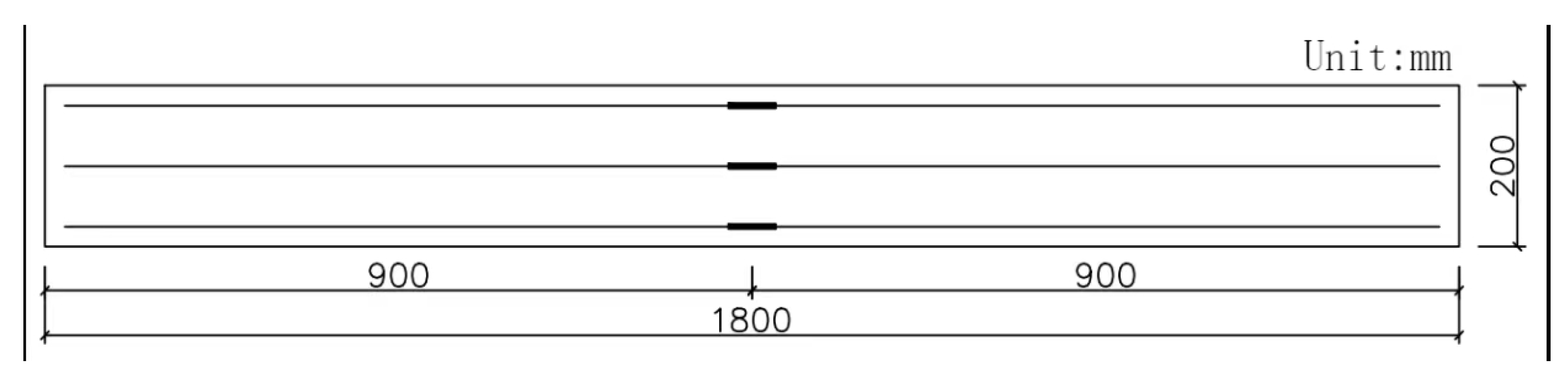
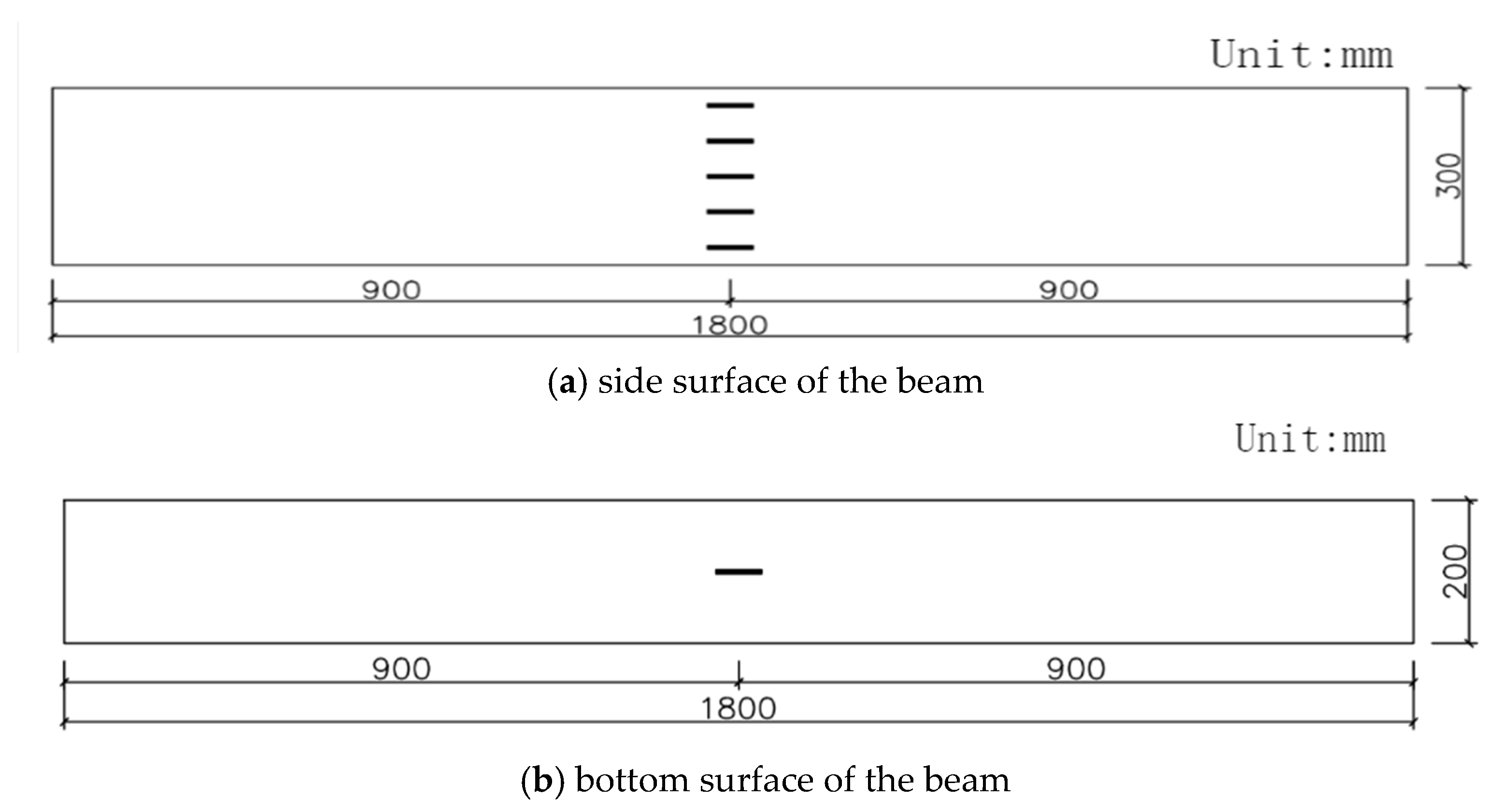
Figure 20.
Dimensions and reinforcement details of test beams.
Figure 20.
Dimensions and reinforcement details of test beams.
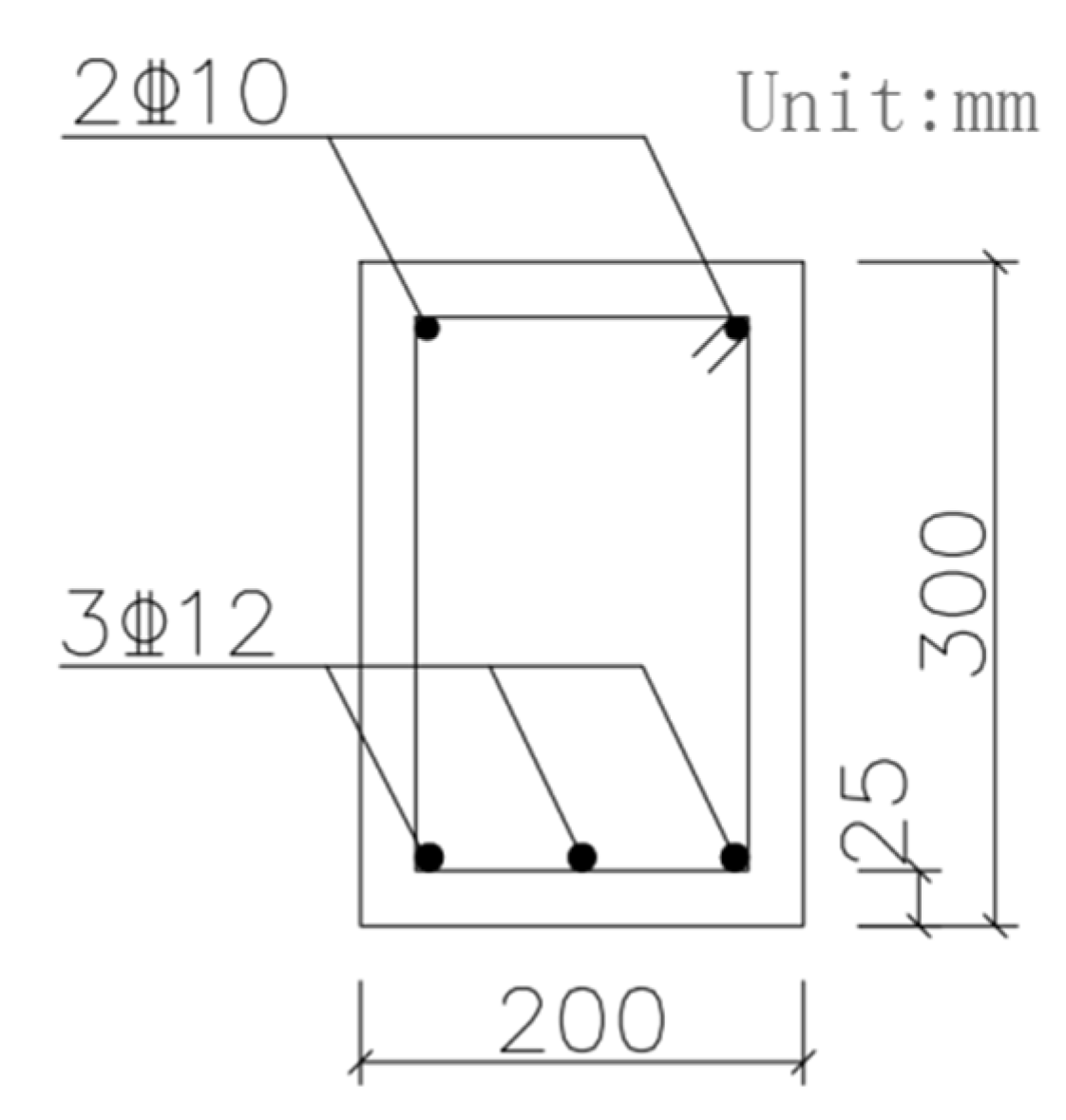
Figure 21.
Cross-sectional reinforcement configuration of test beams.
Figure 21.
Cross-sectional reinforcement configuration of test beams.
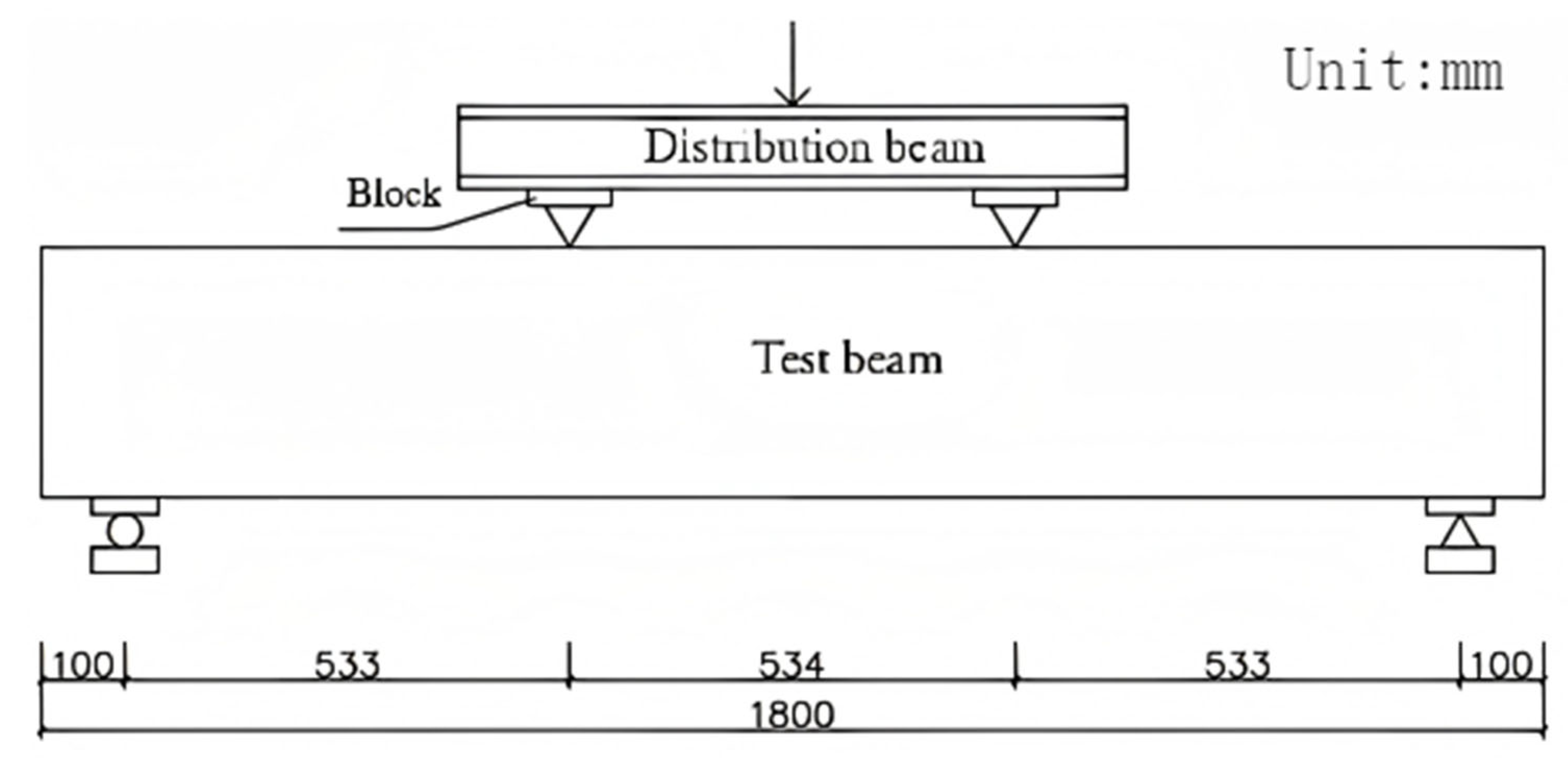
Figure 22.
Schematic diagram of the loading arrangement for test beams.
Figure 22.
Schematic diagram of the loading arrangement for test beams.
Figure 23.
Diagram of the loading device used for beam testing.
Figure 23.
Diagram of the loading device used for beam testing.
Figure 24.
Strain gauge bonding on rebars.
Figure 24.
Strain gauge bonding on rebars.
Figure 25.
Strain gauge bonding on concrete.
Figure 25.
Strain gauge bonding on concrete.
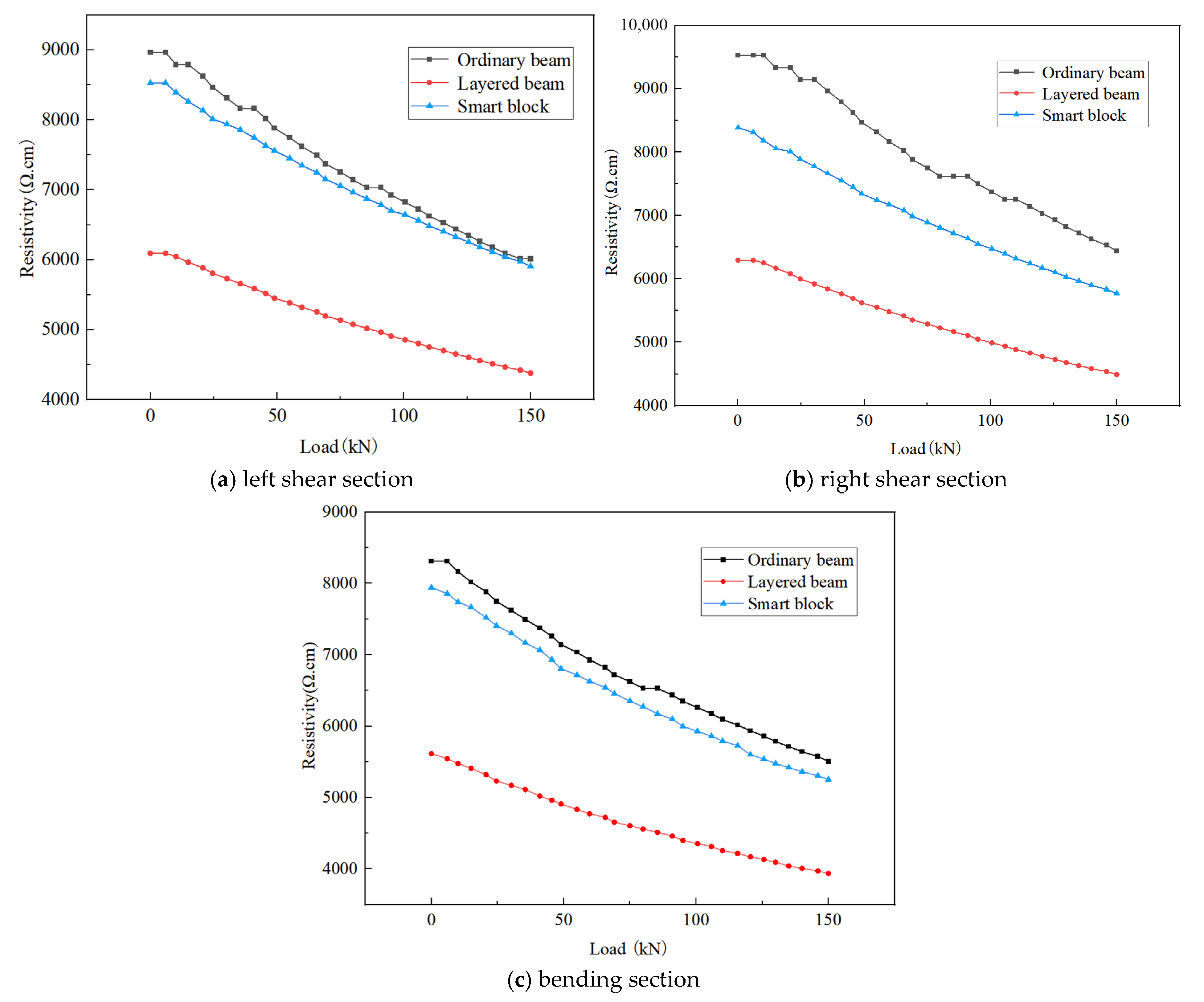
Figure 26.
Load–resistivity curves for bending and shear sections of test beams.
Figure 26.
Load–resistivity curves for bending and shear sections of test beams.
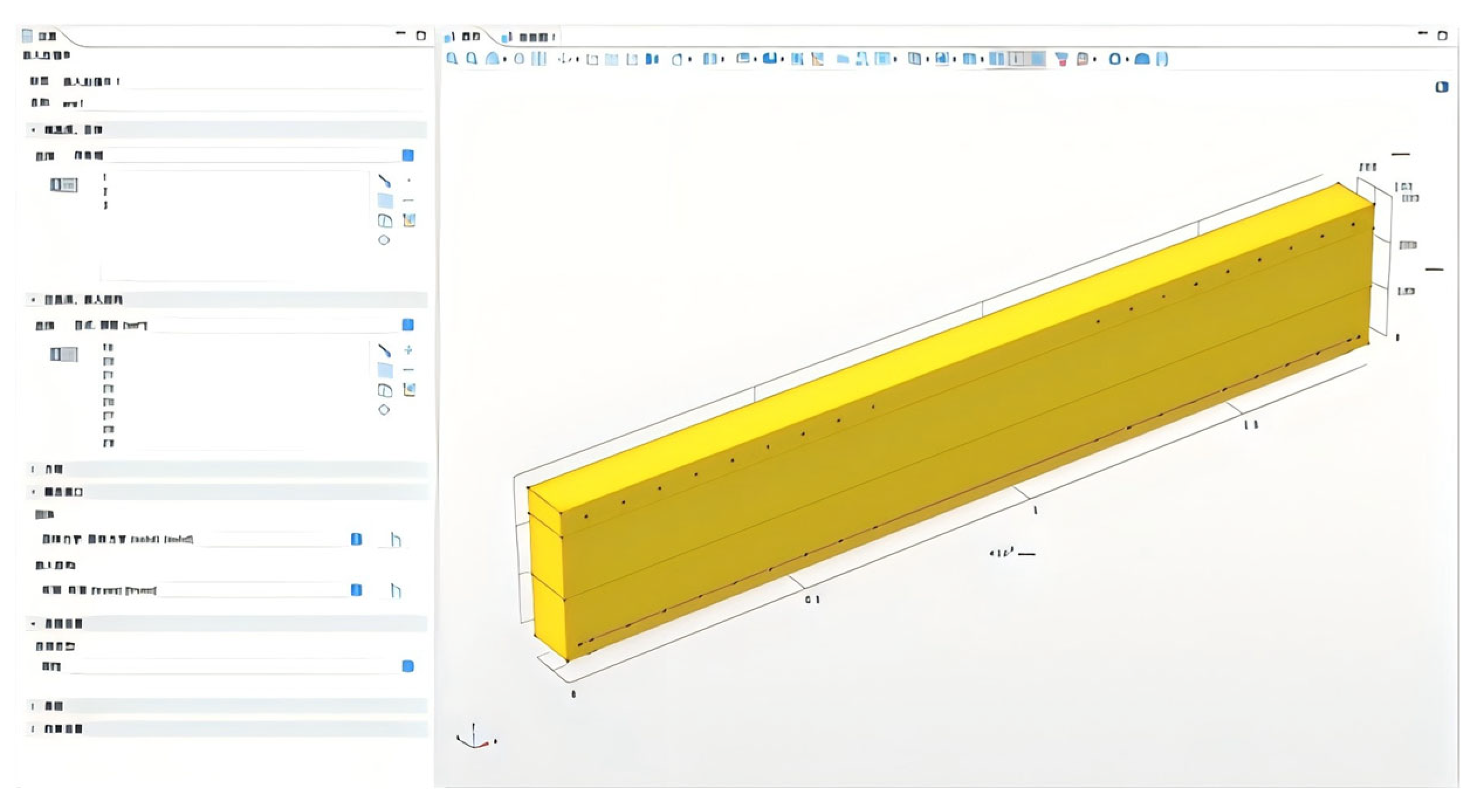
Figure 27.
Model diagram of a beam with an embedded rebar cage.
Figure 27.
Model diagram of a beam with an embedded rebar cage.
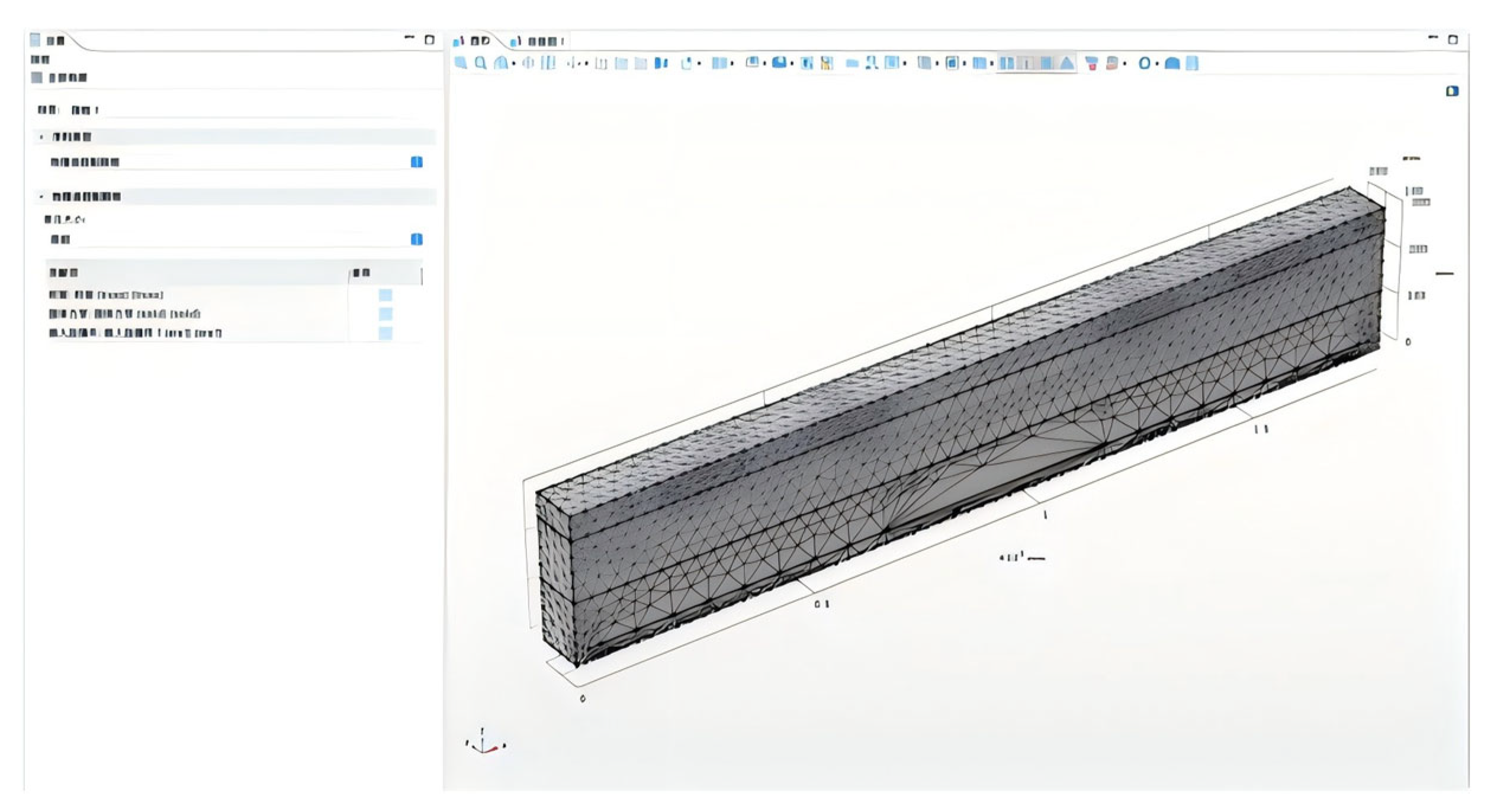
Figure 28.
Finite element mesh generation for the beam model.
Figure 28.
Finite element mesh generation for the beam model.
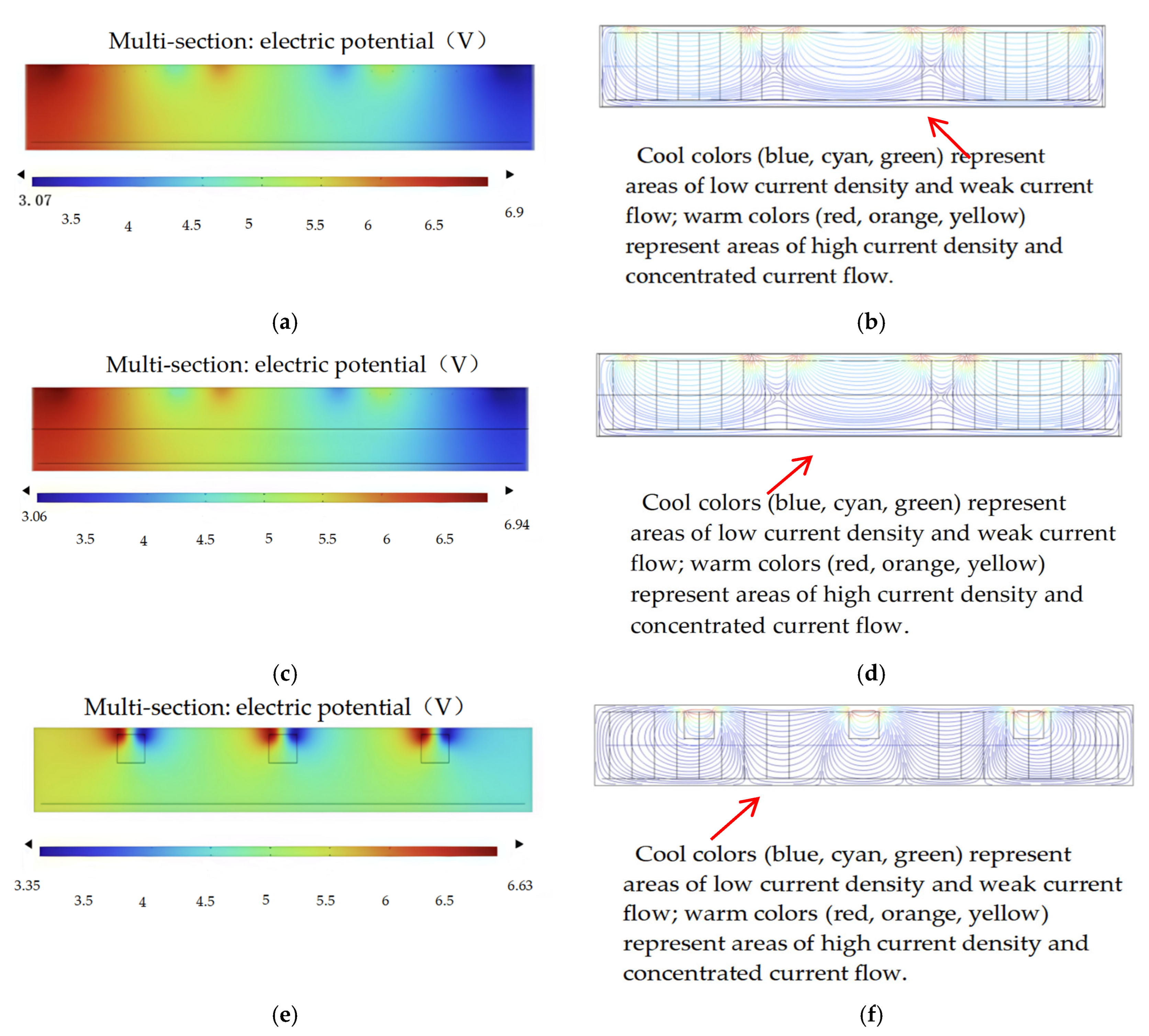
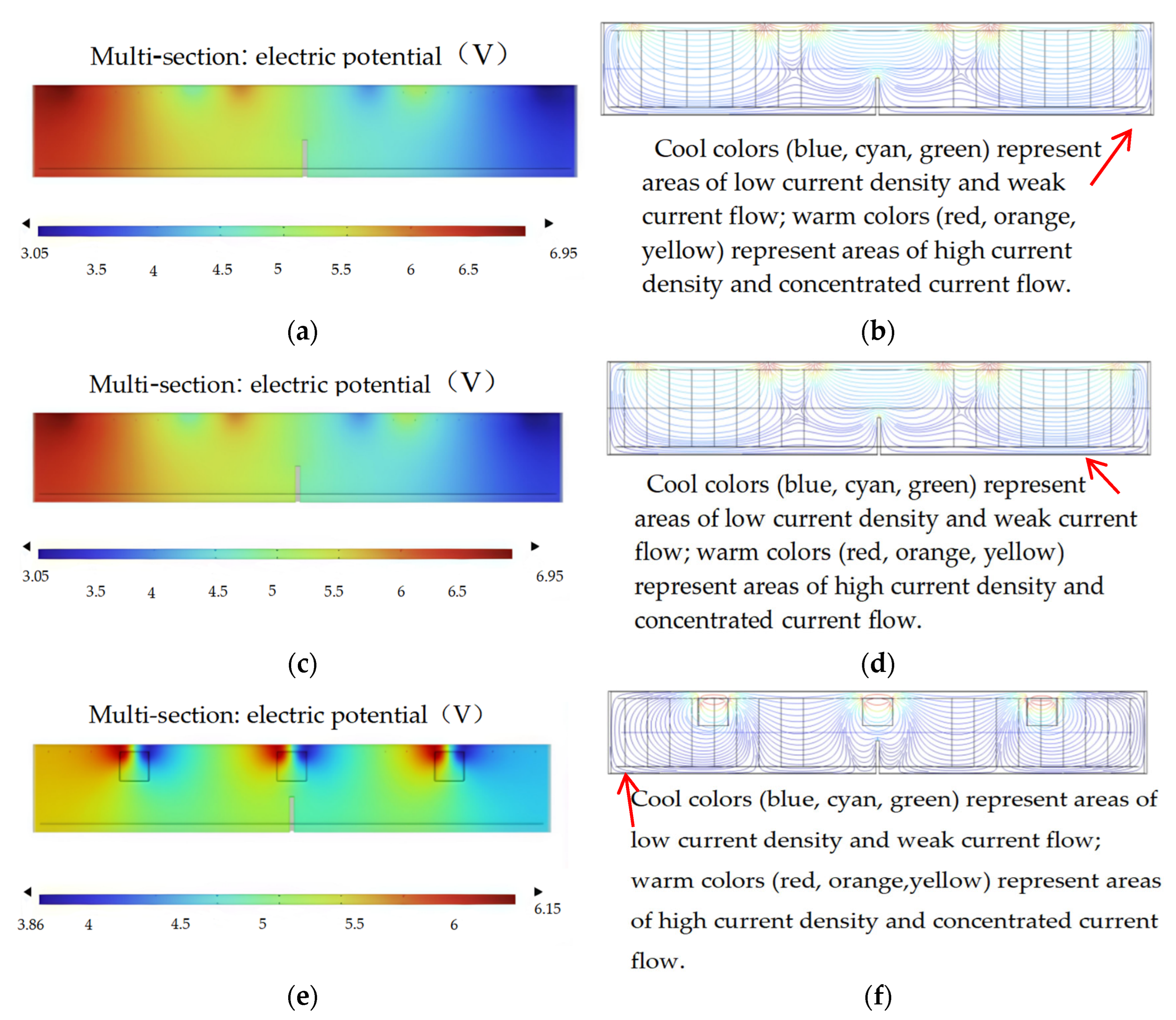
Figure 29.
Simulated potential distribution and current lines for each beam. (a) potential diagram of ordinary concrete; (b) current line diagram of ordinary concrete; (c) potential diagram of a layered GO-modified beam; (d) current line diagram of a layered GO-modified beam; (e) potential diagram of a GO-smart-block beam; (f) current line diagram of a GO-smart-block beam.
Figure 29.
Simulated potential distribution and current lines for each beam. (a) potential diagram of ordinary concrete; (b) current line diagram of ordinary concrete; (c) potential diagram of a layered GO-modified beam; (d) current line diagram of a layered GO-modified beam; (e) potential diagram of a GO-smart-block beam; (f) current line diagram of a GO-smart-block beam.
Figure 30.
Simulated potential distribution and current lines during beam cracking. (a) potential diagram during cracking of ordinary concrete; (b) current line diagram during cracking of ordinary concrete; (c) potential diagram during cracking of a layered GO-modified beam; (d) current line diagram during cracking of a layered GO-modified beam; (e) potential diagram during cracking of a GO-smart-block beam; (f) current line diagram during cracking of a GO-smart-block beam.
Figure 30.
Simulated potential distribution and current lines during beam cracking. (a) potential diagram during cracking of ordinary concrete; (b) current line diagram during cracking of ordinary concrete; (c) potential diagram during cracking of a layered GO-modified beam; (d) current line diagram during cracking of a layered GO-modified beam; (e) potential diagram during cracking of a GO-smart-block beam; (f) current line diagram during cracking of a GO-smart-block beam.
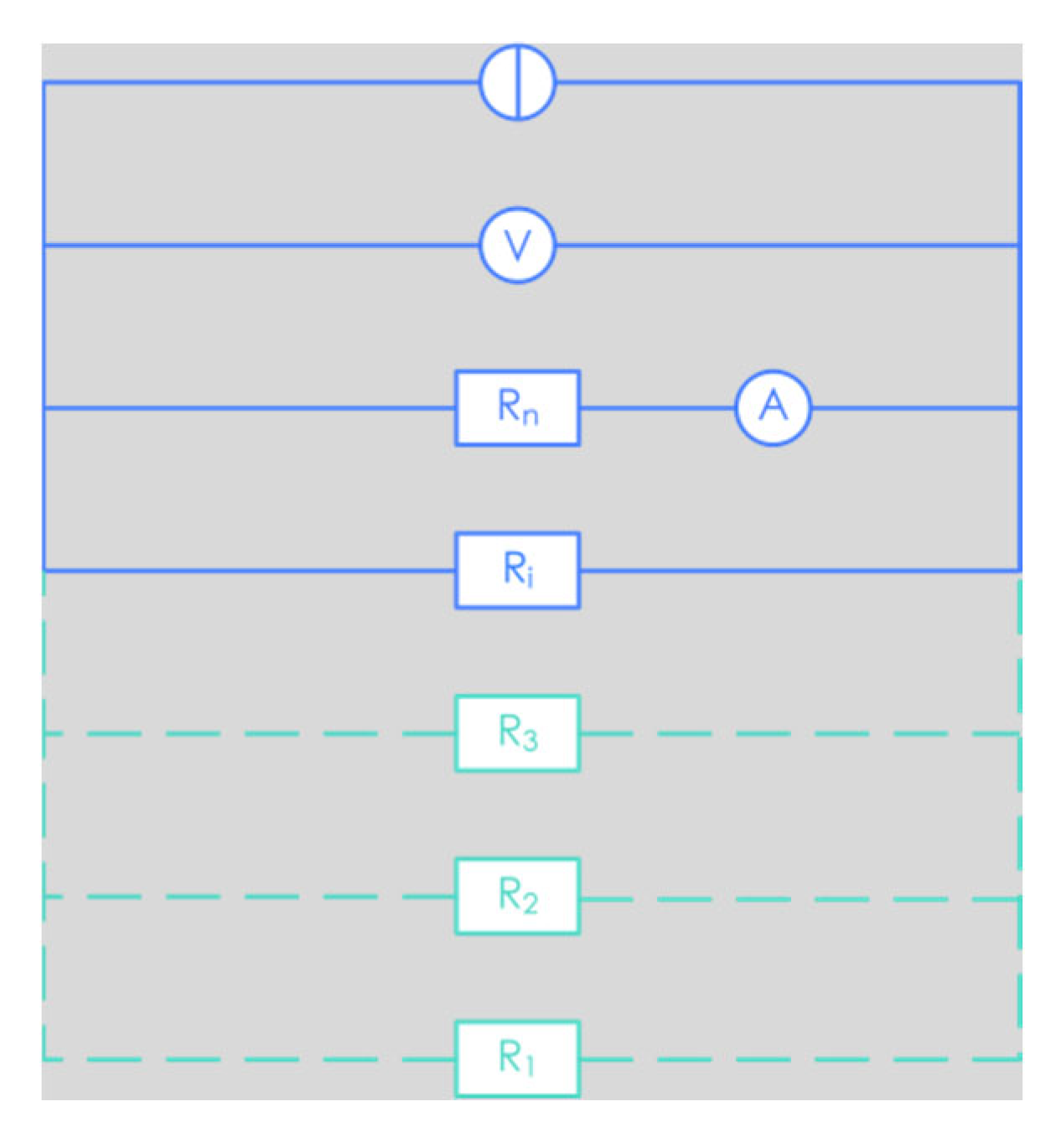
Figure 31.
Equivalent circuit diagram.
Figure 31.
Equivalent circuit diagram.
Table 1.
Physical and mechanical properties of the cement used in this study, including loss on ignition (LOI), initial and final setting times, and compressive strength.
Table 1.
Physical and mechanical properties of the cement used in this study, including loss on ignition (LOI), initial and final setting times, and compressive strength.
| Type | Loss on Ignition (%) | Initial Setting Time (h) | Final Setting Time (h) | Compressive Strength (MPa) |
|---|
| P.O 42.5 | 1.02 | 4 | 5.25 | 28.4 |
Table 2.
Standard and measured chemical composition of copper mesh electrodes used as the conductive interface in the experimental setup. Values are presented in weight percentage, with “N.D.” indicating non-detected components.
Table 2.
Standard and measured chemical composition of copper mesh electrodes used as the conductive interface in the experimental setup. Values are presented in weight percentage, with “N.D.” indicating non-detected components.
| Element | Cu (%) | P (%) | Pb (%) | Fe (%) | Hg (%) | Cd (%) | Cr6+ (%) |
|---|
| Standard content | 60.5–63.5 | ≤0.010 | ≤0.010 | ≤0.15 | ≤0.0020 | ≤0.0020 | ≤0.0020 |
| Measured content | 61.37 | 0.003 | 0.0065 | 0.013 | N.D. | 0.0003 | 0.0003 |
Table 3.
Mix proportions for conductive concrete specimens with varying graphene oxide (GO) dosages.
Table 3.
Mix proportions for conductive concrete specimens with varying graphene oxide (GO) dosages.
| Group | Specimen Code | Material Dose (kg/m3) |
|---|
| GO | Water | Cement | Fine Aggregate | Coarse Aggregate | Water-Reducing Agent | Water-Cement Ratio |
|---|
| 1 | C-GO0 | 0 | 204 | 409.3 | 901 | 1439 | 2.1 | 0.5 |
| 2 | C-GO2 | 0.082 |
| 3 | C-GO6 | 0.246 |
| 4 | C-GO9 | 0.368 |
Table 4.
Compressive strength results of concrete specimens incorporating different GO dosages.
Table 4.
Compressive strength results of concrete specimens incorporating different GO dosages.
| Specimen ID | Number of Replication | Compressive Strength (MPa) | Strength Growth Ratio | Strength Growth Rate (%) | Standard Deviation | Error |
|---|
| C-GO0 | 3 | 30.22 | 1.000 | 0 | 0.5 | 1.243 |
| C-GO2 | 3 | 31.11 | 1.029 | 2.95 | 0.6 | 1.481 |
| C-GO6 | 3 | 32.89 | 1.088 | 8.84 | 0.7 | 1.740 |
| C-GO9 | 3 | 35.56 | 1.177 | 17.67 | 0.8 | 1.988 |
Table 5.
Mechanical properties of HRB400 rebars of different diameters, including yield strength and ultimate tensile strength.
Table 5.
Mechanical properties of HRB400 rebars of different diameters, including yield strength and ultimate tensile strength.
| Material Type | Rebar Diameter (mm) | Rebar Yield Strength (MPa) | Rebar Ultimate Strength (MPa) |
|---|
| HRB400 | 8 | 486 | 648 |
| HRB400 | 10 | 424 | 565 |
| HRB400 | 12 | 421 | 593 |
Table 6.
Detailed parameters of reinforced concrete beams (RCBs) tested in this study, including GO dosage, rebar specifications, reinforcement ratio, beam dimensions, and specimen grouping.
Table 6.
Detailed parameters of reinforced concrete beams (RCBs) tested in this study, including GO dosage, rebar specifications, reinforcement ratio, beam dimensions, and specimen grouping.
| Group | ID | GO Dose (%) | Longitudinal Rebar (mm) | Reinforcement Ratio (%) | Rebar Type | Quantity (Bars) | Dimensions (mm) |
|---|
| 1 | RCB-PT-1 | 0 | 12 | 0.63 | HRB400 | 1 | 200 × 300 × 1800 |
| RCB-PT-2 | 1 |
| RCB-PT-3 | 1 |
| 2 | RCB-GO-F-1 | 0.09 | 1 |
| RCB-GO-F-2 | 1 |
| RCB-GO-F-3 | 1 |
| 3 | RCB-GO-Z-1 | 0.09 | 1 |
| RCB-GO-Z-2 | 1 |
| RCB-GO-Z-3 | 1 |
Table 7.
Parameters of fitted curves.
Table 7.
Parameters of fitted curves.
| Sample Number | a | b | c | CR2 |
|---|
| RCB-PT-1 | 0.9551 | −11.4036 | 0.9612 | 0.9575 |
| RCB-PT-2 | 1.0534 | −12.6187 | 4.2294 | 0.9653 |
| RCB-PT-3 | 1.0606 | −12.852 | 4.9811 | 0.9779 |
| RCB-GO-F-1 | 0.7607 | −9.8436 | 0.4538 | 0.9874 |
| RCB-GO-F-2 | 0.6366 | −7.9233 | 1.9601 | 0.9859 |
| RCB-GO-F-3 | 0.8221 | −11.0407 | 5.038 | 0.9734 |
| RCB-GO-Z-1 | 1.271 | −13.262 | 1.2625 | 0.9859 |
| RCB-GO-Z-2 | 0.9075 | −11.6835 | 3.8544 | 0.9762 |
| RCB-GO-Z-3 | 0.7498 | −11.3056 | 8.9688 | 0.9328 |
Table 8.
Cracking load and ultimate load of the test beam.
Table 8.
Cracking load and ultimate load of the test beam.
| Serial Number | Cracking Load (kN) | Average Cracking Load (kN) | Ultimate Load (kN) | Average Ultimate Load (kN) | Failure Mode |
|---|
| RCB-PT-1 | 55 | 53.33 | 161 | 163.67 | Normal Section Failure |
| RCB-PT-2 | 50 | 160 | Normal Section Failure |
| RCB-PT-3 | 55 | 170 | Normal Section Failure |
| RCB-GO-F-1 | 55 | 51.67 | 165 | 160 | Normal Section Failure |
| RCB-GO-F-2 | 50 | 163 | Normal Section Failure |
| RCB-GO-F-3 | 50 | 152 | Normal Section Failure |
| RCB-GO-Z-1 | 50 | 51.67 | 162 | 163.33 | Normal Section Failure |
| RCB-GO-Z-2 | 50 | 164 | Normal Section Failure |
| RCB-GO-Z-3 | 55 | 164 | Normal Section Failure |
Table 9.
Simulation values and test values of ultimate load of test beam.
Table 9.
Simulation values and test values of ultimate load of test beam.
| Code | Experimental Ultimate Load (kN) | Average Experimental Value (kN) | Simulated Value (kN) | Error (%) |
|---|
| RCB-PT-1 | 161 | 163.67 | 158 | 3.46 |
| RCB-PT-2 | 160 |
| RCB-PT-3 | 170 |
| RCB-GO-F-1 | 165 | 160 | 165 | 3.13 |
| RCB-GO-F-2 | 163 |
| RCB-GO-F-3 | 152 |
| RCB-GO-Z-1 | 162 | 163.33 | 160 | 2.04 |
| RCB-GO-Z-2 | 164 |
| RCB-GO-Z-3 | 164 |
Table 10.
One-Way Analysis of Variance (ANOVA) for Experimental Ultimate Load.
Table 10.
One-Way Analysis of Variance (ANOVA) for Experimental Ultimate Load.
| Source of Variation | Degrees of Freedom (df) | Sum of Squares (ss) | Mean Square | F-Value | p-Value |
|---|
| Between Groups | 2 | 40.22 | 20.11 | 0.87 | 0.466 |
| Within Groups (Error) | 6 | 138.67 | 23.11 | | |
| Total | 8 | 178.89 | | | |