Seismic Fragility Analysis of Shield Tunnels Considering the Flexural Capacity of Longitudinal Joints
Abstract
1. Introduction
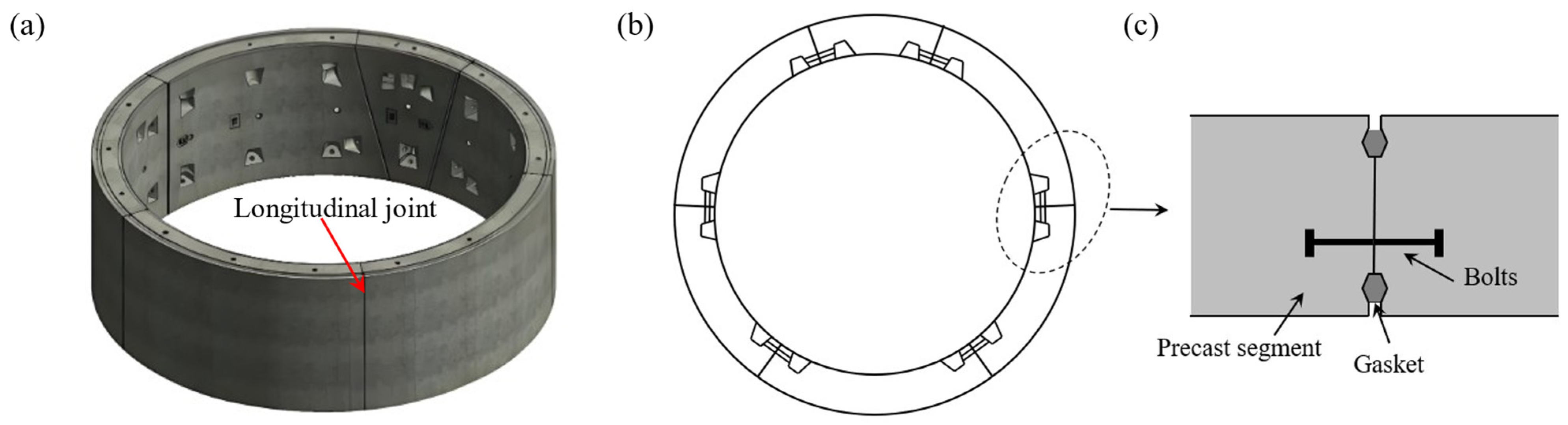
2. Mechanical Properties of Shield Tunnel Longitudinal Joints
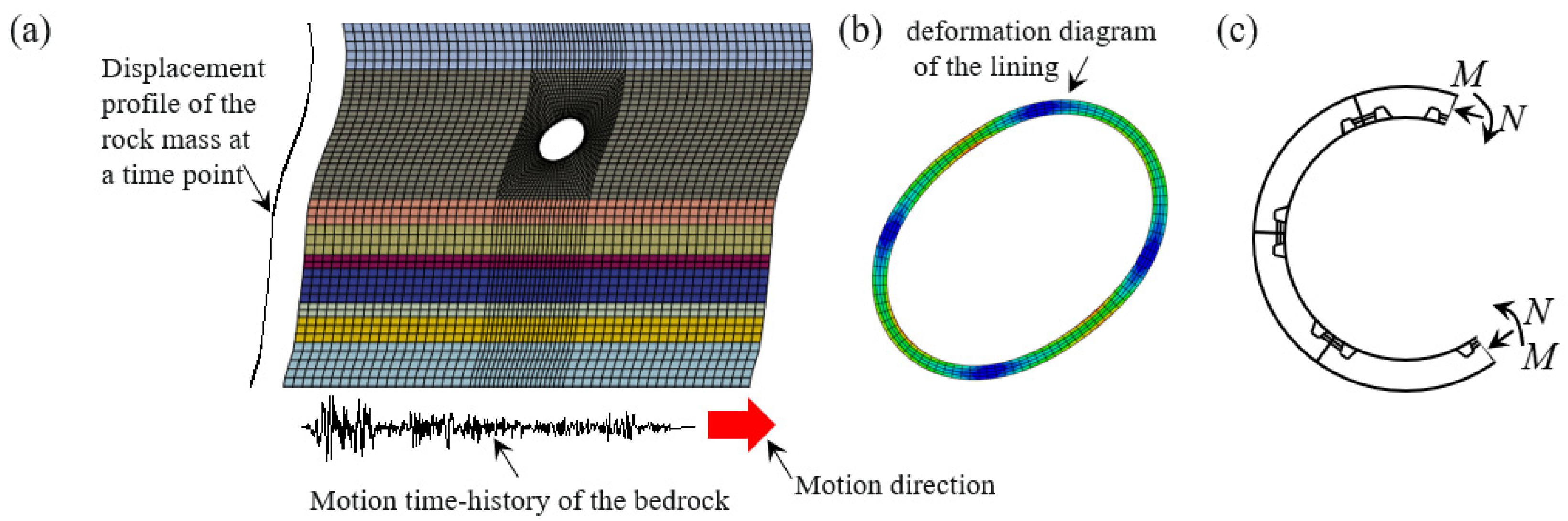
2.1. Characteristics of Longitudinal Joints to Seismic Loads
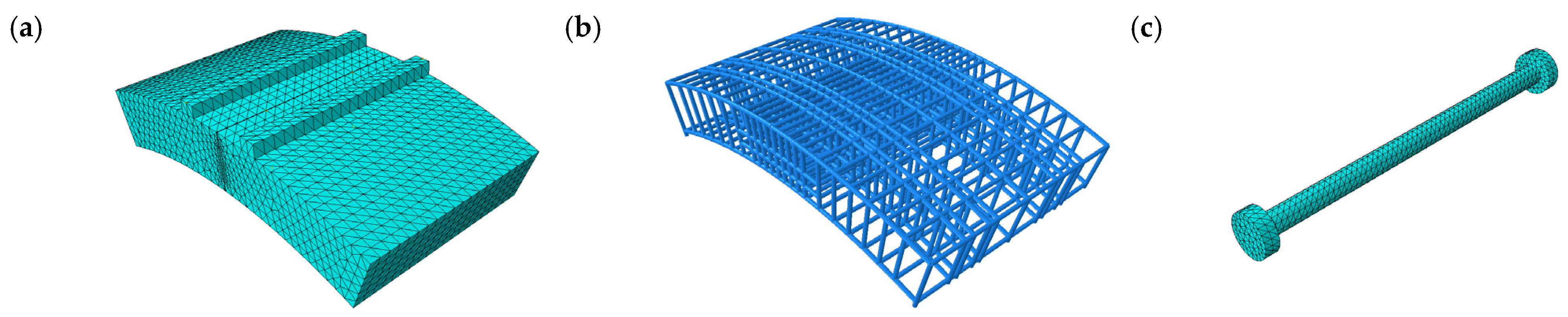
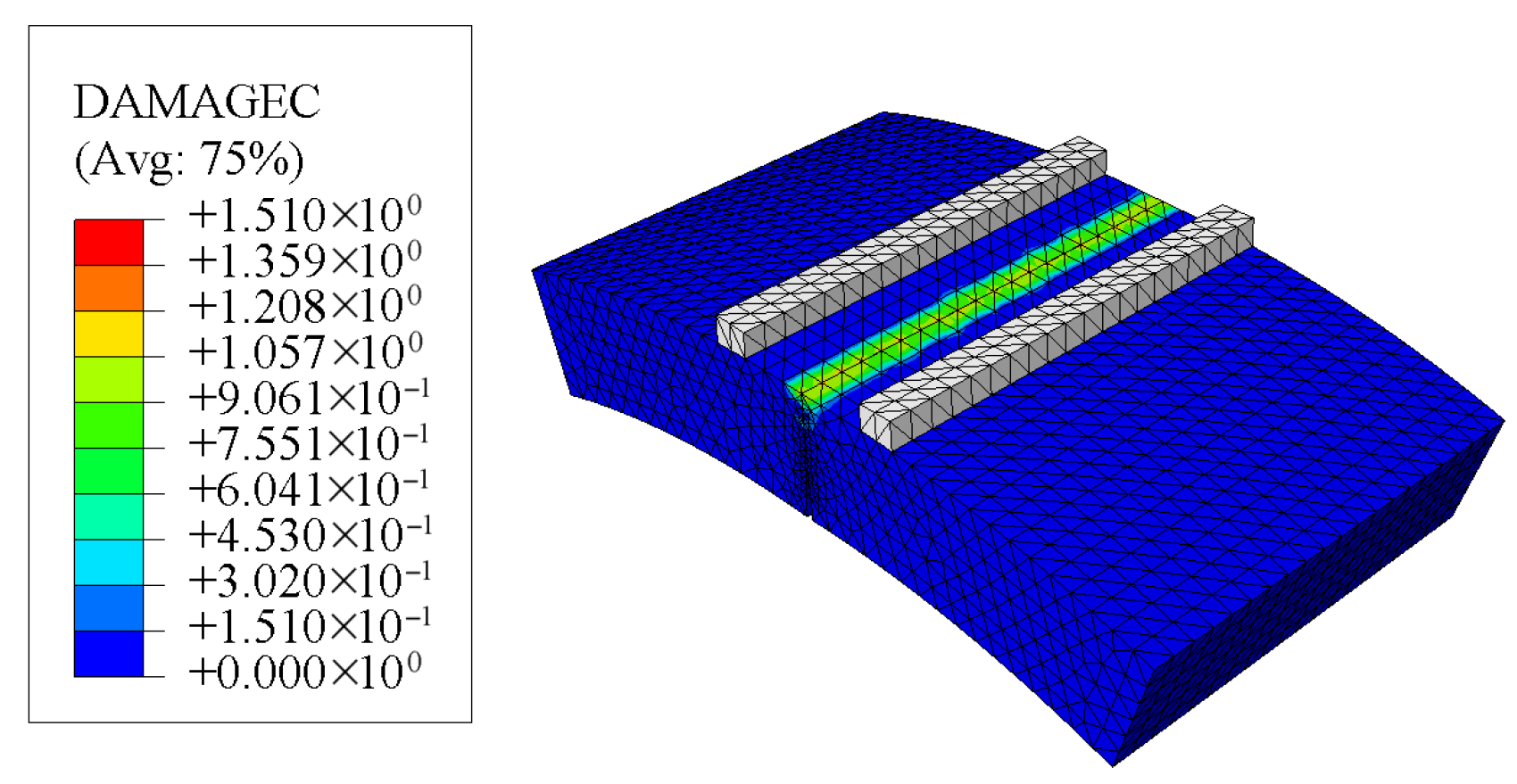
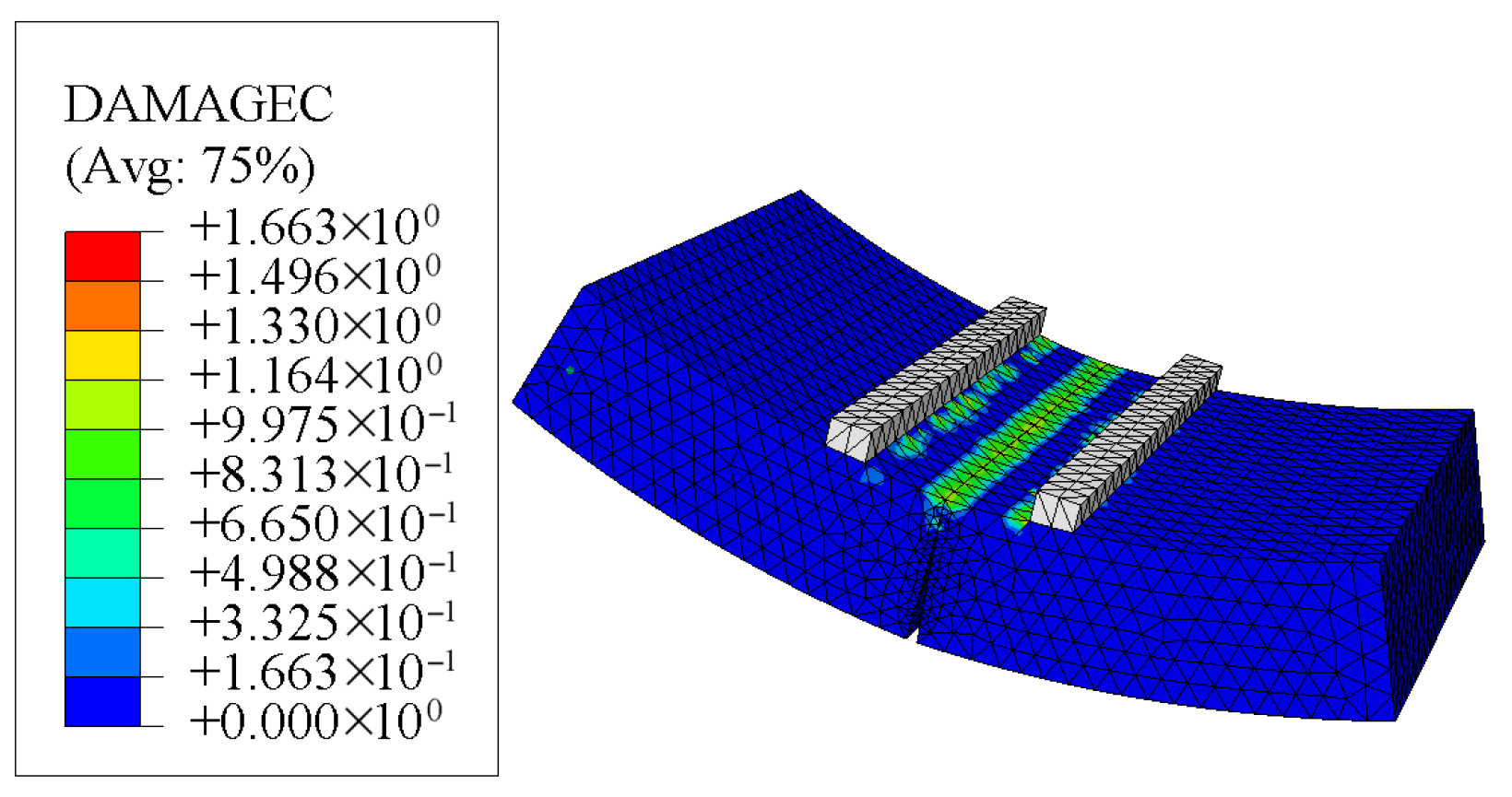
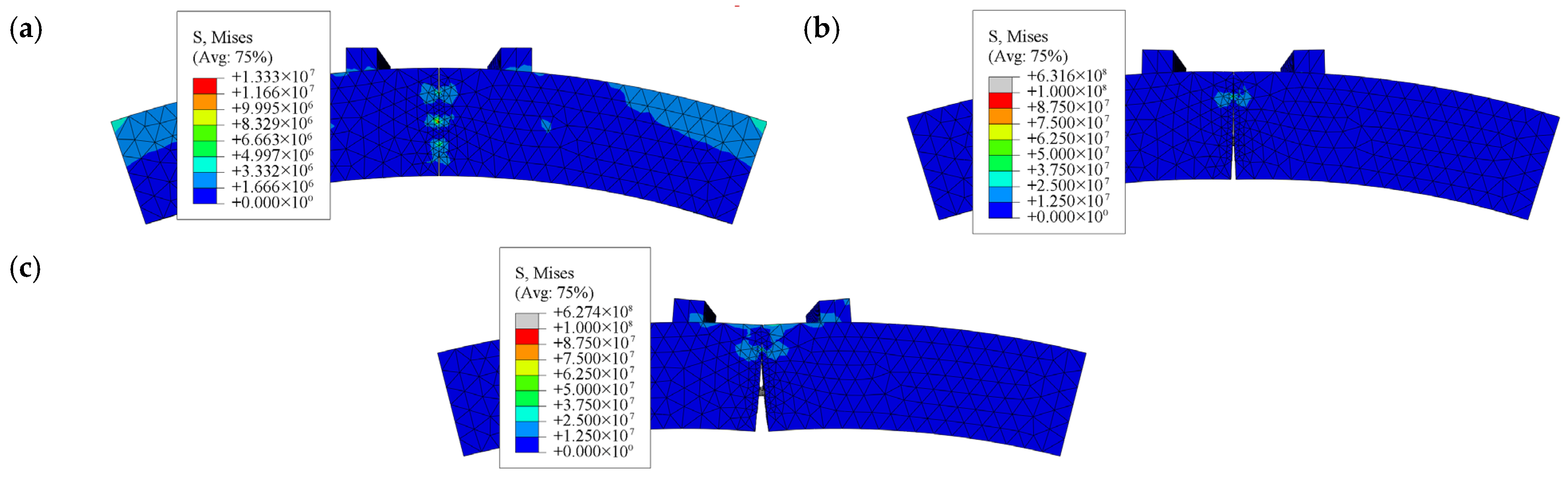
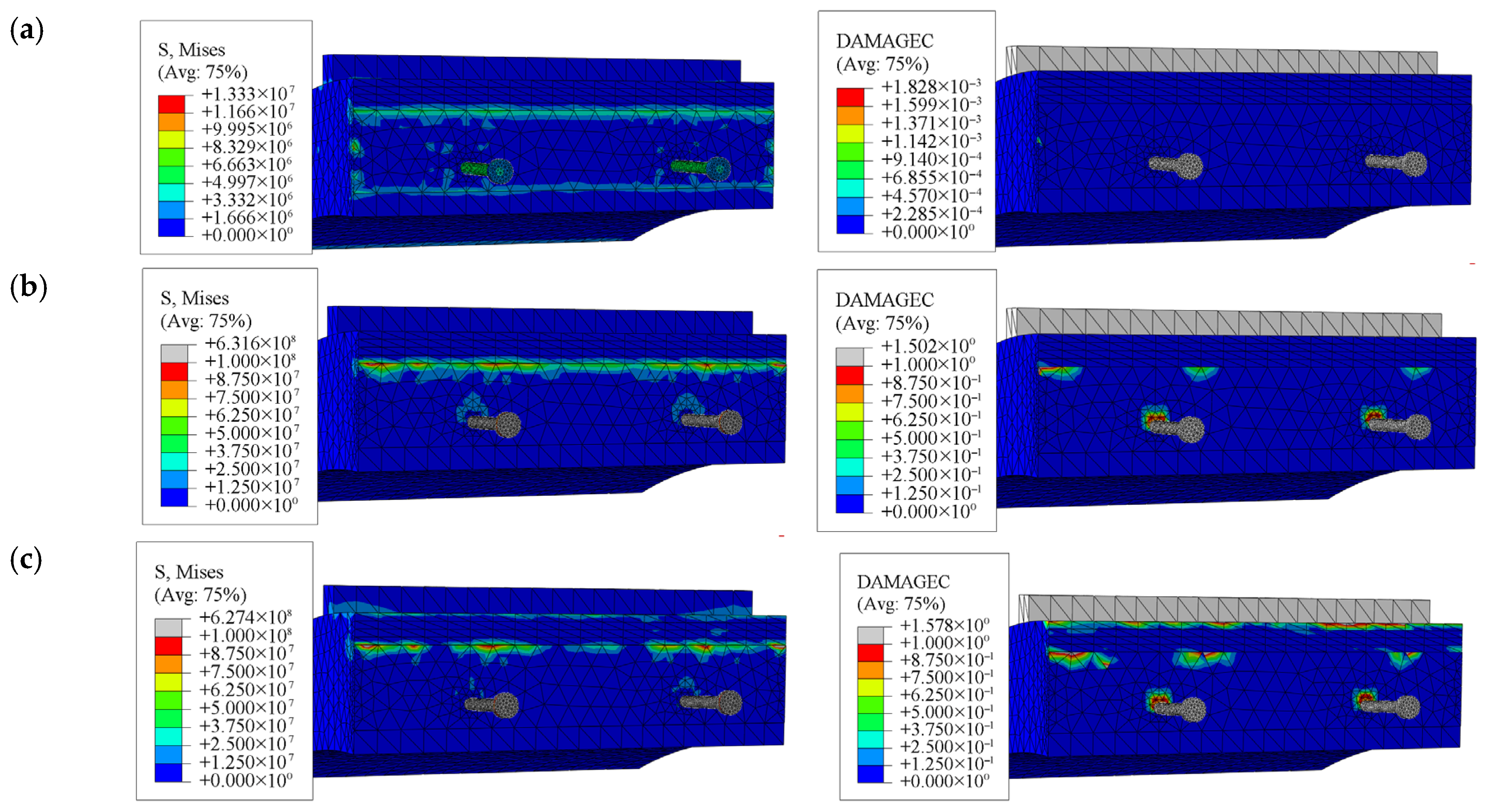
2.2. Numerical Simulation of Shield Tunnel Joints
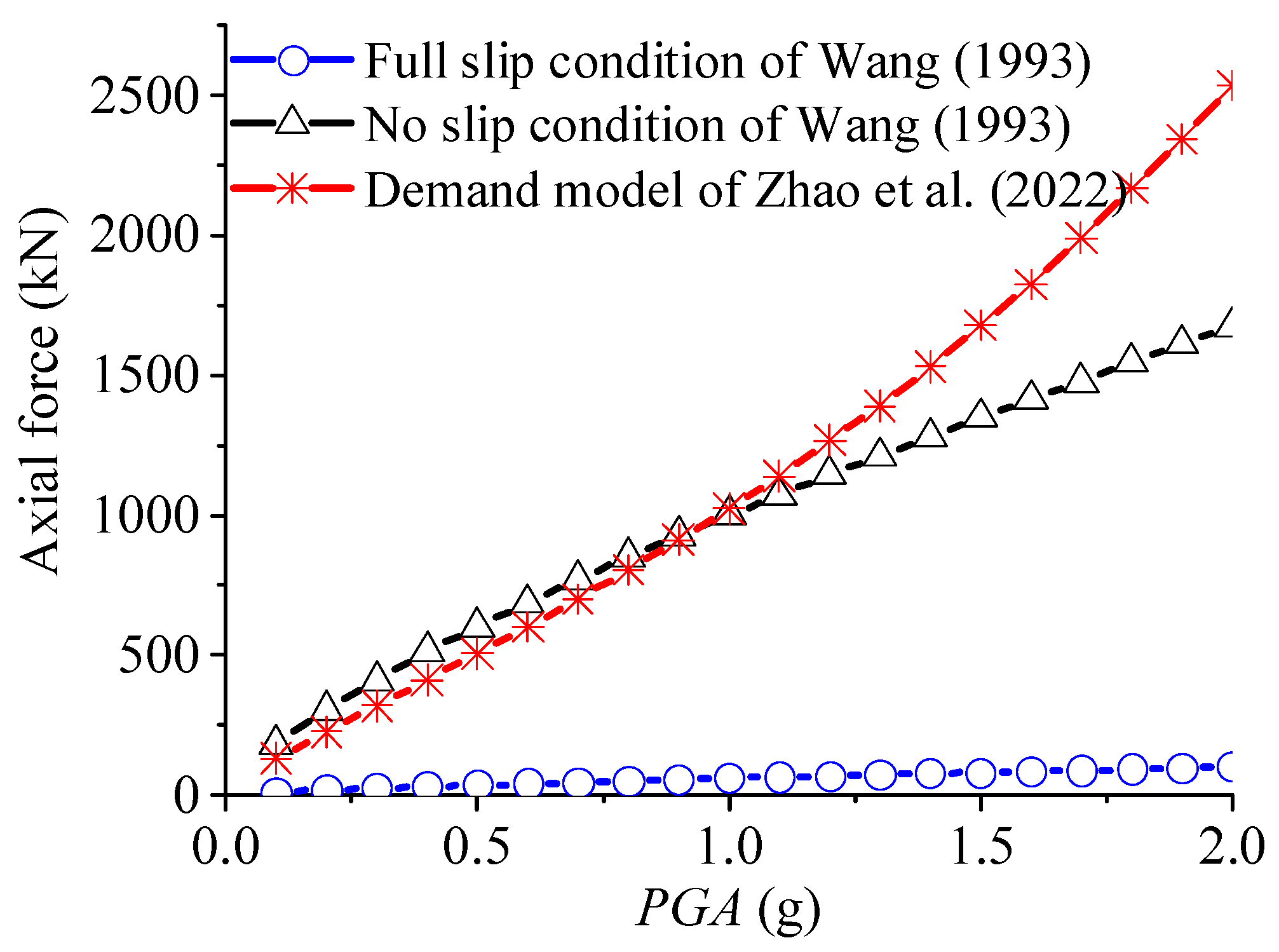
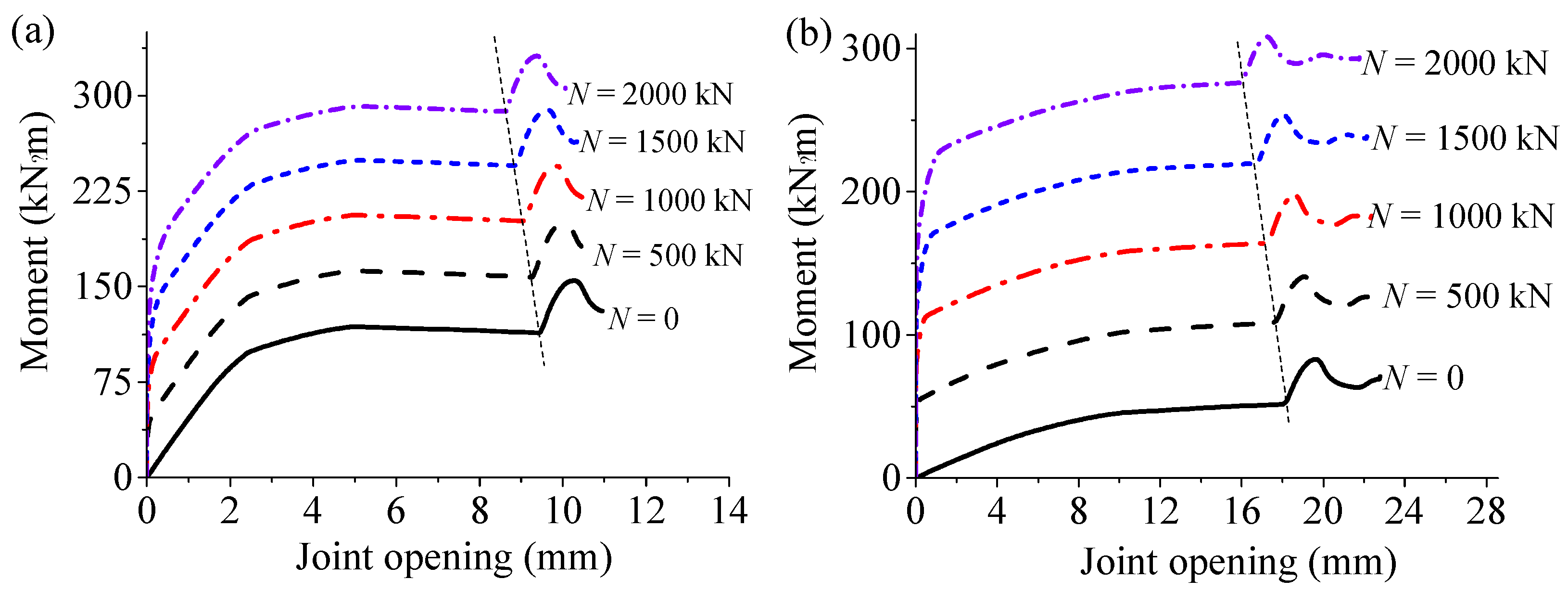
2.3. Mechanical Analysis of Tunnel Joints Based on Numerical Simulations
3. Flexural Capacity Probability Model for the Lining Joints
3.1. Probability Models Used in This Paper
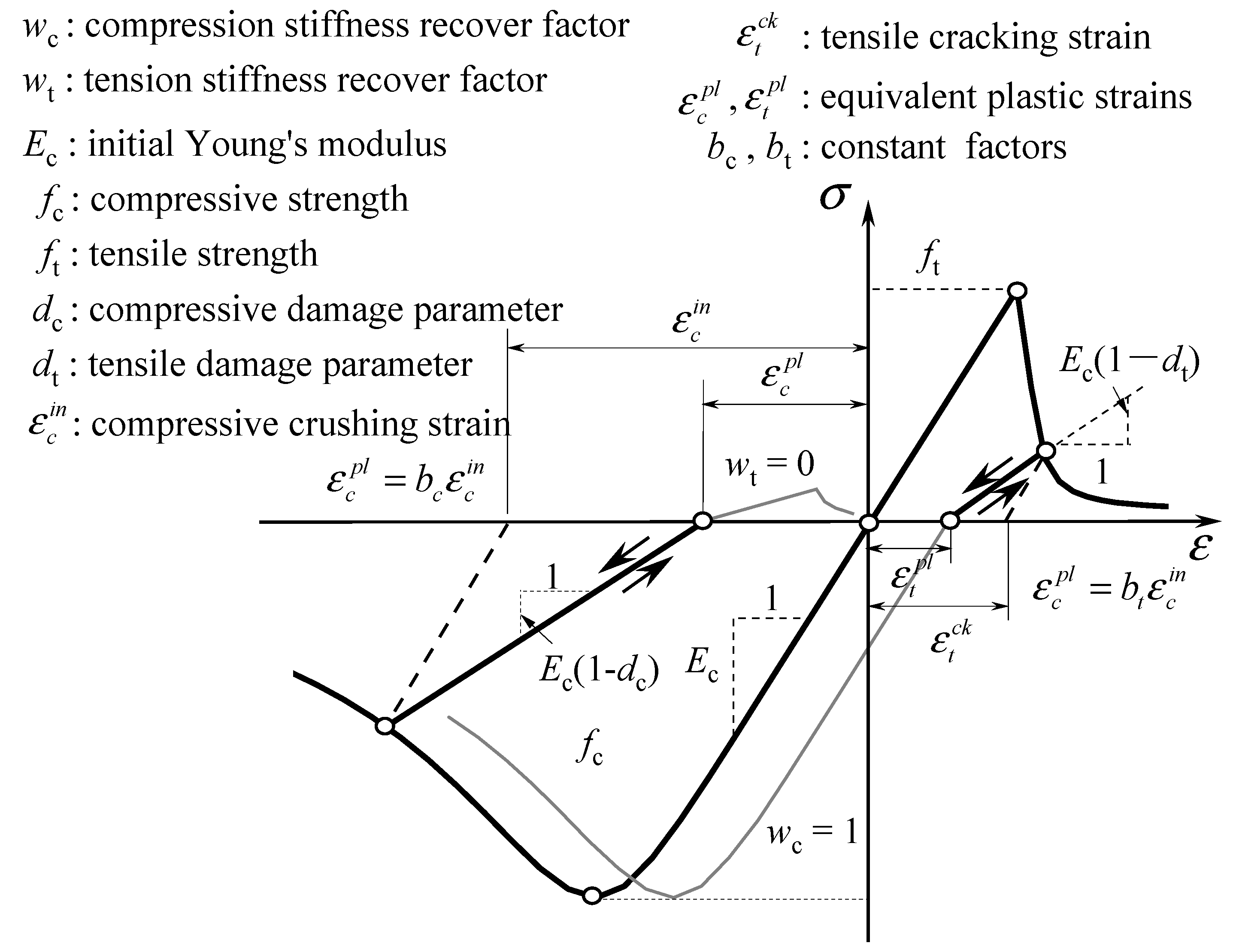
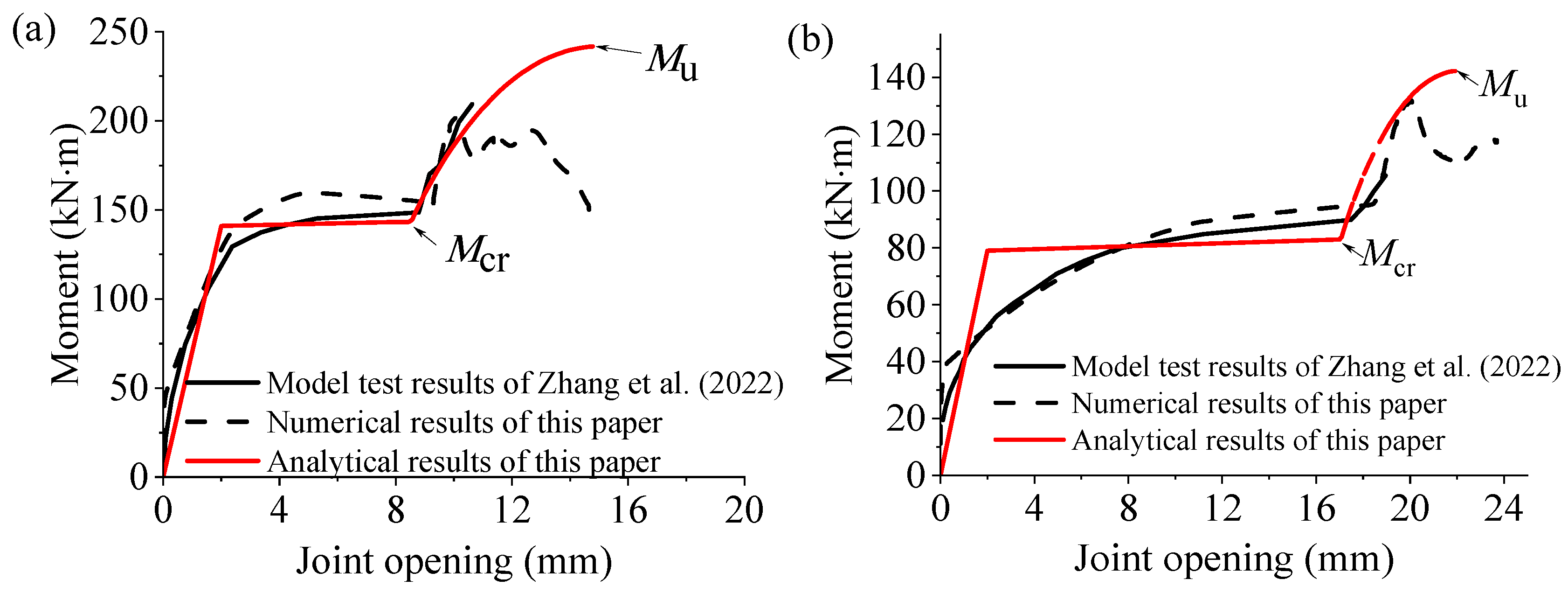
3.2. Deterministic Model Used in the Probability Model
3.3. Sample Points Generation Used for Model Calibration
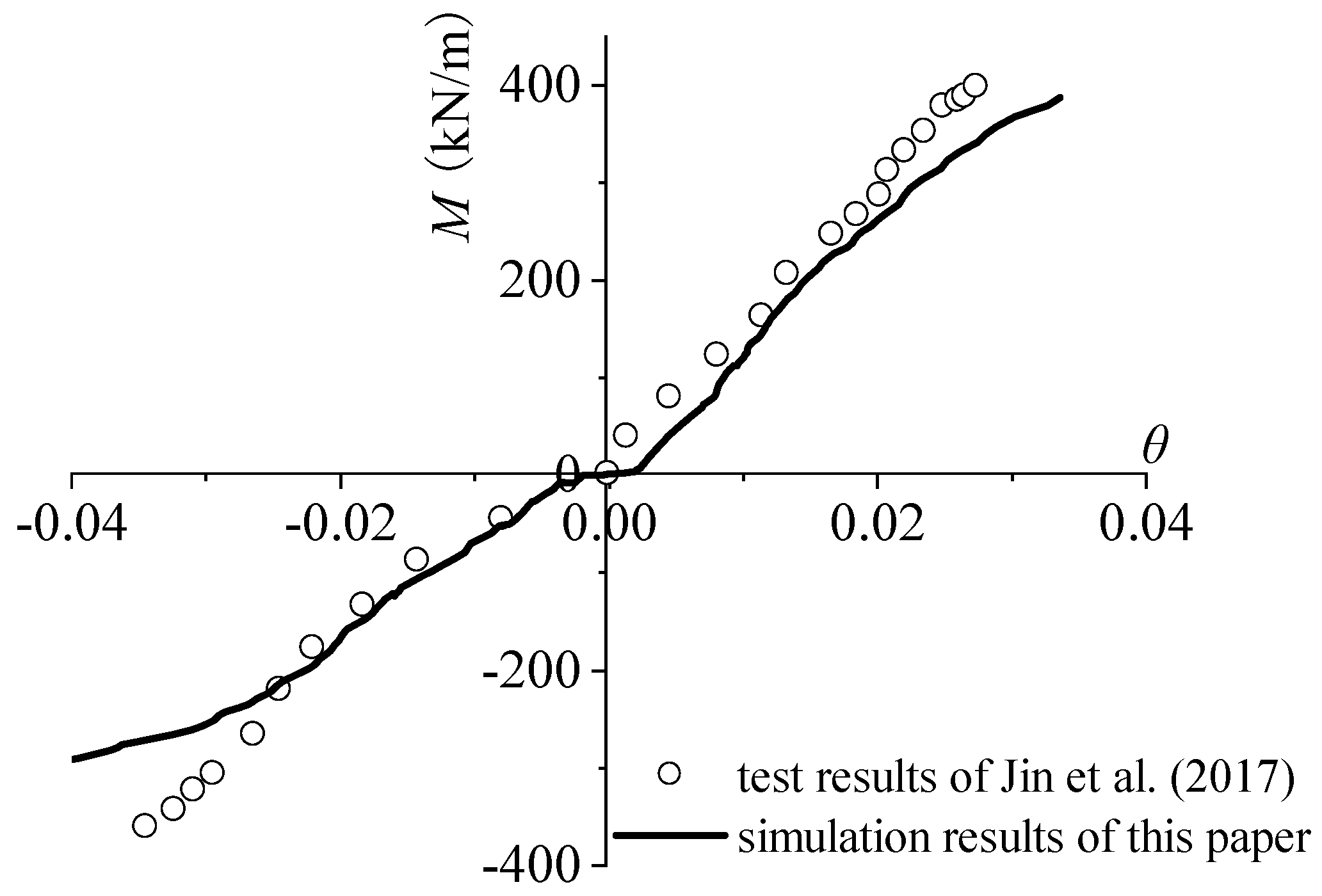
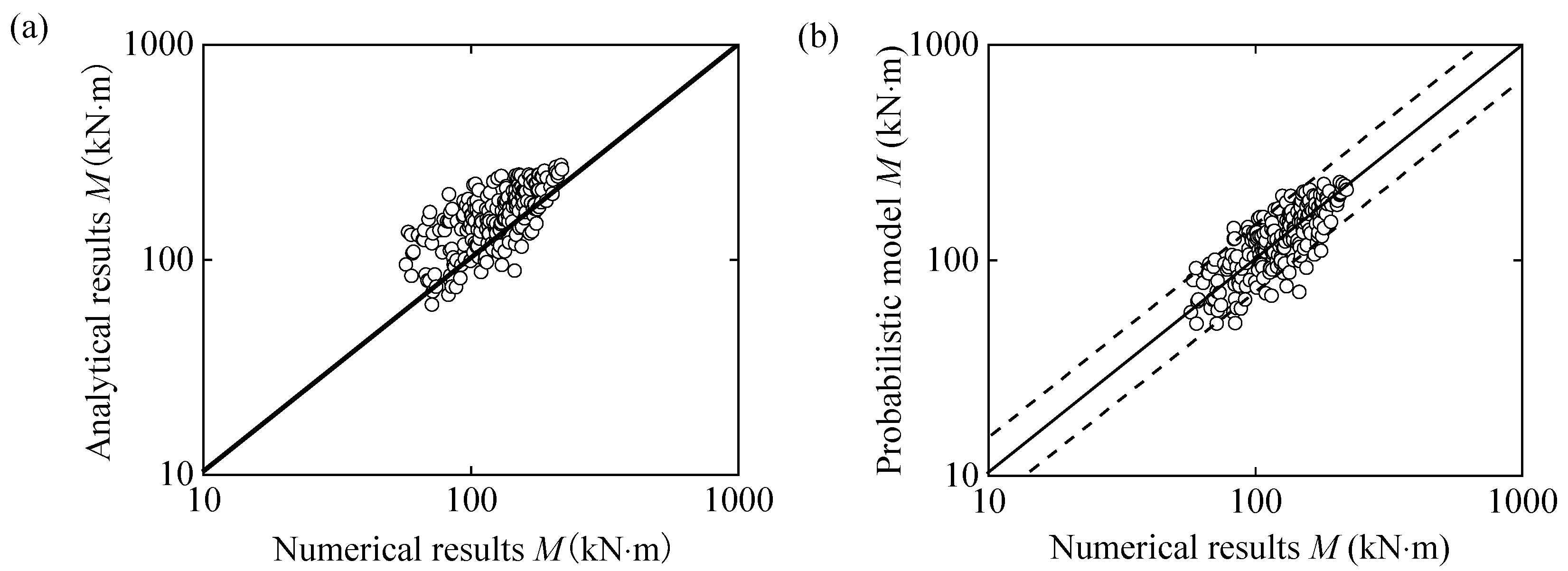
3.4. Model Optimization and Parameter Calibration
4. Seismic Fragility Analysis
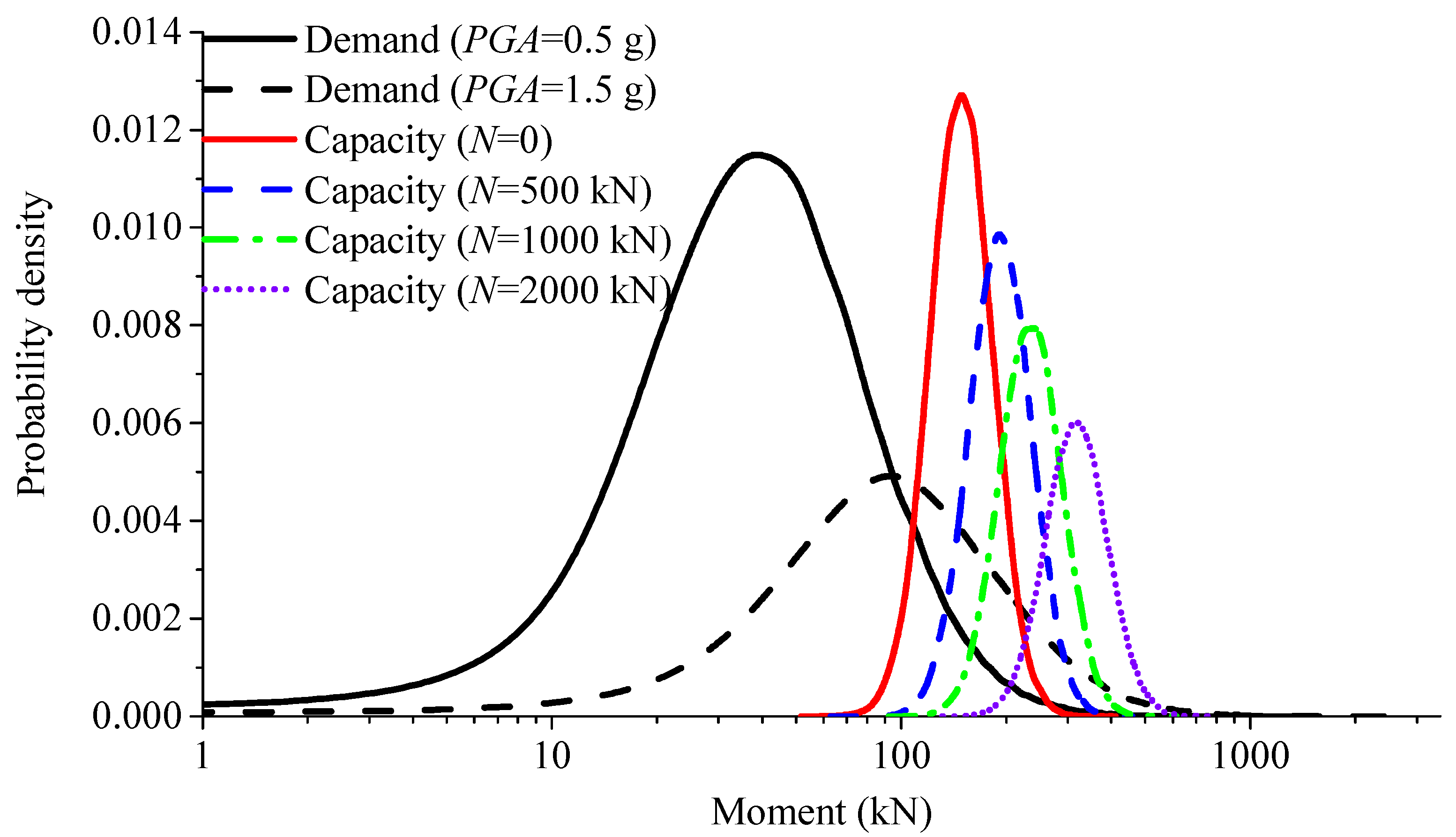
4.1. Fragility Calculation Method and Damage Index
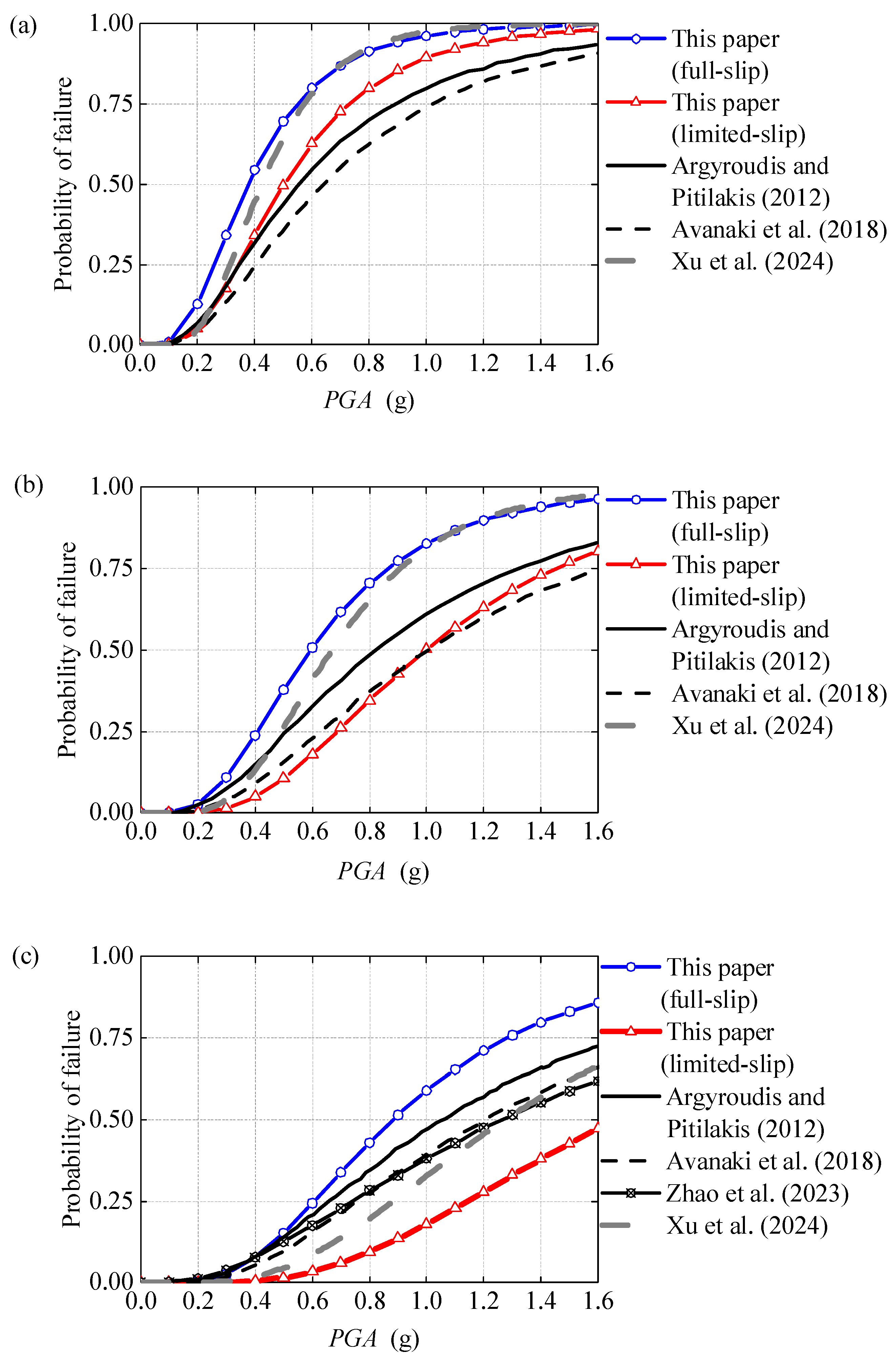
4.2. Fragility Curves and Comparisons with Previous Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Lai, J.; Yang, Y.; Zhou, J.; Shan, Y.; Cui, J. Seismic performance study of immersed tunnel with longitudinal limit device of flexible joint. Undergr. Space 2025, 20, 17–32. [Google Scholar] [CrossRef]
- Wang, T.T.; Kwok, O.L.A.; Jeng, F.S. Seismic response of tunnels revealed in two decades following the 1999 Chi-Chi earthquake (Mw 7.6) in Taiwan: A review. Eng. Geol. 2021, 287, 106090. [Google Scholar] [CrossRef]
- Jiang, X.; Zhu, H.; Yan, Z.; Zhang, F.; Ye, F.; Li, P.; Zhang, X.; Dai, Z.; Bai, Y.; Huang, B. A state-of-art review on development and progress of backfill grouting materials for shield tunneling. Dev. Built. Environ. 2023, 16, 100250. [Google Scholar] [CrossRef]
- Zhao, Z.; Cui, J.; Liu, C.; Liu, H.; ur Rehman, M.; Chen, W.; Peng, Z. Seismic damage characteristics of large-diameter shield tunnel lining under extreme-intensity earthquake. Soil Dyn. Earthq. Eng. 2023, 171, 107958. [Google Scholar] [CrossRef]
- Han, L.; Liu, H.; Zhang, W.; Ding, X.; Chen, Z.; Feng, L.; Wang, Z. Seismic behaviors of utility tunnel-soil system: With and without joint connections. Undergr. Space 2022, 7, 798–811. [Google Scholar] [CrossRef]
- Ye, Z.; Li, Y.; Li, L.; Xu, W.; Wu, H.; Miao, Y.; Liu, H. Seismic response of a long shield tunnel crossing through multiple soil deposits. Comput. Geotech. 2025, 177, 106892. [Google Scholar] [CrossRef]
- Feng, K.; He, C.; Qiu, Y.; Zhang, L.; Wang, W.; Xie, H.; Zhang, Y.; Cao, S. Full-scale tests on bending behavior of segmental joints for large underwater shield tunnels. Tunn. Undergr. Space Technol. 2018, 75, 100–116. [Google Scholar] [CrossRef]
- Shen, Y.; Zhong, Z.; Li, L.; Du, X.; El Naggar, M.H. Seismic response of shield tunnel structure embedded in soil deposit with liquefiable interlayer. Comput. Geotech. 2022, 152, 105015. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, L.; Tang, Z.; Mei, G. An improved theoretical method for assessing tunnel response to pre-excavation dewatering: Time-dependent deflection, internal force, joint opening, and dislocation. Comput. Geotech. 2025, 183, 107216. [Google Scholar] [CrossRef]
- Moayedi Far, A.; Nejati, H.R.; Goshtasbi, K.; Khosrotash, M.; Moosavi, S.A. Seismic Fragility Analysis for Probabilistic Risk Assessment of Underground Structures. J. Earthq. Eng. 2025, 29, 265–287. [Google Scholar] [CrossRef]
- Rajkumari, S.; Thakkar, K.; Goyal, H. Fragility analysis of structures subjected to seismic excitation: A state-of-the-art review. Structures 2022, 40, 303–316. [Google Scholar] [CrossRef]
- Zhu, J.; Zhao, G.; Xu, L.; Li, S. Probabilistic Seismic Demand Models of Circular Tunnels Subjected to Horizontal Ground Motions Based on 2D Dynamic Analyses. J. Earthq. Eng. 2023, 27, 4739–4760. [Google Scholar] [CrossRef]
- Shinozuka, M.; Feng, M.Q.; Lee, J.; Naganuma, T. Statistical analysis of fragility curves. J. Eng. Mech. 2000, 126, 1224–1231. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Pitilakis, K.D. Seismic fragility curves of shallow tunnels in alluvial deposits. Soil Dyn. Earthq. Eng. 2012, 35, 1–12. [Google Scholar] [CrossRef]
- Zhang, X.; Pan, Y.; Su, L.; Ou, E.; Liu, H.; Liu, C.; Cui, J. Seismic fragility assessment of shield tunnels in liquefiable soil-rock strata using fuzzy method for IM optimization. Tunn. Undergr. Space Technol. 2024, 152, 105957. [Google Scholar] [CrossRef]
- Liu, G.; Geng, P.; Wang, T.; Meng, Q.; Huo, F.; Wang, X.; Wang, J. Seismic vulnerability of shield tunnels in interbedded soil deposits: Case study of submarine tunnel in Shantou Bay. Ocean Eng. 2023, 286, 115500. [Google Scholar] [CrossRef]
- Xu, L.Y.; Xi, J.P.; Jiang, J.W.; Cai, F.; Sun, Y.J.; Chen, G.X. Seismic fragility analysis of shield tunnels in liquefiable layered deposits. Soil Dyn. Earthq. Eng. 2025, 191, 109246. [Google Scholar] [CrossRef]
- Shen, Y.; El Naggar, M.H.; Zhang, D.M.; Huang, Z.K.; Du, X. Scalar-and vector-valued seismic fragility assessment of segmental shield tunnel lining in liquefiable soil deposits. Tunn. Undergr. Space Technol. 2025, 155, 106171. [Google Scholar] [CrossRef]
- Avanaki, M.J.; Hoseini, A.; Vahdani, S.; de Santos, C.; de la Fuente, A. Seismic fragility curves for vulnerability assessment of steel fiber reinforced concrete segmental tunnel linings. Tunn. Undergr. Space Technol. 2018, 78, 259–274. [Google Scholar] [CrossRef]
- Yang, Q.; Geng, P.; Wang, L.; Liu, G.; Tang, R. Study on asphalt-cement isolation layer for shield tunnels using seismic fragility curves. J. Earthq. Eng. 2023, 27, 2338–2357. [Google Scholar] [CrossRef]
- Zhao, G.; Gardoni, P.; Xu, L.; Xie, L. Seismic probabilistic capacity models and fragility estimates for the transversal lining section of circular tunnels. J. Earthq. Eng. 2023, 27, 1281–1301. [Google Scholar] [CrossRef]
- Andreotti, G.; Calvi, G.M.; Soga, K.; Gong, C.; Ding, W. Cyclic model with damage assessment of longitudinal joints in segmental tunnel linings. Tunn. Undergr. Space Technol. 2020, 103, 103472. [Google Scholar] [CrossRef]
- Wang, J.; Huang, W.; Xu, R.; Yang, Z.; Xu, R. Analytical approach for circular-jointed shield tunnel lining based on the state space method. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 575–595. [Google Scholar] [CrossRef]
- Zhang, L.; Feng, K.; Li, M.; Sun, Y.; He, C.; Xiao, M. Analytical method regarding compression-bending capacity of segmental joints: Theoretical model and verification. Tunn. Undergr. Space Technol. 2019, 93, 103083. [Google Scholar] [CrossRef]
- Huang, W.M.; Wang, J.C.; Yang, Z.X.; Xu, R.Q. Analytical model for segmental tunnel lining with nonlinear joints. Tunn. Undergr. Space Technol. 2021, 114, 103994. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X. Analytical model regarding compression-bending capacity of segmental joint reinforced by steel plate. Undergr. Space 2025, 20, 157–173. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, R.; Li, Z.; Kang, C.; El Naggar, M.H.; Xiao, M.; Wu, W. Analytical solution for longitudinal deformation of shield tunnel induced by overcrossing tunnelling considering circumferential joints. J. Rock Mech. Geotech. Eng. 2023, 15, 2355–2374. [Google Scholar] [CrossRef]
- Zhao, G.; Gardoni, P.; Xu, L.; Shu, F.; Xie, L. Probabilistic seismic demand models for circular tunnels subjected to transversal seismic load. Tunn. Undergr. Space Technol. 2022, 25, 104527. [Google Scholar] [CrossRef]
- Jin, Y.; Ding, W.; Yan, Z.; Soga, K.; Li, Z. Experimental investigation of the nonlinear behavior of segmental joints in a water-conveyance tunnel. Tunn. Undergr. Space Technol. 2017, 68, 153–166. [Google Scholar] [CrossRef]
- Zhang, D.M.; Zhang, B.L.; Luo, T.L.; Zhang, D.M.; Li, B.J. Full-scale testing and numerical modelling of segmental-joint performance with corroded bolt. Tunn. Undergr. Space Technol. 2022, 119, 104260. [Google Scholar] [CrossRef]
- GB-50010; Code for Design of Concrete Structures. China Architecture and Building Press: Beijing, China, 2010.
- Chen, L.; Graybeal, B.A. Modeling Structural Performance of Ultrahigh Performance Concrete I-Girders. J. Bridge Eng. 2012, 17, 754–764. [Google Scholar] [CrossRef]
- Bahij, S.; Adekunle, S.K.; Al-Osta, M.; Al-Dulaijan, S.U.; Rahman, M.K. Numerical investigation of the shear behavior of reinforced ultra-high-performance concrete beams. Struct. Concr. 2018, 19, 305–317. [Google Scholar] [CrossRef]
- Birtel, V.; Mark, P. Parameterised finite element modelling of RC beam shear failure. In Proceedings of the ABAQUS Users’ Conference, Cambridge, MA, USA, 23 May 2006; pp. 95–108. [Google Scholar]
- Gardoni, P.; Der Kiureghian, A.; Mosalam, K.M. Probabilistic capacity models and fragility estimates for reinforced concrete columns based on experimental observations. J. Eng. Mech. 2002, 128, 1024–1038. [Google Scholar] [CrossRef]
- Fang, K.T. Uniform design: Application of number-theoretic methods in experimental design. Acta Math. Appl. Sin. 1980, 3, 363–372. [Google Scholar]
- Wang, Y.; Fang, K.T. A note on uniform distribution and experimental design. Chin. Sci. Bull. 1981, 26, 485–489. [Google Scholar]
- Hashash, Y.M.; Hook, J.J.; Schmidt, B.; John, I.; Yao, C. Seismic design and analysis of underground structures. Tunn. Undergr. Space Technol. 2001, 16, 247–293. [Google Scholar] [CrossRef]
- Wang, J.N. Seismic Design of Tunnels: A State-of-the-Art Approach; Parsons Brinckerhoff Inc.: New York, NY, USA, 1993. [Google Scholar]
- Xu, L.; Zhu, J.; Zhao, G.; Li, S. Probabilistic seismic capacity models for circular tunnels at different performance levels. Comput. Geotech. 2024, 165, 105906. [Google Scholar] [CrossRef]
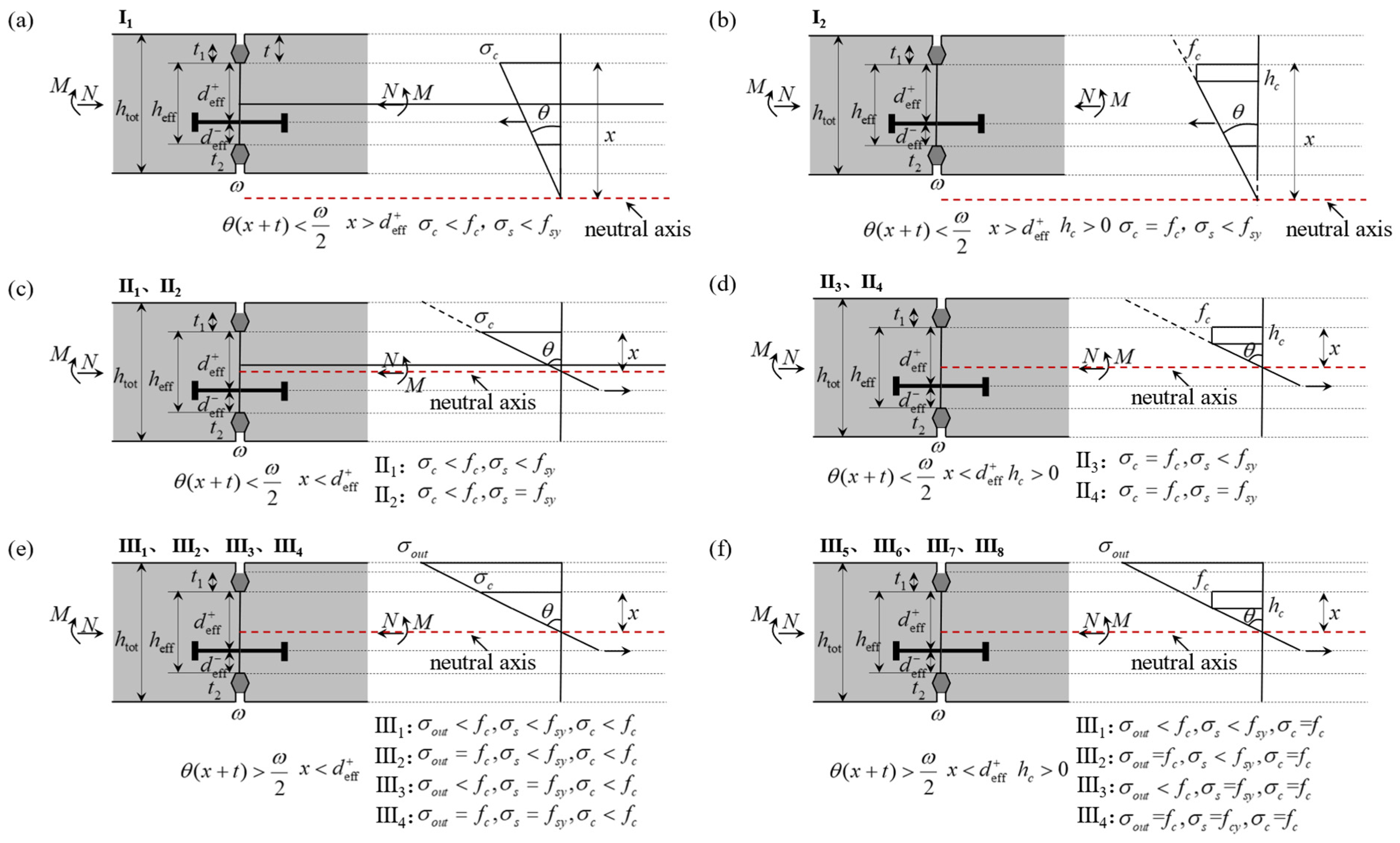
| States | Criteria | Static Equilibrium Equation | |
|---|---|---|---|
| I | I1 | σc < fc, σs < fsy | |
| I2 | σc = fc, σs < fsy | ||
| II | II1 | σc < fc, σs < fsy | |
| II2 | σc < fc, σs = fsy | ||
| II3 | σc = fc, σs < fsy | ||
| II4 | σc = fc, σs = fsy | ||
| III | III1 | σout < fc, σc < fc, σs < fsy | |
| III2 | σout = fc, σc < fc, σs < fsy | ||
| III3 | σout < fc, σc < fc, σs = fsy | ||
| III4 | σout = fc, σc < fc, σs = fsy | ||
| III5 | σout < fc, σc = fc, σs < fsy | ||
| III6 | σout = fc, σc = fc, σs < fsy | ||
| III7 | σout < fc, σc = fc, σs = fsy | ||
| III8 | σout = fc, σc = fc, σs = fsy | ||
| NO. | Concrete Grade | Diameter of Bolt (mm) | Bolt Grade | Axial Force (kN) |
|---|---|---|---|---|
| 1 | C40 | 20 | 9.8 | 1200 |
| 2 | C45 | 26 | 5.8 | 1100 |
| 3 | C50 | 32 | 4.6 | 1100 |
| 4 | C55 | 18 | 10.9 | 900 |
| 5 | C60 | 24 | 6.8 | 800 |
| 6 | C65 | 30 | 4.8 | 700 |
| 7 | C70 | 16 | 12.9 | 600 |
| 8 | C75 | 22 | 8.8 | 500 |
| 9 | C80 | 28 | 5.6 | 400 |
| Physical Quantities | Physical or Mechanical Meaning |
|---|---|
| r | Lining radius |
| t | Lining thickness |
| Ec | Concrete elastic modulus |
| fc | Concrete strength |
| rs | Bolt diameter |
| fsy | Bolt yield strength |
| fsu | Bolt tensile strength |
| N | Axial force level |
| 1 | Constant term |
| Parameters | Mean Value | Standard Deviation | Correlation Coefficient | ||||
|---|---|---|---|---|---|---|---|
| θ1 | θfsy | θfsu | θN | σ | |||
| θ1 | −0.21 | 0.010 | 1 | ||||
| θfsy | 2.1 × 10−9 | 2.35 × 10−10 | −0.021 | 1 | |||
| θfsu | −1.97 × 10−9 | 2.04 × 10−10 | −0.032 | −0.884 | 1 | ||
| θN | 2.32 × 10−7 | 4.26 × 10−8 | 0.124 | 0.432 | −0.542 | 1 | |
| σ | 0.204 | 0.011 | 0.006 | −0.010 | 0.009 | 0.011 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Yang, Z.; Zhu, J.; Lin, S.; Wang, Y. Seismic Fragility Analysis of Shield Tunnels Considering the Flexural Capacity of Longitudinal Joints. Buildings 2025, 15, 4265. https://doi.org/10.3390/buildings15234265
Zhao G, Yang Z, Zhu J, Lin S, Wang Y. Seismic Fragility Analysis of Shield Tunnels Considering the Flexural Capacity of Longitudinal Joints. Buildings. 2025; 15(23):4265. https://doi.org/10.3390/buildings15234265
Chicago/Turabian StyleZhao, Guochen, Zheng Yang, Jingzhou Zhu, Shibin Lin, and Yujin Wang. 2025. "Seismic Fragility Analysis of Shield Tunnels Considering the Flexural Capacity of Longitudinal Joints" Buildings 15, no. 23: 4265. https://doi.org/10.3390/buildings15234265
APA StyleZhao, G., Yang, Z., Zhu, J., Lin, S., & Wang, Y. (2025). Seismic Fragility Analysis of Shield Tunnels Considering the Flexural Capacity of Longitudinal Joints. Buildings, 15(23), 4265. https://doi.org/10.3390/buildings15234265





