Physics-Informed Multi-Task Neural Network (PINN) Learning for Ultra-High-Performance Concrete (UHPC) Strength Prediction
Abstract
1. Introduction
2. Dataset
2.1. Source and Coverage
2.2. Composition and Split
2.3. Data Harmonization, Imputation, and Quality Control
3. Methodology
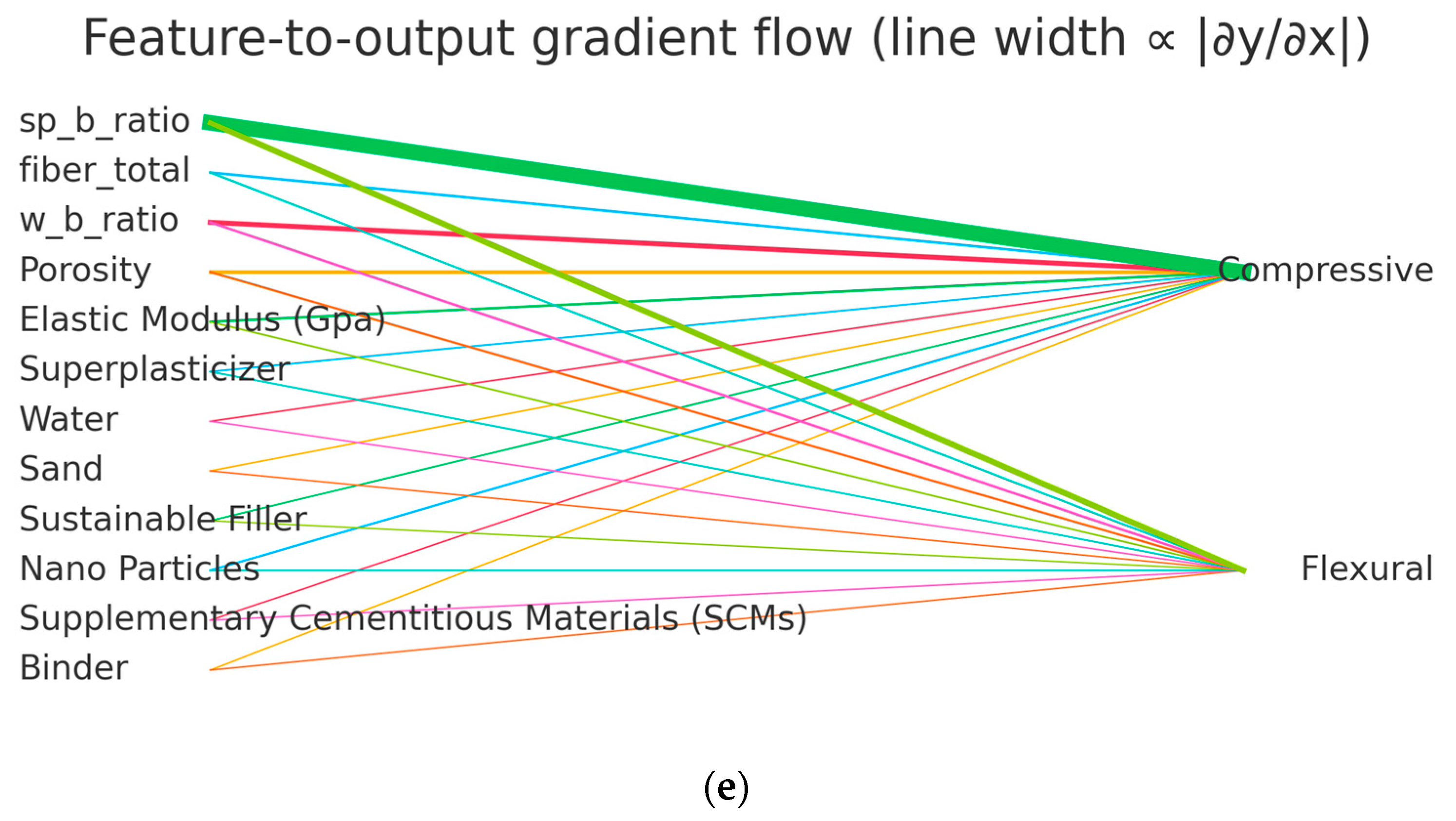
3.1. Data Preparation and Feature Engineering
3.2. Analytical Modeling
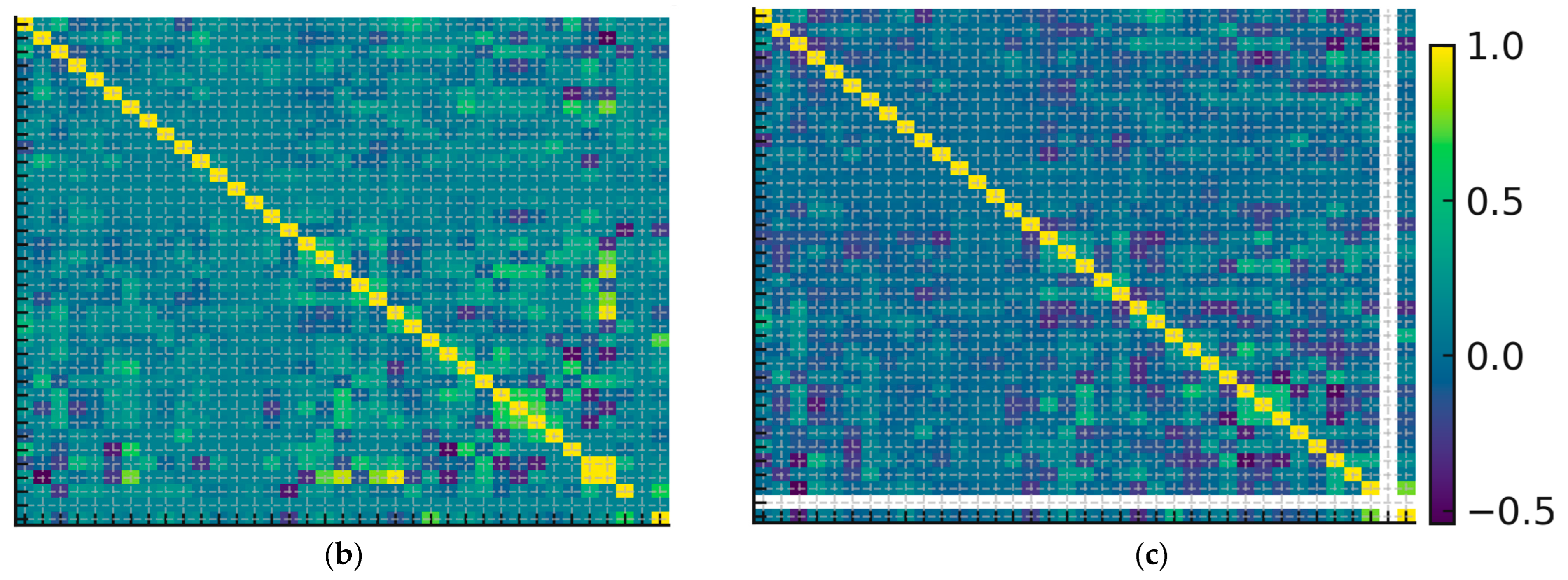
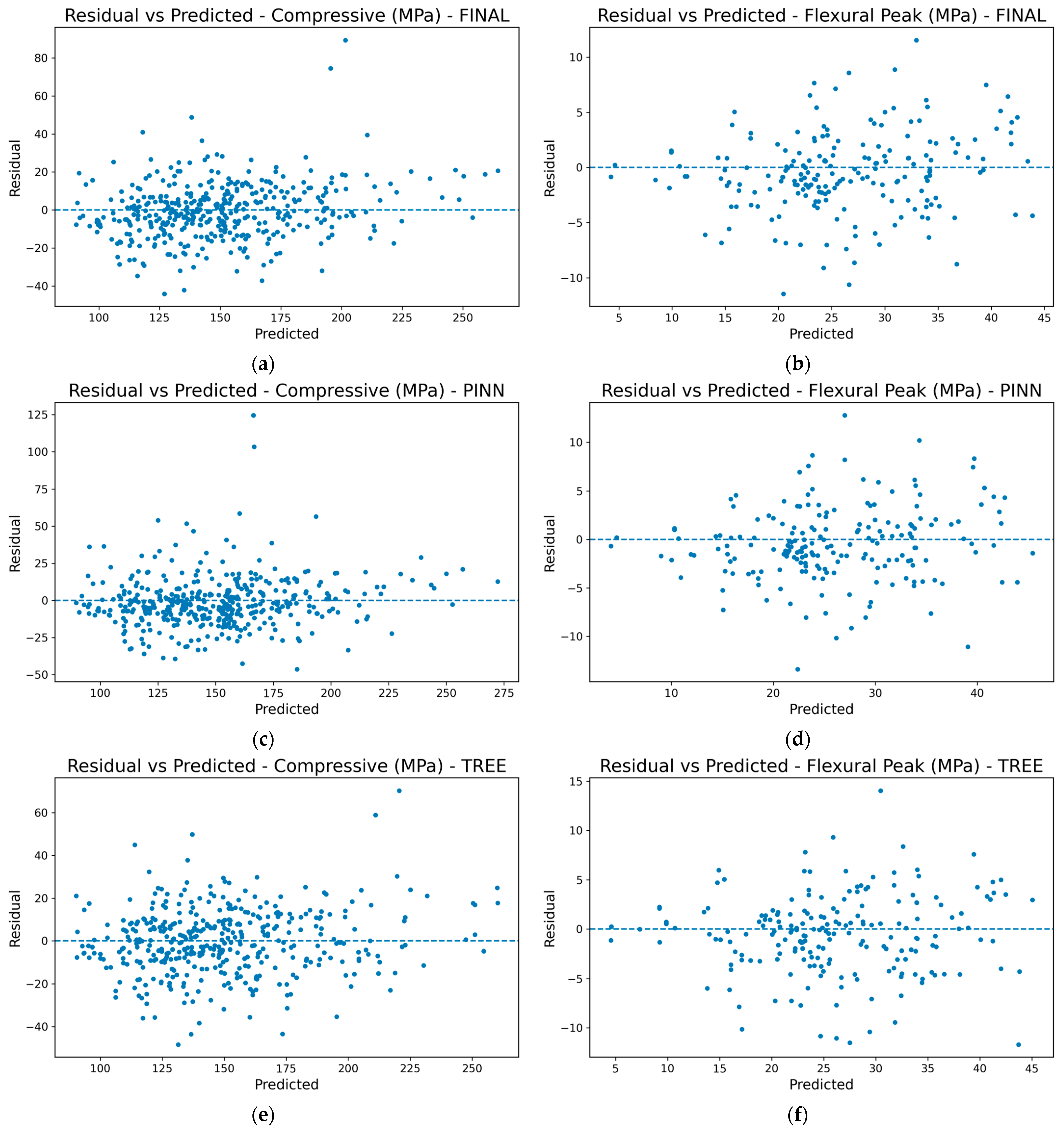
3.3. Evaluation and Residual Analysis
4. Results
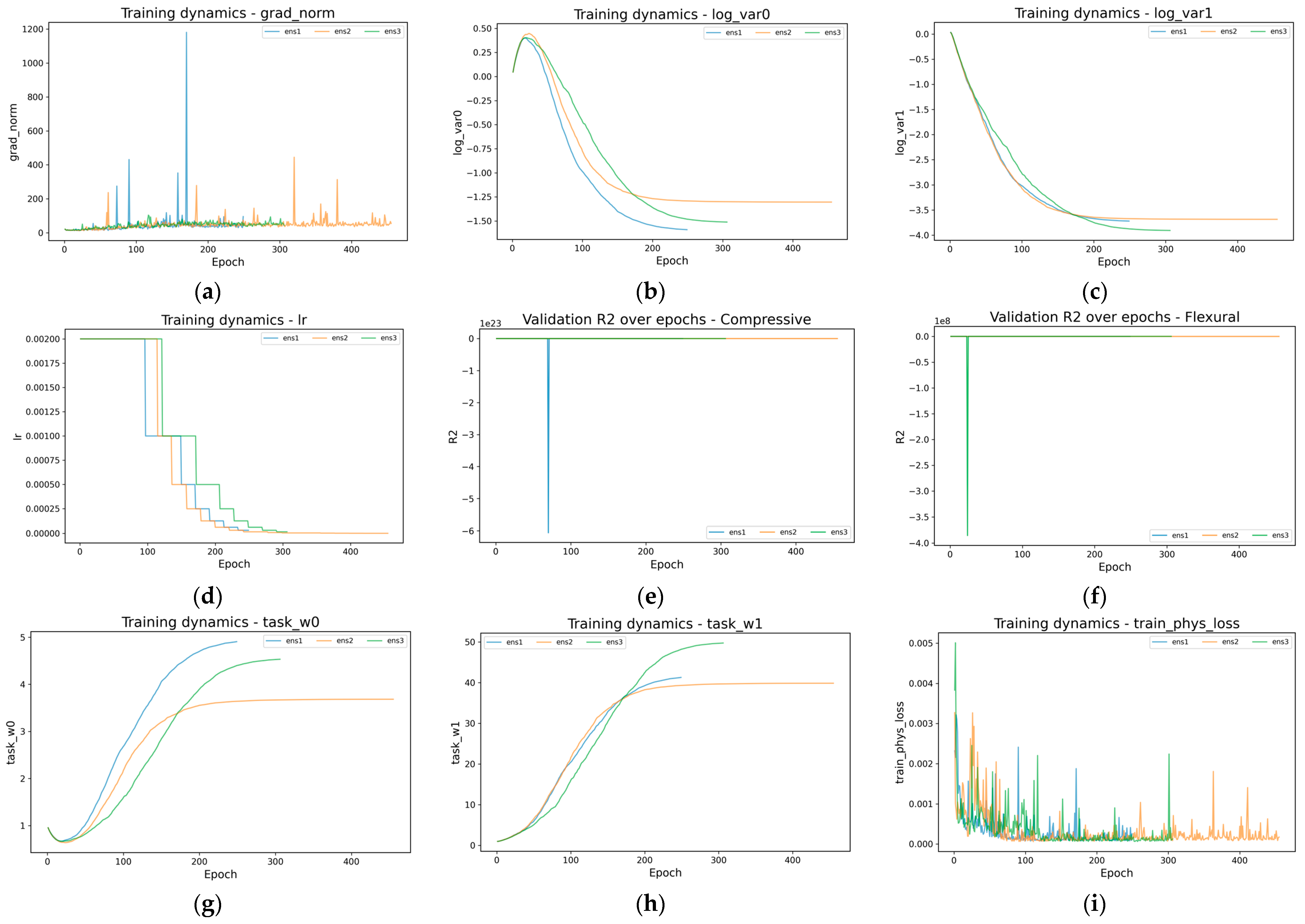
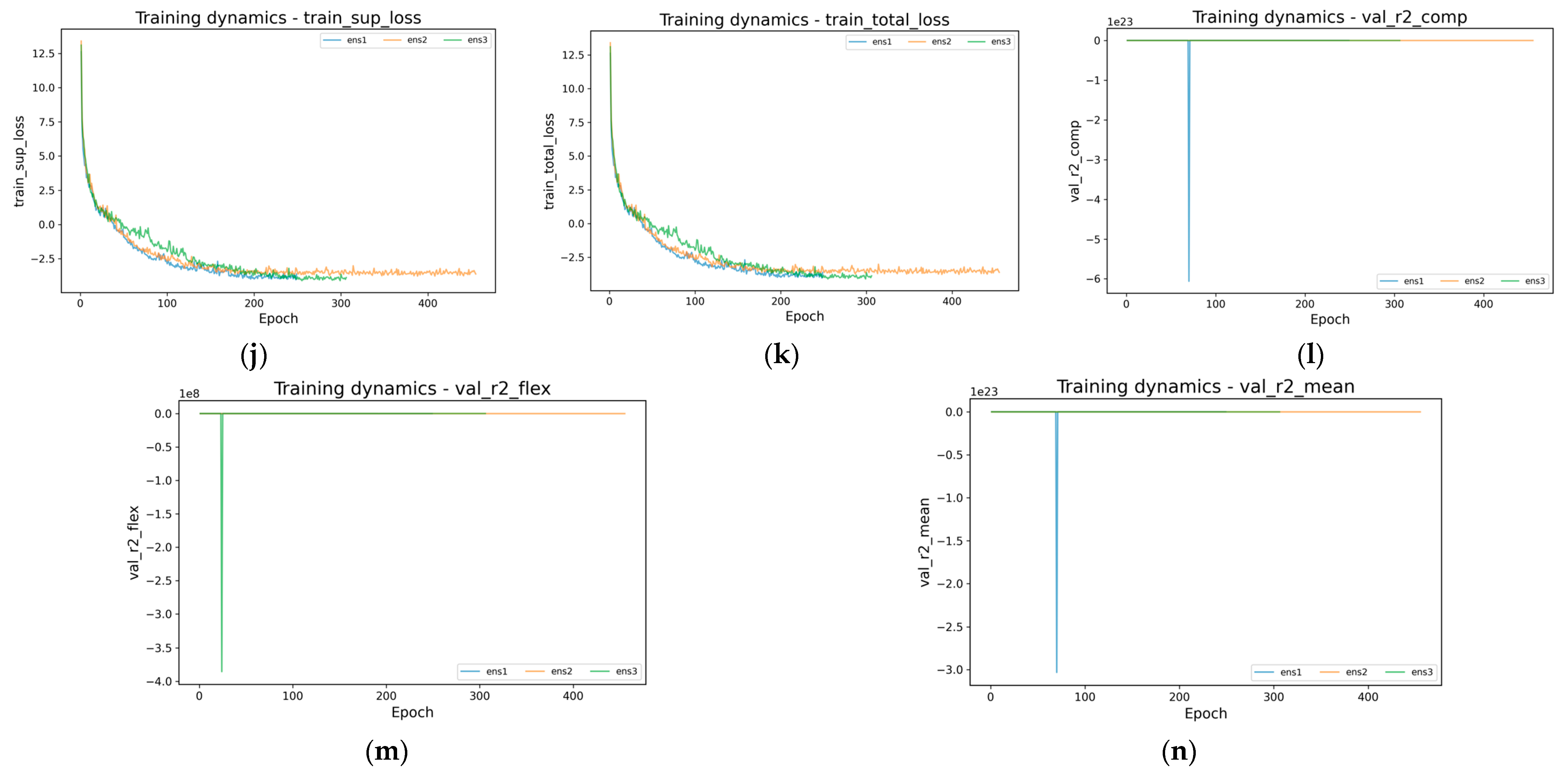
4.1. Training Process
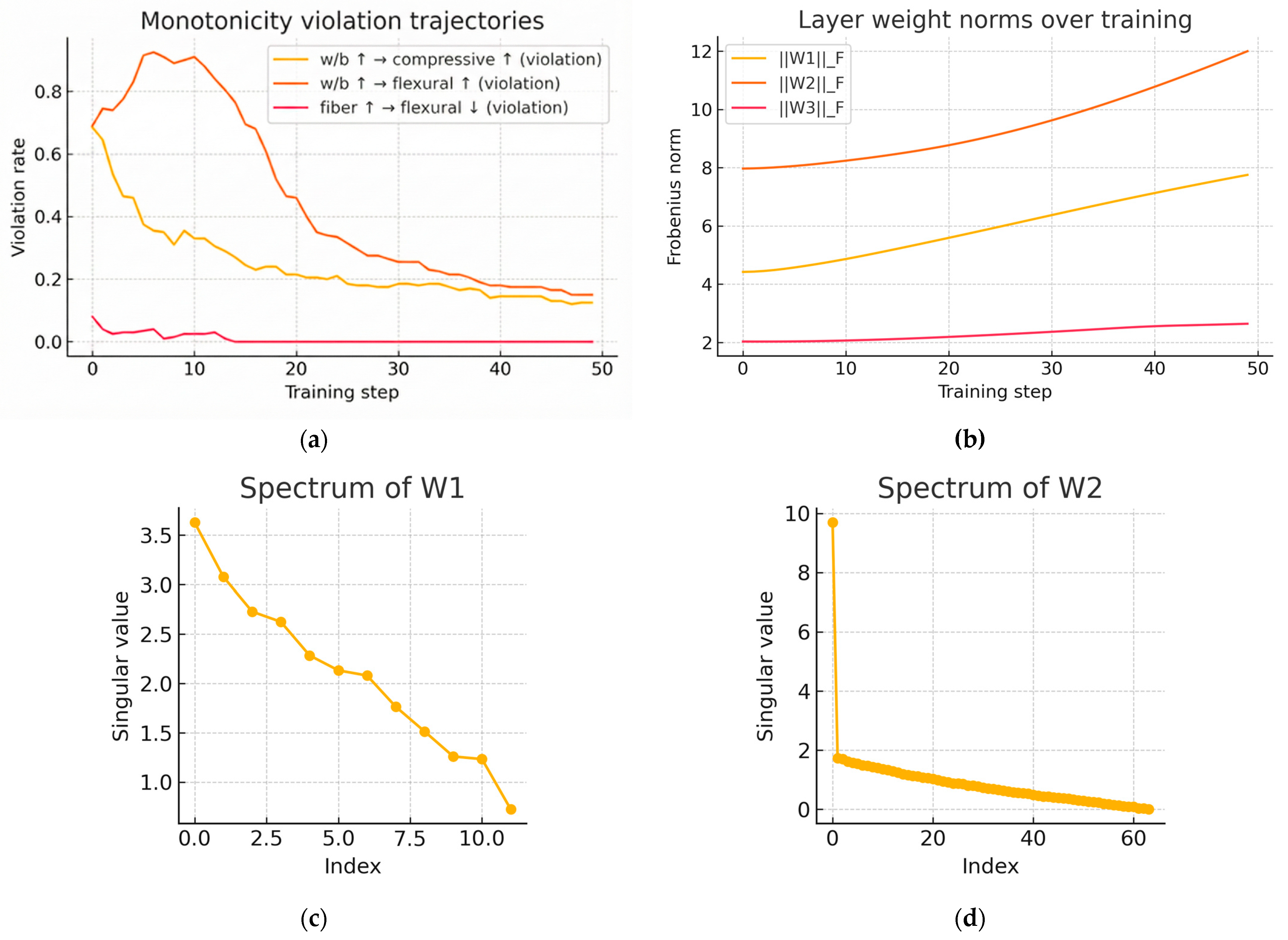
4.2. Physical Parameter Evolution
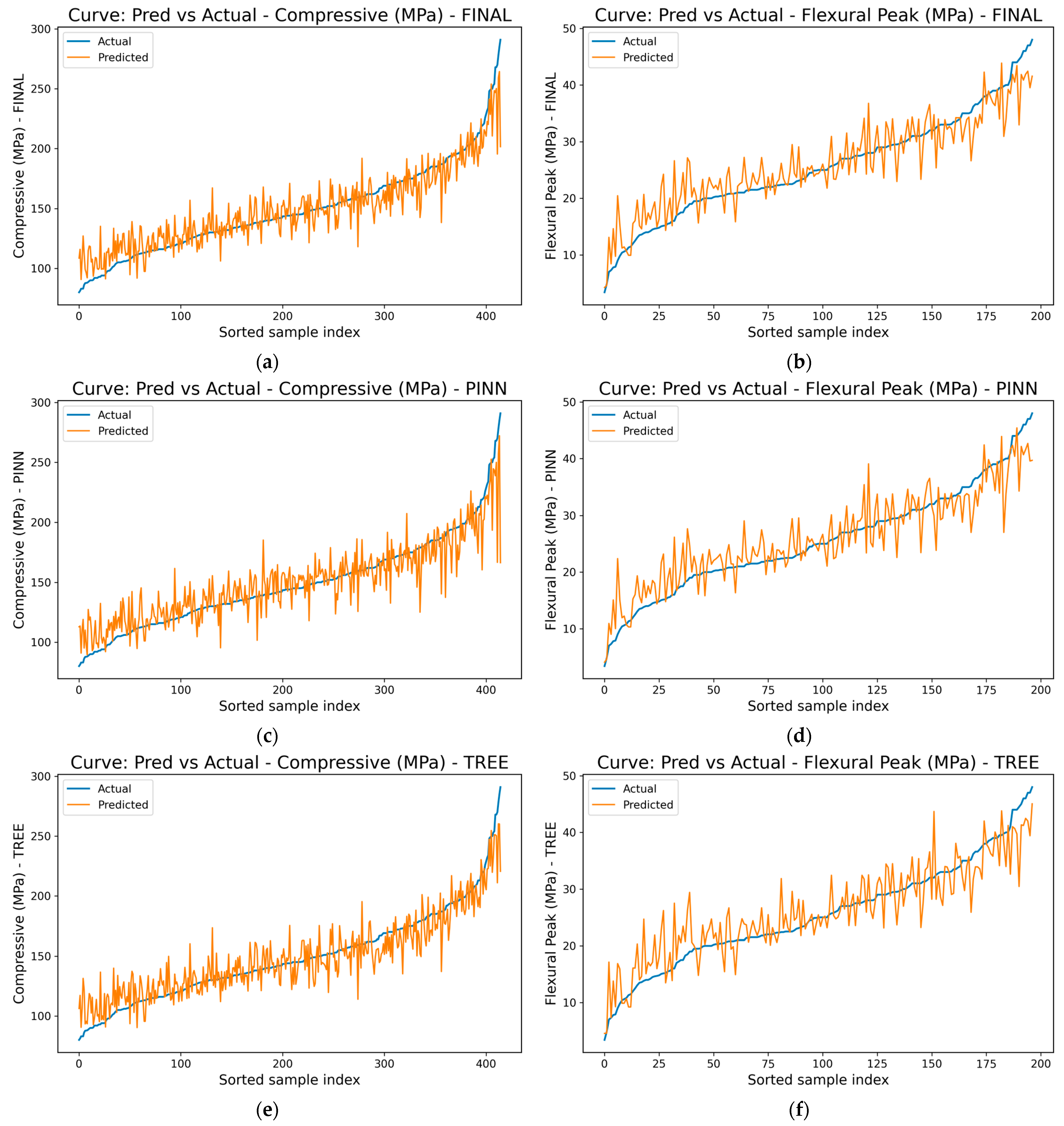
4.3. Model Performance
5. Conclusions
- (1)
- Copula-based data imputation effectively completed missing values, maintained realistic correlations, and supported stable downstream learning compared with mean or median filling.
- (2)
- Feature engineering guided by domain ratios (w/b, sp/b, fiber descriptors) provided interpretable predictors and improved generalization by embedding known physical relationships [45].
- (3)
- The physics-informed PINN reduced monotonicity violations substantially over training, aligning gradients with expected physical trends and yielding smoother, low-rank representations.
- (4)
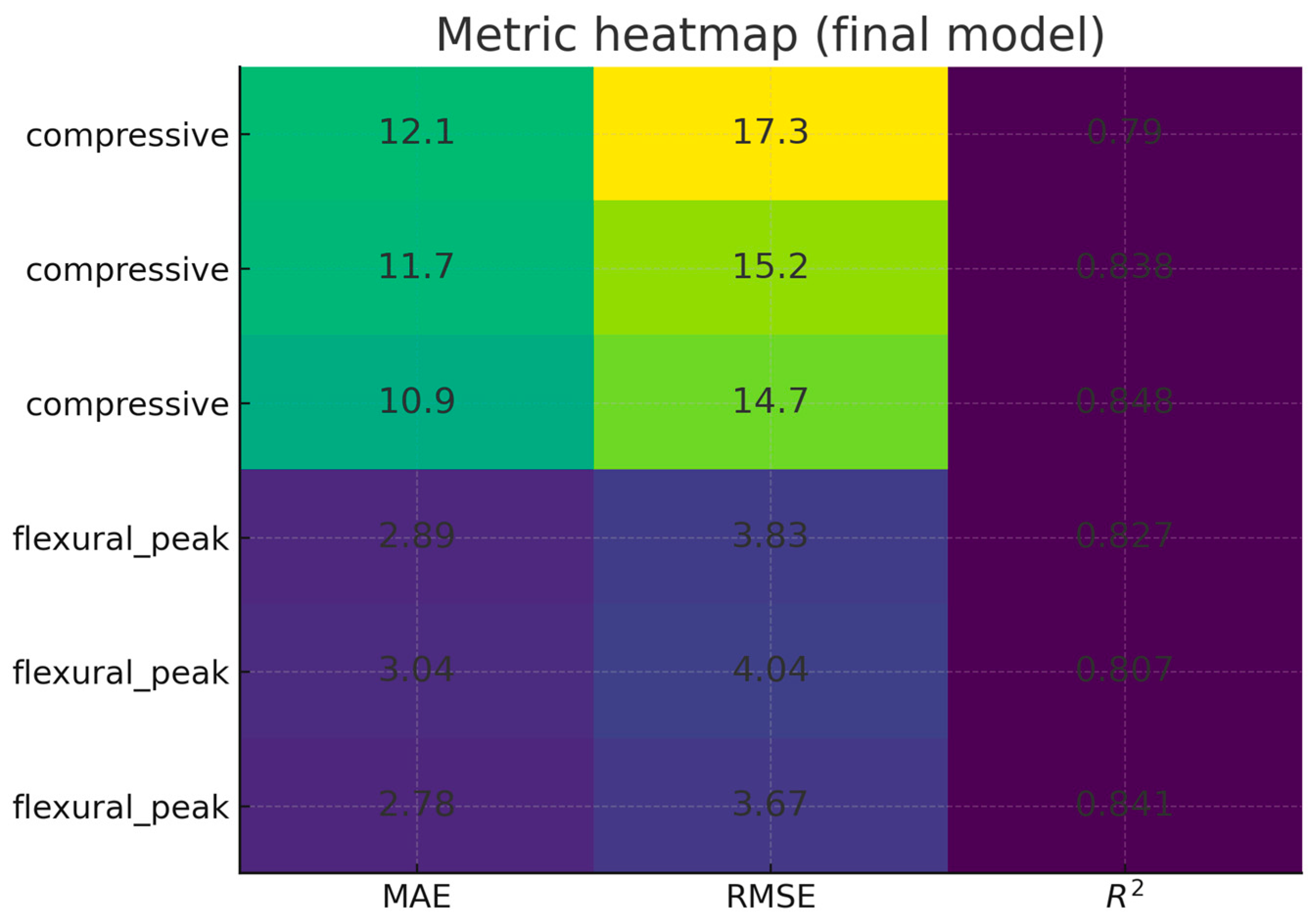
- The convex blend of PINN and HGBT consistently outperformed individual models, achieving an MAE/RMSE/R2 of 10.9/14.7/0.848 for compressive strength and 2.78/3.67/0.841 for flexural strength, thereby improving accuracy and robustness across tasks.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, J.; Meng, W.; Khayat, K.H.; Bao, Y.; Guo, P.; Lyu, Z.; Abu-Obeidah, A.; Nassif, H.; Wang, H. New development of ultra-high-performance concrete (UHPC). Compos. Part B Eng. 2021, 224, 109220. [Google Scholar] [CrossRef]
- Azmee, N.M.; Shafiq, N. Ultra-high performance concrete: From fundamental to applications. Case Stud. Constr. Mater. 2018, 9, e00197. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Yoon, Y.-S. A review on structural behavior, design, and application of ultra-high-performance fiber-reinforced concrete. Int. J. Concr. Struct. Mater. 2016, 10, 125–142. [Google Scholar] [CrossRef]
- Mousavinezhad, S.; Gonzales, G.J.; Toledo, W.K.; Garcia, J.M.; Newtson, C.M.; Allena, S. A comprehensive study on non-proprietary ultra-high-performance concrete containing supplementary cementitious materials. Materials 2023, 16, 2622. [Google Scholar] [CrossRef]
- Abellán-García, J.; Carvajal-Muñoz, J.S.; Ramírez-Munévar, C. Application of ultra-high-performance concrete as bridge pavement overlays: Literature review and case studies. Constr. Build. Mater. 2024, 410, 134221. [Google Scholar] [CrossRef]
- Liao, J.; Yang, K.Y.; Zeng, J.-J.; Quach, W.-M.; Ye, Y.-Y.; Zhang, L. Compressive behavior of FRP-confined ultra-high performance concrete (UHPC) in circular columns. Eng. Struct. 2021, 249, 113246. [Google Scholar] [CrossRef]
- Yu, R.; Spiesz, P.; Brouwers, H. Mix design and properties assessment of ultra-high performance fibre reinforced concrete (UHPFRC). Cem. Concr. Res. 2014, 56, 29–39. [Google Scholar] [CrossRef]
- Nguyen, N.-H.; Abellán-García, J.; Lee, S.; Garcia-Castano, E.; Vo, T.P. Efficient estimating compressive strength of ultra-high performance concrete using XGBoost model. J. Build. Eng. 2022, 52, 104302. [Google Scholar] [CrossRef]
- Zeng, J.-J.; Zeng, W.-B.; Ye, Y.-Y.; Liao, J.; Zhuge, Y.; Fan, T.-H. Flexural behavior of FRP grid reinforced ultra-high-performance concrete composite plates with different types of fibers. Eng. Struct. 2022, 272, 115020. [Google Scholar] [CrossRef]
- ASTM C109; Standard Test Method for Compressive Strength of Hydraulic Cement Mortars. ASTM International: West Conshohocken, PA, USA, 2024.
- ASTM C1609; Standard Test Method for Flexural Performance of Fiber-Reinforced Concrete. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM C1012; Standard Test Method for Length Change of Hydraulic-Cement Mortars Exposed to a Sulfate Solution. ASTM International: West Conshohocken, PA, USA, 2024.
- Mahjoubi, S.; Barhemat, R.; Meng, W.; Bao, Y. AI-guided auto-discovery of low-carbon cost-effective ultra-high performance concrete (UHPC). Resour. Conserv. Recycl. 2023, 189, 106741. [Google Scholar] [CrossRef]
- Wang, D.; Shi, C.; Wu, Z.; Xiao, J.; Huang, Z.; Fang, Z. A review on ultra high performance concrete: Part II. Hydration, microstructure and properties. Constr. Build. Mater. 2015, 96, 368–377. [Google Scholar] [CrossRef]
- Behnood, A.; Golafshani, E.M. Predicting the compressive strength of silica fume concrete using hybrid artificial neural network with multi-objective grey wolves. J. Clean. Prod. 2018, 202, 54–64. [Google Scholar] [CrossRef]
- Bolbolvand, M.; Tavakkoli, S.M.; Alaee, F.J. Prediction of compressive and flexural strengths of ultra-high-performance concrete (UHPC) using machine learning for various fiber types. Constr. Build. Mater. 2025, 493, 143135. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q. A survey on multi-task learning. IEEE Trans. Knowl. Data Eng. 2021, 34, 5586–5609. [Google Scholar] [CrossRef]
- Wen, C.; Zhang, P.; Wang, J.; Hu, S. Influence of fibers on the mechanical properties and durability of ultra-high-performance concrete: A review. J. Build. Eng. 2022, 52, 104370. [Google Scholar] [CrossRef]
- Gong, J.; Ma, Y.; Fu, J.; Hu, J.; Ouyang, X.; Zhang, Z.; Wang, H. Utilization of fibers in ultra-high performance concrete: A review. Compos. Part B Eng. 2022, 241, 109995. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Hanandeh, S.; Ulloa, N.; Barba-Vera, R.; Moghal, A.A.B.; Ebid, A.M.; Arunachalam, K.P.; Ur Rehman, A. Developing machine learning frameworks to predict mechanical properties of ultra-high performance concrete mixed with various industrial byproducts. Sci. Rep. 2025, 15, 24791. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Zhao, Y.; Udell, M. gcimpute: A package for missing data imputation. J. Stat. Softw. 2024, 108, 1–27. [Google Scholar] [CrossRef]
- Aghajanzadeh, E.; Bahraini, T.; Mehrizi, A.H.; Yazdi, H.S. Task weighting based on particle filter in deep multi-task learning with a view to uncertainty and performance. Pattern Recognit. 2023, 140, 109587. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, H.; Wang, Y.; Zhai, Y.; Yang, Y. Deep Isotonic Embedding Network: A flexible Monotonic Neural Network. Neural Netw. 2024, 171, 457–465. [Google Scholar] [CrossRef]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Udell, M. Missing value imputation for mixed data via gaussian copula. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, San Diego, CA, USA, 23–27 August 2020; pp. 636–646. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Peng, R.D. Reproducible research in computational science. Science 2011, 334, 1226–1227. [Google Scholar] [CrossRef] [PubMed]
- Sandve, G.K.; Nekrutenko, A.; Taylor, J.; Hovig, E. Ten simple rules for reproducible computational research. PLoS Comput. Biol. 2013, 9, e1003285. [Google Scholar] [CrossRef]
- Kashem, A.; Karim, R.; Malo, S.C.; Das, P.; Datta, S.D.; Alharthai, M. Hybrid data-driven approaches to predicting the compressive strength of ultra-high-performance concrete using SHAP and PDP analyses. Case Stud. Constr. Mater. 2024, 20, e02991. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, W.; Chen, Y.; Mi, Y.; Lei, J.; Sun, L. Predicting the compressive strength of high-performance concrete using an interpretable machine learning model. Sci. Rep. 2024, 14, 28346. [Google Scholar] [CrossRef]
- Aylas-Paredes, B.K.; Han, T.; Neithalath, A.; Huang, J.; Goel, A.; Kumar, A.; Neithalath, N. Data driven design of ultra high performance concrete prospects and application. Sci. Rep. 2025, 15, 9248. [Google Scholar] [CrossRef]
- Wang, X.Q.; Chow, C.L.; Lau, D. Multiscale perspectives for advancing sustainability in fiber reinforced ultra-high performance concrete. Npj Mater. Sustain. 2024, 2, 13. [Google Scholar] [CrossRef]
- Sun, C.; Wang, K.; Liu, Q.; Wang, P.; Pan, F. Machine-learning-based comprehensive properties prediction and mixture design optimization of ultra-high-performance concrete. Sustainability 2023, 15, 15338. [Google Scholar] [CrossRef]
- Lyngdoh, G.A.; Zaki, M.; Krishnan, N.A.; Das, S. Prediction of concrete strengths enabled by missing data imputation and interpretable machine learning. Cem. Concr. Compos. 2022, 128, 104414. [Google Scholar] [CrossRef]
- Thai, H.-T. Machine learning for structural engineering: A state-of-the-art review. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; pp. 448–491. [Google Scholar] [CrossRef]
- Alabduljabbar, H.; Khan, M.; Awan, H.H.; Eldin, S.M.; Alyousef, R.; Mohamed, A.M. Predicting ultra-high-performance concrete compressive strength using gene expression programming method. Case Stud. Constr. Mater. 2023, 18, e02074. [Google Scholar] [CrossRef]
- Fan, D.; Chen, Z.; Cao, Y.; Liu, K.; Yin, T.; Lv, X.-S.; Lu, J.-X.; Zhou, A.; Poon, C.S.; Yu, R. Intelligent predicting and monitoring of ultra-high-performance fiber reinforced concrete composites—A review. Compos. Part A Appl. Sci. Manuf. 2025, 188, 108555. [Google Scholar] [CrossRef]
- Nithurshan, M.; Elakneswaran, Y. A systematic review and assessment of concrete strength prediction models. Case Stud. Constr. Mater. 2023, 18, e01830. [Google Scholar] [CrossRef]
- Shaban, W.M.; Elbaz, K.; Zhou, A.; Shen, S.-L. Physics-informed deep neural network for modeling the chloride diffusion in concrete. Eng. Appl. Artif. Intell. 2023, 125, 106691. [Google Scholar] [CrossRef]
- Wirz, C.D.; Sutter, C.; Demuth, J.L.; Mayer, K.J.; Chapman, W.E.; Cains, M.G.; Radford, J.; Przybylo, V.; Evans, A.; Martin, T. Increasing the reproducibility and replicability of supervised AI/ML in the Earth systems science by leveraging social science methods. Earth Space Sci. 2024, 11, e2023EA003364. [Google Scholar] [CrossRef]
- Li, S.; Jensen, O.M.; Yu, Q. Influence of steel fiber content on the rate-dependent flexural performance of ultra-high performance concrete with coarse aggregates. Constr. Build. Mater. 2022, 318, 125935. [Google Scholar] [CrossRef]
- Elshaarawy, M.K.; Alsaadawi, M.M.; Hamed, A.K. Machine learning and interactive GUI for concrete compressive strength prediction. Sci. Rep. 2024, 14, 16694. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Nguyen, T.-A.; Ly, H.-B. Ensemble XGBoost schemes for improved compressive strength prediction of UHPC. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; p. 105062. [Google Scholar] [CrossRef]
- Mostafaei, H.; Kelishadi, M.; Bahmani, H.; Wu, C.; Ghiassi, B. Development of sustainable HPC using rubber powder and waste wire: Carbon footprint analysis, mechanical and microstructural properties. Eur. J. Environ. Civ. Eng. 2025, 29, 399–420. [Google Scholar] [CrossRef]
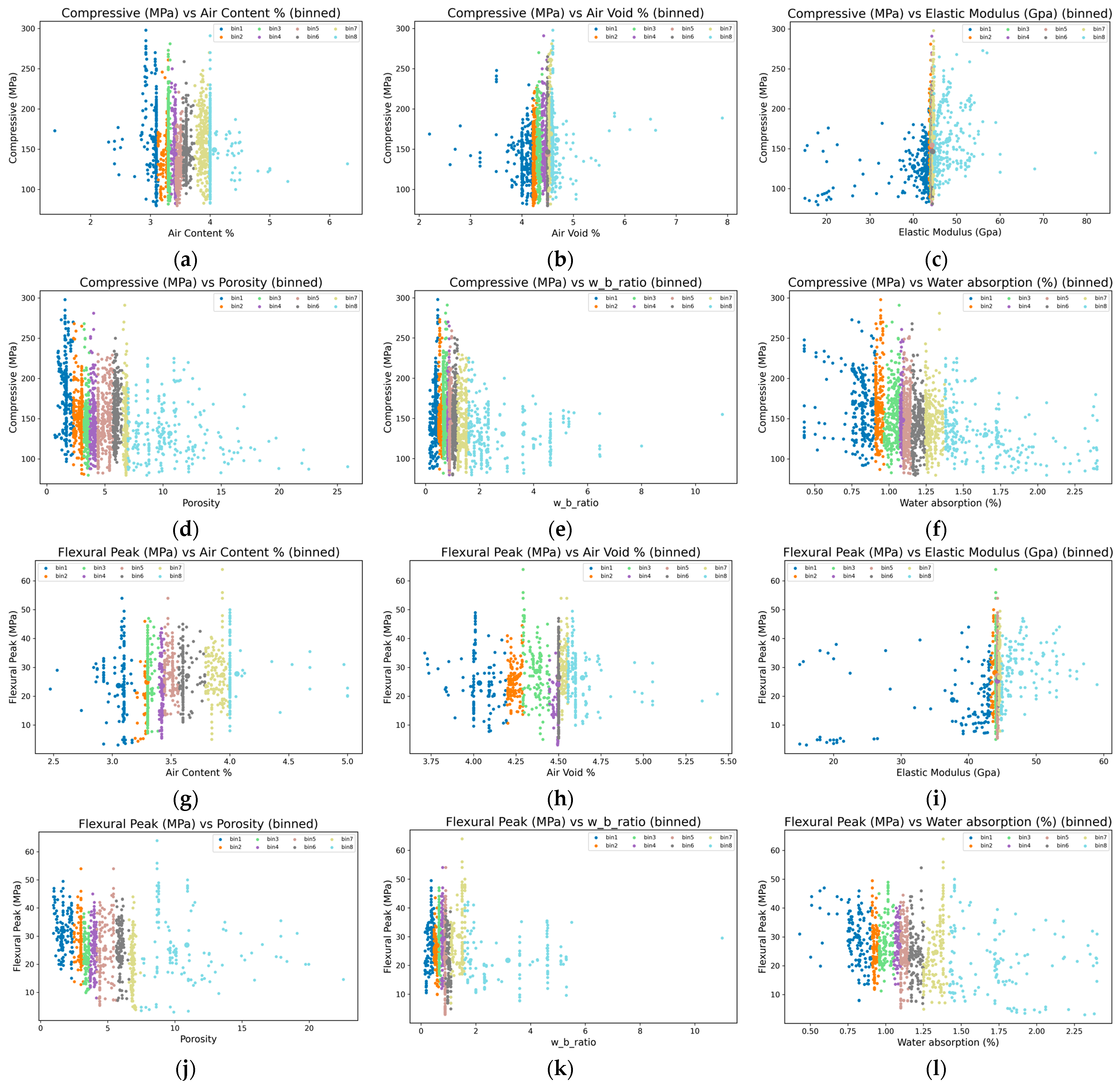
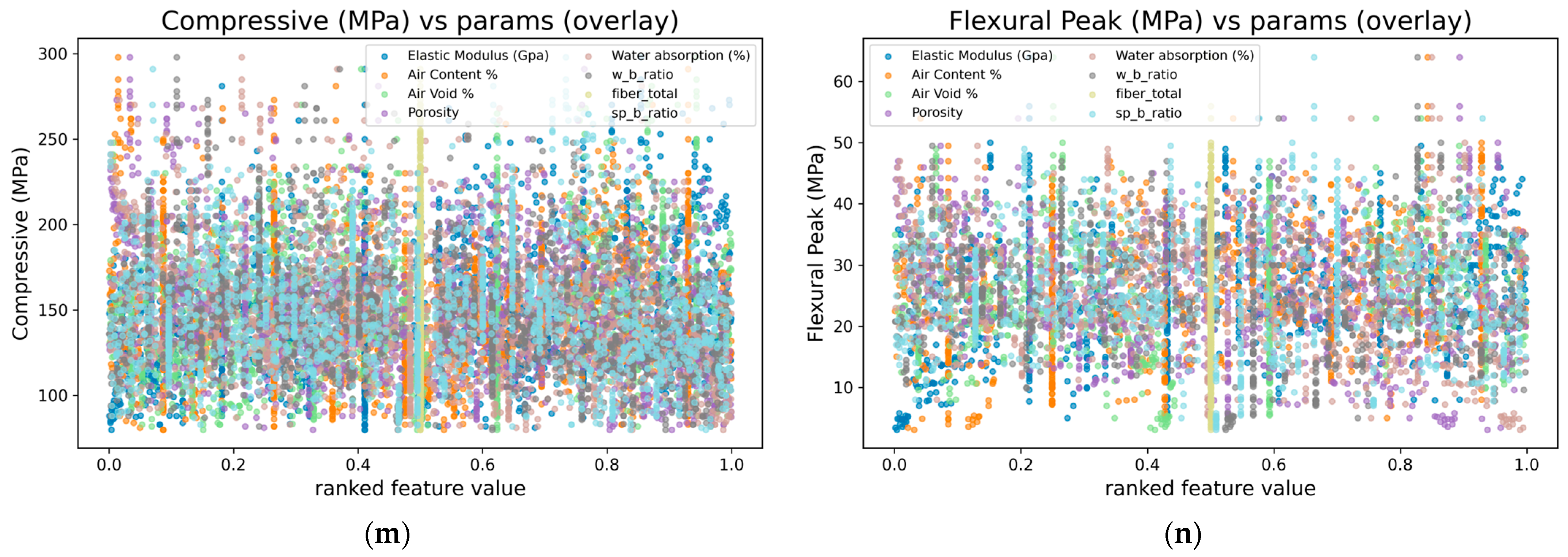
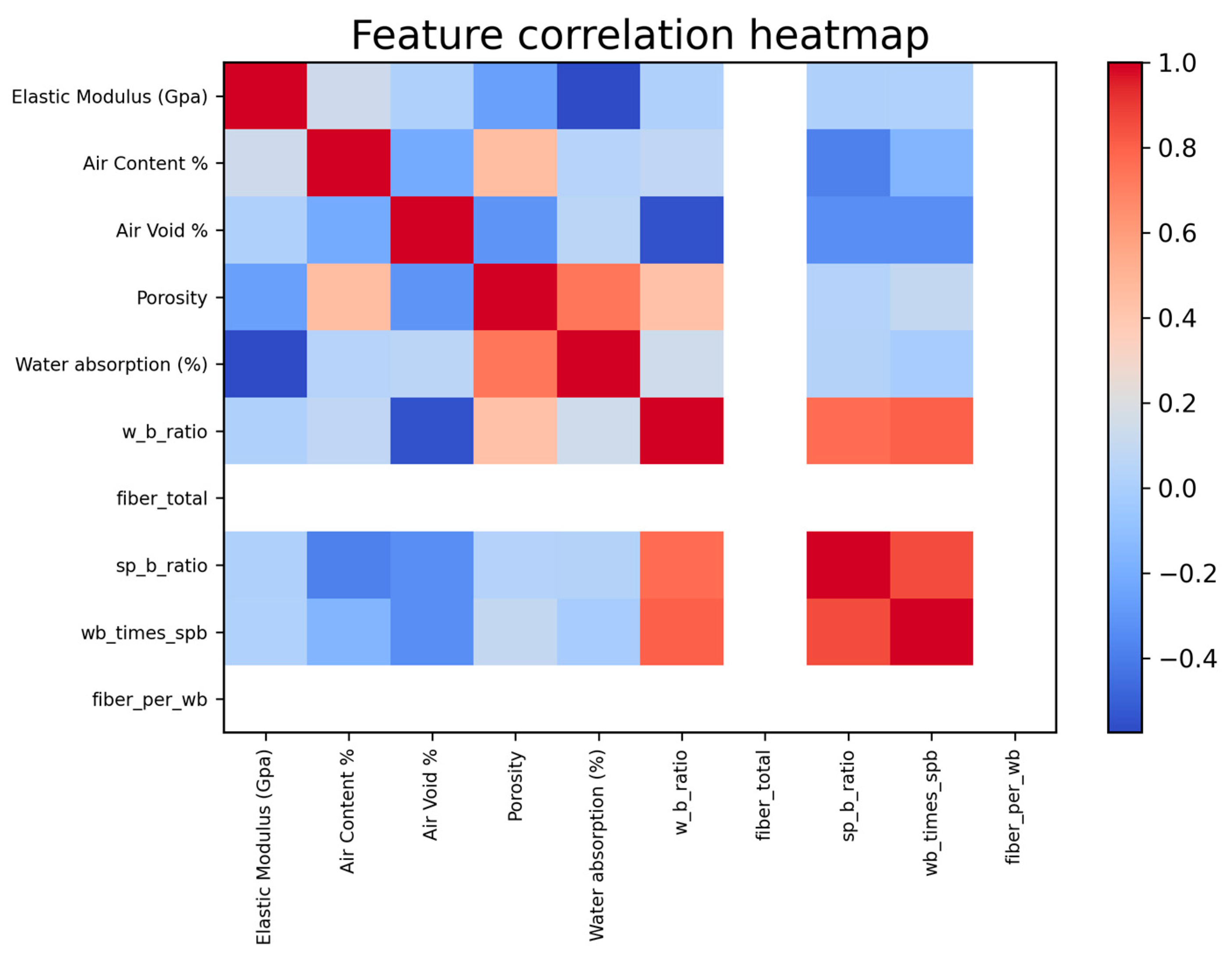
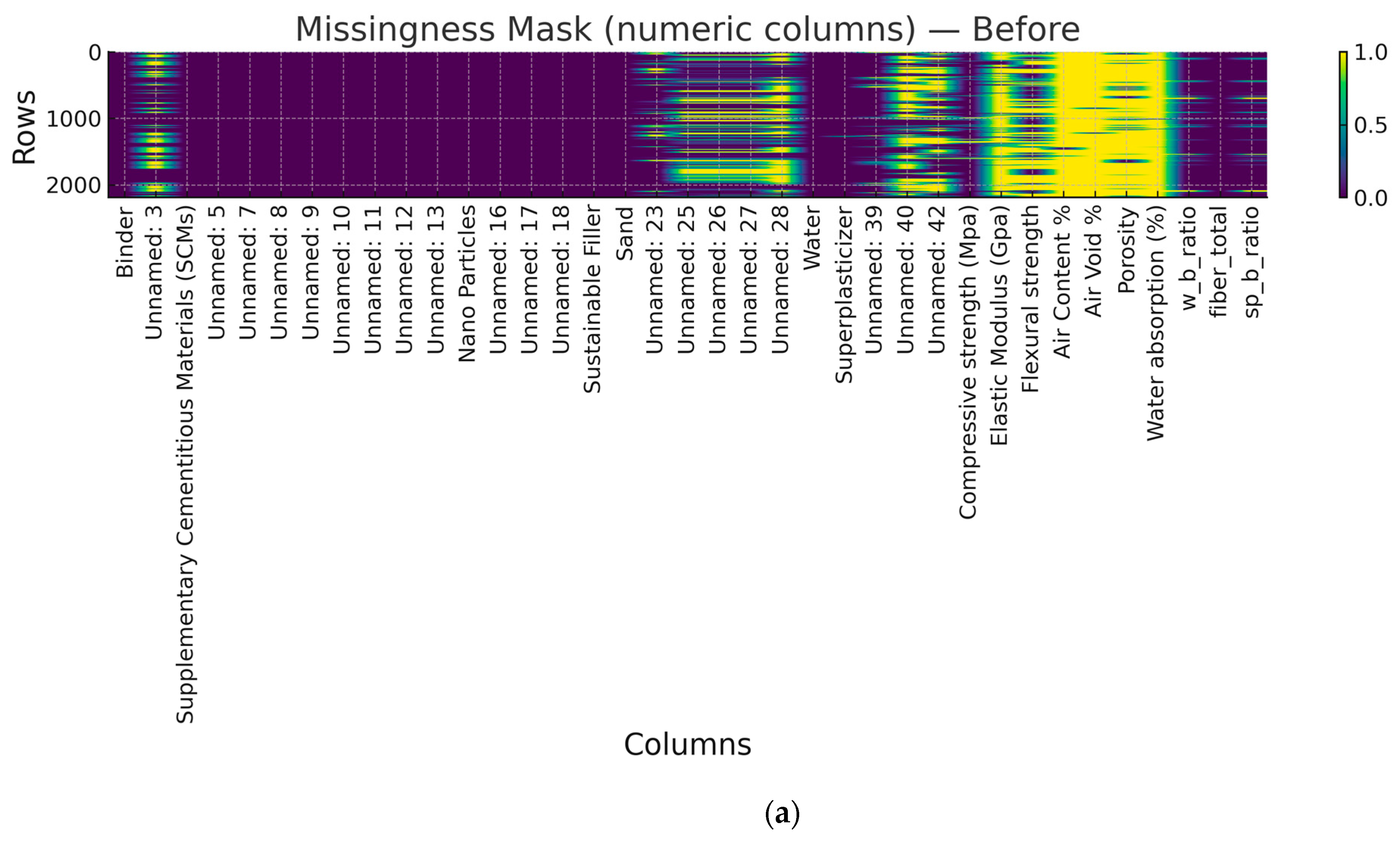
| Category | Variable | Unit | Type | Valid N | Missing (%) | Median [Q1–Q3] | Range (min–max) | P5–P95 | Mean ± SD | Skew/ Kurt |
|---|---|---|---|---|---|---|---|---|---|---|
| Core predictors | Air content (%) | % | Num | 39 | 98.22 | 3.42 [3.01–4] | 1.4–6.3 | 2.39–5.03 | 3.580 ± 0.952 | 0.436/0.698 |
| Air void (%) | % | Num | 29 | 98.68 | 4.5 [3.7–5.5] | 2.2–7.9 | 2.64–6.56 | 4.524 ± 1.322 | 0.44/0.020 | |
| Elastic modulus (GPa) | GPa | Num | 261 | 88.08 | 44.26 [41.5–49.672] | 15–82 | 26–55 | 44.401 ± 8.623 | −0.206 | |
| Porosity (—) | — | Num | 239 | 89.08 | 4.4 [2.15–9.45] | 0.69–25.89 | 1.069–16.52 | 6.223 ± 5.156 | 1.21/0.951 | |
| Water absorption (%) | % | Num | 21 | 99.04 | 1.1 [0.82–1.72] | 0.43–2.4 | 0.58–2.37 | 1.260 ± 0.560 | 0.665/−0.526 | |
| sp_b_ratio | — | Num | 2032 | 7.17 | 0.15 [0.075–0.206] | 0–1.83333 | 0.0283–0.499 | 0.1817 ± 0.185 | 3.97/24 | |
| w_b_ratio | — | Num | 2032 | 7.17 | 0.878 [0.653–1.200] | 0.142857–11 | 0.36–2.663 | 1.114 ± 0.931 | 3.7/20.9 | |
| Mixture amounts | Cement (kg/m3) | kg/m3 | Num | 2188 | 0.05 | 197.1 [133.425–227.25] | 0–617.647 | 0–288 | 180.566 ± 89.329 | 0.29/3.06 |
| Sand (kg/m3) | kg/m3 | Num | 2188 | 0.05 | 960 [820.8–1056] | 0–1994 | 310–1250 | 902.747 ± 291.326 | −0.450 | |
| Water (kg/m3) | kg/m3 | Num | 2188 | 0.05 | 183.26 [166.972–211.5] | 110–355.147 | 147–299.52 | 194.591 ± 42.801 | 1.38/1.97 |
| Target | Model | MAE | RMSE | R2 | Test_n |
|---|---|---|---|---|---|
| compressive | PINN | 12.05 | 17.29 | 0.79 | 415 |
| Tree | 11.71 | 15.18 | 0.84 | 415 | |
| FinalBlend | 10.86 | 14.68 | 0.85 | 415 | |
| flexural_peak | PINN | 2.89 | 3.83 | 0.83 | 197 |
| Tree | 3.04 | 4.04 | 0.81 | 197 | |
| FinalBlend | 2.78 | 3.67 | 0.84 | 197 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Liu, P.; Yao, Y.; Yang, F.; Feng, X. Physics-Informed Multi-Task Neural Network (PINN) Learning for Ultra-High-Performance Concrete (UHPC) Strength Prediction. Buildings 2025, 15, 4243. https://doi.org/10.3390/buildings15234243
Yan L, Liu P, Yao Y, Yang F, Feng X. Physics-Informed Multi-Task Neural Network (PINN) Learning for Ultra-High-Performance Concrete (UHPC) Strength Prediction. Buildings. 2025; 15(23):4243. https://doi.org/10.3390/buildings15234243
Chicago/Turabian StyleYan, Long, Pengfei Liu, Yufeng Yao, Fan Yang, and Xu Feng. 2025. "Physics-Informed Multi-Task Neural Network (PINN) Learning for Ultra-High-Performance Concrete (UHPC) Strength Prediction" Buildings 15, no. 23: 4243. https://doi.org/10.3390/buildings15234243
APA StyleYan, L., Liu, P., Yao, Y., Yang, F., & Feng, X. (2025). Physics-Informed Multi-Task Neural Network (PINN) Learning for Ultra-High-Performance Concrete (UHPC) Strength Prediction. Buildings, 15(23), 4243. https://doi.org/10.3390/buildings15234243






