Construction Control of Long-Span Combined Rail-Cum-Road Continuous Steel Truss Girder Bridge of High-Speed Railway
Abstract
1. Introduction
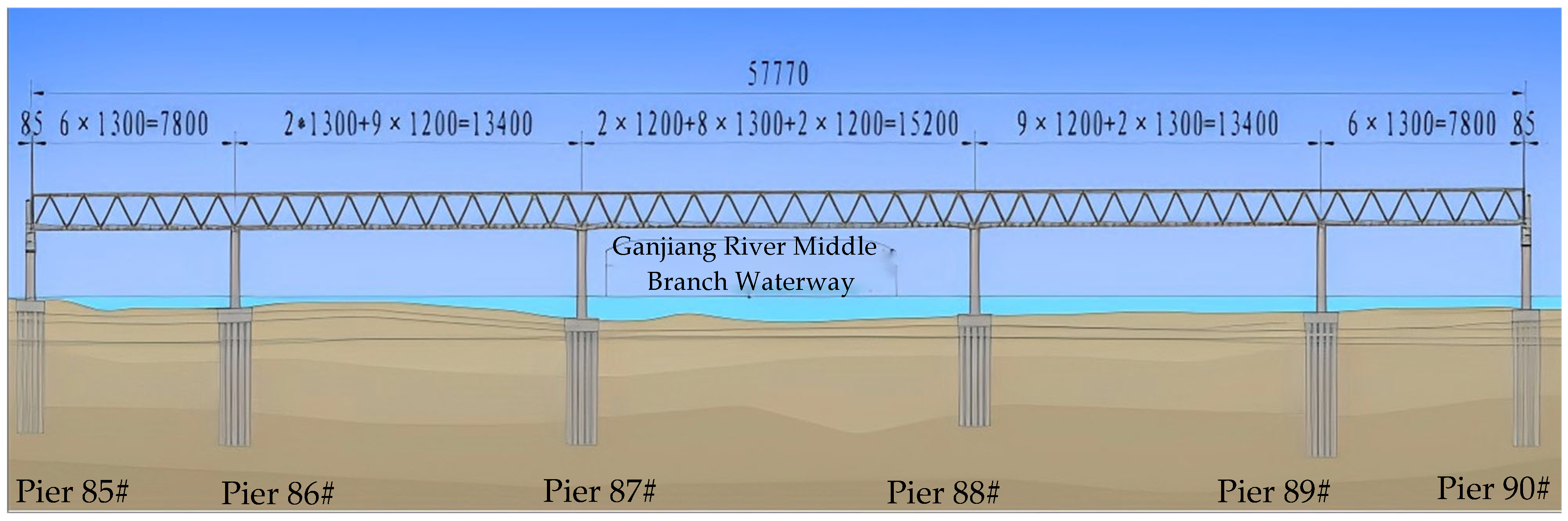
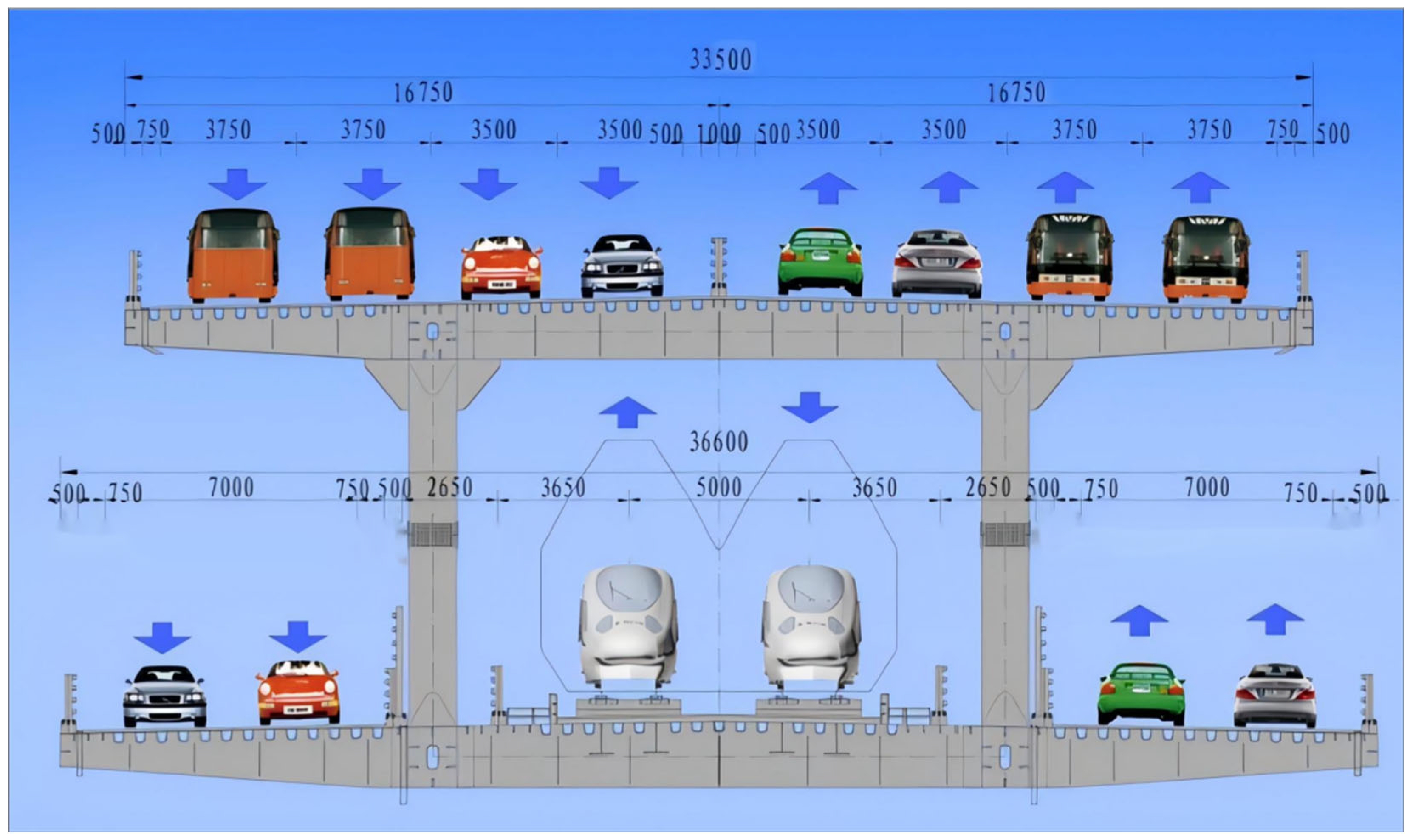
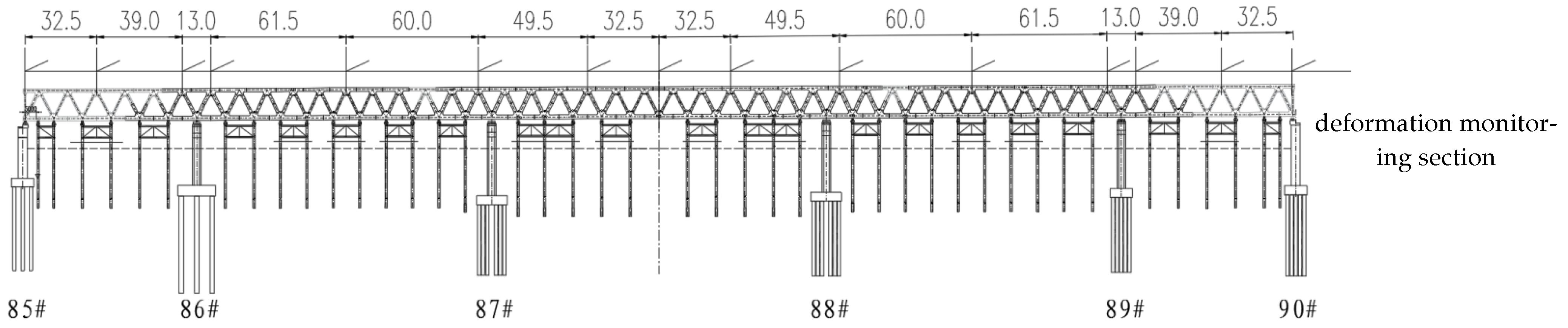
2. Engineering Background
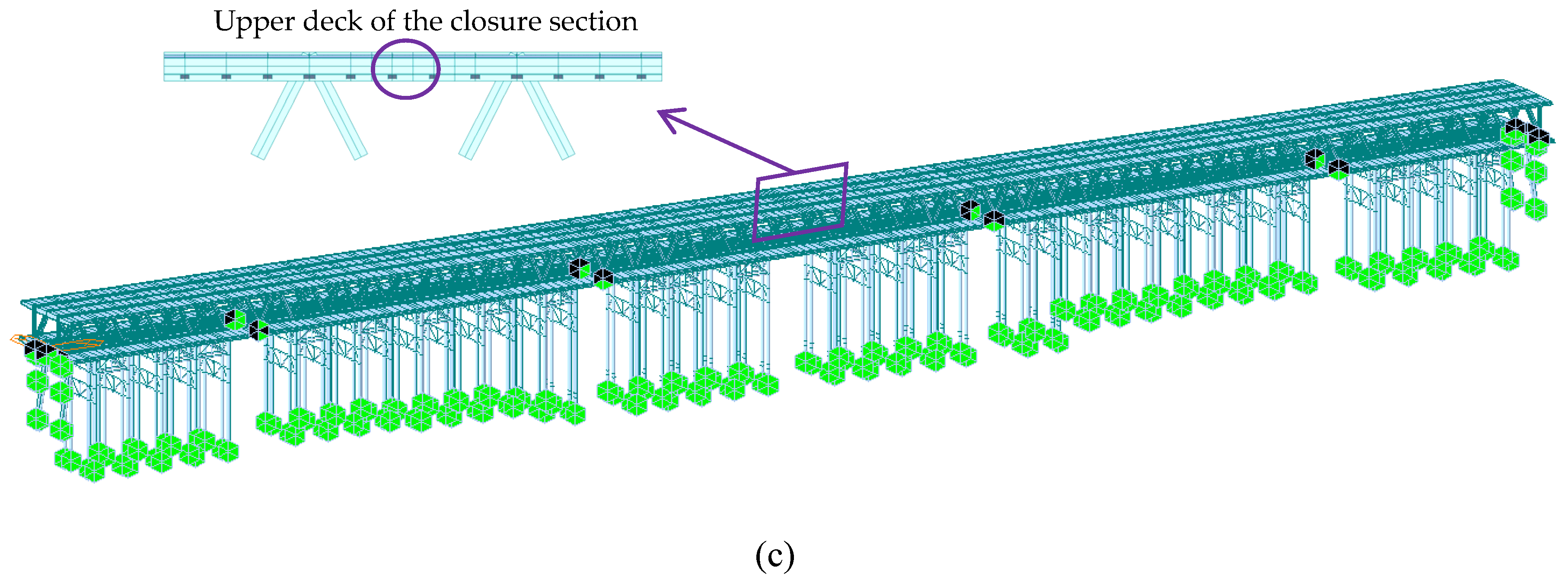
3. Mechanical Performance Analysis
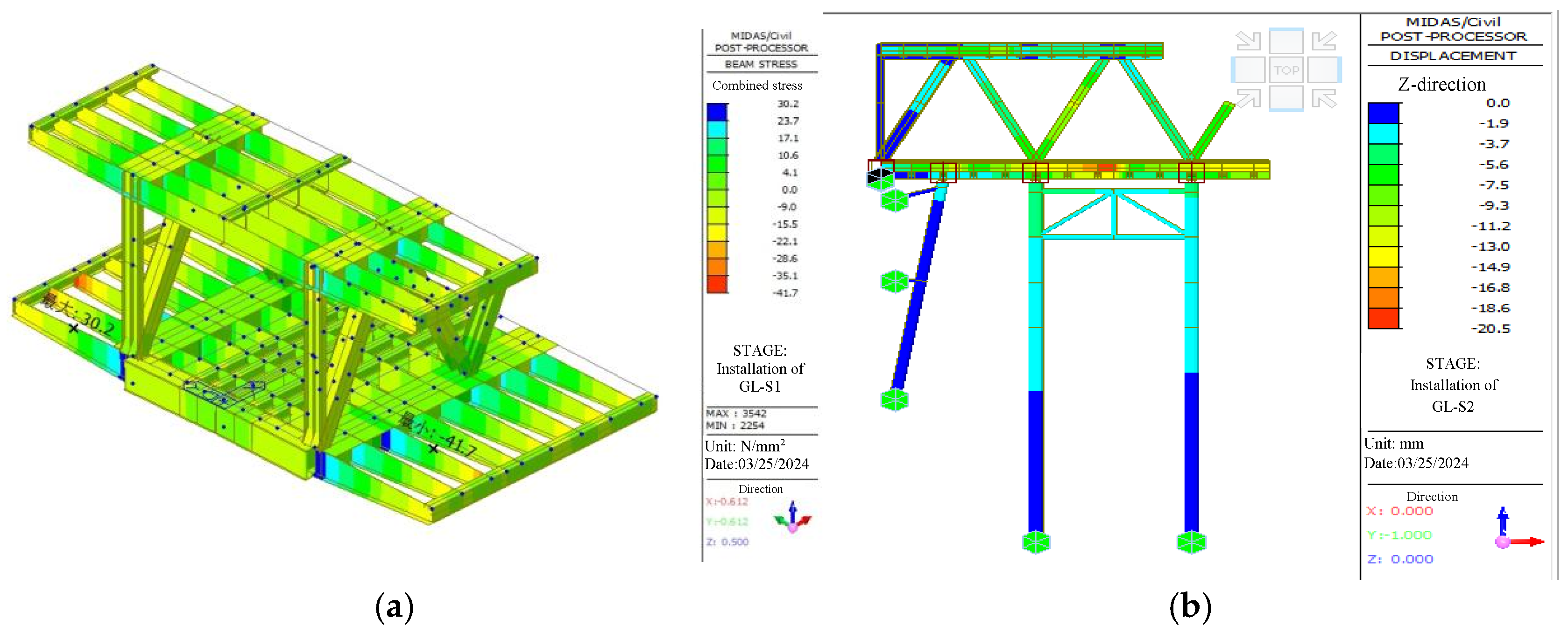
3.1. Finite Element Model (FEM)
3.2. Analysis Results
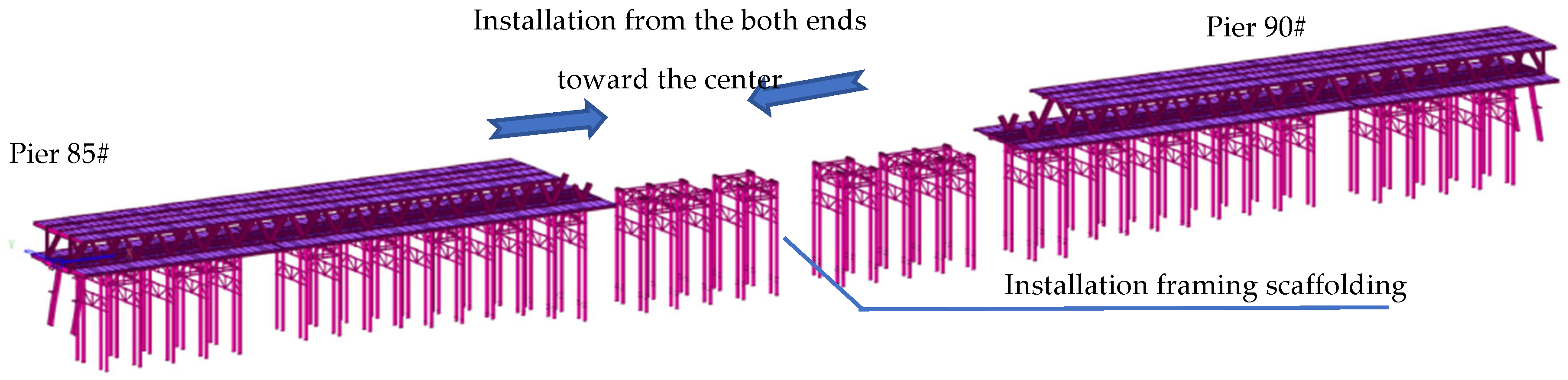
4. Control Method of Construction Process
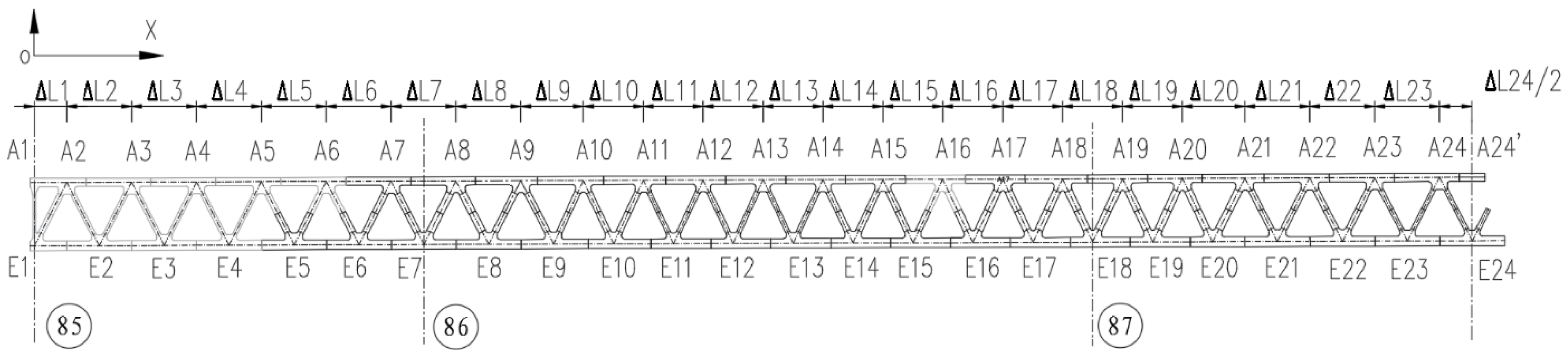
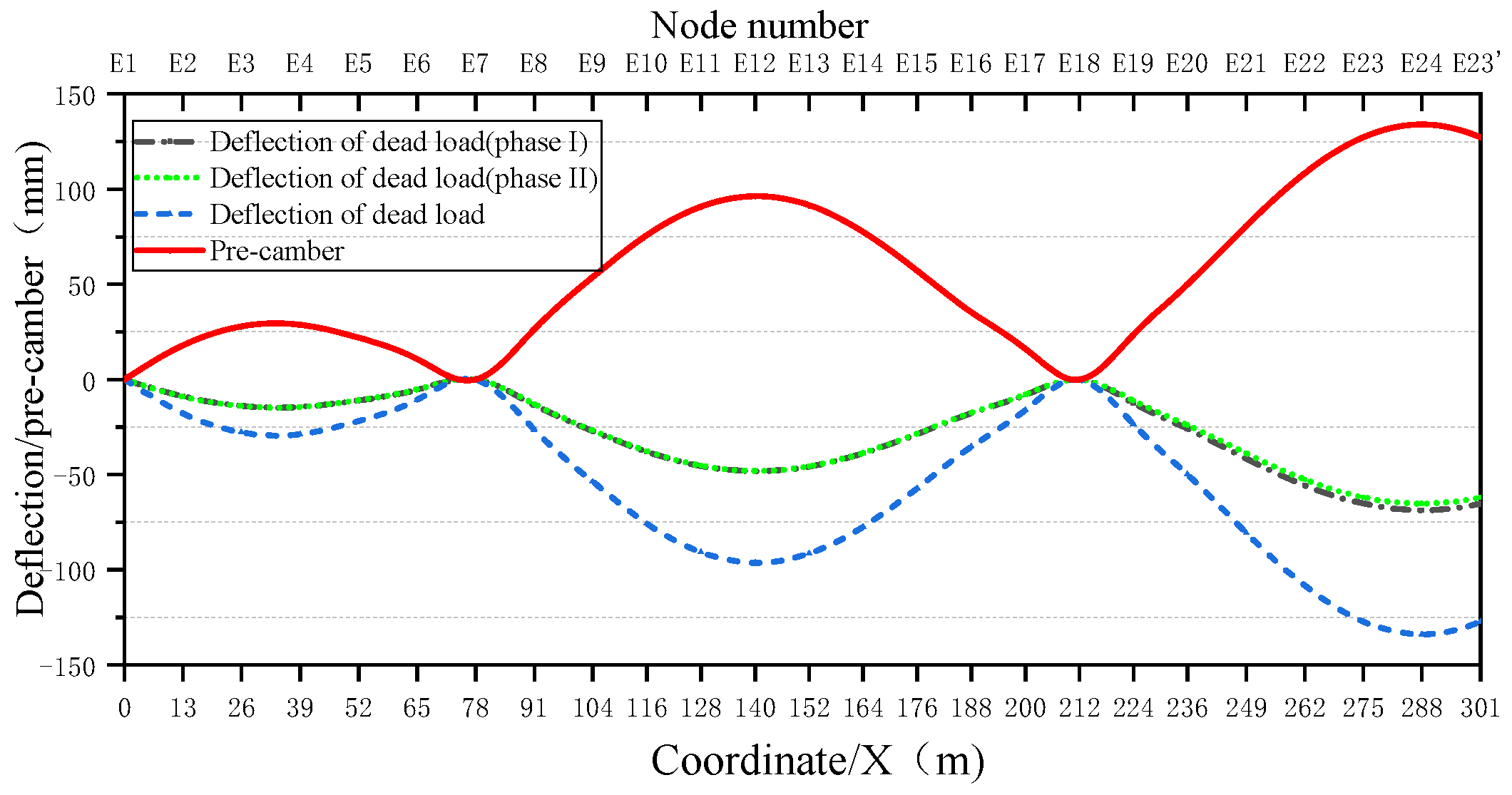
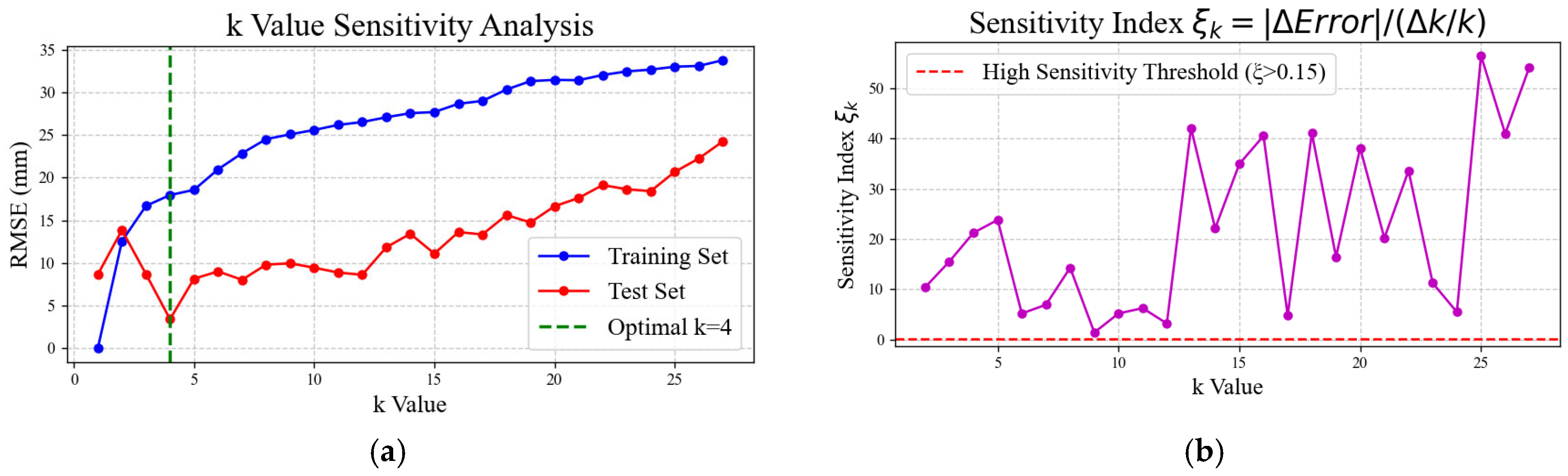
4.1. Application and Prediction of Camber Setting in Steel Truss Girder
- (1)
- Data set Configuration
- (2)
- Training and prediction
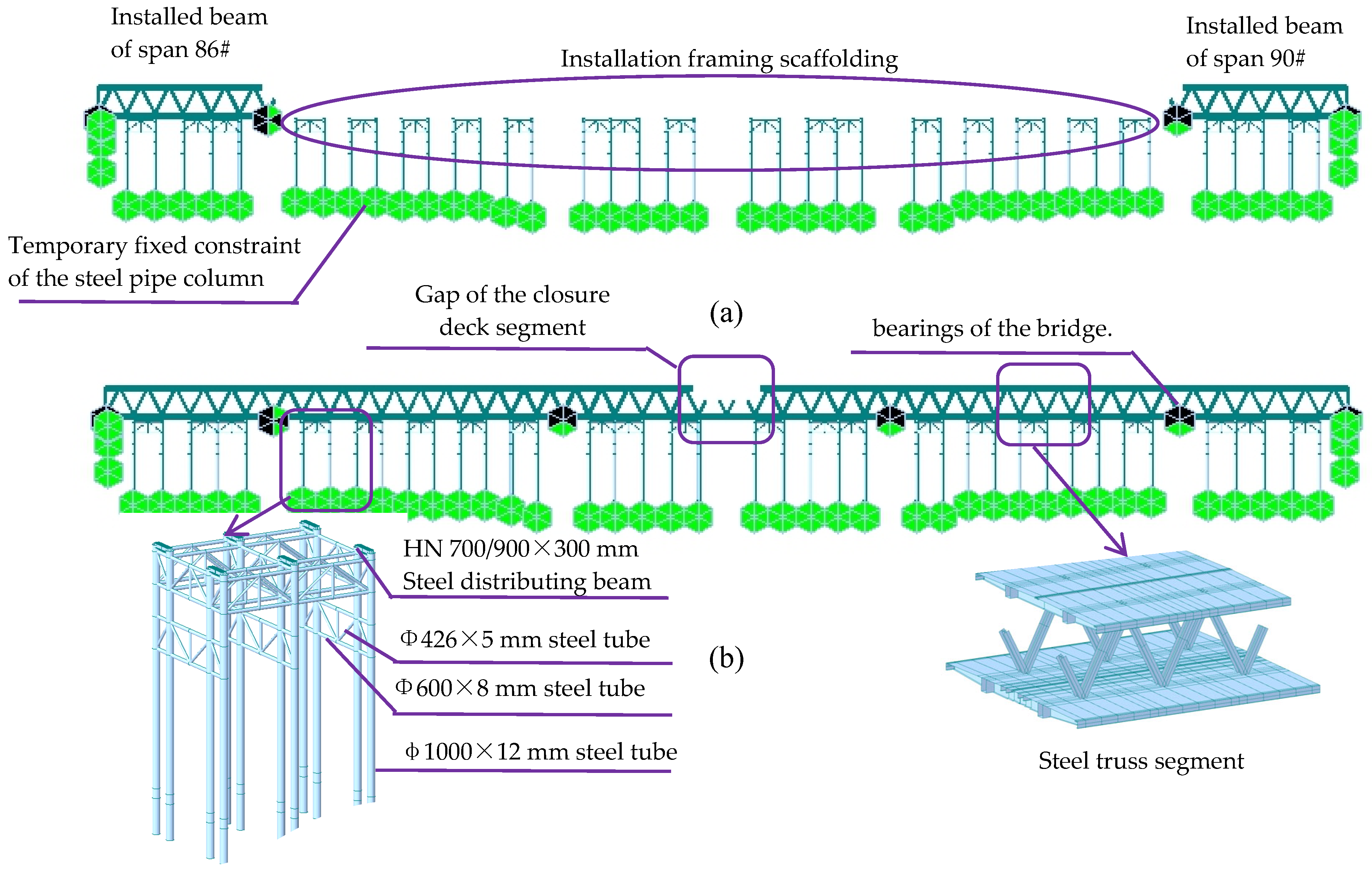
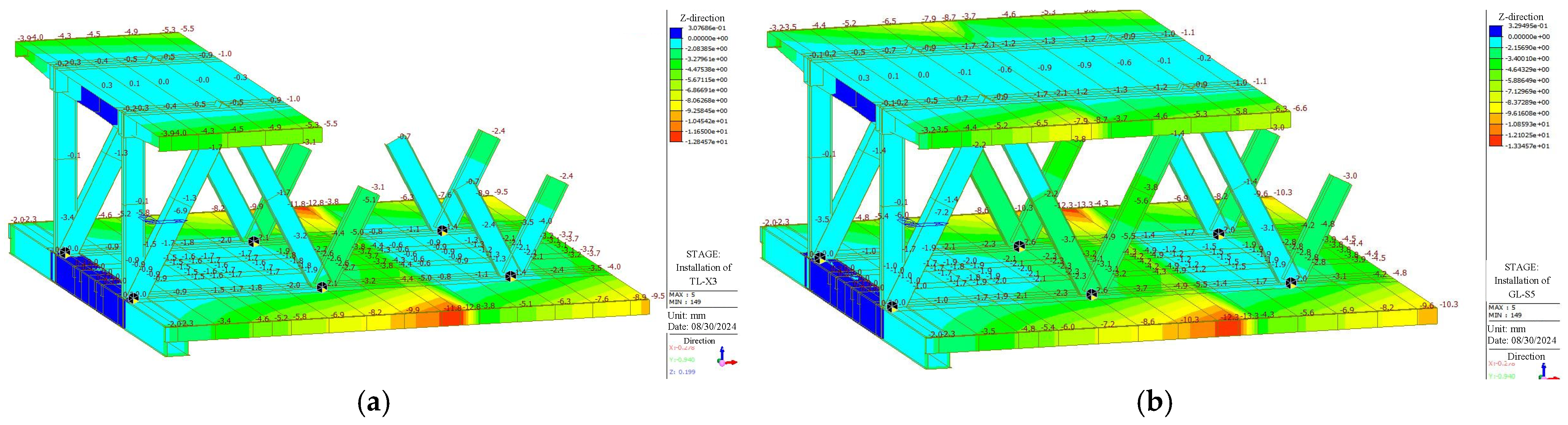
4.2. Closure Segment Construction Control
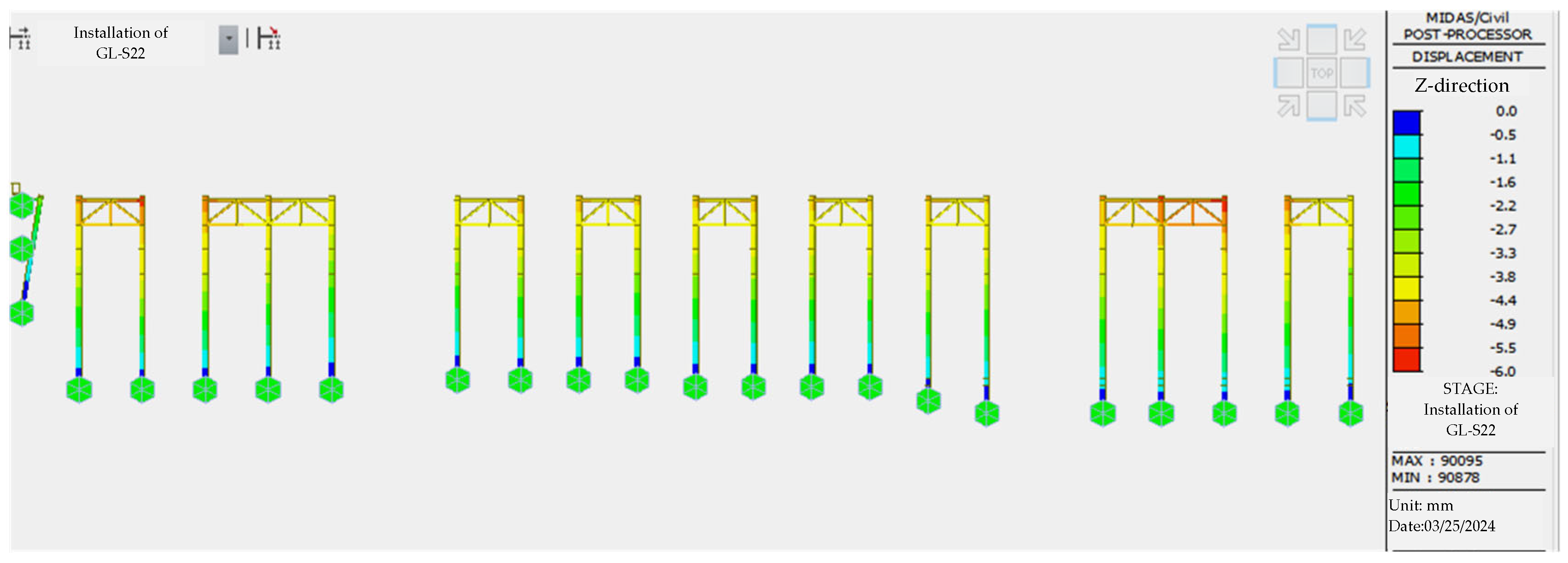
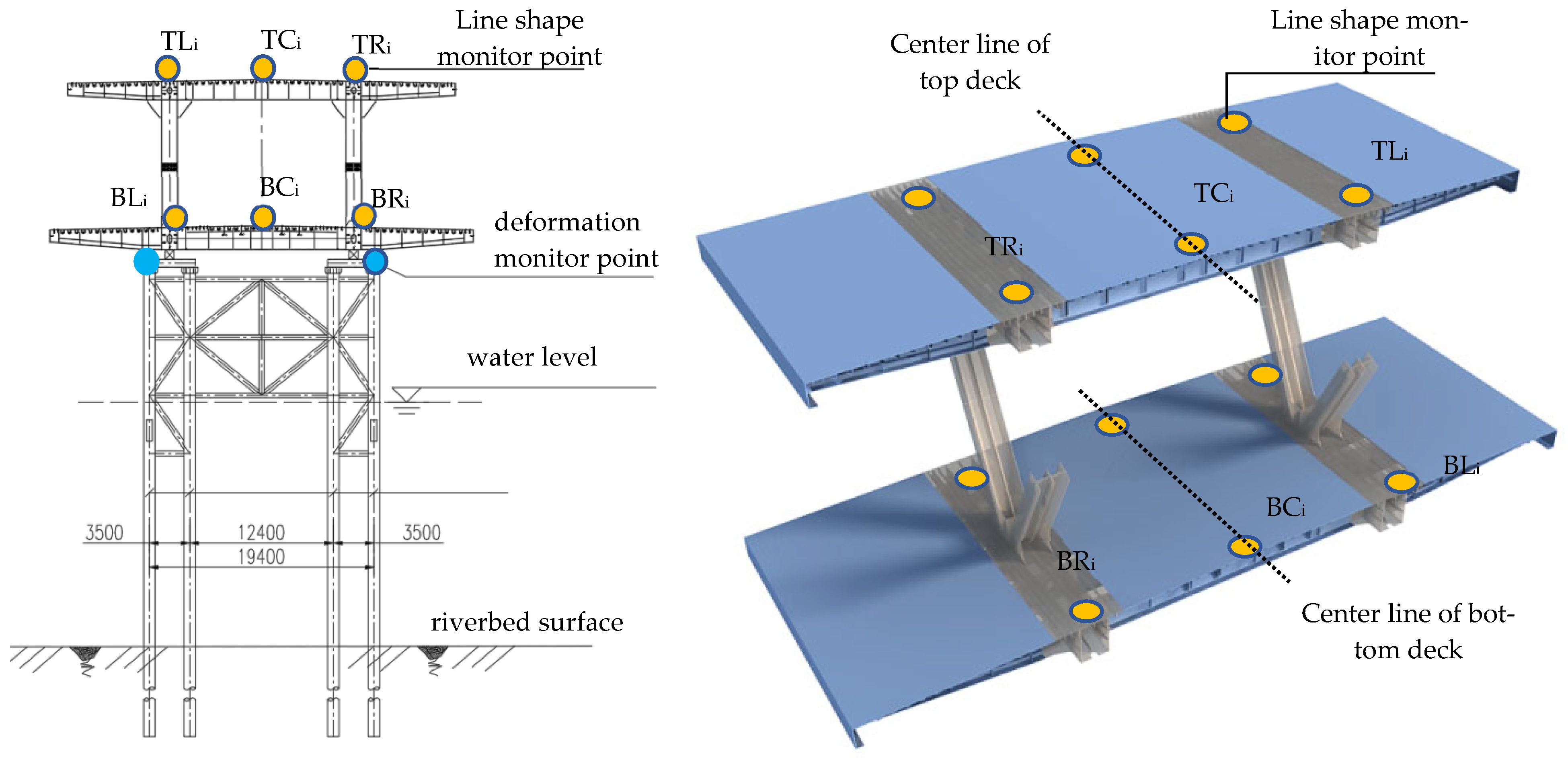
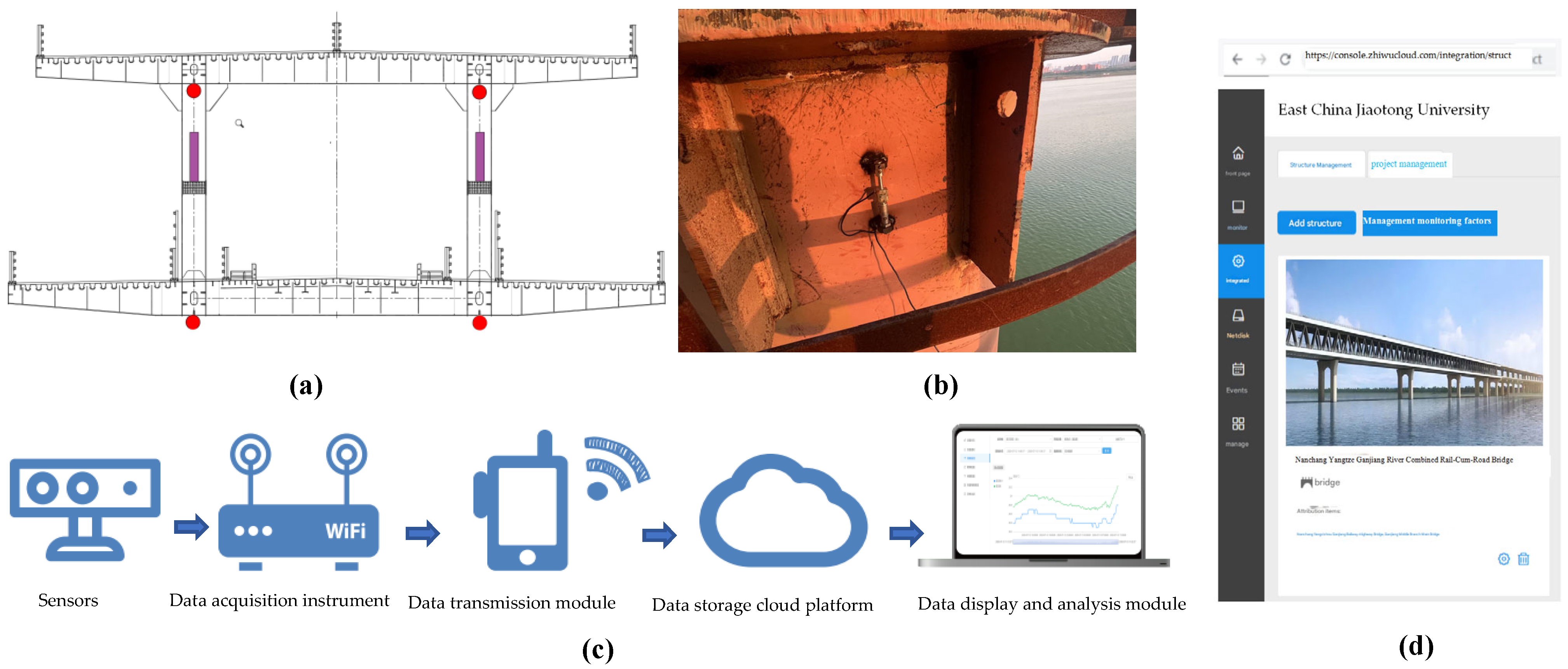
4.3. Real-Time Monitoring
- (1)
- Steel truss girder deformation monitoring
- (2)
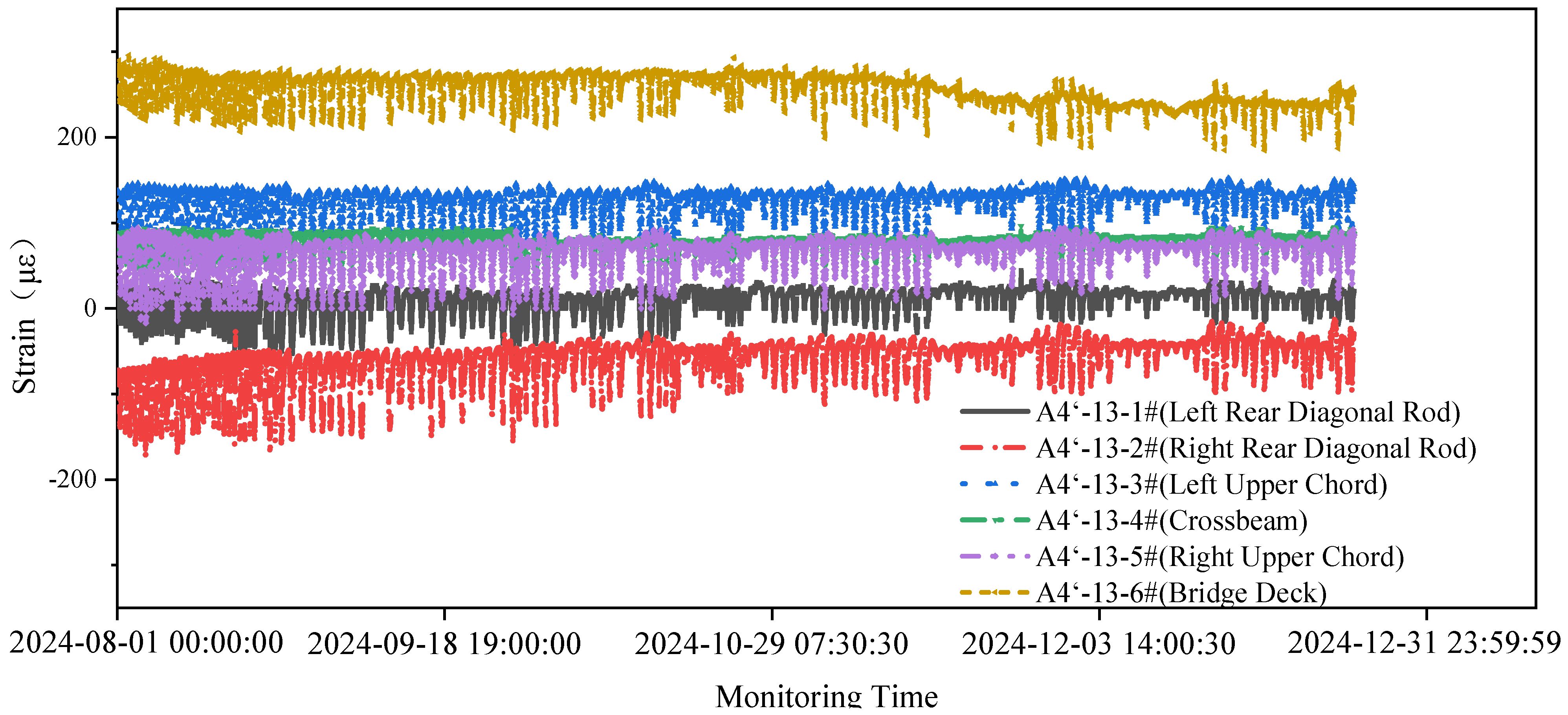
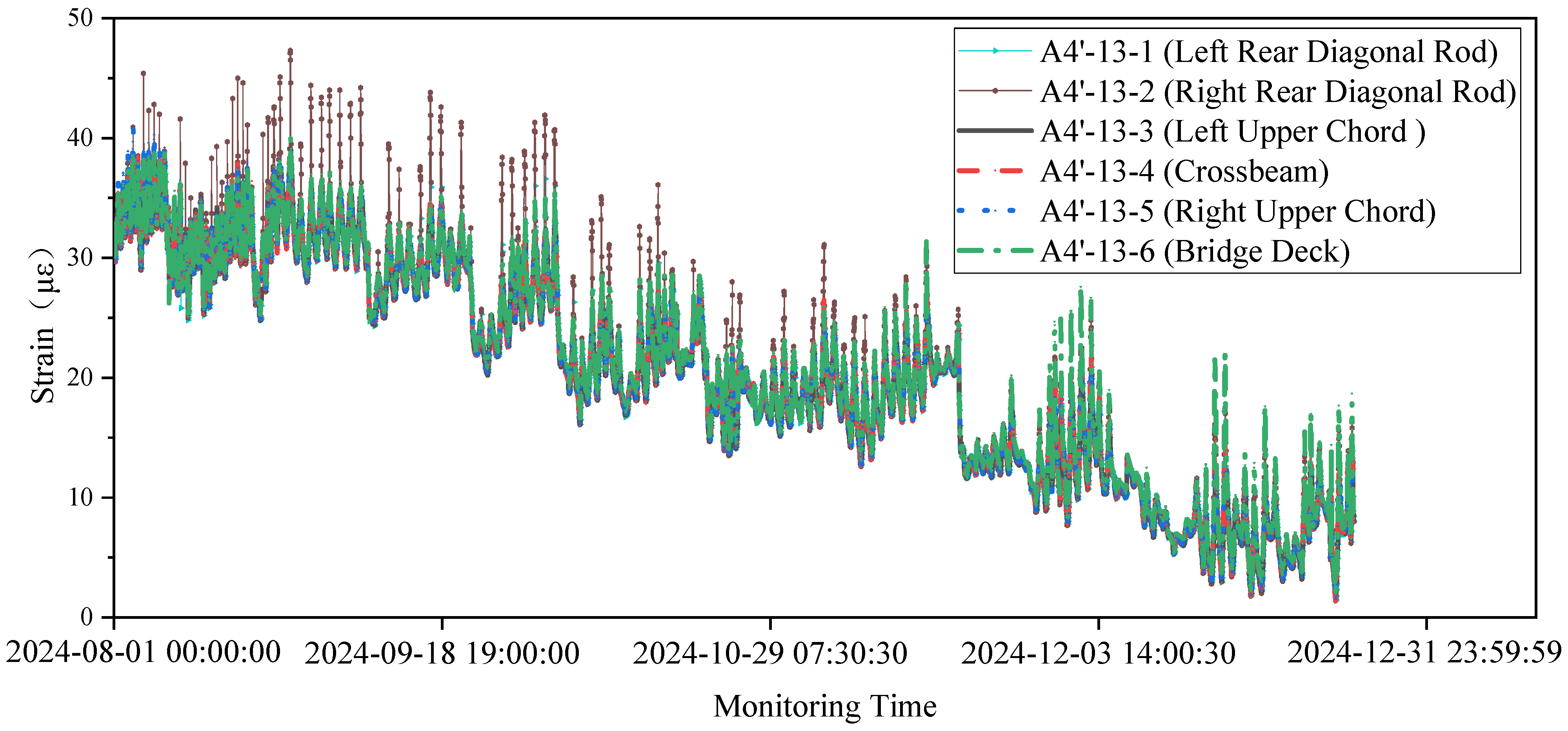
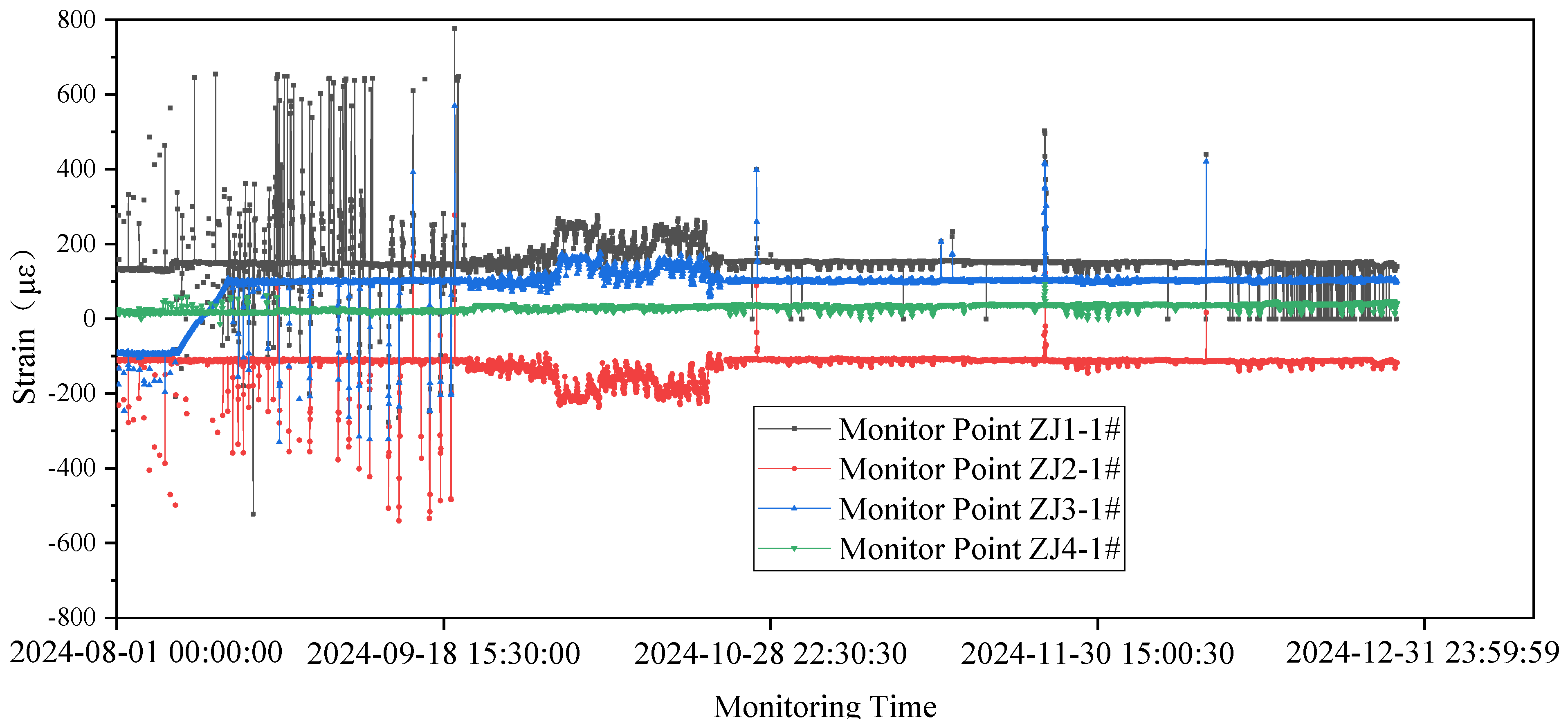
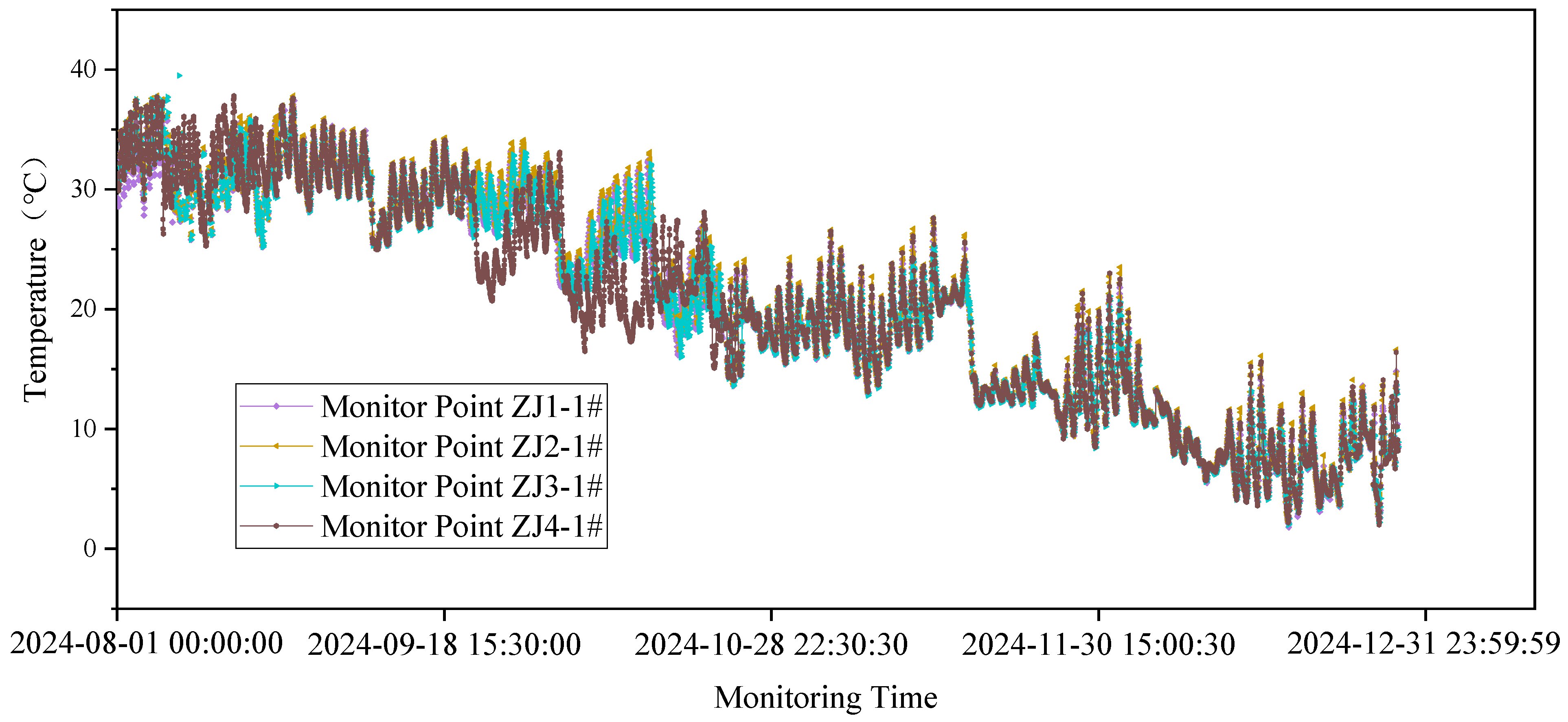
- Stress and temperature monitoring
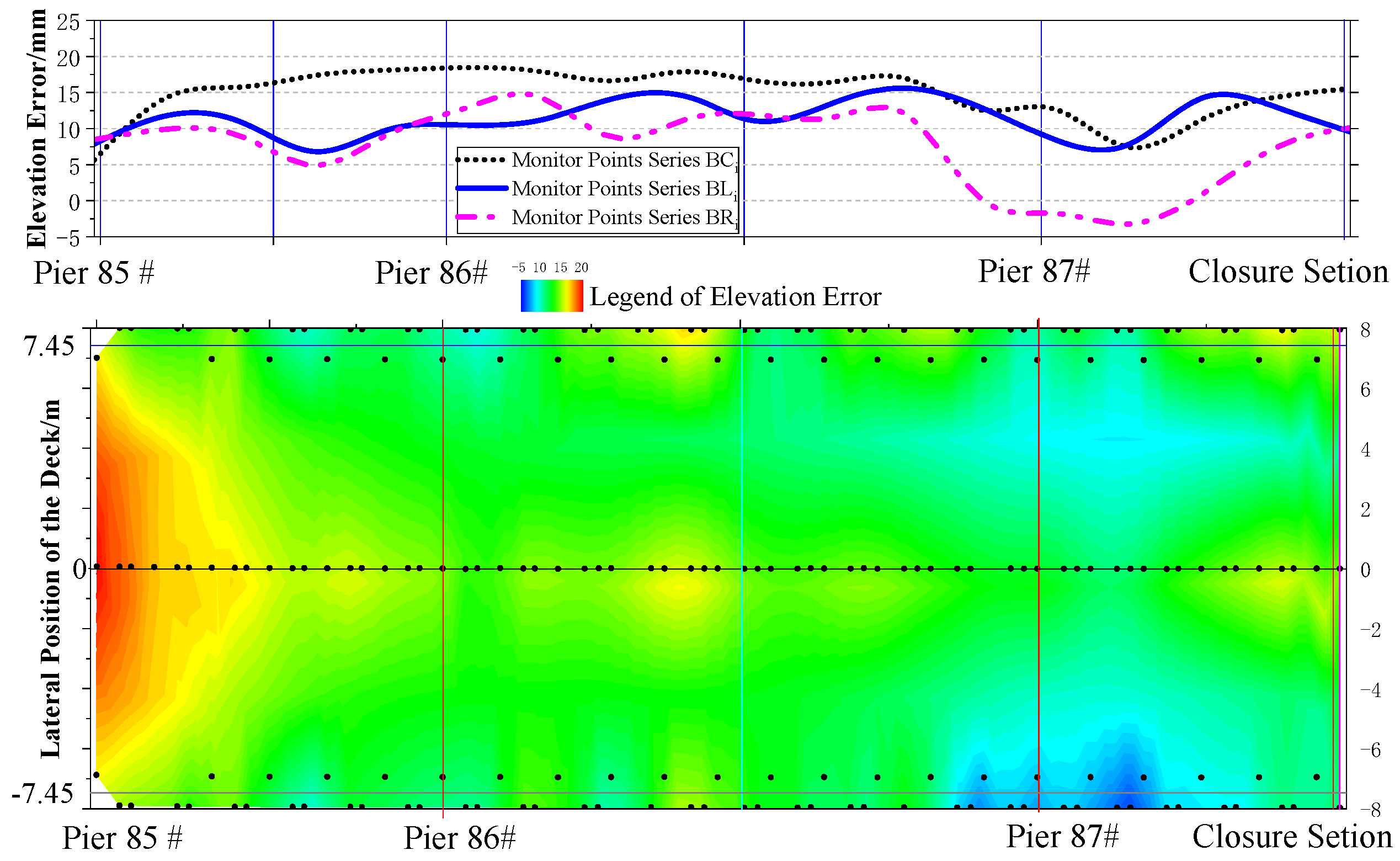
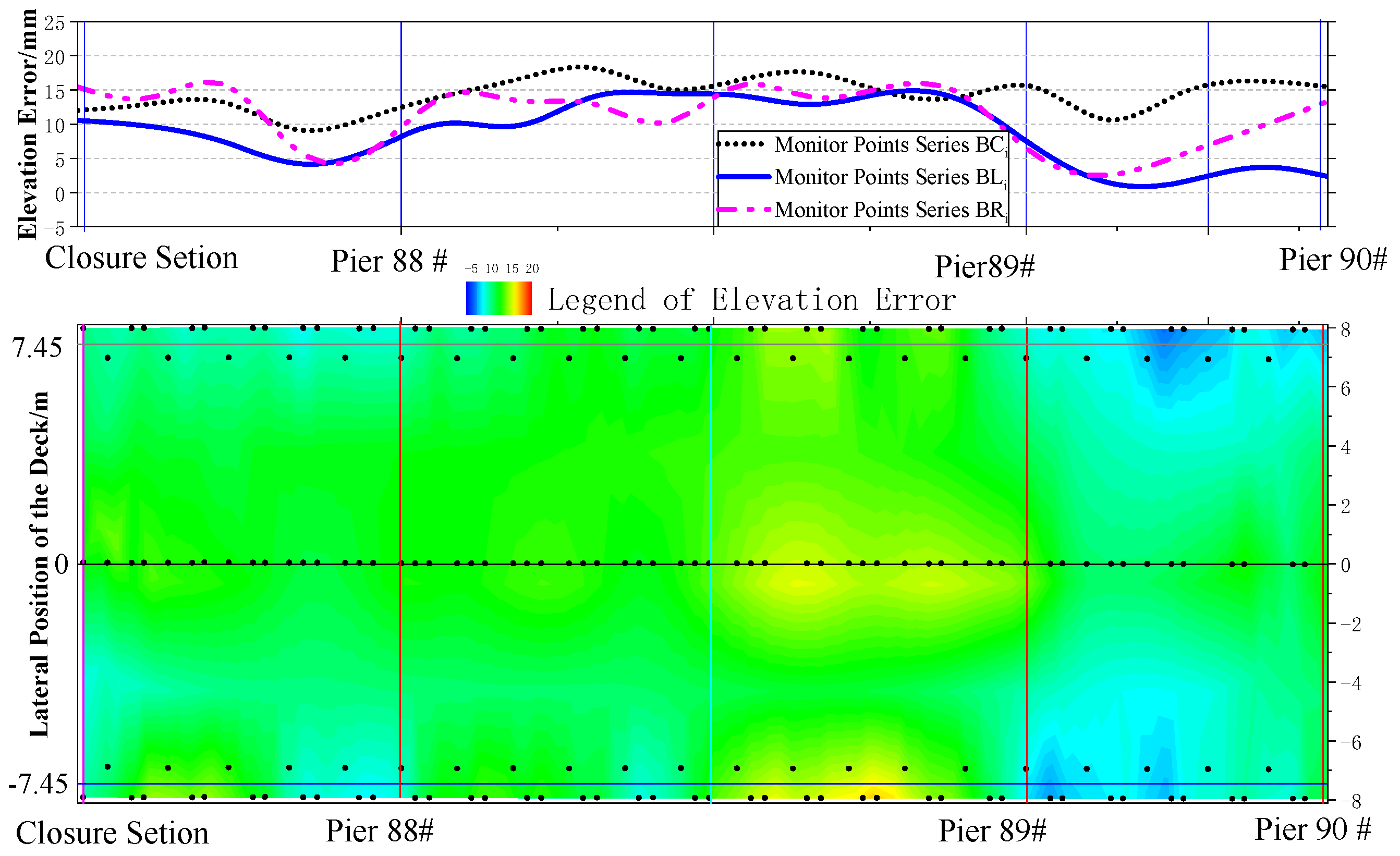
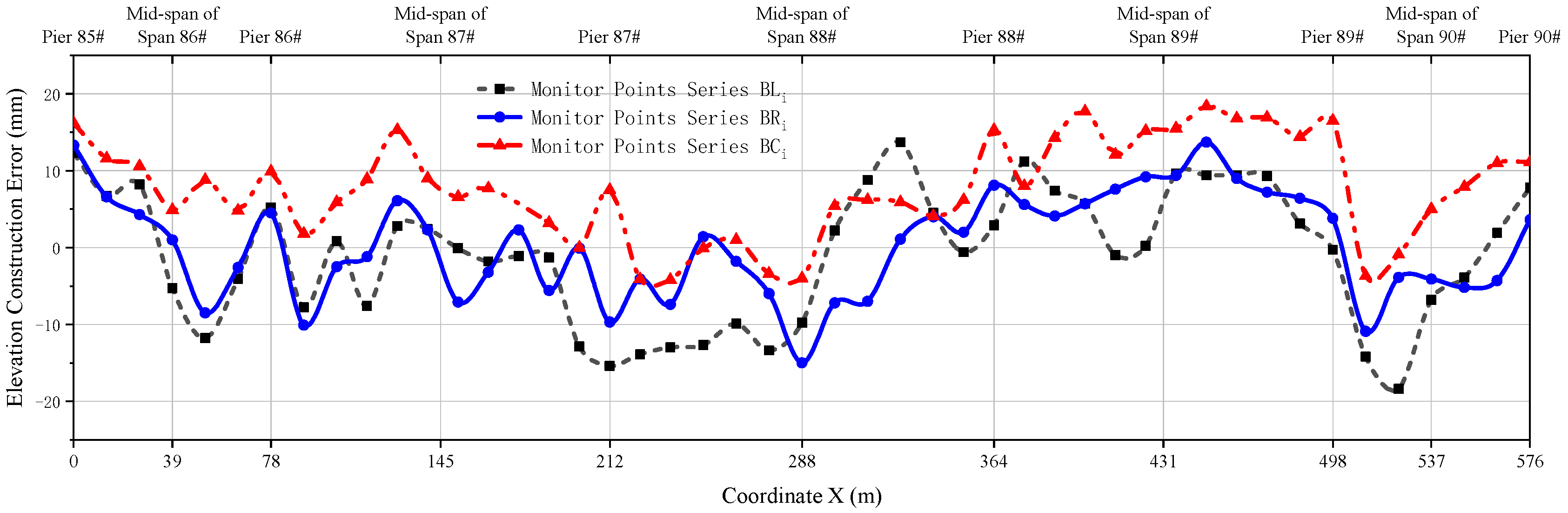
5. Application Results of Engineering
6. Conclusions
- The project validates the effectiveness of an integrated construction control system. This system combined high-fidelity FEM analysis, real-time multi-parameter monitoring, and well-defined closure techniques. The close alignment within 1.8 cm between the predicted and measured final bridge line shape confirms the system’s robustness.
- Continuous high-precision monitoring of geometry, structural stress, and temperature provided a critical feedback mechanism for the early detection of deviations. The closure segment was joined to the existing steel truss sections strictly according to the monitoring temperature of 10 °C using a pre-cut length scheme to ensure proper alignment and minimize residual stresses. This data-informed approach was vital for timely decision-making for steering the structure toward its intended geometric state and mitigating risks associated with cumulative errors.
- The feasibility of machine learning for efficient camber prediction is established, A comparative analysis between ML predictions and theoretical methods for member elongation revealed that the Extra Trees (ET) model and K-Nearest Neighbors (KNN) model achieved the excellent accuracy, with errors within 2 mm, paving the way for future applications whose robustness hinges on the development of more extensive databases of continuous steel truss rail-cum-road bridges.
- Parameter sensitivity analysis quantified the significant impact of temperature on closure precision. Longitudinal displacement (X-direction) of the top chord at the closure interface was highly sensitive to uniform temperature changes, with a 15 °C differential inducing approximately 10–12 mm of movement. Therefore, it is strongly recommended to perform closure welding when the ambient temperature is stable and close to the design reference temperature based on real-time field measurements. Construction under significant thermal differentials should be avoided to ensure closure accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Robin, S.H. Design of the Padma road and rail bridge, Bangladesh. Proc. Inst. Civ. Eng. Bridge Eng. 2015, 168, 181–192. [Google Scholar] [CrossRef]
- Chen, H.P.; Lu, S.H.; Wu, W.B.; Da, I.L.; Ceravolo, R. Fatigue damage assessment of a large rail-cum-road steel truss-arch bridge using structural health monitoring dynamic data. Case Stud. Constr. Mater. 2024, 21, e03772. [Google Scholar] [CrossRef]
- Xie, X.; Su, H.; Pang, M. Mechanical Properties and Experimental Study of a New Laminated Girder Single Tower Cable-Stayed Bridge. Int. J. Steel Struct. 2023, 23, 872–885. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, X.; Ding, Y.; Liu, X. Long-term monitoring of temperature differences in a steel truss bridge with two-layer decks compared with bridge codes: Case study. J. Bridge Eng. 2021, 26, 05020013. [Google Scholar] [CrossRef]
- Wang, Y.; Saul, R. Wide Cable-supported Bridges for r ail-cum-road Traffic. Struct. Eng. Int. 2020, 30, 551–559. [Google Scholar] [CrossRef]
- Xu, W.; Bao, L.X.; Liu, H. Retrofitting design of roadway bridge of main bridge of Jiujiang Changjiang river bridge. Bridge Constr. 2017, 47, 88–93. [Google Scholar]
- Chen, Y.; Sun, H.; Feng, Z. Study on seismic isolation of long span double deck steel truss continuous girder bridge. Appl. Sci. 2022, 12, 2567. [Google Scholar] [CrossRef]
- Yi, L.; Mei, D.P.; Zhou, C. Design of a rail–road asymmetrical low-pylon cable-stayed bridge with a main span of 588 m. Proc. Inst. Civil Eng. Bridge Eng. 2020, 173, 190–197. [Google Scholar] [CrossRef]
- Luo, X.; Fu, S.X.; Gu, X.L.; Cai, L.R. Analysis of Effect of Fetching Girder from Trestle of Long-Span Steel Truss Bridge under Cantilever Erection. Appl. Mech. Mater. 2014, 3308, 1522–1526. [Google Scholar] [CrossRef]
- Nathan, M.; Reuben, Z. Temporary works for dismantling steel cantilever truss bridges in the USA. Proc. Inst. Civ. Eng. Civ. Eng. 2023, 176, 40–47. [Google Scholar]
- Wang, L.; Xu, J.; Li, Y.; Zhou, S. Closure technology of large span steel truss arch bridge with temporarily fixed edge supports. Nonlinear Eng. 2025, 14, 20240067. [Google Scholar] [CrossRef]
- Wu, X.; Wu, T.; Chen, W. Analysis of height difference between three trusses of a steel truss bridge during incremental launching. Stahlbau 2018, 87, 910–922. [Google Scholar] [CrossRef]
- Ding, S.H.; Fang, J.; Zhang, S.L.; Liang, S.S. A Construction Technique of Incremental Launching for a Continuous Steel Truss Girder Bridge with Suspension Cable Stiffening Chords. Struct. Eng. Int. 2020, 31, 93–98. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, M.; Jin, T.; Shi, X.; Zhang, J.; Xu, Y.; Guo, X.; Cai, X.; Peng, W. Computer Vision-Based Monitoring of Bridge Structural Vibration During Incremental Launching Construction. Buildings 2025, 15, 1139. [Google Scholar] [CrossRef]
- Martins, M.H.; Thrall, P.A.; Byers, D.D.; Zoliet, T.P. Behavior of incrementally launched modular steel truss bridges. Eng. Struct. 2025, 326, 119509. [Google Scholar] [CrossRef]
- López, S.; Makoond, N.; Sánchez-Rodríguez, A.; Adam, J.M.; Riveiro, B. Learning from failure propagation in steel truss bridges. Eng. Fail. Anal. 2023, 152, 107488. [Google Scholar] [CrossRef]
- Kim, D.; Kwak, Y.; Sohn, H. Accelerated cable-stayed bridge construction using terrestrial laser scanning. Autom. Constr. 2020, 117, 103269. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Sun, Y.; Mao, X.; Tang, S. Process-independent construction stage analysis of self-anchored suspension bridges. Autom. Constr. 2020, 117, 103227. [Google Scholar] [CrossRef]
- Liu, H.; Li, M.; Dai, Y.; Ou, M. Key Construction Technologies for Steel Truss Bridges in High Water Level and High Flow Velocity Conditions: A Case Study for Shoupanyan Bridge. In Proceedings of the Conference on Sustainable Traffic and Transportation Engineering in 2023. CSTTE 2023, Yinchuan, China, 22–24 November 2023; Lecture Notes in Civil Engineering. Springer: Singapore, 2023; Volume 603. [Google Scholar]
- Zhao, H.; Ding, Y.; Nagarajaiah, S.; Li, A. Longitudinal Displacement Behavior and Girder End Reliability of a Jointless Steel-Truss Arch Railway Bridge during Operation. Appl. Sci. 2019, 9, 2222. [Google Scholar] [CrossRef]
- Chen, Y.; Liao, Y.; Zhu, L.; Chen, L.; Chen, Y. Robustness of a Steel Truss Bridge Subjected to Sudden Member Breakage during the Continuous-to-Simply-Supported Transition. Buildings 2024, 14, 3035. [Google Scholar] [CrossRef]
- Sun, Y.; Tai, X.; Liu, K.; Zhu, A.Z.; Zhu, H.P. Determining launching construction parameters of superlong superwide bridges: A multiobjective optimization method using machine learning techniques. Structures 2022, 41, 15–28. [Google Scholar] [CrossRef]
- Yu, X.; Deng, Y.; Yan, B. Case study of the 156 m simply supported steel truss railway bridge. Struct. Eng. Int. 2017, 27, 563–568. [Google Scholar] [CrossRef]
- Aksar, B.; Ozdemir, M.A.; Tutar, A.I.; Cakir, F. Structural Analysis of Steel Truss and Masonry Bridge Interaction: A Case of Ali Fuat Pasha Bridge in Sakarya, Türkiye. J. Inst. Sci. Technol. 2023, 13, 1784–1798. [Google Scholar]
- Tran, M.Q.; Sousa, H.S.; Ngo, T.V.; Nguyen, B.D.; Nguyen, Q.T.; Nguyen, H.X.; Baron, E.; Matos, J.; Dang, S.N. Structural Assessment Based on Vibration Measurement Test Combined with an Artificial Neural Network for the Steel Truss Bridge. Appl. Sci. 2023, 13, 7484. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, G.; Li, J.; Wang, Y.; Chen, B. Temperature Response of Double-Layer Steel Truss Bridge Girders. Buildings 2023, 13, 2889. [Google Scholar] [CrossRef]
- Li, Z.F.; Niu, Z.G.; Fang, J.; Ding, S.H.; Li, W.J. Mechanical Analysis of Key Joints of Super-spanned Steel Truss Girder in Incremental Launching Construction. J. China Railw. Soc. 2021, 43, 158–165. [Google Scholar]
- Lou, S.; Wu, F.; Jiang, Y.; Wang, J. Mechanical Analysis of Walking—Type Incremental Launching and Sliding Construction of Large Tonnage Steel Truss Girder. Bridge Constr. 2020, 37, 35–40. [Google Scholar]
- Chen, H.; Li, J.; Li, Y.X. Local stress analysis of integral joint of continuous steel truss girder at construction stage. Bridge Constr. 2011, 5, 21–25+58. [Google Scholar]
- Edward, P.; Elena, M.; Daniel, G.; Băncilă, R. Pre-cambering in steel and composite bridge structures. Adv. Mater. Res. 2015, 1111, 169–174. [Google Scholar] [CrossRef]
- UT/T 1246-2019; Technical Specifications for Design of Highway Steel-Concrete Composite Beam Bridges. China Communications Press: Beijing, China, 2019.
- TB 10002-2017; Code for Design of Railway Bridge and Culvert. China Railway Publishing House: Beijing, China, 2017.
- CJJ11-2011; Code of Design for City Bridge. China Architecture & Building Press: Beijing, China, 2011.
- Qin, S.Q. Theory and Practice of Unstressed State Method for Bridge Construction Control; Communications Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- TB10760-2021; Technical Code for Static Acceptance of High-Speed Railway Engineering in China. China Railway Publishing House: Beijing, China, 2011.
- Qin, S.Q. Unstressed state control methodfor bridges constructed in stages. Bridge Constr. 2008, 1, 8–14. (In Chinese) [Google Scholar]
- Li, Z.; Dong, X.; Chen, H.; Chi, L.; Zhang, Z. Overall Lifting Construction Control Method for Large-Segment Steel Arch Bridges Based on Unstressed State Control Theory. Buildings 2025, 15, 523. [Google Scholar] [CrossRef]
- Lin, C.; Doyog, N.D. Applying a Four-Way Factorial Experimental Model to Diagnose Optimum kNN Parameters for Precise Aboveground Biomass Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 18, 479–495. [Google Scholar] [CrossRef]
- Tetteh, E.T.; Zielosko, B. Greedy Algorithm for Deriving Decision Rules from Decision Tree Ensembles. Entropy 2025, 27, 35. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, L.; Feng, Y.; Yan, H.; Mi, Q. Multivariate temperature prediction model based on CNN-BiLSTM and RandomForest. J. Supercomput. 2025, 81, 162. [Google Scholar] [CrossRef]
- Wang, F.; Wang, J. Establishment and validation of a prognostic risk early-warning model for retinoblastoma based on XGBoost. Am. J. Cancer Res. 2025, 15, 99. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Salih, A.K.; Hussein, H.A.A. Lost circulation prediction using decision tree, random forest, and extra trees algorithms for an Iraqi oil field. Iraqi Geol. J. 2022, 55, 111–127. [Google Scholar] [CrossRef]
- Fang, R.; Zhou, T.; Yu, B.; Li, Z.; Ma, L.; Luo, T.; Zhang, Y.; Liu, X. Prediction model of middle school student performance based on MBSO and MDBO-BP-Adaboost method. Front. Big Data 2025, 7, 1518939. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Wang, F.; Wang, W.; Zhang, T.; Wu, H.; Ning, W. Research on intrusion detection model based on improved MLP algorithm. Sci. Rep. 2025, 15, 5159. [Google Scholar] [CrossRef] [PubMed]
- Sun, B. Gray Model and Back Propagation Neural Network Fusion Forecast for Real-Time Temperature in Utility Tunnel Fires. Combust. Sci. Technol. 2025, 1–17. [Google Scholar] [CrossRef]
- Xu, B.; Wang, R.; Zhou, K.; Zhou, X.; Xu, T.; Bian, Q. Research on the physical characteristics of a novel modified foamed cement slurry with non-foamed PVA material. Constr. Build. Mater. 2025, 459, 139710. [Google Scholar] [CrossRef]
- Wang, X.; Miao, C.; Wang, X. Prediction analysis of deflection in the construction of composite box-girder bridge with corrugated steel webs based on MEC-BP neural networks. Structures 2021, 32, 691–700. [Google Scholar] [CrossRef]








| Construction Stage | Max Def. of Span 86 | Max Def. of Span 87 | Max Def. of Span 88 | Max Stress of Truss | Max Def. of Brackets | Max Stress of Brackets |
|---|---|---|---|---|---|---|
| Cantilever Stage | −7.7 mm | −6.7 mm | −7.6 mm | 35.5 MPa | 6 mm | 61.6 MPa |
| Closure Stage | −7.7 mm | −6.6 mm | −9.0 mm | 38.1 MPa | 4 mm | 28.5 MPa |
| Removal of Brackets | −21.8 mm | −53.0 mm | −68.1 mm | 59.5 MPa | / | / |
| Deck Construction | −32.8 mm | −89.4 mm | −117.5 mm | 131.1 MPa | / | / |
| Num. | Seg. Num. | Tp | Sp | x0/m | /m | /T | /T | /mm | /T | /m | /T | /T | /mm | /T | T/T | ΔL/mm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A1–A2 | 5 | 1 | 11.25 | 11.25 | 3.5 | 16 | 149 | 247.8 | 7.35 | 76.5 | 13.3 | 16 | 142.09 | 231.9 | −15.01 |
| 2 | A2–A3 | 5 | 1 | 22.5 | 11.25 | 3.5 | 16 | 147.3 | 237.8 | 13 | 88.5 | 11.2 | 16 | 169.68 | 269.4 | 6.37 |
| 3 | A3–A4 | 5 | 1 | 35.5 | 13 | 3.5 | 16 | 147.3 | 237.7 | 13 | 88.5 | 11.2 | 16 | 169.68 | 269.4 | 7.55 |
| 4 | A4–A5 | 5 | 1 | −39 | 13 | 3.5 | 16 | 147.3 | 240.1 | 13 | 88.5 | 11.2 | 16 | 169.68 | 269.4 | 6.47 |
| 5 | A5–A6 | 5 | 1 | −26 | 13 | 3.9 | 16 | 147.3 | 246.6 | 13 | 98.8 | 12.2 | 16 | 169.68 | 280.7 | 4.12 |
| 6 | A6–A7 | 5 | 1 | −13 | 13 | 3.9 | 24 | 170.1 | 276.3 | 13 | 116.1 | 19.1 | 16 | 169.68 | 304.9 | 0 |
| 7 | A7–A8 | 5 | 1 | 0 | 13 | 3.9 | 24 | 170.1 | 283.3 | 13 | 155.1 | 22.8 | 16 | 204.78 | 382.8 | −33.26 |
| 8 | A8–A9 | 5 | 2 | 13 | 13 | 3.2 | 16 | 142.7 | 247.3 | 13 | 121.9 | 18.3 | 16 | 169.68 | 309.9 | 0.1 |
| 9 | A9–A10 | 5 | 2 | 25.35 | 12.35 | 3.5 | 16 | 149 | 245.3 | 13.5 | 104.2 | 15.1 | 16 | 173.54 | 292.8 | 5.31 |
| 10 | A10–A11 | 5 | 2 | 38.6 | 13.25 | 3.5 | 16 | 143.7 | 230.1 | 12.5 | 88.2 | 11.5 | 16 | 152.74 | 252.4 | 6.37 |
| 11 | A11–A12 | 5 | 2 | 51.1 | 12.5 | 3.5 | 16 | 129.8 | 214 | 12 | 82.1 | 11.2 | 16 | 148.88 | 242.2 | 8.5 |
| 12 | A12–A13 | 5 | 2 | 63.1 | 12 | 3.5 | 16 | 129.8 | 214 | 12 | 82.1 | 11.2 | 16 | 148.88 | 242.2 | 9.03 |
| 13 | A13–A14 | 5 | 2 | −60.5 | 12 | 3.5 | 16 | 129.8 | 215.8 | 12 | 82.1 | 11.2 | 16 | 148.88 | 242.2 | 8.29 |
| 14 | A14–A15 | 5 | 2 | −48.5 | 12 | 3.5 | 16 | 129.8 | 220.1 | 12 | 86.8 | 11.5 | 16 | 148.88 | 247.1 | 5.74 |
| 15 | A15–A16 | 5 | 2 | −36.5 | 12 | 3.9 | 16 | 129.8 | 230.7 | 12 | 97.4 | 15.8 | 16 | 148.88 | 262.1 | 2.02 |
| 16 | A16–A17 | 5 | 2 | −24.5 | 12 | 4.5 | 16 | 129.8 | 247.5 | 12 | 125.5 | 21.2 | 16 | 148.88 | 295.6 | −1.28 |
| 17 | A17–A18 | 5 | 2 | −12.5 | 12 | 4.5 | 24 | 176 | 302.3 | 12 | 144 | 35.7 | 16 | 148.88 | 328.7 | −2.13 |
| 18 | A18–A19 | 5 | 2 | 0 | 12.5 | 4.5 | 24 | 171.6 | 295.6 | 12 | 177.7 | 35.7 | 16 | 196.92 | 410.4 | −39.96 |
| 19 | A19–A20 | 5 | 3 | 12.5 | 12 | 3.9 | 24 | 141.2 | 255.7 | 12 | 136.9 | 28 | 16 | 148.88 | 313.8 | −1.91 |
| 20 | A20-A21 | 5 | 3 | 24.5 | 12.5 | 3.5 | 16 | 143.7 | 250.9 | 11 | 117 | 20.9 | 16 | 141.17 | 279.1 | −2.45 |
| 21 | A21–A22 | 5 | 3 | 37 | 12 | 3.5 | 16 | 147.3 | 243.8 | 13 | 103.5 | 15.1 | 16 | 169.68 | 288.2 | 3.14 |
| 22 | A22–A23 | 5 | 3 | 49 | 12 | 3.5 | 16 | 147.3 | 240 | 13 | 93.6 | 11.5 | 16 | 169.68 | 274.8 | 7.26 |
| 23 | A23–A24 | 5 | 3 | 61 | 12 | 3.5 | 16 | 147.3 | 237.8 | 13 | 88.5 | 11.2 | 16 | 169.68 | 269.4 | 9.9 |
| 24 | A24–A24′ | 5 | 3 | −72.5 | 12 | 0 | 16 | 58 | 80.2 | 13 | 88.2 | 7.1 | 16 | 169.68 | 265 | 0 |
| 25 | A24′–A23′ | 5 | 3 | −60.5 | 12 | 3.5 | 16 | 147.3 | 237.8 | 13 | 88.5 | 11.2 | 16 | 169.68 | 269.4 | 9.81 |
| 26 | A23–A22′ | 5 | 3 | −48.5 | 12 | 3.5 | 16 | 147.3 | 240 | 13 | 93.6 | 11.5 | 16 | 169.68 | 274.8 | 7.45 |
| 27 | A22′–A21’ | 5 | 3 | −36.5 | 12 | 3.5 | 16 | 147.3 | 243.8 | 13 | 103.5 | 15.1 | 16 | 169.68 | 288.2 | 3.04 |
| 28 | A21–A20’ | 5 | 3 | −24.5 | 12.5 | 3.5 | 16 | 143.7 | 250.9 | 11 | 117 | 20.9 | 16 | 141.17 | 279.1 | −2.45 |
| 29 | A20’–A19’ | 5 | 3 | −12 | 12 | 3.9 | 24 | 141.2 | 255.7 | 12 | 136.9 | 28 | 16 | 148.88 | 313.8 | −1.91 |
| 30 | A19’–A18’ | 5 | 3 | 0 | 12.5 | 4.5 | 24 | 171.6 | 295.6 | 12 | 177.7 | 35.7 | 16 | 196.92 | 410.4 | −39.75 |
| 31 | A18’–A17’ | 5 | 2 | 12.5 | 12 | 4.5 | 24 | 176 | 302.3 | 12 | 144 | 35.7 | 16 | 148.88 | 328.7 | −2.44 |
| 32 | A17–A16’ | 5 | 2 | 24.5 | 12 | 4.5 | 16 | 129.8 | 247.5 | 12 | 125.5 | 21.2 | 16 | 148.88 | 295.6 | −1.28 |
| 33 | A15’–A14’ | 5 | 2 | 36.5 | 12 | 3.9 | 16 | 129.8 | 230.7 | 12 | 97.4 | 15.8 | 16 | 148.88 | 262.1 | 2.12 |
| 34 | A14–A13’ | 5 | 2 | 48.5 | 12 | 3.5 | 16 | 129.8 | 220.1 | 12 | 86.8 | 11.5 | 16 | 148.88 | 247.1 | 5.84 |
| 35 | A13’–A12’ | 5 | 2 | 60.5 | 12 | 3.5 | 16 | 129.8 | 215.8 | 12 | 82.1 | 11.2 | 16 | 148.88 | 242.2 | 8.18 |
| 36 | A12–A11’ | 5 | 2 | 72.5 | 12 | 3.5 | 16 | 129.8 | 214 | 12 | 82.1 | 11.2 | 16 | 148.88 | 242.2 | 9.14 |
| ML Model | Training Set Indicators | Test Set Indicators | ||||||
|---|---|---|---|---|---|---|---|---|
| MSE | RMSE | MAE | R2 | MSE | RMSE | MAE | R2 | |
| Random Forest | 5.946 | 2.438 | 1.584 | 0.669 | 7.321 | 2.706 | 1.668 | 0.950 |
| XGBoost | 8.140 | 2.853 | 1.743 | 0.546 | 2.704 | 1.645 | 1.134 | 0.982 |
| Gradient Boosting | 0.225 | 0.474 | 0.326 | 0.987 | 2.718 | 1.649 | 1.040 | 0.982 |
| Extra Trees | 1.079 | 1.039 | 0.908 | 0.940 | 0.542 | 0.736 | 0.630 | 0.996 |
| AdaBoost | 2.087 | 1.445 | 1.390 | 0.884 | 0.644 | 0.802 | 0.651 | 0.995 |
| SVM | 5.628 | 2.372 | 1.721 | 0.686 | 11.064 | 3.326 | 2.684 | 0.925 |
| KNN | 4.754 | 2.180 | 1.818 | 0.735 | 17.100 | 4.135 | 2.608 | 0.884 |
| Decision Tree | 1.308 | 1.144 | 0.951 | 0.936 | 17.571 | 4.192 | 2.687 | 0.881 |
| MLP | 3.734 | 1.932 | 1.541 | 0.818 | 2.688 | 1.640 | 1.197 | 0.982 |
| Num. | Seg. Num. | Theoretical Values | RF | XGBoost | GB | ET | AdB | SVM | KNN | DT | MLP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A11’–A10’ | 6.37 | 6.55 | 6.08 | 6.29 | 7.17 | 7.04 | 8.18 | 6.38 | 6.23 | 10.34 |
| 2 | A10’–A9’ | 5.21 | 3.96 | 4.59 | 5.23 | 4.53 | 4.65 | 4.18 | 4.85 | 3.34 | 5.52 |
| 3 | A9’–A8’ | 0 | −0.44 | 0.07 | 0.10 | 0.02 | −0.59 | −3.66 | 0.18 | −3.11 | 0.57 |
| 4 | A8’–A7’ | −33.26 | −30.48 | −29.26 | −35.05 | −32.91 | −33.26 | −26.57 | −33.66 | −37.66 | −34.58 |
| 5 | A7’–A6’ | 0.29 | −2.10 | −0.48 | −0.07 | 0.12 | −1.34 | 1.22 | 0.41 | −3.11 | −0.90 |
| 6 | A6’–A5’ | 4.32 | 3.34 | 3.95 | 3.80 | 5.17 | 4.65 | 2.58 | 4.05 | 3.34 | 3.87 |
| 7 | A5’–A4’ | 6.37 | 7.01 | 8.22 | 7.51 | 7.46 | 7.04 | 6.14 | 6.05 | 6.23 | 6.25 |
| 8 | A4’–A3’ | 7.65 | 7.27 | 7.17 | 7.38 | 7.52 | 7.04 | 4.48 | 7.01 | 6.23 | 7.57 |
| 9 | A3’–A2’ | 6.28 | 7.05 | 7.47 | 7.38 | 7.49 | 7.04 | 4.68 | 6.05 | 6.23 | 7.43 |
| 10 | A2’–A1’ | −15.01 | −14.08 | −10.27 | −10.35 | −14.17 | −15.01 | −19.67 | −14.99 | −13.11 | −17.60 |
| T (°C) | Upper Chord (A24–A23) Deformation (mm) | Diagonal Web (A24–A23) Deformation (mm) | ||||
|---|---|---|---|---|---|---|
| Dx | Dy | Dz | Dx | Dy | Dz | |
| 22.5 | 2.5 | −0.1 | −2.3 | 7.5 | −1.4 | −9.8 |
| 20 | 0.6 | −0.1 | −3.2 | 6.5 | −1.5 | −10.1 |
| 17.5 | −1.3 | −0.0 | −4.2 | 5.5 | −1.5 | −10.4 |
| 15 | −3.2 | −0.0 | −5.1 | 4.5 | −1.6 | −10.7 |
| 12.5 | −5.1 | 0.0 | −6.1 | 3.5 | −1.6 | −11.1 |
| 10 | −7.0 | 0.0 | −7.1 | 2.5 | −1.7 | −11.3 |
| 7.5 | −8.9 | 0.1 | −8.0 | −1.5 | −1.7 | −11.7 |
| 5 | −10.8 | 0.1 | −9.0 | 0.5 | −1.8 | −11.9 |
| Installation Parts | Left String Pole Deformation (mm) | Right String Pole Deformation (mm) | ||||
|---|---|---|---|---|---|---|
| Dx | Dy | Dz | Dx | Dy | Dz | |
| GL-S20 | 1.1 | 0.7 | −2.2 | 1.1 | −0.6 | −2.1 |
| TL-X22 | −0.4 | −0.4 | −4.0 | −0.4 | 0.5 | −2.1 |
| GL-S21 | 1.1 | 0.7 | −2.3 | 1.1 | −0.6 | −2.3 |
| TL-X23 | −0.4 | −0.5 | −3.8 | −0.4 | 0.5 | −2.9 |
| GL-S22 | 1.0 | 0.7 | −2.3 | 1.0 | −0.6 | −2.3 |
| TL-X24 | 0.3 | −0.7 | −4.2 | 0.4 | 0.8 | −2.2 |
| GL-S23 | 1.8 | 0.7 | −5.0 | 1.8 | 0.5 | −5.2 |
| GL-S24 | 1.7 | 0.8 | −6.3 | 1.7 | −0.8 | −6.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Weng, F.; Liang, Y.; Liao, Z.; Zhang, F.; Fu, M. Construction Control of Long-Span Combined Rail-Cum-Road Continuous Steel Truss Girder Bridge of High-Speed Railway. Buildings 2025, 15, 4204. https://doi.org/10.3390/buildings15224204
Zhou J, Weng F, Liang Y, Liao Z, Zhang F, Fu M. Construction Control of Long-Span Combined Rail-Cum-Road Continuous Steel Truss Girder Bridge of High-Speed Railway. Buildings. 2025; 15(22):4204. https://doi.org/10.3390/buildings15224204
Chicago/Turabian StyleZhou, Jun, Fangwen Weng, Yuxiong Liang, Zhiwei Liao, Feng Zhang, and Meizhen Fu. 2025. "Construction Control of Long-Span Combined Rail-Cum-Road Continuous Steel Truss Girder Bridge of High-Speed Railway" Buildings 15, no. 22: 4204. https://doi.org/10.3390/buildings15224204
APA StyleZhou, J., Weng, F., Liang, Y., Liao, Z., Zhang, F., & Fu, M. (2025). Construction Control of Long-Span Combined Rail-Cum-Road Continuous Steel Truss Girder Bridge of High-Speed Railway. Buildings, 15(22), 4204. https://doi.org/10.3390/buildings15224204






