Optimizing Evacuation for Disabled Pedestrians with Heterogeneous Speeds: A Floor Field Cellular Automaton and Reinforcement Learning Approach
Abstract
1. Introduction
2. Models and Methods
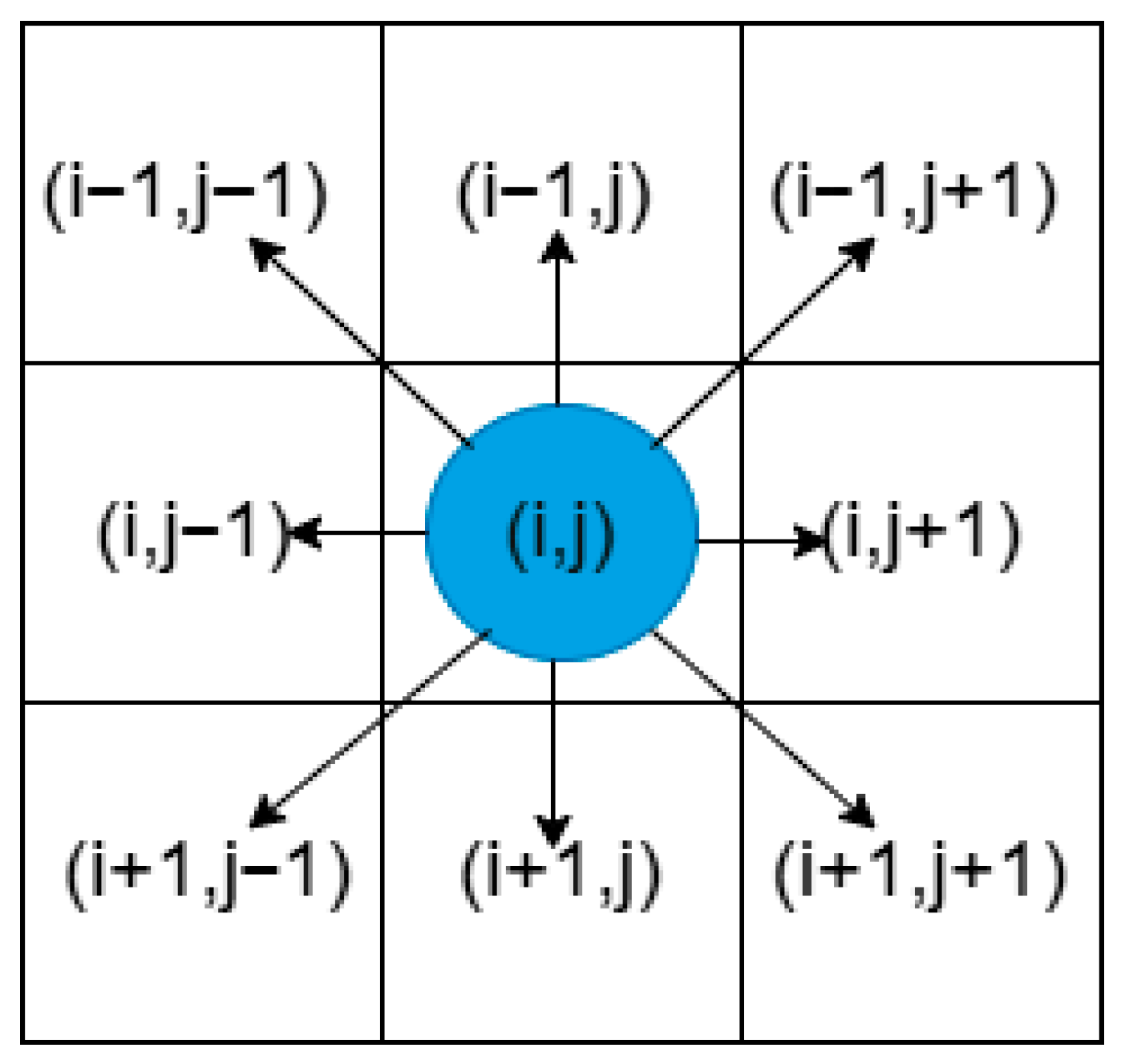
2.1. Cellular Automaton Model
2.2. Floor Field Cellular Automaton Model
2.3. Velocity Heterogeneity Modeling
2.4. Friction-Based Conflict Resolution
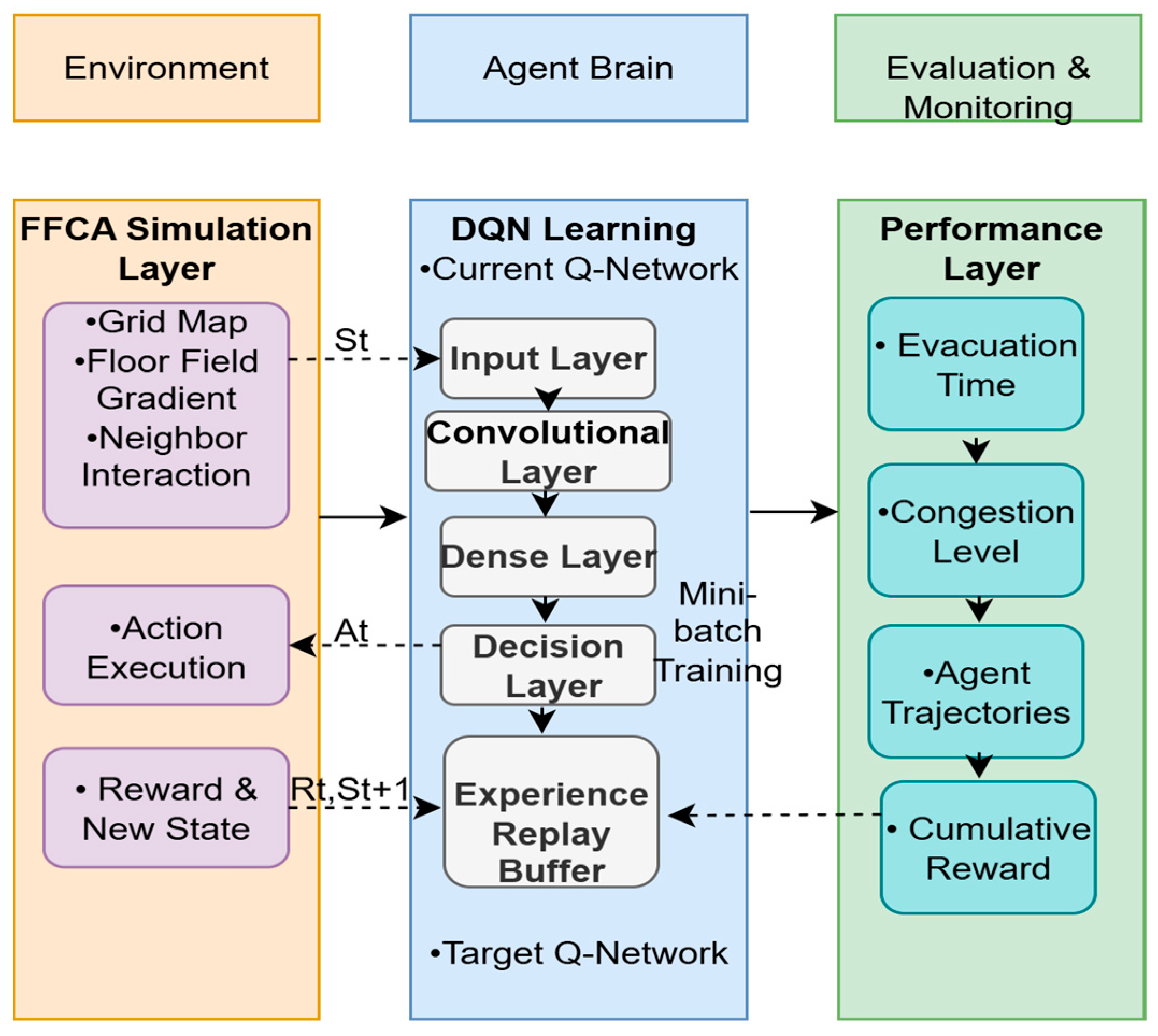
2.5. Reinforcement Learning Integration
2.5.1. Q-Learning Algorithm
2.5.2. Deep Q-Network (DQN)
| Algorithm 1. Hybrid |
| Initialize: Q-table or network Q(s,a;θ), target network θ− = θ, replay buffer D. |
| 1:For episode = 1 to MaxEpisodes: |
| 2: Reset environment; initialize agent states. |
| 3:For t = 1 to Tmax: |
| 4:For each agent: |
| . |
| using ε-greedy policy according to Equation (12). |
| 7:Aggregate action intents for all agents. |
| 8:Apply FFCA feasibility checks; resolve conflicts via friction mechanism. |
| for each agent. |
| . |
| ) in D. |
| 12:If DQN: |
| 13:Sample minibatch from D; update θ using Equation (13). |
| 14:Every C steps: θ− ← θ. |
| 15:Else if Tabular Q: |
| 16:Update Q-table using Equation (10). |
| 17:Decay ε according to Equation (12). |
| 18:End For |
| 19:End For |
2.6. Model Validation
- (1)
- Baseline validation
- (2)
- Dynamic adaptability
- (3)
- Learning-based adaptation
- (4)
- Collective Intelligence
- (5)
- Scalability and Robustness
3. Results and Discussion
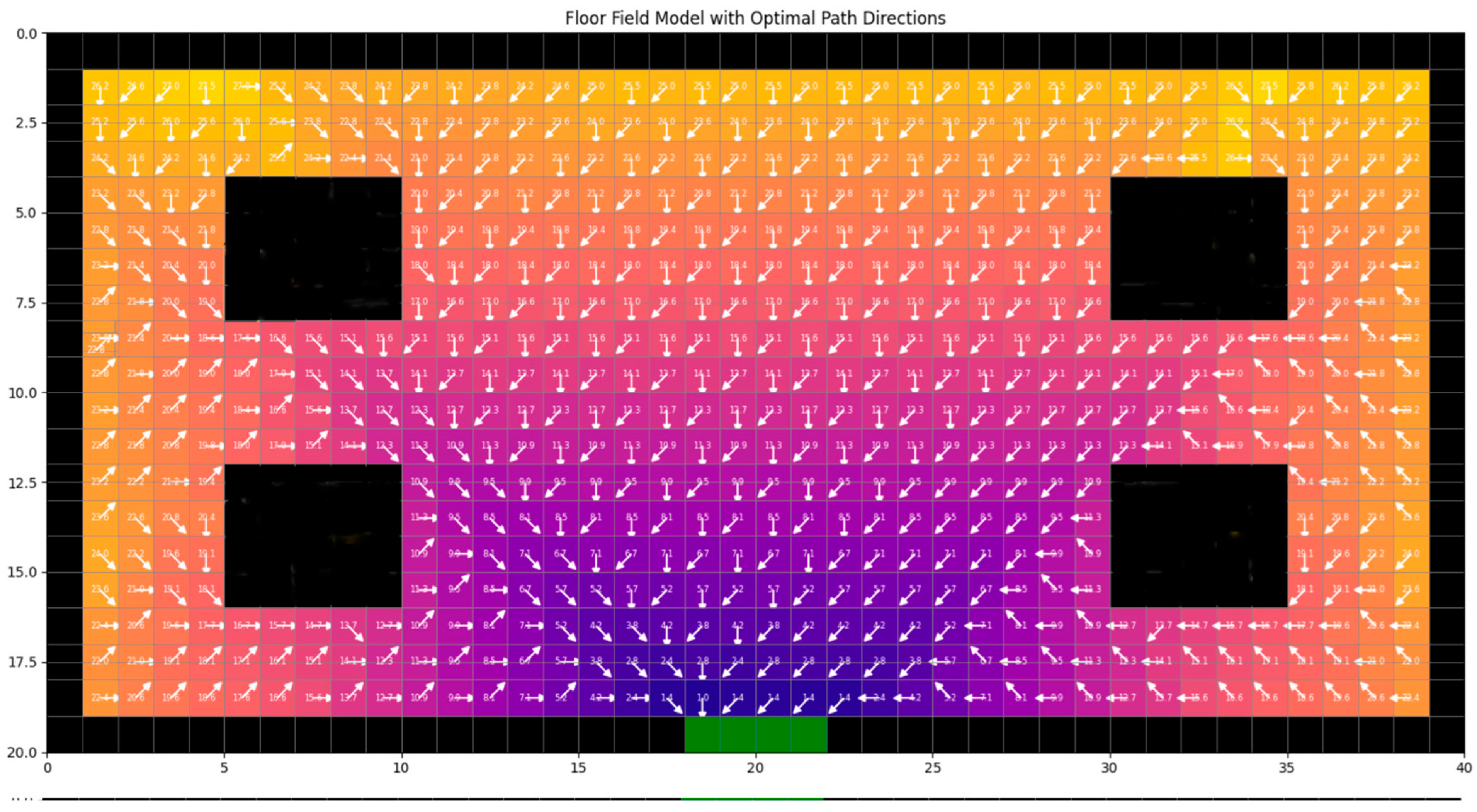
3.1. Static Floor Field Calculation and Optimal Path Planning
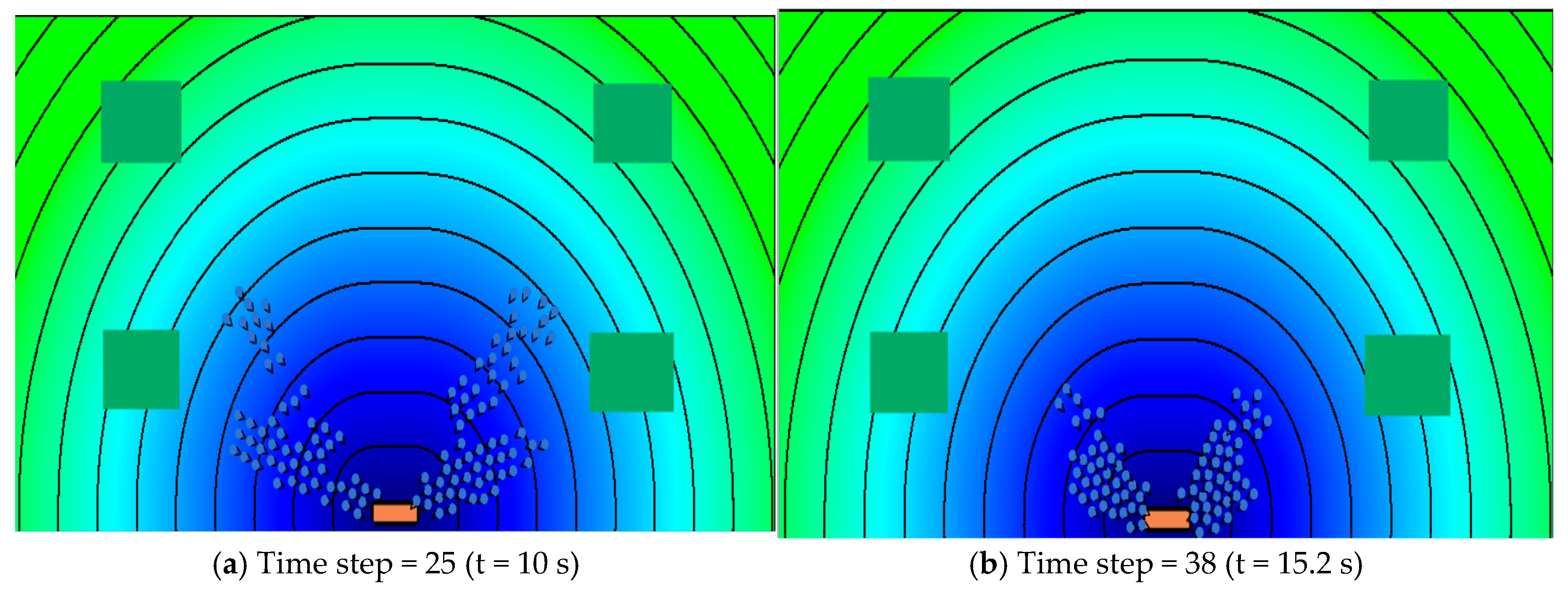
3.2. Dynamic Floor Field Simulation
3.3. Reinforcement Learning-Based Evacuation Optimization
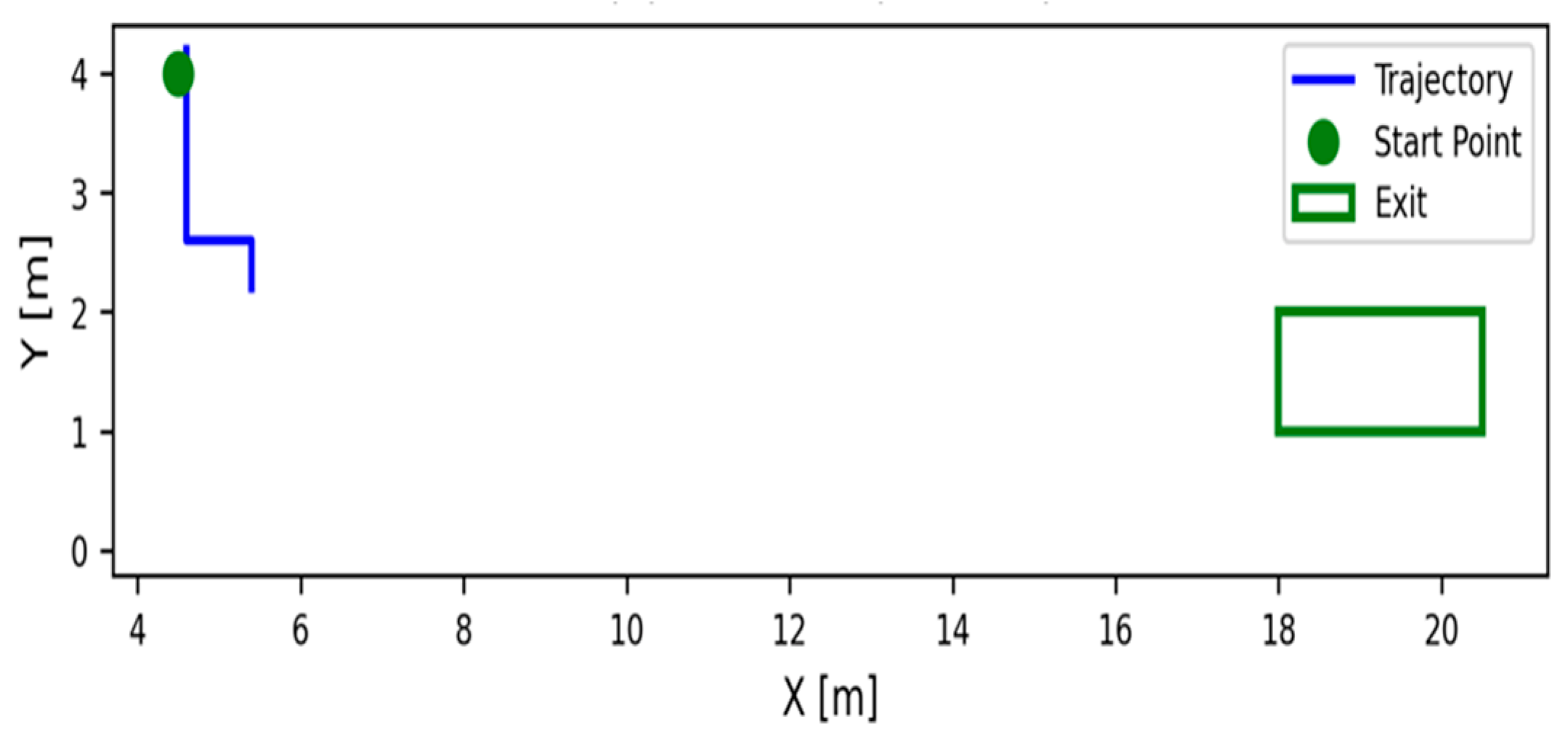
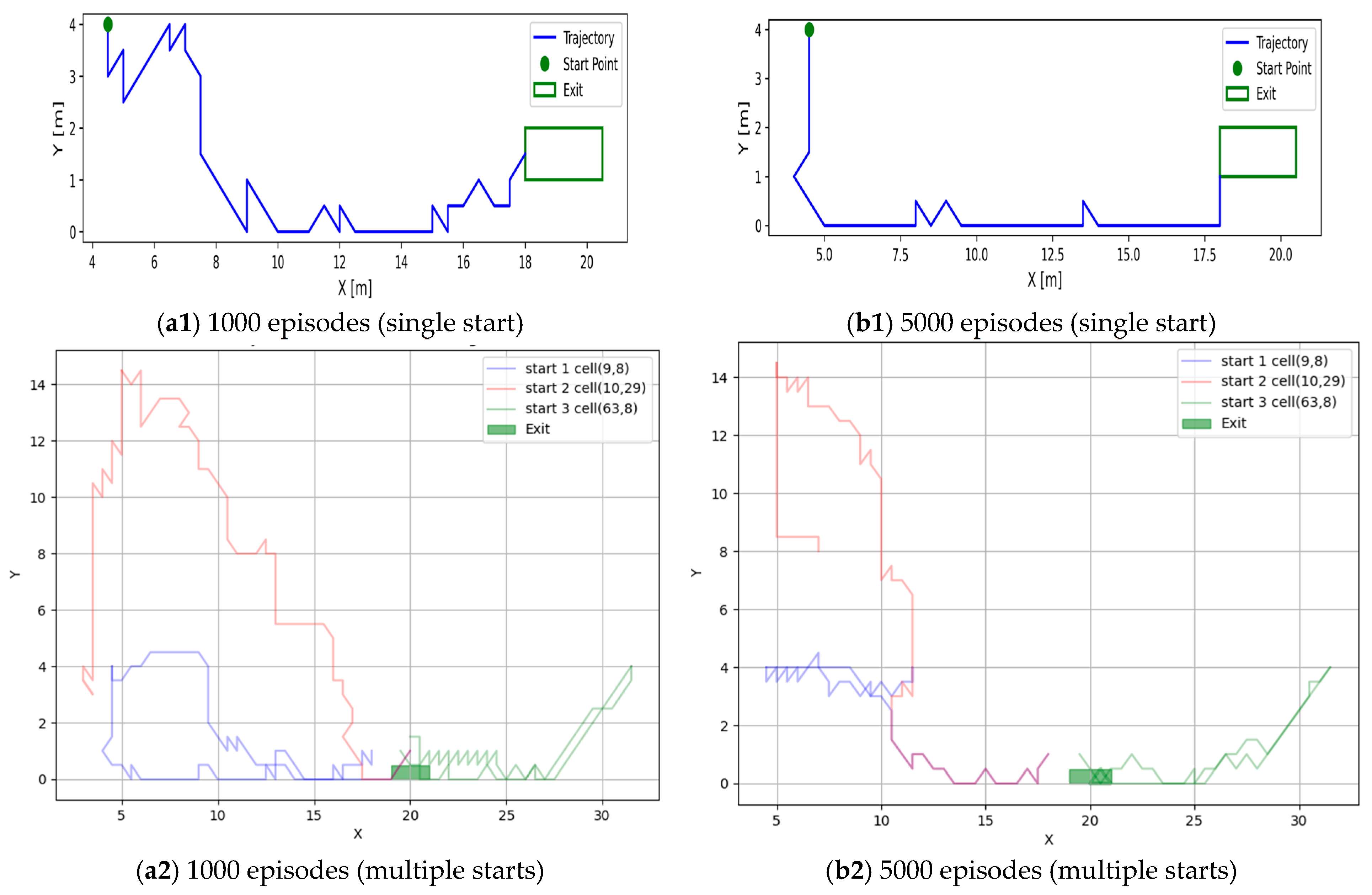
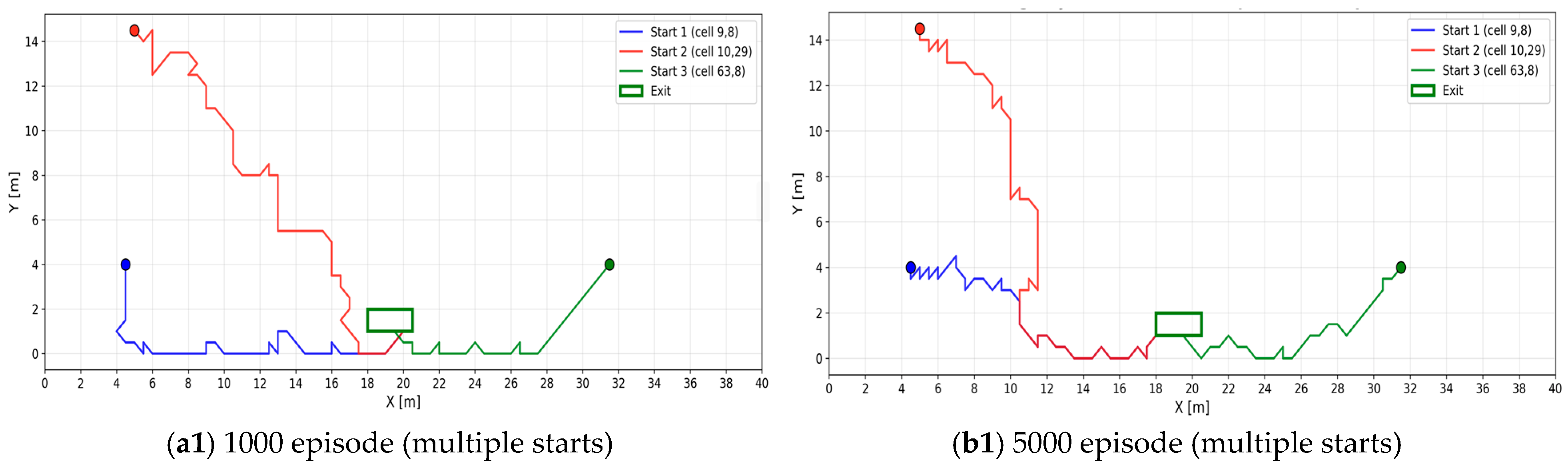
3.3.1. Single-Agent Path Optimization Based on Q-Learning
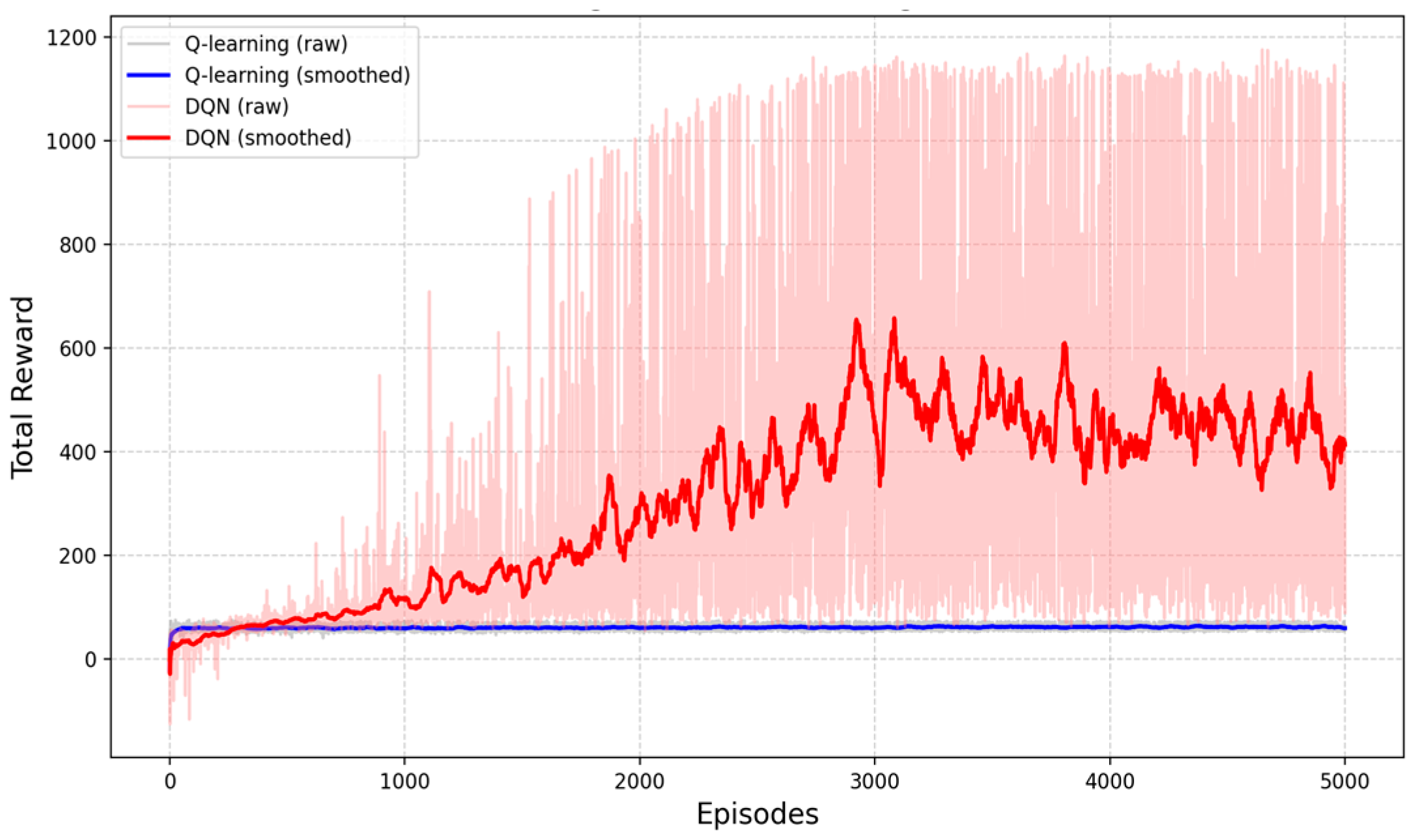
3.3.2. DQN Path Optimization with High-Dimensional State
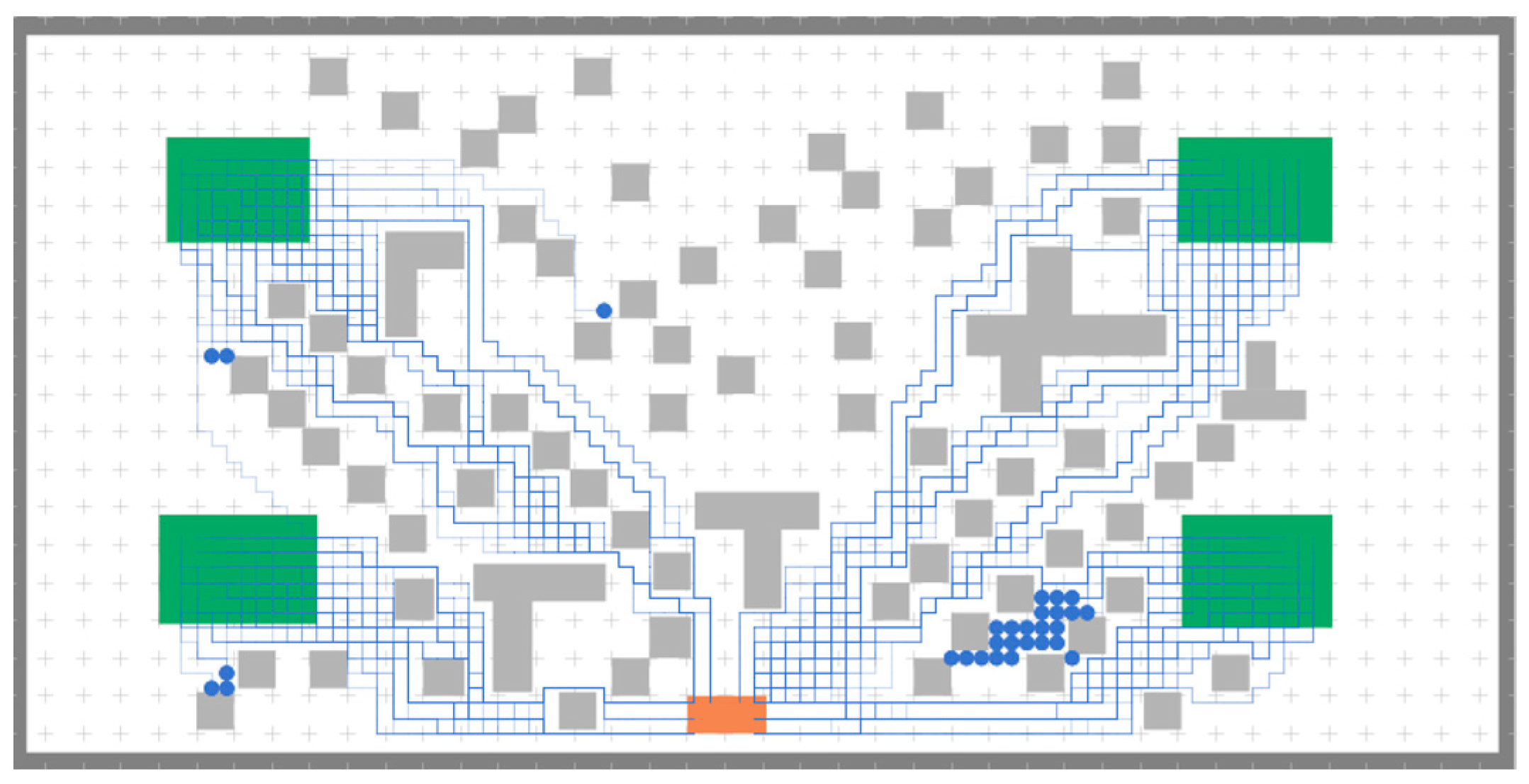
3.4. Multi-Agent Evacuation Optimization
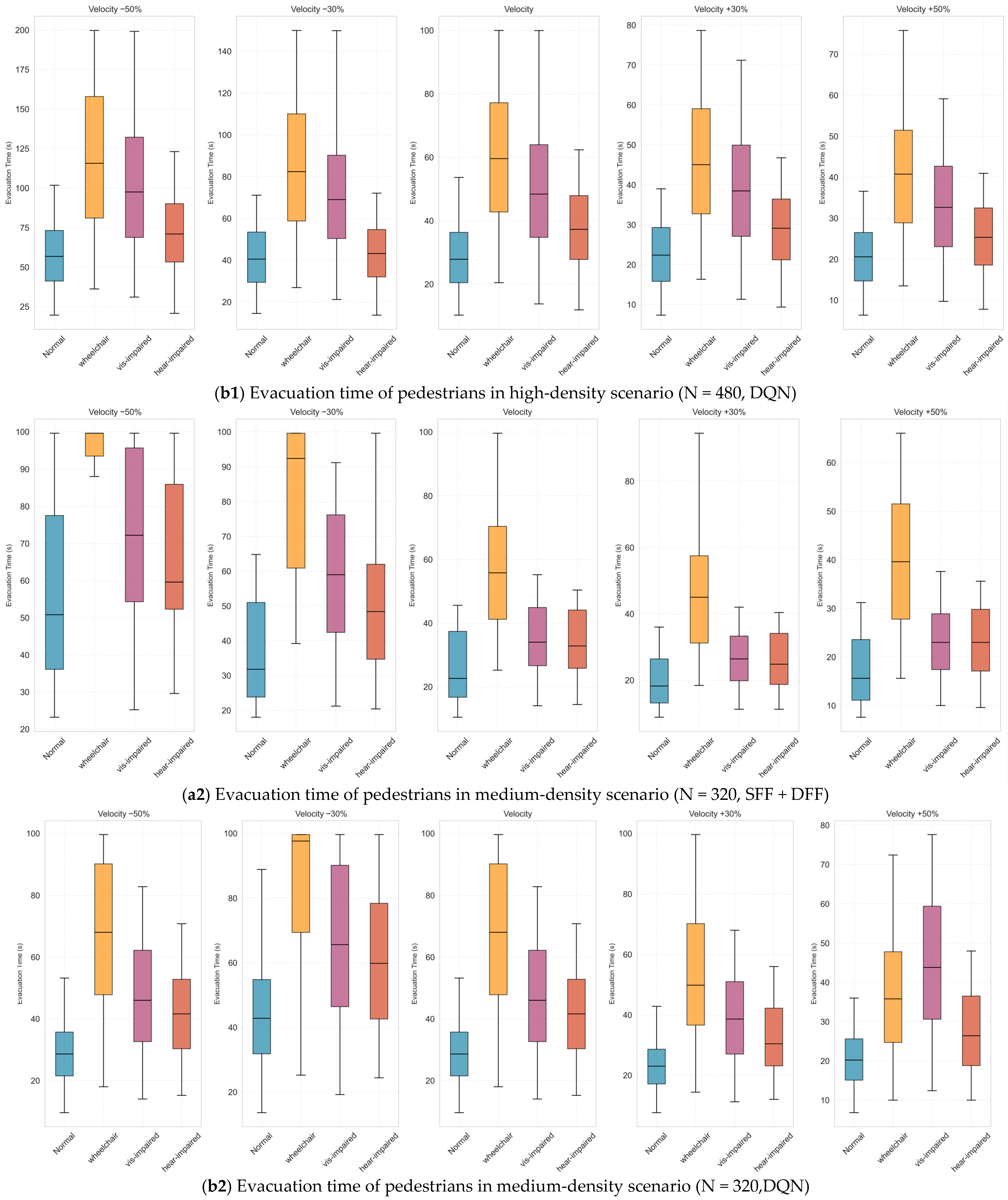
3.5. Sensitivity and Robustness Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CA | Cellular Automaton |
| FFCA | Floor Field Cellular Automaton |
| SFF | Static Floor Field |
| DFF | Dynamic Floor Field |
| RL | Reinforcement Learning |
| DRL | Deep Reinforcement Learning |
| DQN | Deep Q-Network |
Appendix A
| Group | Representative Coefficient (This Study) | Typical Horizontal Speed Range Reported in the Literature (m/s) | Representative References |
|---|---|---|---|
| Able-bodied/normal (adult, horizontal) | 1.2 (study baseline choice) | ≈0.9–1.2 m/s (free/pedestrian studies; dependent on age, sex, context) | Giannoulaki & Christoforou (2024) [72]—systematic review |
| Wheelchair users/mobility-impaired | 0.6 | ≈0.3–0.9 m/s (context dependent; short bouts and community mobility show median ~0.4–0.5 m/s in many studies; some controlled experiments report higher values under unimpeded conditions) | Sonenblum et al. (2012); Tsuchiya et al. (2007); Geoerg et al. (2019) [73,74,75] |
| Visually impaired | 0.8 | ≈0.7–1.0 m/s (horizontal; speeds decline under unfamiliar/low-visibility conditions) | Sørensen (2014)—DTU experiments; Clark-Carter et al. (1986) [76,77] |
| Hearing impaired | 1 | No consistent reduction in steady horizontal walking speed reported (primary impacts are on detection/pre-movement) | Hashemi (2018); Choi et al. (2019) [78,79] |
| Density Level | Group | Velocity Condition | SFF + DFF (1 Exit) | DQN (1 Exit) | Time Difference1 (s) | Improvement (%) |
|---|---|---|---|---|---|---|
| High (N = 480) | Normal | Velocity −50% | 75.6 | 59.4 | 16.2 | 21.4% |
| Velocity −30% | 43.1 | 39.9 | 3.2 | 8% | ||
| Velocity | 38.6 | 26.7 | 11.9 | 30.8% | ||
| Velocity +30% | 29.9 | 23.2 | 6.7 | 22.4% | ||
| Velocity +50% | 28.8 | 20.5 | 8.3 | 28.8% | ||
| Wheelchair User | Velocity −50% | 187.9 | 120.8 | 67.1 | 35.7% | |
| Velocity −30% | 87.2 | 85.0 | 2.2 | 2.5% | ||
| Velocity | 83.1 | 60.6 | 22.5 | 27% | ||
| Velocity +30% | 62.3 | 46.2 | 16.1 | 25.8% | ||
| Velocity +50% | 57.4 | 41.1 | 16.3 | 28.4% | ||
| Visually Impaired | Velocity −50% | 132.7 | 101.1 | 31.6 | 23.8% | |
| Velocity −30% | 65.2 | 64.4 | 0.8 | 1.2% | ||
| Velocity | 63.1 | 49.5 | 13.6 | 21.6% | ||
| Velocity +30% | 53.4 | 39.0 | 14.4 | 26.9% | ||
| Velocity +50% | 45.2 | 33.1 | 12.1 | 26.7% | ||
| Hearing Impaired | Velocity−50% | 103.7 | 72.5 | 31.2 | 30% | |
| Velocity−30% | 53.2 | 43.3 | 9.9 | 18.6% | ||
| Velocity | 48.3 | 37.8 | 10.5 | 21.7% | ||
| Velocity+30% | 38.6 | 28.9 | 9.7 | 25.1% | ||
| Velocity+50% | 30.3 | 25.4 | 4.9 | 16.1% | ||
| Medium (N = 320) | Normal | Velocity−50% | 50.2 | 30.4 | 19.8 | 39.4% |
| Velocity−30% | 43.8 | 35.0 | 8.8 | 25.1% | ||
| Velocity | 25.0 | 23.1 | 1.9 | 7.6% | ||
| Velocity+30% | 21.0 | 19.9 | 1.1 | 5.5% | ||
| Velocity+50% | 20.1 | 18.2 | 1.9 | 10.4% | ||
| Wheelchair User | Velocity−50% | 159.5 | 73.8 | 85.7 | 53.7% | |
| Velocity−30% | 96.3 | 96.1 | 0.2 | 0.2% | ||
| Velocity | 61.1 | 59.2 | 1.9 | 3.2% | ||
| Velocity+30% | 45.2 | 43.1 | 2.1 | 4.6% | ||
| Velocity+50% | 39.8 | 35.2 | 4.6 | 11.6% | ||
| Visually Impaired | Velocity−50% | 73.8 | 46.5 | 27.3 | 36.9% | |
| Velocity−30% | 63.4 | 59.8 | 3.6 | 6% | ||
| Velocity | 41.8 | 38.5 | 3.3 | 7.8% | ||
| Velocity+30% | 36.7 | 32.9 | 3.8 | 10.3% | ||
| Velocity+50% | 42.8 | 23.5 | 19.3 | 45% | ||
| Hearing Impaired | Velocity−50% | 60.0 | 41.2 | 18.8 | 31.3% | |
| Velocity−30% | 59.9 | 48.8 | 11.1 | 18.5% | ||
| Velocity | 41.6 | 38.4 | 3.2 | 7.6% | ||
| Velocity+30% | 32.5 | 28.6 | 3.9 | 12% | ||
| Velocity+50% | 23.5 | 22.9 | 0.6 | 2.5% | ||
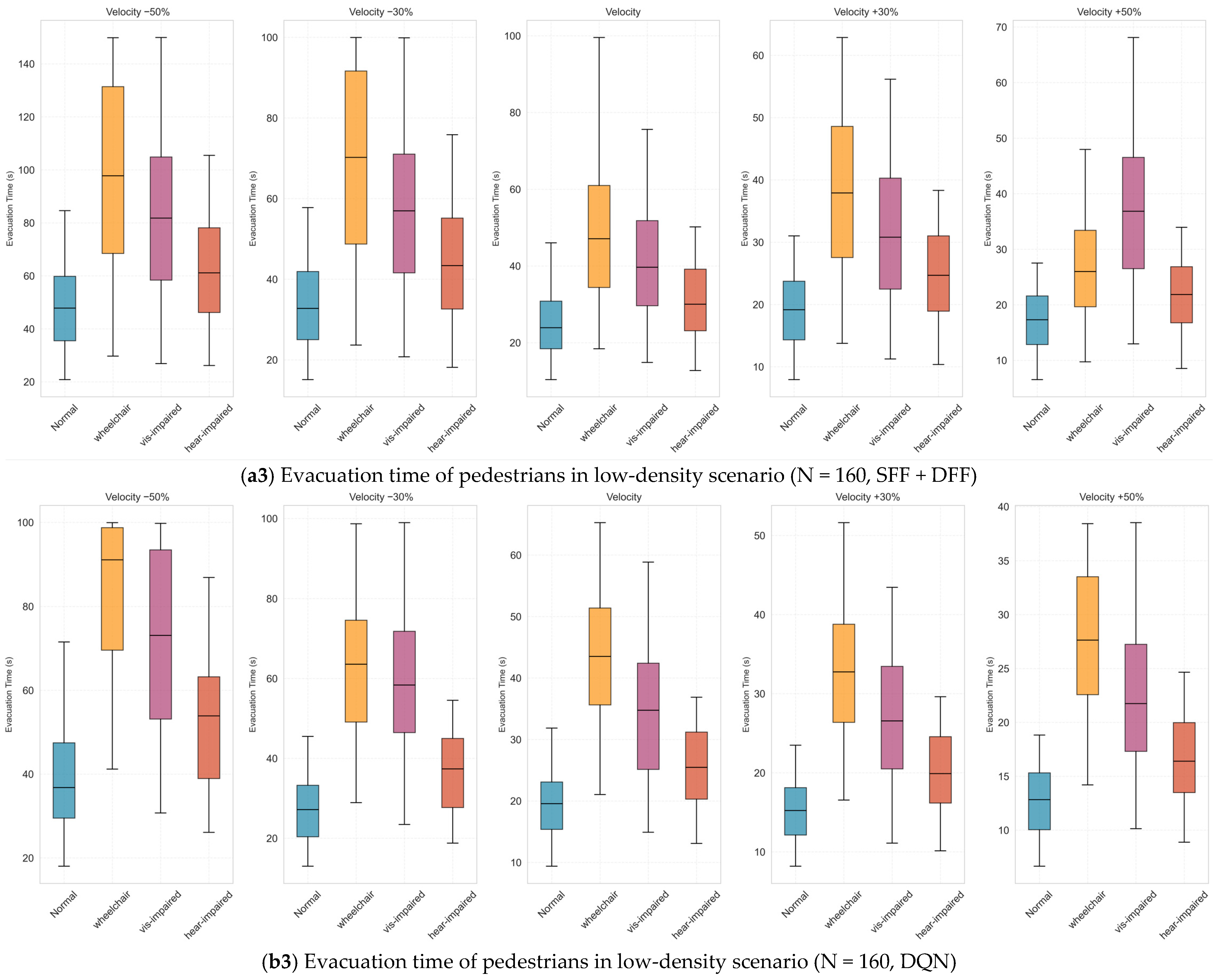
| Low(N = 160) | Normal | Velocity−50% | 46.8 | 39.9 | 6.9 | 14.7% |
| Velocity−30% | 34.3 | 30.1 | 4.2 | 12.2% | ||
| Velocity | 23.9 | 19.6 | 4.3 | 17.9% | ||
| Velocity+30% | 19.8 | 15.2 | 4.6 | 23.2% | ||
| Velocity+50% | 18.6 | 14.8 | 3.8 | 20.4% | ||
| Wheelchair User | Velocity−50% | 98.2 | 88.4 | 9.8 | 9.9% | |
| Velocity−30% | 69.0 | 63.3 | 5.7 | 8.2% | ||
| Velocity | 49.2 | 45.6 | 3.6 | 7.3% | ||
| Velocity+30% | 39.6 | 35.3 | 4.3 | 10.9% | ||
| Velocity+50% | 28.6 | 26.6 | 2 | 6.9% | ||
| Visually Impaired | Velocity−50% | 81.3 | 77.6 | 3.7 | 4.5% | |
| Velocity−30% | 59.4 | 58.1 | 1.3 | 2.1% | ||
| Velocity | 40.0 | 35.1 | 4.9 | 12.2% | ||
| Velocity+30% | 31.9 | 25.3 | 6.6 | 20.6% | ||
| Velocity+50% | 38.6 | 23.2 | 15.4 | 39.9% | ||
| Hearing Impaired | Velocity−50% | 60.5 | 58.4 | 2.1 | 3.4% | |
| Velocity−30% | 43.6 | 38.7 | 4.9 | 11.2% | ||
| Velocity | 35.1 | 25.6 | 9.5 | 27% | ||
| Velocity+30% | 25.0 | 20.0 | 5 | 20% | ||
| Velocity+50% | 23.2 | 16.8 | 6.4 | 27.6% |
References
- Mao, H.; Zhu, L. Simulation and optimization of hybrid evacuation model for high-rise building under emergency condition. Int. J. Model. Simul. Sci. Comput. 2023, 14, 2350039. [Google Scholar] [CrossRef]
- Huang, Z.; Fan, R.; Fang, Z.; Ye, R.; Li, X.; Xu, Q.; Gao, H.; Gao, Y. Performance of occupant evacuation in a super high-rise building up to 583 m. Phys. A Stat. Mech. Its Appl. 2022, 589, 126643. [Google Scholar] [CrossRef]
- Glauberman, G. Scoping review of fire safety behaviors among high-rise occupants: Implications for public health nursing. Public Health Nurs. 2020, 37, 371–379. [Google Scholar] [CrossRef]
- Disability. Available online: https://www.who.int/news-room/fact-sheets/detail/disability-and-health (accessed on 31 October 2024).
- Morris, S.; Fawcett, G.; Brisebois, L.; Hughes, J. A Demographic, Employment and Income Profile of Canadians with Disabilities Aged 15 Years and Over, 2017; Statistics Canada: Ottawa, ON, Canada, 2018. [Google Scholar]
- Zhang, C.; Wu, X.; Shen, H. Research on coupling evacuation of escalator and staircase in fire scenario. PLoS ONE 2025, 20, e0314455. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Zhao, M.; Gao, K.; Zhao, J. The Physiological Experimental Study on the Effect of Different Color of Safety Signs on a Virtual Subway Fire Escape. Int. J. Environ. Res. Public Health 2020, 17, 5903. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, Y.; Chao, L. Simulation study on fire and evacuation of super high-rise commercial building. Case Stud. Therm. Eng. 2023, 52, 103519. [Google Scholar] [CrossRef]
- Fu, L.; Qin, H.; He, Y.; Shi, Y. Application of the social force modelling method to evacuation dynamics involving pedestrians with disabilities. Appl. Math. Comput. 2024, 460, 128297. [Google Scholar] [CrossRef]
- Wang, Z.; He, R.; Rebelo, F.; Vilar, E. Human interaction with virtual reality: Investigating pre-evacuation efficiency in building emergency. Virtual Real. 2023, 27, 1039–1050. [Google Scholar] [CrossRef]
- Zheng, Y.; Jia, B.; Li, X.G.; Jiang, R. Evacuation dynamics considering pedestrians’ movement behavior change with fire and smoke spreading. Saf. Sci. 2017, 92, 180–189. [Google Scholar] [CrossRef]
- Li, Y.; Chen, M.Y.; Dou, Z.; Zheng, X.P.; Cheng, Y.; Mebarki, A. A review of cellular automata models for crowd evacuation. Phys. A Stat. Mech. Its Appl. 2019, 526, 120752. [Google Scholar] [CrossRef]
- Sahin, C. Social Media Emergency Analysis and Realistic Evacuation Modeling. Doctoral Thesis, University of Calgary, Calgary, AB, Canada, 2021. Available online: https://prism.ucalgary.ca (accessed on 24 August 2025).
- Pelechano, N.; Malkawi, A. Evacuation simulation models: Challenges in modeling high rise building evacuation with cellular automata approaches. Auton. Constr. 2008, 17, 377–385. [Google Scholar] [CrossRef]
- Goldengorin, B.; Makarenko, A.; Smelyanec, N. Some applications and prospects of cellular automata in traffic problems. In Proceedings of the International Conference on Cellular Automata for Research and Industry, Heidelberg, Germany, 4–6 October 2004; Springer: Berlin/Heidelberg, Germany, 2006; pp. 532–537. [Google Scholar]
- Wąs, J.; Porzycki, J.; Lubaś, R.; Miller, J.; Bazior, G. Agent-based approach and cellular automata-a promising perspective in crowd dynamics modeling. Acta Phys. Pol. B Proc. Suppl. 2016, 9, 133–144. [Google Scholar] [CrossRef]
- Sirakoulis, G.C. Cellular automata for crowd dynamics. In Proceedings of the International Conference on Implementation and Application of Automata, Giessen, Germany, 30 July–2 August 2014; Springer International Publishing: Cham, Switzerland, 2014; pp. 58–69. [Google Scholar]
- Sirakoulis, G.C. The computational paradigm of cellular automata in crowd evacuation. Int. J. Found. Comput. Sci. 2015, 26, 851–872. [Google Scholar] [CrossRef]
- You, Y.; Ye, R.; Fang, Z.; Ren, X.; Xie, S.; Huang, P.; Yu, L.; Yu, T.; Yan, J. Evacuation dynamics of heterogeneous crowds involving individuals with different types of disabilities. Saf. Sci. 2023, 168, 106297. [Google Scholar] [CrossRef]
- Xing, S.; Wang, C.; Wang, W.; Cao, R.F.; Yuen, A.C.Y.; Lee, E.W.M.; Yeoh, G.H.; Chan, Q.N. A fine discrete floor field cellular automaton model with natural step length for pedestrian dynamics. Simul. Modell. Pract. Theory 2024, 130, 102841. [Google Scholar] [CrossRef]
- Yue, H.; Zhang, J.; Chen, W.; Wu, X.; Zhang, X.; Shao, C. Simulation of the influence of spatial obstacles on evacuation pedestrian flow in walking facilities. Phys. A Stat. Mech. Its Appl. 2021, 571, 125844. [Google Scholar] [CrossRef]
- Fu, L.; Liu, Y.; Shi, Y.; Zhao, Y. Dynamics of bidirectional pedestrian flow in a corridor including individuals with disabilities. Phys. A Stat. Mech. Its Appl. 2021, 580, 126140. [Google Scholar] [CrossRef]
- Fu, L.; Liu, Y.; Shi, Y.; Zhao, Y. Unidirectional pedestrian flow in a corridor involving individuals with disabilities: A modified floor field modelling approach. J. Stat. Mech. Theory Exp. 2021, 2021, 073402. [Google Scholar] [CrossRef]
- Yang, X.; Yang, X.; Wang, Q. Pedestrian evacuation under guides in a multiple-exit room via the fuzzy logic method. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105138. [Google Scholar] [CrossRef]
- Liu, T.; Yang, X.; Wang, Q.; Zhou, M.; Xia, S. A fuzzy-theory-based cellular automata model for pedestrian evacuation from a multiple-exit room. IEEE Access 2020, 8, 106334–106345. [Google Scholar] [CrossRef]
- Rasa, A.R.; Xia, L.; Song, X.; Yu, H.; Karim, R.; Zhang, J.; Song, W. Understanding human-obstacle interaction dynamics on staircases: Implications for emergency evacuation and fire safety in high-rise buildings. J. Build. Eng. 2024, 98, 111082. [Google Scholar] [CrossRef]
- Hu, Y.H.; Bi, Y.B.; Zhang, J.; Lian, L.P.; Song, W.G.; Gao, W. Effect of a static pedestrian as an exit obstacle on evacuation. Chin. Phys. B 2023, 32, 018901. [Google Scholar] [CrossRef]
- Pouw, C.A.; Corbetta, A.; Gabbana, A.; Van der Laan, C.; Toschi, F. High-statistics pedestrian dynamics on stairways and their probabilistic fundamental diagrams. Transp. Res. Part C Emerg. Technol. 2024, 159, 104468. [Google Scholar] [CrossRef]
- Xie, Q.; Wu, Y.; Wang, Y.; Zhang, H. A multi-grid evacuation model considering the effects of different turning types. Phys. A Stat. Mech. Its Appl. 2024, 635, 129497. [Google Scholar] [CrossRef]
- Duan, Y.; Li, C.; He, J. A refined simulation method of building earthquake evacuation processes considering multi-exits and time-variant velocities. Earthq. Spectra. 2024, 40, 705–731. [Google Scholar] [CrossRef]
- Yue, F.R.; Chen, J.; Ma, J.; Song, W.G.; Lo, S.M. Cellular automaton modeling of pedestrian movement behavior on an escalator. Chin. Phys. B 2018, 27, 124501. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Feng, J.; Xu, S.; Liu, J.; Wang, Y. Performance optimization of the obstacle to corner bottleneck under emergency evacuation. J. Build. Eng. 2022, 45, 103658. [Google Scholar] [CrossRef]
- Huo, F.; Li, C.; Li, Y.; Lv, W.; Ma, Y. An extended model for describing pedestrian evacuation considering the impact of obstacles on the visual view. Phys. A Stat. Mech. Its Appl. 2022, 604, 127932. [Google Scholar] [CrossRef]
- Ding, N.; Chen, T.; Zhang, H. Simulation of high-rise building evacuation considering fatigue factor based on cellular automata: A case study in China. In Building Simulation; Tsinghua University Press: Beijing, China, 2017; Volume 10, pp. 407–418. [Google Scholar]
- Zou, B.; Lu, C.; Li, Y. Simulation of a hospital evacuation including wheelchairs based on modified cellular automata. Simul. Model. Pract. Theory. 2019, 99, 102018. [Google Scholar] [CrossRef]
- Wang, K.; Hao, H.; Jiang, S.; Wu, Z.; Cui, C.; Shao, H.; Zhang, W. Escape route optimization by cellular automata based on the multiple factors during the coal mine disasters. Nat. Hazards 2019, 99, 91–115. [Google Scholar] [CrossRef]
- Dong, L.; Yuan, W.; Deng, Y. A Study of Evacuation Model Based on Personnel Vision Change. Intell. Fuzzy Syst. 2023, 44, 6231–6247. [Google Scholar] [CrossRef]
- Zheng, Y.; Jia, B.; Li, X.G. Evacuation dynamics with fire spreading based on cellular automaton. Phys. A Stat. Mech. Its Appl. 2011, 390, 3147–3156. [Google Scholar] [CrossRef]
- Cao, S.; Song, W.; Lv, W.; Fang, Z. A multi-grid model for pedestrian evacuation in a room without visibility. Phys. A Stat. Mech. Its Appl. 2015, 436, 45–61. [Google Scholar] [CrossRef]
- Yue, H.; Guan, H.Z.; Zhang, X.; Shao, C.F. Simulation of pedestrian evacuation with asymmetrical exits layout. Phys. A Stat. Mech. Its Appl. 2010, 390, 198–207. [Google Scholar] [CrossRef]
- Guan, J.B.; Wang, K.H.; Chen, F. A cellular automaton model for evacuation flow using game theory. Phys. A Stat. Mech. Its Appl. 2016, 461, 655–661. [Google Scholar] [CrossRef]
- Song, W.G.; Yu, Y.F.; Wang, B.H.; Fan, W.C. Evacuation behaviors at exit in CA model with force essentials: A comparison with social force model. Phys. A Stat. Mech. Its Appl. 2006, 37, 658–666. [Google Scholar] [CrossRef]
- Henein, C.M.; White, T. Macroscopic effects of microscopic forces between agents in crowd models. Phys. A Stat. Mech. Its Appl. 2007, 373, 694–712. [Google Scholar] [CrossRef]
- Guo, R.Y.; Huang, H.J. A mobile lattice gas model for simulating pedestrian evacuation. Phys. A Stat. Mech. Its Appl. 2008, 387, 580–586. [Google Scholar] [CrossRef]
- Guo, R.Y.; Huang, H.J. A modified floor field cellular automata model for pedestrian evacuation simulation. J. Phys. A Math. Gen. 2008, 41, 385104. [Google Scholar] [CrossRef]
- Georgoudas, G.; Sirakoulis, G.C.; Andreadis, I. An Intelligent Cellular Automaton Model for Crowd Evacuation in Fire Spreading Conditions. In Proceedings of the 19th IEEE International Conference on Tools with Artificial Intelligence (ICTAI 2007), Patra, Greece, 29–31 October 2007; IEEE Computer Society Press: Washington, DC, USA, 2007; pp. 36–43. [Google Scholar] [CrossRef]
- Takabatake, T.; Asai, K.; Kakuta, H.; Hasegawa, N. Optimizing evacuation paths using agent-based evacuation simulations and reinforcement learning. Int. J. Disaster Risk Reduct. 2025, 117, 105173. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, Y.; Liu, D.; Liu, Y.; Namilae, S.; Song, H. Real-Time Deep Reinforcement Learning for Evacuation Under Emergencies (No. CATM-2024-R1-ERAU); Center for Advanced Transportation Mobility, North Carolina A&T State University: Greensboro, NC, USA, 2024. [Google Scholar]
- Pascucci, F.; Rinke, N.; Schiermeyer, C.; Friedrich, B.; Berkhahn, V. Modeling of shared space with multi-modal traffic using a multi-layer social force approach. Transp. Res. Procedia 2015, 10, 316–326. [Google Scholar] [CrossRef]
- Huang, L.; Wu, J.; You, F.; Lv, Z.; Song, H. Cyclist social force model at unsignalized intersections with heterogeneous traffic. IEEE Trans. Ind. Inform. 2017, 13, 782–792. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, B.; Li, X.; Ding, Z. Dynamic navigation field in the social force model for pedestrian evacuation. Appl. Math. Model. 2020, 80, 815–826. [Google Scholar] [CrossRef]
- Wharton, A. Simulation and Investigation of Multi-Agent Reinforcement Learning for Building Evacuation Scenarios. Report, St Catherine’s College. 2009. Available online: https://www.robots.ox.ac.uk/~ash/4YP%20Report.pdf (accessed on 24 August 2025).
- Tian, K.; Jiang, S. Reinforcement learning for safe evacuation time of fire in Hong Kong-Zhuhai-Macau immersed tube tunnel. Syst. Sci. Control Eng. 2018, 6, 45–56. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Alizadeh, B.; Zhang, Z.; Duffield, N.; Meyer, M.A.; Thompson, C.M.; Gao, H.; Behzadan, A.H. A reinforcement learning-based routing algorithm for large street networks. Int. J. Geogr. Inf. Sci. 2024, 38, 183–215. [Google Scholar] [CrossRef]
- Nayeem, G.M.; Fan, M.; Daiyan, G.M. Adaptive Q-Learning Grey Wolf Optimizer for UAV Path Planning. Drones 2025, 9, 246. [Google Scholar] [CrossRef]
- Sharma, J.; Andersen, P.A.; Granmo, O.C.; Goodwin, M. Deep Q-learning with Q-matrix transfer learning for novel fire evacuation environment. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 7363–7381. [Google Scholar] [CrossRef]
- Zhang, Y.; Chai, Z.; Lykotrafitis, G. Deep reinforcement learning with a particle dynamics environment applied to emergency evacuation of a room with obstacles. Phys. A Stat. Mech. Its Appl. 2021, 571, 125845. [Google Scholar] [CrossRef]
- Von Neumann, J.; Taub, A.H. The General and Logical Theory of Automata; MIT Press: Cambridge, MA, USA, 1963; Volume 5. [Google Scholar]
- Ji, J.; Lu, L.; Jin, Z.; Wei, S.; Ni, L. A cellular automata model for high-density crowd evacuation using triangle grids. Phys. A Stat. Mech. Its Appl. 2018, 509, 1034–1045. [Google Scholar] [CrossRef]
- Kirchner, A.; Schadschneider, A. Simulation of evacuation processes using a bionics-inspired cellular automaton model for pedestrian dynamics. Phys. A Stat. Mech. Its Appl. 2002, 312, 260–276. [Google Scholar] [CrossRef]
- Nishinari, K.; Kirchner, A.; Namazi, A.; Schadschneider, A. Extended floor field CA model for evacuation dynamics. IEICE Trans. Inf. Syst. 2004, 87, 726–732. [Google Scholar]
- Burstedde, C.; Klauck, K.; Schadschneider, A.; Zittartz, J. Simulation of pedestrian dynamics using a two-dimensional cellular automaton. Phys. A Stat. Mech. Its Appl. 2001, 295, 507–525. [Google Scholar] [CrossRef]
- Kirchner, A.; Nishinari, K.; Schadschneider, A. Friction effects and clogging in a cellular automaton model for pedestrian dynamics. Phys. Rev. E 2003, 67, 056122. [Google Scholar] [CrossRef]
- Kirchner, A.; Klüpfel, H.; Nishinari, K.; Schadschneider, A.; Schreckenberg, M. Simulation of competitive egress behavior: Comparison with aircraft evacuation data. Phys. A Stat. Mech. Its Appl. 2003, 324, 689–697. [Google Scholar] [CrossRef]
- Helbing, D.; Farkas, I.; Vicsek, T. Simulating dynamical features of escape panic. Nature 2000, 407, 487–490. [Google Scholar] [CrossRef]
- Clifton, J.; Laber, E. Q-learning: Theory and applications. Annu. Rev. Stat. Appl. 2020, 7, 279–301. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; Volume 1. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.J. Self-improving reactive agents based on reinforcement learning, planning and teaching. Mach. Learn. 1992, 8, 293–321. [Google Scholar] [CrossRef]
- Galán, S.F. Fast Evacuation Method: Using an effective dynamic floor field based on efficient pedestrian assignment. Saf. Sci. 2019, 120, 79–88. [Google Scholar] [CrossRef]
- Saeed, M.A.; Ahmed, Z.; Yang, J.; Zhang, W. An optimal approach of wind power assessment using Chebyshev metric for determining the Weibull distribution parameters. Sustain. Energy Technol. Assess. 2020, 37, 100612. [Google Scholar] [CrossRef]
- Giannoulaki, M.; Christoforou, Z. Pedestrian Walking Speed Analysis: A Systematic Review. Sustainability 2024, 16, 4813. [Google Scholar] [CrossRef]
- Sonenblum, S.E.; Sprigle, S.; Lopez, R.A. Manual wheelchair use: Bouts of mobility in everyday life. Rehabil. Res. Pract. 2012, 2012, 753165. [Google Scholar] [CrossRef]
- Tsuchiya, S.; Hasemi, Y.; Furukawa, Y. Evacuation characteristics of group with wheelchair users. In Proceedings of the Asia-Oceania Symposium on Fire Science and Technology, Hong Kong, China, 20–22 September 2007; International Association for Fire Safety Science: London, UK, 2007; pp. 1–12. [Google Scholar]
- Geoerg, P.; Berchtold, F.; Gwynne, S.; Boyce, K.; Holl, S.; Hofmann, A. Engineering egress data considering pedestrians with reduced mobility. Fire Mater. 2019, 43, 759–781. [Google Scholar] [CrossRef]
- Sørensen, J.G. Evacuation of People with Visual Impairments; Technical University of Denmark: Lyngby, Denmark, 2014. [Google Scholar]
- Clark-Carter, D.D.; Heyes, A.D.; Howarth, C.I. The efficiency and walking speed of visually impaired people. Ergo 1986, 29, 779–789. [Google Scholar] [CrossRef] [PubMed]
- Hashemi, M. Emergency evacuation of people with disabilities: A survey of drills, simulations, and accessibility. Cogent. Eng. 2018, 5, 1506304. [Google Scholar] [CrossRef]
- Choi, M.; Lee, S.; Hwang, S.; Park, M.; Lee, H.S. Comparison of emergency response abilities and evacuation performance involving vulnerable occupants in building fire situations. Sustainability 2019, 12, 87. [Google Scholar] [CrossRef]
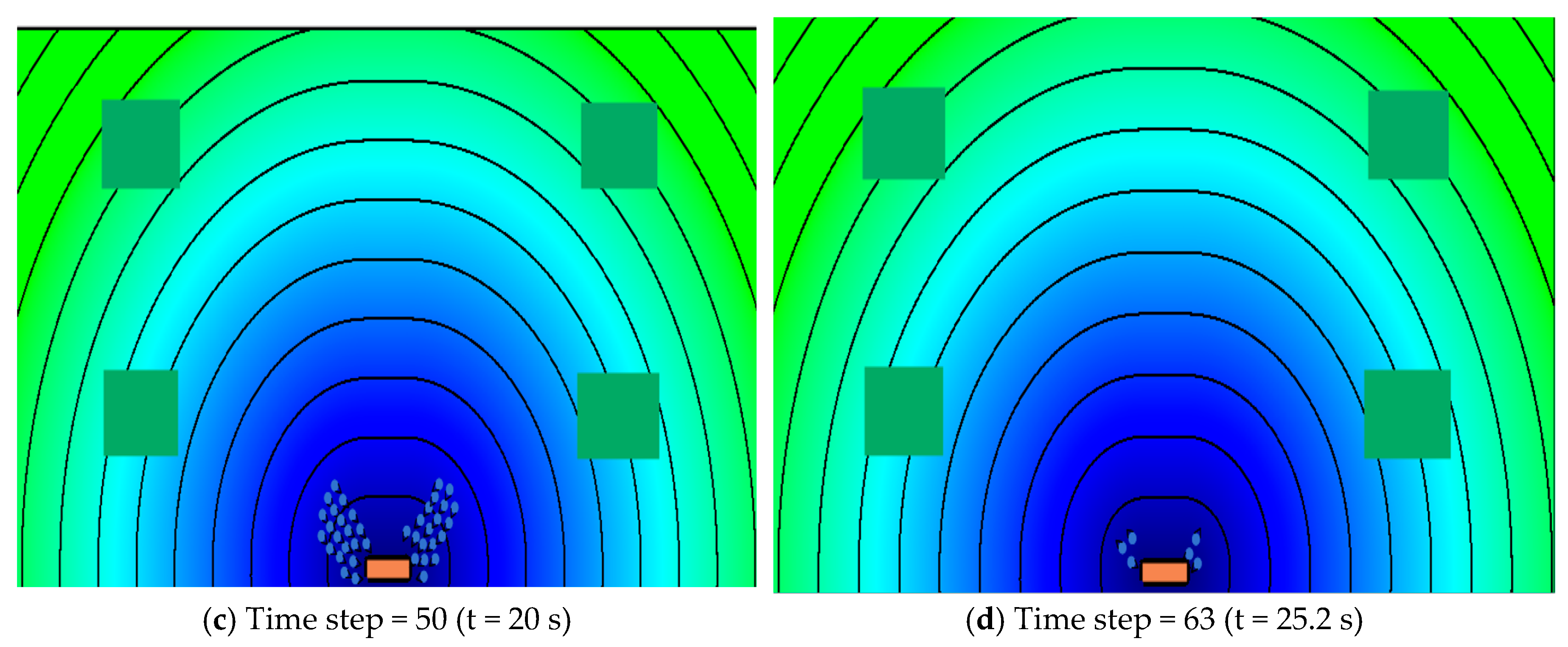
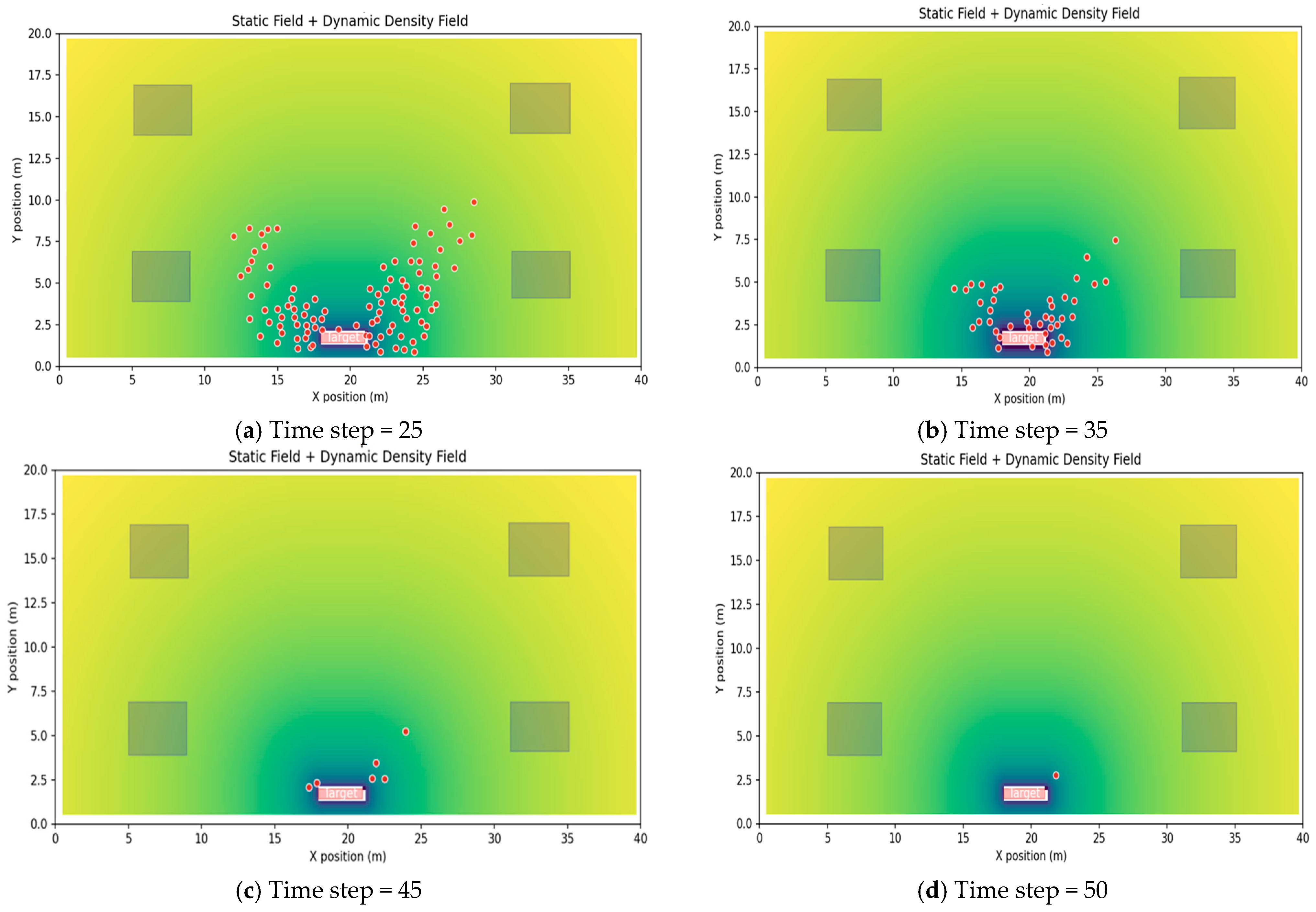
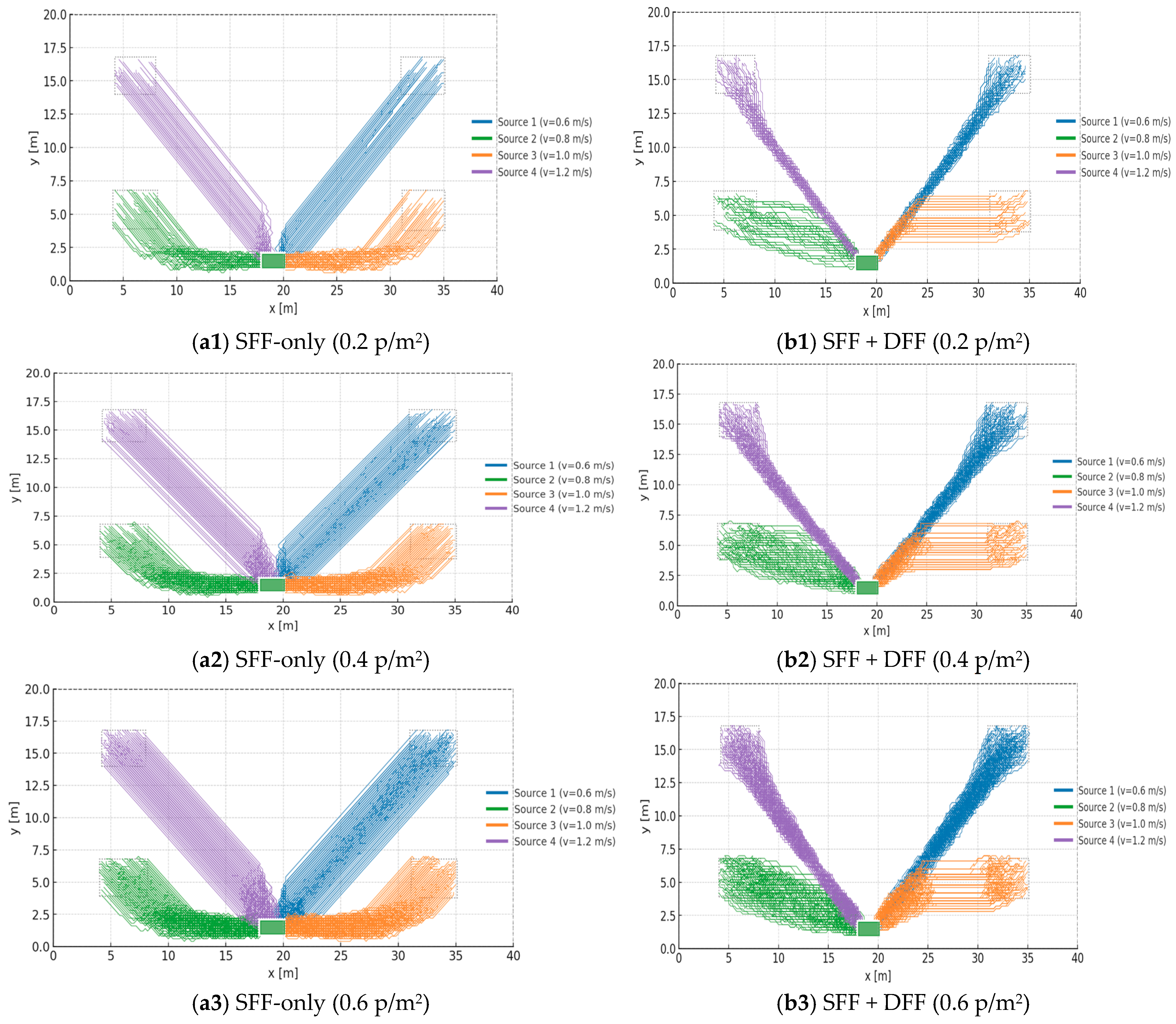
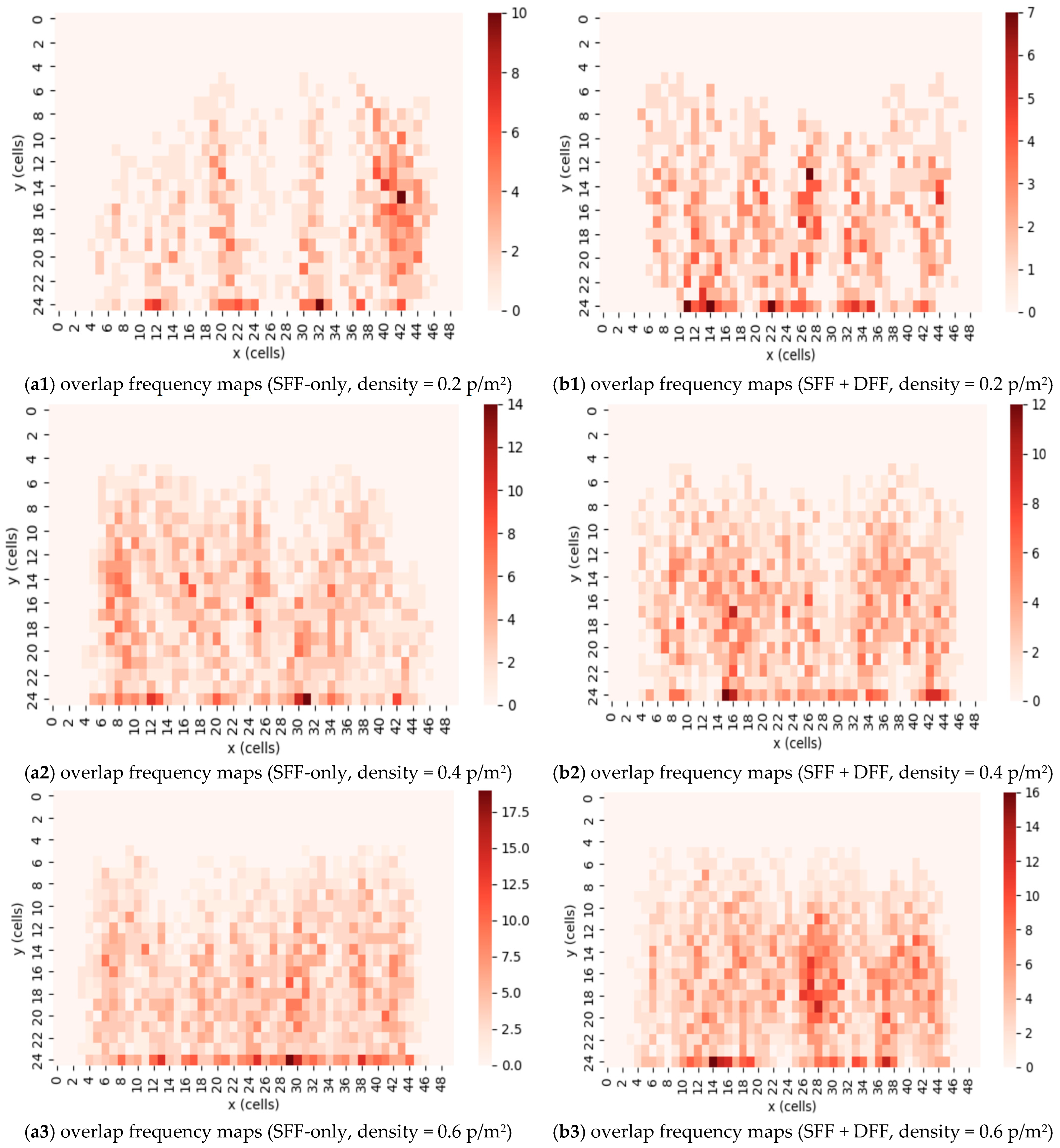

| Reward | Description | Value |
|---|---|---|
| Successful evacuation reward | +100 | |
| Step time penalty | −1 | |
| High-density area penalty | −5 | |
| Obstacle/collision penalty | −10 |
| Parameter | Description | Value/Range |
|---|---|---|
| learning rate | 0.2 | |
| discount factor | 0.98 | |
| initial exploration rate | 1.0 | |
| minimum exploration rate | 0.05 | |
| k | ε decay rate constant | 0.001–0.01 |
| Replay buffer size | capacity of experience storage | 104–105 |
| Target update frequency C | steps between target network updates | 1000 |
| Batch size | training batch size (DQN) | 64–128 |
| Method | Convergence Episodes | Avg. Detour Index | Avg. Evacuation Time (s) | Conflict Count | Success % |
|---|---|---|---|---|---|
| FFCA | - | 1.2912 | 91.12 | 9 | 90.9375 |
| Q-learning | 5000 | 1.9617 | 71.2 | 5 | 100 |
| Algorithm | Avg. Reward | Final Reward | Stability | Avg. Steps |
|---|---|---|---|---|
| Q-learning | 60.42 | 60.92 | 6.08 | 16.9 |
| DQN | 311.51 | 429 | 318.12 | 496.2 |
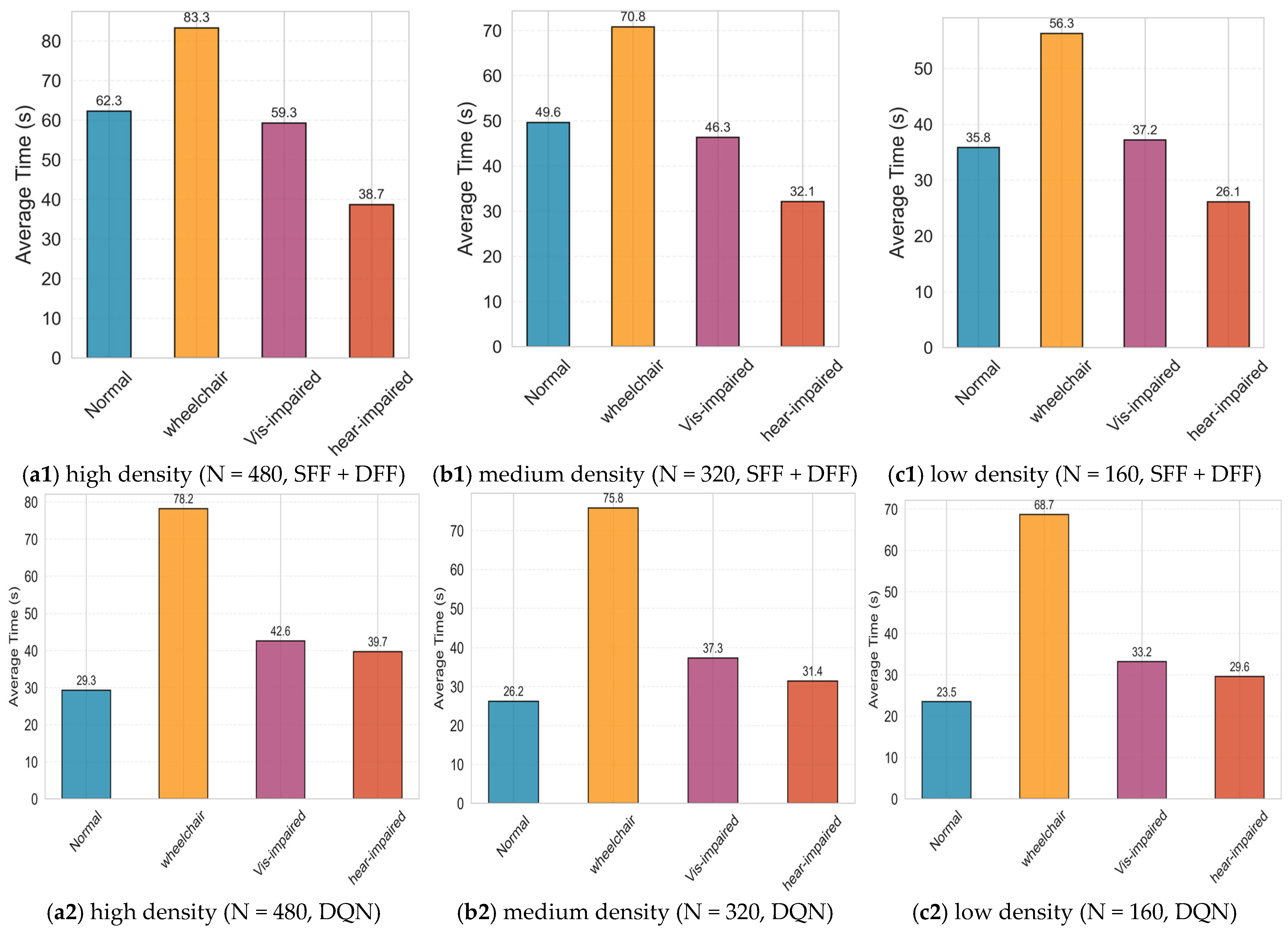
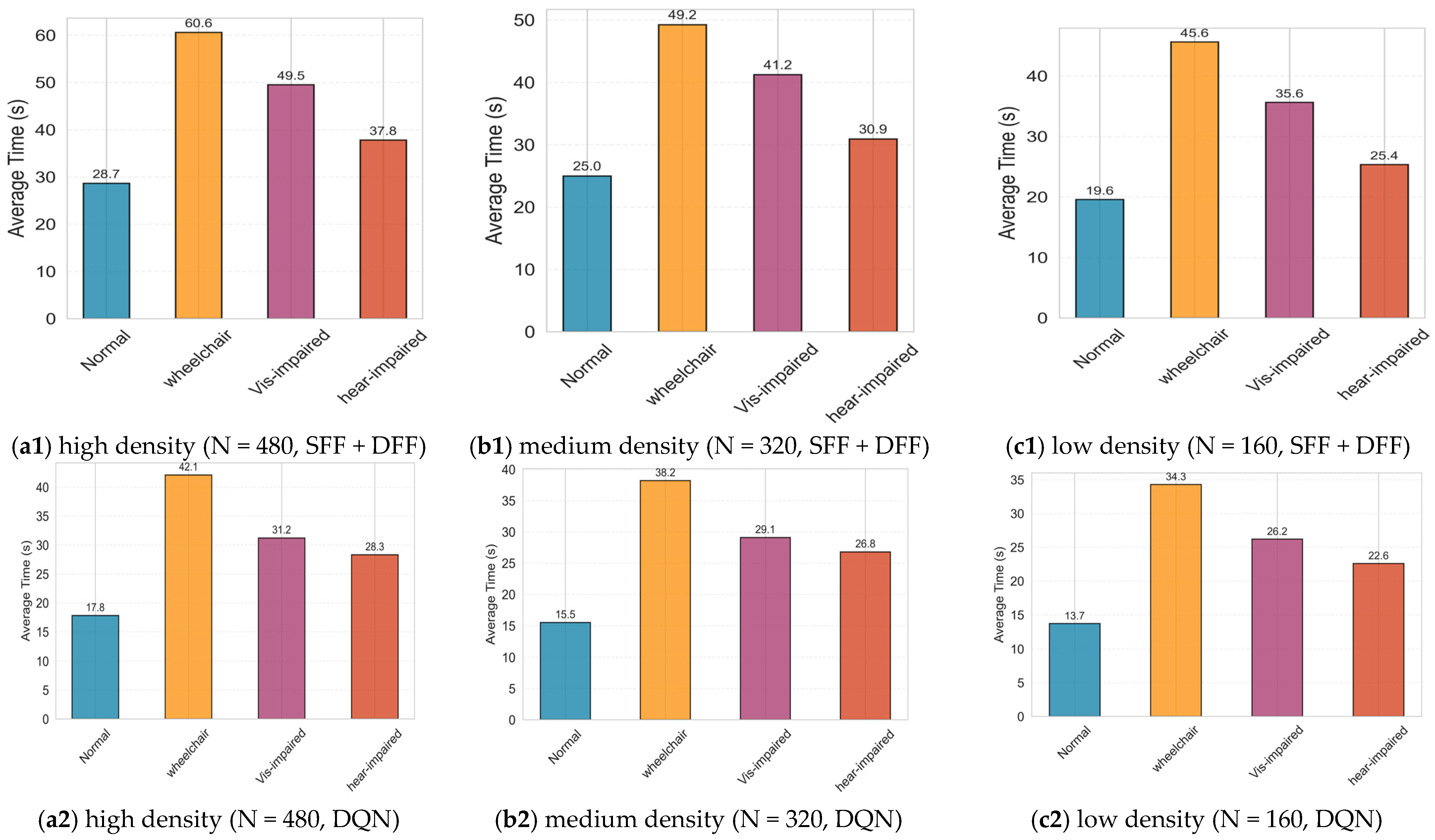
| Density Level | Group | SFF + DFF (1 Exit) | DQN (1 Exit) | Time Difference1 (s) | Improvement (%) | p-Value (1 Exit) | SFF + DFF (2 Exits) | DQN (2 Exits) | Time Difference2 (s) | Improvement (%) | p-Value (2 Exits) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| High (N = 480) | Normal | 62.3 | 29.3 | 33.0 | 52.9 | ** (0.0009) | 28.7 | 17.8 | 10.9 | 37.9 | ** (0.0041) |
| Wheelchair User | 83.3 | 78.2 | 5.1 | 6.1 | * (0.0183) | 60.6 | 42.1 | 18.5 | 30.5 | ** (0.0038) | |
| Visually Impaired | 59.3 | 42.6 | 16.7 | 28.2 | ** (0.0046) | 49.5 | 31.2 | 18.3 | 36.9 | ** (0.0045) | |
| Hearing Impaired | 38.7 | 39.7 | 1 | 2.6 | ns (0.3156) | 37.8 | 28.3 | 4.5 | 11.9 | * (0.0238) | |
| Medium (N = 320) | Normal | 49.6 | 26.2 | 23.4 | 47.1 | ** (0.0078) | 25.0 | 15.5 | 9.5 | 38.0 | ** (0.0093) |
| Wheelchair User | 70.8 | 75.3 | 5.5 | 7.8 | ns (0.1972) | 49.2 | 38.2 | 11.0 | 22.4 | * (0.0263) | |
| Visually Impaired | 46.3 | 37.3 | 9.0 | 19.4 | * (0.025) | 41.2 | 29.1 | 12.1 | 29.4 | ** (0.0052) | |
| Hearing Impaired | 32.1 | 31.4 | 0.7 | 2.2 | ns (0.3023) | 30.9 | 26.8 | 4.1 | 13.3 | ns (0.1237) | |
| Low (N = 160) | Normal | 35.8 | 23.5 | 12.2 | 34.1 | ** (0.0043) | 19.6 | 13.7 | 5.9 | 30.1 | ** (0.0033) |
| Wheelchair User | 56.3 | 68.7 | 12.4 | 22.0 | ** (0.0034) | 45.6 | 34.3 | 11.3 | 24.8 | * (0.0219) | |
| Visually Impaired | 37.2 | 33.2 | 4.0 | 10.8 | ns (0.1272) | 35.6 | 26.2 | 9.4 | 26.4 | * (0.0236) | |
| Hearing Impaired | 26.1 | 29.6 | 3.5 | 13.4 | ns (0.1197) | 25.4 | 22.6 | 2.8 | 11.0 | ns (0.3087) |
| Parameter | Tested Range/Values | Avg. Evac. Time (s) | Std. Dev. | Convergence Stability |
|---|---|---|---|---|
| Velocity coefficient (v) | ±30%, ±50%, baseline | 68.4 → 32.6 | ±2.8 → ±4.2 | Stable |
| Friction coefficient (μ) | 0.2 → 0.8, ±50% of baseline | 34.7 → 39.8 | ±3.1 | Moderate sensitivity |
| Density (N) | 160 → 480 | 26.2 → 78.3 | ±5.7 → ±7.9 | Stable |
| Parameter | Tested Range/Values | Avg. Evac. Time (s) | Episodes to Converge | Convergence Stability |
|---|---|---|---|---|
| Learning rate (α) | 0.1/0.2/0.3/0.5 | 36.8/35.6/35.9/37.5 | 1600/1200/1400/2100 | Stable (0.1–0.3), unstable (≥0.5) |
| Discount factor (γ) | 0.90/0.95/0.98/0.99 | 37.8/35.5/34.9/35.3 | 1800/1400/1300/1500 | Stable near 0.98 |
| Exploration decay (ε) | dynamic (1 → 0.05) vs. fixed 0.1 | 35.6 vs. 38.2 | 1200 vs. 2000 | Dynamic schedule more stable |
| Reward Scaling Factor | Avg. Evac. Time (s) | Episodes to Converge | Stability Assessment | Observed Agent Behavior |
|---|---|---|---|---|
| 0.5× (reduced) | 41.7 | >2000 | Unstable | Frequent oscillation; suboptimal routes; balanced evacuation flow |
| 1.0× (baseline) | 35.6 | 1200 | Stable | Stable near 0.98 |
| 2.0× (amplified) | 34.9 | 1300 | Stable | Slightly faster convergence; reduced exploration |
| 3.0× (over-scaled) | 35.8 | 1700 | Partially unstable | Premature convergence; reduced behavioral diversity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, Y.; Wang, H. Optimizing Evacuation for Disabled Pedestrians with Heterogeneous Speeds: A Floor Field Cellular Automaton and Reinforcement Learning Approach. Buildings 2025, 15, 4191. https://doi.org/10.3390/buildings15224191
Lyu Y, Wang H. Optimizing Evacuation for Disabled Pedestrians with Heterogeneous Speeds: A Floor Field Cellular Automaton and Reinforcement Learning Approach. Buildings. 2025; 15(22):4191. https://doi.org/10.3390/buildings15224191
Chicago/Turabian StyleLyu, Yimiao, and Hongchun Wang. 2025. "Optimizing Evacuation for Disabled Pedestrians with Heterogeneous Speeds: A Floor Field Cellular Automaton and Reinforcement Learning Approach" Buildings 15, no. 22: 4191. https://doi.org/10.3390/buildings15224191
APA StyleLyu, Y., & Wang, H. (2025). Optimizing Evacuation for Disabled Pedestrians with Heterogeneous Speeds: A Floor Field Cellular Automaton and Reinforcement Learning Approach. Buildings, 15(22), 4191. https://doi.org/10.3390/buildings15224191






