The Deterioration of Concrete Based on the Experiments Under the Combined Effects of Freeze-Thaw Cycles, Carbonation Erosion and Sulfate Corrosion
Abstract
1. Introduction
2. Materials and Experiments
2.1. Raw Materials
2.2. Concrete Mix Ratio
2.3. Test Methods
2.3.1. Experimental Instruments and Devices
2.3.2. Test Arrangement
2.3.3. Test Requirements
- The compressive strength is evaluated to assess their performance. To minimize the impact of external factors on these measurements, each type of concrete is tested with three samples, and the average strength is determined from these results.
- The carbonization test is performed under specific conditions, namely, a concentration of 20%, a temperature maintained at 20 ± 2 °C, and a relative humidity of 70 ± 5% [31].
- A freeze–thaw cycle occurs through freezing at −16 ± 2 °C and melting at 3 ± 2 °C. Every freeze–thaw cycle is finished within a time range of 2 to 4 h. The thawing period is at least 1/4 of the length of a freeze–thaw cycle.
3. Results and Discussion
3.1. Apparent Morphology
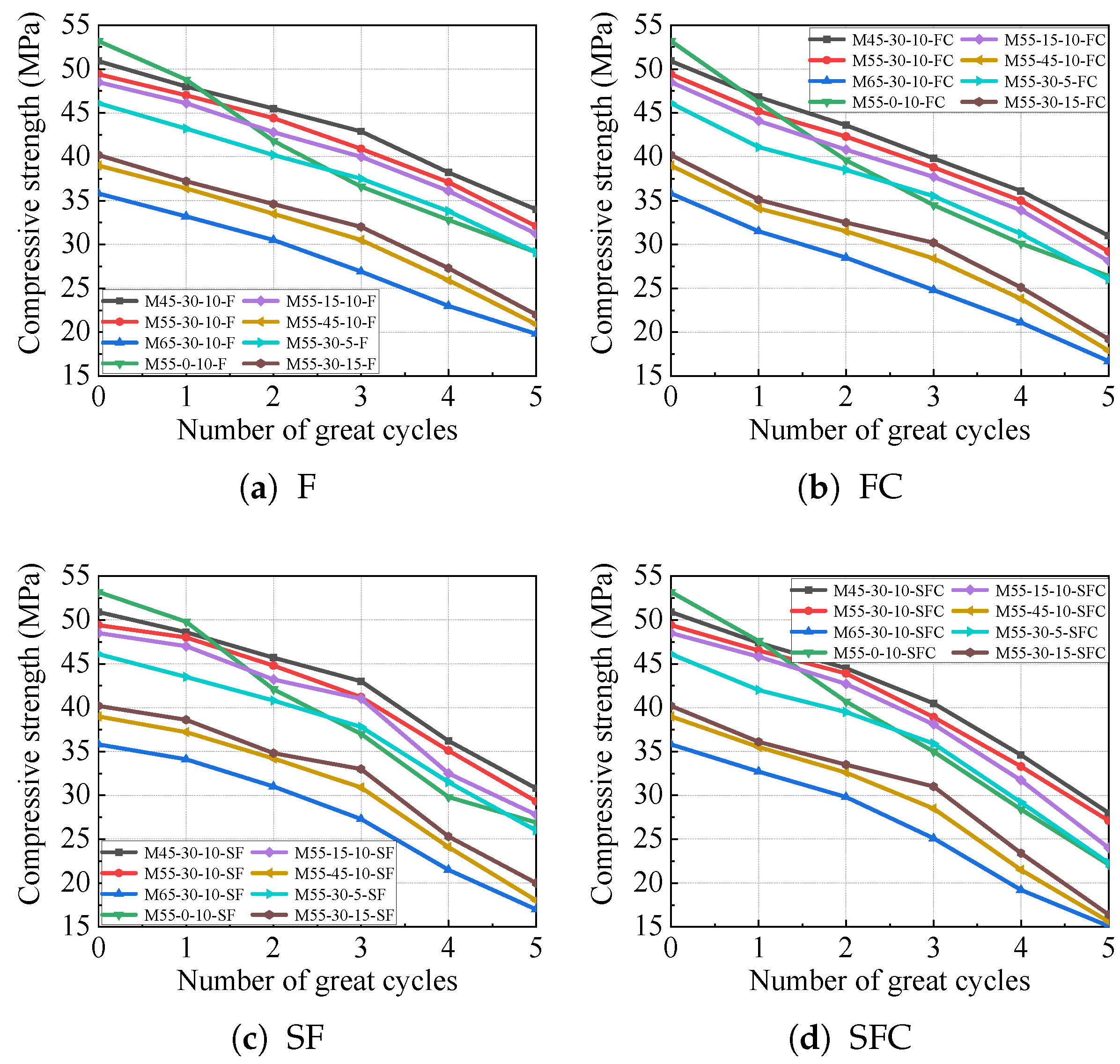
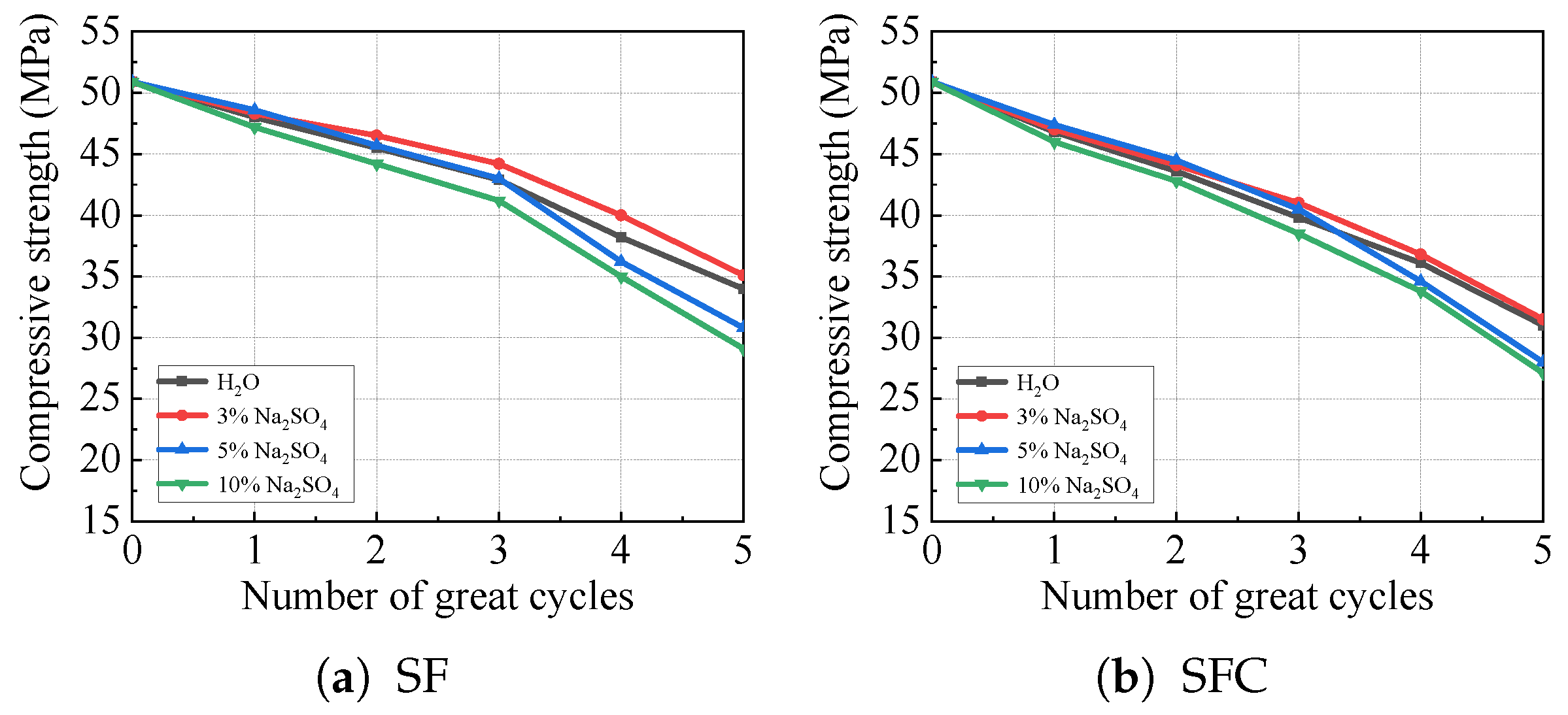
3.2. Compressive Strength
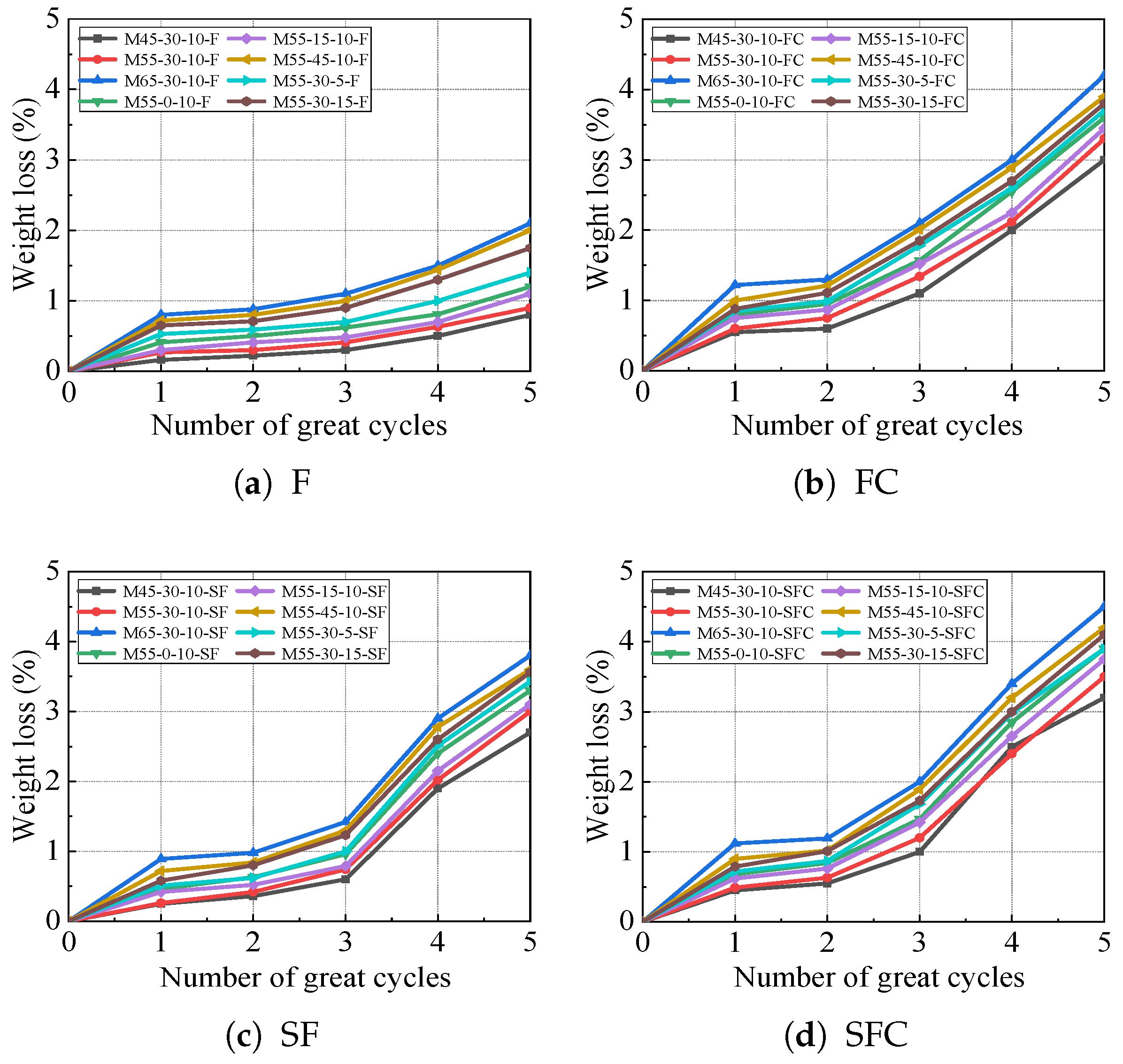
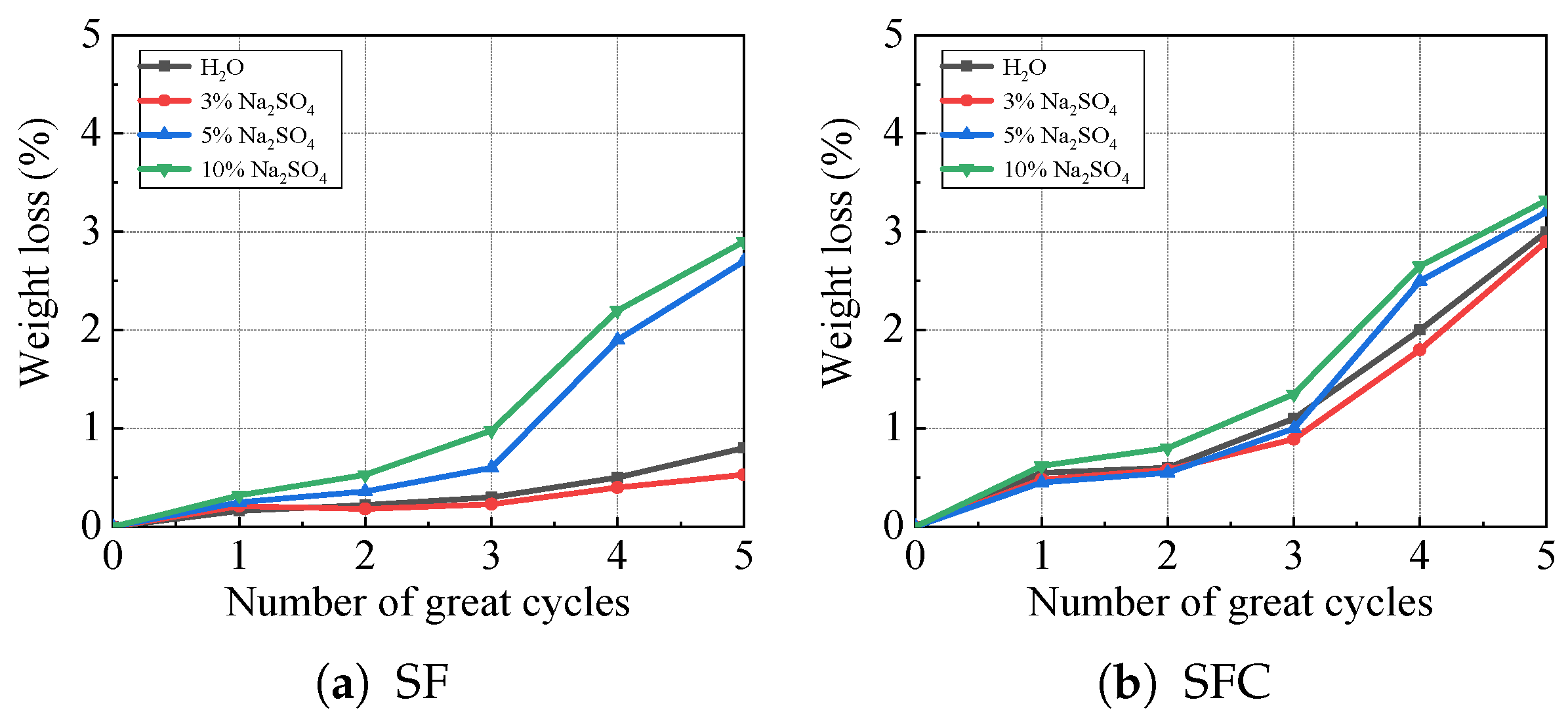
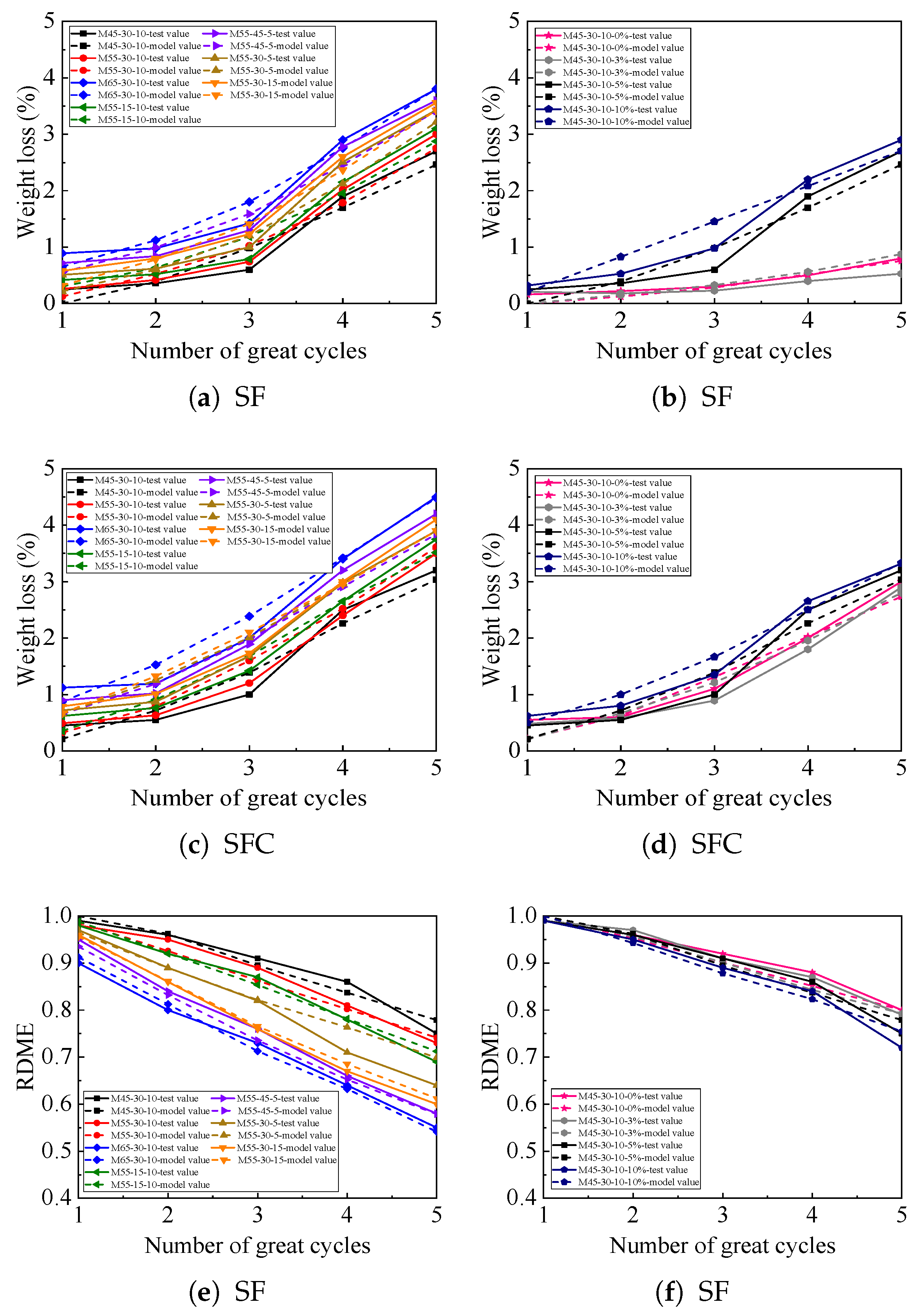
3.3. Weight Change
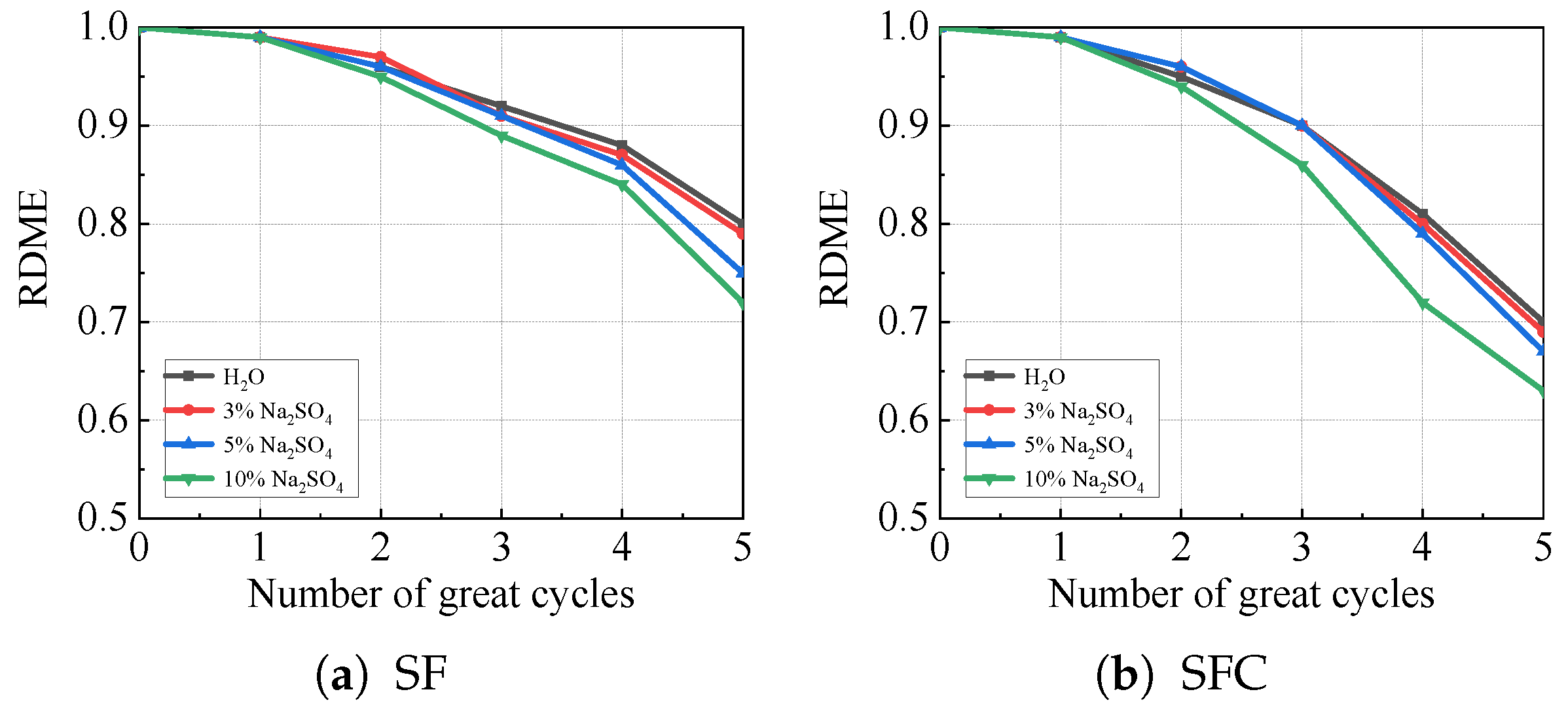
3.4. Relative Dynamic Modulus of Elasticity (RDME)
4. Establishment of the Damage Model and Application of the IOADE Algorithm
4.1. Establishment of the Damage Model
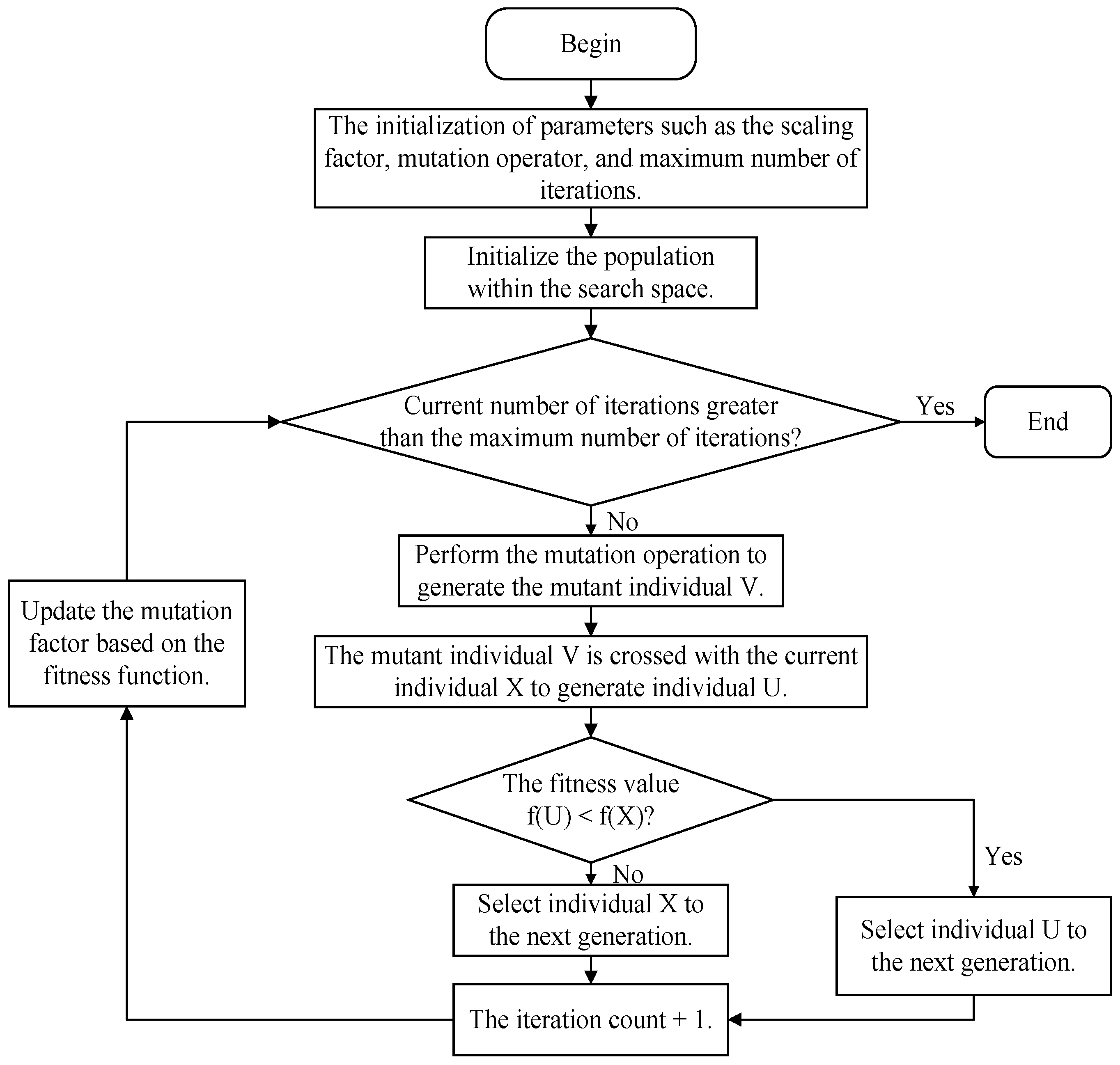
4.2. Application of the IOADE Algorithm and Model Verification
5. Conclusions
- An experimental method has been designed in this paper, which can study the combined effects of freeze–thaw cycles, carbonation erosion, and sulfate corrosion on concrete durability.
- Models for concrete deterioration have been constructed based on the water–binder ratio, fly ash content, polypropylene fiber content, sulfate solution concentration, and compressive strength of concrete, and the interplays of freeze–thaw cycles, carbonation, and sulfate conditions have been obtained.
- To improve the accuracy of the damage evolution models, the IOADE algorithm has been proposed. Meanwhile, the excellent convergence of the proposed IOADE algorithm has been compared with the algorithms of DE and ADE by the , MAE, and RMSE.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, R.J.; Hu, Z.Y.; Li, Y.; Wang, K.; Zhang, H. Review on the deterioration and approaches to enhance the durability of concrete in the freeze-thaw environment. Constr. Build. Mater. 2022, 321, 126371. [Google Scholar] [CrossRef]
- Zhang, R.L.; Zhang, X.P.; Xue, Y.J.; Wang, X.P.; Xiao, P.Z.; Song, Y. Research on the durability degradation mechanism of early-age concrete and life prediction model under freeze-thaw-salt erosion coupling effect. Structures 2025, 71, 107986. [Google Scholar] [CrossRef]
- Taha, A.; Alnahhal, W. Synergistic effects of recycled concrete powder, GGBFS, and basalt fibers on mechanical and durability performance of recycled aggregate concrete. Structures 2025, 71, 108058. [Google Scholar] [CrossRef]
- Harelimana, V.; Zhu, J.A.; Yuan, J.P.; Uwitonze, C. Investigating the bamboo as alternative partial replacement of steel bars in concrete reinforcement members. Struct. Des. Tall Spec. Build. 2022, 31, e1921. [Google Scholar] [CrossRef]
- Ehsan, H.; Behnam, M. Corrosion performance and strain behavior of reinforced concrete: Effect of natural pozzolan as partial substitute for microsilica in concrete mixtures. Structures 2025, 79, 109397. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Cao, Z.Y.; Guan, X.; Li, Q.; Liu, X.L. Damage to recycled concrete with different aggregate substitution rates from the coupled action of freeze-thaw cycles and sulfate attack. Constr. Build. Mater. 2019, 221, 74–83. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Li, Q.; Cao, Z.Y.; Tian, W.Y. The deterioration law of recycled concrete under the combined effects of freeze-thaw and sulfate attack. Constr. Build. Mater. 2019, 200, 344–355. [Google Scholar] [CrossRef]
- Yang, Q.T.; Liu, M.; Li, J.X.; Chen, X. Study on the degradation models based on the experiments considering the coupling effect of freeze-thaw and carbonation. Structures 2024, 64, 106659. [Google Scholar] [CrossRef]
- Roja, S.Y.; Yamini Roja, S.; Murali, K.; Shanthi, V.M. Enhancing Concrete Performance with Waste Foundry Sand Using Ternary Blended Mixes of Ordinary Portland Cement, Silica Fume, and Ground Granulated Blast Furnace Slag. Struct. Des. Tall Spec. Build. 2024, 33, e2180. [Google Scholar]
- Feng, Q.; Jin, J.; Zhang, S.; Liu, W.W.; Yang, X.X.; Li, W.T. Study on a damage model and uniaxial compression simulation method of frozen-thawed rock. Rock Mech. Rock Eng. 2022, 55, 187–211. [Google Scholar]
- Zhang, J.H.; Li, J.; Yun, H.; Long, J.Z.; Zhu, Q.X.; Guan, Z.G. Durability of new-to-old concrete interface under coupling action of freeze-thaw cycle and chloride salt erosion. Structures 2024, 70, 107867. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Y.J.; Liu, Y.; Zhao, M.D. Mechanical properties, pore structure and freeze-thaw resistance of recycled aggregate concrete based on ash of mushroom and corn straw. Structures 2024, 68, 107167. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Zhuang, W.; Li, Z.P.; Yu, Z.Y.; Shao, C.Y. The effect of early-age freeze-thaw cycle damage on hydraulic concrete self-healing. Mech. Time-Depend. Mater. 2023, 27, 529–542. [Google Scholar] [CrossRef]
- Liu, P.; Yu, Z.W.; Chen, Y. Carbonation depth model and carbonated acceleration rate of concrete under different environment. Cem. Concr. Compos. 2020, 114, 103736. [Google Scholar] [CrossRef]
- Xu, R.T.; Liang, Y.; Ning, F.; Chen, Z.P. The effect of NaHCO3 accelerated carbonation method on the early mechanical properties of recycled aggregate concrete. Structures 2024, 70, 107647. [Google Scholar] [CrossRef]
- Feng, M.J.; Li, M.; Qu, H.H.; Tian, D.J.; Lu, M.J.; Gui, T.T.; Li, G. Degradation mechanism and evaluation of the carbonation resistance of concrete after high-temperature exposure. Structures 2023, 58, 105621. [Google Scholar] [CrossRef]
- Bekdas, G.; Yucel, M.; Nigdeli, S.M. Generation of eco-friendly design for post-tensioned axially symmetric reinforced concrete cylindrical walls by minimizing of CO2 emission. Struct. Des. Tall Spec. Build. 2022, 31, e1948. [Google Scholar] [CrossRef]
- Qiao, Y.; Sun, W.; Jiang, J. Damage process of concrete subjected to coupling fatigue load and free/thaw cycles. Constr. Build. Mater. 2015, 93, 806–811. [Google Scholar] [CrossRef]
- Suzuki, T.; Ogata, H.; Takada, R.; Aoki, M.; Ohtsu, M. Use of acoustic emission and X-ray computed tomography for damage evaluation of freezethawed concrete. Constr. Build. Mater. 2010, 24, 2347–2352. [Google Scholar] [CrossRef]
- Tangtermsirikul, S.; Khunthongkeaw, J.; Leelawat, T. A study on carbonation depth prediction for fly ash concrete. Constr. Build. Mater. 2006, 20, 744–753. [Google Scholar] [CrossRef]
- Wang, Y.; An, M.Z.; Yu, Z.R.; Han, S.; Ji, W.Y. Durability of reactive powder concrete under chloride-salt freeze-thaw cycling. Mater. Struct. 2017, 50, 18. [Google Scholar]
- Kessler, S.; Thiel, C.; Grosse, C.U.; Gehlen, C. Effect of freeze-thaw damage on chloride ingress into concrete. Mater. Struct. 2017, 50, 121. [Google Scholar]
- Mu, R.; Miao, C.; Luo, X.; Sun, W. Interaction between loading, freeze-thaw cycles, and chloride salt attack of concrete with and without steel fiber reinforcement. Cem. Concr. Res. 2002, 32, 1061–1066. [Google Scholar] [CrossRef]
- Liang, M.T.; Wang, K.L.; Liang, C.H. Service life prediction of reinforced concrete structure. Cem. Concr. Res. 1999, 29, 1411–1418. [Google Scholar] [CrossRef]
- Jiang, L.; Niu, D.T.; Yuan, L.D.; Fei, Q.N. Durability of concrete under sulfate attack exposed to freeze-thaw cycles. Cold Reg. Sci. Technol. 2015, 112, 112–117. [Google Scholar]
- Wang, D.Z.; Zhou, X.M.; Meng, Y.F.; Chen, Z. Durability of concrete containing fly ash and silica fume against combined freezing-thawing and sulfate attack. Constr. Build. Mater. 2017, 147, 398–406. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.J.; Li, S.Y.; Zhao, Y.; Qin, Y. Resistance of recycled aggregate concrete containing low- and high-volume fly ash against the combined action of freeze-thaw cycles and sulfate attack. Constr. Build. Mater. 2018, 166, 23–34. [Google Scholar]
- Elmoaty, M.A.; Elmoaty, A. Four-years carbonation and chloride induced steel corrosion of sulfate-contaminated aggregates concrete. Constr. Build. Mater. 2018, 163, 539–556. [Google Scholar]
- Oliveira, M.B.; Vazquez, E. The influence of restained moisture in Aggregates from recycling on tbe properties of new hardened concrete. Waste Manag. 1996, 16, 113–117. [Google Scholar]
- Sun, B.; Mao, S.Y.; Wang, J.X.; Di, X.T.; Ren, R.H. Experimental study on correlation between natural carbonation and accelerated carbonation of long-term observation concrete specimens. Build Struct. 2019, 49, 111–114. [Google Scholar]
- GB/T50082-2024; Standard for Test Methods of Long-Term Performance and Durability of Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2024.
- Wang, J.B.; Niu, D.T.; He, H. Frost durability and stress-strain relationship of lining shotcrete in cold environment. Constr. Build. Mater. 2019, 198, 58–69. [Google Scholar] [CrossRef]
- Wang, J.B.; Niu, D.T. Influence of freeze-thaw cycles and sulfate corrosion resistance on shotcrete with and without steel fiber. Constr. Build. Mater. 2016, 122, 628–636. [Google Scholar] [CrossRef]
- Ortega, J.J.; Ruiz, G.; Yu, R.N.C.; Afanador-Garca, N.; Tarifa, M.; Poveda, E.; Zhang, X.; Evangelista, F., Jr. Number of tests and corresponding error in concrete fatigue. Int. J. Fatigue 2018, 116, 210–219. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Nguyen, T.A.; Ly, H.B. Ensemble XGBoost schemes for improved compressive strength prediction of UHPC. Structures 2023, 57, 105062. [Google Scholar] [CrossRef]
- Zhou, S.; Xing, L.; Zheng, X.; Du, N.; Wang, L.; Zhang, Q.F. A self-adaptive differential evolution algorithm for scheduling a single batch-processing machine with arbitrary job sizes and release times. IEEE Trans. Cybern. 2021, 51, 1430–1442. [Google Scholar] [CrossRef]
- Wang, Z.Q.; He, D.K.; Nie, H.T. Operational optimization of copper flotation process based on the weighted Gaussian process regression and index-oriented adaptive differential evolution algorithm. Chin. J. Chem. Eng. 2024, 66, 167–179. [Google Scholar] [CrossRef]




| Cement Variety | Setting Time | Compression Strength (MPa) | Flexural Strength (MPa) | Loss of Ignition (%) | Specific Surface Area (m2/g) | |||
|---|---|---|---|---|---|---|---|---|
| Initial Setting | Final Setting | 3 d | 28 d | 3 d | 28 d | |||
| P.O42.5 | 90 min | 5.5 h | 21.5 | 42.1 | 4.0 | 7.1 | 2.5 | 400 |
| Chemical Composition (%) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cement | 61.35 | 19.78 | 5.69 | 3.03 | 2.96 | 1.55 | 0.75 | 0.13 |
| Fly ash | 6.36 | 52.20 | 21.87 | 7.98 | 0.43 | 2.34 | 1.59 | 2.67 |
| Label | Water to Binder Ratio | Cement (kg/m3) | Fly Ash (kg/m3) | Sand (kg/m3) | Stone (kg/m3) | Water (kg/m3) | Water-Reducing Agent (kg/m3) | Fiber (kg/m3) | Na2SO4 Solution (%) |
|---|---|---|---|---|---|---|---|---|---|
| M45-30-10 | 0.45 | 420 | 180 | 563 | 1047 | 270 | 3 | 9.1 | 0, 3, 5, 10 |
| M55-30-10 | 0.55 | 344 | 147 | 602 | 1117 | 270 | 2.45 | 9.1 | 0, -, 5, - |
| M65-30-10 | 0.65 | 291 | 125 | 628 | 1117 | 270 | 2.08 | 9.1 | 0, -, 5, - |
| M55-0-10 | 0.55 | 491 | 0 | 602 | 1117 | 270 | 2.45 | 9.1 | 0, -, 5, - |
| M55-15-10 | 0.55 | 417 | 74 | 602 | 1117 | 270 | 2.45 | 9.1 | 0, -, 5, - |
| M55-45-10 | 0.55 | 270 | 221 | 602 | 1117 | 270 | 2.45 | 9.1 | 0, -, 5, - |
| M55-30-5 | 0.55 | 344 | 147 | 602 | 1117 | 270 | 2.45 | 4.5 | 0, -, 5, - |
| M55-30-15 | 0.55 | 344 | 147 | 602 | 1117 | 270 | 2.45 | 13.65 | 0, -, 5, - |
| Test Code | Test Conditions | Notations | Test Procedures |
|---|---|---|---|
| 1 | freeze–thaw | F | (1) Water immersion for 4 days (2) Freeze–thaw cycles 50 times (3) Take steps 1–2 as a great cycle and repeat it |
| 2 | freeze–thaw and carbonation | FC | (1) Water immersion for 4 days (2) Freeze–thaw cycles 50 times (3) Oven-dried at 60 °C for 2 days (4) Accelerated carbonation for 3 days (5) Take steps 1–4 as a great cycle and repeat it |
| 3 | sulfate and freeze–thaw | SF | (1) Na2SO4 solution immersion for 4 days (2) Freeze–thaw cycles 50 times (3) Take steps 1–2 as a great cycle and repeat it |
| 4 | sulfate and freeze–thaw and carbonation | SFC | (1) Na2SO4 solution immersion for 4 days (2) Freeze–thaw cycles 50 times (3) Oven-dried at 60 °C for 2 days (4) Accelerated carbonation for 3 days (5) Take steps 1–4 as a great cycle and repeat it |
| a | b | c | d | e | f | g | h | l | m | k | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SF | 6.1685 | −9.7789 | 2.5295 | −0.3734 | −4.4393 | 7.7054 | −3.0650 | −0.1972 | 3.4816 | 0.2098 | −0.4236 | |
| SFC | 3.6801 | 3.1688 | 1.6751 | 0.2333 | 3.8634 | 4.7329 | −4.0047 | −0.0041 | 5.9490 | 3.5623 | −0.8284 | |
| SF | −6.4714 | 1.6279 | 2.8207 | 0.1644 | −0.5890 | −1.2222 | 0.5605 | 0.6774 | −0.8560 | −0.0031 | 0.4967 | |
| SFC | −2.1405 | 7.9662 | −5.2406 | 0.4985 | −0.9421 | 0.3707 | −0.1966 | 1.7825 | −1.7366 | −0.0063 | 0.3848 |
| Gm | Indexes | ||||||
|---|---|---|---|---|---|---|---|
| DE | ADE | IOADE | DE | ADE | IOADE | ||
| 500 | 0.7243 | 0.7936 | 0.8195 | 0.8894 | 0.9324 | 0.9531 | |
| MAE | 0.3989 | 0.3261 | 0.2985 | 0.0305 | 0.0246 | 0.0273 | |
| RMSE | 0.3228 | 0.2983 | 0.2748 | 0.0402 | 0.0349 | 0.0316 | |
| 2000 | 0.8854 | 0.9368 | 0.9530 | 0.9017 | 0.9584 | 0.9755 | |
| MAE | 0.3017 | 0.2634 | 0.2481 | 0.0297 | 0.0231 | 0.0196 | |
| RMSE | 0.2893 | 0.2695 | 0.2544 | 0.0342 | 0.0288 | 0.0219 | |
| 5000 | 0.9058 | 0.9562 | 0.9714 | 0.9534 | 0.9795 | 0.9864 | |
| MAE | 0.2475 | 0.2388 | 0.2264 | 0.0208 | 0.0179 | 0.0165 | |
| RMSE | 0.2503 | 0.2469 | 0.2371 | 0.0265 | 0.0204 | 0.0187 | |
| Gm | Indexes | ||||||
|---|---|---|---|---|---|---|---|
| DE | ADE | IOADE | DE | ADE | IOADE | ||
| 500 | 0.8994 | 0.9136 | 0.9515 | 0.9017 | 0.9256 | 0.9503 | |
| MAE | 0.3849 | 0.3254 | 0.2926 | 0.0576 | 0.3843 | 0.0307 | |
| RMSE | 0.3461 | 0.3027 | 0.2894 | 0.0477 | 0.0395 | 0.0299 | |
| 2000 | 0.9243 | 0.9507 | 0.9615 | 0.9315 | 0.9436 | 0.9717 | |
| MAE | 0.3124 | 0.2918 | 0.2769 | 0.0423 | 0.0318 | 0.0251 | |
| RMSE | 0.3004 | 0.2897 | 0.2722 | 0.0325 | 0.0309 | 0.0272 | |
| 5000 | 0.9506 | 0.9795 | 0.9814 | 0.9614 | 0.9776 | 0.9869 | |
| MAE | 0.2937 | 0.2461 | 0.2368 | 0.0361 | 0.0293 | 0.0226 | |
| RMSE | 0.2983 | 0.2629 | 0.2517 | 0.0293 | 0.0258 | 0.0214 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Wang, Z.; Chen, X.; Li, J. The Deterioration of Concrete Based on the Experiments Under the Combined Effects of Freeze-Thaw Cycles, Carbonation Erosion and Sulfate Corrosion. Buildings 2025, 15, 4179. https://doi.org/10.3390/buildings15224179
Yang Q, Wang Z, Chen X, Li J. The Deterioration of Concrete Based on the Experiments Under the Combined Effects of Freeze-Thaw Cycles, Carbonation Erosion and Sulfate Corrosion. Buildings. 2025; 15(22):4179. https://doi.org/10.3390/buildings15224179
Chicago/Turabian StyleYang, Qianting, Zhiqiang Wang, Xin Chen, and Jiaxu Li. 2025. "The Deterioration of Concrete Based on the Experiments Under the Combined Effects of Freeze-Thaw Cycles, Carbonation Erosion and Sulfate Corrosion" Buildings 15, no. 22: 4179. https://doi.org/10.3390/buildings15224179
APA StyleYang, Q., Wang, Z., Chen, X., & Li, J. (2025). The Deterioration of Concrete Based on the Experiments Under the Combined Effects of Freeze-Thaw Cycles, Carbonation Erosion and Sulfate Corrosion. Buildings, 15(22), 4179. https://doi.org/10.3390/buildings15224179





