Experimental Study and Machine Learning Prediction of Shear Capacity of Panel-Sheathing Nailed Connections in Wood Structures
Abstract
1. Introduction
2. Materials and Methods
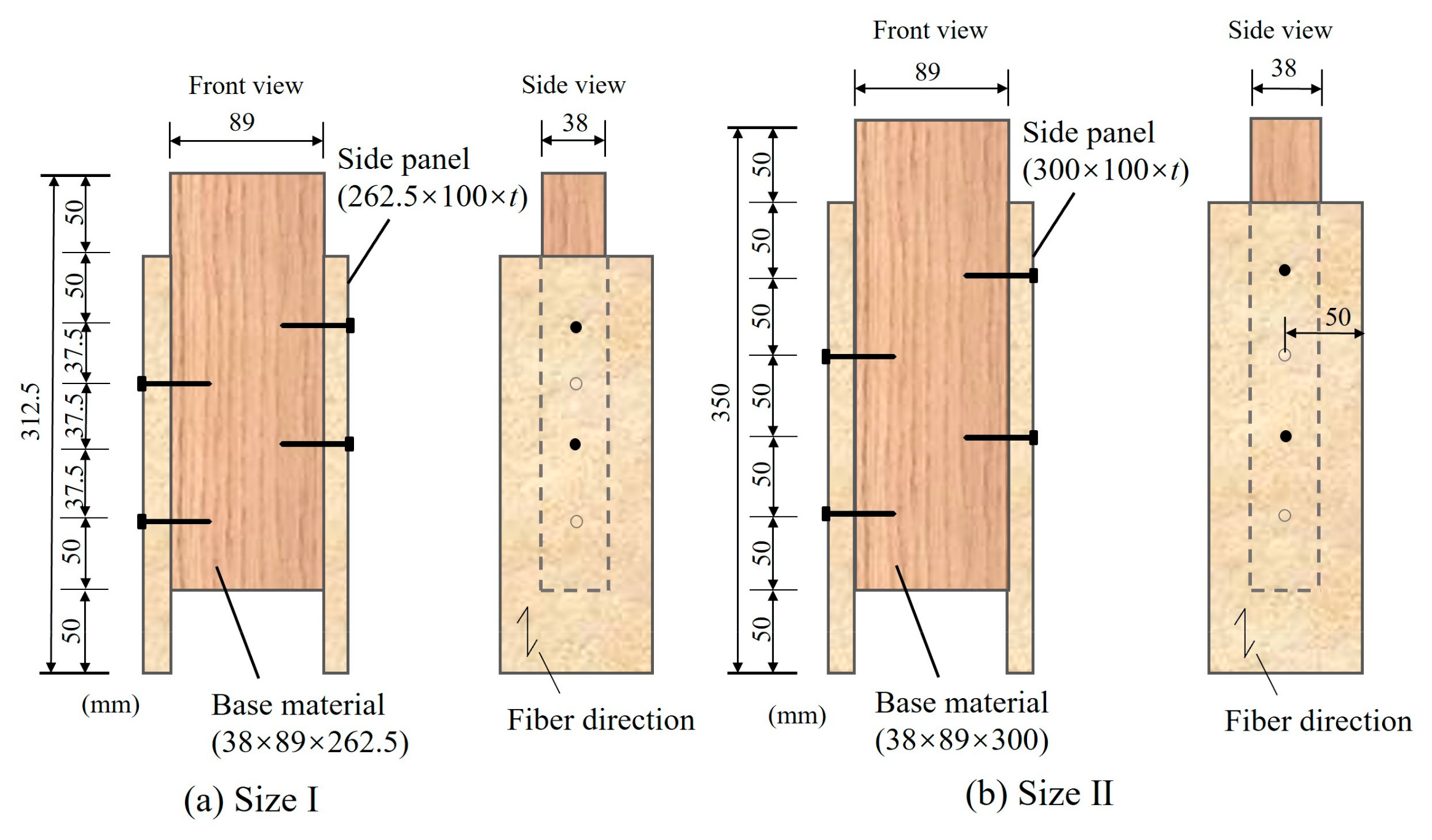
2.1. Specimen Preparation
2.2. Material Properties
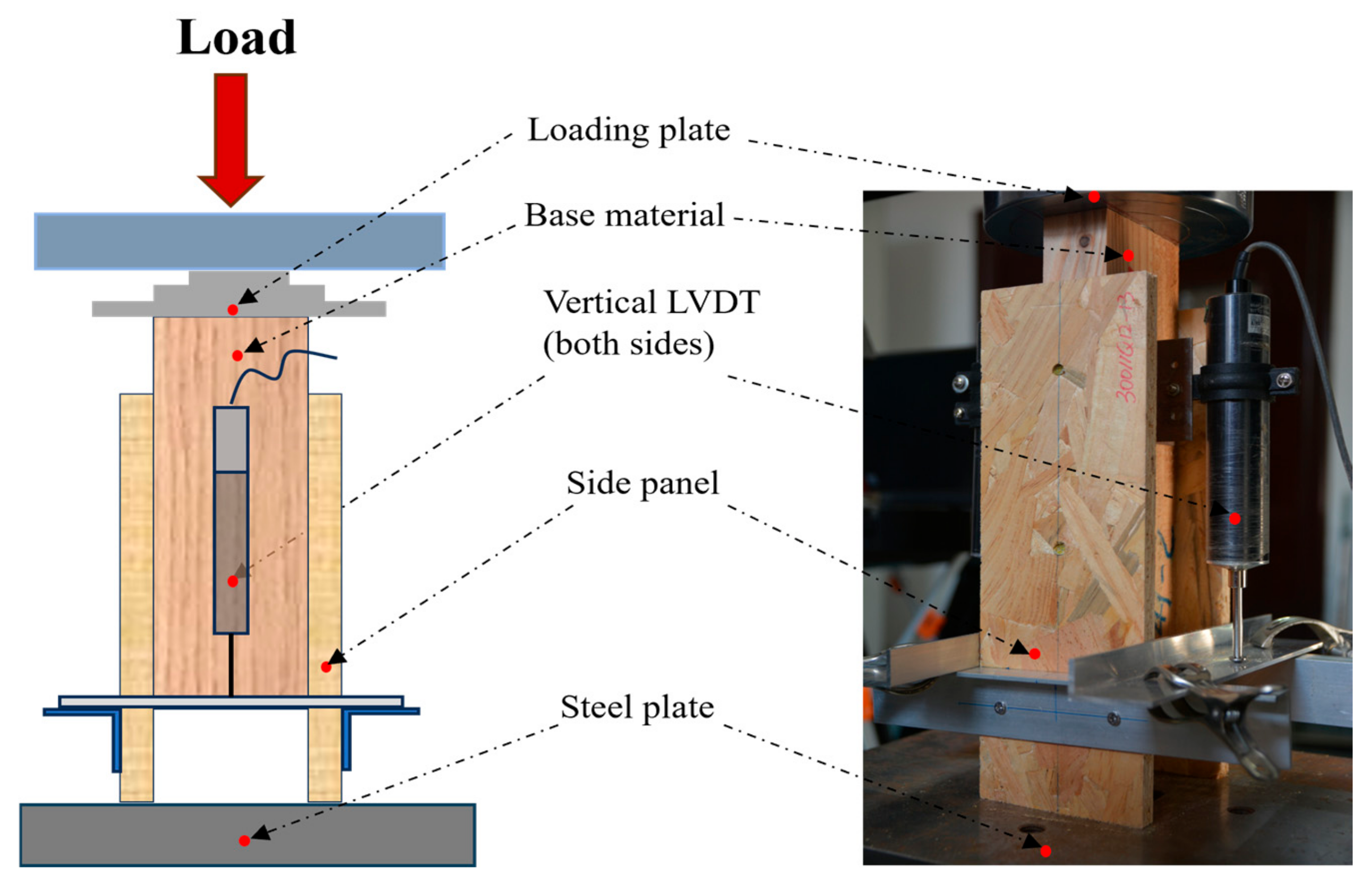
2.3. Experimental Methodology
3. Experimental Results and Analysis
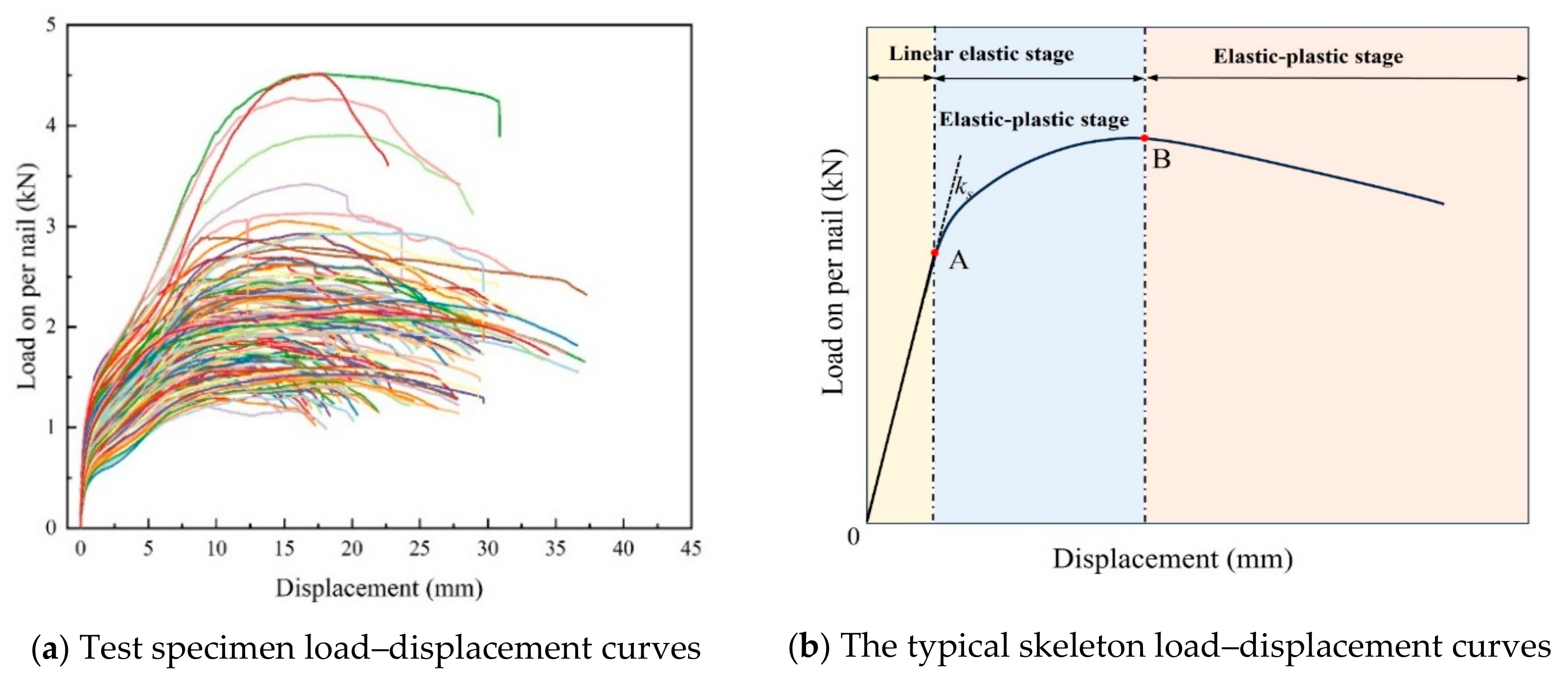
3.1. Load–Displacement Curves
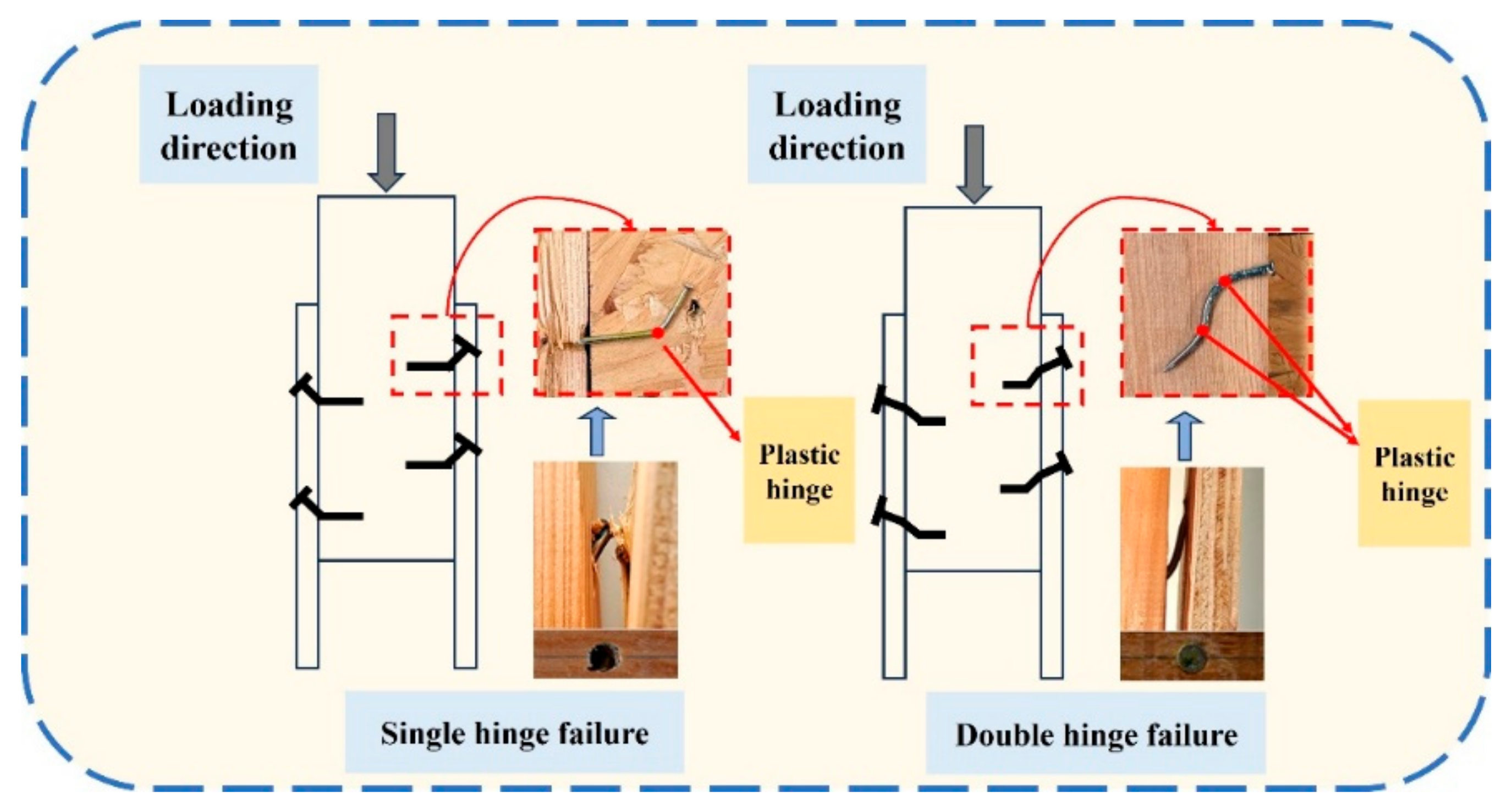
3.2. Observations from the Experiment
4. Machine Learning Model Evaluation
4.1. Dataset for ML Application
- (1)
- Missing or malfunctioning LVDT readings;
- (2)
- Visually observed fixture slippage during testing;
- (3)
- Incomplete specimen failure.
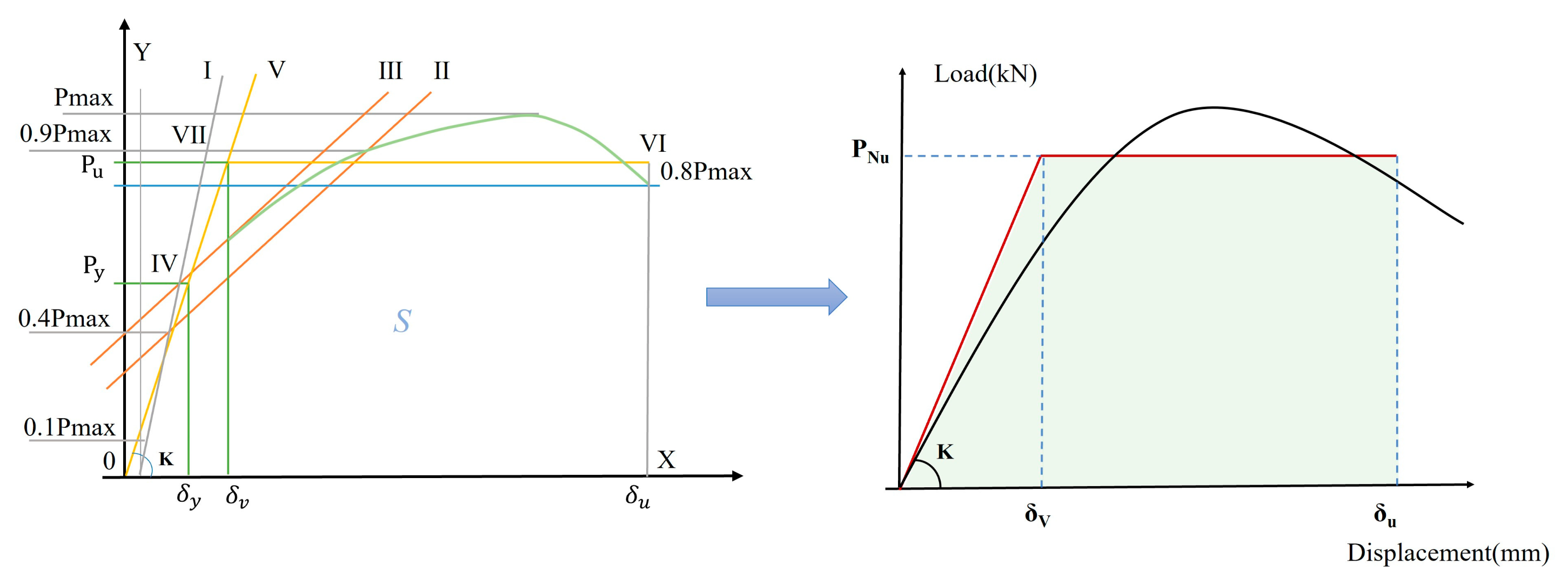
4.2. Model Evaluation Metrics
4.3. Five-Fold Cross-Validation and Hyperparameter Tuning
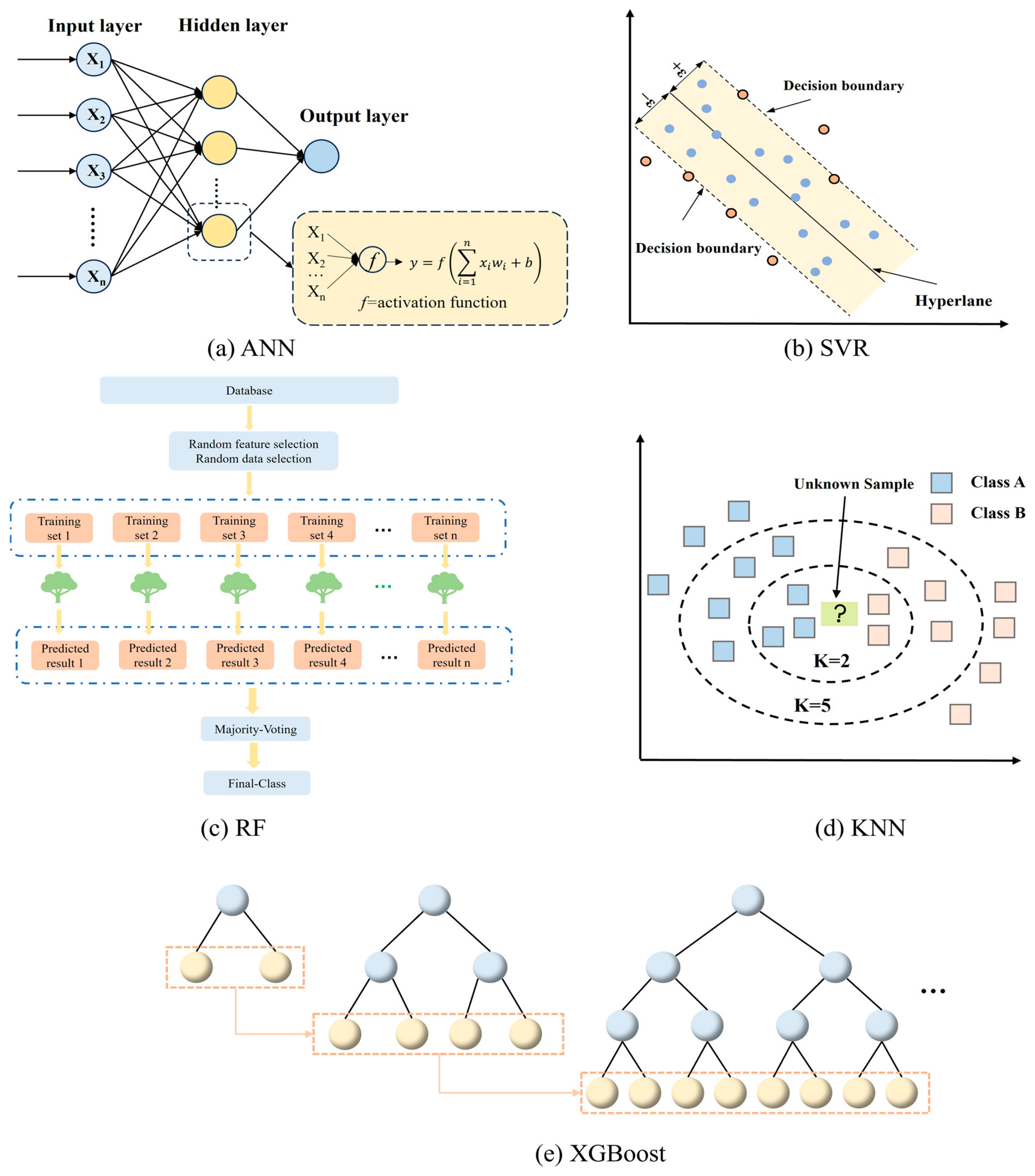
4.4. Machine Learning Algorithm
4.4.1. Artificial Neural Network (ANN)
4.4.2. Support Vector Regression (SVR)
4.4.3. Random Forest (RF)
4.4.4. Extreme Gradient Boosting (XGBoost)
4.4.5. K-Nearest Neighbor (KNN)
4.4.6. Categorical Boosting (CatBoost)
5. Results and Discussion
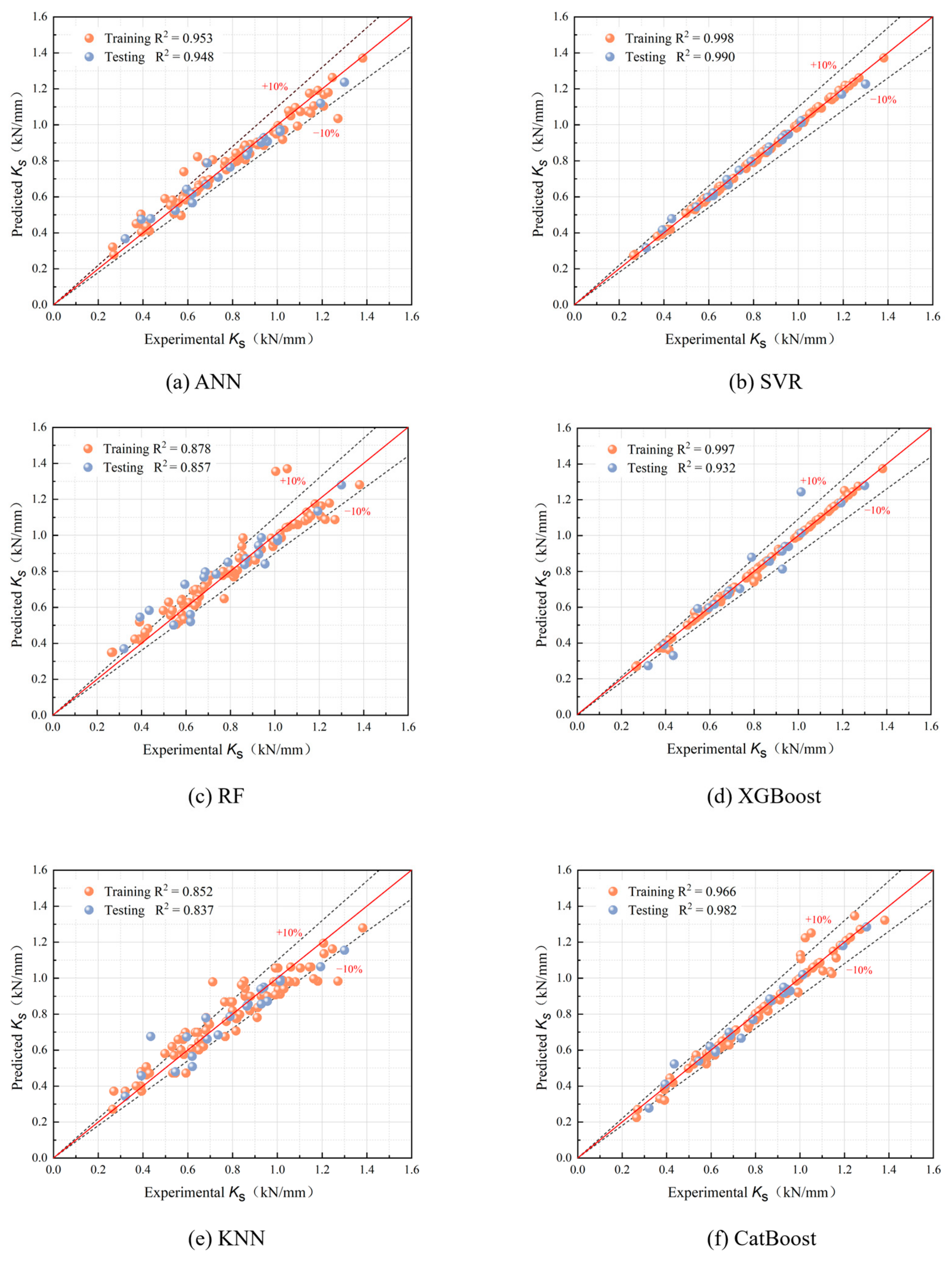
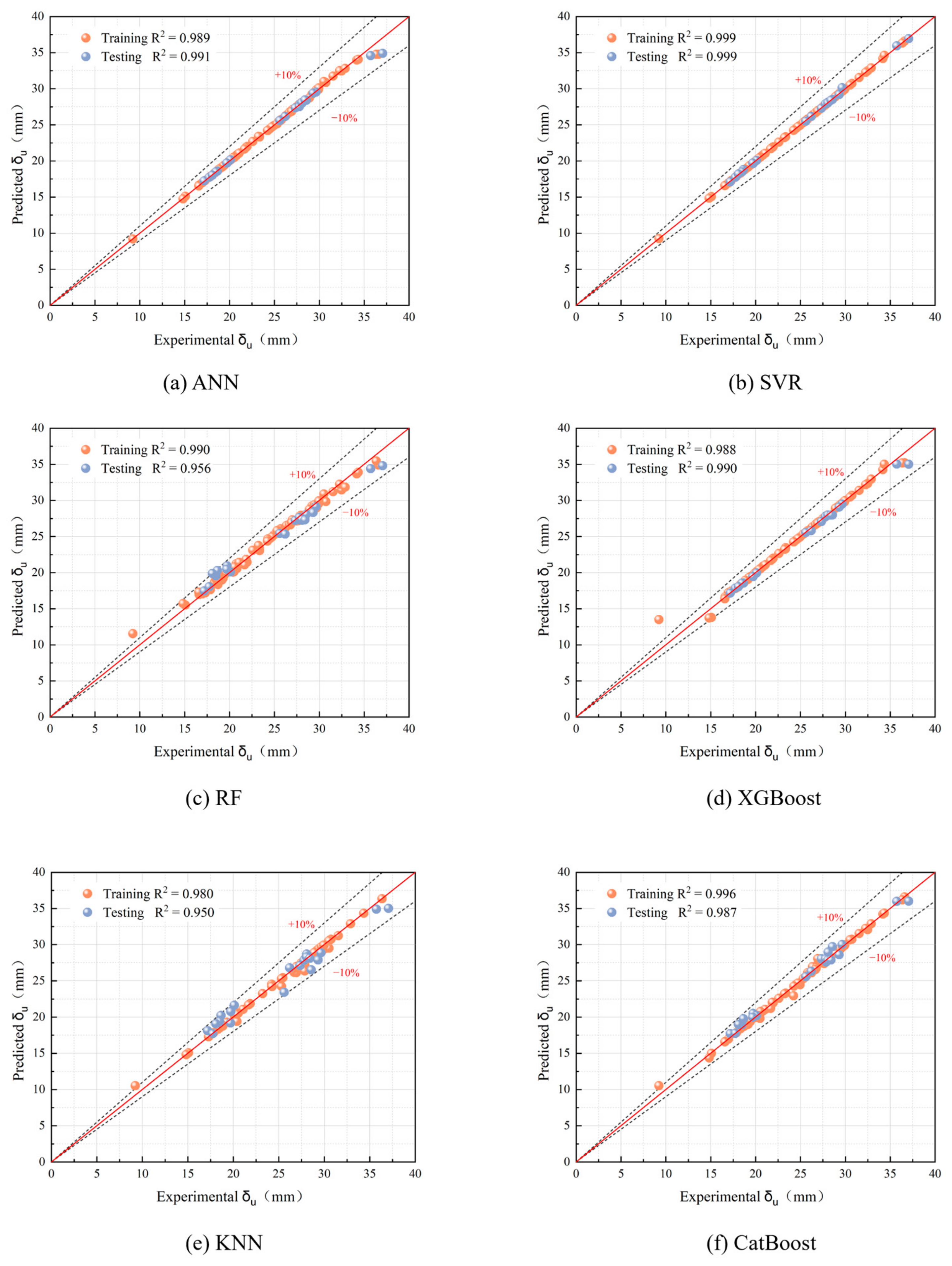
5.1. Model Performance
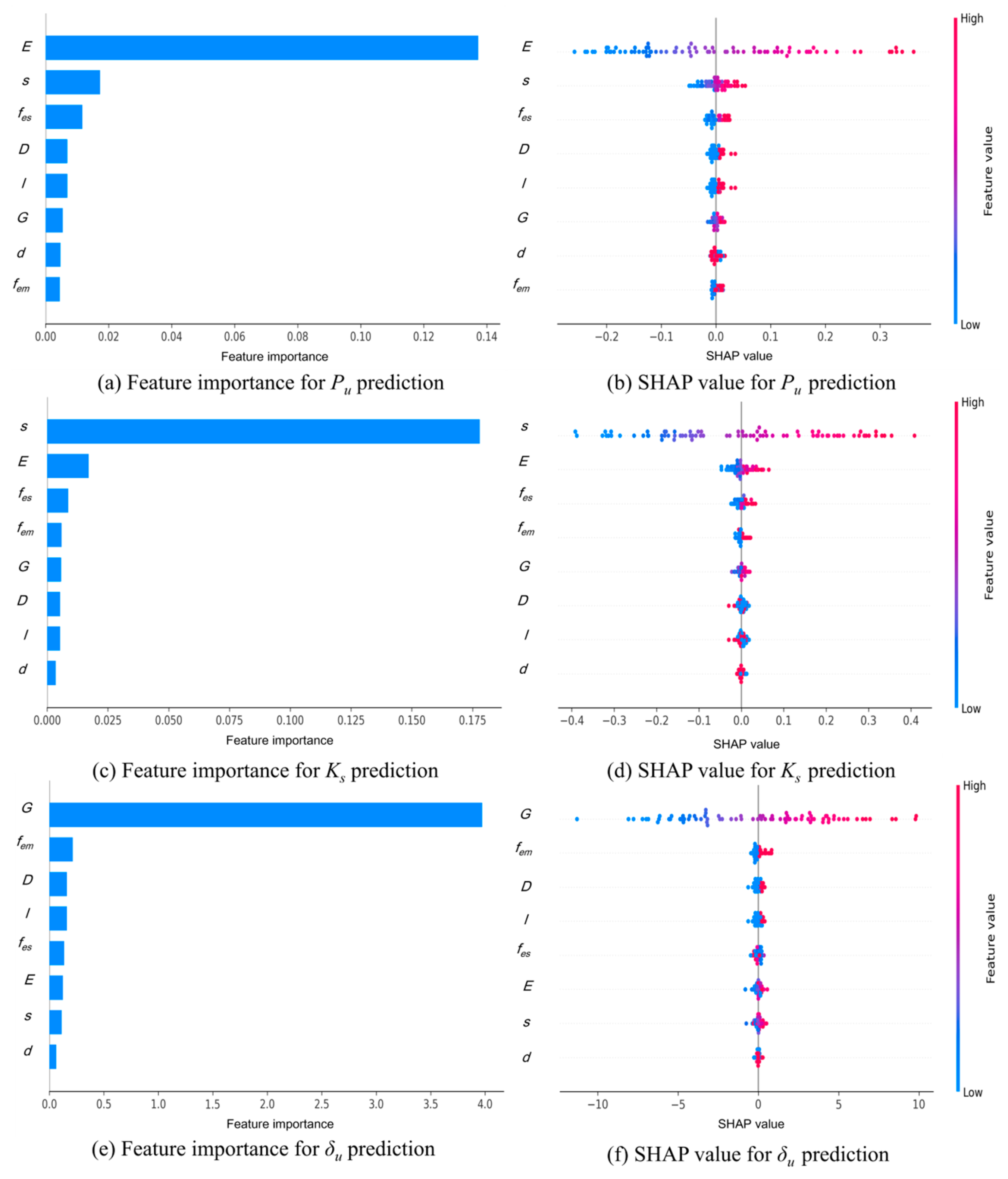
5.2. Model Interpretation
5.3. Calculation of Bearing Capacity
5.3.1. Calculation Using Eurocode 5-1995
5.3.2. Calculation Using GB/T 50005-2017
6. Conclusions
- (1)
- The test results indicate that the performance of nailed connections in wood structures depends on the nail type, substrate, and the thickness and type of the side plates. Thus, it is essential to consider these factors in designing and researching wood structure shear walls or floor slabs to establish an effective collaborative load-bearing mechanism.
- (2)
- The failure modes of the panel-sheathing nailed connection included Mode IIIm (single plastic hinge failure) and Mode IV (double plastic hinge failure). These two failure modes depended on the thickness of the side plates and the length of the nails. Additionally, the grain direction of the side plates had a negligible effect on the shear bearing capacity of the specimens.
- (3)
- The test results demonstrate that the load–displacement curves of the nailed connections exhibited a consistent pattern of three stages: linear elastic, elastoplastic, and failure stages. This finding indicates that employing ML models to predict a simplified load–displacement curve is feasible and justified.
- (4)
- Six ML methods (ANN, SVR, RF, XGBoost, KNN, and CatBoost) were employed to predict the ultimate load, initial shear stiffness, and ultimate displacement of the nailed connections. A comparison analysis revealed that the SVR exhibited the best performance in predicting the three characteristic values of the load–displacement curves of the nailed connection push-out specimens, achieving R2 values of 0.9950, 0.9976, and 0.9994, respectively.
- (5)
- The ML model demonstrated significantly higher predictive accuracy and broader applicability than existing empirical equations in predicting the characteristic values of the load–displacement curves of nailed connections. These models can be used for the structural design of nailed connectors in wood structures.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Derakhshan, S.S.; Zhou, L.; Ni, C. Influence of the Loading Protocol and Loading Rate on the Characteristics of Timber Nail Joints. J. Renew. Mater. 2022, 10, 2655–2667. [Google Scholar] [CrossRef]
- Que, Z.; Ling, Y.; Dan, Z.; Wang, Y.; Yong, W. Experimental Study of Nail Joints of Shear Walls under Different Cladding Conditions in Wood Frame Structures. Build. Struct. 2014, 44, 81–85. [Google Scholar]
- Yan, L.; Zou, X.; Yun, G. Test Research of the Nail Joints on Light Wood Structure. In Proceedings of the World Conference on Timber Engineering 2010, Trentino, Italy, 20–24 June 2010. [Google Scholar]
- Zheng, W.; Lu, W.; Liu, W.; Wang, L.; Ling, Z. Experimental Investigation of Laterally Loaded Double-Shear-Nail Connections Used in Midply Wood Shear Walls. Constr. Build. Mater. 2015, 101, 761–771. [Google Scholar] [CrossRef]
- Wang, S.; Lin, J.; Dong, S.; Chen, Z.; Kong, F.; Ma, P.; Wang, F.; Que, Z. Lateral Resistance Performance of Wood-Frame Shear Walls with Wooden Nail Connections: Experimental and Finite Element Analysis. J. Bioresour. Bioprod. 2025, 10, 410–424. [Google Scholar] [CrossRef]
- Chen, G.; Jiang, H.; Yu, Y.F.; Zhou, T.; Wu, J.; Li, X. Experimental Analysis of Nailed LBL-to-LBL Connections Loaded Parallel to Grain. Mater. Struct. 2020, 53, 81. [Google Scholar] [CrossRef]
- Chen, G.; Yang, W.; Zhou, T.; Yu, Y.; Wu, J.; Jiang, H.; Li, X.; Zhang, Y. Experiments on Laminated Bamboo Lumber Nailed Connections. Constr. Build. Mater. 2021, 269, 121321. [Google Scholar] [CrossRef]
- Wahan, M.Y.; Zhang, Z.; Meng, X.; Gao, Y.; Ji, X. Mechanical Behavior of GFRP-Bamboo Composite Shear Connections. Constr. Build. Mater. 2022, 331, 127333. [Google Scholar] [CrossRef]
- Shahin, A.; Cowled, C.J.; Bailleres, H.; Fawzia, S. Experimental Study on Shear Performance of Nail and Screw-Laminated Timber-Steel Composite and Timber-Timber Systems Using Low-Grade Timber and Mechanical Fasteners. Constr. Build. Mater. 2024, 418, 135403. [Google Scholar] [CrossRef]
- Yan, B.; Zhang, W.; Ye, Y.; Yi, W. Study on the Prediction of Shear Capacity of New and Old Concrete Interfaces Based on Explainable Machine Learning Algorithms. Structures 2025, 71, 108065. [Google Scholar] [CrossRef]
- Zhao, Y.; Tian, J.; Zhou, W.; Liu, G.; Lu, J. Prediction of Shear Capacity of PRC Coupling Beams Using Machine Learning Methods. Structures 2025, 75, 108783. [Google Scholar] [CrossRef]
- Ge, P.; Yang, O.; He, J.; Zhang, K.; Wu, S. A Machine Learning Based Method for Predicting the Shear Strength of Fiber-Reinforced Concrete Joints in Precast Segmental Bridges. Eng. Struct. 2024, 302, 117324. [Google Scholar] [CrossRef]
- Li, X.; Liu, C.; Xue, Y.; Xue, S.; Liao, S.; Zhou, Y. Predicting Bearing Capacity of Angle Steel Bolted Connections Using Machine Learning Based on Experimental and Numerical Database. Structures 2024, 67, 107014. [Google Scholar] [CrossRef]
- Sarothi, S.Z.; Ahmed, K.S.; Khan, N.I.; Ahmed, A.; Nehdi, M.L. Predicting Bearing Capacity of Double Shear Bolted Connections Using Machine Learning. Eng. Struct. 2022, 251, 113497. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Chen, A.; Ruan, X. Auto-Tuning Ensemble Models for Estimating Shear Resistance of Headed Studs in Concrete. J. Build. Eng. 2022, 52, 104470. [Google Scholar] [CrossRef]
- Zhu, J.; Farouk, A.I.B. Development of Hybrid Models for Shear Resistance Prediction of Grouped Stud Connectors in Concrete Using Improved Metaheuristic Optimization Techniques. Structures 2023, 50, 286–302. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, W.; Zheng, Y. Data-Driven Shear Capacity Analysis of Headed Stud in Steel-UHPC Composite Structures. Eng. Struct. 2024, 321, 118946. [Google Scholar] [CrossRef]
- Lu, W.-W.; Chen, Y.-W.; Xu, J.-G.; Yang, H.-F.; Tao, H.-T.; Zheng, W.; Shi, B.-K. Prediction on Slip Modulus of Screwed Connection for Timber–Concrete Composite Structures Based on Machine Learning. Buildings 2025, 15, 2458. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Ghanbari-Ghazijahani, T.; Jankowski, R. Ensemble Machine Learning Models for Estimating Mechanical Curves of Concrete-Timber-Filled Steel Tubes. Eng. Appl. Artif. Intell. 2025, 156, 111234. [Google Scholar] [CrossRef]
- JAS-0360-2019; Structural Panel. Ministry of Agriculture, Forestry and Fisheries of Japan: Tokyo, Japan, 2019. (In Japanese)
- LY/T 1580-2010; Oriented Strand Board. National Forestry and Grassland Administration: Beijing, China, 2010. (In Chinese)
- GB/T 22349-2008; Plywood for Structural Wood Sheathing. National Forestry and Grassland Administration: Beijing, China, 2008. (In Chinese)
- LY/T 2059-2012; Steel Nail for Wood Structure. National Forestry and Grassland Administration: Beijing, China, 2012. (In Chinese)
- ASTM D1761-12; Standard Test Methods for Mechanical Fasteners in Wood. ASTM International: West Conshohocken, PA, USA, 2012.
- Specification for the Evaluation Method of Wood Shear Wall and Its Amplification Performance; Japan Housing and Wood Technology Center (HOWTEC): Tokyo, Japan, 2013. (In Japanese)
- Zhao, H.; Song, W.; Zhang, D.; Jia, K.; Wang, Z. Quasi-Static Test Study of Bamboo-Wood Composite Panel Diaphragm and Its Corresponding Nail Connection. Eng. Struct. 2025, 333, 119994. [Google Scholar] [CrossRef]
- EN 1995-1-1; Eurocode 5: Design of Timber Structures-Part 1-1: General-Common Rules and Rules for Buildings. European Union: Maastricht, The Netherlands, 2004.
- Ueda, R.; Sawata, K.; Sasaki, T.; Sasaki, Y. Effects of Decay on the Shear Properties of Nailed Joints Parallel and Perpendicular to the Grain. J. Wood Sci. 2021, 67, 70. [Google Scholar] [CrossRef]
- Chen, Z. Performance of Nail Connection in Shear-Walls of Light Wood Frame Houses—An Experimental Study. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2006. [Google Scholar]
- Wong, T.T.; Yeh, P.Y. Reliable Accuracy Estimates from k-Fold Cross Validation. IEEE Trans. Knowl. Data Eng. 2019, 32, 1586–1597. [Google Scholar] [CrossRef]
- Ghawi, R.; Pfeffer, J. Efficient Hyperparameter Tuning with Grid Search for Text Categorization Using kNN Approach with BM25 Similarity. Open Comput. Sci. 2019, 9, 160–180. [Google Scholar] [CrossRef]
- Yang, X. Artificial Neural Networks. In Handbook of Research on Geoinformatics; IGI Global: Hershey, PA, USA, 2009; pp. 122–128. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Deng, Z.; Zhu, X.; Cheng, D.; Zong, M.; Zhang, S. Efficient kNN Classification Algorithm for Big Data. Neurocomputing 2016, 195, 143–148. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. In Proceedings of the Advances in Neural Information Processing Systems 31 (NeurIPS 2018), Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Dong, W.; Huang, Y.; Lehane, B.; Ma, G. XGBoost Algorithm-Based Prediction of Concrete Electrical Resistivity for Structural Health Monitoring. Autom. Constr. 2020, 114, 103155. [Google Scholar] [CrossRef]
- GB/T 50005-2017; Wood-Structure Design Standards. China State Engineering and Construction Press: Beijing, China, 2017. (In Chinese)



| ML Models | Hyperparameter | Optimized Hyperparameter Value | ||
|---|---|---|---|---|
| Pu | Ks | δu | ||
| ANN | hidden_layer_sizes | (128, 64) | (128, 64) | (64, 32) |
| learning_rate_init | 0.01 | 0.01 | 0.01 | |
| alpha | 0.1 | 0.1 | 0.1 | |
| activation | relu | relu | tanh | |
| SVR | kernel | rbf | rbf | poly |
| C | 100 | 100 | 50 | |
| epsilon | 0.1 | 0.01 | 0.1 | |
| RF | n_estimators | 500 | 800 | 800 |
| max_depth | 20 | 20 | 20 | |
| min_samples_split | 2 | 2 | 2 | |
| min_samples_leaf | 1 | 2 | 1 | |
| XGBoost | learning_rate | 0.15 | 0.01 | 0.01 |
| max_depth | 5 | 5 | 6 | |
| n_estimators | 500 | 500 | 500 | |
| subsample | 0.8 | 1.0 | 1.0 | |
| KNN | weight | distance | uniform | uniform |
| n_neighbors | 5 | 8 | 4 | |
| CatBoost | depth | 8 | 10 | 6 |
| learning_rate | 0.1 | 0.05 | 0.1 | |
| l2_leaf_reg | 3 | 5 | 3 | |
| Model | R2 | MAE | RMSE | MAPE (%) |
|---|---|---|---|---|
| ANN | 0.9686 | 0.0708 | 0.0950 | 4.05 |
| SVR | 0.9950 | 0.0160 | 0.0370 | 0.89 |
| RF | 0.8887 | 0.1181 | 0.1637 | 6.20 |
| XGBoost | 0.9071 | 0.0899 | 0.1640 | 4.65 |
| KNN | 0.9216 | 0.1049 | 0.1428 | 5.61 |
| CatBoost | 0.9523 | 0.0829 | 0.1156 | 4.53 |
| Model | R2 | MAE | RMSE | MAPE (%) |
|---|---|---|---|---|
| ANN | 0.9487 | 0.0373 | 0.0529 | 5.11 |
| SVR | 0.9976 | 0.0092 | 0.0125 | 1.27 |
| RF | 0.8920 | 0.0551 | 0.0778 | 7.45 |
| XGBoost | 0.9849 | 0.0121 | 0.0326 | 1.86 |
| KNN | 0.8515 | 0.0675 | 0.0854 | 9.33 |
| CatBoost | 0.9693 | 0.0269 | 0.0464 | 3.73 |
| Model | R2 | MAE | RMSE | MAPE (%) |
|---|---|---|---|---|
| ANN | 0.9956 | 0.1248 | 0.3577 | 0.41 |
| SVR | 0.9994 | 0.0294 | 0.0709 | 0.11 |
| RF | 0.9839 | 0.4547 | 0.6438 | 1.99 |
| XGBoost | 0.9891 | 0.1910 | 0.5551 | 0.94 |
| KNN | 0.9750 | 0.4997 | 1.1189 | 2.15 |
| CatBoost | 0.9948 | 0.2164 | 0.3999 | 0.98 |
| Specimen Number | Experimental Value (Kn) | Predicted Value (kN) | Error (%) | GB/T 50005-2017 (kN) | Error (%) | Eurocode 5 (kN) | Error (%) |
|---|---|---|---|---|---|---|---|
| O9PL5A | 1.364 | 1.360 | 0.0029 | 0.578 | −57.61 | 1.5076 | 10.53 |
| O9VL5A | 1.282 | 1.283 | 0.1014 | 0.578 | −54.90 | 1.5076 | 17.60 |
| O9PL5B | 1.380 | 1.375 | 0.3841 | 0.578 | −58.10 | 1.6364 | 18.58 |
| O9PL6A | 1.426 | 1.428 | 0.1192 | 0.756 | −47.01 | 2.0750 | 45.51 |
| O12PL5A | 1.381 | 1.399 | 1.2962 | 0.653 | −52.72 | 1.4761 | 6.88 |
| O12PV5A | 1.543 | 1.564 | 1.3843 | 0.653 | −57.68 | 1.4761 | −4.34 |
| O12PL5B | 1.584 | 1.589 | 0.3447 | 0.653 | −58.78 | 1.4761 | −6.81 |
| O12PL6A | 1.652 | 1.660 | 0.4655 | 0.814 | −50.72 | 2.0395 | 23.45 |
| O12PL7A | 1.852 | 1.863 | 0.5929 | 0.919 | −50.40 | 2.3206 | 25.30 |
| P12PL5A | 1.557 | 1.552 | 0.3141 | 0.653 | −58.06 | 1.4761 | −5.20 |
| P12VL5A | 1.936 | 1.936 | 0.0046 | 0.653 | −66.27 | 1.4761 | −23.76 |
| P12PL5B | 2.005 | 2.009 | 0.1970 | 0.653 | −67.43 | 1.4761 | −26.38 |
| P12PL6A | 2.366 | 2.361 | 0.2075 | 0.814 | −65.59 | 2.0395 | −13.80 |
| P12PL7A | 3.864 | 3.866 | 0.0411 | 0.919 | −76.23 | 2.2531 | −41.69 |
| O18PL6A | 1.928 | 1.979 | 2.6426 | 0.999 | −48.17 | 1.9628 | 1.80 |
| O18VL6A | 2.045 | 2.042 | 0.1462 | 0.999 | −51.14 | 1.9628 | −4.02 |
| O18PL6B | 2.099 | 2.098 | 0.0596 | 0.999 | −52.40 | 1.9628 | −6.49 |
| O18PL7A | 2.505 | 2.499 | 0.2395 | 1.091 | −56.43 | 2.4204 | −3.38 |
| Model | R2 | MAE | RMSE | MAPE (%) |
|---|---|---|---|---|
| ML model | 0.9994 | 0.0085 | 0.0144 | 0.4908 |
| GB/T 50005-2017 | −3.1768 | 1.1004 | 1.2135 | 57.2024 |
| Eurocode 5 | 0.3403 | 0.3192 | 0.4823 | 15.8627 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, W.; Wang, Z.; Jia, K.; Zhao, H.; Wang, X.; Wang, Y. Experimental Study and Machine Learning Prediction of Shear Capacity of Panel-Sheathing Nailed Connections in Wood Structures. Buildings 2025, 15, 4158. https://doi.org/10.3390/buildings15224158
Song W, Wang Z, Jia K, Zhao H, Wang X, Wang Y. Experimental Study and Machine Learning Prediction of Shear Capacity of Panel-Sheathing Nailed Connections in Wood Structures. Buildings. 2025; 15(22):4158. https://doi.org/10.3390/buildings15224158
Chicago/Turabian StyleSong, Weide, Zhaohui Wang, Kai Jia, Hongbo Zhao, Xiaoxia Wang, and Yunxuan Wang. 2025. "Experimental Study and Machine Learning Prediction of Shear Capacity of Panel-Sheathing Nailed Connections in Wood Structures" Buildings 15, no. 22: 4158. https://doi.org/10.3390/buildings15224158
APA StyleSong, W., Wang, Z., Jia, K., Zhao, H., Wang, X., & Wang, Y. (2025). Experimental Study and Machine Learning Prediction of Shear Capacity of Panel-Sheathing Nailed Connections in Wood Structures. Buildings, 15(22), 4158. https://doi.org/10.3390/buildings15224158





