Quantifying Thermal Time Lag Due to PCM Plaster in Model Houses

Abstract

Phase change materials (PCMs) integrated into building envelopes can store and release latent heat, reducing indoor temperature fluctuations and shifting thermal peaks. This study quantifies the time lag and comfort impact of PCM plaster under free-running conditions using two identical, instrumented model houses in Bácsalmás, Hungary. One house served as a reference, while the other was retrofitted with interior PCM plaster panels on four walls (51.2 kg paraffin, ≈8.12 MJ latent heat capacity). The temperatures of the walls, indoor air, and outdoor environment were monitored every five minutes for 105 spring/summer days. Daily peak times were extracted using moving-average smoothing, and time lags between exterior and interior wall peaks were computed. The PCM house exhibited roughly double the average lag compared with the reference (≈200 vs. ≈100 min), with lag distributions well described by lognormal fits. Comfort evaluation based on exceeded degree-hours (EDH) relative to the adaptive comfort range (EN 16798-1) revealed that larger peak-time lags correlated with lower overheating. Results confirm that PCM plaster significantly delays and attenuates daily temperature peaks, extends comfort periods, and supports passive strategies such as night ventilation and demand-side load shifting in lightweight buildings.

1. Introduction

Phase change materials (PCMs) embedded in building envelopes add latent heat storage that boosts effective thermal inertia and damps diurnal temperature swings. By melting and solidifying near the operative comfort range, PCMs shift and reduce peak heat flux and indoor temperature, lowering cooling demand and improving comfort while enabling load shifting to off-peak hours—especially during the warmer periods of the year. These gains are highly design-sensitive—dependent on melting temperature, encapsulation, PCM layer placement and thickness, and their interaction with ventilation strategies, climate, and dwelling typology. Consequently, precise and comparable dynamic metrics are essential: time lag (phase shift in peak temperatures), decrement factor (amplitude attenuation), latent heat utilization, and daily charge–discharge completeness, supported by harmonized experiments and validated models. In this paper, using a full free-running spring/summer measurement campaign on the model houses, we demonstrate how to quantify the peak temperature shift induced by the PCM plaster, its impact on the thermal comfort range time, and the so-called temperature–time exceedance. We reviewed studies on the effectiveness of PCMs in buildings and examined additional research that addressed time lag.

For example, a dynamic PCM wall shift was examined considering the effect of the PCM layer relative to a thin air gap [1]. This boosted latent heat use and, over three hot days, cut interior heat gain by ~100% versus static PCM. It also lowered indoor average temperature by ~9%. Actively timing exposure increased time lag and damped peaks better than any fixed placement. In a foundational multilayer-envelope model, time lag and decrement factor were computed across climates while resolving combined conduction–radiation–convection, providing the scaffold for where and how to seat PCM layers within real stratigraphies and orientations [2]. A modified admittance method embedded PCM effects via adjusted time lag/decrement terms and matched finite-element results, enabling fast early-stage screening of PCM thickness, melting point, and placement [3]. Transient modeling for a hot-humid Indian climate showed that higher mass/thickness lengthened time lag and shifted the peak by ~2 h (for +20% mass), whereas higher conductivity shortened lag—examples of direct sensitivities for PCM sizing and siting to mitigate peaks [4]. In a comprehensive review of solid–solid PCMs, Fallahi et al. [5] linked molecular structure to transition behavior and to thermal properties, making the case for leak-free plasters/boards with good cycling stability while flagging conductivity limits and directions for tailored synthesis. An optimization framework for PCM in external walls identified climate-specific optima for melting temperature, thickness, location, and stresses aiming for daily charge–discharge to avoid PCM acting like a mere phase-stabilized mass [6]. A two-zone numerical study confirmed that PCM location within a multilayer wall lengthened time lag and reduced decrement with facade orientation shaping the payoff by placing PCM where it could maximize the buffering [7]. Whole-building simulations for UK dwellings showed internal PCM placement to be most effective [8]. In this work, detached houses (~30% heat-loss cut) benefited more than apartments (8–14%) due to a larger opaque area. This study aligned PCM strategy with typology and wall-area budget. EnergyPlus modeling of thin PCM layers in a severe-hot location reported 5–6 °C lower indoor swings, 38–59% load-leveling, and strong operative-temperature relief, with the roof contributing the most and indicated benefits translating to CO₂ and cost savings [9]. In Kuwait City, a 20 mm PCM layer in the walls/roof cut summer heat gain by ~14–15% and, annually, RT-31 (≈27–33 °C) outperformed higher melting point (Tm) PCMs by matching Tm to the comfort/operative band and combining roof and wall coverage for larger gains [10]. Full-scale test houses with hydrated-salt PCM recorded peak-flux cuts up to ~31% and time lags ≈ 1.5–2.25 h [11].

Toure et al. [12] set out to measure rather than model the two key dynamic-envelope metrics, i.e., time lag (φ) and decrement factor (f), for a small test cell built from compressed stabilized earth bricks under the warm, sunny conditions of Dakar, Senegal. They quantified time lag ≈ 6 h and decrement factor ≈ 0.4, showing how envelope inertia filtered outdoors swings. Experiments on PCM energy storage blocks with night ventilation showed inner-side PCM placement superior achieving ~7–8 h retardation and large heat-flow reductions in a strong PCM–ventilation synergy [13]. Exterior PCM cladding panels (microencapsulated in cement render/foamed concrete) reduced the peak surface temperature and the heat flux, dropping decrement to ~0.64 and cutting time above 30 °C by ~22%, demonstrating outside placement can work well in hot climates [14]. A commercial PCM-gypsum board exhibited ~45% higher heat storage, a thermal lag increase from ~0.27 to 0.49 h, and only ~2% U-value change, underscoring PCM’s dynamic (not steady-state) value and calling for head-to-head product benchmarks [15]. Simulations for a Polish single-family home showed that the controlled ventilative cooling markedly improved the comfort with modest heating penalties, where the fans outperformed manual airing when optimized [16]. Moreover, in another study, ventilative cooling (window airing or controlled supply) paired with PCM reduced summer discomfort hours by >90% in multi-family dwellings [17]. A systematic review of indoor comfort ranges (15.0–33.8 °C) and behavioral adaptations provided the idea that the target bands of PCMs should straddle daily charge–discharge [18]. A residential “comfort threads” review showed occupants adapted across broad indoor–outdoor bands, implying PCMs can be tuned more broadly than fixed set-points. It linked adaptive ranges to energy-saving potential, guiding Tm selection and PCM plaster thickness [19]. A Bucharest-specific adaptive comfort equation sharpened local neutral temperature targets and acceptability bands, informing PCM Tm selection and layer positioning for that continental climate and supporting regional tailoring [20]. Rural southwest China field data reported neutral temperature ≈29.3 °C and limited willingness to use energy-intensive cooling, since the passive PCM buffering provided favorable conditions, which smoothed late-day peaks and complemented adaptation behaviors [21]. A Romanian passive house case achieved EN 15251 Category I–II summer comfort [22], and indicated how peak damping by envelope strategies (including PCMs) could sustain high comfort in low-energy buildings [23]. A winter monitoring in Belgrade revealed frequent overheating in district-heated homes and system-dependent risks. It argued for time lag/decrement management in heating seasons too, while PCMs could smooth heat delivery and reduce overshoot [24]. Over a full spring season, a model house with PCM-microcapsule plaster showed significant attenuation of indoor temperature extremes against variable outdoor temperature and solar radiation, statistically quantifying diurnal smoothing attributable to PCM lining and supporting demand-shifting and comfort stabilization [25].

EN 16798 is a European standard series on the energy performance of buildings, focusing on ventilation and indoor environmental quality. Part 1 (EN 16798-1:2019) [26] sets the indoor environmental input parameters for design and assessment—covering thermal comfort (including the adaptive method for no-AC periods), indoor air quality, lighting, and acoustics—with practical guidance in CEN/TR 16798-2 [27].

In summary, the literature identifies the following three factors as the primary drivers of peak shifting or time lag of heat peaks at buildings using PCM in order to improve their thermal comfort:

• When a PCM plaster actually melts and refreezes each day, its latent heat compensates for the temperature increase or decrease in the wall, which may be caused by the heat gain or heat loss of the house diminishing the characteristic temperature response inside, also pushing the indoor temperature or heat flux peak later while flattening its magnitude [6,11,14,15].
• Melting temperature aligned with the daily thermal wave. Time lag is largest when the PCM’s melting range overlaps the near-surface temperatures that occur around the outdoor peak. In that window the material absorbs heat most intensely, buffering the incoming pulse and delaying the indoor maximum; if the melting range sits too low or too high, the PCM stays mostly solid or mostly liquid, it provides little latent action, and the wall behaves like ordinary plaster with a shorter delay. The typical metric is a short or a very short period [6,9,10,15,20].
• The physical evaluation of the amount of PCM thickness and completeness of daily cycling. Thicker PCM layers store more energy and typically increase time lag, but only up to the point where the entire layer still melts by day and resolidifies at night. If the layer is so thick or the poorly coupled parts of it never cycle, the effective latent contribution drops and the added delay shrinks toward what would be achieved by simply adding more non-phase change mass; optimal thickness ensures full daily cycling under local climate and operating conditions [3,6,8,11,15].

Compared with the above summarized literature, this paper adopts a different approach: we instrumented model houses with sensors and conducted measurements over a continuous +100-day period, analyzing the time shift between exterior and interior wall temperatures on a large dataset using statistical methods, and benchmarking the results against standardized comfort temperatures.

In the literature, time lag is typically illustrated using arbitrarily selected single-day examples. However, lag depends on multiple weather-related factors that vary stochastically, introduce dispersion, and may render any cherry-picked instance unrepresentative of the technical solution under study. The expected value and variance of the lag can be determined reliably only through statistical evaluation. This was precisely the objective of our research, for which we developed and applied a new methodology using long-duration, free-running temperature sensor records. We analyzed the data using the Python data science stack.

Prior studies typically analyze short windows—often 14 days or less (e.g., Li; Al-Absi, Xu [1,14,15])—whereas the present work processes a 105-day measurement campaign, yielding hundreds of thousands of records per model house. Such data volume enables efficient and precise analysis using statistical and other numerical methods. Across the multi-month period we observed substantial variability in the magnitude of the time lag, making statistical evaluation indispensable. The empirical histogram of measured peak shifts was not normal: it was asymmetric (not centered around zero) and strictly positive, exhibiting a pronounced right-skew toward larger values. This shape is consistent with many natural populations (e.g., particle size distributions) and motivates modeling with non-Gaussian families, such as the lognormal.

2. Materials and Methods

2.1. Aim of the Investigation

This study was carried out in Bácsalmás, southeastern Hungary—the country’s warmest region with the highest annual sunshine duration—using container-based model houses. Two configurations were tested: a control house with standard factory-installed walls, and a variant in which all four interior walls were lined with plaster panels containing phase change material (PCM).

PCM-microcapsule-loaded gypsum plaster panels were cast in forms using 1100 mm × 725 mm, 12.5 mm-thick gypsum boards as backing (framed with timber battens). Additional smaller panels produced to cover residual wall sections were fabricated and installed on the available interior wall surfaces of the model house to assess their impact on thermal behavior. Panels (total area ≈ 15 m²) were fastened with screws and fixed to the interior walls of the PCM-lined house. Differential enthalpy measurements (melting/freezing) of RT25 microencapsulated PCM indicated a plaster composition containing 22 wt% PCM microcapsules. The total PCM mass installed was 51.2 kg, corresponding to a combined latent heat capacity of 8120 kJ. The RT25 paraffin exhibited a melting interval of 22–26 °C and a congealing interval of 26–22 °C, with a peak at 25 °C in both directions [28].

No panels were installed on the floor or ceiling; consequently, the PCM did not cover the entire interior envelope. This design was deliberate: the objective was to model and quantify the heat storage capacity of the PCM and its effectiveness in reduction and shifting of the temperature peaks inside.

The composition of the gypsum-based plaster panels used for casting was as follows (w/w): gypsum powder 32.1%, sand 25.4%, aqueous suspension of microencapsulated PCM 42.4%, and additives 0.2%. The microcapsules were fully embedded within the gypsum plaster matrix, which reduced the fire hazard even for the paraffin-based PCM employed. The latter was used here as a model material for the experiments; for building applications, PCM types with substantially lower fire risk (e.g., fatty acids, esters) are envisaged.

These panels minimally reduced the surface area available for conductive heat transfer; thus, the wall-mounted panels did not act as thermal insulation. Rather, by absorbing and releasing latent heat, they reduced the net heat transmitted from the outdoor environment into the indoor air (and vice versa).

The external and internal surfaces of walls, the floor and roof of the model houses, as well as the indoor air temperature were instrumented with temperature sensors. Twenty-nine thermocouples and other meteo sensors were mounted on the interior and exterior wall surfaces and protected by thin plastic shields; all sensors were connected to a data-logging computer. An otherwise identical reference house was instrumented with sensors in the same positions. The details of the experimental environment have been presented in our earlier publications [24,28].

Solar irradiance and outdoor temperature were also continuously measured on the roof of a nearby house. For the present analysis, we processed raw sensor data collected during spring and summer 2021 (29 March–11 July) over 105 days.

In a previous study [25], we proved that integrating PCM into wall assemblies significantly reduced the indoor temperature amplitude—lowering peak temperatures while raising minima. This thermal buffering was evident even when strong solar gains caused indoor temperatures to exceed outdoor conditions.

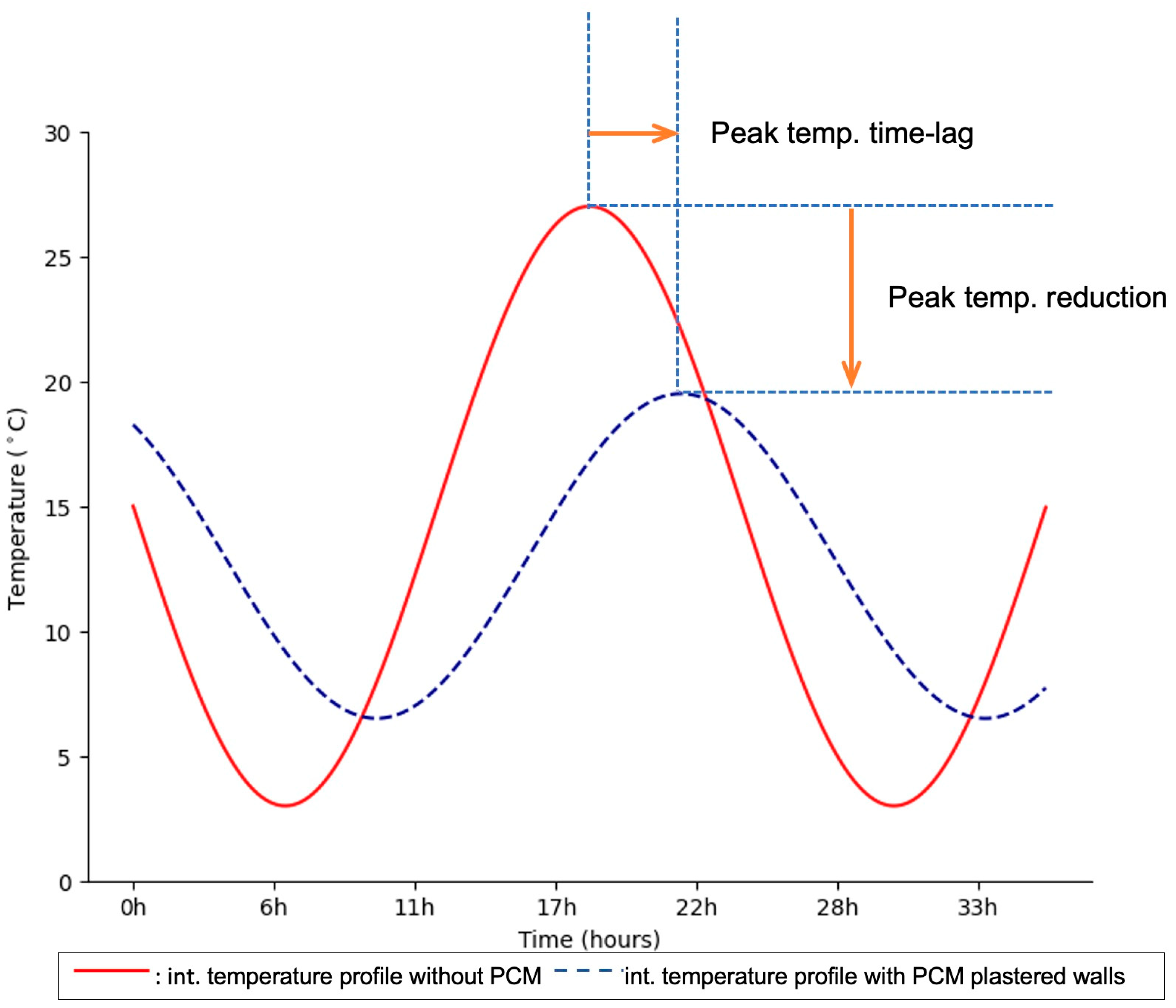
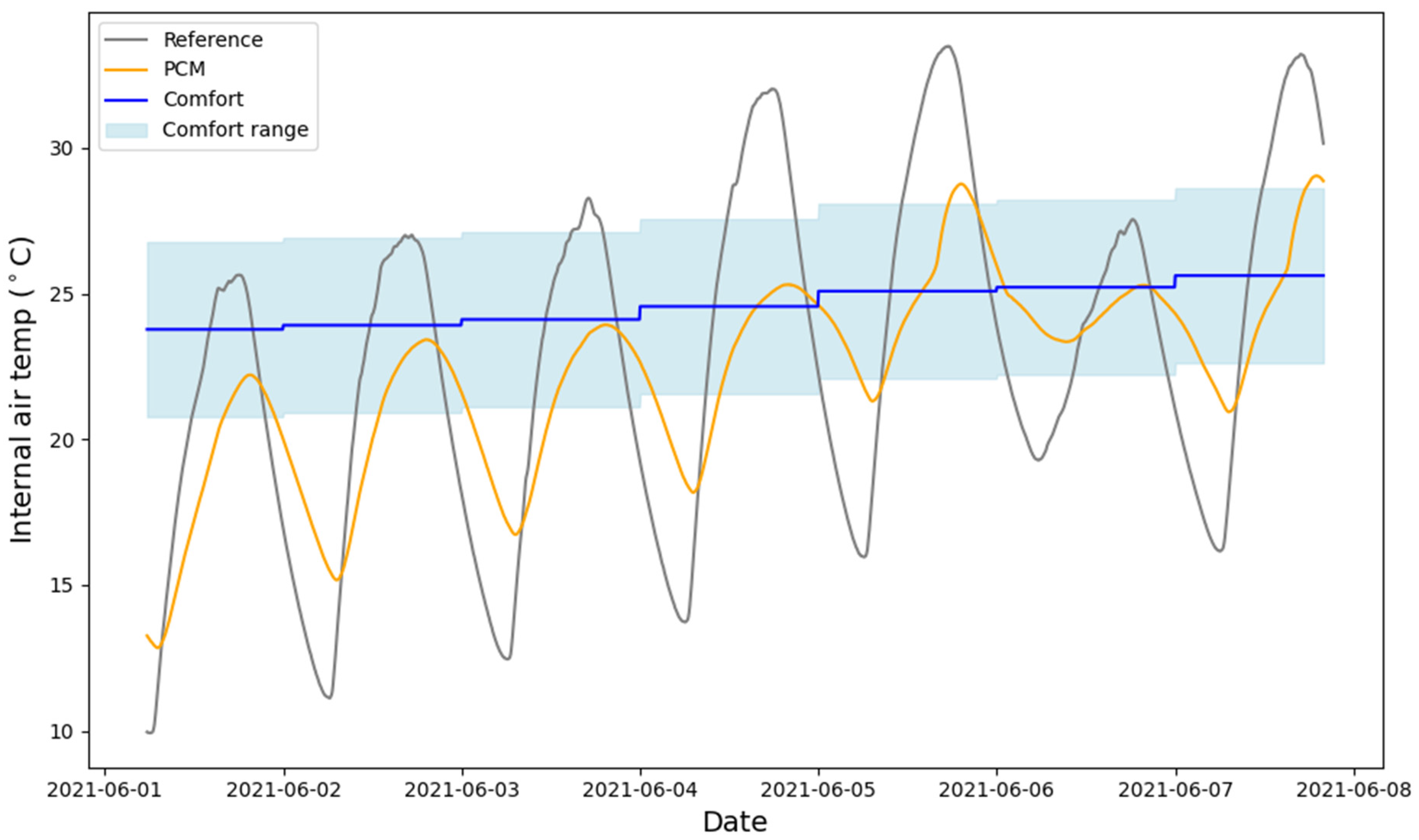
Here, we quantify an additional effect: PCM not only attenuates temperature peaks but also shifts their occurrence in time (Figure 1), thereby enhancing thermal comfort.

2.2. Data Processing and Statistical Approach

When processing the data, it is essential to account for the local climatic conditions which produce substantial differences between temperature records in March and June. In addition, numerous site-specific factors influence the exterior wall temperature, including the intensity of irradiation, cloud cover, wind, precipitation, the wall’s orientation, etc.

For data processing we used the following Python libraries: Matplotlib 3.10.6 for data visualization, Pandas 2.2.3 for data analysis and manipulation, NumPy 2.3.3 for numerical computing, and SciPy 1.16.3 for statistical analysis.

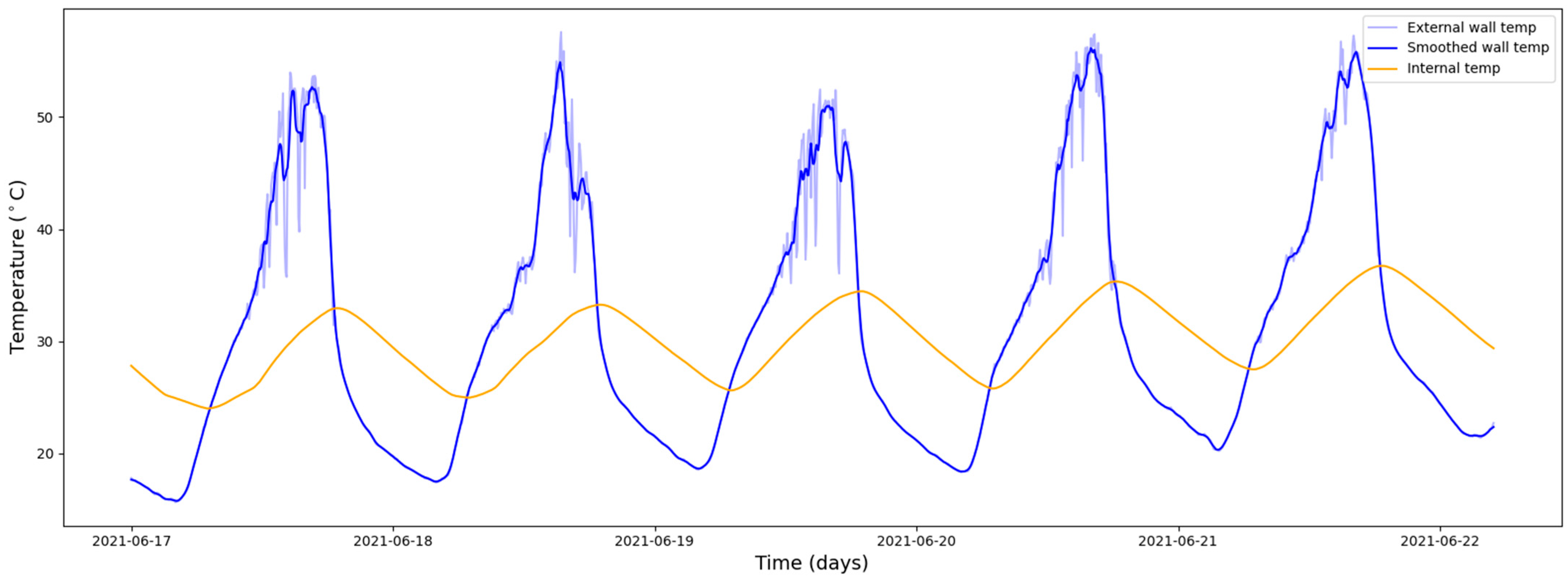
At sufficiently high resolution, the temperature curve exhibits a quasi-periodic pattern with a peak occurrence after midday; however, with 5 min sampling the peak position can be complicated to determine, and during the hottest hours as many as 6–15 local maxima may appear. To address this, we applied a curve-smoothing procedure: moving-average filters were used to suppress noise and short-term fluctuations (Figure 2).

We smoothed the curves using a moving average with a centered 9-point window. By this method the discrete temperature peaks become both interpretable and readily visualizable, which in turn enables subsequent optimization analyses grounded in stable features rather than high-frequency noise. In practical terms, the moving average acts as a low-pass filter over the 5 min sampling series, suppressing short-term fluctuations that can generate multiple spurious local maxima during the hottest hours of the day. This smoothing clarifies the timing and magnitude of the true diurnal maxima and thereby supports downstream tasks such as peak shift estimation, façade orientation comparisons, and selection of PCM loading strategies. Because any smoothing procedure can, in principle, bias amplitude estimates or introduce phase shifts, we explicitly examined the extent to which the chosen window might inject systematic error into the analysis.

The selected centered 9-point window smoothing method does not unduly alter the data and, more importantly, does not distort the physical timing of the peaks. This allows us to compute the day-by-day temporal shift in the peaks with minute-level accuracy.

In this study, we evaluated the indoor temperature time lag relative to the outdoor wall temperature peak for the model houses. We hypothesized that the time lag would be more pronounced in the PCM-plastered house due to latent heat storage. To obtain more precise timing, we compared the average of three temperature sensors mounted on the exterior west façade with the average of three sensors mounted on the interior (west) wall. This configuration yielded the most coherent estimates of peak-time differences, with the exterior temperature curve smoothed as described above.

2.3. The Relevance of the Time Lag of the Peak Temperature

• Reduction of peak indoor temperature/cooling load shifting
  By delaying the time when the indoor surfaces or inner air reach their maximum temperatures, PCM layers help shift the peak heat load to later in the day, often when outdoor temperature (or HVAC cost) is lower, and COP is higher. This reduces cooling demand and expenses during the hottest hours.
• Improved thermal comfort
  With time lag, indoor temperatures fluctuate less abruptly. The interior stays cooler during peak heat times and remains warmer (or at least slower to cool) in the night. This means fewer hours indoors are outside the comfort range.
• Energy savings/lower HVAC peaks
  Shifting peak temperatures means air conditioning or heating systems can run less drastically during peak times. This allows peak loads to be reduced, energy consumption to be smoother, and possibly lower costs if electricity tariffs are time-of-use.
• High thermal inertia and storage capacity
  PCMs store latent heat during melting by absorbing energy that would otherwise raise temperature, then release it later during solidification. Time lag is a measure of how well this storage buffers the external temperature swings. Greater time lag is in relation to more buffering.
• Better alignment with occupant usage/peak electricity pricing
  If peak indoor heat is delayed, occupants might avoid discomfort during highest outside heat, and HVAC systems can be scheduled to pre-cool or shift the load to cheaper or off-peak hours. In places with variable tariffs or demand charges, that can reduce the costs substantially, the literature notes optimizing PCM melting temperatures and thicknesses to match the local climate and usage patterns to maximize these benefits.
• Reduced temperature amplitude (decrement factor)
  Time lag is often considered together with the decrement factor (“how much lower is the internal peak relative to external” + how delayed). Good time lag helps reduce the amplitude of temperature swings indoors. This mitigates discomfort and reduces stress on building materials.

2.4. The Importance of the Comfort Temperature

In central and eastern Europe (CEE) summer comfort in dwellings without air conditioning is best described by the adaptive approach in EN 16798-1 standard, which ties acceptable indoor operative temperature to recent outdoor conditions (

Table 1. Different approaches of the comfort temperature in buildings in CEE countries.

Country	Building/Sample	Season and Mode	Comfort Temperature	Reporting Metric/Notes
Poland [17]	Multi-family (top two floors), simulations (EnergyPlus–CONTAM coupling)	Summer; free-running + ventilative cooling variants	EN 16798	Reported discomfort hours outside Cat II; also tested variable air volume (VAV) fans (on at 24.5 °C, off at 23 °C for control only).
Poland [16]	Single-family house; simulations with fuzzy controllers	Summer; free-running and mixed-mode	EN 16798	Discomfort hours used to compare window opening vs. fan-assisted cooling; category not explicitly specified.
Romania [20]	Six naturally ventilated buildings (Bucharest) with field surveys (2013–2014)	Warm season focus within field campaign; free-running	Local adaptive centerline largely based on old building standard	Provides Romania-specific neutral temperature relation; supports use of adaptive criteria for homes/offices without AC.
Romania [23]	Passive-standard office; field survey + measurements	Summer; largely free-running	Cat I ± 2 K/Cat II ± 3 K around adaptive centerline (as applied for evaluation)	Measured days fell in Category I and Category II.

). For typical CEE summers this yields neutral temperatures around 24–26 °C, with an acceptable band roughly 22–29 °C that shifts day-to-day; homes remain comfortable at the warm end when occupants use fans, shading, and night ventilation.

Field and simulation studies from Poland, Romania, and Slovakia show similar patterns: naturally ventilated flats tolerate warmer interiors during hot spells, while many codes or guidance flag >27 °C for prolonged periods as potential overheating. Bedroom set-points can be slightly lower at night, but residents often accept higher temperatures when air movement is available and clothing is light. Looking beyond CEE, Mediterranean homes tend to prefer and accept warmer summer interiors, Nordic homes slightly cooler, and tropics/subtropics even higher neutral temperatures—whereas fully air-conditioned buildings (e.g., many U.S. offices) follow narrower bands around 23–25 °C.

It is well established that thermal comfort depends on the temperature of the outdoor air—with which building occupants are indirectly in continuous exchange—such that the comfort temperature increases during summer conditions. This dependence is explicitly accounted for in the relevant standard.

Although the standard is not legally mandatory, its use has become common practice in building and comfort studies. Researchers adopt it because it offers a clear, shared method to define comfort temperature. Using a shared method makes results easier to compare across projects and climates. Many journals also prefer studies that follow recognized standards, which further encourages adoption. In central and eastern European (CEE) countries, most papers on comfort temperature now cite this as standard. This is helpful because CEE climates vary, and the standard provides a consistent baseline. Even then, the standard is useful as a reference point for sensitivity checks. For practitioners, following the standard simplifies design decisions and communication with clients and regulators.

2.5. What EN 16798-1 Covers?

EN 16798 is a European standard series on the energy performance of buildings, focusing on ventilation and indoor environmental quality. Part 1 (EN 16798-1:2019) sets the indoor environmental input parameters for design and assessment—covering thermal comfort (including the adaptive method for no-AC periods), indoor air quality, lighting, and acoustics—with practical guidance in CEN/TR 16798-2.

The adaptive comfort method (no-AC periods)

When cooling is not operating, acceptable operative temperature depends on the running-mean outdoor temperature T_rm. EN 16798-1 expresses the centerline as

T_comf = 0.33T_rm + 18.8 (°C)

(1)

with different category bands around it.

The model applies for roughly 10 ≤ T_rm ≤ 30 °C [29,30].

How to find T_rm?

The standard allows a simplified 7-day formula using daily mean outdoor temperatures:

$$T_{rm} ={\displaystyle \frac{T_{ed-1}+ 0.8T_{ed-2} +0.6T_{ed-3}+0.5T_{ed-4}+0.4T_{ed-5}+0.3T_{ed-6}+0.2T_{ed-7}}{3.8}}$$

(2)

(An exponential form with α ≈ 0.8 is also common) [29,30,31].

This adaptive approach is used in buildings (offices and similar types, incl. residential in free-running mode) with operable windows, no active cooling running, mainly sedentary activity, and freedom to adjust clothing [31].

Air speed allowance is also an integral part of the model, but it was not measured or calculated here. As the window of the model houses was not operated, no significant air speed was assumed.

After analyzing numerous literature sources, we defined the comfort range for evaluation as the ±3 °C band around the comfort temperature calculated in accordance with the standard.

3. Results and Discussion

3.1. Quantifying the Time Lag of the Temperature Peak

To evaluate the dynamics of indoor temperature response, this study systematically compares the timing of wall temperature maxima between exterior and interior sides of all walls. By leveraging sensor data from representative wall orientations, the analysis identifies and quantifies delays attributable to latent heat storage effects. In particular, three calibrated temperature sensors were installed on both the outdoor and indoor surfaces of the west-facing wall. This orientation was selected due to its pronounced solar exposure during early afternoon hours, which amplifies thermal loads and drives clear peaks in measured temperatures. For each day of the monitoring campaign, the maximum values recorded by exterior and interior sensors were paired, allowing calculation of the daily time difference between heat peaks for both the PCM-plastered and reference houses. The resulting time shift distributions form the basis for assessing the magnitude and persistence of the PCM-induced thermal lag.

Although temperatures of all other walls were also measured—typically at three representative points—we selected the west wall for analysis because the maxima of outdoor air and exterior wall temperatures occurred in the early afternoon, when the west façade was exposed to direct solar radiation, strongly influencing the formation of indoor air temperature maxima.

For this evaluation, we assessed data from the on-site meteorological station to validate that the evolution of the exterior temperature peak is consistent with the incident solar irradiance. Because air temperature is much more volatile, we used irradiance as a control and focused our analysis on the wall temperature values.

This decision is justified because these quantities directly govern the heat fluxes—i.e., heat transfer through the wall into the indoor air—and thus implicitly capture the influence of other external effects such as solar irradiance, cloud cover, wind, and precipitation. At the same time, the maxima of the exterior wall temperature are correlated with the outdoor air temperature—a relationship that can be demonstrated statistically—yet they also exhibit scatter that reflects the impact of additional stochastic factors.

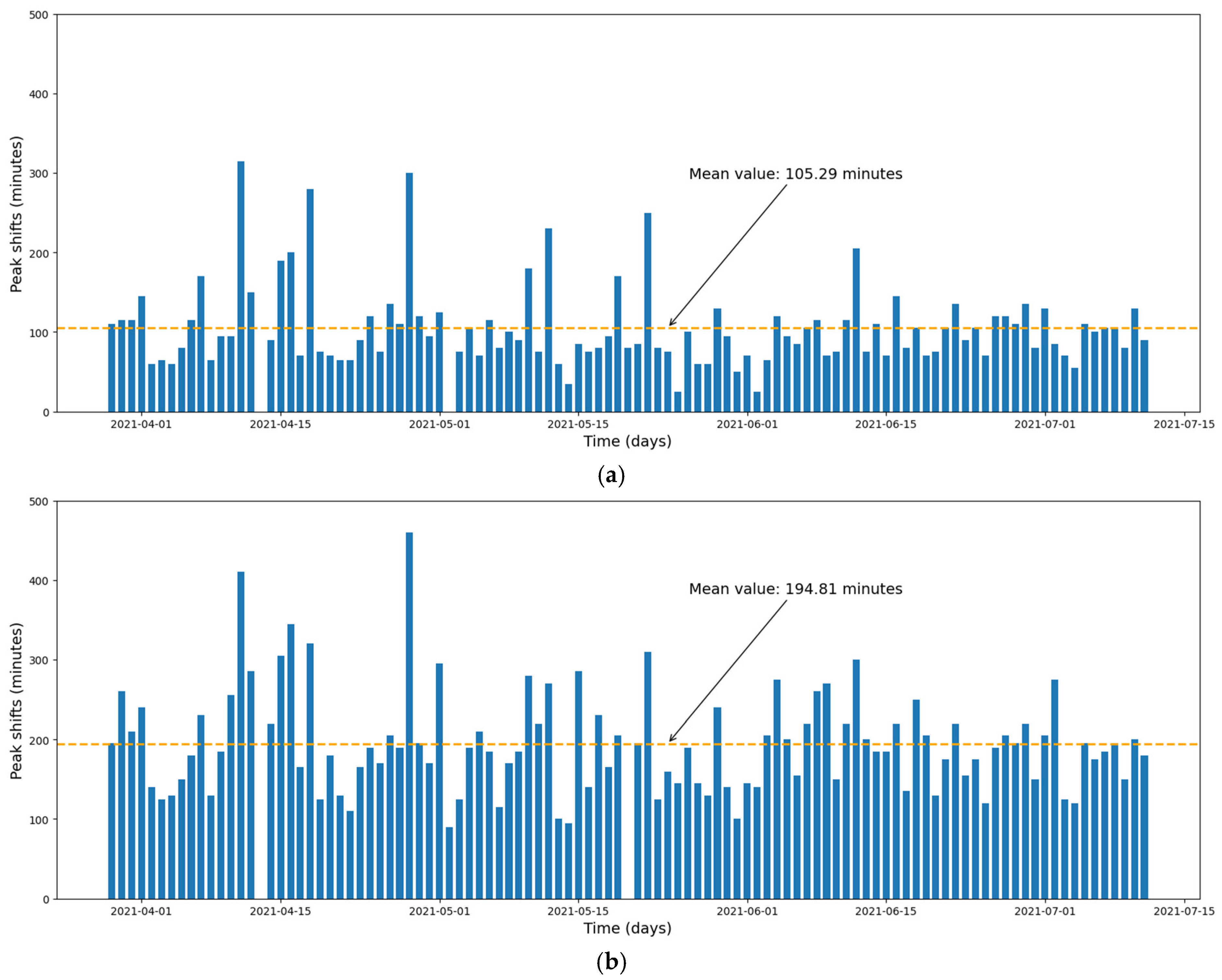
For each day, we paired the occurrence time of the exterior wall-surface temperature maximum with the time of the interior air temperature maximum. From these pairs, the daily time difference between the two peaks was computed for each model house. From the resulting series, frequency distributions of the time differences were compiled and plotted separately for both model houses. We present the day-by-day peak-time shifts in Figure 3a,b.

Visual inspection makes it clear that, in the PCM-plastered model house, the time offset between the exterior and interior wall temperature peaks is approximately twice that of the reference house—about 200 min on average versus roughly 100 min. This twofold difference persists over the entire observation period of more than 100 days.

From the resulting series, frequency distributions of the time differences were compiled and plotted separately for both model houses. As shown in Figure 4a,b, the results are well approximated by a lognormal distribution. In the figure, the red curve indicates the lognormal distribution fit.

The large deviation observed in Figure 4a,b arises from stochastic weather variability that cannot be controlled or measured with exactitude. Eliminating these random factors in real-world applications (building design, construction, and operation) to reduce the variability of outdoor conditions is not feasible; nevertheless, the study shows that employing PCM-containing plaster significantly and beneficially increases—by roughly a factor of two—the temporal shift in temperature peaks toward the late-afternoon/early-evening hours. The deviation attributable to external variability was, in practice, essentially irreducible.

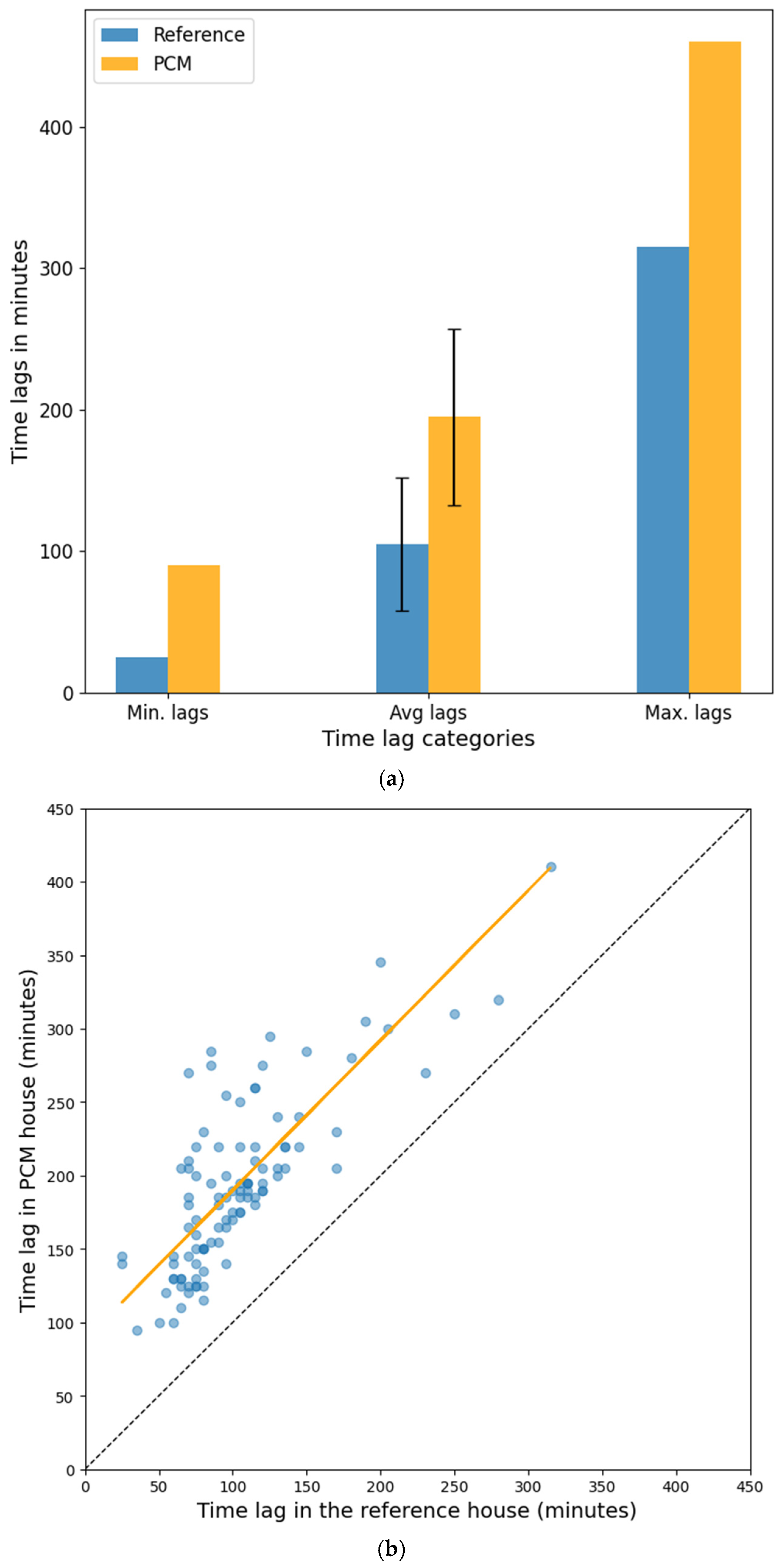
When minima, maxima, and average values of lags—together with the lognormal dispersion—are plotted separately for the two houses, the peak-time offset is unambiguously larger in the PCM house, while the (lognormal) deviation is distinctly smaller (Figure 5).

All temperature sensors in both model houses were individually calibrated, so measurement errors did not introduce any discernible bias into the observed time lags between daily exterior and interior peak temperatures. As evidenced by the extreme values and variance visible in Figure 3a,b and Figure 4a,b, as well as in Figure 5, there is a significant difference between the PCM-plastered house and the plaster-free reference house. Figure 5b plots the relationship between the peak-time shifts measured in the PCM house and in the reference house. It can be seen that the absolute magnitude of the time shift is nearly constant across all measurement points, as the regression line is approximately parallel to the Dt_PCM = Dt_Ref diagonal. The offset between the two lines is about 90 min, which is consistent with the result obtained by an independent method.

In Figure 5b, the regression line fitted to the measurement points can be expressed by the following equation: Y = 1.019*X + 88.19.

3.2. Significance of Peak-Time Lag for Thermal Comfort

The timing of temperature peaks within a building plays a pivotal role in shaping indoor comfort conditions throughout the day, especially when adaptive standards are considered. Exceeded degree-hours (EDH) represent the cumulative sum of the temperature differences by which indoor conditions exceed the defined comfort band integrated over time. Essentially, EDH quantifies not only how far the indoor temperature deviates from acceptable limits but also for how long these deviations persist, providing a comprehensive metric of thermal discomfort. This approach is widely used because it translates complex, time-varying temperature profiles into a single value reflecting total discomfort exposure, facilitating direct comparison between scenarios or interventions. EDH is therefore preferred over simpler measures like exceedance hours or average temperatures, as it captures both the duration and severity of thermal stress experienced by occupants, aligning with current best practices in building performance evaluation and standards such as EN 16798-1.

To assess this relationship in practical terms, the analysis examines the extent and duration of temperature excursions beyond the comfort threshold. By quantifying both the magnitude and persistence of such exceedances, it becomes possible to link observed time shifts in indoor peaks to thermal comfort outcomes as defined by adaptive criteria. This approach ensures that the evaluation reflects not only instantaneous conditions but also the overall occupant experience during periods of thermal stress.

It is self-evident that thermal comfort depends not only on how far the temperature deviates from the comfort setpoint, but also on how long such deviations persist. To express this, the literature commonly uses temperature–time exceedance, also referred to as exceeded degree-hours (EDH—we use this abbreviation). Using the available sensor records we compared the two houses against both the relevant standard and the general building comfort practice. In our calculations, we evaluated the periods lying outside the ±3 °C band around the standardized comfort temperature and computed the corresponding degree-hours (in °C·h) (Figure 6).

In Figure 6, the comfort range is indicated as ±3 °C in accordance with the standard. Figure 6 serves as an illustration; the EDH values were computed for both positive and negative deviations using the standard formulas presented in Section 2.5 and applied to every day in the dataset.

In this analysis we examined the internal air temperature of the model houses, where a peak-time shift also occurs, albeit with a smaller magnitude. The reason is that the physical meaning of the comfort temperature should be assessed within the building interior, in accordance with the referenced standard. It is important to note that at the beginning of the measurement period—in March–April, when the outdoor air was colder—it is not realistic to expect the model house to reach the comfort temperature, since no heating was used in this experiment. The influence of the PCM and the associated peak-time shift manifests as the house cools down less, being less uncomfortable to stay, and, in a hypothetical heated scenario, enabling more efficient heating.

It was also examined to what extent the magnitude of the peak-time shift predicts the time spent within the comfort range—more precisely, how the relationship can be described between a larger peak shift across the wall and the time integral of temperature outside the comfort band (i.e., the physical interpretation of EDH). Due to the physical limits of the “comfort” construct, the relationship was sought within the 10–30 °C range defined by the standard, truncating edge days on which temperatures lay outside the admissible interval (Figure 7).

In Figure 7 the time lag measured in the two houses are plotted as a function of EDH, providing a visually interpretable demonstration of the significance of peak shifting. Higher EDH values indicate greater thermal discomfort and correspond to smaller peak-time shifts in the reference house than in the PCM house.

The results demonstrate that the PCM model house, exhibiting higher peak-time lag values, produced lower EDH (exceeded degree-hours). Thus, beyond the evident improvement in thermal comfort afforded by PCM, evidence is provided that one contributing mechanism is the time lag of the temperature peak.

The PCM wall achieved a larger time lag and consistently showed a lower EDH than the reference wall—the scatter and locally weighted scatterplot smoothing (LOWESS) trend sloped downward.

After adjusting for weather (irradiation and outdoor max/min), the negative shift and EDH link remained, and the EDH reduction per extra minute of shift was stronger for PCM than for the reference case

Tail-focused views (quantile/binned) confirmed the practical impact: on the hottest, high-EDH days, more peak shifting produced the greatest cuts in overheating hours, with median EDH clearly dropping across higher shift bins.

4. Conclusions

Based on the results, we conclude the following:

• The PCM-plastered wall increased the peak-time lag by an average of ~200 min (measured through the west-facing wall). The reference house exhibited an average time lag of only ~100 min.
• This time lag is relevant across the entire observation period; its values follow a lognormal distribution in both houses, but the statistical parameters clearly substantiate the advantage conferred by PCM.
• The temperature peak-time lag contributes to time spent in comfort, because during the hottest part of the day the indoor temperature is lower.
• PCM plaster clearly and significantly increases the fraction of time spent within the comfort range. On most days, only minimal exceedances are observed.
• Approach toward the comfort zone is more pronounced in warm conditions. On cold days, the unheated model house cools down; the PCM’s modulating effect remains evident, but the improvement is not driven by time lag of temperature peaks.
• The PCM effectively brakes the warming and delays the peak by ~200 min in a period when the outside temperature is lower. This suggests substantial energy savings even when air conditioning is used.
• EDH (exceeded degree-hours, i.e., the time integral of temperature above the comfort setpoint) is lower in the PCM house, partly due to the time lag of peaks.
• A similar EDH reduction is detectable in cold periods as a result of the general moderating effect of PCM.