Dynamic Performance and Seismic Response Analysis of Ming Dynasty Masonry Pagodas in the Jiangnan Region: A Case Study of the Great Wenfeng Pagoda

Abstract

To investigate the dynamic performance and seismic response of Ming dynasty masonry pagodas in the Jiangnan region of China, the Great Wenfeng Pagoda in Taizhou, Zhejiang Province, was selected as the study object. Based on on-site inspection and maintenance records, the in situ compressive strength of masonry at each level was measured using a rebound hammer, considering that the pagoda was immovable and no destructive testing was permitted. A numerical model of the pagoda was established using the finite element software ABAQUS 2016 with a hierarchical modeling approach. The seismic response of the pagoda was computed by applying the El Centro wave, Taft wave, and artificial Ludian wave, and the seismic damage mechanism, the distribution of principal tensile stress, and seismic weak zones were analyzed. The results showed that the horizontal acceleration increased progressively along the height of the pagoda. Under minor earthquakes, the pagoda remained largely elastic, whereas under moderate and strong earthquakes, the acceleration at the top and bottom and the story drifts increased markedly, with the effects being most pronounced under the Taft wave. The damage was primarily concentrated in the first and second stories at the lower part of the pagoda and around the doorway. Tensile stress analysis indicated that the masonry blocks in the first and second stories were at risk of tensile failure under strong seismic action, whereas the lower-level stone blocks in the first story remained relatively safe due to their higher material strength. This study not only reveals the seismic weak points of Ming dynasty masonry pagodas in the Jiangnan region but also provides a scientific basis for seismic performance assessment, retrofitting design, and sustainable preservation of traditional historic buildings.

1. Introduction

Ancient masonry pagodas in China are not only symbols of religious belief but also important witnesses to cultural exchange and social transformation, possessing significant historical and artistic value within the context of ancient Chinese architecture. Buddhism was introduced into China during the Han dynasty, and the associated construction of Buddhist pagodas gradually evolved into masonry pagodas with distinctive Chinese characteristics through a long process of localization. Overall, the development of Chinese pagodas can be divided into three main stages: the founding stage (Han to early Tang dynasty), the prosperous stage (Tang and Song dynasties), and the transitional stage (Ming and Qing dynasties). Although wooden pagodas were predominant during the Tang dynasty, their flammability and limited durability led to their gradual replacement by masonry pagodas. Tang dynasty masonry pagodas exhibited diverse types, including pavilion-style, dense-eaved, and single-story pagodas, with representative examples such as the Giant Wild Goose Pagoda and Small Wild Goose Pagoda in Xi’an and the Songyue Temple Pagoda. During the Song and Liao dynasties, the construction quality of masonry pagodas significantly improved, and a considerable number of pagodas have survived, mainly distributed south of the Yellow River. By the Ming and Qing dynasties, masonry had been widely used in the construction of both Buddhist and Wenfeng pagodas, which commonly featured stone bases combined with brick superstructures to enhance structural stability and resistance to moisture.

At present, there are approximately 3000 extant masonry pagodas in China, some of which have been inscribed as World Cultural Heritage sites. The geographic distribution of these pagodas exhibits distinct regional characteristics: wooden pagodas are mainly found in dry areas such as Shanxi Province, whereas masonry pagodas are primarily concentrated in the Jiangnan region, including southern Jiangsu Province, northern Zhejiang Province, and southeastern Anhui Province. On one hand, the humid climate in this region allows masonry structures to be preserved more effectively than wooden ones over long periods; on the other hand, the relatively low seismic activity historically has contributed to the survival of masonry pagodas. Although masonry pagodas generally exhibit high durability, their seismic performance is typically inferior to that of wooden pagodas. Investigations indicate that existing pagodas in the Jiangnan region often sustain varying degrees of damage during earthquakes, manifested as leaning, foundation settlement, brick detachment, and wall cracking, with severe cases leading to total collapse. The primary causes of such damage are the high brittleness of masonry materials, weak bonding strength, and the heavy self-weight of the structures, which render them prone to global instability under seismic loading. In particular, masonry pagodas are constructed from brittle materials with anisotropic mechanical properties, exhibiting tensile strength far lower than their compressive strength. Sudden stiffness changes near the top of the pagoda frequently induce pronounced “whip-like” effects, further threatening the overall structural stability. With the development of the social economy and increasing public awareness of cultural heritage preservation, masonry pagodas have increasingly become a key focus of cultural heritage conservation. The protection of these valuable relics must be based on a systematic evaluation of their structural performance.

Regarding the masonry and mortar properties of ancient masonry pagodas, Liu et al. (2025) analyzed the interior and exterior wall mortars of pagodas in Shaanxi Province, conducting a comparative study on the composition of mortars from different periods [1]. Lu et al. (2022) collected 20 mortar samples from five ancient stone pagodas in Zhejiang Province and investigated the relationship between the shear strength of the mortars and the type of aggregates and additives [2]. Tian et al. (2024) further studied the original formulations of glutinous rice–lime mortar and its shear performance, analyzing the mortar microstructure using shear tests and scanning electron microscopy [3]. Concerning masonry units, Abruzzese et al. (2009) performed small-scale experimental tests on the Songjiang Huzhu Pagoda to determine the mechanical properties of brick and stone materials and assessed static risks using finite element methods [4]. Fahimeh et al. analyzed the uniaxial and triaxial compressive strength, porosity, and water absorption of stone blocks from the Miruksaji Stone Pagoda [5].

The fundamental period of a pagoda is a crucial parameter for evaluating structural damage and for seismic design, and it represents a key factor in analyzing the dynamic characteristics of the structure [6]. However, due to the considerable age of most ancient pagodas and the absence of construction records, precise determination of their fundamental periods is challenging. Based on structural theories of the pagoda, domestic and international scholars have proposed various methods to calculate the natural periods of pagodas, taking into account factors including material properties, wall thickness, cross-sectional geometry, and the presence of openings.

Wei proposed a method for calculating the natural period of masonry pagodas based on the formula for brick chimneys, incorporating the height-to-width ratio and overall pagoda shape [6]. Yuan presented a simplified calculation approach considering masonry material properties, wall thickness, cross-sectional geometry, and the presence of openings, which was validated using 14 typical pagodas [7]. In addition, the Chinese code for technical specifications for the prevention of historic buildings against man-made vibration (GB/T 50452-2008) introduces a weighted average factor of pagoda width by story to adjust the fundamental period [8]. Regarding dynamic property testing, Yang conducted in situ measurements of the Kaiyuan Temple Pagoda using a parallel-direction test method [9]; Mao and Cui performed random vibration response analyses on the Haibao Pagoda in Yinchuan and the Tai Pagoda in Xunyi County, Shaanxi Province, respectively [10,11]; and Fan obtained the dynamic characteristic parameters of the Fang Pagoda in Songjiang, Shanghai, through microtremor tests [12].

Experimental studies mainly include cyclic loading tests and shaking table tests. Due to the large dimensions of existing ancient pagodas, scaled model tests are typically required to obtain overall structural performance. Lu et al. developed a mid-story model of the Xuanzang Pagoda at Xingjiao Temple in Xi’an and simulated the structural behavior of perforated pagodas through low-cycle repeated loading tests combined with finite element analysis [13]. Qian et al. conducted shaking table tests on the Small Wild Goose Pagoda in Xi’an [14].

Numerical simulation serves as an essential approach for evaluating the seismic damage distribution of ancient masonry pagodas, typically requiring the incorporation of tensile and compressive damage parameters into the constitutive model of masonry materials. Two principal modeling strategies are commonly employed: the distinct approach and the homogenized approach. The distinct approach provides a refined representation of the interaction between bricks and mortar but entails high computational cost, whereas the homogenized approach is more convenient and thus widely adopted in practical research.

Pejatovic et al. (2019) conducted a nonlinear dynamic analysis of multi-tier temples in Nepal, showing that extensive cracking occurred even under relatively low peak ground accelerations [15]. Endo et al. (2020, 2025) investigated the Radha Krishna Temple and two other multi-tier pagoda-type structures, respectively, and demonstrated the potential of adaptive pushover analysis in seismic evaluation of tall historic buildings [16,17]. Tra et al. (2024) estimated the 50-year collapse probability of ancient stone pagodas in Korea [18]. De Iasio et al. (2021) developed a three-dimensional model of the Longhu Pagoda in China and analyzed the damage mechanisms of masonry pagodas during the 2008 Wenchuan earthquake using the CDP model [19]. Wu et al. (2022) employed the finite element software ABAQUS to establish a numerical model of the Mafo Temple and investigated its seismic response and failure mechanisms [20]. Li et al. (2023, 2025) carried out discrete element analyses of the Xuanzang Pagoda at Xingjiao Temple and the Small Wild Goose Pagoda in Xi’an [21,22]. Gao et al. (2025) and Lu et al. (2025) performed refined three-dimensional modeling of the Jiufeng Temple brick pagoda and the Changle Pagoda in China, respectively, and analyzed their seismic responses and weak-layer distributions under strong ground motions [23,24]. Hao et al. (2022) [25] investigated the seismic performance of ancient pagoda walls reinforced with GFRP bars embedded in horizontal mortar joints. The results indicated that GFRP reinforcement effectively restrained crack propagation, transformed the failure mode from brittle shear to ductile shear, and led to the derivation of a calculation formula for the shear bearing capacity of reinforced walls [25].

In summary, extensive research has been conducted by domestic and international scholars on the material properties, dynamic characteristics, experimental and numerical approaches, as well as strengthening techniques of masonry pagodas [26]. Numerical simulations have been shown to agree well with shaking table tests in elucidating the seismic damage mechanisms of masonry pagodas, thereby providing a solid theoretical foundation and technical pathways for seismic performance evaluation and restoration. Nevertheless, several limitations remain [27]. Most studies have focused on pagodas located in northern China, while investigations on the dynamic behavior of masonry pagodas in the Jiangnan region are relatively scarce.

Based on the above background, this study selected the Jinshan Great Wenfeng Pagoda (also known as the Big Wenfeng Pagoda on Google Maps) in Taizhou City, Zhejiang Province, a representative Ming dynasty masonry pagoda in the Jiangnan region, as the research object. A systematic on-site survey was conducted, and precise three-dimensional geometric information of the pagoda was obtained through a combination of 3D laser scanning and aerial photogrammetry. On this basis, a three-dimensional finite element model was established according to the material properties and structural characteristics of the pagoda, in which the curved upper structure was refined in detail. The masonry block strength was determined through on-site investigation and comparative analysis of relevant literature. The fundamental period of the pagoda was calculated using a method that integrates empirical formulas and finite element results from multiple domestic and international studies for comparative verification. Time-history analyses were conducted at one intensity level higher than the local seismic fortification intensity to obtain the structural dynamic responses and to evaluate the damage patterns and seismic weak regions. The results provide a reference and methodological basis for inspection and maintenance, seismic retrofitting of the Wenfeng Pagoda, and the structural safety assessment of masonry pagodas in the Jiangnan region of China while also offering a quantitative approach for the preservation and seismic research of historic buildings.

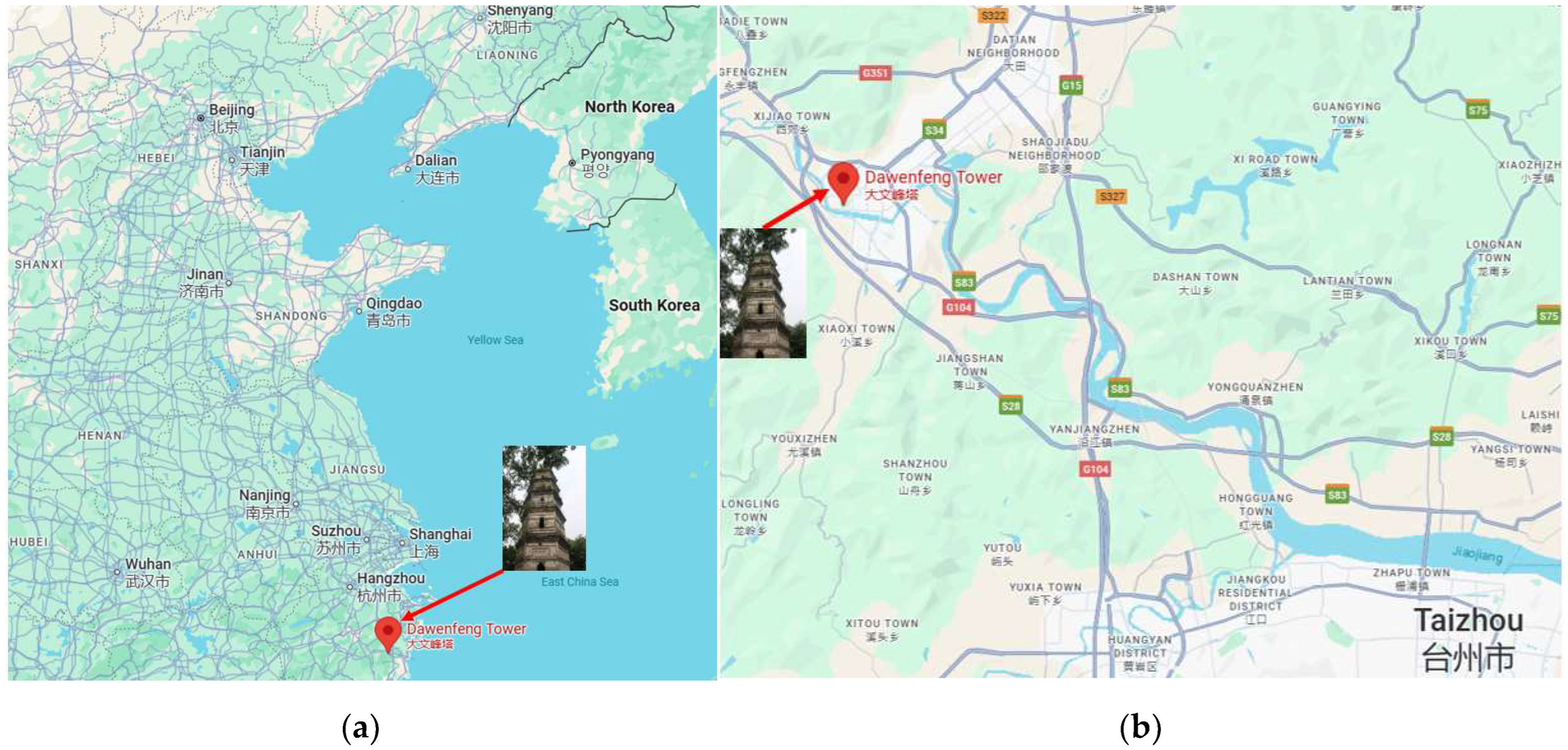
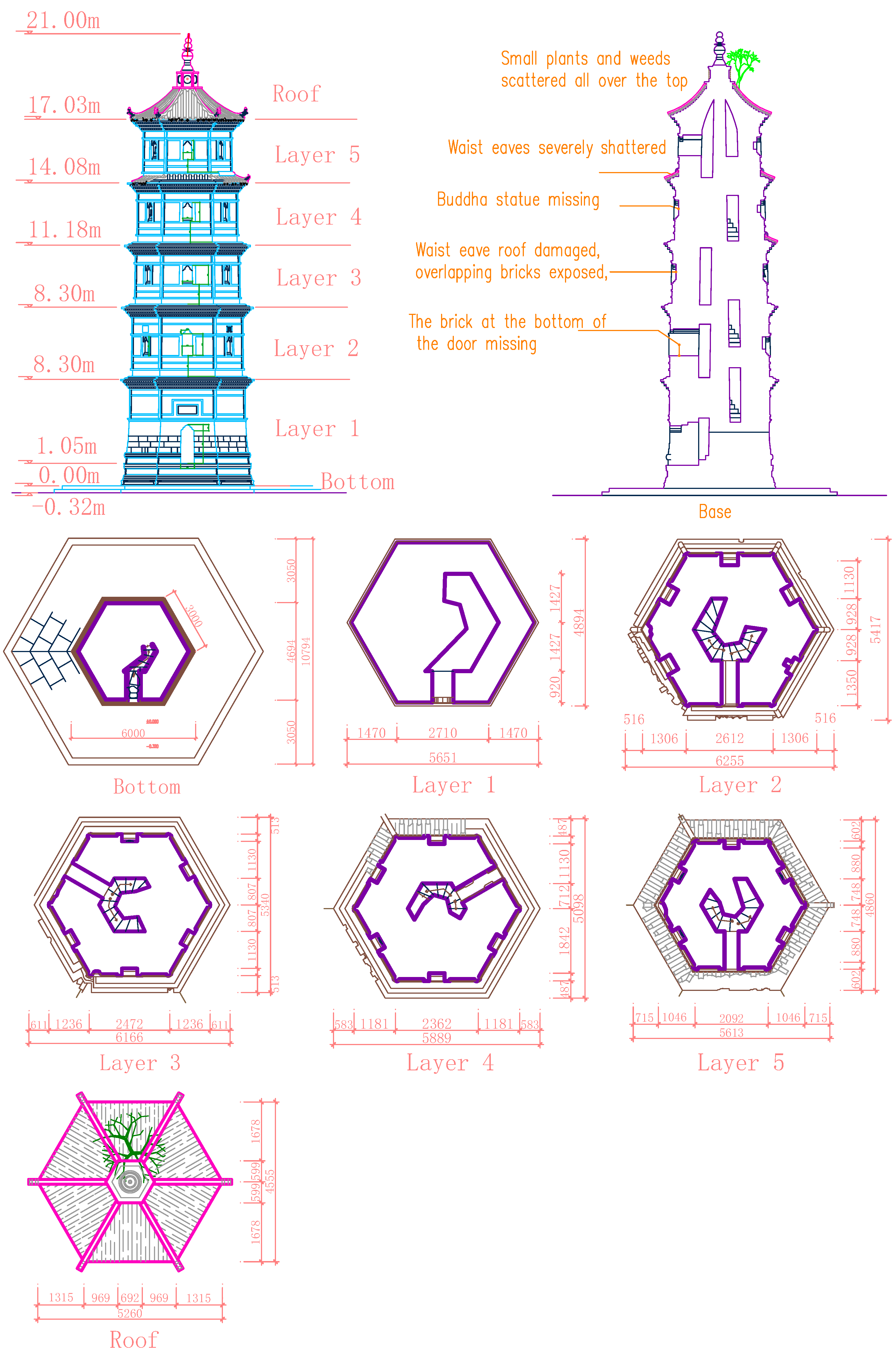
2. Structure Overview

Ancient Chinese pagodas can be broadly classified into four types according to their functions: Buddhist pagodas within temples, fengshui pagodas, Wenfeng pagodas, and commemorative pagodas. Buddhist pagodas were generally constructed alongside temples, serving as symbols of the temple; fengshui pagodas are multi-story pavilion-style pagodas sited according to geomantic principles, typically located at river mouths or around towns to compensate for unfavorable terrain and harmonize local energy; Wenfeng pagodas symbolize the flourishing of literary pursuits and were mostly built in connection with the development of Confucianism, particularly prevalent in the Jiangnan region during the Ming and Qing dynasties; commemorative pagodas were erected to honor historical figures or events. During the Ming dynasty, brick-and-stone construction was widely applied in both residential and religious buildings. Combined with the economic and cultural prosperity of the Jiangnan region and the concurrent prominence of Buddhism and Confucianism, this facilitated the extensive construction of Wenfeng pagodas.

The Great Wenfeng Pagoda is located in Taizhou City, Zhejiang Province (see Figure 1), and is one of the Jinshan Wenfeng Twin Pagodas. It has been designated as a Major Historical and Cultural Site Protected at the National Level. The pagoda was originally built during the Song dynasty and was destroyed by fire twice during the Ming and Qing dynasties. The existing structure was rebuilt in the fourth year of the Tongzhi reign of the Qing dynasty (AD 1865). The pagoda is situated on a hill in the suburb of Linhai City, embodying both feng shui principles and the symbolism of prosperous scholarly pursuits, making it a prominent scenic landmark in the region. Historical records indicate that no destructive earthquakes have occurred directly beneath Linhai City, but moderate seismic effects have been felt from several nearby events, such as those in Ningbo and Wenzhou regions. The pagoda comprises a five-story, hexagonal, multi-eaved brick masonry structure with a total height of 19.02 m. The foundation is a hexagonal stone base, and the ground floor features an entrance with a narrow spiral staircase allowing only single-person access. From the base to the top, the pagoda tapers progressively, forming a conspicuous conical rhythm. The waist eaves (see Figure 2a,d) are constructed using the traditional “stepped corbel” technique, in which bricks are laid layer by layer in a staggered, interlocking manner. This method not only facilitates drainage but also enhances the tiered appearance and decorative effect of the pagoda body. From the second story onward, each level contains Buddha niches (recessed spaces in the wall for placing Buddhist statues) and openings (wall apertures such as doors or windows), as shown in Figure 2b,c. The top of the pagoda is hexagonal with a pointed roof, crowned by a metallic gourd-shaped finial, reflecting the typical form of Ming and Qing dynasty pagodas in the Jiangnan region and contributing to the overall structural stability.

In 2024, an on-site survey of the Great Wenfeng Pagoda was conducted under the leadership of the Cultural Heritage Protection Bureau of Taizhou City, Zhejiang Province. The existing foundation is constructed on bedrock, providing stability and moisture resistance. However, multiple damages were observed on the pagoda: the brickwork on the northern side of the third and fourth stories is cracked, the waist eaves are severely damaged, and the top roofing is almost completely absent, with weeds and small pine trees growing on the surface. The base of the iron finial is damaged, and the iron chain connecting it to the pagoda apex has failed. The stone masonry of the foundation dates back to the Song dynasty, while the exterior walls of the pagoda are covered with patchy plaster. Recent repairs primarily employed traditional Qing dynasty techniques to restore the appearance and surface layers, with exterior walls repainted for visual prominence and moisture protection. Nevertheless, the overall seismic capacity of the structure remains to be assessed. The current condition of the pagoda is shown in Figure 2, while its structural dimensions are presented in

Table 1. Main geometric dimensions of the pagoda (unit: mm).

Layer	Pagoda Body		Openings			Buddha Niche
	Layer Height	Edge Length	Height	Width	Depth	Height	Width	Depth
1	4.95	2.71	1.8	0.65	1.40	/	/	/
2	3.35	2.61	/	/	/	0.88	0.50	0.35
3	2.88	2.47	1.69	0.46	1.35	0.88	0.49	0.22
4	2.90	2.36	/	/	/	0.88	0.44	0.22
5	2.95	2.09	1.31	0.4	1.08	0.88	0.40	0.22
Roof	0.77	0.69	/	/	/	/	/	/

and Figure 3.

Although the Great Wenfeng Pagoda has been maintained in terms of appearance, a systematic analysis of the dynamic characteristics and damage evolution of the entire pagoda structure is still lacking. The dynamic properties of the pagoda are a key basis for evaluating its mechanical performance and damage state. Therefore, conducting a scientific study on the structural dynamic performance is of significant importance for the long-term preservation of the pagoda and for formulating rational seismic retrofitting strategies.

3. Dynamic Characteristic Analysis

3.1. Material Properties of Masonry Blocks

The mechanical properties of masonry blocks form the basis for assessing the seismic performance of ancient pagodas. Common testing methods can be broadly divided into laboratory sampling tests and in situ non-destructive tests. Laboratory tests typically involve uniaxial compression experiments on samples taken from the structure to obtain the mechanical parameters of brick and stone materials, whereas in situ tests, such as rebound hammer and penetration methods, can estimate the properties of masonry and mortar without damaging the structure. Since the Great Wenfeng Pagoda is a nationally protected cultural relic, destructive testing is strictly prohibited; therefore, only non-destructive methods were employed to obtain mechanical data in this study.

Field investigations revealed that the first story of the Great Wenfeng Pagoda consists of two materials: the lower 3.14 m is constructed with stone blocks, while the upper 1.81 m is built with blue bricks; all the upper stories are entirely of blue-brick masonry. The Linhai Institute for Cultural Relics Protection conducted rebound hammer tests on brick masonry across different stories, as shown in Figure 4. For each story, test zones were selected, and within each zone, 10 intact and relatively flat bricks were chosen as test points. Five rebound readings were taken on each brick, and their mean value was calculated. The measurement points were arranged at the stairs and openings corresponding to the target heights inside the pagoda body.

Table 2. Rebound data of compressive strength.

Layer	Rebound Value
	No. 1	No. 2	No. 3	No. 4	No. 5	No. 6	No. 7	No. 8	No. 9	No. 10
1s	42.2	40.0	39.2	32.3	36.5	/	/	/	/	/
1	25.2	30.0	28.4	30.0	26.4	24.2	32.0	28.8	33.0	24.4
2	35.6	45.0	42.0	36.8	35.4	36.4	43.0	33.6	33.0	34.0
3	35.0	32.8	24.2	35.8	42.2	41.6	35.6	47.2	24.8	40.0
4	27.6	40.8	28.4	30.4	31.6	42.8	41.2	42.0	42.8	42.6
5	39.4	32.8	23.8	29.6	31.0	38.8	31.5	22.5	24.6	34.0

Note: 1s represents stone blocks.

presents the rebound test results of the compressive strength of the bricks. Based on the strength conversion curve recommended for the rebound hammer, the compressive strength of the blue bricks was estimated to range between 12 and 15 MPa. Considering the effects of weathering on ancient structures and with reference to strength values reported in previous studies, the compressive strength of the brick masonry was conservatively taken as f₁ = 11 MPa in this study. For the mortar strength test, due to severe weathering on site and the difficulty of direct measurement, the compressive strength of mortar was assumed as f₂ = 1.5 MPa based on construction techniques of contemporaneous Qing dynasty masonry structures and related studies. The axial compressive strength of masonry was calculated according to Equations (1) and (2), as specified in the Code for Design of Masonry Structures (GB 50003-2011) [28].

$$f_m=k_1{f}_1^{\alpha }(1+0.07f_2)k_2$$

(1)

$$f_t=k_3\sqrt{f_2}$$

(2)

where k₁, α are parameters related to the type of block and the masonry method, respectively, and k₂ is the correction factor for masonry compressive strength, with corresponding values of 0.78, 0.5, and 1. k₃ is the correction factor for masonry tensile strength, with corresponding values of 0.141.

The elastic modulus E of the masonry was determined using Equation (3) in accordance with the same code [28].

$$E=370f_m^{1.5}$$

(3)

The compressive strength f_m and elastic modulus E of the existing blue-brick masonry in the Great Wenfeng Pagoda were calculated from on-site test results as 2.85 MPa and 1788 MPa, respectively.

Due to the long-term weathering and water erosion in the Jiangnan region, the stone blocks at the base of the pagoda, which were constructed centuries ago, have experienced significant surface deterioration. According to the testing code, ten rebound test areas were delineated on the first story, but only five groups of valid data were obtained because of the rough and corroded surface condition. Based on the test data and relevant literature, the compressive and tensile strengths of the stone masonry at the lower part of the first story were estimated to be 3.38 MPa and 0.24 MPa, respectively, and the elastic modulus was taken as 2300 MPa.

3.2. Vibration Mode and Frequency

The calculation parameters for the fundamental period of masonry pagodas primarily consider the pagoda height and the cross-sectional width of the pagoda body while also being influenced by key factors such as the material properties of the masonry, the thickness of the pagoda body, the cross-sectional shape of the pagoda, and the opening ratio. The Chinese code for technical specifications for the prevention of historic buildings against man-made vibration (GB/T 50452-2008) recommends the following empirical formula for the horizontal natural frequency of masonry pagodas, as shown in Equation (4):

$$f_j={\displaystyle \frac{(a_j{b}_0)}{2\pi H^2}}\phi$$

(4)

where f_j is the j-th natural frequency of the structure; H is the total design height of the pagoda, measured from the top of the podium to the base of the finial; b₀ is the width at the base of the structure, measured as the distance between two opposite sides; a_j is the comprehensive deformation coefficient for the j-th natural frequency, determined from tables according to the values of H/b_m and b_m/b₀. Here, b_m is the weighted average width of each story within the height H relative to the story height, and φ is the mass–stiffness parameter of the structure. For masonry pagodas, φ is taken as 5.4H + 615 in this study.

Yuan [6] recommended the following simplified formula for the fundamental period of masonry pagodas, as shown in Equation (5):

$$T=0.0065{\eta }_1{\eta }_2{\eta }_3{\eta }_4{H}^2/D$$

(5)

where H is the design height of the pagoda, measured from the base to the top; D is the external diameter at the base, which in this study is taken as the distance between two pairs of sides; ${\eta }_1$ is the wall thickness influence factor, ${\eta }_2$ is the cross-sectional shape influence factor, ${\eta }_3$ is the masonry material influence factor (taken as 1.0 for the brick masonry in this study), and ${\eta }_4$ is the influence factor of openings in the pagoda body.

Wei [7] obtained the following formula for calculating the natural period of brick pagodas using the least squares method, as shown in Equation (6):

$$T=\alpha \beta (0.4116+{\displaystyle \frac{0.00287H^2}{D}})$$

(6)

where H and D are the same as in Equation (4); α and β are the coefficients accounting for the effects of the height-to-width ratio and the structural configuration of the pagoda, respectively.

The natural vibration periods of the Great Wenfeng Pagoda were calculated as 0.51 s, 0.58 s, and 0.53 s using Equations (4)–(6), respectively. It can be seen that the results obtained from these commonly used period calculation formulas are relatively close. They will be compared with the subsequent finite element analysis results to verify the accuracy of the finite element model.

3.3. Constitutive Relationships of Masonry Materials

In this study, a finite element model of the Great Wenfeng Pagoda was established using ABAQUS. Field investigations revealed that the masonry was composed of bricks, mortar, and sticky rice–lime paste. To improve computational efficiency, the interaction between the mortar and brick units was not considered at the material level. Instead, a homogenized modeling approach was adopted, in which the bricks and mortar were regarded as a single continuous medium. In terms of geometric modeling, a hierarchical modeling approach was employed to reflect the structural hierarchy of the brick pagoda, which consists of the foundation, the pagoda body, and the spire. Due to temporal and regional variations, no unified compressive constitutive model exists for historic masonry, and most previous studies only addressed the ascending branch of the stress–strain curve, without considering the descending branch. However, in dynamic response analysis, the nonlinear behavior of the structure must be represented. Therefore, a constitutive relationship including the descending branch is necessary. The constitutive model proposed in [13], which accounts for the descending branch, is expressed by Equations (7)–(10).

$${\displaystyle \frac{\sigma }{f_m}}={\displaystyle \frac{\eta }{1+(\eta -1){(\epsilon /{\epsilon }_m)}^{\eta /(\eta -1)}}}{\displaystyle \frac{\epsilon }{{\epsilon }_m}}$$

(7)

$$D_{\mathrm{c}}=1-{\displaystyle \frac{1}{1+(\eta -1){(\frac{\epsilon }{{\epsilon }_{\mathrm{m}}})}^{\frac{\eta }{\eta -1}}}}$$

(8)

where σ represents the axial compressive stress of the masonry; ε is the axial compressive strain; η denotes the ratio of the secant modulus to the initial elastic modulus, taken as 1.633; f_m is the average axial compressive strength of the masonry; ε_m corresponds to the design compressive strain at the axial compressive strength; and D_c is the uniaxial compressive damage variable of the masonry.

The tensile stress–strain relationship of the masonry is expressed by Equations (9) and (10):

$$\left\{\begin{array}{c}{\displaystyle \frac{\sigma }{f_t}}={\displaystyle \frac{\epsilon }{{\epsilon }_t}}\begin{array}{cc}& {\displaystyle \frac{\epsilon }{{\epsilon }_t}}\le 1\end{array}\\ \begin{array}{c}\\ {\displaystyle \frac{\sigma }{f_t}}={\displaystyle \frac{\frac{\epsilon }{{\epsilon }_t}}{2{(\frac{\epsilon }{{\epsilon }_t}-1)}^{1.7}+\frac{\epsilon }{{\epsilon }_t}}}\begin{array}{cc}& {\displaystyle \frac{\epsilon }{{\epsilon }_t}}>1\end{array}\end{array}\end{array}\right\}$$

(9)

$$D_t=\left\{\begin{array}{c}1-{\displaystyle \frac{f_t}{E_c{\epsilon }_t}}\begin{array}{cc}& {\displaystyle \frac{\epsilon }{{\epsilon }_t}}\le 1\end{array}\\ \begin{array}{c}\\ 1-{\displaystyle \frac{\frac{f_t}{E_c{\epsilon }_t}}{2{(\frac{\epsilon }{{\epsilon }_t}-1)}^{1.7}+\frac{\epsilon }{{\epsilon }_t}}}\begin{array}{cc}& {\displaystyle \frac{\epsilon }{{\epsilon }_t}}>1\end{array}\end{array}\end{array}\right\}$$

(10)

where σ_t is the tensile stress of the masonry; ε is the tensile strain of the masonry; f_t is the average axial tensile strength of the masonry; ε_t is the tensile strain corresponding to the design axial tensile strength; D_t is the uniaxial tensile damage variable of the masonry; E_c is the elastic modulus of the masonry.

Studies have shown that this constitutive model exhibits good generality, involves a small number of easily calibrated parameters, and features a simple expression, which conforms to the mathematical characteristics of the masonry compressive stress–strain curve.

Since ABAQUS does not provide a built-in constitutive model for masonry, both bricks and stone blocks in this study were simulated using the Concrete Damaged Plasticity (CDP) model, with their material parameters adjusted according to their respective strength values. This model exhibits good convergence in simulating the failure of brittle materials and can account for both compressive and tensile failures. The main parameters of the model are referenced from similar literature [24,25,26,27] and set as follows: dilation angle of 34°, eccentricity of 0.1, ratio of biaxial to uniaxial compressive strength of 1.16, ratio of the second stress invariant on the tensile meridian of 0.6667, and viscosity parameter of 0.005. According to literature data for contemporaneous brick masonry pagodas in China, the densities of the bricks and stone blocks were taken as 1800 kg/m³ and 2800 kg/m³, respectively, and the damping ratio was set to 0.04.

3.4. Modal Analysis

The internal spiral staircase of the Great Wenfeng Pagoda is extremely narrow; therefore, to improve computational efficiency, the staircase and the pagoda finial were not included in the model. The bottom boundary condition of the model was set as fixed. As waist eaves, Buddha niches, doorways, and other openings are decorative components of masonry pagodas, their weight and size are relatively small compared to the entire pagoda. Therefore, their influence on the overall structural dynamic response is limited. In the FEA, these components were appropriately simplified to balance computational efficiency and analytical accuracy. The finite element model adopted C3D8R three-dimensional solid elements, and the model and mesh division are shown in Figure 5, where different colors indicate separate parts in the ABAQUS model.

According to the Code for Seismic Design of Buildings (GB50011-2010) [29] and the Technical Specification for Concrete Structures of Tall Buildings (JGJ3-2010) [30], the selected vibration modes accounted for more than 90% of the total mass in both horizontal and vertical directions, satisfying the requirement for the number of vibration modes. The first three vibration modes along the north–south direction were extracted and are shown in Figure 6. The model excited 90% of the total mass in the X, Y, and Z directions at the 7th, 11th, and 13th modes, respectively, as shown in

Table 3. Cumulative mass fraction table of each vibration mode.

Mode	X (%)	X_Cum (%)	Y (%)	Y_Cum (%)	Z(%)	Z_Cum (%)
1	0.01	0.01	55.39	55.39	0	0
2	55.57	55.58	0.01	55.4	0	0
3	8.19	63.77	0.01	55.41	0	0
4	0.01	63.78	23.29	78.7	0	0
5	15.69	79.47	0.02	78.72	0	0
6	0	79.47	0	78.72	84.85	84.85
7	11.11	90.58	0.01	78.73	0	84.85
8	0.01	90.59	10.76	89.49	0	84.85
9	0.04	90.63	0	89.49	0	84.85
10	5.53	96.16	0.02	89.51	0	84.85
11	0.01	96.17	6.62	96.13	0.01	84.86
12	0.47	96.63	0	96.13	0	84.86
13	0	96.63	0.02	96.15	15.09	99.96

Note: X and X_Cum represent the sum in the X direction, respectively.

.

To verify the rationality of the model and parameter selection, the natural periods obtained from the finite element analysis were compared with the results calculated using empirical Equations (3)–(5). The comparison indicated that the finite element model could accurately reflect the dynamic characteristics of the Great Wenfeng Pagoda.

The first two horizontal vibration modes of the pagoda corresponded to first-order bending, with frequencies of 2.12 Hz and 2.16 Hz. The third mode was dominated by second-order bending translation, with a frequency of 9.11 Hz. The first-order frequency obtained from the finite element model exhibited a small deviation from the value calculated using the empirical formula. Based on the first- and second-order frequencies, the Rayleigh damping parameters α and β required for the pagoda in the finite element model were determined as 0.515 and 0.003, respectively, according to the method in [11].

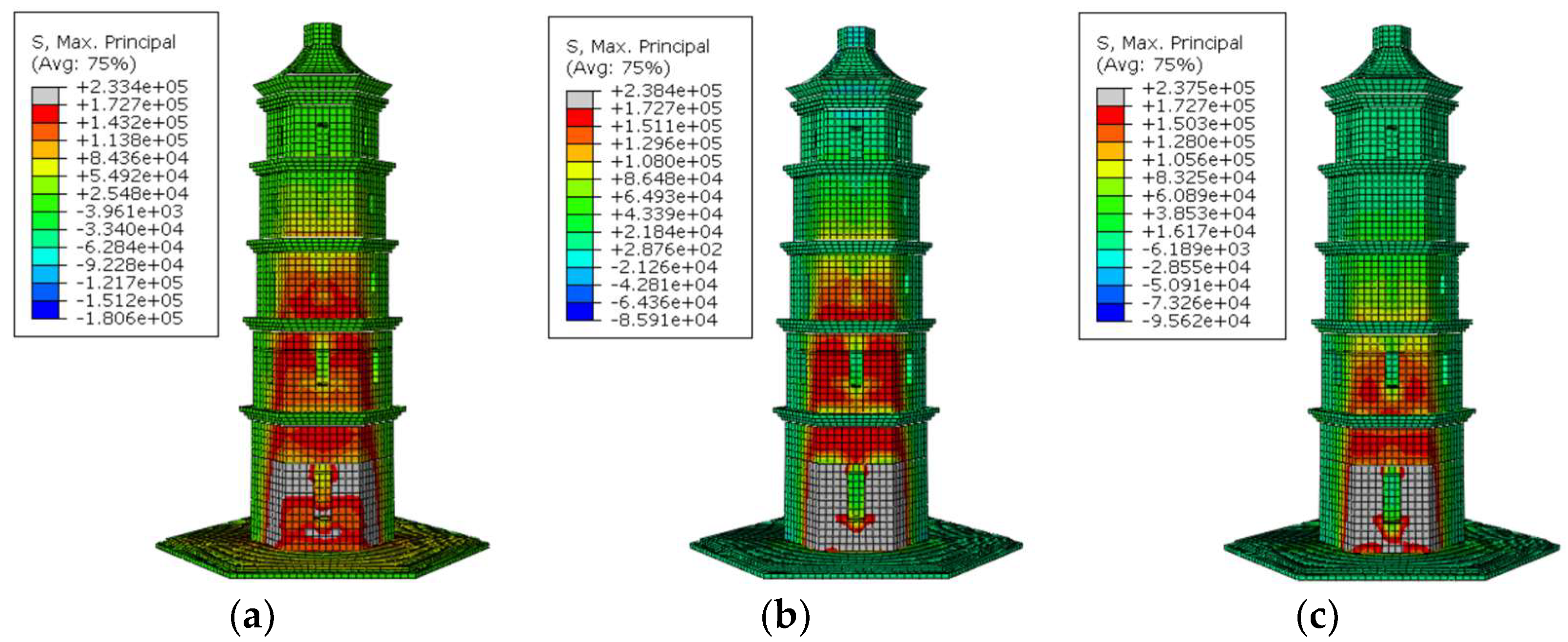
4. Seismic Response

4.1. Selection of Seismic Wave

According to the Seismic Ground Motion Parameter Zonation Map of China (GB 18306-2015) [31], the Great Wenfeng Pagoda is located in Taizhou, Zhejiang Province, where the seismic fortification intensity is 6, and the design seismic group is the first, with a basic design earthquake acceleration of 0.05 g. As the pagoda is a nationally protected cultural relic, the analysis was conducted with the fortification intensity increased by one level, corresponding to a 7-degree design earthquake. The pagoda is located on a hill composed of moderately weathered granite, corresponding to a Class II site condition; the acceleration amplification coefficient for such site conditions ranges from 1.0 to 1.2. According to the Chinese Code for Seismic Design of Buildings (GB 50011-2010) [29], one artificial seismic wave and two recorded earthquake waves were selected, namely the artificial Ludian wave (in 2014, Yunnan Province), the Taft wave, and the El Centro wave (EL wave), as shown in Figure 7. The peak accelerations of these waves were scaled according to small, moderate, and large earthquakes to 0.35 m/s², 1.5 m/s², and 2.2 m/s², respectively. Seismic dynamic response analyses of the pagoda were conducted in the east–west direction. According to the Code for Seismic Design of Buildings (GB 50011-2010), the duration of seismic acceleration records should not be less than five times the fundamental period of the structure and not shorter than 15 s. As the fundamental period of the Great Wenfeng Pagoda is approximately 0.5 s, a seismic input duration of 15 s was adopted.

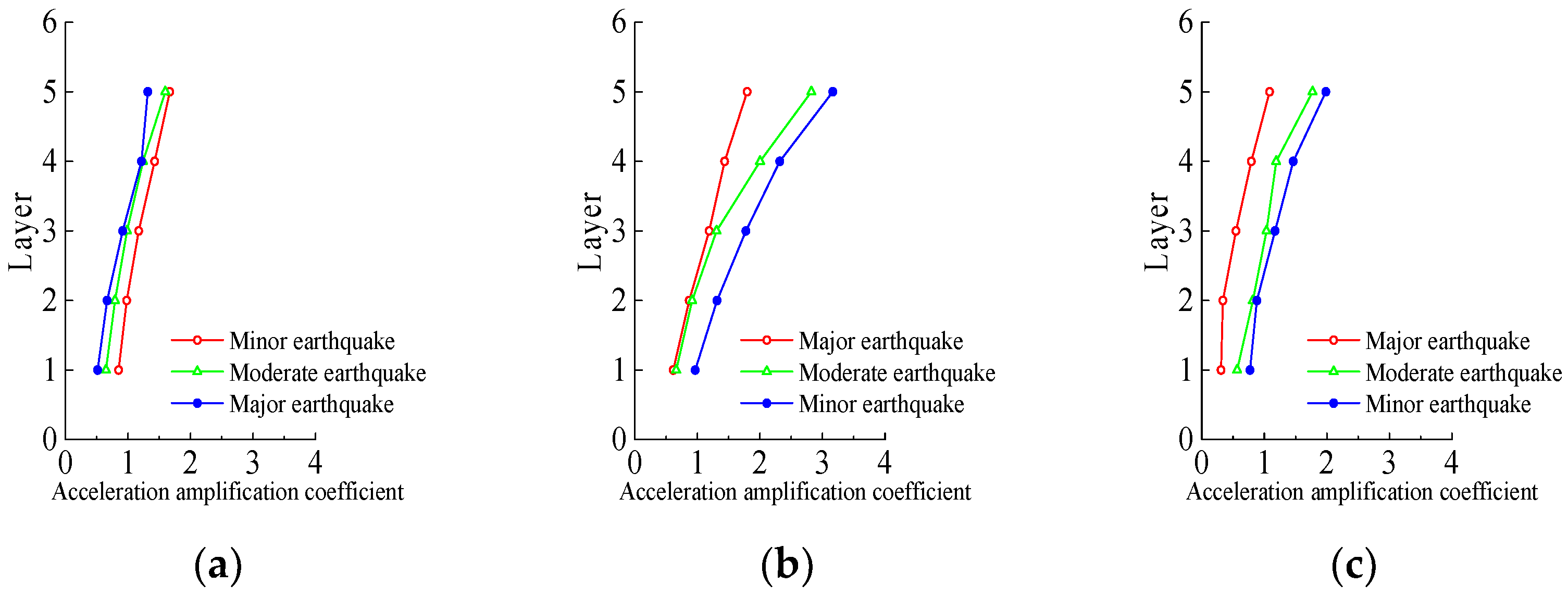
4.2. Horizontal Acceleration

The relationship between the horizontal acceleration amplification factor and the height of the pagoda was presented in Figure 8. It was observed that the amplification factor curve along the height, composed of five characteristic points, approximately exhibited a “C”-shaped profile. The acceleration amplification at the top was markedly larger than that at the base, and the horizontal acceleration amplification gradually increased with height, particularly above the third level. This was primarily attributed to the reduction in cross-sectional stiffness with increasing height. Under minor seismic action, the acceleration amplification was more pronounced than under moderate and severe seismic conditions. Owing to the architectural form and the influence of Buddhist culture in the Jiangnan region, the tops of masonry pagodas were typically abruptly reduced to accommodate metal finials. The top acceleration amplification of the Great Wenfeng Pagoda exhibited a trend similar to that of conventional pagoda structures, and the increase in horizontal acceleration at the top was mainly caused by the inherent structural whip effect, which was particularly pronounced at the top. Compared with the EL and synthetic waves, the Taft wave induced the most significant acceleration amplification at the top. For instance, for the Taft wave, the maximum amplification factor at the top reached 3.16 under the minor earthquake scenario, whereas the maximum amplification at the top under the EL and Ludian waves was 1.66 and 1.77, respectively.

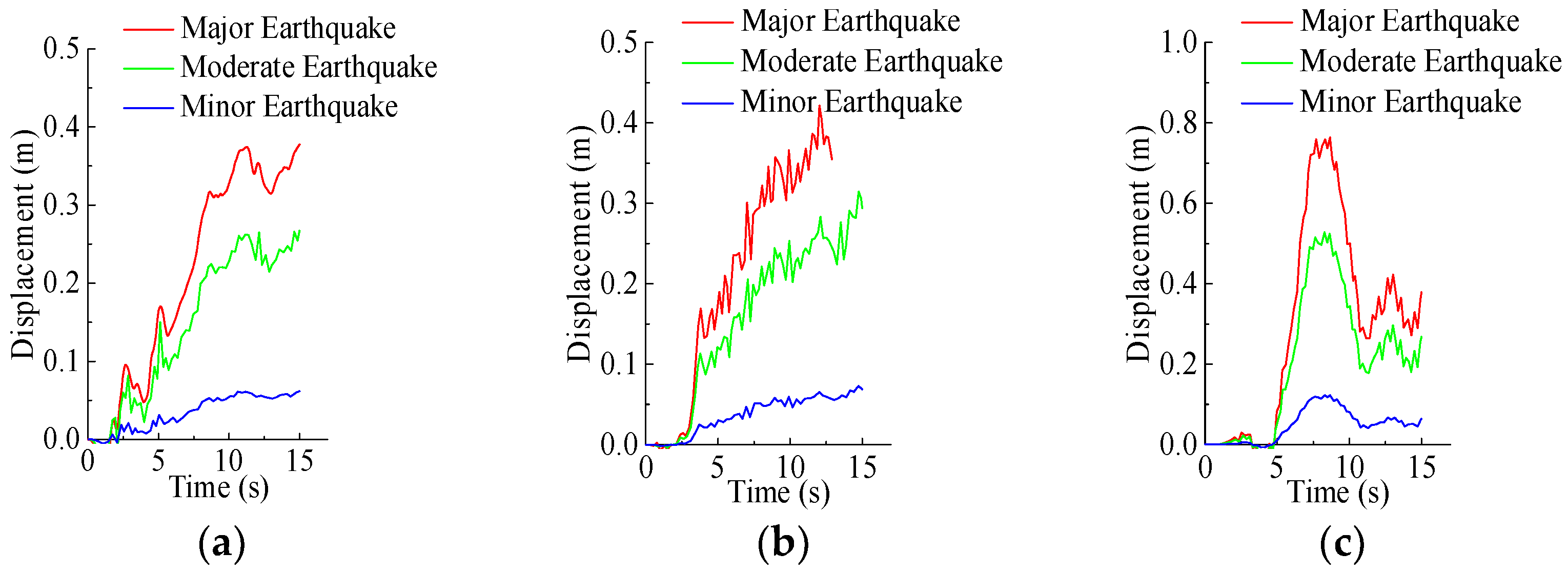
4.3. Horizontal Displacement

The time-history responses of the top displacement and horizontal inter-story displacements of the Great Wenfeng Pagoda under a seismic intensity of 7 were presented in Figure 9 and Figure 10, respectively. It was observed that the top horizontal displacement increased markedly with seismic intensity. As the duration of seismic wave input increased, the displacement gradually accumulated toward one side, resulting in significant residual deformation at the top of the pagoda. Among the three seismic waves, the top displacement induced by the synthetic wave was considerably larger than that induced by the Taft and El waves. Under moderate and severe seismic conditions, the displacement curves exhibited similar trends.

When the pagoda was regarded as a cantilever structure fixed at the base, the overall deformation was primarily dominated by bending-shear effects. Compared with sectional displacements, inter-story drift angles were more effective in reflecting locations of structural weakness. Existing masonry pagodas generally exhibited varying degrees of damage accumulated over long-term preservation, causing certain structural discontinuities. Therefore, sectional displacement alone was insufficient to identify weak links. Inter-story drift angles were analyzed (see Figure 11), and the results indicated that under all three seismic waves, the inter-story drift angles varied similarly with height: during minor and moderate earthquakes, the pagoda remained largely in the elastic stage, and the drift angles increased approximately linearly with height; under severe seismic action, the drift angles at the top increased significantly and reached their maximum, exhibiting clear nonlinear behavior. Notably, for the EL wave, a pronounced inflection appeared at the second level, whereas for the Taft and synthetic waves, abrupt changes occurred at the third and fourth levels.

Overall, under all three seismic waves, the inter-story drift angles in the minor earthquake scenario remained below 1/550, indicating that the structure was largely intact without evident cracking. Under moderate and severe seismic conditions, inter-story drift increased progressively with height, particularly above the third level. The relatively low seismic fortification intensity in Zhejiang, coupled with the historically low frequency of strong earthquakes compared with high-intensity regions such as Yunnan and Sichuan, contributed to the good preservation of masonry pagodas in this region.

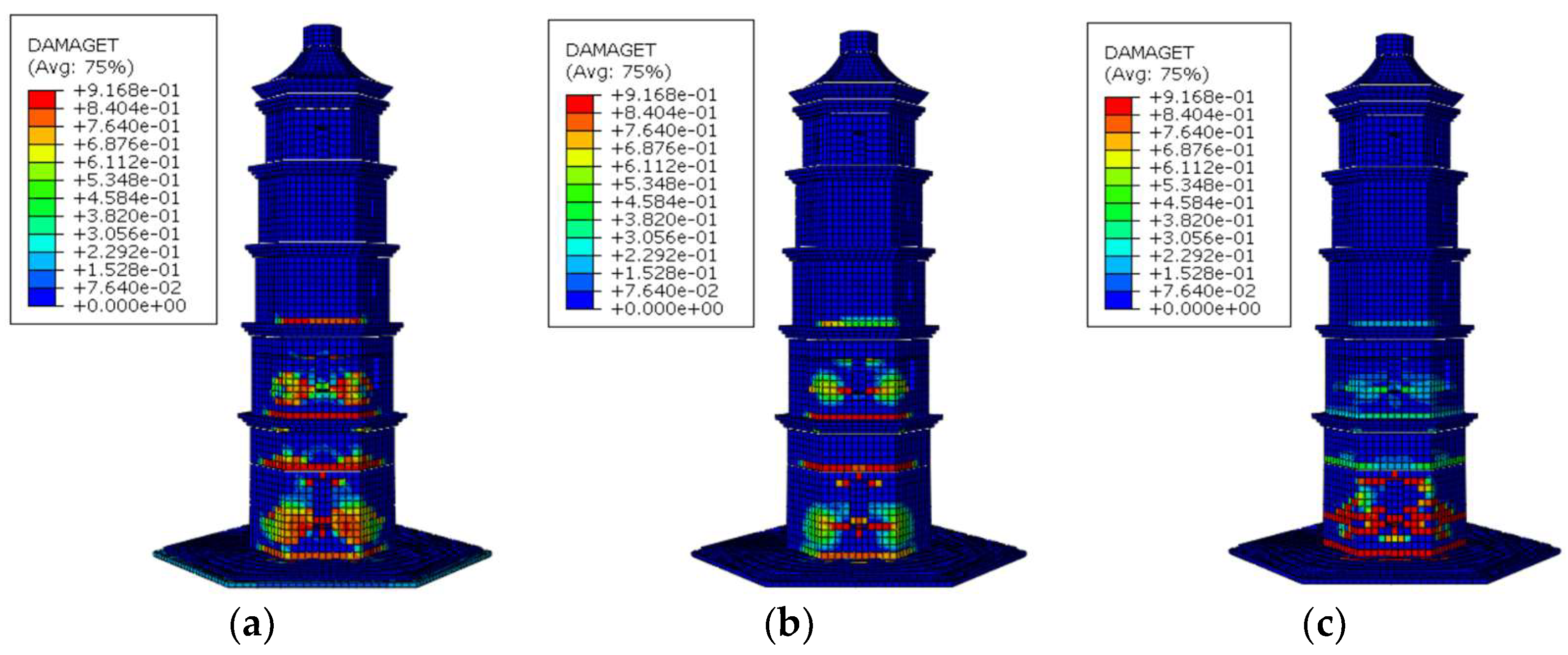
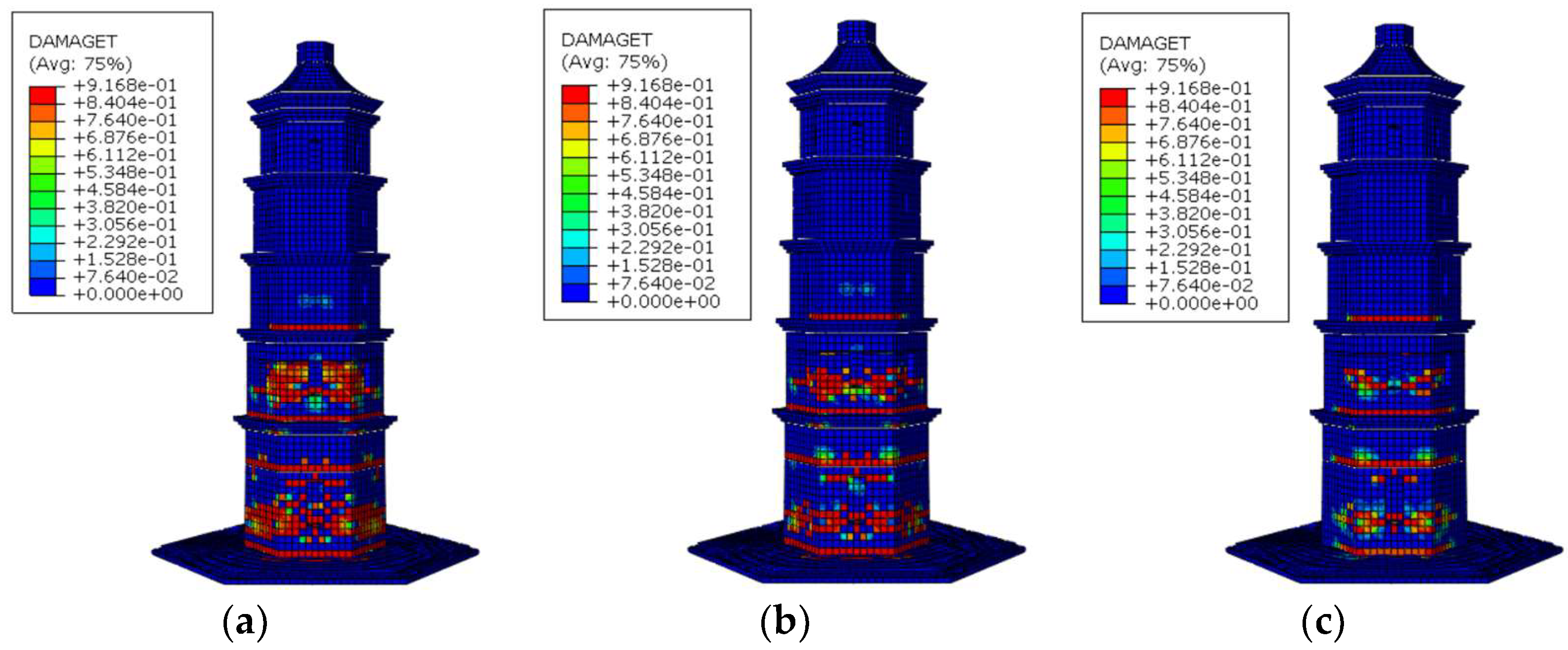
5. Damage Analysis of Ancient Pagoda

In the research of masonry pagodas and historical masonry structures, the tensile damage cloud chart and the main tensile stress cloud chart have been widely adopted to illustrate the evolution of structural damage and to identify vulnerable regions. In this study, the seismic failure mechanism of the Great Wenfeng Pagoda was analyzed based on the distribution of the main tensile stress, particularly under moderate and strong earthquake excitations, by evaluating the tensile damage factor and the principal tensile stress limits.

The tensile damage cloud chart of the pagoda under moderate and severe seismic actions induced by the El wave, Taft wave, and artificial Ludian wave was extracted, as shown in Figure 12 and Figure 13. The results indicated that the major damage regions induced by the three seismic waves were consistent, primarily concentrated in the first and second levels at the base of the pagoda, which was in agreement with the damage patterns reported for masonry pagodas in previous studies. Compared with minor seismic action, the damaged areas under moderate seismic action were significantly enlarged, with the tensile damage factor in some regions exceeding 1.0, primarily concentrated in the first and second levels at the base of the pagoda. Under severe seismic action, the damage factor in these levels further increased, and the damaged regions progressively extended toward the middle and upper portions of the pagoda. The maximum damage factor was observed near the doorway and gradually propagated to the surrounding areas. Masonry near openings experienced severe tensile damage, mainly around the doorways. Field investigation revealed that the lower portion of the base was constructed with stone blocks, whose higher strength contributed to enhanced seismic resistance of the pagoda.

The main tensile stress cloud images of the pagoda were obtained and are presented in Figure 14 and Figure 15. The results indicated that the first and second segments reached the tensile strength of the masonry material first and entered the failure stage, followed by a gradual expansion of the tensile damage zone to adjacent segments. Taking the Taft wave as an example, under the minor seismic intensity, the overall tensile stress of the pagoda remained low, with only a few bricks in the first and second layers exceeding the material tensile strength, and the pagoda structure remained relatively intact. Under moderate and strong seismic intensities, however, the pagoda suffered severe damage.

The tensile regions were primarily concentrated in the lower part of the first layer. Under strong seismic excitation, the maximum principal tensile stresses of the pagoda were 0.233, 0.238, and 0.237 MPa, approaching the tensile strength of the lower-layer stone blocks. Under strong seismic action, the masonry at the first layer experienced significant tensile stress, particularly in the regions near the doorway. The principal tensile stress in the second layer was also close to the tensile strength of the upper brick masonry, with local tensile stresses even reaching or exceeding the material limits. Field strength tests in Section 3.1 further revealed that the stone blocks at the base of the pagoda were severely damaged, and effective rebound test data could not be obtained in most areas, partly due to long-term rainwater erosion in the lower regions. These findings indicate that under moderate seismic action, the first-layer stone blocks remain relatively safe due to their higher strength, but under strong seismic action, they still present a risk of damage.

6. Discussion and Conclusions

The Jinshan Great Wenfeng Pagoda was selected as the research object, and a full-scale finite element model was established in ABAQUS based on on-site inspections and maintenance records to perform dynamic analysis, seismic response evaluation, and damage assessment. Given the long construction history of ancient pagodas, original design and construction documentation is often unavailable, and the physical properties and current damage state of the masonry materials are difficult to ascertain. These factors pose significant challenges for establishing reliable dynamic models. The present study provides a refined modeling methodology for Ming and Qing dynasty masonry pagodas in the Jiangnan region, offering practical guidance on several critical aspects, including precise dimension measurement, estimation of masonry strength when destructive testing is not feasible, calculation of the fundamental period, simplification of local structural components, and selection of material constitutive models.

Based on the above analyses and discussions, the main conclusions of this study are summarized as follows:

1.

The calculated natural periods of the pagoda were consistent with those obtained from the finite element analysis. Horizontal acceleration increased with height, and significant acceleration amplification was observed at the top, primarily governed by the inherent whip effect of the structure. Under minor earthquake excitation, the pagoda remained generally elastic, whereas under moderate and major earthquakes, significant increases in top acceleration were observed, with the most pronounced effect occurring under the Taft wave.

2.

The top horizontal displacement increased markedly with seismic intensity. The first and second stories at the base were identified as structural weak zones. Under minor earthquake conditions, the inter-story drift angle was less than 1/550, indicating that the pagoda remained largely intact. Under moderate and major earthquakes, the lower stories and areas surrounding the door openings were the most vulnerable regions.

3.

The distribution of damage under different seismic waves was generally consistent, mainly concentrated in the first and second stories, with tensile damage to masonry around the doorways being most pronounced. Under moderate and major earthquakes, tensile stresses in the lower-story masonry approached or exceeded the material tensile strength, resulting in localized cracking or failure. The lower part of the first story, constructed with stone blocks, provided an additional safety reserve, demonstrating the overall good seismic performance of the pagoda.

4.

The hierarchical modeling approach can accurately capture the overall mechanical behavior of the Jinshan Great Wenfeng Pagoda masonry structure and can be applied to analyze the dynamic response of dense-eave masonry pagodas in the Jiangnan region, providing a scientific basis for seismic retrofitting and long-term preservation of such historical buildings, with significant implications for cultural sustainability.

5.

This study followed the common practice in heritage structure seismic assessment of increasing the local fortification intensity by one level. Seismic time-history analyses were performed using inputs corresponding to intensity 7, resulting in conservative estimates. Future research will further incorporate site-specific ground motion parameters to analyze the response characteristics under regional seismic actions.