Energy-Consistent Mapping for Concrete Tensile Softening Within a Framework Combining Concrete Damaged Plasticity and Crack Band Theory

Abstract

As concrete exhibits localized strain softening, for example, under tension, fracture-energy consistency is essential for obtaining mesh-insensitive results of finite-element (FE) analyses. Accordingly, element- and structural-level parametric studies of uniaxial tensile behavior are performed within an FE framework coupling the Concrete Damaged Plasticity (CDP) model, the Crack Band Theory, and the Newton–Raphson solver in Abaqus. The effects of several CDP parameters and the mesh size are quantified using a sensitivity index ($SI$). A damage evolution law with several tensile parameters is proposed for energy consistency in addition to scaling of the softening strain. Besides tensile strength, elastic modulus, and an estimated uniaxial stress–strain curve, three key parameters are validated: the ratio between fracture energy from pure tension in the crack band and that from direct-tension tests, and two mesh-independent damage evolution parameters. An inverse calibration is proposed, in which the damage parameters and the fracture-energy ratio are identified in one-element ($SI\le 5\%$) and multi-element models, respectively. With these calibrations, the tensile response of the crack band is obtained, and multi-element analyses achieve mesh insensitivity when meshes are not smaller than the crack-band width. For finer meshes violating continuum assumptions, the initial damage rate parameter is reduced to preserve energy consistency.

1. Introduction

The meso-scale heterogeneity of concrete leads to variations in the mechanical response of neighboring elements, with weak zones (e.g., ITZ) cracking first and macro-cracks forming after stress redistribution (Figure 1). Localized strain softening is therefore the average response of a fracture process zone (FPZ) rather than a material property. The energy dissipated per unit of crack length should be mesh-independent [1]. Without explicit energy regularization, finite-element analyses exhibit mesh sensitivity, a phenomenon common to failure mechanisms governed by softening [1,2]. For example, in shear connections, degradation of shear transfer is strongly influenced by tensile micro-cracking and aggregate interlock, making the response particularly sensitive to tensile-softening regularization [3,4]. For uniaxial tension, the fictitious crack model (FCM) treats the FPZ as a crack-like zone at the tip to describe growth and stress release [5], while crack band theory (CBT) represents the FPZ as a narrow band of continuously distributed micro0cracks and restores energy consistency through a physical crack-band width [1]. In continuum FE models, tensile softening is represented via a smeared-crack approach with element-averaged properties, with CBT providing the energy constraint in a manner compatible with FCM. On this basis, isotropic plastic damage models such as the Concrete Damaged Plasticity (CDP) model proposed by Lubliner et al. (1989) and Lee & Fenves (1998) [6,7] are widely used for large-scale structural analysis.

Within the CDP framework, concrete is treated as an effective homogeneous and isotropic medium. Material heterogeneity is not modeled explicitly but is accounted for implicitly through the fracture energy and crack-band width, which represent the average behavior of the FPZ, and through strain-softening-induced localization in the constitutive law. In this setting, variability in crack initiation and the crack path can be reproduced at the structural scale using small geometric or boundary imperfections, notches, or a prescribed weak layer, while retaining computational efficiency without resolving meso-scale anisotropy [8]. To achieve convergence, accuracy, and mesh insensitivity in homogeneous FE models, the evolutions of tensile damage, stiffness degradation, and plastic deformation that govern the softening law must be explicitly characterized.

Li and Ren (2009) proposed a stochastic damage model for concrete based on an energy-equivalent strain [9]. The microscopic fracture strain is treated as a random variable, and statistical averaging of local rupture thresholds yields a macroscopic damage law, thereby bridging continuum damage mechanics and micro-scale stochastic fracture. The model derives a uniaxial stochastic damage evolution and, via the definition of an energy-equivalent strain, extends the result to multiaxial stress–strain spaces. Recent developments continue along this energy-equivalence principle, including unified or three-dimensional stochastic damage formulations by Guo and Li (2024) and Wang (2023), recommendations to control tensile softening using the tensile stress–crack opening relation and fracture energy to mitigate mesh sensitivity by Shamsi and Simer (2024), energy-regularization improvements of the Mazars model consistent with the crack-band concept by Arruda et al. (2022), and consistent crack-band strategies for higher-order elements emphasizing objectivity by Shen et al. (2024) [10,11,12,13,14].

In practice, however, damaged plasticity details are often underrepresented in structural-scale experimental validations and parametric studies [3,4,15,16,17]. Commercial workflows rely on tabulated post-peak inputs. Although models, codes, or empirical formulas [8] allow for the extraction of uniaxial tensile stress–strain or stress–crack opening relations from tests, experimental constraints, i.e., boundary conditions and multiaxial stress weighting under cyclic loading, make it difficult to isolate pure tensile behavior with damage evolution directly from data [18,19,20]. On the other hand, the energy-equivalent-strain principle has not been integrated with CDP–CBT in commercial FE workflows. For example, Li and Ren (2009) do not address the implementation details of CDP in FE software such as Abaqus but focus on statistical/mechanistic derivations [9]. Likewise, Guo and Li (2024) and Wang (2023) have not provided a CDP-CBT route that yields an operational inverse calibration and an energy-consistent closure [10,11]. If an inverse-calibration pathway could maintain fracture-energy consistency under limited experimental data, it would substantially enhance the engineering applicability of CDP models while safeguarding simulation reliability.

At the application level, most recent CDP-parameters validations including fracture energy and damage evolution are performed at the structural scale, reporting pronounced effects of mesh size and CDP parameters on global responses. Nastri et al. (2023) compiled practical CDP inputs and modeling guidance for a specific material class (tuff masonry in the Campania area), facilitating model establishment in commercial software [21]. Fakeh et al. (2023/2025) and Feng et al. (2020/2023) provided CDP calibration and parameter recommendations for ultra-high-performance concrete and reactive-powder concrete based on case studies at the structural scale [4,17,22,23]. Spozito et al. (2024) showed strong mesh influence on structural results, underscoring that table-based inputs are prone to sensitivity without internally enforced energy regularization and a consistent algorithmic tangent [24]. Ayhan and Lale (2022) introduced a rate-sensitive CDP modification, illustrating the impact of viscoplastic regularization on strength and softening and the need to delineate when viscosity serves only as a numerical aid [25]. Yet the quantitative roles at the element level of mesh size relative to crack-band width, viscoplastic regularization, dilation angle, and tensile damage evolution parameters in shaping both element- and structure-scale responses remain insufficiently specified. Qasem et al. (2025) discussed interactions among viscosity parameter, damage variables, and mesh and proposed a general calibration framework, but they did not discuss the calculation criteria of uniaxial simulations in detail [26]. Despite numerous advances, critical gaps remain in the CDP parameters and constitutive relations for concrete under quasi-static uniaxial tension.

If the tabulated stress–inelastic strain and damage–history relations are not mutually consistent, the return mapping follows an effective tangent between them, and the computed response departs from the target even in pure tension. Furthermore, the structural response depends on how softening is regularized with respect to the crack-band width and on how assembly effects enter the global tangent. This study develops an internally closed CDP–CBT constitutive model for quasi-static uniaxial tension at the element and structural scales, based on a mathematical constitutive solution, implemented within the Abaqus Newton–Raphson framework [1,5,6,7]. Using only limited test data, the crack-band width, fracture energy, tensile strength, elastic modulus, and an estimated uniaxial tensile stress–strain curve, an energy-consistent, invertible mapping is established from material inputs to three key tensile parameters, namely the ratio between fracture energy from pure tension in the physical crack band and that from direct-tension tests, and two mesh-independent damage evolution parameters (initial and overall). Parametric studies without viscoplastic regularization confirm the negligible role of dilation in pure tension in the embedded CDP model, while using a small viscosity parameter, increasing input-data density, or prescribing a predefined weak layer helps stabilize the stress-concentration path. A residual-based sensitivity index ($SI$) quantifies the effects of these parameters and mesh size, and a material-level stability indicator is validated to link element calibration to the assembled global tangent and the onset of localization, as one-element calibration does not guarantee structural validity. An inverse calibration is proposed in which the damage parameters and the fracture-energy ratio are identified in one-element ($SI\le 5\%$) and multi-element models, respectively. With these calibrations, the tensile response of the physical crack band is obtained, and multi-element analyses achieve mesh insensitivity when meshes are not smaller than the crack-band width. For energy regularization and mesh robustness, a value of approximately 0.01 for the initial tensile-damage-rate parameter is recommended to increase the material-level stability indicator and suppress spurious sensitivity for fine meshes that violate continuum assumptions. This work is methodological and does not introduce new experiments, while it can make use of any independently reported direct-tension datasets as boundary constraints. The framework is extensible to three-point bending for additional experimental corroboration.

2. Materials and Methods

In continuum CDP-CBT models, local softening is represented by element-averaged properties, i.e., the smeared-crack approach, in which the crack is assumed to develop continuously within an element. Under the corresponding assumption, the averaged cracking band observed in real tensile fracture is regarded as a material constant. In a finite-element model, the element width, i.e., mesh size, is taken to be the crack-band width.

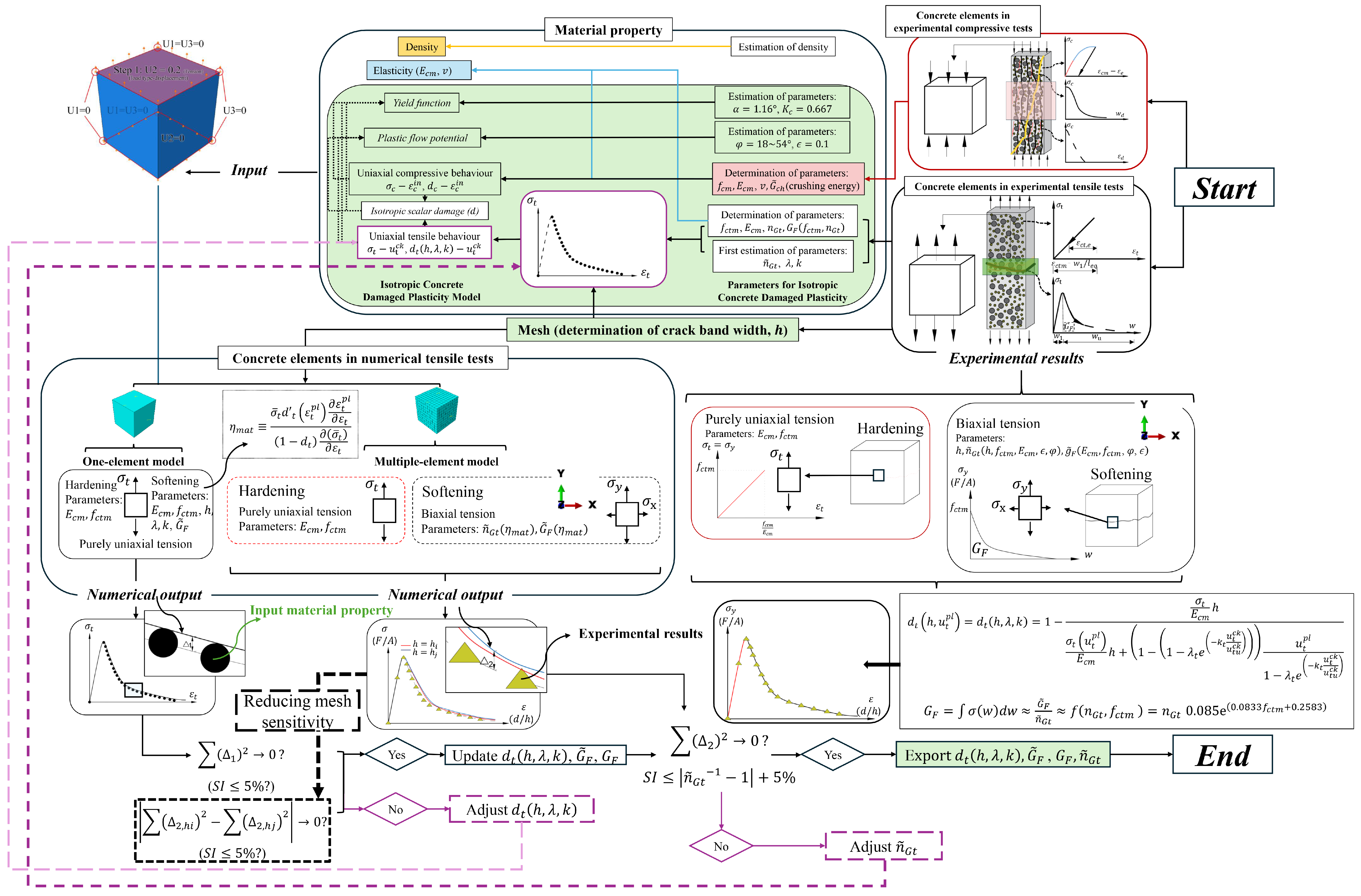
2.1. Isotropic Concrete Damaged Plasticity Model

In this paper, parameters with commonly suggested default values in commercial CDP implementations are treated as defaults [6,7,27].

The model utilizes the yield function as shown in Equation (1), which captures the evolutions of strength under tension and compression with three yield-surface shape parameters ($\alpha$, $\gamma$, and $\beta$),

$$F={\displaystyle \frac{1}{1-\alpha }}\left(\overline{q}-3\alpha \overline{p}+\beta 〈{\widehat{\overline{\sigma }}}_{max}〉-\gamma 〈-{\widehat{\overline{\sigma }}}_{max}〉\right)-{\overline{\sigma }}_c=0$$

(1)

where $\alpha \left({\sigma }_{b0}/{\sigma }_{c0}\right)={\displaystyle \frac{\left({\sigma }_{b0}/{\sigma }_{c0}\right)-1}{2\left({\sigma }_{b0}/{\sigma }_{c0}\right)-1}}$ and ${\sigma }_{b0}/{\sigma }_{c0}$ denotes the biaxial to uniaxial compressive strength ratio at initial yield, $\gamma \left(K_c\right)={\displaystyle \frac{3\left(1-K_c\right)}{2K_c-1}}$ and $K_c$ denotes the deviatoric-plane shape parameter, and $\beta \left({\tilde{\epsilon }}^{pl},\alpha \right)={\displaystyle \frac{{\overline{\sigma }}_c\left({\tilde{\epsilon }}_c^{pl}\right)}{{\overline{\sigma }}_t\left({\tilde{\epsilon }}_t^{pl}\right)}}\left(1-\alpha \right)-\left(1+\alpha \right)$ and $\beta$ denotes a tension–compression coupling factor that uses the current ratio of ${\overline{\sigma }}_c\left({\tilde{\epsilon }}_c^{pl}\right)$ to ${\overline{\sigma }}_t\left({\tilde{\epsilon }}_t^{pl}\right)$ together with $\alpha$ to shift and contract the yield surface along the tensile meridian.

${\sigma }_{b0}/{\sigma }_{c0}$ and $K_c$ are set as 1.16 and 0.667, respectively, as their impact is secondary within the present uniaxial tension scope once the tensile damage law is calibrated.

The scalar degradation in elastic stiffness ($d$) in Equation (1) is assumed to be isotropic following Equations (2) and (3) in the CDP model,

$$E=\left(1-d\right)E_{cm}$$

(2)

$$1-d=\left(1-s_c{d}_c\right)\left(1-s_t{d}_t\right)$$

(3)

where $s_c=1-w_c\left(1-r^{*}\left({\sigma }_{11}\right)\right)$, $s_t=1-w_t{r}^{*}\left({\sigma }_{11}\right)$ and $r^{*}\left({\sigma }_{11}\right)=H\left({\sigma }_{11}\right)=\left\{\begin{array}{c}1, {\sigma }_{11}>0\\ 0, {\sigma }_{11}<0\end{array}\right.$ and $d$ involves the opening, closing, and the interaction of previously formed micro-cracks.

The values of the weight factors, $w_c$ ($0\le w_c\le 1$) and $w_t$ ($0\le w_t\le 1$), are assumed to be 1 and 0, respectively, as first-order idealizations, indicating that there is full stiffness recovery upon crack closure in compression and no recovery in tension under monotonic loading. When cyclic direct-tension data are available, $w_c$ and $w_t$ can be identified within the same inverse calibration framework.

A non-associated multi-hardening plasticity is combined with the isotropic scalar damaged elasticity (Equation (4)).

$$\mathit{G}\left(\mathsf{\sigma }\right)=\sqrt{{\left(ϵ{\sigma }_{t0}\tan \phi \right)}^2+{\overline{q}}^2}-\overline{p}\tan \phi$$

(4)

The flow potential $\mathit{G}\left(\mathsf{\sigma }\right)$ used for this model is the Drucker–Prager hyperbolic function, including the direction (${\displaystyle \frac{\partial G}{\partial \sigma }}$) and the length of the plastic strain increment ($\mathit{\lambda }$) (Equation (5)).

$$d{\mathit{\epsilon }}^{pl}=\mathit{\lambda }{\displaystyle \frac{\partial G}{\partial \mathit{\sigma }}}$$

(5)

If $ϵ{\sigma }_{t0}$ increases, and/or $\phi$ decreases, the dilation angle decreases more rapidly in the hardening process (i.e., the dilation angle increases more rapidly in the softening process). In the CDP hyperbolic plastic potential, the flow potential eccentricity $ϵ$ primarily controls the curvature near low confinement, thus slightly affecting the flow direction close to the hydrostatic axis. In pure tension, its influence is minor relative to parameter $\phi$, which directly governs the volumetric–deviatoric partition of plastic flow. Therefore, $ϵ$ is kept at the default (0.1), while the sensitivity study focuses on $\phi$.

The scalar stress–strain relation in this CDP model is written as Equation (6).

$$\mathit{\sigma }=\left(1-d\right){\mathit{D}}_0^{\mathit{e}\mathit{l}}:\left(\mathit{\epsilon }-{\mathit{\epsilon }}^{pl}\right)=\left(1-d\right)\overline{\mathit{\sigma }}$$

(6)

The expression in Equation (3) for $d$ is generalized to the multiaxial stress case in Equation (6) by replacing the unit step function ($r^{*}\left({\sigma }_{11}\right)$ in Equation (3)) with a multiaxial stress weight factor, $r\left(\widehat{\sigma }\right)$,

• where $r\left(\widehat{\sigma }\right)={\displaystyle \frac{{\sum }_{i=1}^3〈{\widehat{\sigma }}_i〉}{{\sum }_{i=1}^3\left|{\widehat{\sigma }}_i\right|}}$, $0\le r\left(\widehat{\sigma }\right)\le 1$.

The elastic stiffness recovery effects during cyclic load reversals ($w_c$ and $w_t$ in Equation (3)) are considered, also known as the “unilateral effect”, which is usually more pronounced as the load changes from tension to compression, causing tensile cracks to close and resulting in the recovery of the compressive stiffness.

The uniaxial stress–strain relations can be described by Equations (7) and (8).

$${\sigma }_c=\left(1-d_c\right)E_{cm}\left({\epsilon }_c-{\tilde{\epsilon }}_c^{pl}\right)$$

(7)

$${\sigma }_t=\left(1-d_t\right)E_{cm}\left({\epsilon }_t-{\tilde{\epsilon }}_t^{pl}\right)$$

(8)

The hardening and softening processes can be described by the stress–inelastic strain relation, where the inelastic strain is defined as the total strain minus the elastic strain corresponding to the undamaged material (Equations (9) and (10)).

$${\tilde{\epsilon }}_c^{in}={\epsilon }_c-{\epsilon }_{oc}^{el}={\epsilon }_c-{\displaystyle \frac{{\sigma }_c}{E_{cm}}}$$

(9)

$${\tilde{\epsilon }}_t^{ck}={\epsilon }_t-{\epsilon }_{ot}^{el}={\epsilon }_t-{\displaystyle \frac{{\sigma }_t}{E_{cm}}}$$

(10)

Unloading data of the damaged material is provided in terms of the relations shown in Equations (11) and (12). For uniaxial tension, the hardening and softening processes can also be described by the stress–cracking displacement relation (Equation (13)).

$${\tilde{\epsilon }}_c^{pl}={\tilde{\epsilon }}_c^{in}-{\displaystyle \frac{d_c}{\left(1-d_c\right)}}{\displaystyle \frac{{\sigma }_c}{E_{cm}}}$$

(11)

$${\tilde{\epsilon }}_t^{pl}={\tilde{\epsilon }}_t^{ck}-{\displaystyle \frac{d_t}{\left(1-d_t\right)}}{\displaystyle \frac{{\sigma }_t}{E_{cm}}}$$

(12)

$${\tilde{u}}_t^{pl}={\tilde{u}}_t^{ck}-{\displaystyle \frac{d_t}{\left(1-d_t\right)}}{\displaystyle \frac{{\sigma }_t}{E_{cm}}}h$$

(13)

where ${\tilde{u}}_t^{pl}=h{\tilde{\epsilon }}_t^{pl}$; ${\tilde{u}}_t^{ck}=h{\tilde{\epsilon }}_t^{ck}$.

In multiaxial stress states, all the equivalent strains and deformations (${\tilde{\epsilon }}_c^{pl}$, ${\tilde{\epsilon }}_t^{pl}$, ${\tilde{\epsilon }}_c^{in}$, ${\tilde{\epsilon }}_t^{ck}$, ${\tilde{u}}_t^{pl}$ and ${\tilde{u}}_t^{ck}$) should be calculated automatically according to the input uniaxial strain (${\epsilon }_t^{pl}$, ${\epsilon }_c^{pl}$, ${\epsilon }_t^{ck}$, ${\epsilon }_c^{in}$, $u_t^{pl}$ and $u_t^{ck}$), yield function, and plastic flow.

2.2. Uniaxial Constitutive Law Coupled with Concrete Damaged Plasticity Model

2.2.1. Parameters in the Concrete Damaged Plasticity Model

The case of uniaxial tension can be deduced from Equation (8), resulting in Equation (14a).

$${\sigma }_t\left({\epsilon }_t^{pl}\right)={\displaystyle \frac{E_{cm}{\epsilon }_t^{pl}}{b_t^{\prime }}}\left(1-b_t^{\prime }\right)$$

(14a)

When the stress–cracking displacement relation is adopted for defining the uniaxial tension, Equation (14b) is obtained.

$${\sigma }_t\left(u_t^{pl}\right)={\displaystyle \frac{E_{cm}{u}_t^{pl}}{b_t^{\prime }h}}\left(1-b_t^{\prime }\right)$$

(14b)

where $b_t^{\prime }={\displaystyle \frac{{\epsilon }_t^{pl}}{{\epsilon }_t^{ck}}}$.

Theoretically, using the incremental integration algorithm according to Equation (14a) (or Equation (14b)), the non-associated plastic potential function (Equation (4)), and the yield function (Equation (1)), the uniaxial tensile stress–strain (${\sigma }_t-{\epsilon }_t$) relationship can be obtained with the given values of $f_{ctm}$, $E_{cm}$, ${\sigma }_{t0}$, $\phi$, and $ϵ$. Assuming ${\sigma }_{t0}=a_{t0}{f}_{ctm}$ while $a_{t0}$ is pre-defined (e.g., $a_{t0}=1.0$), ${\epsilon }_t^{pl}$ and $b_t^{\prime }$ in uniaxial tensile cases can be derived in this way to relate to several parameters, as shown in Equations (15) and (16).

$${\epsilon }_t^{pl}={\epsilon }_t^{pl}\left(\phi ,{ϵ,f}_{ctm},E_{cm}\right)$$

(15)

$$b_t^{\prime }=b_t^{\prime }\left({\epsilon }_t^{pl},E_{cm},{\sigma }_{t0}\right)=b_t^{\prime }\left(\phi ,{ϵ,f}_{ctm},E_{cm}\right)$$

(16)

Notice that ${\tilde{g}}_F={\tilde{G}}_F/h=\int {\sigma }_t\left({\epsilon }_t^{ck}\right)d{\epsilon }_t^{ck}$, and therefore Equation (17) can be derived.

$${\tilde{g}}_F={\int }_0^{\mathrm{\infty }}{\sigma }_t\left({\displaystyle \frac{{\epsilon }_t^{pl}\left(\phi ,{ϵ,f}_{ctm},E_{cm}\right)}{b_t^{\prime }\left(\phi ,{ϵ,f}_{ctm},E_{cm}\right)}}\right)d\left({\displaystyle \frac{{\epsilon }_t^{pl}\left(\phi ,{ϵ,f}_{ctm},E_{cm}\right)}{b_t^{\prime }\left(\phi ,{ϵ,f}_{ctm},E_{cm}\right)}}\right)={\tilde{g}}_F\left(\phi ,{ϵ,f}_{ctm},E_{cm}\right)$$

(17)

Equation (17) reveals that there are certain relationships between $\phi$ and ${\tilde{g}}_F$ with parameters including $ϵ$, ${ E}_{cm}$, and $f_{ctm}$ determined. As $ϵ$ can be set to 0.1 and $h$ can be pre-defined, at least three parameters, ${\tilde{G}}_F, E_{cm}$, and $f_{ctm}$ (or $\phi , E_{cm}$, and $f_{ctm}$), should be utilized to derive the ${\sigma }_t$ − ${\epsilon }_t$ relationship incorporating damaged plasticity ($b_t^{\prime }$ − ${\epsilon }_t^{pl}$ evolution and $d_t$ − ${\epsilon }_t^{pl}$ evolution). Therefore, Equations (15)–(17) can be further transformed into Equation (18), which shows the functional dependency of ${\epsilon }_t^{pl}$, $b_t^{\prime }$, and ${\tilde{G}}_F$ (or ${\tilde{g}}_F$ and $h$) on various parameters. The corresponding evolution of $d_t$ can be uniquely derived from a set of variables including $f_{ctm}$, $E_{cm}$, $\phi$, and $ϵ$ within the framework of the CDP model, as shown in Figure 2.

$$\begin{gathered} b_t^{\prime }=b_t^{\prime }\left({\tilde{G}}_F,f_{ctm},E_{cm}\right), {\epsilon }_t^{pl}={\epsilon }_t^{pl}\left({\tilde{G}}_F,f_{ctm},E_{cm}\right), \\ {\tilde{G}}_F={\tilde{G}}_F\left(b_t^{\prime },f_{ctm},E_{cm},h\right)={\tilde{G}}_F\left({\epsilon }_t^{pl},f_{ctm},E_{cm},h\right)\mathrm{or} \\ {\tilde{g}}_F=g_F\left(b_t^{\prime },f_{ctm},E_{cm}\right)=g_F\left({\epsilon }_t^{pl},f_{ctm},E_{cm}\right) \end{gathered}$$

(18)

The parametric relationships for uniaxial compression can be derived as shown in Equations (19)–(21).

$${\sigma }_c\left({\epsilon }_c^{pl}\right)={\displaystyle \frac{E_{cm}{\epsilon }_c^{pl}}{b_c^{\prime }}}\left(1-b_c^{\prime }\right)$$

(19)

$${\tilde{g}}_{ch}={\tilde{g}}_{ch}\left({\phi ,f_{ctm},ϵ,E}_{cm},f_{cm}\right)$$

(20)

$$\begin{gathered} b_c^{\prime }=b_c^{\prime }\left({{\tilde{G}}_{ch},f_{ctm},E}_{cm},f_{cm}\right), {\epsilon }_c^{pl}={\epsilon }_c^{pl}\left({{\tilde{G}}_{ch},f_{ctm},E}_{cm},f_{cm}\right), \\ {\tilde{G}}_{ch}={\tilde{G}}_{ch}\left(b_c^{\prime },f_{ctm},E_{cm},f_{cm},h\right)={\tilde{G}}_{ch}\left({\epsilon }_c^{pl},f_{ctm},E_{cm},f_{cm},h\right)\mathrm{or} \\ {\tilde{g}}_{ch}={\tilde{g}}_{ch}\left(b_c^{\prime },f_{ctm},E_{cm},f_{cm}\right)={\tilde{g}}_{ch}\left({\epsilon }_c^{pl},f_{ctm},E_{cm},f_{cm}\right) \end{gathered}$$

(21)

When the constitutive model is internally closed, i.e., with the yield surface, plastic potential, and an explicitly defined tensile-damage evolution (e.g., prescribing the initial value $b_t^{\prime }$ ($b_{t0}^{\prime }$) under a small initial-softening increment), the post-peak softening law is uniquely generated by incremental integration, so the uniaxial tensile stress–strain relation should be treated as an output rather than an input. This is a theoretical constitutive solution at the material-point level, and its uniqueness is model-conditional and depends on the specified evolution law and parameters. For practical use, external experimental validation and parameter identification are still required, and mesh objectivity at the structural scale demands crack-band scaling and fracture-energy consistency.

Experimentally, the relationships in Equations (18) and (21) are influenced by concrete design variables, including mix variations that alter chemical composition and mechanical properties. Given this variability and the absence of a universal and closed-form mapping from parameters to a unique post-peak law across mixes, geometries, and boundary conditions, commercial CDP implementations adopt an interface-oriented design that allows the user to specify the tensile softening. Accordingly, in the CDP model embedded in most commercial FE software such as Abaqus, the tabulated post-peak tensile inputs are treated as the constitutive law, so that the return mapping is closed and fracture-energy dissipation and crack-band scaling can be enforced when the fracture energy and the equivalent crack-band width are supplied consistently, enabling alignment with mix-specific test data.

However, if the $d_t$ − ${\epsilon }_t^{pl}$ relation and the ${\sigma }_t$ − ${\epsilon }_t^{ck}$ curve are not mutually consistent, i.e., they do not satisfy Equation (6) and imply the same unloading stiffness and softening slope, the return mapping follows an effective tangent between them, and the uniaxial response obtained from the FE calculation departs from the target, as shown in Figure 2. Moreover, in a multiaxial stress state, the progression of the yield surface (Equation (1)), which is governed by the plastic strain ${\mathit{\epsilon }}^{pl}$ and the corresponding damage variable $d$, could be significantly altered even if the global equilibrium can be achieved, leading to numerical differences compared with the real concrete behavior (Equation (6)).

Therefore, under the background of the CBT, the continuum assumption, and the strain-softening hypothesis, the one-element tensile damage can be identified using a theoretical constitutive solution. Structural-scale predictions under uniaxial tensile loading should then be verified on multi-element models by inputting the calibrated results from a one-element model based on the same assumptions. This solution is model-conditional and energy-consistent when the element size matches the physical crack-band width, which is applicable using results from the CDP model embedded in Abaqus, although experimental data of elastic degradation is limited, as shown in Figure 2.

2.2.2. Elastic Stiffness Damage Evolution

Theoretical formulas are commonly employed to estimate damage evolution based on experimental or standardized monolithic stress–strain relationships. Three commonly used methods to define damage evolution variables for the degradation of elastic stiffness are described as follows.

1.

Damage Evolution Law 1 ($d_1$)

The most basic concept of CDP from Lubliner et al. (1989) gives the damage evolution as shown in Equations (22) and (23) [6], which should be non-dimensional if the relationships of uniaxial stresses and the corresponding inelastic displacements are considered as material constants.

$$d_c={\mathrm{k}}_{\mathrm{c}}={\displaystyle \frac{\int {\sigma }_c\left({\epsilon }_c^{in}\right)d{\epsilon }_c^{in}}{{\tilde{G}}_{ch}/l_{eq}}}$$

(22)

$$d_t={\mathrm{k}}_{\mathrm{t}}={\displaystyle \frac{\int {\sigma }_t\left({\epsilon }_t^{ck}\right)d{\epsilon }_t^{ck}}{{\tilde{G}}_F/h}}$$

(23)

The size independence of this law ($d_1$), defining the elastic stiffness damage as the portion of normalized energy dissipated by damage [28], is consistent with the derivation from Equations (18) and (21) that five parameters—${\tilde{G}}_F, {{\tilde{G}}_{ch}, f_{ctm}, E}_{cm}, f_{cm}$ can be utilized to describe the damaged plasticity. However, it should also be noticed that ${\mathrm{k}}_{\mathrm{c}}$ and ${\mathrm{k}}_{\mathrm{t}}$ do not share the same definition as the damage of elastic stiffnesses.

2.

Damage Evolution Law 2 ($d_2$)

According to the energy equivalence principle from Sidoroff (1981) [29], elastic energy due to stress in the undamaged material ($W_o^e$) and elastic energy due to stress in the damaged material ($W_d^e$) are, respectively, represented by Equations (24a) and (24b).

$$W_o^e={\displaystyle \frac{{\sigma }^2}{2E_{cm}{\left(1-d_s\right)}^2}}$$

(24a)

$$W_d^e=\left(1-d_s\right)W_o^e={\displaystyle \frac{{\sigma }^2}{2E_{cm}\left(1-d_s\right)}}$$

(24b)

where $d_s$ and $d$ are the damage of secant and elastic stiffnesses, respectively.

If $W_d^e$ is assumed to be approximately equal to $W_{d,CDP}^e$, i.e., the energy caused by the effective stress in the damaged material in the CDP model, as expressed in Equations (24c) and (24d) with $n_{\mathsf{\Psi }}\approx 1$, $d_c$ and $d_t$ can be estimated by Equations (25a) and (25b), respectively.

$$W_{d,CDP}^e={\displaystyle \frac{{\overline{\sigma }}^2}{2E_{cm}}}={\displaystyle \frac{{\sigma }^2}{{\left(1-d\right)}^{2}2E_{cm}}}$$

(24c)

$${\displaystyle \frac{{\sigma }^2}{2E_{cm}\left(1-d_s\right)}}=n_{\mathsf{\Psi }}{\displaystyle \frac{{\sigma }^2}{{\left(1-d\right)}^{2}2E_{cm}}}, n_{\mathsf{\Psi }}={\displaystyle \frac{{\epsilon }^{pl}}{{\epsilon }^{el}}}\left(2+{\displaystyle \frac{{\epsilon }^{pl}}{{\epsilon }^{el}}}\right)+1$$

(24d)

$$d_c=1-\sqrt{{\displaystyle \frac{{\sigma }_c}{E_{cm}{\epsilon }_c}}}$$

(25a)

$$d_t=1-\sqrt{{\displaystyle \frac{{\sigma }_t}{E_{cm}{\epsilon }_t}}}$$

(25b)

However, $n_{\mathsf{\Psi }}\approx 1$ is only valid when ${\displaystyle \frac{{\epsilon }^{pl}}{{\epsilon }^{el}}}$ can be estimated to be zero in the hardening states. When damage develops to its limit, cracks fully open, and the concrete reaches its maximum load-bearing capacity, localized deformation and crack surface sliding become dominant. Energy dissipation primarily occurs through crack propagation rather than through internal micro-damage. As a result, the energy equivalence principle may no longer be applicable.

3.

Damage Evolution Law 3 ($d_3$)

From Equations (11) and (13), the relationships for uniaxial compression and tension can be derived to Equation (26) and Equation (27), respectively, and this study adopts their basic concept to establish a damage evolution law ($d_3$) that can determine the uniaxial elastic-stiffness degradation. However, the energy regularization could not be obtained given the complex coupling effect of the CDP-CBT model in FE simulations. The damage evolution laws $d_1$ and $d_2$ will also be further verified in the following discussion along with the establishment of $d_3$.

$$d_c=1-{\displaystyle \frac{\frac{{\sigma }_c}{E_{cm}}}{\frac{{\sigma }_c}{E_{cm}}+\left(1-b_c^{\prime }\right){\epsilon }_c^{in}}}$$

(26)

$$d_t=1-{\displaystyle \frac{{\sigma }_t/E_{cm}}{\frac{{\sigma }_t}{E_{cm}}+\left(1-b_t^{\prime }\right){\epsilon }_t^{ck}}}$$

(27)

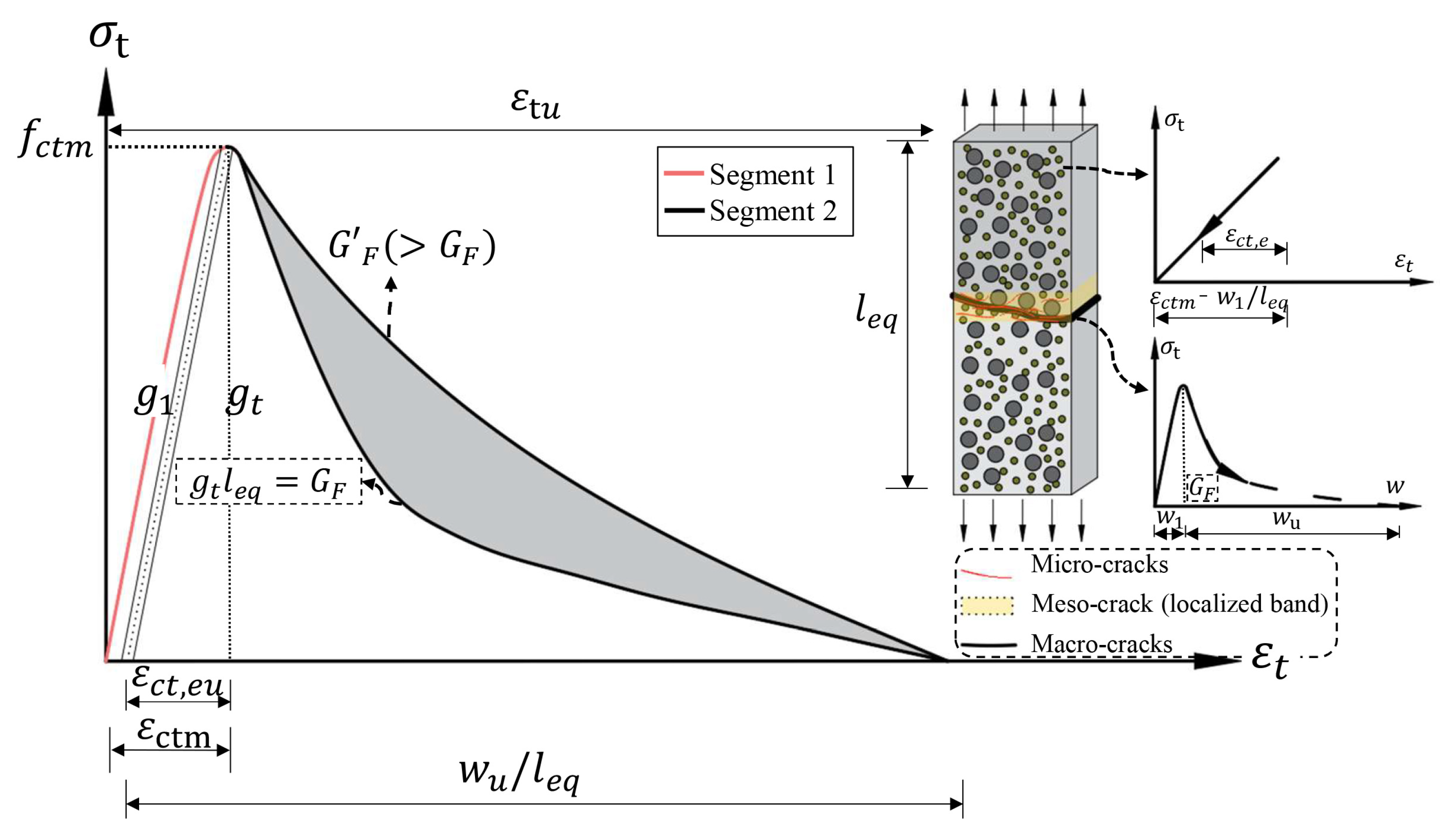
2.2.3. Uniaxial Tensile Behavior

• Uniaxial Tensile Relations from the Fictious Crack Model

In the FCM, only the tensile behavior of the uncracked concrete can be described using a stress–strain (${\sigma }_t$ − ${\epsilon }_t$) relation, as tensile failure of concrete is described as a discrete phenomenon [5]. $w$ of micro-cracks in a FPZ increases as these micro-cracks grow and form a discrete crack at stress close to $f_{ctm}$ (Figure 1), leaving a large area outside the FPZ uncracked.

For the process where $w$ of the micro-cracks ranges from zero to $w_1$ (i.e., segment 1 shown in Figure 1), it is assumed that the micro-cracking starts to reduce the material stiffness in the fracture zone at tensile stresses of $0.9f_{ctm}$ [5]. Therefore, in this initial process, the ${\sigma }_t$ − ${\epsilon }_t$ relation in the hardening fracture zone and the rest area can be presented by Equations (28) and (29), respectively.

$${\sigma }_t\left({\epsilon }_t\right)=\left\{\begin{array}{c}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{E}_{cm}{\epsilon }_t,\hspace{1em}\hspace{1em}\hspace{1em}0\le {\epsilon }_t<0.9{\displaystyle \frac{f_{ctm}}{E_{cm}}}\\ f_{ctm}\left(1-0.1{\displaystyle \frac{{\epsilon }_{ctm,l}-{\epsilon }_t}{{\epsilon }_{ctm,l}-0.9\frac{f_{ctm}}{E_{cm}}}}\right)={\sigma }_t\left({\delta }_t^{pl}\right),\hspace{1em}\hspace{1em}\hspace{1em}0.9{\displaystyle \frac{f_{ctm}}{E_{cm}}}\le {\epsilon }_t<{\epsilon }_{ctm,l},{\delta }_t^{pl}>0 \end{array}\right.$$

(28)

$${\sigma }_t\left({\epsilon }_t\right)=E_{cm}{\epsilon }_t, {0\le \epsilon }_t<{\displaystyle \frac{f_{ctm}}{E_{cm}}}, {\delta }_t^{pl}=0$$

(29)

After the macro-cracks propagate in this zone (i.e., segment 2 shown in Figure 1), $w_1\le w\le w_u+w_1$, the crack opening continues to grow until it reaches a critical point, at which the tensile stress drops to zero. A stress–crack opening (${\sigma }_t-w$) relation is used in the FCM. Based on this, an exponential relationship (Equation (30)) for NC is proposed by Hillerborg 1991 and given by fib MC2020 [15,30].

$${\sigma }_t\left(w\right)=f_{ctm}\left\{\left\{1+{\left(c_1{\displaystyle \frac{w-w_1}{w_u}}\right)}^3\right\}{e}^{\left(-c_2{\displaystyle \frac{w-w_1}{w_u}}\right)}-\left({\displaystyle \frac{w-w_1}{w_u}}\right)\left(1+{c_1}^3\right)e^{\left(-c_2\right)}\right\}={\sigma }_t\left({\delta }_t^{pl}\right)$$

(30)

in which $w_1\le w\le w_u+w_1$, ${\delta }_t^{pl}>0$,

$$w_u={\displaystyle \frac{5.14\left(G_F-{\int }_0^{w_1}{\sigma }_t\left(w\right)dw\right)}{f_{ctm}}}; c_1=3, c_2=6.93$$

(31)

According to fib MC2020, $f_{ctm}$ and $G_F$ can be estimated by Equations (32) and (33) in cases of no specific experimental data [15].

$$f_{ctm}\approx 1.8\ln \left(f_{cm}-8\right)-3.1$$

(32)

$$G_F={\int }_0^{w_1+w_{\mathrm{u}}}{\sigma }_t\left(w\right)dw\approx 0.085{\left(f_{cm}-8\right)}^{0.15}\approx 0.085{\mathrm{e}}^{\left(0.0833f_{ctm}+0.2583\right)}$$

(33)

While Equations (32) and (33) are derived from statistical analyses of the results obtained for NC, this study introduces two coefficients, $n_t$ (Equation (34)) and $n_{Gt}$ (Equation (35)), to refine the validation between actual measurements and statistical predictions of $f_{ctm}$ and $G_F$ from Equations (32) and (33), respectively. This adjustment allows various concrete types to utilize the unified exponential model described in Equation (30) for more accurate ${\sigma }_t-w$ relationships.

$$f_{ctm}\approx n_t\times \left[1.8\ln \left(f_{cm}-8\right)-3.1\right]$$

(34)

$$G_F\approx n_{Gt}0.085{\left(f_{cm}-8\right)}^{0.15}=f\left(n_{Gt},n_t,f_{cm}\right)\approx n_{Gt}0.085{\mathrm{e}}^{\left(0.0833f_{ctm}+0.2583\right)}=f\left(n_{Gt},f_{ctm}\right)$$

(35)

Once the tensile stress decreases from $f_{ctm}$ to zero (i.e., fracture energy releasing process), the cracks become stress-free. At the same time, the uncracked concrete experiences unloading (Equation (29)).

2.

Coupling the Fictious Crack model with the Crack Band Theory

The formation of cracks in the FCM can be modeled by introducing the damaged elasticity and plastic deformations in finite elements and coupling this with the CBT [1], which models the FPZ as a narrow band of uniformly and continuously distributed micro-cracks within a width in FE analysis. In experimental tests, $h$ refers to crack-band width [1]. In the FE model, as shown in Figure 2, these crack bands can be simulated in the damaged elements with a mesh size, $h$ (Equation (36)).

$$h={\displaystyle \frac{\sqrt{A_e}}{\cos \theta }}$$

(36)

Unlike FCM, a ${\sigma }_t$ − ${\epsilon }_t$ relation is applied in the CBT, while the strain at complete rupture in the crack band model can be associated with $w$ in the FCM. $w_1$ in Figure 1 can be computed as presented in Equation (37).

$$w_1={(\epsilon }_{ctm,l}-{\displaystyle \frac{f_{ctm}}{E_{cm}}})h; {\epsilon }_{ctm,l}={\displaystyle \frac{f_{ctm}}{E_{cm}}}+{\displaystyle \frac{w_1}{h}}$$

(37)

For regular-shaped concrete specimens, the average tensile strain in the softening phase can be computed by simply adopting the FCM (Equation (38a)) or the CBT (Equation (38b)).

$${\displaystyle \frac{{\delta }_t}{l_{eq}}}={\displaystyle \frac{{\delta }_{ii}}{l_{eq}}}=\left\{\begin{array}{c}{\displaystyle \frac{{\sigma }_t}{E_{cm}}}+{\displaystyle \frac{\mathrm{w}}{l_{eq}}}, 0\le w\le w_1 \\ {\displaystyle \frac{f_{ctm}}{E_{cm}}}+{\displaystyle \frac{\mathrm{w}}{l_{eq}}}-{\epsilon }_{ct,e}={\displaystyle \frac{{\sigma }_t}{E_{cm}}}+{\displaystyle \frac{\mathrm{w}}{l_{eq}}},w_1\le w\le w_1+w_{\mathrm{u}} \end{array}={\displaystyle \frac{{\sigma }_t}{E_{cm}}}+{\displaystyle \frac{\mathrm{w}}{l_{eq}}}\right.$$

(38a)

$${\displaystyle \frac{{\delta }_t}{h}}={\displaystyle \frac{{\delta }_{ii}}{h}}=\left\{\begin{array}{c}{\displaystyle \frac{{\sigma }_t}{E_{cm}}}+{\displaystyle \frac{\mathrm{w}}{h}}, 0\le w\le w_1 \\ {\displaystyle \frac{f_{ctm}}{E_{cm}}}+{\displaystyle \frac{\mathrm{w}}{h}},w_1<w\le w_1+w_{\mathrm{u}} \end{array}\right.$$

(38b)

3.

Clarification of Global Strain in the ${ii}^{th}$ Direction, Uniaxial Strain in Purely Uniaxial Stress States, and Scalar Equivalent Strain in Multiaxial Stress States

Based on the curve-fitting results from cyclic tests by Sinha et al. (1964), the ratios of ${\epsilon }_{ii}^{pl}$ and ${\epsilon }_{ii}^{ck}$ were found to range from 0.6 to 0.9 [31]. Nevertheless, the tensile damage variables for different types of concrete should be based on distinct evolutions of $b_t^{\prime }$.

One should notice from this experimental observation that ${\epsilon }_{ii}^{pl}/{\epsilon }_{ii}^{ck}\ne b_t^{\prime }$. Only in uniaxial tensile cases is the following true: ${\epsilon }_{ii}^{pl}/{\epsilon }_{ii}^{ck}=b_t^{\prime }$. The tensile plastic strain (${\epsilon }_{ii}^{pl}$) in the ${ii}^{th}$ direction is a one-direction strain corresponding to the multiaxial stress states, which differs from the tensile plastic strain in purely uniaxial tensile stress states (${\epsilon }_t^{pl}$) and the equivalent tensile plastic strain (${\tilde{\epsilon }}_t^{pl}$ and ${\tilde{\epsilon }}_t^{pl}\ge {\epsilon }_{ii}^{pl}>{\epsilon }_t^{pl}$) of concrete elements under uniaxial loading (i.e., in multiaxial stresses cases, as shown in Figure 2). The form of the ${\sigma }_t-w$ relation (the FCM) is deduced from non-purely uniaxial tensile stress states of cracking concrete elements, so that the ${\sigma }_t-w$ relation is indeed a ${\sigma }_t-{\delta }_{ii}^{ck}$ relation. More specifically, ${{\tilde{u}}_t^{ck}\ge \delta }_t^{ck}={\delta }_{ii}^{ck}=w>u_t^{ck}$, ${{\tilde{u}}_t^{pl}\ge \delta }_t^{pl}={\delta }_{ii}^{pl}=b_{\delta t}^{\prime }w>u_t^{pl}$, ${\delta }_{t,l}>u_{t,l}$, ${\delta }_t>u_t$, and ${\tilde{G}}_F$ measured in purely uniaxial tensile stress states should follow ${\tilde{G}}_F<G_F=\int {\sigma }_t\left(w\right)dw$.

This study assumes a relationship between ${\tilde{G}}_F$ and ${\tilde{n}}_{Gt}$ (the ratio between fracture energy from pure tension in the physical crack band and that from direct-tension tests) according to Equation (39).

$${\tilde{G}}_F={\tilde{n}}_{Gt}{G}_F, {0<\tilde{n}}_{Gt}<1$$

(39)

That is to say, the ${\sigma }_t$ − $w$ relation (FCM) should be the output numerical results using the input data of the corresponding ${\sigma }_t$ − $u_t^{ck}$ relation. Coupling the FCM and CBT, in the CDP theory the experimental crack opening ($w$) can be defined as the inelastic deformation and the average tensile strain (Equation (40)) follows the same relation shown in Equation (38a). However, numerical models cannot output the same results as those calculated by Equation (38a) if the $d_t$ − ${\epsilon }_t^{pl}$ and the ${\sigma }_t$ − ${\epsilon }_t^{ck}$ curves are not mutually consistent.

$${\displaystyle \frac{{\delta }_t}{l_{eq}}}={\displaystyle \frac{{\delta }_{ii}}{l_{eq}}}=\left\{\begin{array}{c}{\displaystyle \frac{{\sigma }_t}{E_{cm}}}+{\displaystyle \frac{w}{h}}, 0\le w\le w_1 \\ {\displaystyle \frac{\left[\left(\frac{{\sigma }_t}{E_{cm}}+\frac{\mathrm{w}}{h}\right)h+\frac{{\sigma }_t}{E_{cm}}\left(l_{eq}-h\right)\right]}{l_{eq}}}={\displaystyle \frac{{\sigma }_t}{E_{cm}}}+{\displaystyle \frac{\mathrm{w}}{l_{eq}}},w_1<w\le w_1+w_{\mathrm{u}} \end{array}\right.$$

(40)

Furthermore, $b_t^{\prime }$ related to the parameters $\phi , {ϵ, f}_{ctm}{, E}_{cm}$ cannot be assumed as fixed values. ${\epsilon }_t^{ck}$ encompasses recoverable strains caused by other factors such as porosity and frictional displacement from cracking and localization. When the effects of these additional factors are less significant, e.g., when the localized deformation becomes larger and the damage effects become less pronounced, the value of $b_t^{\prime }$ and $b_{\delta t}^{\prime }$ tend to become higher. Therefore, we propose an exponential assumption for the evolutions of $b_t^{\prime }$ and $b_{\delta t}^{\prime }$ with two damage evolution parameters, the initial and overall damage evolution rate parameters (${\lambda }_t$ and $k_t$), as shown in Equations (41) and (42). With ${\tilde{n}}_{Gt}$ estimated as 1.0, ${\epsilon }_{ii}^{pl}/{\epsilon }_{ii}^{ck}$ can be assumed to be equal to ${\epsilon }_t^{pl}/{\epsilon }_t^{ck}$, and $b_t^{\prime }=b_{\delta t}^{\prime }$.

$$b_t^{\prime }={\epsilon }_t^{pl}/{\epsilon }_t^{ck}=1-{\lambda }_t{e}^{\left(-k_t{\displaystyle \frac{u_t^{ck}}{u_{tu}^{ck}}}\right)}$$

(41)

$$b_{\delta t}^{\prime }={\epsilon }_{ii}^{pl}/{\epsilon }_{ii}^{ck}=1-{\lambda }_t{e}^{\left(-k_t{\displaystyle \frac{w}{w_u}}\right)}$$

(42)

4.

Coupling the Fictious Crack Model and the Crack Band Theory with the Concrete Damaged Plasticity Model

At the elastic stage, where $w=0$, ${\tilde{\epsilon }}_t^{pl}=0$, the uniaxial tensile behavior follows Equation (43).

$${\sigma }_t=E_{cm}{\epsilon }_t, {0\le \epsilon }_t<0.9{\displaystyle \frac{f_{ctm}}{E_{cm}}} \mathrm{or} {0\le \epsilon }_t<{\displaystyle \frac{f_{ctm}}{E_{cm}}}$$

(43)

When coupling with the CDP model (Equation (6)), the uniaxial tensile inelastic behavior at the meso-scale can be expressed as shown in Equation (44).

$$\begin{gathered} {\sigma }_t\left({\delta }_t^{pl}\right)=\left(1-d_{t,l}\right)E_{cm}{\displaystyle \frac{\left({\delta }_{t,l}-{\delta }_t^{pl}\right)}{h}} \\ {\delta }_{t,l}={\delta }_{t,lii}=w-w_1+\left({\epsilon }_{ctm,l}-{\epsilon }_{ct,el}\right)h={\displaystyle \frac{{\sigma }_t\left({\delta }_t^{pl}\right)}{E_{cm}}}h+w \end{gathered}$$

(44)

$${\delta }_{t,le}={\epsilon }_{ot,l}^{el}h={\displaystyle \frac{{\sigma }_t\left({\delta }_t^{pl}\right)}{E_{cm}}}h$$

(45a)

$${\delta }_t^{ck}={\delta }_{ii}^{ck}={\delta }_{t,l}-{\delta }_{t,le}={\displaystyle \frac{{\delta }_t^{pl}}{b_{\delta t}^{\prime }}}=w, 0<b_{\delta t}^{\prime }<1$$

(45b)

$${\delta }_t^{pl}={\delta }_{ii}^{pl}=b_{\delta t}^{\prime }{\delta }_t^{ck}=b_{\delta t}^{\prime }w, 0<b_{\delta t}^{\prime }<1$$

(45c)

$$d_{t,l}\left(h,{\delta }_t^{pl}\right)=1-{\displaystyle \frac{\frac{{\sigma }_t\left({\delta }_t^{pl}\right)}{E_{cm}}h}{\frac{{\sigma }_t\left({\delta }_t^{pl}\right)}{E_{cm}}h+\left(1-b_{\delta t}^{\prime }\right)\frac{{\delta }_t^{pl}}{b_{\delta t}^{\prime }}}}=d_{t,l}\left(b_{\delta t}^{\prime },h,f_{ctm},E_{cm},G_F\right)$$

(46)

where $0\le w\le w_1+w_{\mathrm{u}}$, ${\tilde{\epsilon }}_t^{pl}>0$, $b_{\delta t}^{\prime }$ can be assumed as shown in Equation (42) when ${\sigma }_t\left(w\right)$ is provided (e.g., Equation (30)) and ${\lambda }_t$ and $k_t$ can be initially estimated to be 0.1~0.4 and a value larger than 0 for NC, respectively.

The uniaxial tensile behavior of the macro-scale can be expressed as shown in Equation (47).

$$\begin{gathered} {\sigma }_t\left({\delta }_t^{pl}\right)=\left(1-d_{t,s}\right)E_{cm}{\displaystyle \frac{\left({\delta }_t-{\delta }_t^{pl}\right)}{l_{eq}}} \\ {\delta }_t={\delta }_{ii}=w-w_1+\left({\epsilon }_{ctm}-{\epsilon }_{ct,e}\right)l_{eq}={\displaystyle \frac{{\sigma }_t\left({\delta }_t^{pl}\right)}{E_{cm}}}{l}_{eq}+w \end{gathered}$$

(47)

$${\delta }_{t,e}={\epsilon }_{ot}^{el}{l}_{eq}={\displaystyle \frac{{\sigma }_t\left({\delta }_t^{pl}\right)}{E_{cm}}}{l}_{eq}$$

(48a)

$${\delta }_t^{ck}={\delta }_{ii}^{ck}={\delta }_t-{\delta }_{t,e}={\displaystyle \frac{{\delta }_t^{pl}}{b_{\delta t}^{\prime }}}=w, 0<b_{\delta t}^{\prime }<1$$

(48b)

$${\delta }_t^{pl}={\delta }_{ii}^{pl}=b_{\delta t}^{\prime }{\delta }_t^{ck}=b_{\delta t}^{\prime }w, 0<b_{\delta t}^{\prime }<1$$

(48c)

$$d_{t,s}\left(l_{eq},{\delta }_t^{pl}\right)=1-{\displaystyle \frac{\frac{{\sigma }_t}{E_{cm}}{l}_{eq}}{\frac{{\sigma }_t\left({\delta }_t^{pl}\right)}{E_{cm}}{l}_{eq}+\left(1-b_{\delta t}^{\prime }\right)\frac{{\delta }_t^{pl}}{b_{\delta t}^{\prime }}}}=d_{t,s}\left(b_{\delta t}^{\prime },l_{eq},f_{ctm},E_{cm},G_F\right)$$

(49)

Theoretically, the evolution of $d_t\left(h,u_t^{pl}\right)$ (Equation (50)) in uniaxial tensile stress states can be expressed by Equation (51a) with four parameters ($h,f_{ctm},E_{cm}$, and ${\tilde{G}}_F$) if the shape of the ${\sigma }_t$ − $u_t^{ck}$ response or the initial value $b_t^{\prime }$ ($b_{t0}^{\prime }$) is estimated, based on the derivation from Equation (18) ($b_t^{\prime }=b_t^{\prime }\left(f_{ctm},E_{cm},{\tilde{G}}_F\right)$).

$$d_t\left(h,u_t^{pl}\right)=1-{\displaystyle \frac{\frac{{\sigma }_t}{E_{cm}}h}{\frac{{\sigma }_t\left(u_t^{pl}\right)}{E_{cm}}h+\left(1-b_t^{\prime }\right)\frac{u_t^{pl}}{b_t^{\prime }}}}=d_t\left(b_t^{\prime },h,f_{ctm},E_{cm},{\tilde{G}}_F\right)$$

(50)

$$d_t\left(h,u_t^{pl}\right)=d_t\left(h,f_{ctm},E_{cm},{\tilde{G}}_F \right)\approx d_t\left(h,f_{cm},E_{cm},n_{Gt},n_t, {\tilde{n}}_{Gt}\right)$$

(51a)

In cases where $f_{ctm}$ is not provided, according to Equations (30), (31), (34), (35) and (38)–(40), $d_t\left(h,u_t^{pl}\right)$ can be related to six coefficients ($h,f_{cm},E_{cm},n_{Gt},n_t$, and ${\tilde{n}}_{Gt}$).

In multiaxial stresses states, $d_t\left(h,{\tilde{u}}_t^{pl}\right)$ should be calculated automatically according to the corresponding ${\tilde{u}}_t^{pl}$, so that the $d_t\left(h,{\tilde{u}}_t^{pl}\right)$ − ${\tilde{u}}_t^{pl}$ relationship and $d_t\left(h,u_t^{pl}\right)$ − $u_t^{pl}$ relationship curves merge, and the $d_{t,l}\left(h,{\delta }_t^{pl}\right)$ − ${\delta }_t^{pl}$ relationship and $d_{t,s}\left(l_{eq},{\delta }_t^{pl}\right)$ − ${\delta }_t^{pl}$ can be computed as the output results. Assuming $b_{\delta t}^{\prime }=b_{\delta t}^{\prime }\left(f_{ctm},E_{cm},{\tilde{G}}_F \right)$, similarly to the derivation from Equation (18), for a concrete specimen/model with a specific $l_{eq}$ and $h$, $d_{t,l}\left(h,{\delta }_t^{pl}\right)$ (CBT, meso-scale) and $d_{t,s}\left(l_{eq},{\delta }_t^{pl}\right)$ (FCM, macro-scale) can be interpreted from Equations (51b) and (51c), respectively.

$$d_{t,l}\left(h,{\delta }_t^{pl}\right)\approx d_{t,l}\left(h,f_{ctm},E_{cm},{\tilde{G}}_F\right)\approx d_{t,l}\left(h,f_{cm},E_{cm},n_{Gt},n_t, {\tilde{n}}_{Gt}\right)$$

(51b)

$$d_{t,s}\left(l_{eq},{\delta }_t^{pl}\right)\approx d_{t,s}\left(l_{eq},f_{ctm},E_{cm},{\tilde{G}}_F\right)\approx d_{t,s}\left(l_{eq},f_{cm},E_{cm},n_{Gt},n_t, {\tilde{n}}_{Gt}\right)$$

(51c)

Equation (51a), Equation (51b), and Equation (51c) indicate that once these parameters (${\tilde{G}}_F,f_{ctm}$, and $E_{cm}$) are determined with an estimation of the shape of the ${\sigma }_t$ − $u_t^{ck}$ response or the initial value $b_t^{\prime }$ ($b_{t0}^{\prime }$), the corresponding damage evolution (e.g., $d_t\left(h,u_t^{pl}\right)$, $d_{t,l}\left(h,{\delta }_t^{pl}\right)$ and $d_{t,s}\left(l_{eq},{\delta }_t^{pl}\right)$) can be obtained, which will be clarified in subsequent numerical tests.

Pre-peak tensile hardening is taken as insignificant ($w_1\approx 0$) for normal concrete under monotonic uniaxial tension, which is a scope-specific assumption. This study assumes $w_1=0$). If test data indicates a discernible pre-peak hardening, a short linear segment can be included in segment 1 ($w_1>0$ in Figure 1), which can be handled by the same CDP–CBT mapping and inverse-calibration procedure.

2.2.4. Uniaxial Compressive Behavior

The compressive stress–strain curve can be divided into three segments which include three states, i.e., elastic state, hardening state, and softening state. Three compositions, namely segment 1 (elastic phase) [15], segment 2 (strain hardening phase where the energy equivalence principle is adopted) [15,16,29], and segment 3 (strain softening phase) [2].

This study excludes the effect of the uniaxial compressive stress–strain relation. For the first and second segments, they follow the relationships given by fib MC2020 [15], using the damage evolution law expressed by Equation (25a) [29].

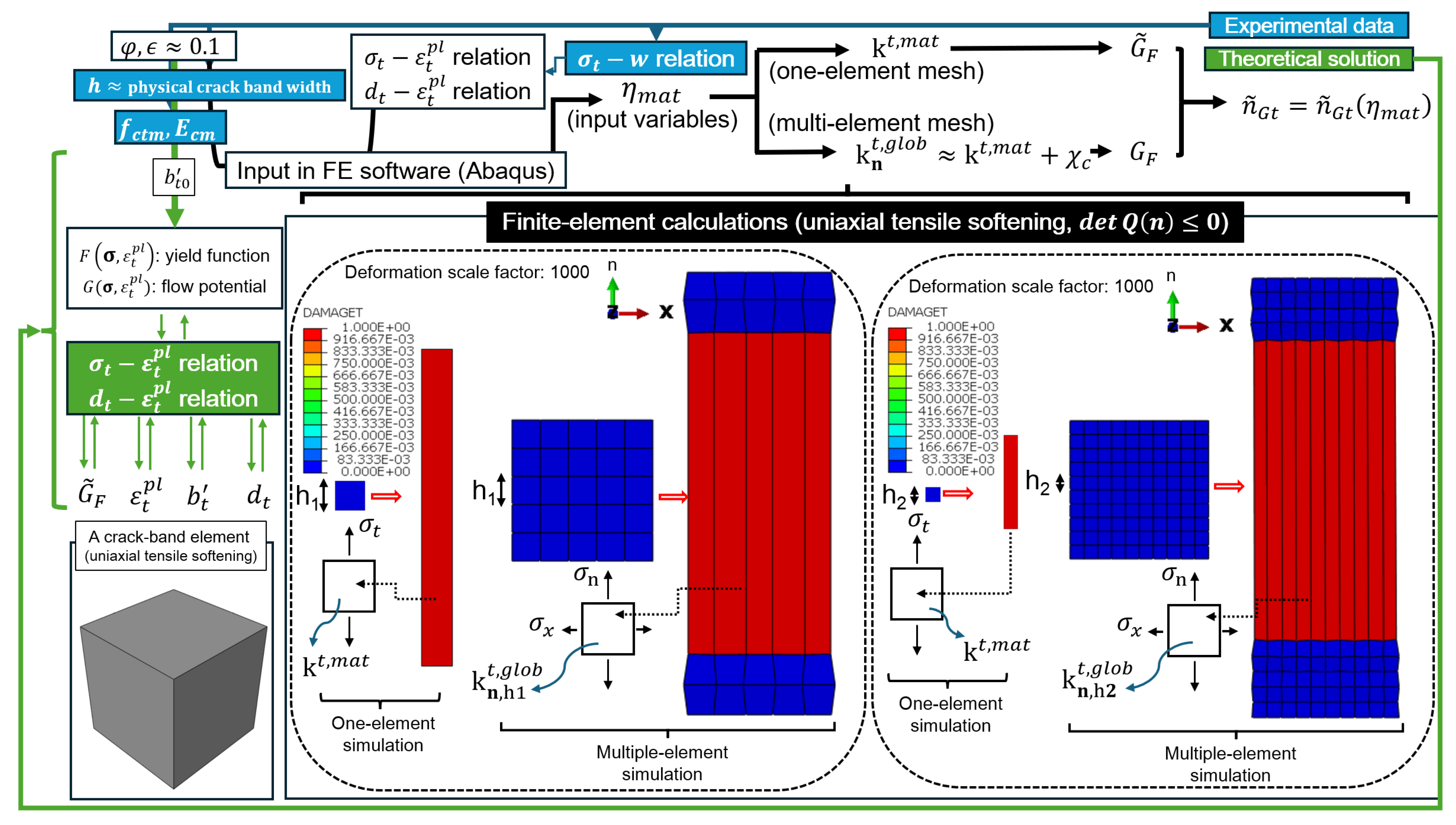
2.3. Accuracy of the Solution by Newton–Raphson Method

The implicit Full-Newton method from ABAQUS/Standard with viscoplastic regularization is adopted in the following numerical modeling, with the geometric nonlinearity and viscoplastic regularization accounted for. C3D8R is selected as the type of element of concrete.

2.3.1. Convergence Criteria for Nonlinear Problems

Newton iterations exhibit quadratic convergence once the iterates enter the local radius of convergence (e.g., [32]). In practice, convergence of increment $\mathrm{t}$ is accepted when the residual and the correction measures satisfy the default solution control tolerances (Equations (52a) and (52b)) with default solution control parameters and the averaged norms (Equations (52c) and (52d)).

Residual criterion:

$${\mathrm{r}}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathsf{\alpha }}\left(\mathrm{t}\right)\le {\mathrm{R}}_{\mathrm{n}}^{\mathsf{\alpha }}{\tilde{\mathrm{q}}}^{\mathsf{\alpha }}\left(\mathrm{t}\right)$$

(52a)

Correction criterion:

$$c_{max}^{\alpha }\left(t\right)\le C_n^{\alpha }∆u_{max}^{\alpha }\left(t\right)$$

(52b)

Averaging of the residual measure over elements:

$${\tilde{q}}^{\alpha }\left(t\right)\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\displaystyle \frac{1}{N_t}}\sum _{i=1}^{N_t}{\overline{q}}^{\alpha }\left({t|}_i\right)$$

(52c)

$${\overline{q}}^{\alpha }\left(t\right)\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\displaystyle \frac{1}{{\sum }_{e=1}^E{\sum }_{n_e=1}^{N_e}{N}_{n_e}^{\alpha }+N_{e_f}^{\alpha }}}\left(\sum _{e=1}^E\sum _{n_e=1}^{N_e}\sum _{i=1}^{N_{n_e}^{\alpha }}\left|q_{i,n_e}^{\alpha }\right|+\sum _{i=1}^{N_{e_f}^{\alpha }}{\left|q\right|}_i^{\alpha ,ef}\right)$$

(52d)

Quadratic convergence may degrade near non-smooth events (yield-surface corners, damage table kinks, contact), in which case the order becomes linear/super-linear.

Viscoplastic regularization can be used to address convergence issues from nonsymmetric Jacobians in non-associated plasticity or Coulomb friction, allowing stress outside the yield surface (Duvaut-Lions, see Equations (53)–(55)). This keeps the tangent stiffness positive with small time steps (Equations (53) and (54)), but it does not always guarantee accuracy.

$${\dot{\epsilon }}_{\mu }^{pl}={\displaystyle \frac{1}{\mu }}\left({\epsilon }^{pl}-{\epsilon }_{\mu }^{pl}\right)$$

(53a)

$${\epsilon }_{\mu }^{pl}\approx {\epsilon }^{pl}-\mu {\displaystyle \frac{∆{\epsilon }_{\mu }^{pl}}{∆t}}$$

(53b)

$${\dot{d}}_{\mu }={\displaystyle \frac{1}{\mu }}\left(d-d_{\mu }\right)$$

(54a)

$$d_{\mu }\approx d-\mu {\displaystyle \frac{∆d_{\mu }}{∆t}}$$

(54b)

$$\sigma =\left(1-d_{\mu }\right)D_0^{el}:\left(\epsilon -{\epsilon }_{\mu }^{pl}\right)$$

(55)

The mesh refinement method is considered in parametric studies as well. As shown in Equation (52d), element discretization affects convergence and finer meshes are expected to improve accuracy, but the nonlinear calculation is complex, especially using models coupled with damaged plasticity.

2.3.2. Local and Global Consistent Tangents

Given the geometric nonlinearity, the stiffness matrix of element (${\mathrm{k}}_e$) and the consistent global Jacobian (${\mathbf{K}}_t$, global algorithmic tangent) at each Newton iteration within increment $\mathrm{t}$ are expressed as shown in Equations (56) and (57).

$${\mathrm{k}}_e=\iiint {\mathrm{B}}^T{\mathrm{C}}_{\mathrm{a}\mathrm{l}\mathrm{g}}\mathrm{B}d{\mathrm{V}}_e+\iiint {\mathrm{G}}^T\tau \mathrm{G}d{\mathrm{V}}_e$$

(56)

$${\mathbf{K}}_t={\displaystyle \frac{\partial \mathbf{R}}{\partial \mathbf{U}}}=\iiint {\mathbf{B}}^T{\mathbf{C}}_{\mathrm{a}\mathrm{l}\mathrm{g}}\mathbf{B}d{\mathbf{V}}_{\mathbf{e}}+\iiint {\mathbf{G}}^T\mathit{\tau }\mathbf{G}d{\mathbf{V}}_{\mathbf{e}}=\sum _{e=1}^E{\mathrm{A}}_e^T{\mathrm{k}}_e{\mathrm{A}}_e$$

(57)

where $\mathbf{R}\left(\mathbf{U}\right)$ is the residual vector.

According to the plastic consistency framework [32,33], at the material level in the CDP model, the element directional tangent under uniaxial tension (${\mathrm{k}}^{t,mat}$) can be written as follows:

$${\mathrm{k}}^{t,mat}=h{\displaystyle \frac{d{\sigma }_t}{d{\epsilon }_t}}=h\left[{\displaystyle \frac{\left(1-d_t\right)d\left({\overline{\sigma }}_t\right)-{\overline{\sigma }}_{t}d\left(d_t\right)}{d{\epsilon }_t}}\right]=h\left[\left(1-d_t\right)H-{\overline{\sigma }}_t{d^{\prime }}_t\left({\epsilon }_t^{pl}\right){\beta }_{Hp}\right]$$

(58)

where $d\left({\overline{\sigma }}_t\right)=Hd{\epsilon }_t$ and $d\left({\epsilon }_t^{pl}\right)={\beta }_{Hp}d{\epsilon }_t$.

Tensile localization is expected to be simulated in the CDP model regardless of the mesh sizes. A negative post-peak slope (${\mathrm{k}}^{t,mat}<0$) is necessary but not sufficient for tensile localization. Let $\mathbf{Q}\left(\mathbf{n}\right)=\mathbf{n}·{\mathbf{C}}_{\mathrm{a}\mathrm{l}\mathrm{g}}·\mathbf{n}$ denote the acoustic tensor, and strong ellipticity requires $\det \mathbf{Q}\left(\mathbf{n}\right)>0$ [32]. The loss of strong ellipticity occurs when $\det \mathbf{Q}\left(\mathbf{n}\right)=0$, which should be linked to the values of ${\displaystyle \frac{{\mathrm{k}}^{t,mat}}{h}}$ (Equation (58)).

At the structural level in the CDP model with expected tensile localizations, as shown in Figure 2, the global directional tangent under uniaxial tension (${\mathrm{k}}_{\mathbf{n}}^{t,glob}$) can be additively split into a material term (${\mathrm{k}}^{t,mat}$) and an assembly term (${\chi }_c$):

$$\begin{gathered} {\mathrm{k}}_{\mathbf{n}}^{t,glob}={\mathbf{e}}^T{\mathbf{K}}_t\mathbf{e}=h{\displaystyle \frac{d{\sigma }_{\mathrm{n}}}{d{\epsilon }_{\mathrm{n}}}}=h\left[\left(1-d\right){\displaystyle \frac{\partial \left({\overline{\sigma }}_{\mathrm{n}}\right)}{\partial {\epsilon }_{\mathrm{n}}}}-{\overline{\sigma }}_{\mathrm{n}}{d}^{\prime }\left({\epsilon }_{\mathrm{n}}^{pl}\right){\displaystyle \frac{\partial {\epsilon }_{\mathrm{n}}^{pl}}{\partial {\epsilon }_{\mathrm{n}}}}\right] \\ {\mathrm{k}}_{\mathbf{n}}^{t,glob}\approx h\left[\left(1-d\right){\displaystyle \frac{\partial \left({\widehat{\overline{\sigma }}}_{max}\right)}{\partial {\widehat{\overline{\epsilon }}}_{max}}}-{\widehat{\overline{\sigma }}}_{max}{d}^{\prime }\left({\tilde{\epsilon }}_t^{pl}\right){\displaystyle \frac{\partial {\tilde{\epsilon }}_t^{pl}}{\partial {\widehat{\overline{\epsilon }}}_{max}}}\right]\approx {\mathrm{k}}^{t,mat}+{\chi }_c \end{gathered}$$

(59)

where ${\sigma }_{\mathrm{n}}$/${\epsilon }_{\mathrm{n}}$/${\epsilon }_{\mathrm{n}}^{pl}$ is the normal stress/total strain/plastic strain in the loading direction, and ${\chi }_c$ represents the additional directional stiffness that originates from the lateral confinement stiffness of the surrounding elements and boundary conditions (Equation (60a)), which is condensed via a Schur complement to the crack-band integration point and then projected onto $\mathbf{n}$ (the loading direction), giving a term with the same units as a modulus.

$${\chi }_c={\displaystyle \frac{1}{{\mathrm{V}}_e}}{{\mathbf{B}}_{\mathbf{n}}}^T{\mathbf{S}}_{\mathit{L}\mathit{L}}{\mathbf{B}}_{\mathbf{n}}$$

(60a)

A practical estimate of ${\chi }_c$ is

$${\chi }_c={\chi }_c\left({\epsilon }_{v,mat}^{pl},{\epsilon }_{v,glob}^{pl},{\mathbf{C}}_{\mathrm{a}\mathrm{l}\mathrm{g}},\mathbf{n},h\right)\approx \left(1-{\displaystyle \frac{{\epsilon }_{v,mat}^{pl}}{{\epsilon }_{v,glob}^{pl}}}\right)\left(\mathbf{n}:{\mathbf{C}}_{\mathrm{a}\mathrm{l}\mathrm{g}}^{\mathrm{i}\mathrm{n}\mathrm{i}}:\mathbf{n}\right)h$$

(60b)

2.3.3. Clarification of Physical and Simulated Crack Band

As shown in Figure 2, under the CBT assumption, the average crack band observed in real tensile fracture is regarded as a material constant. In a finite-element model, the element width is taken to be the crack-band width. By extracting the cracked portion and representing it with a C3D8R element whose width equals the crack-band width, and by comparing a single-element computation with a multi-element specimen using the same mesh, one can obtain the stiffness difference (${\chi }_c$, Equations (59)–(61a)) and the corresponding values of ${\tilde{n}}_{Gt}$ (Equation (39)). These quantities, together with ${\mathrm{k}}^{t,mat}$, are material constants associated with the crack band characteristics.

$$∆{\mathrm{k}}^t={\mathrm{k}}_{\mathbf{n},h}^{t,glob}-{\mathrm{k}}^{t,mat}\approx {\chi }_{c,h}$$

(61a)

On the other hand, if the mesh size applied in FE models differs from the physical crack band where ${\chi }_{c,h}={\chi }_{c,h1}$, the mesh sensitivities of global consistent tangent can be expressed as follows:

$$∆{\mathrm{k}}_{\mathbf{n},h}^{t,glob}={\mathrm{k}}_{\mathbf{n},h2}^{t,glob}-{\mathrm{k}}_{\mathbf{n},h1}^{t,glob}\approx {\chi }_{c,h2}-{\chi }_{c,h1}$$

(61b)

Uniaxial residual tensile strength, ${\dot{d}}_{\mu }$, and ${\dot{\epsilon }}_{\mu }^{pl}$ (i.e., input $\mu$, ${\sigma }_t$ − ${\epsilon }_t^{pl}$ relation, $d_t$ − ${\epsilon }_t^{pl}$ relation, $ϵ$, and $\phi$) should have an effect on ${\mathrm{k}}^{t,mat}$ (Equation (58)) as well as ${\chi }_c$ (Equation (59)). To achieve reduced mesh sensitivity ($∆{\mathrm{k}}_{\mathbf{n},h}^{t,glob}\approx 0$), one needs ${\chi }_{c,h}\approx 0$ (weak lateral coupling), or ${\chi }_{c,h2}\approx {\chi }_{c,h1}$ (balanced confinement between compared meshes). However, ${\chi }_c\ne 0$ is always valid in multiple-element simulations in the default CDP model. According to Equation (60a), finer mesh will lead to larger values of ${\chi }_c$ with the decrease of ${\mathrm{V}}_e$, especially under the assumption of the CBT energy consistency with increase of ${\epsilon }_{\mathrm{n}}$. Different types of elements produce different ${\chi }_c$ levels. C3D8R elements typically produce smaller ${\chi }_c$ (partly due to the effective ${\mathrm{V}}_e$ and the way lateral stiffness is condensed), which motivates the choice of C3D8R for subsequent parametric studies.

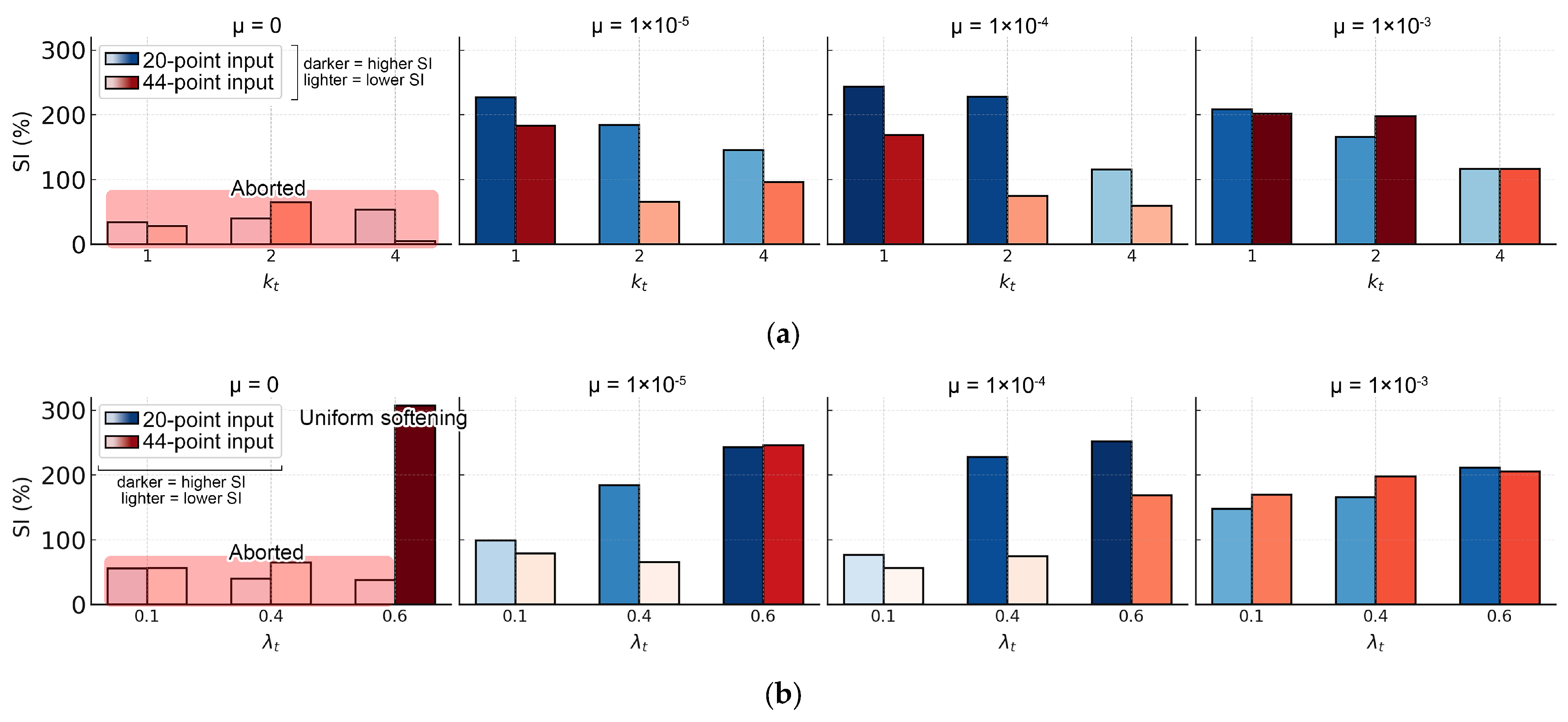
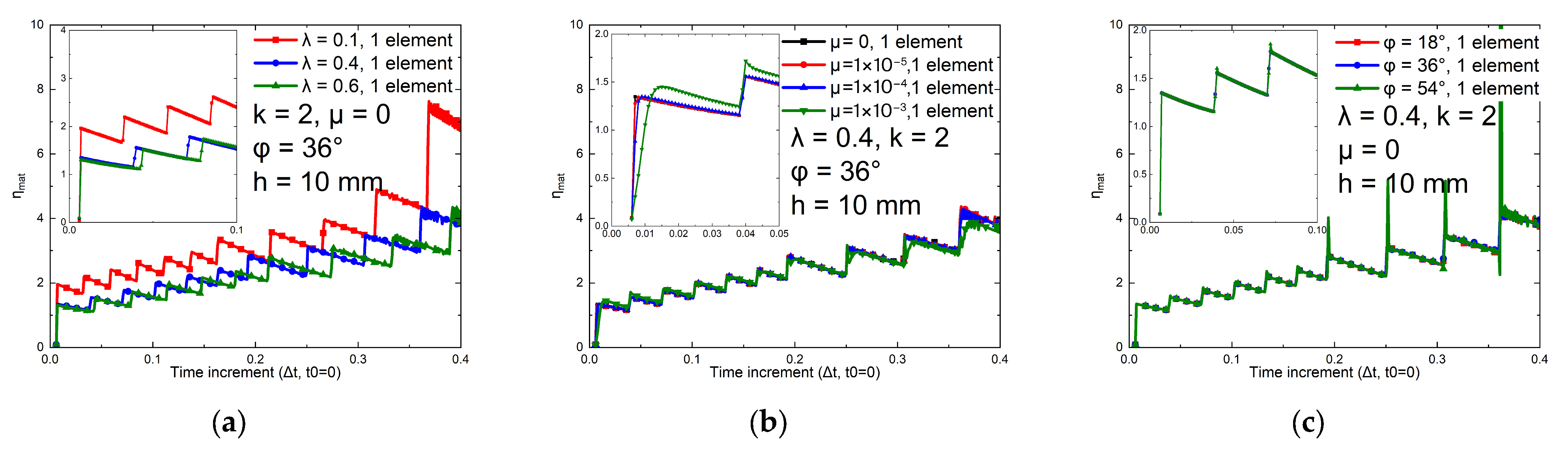
2.3.4. A Sensitivity Indicator Linking Newton–Raphson Solver, CDP Coupling, and CBT Energy Consistency

To analytically link the Newton–Raphson solver with the CDP model and the CBT, ${\mathrm{k}}^{t,mat}$ (${\mathrm{k}}^{t,mat}\approx h\left(1-{\eta }_{mat}\right)\left(1-d_t\right)H$) and ${\mathrm{k}}_{\mathbf{n}}^{t,glob}$ (${\mathrm{k}}_{\mathbf{n}}^{t,glob}\approx h\left(1-{\eta }_{mat}\right)\left(1-d_t\right)H$ $+{\chi }_c$) can be introduced with a material parameter, ${\eta }_{mat}$:

$${\eta }_{mat}\equiv {\displaystyle \frac{{\overline{\sigma }}_t{d\prime }_t\left({\epsilon }_t^{pl}\right){\beta }_{Hp}}{\left(1-d_t\right)H}}$$

(62)

A first-order perturbation of $∆{\mathrm{k}}^t$ with respect to ${\eta }_{mat}$ yields the following:

$${\displaystyle \frac{\partial ∆{\mathrm{k}}^t}{\partial {\eta }_{mat}}}\approx {\displaystyle \frac{\partial {\chi }_{c,h}}{\partial {\eta }_{mat}}}=-{\mathsf{\alpha }}_h\left(1-d_t\right)H$$

(63a)

$$\mathsf{\alpha }={\displaystyle \frac{1}{{\mathrm{V}}_e\left(1-d_t\right)H}}{{\mathbf{B}}_{\mathbf{n}}}^T{\displaystyle \frac{\partial {\mathbf{S}}_{\mathit{L}\mathit{L}}}{\partial {\eta }_{mat}}}{\mathbf{B}}_{\mathbf{n}}$$

(63b)

For practical use, linearization around a reference value ${\eta }_0={\eta }_{mat}\left(t=s_0\right)$ gives the following:

$$∆{\mathrm{k}}^t\left({\eta }_{mat}\right)\approx {\chi }_{c,h}\approx ∆{\mathrm{k}}^t\left({\eta }_0\right)-{\mathsf{\alpha }}_h\left(1-d_t\right)H\left({\eta }_{mat}-{\eta }_0\right)$$

(63c)

Similarly, for the inter-mesh sensitivity:

$${\displaystyle \frac{\partial ∆{\mathrm{k}}_{\mathbf{n},h}^{t,glob}}{\partial {\eta }_{mat}}}\approx {\displaystyle \frac{\partial \left({\chi }_{c,h2}-{\chi }_{c,h1}\right)}{\partial {\eta }_{mat}}}=-\left({\mathsf{\alpha }}_{h2}-{\mathsf{\alpha }}_{h1}\right)\left(1-d_t\right)H$$

(64a)

$$∆{\mathrm{k}}_{\mathbf{n},h}^{t,glob}\left({\eta }_{mat}\right)\approx {\chi }_{c,h2}-{\chi }_{c,h1}\approx -\left({\mathsf{\alpha }}_{h2}-{\mathsf{\alpha }}_{h1}\right)\left(1-d_t\right)H\left({\eta }_{mat}-{\eta }_0\right)$$

(64b)

where ${\mathsf{\alpha }}_{h2}$ and ${\mathsf{\alpha }}_{h1}$ denote the confinement-geometry coefficients corresponding to different mesh sizes, and ${\eta }_0={\eta }_{mat}\left(t=s_0\right)$ is taken as the baseline value, i.e., ${\eta }_{mat}$ at the first increment of the softening stage.

As softening proceeds, the crack band exhausts the lateral confinement paths so that ${\mathsf{\alpha }}_h$ and $\left(1-d_t\right)H$ decrease. Hence, in the early softening regime ($H>0$ and $\mathsf{\alpha }>0$), increasing ${\eta }_{mat}$ will decrease $∆{\mathrm{k}}^t$, while the sensitivity of ${\eta }_{mat}$ to $∆{\mathrm{k}}^t$ is reduced as softening proceeds.

Therefore, in a general assumption, $∆{\mathrm{k}}^t$, $∆{\mathrm{k}}_{\mathbf{n},h}^{t,glob}$, ${\displaystyle \frac{{\tilde{G}}_F}{G_F}}={\tilde{n}}_{Gt}={\tilde{n}}_{Gt}\left({\eta }_{mat}\right)$, and the loss of strong ellipticity ($\det \mathbf{Q}\left(\mathbf{n}\right)\le 0$, i.e., presence of expected tensile localization) can be linked to ${\eta }_{mat}$ (Figure 2), particularly at the initial stage of softening.

Note that Abaqus does not disclose the exact implementation of calculations of local and global consistent tangents, meaning that the instantaneous ${\eta }_{mat}$ cannot be exported directly. Based on these, a computable indicator of ${\eta }_{mat}$ is proposed as expressed in Equation (65). It is expected that ${\chi }_{c,h}$, $∆{\mathrm{k}}^t$, and $∆{\mathrm{k}}_{\mathbf{n},h}^{t,glob}$ are approximately equal to zero (${\chi }_{c,h}\approx 0$ so that ${\chi }_{c,A}\approx {\chi }_{c,B}$) to achieve numerical results of mesh-insensitive structural responses when ${\eta }_{mat}^{sec}\ge {\eta }_{min}^{sec}$ at the initial stage of tensile softening.

$${\eta }_{mat}^{sec}\approx {\displaystyle \frac{{\overline{\sigma }}_t\frac{\mathsf{\Delta }{d}_t}{\mathsf{\Delta }{\epsilon }_t^{pl}}\frac{\mathsf{\Delta }{\epsilon }_t^{pl}}{\mathsf{\Delta }{\epsilon }_t}}{\left(1-d_t\right)\frac{\mathsf{\Delta }{\overline{\sigma }}_t}{\mathsf{\Delta }{\epsilon }_t}}}\ge {\eta }_{min}^{sec}$$

(65)

The coupling effect of the CDP model and the assumption of CBT using the Newton–Raphson solver on the numerical results are complex. Hence, how the input ${\sigma }_t-{\epsilon }_t^{pl}$ relation, $d_t-{\epsilon }_t^{pl}$ relation, $\mu$, $\phi$, and the mesh size affect $∆{\mathrm{k}}^t\left({\eta }_{mat}\right)$, $∆{\mathrm{k}}_{\mathbf{n},h}^{t,glob}\left({\eta }_{mat}\right)$, ${\tilde{n}}_{Gt}\left({\eta }_{mat}\right)$, and the loss of strong ellipticity should be evaluated through a series of numerical tests (here C3D8R is shown as an example).

3. Verification of the Proposed Model

This section aims to provide verifications of the proposed uniaxial tensile constitutive laws at the macro-scale before the numerical investigation at the element and structural scales. The stress–crack opening relation follows the exponential curve given in fib MC2020 based on the FCM (Equation (30)) [5,15,30]. The total strain is calculated according to Equation (38a), and the corresponding total deformation is equal to the total strain times $l_{eq}$. In this way, three methods for the derivation of elastic stiffness damage are compared.

3.1. Verification of the Proposed Damaged Constitutive Law at the Macro-Scale

3.1.1. Analytical Expression

Only experimental verifications for normal concrete (NC) and steel-fiber reinforced concrete (SFRC) of direct-tensile tests of dog-bone (DB), prismatic (PR), or cylinder (CY) specimens are considered. The summary of the test details is shown in

Table 1. Summary of experimental tests on uniaxial tension.

Tests	Specimen Dimensions				Mechanical Properties
	Type	Depth (d)	Height/d	Gauge Length	Type	${\mathit{f}}_{\mathit{c}\mathit{t}\mathit{m}}$	${\mathit{G}}_{\mathit{F}}$35	${\mathit{n}}_{\mathit{G}\mathit{t}}$35	${\mathit{\lambda }}_{\mathit{t}}$41	${\mathit{k}}_{\mathit{t}}$41
Van Vliet (2000) [34]	DB	50, 100, 200	0.725	30, 60, 120	NC	2.75	0.090	0.650	/	/
Chen (2017) [35]	CY	73	2	135	NC	2.91	0.063	0.450	0.400	2.00
Yankelevsky (1987) [36]	PR	50	5	35	NC	3.45	0.117	0.800	0.250	1.00
Wang (2023) [18]	CY	75	2.67	20	SFRC	6.80	11.6	60.0	0.400	20.0
						7.07	12.9	65.0	0.400	30.0
						7.20	13.0	65.0	0.400	25.0

, and the corresponding expressions of the analytical results for the tests are presented in Figure 3 and Figure 4. In this part, the characteristic lengths are equal to the gauge length.

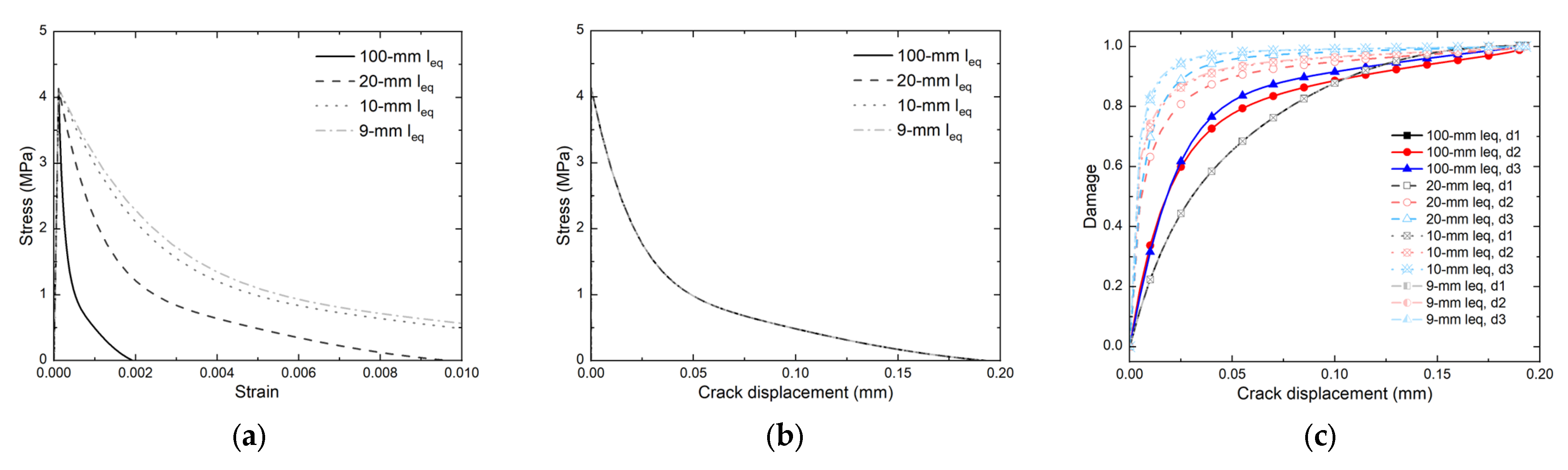
3.1.2. Estimation of Fracture Energy ($G_F$)

Figure 3 demonstrates that the calibration of the constitutive law (Equation (38a)) with $n_{Gt}$ (Equation (35)) set consistently as 0.65 aligns well with monotonic tensile test data, regardless of different specimen sizes. The similar patterns observed in cyclic tensile tests, as depicted in Figure 3 and Figure 4, further validate the importance of incorporating $n_{Gt}$ to refine the estimation of $G_F$. For NC, as shown in Figure 3 and Figure 4a,b, $n_{Gt}$ ranges from 0.450 to 0.800, which tends to decrease from 1.0 for low-strength concrete. For SFRC, as shown in Figure 4c, $n_{Gt}$ ranges from 60 to 65. These results necessitate the coefficient $n_{Gt}$ in order to modify the estimation of the ${\sigma }_t\left(w\right)-w$ relation when $G_F$ is purely dependent on $f_{cm}$ or $f_{ctm}$ according to fib MC2020 (Equations (34) and (35)).

Figure 3. Comparisons between experimental results and analytical implementation: size effect (monotonic tensile loading) [34]: (a) stress–strain relation; (b) force–deformation relation.

Figure 3. Comparisons between experimental results and analytical implementation: size effect (monotonic tensile loading) [34]: (a) stress–strain relation; (b) force–deformation relation.

Figure 4. Comparisons between experimental results and analytical implementation (cyclic tensile loading): (a) stress–deformation relation of NC [36]; (b) stress–strain relation of NC [35]; (c) stress–strain relation of SFRC [18].

Figure 4. Comparisons between experimental results and analytical implementation (cyclic tensile loading): (a) stress–deformation relation of NC [36]; (b) stress–strain relation of NC [35]; (c) stress–strain relation of SFRC [18].

It is clarified by Equation (39) that $G_F={\tilde{G}}_F/{\tilde{n}}_{Gt}$, in which ${\tilde{G}}_F$ is influenced by the parameters $h,{ϵ,f}_{ctm},E_{cm}$, and $\phi$ according to Equation (17) and ${\tilde{n}}_{Gt}$ should be a material parameter relying on the corresponding fracture mechanisms. Therefore, if $G_F$ is computed according to Equation (35) ($G_F\approx n_{Gt}0.085{\mathrm{e}}^{\left(0.0833f_{ctm}+0.2583\right)}$), $n_{Gt}$ should be related to at least four parameters, $h,$ $E_{cm}$, $ϵ$, and $\phi$.

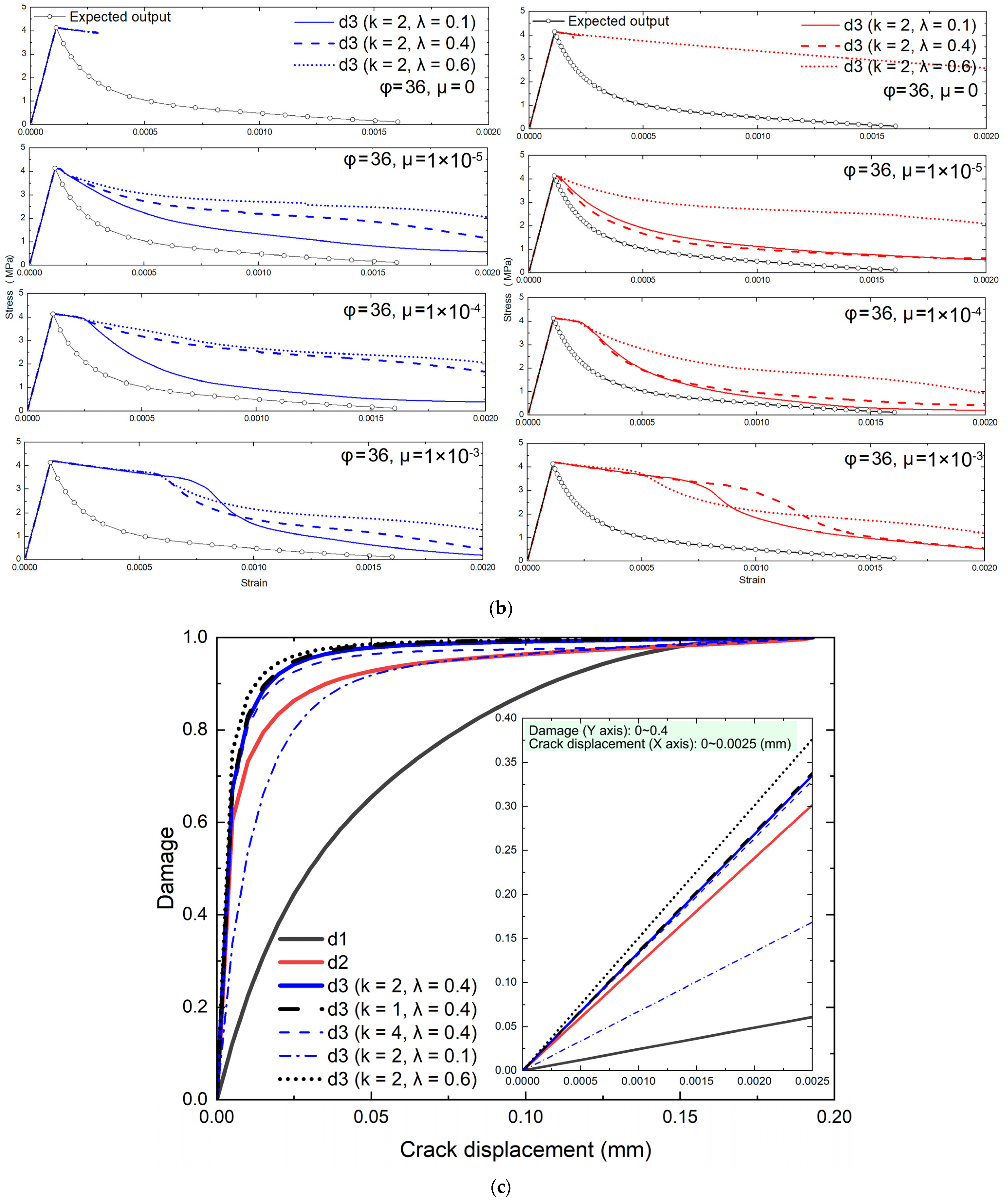
3.1.3. Estimation of Tensile Damage Evolution ($d_{t,s}$)

From a material perspective, the unloading slope better captures meso-scale damage evolution, while for engineering assessment of residual stiffness and capacity, the reloading stiffness is more suitable for calibration herein (Figure 4). Overall, $d_t=d_1$ (underestimation) and $d_t=d_2$ (overestimation) were not proposed for describing the concrete mechanical behavior at the macro-scale. $d_t=d_3\approx d_{t,s}$ following Equation (49) can give a more precise reflection of different concrete types using the CDP model by adjusting the estimation of ${\lambda }_t$ and $k_t$ from Equations (41) and (42).

Different types of concrete in Table 1, both NC and SFRC, have a similar estimation of ${\lambda }_t$ (0.4). Taking examples from Chen et al. (2017) (Figure 4b) [35], it can be found that $b_{\delta t}^{\prime }$ (Equations (42) and (49)) at the initial state of strain softening is roughly equal to 0.6, with ${\lambda }_t$ estimated as 0.4. At the end of the strain softening loading, $b_{\delta t}^{\prime }$ (Equations (42) and (49)) can range from 0.9 to 0.99, depending on the different types of concrete in the examples shown ($k_t=2.00$ for NC, shown in Figure 4b and $k_t$ ranges from 20 to 30 for SFRC, shown in Figure 4c).

According to the results shown in Table 1, the subsequent numerical modeling for non-steel-fiber-reinforced high-strength concrete (HSC) adopts 1.00, 1.00, 0.40, and 2.00 as the initial estimates of ${\tilde{n}}_{Gt}$, $n_{Gt}$, ${\lambda }_t$, and $k_t$ respectively. Considering that the values of $n_{Gt}$ and $k_t$ for SFRC are well beyond the typical ranges for NC and are strongly affected by fiber characteristics, SFRC is excluded from the numerical parameter analysis herein.

3.2. Verification of the Proposed Damaged Constitutive Law at Element and Structural Scales

Utilizing the CDP model in Abaqus, parametric analyses were performed on a type of concrete from a joint test [4] as an example to assess the sensitivities of the proposed constitutive law, using three different derivations of the tensile damage evolution law ($d_1$, $d_2$, and $d_3$), along with various mesh assignments, viscosity parameters, and dilation angles. A sensitivity index is proposed as expressed in Equation (66) to quantify the difference between the numerical calculations (${\sigma }_{inp}$) and the expected output results (${\sigma }_{opd}$), using the same input uniaxial tensile stress–strain relationship. Within this framework, a robust calibration platform is established for the uniaxial tensile response of concrete using the CDP model and the Newton–Raphson method in Abaqus.

$$SI={\displaystyle \frac{\int \left|{\sigma }_{inp}-{\sigma }_{opd}\right|d{\epsilon }_t}{\int {\sigma }_{inp}d{\epsilon }_t}}$$

(66)

3.2.1. Numerical Model Details

A 100 mm cube model is simulated with frictionless boundary conditions, as shown in Figure 5, so that the effect of boundary conditions can be removed for simulating the true softening phase in uniaxial tensile behavior with homogeneous and isotropic elements in the FE model. The experimental values of the mechanical properties of the concrete ($f_{cm}=111.18 \mathrm{M}\mathrm{P}\mathrm{a}$, $f_{ctm}=4.13 \mathrm{M}\mathrm{P}\mathrm{a}$, $E_{cm}=\mathrm{37,004} \mathrm{M}\mathrm{P}\mathrm{a}$, $E_{c1}=\mathrm{34,221} \mathrm{M}\mathrm{P}\mathrm{a}$, Poisson’s ratio $=$ 0.219) [4] are used directly to describe the stress–strain relationships in the above equations where needed (Figure 6), where the characteristic length ($l_{eq}$) is equal to the mesh size ($h$), and the input relation curves are presented by 20 continuous points (i.e., 20-point input).

3.2.2. Result Overview

An overview of the numerical output results of uniaxial tension CDP modeling is shown in Figure 7 and Figure 8.

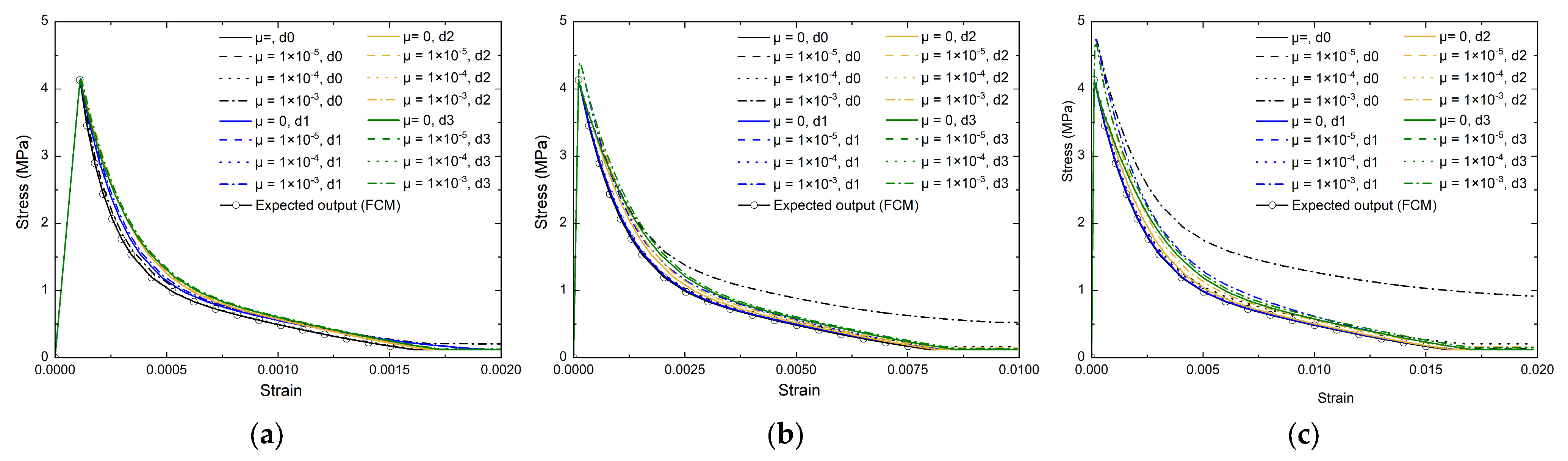
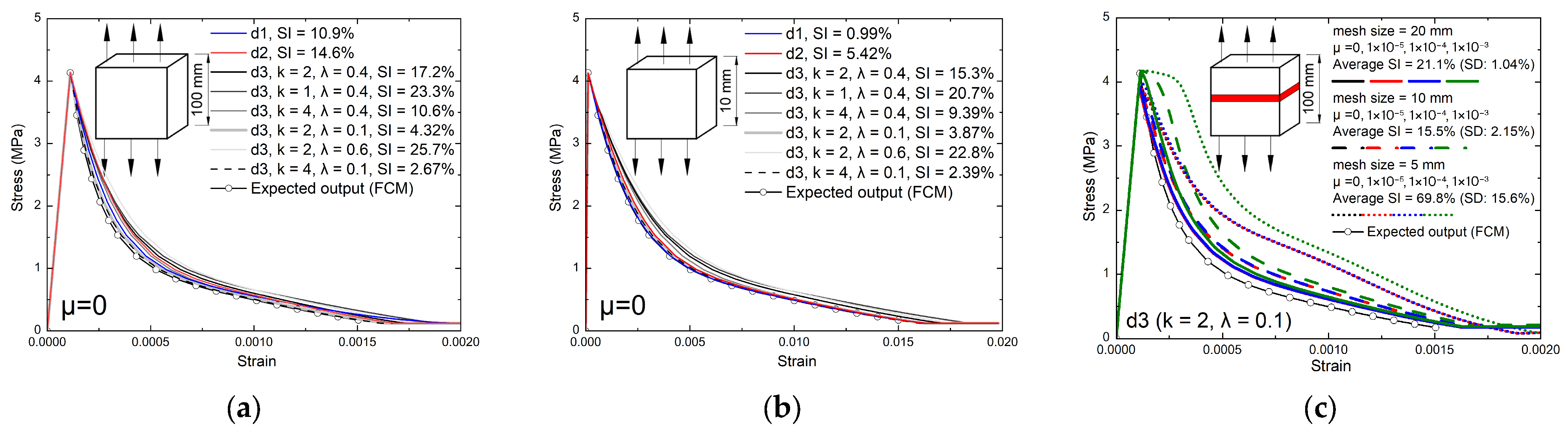
3.2.3. Numerical Results for a Single Element at Element Scale

As for the one-element simulation shown in Figure 7, Figure 8 and Figure 9a, the stress state of cube model is purely uniaxial tension, as expected.

The effects of viscoplastic regularization and the definition of damage variables on the numerical results for one single element are minor (Figure 8 and

Table 2. Summary of $SI$ of one-element simulations with different tensile damage variables, viscosity parameters, and mesh sizes (unit: %).

${\mathit{l}}_{\mathit{e}\mathit{q}}=\mathit{h}$ = 100 mm					${\mathit{l}}_{\mathit{e}\mathit{q}}=\mathit{h}$ = 100/5 mm					${\mathit{l}}_{\mathit{e}\mathit{q}}=\mathit{h}$ = 100/10 mm
$\mathit{\mu }$	0	1 × 10−5	1 × 10−4	1 × 10−3	$\mathit{\mu }$	0	1 × 10−5	1 × 10−4	1 × 10−3	$\mathit{\mu }$	0	1 × 10−5	1 × 10−4	1 × 10−3
${d_t=d}_0$	0.00	0.11	1.06	10.5	${d_t=d}_0$	0.00	0.53	5.24	50.8	${d_t=d}_0$	0.00	1.05	10.3	99.4
${d_t=d}_1$	10.9	10.9	11.2	13.7	${d_t=d}_1$	2.09	2.21	3.32	14.5	${d_t=d}_1$	0.99	1.23	3.41	25.7
$d_t=d_2$	14.6	14.6	14.9	17.2	$d_t=d_2$	7.69	7.76	8.38	14.7	$d_t=d_2$	5.42	5.53	6.51	16.4
$d_t=d_3$	17.2	17.2	17.4	19.6	$d_t=d_3$	16.3	16.3	16.8	21.7	$d_t=d_3$	15.3	15.3	16.0	23.12

) under monolithic (Figure 7a–c) and cyclic loading (Figure 7d–f). However, no matter how the tensile damage is defined based on different damage evolution laws, the output residual strength corresponding to the same vertical strain (i.e., displacement divided by $l_{eq}$) tends to be overestimated in comparison with the input uniaxial tensile stress–strain relationship ($\mathrm{S}I\ge 10.9\%$), unless the tensile damage is not defined with the viscosity parameter ($\mu$) set to be zero ($\mathrm{S}I=0$). Different tensile-damage variables lead to observable differences in the output results of the uniaxial tensile stress–strain relationship.

For further investigation into one-element simulation, several cube models with $l_{eq}=h$ = 100/5 mm and $l_{eq}=h$ = 100/10 mm are established using the same method as that for models shown in Figure 5a. As shown in Figure 9 and Table 2, when $l_{eq}=h$ decreases and $0\le \mu \le 0.0001$, the convergence of the numerical results for a single element generally improves and $SI$ generally decreases when tensile damage is defined. As $\mu$ increases, the residual strength is increasingly overestimated, with $\mathrm{S}I$ increasing, particularly for simulations without tensile damage defined. The calculated overestimation caused by the effect of viscoplastic regularization can be reduced when tensile-damage variables are used as input, especially for fine-mesh simulations.

Overall, ${\mathrm{k}}^{t,mat}$ (Equation (58) and Figure 2) is validated to be affected by mesh size ($h$), the choice of tensile damage evolution, and the value of the viscosity parameter ($\mu$). Generally, a smaller mesh size (e.g., $h=10$ mm), a lower initial tensile-damage evolution rate (e.g., ${d_t=d}_1$), or a smaller value of $\mu$ ($\mu \to 0$) is beneficial to avoid overestimation of ${\mathrm{k}}^{t,mat}$ relative to the input stress–displacement relationships. These results further validate the assumption presented in Equation (51a) and Figure 2 that a specific tensile-damage evolution is the necessary and sufficient condition for a specific value of ${\tilde{G}}_F$, given an estimate of the shape of the ${\sigma }_t$ − $u_t^{ck}$ response under the CDP framework in FE simulations.

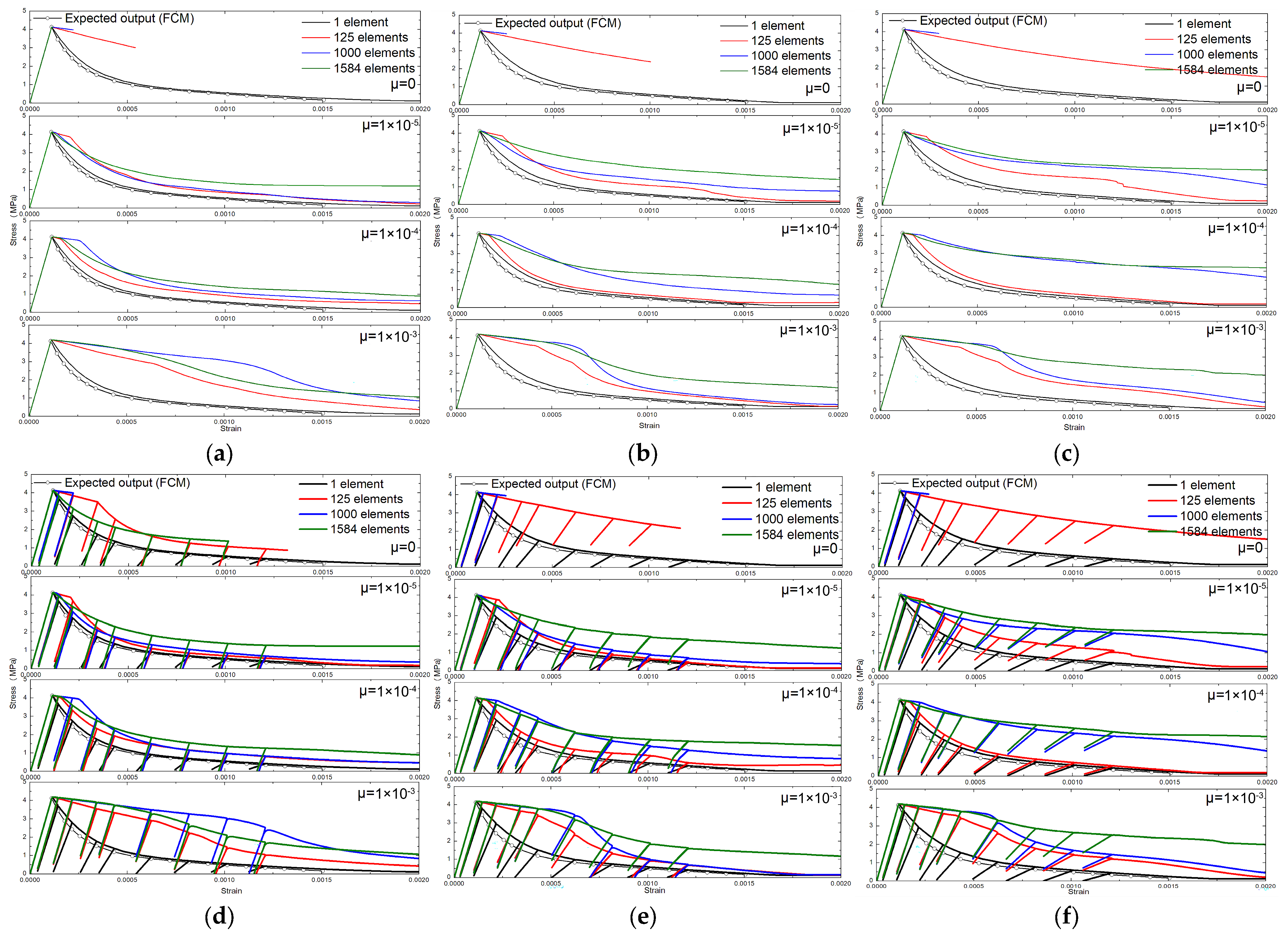
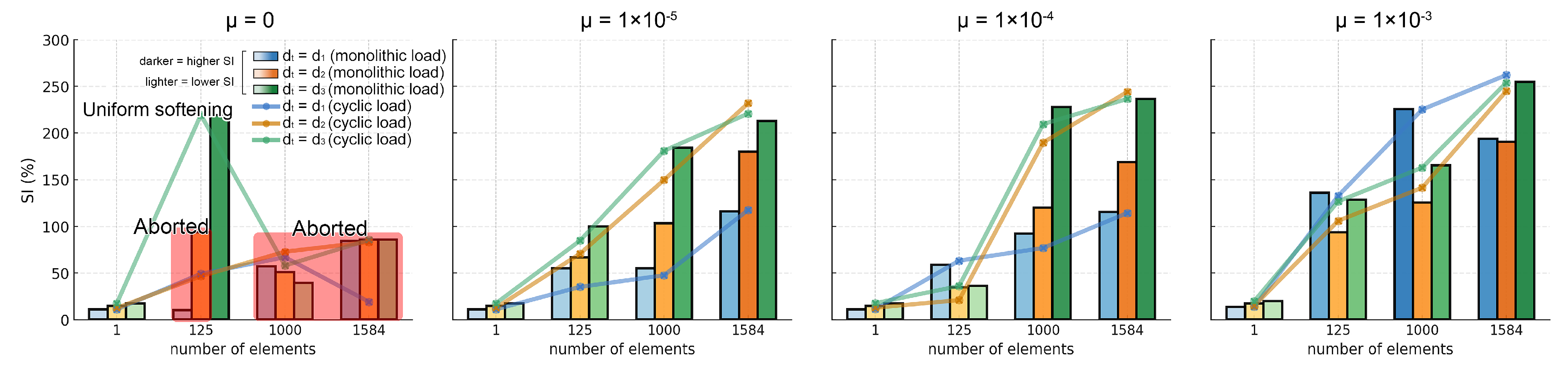
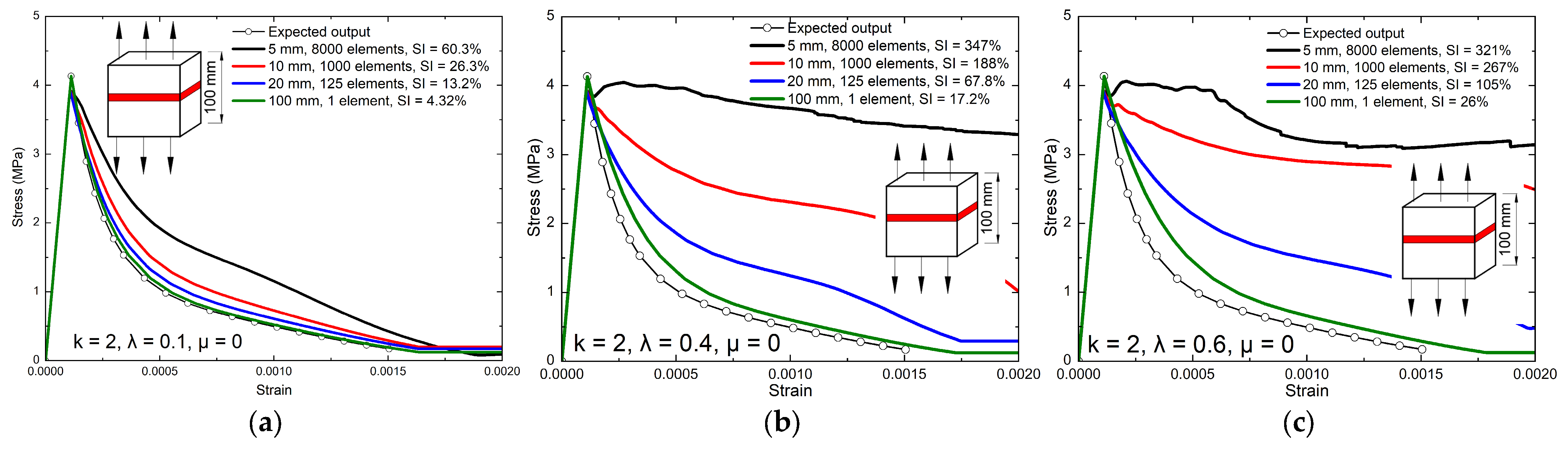
3.2.4. Numerical Results for Multiple-Element Models at the Structural Scale

In structural simulations, purely uniaxial tension rarely exists where tensile cracks localize. Element-scale behavior should be modeled using multi-element cube models. However, as shown in Figure 7, these models fail to capture either uniform nor localized deformation accurately, regardless of mesh type, damage variable definition, or viscosity values, under both monotonic and cyclic loading. This discrepancy in $SI$ is summarized in Figure 8, which is mainly due to four sources of numerical instability.

1.

Loss of Strong Ellipticity

In FE simulations, localization is present only after the loss of strong ellipticity occurs and $\det \mathbf{Q}\left(\mathbf{n}\right)\le 0$, whereas uniform deformation can be simulated only when $\det \mathbf{Q}\left(\mathbf{n}\right)>0$ [37]. As shown in Figure 7 and Figure 8, when $\mu =0$, uniform tensile deformation in the softening stage cannot be simulated in multi-element models, and calculations are typically aborted just after the peak strength, indicating $\det \mathbf{Q}\left(\mathbf{n}\right)>0$, except for the case shown in Figure 7c,f (i.e., 125-element models with $d_t=d_3$). In contrast, when $\mu >0$, localization is observed in the softening stage (Figure 7, Figure 8 and Figure 10), indicating $\det \mathbf{Q}\left(\mathbf{n}\right)\le 0$ and the occurrence of the loss of strong ellipticity.

When $0.00001\le \mu \le 0.0001$, a slight increase in ${\mathrm{k}}^{t,mat}/h$ is observed, and the loss of strong ellipticity as well as the consequent tensile localization can be more readily triggered immediately after the peak strength. As $\mu$ increases to 0.001 and a larger difference in ${\mathrm{k}}^{t,mat}/h$ appears, the loss of strong ellipticity and the consequent tensile localization occur at a higher strain level. In other words, $\mu =0$ fails to capture tensile localization, whereas $\mu >0.0001$ may overestimate the response by delaying the onset of softening localization and by increasing the values of ${\mathrm{k}}^{t,mat}/h$ and ${\mathrm{k}}^{t,glob}/h$ (Figure 2), which is reflected in the $SI$ results shown in Figure 8.

This pattern indicates that the loss of strong ellipticity occurs ($\det \mathbf{Q}\left(\mathbf{n}\right)\le 0$) only when ${\mathrm{k}}^{t,mat}$ lies within a certain negative range (${\mathrm{k}}^{min}{\le \mathrm{k}}^{t,mat}\le {\mathrm{k}}^{max}$), which is affected by different choices of tensile damage evolution, different mesh sizes ($h$), and different values of $\mu$ (Figure 7, Figure 8 and Figure 9 and Table 2). When ${\mathrm{k}}^{t,mat}\le {\mathrm{k}}^{min}<0$ ($\det \mathbf{Q}\left(\mathbf{n}\right)\ll 0$), calculations are aborted. When ${0>\mathrm{k}}^{t,mat}\ge {\mathrm{k}}^{max}$ ($\det \mathbf{Q}\left(\mathbf{n}\right)>0$), uniform tensile softening deformation can be simulated. After the loss of strong ellipticity occurs ($\det \mathbf{Q}\left(\mathbf{n}\right)\le 0$), cracked elements propagate randomly due to numerical instability, being similar to the crack patterns observed in heterogeneous concrete specimens. These cracked elements experience multiaxial stresses, unlike the purely uniaxial tension in single-element models, which leads to uneven shear stress and tensile damage among elements (Figure 11 and Figure 12).

Under cyclic loading involving both tensile ($d_t$) and compressive ($d_c$) damage, local stress redistribution occurs, leading to inconsistencies between cyclic and monotonic results regardless of the damage law used (Figure 7 and Figure 8), which is influenced by the multiaxial stress weight factor ($r\left(\widehat{\sigma }\right)$). As ${\mathrm{k}}^{t,glob}\left({\mathrm{k}}^{t,mat},{\chi }_c\right)$ plays a key role in the development of tensile softening localization, mesh sensitivity induced by ${\chi }_c$ can also be observed (Figure 7 and Figure 8).

2.

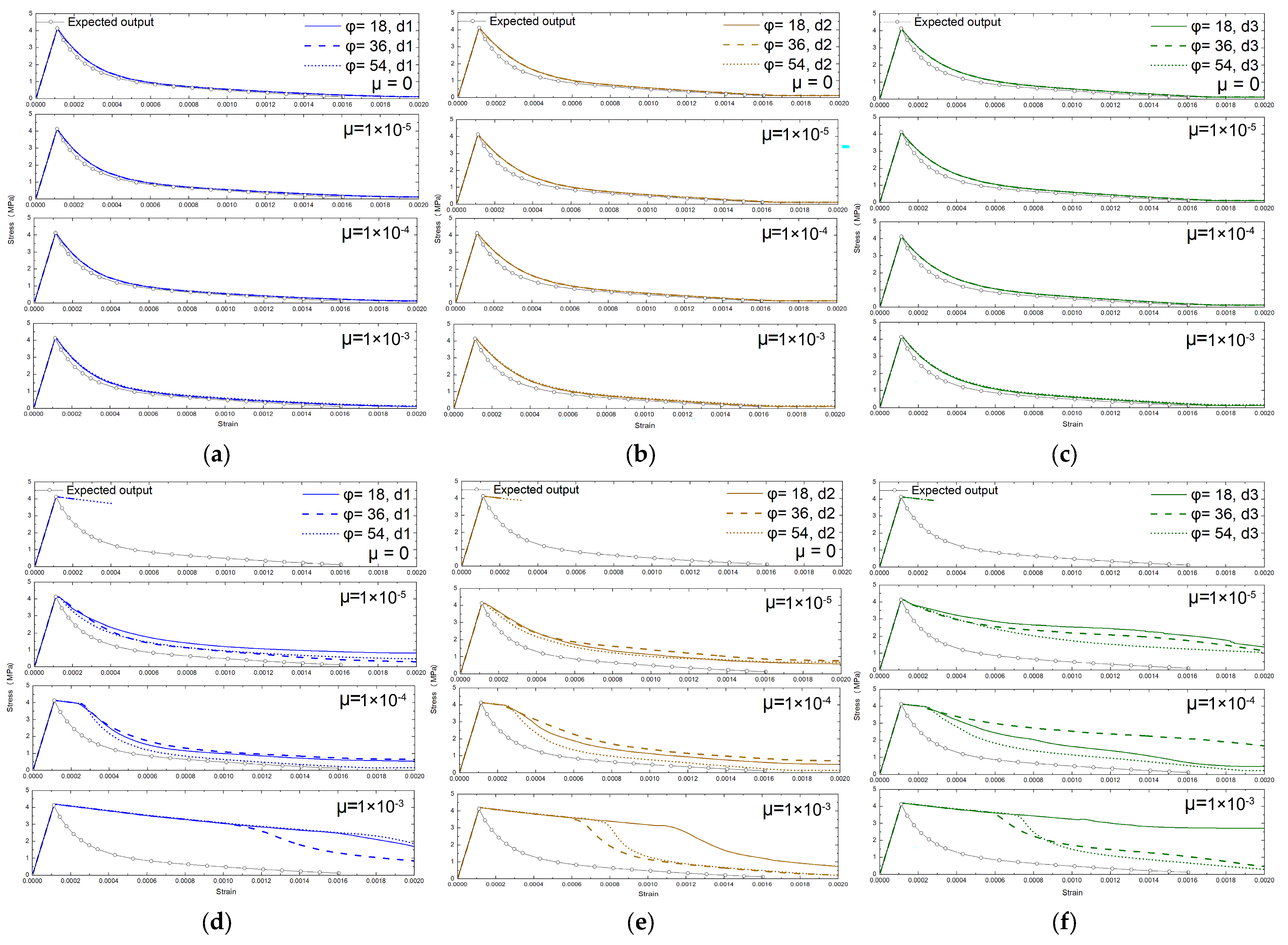
Effect of Dilation Angle

As shown in Figure 13a–c and

Table 3. Summary of $SI$ of one-element simulations with different tensile damage variables, viscosity parameters, and $\phi$ (unit: %).

${\mathit{d}}_1$ (1 Element)					${\mathit{d}}_2$ (1 Element)					${\mathit{d}}_3$ (1 Element)
$\mathit{\mu }$	0	1 × 10−5	1 × 10−4	1 × 10−3	$\mathit{\mu }$	0	1 × 10−5	1 × 10−4	1 × 10−3	$\mathit{\mu }$	0	1 × 10−5	1 × 10−4	1 × 10−3
$\phi =18$	10.9	10.9	11.1	13.2	$\phi =18$	14.6	14.6	14.8	16.7	$\phi =18$	17.2	17.2	17.4	19.1
$\phi =36$	10.9	10.9	11.2	13.7	$\phi =36$	14.6	14.6	14.9	17.2	$\phi =36$	17.2	17.2	17.4	19.6
$\phi =54$	10.9	10.9	11.6	17.9	$\phi =54$	14.6	14.7	15.3	22.0	$\phi =54$	17.2	17.2	17.9	24.2

, varying $\phi$ ($18°$, $36°$ and $54°$) has little impact on the uniaxial tensile response for single-element models across values of $\mu$ from 0 to 0.001. Even with a 1000-element mesh (Figure 13d–f and

Table 4. Summary of $SI$ of 1000-element simulations with different tensile damage variables, viscosity parameters, and $\phi$ (unit: %).

${\mathit{d}}_1$ (1000 Elements)					${\mathit{d}}_2$ (1000 Elements)					${\mathit{d}}_3$ (1000 Elements)
$\mathit{\mu }$	0	1 × 10−5	1 × 10−4	1 × 10−3	$\mathit{\mu }$	0	1 × 10−5	1 × 10−4	1 × 10−3	$\mathit{\mu }$	0	1 × 10−5	1 × 10−4	1 × 10−3
$\phi =18$	76.0	93.2	78.7	273	$\phi =18$	67.3	82.8	92.8	227	$\phi =18$	69.5	217.1	129	300
$\phi =36$	57.2	55.1	92.2	226	$\phi =36$	50.7	103.2	120	126	$\phi =36$	39.7	184.3	228	165
$\phi =54$	12.3	59.9	40.5	280	$\phi =54$	34.9	74.6	49.5	142	$\phi =54$	46.4	147.8	85.7	150

), the effect of $\phi$ remains insignificant, especially at the viscosity parameter equal to 1 × 10⁻⁵, due to minimal lateral and shear plastic strains under localized tension.

Consequently, it can be deduced that the dilation angle (with parameters including $\phi , ϵ$, and ${\sigma }_{t0}$) is not a critical factor when calibrating the tensile response in the CDP model for a given estimated shape of uniaxial tensile stress–strain curve, $G_F$ and ${\tilde{n}}_{Gt}$ (Equation (39)), although increasing its values has a slightly positive effect on increasing ${\mathrm{k}}^{t,mat}$ and ${\chi }_c$ (i.e., ${\mathrm{k}}^{t,glob}\left({\mathrm{k}}^{t,mat},{\chi }_c\right)$) (Figure 2), especially when $\mu >0$.

3.

Effect of Damage Evolution

On the other hand, from Figure 7 and Figure 8, it can be generalized that the results of models meshed with multiple elements differ significantly for different choices of tensile damage evolution, particularly for finer meshes (i.e., 1000-element and 1584-element simulations). This indicates that the damage evolution variables, mesh sizes ($h$), and viscosity parameter ($\mu$) have a greater influence on ${\mathrm{k}}^{t,glob}\left({\mathrm{k}}^{t,mat},{\chi }_c\right)$ than on ${\mathrm{k}}^{t,mat}$ in the CDP model (Figure 2).

Further numerical results of models meshed with 1000 elements using $d_3$ with different parameters are shown in Figure 14 and Figure 15. The $SI$ values (Figure 15) are lower when the initial damage variables are smaller ($\lambda =0.1$ and $k=2$) or when the overall damage evolution rate is lower (${\lambda }_t=0.4$ and $k_t=4$). ${\mathrm{k}}^{t,glob}\left({\mathrm{k}}^{t,mat},{\chi }_c\right)$ are validated to be significantly sensitive to tensile damage evolution rates, particularly at the initial softening stage.

4.

Effect of the Density of Data Points

The effect of the density of data points in the uniaxial tensile stress–strain relationship is also investigated, as shown in Figure 14 and Figure 15. For numerical tests with ${\lambda }_t=0.6$, $k_t=2$, and $\mu =0$, uniform tensile deformation in the softening stage can be simulated when denser input data points are used. Denser input data points depict a sharper initial tensile-damage evolution, indicating an increase in ${\mathrm{k}}^{t,mat}$ at the onset of tensile softening. However, the $SI$ values are generally reduced as the input-point density increases, which can be attributed to improved representation of the localized path with reduced randomness.

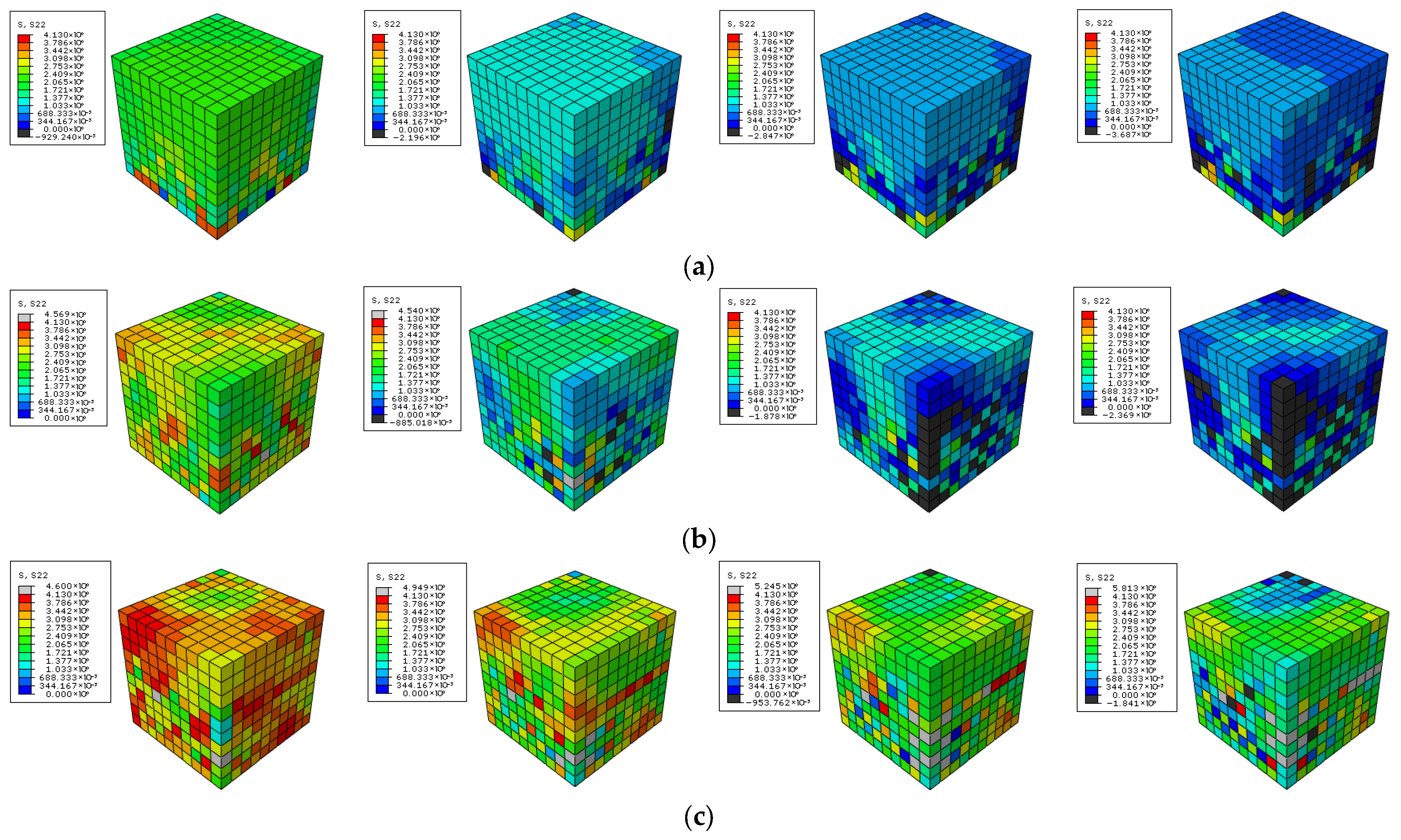
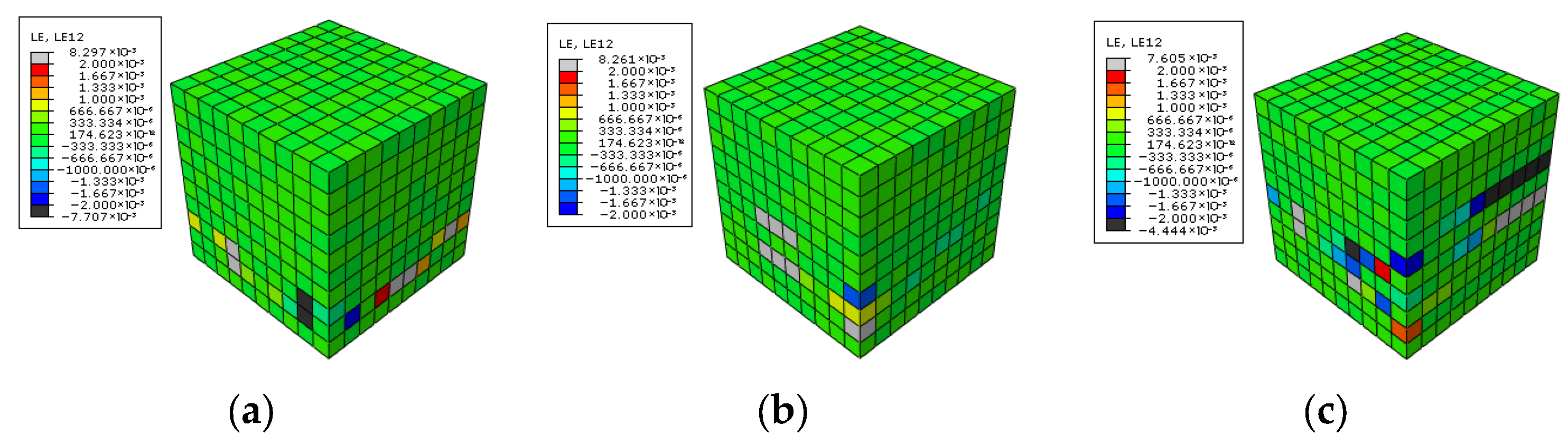
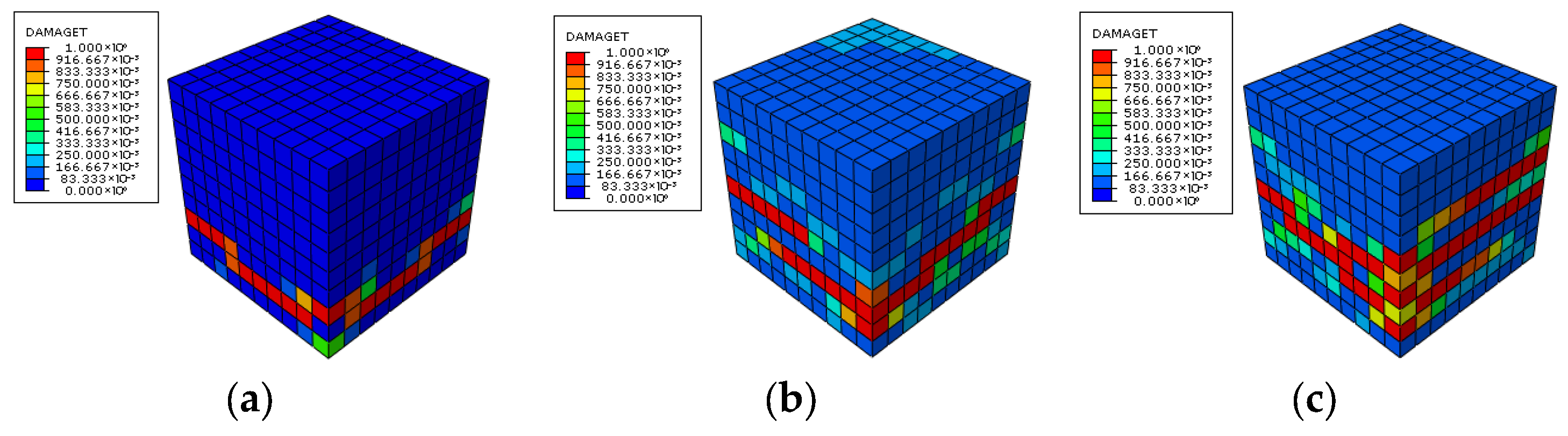
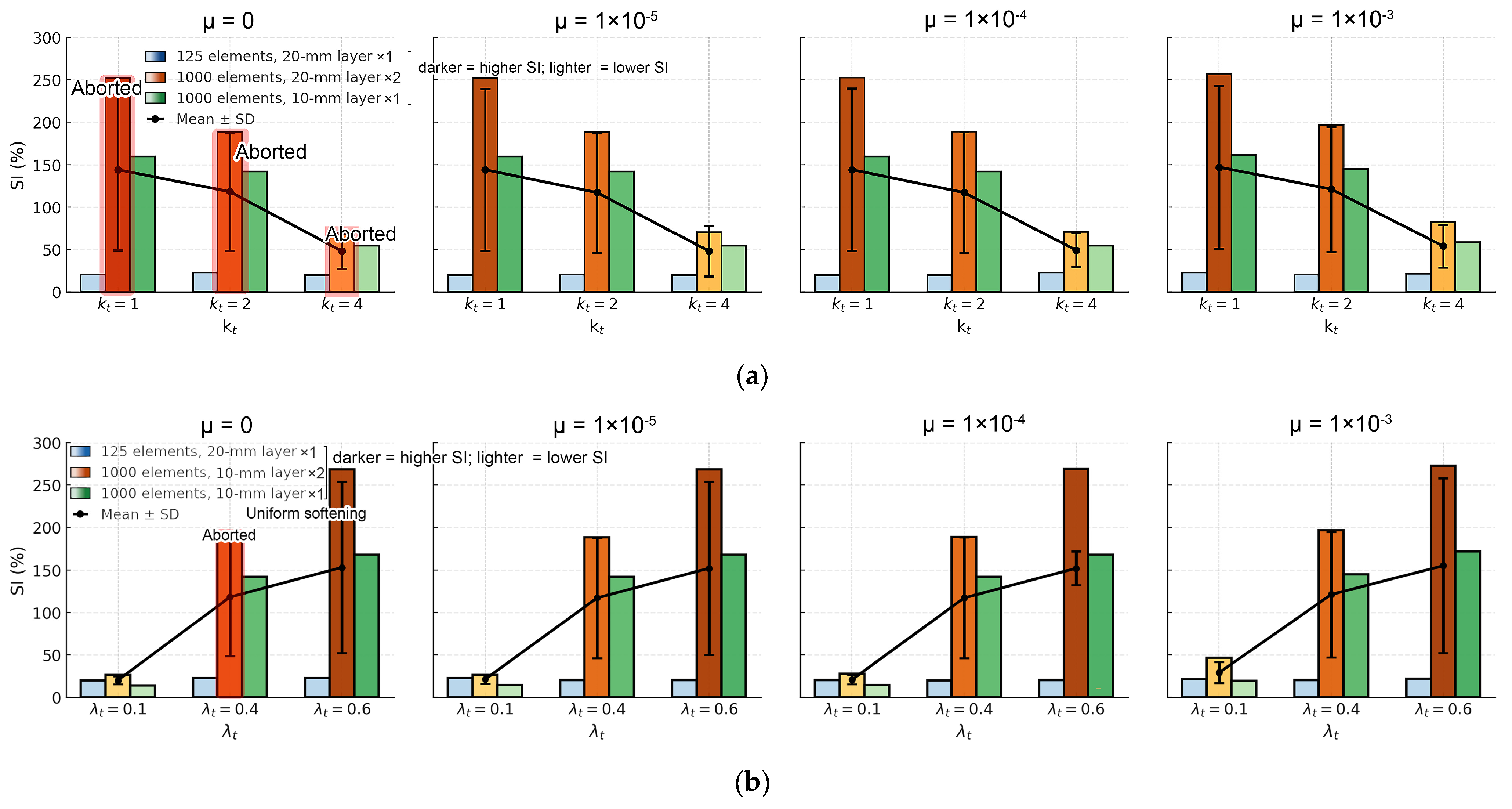
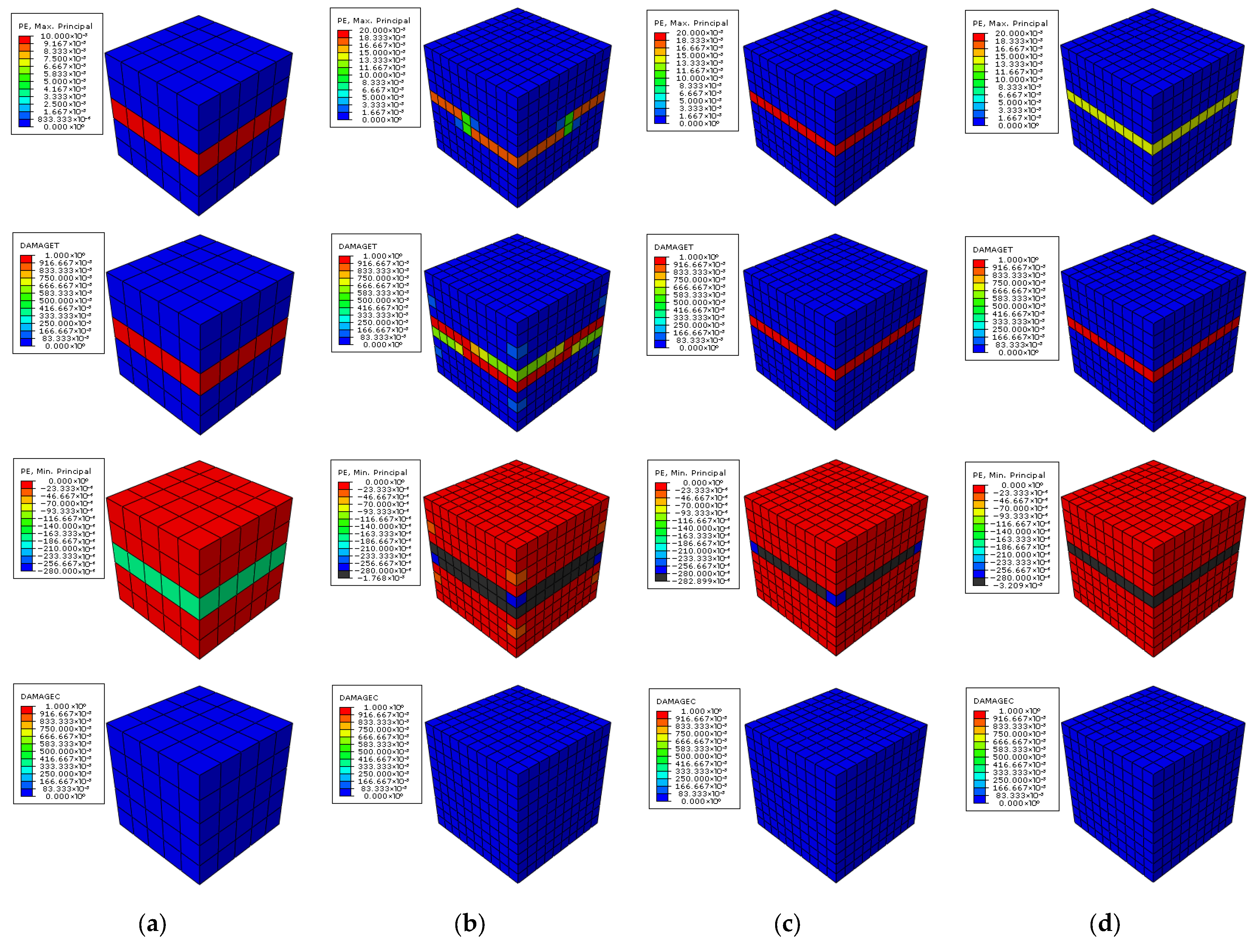
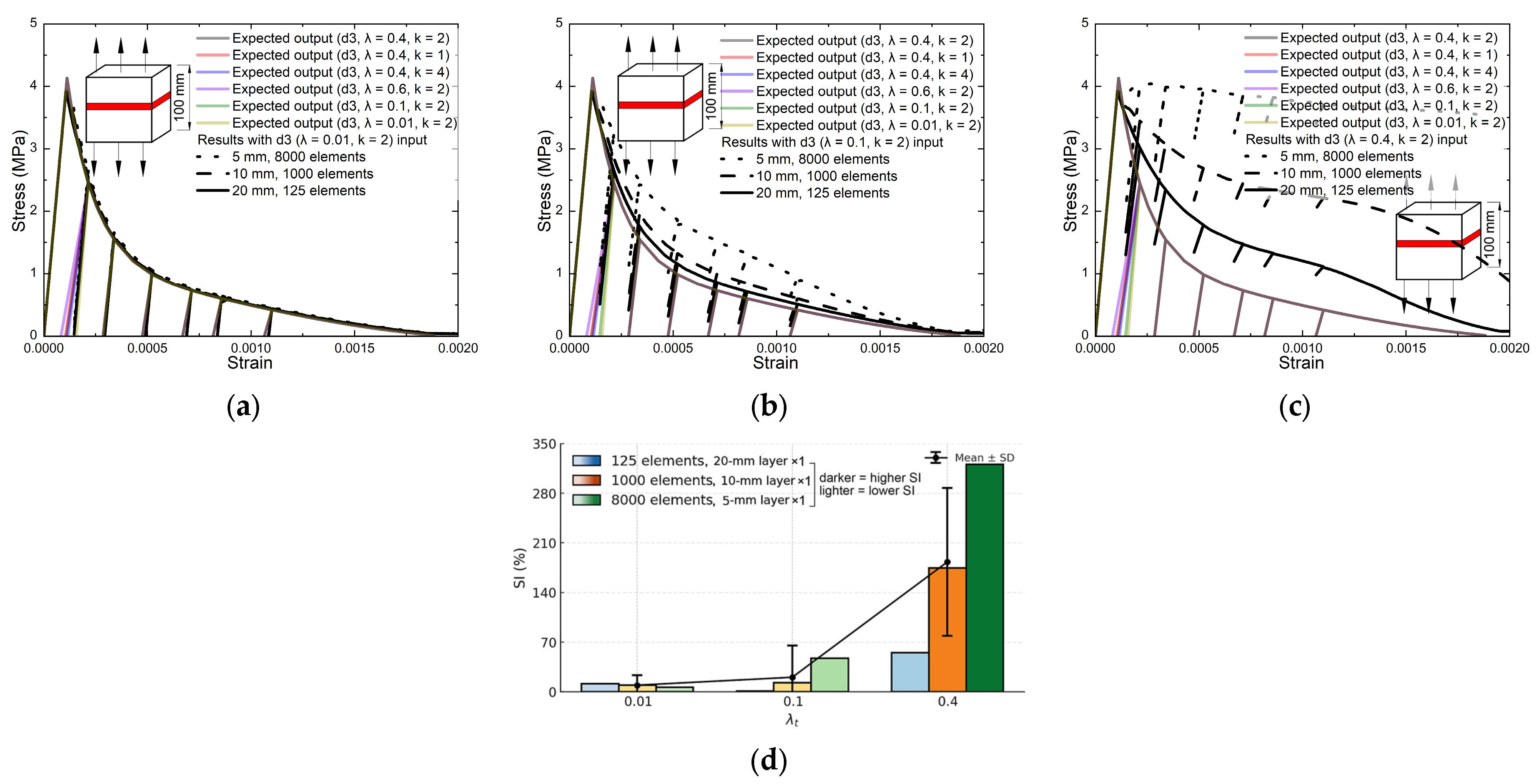
3.2.5. Numerical Results Simulation with a Predefined Weaker Layer at Structural Scale

Cracked elements that propagate randomly due to the numerical instability induced by the loss of strong ellipticity ($\det \mathbf{Q}\left(\mathbf{n}\right)\le 0$) exhibit crack patterns similar to those observed in heterogeneous concrete specimens. However, in structural models, even without concrete strength randomness, macro-scale factors such as stress concentration and joint geometry inherently promote specific paths of localized deformation. To emulate this behavior, cube models with a predefined weaker layer are introduced, representing a prescribed path for tensile localization which is consistent with the CBT assumption. This setup is then used to evaluate the mesh sensitivity governed by ${\mathrm{k}}^{t,glob}\left({\mathrm{k}}^{t,mat},{\chi }_c\right)$ in CDP-based FE simulations. In the predefined weaker layers, the average tensile strength within the crack band is typically lower than that of the adjacent concrete, and therefore the tensile strength is reduced by 5%, so it is large enough to suppress mesh-noise-driven path wandering, yet sufficiently small to avoid biasing force–displacement and energy measures.

As assumed in Figure 2, ${\mathrm{k}}^{t,mat}$, ${\chi }_c$ and the corresponding values of ${\tilde{n}}_{Gt}$ are material constants associated with the characteristics of the crack band. In the CBT assumption, the crack-band width should range from 1.5 to 4 times the maximum aggregate size (9.5 mm for C2 concrete [2]) to ensure continuum-scale smoothing [1]. For concrete with reduced stiffness contrast between aggregate and mortar (e.g., high-strength concrete), the crack-band width ($h$) is expected to be smaller. Based on the CDP and CBT model, the calibrated tensile damage evolution is assumed to be valid in FE simulations solved by the implicit Full-Newton method and using mesh sizes appropriately selected corresponding to the physical crack-band width (14.25–38 mm) [1]. Two mesh sizes (10 mm and 20 mm) are used in cube models with predefined weaker layers of $h$.

1.

Results and Discussion

As shown in Figure 16, Figure 17 and Figure 18, results with a specific path of tensile localized deformation still vary with different tensile damage variables, particularly in 1000-element models (Figure 16b,c and Figure 18b–d). The predefined weak layer undergoes biaxial tensile stress, while negative minimum principal strains arise due to the Poisson effect. A zero value of the viscosity parameter still fails to capture localized tensile deformation in the absence of significant macro force concentration (Figure 16b and Figure 18b). These results further confirm that multi-element models are sensitive to $d_t\left(h,u_t^{pl}\right)$ (Figure 16 and Figure 17), especially when the initial damage parameters are large and mesh sizes are small ($\mathrm{S}I>150\%$ when ${\lambda }_t=0.6$ and $h=10$ mm).

For comparison, Figure 19a,b present results for 100 mm-$l_{eq}$ and 10 mm-$l_{eq}$ single-element cubes with different tensile damage evolution variables and $\mu =0$. Although the sensitivity to $d_t\left(h,u_t^{pl}\right)$ (Equation (51a)) is insignificant compared with multi-element models ($SI<26\%$), different tensile-damage evolution variables, i.e., the parameters ${\lambda }_t$ and $k_t$ used in $d_3$, lead to different calculated dissipated fracture energies, ${\tilde{G}}_F=h{\int }_{{\epsilon }_{ctm}}^{w_u/h}{\sigma }_t\left({\epsilon }_t\right)d{\epsilon }_t$.

2.

Increase in Mesh Sensitivity in Fine-Mesh Simulations

Element size should be large enough to reflect the continuum smoothing of aggregate heterogeneity according to the CBT. Notably, the optimal choice identified in Figure 16 and Figure 19a,b (Equation (51a), $d_t=d_t\left(h,u_t^{pl}\right)=d_t\left(h,{\lambda }_t,k_t\right)\approx d_t\left(\mathrm{10,0.1,2}\right)\approx d_t\left(\mathrm{10,0.1},4\right)$ with ${\tilde{n}}_{Gt}\approx 0.80$) yields less mesh-sensitive responses for simulations with mesh sizes larger than 10 mm, even in the presence of a non-zero viscosity parameter (Figure 19c). However, in some simulations with small structural dimensions, such as keyed joints, the mesh size must be smaller than the physical crack-band width (e.g., $h=5$ mm) to capture stress concentration paths. In this case, mesh sensitivity increases sharply (Figure 20).

3.3. Discussion on the Effect of ${\eta }_{mat}$

As assumed in Section 2.3 and confirmed by the parametric studies in this section, changes in the finite-element mesh size, the damage evolution law, and the viscoplastic regularization alter the material-level tangent stiffness (${\mathrm{k}}^{t,mat}$) and ${\chi }_c$, and therefore the assembled global tangent stiffness (${\mathrm{k}}^{t,glob}\left({\mathrm{k}}^{t,mat},{\chi }_c\right)$). These dependencies induce simulation sensitivity, which becomes particularly pronounced on fine meshes (see Figure 20). In multi-element models, the total energy dissipated by localized tensile failure then fails to comply with the fracture-energy regularization requirement.

As shown in Figure 21, $∆{\mathrm{k}}^t$, $∆{\mathrm{k}}_{\mathbf{n},h}^{t,glob}$, ${\displaystyle \frac{{\tilde{G}}_F}{G_F}}={\tilde{n}}_{Gt}={\tilde{n}}_{Gt}\left({\eta }_{mat}\right)$, and the loss of strong ellipticity ($\det \mathbf{Q}\left(\mathbf{n}\right)\le 0$, i.e., the presence of expected tensile localization) can be quantitatively linked to ${\eta }_{mat}$, particularly at the initial stage of softening.

When ${\eta }_{mat}$ at the initial stage of softening decreases, the total energy dissipation ($G_F$) increases, while ${\displaystyle \frac{{\tilde{G}}_F}{G_F}}={\tilde{n}}_{Gt}={\tilde{n}}_{Gt}\left({\eta }_{mat}\right)$ decreases significantly (e.g., ${\lambda }_t-0.6$ simulation in Figure 20c and Figure 21a and $\mu -0.001$ simulation in Figure 16 and Figure 21b). Unexpected uniform softening appears ($\det \mathbf{Q}\left(\mathbf{n}\right)>0$) when ${\eta }_{mat}$ at the initial stage of softening decreases to a certain level (e.g., ${\lambda }_t-0.6$ simulation in Figure 14b and Figure 21a), whereas abortion of the calculation occurs ($\det \mathbf{Q}\left(\mathbf{n}\right)\ll 0$) when ${\eta }_{mat}$ at the initial stage of softening increases to a certain level (e.g., $\mu -0$ simulation in Figure 14a and Figure 21b). The mesh sensitivity ($∆{\mathrm{k}}^t$ and $∆{\mathrm{k}}_{\mathbf{n},h}^{t,glob}$) of multi-element simulations with expected localized deformation ($\det \mathbf{Q}\left(\mathbf{n}\right)\le 0$) is reduced as ${\eta }_{mat}$ is slightly increased (e.g., ${\lambda }_t-0.1$ simulation in Figure 20a and Figure 21a). Decreasing $\phi$ from $54$ to $18°$ slightly decreases ${\eta }_{mat}$, which is almost unobservable, although a larger effect on $∆{\mathrm{k}}^t$ is produced (Figure 13 and Figure 21c). In general, it can be deduced from the pattern in Figure 21 that increasing ${\eta }_{mat}$ at the initial stage of softening from 2 (${\eta }_{min}^{sec}\approx 2$ and ${\eta }_{mat}\ge {\eta }_{min}^{sec}$), for example by decreasing the value of ${\lambda }_t$, can further reduce the mesh sensitivity of multi-element simulations with expected localized deformation (Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20).

As shown in Figure 22, when ${\lambda }_t$ decreases to 0.01, the mesh sensitivity of the structural responses investigated using the same method expressed in Section 3.2.5. is significantly reduced, as expected. However, in this case, the simulated tensile behavior deviates slightly from the calibrated one, as $G_F\approx {\tilde{G}}_F$ and ${\tilde{n}}_{Gt}\approx 1.00$ rather than $0<{\tilde{n}}_{Gt}<1$. Variations in ${\lambda }_t$ and $k_t$ mainly affect the theoretical macroscopic tensile response of elastic degradation at the onset of tensile softening, but $d_t\approx d_{t,l}\approx d_{t,s}$ (Equation (51a), Equation (51b), and Equation (51c)) at a specific deformation along the loading direction.

4. A Calibration Framework for Concrete Tensile Behavior

The validation provided by analytical and numerical results in Section 3 enables the inverse calibration of the uniaxial tensile response by a theoretical constitutive solution and experimental fracture-energy consistency under the background of the CBT, the continuum assumption, and the strain-softening hypothesis.

4.1. Assumption Validations

4.1.1. Single-Element Validation

Within the CDP–CBT framework solved by a Newton–Raphson scheme, the model was closed internally, so that the post-peak softening was uniquely generated by incremental integration and the uniaxial tensile stress–strain relation acted as an output. One-element simulations in Figure 19a,b, consistent with Figure 9, confirm Equation (51a). Once the shape of the ${\sigma }_t$ − $u_t^{ck}$ curve is specified by ${\tilde{G}}_F,f_{ctm}$, and $E_{cm}$, the corresponding evolution of $d_t\left(h,u_t^{pl}\right)$ for an element of width $h$ is uniquely induced and reproduced with $SI\le 5\%$, using the proposed two-parameter damage law, as expressed by Equation (41). The dilation angle in the range ${18}^{°}-{54}^{°}$ has negligible effect, while the viscosity parameter is required to be approximately zero. Dense input data points near early post-peak are found necessary to avoid interpolation-induced tangent bias. Under the CBT assumption, taking the element width equal to the physical crack-band width ensures energy consistency at the element level.

4.1.2. Multi-Element Validation and Localization

In the CDP model, plastic flow and damage evolution are tightly coupled. In multi-element models, assembling the global tangent stiffness becomes more complex. It is commonly understood that energy regularization based on the CBT primarily acts by scaling the softening strain. However, the results of numerical tests in Section 3 present that varying the tensile-damage evolution $d_t\left(h,u_t^{pl}\right)$ while keeping other inputs fixed led to different dissipated energies (Figure 16 and Figure 17), confirming that energy is governed by the damage evolution rather than by purely scaling the softening strain.

The onset of localization coincided with the loss of strong ellipticity, and a larger initial damage rate parameter ${\lambda }_t$ (or a larger viscosity if used) delays localization and increases residual strength and energy.

Overall, the assumptions illustrated in Figure 2 and expressed by Equation (18), Equation (39), Equation (51a), Equation (51b), and Equation (51c) are validated. For any purely uniaxial tensile response with a prescribed $h$, there exists a unique solution for the uniaxial tensile-damage evolution ($d_t\left(h,u_t^{pl}\right)$), the evolution of the total fracture-energy dissipation ($G_F=G_F\left({\tilde{G}}_F,{\tilde{n}}_{Gt}\right)$), and $d_t\left(h,u_t^{pl}\right)\approx d_{t,l}\left(h,{\delta }_t^{pl}\right)\approx d_{t,s}\left(l_{eq},{\delta }_t^{pl}\right)$ at a specific deformation to the loading direction.

4.1.3. Material-Level Stability Indicator Linking Element Calibration to Structural Response

The material-level stability indicator ${\eta }_{mat}$ is read at the onset of softening from the initial post-peak tangent, together with the associated energy release consistent with the target fracture energy. It serves as a compact descriptor of the initial softening kinetics. The key driver is $b_{t0}^{\prime }$, i.e., the initial value of $b_t^{\prime }$, which sets how the inelastic increment is partitioned between plasticity and cracking. A smaller $b_{t0}^{\prime }$ (or a larger ${\lambda }_t$, i.e., the initial damage rate parameter) triggers faster initial damage growth, and thus a smaller ${\eta }_{mat}$. In one-element simulations, the dilation angle and viscosity parameter only have a weak influence on ${\eta }_{mat}$, and different ${\eta }_{mat}$ has less impact on the simulated tensile response than in multi-element simulations. In a multi-element model with the same mesh size as the one-element simulations, a larger ${\eta }_{mat}$ yields an earlier localization, lower residual tension, and energy dissipation closer to the target crack band law. A multi-element response aligns better with the single-element results when ${\eta }_{mat}\ge {\eta }_{min}^{sec}$.

4.1.4. Energy Regularization and Mesh Sensitivity

When the analysis mesh differs, the global consistent tangent exhibits mesh-scale effects captured by the confinement-related stiffness term ${\chi }_c$ (Equations (59), (60a,b) and (61a)). Finer meshes generally increase ${\chi }_c$ as the element volume decreases. The sensitivity of the mesh is minimized when ${\chi }_{c,h}\approx 0$ (weak lateral coupling) or ${\chi }_{c,h2}\approx {\chi }_{c,h1}$ (balanced confinement). To fix energy regularization, ${\chi }_c$ (equivalently $∆{\mathrm{k}}^t$) should be calibrated in a reference simulation with mesh size approximately equal to the crack-band width, and then used to revise the tangent stiffness formulation. Under this criterion, multi-element results become effectively mesh-insensitive and the variation in dissipated energy arises from the chosen damage evolution law, not from the mesh.

In practice with the embedded CDP in Abaqus, record ${\eta }_{mat}$ after single-element calibration and use it as a predictor for the assembled response under the same assumptions. If a fine-mesh model shows unexpected sensitivity, increase ${\eta }_{mat}$ at softening onset by reducing the initial damage rate (e.g., decrease ${\lambda }_t$ in Equation (41)). A commonly used workaround is to specify the uniaxial tensile behavior by $G_F$, i.e., the total fracture energy dissipation from direct-tension tests, instead of ${\tilde{G}}_F$, and enforce a near-zero initial tensile-damage rate (e.g., ${\lambda }_t=0.01$ in Equation (41), which reproduces the calibrated tensile response at a structural level (e.g., Figure 22a). However, the input fracture energy becomes effectively overestimated (${\tilde{n}}_{Gt}\approx 1.00$), and under multiaxial states the simulated response may deviate from that obtained with the expected, optimized CDP formulation.

4.2. Inverse Calibration Framework Based on Numerical Validations

The validations above support an inverse calibration workflow of uniaxial tensile behavior for normal (non-fiber) concrete via the CDP model in FE simulations using limited experimental data. In typical tests, isolating the purely uniaxial tensile behavior of the concrete within the crack band alone is practically infeasible. However, if the measured data include the crack-band width, $G_F$, $f_{ctm}$, $E_{cm}$, and an estimated shape of ${\sigma }_t$ − ${\epsilon }_t$ curve, as shown in Figure 2, multi-element simulations conducted with mesh size approximately equal to the crack-band width can reproduce the elastic degradation, the force–deformation response, and the crack-band energy in agreement with the CBT, the continuum assumption, and the strain-softening hypothesis. Figure 23 shows an example based on direct tensile tests.

The calibrated parameters include the local fracture-energy parameter (${\tilde{G}}_F$), or the partition factor (${\tilde{n}}_{Gt}$), and the corresponding tensile-damage evolution ($d_t\left(h,u_t^{pl}\right)=d_t\left(h,{\lambda }_t,k_t\right)$), identified according to the total dissipated fracture response ($G_F$ and ${\sigma }_n-w$ curve) in direct-tensile tests (i.e., $SI\le 5\%$ for one-element simulation and $SI\le \left|{{\tilde{n}}_{Gt}}^{-1}-1\right|+5\%$ for multiple-element simulation). Using C2 concrete as an example, if the experiment indicates that $G_F=n_{Gt}0.085{\mathrm{e}}^{\left(0.0833f_{ctm}+0.2583\right)}$ with $n_{Gt}\approx 1.26$ and the crack-band width ($h$) is approximately equal to 10 mm, the optimal choice identified in Figure 16 and Figure 19a,b is $d_t=d_t\left(h,u_t^{pl}\right)=d_t\left(h,{\lambda }_t,k_t\right)\approx d_t\left(\mathrm{10,0.1,2}\right)\approx d_t\left(\mathrm{10,0.1},4\right)$ with ${\tilde{n}}_{Gt}\approx 0.80$, for which $SI\le 5\%$ $SI\le 5\%$ for one-element simulations and $SI\le \left|{{\tilde{n}}_{Gt}}^{-1}-1\right|+5\%$ for multiple-element simulations. Otherwise, the input value of ${\tilde{n}}_{Gt}$ (or ${\tilde{G}}_F$) is changed and the corresponding tensile-damage evolution ($d_t=d_t\left(h,u_t^{pl}\right)=d_t\left(h,{\lambda }_t,k_t\right)=d_t\left(10,{\lambda }_t,k_t\right)$) is recalibrated as well (Figure 23).

Overall, the method enables the iterative optimization of three key parameters: ${\tilde{n}}_{Gt}$ (Equation (39)), ${\lambda }_t$, and $k_t$ (Equation (41)), by comparing the numerical and experimental results of direct-tensile tests, as the influence of $\phi$ and $ϵ$ in the plastic potential function is theoretically and numerically negligible. Practical starting values are ${0.1\le \lambda }_t\le 0.4$, ${2\le k}_t\le 4$, and ${\tilde{n}}_{Gt}=0.8$, which are initial guesses according to several published experimental studies and numerical tests in this study and should be re-identified for each mix and geometry using the $SI$ criteria.

In this study, ${\tilde{n}}_{Gt}$ is defined for direct tension. Other tests such as three-point bending introduce geometry-dependent effects (e.g., notch height and non-uniform stress fields), so ${\tilde{n}}_{Gt}$ should be treated as mix- and test-specific and mapped as a function of $h,f_{ctm},E_{cm}$, ${\tilde{G}}_F$, and the test type.

Calibration in this framework is driven by the theoretical constitutive solutions that are mathematical, with a limited set of measurements serving as boundary conditions to anchor the parameters. Since the numerical results show that the local law $d_t\left(h,u_t^{pl}\right)$ closely matches the measured global stiffness degradation in direct tension ($d_t\left(h,u_t^{pl}\right)\approx d_{t,l}\left(h,{\delta }_t^{pl}\right)\approx d_{t,s}\left(l_{eq},{\delta }_t^{pl}\right)$), an experimentally obtained global degradation curve can be used to further refine the framework. As additional data become available, inverse analysis can progressively update ${\tilde{n}}_{Gt}$ (Equation (39)), ${\lambda }_t$, and $k_t$ (Equation (41)) under a weak-coupling assumption without altering the theoretical formulation, which can contain more experimental factors such as a strength distribution model in test specimens.

5. Conclusions

This study formulates a CBT-compatible uniaxial tensile softening law within the CDP framework, provides an invertible mapping from fracture-mechanics inputs to CDP tensile variables, and introduces a residual-based sensitivity index ($SI$) to quantify the roles of mesh size, dilation angle, viscoplastic regularization, and tensile damage evolution variables. Within the scope of normal (non-fiber) concrete, verifications against published tests and parametric FE studies show fracture-energy consistency and mesh-robust predictions when the FE mesh is not smaller than the physical crack-band width. The framework clarifies when viscoplastic regularization aids convergence versus biases strength/energy, and links one-element calibration to structural behavior through a material-level stability indicator ${\eta }_{mat}$ and a structural-level global tangent. Based on a mathematical constitutive solution, a practical inverse calibration framework and a reliable basis for commercial FE simulation of tensile softening in concrete is thereby provided, which requires only limited experimental data, including stress–crack opening response and crack-band width in direct-tensile tests, tensile strength, and elastic modulus. The main conclusions are as follows:

1.

Tensile damage and plastic flow are tightly coupled. A damage evolution law with several tensile parameters in the CDP model is proposed for energy consistency in addition to scaling of the softening strain. For a prescribed uniaxial tensile stress–strain (${\sigma }_t$ − ${\epsilon }_t$) curve, the dilation angle ($18$ to $54°$) has negligible effect in one-element tension, whereas using viscoplastic regularization without an explicit tensile-damage law biases the response. Given elastic modulus, tensile strength, fracture energy from pure tension, and an estimated shape of the ${\sigma }_t$ − ${\epsilon }_t$ curve, the evolutions of damage variables are uniquely determined. Using the proposed damage law with calibrated damage evolution parameters (${\lambda }_t$ and $k_t$), the one-element $SI$ can be reduced to less than 5%, in which target tensile damage evolution for the corresponding ${\sigma }_t-{\epsilon }_t$ relationship is obtained. One-element analyses are thus suitable for calibrating the purely uniaxial tensile behavior of concrete.

2.

One-element calibration does not guarantee structural validity. In multi-element models, responses depend on mesh size, viscosity parameter, tensile-damage evolution rate, and assembly/constraint effects condensed in the global tangent with a confinement factor, while they are weakly sensitive to the dilation angle. Localization begins at the loss of strong ellipticity. A large viscosity parameter or high initial damage rate delays localization and overestimates residual strength and energy. Without a prescribed stress-concentration path, it is advised to use very small viscosity parameters purely for convergence to avoid uniform softening or aborted runs. Decreasing the initial damage rate parameter (${\lambda }_t$) markedly reduces mesh sensitivity, especially with a specific localization path. Denser target data points for inputting uniaxial tensile behavior in the CDP model reduce the path randomness of stress concentration. A predefined weak layer reproduces crack concentration and sharpens localization (here its tensile strength is reduced by 5%).

3.

In addition to tensile strength, elastic modulus, and an estimated uniaxial tensile stress–strain curve, three key tensile parameters are validated by parametric analyses at the element and structural levels, i.e., the ratio between fracture energy from pure tension in the physical crack band and that from direct-tension tests, and two mesh-independent damage evolution parameters (${\lambda }_t$ and $k_t$). Accordingly, an inverse calibration workflow under a framework coupling the CDP model, the CBT, and the Newton–Raphson solver in Abaqus is proposed, separating the material-scale crack band tensile law from structural responses. The damage evolution parameters and the fracture-energy ratio are identified in a one-element model subjected to uniaxial tension ($SI\le 5\%$) and multi-element models with boundary effects, respectively.

4.

During calibration in the proposed framework, the mesh size should be matched to the physical crack-band width, with a viscosity parameter set to approximately zero. With these calibrations, the tensile response of the physical crack band is obtained, and multi-element analyses achieve mesh insensitivity and CBT-consistent energy dissipation when meshes are at or above typical admissible sizes in the CBT (e.g., $h\ge 10$ mm in this study). Practical starting values are ${0.1\le \lambda }_t\le 0.4$, ${2\le k}_t\le 4$, and ${\tilde{n}}_{Gt}=0.8$ based on numerical and experimental observation.

5.

In the embedded CDP model in Abaqus, the input parameter for determining the uniaxial tensile response must be recalibrated to ensure both CBT-consistent energy dissipation (i.e., target fracture energy dissipation at structural level) and mesh-robust predictions. For fine meshes required by structural details, continuum assumptions for concrete are violated and thus mesh sensitivity rises, unless the initial tensile-damage rate is moderated by decreasing the initial damage rate parameter ${\lambda }_t$ (e.g., ${\lambda }_t=0.01$).

6.

A computable indicator, ${\eta }_{mat}$, obtained from one-element simulations is proposed, which is mainly affected by tensile damage evolution. A small value of ${\eta }_{mat}$ at the start of softening indicates a rapid initial tensile damage evolution rate, which increases the value of $SI$ in multiple-element simulations using fine meshes as well as delays of the loss of strong ellipticity, i.e., tensile localization. Using a near-zero initial damage rate in commercial implementations means that the results behave as if ${\eta }_{mat}$ were large, which decreases mesh sensitivity led by tensile damage variables but underestimates the total dissipated energy at a structural level.

7.

The CDP algorithm should be refined in future work. While energy regularization based on crack band theory is often regarded as a simple scaling of the softening strain, the numerical results indicate that regularization is also coupled with plastic-damage quantities, particularly the damage evolution variables. To enforce fracture-energy consistency, the confinement-related stiffness term and the corresponding tangent-stiffness increment should be calibrated and fixed using a reference simulation in which the mesh size equals the physical crack-band width. Adopting this criterion allows the tangent-stiffness formulation in the CDP algorithm to be revised so that multi-element analyses become effectively mesh-insensitive and energy regularization is achieved. Under the revised formulation, any variation in dissipated energy arises from the chosen damage evolution law rather than from the discretization.