The Spatiotemporal Distribution Characteristics and Sensitivity Analysis of Stress in the Galleries of a Super-High Arch Dam During Construction
Abstract
1. Introduction
2. Case of Gallery Cracking
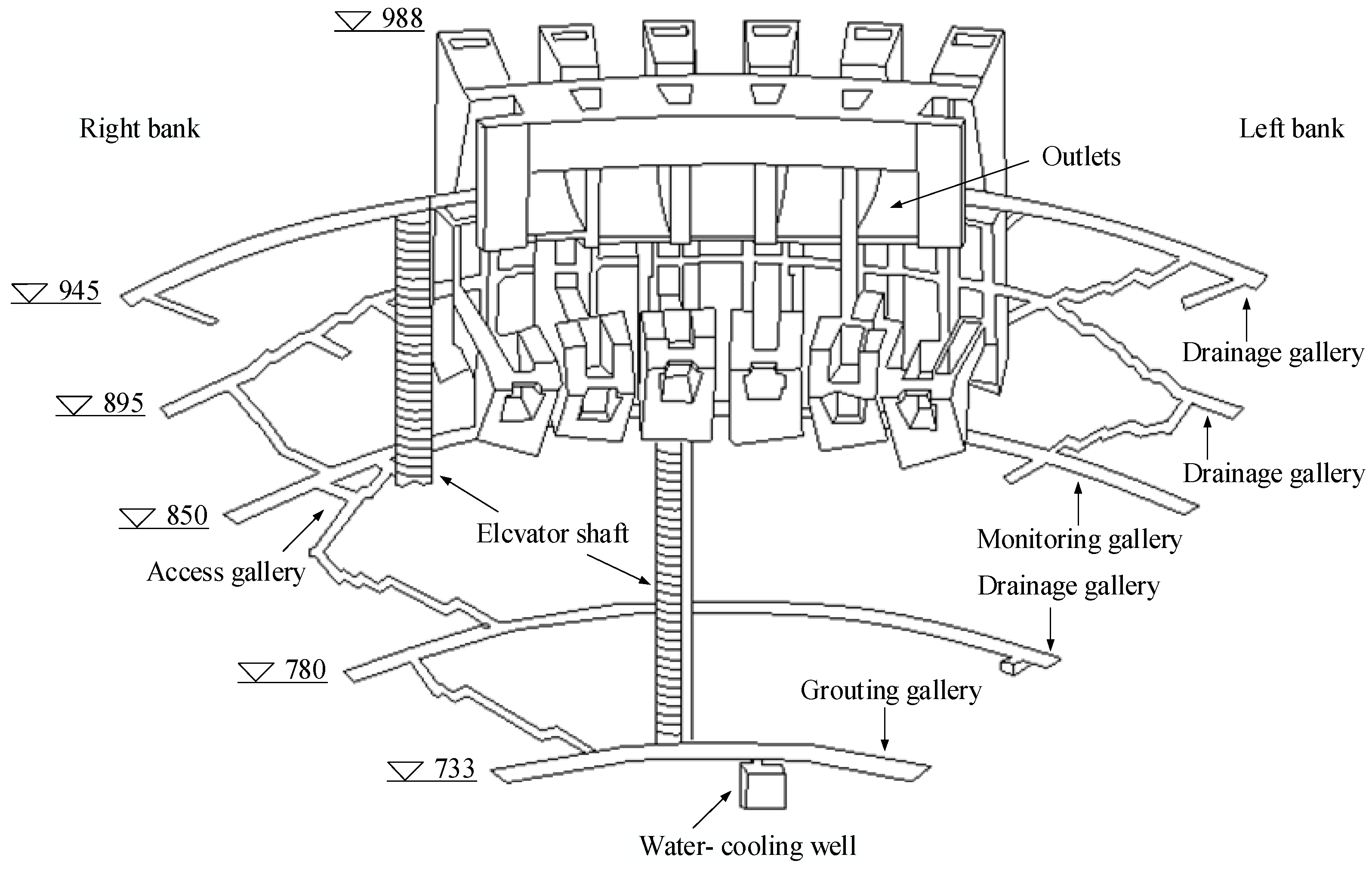
2.1. Basic Information of the Dam and the Gallery at an Elevation of 733 m
2.2. Basic Information on the Cracks in the 733 Gallery of Dam Section 7# on the Riverbed
3. Calculation Methods and Conditions
3.1. Analysis Method and Software
3.2. Main Calculation Parameters
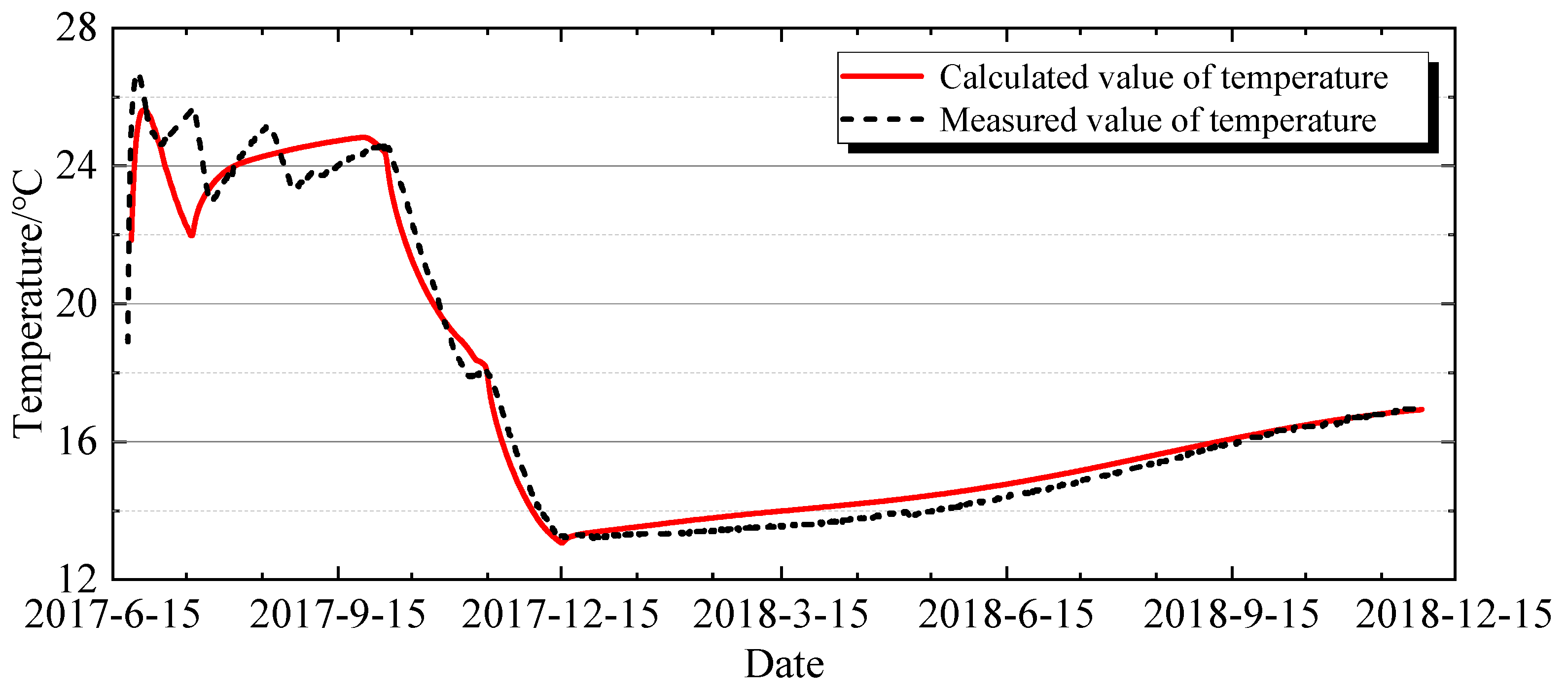
3.2.1. Temperature Data
3.2.2. Main Thermodynamic Parameters of Foundation and Concrete
3.3. Construction and Measures
3.4. Calculation Model and Conditions
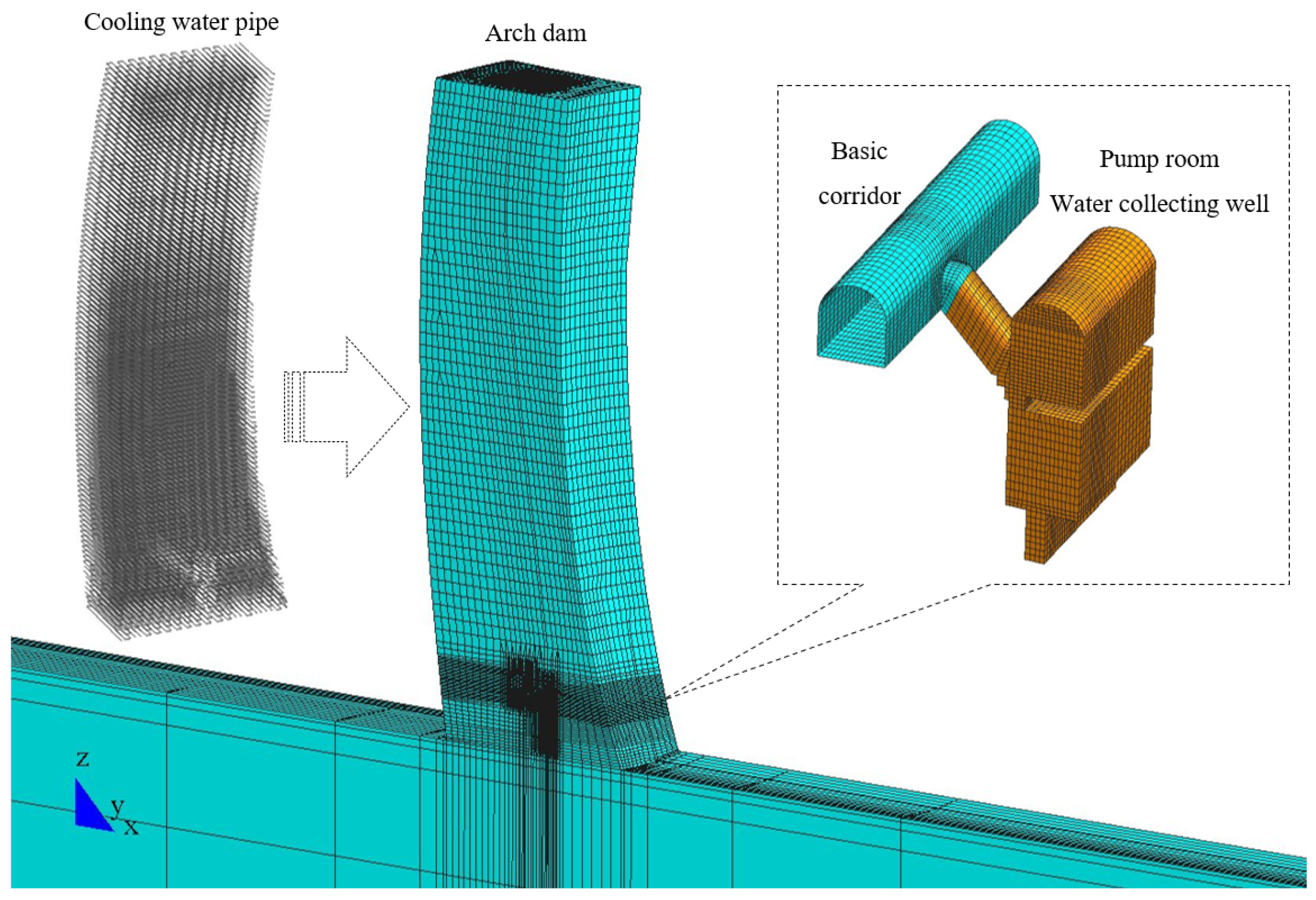
3.4.1. Calculation Model
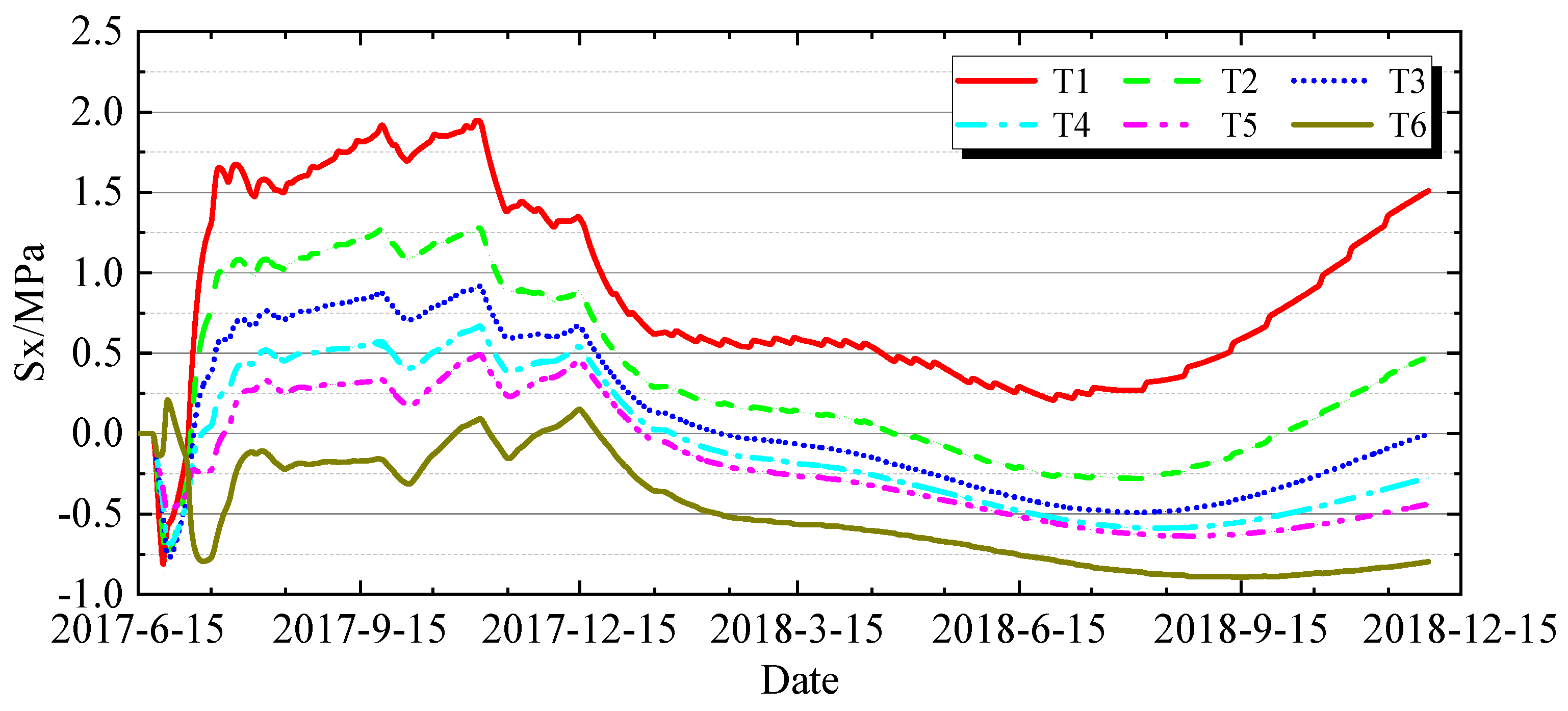
3.4.2. Feature Points and Feature Sections
3.4.3. Calculation Conditions
4. Results Analysis and Discussion
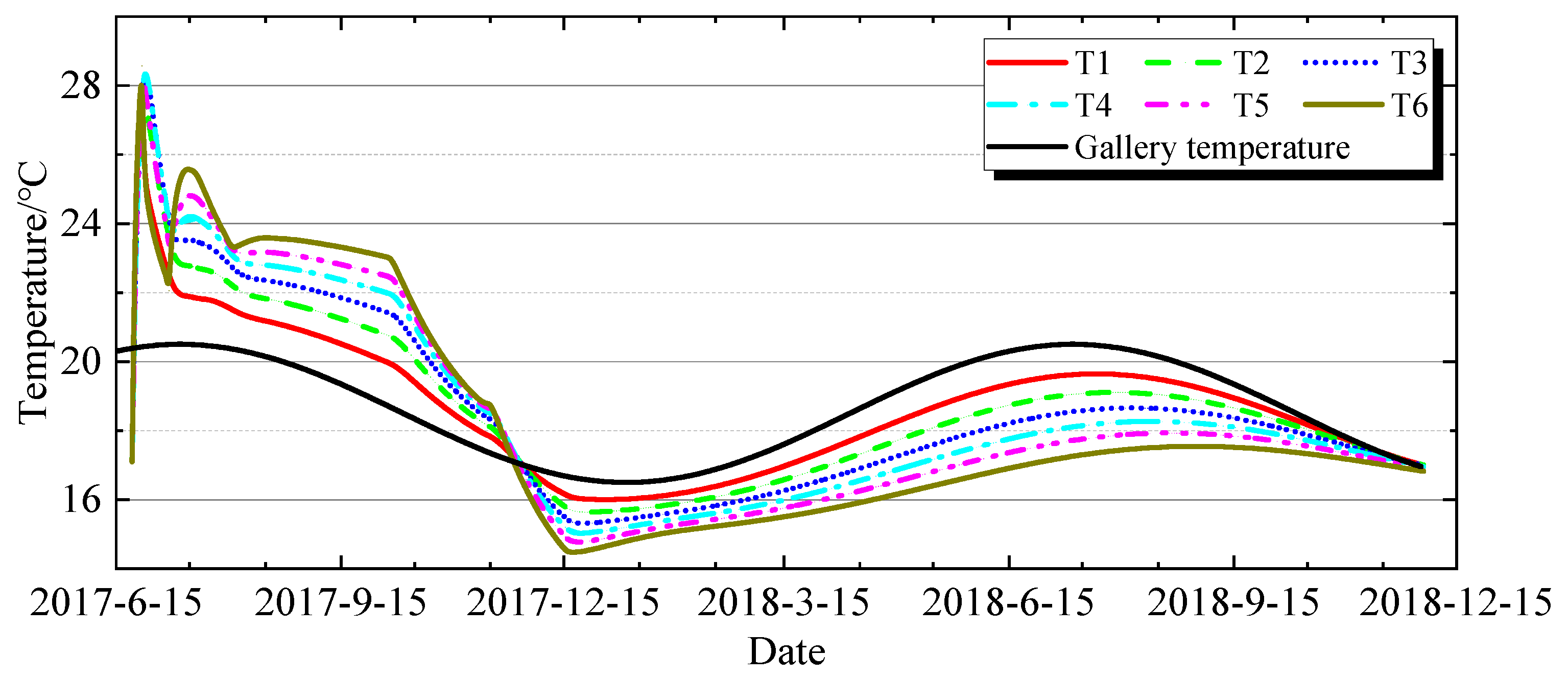
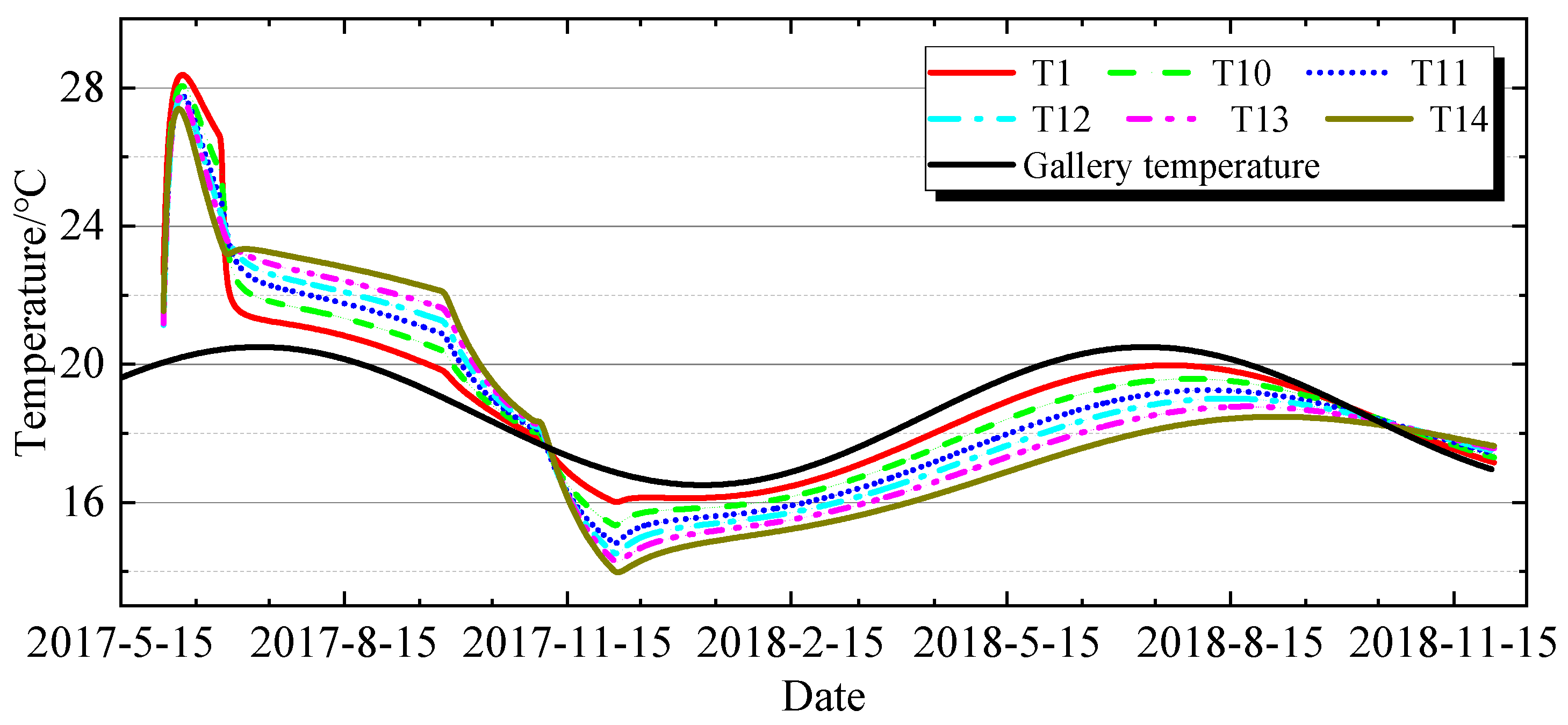
4.1. Analysis of Temperature Characteristics of the 733 Gallery
4.2. Analysis of Spatiotemporal Distribution Characteristics of Stress in the 733 Gallery
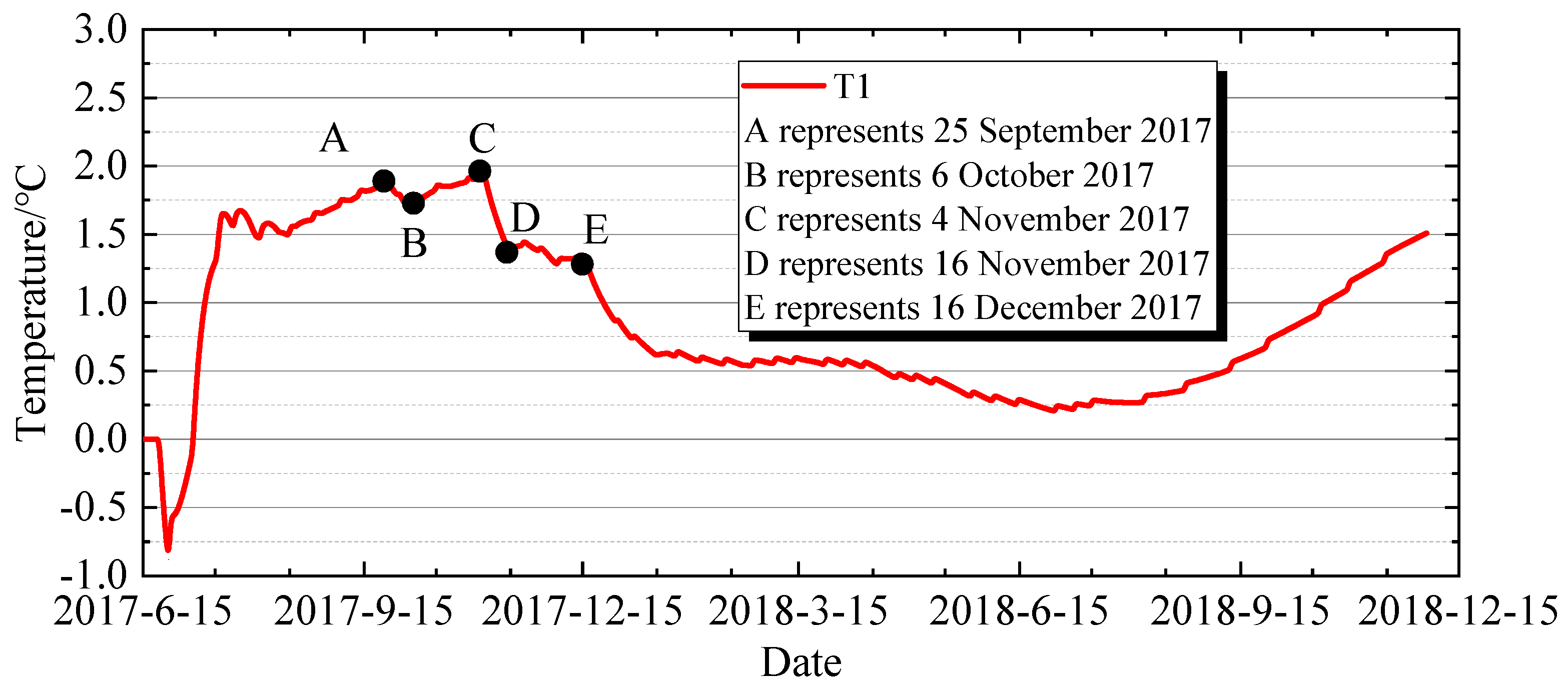
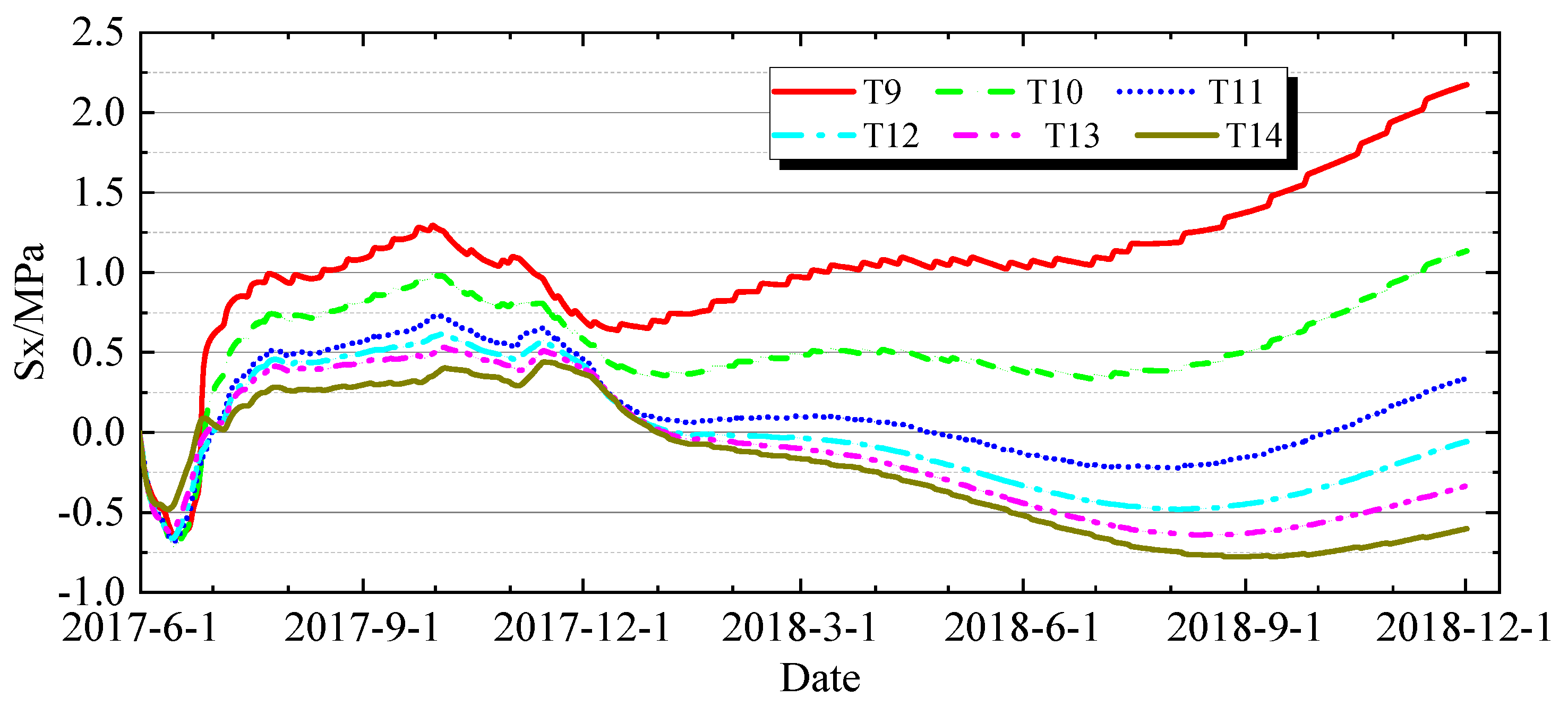
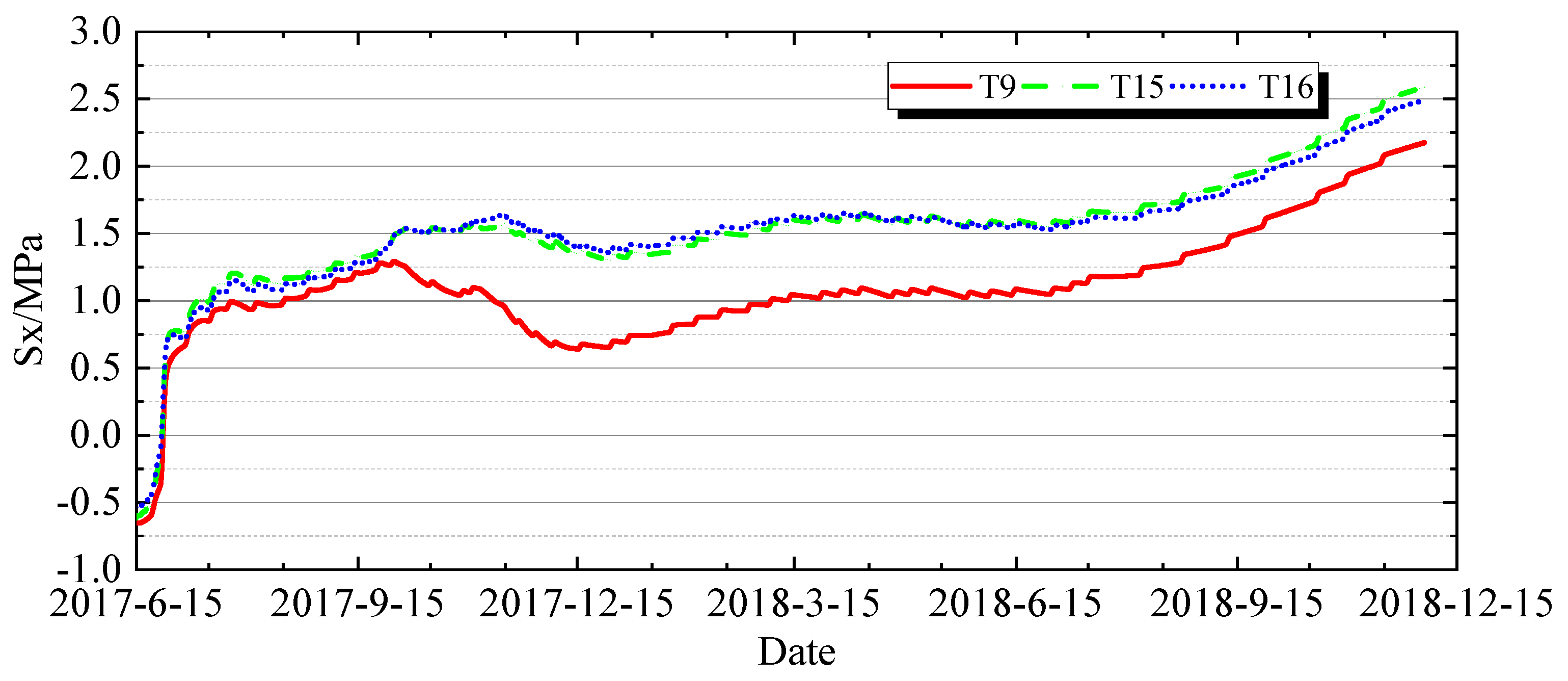
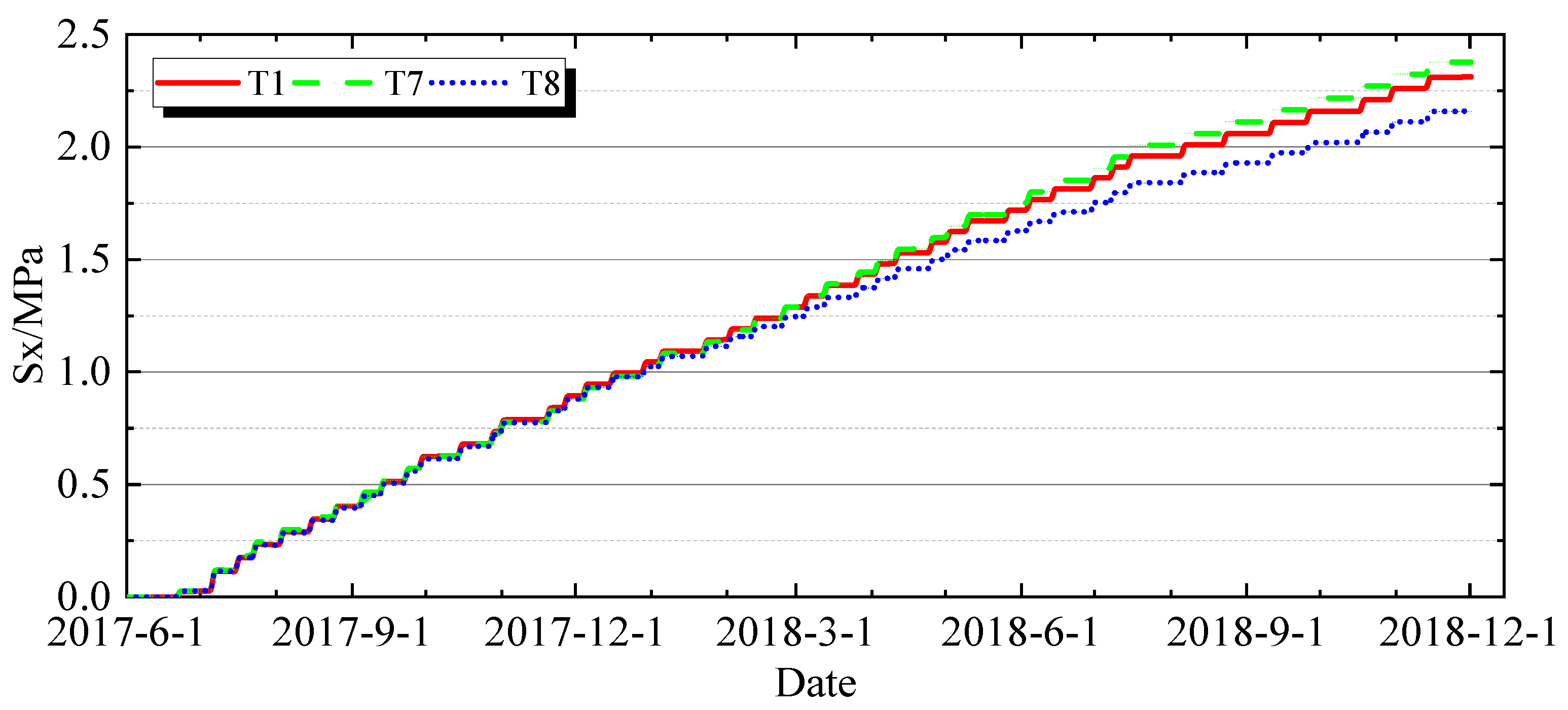
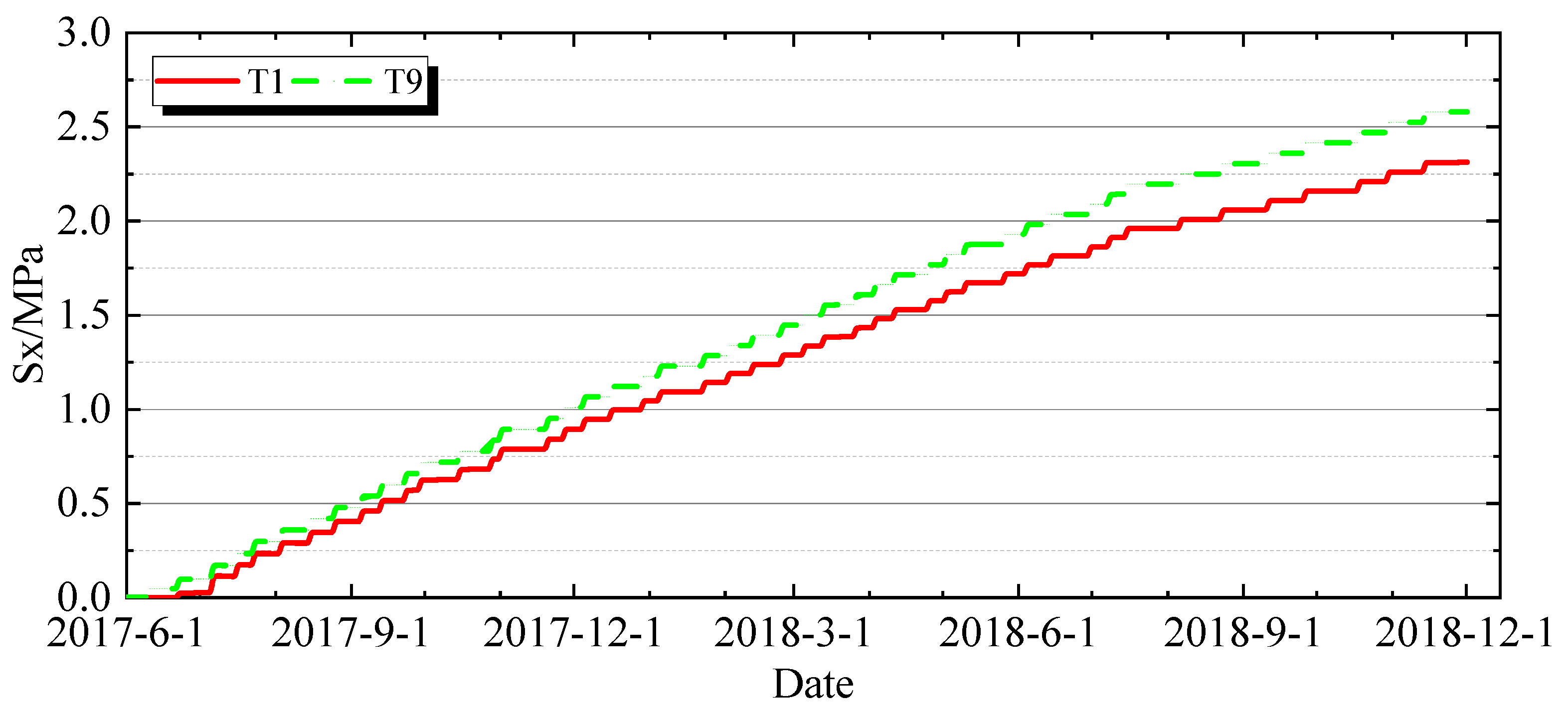
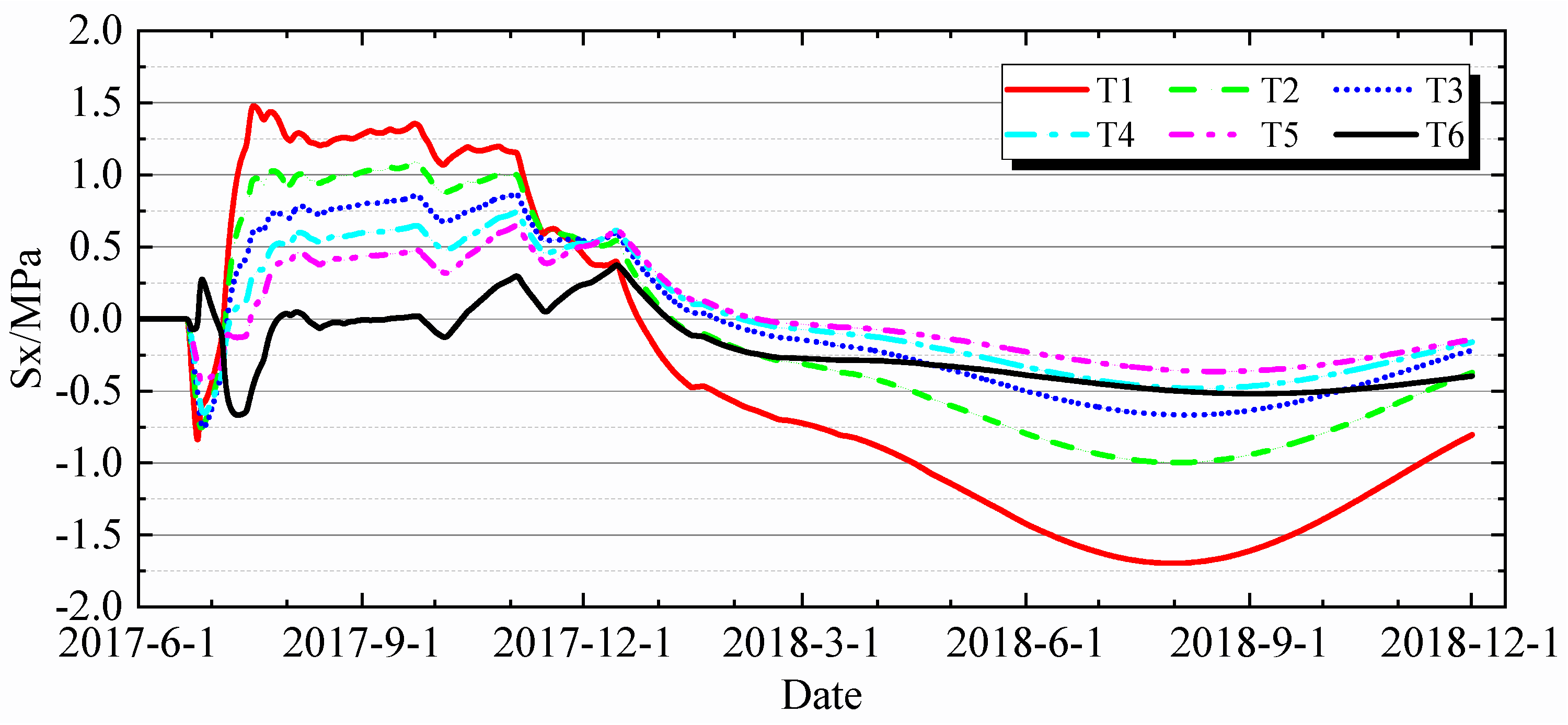
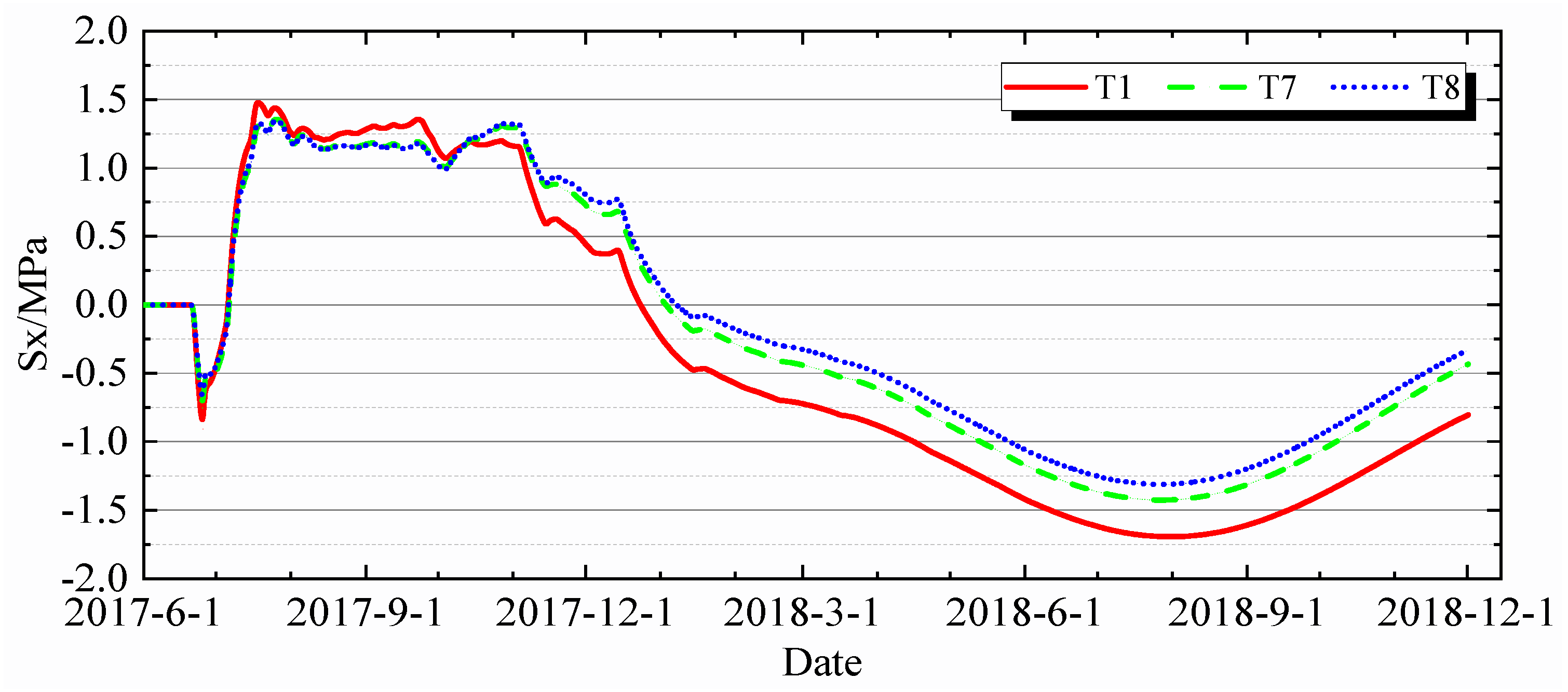
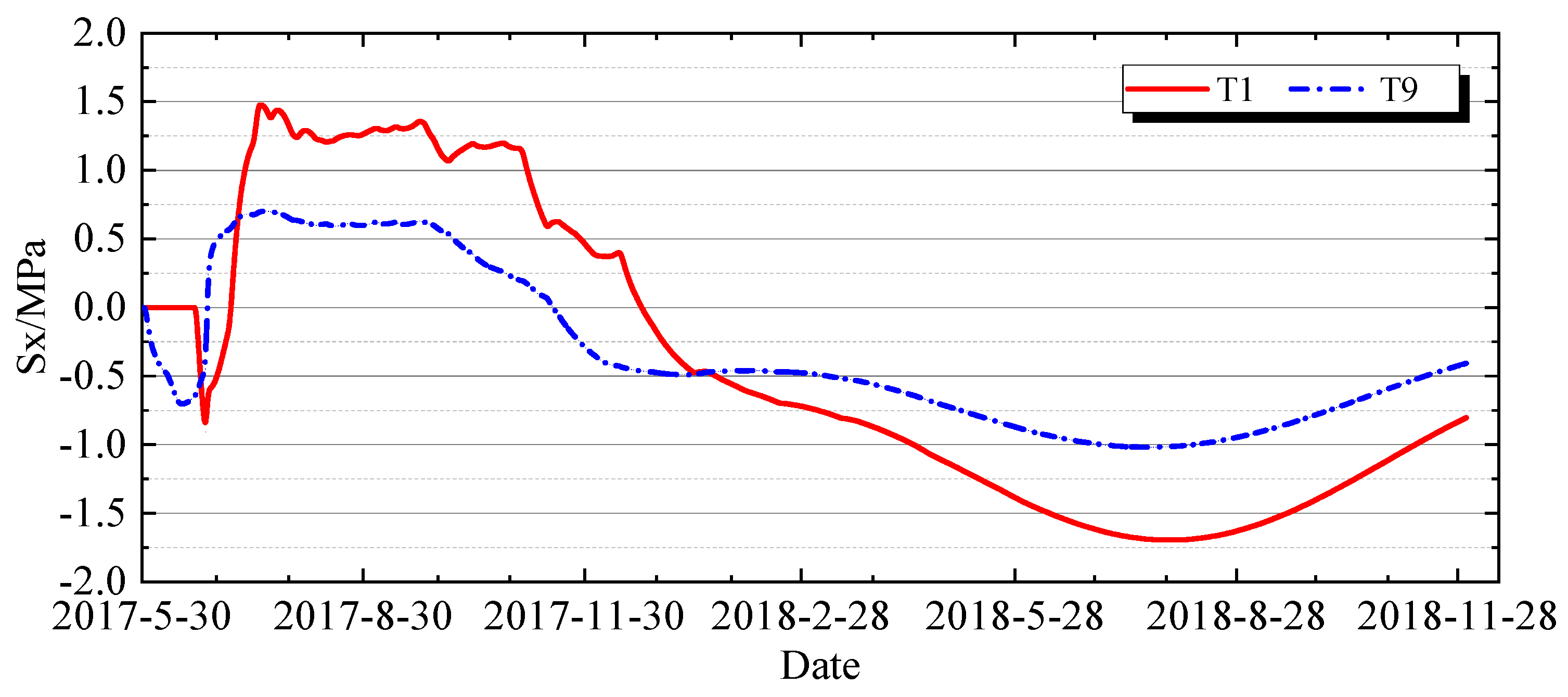
4.2.1. Characteristics of Stress Variation over Time
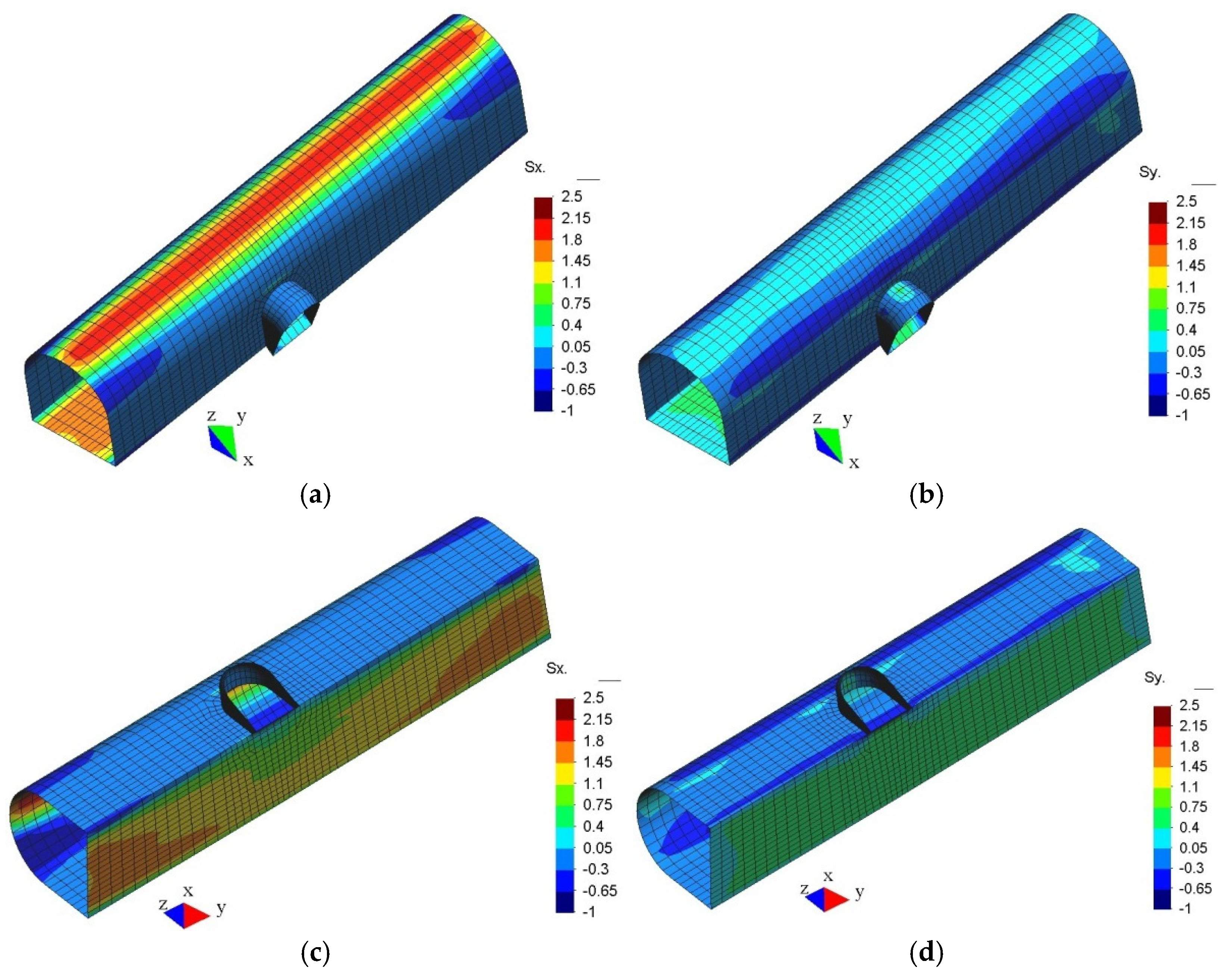
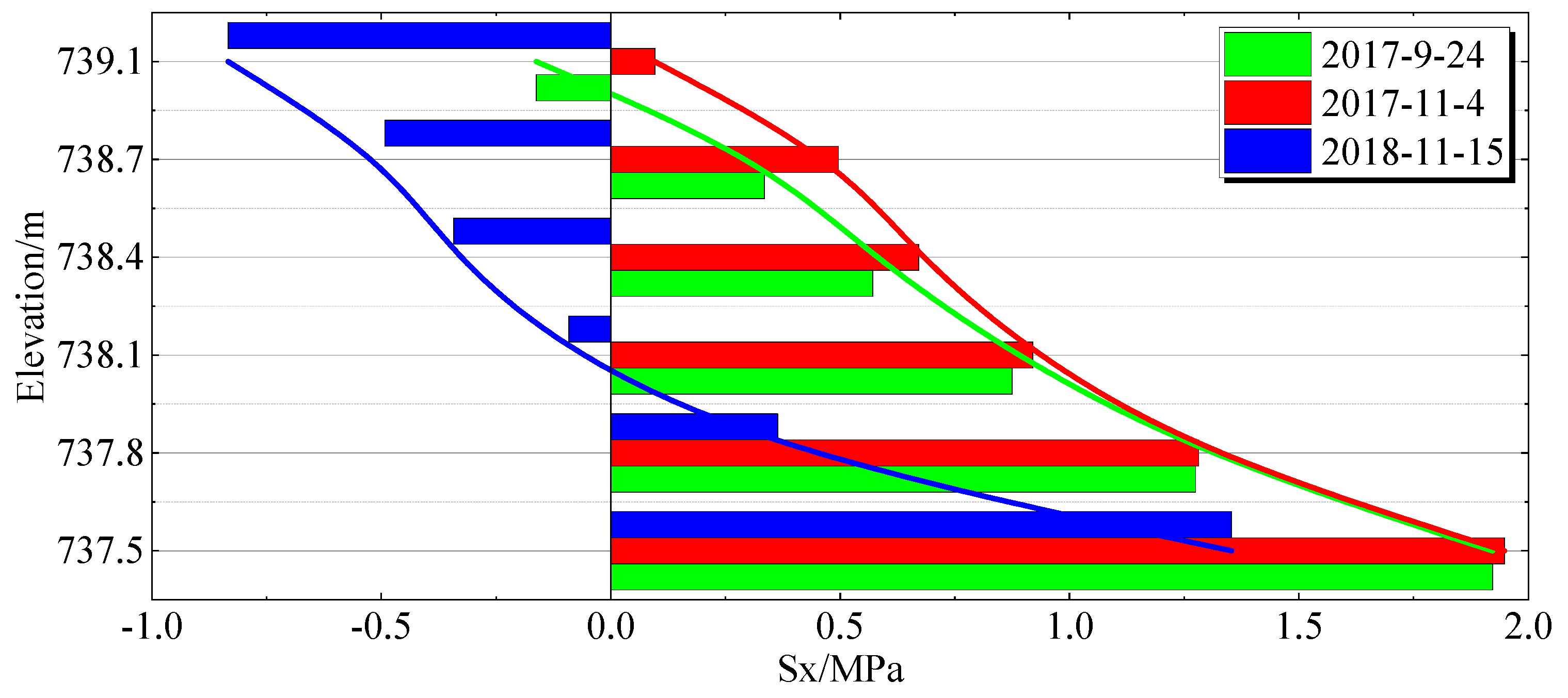
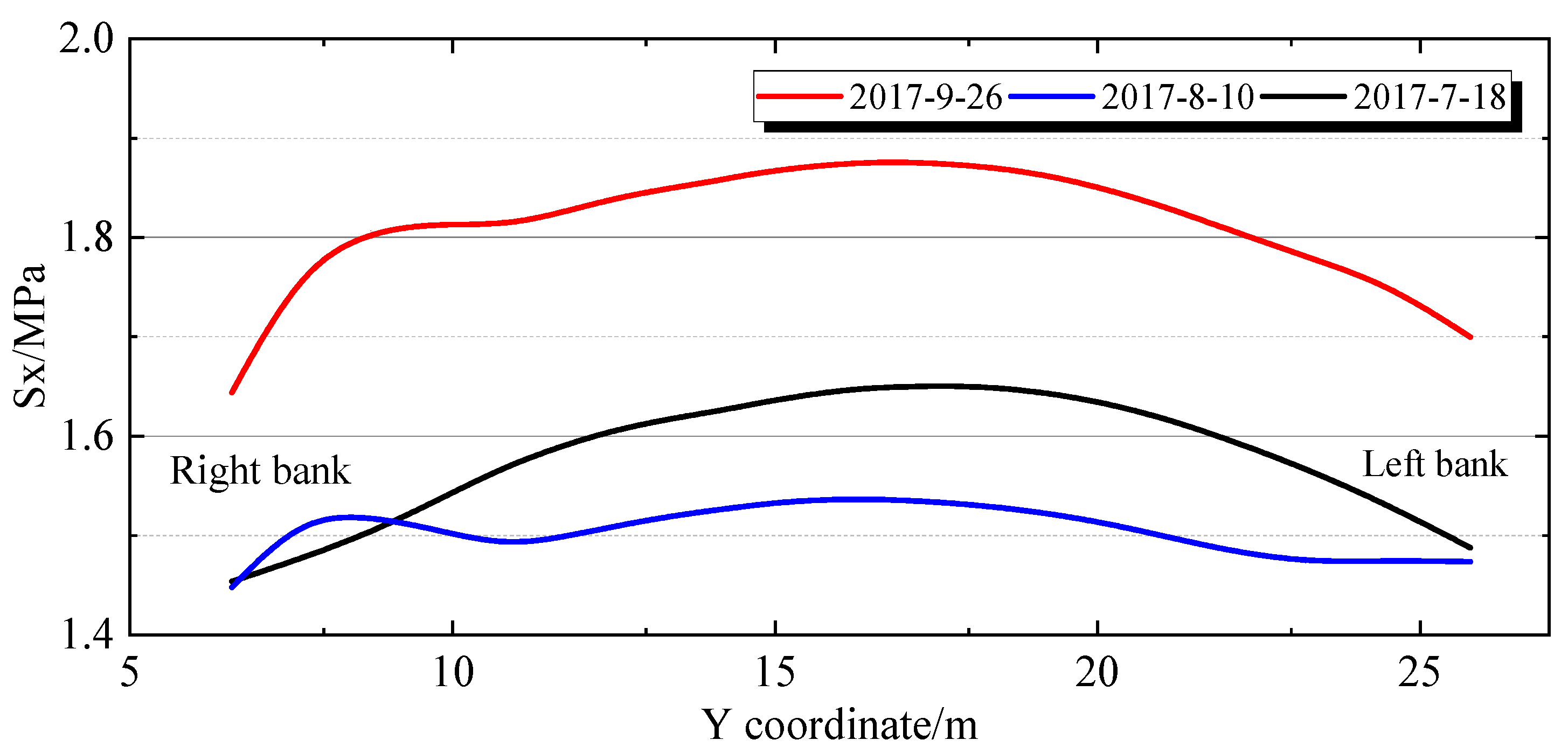
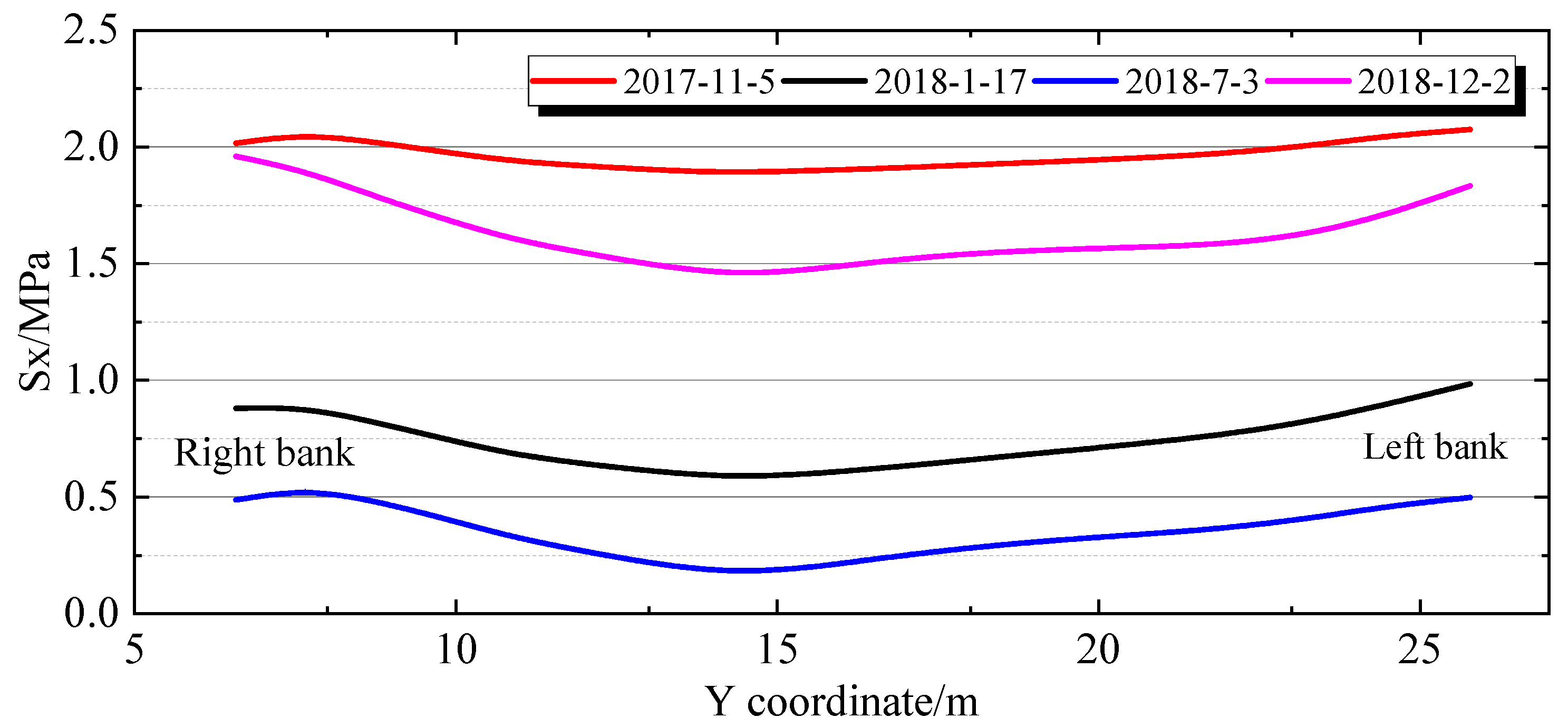
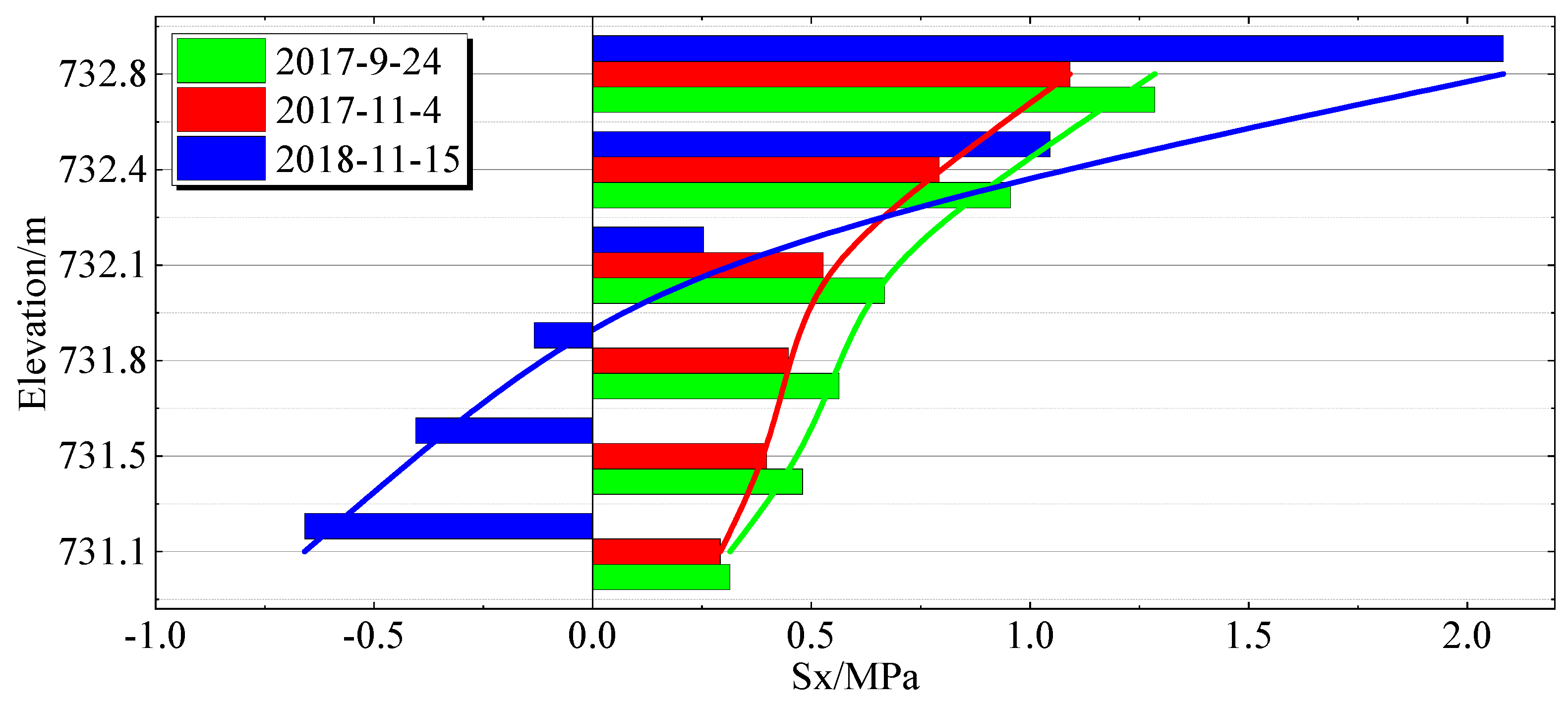
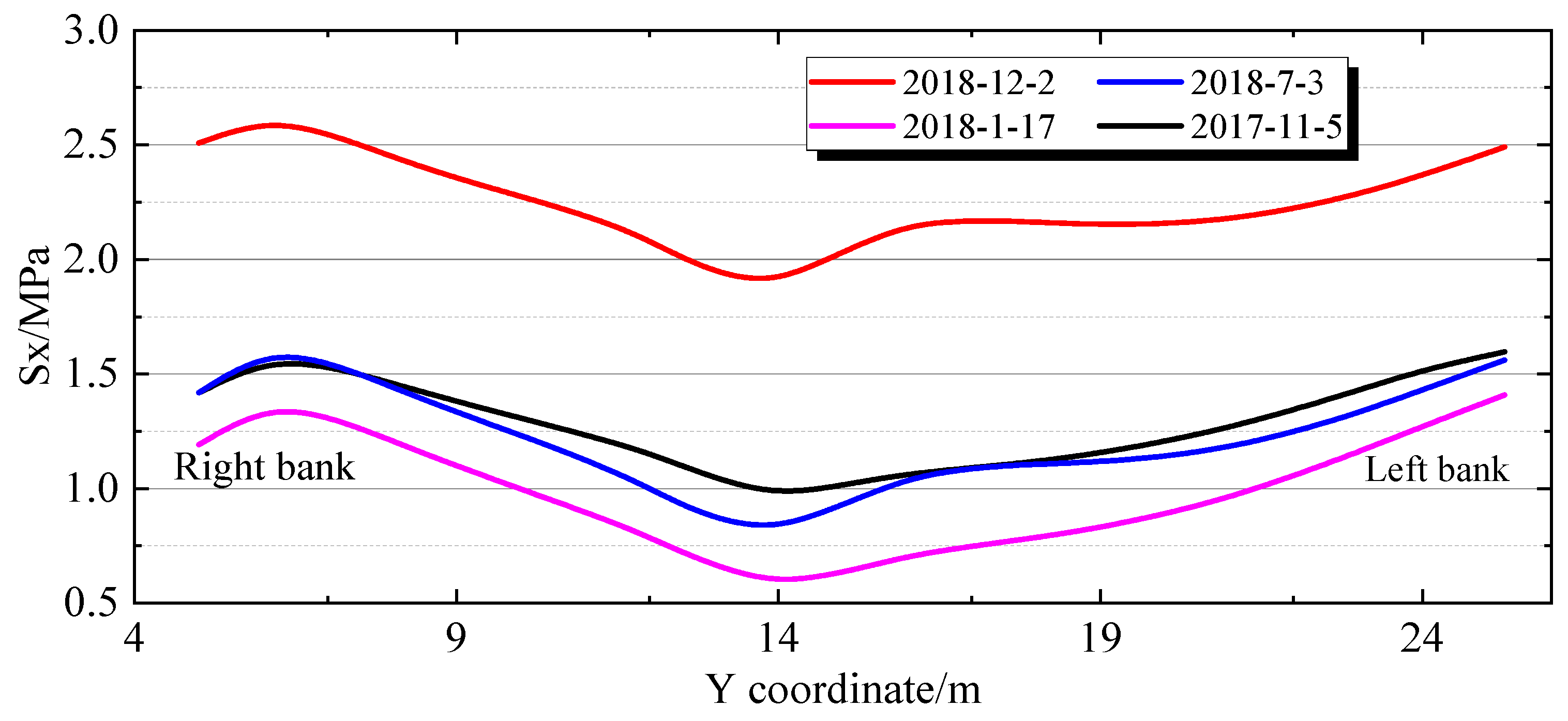
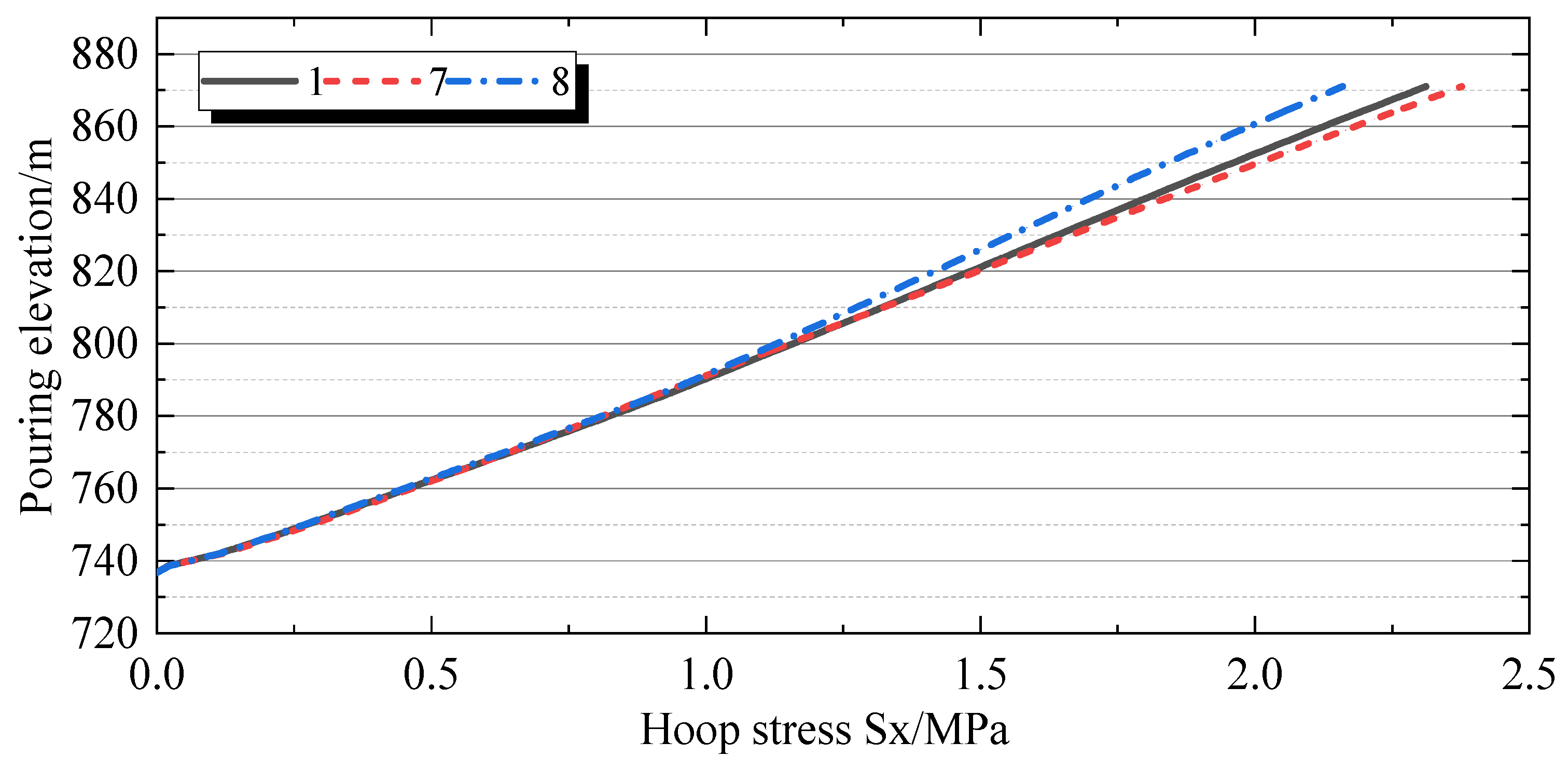
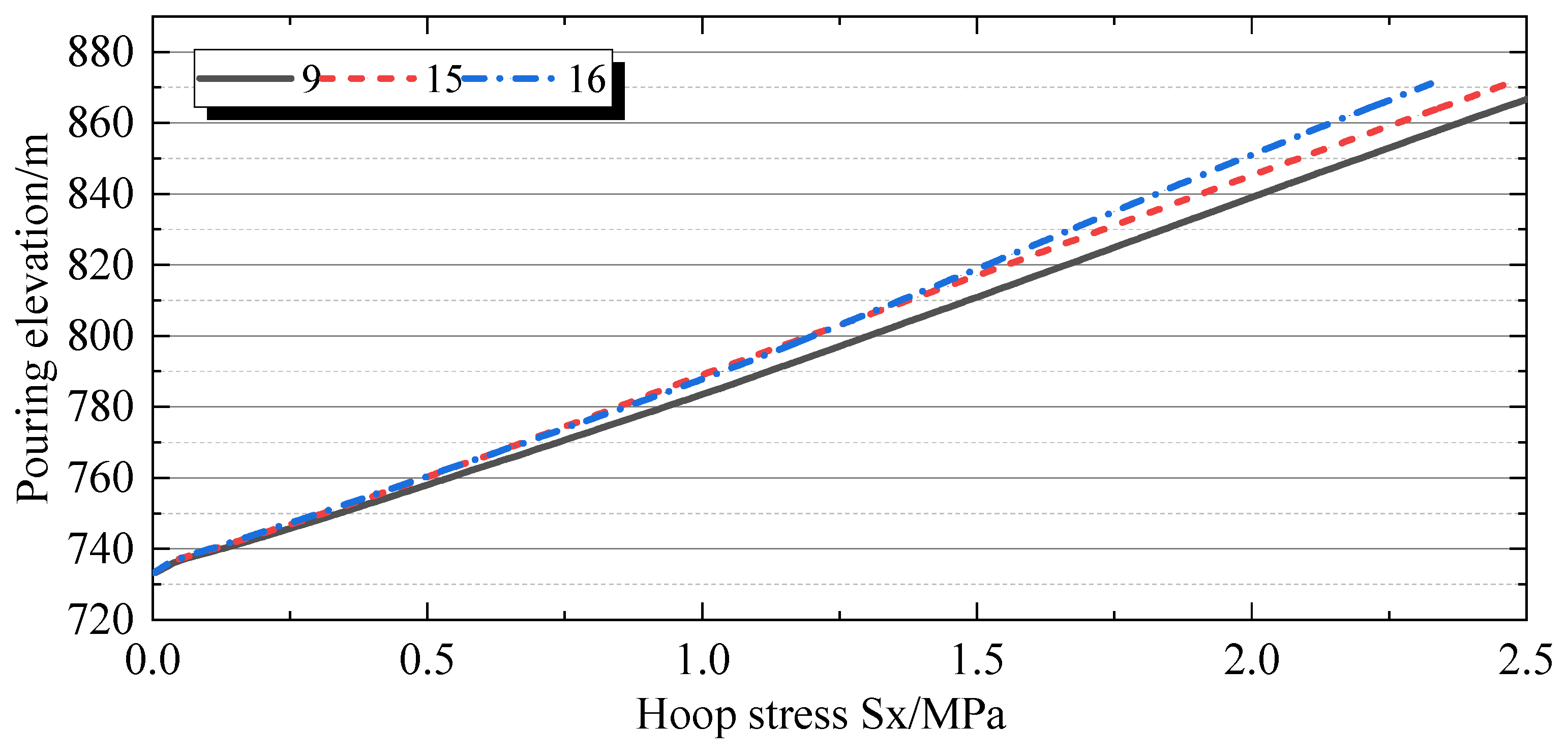
4.2.2. Stress Spatial Distribution Characteristics
4.3. Stress Sensitivity Analysis of the 733 Gallery
4.3.1. Influence of Self-Weight
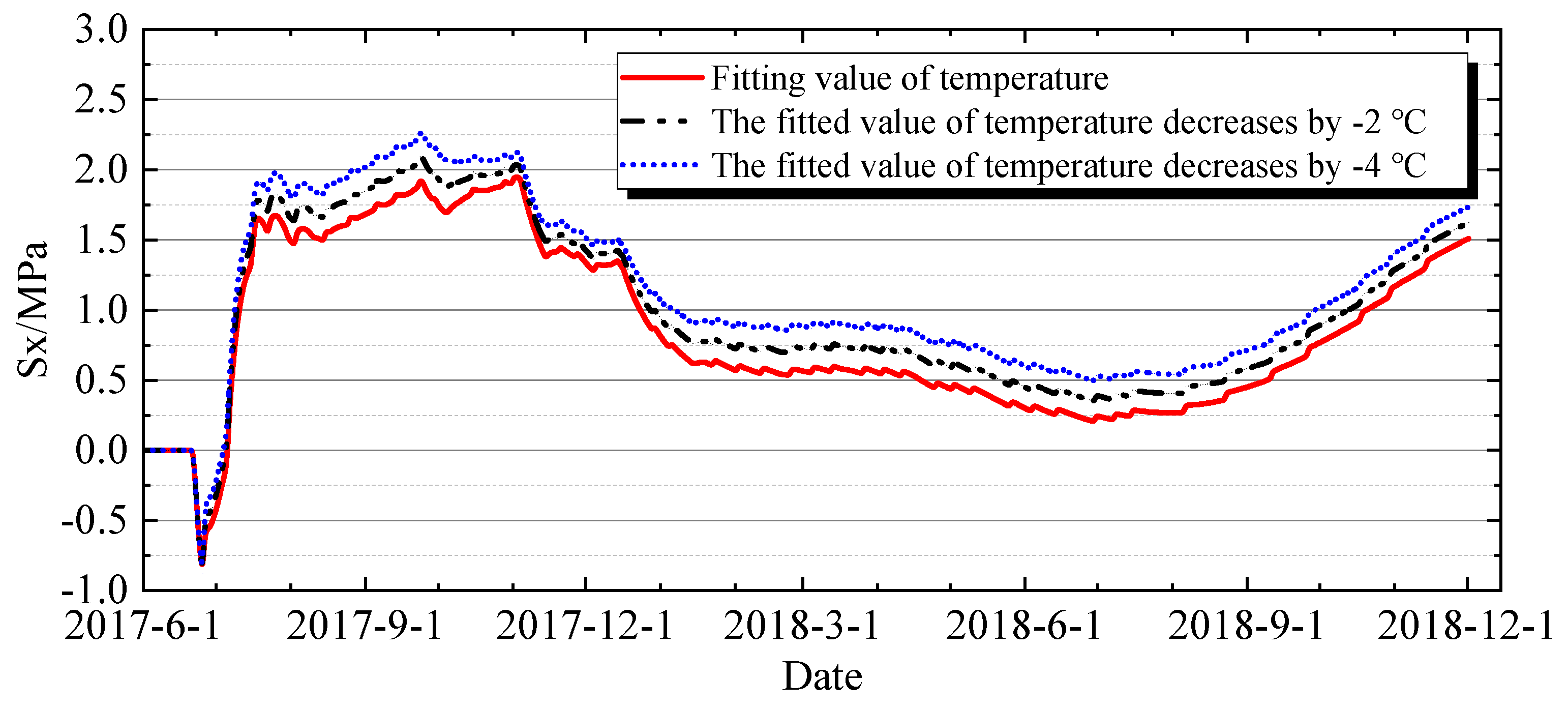
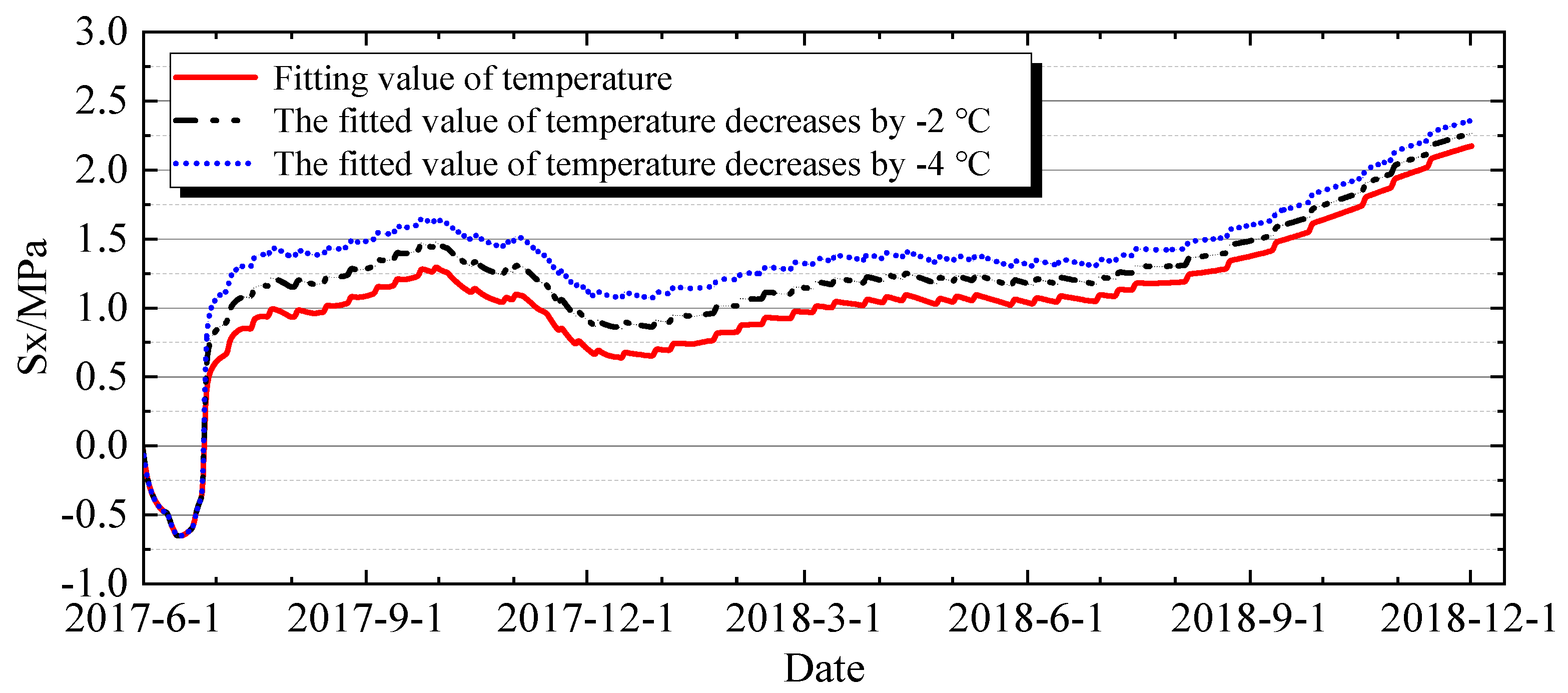
4.3.2. Impact of Temperature Loads
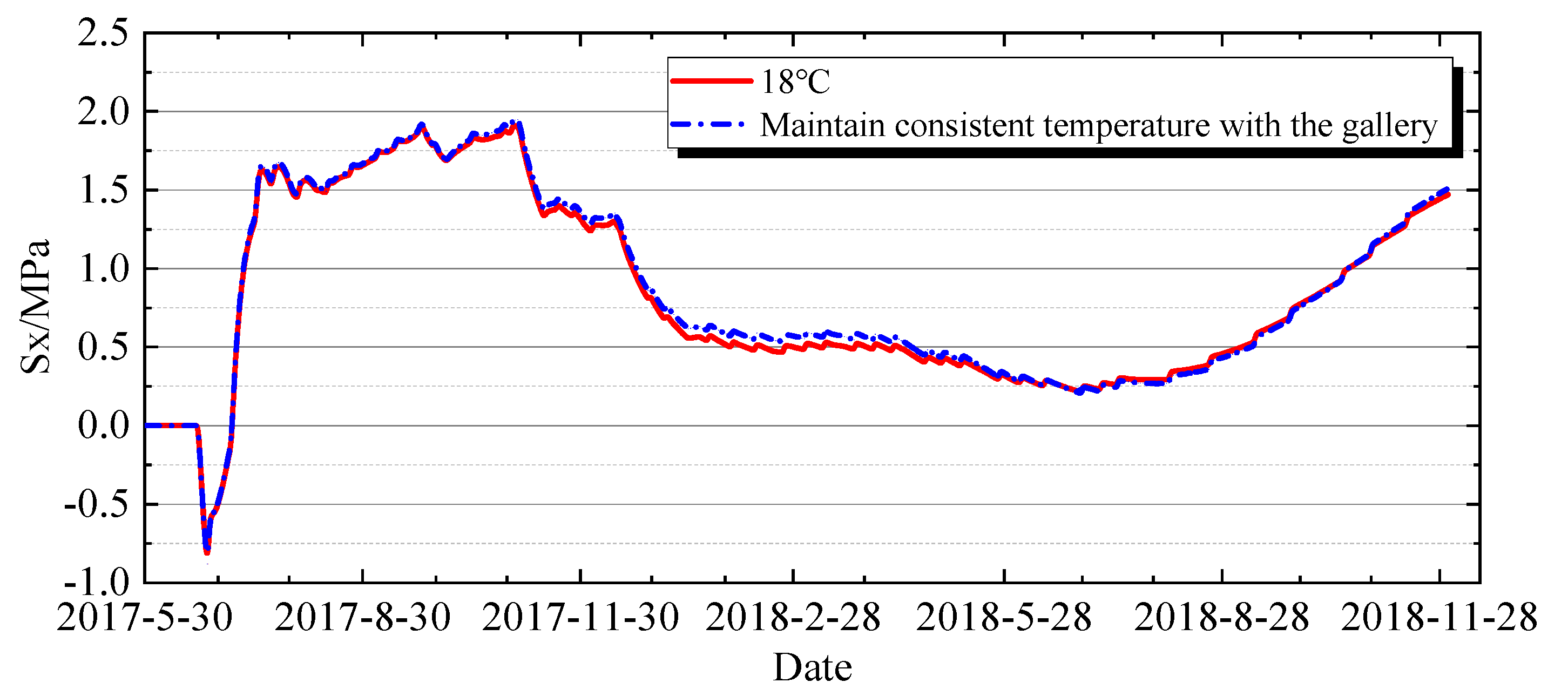
4.3.3. Impact of Air Temperature on the Gallery
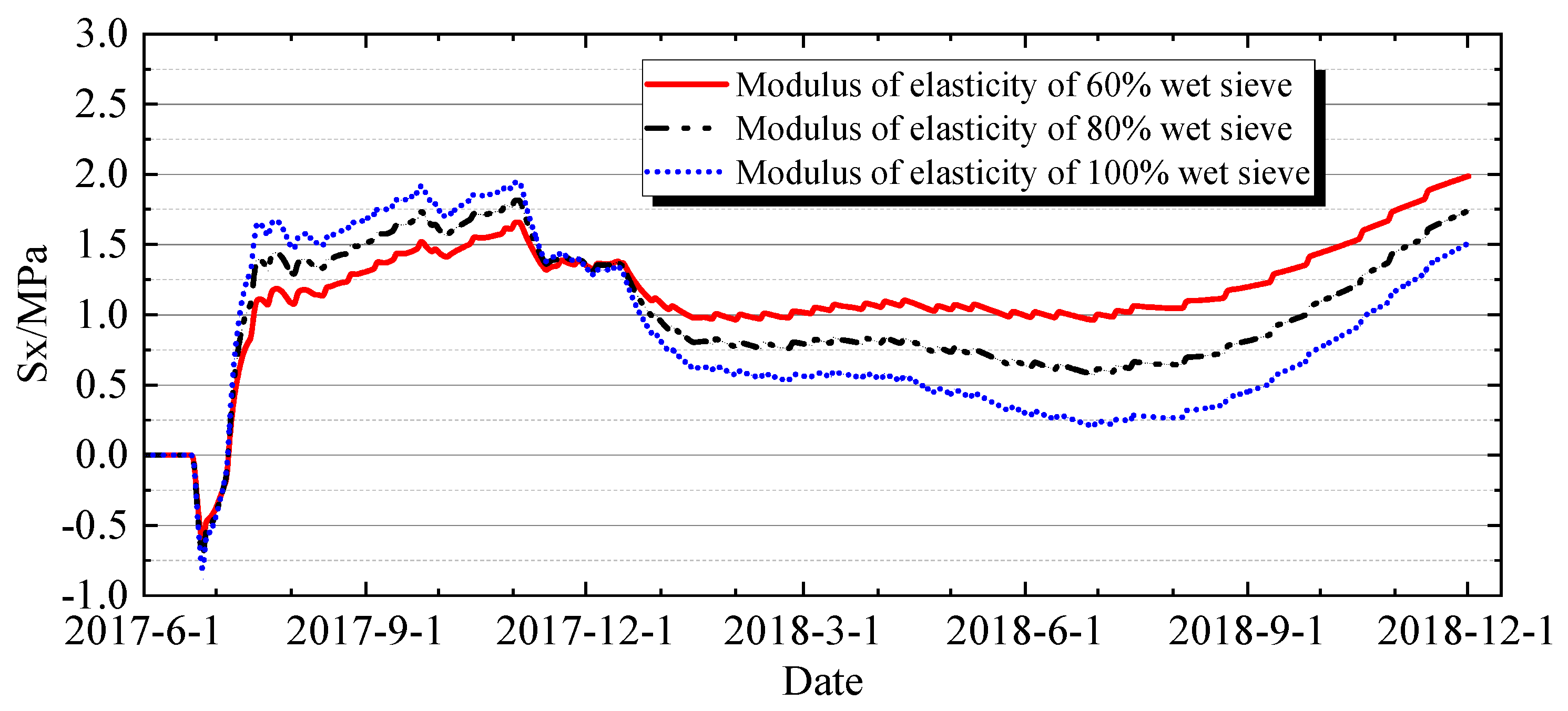
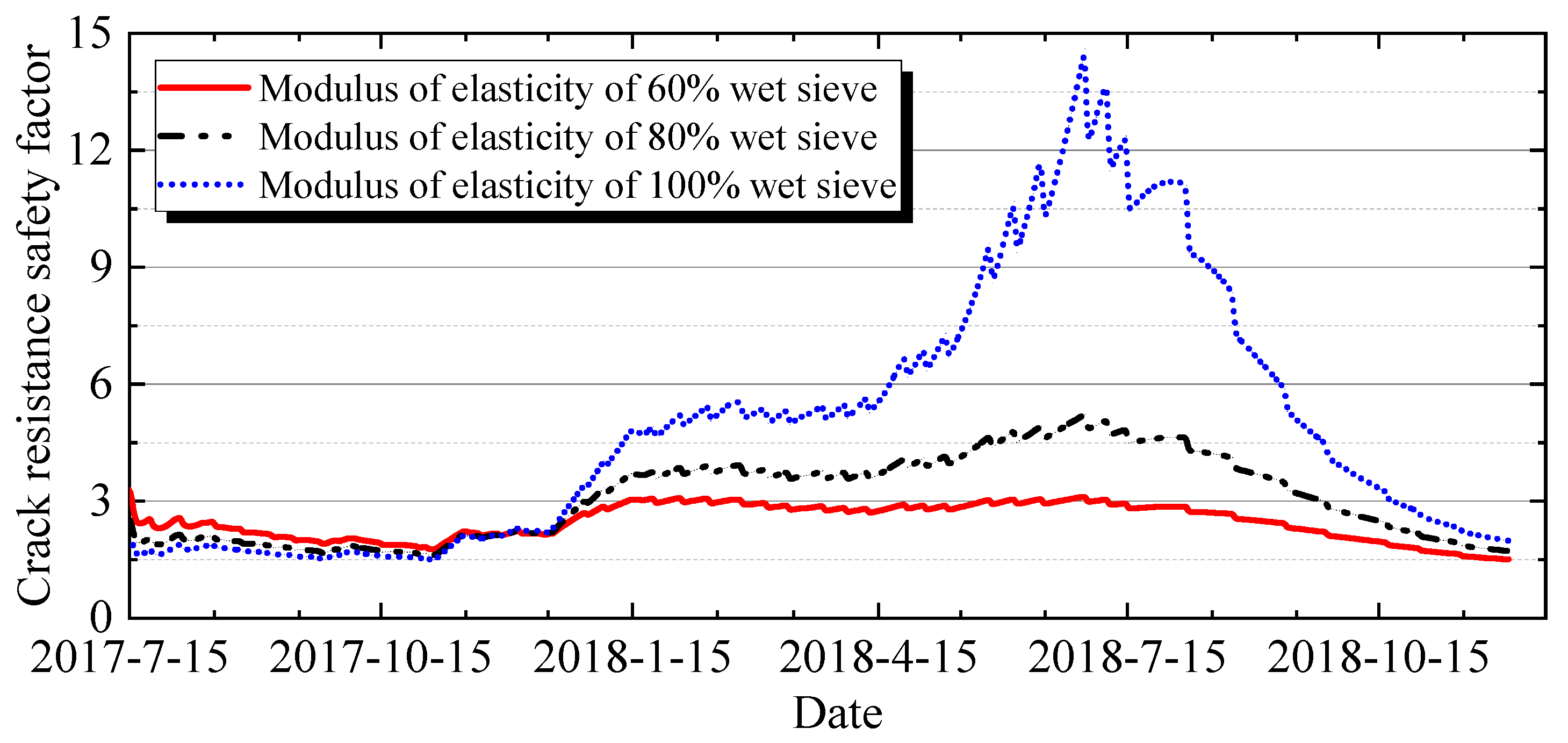
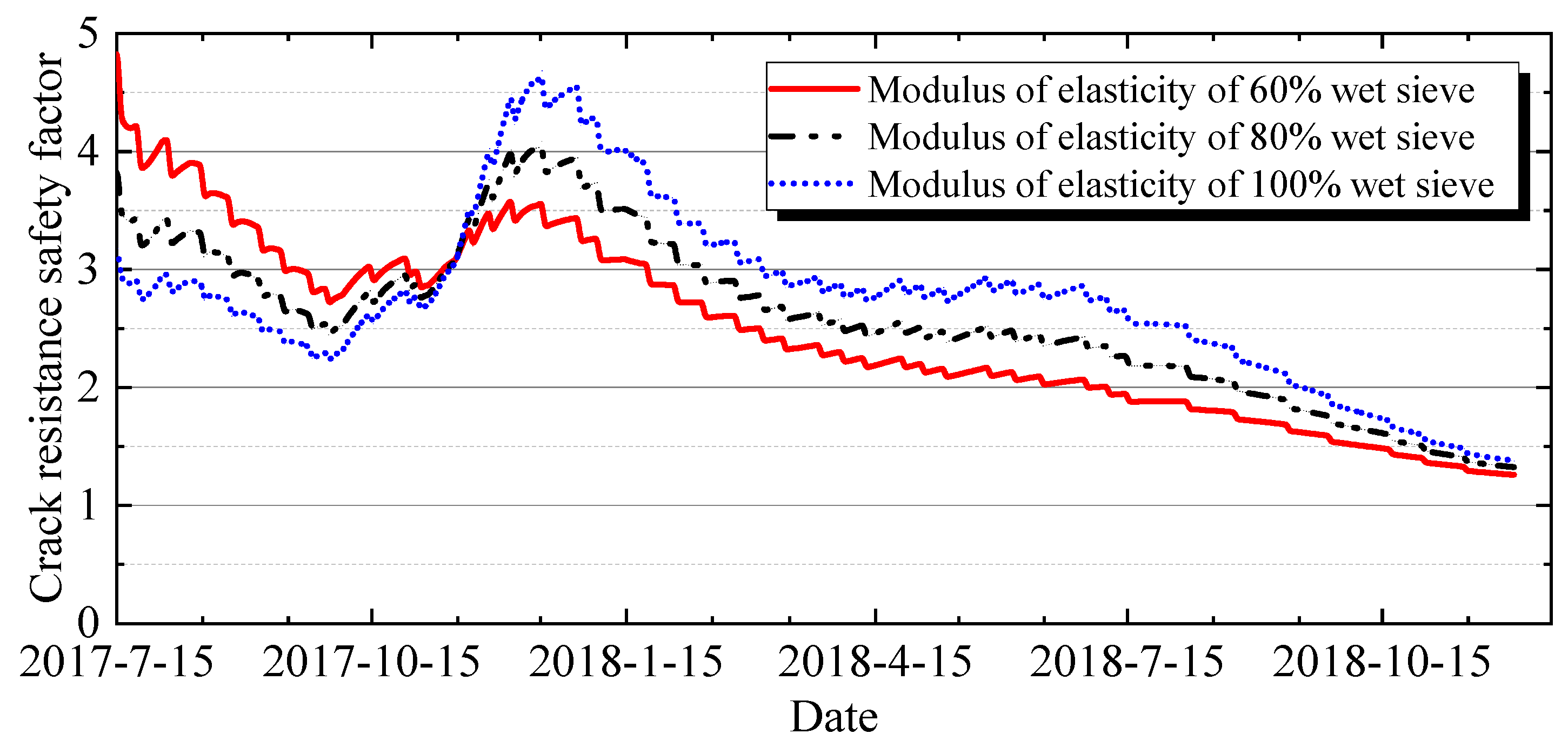
4.3.4. Impact of Wet-Screened and Fully Graded Aggregate Parameters on Thermal Stress
4.3.5. Impact of Cooling Water Pipes on the Top of the Gallery
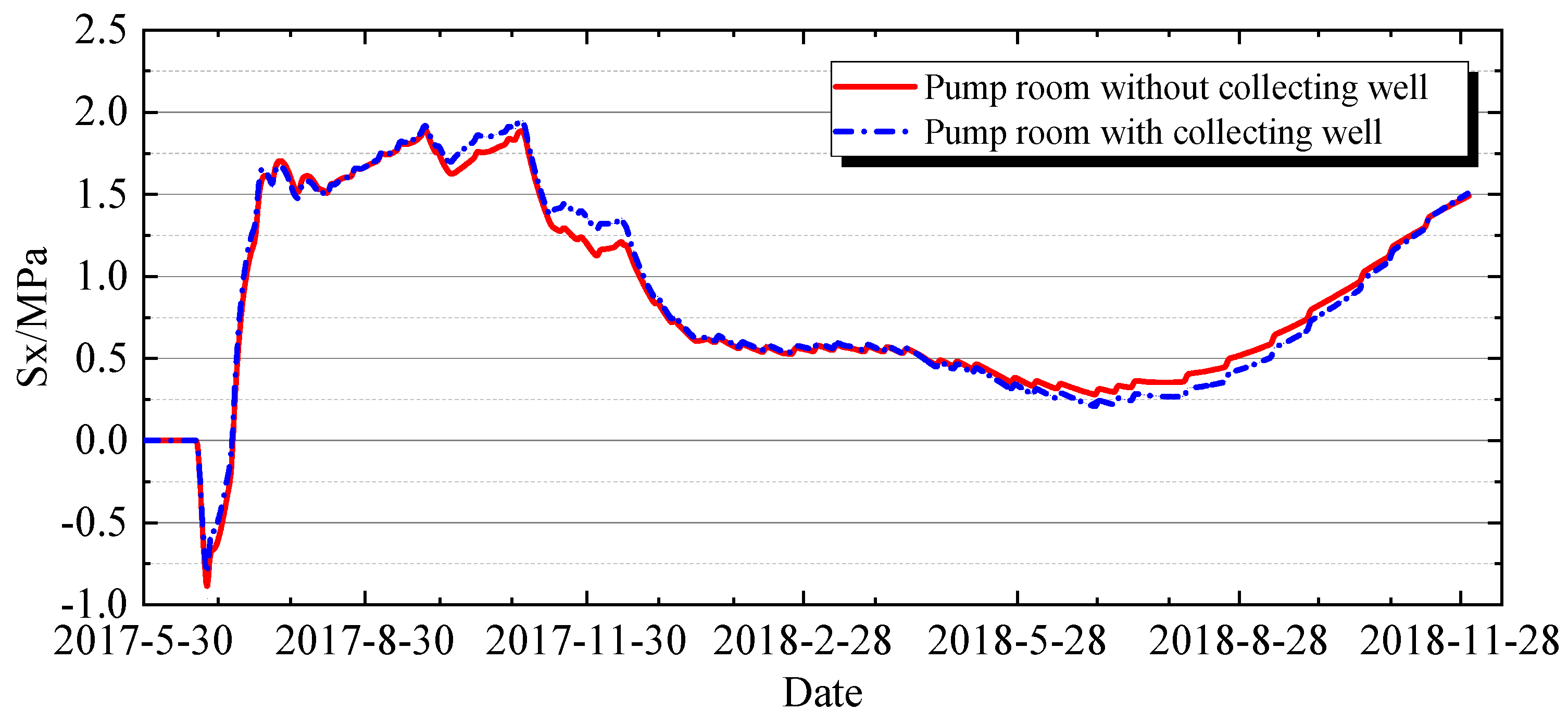
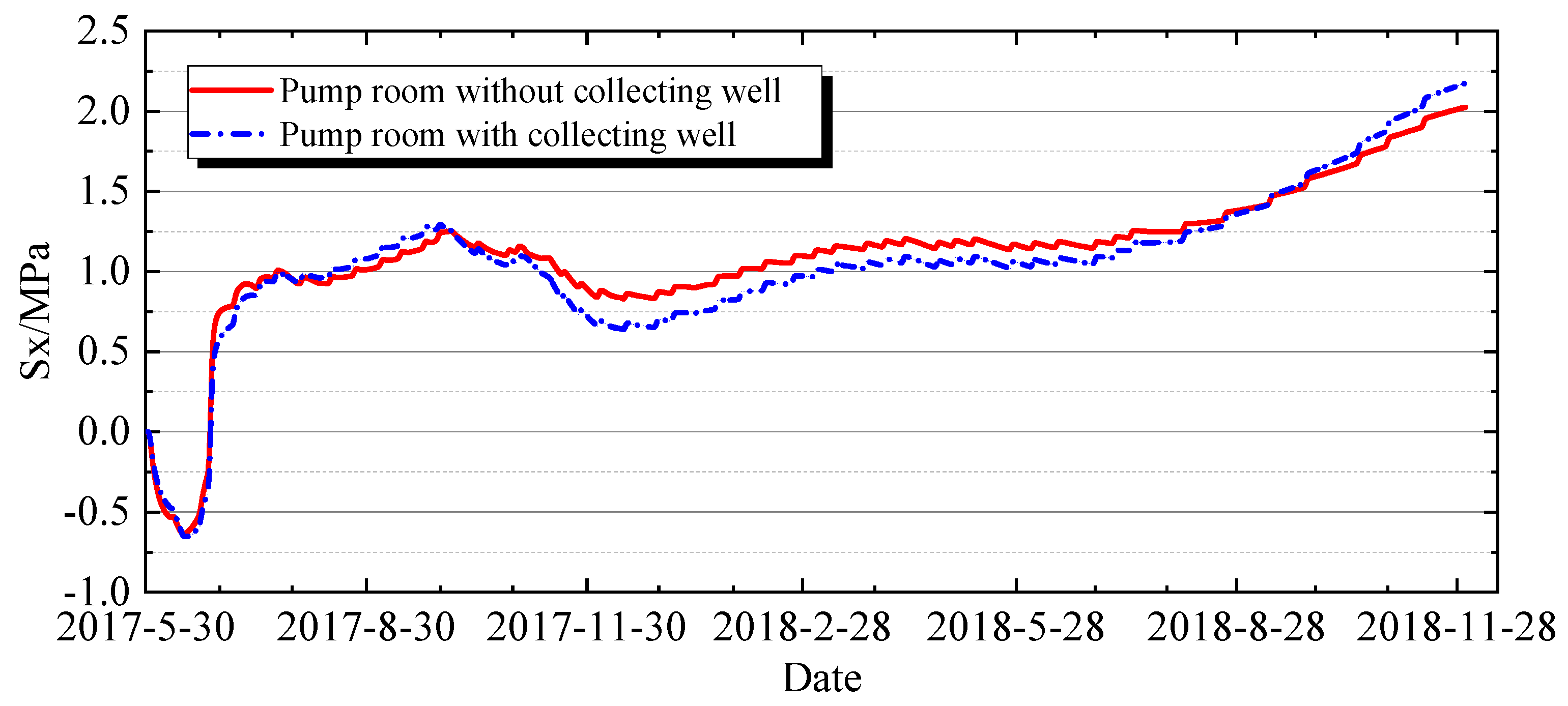
4.3.6. Impact of Pump Room and Collecting Well
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- John, R.; Balakrishnan, S.D. Investigations on seismic response of Idukki Arch Dam considering concrete ageing. Innov. Infrastruct. Solut. 2025, 10, 404. [Google Scholar] [CrossRef]
- Pan, X.; Wang, G.; Lu, W.; Qi, Z.; Chen, M.; Yan, P. Fragility analysis of high arch dam against far-field underwater blast. Eng. Struct. 2024, 316, 118568. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, X.; Liu, Y.; Wang, J.; Yi, K.; Yan, J.; Chen, H. Effect of attached outlets on the dynamic response of arch dams. Eng. Struct. 2024, 302, 117392. [Google Scholar] [CrossRef]
- Liu, J.; Wang, F.; Wang, X.; Hu, Z.; Liang, C. Temperature monitoring and cracking risk analysis of corridor top arch of Baihetan arch dam during construction period. Eng. Fail. Anal. 2025, 16, 108903. [Google Scholar] [CrossRef]
- Lin, P.; Shi, J.; Wei, P.; Fan, Q.; Wang, Z. Shallow unloading deformation analysis on Baihetan super-high arch dam foundation. Bull. Eng. Geol. Environ. 2019, 78, 5551–5568. [Google Scholar] [CrossRef]
- Lin, P.; Guan, J.; Peng, H.; Shi, J. Horizontal cracking and crack repair analysis of a super high arch dam based on fracture toughness. Eng. Fail. Anal. 2019, 97, 72–90. [Google Scholar] [CrossRef]
- Zhuang, D.; Ma, K.; Tang, C.; Cui, X.; Yang, G. Study on crack formation and propagation in the galleries of the Dagangshan high arch dam in Southwest China based on microseismic monitoring and numerical simulation. Int. J. Rock Mech. Min. Sci. 2019, 115, 157–172. [Google Scholar] [CrossRef]
- Lin, P.; Liu, H.; Li, Q.; Hu, H. Effects of Outlets on Cracking Risk and Integral Stability of Super-High Arch Dams. Sci. World J. 2014, 2014, 312827. [Google Scholar] [CrossRef] [PubMed]
- Luo, D.; Lin, P.; Li, Q.; Zheng, D.; Liu, H. Effect of the impounding process on the overall stability of a high arch dam: A case study of the Xiluodu dam, China. Arab. J. Geosci. 2015, 8, 9023–9041. [Google Scholar] [CrossRef]
- Yang, G.; Zhao, A.; Sun, J.; Niu, J.; Zhang, J.; Wang, L. Progressive failure process-considered deformation safety diagnosis method for in-service high arch dam. Eng. Fail. Anal. 2024, 163, 108570. [Google Scholar] [CrossRef]
- Yan, C.; Tu, J.; Liang, H.; Guo, S.; Li, D. Seismic failure analysis of a high arch dam-foundation multiple nonlinear coupling system. Soil Dyn. Earthq. Eng. 2024, 187, 109001. [Google Scholar] [CrossRef]
- Xin, J.; Tang, Q.; Zhou, J.; Zhou, Y.; Luo, C.; Jiang, Y. A novel method for calculating the ultimate bearing capacity of in-service RC arch bridges using sectional constitutive relation. Appl. Math. Model. 2025, 138, 115829. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, L.; Yang, B.Q.; Dong, J.; Chen, J. Geomechanical model test on dam stability and application to Jinping High arch dam. Int. J. Rock Mech. Min. Sci. 2015, 76, 1–9. [Google Scholar] [CrossRef]
- Ma, K.; Zhuang, D.; Tang, C.; Jin, F.; Tang, S. Study on formation causes of gallery cracks in Dagangshan high arch dam based on microseismic monitoring. Chin. J. Rock Mech. Eng. 2018, 37, 1608–1617. [Google Scholar]
- Wieland, M.; Kirchen, G.F. Long-term dam safety monitoring of Punt dal Gall arch dam in Switzerland. Front. Struct. Civ. Eng. 2012, 6, 76–83. [Google Scholar] [CrossRef]
- Dubey, C.S.; Venkatachalam, K.; Ratnam, M.; Shekhar, P. Causes of seepage water in drainage and grouting galleries of the Pandoh Dam, Central Himalaya. Bull. Eng. Geol. Environ. 2004, 63, 19–23. [Google Scholar] [CrossRef]
- Zhu, B.F. Thermal Stresses and Temperature Control of Mass Concrete; Water and Power Press: Beijing, China, 2012. [Google Scholar]
- Wang, W.; Ding, J.; Wang, G.; Zou, L.; Chen, S. Stability analysis of the temperature cracks in Xiaowan arch dam. Sci. China (Technol. Sci.) 2011, 54, 547–555. [Google Scholar] [CrossRef]
- Sheibany, F.; Ghaemian, M. Effects of Environmental Action on Thermal Stress Analysis of Karaj Concrete Arch Dam. J. Eng. Mech. 2006, 132, 532–544. [Google Scholar] [CrossRef]
- Pan, J.; Feng, Y.; Xu, Y.; Jin, F.; Zhang, C.; Zhang, B. Chemo-damage modeling and cracking analysis of AAR-affected concrete dams. Sci. China (Technol. Sci.) 2013, 56, 1449–1457. [Google Scholar] [CrossRef]
- Wei, P.; Lin, P.; Peng, H.; Yang, Z.; Qiao, Y. Analysis of cracking mechanism of concrete galleries in a super high arch dam. Eng. Struct. 2021, 248, 113227. [Google Scholar] [CrossRef]
- Satoru, I.; Mitsuo, N. Temperature Distribution Analysis of Concrete in Fill Dam Gallery. Bull. Univ. Osaka Prefect. Ser B Agric. Biol. 1986, 38, 35–43. [Google Scholar]
- Malla, S.; Wieland, M. Analysis of an arch-gravity dam with a horizontal crack. Comput. Struct. 1999, 72, 267–278. [Google Scholar] [CrossRef]
- Lin, P.; Ning, Z.; Shi, J.; Liu, C.; Chen, W.; Tan, Y. Study on the gallery structure cracking mechanisms and cracking control in dam construction site. Eng. Fail. Anal. 2021, 121, 105135. [Google Scholar] [CrossRef]
- Cavuslu, M. Evaluating the Relationship between Reservoir Level Changes and Earthquake Damage Responses of High Arch Dams: A 3D Numerical Study of Ermenek Arch Dam (220 m) in Turkey. Adv. Civ. Eng. 2023, 2023, 8944853. [Google Scholar] [CrossRef]
- Lin, S.; Xie, Z. A Jacobi_PCG solver for sparse linear systems on multi-GPU cluster. J. Supercomput. 2017, 73, 433–454. [Google Scholar] [CrossRef]
- Lin, S.; Xie, Z. A new recursive formula for integration of polynomial over simplex. Appl. Math. Comput. 2020, 376, 125140. [Google Scholar] [CrossRef]
- Yuan, M.; Zhu, X.; Han, L.; Qi, Y.; Xie, Z.; Qin, X.; Dong, Y. Research on the Full Life Cycle Deformation, Stress Response, and Dynamic Fatigue Performance of Concrete Structures in Pump Stations. Buildings 2024, 14, 4052. [Google Scholar] [CrossRef]
- SL/T 352-2020; Test Code for Hydraulic Concrete. China Water and Power Press: Beijing, China, 2020.
- Xie, Z. Study and Application of Several Key Algorithms for Hydraulic Concrete Temperature Control Simulation; Hohai University: Nanjing, China, 2012. [Google Scholar]











| Category | Thermal Conductivity Coefficient / (kJ·m−1·h−1·°C−1) | Specific Heat / (kJ·kg−1·°C−1) | Thermal Diffusivity / (m2·h−1) | Linear Expansion Coefficient / (10−6·°C−1) | Final Modulus of Elasticity (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| Foundation | 7.598 | 0.886 | 0.003200 | 6.8 | 35,000 | 0.2 |
| C18035 | 7.700 | 0.839 | 0.003656 | 7.1 | 36,500 | 0.167 |
| Number of Periods | Water Temperature (°C) | Flow (m3/h) | Duration (d) |
|---|---|---|---|
| Initial stage | 8~16 | 1.5~2.3 | 15 |
| Intermediate stage | 14 | 1.2 | 30 |
| Second stage | 9~10 | 1.5 | 30 |
| Insulation Area | Insulation Material | Equivalent Heat Transfer Coefficient W/(m2·°C) | Insulation Time |
|---|---|---|---|
| Warehouse Surface | Insulation Roll Material | 3.0 | Insulate immediately after pouring |
| Upstream and Downstream Surfaces | Polyurethane/Styrofoam | 2.0 | 30 d |
| Galleries, etc. | Insulation Roll Material | 5.0 | Consider it as exposed after closure |
| Conditions | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | |
|---|---|---|---|---|---|---|---|---|
| Self-Weight | Creep | Vault Water Pipe | External Ambient Temperature | Gallery Temperature | Elastic Modulus | Collecting Well and Pump Room | Describe | |
| 1 | √ | √ | √ | × | × | √ | √ | |
| 2 | √ | √ | √ | √ | √ | √ | ||
| 3 | √ | √ | √ | √ | √ | √ | √ | |
| 4 | √ | √ | √ | √ | √ | √ | √ | Item ⑤ reduce by 2 °C |
| 5 | √ | √ | √ | √ | √ | √ | √ | Item ⑤ reduce by 4 °C |
| 6 | √ | √ | √ | √ | √ | √ | √ | 60% of item ⑥ |
| 7 | √ | √ | √ | √ | √ | √ | √ | 80% of item ⑥ |
| 8 | √ | √ | × | √ | √ | √ | √ | Item ③ is not considered |
| 9 | √ | √ | √ | √ | √ | √ | √ | Item ⑧ remains constant at 18 °C |
| 10 | √ | √ | √ | √ | √ | √ | × | Item ⑧ filling of cavity entities |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Yuan, M.; Xu, H.; Peng, J.; Chen, Q. The Spatiotemporal Distribution Characteristics and Sensitivity Analysis of Stress in the Galleries of a Super-High Arch Dam During Construction. Buildings 2025, 15, 3967. https://doi.org/10.3390/buildings15213967
Xie Z, Yuan M, Xu H, Peng J, Chen Q. The Spatiotemporal Distribution Characteristics and Sensitivity Analysis of Stress in the Galleries of a Super-High Arch Dam During Construction. Buildings. 2025; 15(21):3967. https://doi.org/10.3390/buildings15213967
Chicago/Turabian StyleXie, Zhiqiang, Min Yuan, Hang Xu, Jiaxu Peng, and Qin Chen. 2025. "The Spatiotemporal Distribution Characteristics and Sensitivity Analysis of Stress in the Galleries of a Super-High Arch Dam During Construction" Buildings 15, no. 21: 3967. https://doi.org/10.3390/buildings15213967
APA StyleXie, Z., Yuan, M., Xu, H., Peng, J., & Chen, Q. (2025). The Spatiotemporal Distribution Characteristics and Sensitivity Analysis of Stress in the Galleries of a Super-High Arch Dam During Construction. Buildings, 15(21), 3967. https://doi.org/10.3390/buildings15213967







