Reuse of Solid Bricks in Construction: An Experimental Work
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Program
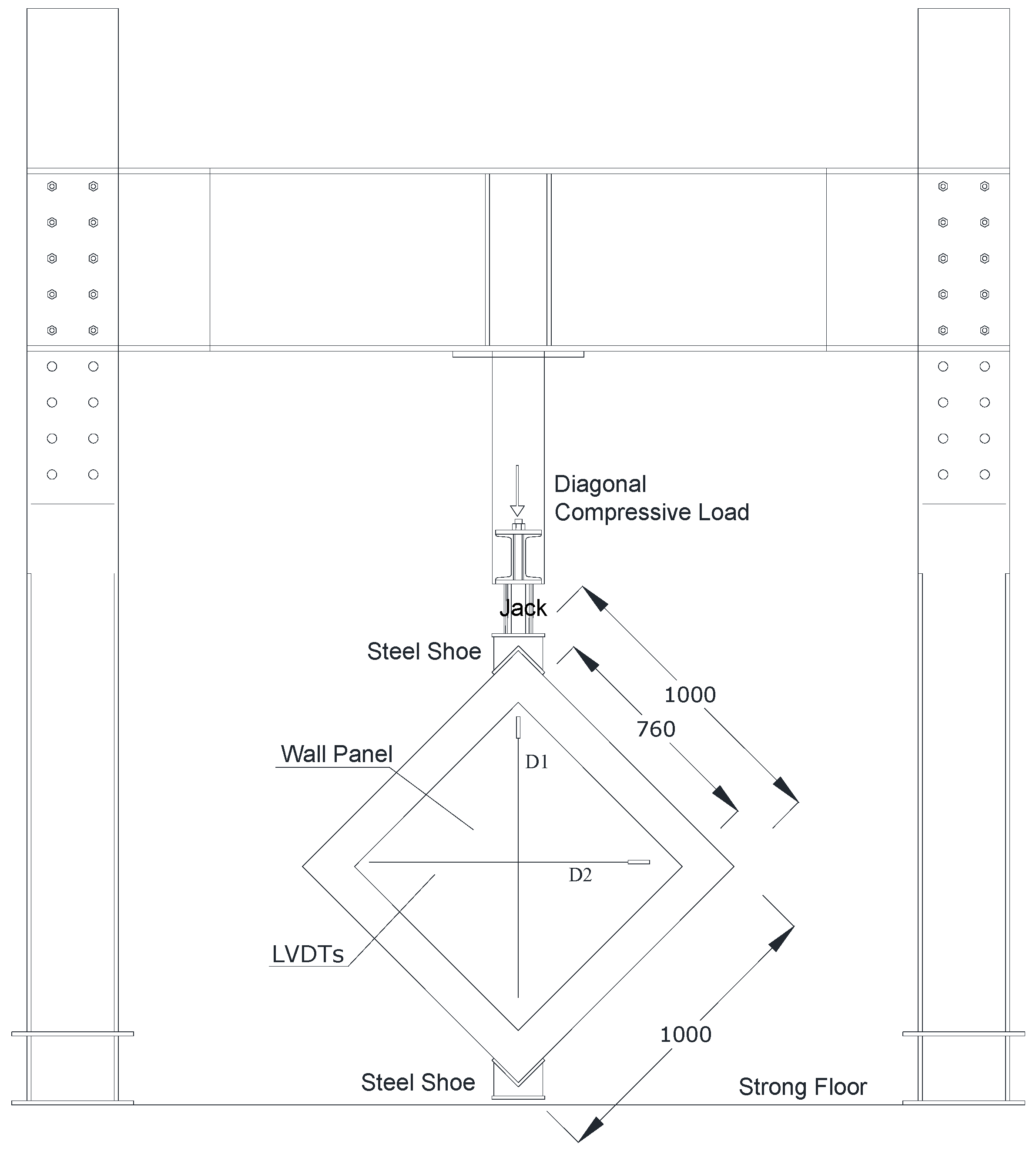
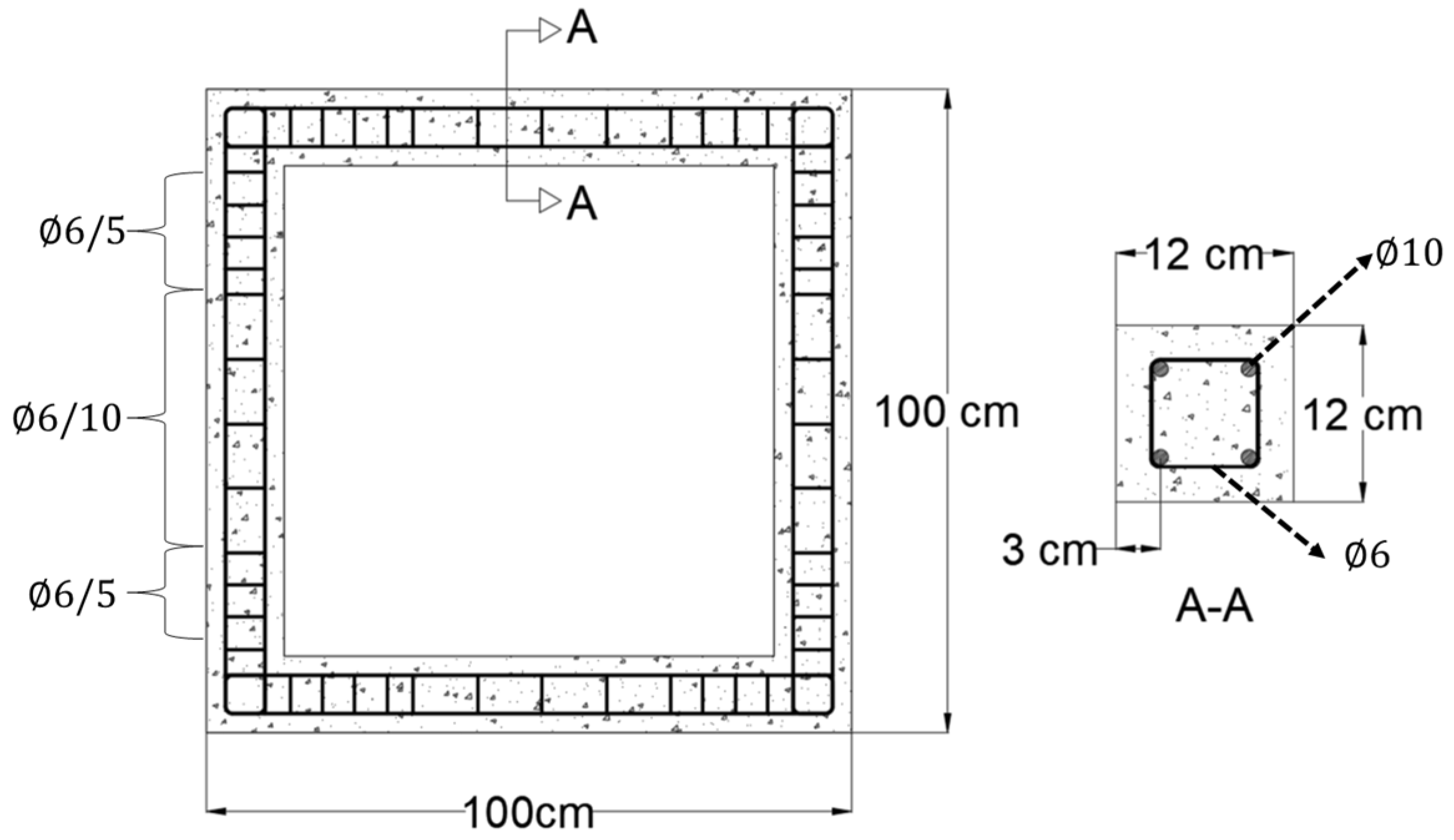
2.1.1. Design of Wall Specimens
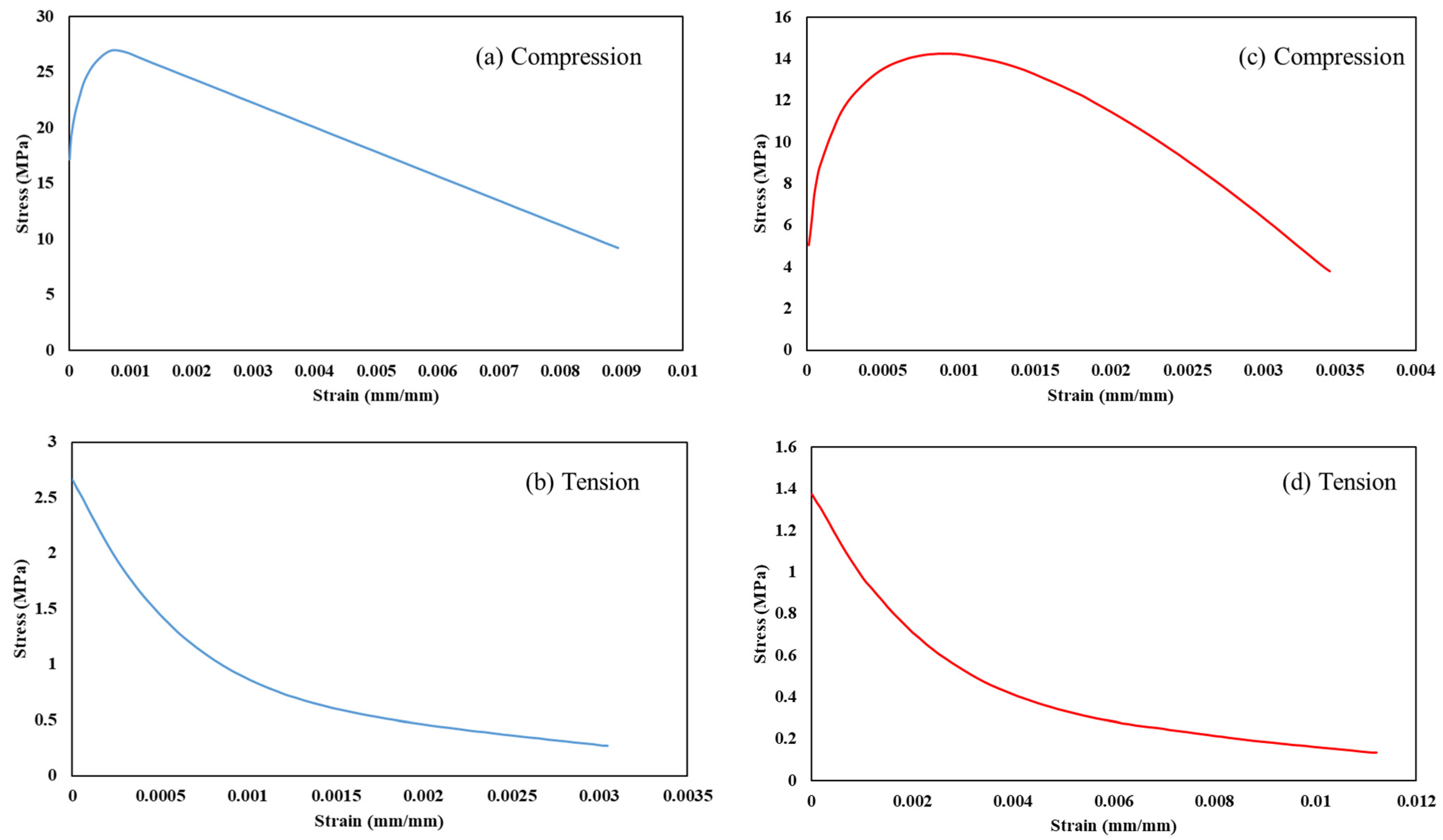
2.1.2. Material Testing
2.1.3. Wall Panels and Testing
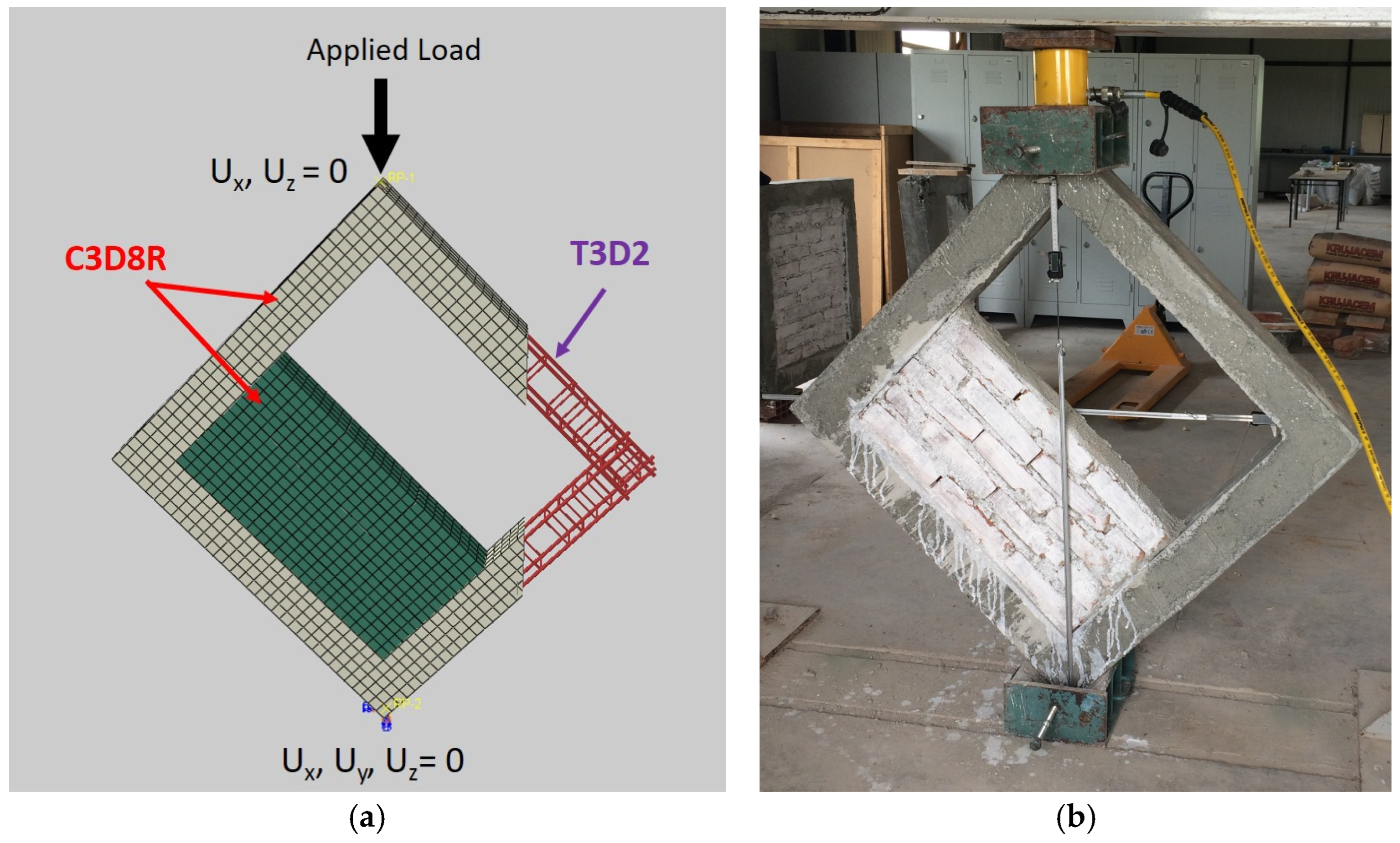
2.2. Finite Element Modeling
3. Results and Discussion
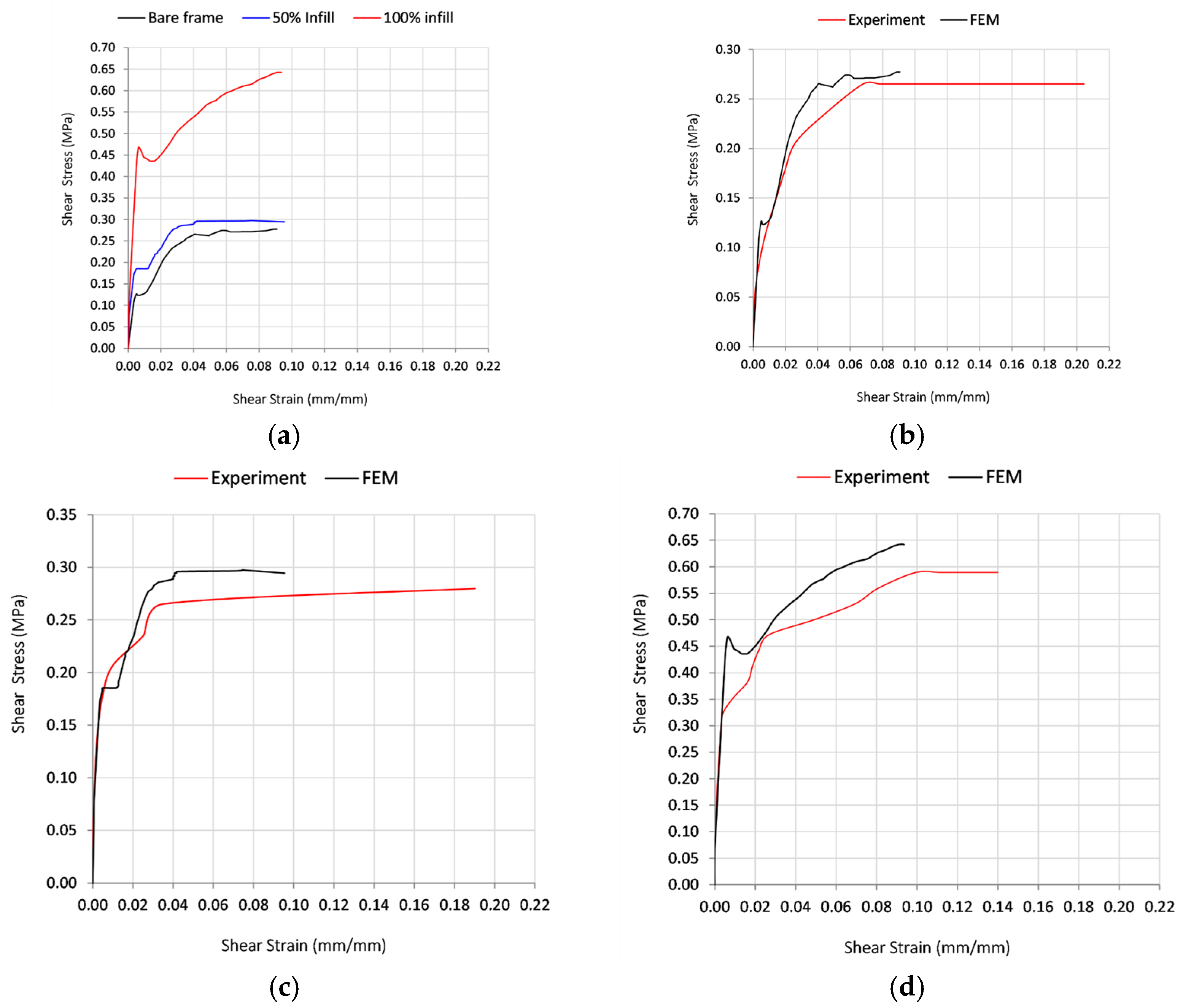
3.1. Experimental Results
3.2. FEM Results
4. Discussion: Engineering Background, Practical Value, and Limitations
5. Significance of the Study
6. Conclusions
- Recycled solid-brick infills significantly enhanced the in-plane capacity of reinforced concrete (RC) frames, leading to an increase of approximately 149% in diagonal shear strength compared with the bare frame, while maintaining acceptable deformation compatibility.
- A clear trade-off between strength and ductility was observed: fully infilled frames exhibited the highest stiffness and strength but reduced ductility by around 40%, indicating that partial or discontinuous infills may offer a balanced seismic response.
- The finite element model, based on the Concrete Damaged Plasticity (CDP) formulation with cohesive interface contact, accurately reproduced the experimental load–displacement behavior with deviations in peak load below 8%, confirming its adequacy for macro-scale structural analysis.
- The reuse of intact solid bricks presents both structural and environmental advantages, reducing construction waste and embodied CO2 emissions while enhancing seismic resilience. The approach supports circular-construction practices and aligns with Sustainable Development Goal 11 (Sustainable Cities and Communities).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Seco, A.; Omer, J.; Marcelino, S.; Espuelas, S.; Prieto, E. Sustainable unfired bricks manufacturing from construction and demolition wastes. Constr. Build. Mater. 2018, 167, 154–165. [Google Scholar] [CrossRef]
- Dos Reis, G.S.; Cazacliu, B.G.; Cothenet, A.; Poullain, P.; Wilhelm, M.; Sampaio, C.H.; Lima, E.C.; Ambros, W.; Torrenti, J.-M. Fabrication, microstructure, and properties of fired clay bricks using construction and demolition waste sludge as the main additive. J. Clean. Prod. 2020, 258, 120733. [Google Scholar] [CrossRef]
- Hopkinson, P.; Chen, H.M.; Zhou, K.; Wang, Y.; Lam, D. Recovery and reuse of structural products from end-of-life buildings. Proc. Inst. Civ. Eng.—Eng. Sustain. 2018, 172, 119–128. [Google Scholar] [CrossRef]
- Richardson, H.G.; Richardson, E.M. The English Brickmaker: A History of Brickmaking and Brick Building in England from the Roman Times to the Present Day; Osprey Publishing: London, UK, 1961. [Google Scholar]
- Erdem, I.; Akyuz, U. Analytical investigation of lateral strength of masonry infilled RC frames retrofitted with CFRP. J. Perform. Constr. Facil. 2010, 24, 302–310. [Google Scholar] [CrossRef]
- Zhai, C.; Wang, X.; Kong, J.; Li, S.; Xie, L. Numerical simulation of masonry-infilled RC frames using XFEM. J. Struct. Eng. 2017, 143, 04017144. [Google Scholar] [CrossRef]
- Hammoudah, S.M.W.; Chaudhary, M.T.A.; Essawy, A.S. Analytical and parametric study on masonry infilled reinforced concrete frames using finite element method. Adv. Struct. Eng. 2017, 20, 1891–1906. [Google Scholar] [CrossRef]
- Tanjung, J.; Mohamed Nazri, F.; Hayati, Y. A simple strengthening method for preventing collapse of vulnerable masonry infills. Buildings 2022, 12, 1496. [Google Scholar] [CrossRef]
- Cumhur, A.; Altundal, A.; Aykac, S.; Aykac, B. Strengthening of hollow brick infill walls with expanded steel plates. Earthq. Struct. 2016, 11, 887–904. [Google Scholar] [CrossRef]
- Mutsuddy, R.; Das, S.S.; Majumder, S.N. Influence of nylon fiber on the response of carbon fiber reinforced polymer (CFRP)-retrofitted RC frame under cyclic load. Asian J. Civ. Eng. 2024, 25, 3011–3024. [Google Scholar] [CrossRef]
- Dehghani, A.; Nateghi-Alahi, F.; Fischer, G. Engineered cementitious composites for strengthening masonry infilled reinforced concrete frames. Eng. Struct. 2015, 105, 197–208. [Google Scholar] [CrossRef]
- Selvaraj, B.R.; Rai, D.C. Effect of in-plane damage on out-of-plane response of FRCM strengthened masonry infilled RC frames. J. Compos. Constr. 2022, 26, 04022070. [Google Scholar] [CrossRef]
- Lu, X.; Zha, S. Full-scale experimental investigation of the in-plane seismic performance of a novel resilient infill wall. Eng. Struct. 2021, 232, 111826. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Y.; Kinoshita, T.; DeJong, M.J. Distinct element modeling of the in-plane and out-of-plane response of ordinary and innovative masonry infill walls. Structures 2023, 50, 1447–1460. [Google Scholar] [CrossRef]
- Guettala, S.; Khelaifia, A.; Abdesselam, I.; Chebili, R.; Guettala, S. Assessment of seismic fragility of 3D reinforced concrete structures with masonry infill walls under different distribution arrangements. Asian J. Civ. Eng. 2024, 25, 5525–5532. [Google Scholar] [CrossRef]
- Zare, A.R.; Vosoughi, A.R.; Najafgholipour, M.A. Steel honeycomb elements for improving the seismic performance of moment-resisting frames with masonry infills. Structures 2023, 57, 105237. [Google Scholar] [CrossRef]
- Stazi, F.; Serpilli, M.; Maracchini, G.; Pavone, A. An experimental and numerical study on CLT panels used as infill shear walls for RC buildings retrofit. Constr. Build. Mater. 2019, 211, 605–616. [Google Scholar] [CrossRef]
- Furtado, A.; Rodrigues, H.; Arêde, A.; Varum, H. Experimental tests on strengthening strategies for masonry infill walls: A literature review. Constr. Build. Mater. 2020, 263, 120520. [Google Scholar] [CrossRef]
- Ricci, P.; Di Domenico, M.; Verderame, G.M. Experimental assessment of the in-plane/out-of-plane interaction in unreinforced masonry infill walls. Eng. Struct. 2018, 173, 960–978. [Google Scholar] [CrossRef]
- Xue, J.; Huang, X.; Luo, Z.; Gao, L. Experimental and numerical studies on the frame-infill interaction in steel-reinforced recycled concrete frames. Steel Compos. Struct. 2016, 20, 1391–1409. [Google Scholar] [CrossRef]
- E519-02; Test Method for Diagonal Tension (Shear) in Masonry Assemblages. C15 Committee: West Conshohocken, PA, USA, 2017. [CrossRef]
- BS 4449:2005+A3:2016; Steel for the Reinforcement of Concrete—Weldable Reinforcing Steel—Bar, Coil and Decoiled Product—Specification. BSI: London, UK, 2016.
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- EN 206-1; Concrete—Specification, Performance, Production, and Conformity. European Committee for Standardization (CEN): Brussels, Belgium, 2000.
- EN 771-1; Specification for Masonry Units—Part 1: Clay Masonry Units. European Committee for Standardization (CEN): Brussels, Belgium, 2011.
- EN 196-1; Methods of Testing Cement—Part 1: Determination of Strength. European Committee for Standardization (CEN): Brussels, Belgium, 2016.
- Elkady, A. ABAQUS CDP Generator, Version v23.04; Zenodo: Geneva, Switzerland, 2023. [CrossRef]
- Nasiri, E.; Liu, Y. Effect of prior in-plane damage on the out-of-plane performance of concrete masonry infills. Eng. Struct. 2020, 222, 111149. [Google Scholar] [CrossRef]
- Lourenço, P. Computational Strategies for Masonry Structures. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1996. [Google Scholar]
- Simulia. ABAQUS Analysis User’s Manual; Hibbitt, Karlsson, and Sorenson: Pawtucket, RI, USA, 2024. [Google Scholar]
- Kim, M.; Yu, E. Experimental Study on Lateral-Load-Resisting Capacity of Masonry-Infilled Reinforced Concrete Frames. Appl. Sci. 2021, 11, 9950. [Google Scholar] [CrossRef]
- Wang, C.; Guo, J.; Wang, X.; Zhang, Y.; Ma, Z. Dynamic mechanical properties and damage constitutive model of high-toughness recycled aggregate concrete under high strain rate impact loads. Constr. Build. Mater. 2025, 400, 133157. [Google Scholar] [CrossRef]
- Grubišić, M.; Šipoš, T.K.; Grubišić, A.; Pervan, B. Testing of damaged single-bay reinforced concrete frames strengthened with masonry infill walls. Buildings 2023, 13, 1021. [Google Scholar] [CrossRef]









| Symbol | (MPa) | COV | |
|---|---|---|---|
| Concrete compressive strength | fcc | 34.01 | (0.21) |
| Reinforcing steel bar tensile strength | fy | 527 | (0.07) |
| Steel reinforcement’s ultimate strength | fu | 618 | (0.05) |
| Solid brick compressive strength | fcb | 18.25 | (0.25) |
| Solid brick flexural strength | ffb | 4.53 | (0.33) |
| Mortar compressive strength | fcm | 4.3 | (0.24) |
| Mortar flexural strength | ffm | 0.9 | (0.13) |
| Masonry compressive strength | fcm | 14.01 | (0.1) |
| Wall Panel | Pmax (kN) | Ss (MPa) | μ | G10 (MPa) | G20 (MPa) | |
|---|---|---|---|---|---|---|
| P1-00 | 0% infill | 45.0 | 0.265 | 8.66 | 39.3 | 14.1 |
| P2-50 | 50% infill | 47.5 | 0.280 | 4.96 | 153.7 | 76.8 |
| P3-100 | 100% infill | 112.1 | 0.590 | 5.03 | 392.8 | 196.4 |
| P4-Al | aluminum frame infill | 45.3 | 0.265 | 2.65 | 53.6 | 13.2 |
| P5-SB | solid brick wall | 39.9 | 0.094 | 1.01 | 71.0 | 39.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luga, E.; Mustafaraj, E.; Tasdemir, E.; Corradi, M.; Lika, E.; Periku, E. Reuse of Solid Bricks in Construction: An Experimental Work. Buildings 2025, 15, 3935. https://doi.org/10.3390/buildings15213935
Luga E, Mustafaraj E, Tasdemir E, Corradi M, Lika E, Periku E. Reuse of Solid Bricks in Construction: An Experimental Work. Buildings. 2025; 15(21):3935. https://doi.org/10.3390/buildings15213935
Chicago/Turabian StyleLuga, Erion, Enea Mustafaraj, Emrah Tasdemir, Marco Corradi, Ervis Lika, and Erion Periku. 2025. "Reuse of Solid Bricks in Construction: An Experimental Work" Buildings 15, no. 21: 3935. https://doi.org/10.3390/buildings15213935
APA StyleLuga, E., Mustafaraj, E., Tasdemir, E., Corradi, M., Lika, E., & Periku, E. (2025). Reuse of Solid Bricks in Construction: An Experimental Work. Buildings, 15(21), 3935. https://doi.org/10.3390/buildings15213935








