Seismic Response Control of High-Speed Railway Bridges with Prefabricated Multi-Layer Parallel-Connected Slit Steel Plate Shear Dampers
Abstract
1. Introduction
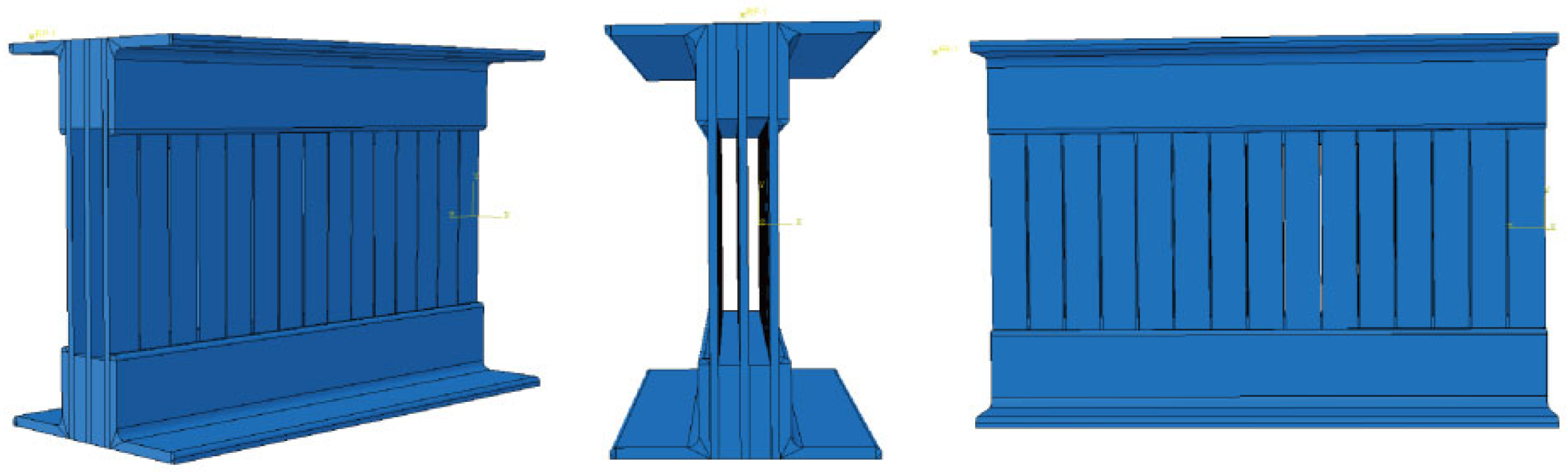
2. Prefabricated Multi-Layer Parallel-Connected Slit Steel Plate Shear Damper
2.1. Configuration and Fabrication
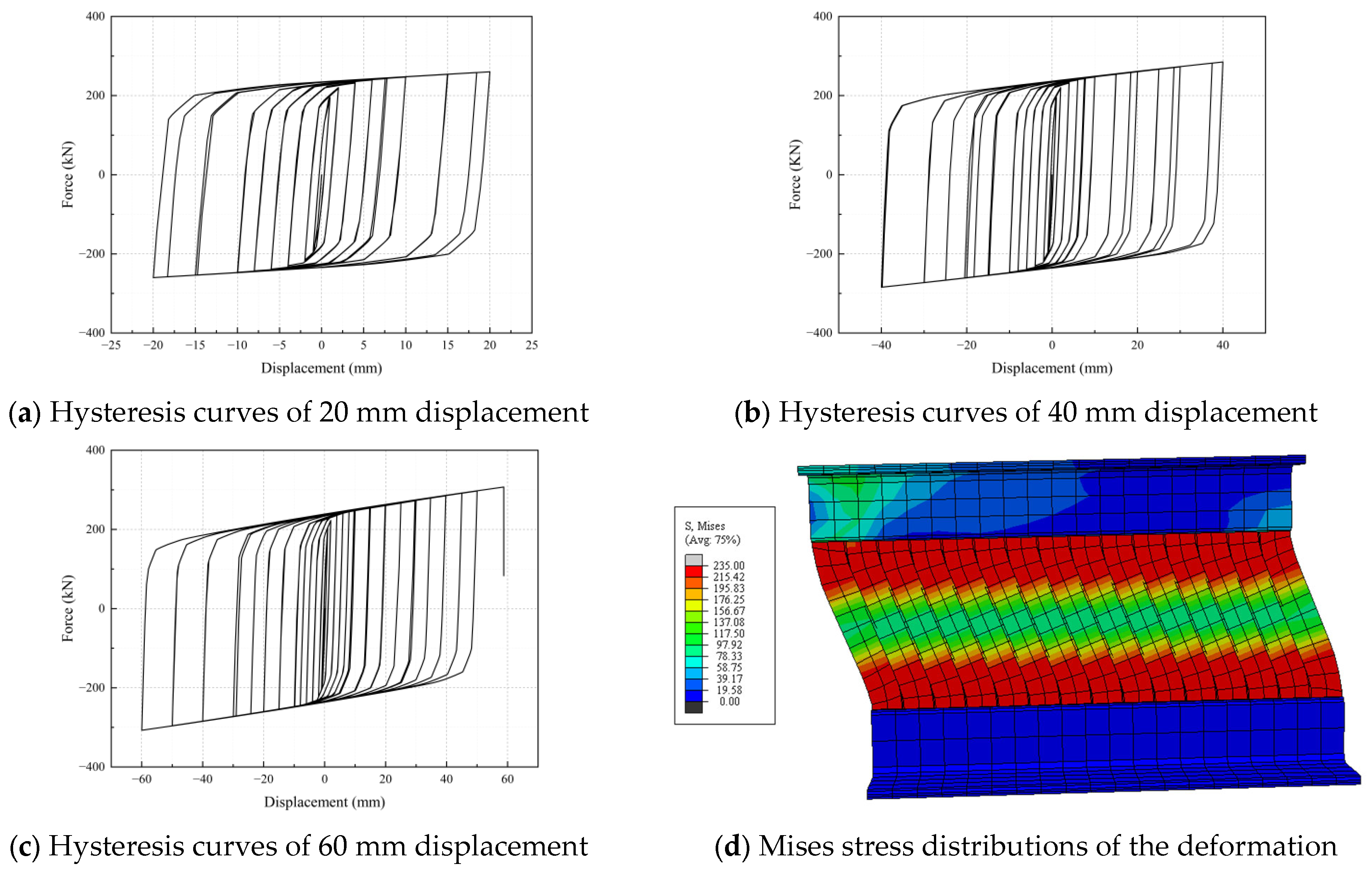
2.2. Mechanical Properties
2.3. Finite Element Modelling
2.4. Research Limitations and Future Prospects
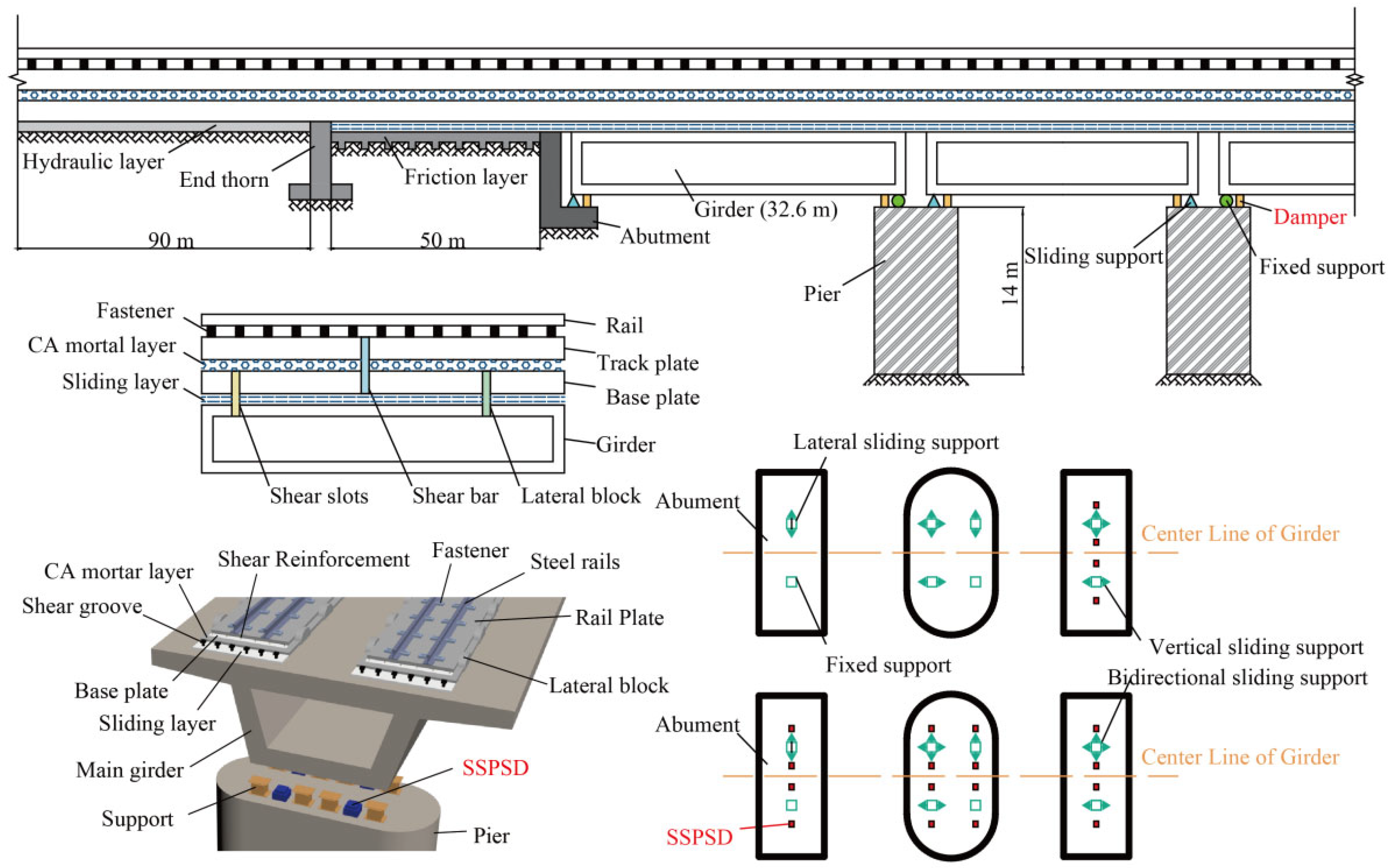
3. The High-Speed Railway Track-Bridge System with SSPSDs
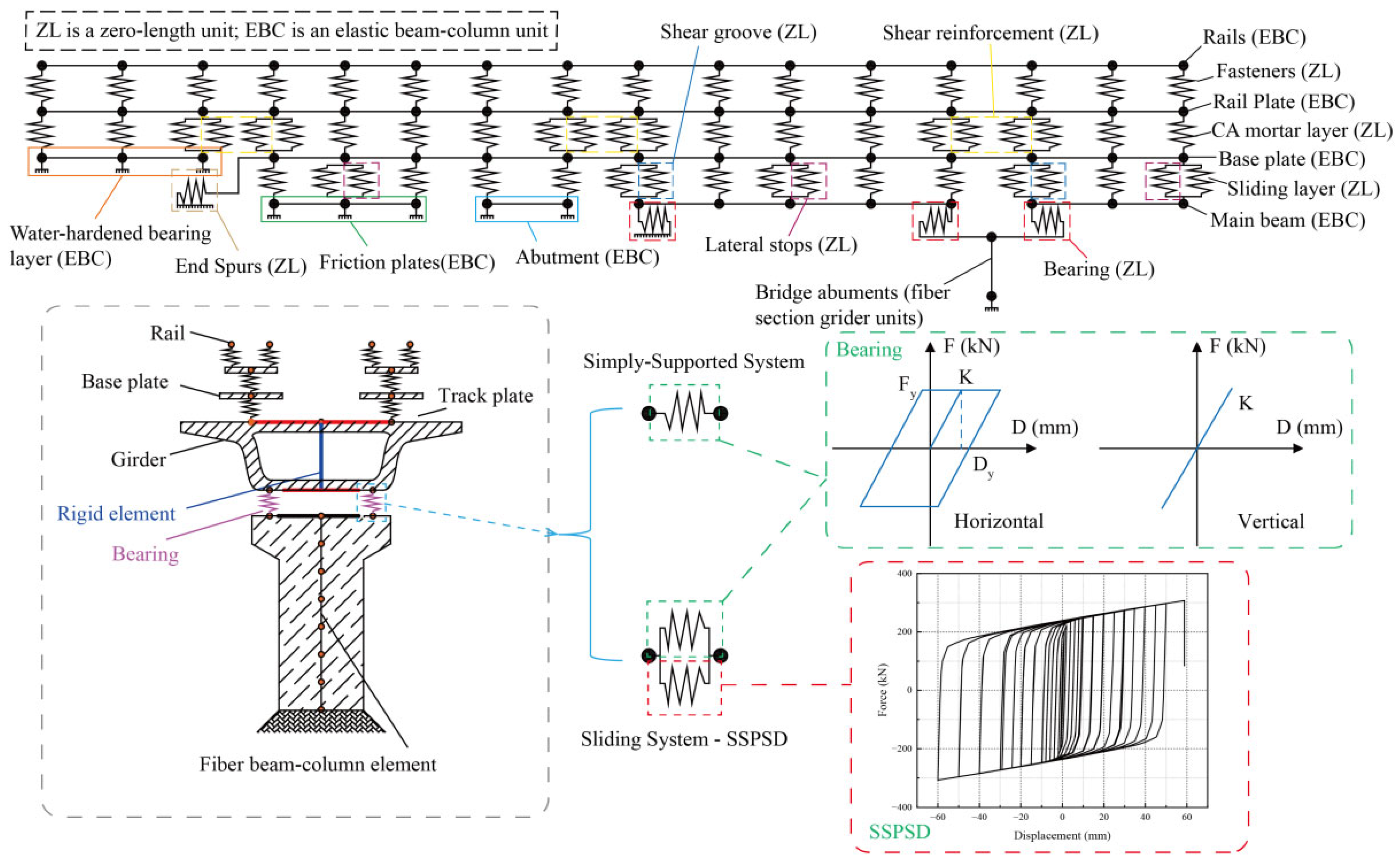
3.1. Numerical Model of HSRTBS with SSPSD
3.2. The Influence of Boundary Conditions
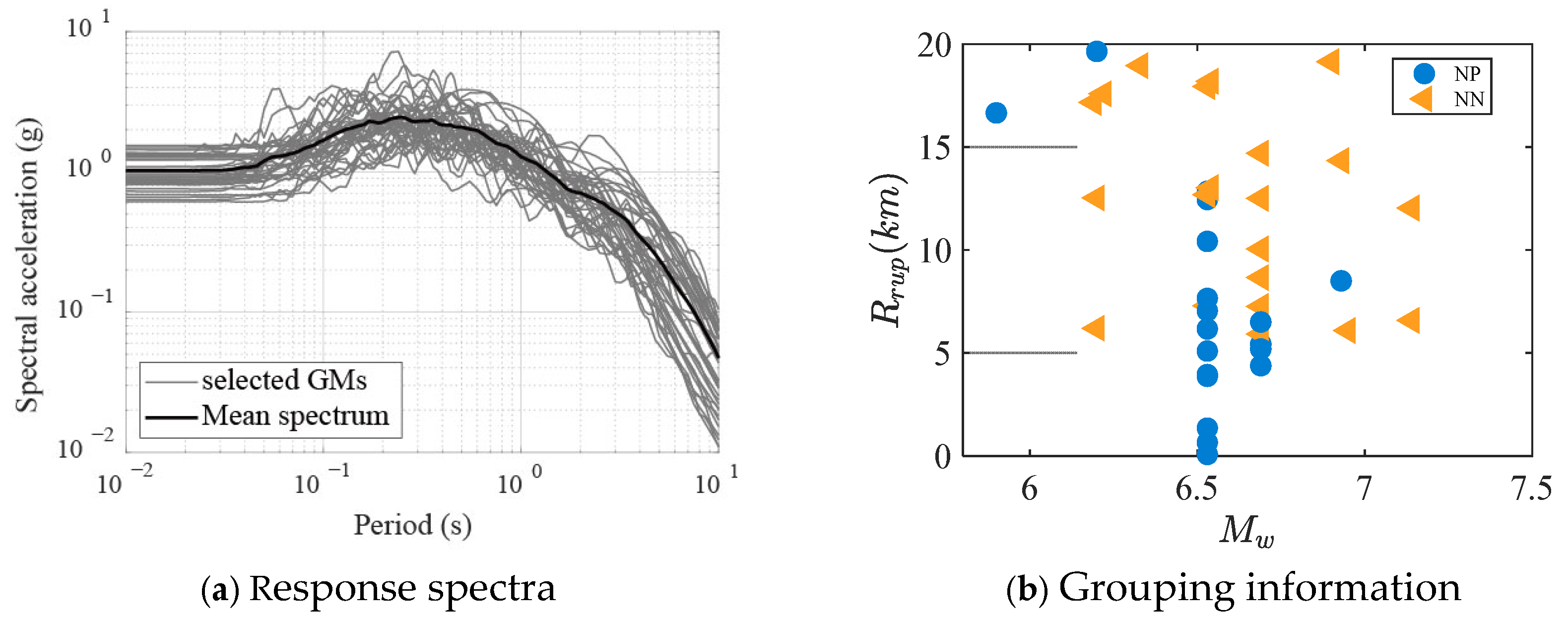
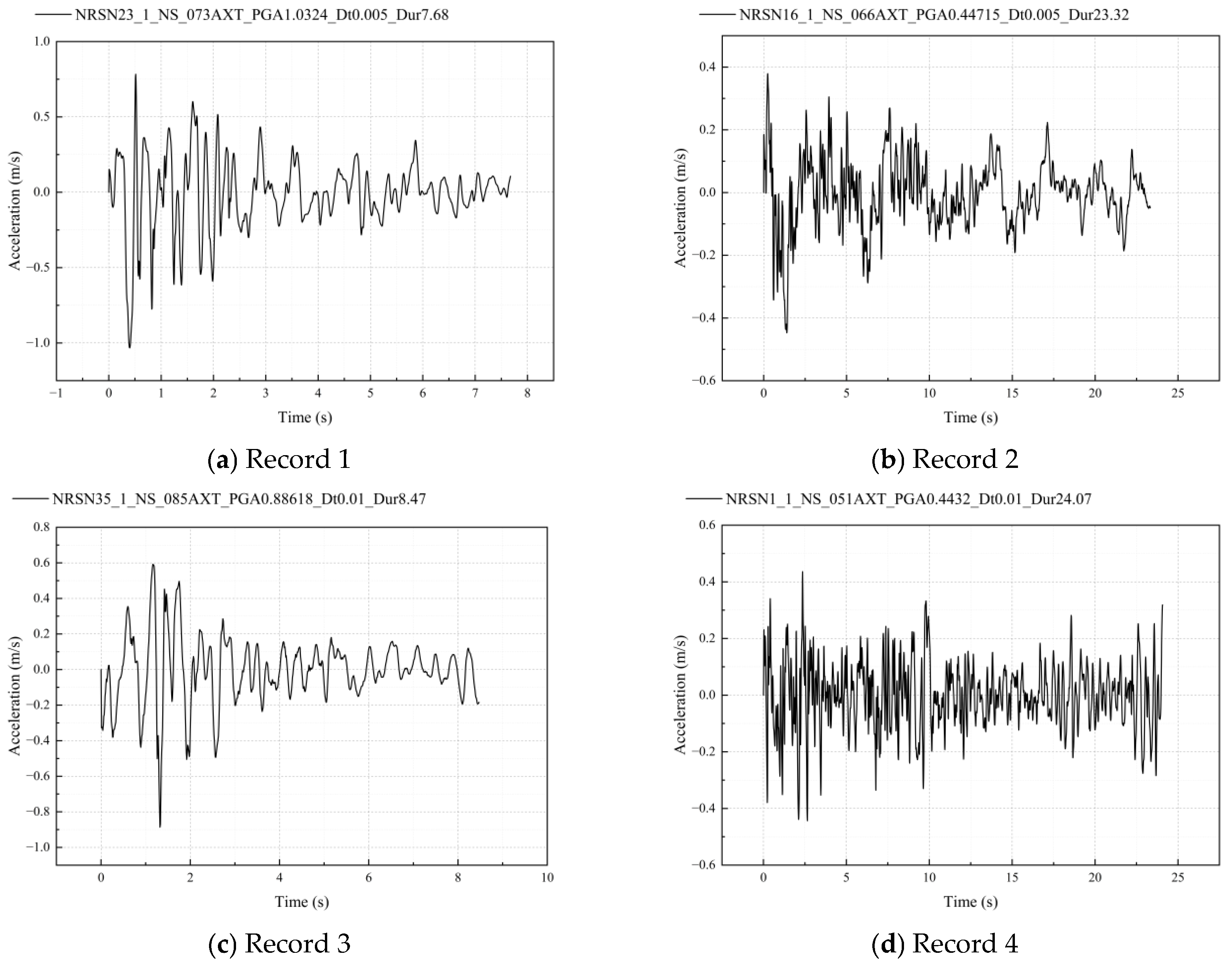
3.3. Ground Motion Selection and Spectral Matching
4. Seismic Mitigation Efficacy of SSPSD in HSRTBS
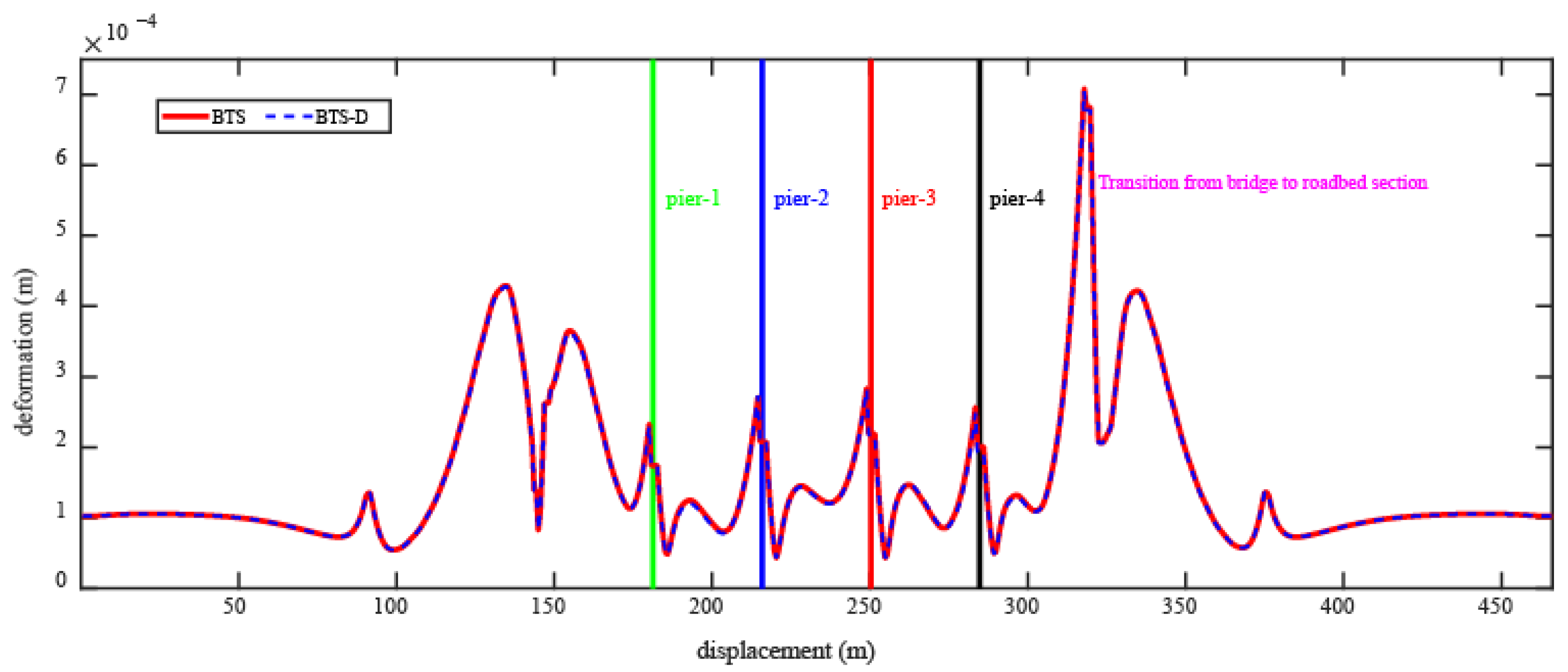
4.1. Seismic Response Analysis of Critical Components
4.2. Comprehensive Analysis of Seismic Mitigation Effectiveness
5. Conclusions
- SSPSD design and performance verification. A modular prefabricated multi-layer parallel-connected slit steel plate shear damper slitted steel plate damper was designed, where energy dissipation plates achieve high-efficiency energy absorption through flexure-shear coupling deformation. Theoretical models for stiffness and load-bearing capacity were derived, demonstrating <8% error in initial stiffness prediction. Abaqus hysteresis analysis confirms stable hysteretic loops with negligible pinching at 60 mm displacement. These results satisfy the large-deformation energy dissipation demands of high-speed railway bridges. The modular design reduces replacement costs by 40%, aligning with resilient infrastructure principles.
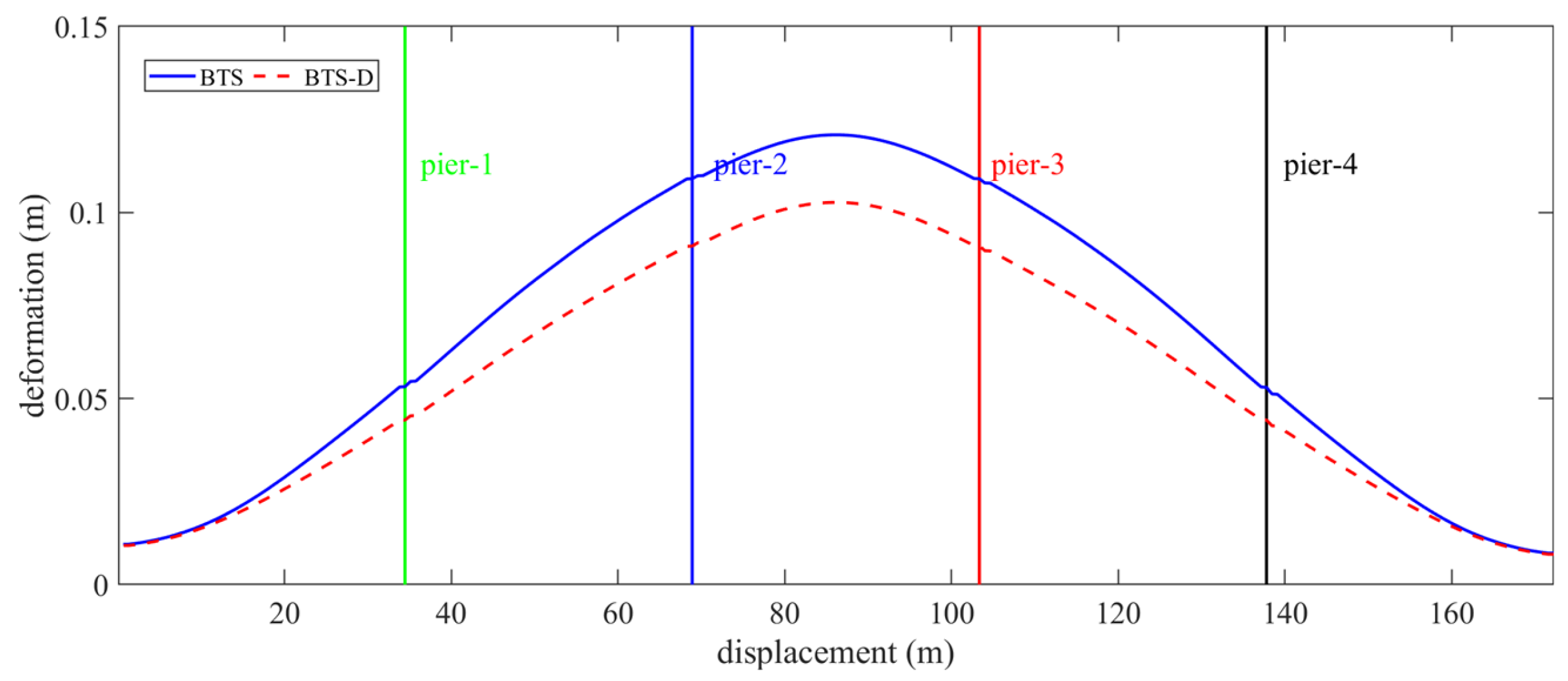
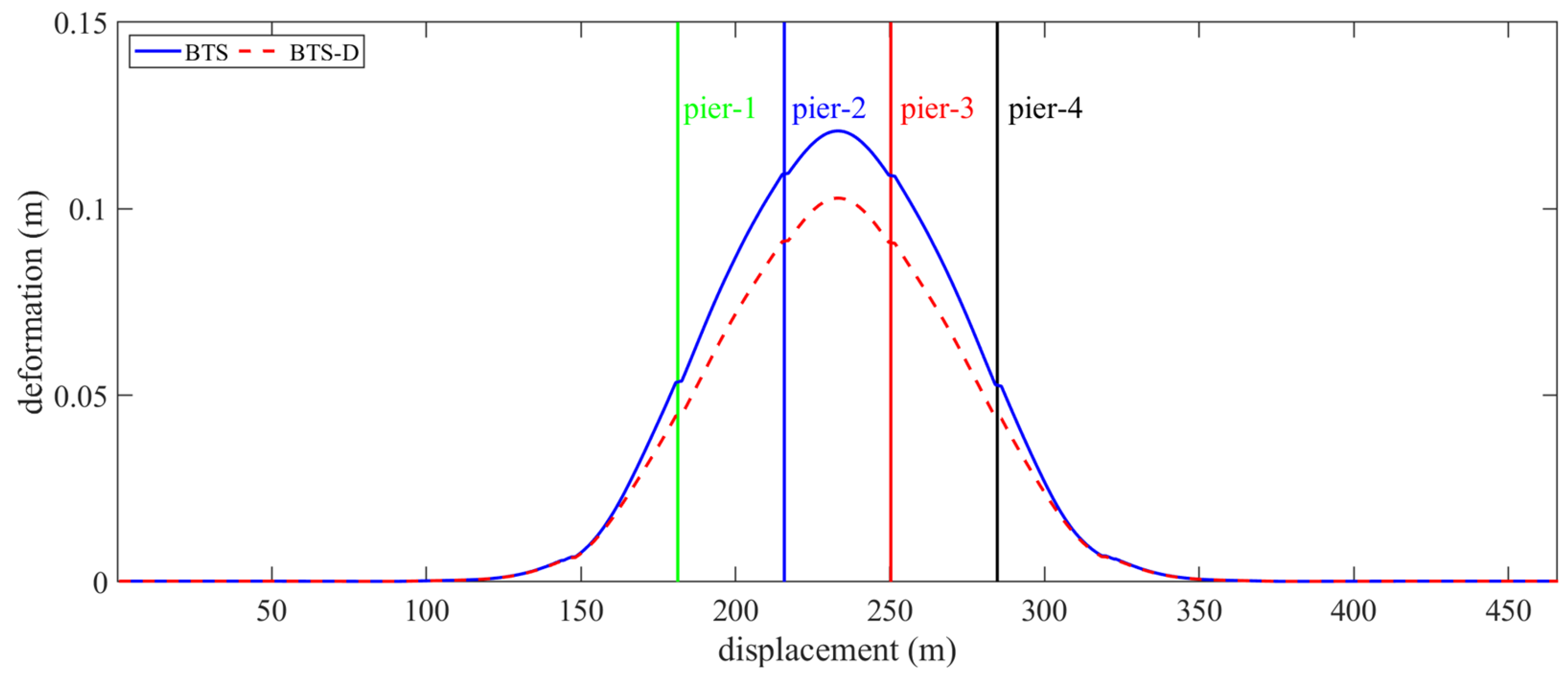
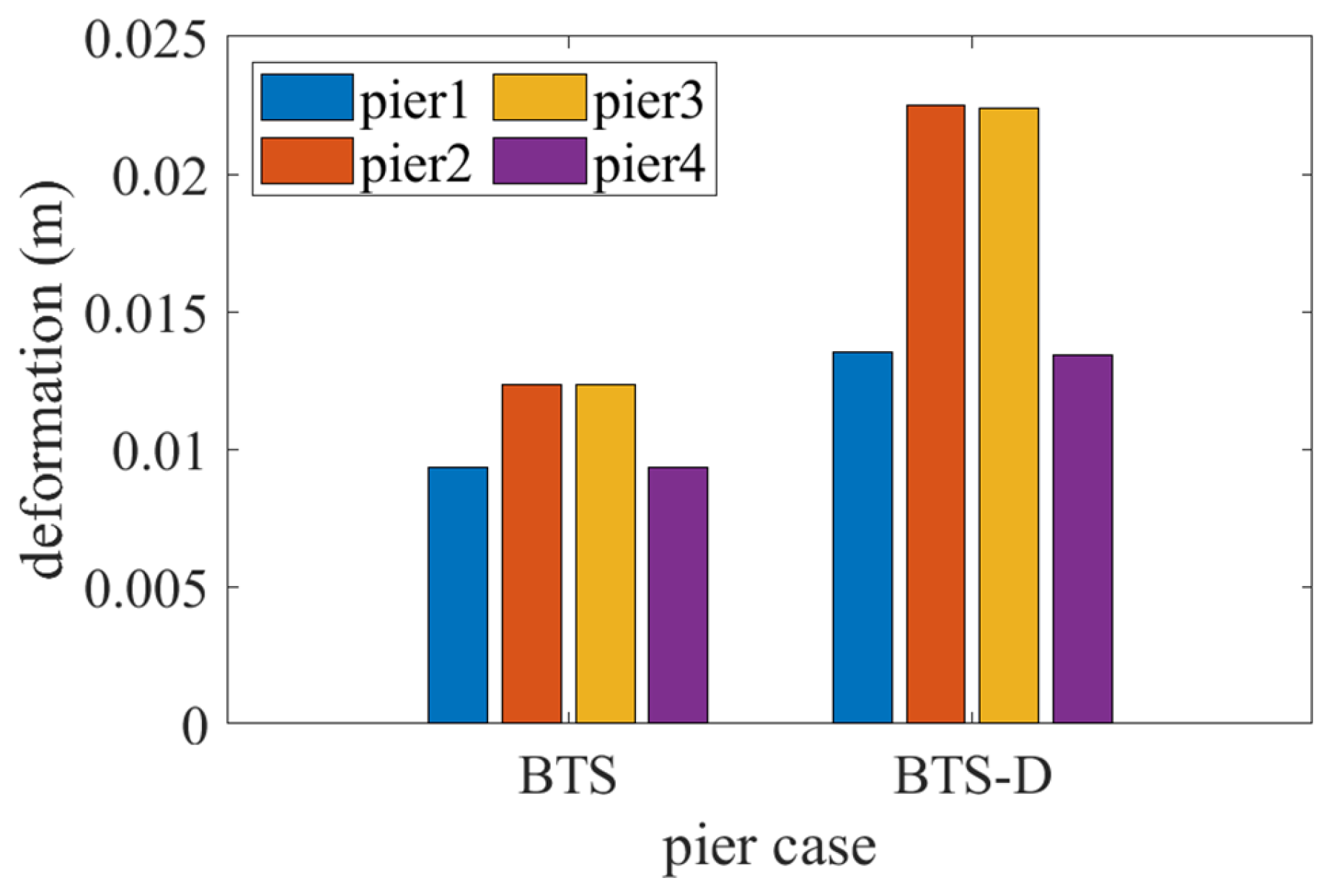
- Track-bridge system response control mechanism. The SSPSD significantly reduces peak deformations: fixed bearings by 29.13%, movable bearings by 34.12%, girder midspan by 15%, and track systems by 14.9%. Although pier deformations increase by 62.97%, absolute values remain below code limits (<30 mm), validating the energy redistribution strategy for preventing critical component overload.
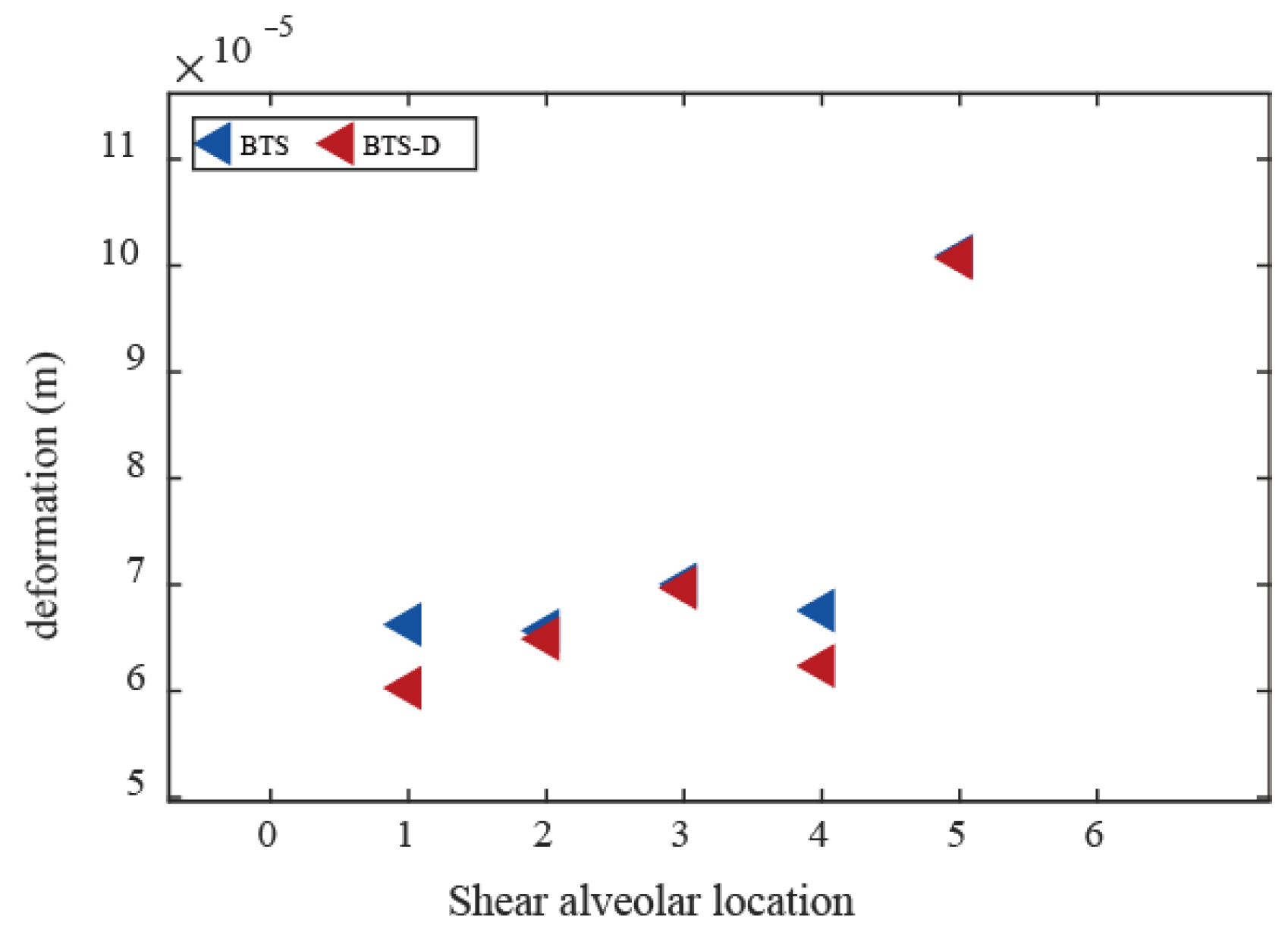
- System coupling effects and engineering applicability. By suppressing global bridge vibrations, the SSPSD optimizes track-girder interaction, markedly reducing dynamic shear demands on fasteners and track slabs. Spatial heterogeneity in shear key responses highlights the need for further optimization of damper placement parameters to balance constraint effects.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Su, M.; Dai, G.; Marx, S.; Liu, W.; Zhang, S. A Brief Review of Developments and Challenges for High-speed Rail Bridges in China and Germany. Struct. Eng. Int. 2019, 29, 160–166. [Google Scholar] [CrossRef]
- Yan, W.; Tian, X.; Wu, Z.; Ping, W.; Lin, K. Seismic response of concrete bridge of Lanzhou-Xinjiang high-speed railway under the near-fault strong earthquake. Structures 2023, 50, 1416–1428. [Google Scholar]
- Parsons, T.; Ji, C.; Kirby, E. Stress changes from the 2008 Wenchuan earthquake and increased hazard in the Sichuan basin. Nature 2008, 454, 509–510. [Google Scholar] [CrossRef]
- Sun, A.; Chen, X.; Fu, W. Improvement of seismic resilience for existing buildings based on hybrid seismic reduction technology. Shock. Vib. 2024, 43, 238–246. [Google Scholar]
- Jaehoon, B.; Huang, X.; Zhang, Z. Advanced seismic resilient performance of steel MRF equipped with viscoelastic friction dampers. Sci. Rep. 2024, 14, 19403. [Google Scholar] [CrossRef] [PubMed]
- Su, L.; Wang, Y.; Li, P.; Mei, S.; Guo, K. Seismic analysis of bridges based on stress-dependent damping. Struct. Eng. Mech. 2017, 62, 281–289. [Google Scholar] [CrossRef]
- Javanmardi, A.; Ibrahim, Z.; Ghaedi, K.; Ghadim, H.B.; Hanif, M.U. State-of-the-Art Review of Metallic Dampers: Testing, Development and Implementation. Arch. Comput. Methods Eng. 2020, 27, 455–478. [Google Scholar] [CrossRef]
- Dai, K.; He, Z.; Li, T.; Yang, Y. Mitigating ground motion duration impact on steel moment-resisting frames using viscous dampers. J. Constr. Steel Res. 2024, 213, 108430. [Google Scholar] [CrossRef]
- Xing, L.; Zhou, Y.; Zhang, P. Optimal tuned outrigger-ATMD systems considering seismic and wind loads. Soil Dyn. Earthq. Eng. 2023, 172, 108023. [Google Scholar] [CrossRef]
- Di Egidio, A.; Olivieri, C.; Contento, A.; Pagliaro, S. Improving the dynamic and seismic behaviour of rigid block-like elements through active mass dampers. Eng. Struct. 2023, 275, 115312. [Google Scholar] [CrossRef]
- Amjadian, M.; Agrawal, A.K. Feasibility study of using a semiactive electromagnetic friction damper for seismic response control of horizontally curved bridges. Struct. Control Health Monit. 2019, 26, e2333. [Google Scholar] [CrossRef]
- Zhu, X.; Jing, X.; Cheng, L. Magnetorheological fluid dampers: A review on structure design and analysis. J. Intell. Mater. Syst. Struct. 2012, 23, 839–873. [Google Scholar] [CrossRef]
- Luu, M.; Rodrigo, M.; Zabel, V.; Könke, C. Semi-active magnetorheological dampers for reducing response of high-speed railway bridges. Control Eng. Pract. 2014, 32, 147–160. [Google Scholar] [CrossRef]
- Guo, T.; Liu, J.; Zhang, Y.; Pan, S. Displacement monitoring and analysis of expansion joints of long-span steel bridges with viscous dampers. J. Bridg. Eng. 2015, 20, 04014099. [Google Scholar] [CrossRef]
- Guo, W.; Li, J.; Guan, Z. Shake table test on a long-span cable-stayed bridge with viscous dampers considering wave passage effects. J. Bridg. Eng. 2021, 26, 04020118. [Google Scholar] [CrossRef]
- Yan, X.; Alam, M.S.; Shu, G.; Qin, Y. A novel self-centering viscous damper for improving seismic resilience: Its development, experimentation, and system response. Eng. Struct. 2023, 279, 115632. [Google Scholar] [CrossRef]
- He, Z.; Shi, F.; Lin, Z.; Zhang, C.; Zhou, Y.; Zhao, F. Experimental characterization on cyclic stability behavior of a high-damping viscoelastic damper, Constr. Build. Mater. 2023, 371, 130749. [Google Scholar] [CrossRef]
- Dai, J.; Xu, Z.-D.; Gai, P.-P.; Yan, X. Seismic performance of viscoelastically damped structures at different ambient temperatures. J. Vib. Control 2020, 27, 2819–2834. [Google Scholar] [CrossRef]
- Paronesso, M.; Lignos, D.G. Experimental study of sliding friction damper with composite materials for earthquake resistant structures. Eng. Struct. 2021, 248, 113063. [Google Scholar] [CrossRef]
- Xu, G.; Ou, J. Seismic performance of combined rotational friction and flexural yielding metallic dampers. J. Build. Eng. 2022, 49, 104059. [Google Scholar] [CrossRef]
- De Matteis, G.; Brando, G.; Mazzolani, F.M. Hysteretic behaviour of bracing-type pure aluminium shear panels by experimental tests. Earthq. Eng. Struct. Dyn. 2011, 40, 1143–1162. [Google Scholar] [CrossRef]
- Xiang, N.; Alam, M.S.; Li, J. Yielding steel dampers as restraining devices to control seismic sliding of laminated rubber bearings for highway bridges: Analytical and experimental study. J. Bridg. Eng. 2019, 24, 04019103. [Google Scholar] [CrossRef]
- Briones, B.; De La Llera, J.C. Analysis, design and testing of an hourglass-shaped copper energy dissipation device. Eng. Struct. 2014, 79, 309–321. [Google Scholar] [CrossRef]
- Guo, W.; Wang, Y.; Zhai, Z.; Du, Q. Seismic control of high-speed railway bridge using S-shaped steel damping friction bearing. Smart Struct. Syst. 2022, 30, 479–500. [Google Scholar]
- Xie, X.; Chen, S.X.; Zhou, X. A simplified analytical model for U-shaped steel dampers considering horizontal bidirectional deformation. Bull. Earthq. Eng. 2018, 16, 6243–6268. [Google Scholar] [CrossRef]
- Zhai, Z.; Guo, W.; Yu, Z.; He, C.; Zeng, Z. Experimental and numerical study of S-shaped steel plate damper for seismic resilient application. Eng. Struct. 2020, 221, 111006. [Google Scholar] [CrossRef]
- Cao, X.; Shen, D.; Ji, K.; Qu, Z.; Wang, C. Recovery resilience framework of replaceable AB-BRB for seismic strengthening during the aftershock stage. ThinWalled Struct. 2024, 205, 112389. [Google Scholar] [CrossRef]
- Zhong, J.; Zheng, X.; Wu, Q.; Jiang, L.; He, M.; Dang, X. Seismic fragility and resilience assessment of bridge columns with dual-replaceable composite link beam under near-fault GMs. Structures 2023, 47, 412–424. [Google Scholar] [CrossRef]
- Fu, P.; Li, X.; Xu, L.; Wang, M. An advanced assessment framework for seismic resilience of railway continuous girder bridge with multiple spans considering 72 h golden rescue requirements. Soil. Dyn. Earthq. Eng. 2024, 177, 108370. [Google Scholar] [CrossRef]
- Andrić, J.M.; Lu, D.-G. Fuzzy methods for prediction of seismic resilience of bridges. Int. J. Disaster Risk Reduct. 2017, 22, 458–468. [Google Scholar] [CrossRef]
- Biondini, F.; Camnasio, E.; Titi, A. Seismic resilience of concrete structures under corrosion. Earthq. Eng. Struct. Dyn. 2015, 44, 2445–2466. [Google Scholar] [CrossRef]
- Yang, G.; Tian, L.; Du, Y.; Tang, G.; Ye, S.; Mao, J. Research on seismic resilience factors and improved evaluation of continuous beam bridges based on recovery function. China Civ. Eng. J. 2022, 55, 219–226. [Google Scholar]
- Xu, X.; Chen, X.; Hu, H.; Zhou, X.; Cheng, M.; Sun, L.; Li, X. Energy Dissipation and Seismic Response Reduction System for High-Speed Railway Bridges Based on Multiple Performance Requirements. Eng. Struct. 2024, 307, 117919. [Google Scholar] [CrossRef]
- Wang, X.; Liu, B.; Di Gialleonardo, E.; Kovacic, I.; Bruni, S. Application of Semi-Active Yaw Dampers for the Improvement of the Stability of High-Speed Rail Vehicles: Mathematical Models and Numerical Simulation. Veh. Syst. Dyn. 2022, 60, 2608–2635. [Google Scholar] [CrossRef]
- Liu, C.N.; Lai, S.K.; Ni, Y.Q.; Chen, L. Dynamic modelling and analysis of a physics-driven strategy for vibration control of railway vehicles. Vehicle. Syst. Dyn. 2024, 63, 1080–1110. [Google Scholar] [CrossRef]
- Alehashem, S.M.S.; Ni, Y.Q.; Liu, X.Z. A Full-Scale Experimental Investigation on Ride Comfort and Rolling Motion of High-Speed Train Equipped with MR Dampers. IEEE Access 2021, 9, 118113–118123. [Google Scholar] [CrossRef]
- Zhou, W.; Yu, J.; Jiang, L.; Lai, Z.; Zuo, Y.; Peng, K. Component Damage and Failure Sequence of Track-bridge System for High-speed Railway under Seismic Action. J. Earthq. Eng. 2023, 27, 27656–27678. [Google Scholar]
- Chen, X.; De Domenico, D.; Li, C. Seismic resilient design of rocking tall bridge piers using inerter-based systems. Eng. Struct. 2023, 281, 115819. [Google Scholar] [CrossRef]
- Chen, X., Jr.; Spencer, B.F.; Li, J.; Guan, Z.; Pang, Y. Optimization of distribution patterns of link beams in a double-column tall pier bent subjected to earthquake excitations. Earthq. Eng. Struct D 2023, 52, 52641–52659. [Google Scholar] [CrossRef]
- Kent, D.C.; Park, R. Inelastic behaviour of reinforced concrete members with cyclic loading. Bull. N. Z. Soc. Earthq. Eng. 1971, 4, 108–125. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Filippou, F.; Popov, E.; Bertero, V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints; University of California: Berkeley, CA, USA, 1983. [Google Scholar]
- Li, S.; Wu, D. Effects of pier design on superstructure vibration. J. China Railw. Soc. 2002, 24, 73–77. [Google Scholar]
- Jiang, L.; Yu, K.; Jiang, L.; Wen, T.; Hu, Y.; Pang, L. Effects of shear panel dampers on seismic response mitigation of high-speed railway simply supported bridge-track system under far-field and near-field ground motions. Arch. Civ. Mech. Eng. 2023, 23, 93. [Google Scholar] [CrossRef]
- Yan, B.; Liu, S.; Pu, H.; Dai, G.; Cai, X. Elastic-plastic seismic response of CRTS II slab ballastless track system on high-speed railway bridges. Sci. China Technol. Sci. 2017, 60, 865–871. [Google Scholar] [CrossRef]
- Hibbit, D.; Karlsson, B.; Sorensen, P. ABAQUS/Standard Analysis User’s Manual, version 6.13; Dassault Systèmes/Simulia: Providence, RI, USA, 2013.
- Khalili, M.; Sivandi-Pour, A.; Noroozinejad Farsangi, E. Experimental and numerical investigations of a new hysteretic damper for seismic resilient steel moment connections. J. Build. Eng. 2021, 43, 102811. [Google Scholar] [CrossRef]
- Zahrai, S.M.; Motezagholi, M.H. Cyclic Performance of an Elliptical-Shaped Damper with Shear Diaphragms in Chevron Braced Steel Frames. J. Earthq. Eng. 2018, 22, 1209–1232. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, X.; Yan, Y.; Jiang, L. U-shape energy-dissipation device for enhancing seismic resilience of high-speed railway track-bridge systems. J. Constr. Steel Res. 2024, 226, 109257. [Google Scholar] [CrossRef]
- Mou, B.; Wang, Z.; Zhang, Z.; Wu, C. Seismic behavior of steel frames with H-shaped damper. J. Constr. Steel Res. 2024, 213, 108401. [Google Scholar] [CrossRef]
- Jiang, L.; Yan, Y.; Wen, T.; Jiang, L.; Yu, K.; Pang, L. System-level seismic fragility of high-speed railway track-bridge system with component-replaceable U-shaped combined steel damper. Structures 2023, 58, 105452. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, C.; Lai, S.-K.; Chen, Z.; Chen, L. Frequency-dependent equivalent impedance analysis for optimizing vehicle inertial suspensions. Nonlinear Dyn. 2025, 113, 9373–9398. [Google Scholar] [CrossRef]



| Component | Material | E (MPa) | S (m2) |
|---|---|---|---|
| Main girder (mid-span) | C50 | 3.55 × 104 | 8.722 |
| Main girder (end) | C50 | 3.55 × 104 | 14.22 |
| Steel rail | Q235 | 2.06 × 105 | 0.007745 |
| Rail plate | C55 | 3.65 × 104 | 0.51 |
| Base plate | C30 | 3.25 × 104 | 0.5605 |
| Friction plate | C30 | 3.25 × 104 | 3.6 |
| Water-hardened bearing layer | water-hard material | 1.80 × 104 | 0.92 |
| Component | Horizontal Direction | Vertical Direction | |||
|---|---|---|---|---|---|
| Fl (kN) | Dl (mm) | Ft (kN) | Dt (mm) | Kv (kN/mm) | |
| Fastener | 15 | 2 | 15 | 2 | 2.4 × 103 |
| CA mortar layer | 45 | 0.5 | 45 | 0.5 | 2.0 × 103 |
| Sliding layer on bridge | 6 | 0.5 | 6 | 0.5 | / |
| Friction plate sliding layer | 14 | 0.5 | 14 | 0.5 | / |
| Shear groove | 1200 | 0.12 | 1200 | 0.12 | 2.3 × 104 |
| Shear reinforcement | 173 | 0.075 | 173 | 0.075 | 0 |
| Lateral block | 0 | 0 | 453 | 2 | 0 |
| Fixed end of support | 1000 | 2 | 1000 | 2 | 1.0 × 104 |
| Sliding end of support | 100 | 2 | 100 | 2 | 1.0 × 104 |
| Force–displacement curve | 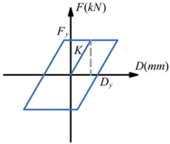 |  | |||
| Record | Seismic Intensity | Epicenter Distance (km) | Nearest Distance (km) | Preferred Vs30 (m/s) | FN Pulse | Pulse Period (s) | Conversion Factor |
|---|---|---|---|---|---|---|---|
| 1 | 7.0 | 13.0 | 6.1 | 213 | 0 | −99.00 | 3.63 |
| 2 | 6.5 | 2.6 | 0.7 | 275 | 1 | 2.30 | 4.28 |
| 3 | 6.5 | 43.2 | 10.4 | 209 | 1 | 4.03 | 5.23 |
| 4 | 6.5 | 18.9 | 7.3 | 275 | 0 | −99.00 | 3.54 |
| 5 | 6.5 | 19.4 | 0.1 | 186 | 1 | 3.35 | 2.41 |
| 6 | 6.5 | 26.3 | 6.2 | 203 | 1 | 4.49 | 4.10 |
| 7 | 6.5 | 29.4 | 12.5 | 196 | 1 | 7.36 | 3.96 |
| 8 | 6.5 | 32.0 | 17.9 | 197 | 0 | −99.00 | 7.18 |
| 9 | 6.5 | 28.7 | 12.9 | 163 | 1 | 5.24 | 4.41 |
| 10 | 6.5 | 27.1 | 7.1 | 209 | 1 | 4.61 | 2.48 |
| 11 | 6.5 | 27.8 | 4.0 | 206 | 1 | 4.05 | 2.33 |
| 12 | 6.5 | 27.5 | 1.4 | 203 | 1 | 3.84 | 2.08 |
| 13 | 6.5 | 28.1 | 3.9 | 206 | 1 | 5.39 | 2.87 |
| 14 | 6.5 | 27.2 | 5.1 | 202 | 1 | 5.86 | 2.43 |
| 15 | 6.5 | 19.8 | 7.7 | 203 | 1 | 4.80 | 3.93 |
| 16 | 6.5 | 48.6 | 12.7 | 349 | 0 | −99.00 | 8.00 |
| 17 | 6.3 | 36.7 | 19.0 | 275 | 0 | −99.00 | 5.82 |
| 18 | 5.9 | 20.5 | 16.7 | 349 | 1 | 3.58 | 3.66 |
| 19 | 6.2 | 20.3 | 17.2 | 271 | 0 | −99.00 | 6.20 |
| 20 | 6.2 | 24.8 | 17.6 | 207 | 0 | −99.00 | 8.00 |
| 21 | 6.5 | 35.8 | 18.2 | 192 | 0 | −99.00 | 3.13 |
| 22 | 6.5 | 19.5 | 13.0 | 194 | 0 | −99.00 | 3.88 |
| 23 | 6.9 | 32.4 | 14.3 | 222 | 0 | −99.00 | 3.84 |
| 24 | 6.9 | 27.2 | 8.5 | 371 | 1 | 4.47 | 2.97 |
| 25 | 6.7 | 9.0 | 4.4 | 275 | 1 | 2.65 | 1.78 |
| 26 | 6.7 | 11.1 | 8.7 | 298 | 0 | −99.00 | 3.59 |
| 27 | 6.7 | 4.9 | 14.7 | 267 | 0 | −99.00 | 2.45 |
| 28 | 6.7 | 13.0 | 5.4 | 373 | 1 | 3.53 | 1.60 |
| 29 | 6.7 | 13.1 | 12.5 | 446 | 0 | −99.00 | 4.13 |
| 30 | 6.7 | 20.3 | 5.9 | 269 | 0 | −99.00 | 1.70 |
| 31 | 6.7 | 19.3 | 7.3 | 508 | 0 | −99.00 | 2.90 |
| 32 | 6.7 | 10.9 | 6.5 | 282 | 1 | 1.23 | 1.42 |
| 33 | 6.7 | 12.4 | 10.1 | 309 | 0 | −99.00 | 3.17 |
| 34 | 6.7 | 13.6 | 5.2 | 371 | 1 | 3.49 | 1.45 |
| 35 | 6.9 | 46.0 | 19.2 | 256 | 0 | −99.00 | 3.67 |
| 36 | 7.1 | 41.3 | 12.0 | 326 | 0 | −99.00 | 1.93 |
| 37 | 7.1 | 1.6 | 6.6 | 276 | 0 | −99.00 | 1.85 |
| 38 | 6.2 | 25.5 | 19.7 | 428 | 1 | 3.19 | 6.82 |
| 39 | 6.2 | 10.1 | 6.2 | 553 | 0 | −99.00 | 2.85 |
| 40 | 6.2 | 14.5 | 12.5 | 553 | 0 | −99.00 | 8.00 |
| Fixed Bearings | BTS | BTS-D | Difference | Reduced Response |
|---|---|---|---|---|
| Pier 1 | 47.097 | 30.898 | 16.199 | 34.39% |
| Pier 2 | 104.481 | 68.655 | 35.826 | 34.29% |
| Pier 3 | 106.305 | 70.584 | 35.721 | 33.60% |
| Pier 4 | 49.668 | 33.107 | 16.561 | 33.34% |
| Movable Bearings | BTS | BTS-D | Difference | Reduced Response |
|---|---|---|---|---|
| Pier 1 | 51.357 | 34.052 | 17.305 | 33.66% |
| Pier 2 | 107.113 | 71.249 | 35.864 | 33.48% |
| Pier 3 | 103.289 | 67.527 | 35.762 | 34.62% |
| Pier 4 | 45.071 | 29.421 | 15.650 | 34.72% |
| Girder | BTS | BTS-D | Difference | Reduced Response |
|---|---|---|---|---|
| Pier 1 | 53.201 | 44.231 | 8.970 | 16.86% |
| Pier 2 | 109.076 | 90.968 | 18.108 | 16.60% |
| Pier 3 | 109.078 | 91.075 | 18.003 | 16.50% |
| Pier 4 | 53.013 | 44.223 | 8.790 | 16.58% |
| Girder | BTS | BTS-D | Difference | Reduced Response |
|---|---|---|---|---|
| Pier 1 | 53.451 | 44.480 | 8.971 | 16.78% |
| Pier 2 | 109.312 | 91.301 | 18.011 | 16.48% |
| Pier 3 | 108.928 | 90.931 | 17.997 | 16.52% |
| Pier 4 | 52.743 | 44.030 | 8.713 | 16.52% |
| Pier | BTS | BTS-D | Difference | Response Amplification |
|---|---|---|---|---|
| Pier 1 | 9.348 | 13.546 | 4.198 | 44.91% |
| Pier 2 | 12.346 | 22.487 | 10.141 | 82.14% |
| Pier 3 | 12.340 | 22.377 | 10.037 | 81.34% |
| Pier 4 | 9.344 | 13.410 | 4.066 | 43.51% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, Z.; Jiang, L.; Zhao, Z.; Tan, S.; Jiang, L.; Huang, Y.; Zhou, F.; Rao, L.; Zou, L. Seismic Response Control of High-Speed Railway Bridges with Prefabricated Multi-Layer Parallel-Connected Slit Steel Plate Shear Dampers. Buildings 2025, 15, 3902. https://doi.org/10.3390/buildings15213902
Kong Z, Jiang L, Zhao Z, Tan S, Jiang L, Huang Y, Zhou F, Rao L, Zou L. Seismic Response Control of High-Speed Railway Bridges with Prefabricated Multi-Layer Parallel-Connected Slit Steel Plate Shear Dampers. Buildings. 2025; 15(21):3902. https://doi.org/10.3390/buildings15213902
Chicago/Turabian StyleKong, Ziyi, Liqiang Jiang, Zhen Zhao, Sui Tan, Lizhong Jiang, Yifan Huang, Fangzheng Zhou, Lanzhe Rao, and Lifeng Zou. 2025. "Seismic Response Control of High-Speed Railway Bridges with Prefabricated Multi-Layer Parallel-Connected Slit Steel Plate Shear Dampers" Buildings 15, no. 21: 3902. https://doi.org/10.3390/buildings15213902
APA StyleKong, Z., Jiang, L., Zhao, Z., Tan, S., Jiang, L., Huang, Y., Zhou, F., Rao, L., & Zou, L. (2025). Seismic Response Control of High-Speed Railway Bridges with Prefabricated Multi-Layer Parallel-Connected Slit Steel Plate Shear Dampers. Buildings, 15(21), 3902. https://doi.org/10.3390/buildings15213902






