A* Algorithm for On-Site Collaborative Path Planning in Building Construction Robots
Abstract
1. Introduction
- ➢
- The traditional A* algorithm was improved by incorporating obstacle density into the heuristic function and introducing a path-smoothing post-processing step to generate more efficient and realistic trajectories;
- ➢
- A collaborative path planning framework for construction robot groups was developed based on the leader–follower and BIM-based grid mapping approaches, enabling coordinated task execution in complex construction scenarios;
- ➢
- The effectiveness (i.e., planning time, planning length, path variation range, and success rate) was validated through real-world construction case studies, which also demonstrated its practical applicability.
2. Literature Review
2.1. Path Planning Algorithms
2.2. Robot Group Formation Control
- ➢
- The leader–follower approach is easy to implement and highly effective in environments with clear navigation paths but is susceptible to leader failure and communication delays, making robustness a key concern.
- ➢
- The virtual structure method ensures rigid formation and accurate coordination but suffers from high computational overhead and limited scalability in complex or crowded construction sites.
- ➢
- Behavior-based control offers better fault tolerance and flexibility in dynamic environments but may lack formation stability and requires fine-tuned behavior rules.
2.3. Summary of Current Research
3. Methodology
3.1. Analysis of Collaborative Work Scenarios for Construction Robots
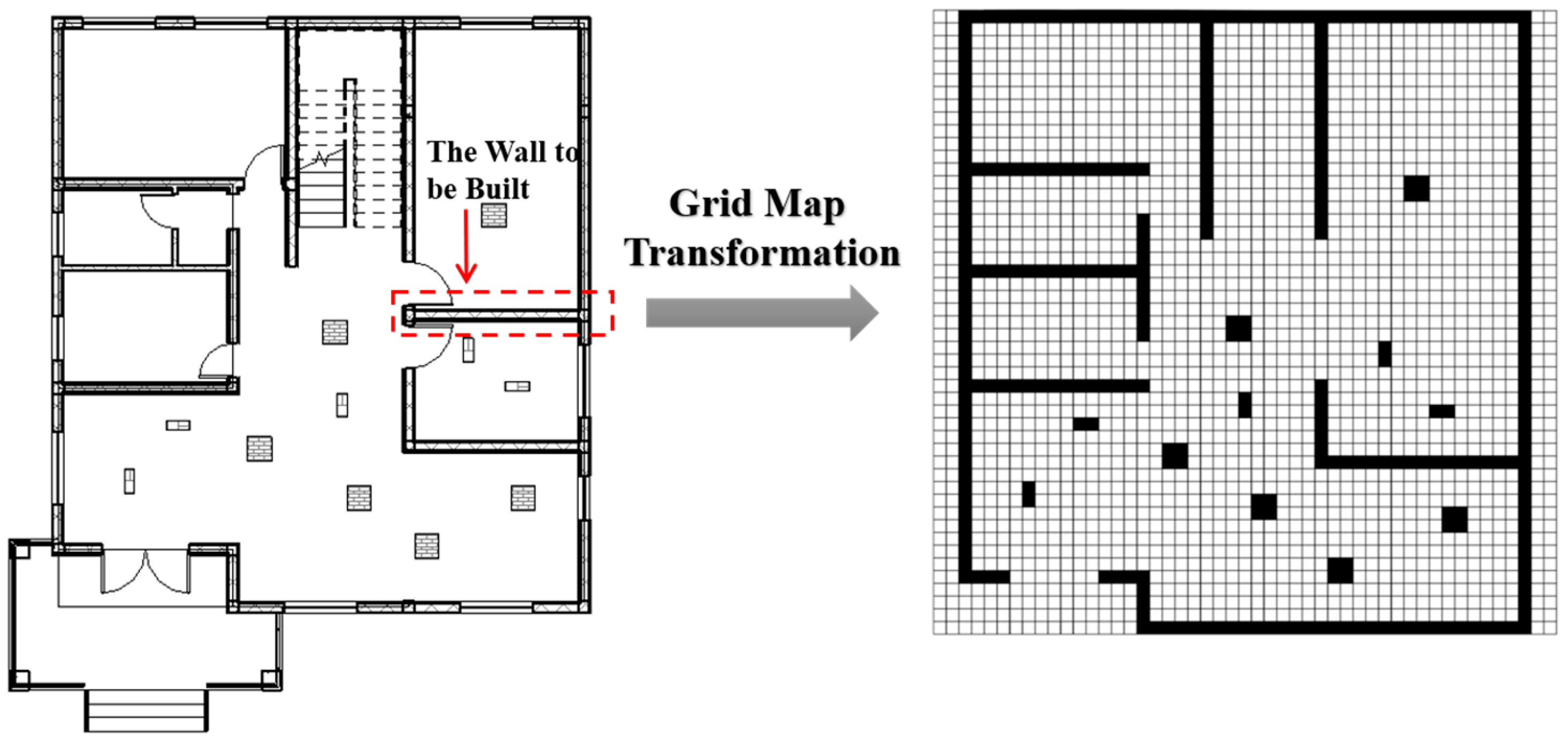
3.2. Formalization of Robots’ Work Map
- ➢
- Step 1: Collect building blueprint information to determine the geometry and location of each floor of the building.
- ➢
- Step 2: Use Building Information Modeling (BIM) technology to draw the building’s geometric and locational information diagram and create the construction robot’s working environment model.
- ➢
- Step 3: Set the grid plane parameters and mapping rules based on the construction robot’s working environment model.
- ➢
- Step 4: Complete the actual mapping of the work map based on the grid map and mapping rules, thus obtaining the construction robot’s working grid map.
3.3. Path Planning and Obstacle Avoidance for the Leader Robot Based on A* Algorithm
- ➢
- Obtain the complete set of nodes U = {Pi∣1 ≤ I ≤ n} from the A* algorithm’s planned path, where P1 represents the starting node and Pn represents the end node of the path. Create an initial key node set V = {P1, Pn}, which initially includes only the starting and ending nodes of the path and is used to store the optimized key nodes.
- ➢
- Starting from P1, draw a straight line connecting the nodes sequentially in U, i.e., P2, P3, …, Pi, and check if the straight line P1Pi intersects any obstacles:
- ➢
- If the line P1Pi does intersect an obstacle, the node Pi−1 is deemed a critical node and a necessary turning node in the path and is added to the set V.
- ➢
- If the line P1Pi does not intersect any obstacles, nodes P2, …, Pi−1 are considered redundant. Continue extending the line from Pi to subsequent nodes in U until it reaches the end node Pn, adding all identified key nodes to V.
- ➢
- After selecting the key nodes, the set V contains all critical nodes. Sequentially connect all nodes in V to globally optimize the path, i.e., remove redundant nodes and smooth the planned path.
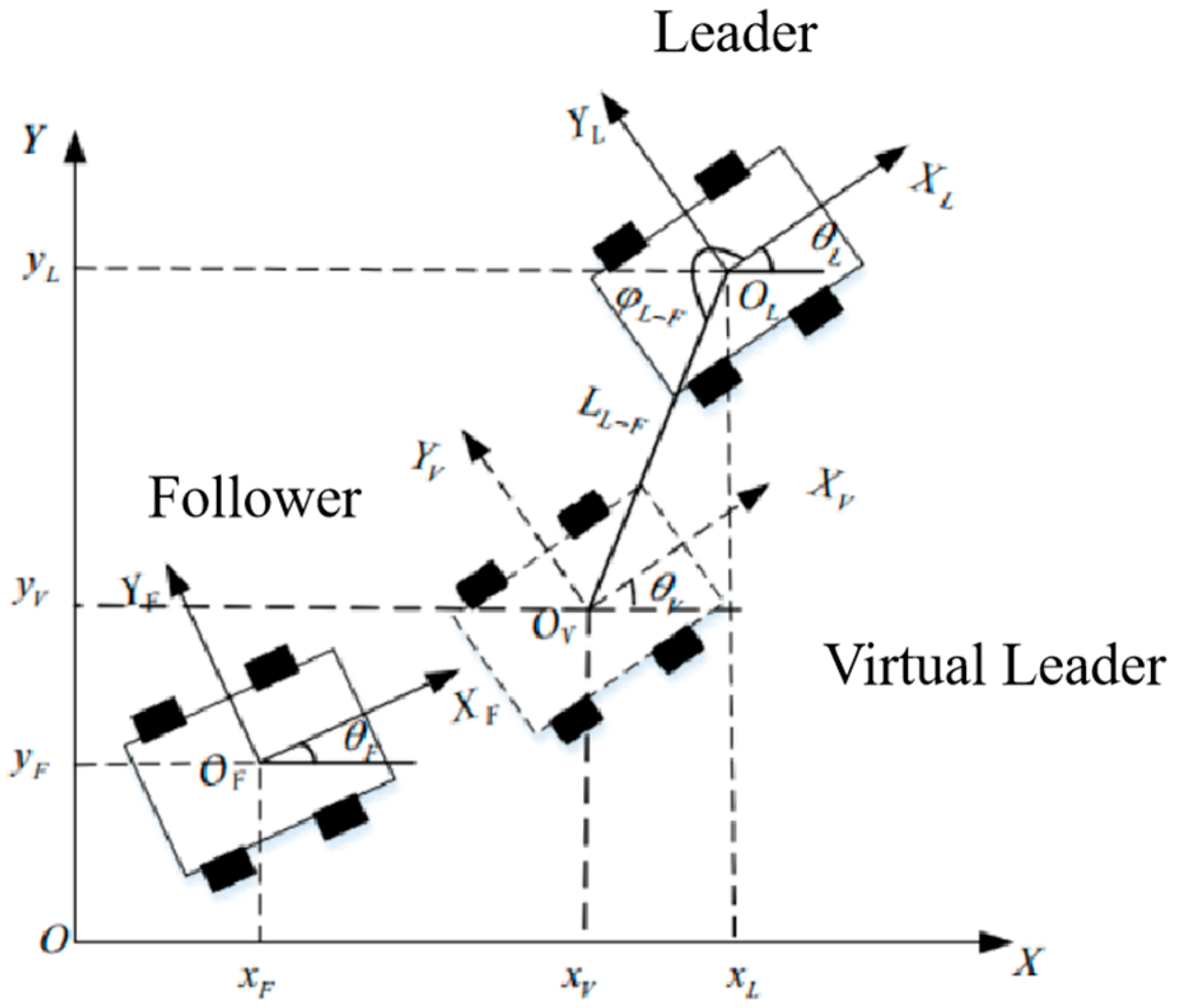
3.4. Path Planning for Collaborative Construction Robot Groups
- ➢
- The global coordinate system is represented by X–O–Y.
- ➢
- The local coordinate system of the leader robot is represented by XL–OL–YL.
- ➢
- The position of the leader robot in the global coordinate system is defined as (xL, yL, θL), where
- ➢
- xL, yL are the coordinates of the leader robot in the global coordinate system;
- ➢
- θL is the angle between the orientation of the leader robot and the X-axis in the global coordinate system.
- ➢
- The velocity vector of the leader robot in the global coordinate system is expressed as [44].
- ➢
- represent the leader robot’s linear velocities in the x and y directions and angular velocity in the global coordinate system;
- ➢
- vx, vy, and ω represent the leader robot’s linear velocities in the x and y directions and angular velocity in the local coordinate system.
4. Case Studies
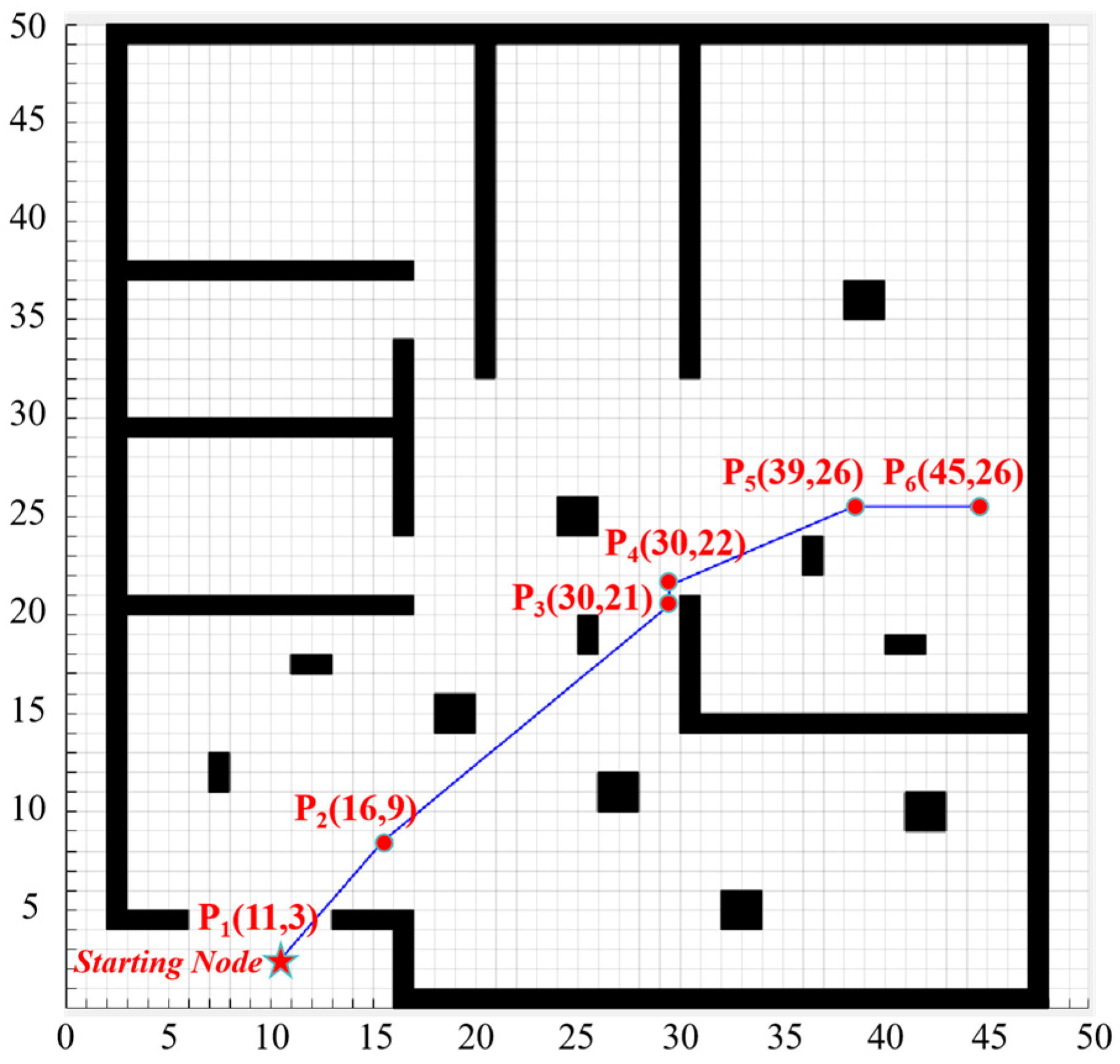
4.1. A* Algorithm-Based Path Planning and Obstacle Avoidance Model for the Leader Robot
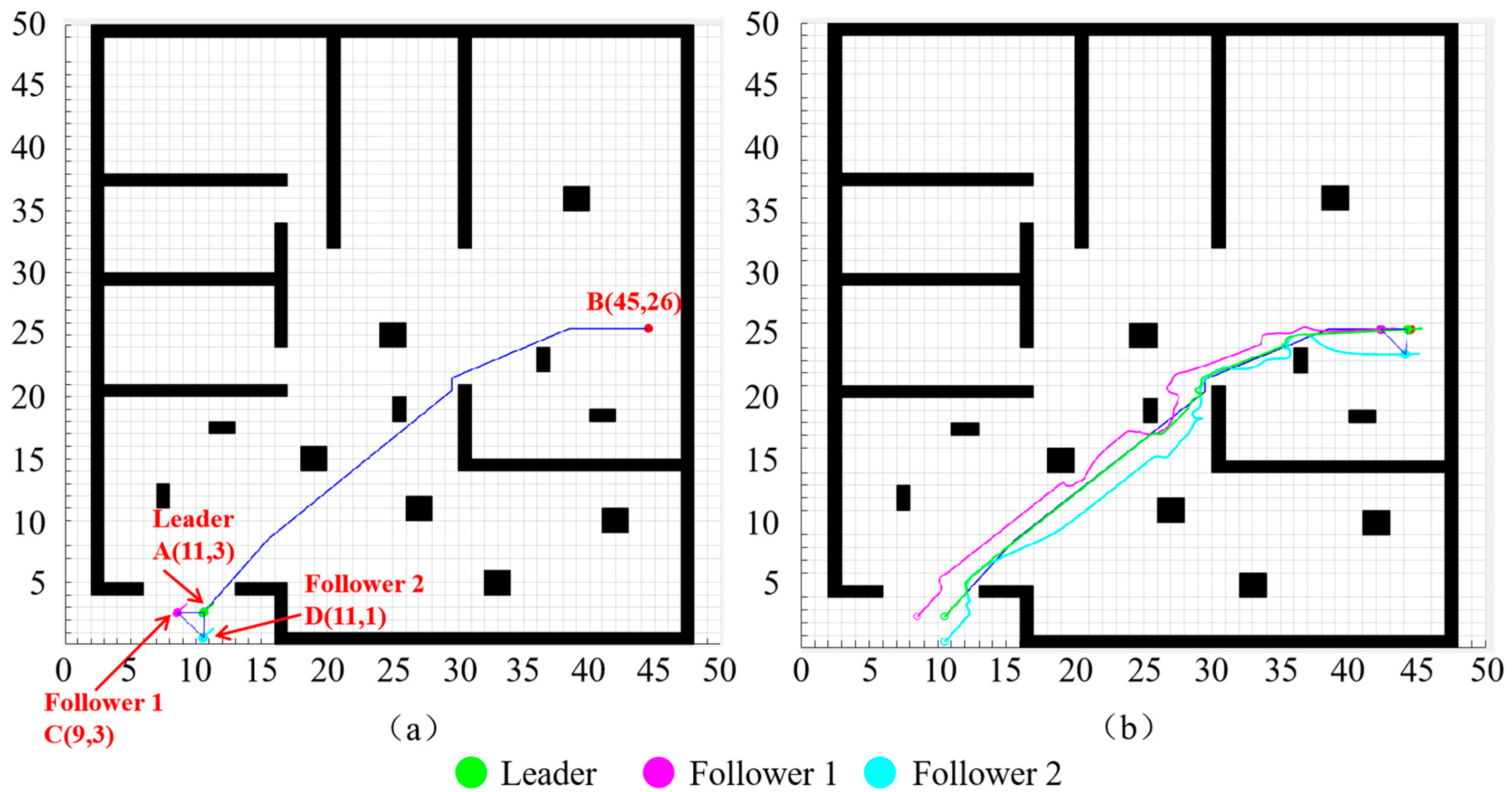
4.2. Collaborative Path Planning for a Group of Construction Robots
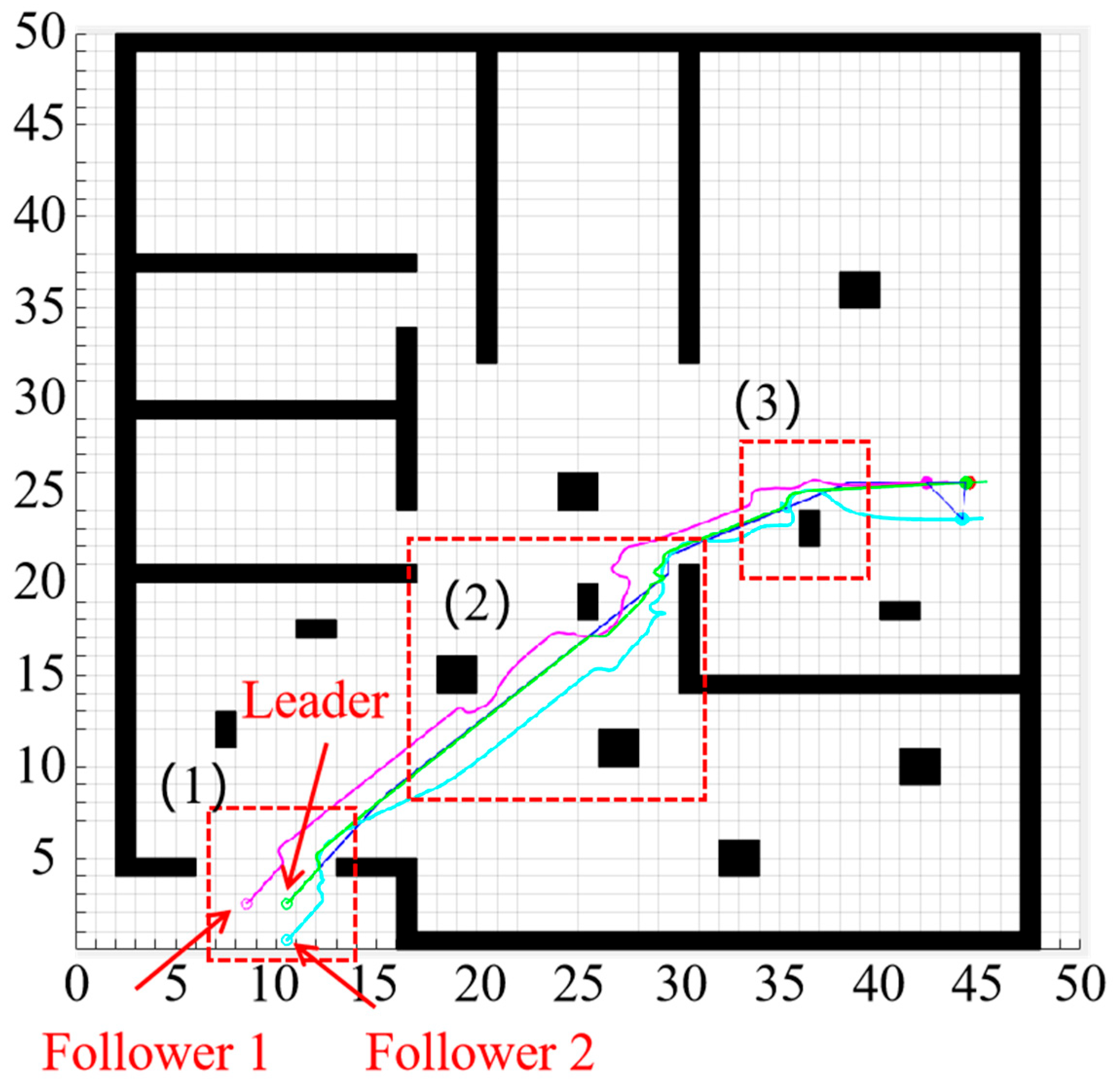
4.3. Discussion
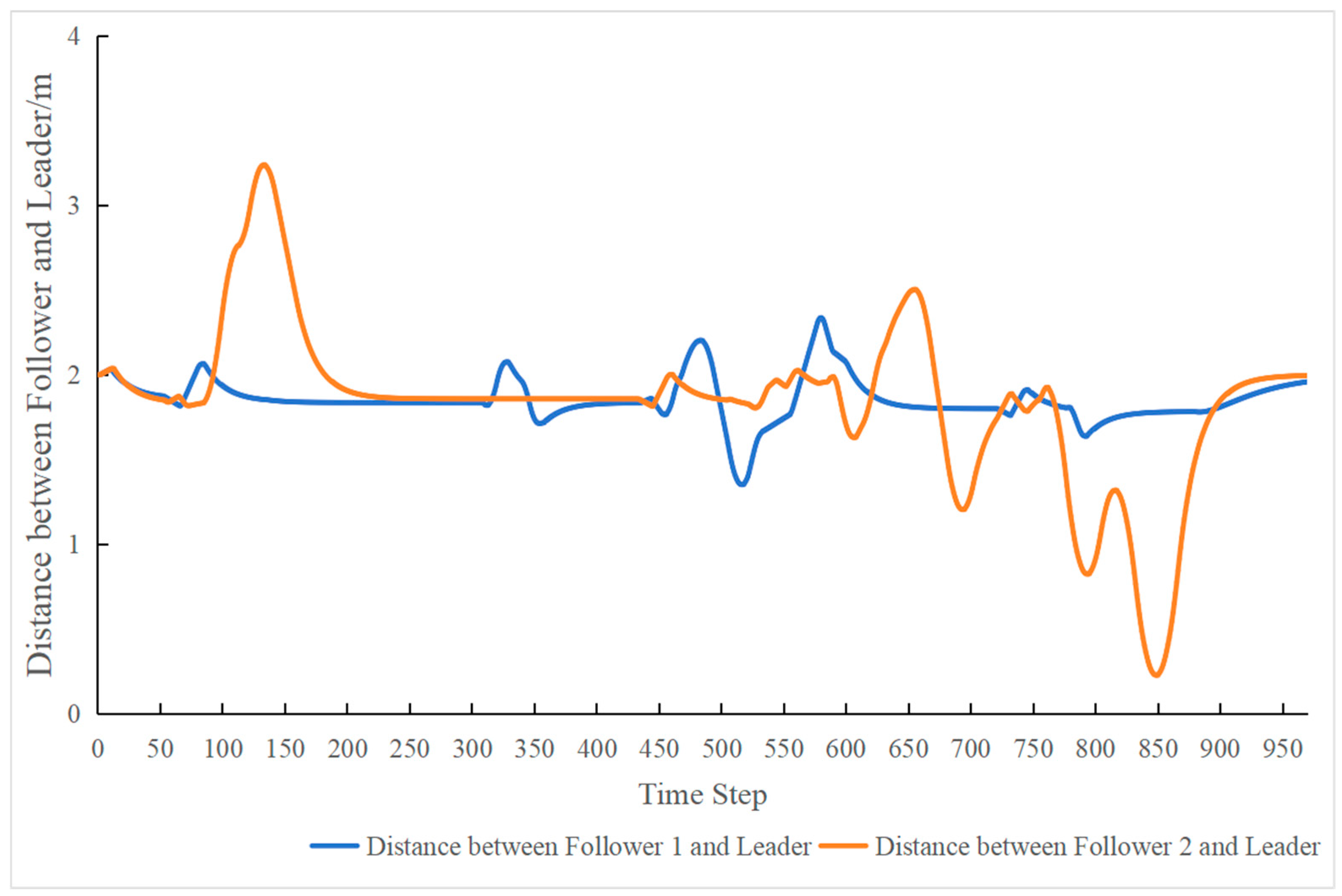
4.4. Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, Z.; Ning, S. Corporate digital transformation and strategic investments of construction industry in China. Heliyon 2023, 9, e17879. [Google Scholar] [CrossRef]
- Guo, Q.; Zhong, J. The effect of urban innovation performance of smart city construction policies: Evaluate by using a multiple period difference-in-differences model. Technol. Forecast. Soc. Change 2022, 184, 122003. [Google Scholar] [CrossRef]
- Lindsay, N.; Buehling, R.K.; Sun, L. A Sequential Task Addition Distributed Assignment Algorithm for Multi-Robot Systems. J. Intell. Robot. Syst. 2021, 102, 51. [Google Scholar] [CrossRef]
- Zhao, X.; Cheah, C.C. BIM-based indoor mobile robot initialization for construction automation using object detection. Autom. Constr. 2023, 146, 104647. [Google Scholar] [CrossRef]
- Gharbia, M.; Chang-Richards, A.; Lu, Y.; Zhong, R.Y.; Li, H. Robotic technologies for on-site building construction: A systematic review. J. Build. Eng. 2020, 32, 101584. [Google Scholar] [CrossRef]
- Melenbrink, N.; Werfel, J.; Menges, A. On-site autonomous construction robots: Towards unsupervised building. Autom. Constr. 2020, 119, 103312. [Google Scholar] [CrossRef]
- Pan, W.; Li, R.; Bock, T. Design and synthesis of the localization system for the onsite construction robot. In ISARC. Proceedings of the International Symposium on Automation and Robotics in Construction, Online, 27–29 October 2020; IAARC Publications: Edinburgh, UK, 2020; Volume 37, pp. 1501–1507. [Google Scholar]
- Wang, X.; Wang, S.; Menassa, C.C.; Kamat, V.R.; McGee, W. Automatic high-level motion sequencing methods for enabling multi-tasking construction robots. Autom. Constr. 2023, 155, 105071. [Google Scholar] [CrossRef]
- Wang, D.; Deng, H. Multirobot coordination with deep reinforcement learning in complex environments. Expert Syst. Appl. 2021, 180, 115128. [Google Scholar] [CrossRef]
- Ye, X.; Guo, H.; Luo, Z. Two-stage task allocation for multiple construction robots using an improved genetic algorithm. Autom. Constr. 2024, 165, 105583. [Google Scholar] [CrossRef]
- Fang, W.; Liao, Z.; Bai, Y. Improved ACO algorithm fused with improved Q-Learning algorithm for Bessel curve global path planning of search and rescue robots. Robot. Auton. Syst. 2024, 182, 104822. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Z.; Xue, Y.; Deng, Z.; Qin, H. Local path planning of under-actuated AUV based on VADWA considering dynamic model. Ocean Eng. 2024, 310, 118705. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. Ieee Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Li, R.; Zhou, C.; Dou, Q.; Hu, B. Complete coverage path planning and performance factor analysis for autonomous bulldozer. J. Field Robot. 2022, 39, 1012–1032. [Google Scholar] [CrossRef]
- Auh, E.; Kim, J.; Joo, Y.; Park, J.; Lee, G.; Oh, I.; Pico, N.; Moon, H. Unloading sequence planning for autonomous robotic container-unloading system using A-star search algorithm. Eng. Sci. Technol. Int. J. 2024, 50, 101610. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, S.; Zhou, J. A-star algorithm for expanding the number of search directions in path planning. In Proceedings of the 2021 2nd International Seminar on Artificial Intelligence, Networking and Information Technology (AINIT), Shanghai, China, 15–17 October 2021. [Google Scholar]
- Zheng, H.; Dai, M.; Zhang, Z.; Xia, Z.; Zhang, G.; Jia, F. The Navigation Based on Hybrid A Star and TEB Algorithm Implemented in Obstacles Avoidance. In Proceedings of the 2023 29th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Queenstown, New Zealand, 21–24 November 2023. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Liu, L.; Lin, J.; Yao, J.; He, D.; Zheng, J.; Huang, J.; Shi, P. Path Planning for Smart Car Based on Dijkstra Algorithm and Dynamic Window Approach. Wirel. Commun. Mob. Comput. 2021, 2021, 8881684. [Google Scholar] [CrossRef]
- Alshammrei, S.; Boubaker, S.; Kolsi, L. Improved Dijkstra Algorithm for Mobile Robot Path Planning and Obstacle Avoidance. Comput. Mater. Contin. 2022, 72, 5939–5954. [Google Scholar] [CrossRef]
- Yen, C.; Cheng, M. A study of fuzzy control with ant colony algorithm used in mobile robot for shortest path planning and obstacle avoidance. Microsyst. Technol. 2018, 24, 125–135. [Google Scholar] [CrossRef]
- Li, J.; Wang, H. Research on AUV Path Planning Based on Improved Ant Colony Algorithm. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 13–16 October 2020. [Google Scholar]
- Wu, L.; Huang, X.; Cui, J.; Liu, C.; Xiao, W. Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot. Expert Syst. Appl. 2023, 215, 119410. [Google Scholar] [CrossRef]
- Wang, P.K.C. Navigation strategies for multiple autonomous mobile robots moving in formation. J. Robot. Syst. 1991, 8, 177–195. [Google Scholar] [CrossRef]
- Desai, J.P.; Ostrowski, J.; Kumar, V. Controlling formations of multiple mobile robots. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No.98CH36146), Leuven, Belgium, 20 May 1998. [Google Scholar]
- Wu, X.; Wang, S.; Xing, M. Observer-Based Leader-Following Formation Control for Multi-Robot with Obstacle Avoidance. IEEE Access 2019, 7, 14791–14798. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Yang, S.; Shan, M. A Practical Leader–Follower Tracking Control Scheme for Multiple Nonholonomic Mobile Robots in Unknown Obstacle Environments. IEEE Trans. Control Syst. Technol. 2019, 27, 1685–1693. [Google Scholar] [CrossRef]
- Park, B.S.; Yoo, S.J. Connectivity-maintaining obstacle avoidance approach for leader-follower formation tracking of uncertain multiple nonholonomic mobile robots. Expert Syst. Appl. 2021, 171, 114589. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Wang, G.; Wu, S.; Li, W. Adaptive virtual leader–leader–follower based formation switching for multiple autonomous tracked mobile robots in unknown obstacle environments. J. Frankl. Inst. 2024, 361, 106762. [Google Scholar] [CrossRef]
- Lewis, M.A.; Kar-Han, T. High Precision Formation Control of Mobile Robots Using Virtual Structures. Auton. Robot. 1997, 4, 387–403. [Google Scholar] [CrossRef]
- Beard, R.W.; Lawton, J.; Hadaegh, F.Y. A coordination architecture for spacecraft formation control. IEEE Trans. Control Syst. Technol. 2001, 9, 777–790. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, L.; Zhang, G.; Wang, C.; Chai, Y.; Yang, T.; Mao, Z. Research on obstacle avoidance of multi-AUV cluster formation based on virtual structure and artificial potential field method. Comput. Electr. Eng. 2024, 117, 109250. [Google Scholar] [CrossRef]
- Cai, Z.; Wang, L.; Zhao, J.; Wu, K.; Wang, Y. Virtual target guidance-based distributed model predictive control for formation control of multiple UAVs. Chin. J. Aeronaut. 2020, 33, 1037–1056. [Google Scholar] [CrossRef]
- Zhen, Q.; Wan, L.; Li, Y.; Jiang, D. Formation control of a multi-AUVs system based on virtual structure and artificial potential field on SE(3). Ocean Eng. 2022, 253, 111148. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Cheung, C.; Rawashdeh, S.; Mohammadi, A. Jam Mitigation for Autonomous Convoys via Behavior-Based Robotics. Appl. Sci. 2022, 12, 9863. [Google Scholar] [CrossRef]
- Chen, G.; Shen, Y.; Qu, N.; He, B. Path planning of AUV during diving process based on behavioral decision-making. Ocean Eng. 2021, 234, 109073. [Google Scholar] [CrossRef]
- Ding, L.; Jiang, W.; Zhou, Y.; Zhou, C.; Liu, S. BIM-based task-level planning for robotic brick assembly through image-based 3D modeling. Adv. Eng. Inform. 2020, 43, 100993. [Google Scholar] [CrossRef]
- Cho, J.; Lee, J.; Kim, Y.; Shin, K. An analysis model for wind resistance performance of automated exterior wall painting robots in apartment buildings. KSCE J. Civ. Eng. 2014, 18, 909–919. [Google Scholar] [CrossRef]
- Jung, J.; Lee, S.; Myung, H. Indoor Mobile Robot Localization and Mapping Based on Ambient Magnetic Fields and Aiding Radio Sources. IEEE Trans. Instrum. Meas. 2015, 64, 1922–1934. [Google Scholar] [CrossRef]
- Yu, S.; Ryu, B.; Lim, S.; Kim, C.; Kang, M.; Han, C. Feasibility verification of brick-laying robot using manipulation trajectory and the laying pattern optimization. Autom. Constr. 2009, 18, 644–655. [Google Scholar] [CrossRef]
- Ben Salah, I.; Kramm, S.; Demonceaux, C.; Vasseur, P. Summarizing large scale 3D mesh for urban navigation. Robot. Auton. Syst. 2022, 152, 104037. [Google Scholar] [CrossRef]
- Thrun, S. Learning metric-topological maps for indoor mobile robot navigation. Artif. Intell. 1998, 99, 21–71. [Google Scholar] [CrossRef]
- Dierks, T.; Jagannathan, S. Control of Nonholonomic Mobile Robot Formations: Backstepping Kinematics into Dynamics. In Proceedings of the 2007 IEEE International Conference on Control Applications, Singapore, 1–3 October 2007. [Google Scholar]
- Zhang, H.; Wu, Z. The general goodness-of-fit tests for correlated data. Comput. Stat. Data Anal. 2022, 167, 107379. [Google Scholar] [CrossRef]





| Type of Algorithm | Scalability in Path Generation | Suitability in Path Optimization | Computational Efficiency |
|---|---|---|---|
| A* algorithm | Yes | Yes | Fastest |
| Dijkstra algorithm | Yes | Yes | Relatively Fast |
| Ant Colony algorithm | Yes | No | Slow |
| Type of Formation Methods | Advantages | Disadvantages |
|---|---|---|
| Leader–Follower Method | Simple formation control structure, easy to implement | Highly dependent on the leader |
| Virtual Structure Method | Clear formation feedback, easy to determine and maintain formation behavior | Restricted in flexibility and adaptability, especially in case of obstacle avoidance |
| Behavior-Based Formation Method | Strong adaptability, better handle collision avoidance issues | Limited in clearly defining the overall behavior of the formation system, leading to lower stability |
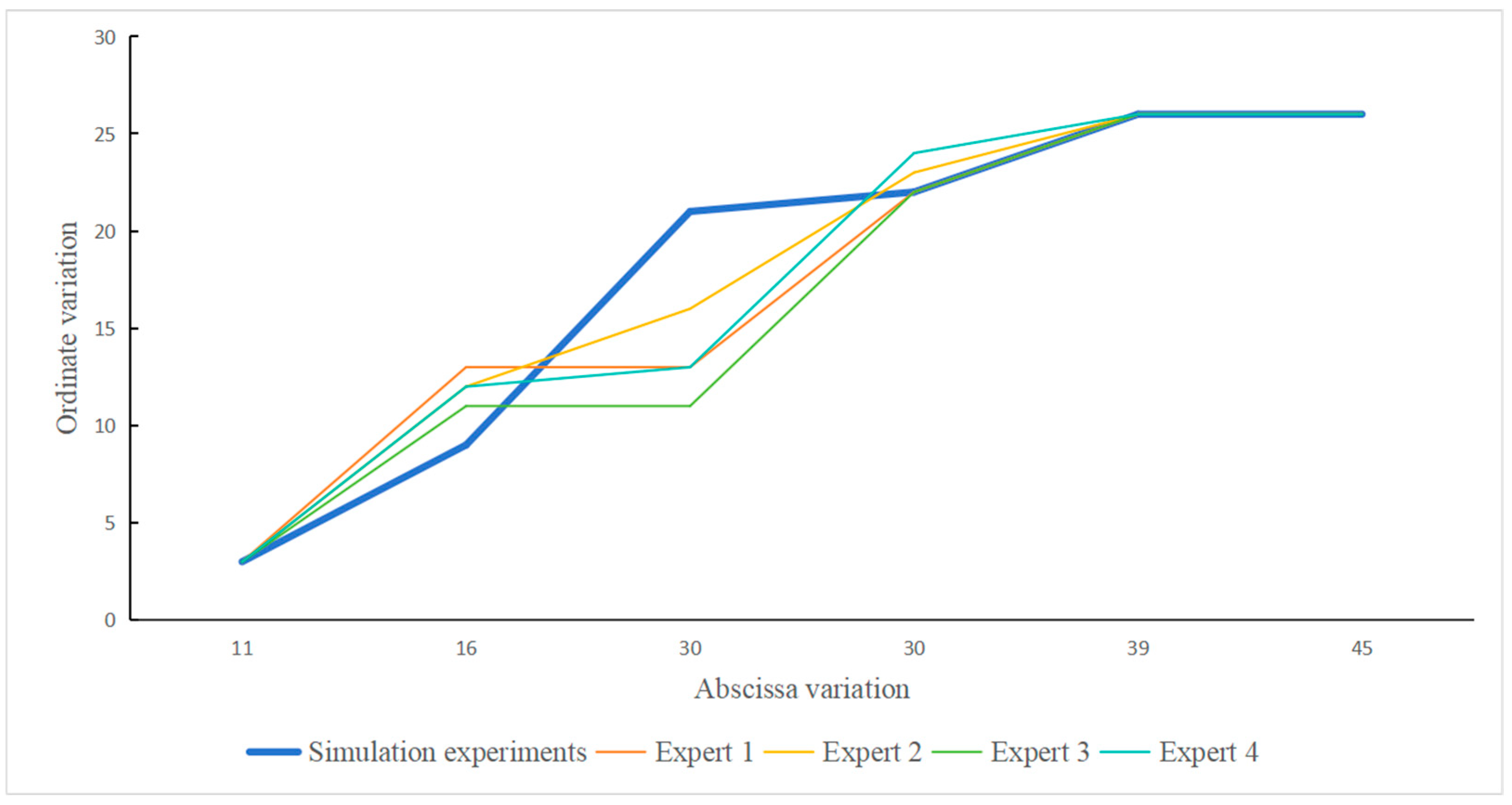
| Key Node | Horizontal Coordinate Value | Vertical Coordinate Value |
|---|---|---|
| (Star Node) | 11 | 3 |
| 16 | 9 | |
| 30 | 21 | |
| 30 | 22 | |
| 39 | 26 | |
| (End Node) | 45 | 26 |
| Parameter Types | Value |
|---|---|
| Initial heading angle of the leader robot | π/4 |
| Initial heading angle of the follower robot | π/4 |
| Desired distance between the leader and the followers | 2 m |
| Initial angle between the leader and follower | π/2 |
| Initial angle between the leader and follower | 3π/4 |
| Maximum linear velocity of the robot | 0.7 m/s |
| Minimum linear velocity of the robot | 0 m/s |
| Maximum linear acceleration of the robot | 0.4 m/s2 |
| Minimum linear acceleration of the robot | 0 m/s2 |
| Investigator | TSS | RSS | R2 |
|---|---|---|---|
| Expert 1 | 415 | 64 | 0.84 |
| Expert 2 | 414 | 35 | 0.91 |
| Expert 3 | 452 | 104 | 0.77 |
| Expert 4 | 444 | 84 | 0.81 |
| Path Planning Method | Planning Time (s) | Path Length/m | Path Variation Range | Success Rate |
|---|---|---|---|---|
| The proposed method | 547.7 | 22 | Minor | 100% |
| Manual method | 604.9 | 24.3 | Significant | 75% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; He, J.; Wang, X.; Xu, W.; Kim, J.I.; Chen, X. A* Algorithm for On-Site Collaborative Path Planning in Building Construction Robots. Buildings 2025, 15, 3876. https://doi.org/10.3390/buildings15213876
Fang Y, He J, Wang X, Xu W, Kim JI, Chen X. A* Algorithm for On-Site Collaborative Path Planning in Building Construction Robots. Buildings. 2025; 15(21):3876. https://doi.org/10.3390/buildings15213876
Chicago/Turabian StyleFang, Yuan, Jialiang He, Xi Wang, Wensheng Xu, Jung In Kim, and Xingbin Chen. 2025. "A* Algorithm for On-Site Collaborative Path Planning in Building Construction Robots" Buildings 15, no. 21: 3876. https://doi.org/10.3390/buildings15213876
APA StyleFang, Y., He, J., Wang, X., Xu, W., Kim, J. I., & Chen, X. (2025). A* Algorithm for On-Site Collaborative Path Planning in Building Construction Robots. Buildings, 15(21), 3876. https://doi.org/10.3390/buildings15213876





