Research on Cooling-Load Characteristics of Subway Stations Based on Co-Simulation Method and Sobol Global Sensitivity Analysis
Abstract
1. Introduction
1.1. Research Background
1.2. Literature Review
1.2.1. Research on Influencing Factors of Building Load
1.2.2. Sensitivity Analysis Methods
2. Materials and Methods
- (1)
- Parameter determination
- (2)
- Variable values
- (3)
- Saltelli quasi-Monte Carlo sampling
- (4)
- EnergyPlus–Python co-simulation
- (5)
- Sobol global sensitivity analysis
2.1. Saltelli Quasi-Monte Carlo Sampling Method
2.2. Sobol Global Sensitivity Analysis Theory
2.3. Co-Simulation Method for the Subway Station Cooling Load
3. Establishment of the Cooling-Load Simulation Database
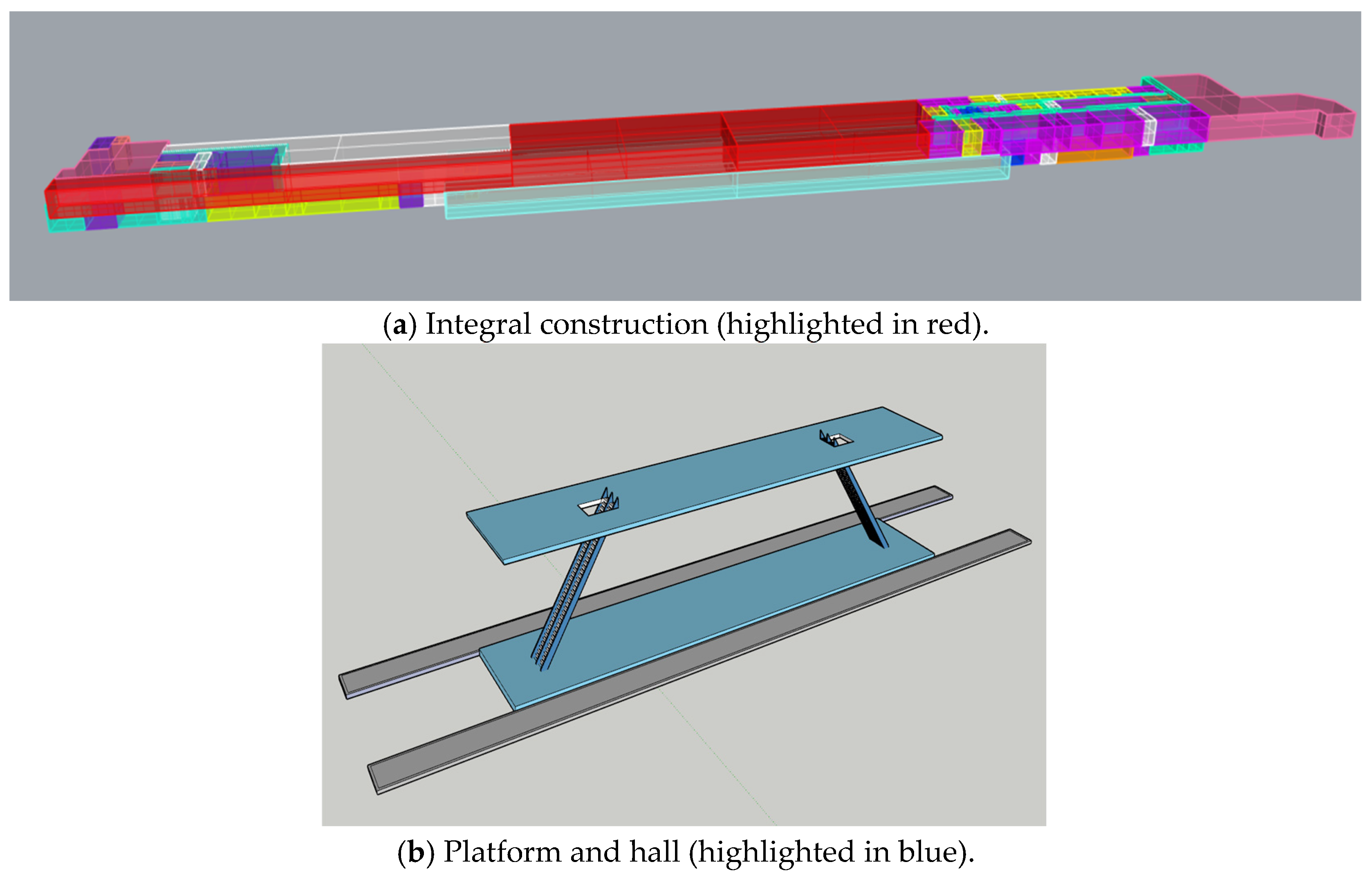
3.1. Baseline Model of the Case Subway Station
3.1.1. Basic Information of the Case Subway Station
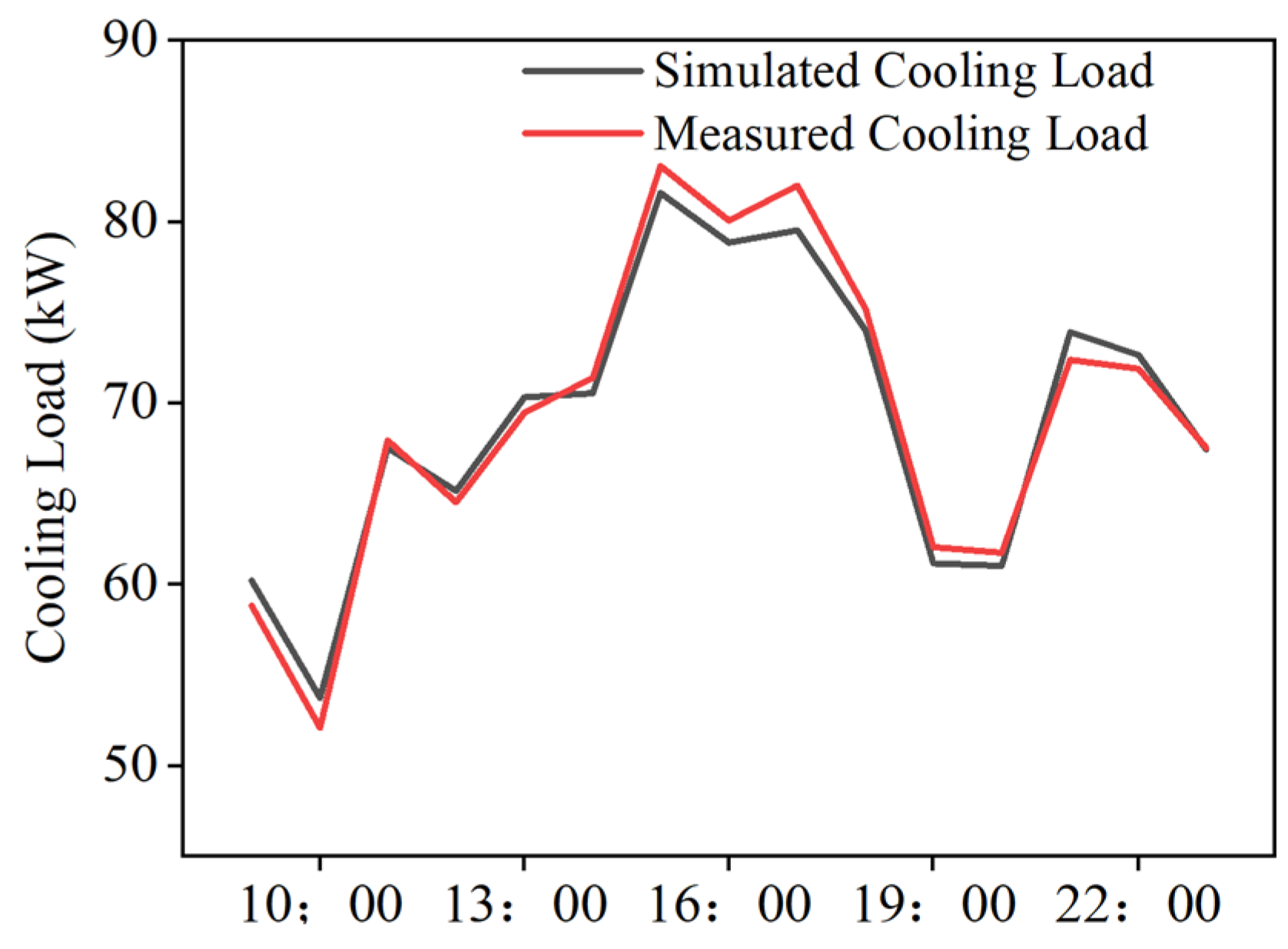
3.1.2. Verification of Simulation Results for the Case Station
3.2. Input Parameter Range and Distribution
3.3. Saltelli Sampling Implementation
3.4. Generation of Simulated Database
4. Result
4.1. Single-Parameter Sensitivity Analysis Results
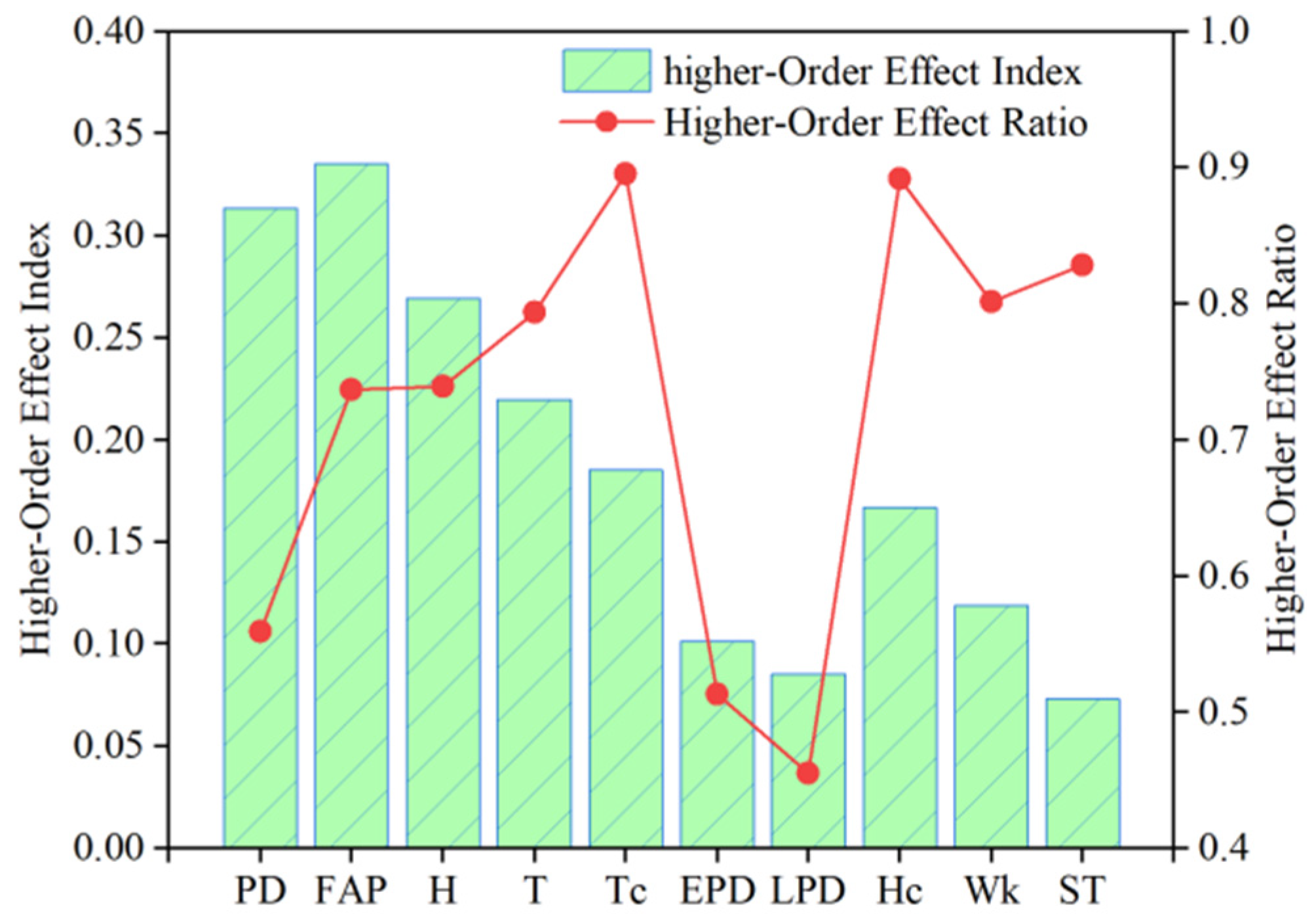
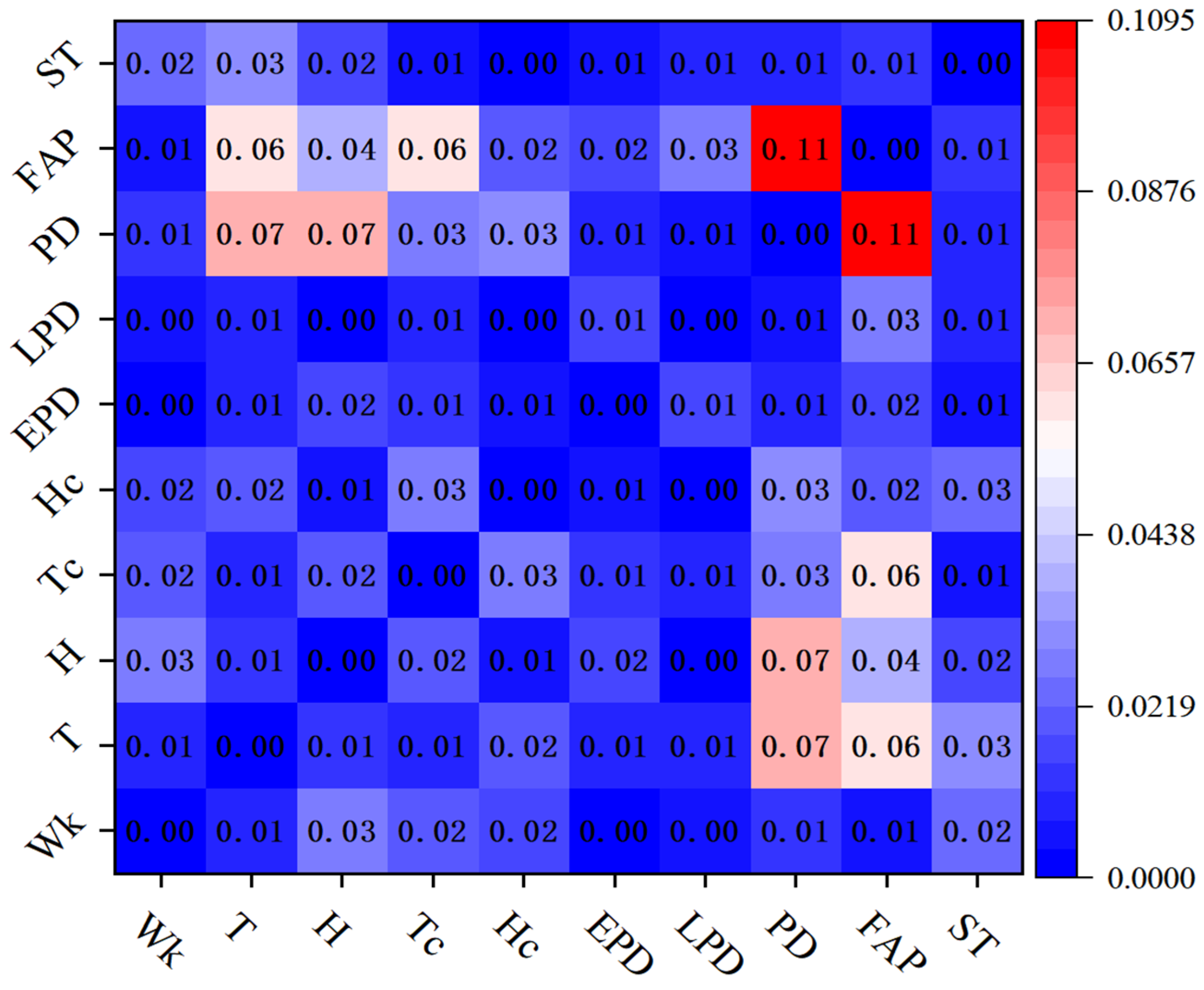
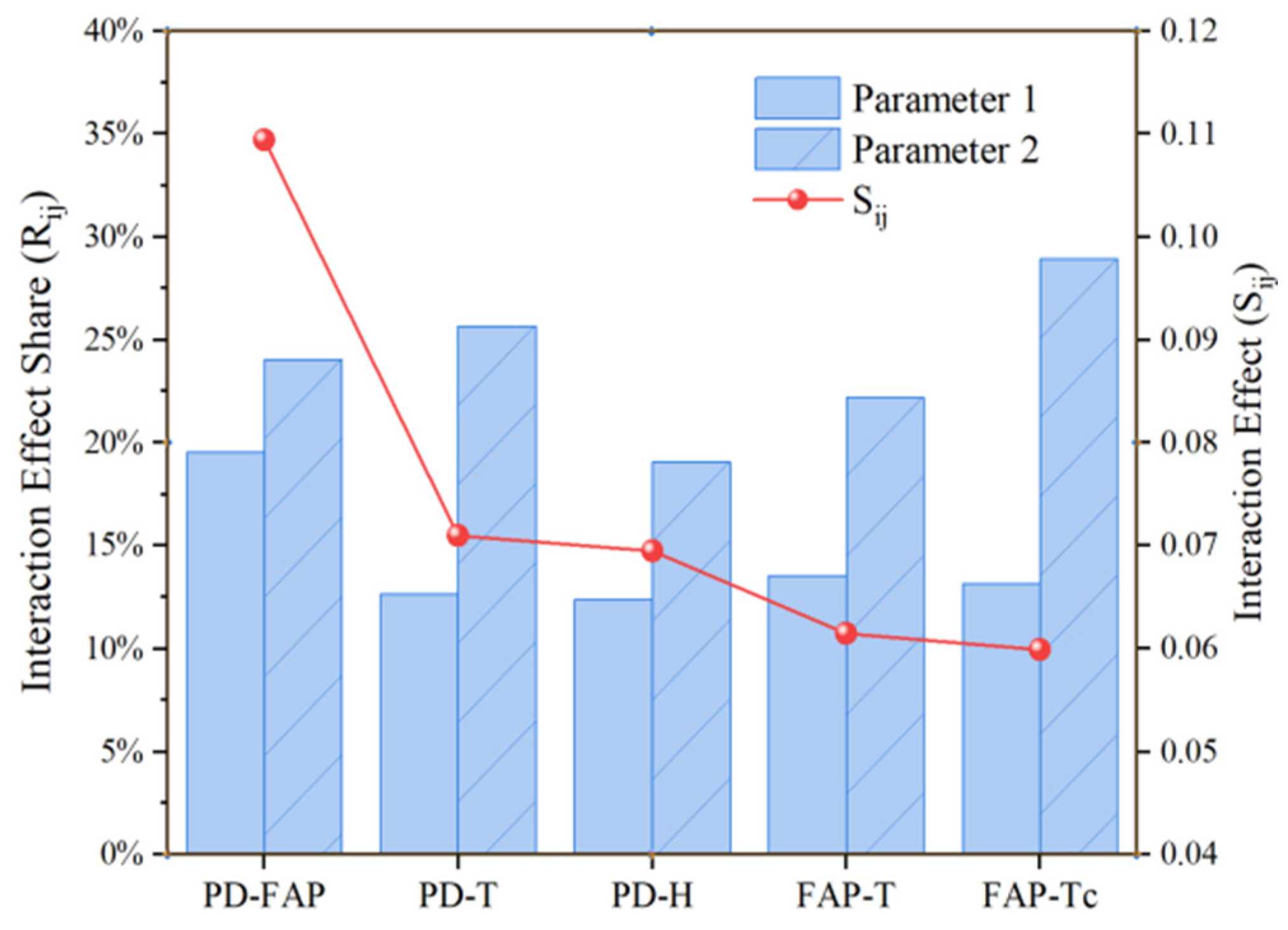
4.2. Parameter Interaction Effects
5. Discussion
5.1. Influence Factors and Comparative Analysis
5.2. Significance of Interaction Effects
6. Conclusions
- (1)
- Based on the total sensitivity index, the ranking of the importance of factors influencing the cooling load in subway stations is as follows: occupant density > fresh air volume > outdoor relative humidity > outdoor dry-bulb temperature > air-conditioning setpoint temperature > lighting power density > equipment power density > air-conditioning setpoint humidity > building-envelope heat transfer coefficient > soil temperature. Among them, occupant density (SiT = 0.5605) fresh air volume (SiT = 0.4546) are the dominant factors influencing the total cooling load. These two parameters contribute approximately 50% of the total load variance together.
- (2)
- Among meteorological parameters, outdoor relative humidity (SiT = 0.3642) and outdoor dry-bulb temperature (SiT = 0.2768) affect the load by changing the enthalpy value of fresh air. However, their influence is significantly weaker compared to above-ground buildings. This is mainly due to the low and stable soil temperature in the external environment of the underground building envelope. The influence of the building-envelope heat transfer coefficient (SiT = 0.1482) and soil temperature (SiT = 0.0881) is very limited.
- (3)
- Passenger density (Si = 0.2471) is the most influential independent parameter, driving load variations through passenger heat and moisture dissipation. Lighting power density (Si = 0.1022) and equipment power density (Si = 0.0961) as stable internal heat sources, also exhibit significant independent influences. Although the total effect of fresh air volume and outdoor meteorological parameters is high, their first-order effect index are relatively low, indicating that their independent effects are limited, and the load influence is highly dependent on the interactions with other parameters.
- (4)
- Five significant second-order interactions were identified according to the Sobol sensitivity analysis, including occupant density and fresh air volume (Sij = 0.1094), occupant density and outdoor dry-bulb temperature (Sij = 0.07098), fresh air volume and outdoor dry-bulb temperature (Sij = 0.06947), fresh air volume and outdoor relative humidity (Sij = 0.06145), air-conditioning setpoint temperature and fresh air volume (Sij = 0.05985). These interactions reveal the nonlinear load response characteristics when multiple parameters change in concert.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schwanitz, S.; Wittkowski, M.; Rolny, V.; Samel, C.; Basner, M. Continuous assessments of pressure comfort on a train—A field-laboratory comparison. Appl. Ergon. 2013, 44, 11–17. [Google Scholar] [CrossRef]
- Mohammadi, A.; Amador-Jimenez, L.; Nasiri, F. A multi-criteria assessment of the passengers’ level of comfort in urban railway rolling stock. Sustain. Cities Soc. 2020, 53, 101892. [Google Scholar] [CrossRef]
- Niu, J.; Zhou, D.; Liang, X.; Liu, T.; Liu, S. Numerical study on the aerodynamic pressure of a metro train running between two adjacent platforms. Tunn. Undergr. Space Technol. 2017, 65, 187–199. [Google Scholar] [CrossRef]
- China Association of Metros. 2024 Annual Statistics and Analysis Report on Urban Rail Transit. 2024. Available online: https://www.camet.org.cn/xytj/tjxx/660844283682885.shtml (accessed on 28 March 2025).
- Su, X.; Huang, Y.; Wang, L.; Tian, S.; Luo, Y. Operating optimization of air-conditioning water system in a subway station using data mining and dynamic system models. J. Build. Eng. 2021, 44, 103379. [Google Scholar] [CrossRef]
- Yang, G.; Zhai, X. Optimal design and performance analysis of solar hybrid CCHP system considering influence of building type and climate condition. Energy 2019, 174, 647–663. [Google Scholar] [CrossRef]
- Yang, G.; Zhai, X. Optimization and performance analysis of solar hybrid CCHP systems under different operation strategies. Appl. Therm. Eng. 2018, 133, 327–340. [Google Scholar] [CrossRef]
- State Council of the People’s Republic of China. *Energy Conservation and Carbon Reduction Action Plan for 2024–2025. 2024. Available online: http://www.gov.cn/zhengce/content/2024-05/23/content_6954682.htm (accessed on 23 May 2024).
- GB/T 45902-2025; General Technical Requirements for Energy-Saving Control Systems of Ventilation and Air Conditioning in Urban Rail Transit Stations. Standardization Administration of the People’s Republic of China: Beijing, China, 2025. Available online: https://std.samr.gov.cn/gb/search/gbDetailed?id=E711ED782A31B4BAE05397BE0A0AED40 (accessed on 30 June 2025).
- Mastrucci, A.; Pérez-López, P.; Benetto, E.; Leopold, U.; Blanc, I. Global sensitivity analysis as a support for the generation of simplified building stock energy models. Energy Build. 2017, 149, 368–383. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Su, Z.; Li, X. Energy benchmarking analysis of subway station with platform screen door system in China. Tunn. Undergr. Space Technol. 2022, 128, 104655. [Google Scholar] [CrossRef]
- Li, H.; Tang, B.; Che, L.; Liu, J.; Su, X. Energy Saving Potential of Air Conditioning System of Equipment Stations in Metro Systems. Procedia Eng. 2017, 205, 3519–3524. [Google Scholar] [CrossRef]
- Jiao, H.; Feng, H.; Wei, D.; Ran, Y.; Hu, Z. Energy saving control for the subway station air conditioning systems based on reinforcement learning. Control. Decis. 2021, 37, 3139–3148. (In Chinese) [Google Scholar]
- Wang, J.; Yin, Y.; Wei, Z.; Zhai, X. Cooling load analysis based on theory-based models and field tests for VAC system in subway station: A case study. Energy 2025, 314, 134219. [Google Scholar] [CrossRef]
- Hu, Y.; Qin, L.; Li, S.; Li, X.; Zhou, R.; Li, Y.; Sheng, W. Adaptive corrected parameters algorithm applied in cooling load prediction based on black-box model: A case study for subway station. Energy Build. 2023, 297, 113429. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Fan, X.; Duan, D.; Zheng, W. Air-conditioning load characteristics and grey box predicting model in subway stations. J. Build. Eng. 2024, 91, 109656. [Google Scholar] [CrossRef]
- Guan, B.; Liu, X.; Zhang, T.; Wang, X. Hourly energy consumption characteristics of metro rail transit: Train traction versus station operation. Energy Built Environ. 2023, 4, 568–575. [Google Scholar] [CrossRef]
- Lian, H.; Wei, H.; Wang, X.; Chen, F.; Ji, Y.; Xie, J. Research on Real-Time Energy Consumption Prediction Method and Characteristics of Office Buildings Integrating Occupancy and Meteorological Data. Buildings 2025, 15, 404. [Google Scholar] [CrossRef]
- Guan, Y.; Hu, C.; Meng, X. Formation analysis of cooling load from envelopes under air-conditioning intermittent operation. Sol. Energy 2025, 292, 113428. [Google Scholar] [CrossRef]
- Ao, J.; Du, C.; Bellamy, L.; Li, B. Integration of thermal-daylighting climate subzones and energy efficiency design optimization for office buildings. J. Build. Eng. 2025, 99, 111669. [Google Scholar] [CrossRef]
- Lian, H.; Ji, Y.; Niu, M.; Gu, J.; Xie, J.; Liu, J. A hybrid load prediction method of office buildings based on physical simulation database and LightGBM algorithm. Appl. Energy 2025, 377, 124620. [Google Scholar] [CrossRef]
- Yu, Y.; You, S.; Zhang, H.; Wei, S.; Liu, T.; Guo, X.O.; Luo, N.; Chen, W. An empirical study estimating train-induced airflow rate and its effect on the cooling load of underground stations. J. Build. Eng. 2025, 105, 112413. [Google Scholar] [CrossRef]
- Kong, G.; Hu, S.; Yang, Q. Uncertainty method and sensitivity analysis for assessment of energy consumption of underground metro station. Sustain. Cities Soc. 2023, 92, 104504. [Google Scholar] [CrossRef]
- Jiang, X.; Ding, Y.; Zhang, D.; He, Y.; Yan, H.; Yao, Y.; Hou, Y. How does heat move seasonally in deep-buried underground stations? Insights into the “Source-Path-Sink” mechanism from Chongqing. Build. Environ. 2025, 283, 113369. [Google Scholar] [CrossRef]
- Ren, T.; Li, M.; Wang, D.; Yang, J.; Kong, L.; He, L. Theoretical and numerical studies of heat and humidity transfer in underground ventilation corridor. Int. J. Heat Fluid Flow 2025, 112, 109765. [Google Scholar] [CrossRef]
- Akram, M.W.; Guo, H.; Hu, W. Numerical simulation of heat transfer through rock envelope of a plant factory in an underground mine tunnel. Energy Built Environ. 2025, in press. [Google Scholar] [CrossRef]
- Yin, H.; Yang, C.; Yi, L.; Yu, J.; Wu, Y.; Deng, Y.; Tang, Z. Ventilation and air conditioning system of deep-buried subway station in sub-tropical climates: Energy-saving strategies. Appl. Therm. Eng. 2020, 178, 115555. [Google Scholar] [CrossRef]
- Bi, H.; Zhou, Y.; Liu, J.; Wang, H.; Yu, T. Load forecast and fuzzy control of the air-conditioning systems at the subway stations. J. Build. Eng. 2022, 49, 104029. [Google Scholar] [CrossRef]
- Ahn, J.; Cho, S.; Chung, D.H. Development of a statistical analysis model to benchmark the energy use intensity of subway stations. Appl. Energy 2016, 179, 488–496. [Google Scholar] [CrossRef]
- Guan, B.; Liu, X.; Zhang, T.; Xia, J. Energy consumption of subway stations in China: Data and influencing factors. Sustain. Cities Soc. 2018, 43, 451–461. [Google Scholar] [CrossRef]
- Ren, Z.; Kim, J.I.; Kim, J. Assessment methodology for dynamic occupancy adaptive HVAC control in subway stations integrating passenger flow simulation into building energy modeling. Energy Build. 2023, 300, 113667. [Google Scholar] [CrossRef]
- Su, Z.; Li, X. Extraction of key parameters and simplification of sub-system energy models using sensitivity analysis in subway stations. Energy 2022, 261, 125285. [Google Scholar] [CrossRef]
- Sanchez, D.G.; Lacarrière, B.; Musy, M.; Bourges, B. Application of sensitivity analysis in building energy simulations: Combining first- and second-order elementary effects methods. Energy Build. 2014, 68, 741–750. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis the Primer; John Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Tian, W. A review of sensitivity analysis methods in building energy analysis. Renew. Sustain. Energy Rev. 2013, 20, 411–419. [Google Scholar] [CrossRef]
- Mechri, H.E.; Capozzoli, A.; Corrado, V. USE of the ANOVA approach for sensitive building energy design. Appl. Energy 2010, 87, 3073–3083. [Google Scholar] [CrossRef]
- Tian, W.; de Wilde, P. Uncertainty and sensitivity analysis of building performance using probabilistic climate projections: A UK case study. Autom. Constr. 2011, 20, 1096–1109. [Google Scholar] [CrossRef]
- Wilde, P.; Tian, W. Identification of key factors for uncertainty in the prediction of the thermal performance of an office building under climate change. Build. Simul. 2009, 2, 157–174. [Google Scholar] [CrossRef]
- Neale, J.; Shamsi, M.H.; Mangina, E.; Finn, D.; O’Donnell, J. Accurate identification of influential building parameters through an integration of global sensitivity and feature selection techniques. Appl. Energy 2022, 315, 118956. [Google Scholar] [CrossRef]
- Ebrahimi-Moghadam, A.; Farzaneh-Gord, M.; Abadi, M.K. Sensitivity analysis and working fluid selection for a biogas-fueled hybrid energy system based on nearly zero energy building concept: A case study. J. Clean. Prod. 2024, 435, 140499. [Google Scholar] [CrossRef]
- Tootkaboni, M.P.; Ballarini, I.; Corrado, V. Towards climate resilient and energy-efficient buildings: A sensitivity analysis on building components and cooling strategies. Build. Environ. 2025, 270, 112473. [Google Scholar] [CrossRef]
- Tajuddeen, I.; Rodrigues, E. A Morris sensitivity analysis of an office building’s thermal design parameters under climate change in sub-Saharan Africa. Build. Environ. 2024, 262, 111771. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, J.; Gao, Y.; Tian, W.; Yan, Z.; Ye, X.; Sun, Y.; Wu, C. Uncertainty and sensitivity analysis of cooling and heating loads for building energy planning. J. Build. Eng. 2022, 45, 103440. [Google Scholar] [CrossRef]
- Pang, Z.; O’Neill, Z. Uncertainty quantification and sensitivity analysis of the domestic hot water usage in hotels. Appl. Energy 2018, 232, 424–442. [Google Scholar] [CrossRef]
- Delgarm, N.; Sajadi, B.; Azarbad, K.; Delgarm, S. Sensitivity analysis of building energy performance: A simulation-based approach using OFAT and variance-based sensitivity analysis methods. J. Build. Eng. 2018, 15, 181–193. [Google Scholar] [CrossRef]
- Zhang, H.; Tian, W.; Tan, J.; Yin, J.; Fu, X. Sensitivity analysis of multiple time-scale building energy using Bayesian adaptive spline surfaces. Appl. Energy 2024, 363, 123042. [Google Scholar] [CrossRef]
- Gauch, H.L.; Dunant, C.F.; Hawkins, W.; Serrenho, A.C. What really matters in multi-storey building design? A simultaneous sensitivity study of embodied carbon, construction cost, and operational energy. Appl. Energy 2023, 333, 120585. [Google Scholar] [CrossRef]
- Mavromatidis, G.; Orehounig, K.; Carmeliet, J. Uncertainty and global sensitivity analysis for the optimal design of distributed energy systems. Appl. Energy 2018, 214, 219–238. [Google Scholar] [CrossRef]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Shi, Q.; Xu, Z.; Lv, X.; Zhang, P. Parameter sensitivity analysis of SWMM Model based on local and global methods. Water Resour. Hydropower Eng. 2025, 1–23. Available online: https://link.cnki.net/urlid/10.1746.TV.20241227.1138.002 (accessed on 28 March 2025). (In Chinese).
- Xiang, X.; Ao, T.; Xiao, Q.; Li, X.; Zhou, L.; Chen, Y.; Bi, Y.; Guo, J. Parameter Sensitivity Analysis of SWAT Modeling in the Upper Heihe River Basin Using Four Typical Approaches. Appl. Sci. 2022, 12, 9862. [Google Scholar] [CrossRef]
- ISO 7730:2005; Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. International Organization for Standardization: Geneva, Switzerland, 2005.
- GB 50176-2016; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Thermal Design of Civil Buildings. China Architecture & Building Press: Beijing, China, 2016.
- National Renewable Energy Laboratory. EnergyPlus Weather Data [Data set]. U.S. Department of Energy. 2023. Available online: https://energyplus.net/weather (accessed on 1 April 2005).
- Zhang, Z.; Shi, X.; Yu, D.; Wang, H.; Zhao, Y.; Sun, W.; Huang, B. Seasonal variation and regional differentiation of soil temperature in China. Acta Pedol. Sin. 2009, 46, 227–234. (In Chinese) [Google Scholar]
- GB 50189-2015; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Design Standard for Energy Efficiency of Public Buildings. China Architecture & Building Press: Beijing, China, 2015.
- GB/T 16275-2008; Standardization Administration of the People’s Republic of China. Classification and Terminology for Urban Rail Transit. Standards Press of China: Beijing, China, 2008.
- GB 50137-2013; Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of Urban Rail Transit. China Architecture & Building Press: Beijing, China, 2013.
- Wang, Z.; Jia, S.; Dai, Z.; Yin, S.; Zhang, X.; Yang, Z.; Thanh, H.V.; Ling, H.; Soltanian, M.R. Environmental risk evaluation for radionuclide transport through natural barriers of nuclear waste disposal with multi-scale streamline approaches. Sci. Total Environ. 2024, 953, 176084. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, Z.; Zhang, Z.; Liu, G.; Fang, Y.; Song, Y.; Li, J.; Sun, K.; Feng, Y. Coupled LCA, AHP- and Monte Carlo sensitivity analysis: A comprehensive assessment of estrogen-containing municipal wastewater treatment by AO and AAO processes. Chem. Eng. J. 2025, 511, 161922. [Google Scholar] [CrossRef]





| Category | Method | Significance | Mathematical Expression |
|---|---|---|---|
| Regression-based sensitivity method [36] | PEAR | Measures the linear correlation coefficient between the output variable Y and a single input parameter Xi Suitable for linear regression models. | |
| SRC | Computes the strength of correlation between Y and Xj via a linear regression model. Applicable to linear models. | ||
| PCC | Partial Correlation Coefficient; quantifies the independent linear influence of Xj on Y through regression, ignoring interactions among input parameters. | ||
| Screening-based sensitivity method [37] | Morris | A model-agnostic method that computes partial derivatives of the model at uniformly distributed points across the input parameter space and averages these derivatives as an indicator of each parameter’s influence. | |
| Variance-based sensitivity analysis method [11] | Sobol | A model-independent method based on variance decomposition; quantifies the contribution of input parameters to output uncertainty. Capable of accurately distinguishing main effects, interaction effects, and total effects. | |
| Metamodel-based sensitivity analysis method | MARS | Multivariate Adaptive Regression Splines; combines spline regression with stepwise model fitting and recursive partitioning. | / |
| Sort | Parameter | Label | Value Range | Discrete Step | Unit | Selection Basis |
|---|---|---|---|---|---|---|
| Basic thermal parameters of the station | Heat transfer coefficient | Wk | 0.1–1.9 | 0.3 | W/(m2·K) | [56] |
| Meteorological information | Dry-bulb temperature | T | 26–40 | 2 | °C | [57] |
| Relative humidity | H | 20–100 | 10 | / | ||
| Soil temperature | ST | 18–26 | 2 | °C | [58] | |
| Internal load disturbance | Occupant density | PD | 0–5000 | 500 | p/h | From history data |
| Equipment power density | EPD | 5–30 | 5 | W/m2 | [59] | |
| Lighting power density | LPD | 0–15 | 3 | W/m2 | [60] | |
| Indoor environment control | Temperature | Tc | 26–30 | 1 | °C | [61] |
| Relative humidity | Hc | 40–70 | 5 | / | ||
| Fresh air | FAP | 0–30 | 5 | m3/(h·p) |
| Label | Si | SiT | SiT − Si |
|---|---|---|---|
| PD | 0.2471 | 0.5605 | 0.3134 |
| FAP | 0.1196 | 0.4546 | 0.335 |
| H | 0.095 | 0.3642 | 0.2692 |
| T | 0.0572 | 0.2768 | 0.2196 |
| Tc | 0.0217 | 0.2069 | 0.1852 |
| EPD | 0.0961 | 0.1973 | 0.1012 |
| LPD | 0.1022 | 0.1876 | 0.0854 |
| Hc | 0.0202 | 0.1869 | 0.1667 |
| Wk | 0.0294 | 0.1482 | 0.1188 |
| ST | 0.0151 | 0.0881 | 0.073 |
| Aspect | This Study | Yu et al. [23] | Kong et al. [24] | Ahn et al. [30] |
|---|---|---|---|---|
| Key Findings | Quantified parameter ranking Strong interaction effects identified | Train-induced airflow significantly impacts load | Outdoor temperature and equipment parameters dominate | Passenger flow as a key variable in multi-factor benchmark model |
| Significance | Systematic quantification and ranking Interaction effects introduced | Corrects inaccuracies in traditional design methods | Highlights load driver differences by functional zone | Establishes a energy benchmark regression model |
| Advantages | Comprehensive and quantitative method Novel insight into interaction mechanisms | Strong empirical evidence (field measurements) | Considers parameter uncertainty | Based on extensive operational data (157 stations) |
| Disadvantages | Excludes dynamic disturbances No specific control strategy | Single-factor focus, lacks multi-factor comparison | Excludes passenger factors | Cannot reveal physical mechanisms or interactions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Z.; Tian, W.; Lu, Q.; Li, M.; Dai, B.; Ji, Y.; Zhang, L.; Wang, J. Research on Cooling-Load Characteristics of Subway Stations Based on Co-Simulation Method and Sobol Global Sensitivity Analysis. Buildings 2025, 15, 3858. https://doi.org/10.3390/buildings15213858
Lv Z, Tian W, Lu Q, Li M, Dai B, Ji Y, Zhang L, Wang J. Research on Cooling-Load Characteristics of Subway Stations Based on Co-Simulation Method and Sobol Global Sensitivity Analysis. Buildings. 2025; 15(21):3858. https://doi.org/10.3390/buildings15213858
Chicago/Turabian StyleLv, Zhirong, Wei Tian, Qianwen Lu, Minfeng Li, Baoshan Dai, Ying Ji, Linfeng Zhang, and Jiaqiang Wang. 2025. "Research on Cooling-Load Characteristics of Subway Stations Based on Co-Simulation Method and Sobol Global Sensitivity Analysis" Buildings 15, no. 21: 3858. https://doi.org/10.3390/buildings15213858
APA StyleLv, Z., Tian, W., Lu, Q., Li, M., Dai, B., Ji, Y., Zhang, L., & Wang, J. (2025). Research on Cooling-Load Characteristics of Subway Stations Based on Co-Simulation Method and Sobol Global Sensitivity Analysis. Buildings, 15(21), 3858. https://doi.org/10.3390/buildings15213858








