Mechanisms of Seismic Failure in Multistory Masonry and Infilled Frame Buildings: Field Investigation and Numerical Validation from the 2022 Luding Earthquake
Abstract
1. Introduction
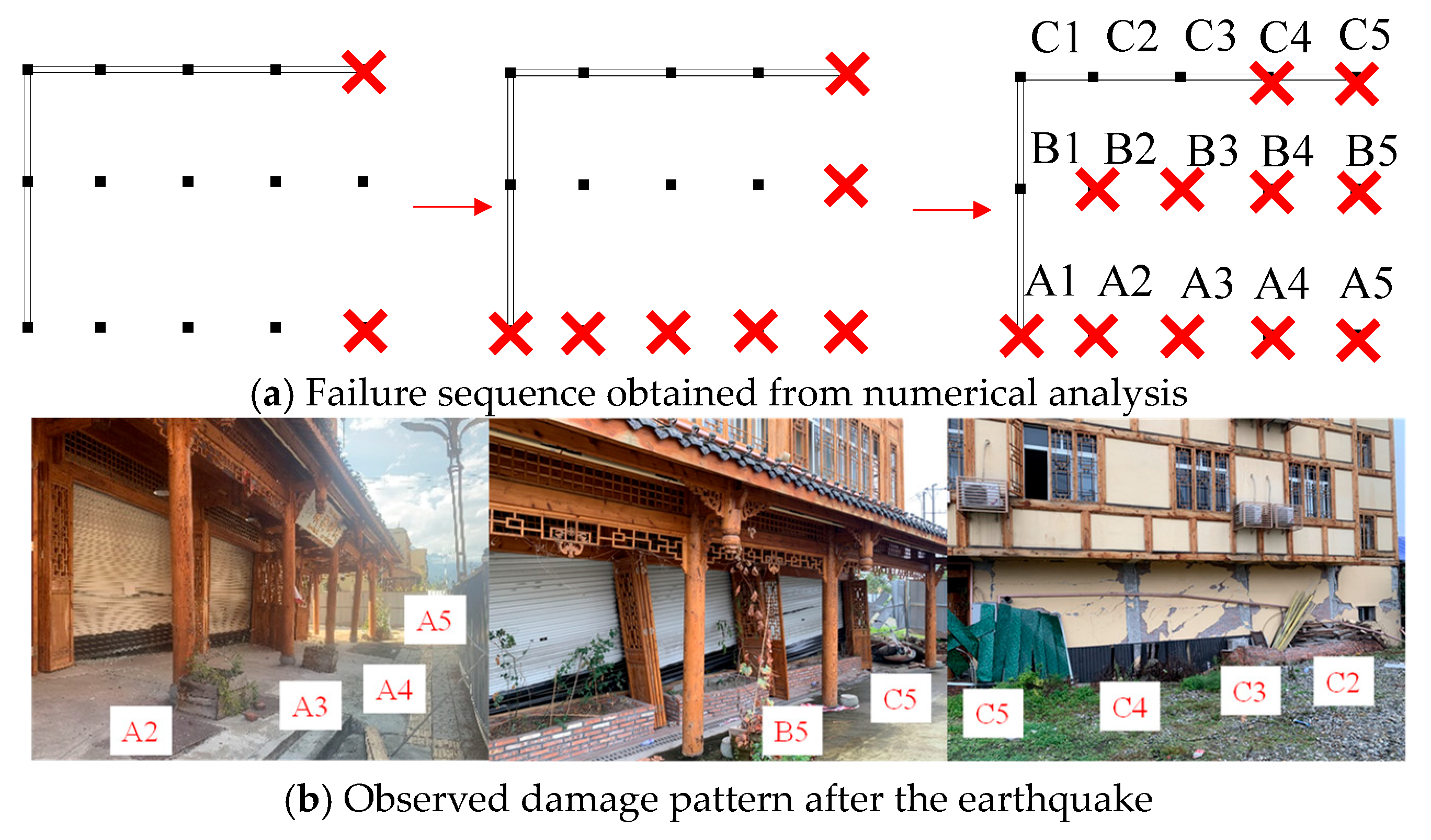
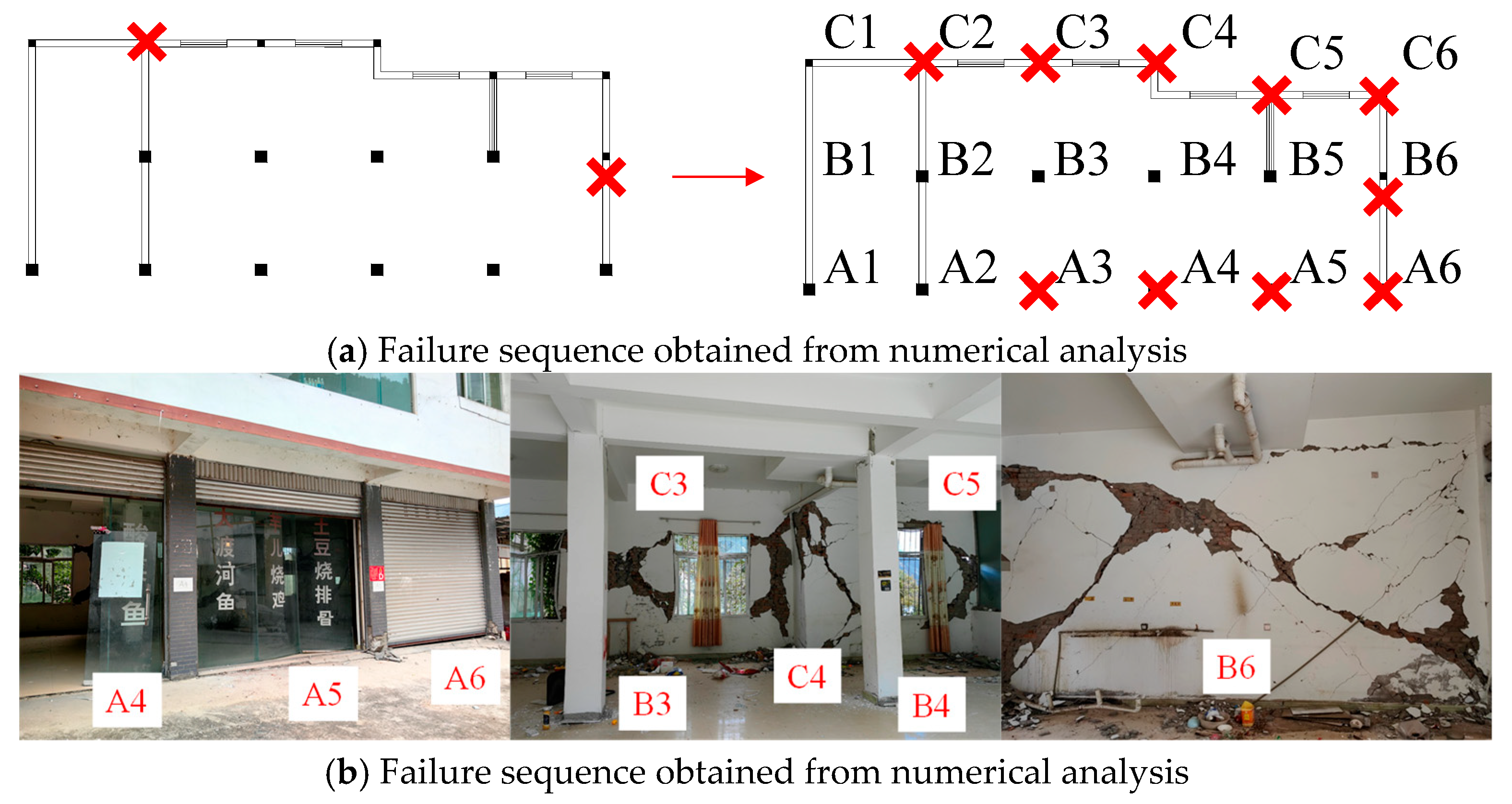
2. Typical Building Damage Patterns
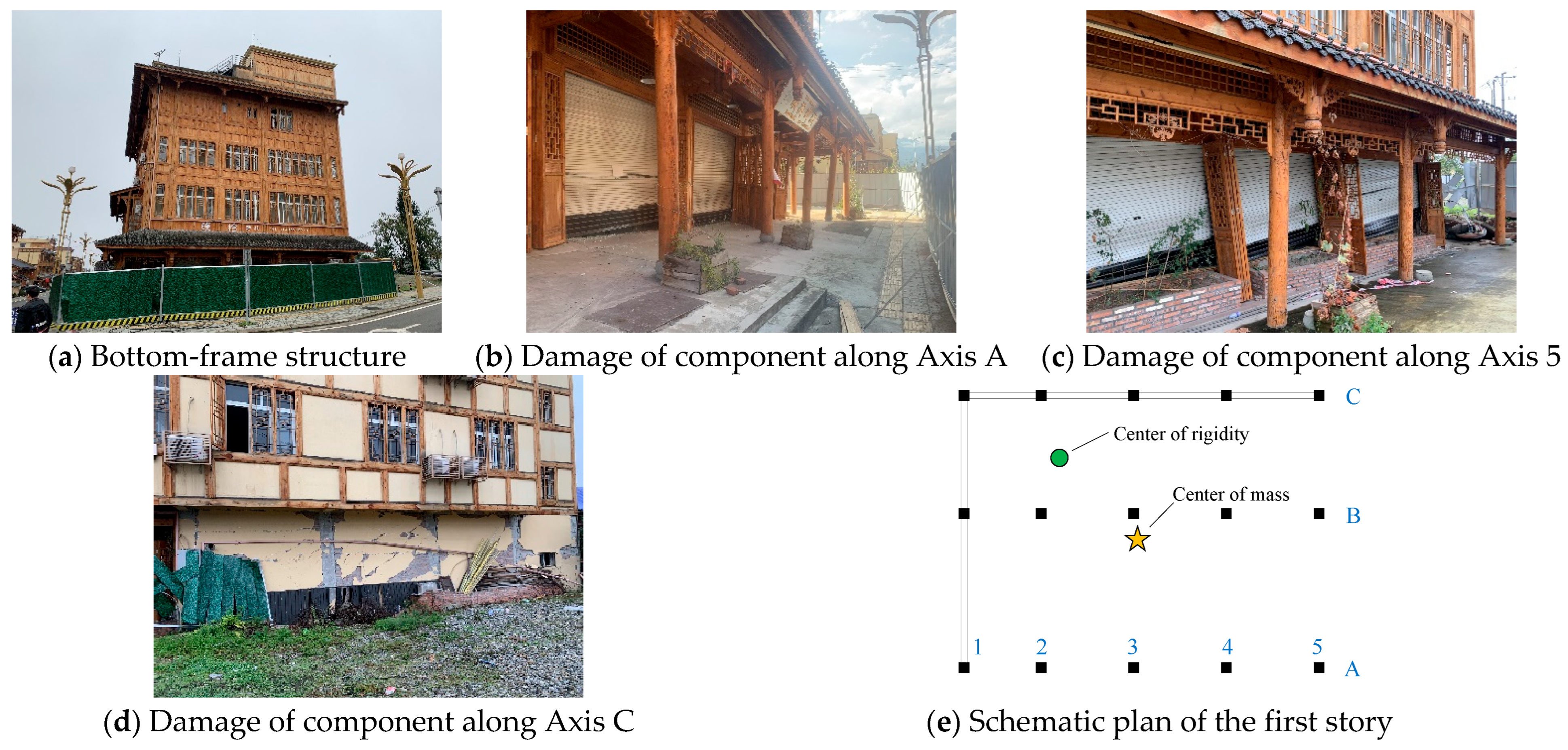
2.1. Failure of Low-Stiffness Components
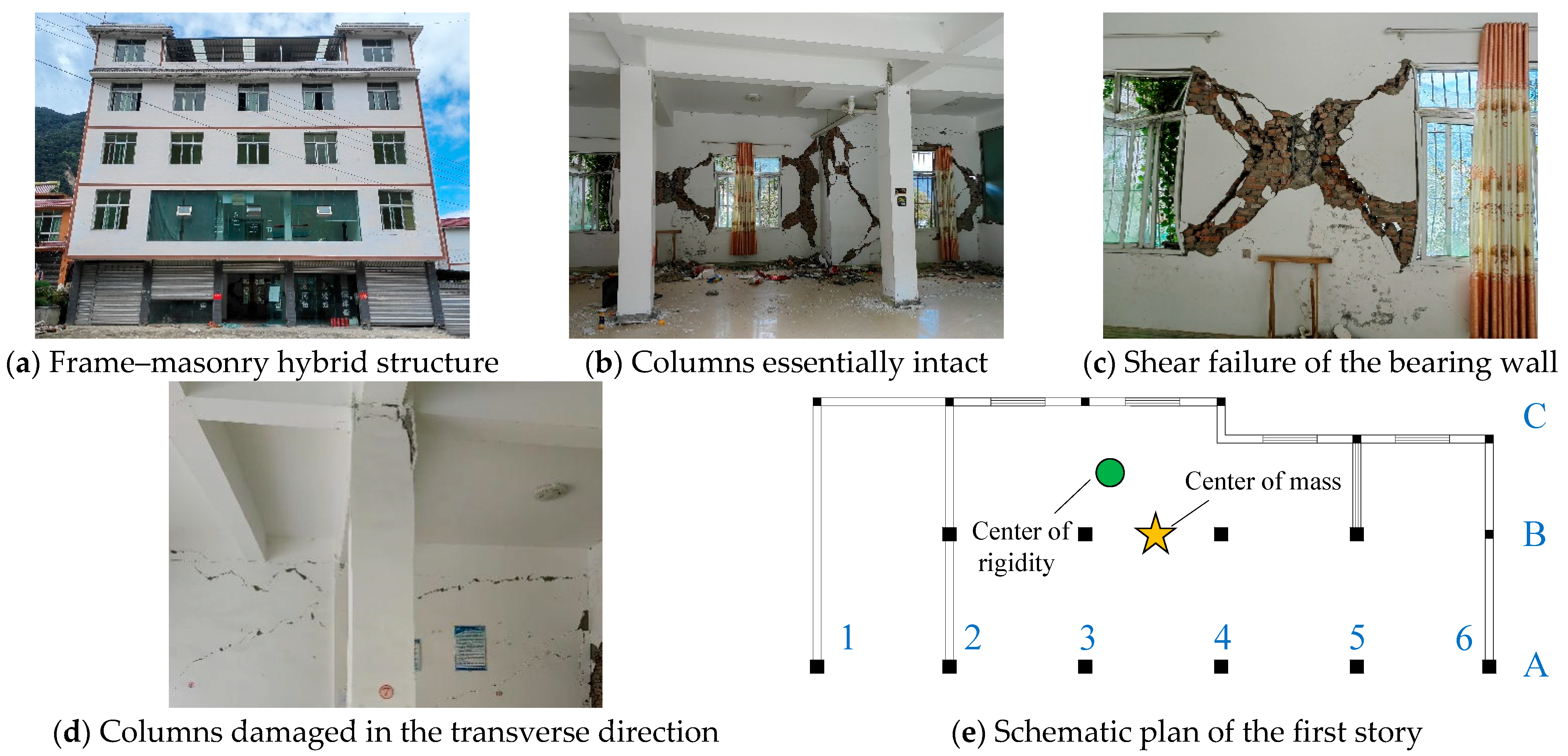
2.2. Failure of High-Stiffness Components
2.3. Undamaged Buildings
3. Structural Failure Mechanisms
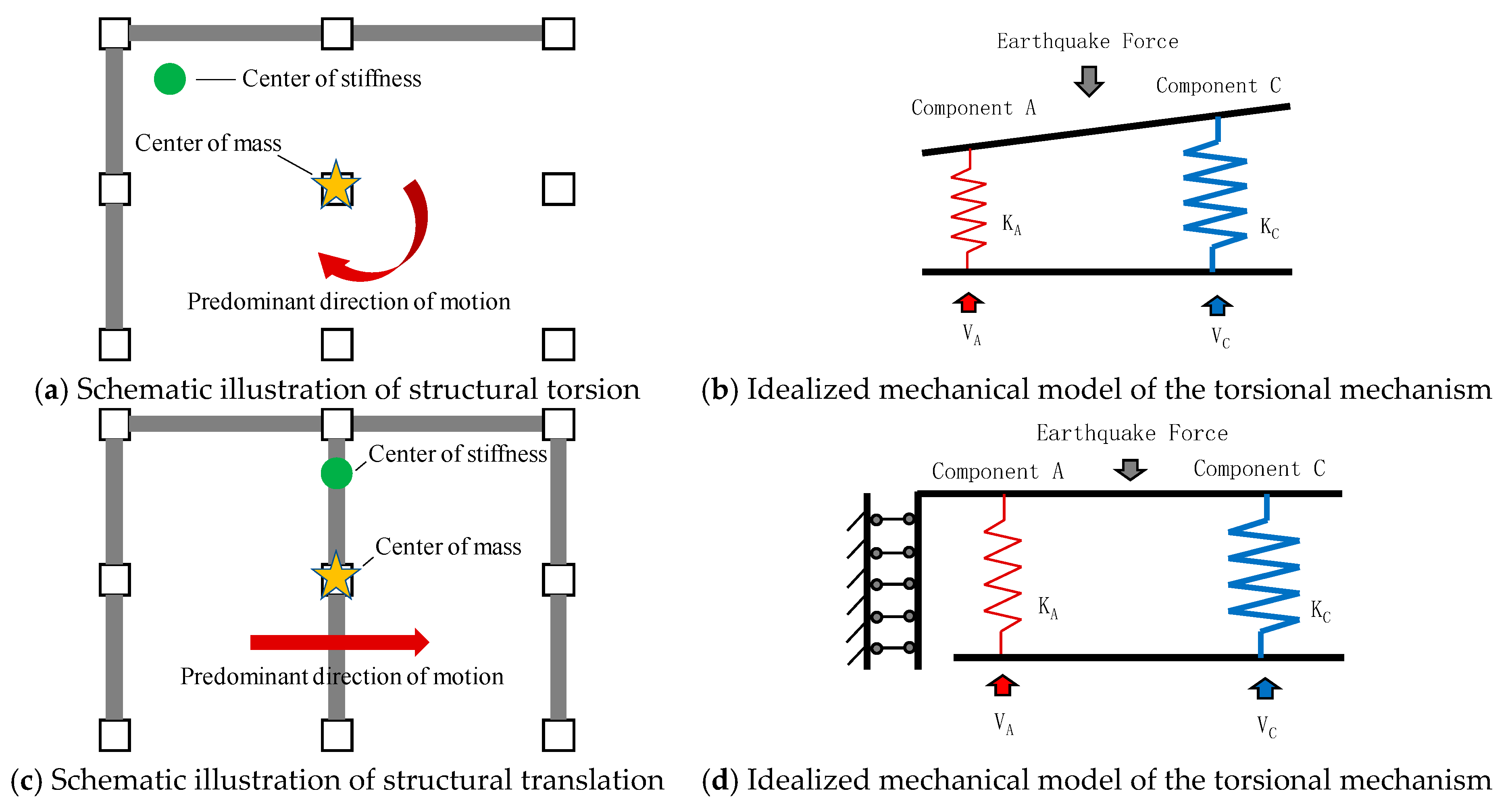
3.1. Translational and Torsional Motion Mechanisms
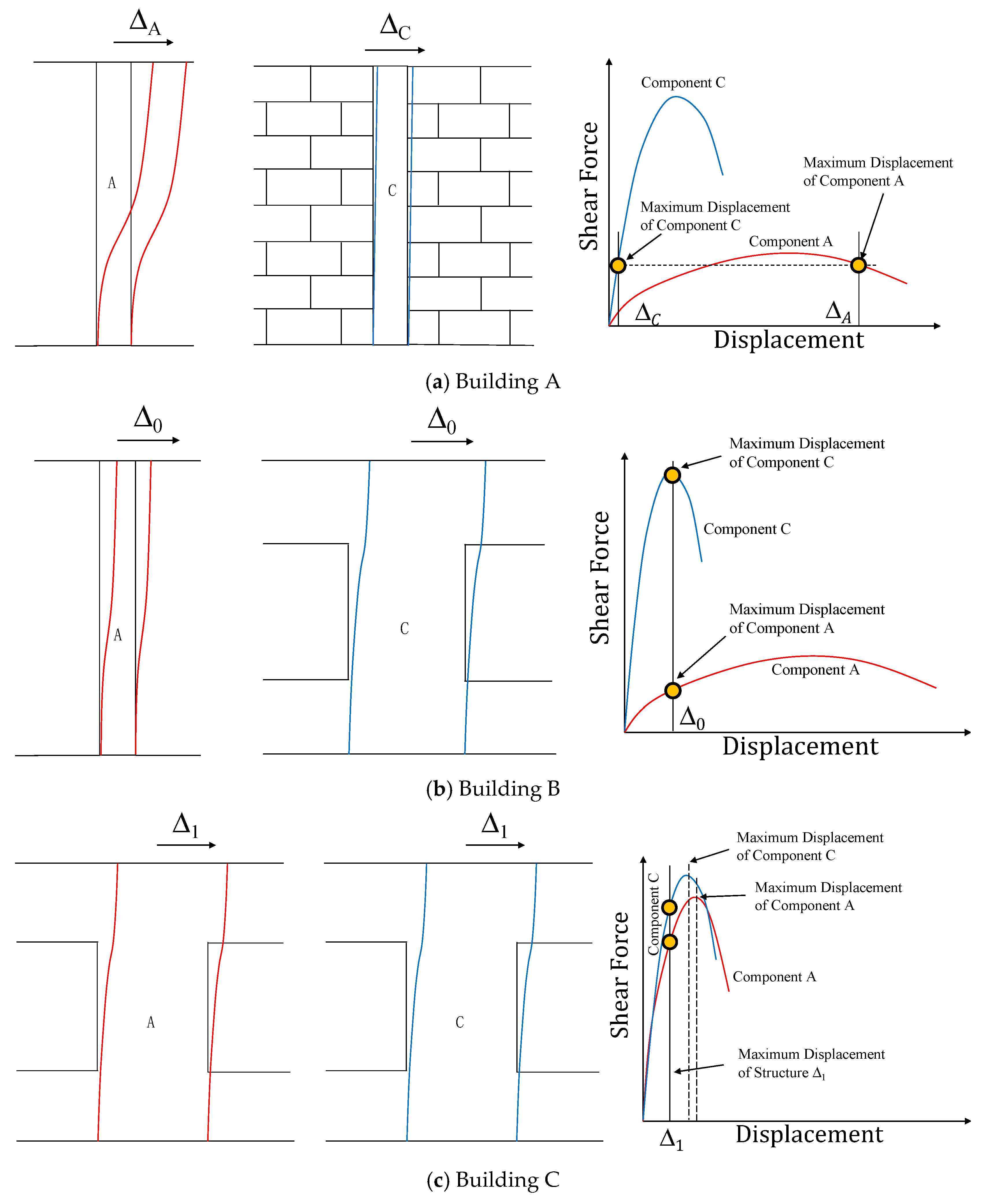
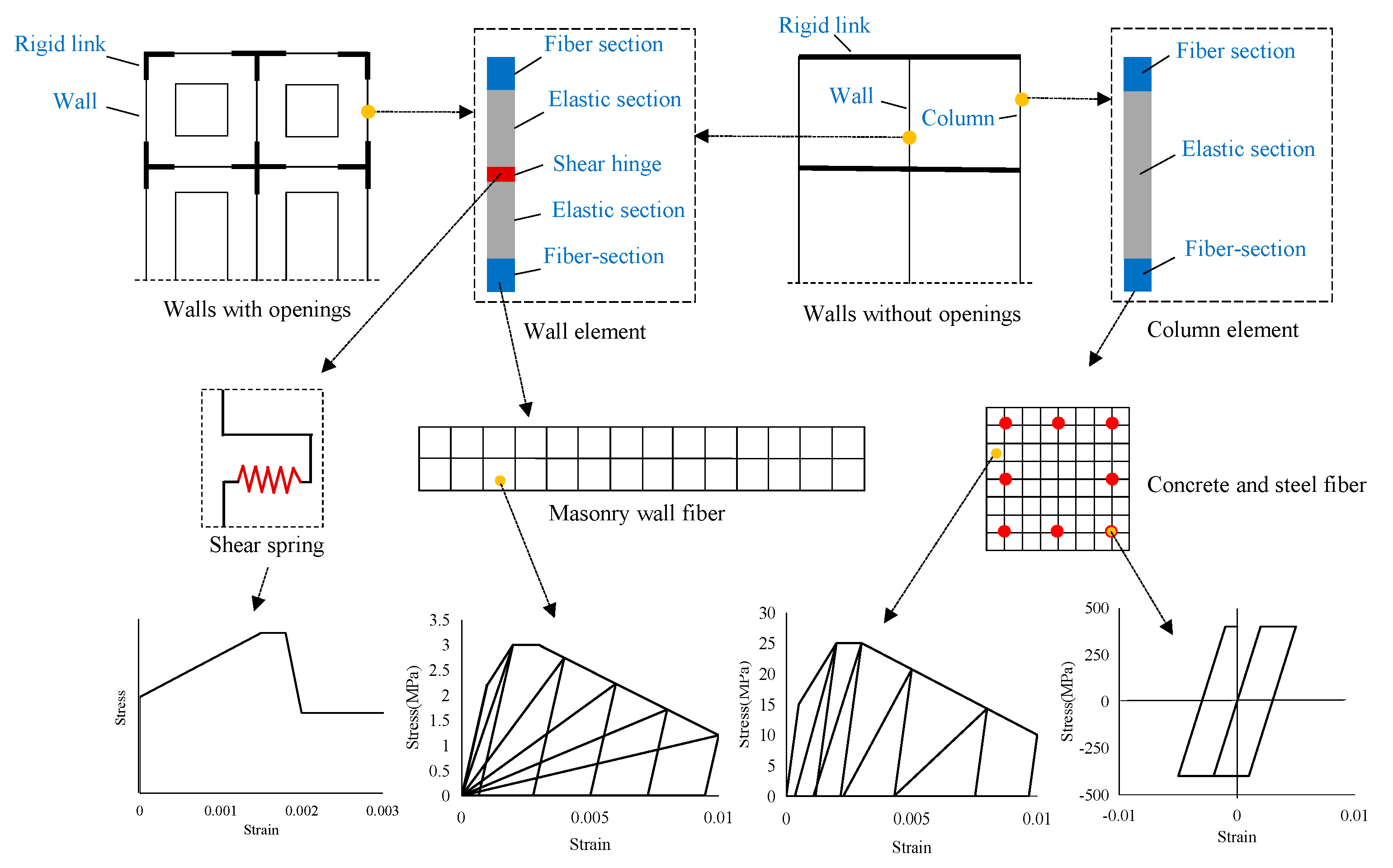
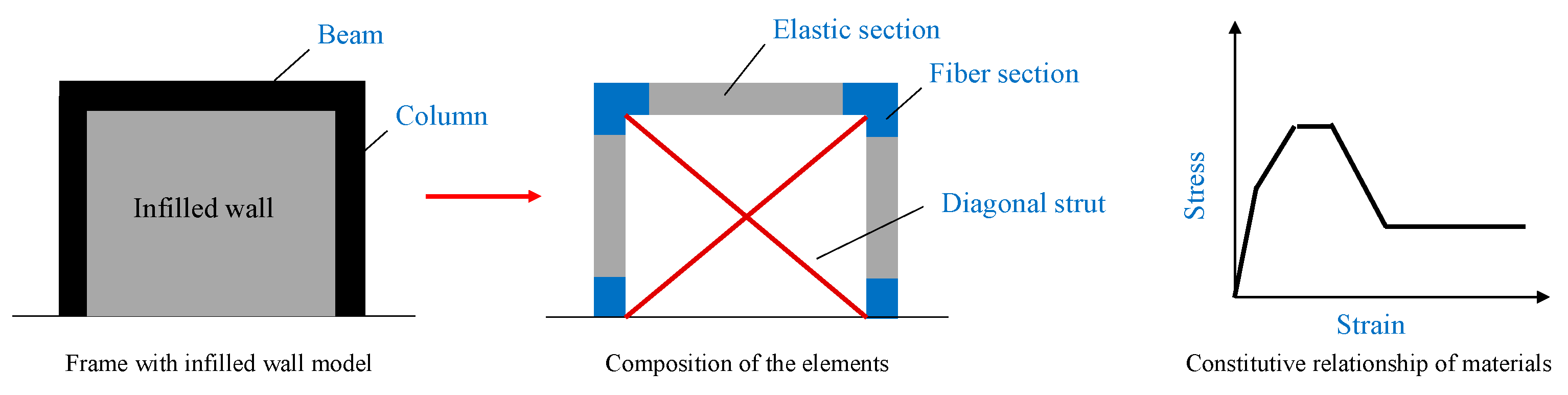
3.2. Constitutive Behavior and Component Failure Modes
4. Numerical Validation of Structural Motion and Failure Mechanisms
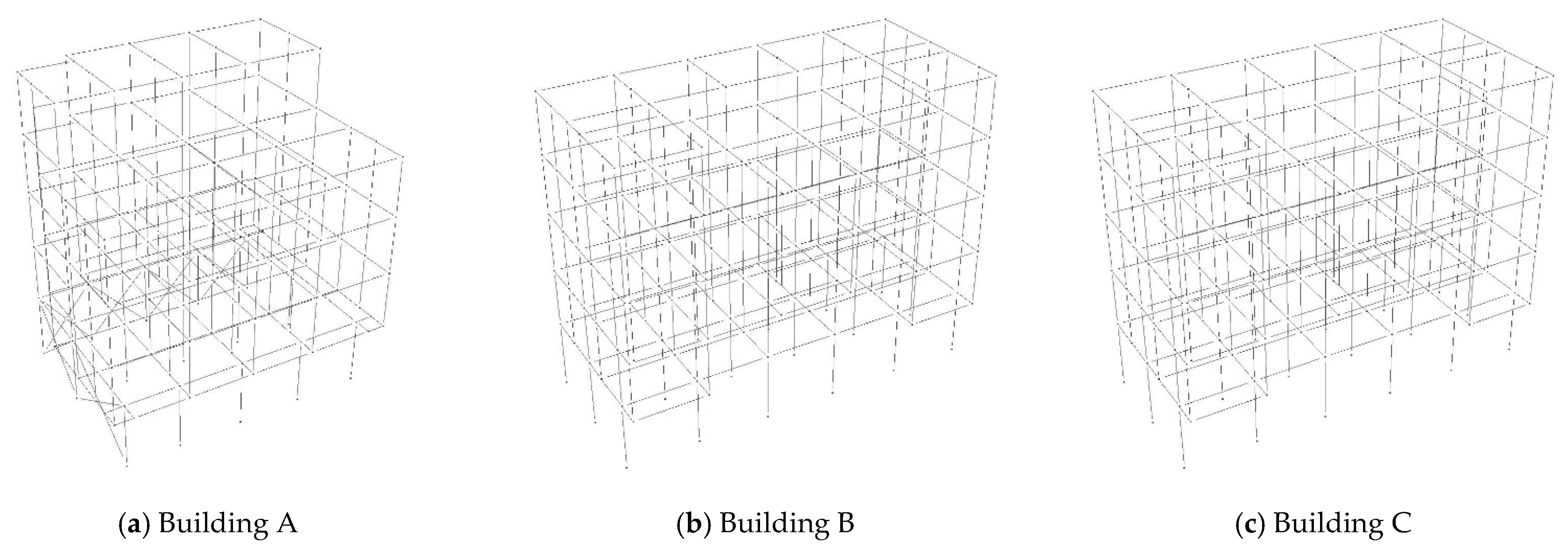
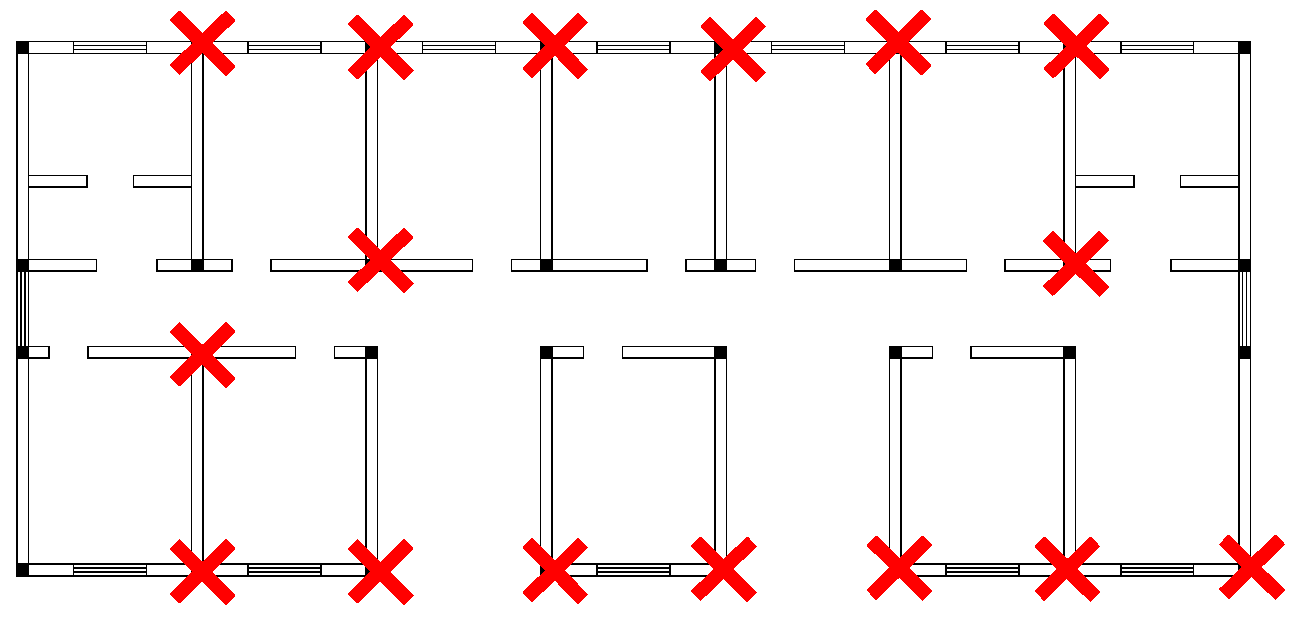
4.1. Representative Buildings
4.2. Modeling Method
4.2.1. Element Types and Material Properties
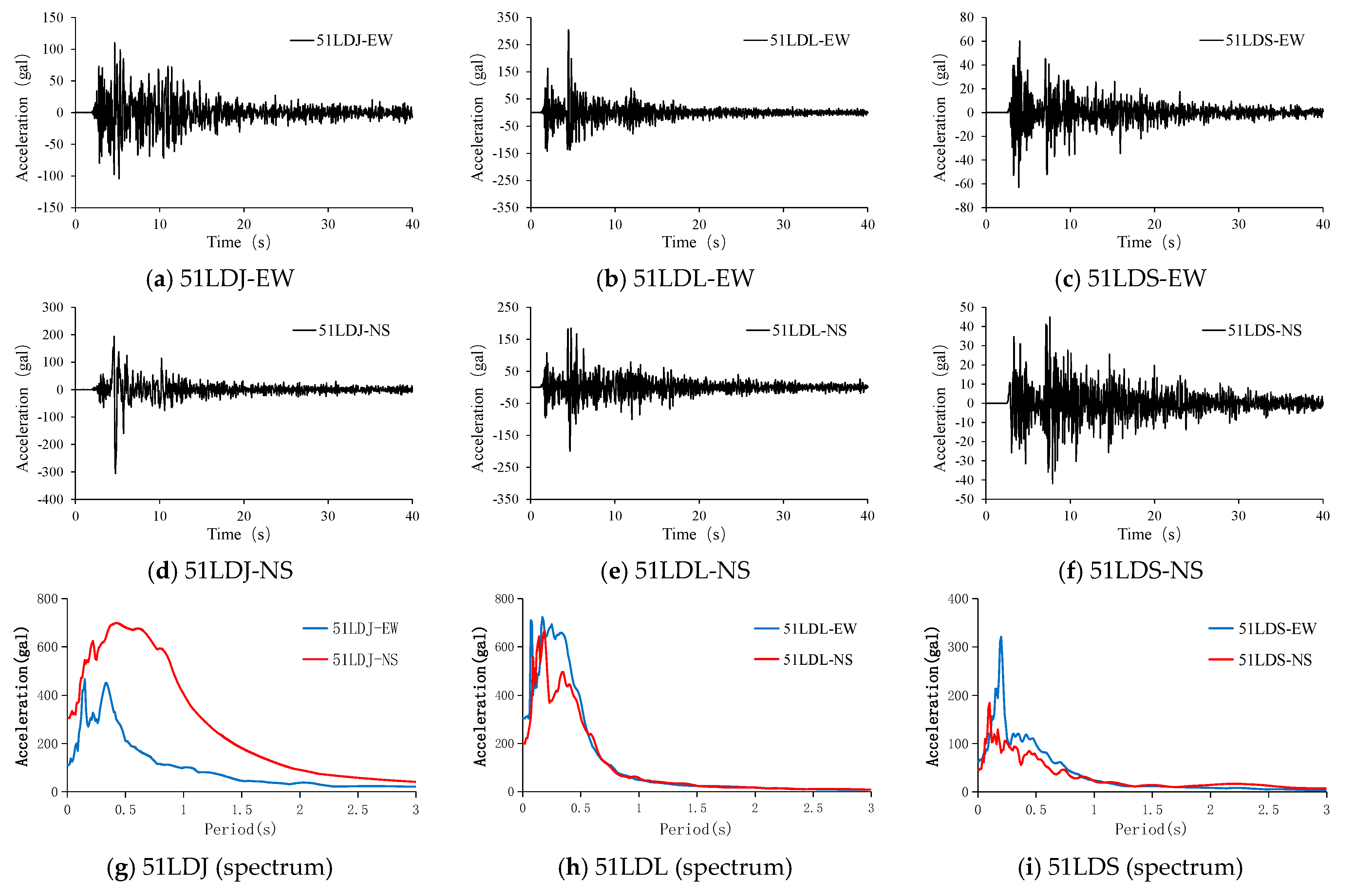
4.2.2. Loading Conditions
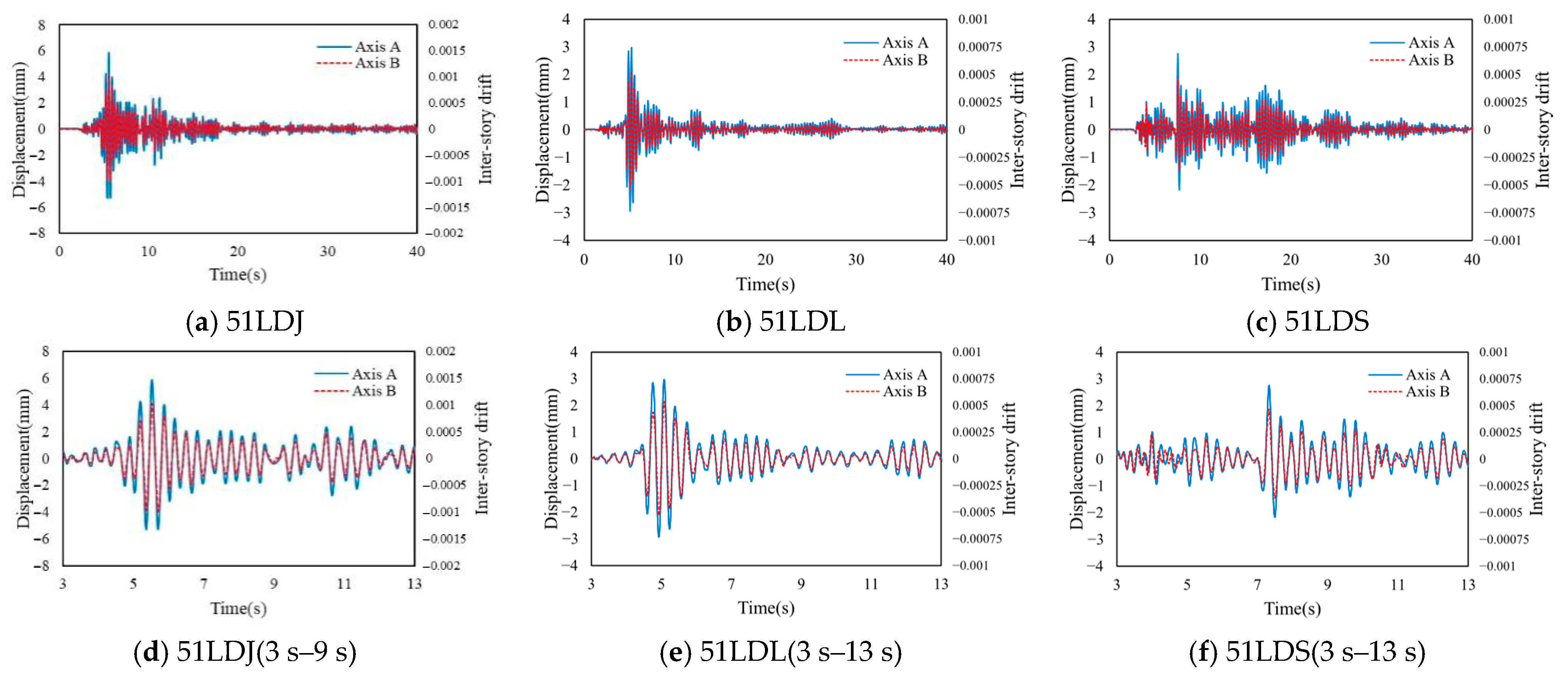
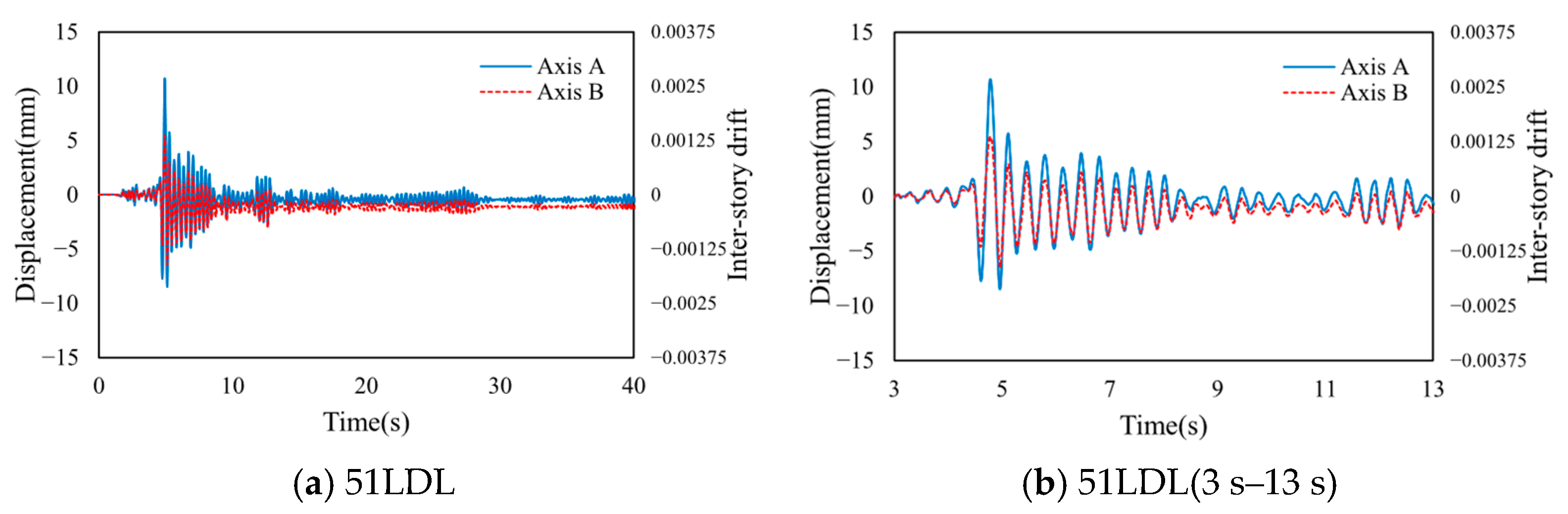
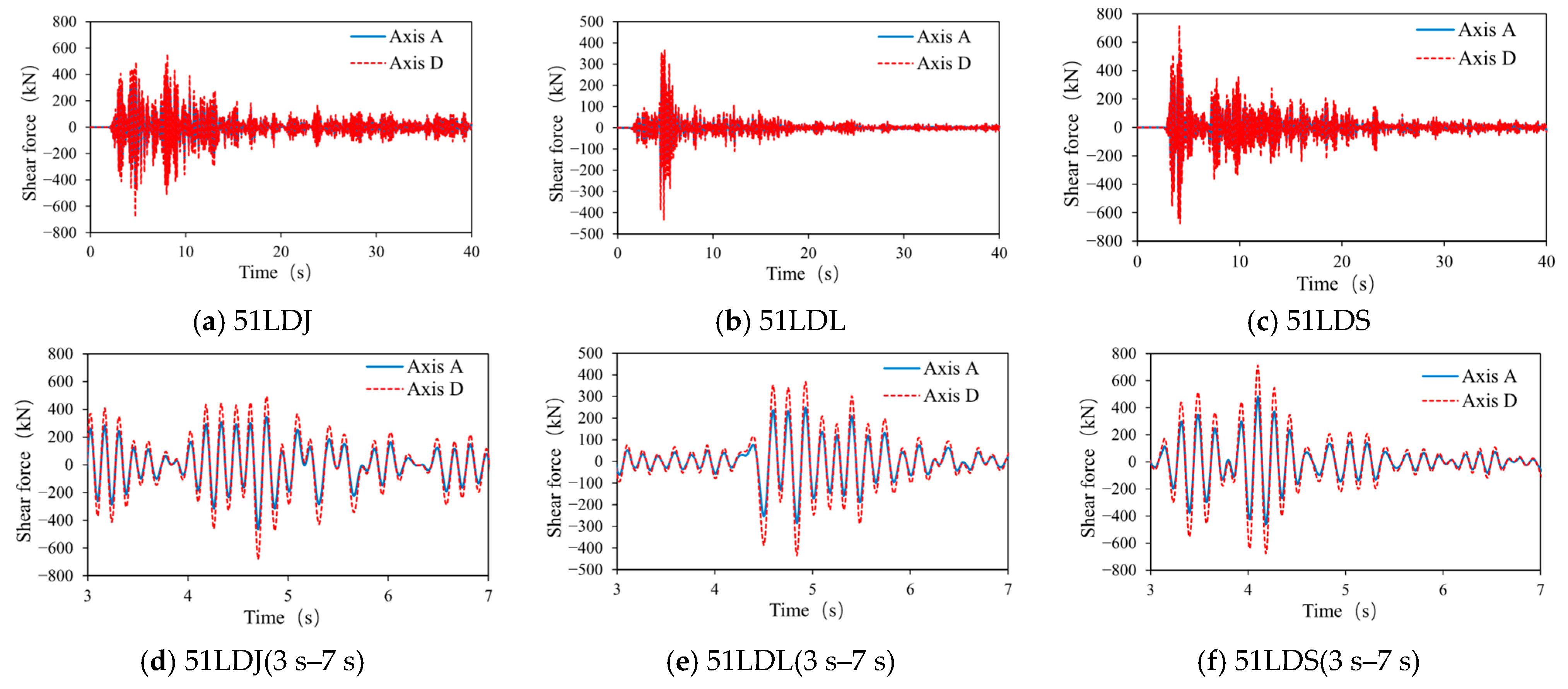
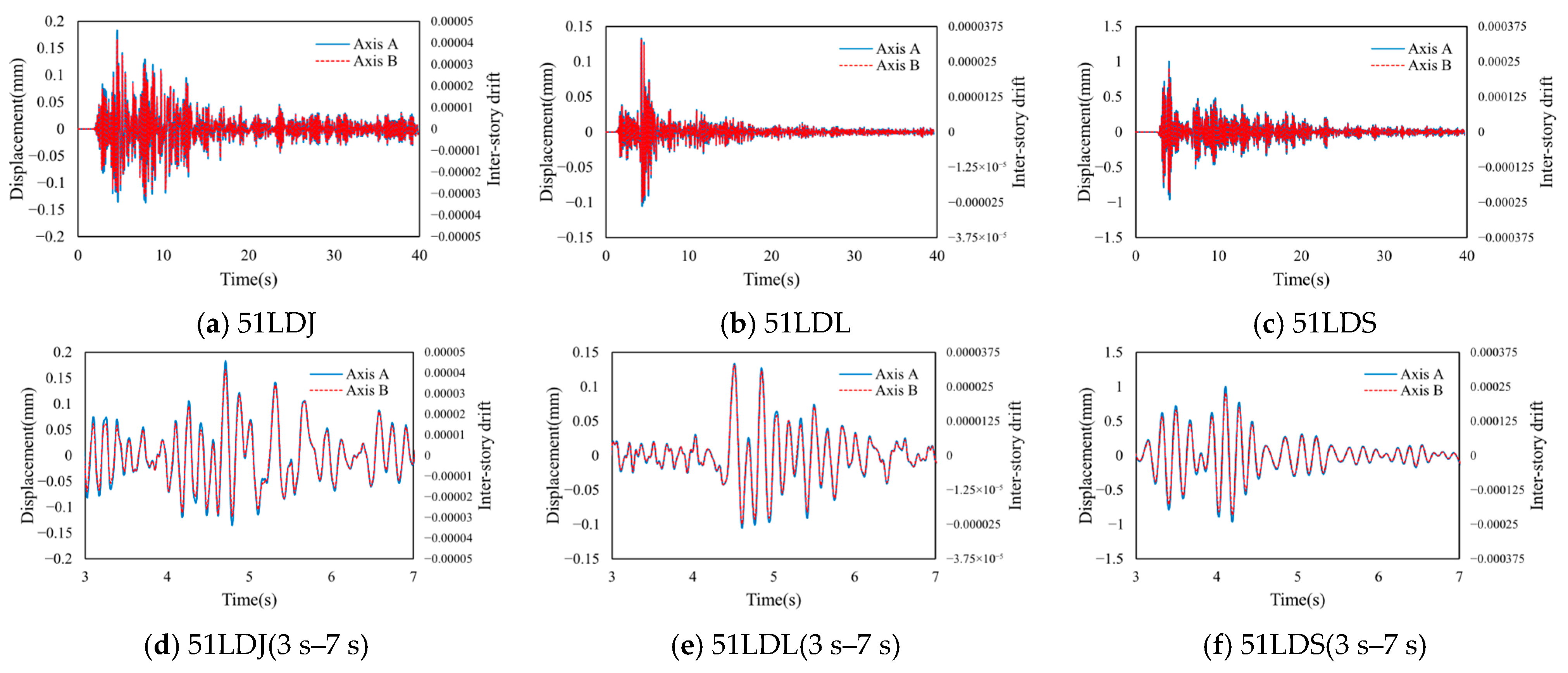
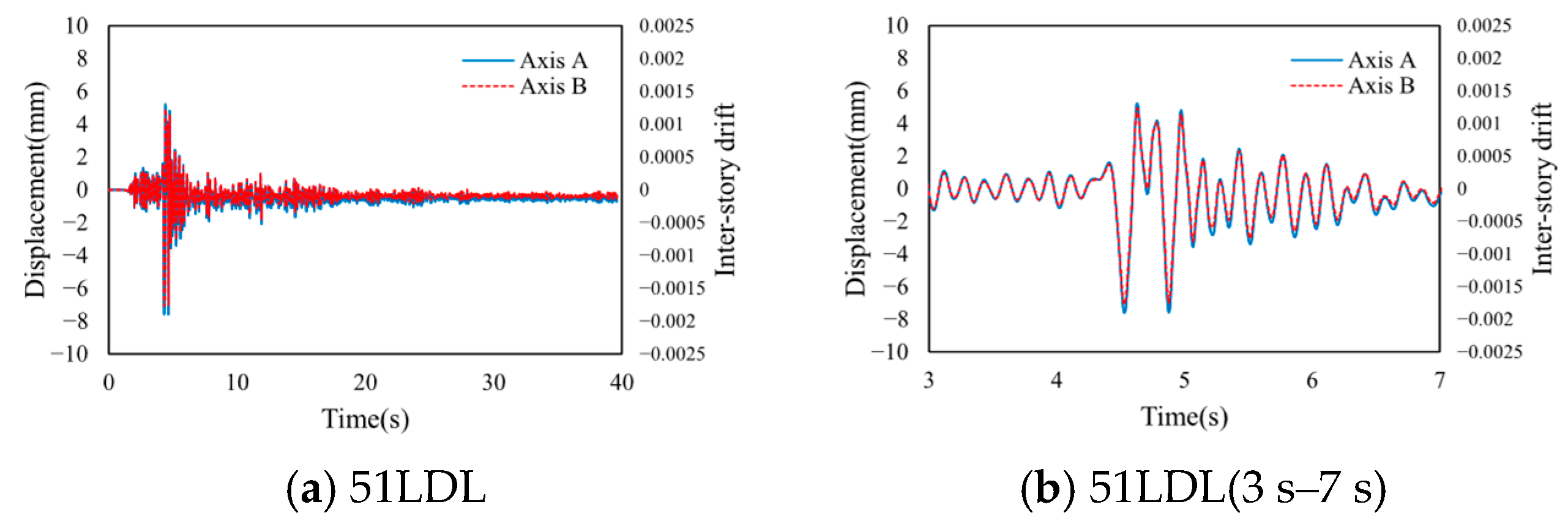
4.3. Result and Analysis
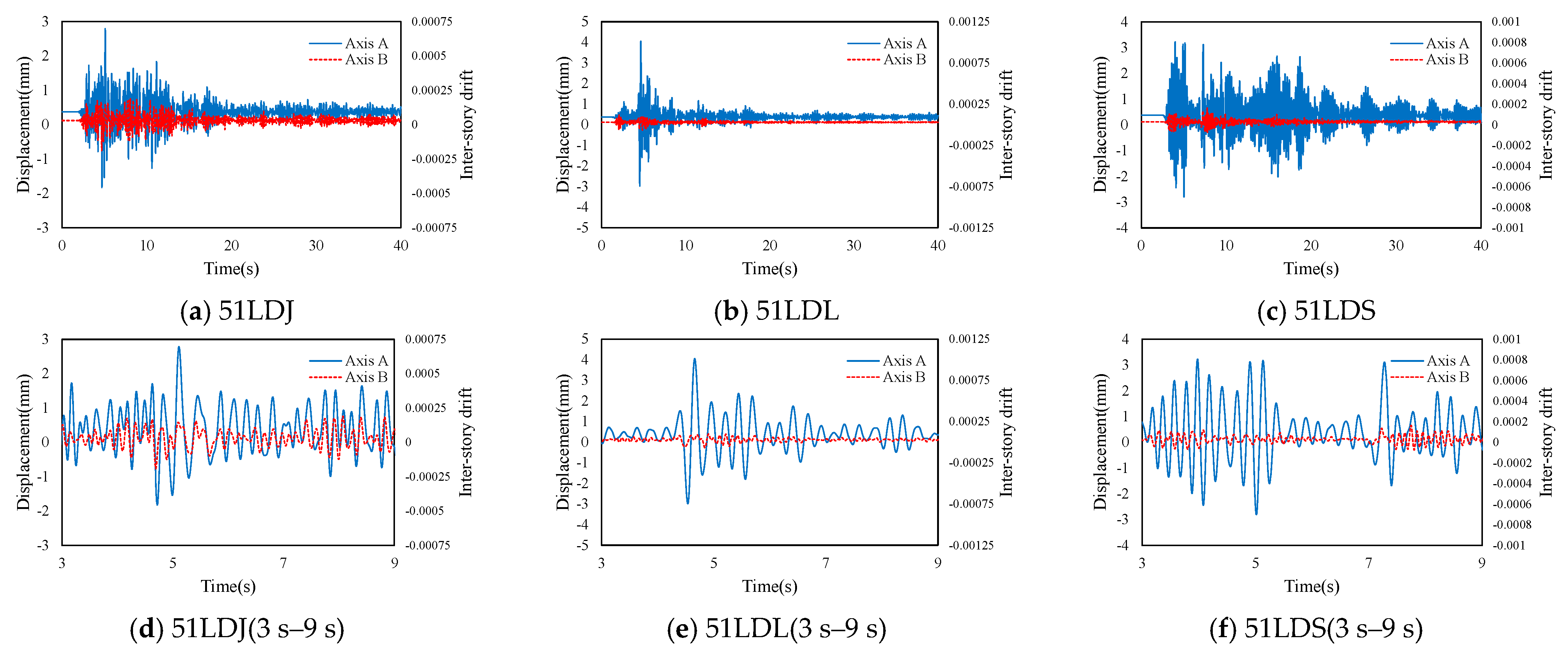
4.3.1. Building A
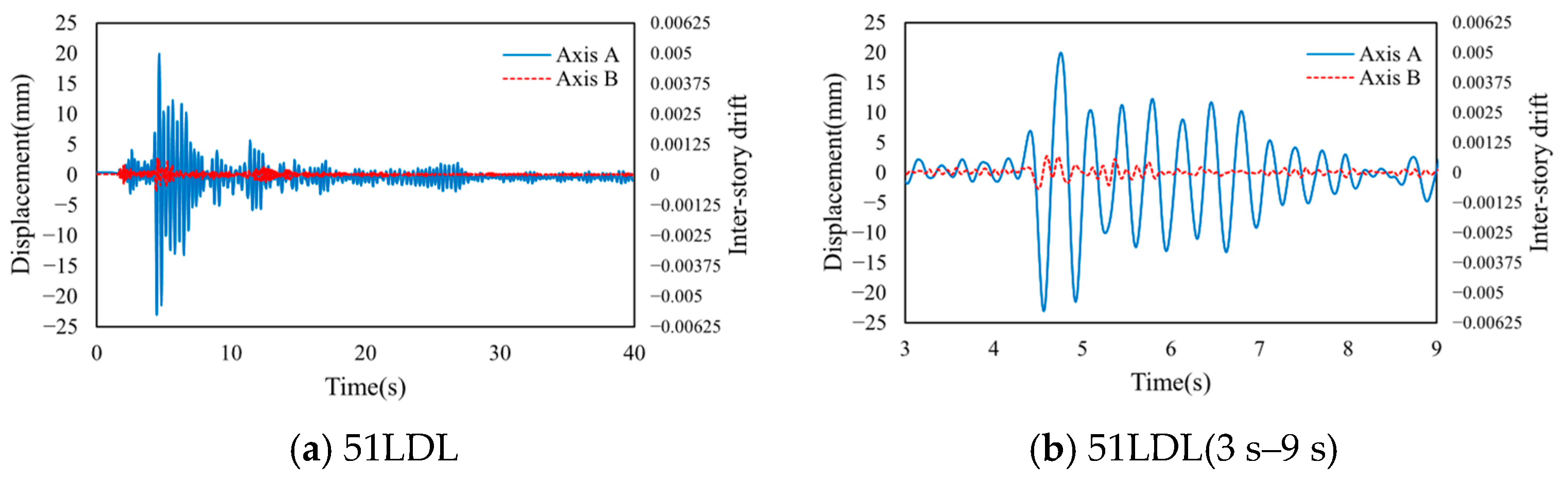
4.3.2. Building B
4.3.3. Building C
5. Conclusions
5.1. Summary of Findings
- (1)
- Three typical failure mechanisms were identified: torsion-dominated behavior in corner buildings with L-shaped infilled walls, translation-dominated behavior in street-front buildings with large façade openings, and strength-controlled behavior in buildings with uniformly distributed walls. These patterns correspond to distinct stiffness distributions and deformation compatibilities among components.
- (2)
- The essential difference among these mechanisms lies in the relative stiffness and ductility balance of components. Torsion-dominated structures exhibit similar force but uncoordinated deformation among elements, while translation-dominated ones show uniform displacement but concentrated stress in stiff components. Uniform wall distribution achieves coordinated deformation and balanced strength utilization.
- (3)
- Numerical analyses corroborate the proposed mechanisms and demonstrate that stiffness nonuniformity governs the shift between torsional, translational, and balanced responses.
- (4)
- Design implications: To improve seismic resilience, two conceptual strategies are suggested—(a) ensuring uniformly high ductility among primary components, or (b) maintaining balanced stiffness and strength through rational wall configurations. Both approaches enhance seismic capacity and collapse prevention.
5.2. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shibata, A. Estimation of earthquake damage to urban systems. Struct. Control Health Monit. 2006, 13, 454–471. [Google Scholar] [CrossRef]
- Chan, C.C.; Lin, Y.P.; Chen, H.H.; Chang, T.-Y.; Cheng, T.-J.; Chen, L.-S. A population-based study on the immediate and prolonged effects of the 1999 Taiwan earthquake on mortality. Ann. Epidemiol. 2003, 13, 502–508. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Chen, W.; Liu, J. Secondary geological hazard analysis in Beichuan after the Wenchuan earthquake and recommendations for reconstruction. Environ. Earth Sci. 2012, 66, 1001–1009. [Google Scholar] [CrossRef]
- Gao, S.; Lu, Y.; Mao, L. Risk assessment of earthquake-induced geological hazards considering cultivated land factor: A case study of the Jishishan Ms 6.2 earthquake. J. Mt. Sci. 2025, 22, 913–930. [Google Scholar] [CrossRef]
- Sepúlveda, S.A.; Serey, A. Tsunamigenic, earthquake-triggered rock slope failures during the April 21, 2007 Aisén earthquake, southern Chile (45.5° S). Andean Geol. 2009, 36, 131–136. [Google Scholar] [CrossRef]
- Furtado, A.; Rodrigues, H.; Arêde, A.; Varum, H. A review of the performance of infilled RC structures in recent earthquakes. Appl. Sci. 2021, 11, 5889. [Google Scholar] [CrossRef]
- Kawashima, K.; Unjoh, S.; Hoshikuma, J.I.; Kosa, K. Damage of bridges due to the 2010 Maule, Chile, earthquake. J. Earthq. Eng. 2011, 15, 1036–1068. [Google Scholar] [CrossRef]
- Perrone, D.; Calvi, P.M.; Nascimbene, R.; Fischer, E.C.; Magliulo, G. Seismic performance of non-structural elements during the 2016 Central Italy earthquake. Bull. Earthq. Eng. 2019, 17, 5655–5677. [Google Scholar] [CrossRef]
- Aydın, M.C.; Işık, E.; Büyüksaraç, A.; Ulu, A.E.; Avcil, F. Technical and Socio-Economic Perspective on the Disaster of the Century (6 February 2023 Earthquake) in Türkiye on the Second Anniversary. Geol. J. 2025, 1–18. [Google Scholar] [CrossRef]
- Aksoy, C.G.; Chupilkin, M.; Koczan, Z.; Plekhanov, A. Unearthing the impact of earthquakes: A review of economic and social consequences. J. Policy Anal. Manag. 2024, 44, 1450–1471. [Google Scholar] [CrossRef]
- Kaushik, H.B.; Jain, S.K. Impact of great December 26, 2004 Sumatra earthquake and tsunami on structures in Port Blair. J. Perform. Constr. Facil. 2007, 21, 128–142. [Google Scholar] [CrossRef]
- Ye, S.; Zhai, G.; Hu, J. Damages and lessons from the Wenchuan earthquake in China. Hum. Ecol. Risk Assess. Int. J. 2011, 17, 598–612. [Google Scholar] [CrossRef]
- DesRoches, R.; Comerio, M.; Eberhard, M.; Mooney, W.; Rix, G.J. Overview of the 2010 Haiti earthquake. Earthq. Spectra 2011, 27 (Suppl. S1), S1–S21. [Google Scholar] [CrossRef]
- Saatcioglu, M.; Tremblay, R.; Mitchell, D.; Ghobarah, A.; Palermo, D.; Simpson, R.; Adebar, P.; Ventura, C.; Hong, H. Performance of steel buildings and nonstructural elements during the 27 February 2010 Maule (Chile) Earthquake. Can. J. Civ. Eng. 2013, 40, 722–734. [Google Scholar] [CrossRef]
- Kabeyasawa, T. Damages to RC school buildings and lessons from the 2011 East Japan earthquake. Bull. Earthq. Eng. 2017, 15, 535–553. [Google Scholar] [CrossRef]
- Gautam, D. Unearthed lessons of 25 April 2015 Gorkha earthquake (MW 7.8): Geotechnical earthquake engineering perspectives. Geomat. Nat. Hazards Risk 2017, 8, 1358–1382. [Google Scholar] [CrossRef]
- Tapia-Hernández, E.; Genes, M.C.; Guerrero-Bobadilla, H. Damages observed in Turkey due to the Kahramanmaras earthquakes of February 6, 2023. J. Earthq. Eng. 2024, 1–19. [Google Scholar] [CrossRef]
- Hao, L.N.; Zhang, Y.S. Natural Vibration Period Analysis of Multi-Storey Reinforced Concrete Frame Structure. Appl. Mech. Mater. 2012, 226, 351–354. [Google Scholar] [CrossRef]
- Luo, R.; Guo, X.; Wang, B.; Dong, X.; Zhang, Q.; Ouyang, Z. The impact of infill wall distribution on the mechanical behavior and failure patterns of multi-story RC frame structures: An acceleration–strain coupled testing approach. Structures 2024, 59, 105737. [Google Scholar] [CrossRef]
- Blume, J.A.; Newmark, N.M.; Corning, L.H. Design of Multistory Reinforced Concrete Buildings for Earthquake Motions; Portland Cement Association: Chicago, IL, USA, 1961. [Google Scholar]
- Hollings, J.P. Reinforced concrete seismic design. Bull. New Zealand Soc. Earthq. Eng. 1969, 2, 217–250. [Google Scholar] [CrossRef]
- Park, R. State of the art report ductility evaluation from laboratory and analytical testing. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo-Kyoto, Japan, 2–9 August 1988; pp. 605–616. [Google Scholar]
- Paulay, T.; Priestley, M.J.N. Seismic Design of Reinforced Concrete and Masonry Buildings; John Wiley & Sons, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Fardis, M.N. Capacity design: Early history. Earthq. Eng. Struct. Dyn. 2018, 47, 2887–2896. [Google Scholar] [CrossRef]
- SEAOC. Recommended Lateral Force Requirements and Commentary; Seismology Committee, Structural Engineers Association of California: San Francisco, CA, USA, 1968. [Google Scholar]
- ACI 318; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- NZS-3101; Concrete Structures Standard. Standards New Zealand: Wellington, New Zealand, 2006.
- GB-50011; Code for Seismic Design of Buildings. Architectural & Building Press: Beijing, China, 2016. (In Chinese)
- Luo, R.; Guo, X.; Lata, A.; Wang, B.; Qi, F.; Dong, X. Investigation and Analysis of Seismic Damage to Side Corridor School Buildings in M6.4 Yangbi Earthquake. World Earthq. Eng. 2021, 37, 54–63. (In Chinese) [Google Scholar]
- Dong, X.; Guo, X.; Lata, A.; Luo, R.; Yan, C. Seismic Response of Multi-Story Buildings Subjected to Luding Earthquake 2022, China Considering the Deformation Saturation Theory. Buildings 2024, 14, 2887. [Google Scholar] [CrossRef]
- Wang, T.; Chen, J.; Zhou, Y.; Lin, X.; Wang, X.; Shang, Q. Preliminary investigation of building damage in Hatay under February 6, 2023 Turkey earthquakes. Earthq. Eng. Eng. Vib. 2023, 22, 853–866. [Google Scholar] [CrossRef]
- Peng, Q.; Zhou, X.; Yang, C. Influence of connection and constructional details on masonry-infilled RC frames under cyclic loading. Soil Dyn. Earthq. Eng. 2018, 108, 96–110. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, X.; Mao, J. Full-scale experimental study on masonry infilled RC moment-resisting frames under cyclic loads. Eng. Struct. 2015, 91, 70–84. [Google Scholar] [CrossRef]
- Zovkic, J.; Sigmund, V.; Guljas, I. Cyclic testing of a single bay reinforced concrete frames with various types of masonry infill. Earthq. Eng. Struct. Dyn. 2013, 42, 1131–1149. [Google Scholar] [CrossRef]
- Misir, S.; Ozcelik, O.; Girgin, S.C.; Kahraman, S. Experimental work on seismic behavior of various types of masonry infilled RC frames. Struct. Eng. Mech. 2012, 44, 763–774. [Google Scholar] [CrossRef]
- Kakaletsis, D.J.; Karayannis, C.G. Influence of masonry strength and openings on infilled R/C frames under cycling loading. J. Earthq. Eng. 2008, 12, 197–221. [Google Scholar] [CrossRef]
- Tasnimi, A.A.; Mohebkhah, A. Investigation on the behavior of brick-infilled steel frames with openings, experimental and analytical approaches. Eng. Struct. 2011, 33, 968–980. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Y.; Liu, X.; Zheng, Y.; Qi, Z. Study on seismic performance of RC frame structures considering the effect of infilled walls. Buildings 2024, 14, 1907. [Google Scholar] [CrossRef]
- Lazaridis, P.C.; Kavvadias, I.E.; Demertzis, K.; Iliadis, L.; Vasiliadis, L.K. Structural damage prediction of a reinforced concrete frame under single and multiple seismic events using machine learning algorithms. Appl. Sci. 2022, 12, 3845. [Google Scholar] [CrossRef]
- Stavridis, A.; Koutromanos, I.; Shing, P.B. Shake-table tests of a three-story reinforced concrete frame with masonry infill walls. Earthq. Eng. Struct. Dyn. 2012, 41, 1089–1108. [Google Scholar] [CrossRef]
- Wang, B.; Guo, X.; Xuan, Y.; Fan, X.-Q.; Chen, B. The effects of infilled walls on seismic performance of RC frame structures with eccentrically placed open corridor. Sustainability 2022, 14, 5299. [Google Scholar] [CrossRef]
- Dong, X.; Guo, X.; Wang, B.; Lata, A.; Luo, R. Suggestions for a Collapse-Resistant Design for Frame–Masonry Hybrid Buildings Based on the Concept of Balancing Seismic Shear Forces. Buildings 2025, 15, 1357. [Google Scholar] [CrossRef]
- Dong, X.; Lata, A.; Guo, X.; Luo, R.; Yan, C. Study on seismic performance of semi-enclosed buildings based on shaking table test. Structures 2025, 81, 110315. [Google Scholar] [CrossRef]
- Luo, R.; Guo, X.; Dong, X.; Zhang, Q. New recognition of failure and collapse mechanism of multi-story building suffered from earthquake. Earthq. Eng. Eng. Dyn. 2022, 42, 95–103. (In Chinese) [Google Scholar]
- Zhang, J.; Guo, X.; Luo, R.; Dong, X.; Dong, C.; Zhang, Q. Seismic damage investigation and analysis of buildings in Ms6.8 Luding earthquake. Earthq. Eng. Eng. Dyn. 2024, 44, 190–199. (In Chinese) [Google Scholar]
- Luo, R.; Jin, X.; Guo, X.; Dong, C.; Dong, X.; Zhang, Q.; Zhang, J. Investigation and analysis of structure damage in the Sichuan Luding Ms6.8 earthquake in 2022. J. Inst. Disaster Prev. 2022, 24, 46–55. (In Chinese) [Google Scholar]
- Lowes, L.N.; Lehman, D.E.; Baker, C.; Lundeen, C.P. Recommendations for modeling the nonlinear response of slender reinforced concrete walls using PERFORM-3D. In Proceedings of the 2016 SEAOC Convention, Maui, HI, USA, 12–15 October 2016. [Google Scholar]
- Powell, G.H. Modeling for Structural Analysis: Behavior and Basics; Computers and Structures: Berkeley, CA, USA, 2010. [Google Scholar]
- Peruch, M.; Spacone, E.; Camata, G. Nonlinear analysis of masonry structures using fiber-section line elements. Earthq. Eng. Struct. Dyn. 2019, 48, 1345–1364. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency. FEMA 356 Pre-Standard and Commentary for the Seismic Rehabilitation of Buildings; Federal Emergency Management Agency: Washington, DC, USA, 2000.

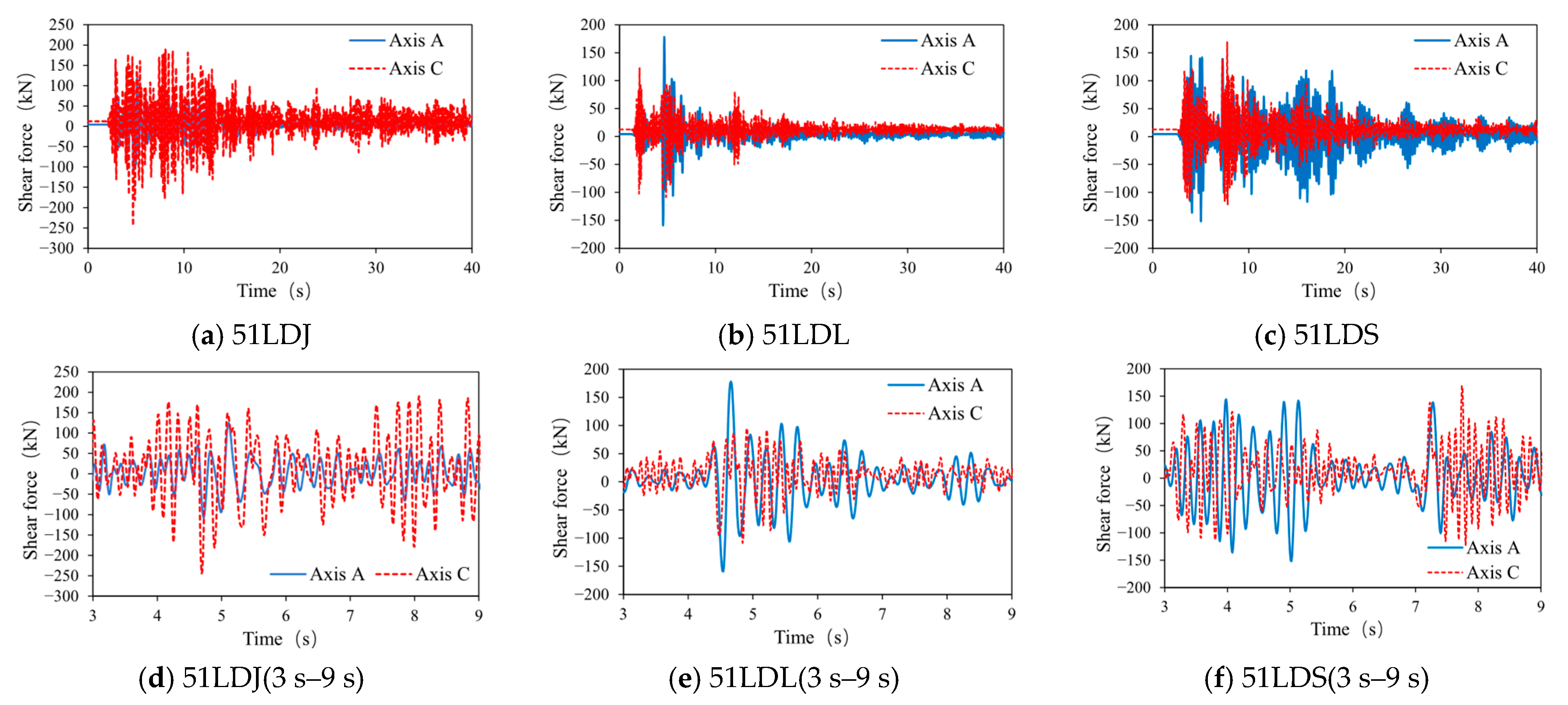
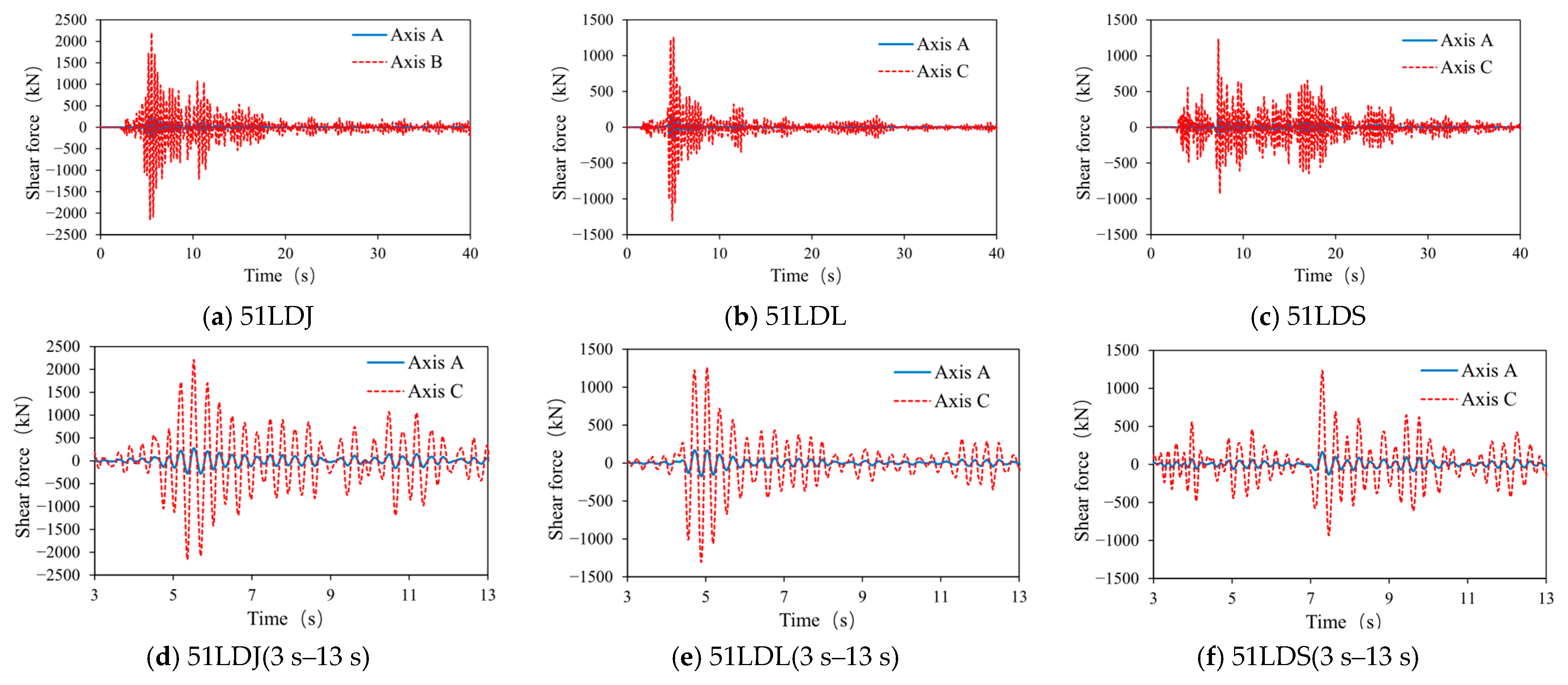
| 51LDJ | 51LDL | 51LDS | ||||
|---|---|---|---|---|---|---|
| Axis | A | C | A | C | A | C |
| Shear force | 1.00 | 1.28 | 1.00 | 0.79 | 1.00 | 1.39 |
| Displacement | 4.79 | 1.00 | 8.44 | 1.00 | 4.94 | 1.00 |
| 51LDJ | 51LDL | 51LDS | ||||
|---|---|---|---|---|---|---|
| Axis | A | C | A | C | A | C |
| Shear force | 1.00 | 7.97 | 1.00 | 7.81 | 1.00 | 7.59 |
| Displacement | 1.28 | 1.00 | 1.31 | 1.00 | 1.28 | 1.00 |
| 51LDJ | 51LDL | 51LDS | ||||
|---|---|---|---|---|---|---|
| Axis | A | D | A | D | A | D |
| Shear force | 1.00 | 1.47 | 1.00 | 1.51 | 1.00 | 1.48 |
| Displacement | 1.10 | 1.00 | 1.03 | 1.00 | 1.09 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, R.; Chiu, C.; Wang, S.; Dong, X.; Guo, X. Mechanisms of Seismic Failure in Multistory Masonry and Infilled Frame Buildings: Field Investigation and Numerical Validation from the 2022 Luding Earthquake. Buildings 2025, 15, 3801. https://doi.org/10.3390/buildings15203801
Luo R, Chiu C, Wang S, Dong X, Guo X. Mechanisms of Seismic Failure in Multistory Masonry and Infilled Frame Buildings: Field Investigation and Numerical Validation from the 2022 Luding Earthquake. Buildings. 2025; 15(20):3801. https://doi.org/10.3390/buildings15203801
Chicago/Turabian StyleLuo, Ruofan, Chenyuan Chiu, Shicheng Wang, Xiaoyao Dong, and Xun Guo. 2025. "Mechanisms of Seismic Failure in Multistory Masonry and Infilled Frame Buildings: Field Investigation and Numerical Validation from the 2022 Luding Earthquake" Buildings 15, no. 20: 3801. https://doi.org/10.3390/buildings15203801
APA StyleLuo, R., Chiu, C., Wang, S., Dong, X., & Guo, X. (2025). Mechanisms of Seismic Failure in Multistory Masonry and Infilled Frame Buildings: Field Investigation and Numerical Validation from the 2022 Luding Earthquake. Buildings, 15(20), 3801. https://doi.org/10.3390/buildings15203801






